1. Introduction
With the rapid development of urban, high-speed railway, tunnel, and bridge projects, underground construction in complex geological structures has increased, leading to frequent potential engineering issues. Grouting technology, a critical measure for preventing and controlling such problems, has been widely applied in tunnel construction, pile foundation engineering, and other fields. However, the grouting process is usually hidden from view and highly uncertain. To better guide the design and implementation of grouting projects, researchers have proposed various grouting theories. These theories aim to study the flow and diffusion patterns of grout in rock and soil voids and establish relationships between key variables such as the diffusion radius, grouting time, grout flow rate, and injection pressure. Current theories include permeation grouting theory [
1,
2,
3], compaction grouting theory [
4,
5,
6], fracture grouting theory [
7,
8,
9], and fissure grouting theory [
10,
11,
12].
Numerical simulation serves as a crucial method for studying grouting mechanisms. This includes Olivier’s time domain random walk (TDRW) method for simulating solute transport in one-dimensional heterogeneous media [
13]; Bodin and Porel abstracted fracture networks into one-dimensional pipeline networks and combining random walk with particle tracking to improve computational efficiency [
14,
15]; Zou and Håkansson extended the two-phase flow model of Bingham fluid in single fractures to saturated fracture networks to simulate cement grout propagation [
16]; Koyama et al. established a 3D model based on the equivalent continuum method to study temporal variations in grout density and flow fields, an approach validated through experiments [
17]; Ivanova et al. utilized an improved GEOFRAC model and FRACSIM program to analyze the effects of fracture intensity, size, and orientation on connectivity via statistical parameter studies [
18]; and Mohajerani et al. developed a new grout diffusion algorithm restricted to uncoupled smooth fractures [
19]. While the aforementioned numerical simulation methods have achieved notable advances in theoretical modeling and computational efficiency, they commonly suffer from oversimplifications of geological complexity. Most models also rely on idealized coupling boundary conditions, severely limiting their predictive reliability in scenarios involving heterogeneous multiphase fluid interactions or dynamically evolving fracture networks.
In the field of grouting effect detection, extensive research and applications have been conducted both domestically and internationally. Common techniques include the borehole inspection method [
20], excavation sampling method [
21], and geophysical detection methods [
22,
23,
24]. Grouting pressure monitoring involves installing sensors in pipelines or holes to track pressure changes in real time and evaluating slurry permeability and filling conditions [
25,
26,
27]. The sonic detection method assesses the grouting quality and distribution by analyzing the acoustic signal characteristics [
28,
29,
30]. Additionally, wireless sensor networks are employed to collect real-time data on parameters such as pressure, flow rate, and temperature, enhancing the flexibility of indirect monitoring.
However, existing monitoring methods still face significant limitations in the real-time acquisition of grout diffusion patterns [
31,
32,
33]. This results in a lack of effective data support for interpreting grouting mechanisms, making accurate determination of key parameters such as fracture channels and grouting coverage area difficult. Additionally, insufficient research on grout rheology and diffusion theory often leaves engineering design and construction techniques without adequate theoretical backing, leading to poor adaptability. Therefore, developing technologies capable of dynamic monitoring of grout flow, grout body morphology, and consolidation dynamics is highly important for studying the fluid-solid coupling mechanisms of grouting and advancing precise, controllable grouting techniques.
Compared with other geophysical methods, shallow seismic techniques are limited in deep exploration; ground-penetrating radar (GPR) is susceptible to surface cover and conductivity, restricting its penetration depth; and distributed fiber optic technology faces challenges in data interpretation [
34,
35,
36,
37,
38]. In contrast, electrical resistivity tomography (ERT) has advantages such as dynamic imaging capability, flexible deployment, and high cost effectiveness [
39,
40,
41]. Considering the complex environments, detection requirements, and cost efficiency of grouting monitoring, 3D electrical imaging has emerged as a more suitable choice. Its theoretical basis lies in the significant resistivity contrast between grout materials and the surrounding rock/soil, as well as the varying resistivity of grout at different consolidation stages. With the rapid advancement of big data processing and parallel computing technologies, dynamic inversion of grout flow during injection using geophysical methods, particularly ERT, has become feasible.
In summary, to address the core challenge of real-time acquisition of grout diffusion patterns, a novel dynamic monitoring method based on 3D ERT is proposed. Compared with traditional approaches such as numerical simulations and postconstruction excavation, this method achieves comprehensive improvements in both accuracy and real-time capability. This research involves the development and testing of corresponding technical equipment, providing a groundbreaking solution for dynamic grouting monitoring and the advancement of grouting technologies.
2. Electrical Properties of Geotechnical Media
Under natural conditions, geotechnical media contain varying amounts of water, which exists in the form of aqueous solutions containing various ions. Thus, natural rock and soil masses possess a certain degree of conductivity. The electrical properties of conductors are typically characterized by their resistivity or conductivity, which are reciprocal to each other and expressed as follows:
In Equation (1), R represents the resistance of the conductor, S denotes the cross-sectional area of the conductor, and L represents the length of the conductor.
Geotechnical materials exhibit complex and variable characteristics in terms of their conductivity and resistivity. Through extensive measurements and statistical analysis of porous rock resistivity, Archie established an empirical relationship between the resistivity of saturated cohesionless soils/pure sandstones and pore water resistivity by correlating geotechnical resistivity with its internal structure [
42,
43,
44]. The formula is expressed as follows:
In Equation (2), ρ represents the resistivity of saturated soil, n represents the porosity, ρw is the resistivity of pore water, and a and m are physical constants related to the cementation state of the geotechnical material.
Archie’s resistivity model is relatively simplified, neglecting the influence of conductive charged ions adsorbed on the surface of geotechnical media on the overall conductivity of the soil. Bruckshaw et al. [
45] expanded Archie’s model and established the Archie equation for unsaturated geotechnical materials:
In Equation (3), ρ represents the resistivity of unsaturated geotechnical materials, Sr denotes the degree of saturation, and ρw is the saturation exponent.
On the basis of the relationships among saturation, water content, and porosity, Equation (3) can be transformed into the following equation:
In Equation (4), Φ represents the porosity of the geotechnical material and θ denotes the water content of the geotechnical material. Equation (4) indicates that the resistivity of the geotechnical material is inversely proportional to its water content—the higher the water content is, the lower the resistivity.
Commonly used grouting materials include Portland cement. Portland cement is a complex mixture composed of various mineral components. The hydration process of cement and its electrical characteristics serve as the foundation for electrical monitoring of the grout permeation and consolidation process. The relationship between the composite resistivity (the resistivity of the medium after cement grout injection) and the liquid-phase resistivity (the resistivity of the cement grout) can be expressed by the Archie equation as follows:
Equation (5) indicates that the resistivity of cement grout is a crucial parameter for characterizing the diffusion process of the grout. After grouting, the composite resistivity is closely related to both the resistivity of the cement grout and the porosity of the porous medium. Additionally, for the same medium with a fixed porosity, the composite resistivity is directly proportional to the resistivity of the cement grout and exhibits similar variation characteristics.
3. Grouting Monitoring System
Existing geophysical monitoring methods face significant technical bottlenecks in grouting engineering remediation scenarios. GPR is constrained by construction interface flatness and antenna coupling conditions, making it unsuitable for complex terrains. The transient electromagnetic method (TEM) is vulnerable to industrial electromagnetic interference and suffers from detection blind zones and insufficient resolution. Although the ERT method achieves automated data collection through preset electrode arrays (e.g., a 60-electrode Wenner array can collect 570 data points per cycle with 2 s per point, requiring approximately 20 min per cycle), its serial operation mode results in low time efficiency. These methods are fundamentally premised on the assumption of “static stability of underground medium physical parameters,” which contradicts the dynamic evolution of electrical parameters during grouting remediation, leading to reduced applicability of inversion models and diminished monitoring accuracy. When the construction time window (e.g., railway maintenance “time windows”) is significantly shorter than the data acquisition cycle, traditional serial modes cannot capture dynamic grout diffusion boundaries or physical parameter gradients, severely limiting the timeliness and reliability of remediation quality assessment. Therefore, it is imperative to develop an ERT monitoring system based on parallel acquisition architecture to overcome the temporal constraints of serial modes and achieve synchronous monitoring of dynamic processes.
3.1. System Functional Design
The distributed and parallel dynamic grouting monitoring system (
Figure 1) consists of three core subsystems: the data acquisition system, the data processing system, and the energy system. It forms a technical framework for dynamic underground medium resistivity monitoring through the collaborative operation of parallel data acquisition, IoT data transmission, intelligent inversion algorithms, and solar power supply technologies. Each subsystem fulfills critical functions: the data acquisition system handles real-time parameter collection, the data processing system manages remote transmission and intelligent analysis, and the energy system ensures a sustained power supply. This integrated approach enables dynamic monitoring and three-dimensional visual analysis of subsurface medium parameters during grouting operations.
In the architectural design of a distributed and parallel dynamic grouting monitoring system, two core challenges must be addressed: first, achieving high-precision time synchronization control between distributed acquisition modules, and second, optimizing the configuration of the multielectrode power supply and measurement modes (as shown in
Figure 2).
For the former, this study employs a hierarchical control strategy in which the master module generates unified synchronization clock signals and issues acquisition commands, ensuring strict adherence to preset timing sequences across submodules (each containing 32 channels: 4 communication channels and 28 electrode channels supporting 28 electrodes). A hardware architecture incorporating a common power supply negative terminal (B-pole) is introduced to effectively reduce system noise interference in multichannel potential measurements.
For the latter, a dynamic optimization combination algorithm is proposed on the basis of the scalar characteristics of DC electrical potential observations and the polarity symmetry principle of AB electrodes. By fixing the B pole as the reference point and sequentially switching the power supply positive terminal (A pole) while synchronously collecting potential data from the remaining electrodes, this approach simplifies topological complexity through electrode polarity interchange. The parallel acquisition mechanism enables synchronous spatial field information collection across the entire electrode array, significantly enhancing data throughput per unit time and system resolution. Theoretical analysis and experimental validation confirm that this design satisfies the efficient synchronous operation requirements of large-scale electrode networks, providing technical support for dynamic monitoring of dynamic subsurface media evolution processes.
3.2. Component Selection and Hardware Design
The data acquisition terminal, which serves as the core unit of the distributed and parallel dynamic monitoring system, plays a pivotal role in the monitoring system. This terminal integrates a complete hardware architecture comprising data acquisition circuits, communication modules, relay banks, and electrode arrays. The coordinated operation of its embedded control system and high-precision data acquisition modules enables effective monitoring of the grouting process. Powered by a dedicated battery pack as the discharge source, the system utilizes microprocessor-controlled switching operations of the relay bank to achieve intelligent gating of the four-electrode configuration (A, M, N, and B electrodes), ensuring reliable and precise resistivity data acquisition.
With respect to hardware architecture design, the system employs an STM32H750 core board as the main controller. This ARM Cortex-M7-based controller operates at 480 MHz with 128 KB of flash memory and a 1 MB RAM configuration, achieving low-power operation (263 µA/MHz in active mode, 4 µA in standby mode) while maintaining processing efficiency. Equipped with 34 programmable I/O ports, it fulfills multiperipheral parallel control requirements. The data acquisition module uses ADS1263 [Texas Instruments, Dallas, TX, United States] devices—32-bit high-precision analog-to-digital converters—which support a 38.4 ksps sampling rate with a 10-channel simultaneous acquisition capability. The implementation adopts a configuration in which one STM32H750 [STMicroelectronics, Geneva, Switzerland] master controller drives three ADS1263 units (as shown in
Figure 3). Through an optimized reference voltage channel configuration, each acquisition module effectively manages 28 electrode channels, significantly increasing the collection density of the unit modules.
The system incorporates a flexible cascading expansion mechanism to address large-scale grouting monitoring requirements. Each data acquisition terminal features two standardized cascading interfaces, enabling multiterminal serial connections through a five-wire transmission line (including power supply positive/negative terminals, ADG5208 [Analog Devices, Norwood, MA, United States] common output, and ground). When monitoring areas exceed the 32-channel capacity of a single terminal or encounter inconvenient measurement-line arrangements, multichannel acquisition networks can be constructed by cascading. For instance, cascading two terminals to form a 56-electrode system with a dual-power negative terminal configuration achieves approximately 1 min per acquisition cycle, yielding 5940 valid data points. Compared with serial operation modes, this configuration reduces the single-cycle data acquisition time by approximately 20 times and improves the data collection efficiency by nearly 200 times.
With respect to system performance optimization, significant breakthroughs have been achieved through coordinated hardware architecture innovation and software algorithm improvements. First, the distributed acquisition architecture reduces the collection time to approximately 1 min, simultaneously satisfying the temporal constraints of inversion algorithms while ensuring real-time data performance. Compared with the serial mode, the parallel acquisition strategy increases the effective data volume by an order of magnitude (10×), establishing a robust informational foundation for subsequent data processing.
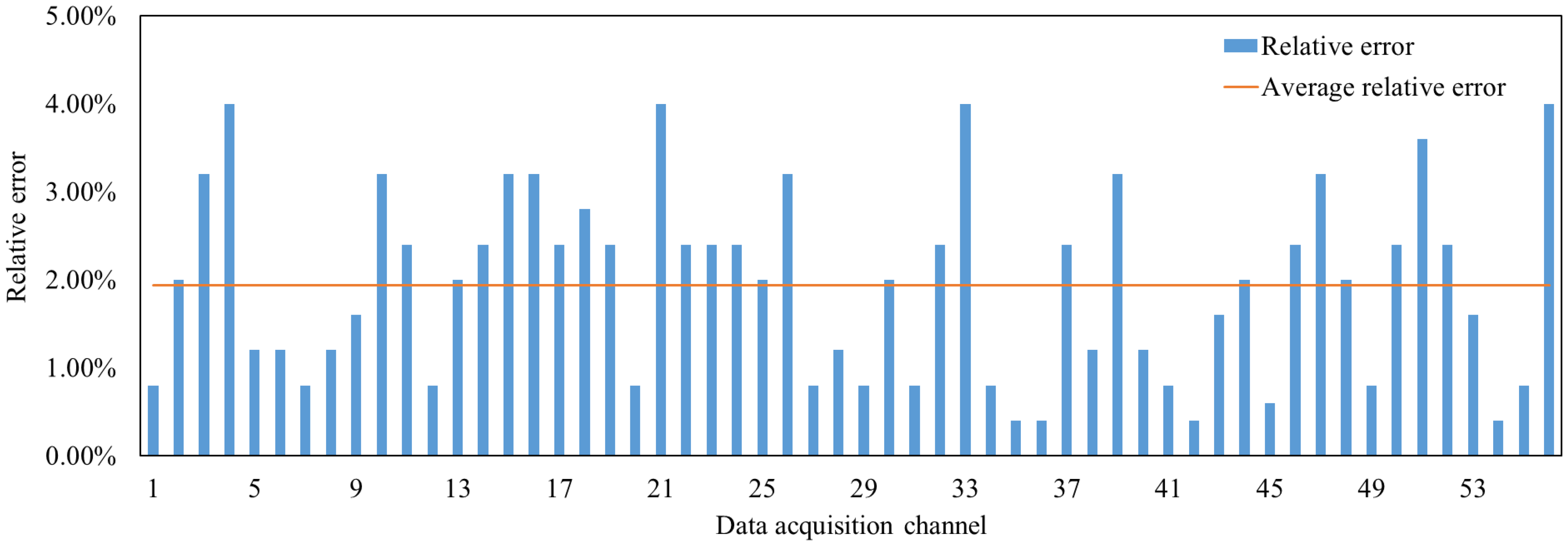
The precision characterization of the data acquisition system was conducted through calibration using a 250 Ω reference resistor, implemented in a master-slave cascaded architecture comprising one primary unit and one secondary unit. As illustrated in the calibration outcomes (
Figure 4), the relative error distribution demonstrated a peak value of 4.00%, a minimum value of 0.4%, and a weighted mean of 1.94% across the measurement spectrum. These metrics underscore the system’s statistically robust performance in accuracy, with error magnitudes consistently confined within an industrially acceptable tolerance range. Such precision stability validates the system’s suitability for high-precision measurement scenarios requiring traceable metrological rigor.
4. Inversion Imaging Algorithm
In practical electrical exploration, the background conditions of data acquisition vary, making it impossible to apply the same set of parameters to different collection environments or data with varying accuracy requirements. For instance, under high-precision exploration requirements, setting the threshold too high can lead to significant errors in the final inversion results. Conversely, if the background noise in the collection environment is substantial, the threshold needs to be set lower, but this would prolong the computation time. Therefore, a balance must be struck between these two aspects, necessitating the preprocessing of noise in the measured data. On the basis of this rationale, Bayesian estimation framework is introduced to dynamically adapt inversion parameters to variable field noise conditions and precision requirements by integrating geological prior knowledge, thereby optimizing the balance between measurement accuracy and computational efficiency without manual threshold tuning.
4.1. Bayesian Estimation Theory
Bayesian estimation involves prior probability and posterior probability. At its core, Bayesian estimation combines sample information with prior information related to unknown parameters. Afterward, on the basis of Bayes’ theorem, it derives the posterior information and distribution associated with these parameters, ultimately using the posterior information to make further estimates of the unknown parameters.
The Bayesian algorithm holds that inference requires three types of information: population information, sample information, and prior information. Assume that the population data depend on a parameter
θ, with its probability function denoted as
P(
x∣
θ) and its prior distribution as
π(
θ). First, a sample
θ0 is drawn from
π(
θ), and then a set of samples is generated from
P(
x∣
θ0). Through these two steps, the joint conditional probability function of the sample
x = (
x1,
x2, ⋯ ,
xn) can be expressed as follows:
The joint distribution of the sample and the parameter
θ is as follows:
The marginal probability function of sample
x is as follows:
Thus, we obtain the density function form of Bayes’ theorem, expressed as follows:
4.2. Geological Unit Merging Inversion Based on Bayesian Estimation
Taking resistivity as the target parameter, the Bayesian formulation can be expressed as follows:
In Equation (11), ρs is the theoretical resistivity, ρr is the actual measured resistivity, P(ρr|ρs) represents the prior probability density function, P(ρs|ρr) represents the posterior probability density function, P(ρr) is the prior probability density function of the actual measurement data, which can be replaced by a constant, and P(ρs) represents the prior probability density of the model.
Owing to environmental influences, the data may contain noise, leading to certain errors in the inverted resistivity. In this paper, Bayesian estimation is introduced to assess the level of error in the noise after inversion. If the difference falls within the error range, cell merging can be performed.
During the data acquisition process, the influence of environmental factors should be treated as random noise, which follows a normal distribution. Therefore, in this inversion process, the inversion equation can be expressed as follows:
In Equation (12),
G is the stiffness matrix. If the collected data contain no noise, the theoretical resistivity value of the model can be derived as follows:
If the influence of noise is present, the inversion of the measured data transforms into:
In Equation (14), is the data covariance matrix, which represents the noise level.
Bayesian theory indicates that the posterior distribution of the inversion results can be obtained by performing maximum likelihood estimation on the prior distribution of noise and the theoretical model values derived from least-squares inversion. From Equation (14), the noise can be expressed as follows:
According to Bayesian estimation theory, the posterior probability distribution of the noise follows a chi-square distribution, i.e.,
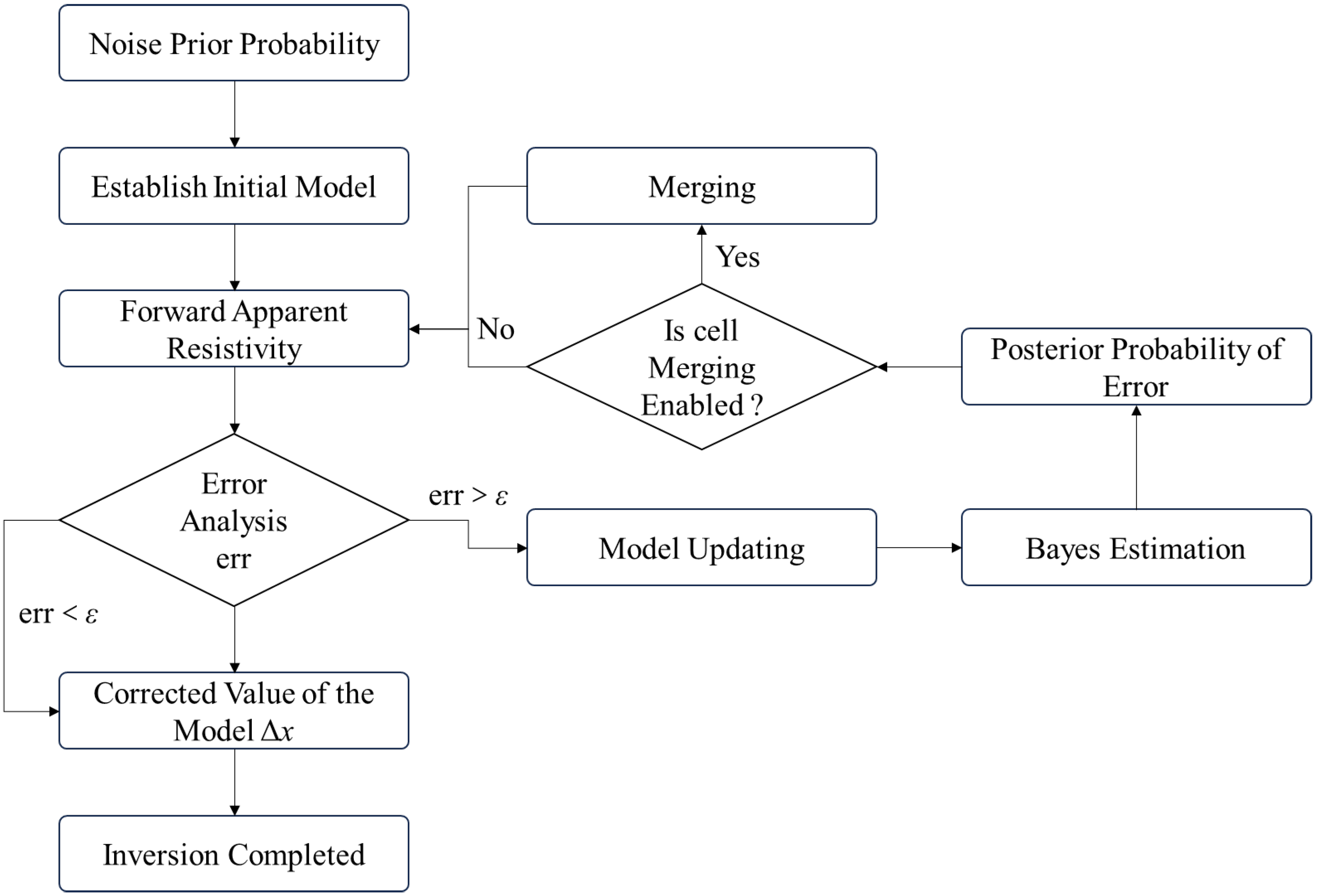
On the basis of the chi-square distribution derived from the above equation, the posterior probability of the noise (assumed as additive Gaussian noise) is calculated under explicitly defined Gaussian prior distributions for model parameters. This posterior probability serves as a dynamic threshold to evaluate whether adjacent grid cells should be merged during the iterative Bayesian merging inversion process. The merging criterion is updated at each iteration step by balancing the likelihood of observed data (computed via forward modeling) and the prior constraints on geological unit continuity. The inversion loop continues until convergence is achieved, defined by a minimal change in posterior probability or a maximum iteration count. The geological unit inversion flowchart incorporating Bayesian estimation is shown in
Figure 5 which illustrates key stages including (1) initialization of priors and noise parameters, (2) forward simulation of geophysical responses, (3) posterior probability calculation, (4) adaptive grid merging based on the threshold, and (5) iterative refinement of the geological model.
4.3. Inversion Algorithm Validation
For the geological units, Bayesian estimation is used to filter the data to obtain the prior probability of noise (
Figure 6). The inversion evaluation process includes the calculation of the posterior error probability, which is used to determine the threshold for grid cell merging, thereby further improving the inversion accuracy.
To verify the merging and convergence effects of Bayesian estimation on inversion, a simple demonstration of the merging process was conducted using a small number of grid cells. In this paper, a model with a length of 500 m and a thickness of 100 m is adopted and divided into 20 grids, with a low-resistivity body placed between the depths of 25–50 m. The initial inversion model is shown in
Figure 6. Each cell in the first layer has an initial resistivity value of 100 Ω·m, each cell in the second layer has an initial resistivity value of 160 Ω·m, and the resistivity value of the low-resistivity zone is 40 Ω·m.
Before performing the inversion, it is necessary to preprocess the resistivity values through filtering. During the inversion process, the threshold for grid cell merging is determined on the basis of the posterior probability of noise. If the difference in resistivity values between adjacent cells is below this threshold, merging can be performed; otherwise, iterative inversion continues.
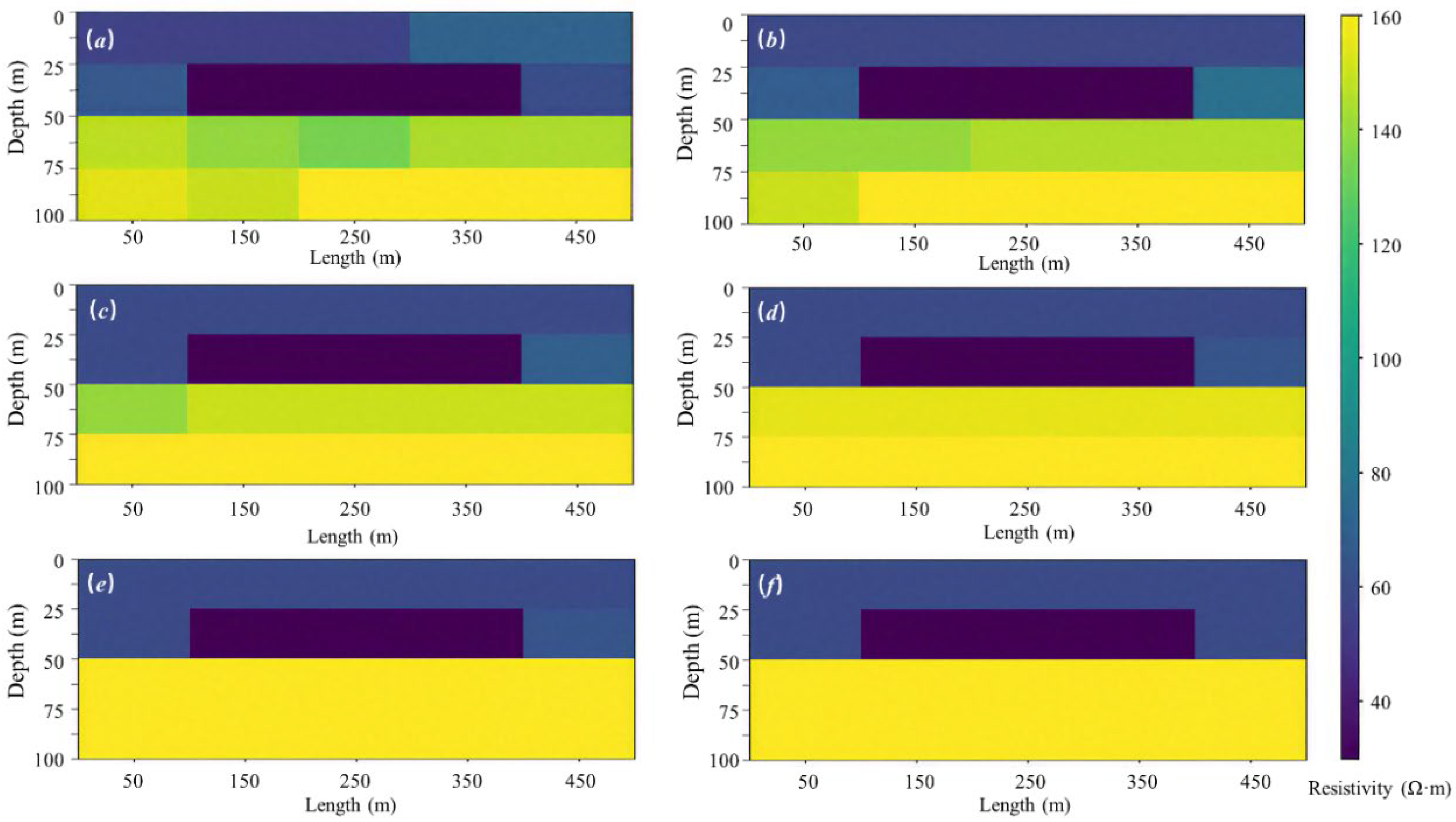
The inversion merging of geological units combined with Bayesian estimation after the addition of 10% noise is shown in
Figure 7. The results after 2, 3, …, up to 7 iterations are presented in
Figure 7a–f, respectively. The results after the 7th iteration are shown in
Figure 7f. Continuing the iterative inversion completes the merging of grid cells, with the central part identified as a low-resistivity anomaly.
From this inversion process, it can be observed that Bayesian merging effectively evaluates noise during inversion and provides a reliability threshold for merging, enabling rapid cell consolidation. This reduces the number of grid cells, sharpens the inversion boundaries, and enhances the accuracy of the model.
To evaluate the accuracy of the Bayesian estimation-based geological unit merging algorithm, this study applied least-squares inversion processing using the mainstream inversion software RES2DINV (version 3.5.44) [
46,
47,
48] on resistivity data with 10% artificial noise. As shown in
Figure 8, the inversion results reveal the following:
- (1)
The low-resistivity body obtained by least-squares inversion has a burial depth range of 20–60 m (compared with the theoretical model’s true burial depth of 25–50 m), indicating significant positional deviation;
- (2)
The boundaries of the low-resistivity anomaly are blurred, with low discernibility in the electrical interface between the anomaly and surrounding medium-to high-resistivity materials (120–160 Ω·m);
- (3)
The dual-layer geological structure with a basal resistivity of 160 Ω·m is not accurately reconstructed, and high-resistivity responses are distributed only in localized areas of the basement;
- (4)
Significant discrepancies exist between the inversion results on the right side of the profile and the theoretical model. Compared with the Bayesian estimation-based geological unit merging algorithm, the traditional least-squares inversion markedly reduces accuracy [
49].
As shown in
Table 1, the Bayesian merging inversion algorithm demonstrates a computational runtime of 3.01 s per iteration for a typical 2D geological model with 10
4 grid cells, achieving convergence within 7 iterations. In comparison, conventional least-squares inversion requires 3.15 s per iteration but necessitates 7 iterations to reach comparable data misfit thresholds, resulting in a total runtime is almost the same. Over 50 independent trials, proposed method demonstrated a mean accuracy improvement of 12.7%. These results confirm not only the numerical superiority but also the statistical significance of the proposed method’s advantages.
Comprehensive analysis demonstrates that the Bayesian estimation-based geological unit merging inversion algorithm successfully reconstructs the location and boundaries of the anomalous body, resulting in higher precision and accuracy. The inversion results are highly satisfactory, confirming the strong feasibility of this approach.
While the Bayesian inversion framework demonstrated robust stability across all tested scenarios, it is important to note that accuracy inevitably degrades as noise increases. High noise levels introduce greater uncertainty into the observed data, which propagates into the posterior parameter estimates, leading to wider credible intervals and potentially biased point estimates.
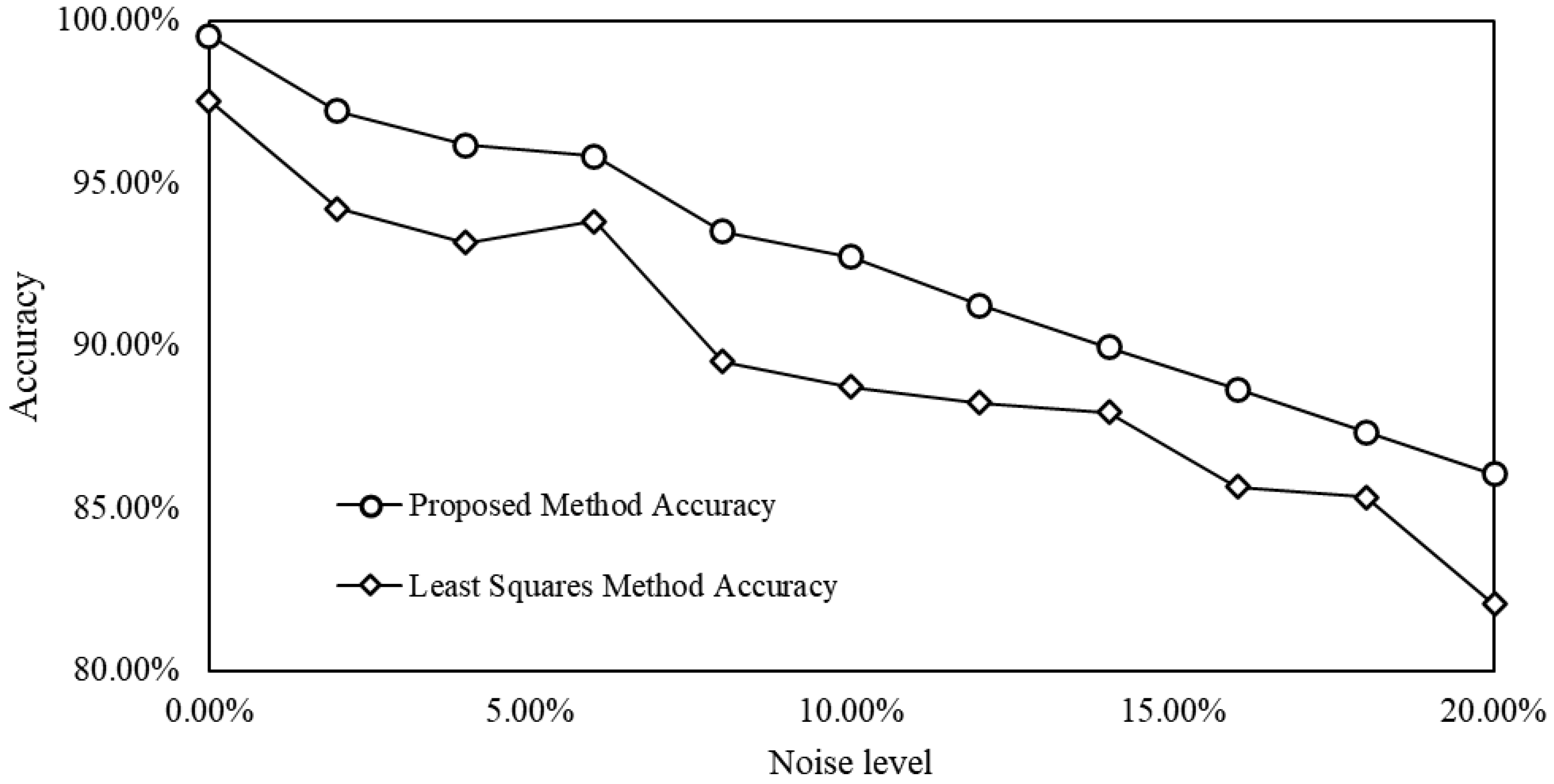
A comparative analysis was conducted between our proposed algorithm and the conventional least squares method to evaluate robustness under varying noise conditions. As depicted in the experimental results (
Figure 9), field data acquisition noise levels predominantly remained below 20%, with over 80% of cases exhibiting noise below 10%. Within this operational range, our algorithm consistently outperformed the least squares method in accuracy. Notably, inversion accuracy exceeded 93% at noise levels ≤ 10%, while maintaining > 85% precision even under high noise conditions (20%). These results validate the algorithm’s enhanced tolerance to noise-induced perturbations compared to classical approaches.
5. Application of the Grouting Monitoring System
5.1. Optimization of Array and Electrode Spacing
The key aspects for the effective use of a grouting monitoring system primarily include the selection of measurement arrays and the determination of electrode spacing. On the basis of the actual conditions of the grouting process, a grouting model is established for numerical simulation. The forward model of the grouting is illustrated in
Figure 10. The model has a length of 20 m and a depth of 8 m. In this model, commonly used measurement devices are employed for data acquisition and the imaging simulation.
5.1.1. Wenner Array
As shown in
Figure 11, the Wenner array is characterized by four electrodes arranged at specific intervals in a rectangular or square configuration. Current is applied through the outer two electrodes, while the voltage is measured between the inner two electrodes. Its advantages include simple setup and measurement procedures, making it suitable for medium-depth exploration and providing relatively accurate resistivity measurements for homogeneous media. However, for heterogeneous media, interpretation and analysis of the results may prove more challenging.
5.1.2. Schlumberger Array
As shown in
Figure 12, the Schlumberger array is characterized by fixed outer electrodes, whereas the inner electrodes are measured at varying distances, enabling resistivity measurements at different depths. Its advantage lies in its suitability for deep exploration, allowing the acquisition of resistivity data over extensive depth ranges. However, owing to the wide spacing between its measurement electrodes, the Schlumberger array has lower spatial resolution and limited ability to detect small-scale subsurface structures.
5.1.3. Dipole–Dipole Array
As shown in
Figure 13, the dipole-dipole array is characterized by the use of multiple electrode pairs for measurements. Each pair consists of a current-injecting electrode and a potential-measuring electrode, with the spacing between pairs adjustable as needed. Its advantages include providing richer resistivity information while balancing depth investigation capability and spatial resolution requirements. However, the dipole-dipole array requires longer measurement times because of the multiple required readings, and both electrode configuration selection and data processing are relatively complex.
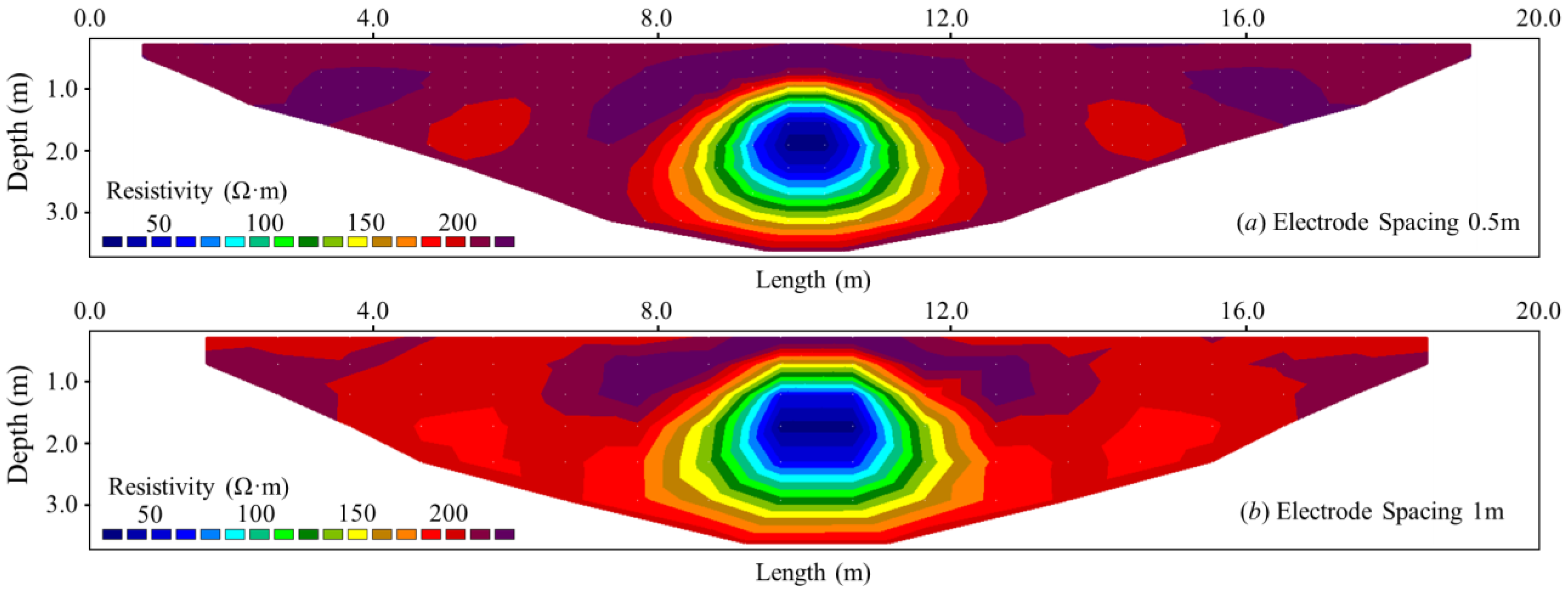
As shown in
Figure 14,
Figure 15 and
Figure 16, selecting an appropriate electrode array is crucial for efficient grouting monitoring. This requires comprehensive consideration of exploration objectives, geological conditions, and budgetary constraints and may involve combining different array configurations to leverage their respective advantages.
With respect to the specific objective of precisely locating grout boundaries in rock–soil masses postinjection, the primary consideration is the resolution characteristics of different electrical resistivity configurations. This directly affects the accuracy and effectiveness of subsequent work. Among commonly used configurations, the dipole-dipole array has notable advantages. It is highly sensitive to minor resistivity variations between electrodes (particularly with good electrode grounding), making it especially effective at detecting vertical anomalies. This array also has the potential to probe deeper targets. By employing smaller electrode spacings (e.g., 0.5 m) and extending the survey line, the detection depth can be effectively increased, significantly enhancing its suitability for dynamic grouting process monitoring. While a 0.5 m electrode spacing was determined as optimal under controlled numerical simulation, field deployments allow flexible adjustment based on site-specific requirements. The appropriate spacing should be determined by: geological complexity, required resolution (where spatial resolution ≈ 0.5 × electrode spacing), and economic constraints. This adaptive approach ensures practical implementation across diverse environments while maintaining detection capabilities.
Owing to these advantages, as illustrated in
Figure 17a–e, the dipole-dipole configuration can accurately capture subtle resistivity changes induced by the diffusion, permeation, and solidification of cement grout. The method is capable of long-term monitoring of grout consolidation beyond the injection stage, as demonstrated by the temporal evolution of the grout’s apparent resistivity. The apparent resistivity progressively increases over time following injection until reaching a stable plateau. This characteristic trend allows the system to effectively track the consolidation process and determine its completion point. However, while this method reliably indicates consolidation status, it does not provide direct quantitative measurement of the strength of the consolidated grout matrix. This provides highly valuable insights into the dynamic process of grout permeation and solidification.
5.2. Experiment
This experiment was performed to verify the applicability and reliability of the distributed and parallel grouting monitoring system. By constructing a physical simulation test bed, the system’s dynamic monitoring capability for grout diffusion processes, spatial resolution, and anti-interference performance were specifically evaluated:
- (1)
Grout diffusion can be quantitatively characterized through variations in the dielectric properties;
- (2)
Background field differential algorithms effectively highlight valid signals induced by grouting;
- (3)
The spatial resolution capability of the system for delineating grout diffusion boundaries is demonstrated.
While water was chosen as a simplified proxy for grout in experiments owing to its ease of control and measurement repeatability, it is important to emphasize that water and cement grout exhibit distinct rheological behaviors (e.g., viscosity, shear-thinning properties) and electrical characteristics (e.g., conductivity, permittivity). These differences may lead to underestimation of flow resistance in fractures or inaccuracies in electrical tomography interpretations for field-scale grouting. Future work will incorporate cement-based analogs or scaled grout mixtures to better replicate field conditions.
The test area is 7 m in length and 2 m in width and is primarily composed of loose clay (
Figure 18). A water permeation zone was established in the central area (coordinates x = 2~3 m, y = 1 m) with an infiltration volume of 8 L to simulate typical grout diffusion scenarios in grouting engineering. The electrode array system adopted a dual-survey-line three-dimensional deployment mode: Two parallel survey lines were arranged along the longitudinal axis (x-axis) with 2 m spacing between them, forming a parallel observation network. Each survey line was equipped with 14 stainless steel electrodes maintaining a constant 0.5 m electrode spacing, with proper watering ensuring optimal electrode–ground contact.
The data acquisition system employs a multichannel parallel acquisition architecture. By automatically switching between current electrode pairs (ABs) and measuring electrode pairs (MNs), full-waveform data collection of the three-dimensional resistivity field is achieved, with a sampling interval of 1 s per measurement. Each complete acquisition cycle lasts approximately 1 min, after which the data are automatically saved and timestamped with the completion time. A 1 min interval is maintained between two consecutive full acquisition cycles.
This monitoring system employs a background field differential method to highlight the dynamic resistivity variations induced by grouting operations. The implementation involves using initial monitoring data as the reference background field. Through differential calculations between dynamic monitoring profiles and the initial background field, the system effectively extracts anomalous variation zones of apparent resistivity in geomaterials (corresponding to the extent of grout diffusion). The typical application effect of this method is shown in
Figure 19, where the black dots represent electrode spatial coordinates. During the preliminary experimental phase, watering operations were conducted to ensure that electrode–ground coupling effects created localized low-resistivity anomaly zones around the electrodes.
In the monitoring results of the water permeation test (
Figure 19), the blue zones represent regions of reduced apparent resistivity, with darker shades indicating greater resistivity reduction. The spatial distribution of these zones is significantly correlated with water migration paths. This arises from the physical properties of water as a typical low-resistivity medium—its movement through soil/rock pores enhances overall conductivity, manifesting as negative anomalies (Δρ < 0) in resistivity imaging. Experimental data demonstrate that water permeation effectively induces resistivity reduction, and the spatial distribution of anomalous zones provides direct evidence for evaluating the extent of grout diffusion.
5.3. Field Application
Field validation of the distributed and parallel dynamic grouting monitoring system was conducted for the subgrade settlement treatment project on a section of the Lanzhou–Xinjiang Passenger Dedicated Line. The strata in this section mainly consist of Quaternary alluvial sand gravel (8–12 m thick) overlaying mudstone, with a groundwater depth of 18 m. The sleeve–valve pipe grouting method was employed for foundation reinforcement, featuring designed grouting pressures of 0.1–0.8 MPa. The primary objective was to verify the engineering applicability of the developed distributed and parallel dynamic grouting monitoring system under complex stratigraphic conditions. Field tests captured dynamic resistivity response characteristics during grouting processes, providing critical data support for establishing an intelligent evaluation system correlating “resistivity variation–grout diffusion patterns–reinforcement effectiveness”.
A three-dimensional electrode array system was constructed in the grouting zone: Main survey line 1 was deployed along the downslope shoulder of the route, and auxiliary survey line 2 was arranged along the toe of the slope, forming a 20 m × 7 m three-dimensional observation network (
Figure 20). Each survey line contained 30 electrodes with a spacing of approximately 0.7 m. Premonitoring tests ensured proper grounding of all the electrodes. The parallel arrangement of lines 1 and 2 covered a three-dimensional monitoring zone encompassing the grouting holes. Each data acquisition cycle lasted 60 s, with a 60 s monitoring interval, resulting in a total monitoring duration of 40 min during the construction window. This process yielded 20 complete three-dimensional datasets.
The experimental data (
Figure 21) revealed significant resistivity variations following grout injection, with low-resistivity anomaly zones observed within 0–2 m around the grouting holes. The three-dimensional morphology of grout diffusion was reconstructed using our inversion algorithm. The main grout vein extended 5 m along the route orientation, spread 2 m perpendicular to the alignment, and achieved a maximum penetration depth of 4.5 m, forming an inverted conical diffusion pattern. The primary technique employed in the field application is compaction grouting, where highly viscous grout is injected into the soil through boreholes, forming localized grout bulbs. These bulbs induce significant compression on the surrounding soil matrix. Specifically, the proximal zone adjacent to the grout bulb undergoes plastic deformation due to high shear stresses, while the distal zone experiences elastic deformation, resulting in a measurable increase in soil density. Sequential bottom-up grouting creates a composite grout column. This mechanistic behavior aligns with the slurry diffusion mechanism variations observed in our monitoring data, thereby validating the effectiveness of the proposed method in achieving grouting monitoring.
The core sampling results indicated an actual grout diffusion radius that deviated by 0.3 m from the resistivity monitoring results. This discrepancy is primarily attributed to the over smoothing effect of the inversion algorithm for low-resistivity thin layers. The research outcomes indicate that the proposed approach is a critical process monitoring methodology for grouting technology.
While this study focused on a railway project, the developed Distributed and Parallel Dynamic Grouting Monitoring System exhibit significant transferability to other geotechnical and infrastructure monitoring scenarios. Key applications include, but are not limited to, the following: dynamic assessment of grout spread and consolidation during tunnel construction or rehabilitation; tracking moisture movement and potential instability triggers in sensitive slopes. The core principles of Distributed and Parallel Dynamic Grouting Monitoring System for detecting fluid movement within geomaterials are directly applicable to these domains.
5.4. Limitations
Two key limitations should be noted in applying this method. First, the volume averaging effect inherent in electrical resistivity tomography—where coarse spatial resolutions smooth sharp geological boundaries—may reduce the accuracy of fracture boundary delineation, particularly in narrow or irregular fractures. Second, interpreting inversion results in highly heterogeneous media (e.g., layered or fractured bedrock with contrasting resistivity)—due to ambiguous electrical property contrasts—remains challenging and may require prior geological constraints or multi-method validation. Future work will focus on integrating high-resolution seismic or ground penetrating radar data to mitigate these limitations.
6. Conclusions
In this study, a distributed and parallel dynamic grouting monitoring system based on electrical resistivity tomography was developed, achieving dynamic monitoring of grout diffusion patterns underground through integrated hardware architecture innovation and inversion algorithm optimization.
- (1)
The system employs distributed electrode arrays, cascadable data acquisition terminals, and parallel acquisition architecture, significantly improving data collection efficiency. The single acquisition time was reduced by approximately 20 times compared with that of traditional serial modes, with a 200-fold increase in data acquisition efficiency, meeting dynamic monitoring demands for grouting in railway subgrade, urban underground space and tunnel engineering.
- (2)
A Bayesian estimation-based geological unit merging algorithm was proposed, which dynamically adjusts inversion thresholds through noise posterior probability calculations to effectively suppress environmental interference and significantly increase grout boundary identification accuracy. Numerical simulations and experimental validation demonstrated that the algorithm maintains high inversion stability under 10% noise conditions, with the boundary resolution markedly improving over that of traditional least-squares methods while effectively reducing the positioning errors of low-resistivity anomalies.
- (3)
In a study of the Lanzhou–Xinjiang Passenger Dedicated Line subgrade grouting project, the system successfully captured the grout diffusion dynamics, with the inversion results strongly agreeing (0.3 m grout diffusion radius error) with the actual core sampling data. Three-dimensional imaging clearly revealed underground grout diffusion patterns.
This research addresses the limitations of traditional blind grouting monitoring, providing reliable technical support for the precise control and quality assessment of underground engineering grouting processes.
In the future, efforts can focus on further developing miniaturized, low-power hardware devices to enhance the system’s adaptability in confined spaces or harsh environments. Integrating deep learning algorithms to optimize inversion processes will strengthen noise resistance and resolution under complex geological conditions. Exploration of integrated applications combining resistivity imaging with fiber-optic sensing, micro seismic monitoring, and other technologies should aim to establish a multi-physical-field joint monitoring system, achieving comprehensive perception of mechanical–seepage–electrical parameters during underground engineering grouting processes. Extending the system to domains such as geohazard prevention and environmental remediation will validate its universality and cross-scenario applicability, driving technological expansion from engineering monitoring toward disaster early warning and ecological governance.
Author Contributions
Conceptualization, H.Z., Q.Z., and J.L.; methodology, H.Z., Q.Z., and J.L.; formal analysis, H.Z. and Y.L.; investigation, Y.L.; resources, C.D.; data curation, H.Z. and Y.L.; writing—original draft preparation, H.Z.; writing—review and editing, Q.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of the China (U2468222) and the Scientific Research Fund of China Academy of Railway Sciences Corporation Limited (2023YJ197).
Data Availability Statement
Data associated with this study are available and can be obtained by contacting the corresponding author.
Conflicts of Interest
Authors Hu Zeng, Qianli Zhang, Jie Liu, Cui Du and Yilin Li were employed by the company China Academy of Railway Sciences Corporation Limited (CARS). All authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Zhang, L.; Yu, R.; Zhang, Q.; Liu, R.; Feng, H.; Chu, Y. Permeation Grouting Diffusion Mechanism of Quick Setting Grout. Tunn. Undergr. Space Technol. 2022, 124, 104449. [Google Scholar] [CrossRef]
- Fu, Y.; Wang, X.; Zhang, S.; Yang, Y. Modelling of Permeation Grouting Considering Grout Self-Gravity Effect: Theoretical and Experimental Study. Adv. Mater. Sci. Eng. 2019, 2019, 7968240. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, T.; Jin, X. Study on Permeation Grouting Rules for Loess and Method for Predicting Migration Radius. KSCE J. Civ. Eng. 2021, 25, 2876–2883. [Google Scholar] [CrossRef]
- Wang, D.; Xing, X.; Qu, H.; Zhang, L.-M. Simulated Radial Expansion and Heave Caused by Compaction Grouting in Noncohesive Soils. Int. J. Geomech. 2015, 15, 04014069. [Google Scholar] [CrossRef]
- Yang, X.; Zou, J. Estimation of Compaction Grouting Pressure in Strain Softening Soils. J. Cent. South Univ. Technol. 2009, 16, 653–657. [Google Scholar] [CrossRef]
- Shrivastava, N.; Zen, K.; Shukla, S.K. Modeling of Compaction Grouting Technique with Development of Cylindrical Cavity Expansion Problem in a Finite Medium. Int. J. Geosynth. Ground Eng. 2017, 3, 40. [Google Scholar] [CrossRef]
- Cheng, H.; Liu, X.; Lin, J.; Zhang, L.; Li, M.; Rong, C. Study on Fracturing and Diffusion Mechanism of Nonslab Fracturing Grouting. Geofluids 2020, 2020, 8838135. [Google Scholar] [CrossRef]
- Bezuijen, A.; te Grotenhuis, R.; van Tol, A.F.; Bosch, J.W.; Haasnoot, J.K. Analytical Model for Fracture Grouting in Sand. J. Geotech. Geoenviron. Eng. 2011, 137, 611–620. [Google Scholar] [CrossRef]
- Liu, X.; Cheng, H.; Lin, J.; Rong, C.; Li, M.; Xu, H. Study of the Mechanism of Fracture Grouting in Deeply Buried Rock Strata Based on Bingham Fluid Slurry. Adv. Civ. Eng. 2019, 2019, 6943239. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, C.; Zhou, X.; Gao, G.; Feng, X. Full-Scale Physical Modelling of Fissure Grouting in Deep Underground Rocks. Tunn. Undergr. Space Technol. 2019, 89, 249–261. [Google Scholar] [CrossRef]
- Li, W.; Zhang, J.; Wang, N.; Zhang, L.; Qiu, Q.; Zhang, H. Experimental Study on Morphological Characteristics of Vertical Fissure Grouting in Earthen Sites. Measurement 2025, 239, 115537. [Google Scholar] [CrossRef]
- Du, X.; Li, Z.; Fang, H.; Li, B.; Zhao, X.; Zhai, K.; Xue, B.; Wang, S. A State-of-the-Art Review on the Study of the Diffusion Mechanism of Fissure Grouting. Appl. Sci. 2024, 14, 2540. [Google Scholar] [CrossRef]
- Banton, O.; Delay, F.; Porel, G. A New Time Domain Random Walk Method for Solute Transport in 1–D Heterogeneous Media. Groundwater 1997, 35, 1008–1013. [Google Scholar] [CrossRef]
- Bodin, J.; Porel, G.; Delay, F. Simulation of Solute Transport in Discrete Fracture Networks Using the Time Domain Random Walk Method. Earth Planet Sci. Lett. 2003, 208, 297–304. [Google Scholar] [CrossRef]
- Bodin, J.; Porel, G.; Delay, F.; Ubertosi, F.; Bernard, S.; de Dreuzy, J.-R. Simulation and Analysis of Solute Transport in 2D Fracture/Pipe Networks: The SOLFRAC Program. J. Contam. Hydrol. 2007, 89, 1–28. [Google Scholar] [CrossRef] [PubMed]
- Zou, L.; Håkansson, U.; Cvetkovic, V. Cement Grout Propagation in Two-Dimensional Fracture Networks: Impact of Structure and Hydraulic Variability. Int. J. Rock Mech. Min. Sci. 2019, 115, 1–10. [Google Scholar] [CrossRef]
- Koyama, T.; Katayama, T.; Tanaka, T.; Kuzuha, Y.; Ohnishi, Y. Development of a Numerical Model for Grout Injection and Its Application to the in Situ Grouting Test at the Grimsel Test Site, Switzerland. Geosystem Eng. 2013, 16, 26–36. [Google Scholar] [CrossRef]
- Ivanova, V.M.; Sousa, R.; Murrihy, B.; Einstein, H.H. Mathematical Algorithm Development and Parametric Studies with the GEOFRAC Three-Dimensional Stochastic Model of Natural Rock Fracture Systems. Comput. Geosci. 2014, 67, 100–109. [Google Scholar] [CrossRef]
- Mohajerani, S.; Baghbanan, A.; Wang, G.; Forouhandeh, S.F. An Efficient Algorithm for Simulating Grout Propagation in 2D Discrete Fracture Networks. Int. J. Rock Mech. Min. Sci. 2017, 98, 67–77. [Google Scholar] [CrossRef]
- Wang, Q.; Gao, H.; Jiang, B.; Li, S.; He, M.; Qin, Q. In-Situ Test and Bolt-Grouting Design Evaluation Method of Underground Engineering Based on Digital Drilling. Int. J. Rock Mech. Min. Sci. 2021, 138, 104575. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, L.; Sun, D.; Zhang, Q.; Wang, D.; Wang, L. Quantitative Design Method for Grouting in Sand Layers: Practice in Qingdao Metro Line 2. Processes 2022, 10, 840. [Google Scholar] [CrossRef]
- Hu, Y.; Zhao, M.Y.; Liang, S. Research on Detection Standard of Karst Roadbed Grouting Effect Based on the Geophysical Methods. Appl. Mech. Mater. 2014, 556–562, 659–662. [Google Scholar] [CrossRef]
- Peng, M.; Wang, D.; Liu, L.; Shi, Z.; Shen, J.; Ma, F. Recent Advances in the GPR Detection of Grouting Defects behind Shield Tunnel Segments. Remote Sens. 2021, 13, 4596. [Google Scholar] [CrossRef]
- Ma, X.; Su, M.; Xue, Y.; Wang, P.; Qiu, D.; Han, M.; Ju, Z.; Liao, Z. Comprehensive Geophysical Evaluation of Grouting in the Goaf of an Urban Underground Coal Mine. Mine Water Environ. 2023, 42, 513–526. [Google Scholar] [CrossRef]
- Rafi, J.Y.; Stille, H. Control of Rock Jacking Considering Spread of Grout and Grouting Pressure. Tunn. Undergr. Space Technol. 2014, 40, 1–15. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, S.; Sloan, S.W.; Sheng, D.; Pakzad, R. Experimental Investigation of Pressure Grouting in Sand. Soils Found. 2016, 56, 161–173. [Google Scholar] [CrossRef]
- Hossain, M.A.; Yin, J.-H. Influence of Grouting Pressure on the Behavior of an Unsaturated Soil-Cement Interface. J. Geotech. Geoenviron. Eng. 2012, 138, 193–202. [Google Scholar] [CrossRef]
- Wang, B.; Zhou, X.; Liu, L.; Liu, T. Detection of Grouting Defects behind Shield Segments via Shear Wave Ultrasound Arrays: Numerical and Full-Scale Model Experiments. Tunn. Undergr. Space Technol. 2025, 157, 106287. [Google Scholar] [CrossRef]
- Cao, D.; Pan, Z.; Zhang, Z.; Zeng, B. Experimental and Numerical Study on Detection of Sleeve Grouting Defect with Impact-Echo Method. Structures 2023, 52, 632–650. [Google Scholar] [CrossRef]
- Krause, M.; Milmann, B.; Mielentz, F.; Streicher, D.; Redmer, B.; Mayer, K.; Langenberg, K.-J.; Schickert, M. Ultrasonic Imaging Methods for Investigation of Post-Tensioned Concrete Structures: A Study of Interfaces at Artificial Grouting Faults and Its Verification. J. Nondestruct. Eval. 2008, 27, 67–82. [Google Scholar] [CrossRef]
- Stille, B.; Stille, H.; Gustafson, G.; Kobayashi, S. Experience with the real time grouting control method. Geomech. Tunn. 2009, 2, 447–459. [Google Scholar] [CrossRef]
- Gaspar, G.; Budjac, R.; Sedivy, S.; Stremy, M.; Benka, D.; Nemlaha, E.; Elias, R. Innovative Grouting Process Monitoring: Design and Implementation of a Measurement Device with Datalogger Function. IEEE Access 2025, 13, 19340–19352. [Google Scholar] [CrossRef]
- Naskar, J.; Jha, A.K.; Singh, T.N. A Comprehensive Review of Grouts: Unraveling Biogrout Technologies for Environmental Sustainability and Limitations. J. Hazard. Toxic Radioact. Waste 2024, 28, 03124001. [Google Scholar] [CrossRef]
- Lin, C.; Wang, X.; Li, Y.; Zhang, F.; Xu, Z.; Du, Y. Forward Modelling and GPR Imaging in Leakage Detection and Grouting Evaluation in Tunnel Lining. KSCE J. Civ. Eng. 2020, 24, 278–294. [Google Scholar] [CrossRef]
- Zhu, L.; Gu, W.; Qiu, F.; Ouyang, Y. Grouting Slurry Diffusion Range Based on Active Heating Fiber Optics Monitoring. Sci. Rep. 2022, 12, 19162. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.; Xu, H.; Wei, G.; Yu, X.; Ma, D.; Tang, Y.; Ma, H. Evaluation of Grouting Effectiveness for Semi-Rigid Pavement Base Layer Cracks Based on Time-Frequency Domain Signal Characteristics of 3D GPR. Measurement 2024, 237, 115228. [Google Scholar] [CrossRef]
- Cai, G.; Xie, X.; Li, K. Intelligent GPR Detection of Backfill Grouting Quality and Adjacent Soil Cavities in Shield Tunnels: A Case Study. Adv. Civ. Eng. 2025, 2025, 5558241. [Google Scholar] [CrossRef]
- Li, P.; Liu, Y.; Fan, J.; Qiu, Y.; Li, Y.; Xu, C.; Wang, C. Intelligent Identification of Synchronous Grouting GPR Detection in Shield Tunnel and Field Test Research. J. Basic Sci. Eng. 2025, 33, 743–754. [Google Scholar] [CrossRef]
- Karaoulis, M. Optimization of 3D Borehole Electrical Resistivity Tomography (ERT) Measurements for Real-Time Subsurface Imaging. Water 2025, 17, 1695. [Google Scholar] [CrossRef]
- Lapenna, V.; Perrone, A. Time-Lapse Electrical Resistivity Tomography (TL-ERT) for Landslide Monitoring: Recent Advances and Future Directions. Appl. Sci. 2022, 12, 1425. [Google Scholar] [CrossRef]
- Su, B.; Yang, H.; Królczyk, G.; Yang, Q.; Liu, S.; Siarry, P.; Li, Z. Geophysical Electrical Potential Inversion for Grouting Remote Monitoring of Coal Mine Double-Layered Wellbores. Alex. Eng. J. 2024, 96, 279–294. [Google Scholar] [CrossRef]
- Archie, G.E. The Electrical Resistivity Log as an Aid in Determining Some Reservoir Characteristics. Trans. AIME 1942, 146, 54–62. [Google Scholar] [CrossRef]
- Zhou, Q.Y.; Shimada, J.; Sato, A. Three-Dimensional Spatial and Temporal Monitoring of Soil Water Content Using Electrical Resistivity Tomography. Water Resour. Res. 2001, 37, 273–285. [Google Scholar] [CrossRef]
- Kennedy, W.D.; Herrick, D.C. Conductivity Models for Archie Rocks. Geophysics 2012, 77, WA109–WA128. [Google Scholar] [CrossRef]
- Bruckshaw, J.M. Electrical Methods of Geophysical Prospecting. J. Inst. Electr. Eng. 1933, 73, 521–533. [Google Scholar] [CrossRef]
- Parwatiningtyas, D.; Astuti, R.Y.; Hartoyo, P. Application of 2D Resistivity from Geoelectrical Methods with Dipole Dipole Configuration for Identification of Land Slides in Citeko Village, Cisarua, Bogor District, West Java. J. Phys. Conf. Ser. 2021, 1832, 12015. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, Z.; Yang, Y.; Tian, Y. Application of Electrical Resistivity Tomography for Underground Box Culvert Detection. J. Phys. Conf. Ser. 2024, 2895, 12039. [Google Scholar] [CrossRef]
- Yasir, S.F.; Jani, J.; Mukri, M. A Dataset of Visualization Methods to Assessing Soil Profile Using RES2DINV and VOXLER Software. Data Brief. 2019, 24, 103821. [Google Scholar] [CrossRef]
- Tsourlos, P.; Papadopoulos, N.; Papazachos, C.; Yi, M.-J.; Kim, J.-H. Efficient 2D Inversion of Long ERT Sections. J. Appl. Geophys. 2014, 105, 213–224. [Google Scholar] [CrossRef]
Figure 1.
Structure of the monitoring system.
Figure 1.
Structure of the monitoring system.
Figure 2.
Distributed and parallel dynamic grouting monitoring system architecture.
Figure 2.
Distributed and parallel dynamic grouting monitoring system architecture.
Figure 3.
Distributed and parallel dynamic grouting monitoring system PCB schematic diagram.
Figure 3.
Distributed and parallel dynamic grouting monitoring system PCB schematic diagram.
Figure 4.
Channel-specific relative error distribution of the distributed and parallel dynamic grouting monitoring system.
Figure 4.
Channel-specific relative error distribution of the distributed and parallel dynamic grouting monitoring system.
Figure 5.
Geological unit inversion workflow incorporating Bayesian estimation.
Figure 5.
Geological unit inversion workflow incorporating Bayesian estimation.
Figure 6.
Initial model for inversion.
Figure 6.
Initial model for inversion.
Figure 7.
Inversion iteration results. (a) Second iteration result; (b) Third iteration result; (c) Fourth iteration result; (d) Fifth iteration result; (e) Sixth iteration result; (f) Seventh iteration result.
Figure 7.
Inversion iteration results. (a) Second iteration result; (b) Third iteration result; (c) Fourth iteration result; (d) Fifth iteration result; (e) Sixth iteration result; (f) Seventh iteration result.
Figure 8.
Inversion results based on the least squares method.
Figure 8.
Inversion results based on the least squares method.
Figure 9.
Accuracy comparison across noise levels.
Figure 9.
Accuracy comparison across noise levels.
Figure 10.
Forward modeling of grouting.
Figure 10.
Forward modeling of grouting.
Figure 12.
Schlumberger array.
Figure 12.
Schlumberger array.
Figure 13.
Dipole-dipole array.
Figure 13.
Dipole-dipole array.
Figure 14.
Simulation results of the Wenner array: (a) electrode spacing of 0.5 m; (b) electrode spacing of 1 m.
Figure 14.
Simulation results of the Wenner array: (a) electrode spacing of 0.5 m; (b) electrode spacing of 1 m.
Figure 15.
Simulation results of the Schlumberger array: (a) electrode spacing of 0.5 m; (b) electrode spacing of 1 m.
Figure 15.
Simulation results of the Schlumberger array: (a) electrode spacing of 0.5 m; (b) electrode spacing of 1 m.
Figure 16.
Simulation results of the dipole-dipole array: (a) electrode spacing of 0.5 m and (b) electrode spacing of 1 m.
Figure 16.
Simulation results of the dipole-dipole array: (a) electrode spacing of 0.5 m and (b) electrode spacing of 1 m.
Figure 17.
The resistivity profile illustrating the grout diffusion-consolidation process. (a–d) Grout diffusion process; (e–g) Grout consolidation process.
Figure 17.
The resistivity profile illustrating the grout diffusion-consolidation process. (a–d) Grout diffusion process; (e–g) Grout consolidation process.
Figure 18.
Grouting monitoring test site and array layout.
Figure 18.
Grouting monitoring test site and array layout.
Figure 19.
Results of the 3D grouting monitoring experiment: (a) top view; (b) main view; (c) side view; (d) three-dimensional view.
Figure 19.
Results of the 3D grouting monitoring experiment: (a) top view; (b) main view; (c) side view; (d) three-dimensional view.
Figure 20.
Layout of the grouting field monitoring system.
Figure 20.
Layout of the grouting field monitoring system.
Figure 21.
Monitoring results of railway subgrade grouting: (a) top view; (b) main view; (c) side view; (d) three-dimensional view.
Figure 21.
Monitoring results of railway subgrade grouting: (a) top view; (b) main view; (c) side view; (d) three-dimensional view.
Table 1.
Statistical Comparison of Accuracy and Computational Efficiency.
Table 1.
Statistical Comparison of Accuracy and Computational Efficiency.
| Metric | Least Squares (Mean ± SD) | Proposed Method (Mean ± SD) | Improvement |
|---|
| Accuracy (%) | 82.3 ± 3.1 | 92.7 ± 2.4 | 12.70% |
| Computation Time (s/iter) | 0.45 ± 0.08 | 0.43 ± 0.05 | 4.44% |
| Number of iterations | 7 ± 0.08 | 7 ± 0.06 | 12.50% |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).