Quasi-Synchronization Control of Discrete-Time Leader–Follower Neural Networks with Parameter Uncertainties and Markovian Channel Fading

Abstract

Leader–follower neural networks deployed over wireless platforms are subject to parameter uncertainties and stochastic channel fading. The combined impact of these effects on quasi-synchronization control remains largely unexplored. The paper addresses the problem of quasi-synchronization performance degradation in discrete-time leader–follower neural networks caused by randomly occurring parameter uncertainties and stochastic channel fading. Discrete leader–follower neural networks are constructed in state-space form. Randomly occurring parameter uncertainties in the leader neural networks are described using a Bernoulli probability distribution and time-varying parameter matrices. Channel fading is represented by a finite-state Markovian model that captures state switching. For the follower neural networks, an intermittent impulsive control strategy is designed based on linear matrix inequalities and the Lyapunov stability principle. A computable bound on the synchronization error is derived as well. A simulation study validates that the proposed impulsive control strategy effectively suppresses synchronization error caused by parameter uncertainties and Markovian channel fading, thereby ensuring mean-square boundedness. Compared with an existing method, the proposed approach consumes less control energy but achieves better performance in terms of synchronization error. The average norms of the synchronization error and the control input signal are reduced by 24.00% and 58.64%, respectively.

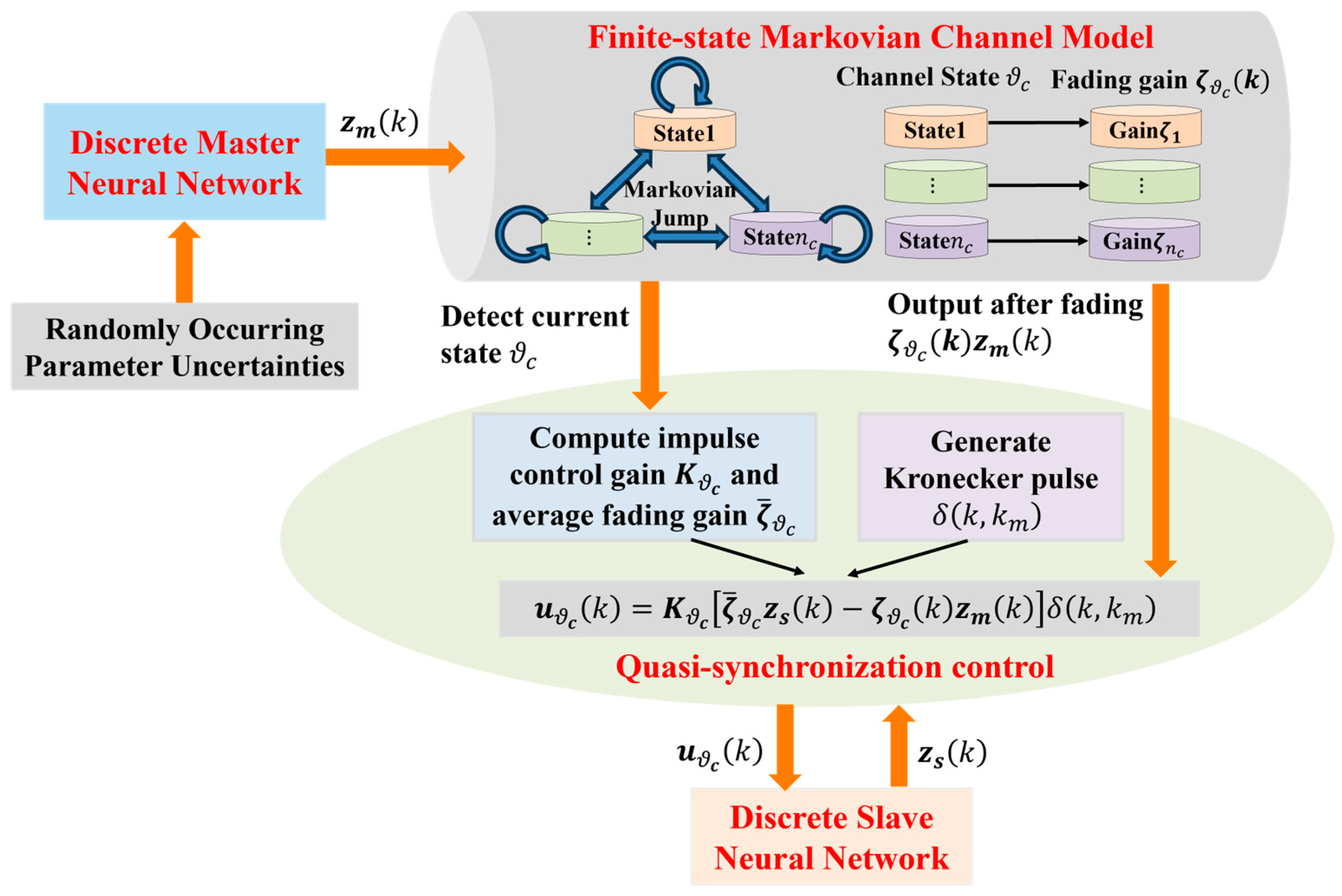
1. Introduction

The growing demand for remote and distributed control in complex engineering applications has driven significant interest in network-based control systems due to their flexibility and scalability [1,2]. Leader–follower neural networks play a crucial role in such systems owing to their outstanding advantages in terms of self-learning ability, associative memory, and fault tolerance [3].

Achieving synchronization between leader–follower neural networks constitutes a fundamental performance requirement for the efficient coordinated control of complex remote distributed systems, such as satellite constellations, microgrids, multiple unmanned aerial vehicles, and financial systems [4,5,6,7]. Synchronization entails driving the follower neural networks to reach a state that is consistent, either completely or approximately, with the leader neural networks. In practical applications, leader–follower neural networks are implemented using electronic components. Consequently, their performance is significantly affected by stochastic environmental disturbances such as temperature fluctuations, humidity variations, and electromagnetic interference. These disturbances induce system parameter uncertainties, posing substantial challenges for synchronization control [8,9]. Due to these parameter uncertainties, achieving absolute synchronization is infeasible in actual leader–follower neural networks. Instead, the synchronization error can only be controlled within a bounded region, referred to as quasi-synchronization [10].

Numerous studies have investigated the quasi-synchronization behavior and control approaches for leader–follower neural networks with various types of uncertainties. Typically, uncertainties induced by discontinuous activation functions, mismatched connection weight parameters, and unknown connection weight parameters have significant impacts on the quasi-synchronization performance [8]. Foundational work by Liu et al. [11] established the quasi-synchronization criteria in leader–follower neural networks characterized by discontinuous activation functions and parameter mismatches. By utilizing a Filippov solution framework, matrix measure techniques, and generalized Halanay inequalities, their control approach ensured the existence and dissipativity of solutions, thereby providing a basis for understanding quasi-synchronization in such systems. Sliding mode control has proven effective for uncertain hyperchaotic systems, as evidenced by Singh et al. [12]. This approach ensures stabilization and synchronization despite parameter uncertainties. Hui [13,14,15] developed discrete-time sliding mode controllers for nuclear reactors with model uncertainties, exogenous disturbances and discretization errors. Loría et al. [16] broadened the train of thought to achieve the leader–follower synchronization under parameter uncertainty via an observer design method. The leader system was regarded as a system of differential equations with a state and a measurable output. A state observer was designed as the follower system to reconstruct the dynamics of the leader system. The randomness of many system parameters occurs intermittently. Thus, a Bernoulli process was employed by Rao et al. [17] to describe the randomly occurring system parameter uncertainties in discrete leader–follower neural networks, concurrently considering parameter mismatch. A quasi-synchronization control algorithm based on Lyapunov stability theory was provided. Further, the randomly occurring uncertainties in system parameters have been extended to connection weight parameters. Soundararajan et al. [18,19] considered randomly occurring uncertainties in both system parameters and connection weight parameters in discrete-time complex-valued neural networks. The developed less conservative output feedback control algorithm based on Jensen’s weight summation inequalities and the extended reciprocal convex matrix inequality significantly reduced the impact of randomly occurring uncertainties on the synchronization behavior. In addition, some adaptive quasi-synchronization control methods [20,21] were proposed to reduce the effects of uncertain network topologies on quasi-synchronization behavior.

It is noteworthy that uncertainties can stem from the signal transmission process and deserve to be explored in depth as well. Utilizing recursive matrix inequalities and stochastic analysis, Zhao et al. [22] ensured that the networks achieved the desired quasi-synchronization performance despite the uncertainties introduced by stochastic communication channels. In recent years, the evolution of wireless communication within leader–follower neural networks has garnered significant attention, driven by technological advancements and increasing demands for efficient, reliable, and scalable communication protocols [23]. Wireless transmission links inherently suffer from channel fading and delay due to the reflection, diffraction, and scattering of radio waves caused by terrain and obstacles [24]. Notably, the channel fading and delay during the signal transmission process are stochastic. Many studies have addressed the quasi-synchronization problems of delayed leader–follower systems. Zhang et al. [25] addressed the problem of leader–follower synchronization under unbounded delays. They proposed an adaptive control approach without restrictive delay assumptions, providing a rigorous proof of error convergence and expanding the theoretical understanding of neural network synchronization under challenging delay scenarios. Zhang et al. [26] integrated the tempered fractional-order operators with memristive neural networks to establish a synchronization criterion under time-delay state feedback control. However, most existing quasi-synchronization control strategies neglect the channel fading characteristics, which often result in residual steady-state synchronization errors. A widely adopted model for channel fading is the finite-state Markovian model, where fading variations are described by Markovian jumps [27,28]. While Markovian channel fading has received preliminary attention, the specific problem of quasi-synchronization control for discrete-time leader–follower systems under the combined effects of randomly occurring parameter uncertainties and Markovian channel fading remains largely unexplored.

While continuous control strategies have been widely studied for networked systems, their effectiveness fundamentally depends on the persistent and reliable transmission of sensor feedback to the controller [29]. However, this dependency poses a significant challenge in practical implementations where feedback signals are frequently degraded or interrupted due to sensor failures, external disturbances, or inherent communication imperfections. Consequently, continuous control often becomes infeasible or suboptimal when signal integrity is compromised. To address this limitation, impulsive control emerges as a promising alternative. By allowing systems to generate discontinuous control inputs at specific instants, it offers distinct advantages such as rapid response and reduced energy consumption, making it particularly suitable for discrete leader–follower neural networks. Building upon this potential, recent research has explored impulsive control for quasi-synchronization in leader–follower systems. Tang et al. [30] demonstrated its efficacy for facilitating exponential quasi-synchronization in leader–follower systems with parameter mismatches and time-varying delays. Rao et al. [31] modeled parameter uncertainties in leader–follower neural networks via the Markovian jump process and described the communication channel fading phenomenon using random variables with distinct gains. They designed an impulsive transmission-driven synchronization strategy. Suo et al. [32] proposed an impulsive control method based on delay effects, improving the lagging quasi-synchronization performance of stochastic complex neural networks considering communication delays. Fan et al. [29] introduced aperiodic intermittent control to achieve quasi-synchronization in delayed memristive neural networks with switching mismatches, emphasizing reduced conservativeness. Gu et al. [33] provided an event-triggered impulsive control scheme to impair the effects of nonlinear disturbances on the multi-agent system quasi-synchronization. Despite these valuable contributions, the combined impact of randomly occurring parameter uncertainties and stochastic channel fading on discrete-time leader–follower neural network synchronization has received insufficient attention.

Motivated by the aforementioned research gaps, this paper deeply investigates the quasi-synchronization control problem oriented for the discrete-time leader–follower neural networks subject to randomly occurring parameter uncertainties and stochastic channel fading. Discrete leader–follower neural networks are constructed using the state-space method. Parameter uncertainties that randomly occur in the leader neural networks are characterized using a Bernoulli probability distribution and time-varying parameter matrices. Channel fading is represented by a finite-state Markovian model that captures state switching. Based on linear matrix inequalities and the Lyapunov stability principle, an intermittent impulsive control strategy is designed for the follower neural networks. Crucially, the impulsive control gain is automatically adjusted according to the channel fading states. Furthermore, the bound on the synchronization error is rigorously derived as well.

The rest of the paper is structured as follows. Section 2 presents the modeling process of the discrete-time leader–follower neural networks including the leader neural networks, the follower neural networks, and the Markovian channel fading model. Section 3 provides the concept of synchronization error and its dynamic characteristics. The intermittent impulsive control strategy is proposed in Section 4. Section 5 verifies the effectiveness of the proposed approach. Section 6 concludes the paper.

2. Modeling of the Leader–Follower Neural Networks

The modeling and control flow for the quasi-synchronization of leader–follower neural networks is illustrated in Figure 1. Discrete leader neural networks, subject to randomly occurring parameter uncertainties, generate output signal. The output signal suffers from channel fading when transmitted to the follower neural networks through a finite-state Markovian channel. Within this channel model, each discrete Markovian state corresponds uniquely to a specific channel fading gain. State transitions are governed by a Markovian transition probability matrix. The terminal of the follower neural networks detects the current channel state, calculates the impulse control gain and average fading gain under the current state based on the Lyapunov stability principle and linear matrix inequalities. It then receives the state of the follower neural networks and the fading state of the leader neural networks, calculates the impulse control signal applied to the follower neural networks, and thereby achieves quasi-synchronization of the leader–follower neural networks.

2.1. Leader Neural Networks

Consider the following discrete-time leader neural networks with randomly occurring uncertainties in system parameters and weight parameters,

$$\begin{array}{cc}\hfill {\mathit{z}}_{\mathit{m}}\left(k+1\right)& =\left[{\mathit{A}}_1+\beta \left(k\right)\mathrm{\Delta }{\mathit{A}}_1\left(k\right)+\left(1-\beta \left(k\right)\right)\gamma \left(k\right)\mathrm{\Delta }{\mathit{A}}_2\left(k\right)\right]{\mathit{z}}_{\mathit{m}}\left(k\right)\hfill \\ & +\left[{\mathit{B}}_1+\alpha \left(k\right)\mathrm{\Delta }{\mathit{B}}_1\left(k\right)+\left(1-\alpha \left(k\right)\right)\rho (k)\mathrm{\Delta }{\mathit{B}}_2\left(k\right)\right]\mathit{f}\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)\hfill \end{array}$$

(1)

where $k\in \mathbb{N}$ denotes the discrete time step. $\alpha \left(k\right)$, $\beta \left(k\right)$, $\gamma \left(k\right)$, and $\rho (k)$ are random variables. ${\mathit{z}}_{\mathit{m}}\left(k\right)\in {ℝ}^n$ is the n-dimensional discrete-time state vector of the leader neural networks, satisfying the energy-bounded constraint $‖{\mathit{z}}_{\mathit{m}}\left(k\right)‖\le h$. $‖\cdot ‖$ denotes the Euclidean norm. $h$ is a constant. ${\mathit{A}}_1\in {ℝ}^{n\times n}$ and ${\mathit{B}}_1\in {ℝ}^{n\times n}$ are known constant parameter matrices. $\mathrm{\Delta }{\mathit{A}}_1\left(k\right)\in {ℝ}^{n\times n}$, $\mathrm{\Delta }{\mathit{A}}_2\left(k\right)\in {ℝ}^{n\times n}$, $\mathrm{\Delta }{\mathit{B}}_1\left(k\right)\in {ℝ}^{n\times n}$, and $\mathrm{\Delta }{\mathit{B}}_2\left(k\right)\in {ℝ}^{n\times n}$ are time-varying parameter matrices of the leader neural networks, satisfying the bounded constraints $‖\mathrm{\Delta }{\mathit{A}}_1\left(k\right)‖\le h_1$, $‖\mathrm{\Delta }{\mathit{A}}_2\left(k\right)‖\le h_2$, $‖\mathrm{\Delta }{\mathit{B}}_1\left(k\right)‖\le h_1$, and $‖\mathrm{\Delta }{\mathit{B}}_2\left(k\right)‖\le h_2$. $h_1$ and $h_2$ are constants. $\mathit{f}\left(\cdot \right)={\left[f_1\left(\cdot \right),\dots f_n\left(\cdot \right)\right]}^T\in {ℝ}^n$ is the n-dimensional nonlinear activation function of the neural networks.

In practical applications, Equation (1) can stand for different types of neural networks [19]. The detailed mapping from neural networks to Equation (1) varies with the type of neural networks, which is beyond the scope of this paper. In general, ${\mathit{z}}_{\mathit{m}}\left(k\right)$ is associated with the values of the n-neurons of the leader neural networks. ${\mathit{A}}_1$ and ${\mathit{B}}_1$ represent the neuronal self-feedback matrix and the connection weight matrix, respectively. $\mathit{f}\left(\cdot \right)$ corresponds to the n-dimensional nonlinear activation function in neural networks.

Considering that the parameter uncertainties are norm-bounded and occur randomly, the stochastic characteristics of $\alpha \left(k\right)$, $\beta \left(k\right)$, $\gamma \left(k\right)$, and $\rho (k)$ are described by mutually independent Bernoulli probability distributions:

$$\left\{\begin{array}{l}\begin{array}{c}\mathbb{P}\left\{\alpha \left(k\right)=1\right\}=\overline{\alpha },\begin{array}{c}P\left\{\alpha \left(k\right)=0\right\}=1-\overline{\alpha }\end{array}\\ \mathbb{P}\left\{\beta \left(k\right)=1\right\}=\overline{\beta },\begin{array}{c}P\left\{\beta \left(k\right)=0\right\}=1-\overline{\beta }\end{array}\end{array}\\ \begin{array}{c}\mathbb{P}\left\{\gamma \left(k\right)=1\right\}=\overline{\gamma },\begin{array}{c}P\left\{\gamma \left(k\right)=0\right\}=1-\overline{\gamma }\end{array}\\ \mathbb{P}\left\{\rho \left(k\right)=1\right\}=\overline{\rho },\begin{array}{c}P\left\{\rho \left(k\right)=0\right\}=1-\overline{\rho }\end{array}\end{array}\end{array}\right.$$

(2)

where $\overline{\alpha },\overline{\beta },\overline{\gamma },\overline{\rho }\in [0,1]$ are constants while $\mathbb{P}\left\{\cdot \right\}$ denotes probability.

Assume that the continuous nonlinear activation function $f_i\left(\cdot \right)$ satisfies the zero initial condition and the following condition [26],

$${\alpha }_i\le {\displaystyle \frac{f_i\left(a\right)-f_i\left(b\right)}{a-b}}\le {\beta }_i$$

(3)

where $a,b\in ℝ$ and $a\ne b$ while ${\alpha }_i$ and ${\beta }_i$ are constants.

2.2. Markovian Channel Fading Model

Radio waves are susceptible to reflection, diffraction, and scattering during propagation, which cause signal energy loss, known as channel fading. The stochastic characteristics of channel fading in wireless communications are strongly influenced by factors such as terrain and obstacles encountered during transmission, exhibiting significant randomness. A finite-state Markovian model is employed to characterize the randomness of channel fading, where a Markovian chain ${\vartheta }_c\in \left\{1,2,\dots n_c\right\}$ represents distinct fading states. Each channel fading characteristic corresponds to a channel state. $n_c$ is a positive integer representing the number of states for the Markovian chain. Assume that the state transition probability matrix of ${\vartheta }_c$ is $\mathit{\pi }=\left\{{\pi }_{ij}\right\}\in {\mathit{R}}^{n_c\times n_c}$, with each element defined as,

$${\pi }_{ij}=\mathbb{P}\left\{{\vartheta }_c(k+1)=j|{\vartheta }_c(k)=i\right\}$$

(4)

where ${\pi }_{ij}$ represents the probability that the next state ${\vartheta }_c(k+1)$ will be $j$ given that the current state ${\vartheta }_c(k)$ is $i$. For all $i\in \left\{1,2,\dots n_c\right\}$, the sum ${\displaystyle \sum _{j=1}^{n_c}}{\pi }_{ij}=1$.

The fading gains of communication channels under different states ${\vartheta }_c$ are described by a random diagonal matrix ${\mathit{\zeta }}_{{\vartheta }_c}\left(k\right)=\mathrm{diag}\left\{{\zeta }_{{\vartheta }_{c1}}\left(k\right),{\zeta }_{{\vartheta }_{c2}}\left(k\right),\dots ,{\zeta }_{{\vartheta }_{cn}}\left(k\right)\right\}$. It is assumed that the random variables ${\zeta }_{{\vartheta }_{c1}}\left(k\right),{\zeta }_{{\vartheta }_{c2}}\left(k\right),\dots ,{\zeta }_{{\vartheta }_{cn}}\left(k\right)$ for the signal fading gains are mutually independent, meaning there is no interference among channels, which aligns with practical engineering backgrounds. Assume that ${\zeta }_{{\vartheta }_{ci}}\left(k\right)$ follows a Gaussian distribution, with its expectation and variance represented by diagonal matrices,

$$\left\{\begin{array}{c}{\overline{\mathit{\zeta }}}_{{\vartheta }_c}=\mathrm{diag}\left\{{\overline{\zeta }}_{{\vartheta }_{c1}},{\overline{\zeta }}_{{\vartheta }_{c2}},\dots ,{\overline{\zeta }}_{{\vartheta }_{cn}}\right\}\\ S_{\vartheta c}=\mathrm{diag}\left\{{\sigma }_{{\vartheta }_{c1}}^2,{\sigma }_{{\vartheta }_{c2}}^2,\dots ,{\sigma }_{{\vartheta }_{cn}}^2\right\}\end{array}\right.$$

(5)

where the expectation is expressed as ${\overline{\zeta }}_{{\vartheta }_{ci}}=E\left\{{\zeta }_{{\vartheta }_{ci}}\left(k\right)\right\}$, while the variance is expressed as ${\sigma }_{{\vartheta }_{ci}}^2=E\left\{{\left[{\zeta }_{{\vartheta }_{ci}}\left(k\right)-{\overline{\zeta }}_{{\vartheta }_{ci}}\right]}^2\right\}$.

2.3. Follower Neural Networks

The follower neural networks have a structure similar to that of the leader neural networks, but with different parameters. Neglecting parameter randomness in the follower neural networks, the follower neural networks are formulated as

$${\mathit{z}}_{\mathit{s}}\left(k+1\right)={\mathit{A}}_2{\mathit{z}}_{\mathit{s}}\left(k\right)+{\mathit{B}}_2\mathit{f}\left({\mathit{z}}_{\mathit{s}}\left(k\right)\right)+{\mathit{u}}_{{\vartheta }_c}\left(k\right)$$

(6)

where ${\mathit{z}}_{\mathit{s}}\left(k\right)\in {ℝ}^n$ denotes the state vector of the follower neural networks. ${\mathit{A}}_2\in {ℝ}^{n\times n}$ and ${\mathit{B}}_2\in {ℝ}^{n\times n}$ are the known neuronal self-feedback matrix and connection weight matrix, respectively. ${\mathit{u}}_{{\vartheta }_c}\left(k\right)\in {ℝ}^n$ represents the control input signal under channel state ${\vartheta }_c$.

3. Synchronization Error and Its Dynamic Characteristics

The synchronization error of the leader–follower neural networks is defined as

$${\mathit{z}}_{\mathit{e}}\left(k\right)={\mathit{z}}_{\mathit{s}}\left(k\right)-{\mathit{z}}_{\mathit{m}}\left(k\right)$$

(7)

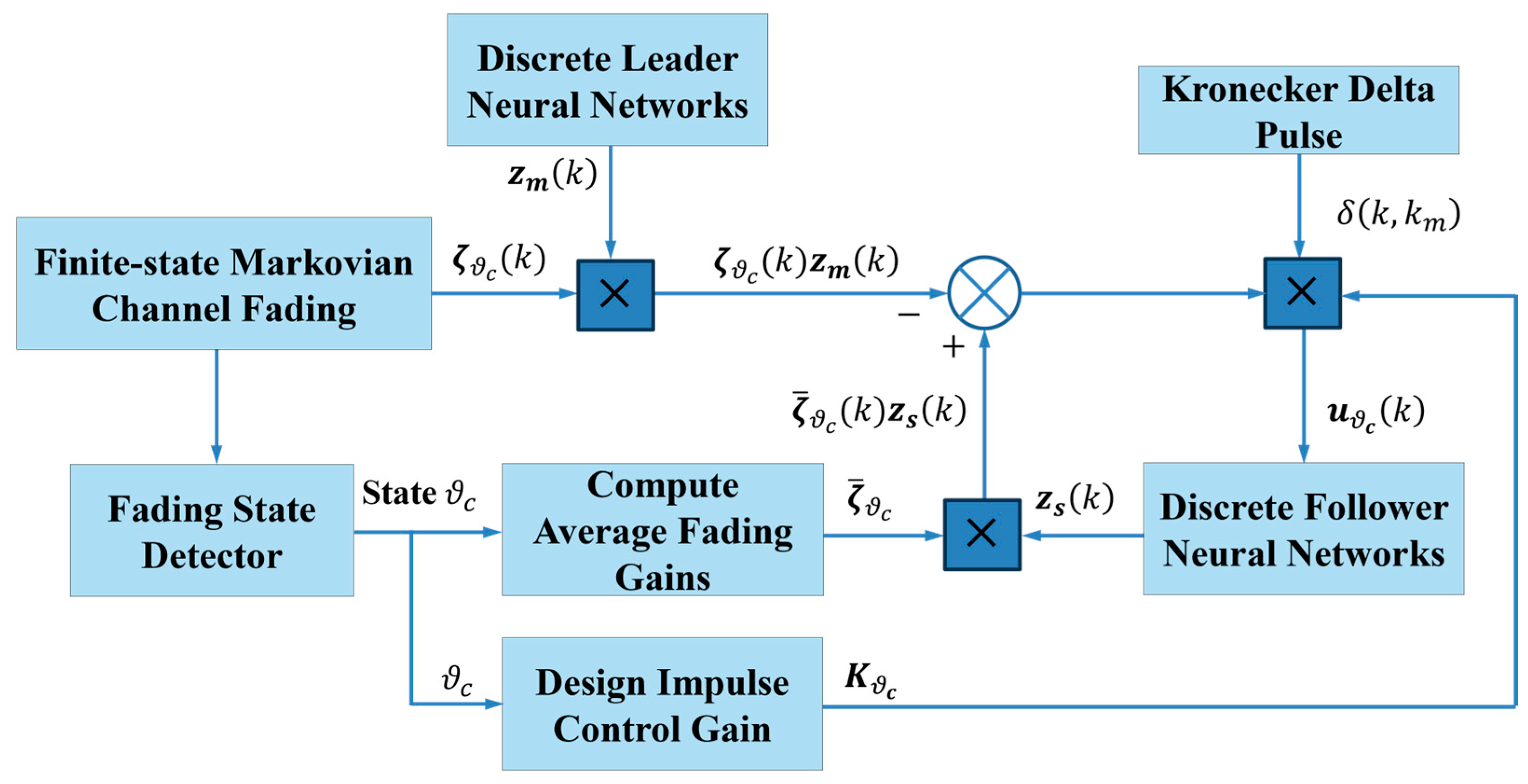
Detailed synchronization control structure based on error feedback and discrete impulse is depicted in Figure 2. A finite-state Markovian channel model is used to generate the random fading gain ${\mathit{\zeta }}_{{\vartheta }_c}\left(k\right)$. The current state of the Markovian chain ${\vartheta }_c$ is detected by a fading state detector. Based on the detected fading state, the control system computes the average fading gain ${\overline{\mathit{\zeta }}}_{{\vartheta }_c}$ and designs the impulse control gain via linear matrix inequalities and the Lyapunov stability principle. A Kronecker delta pulse with constant time interval is generated for discrete impulse control. Then the synchronization control input based on the synchronization error after channel fading ${\overline{\mathit{\zeta }}}_{{\vartheta }_c}{\mathit{z}}_{\mathit{s}}\left(k\right)-{\mathit{\zeta }}_{{\vartheta }_c}\left(k\right){\mathit{z}}_{\mathit{m}}\left(k\right)$ is applied to the follower neural networks, with the controller designed as

$${\mathit{u}}_{{\vartheta }_c}\left(\mathit{k}\right)={\mathit{K}}_{{\vartheta }_c}\left[{\overline{\mathit{\zeta }}}_{{\vartheta }_c}{\mathit{z}}_{\mathit{s}}\left(k\right)-{\mathit{\zeta }}_{{\vartheta }_c}\left(k\right){\mathit{z}}_{\mathit{m}}\left(k\right)\right]\delta \left(k,k_m\right)$$

(8)

where ${\mathit{K}}_{{\vartheta }_c}$ is the control gain to be determined under channel state ${\vartheta }_c$. $\delta \left(k,k_m\right)$ denotes the Kronecker delta function. $k_m$ is an integer for indexing the driving pulses within specified time intervals, with $m\in \mathbb{Z}$ and $k_0=1$. The time interval between consecutive pulses is denoted by a fixed positive integer $h_m$, with $h_m\triangleq k_{m+1}-k_m$. The detailed definition of $\delta \left(k,k_m\right)$ is

$$\delta \left(k,k_m\right)=\left\{\begin{array}{c}1,\mathrm{if}k=k_m\\ 0,\mathrm{if}k\ne k_m\end{array}\right.$$

(9)

Define the nonlinear activation function of the synchronization error as

$${\mathit{f}}_{\mathit{e}}\left({\mathit{z}}_{\mathit{e}}\left(k\right)\right)=\mathit{f}\left({\mathit{z}}_s\left(k\right)\right)-\mathit{f}\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)$$

(10)

Let $\mathit{A}={\mathit{A}}_2-{\mathit{A}}_1$ and $\mathit{B}={\mathit{B}}_2-{\mathit{B}}_1$. Assuming ${\overline{\mathit{\zeta }}}_{{\vartheta }_k}\approx {\mathit{\zeta }}_{{\vartheta }_k}\left(k\right)$, and combining Equations (1), (6), and (8), the dynamic difference equation of the synchronization error is

$${\mathit{z}}_{\mathit{e}}\left(k+1\right)={\mathit{N}}_{{\vartheta }_k}^T{\mathit{z}}_{\mathit{e}}\left(k\right)+{\mathit{B}}_2{\mathit{f}}_{\mathit{e}}\left({\mathit{z}}_{\mathit{e}}\left(k\right)\right)+\mathit{M}\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)$$

(11)

where

$$\begin{array}{cc}\hfill \mathit{M}\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)& =\left[\mathit{A}-\beta \left(k\right)\mathrm{\Delta }{\mathit{A}}_1\left(k\right)-\left(1-\beta \left(k\right)\right)\gamma \left(k\right)\mathrm{\Delta }{\mathit{A}}_2\left(k\right)\right]{\mathit{z}}_{\mathit{m}}\left(k\right)\hfill \\ & +\left[\mathit{B}-\alpha \left(k\right)\mathrm{\Delta }{\mathit{B}}_1\left(k\right)-\left(1-\alpha \left(k\right)\right)\rho (k)\mathrm{\Delta }{\mathit{B}}_2\left(k\right)\right]\mathit{f}\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)\hfill \end{array}$$

(12)

$${\mathit{N}}_{{\vartheta }_c}={\mathit{A}}_2+{\mathit{K}}_{{\vartheta }_c}{\overline{\mathit{\zeta }}}_{{\vartheta }_c}\delta \left(k,k_m\right)$$

(13)

The mathematical definition of the quasi-synchronization of the leader–follower neural networks is then presented.

Definition 1.

([30,34]). Consider the leader neural networks in Equation (1) and the follower neural networks in Equation (6). Quasi-synchronization is achieved with an error bound ${\epsilon }_b>0$, if there exists a compact region $\Theta$ such that the error ${\mathit{z}}_{\mathit{e}}\left(k\right)$ ultimately enters and remains within the region $\Theta =\left\{{\mathit{z}}_{\mathit{e}}\left(k\right)\in {ℝ}^n\left|‖{\mathit{z}}_{\mathit{e}}\left(k\right)‖\le {\epsilon }_b\right.\right\}$ as $k\to \infty$ for all initial conditions in the domain of interest. Synchronization is achieved if $‖{\mathit{z}}_{\mathit{e}}\left(k\right)‖=0$ as $k\to \infty$ for all initial conditions in the domain of interest.

Remark 1.

In nonlinear dynamical systems, ‘synchronization’ and ‘quasi-synchronization’ mainly target phase/frequency or partial synchronization [35,36,37]. In Fujisaka’s framework [38], ‘synchronization’ means that the vertical distance of the state phase points shrinks as time goes on. In contrast, ‘synchronization’ and ‘quasi-synchronization’ in this paper concern complete state synchronization with an explicit uniform or zero bound. It aims at the norm of the synchronization error and does not directly address phase/frequency locking.

4. Design of Impulse Control Gain

The sufficient conditions for the quasi-synchronization of the leader–follower neural networks with randomly occurring parameter uncertainties and Markovian channel fading, as described in (1)–(6), are derived in this section. The impulse control gain is then designed based on linear matrix inequalities and the Lyapunov stability principle.

Lemma 1

([39]). For any vector $\mathit{x},\mathit{y}\in {ℝ}^n$, there exists a positive definite matrix $\mathit{Q}\in {ℝ}^{n\times n}$ such that the following inequality holds,

$$2{\mathit{x}}^{\mathit{T}}\mathit{y}\le {\mathit{x}}^{\mathit{T}}\mathit{Q}\mathit{x}+{\mathit{y}}^{\mathit{T}}{\mathit{Q}}^{-1}\mathit{y}$$

(14)

Theorem 1.

For a given $\mu \in \left(0,1\right)$, the leader–follower neural networks with randomly occurring parameter uncertainties and Markovian channel fading, as described in (1)–(6), achieve quasi-synchronization, if there exist a positive scalar constant $\epsilon$, positive definite matrices  $\mathit{P}$, ${\mathit{Q}}_1$, ${\mathit{Q}}_2$, ${\mathit{Q}}_3$, and  ${\mathit{K}}_{{\vartheta }_c}$ for each channel state  ${\vartheta }_c$ such that condition (15) holds,

$$\left[\begin{array}{cccccc}-\mu \mathit{P}-\epsilon {\mathit{\Psi }}_1& {\mathit{N}}_{{\vartheta }_c}^T\mathit{P}{\mathit{B}}_2+\epsilon {\mathit{\Psi }}_2& {\mathit{N}}_{{\vartheta }_c}^T\mathit{P}& {\mathit{N}}_{{\vartheta }_c}^T\mathit{P}& 0& {\mathit{N}}_{{\vartheta }_c}^T\mathit{P}\\ *& {\mathit{B}}_2^T\mathit{P}{\mathit{B}}_2+{\mathit{B}}_2^T{\mathit{Q}}_3^{-1}{\mathit{B}}_2-\epsilon \mathit{I}& 0& 0& {\mathit{B}}_2^T\mathit{P}& 0\\ *& *& -{\mathit{Q}}_1^{-1}& 0& 0& 0\\ *& *& *& -\mathit{P}& 0& 0\\ *& *& *& *& -{\mathit{Q}}_2^{-1}& 0\\ *& *& *& *& *& -{\mathit{Q}}_3^{-1}\end{array}\right]<0$$

(15)

Then the synchronization error is bounded within the range of $\sqrt{{\displaystyle \frac{\delta }{\left(1-\mu \right){\lambda }_{\mathit{M}}\left(\mathit{P}\right)}}}$. Where $\mathit{I}\in {ℝ}^{n\times n}$ denotes the identity matrix, and

$$\left\{\begin{array}{l}{\mathit{\Psi }}_1=\mathrm{diag}\left\{{\alpha }_1{\beta }_1,{\alpha }_2{\beta }_2,\dots ,{\alpha }_n{\beta }_n\right\}\\ {\mathit{\Psi }}_2=\mathrm{diag}\left\{{\displaystyle \frac{{\alpha }_1+{\beta }_1}{2}},{\displaystyle \frac{{\alpha }_2+{\beta }_2}{2}},\dots ,{\displaystyle \frac{{\alpha }_n+{\beta }_n}{2}}\right\}\end{array}\right.$$

(16)

$$\begin{array}{l}\delta ={\lambda }_M\left(\mathit{P}+{\mathit{Q}}_1^{-1}+{\mathit{Q}}_2^{-1}\right)\times \left\{{\left[‖\mathit{A}‖+\max \left\{\overline{\beta }{h}_1,(1-\overline{\beta })\overline{\gamma }{h}_2\right\}\right]}^2{h}^2\right.\\ +{\left[‖\mathit{B}‖+\max \left\{\overline{\alpha }{h}_1,(1-\overline{\alpha })\overline{\rho }{h}_2\right\}\right]}^2\times \max \left\{{\left|f_1\left(h\right)\right|}^2,\mathrm{\dots },{\left|f_1\left(h\right)\right|}^2,{\left|f_1\left(-h\right)\right|}^2,\mathrm{\dots },{\left|f_1\left(-h\right)\right|}^2\right\}\\ +2h\left[‖\mathit{A}‖+\max \left\{\overline{\beta }{h}_1,(1-\overline{\beta })\overline{\gamma }{h}_2\right\}\right]\times \left[‖\mathit{B}‖+\max \left\{\overline{\alpha }{h}_1,(1-\overline{\alpha })\overline{\rho }{h}_2\right\}\right]\\ \left.\times \max \left\{\left|f_1\left(h\right)\right|,\mathrm{\dots },\left|f_n\left(h\right)\right|,\left|f_1\left(-h\right)\right|,\mathrm{\dots },\left|f_n\left(-h\right)\right|\right\}\right\}\end{array}$$

(17)

where ${\lambda }_M\left(\cdot \right)$ is the maximum eigenvalue of the positive definite matrix. $\delta$ is a constant.

Proof of Theorem 1.

In view of the Lyapunov stability principle, the impulse control gain ${\mathit{K}}_{{\vartheta }_c}$ is designed. The following Lyapunov function with a positive definite matrix $\mathit{P}$ is introduced for stability analysis of the leader–follower neural networks

$$V\left(k\right)={\mathit{z}}_{\mathit{e}}^T\left(k\right)\mathit{P}{\mathit{z}}_{\mathit{e}}\left(k\right)$$

(18)

The fundamental principle for designing the impulse control gain of discrete leader–follower neural networks in this paper is to ensure the synchronization error remains bounded in the mean square sense. This is to say, $E\left\{{‖{\mathit{z}}_{\mathit{e}}\left(k\right)‖}^2\right\}$ is bounded. For a given constant $\mu \in \left(0,1\right)$, the Lyapunov difference function of the discrete stochastic neural networks in the mean square sense is

$$E\left\{\mathrm{\Delta }V\left(k+1\right)\right\}\triangleq E\left\{V\left(k+1\right)\right\}-\mu E\left\{V\left(k\right)\right\}$$

(19)

Since the activation function $\mathit{f}\left(\cdot \right)$ satisfies the condition in Equation (3), there must exist a positive constant $\epsilon$ such that the following inequality holds,

$$\varphi \left(k\right)={\mathit{\rho }}^T\left(k\right)\left[\begin{array}{cc}\epsilon {\mathit{\Psi }}_1& -\epsilon {\mathit{\Psi }}_2\\ -\epsilon {\mathit{\Psi }}_2& \epsilon \mathit{I}\end{array}\right]\mathit{\rho }\left(k\right)\le 0$$

(20)

where $\mathit{\rho }\left(k\right)={\left[\begin{array}{cc}{\mathit{z}}_{\mathit{e}}^T\left(k\right)& {\mathit{f}}_{\mathit{e}}^T\left({\mathit{z}}_{\mathit{e}}\left(k\right)\right)\end{array}\right]}^T$.

Substituting the error dynamic Equation (11) into the Lyapunov function (18) yields:

$$\begin{array}{cc}\hfill V\left(k+1\right)& ={\mathit{z}}_{\mathit{e}}^{\mathit{T}}\left(k+1\right)\mathit{P}{\mathit{z}}_{\mathit{e}}\left(k+1\right)\hfill \\ & ={\mathit{z}}_{\mathit{e}}^T\left(k\right){\mathit{N}}_{{\vartheta }_k}^T\mathit{P}{\mathit{N}}_{{\vartheta }_k}{\mathit{z}}_{\mathit{e}}\left(k\right)+{\mathit{f}}_{\mathit{e}}^T\left({\mathit{z}}_{\mathit{e}}\left(k\right)\right){\mathit{B}}_2^T\mathit{P}{\mathit{B}}_2{\mathit{f}}_{\mathit{e}}\left({\mathit{z}}_{\mathit{e}}\left(k\right)\right)\hfill \\ & +{\mathit{M}}^{\mathit{T}}\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)\mathit{P}\mathit{M}\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)+2{\mathit{z}}_{\mathit{e}}^T\left(k\right){\mathit{N}}_{{\vartheta }_k}^T\mathit{P}{\mathit{B}}_2{\mathit{f}}_{\mathit{e}}\left({\mathit{z}}_{\mathit{e}}\left(k\right)\right)\hfill \\ & +2{\mathit{z}}_{\mathit{e}}^T\left(k\right){\mathit{N}}_{{\vartheta }_k}^T\mathit{P}\mathit{M}\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)+2{\mathit{f}}_{\mathit{e}}^T\left({\mathit{z}}_{\mathit{e}}\left(k\right)\right){\mathit{B}}_2^T\mathit{P}\mathit{M}\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)\hfill \end{array}$$

(21)

By Lemma 1, there exist positive definite matrices ${\mathit{Q}}_1$, ${\mathit{Q}}_2$, and ${\mathit{Q}}_3$ such that the following inequality holds:

$$\left\{\begin{array}{cc}\hfill 2{\mathit{z}}_{\mathit{e}}^T\left(k\right){\mathit{N}}_{{\vartheta }_k}^T\mathit{P}\mathit{M}\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)& \le {\mathit{z}}_{\mathit{e}}^T\left(k\right){\mathit{N}}_{{\vartheta }_k}^T\mathit{P}{\mathit{Q}}_1\mathit{P}{\mathit{N}}_{{\vartheta }_k}{\mathit{z}}_{\mathit{e}}\left(k\right)\hfill \\ & +{\mathit{M}}^{\mathit{T}}\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right){\mathit{Q}}_1^{-1}\mathit{M}\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)\hfill \\ \hfill 2{\mathit{f}}_{\mathit{e}}^T\left({\mathit{z}}_{\mathit{e}}\left(k\right)\right){\mathit{B}}_2^T\mathit{P}\mathit{M}\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)& \le {\mathit{f}}_{\mathit{e}}^T\left({\mathit{z}}_{\mathit{e}}\left(k\right)\right){\mathit{B}}_2^T\mathit{P}{\mathit{Q}}_2\mathit{P}{\mathit{B}}_2{\mathit{f}}_{\mathit{e}}\left({\mathit{z}}_{\mathit{e}}\left(k\right)\right)\hfill \\ & +{\mathit{M}}^{\mathit{T}}\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right){\mathit{Q}}_2^{-1}\mathit{M}\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)\hfill \\ \hfill 2{\mathit{z}}_{\mathit{e}}^T\left(k\right){\mathit{N}}_{{\vartheta }_k}^T\mathit{P}{\mathit{B}}_2{\mathit{f}}_{\mathit{e}}\left({\mathit{z}}_{\mathit{e}}\left(k\right)\right)& \le {\mathit{z}}_{\mathit{e}}^T\left(k\right){\mathit{N}}_{{\vartheta }_k}^T\mathit{P}{\mathit{Q}}_3\mathit{P}{\mathit{N}}_{{\vartheta }_k}{\mathit{z}}_{\mathit{e}}\left(k\right)\hfill \\ & +{\mathit{f}}_{\mathit{e}}^T\left({\mathit{z}}_{\mathit{e}}\left(k\right)\right){\mathit{B}}_2^T{\mathit{Q}}_3^{-1}{\mathit{B}}_2{\mathit{f}}_{\mathit{e}}\left({\mathit{z}}_{\mathit{e}}\left(k\right)\right)\hfill \end{array}\right.$$

(22)

Combining Equations (21) and (22) produces:

$$\begin{array}{cc}V\left(k+1\right)& \le {\mathit{z}}_{\mathit{e}}^T\left(k\right)\left({\mathit{N}}_{{\vartheta }_k}^T\mathit{P}{\mathit{N}}_{{\vartheta }_k}+{\mathit{N}}_{{\vartheta }_k}^T\mathit{P}{\mathit{Q}}_1\mathit{P}{\mathit{N}}_{{\vartheta }_k}+{\mathit{N}}_{{\vartheta }_k}^T\mathit{P}{\mathit{Q}}_3\mathit{P}{\mathit{N}}_{{\vartheta }_k}\right){\mathit{z}}_{\mathit{e}}\left(k\right)\\ & +{\mathit{f}}_{\mathit{e}}^T\left({\mathit{z}}_{\mathit{e}}\left(k\right)\right)\left({\mathit{B}}_2^T\mathit{P}{\mathit{B}}_2+{\mathit{B}}_2^T\mathit{P}{\mathit{Q}}_2\mathit{P}{\mathit{B}}_2+{\mathit{B}}_2^T{\mathit{Q}}_3^{-1}{\mathit{B}}_2\right){\mathit{f}}_{\mathit{e}}\left({\mathit{z}}_{\mathit{e}}\left(k\right)\right)\hfill \\ & +{\mathit{M}}^{\mathit{T}}\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)\left(\mathit{P}+{\mathit{Q}}_1^{-1}+{\mathit{Q}}_2^{-1}\right)\mathit{M}\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)\hfill \end{array}$$

(23)

Considering Equations (19)–(23) yields:

$$\begin{array}{cc}\hfill E\left\{\mathrm{\Delta }V\left(k+1\right)\right\}& \le E\left\{V\left(k+1\right)-\mu V\left(k\right)-\varphi \left(k\right)\right\}\hfill \\ & =E\left\{{\mathit{M}}^{\mathit{T}}\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)\left(\mathit{P}+{\mathit{Q}}_1^{-1}+{\mathit{Q}}_2^{-1}\right)\mathit{M}\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)\right\}+E\left\{{\mathit{\rho }}^T\left(k\right)\Omega \mathit{\rho }\left(k\right)\right\} \end{array}$$

(24)

where

$$\Omega =\left[\begin{array}{cc}{\mathit{N}}_{{\vartheta }_c}^T\mathit{P}{\mathit{N}}_{{\vartheta }_c}+{\mathit{N}}_{{\vartheta }_c}^T\mathit{P}{\mathit{Q}}_1\mathit{P}{\mathit{N}}_{{\vartheta }_c}+{\mathit{N}}_{{\vartheta }_c}^T\mathit{P}{\mathit{Q}}_3\mathit{P}{\mathit{N}}_{{\vartheta }_c}-\mu \mathit{P}-\epsilon {\mathit{\Psi }}_1& \epsilon {\mathit{\Psi }}_2\\ *& {\mathit{B}}_2^T\mathit{P}{\mathit{B}}_2+{\mathit{B}}_2^T{\mathit{Q}}_3^{-1}{\mathit{B}}_2+{\mathit{B}}_2^T\mathit{P}{\mathit{Q}}_2\mathit{P}{\mathit{B}}_2-\epsilon \mathit{I}\end{array}\right]$$

(25)

According to Equation (25), the necessary and sufficient conditions for the error ${\mathit{z}}_{\mathit{e}}\left(k\right)$ to be bounded in the mean square sense are: (1) the first term $E\left\{{\mathit{M}}^T\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)\left(\mathit{P}+{\mathit{Q}}_1^{-1}+{\mathit{Q}}_2^{-1}\right)\mathit{M}\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)\right\}$ is bounded, (2) the matrix $\Omega$ is negative definite.

Using multiple applications of the Schur complement lemma, the negative definiteness of matrix $\mathbf{\Omega }$ is equivalent to solving the matrix inequality (15).

According to the condition of the nonlinear activation function assumed in Equation (3), and considering the energy boundedness of the leader state vector and the boundedness of time-varying parameters, the boundedness of $E\left\{{\mathit{M}}^T\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)\left(\mathit{P}+{\mathit{Q}}_1^{-1}+{\mathit{Q}}_2^{-1}\right)\mathit{M}\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)\right\}$ is proven as follows.

Considering the energy-bounded constraint $‖{\mathit{z}}_{\mathit{m}}\left(k\right)‖\le h$, we obtain

$$\left\{\begin{array}{l}‖\mathit{f}\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)‖\le \max \left\{\left|f_1\left(h\right)\right|,\mathrm{\dots },\left|f_n\left(h\right)\right|,\left|f_1\left(-h\right)\right|,\mathrm{\dots },\left|f_n\left(-h\right)\right|\right\}\\ {\mathit{f}}^{\mathit{T}}\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)\mathit{f}\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)\le \max \left\{{\left|f_1\left(h\right)\right|}^2,\mathrm{\dots },{\left|f_1\left(h\right)\right|}^2,{\left|f_1\left(-h\right)\right|}^2,\mathrm{\dots },{\left|f_1\left(-h\right)\right|}^2\right\}\end{array}\right.$$

(26)

Then,

$$\begin{array}{l}E\left\{{\mathit{M}}^{\mathit{T}}\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)\left(\mathit{P}+{\mathit{Q}}_1^{-1}+{\mathit{Q}}_2^{-1}\right)\mathit{M}\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)\right\}\\ \le {\lambda }_{\mathit{M}}\left(\mathit{P}+{\mathit{Q}}_1^{-1}+{\mathit{Q}}_2^{-1}\right)\\ \times E\left\{\begin{array}{l}\left[\left(\mathit{A}-\beta \left(k\right)\mathrm{\Delta }{\mathit{A}}_1\left(k\right)\right){\mathit{z}}_{\mathit{m}}\left(k\right)-\left(1-\beta \left(k\right)\right)\gamma \left(k\right)\mathrm{\Delta }{\mathit{A}}_2\left(k\right){\mathit{z}}_{\mathit{m}}\left(k\right)\right.\\ {\left.+\left(\mathit{B}-\alpha \left(k\right)\mathrm{\Delta }{\mathit{B}}_1\left(k\right)\right)f\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)-\left(1-\alpha \left(k\right)\right)\rho (k)\mathrm{\Delta }{\mathit{B}}_2\left(k\right)f\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)\right]}^T\end{array}\right.\\ \left.\begin{array}{l}\times \left[\left(\mathit{A}-\beta \left(k\right)\mathrm{\Delta }{\mathit{A}}_1\left(k\right)\right){\mathit{z}}_{\mathit{m}}\left(k\right)-\left(1-\beta \left(k\right)\right)\gamma \left(k\right)\mathrm{\Delta }{\mathit{A}}_2\left(k\right){\mathit{z}}_{\mathit{m}}\left(k\right)\right.\\ \left.+\left(\mathit{B}-\alpha \left(k\right)\mathrm{\Delta }{\mathit{B}}_1\left(k\right)\right)f\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)-\left(1-\alpha \left(k\right)\right)\rho (k)\mathrm{\Delta }{\mathit{B}}_2\left(k\right)f\left({\mathit{z}}_{\mathit{m}}\left(k\right)\right)\right]\end{array}\right\}\\ \le {\lambda }_{\mathit{M}}\left(\mathit{P}+{\mathit{Q}}_1^{-1}+{\mathit{Q}}_2^{-1}\right)\times \left\{{\left[‖\mathit{A}‖+\max \left\{\overline{\beta }{h}_1,(1-\overline{\beta })\overline{\gamma }{h}_2\right\}\right]}^2{h}^2\right.\\ +{\left[‖\mathit{B}‖+\max \left\{\overline{\alpha }{h}_1,(1-\overline{\alpha })\overline{\rho }{h}_2\right\}\right]}^2\times \max \left\{{\left|f_1\left(h\right)\right|}^2,\mathrm{\dots },{\left|f_1\left(h\right)\right|}^2,{\left|f_1\left(-h\right)\right|}^2,\mathrm{\dots },{\left|f_1\left(-h\right)\right|}^2\right\}\\ +2h\left[‖\mathit{A}‖+\max \left\{\overline{\beta }{h}_1,(1-\overline{\beta })\overline{\gamma }{h}_2\right\}\right]\times \left[‖\mathit{B}‖+\max \left\{\overline{\alpha }{h}_1,(1-\overline{\alpha })\overline{\rho }{h}_2\right\}\right]\\ \times \left.\max \left\{\left|f_1\left(h\right)\right|,\mathrm{\dots },\left|f_n\left(h\right)\right|,\left|f_1\left(-h\right)\right|,\mathrm{\dots },\left|f_n\left(-h\right)\right|\right\}\right\}\\ =\delta \end{array}$$

(27)

Combining Equation (24) and Equation (27) gives

$$E\left\{\mathrm{\Delta }V\left(k+1\right)\right\}\triangleq E\left\{V\left(k+1\right)\right\}-\mu E\left\{V\left(k\right)\right\}\le \delta$$

(28)

For a given constant $\mu \in \left(0,1\right)$, ${\mu }^k$ approaches zero when $k\to +\infty$. Utilizing the recursive Equation (27) results in

$$E\left\{V\left(k\right)\right\}\le {\displaystyle \frac{1}{1-\mu }}\delta$$

(29)

From the Lyapunov function in Equation (18) and Definition 1, the bound of the synchronization error is calculated by,

$$E\left\{‖{\mathit{z}}_{\mathit{e}}\left(k\right)‖\right\}\le \sqrt{{\displaystyle \frac{E\left\{V\left(k\right)\right\}}{{\lambda }_{\mathit{M}}\left(\mathit{P}\right)}}}=\sqrt{{\displaystyle \frac{\delta }{\left(1-\mu \right){\lambda }_{\mathit{M}}\left(\mathit{P}\right)}}}$$

(30)

The proof is completed. The impulse control gain is designed in the following theorem. □

Theorem 2.

For a given  $\mu \in \left(0,1\right)$, the leader–follower neural networks with randomly occurring parameter uncertainties and Markovian channel fading, as described in (1)–(6),achieve quasi-synchronization, if there exist a positive scalar constant  $\epsilon$, positive definite matrices  $\mathit{P}$, ${\mathit{Q}}_1$, ${\mathit{Q}}_2$, ${\mathit{Q}}_3$, and  $\mathit{L}$ such that condition (31) holds,

$$\left[\begin{array}{cccccc}-\mu \mathit{P}-\epsilon {\mathit{\Psi }}_1& \mathit{L}{\mathit{B}}_2+\epsilon {\mathit{\Psi }}_2& \mathit{L}& \mathit{L}& 0& \mathit{L}\\ *& {\mathit{B}}_2^T\mathit{P}{\mathit{B}}_2+{\mathit{B}}_2^T{\mathit{Q}}_3^{-1}{\mathit{B}}_2-\epsilon \mathit{I}& 0& 0& {\mathit{B}}_2^T\mathit{P}& 0\\ *& *& -{\mathit{Q}}_1^{-1}& 0& 0& 0\\ *& *& *& -\mathit{P}& 0& 0\\ *& *& *& *& -{\mathit{Q}}_2^{-1}& 0\\ *& *& *& *& *& -{\mathit{Q}}_3^{-1}\end{array}\right]<0$$

(31)

where $\mathit{L}={\mathit{N}}_{{\vartheta }_c}^T\mathit{P}$.

Then the impulse control gain under channel state ${\vartheta }_c$ is derived

$${\mathit{K}}_{{\vartheta }_c}=\left({\mathit{P}}^{-1}{\mathit{L}}^T-{\mathit{A}}_2\right){\overline{\mathit{\zeta }}}_{{\vartheta }_c}^{-1}$$

(32)

Proof of Theorem 2.

In the matrix inequality (15), the known quantities include $\mu$, ${\mathit{\Psi }}_1$, and ${\mathit{\Psi }}_2$ while the unknown variables include $\epsilon$, $\mathit{P}$, ${\mathit{Q}}_1$, ${\mathit{Q}}_2$, ${\mathit{Q}}_3$ and $\mathit{N}$. Given the presence of nonlinear terms in matrix inequality (15), the unknown variables are redefined as $\epsilon$, $\mathit{P}$, ${\mathit{Q}}_1^{-1}$, ${\mathit{Q}}_2^{-1}$, ${\mathit{Q}}_3^{-1}$ and $\mathit{L}={\mathit{N}}^T\mathit{P}$. The nonlinear inequality condition (15) is then transformed into a linear inequality condition (31). According to Equation (13), the impulse control gain in Equation (32) is obtained. □

Remark 2.

The LMI toolkit in MATLAB R2025a is employed to solve the linear inequality conditions (15) and (31). The numerical solution tool internally uses efficient convex optimization algorithms to find a feasible solution. If the toolkit returns a specific feasible solution, these conditions hold. If the toolkit returns an “infeasible” statement, these conditions do not hold. We do not seek to prove the existence of a feasible solution for LMIs from an analytical perspective. In this paper, the parameter $\mu$ can affect the existence of a feasible solution for these conditions. Therefore, if these conditions do not hold, setting value of the parameter  $\mu$ can be altered to find a feasible solution.

5. Result and Discussion

A simulation study was conducted to validate the effectiveness of the proposed impulse quasi-synchronization control algorithm. The control approach proposed in [17] was employed for comparison. Its control input signal for the follower neural networks was defined as

$${\mathit{u}}_{cp}\left(k\right)={\mathit{K}}_{cp}\left[{\mathit{z}}_{\mathit{s}}\left(k\right)-{\mathit{z}}_{\mathit{m}}\left(k\right)\right]$$

(33)

where ${\mathit{K}}_{cp}$ is a constant control gain and its value is given by [17]

$${\mathit{K}}_{cp}=-\left[\begin{array}{ccc}0.7462& 0.0176& -0.0034\\ 0.0200& 0.6760& 0.0201\\ 0.0040& 0.0308& 0.5371\end{array}\right]$$

(34)

It is assumed that the discrete leader–follower neural networks have three communication channels, with parameters set as

$$\begin{gathered} {\mathit{A}}_1=\left[\begin{array}{ccc}0.75& 0& 0\\ 0& 0.67& 0\\ 0& 0& 0.56\end{array}\right],{\mathit{A}}_2=\left[\begin{array}{ccc}0.74& 0& 0\\ 0& 0.65& 0\\ 0& 0& 0.5\end{array}\right] \\ {\mathit{B}}_1=\left[\begin{array}{ccc}0.13& 0.24& 0\\ 0.14& 0.21& 0.23\\ 0& 0.25& 0.23\end{array}\right],{\mathit{B}}_2=\left[\begin{array}{ccc}0.11& 0.26& 0\\ 0.15& 0.23& 0.21\\ 0& 0.24& 0.33\end{array}\right] \end{gathered}$$

Define the uncertain parameter matrices of the leader neural networks,

$$\begin{gathered} \mathrm{\Delta }{\mathit{A}}_1\left(k\right)=\mathrm{diag}\left\{0.1\cos \left(k\right),0.1\cos \left(k\right),0.1\cos \left(k\right)\right\} \\ \mathrm{\Delta }{\mathit{B}}_1\left(k\right)=\mathrm{diag}\left\{0.1\sin \left(k\right),0.1\sin \left(k\right),0.1\sin \left(k\right)\right\} \\ \mathrm{\Delta }{\mathit{A}}_2\left(k\right)=\mathrm{diag}\left\{0.2\cos \left(0.5k\right),0.2\cos \left(0.5k\right),0.2\cos \left(0.5k\right)\right\} \\ \mathrm{\Delta }{\mathit{B}}_2\left(k\right)=\mathrm{diag}\left\{0.2\sin \left(0.5k\right),0.2\sin \left(0.5k\right),0.2\sin \left(0.5k\right)\right\} \end{gathered}$$

All of them satisfy the bounded constraints $‖\mathrm{\Delta }{\mathit{A}}_1\left(k\right)‖\le h_1$, $‖\mathrm{\Delta }{\mathit{A}}_2\left(k\right)‖\le h_2$, $‖\mathrm{\Delta }{\mathit{B}}_1\left(k\right)‖\le h_1$, and $‖\mathrm{\Delta }{\mathit{B}}_2\left(k\right)‖\le h_2$, where $h_1=0.1$ and $h_2=0.2$. Assume that the state of the leader neural networks is constrained by $‖{\mathit{z}}_{\mathit{m}}\left(k\right)‖\le h$, where $h=1$. 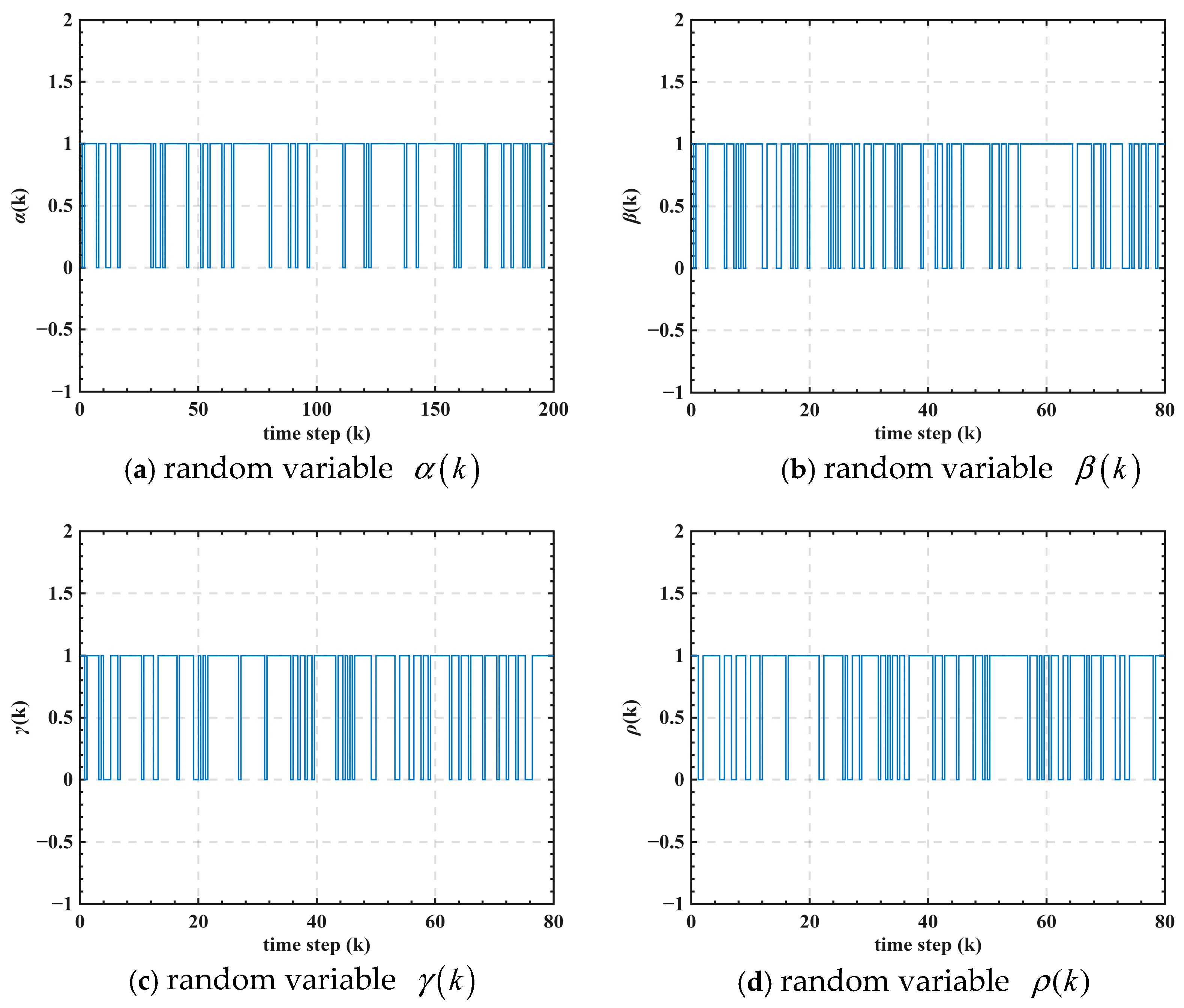The probabilities of the Bernoulli-distributed random variables $\alpha \left(k\right)$, $\beta \left(k\right)$, $\gamma \left(k\right)$, and $\rho (k)$ governing the stochastic occurrence of parameter uncertainties are defined as $\overline{\alpha }=\overline{\beta }=\overline{\gamma }=\overline{\rho }=0.8$. Figure 3 shows the states of the mutually independent random variables $\alpha \left(k\right)$, $\beta \left(k\right)$, $\gamma \left(k\right)$, and $\rho (k)$ whose values indicate the occurrence of parameter uncertainties in leader neural networks.

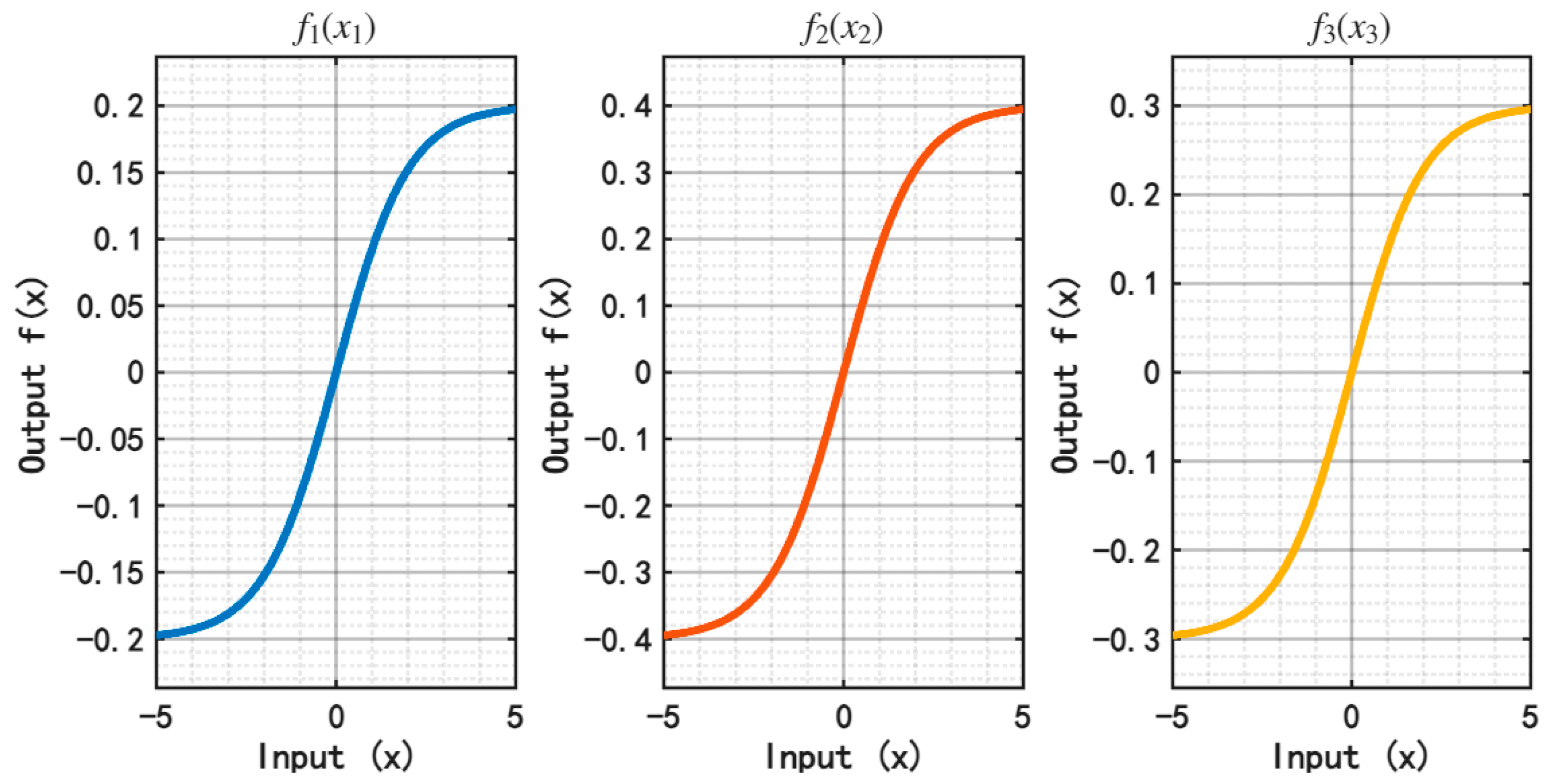
Define the initial states of the discrete leader and follower neural networks as ${\mathit{z}}_{\mathit{m}0}\left(k\right)={\left[\begin{array}{ccc}0.2& 0.2& 0.2\end{array}\right]}^T$, ${\mathit{z}}_{\mathit{s}0}\left(k\right)={\left[\begin{array}{ccc}0.1& 0.1& 0.1\end{array}\right]}^T$. The nonlinear activation function $\mathit{f}\left(\cdot \right)$ of the leader–follower neural networks is assumed as,

$$\begin{array}{c}{f}_1\left(x_1\right)={\displaystyle \frac{0.2(1-e^{-x_1})}{1+e^{-x_1}}}\\ f_2\left(x_2\right)={\displaystyle \frac{0.4(1-e^{-x_1})}{1+e^{-x_2}}}\\ f_3\left(x_3\right)={\displaystyle \frac{0.3(1-e^{-x_1})}{1+e^{-x_3}}}\end{array}$$

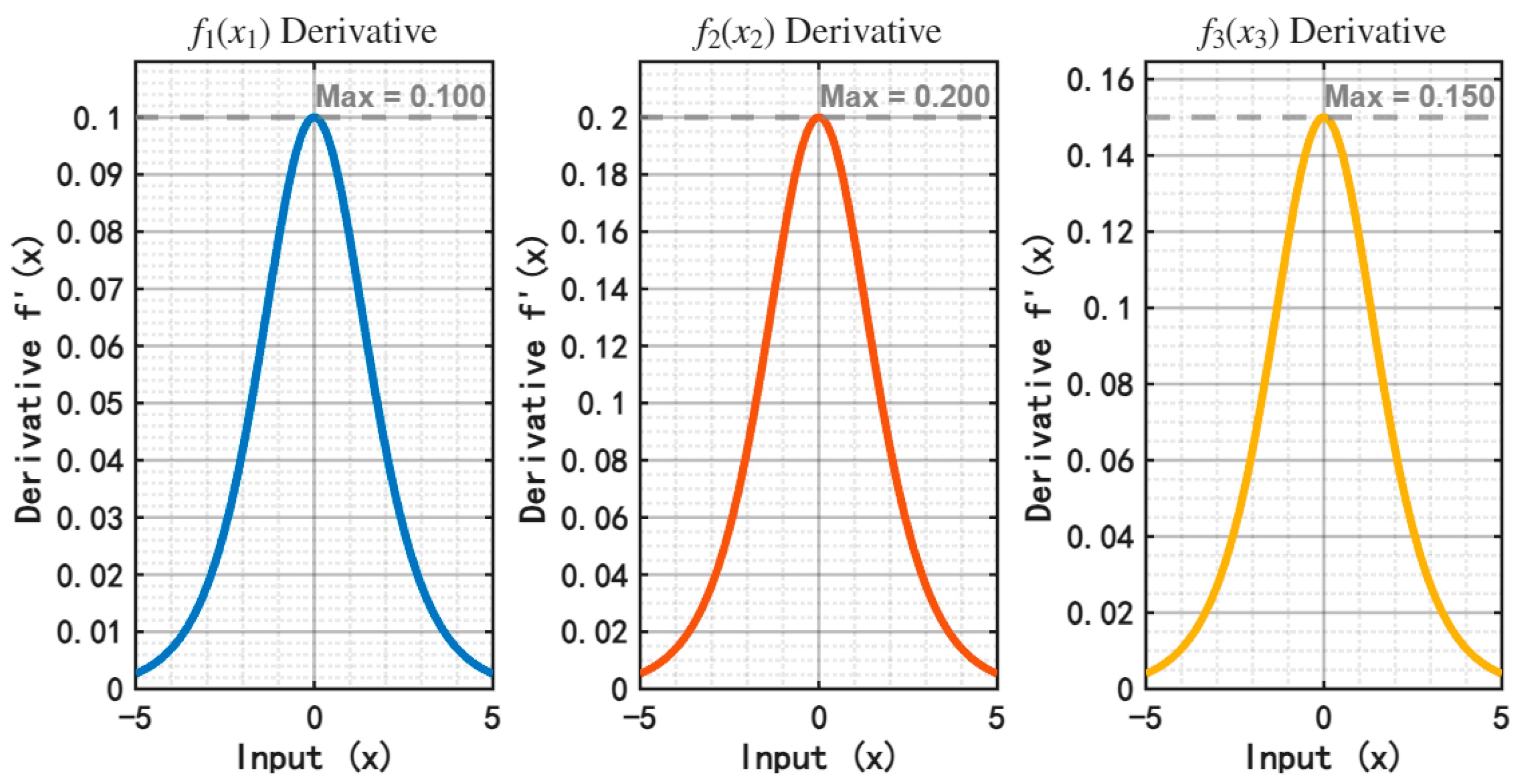
If the derivative of the nonlinear activation function is globally bounded, then the condition shown in Equation (3) is satisfied. The curves of the above nonlinear activation function and its derivative are given in Figure 4 and Figure 5, which indicate ${\alpha }_1={\alpha }_2={\alpha }_3=0$, ${\beta }_1=0.1$, ${\beta }_2=0.2$, ${\beta }_3=0.15$, ${\mathit{\Psi }}_1=\mathrm{diag}\left\{0,0,0\right\}$, and ${\mathit{\Psi }}_2=\mathrm{diag}\left\{0.05,0.1,0.075\right\}$.

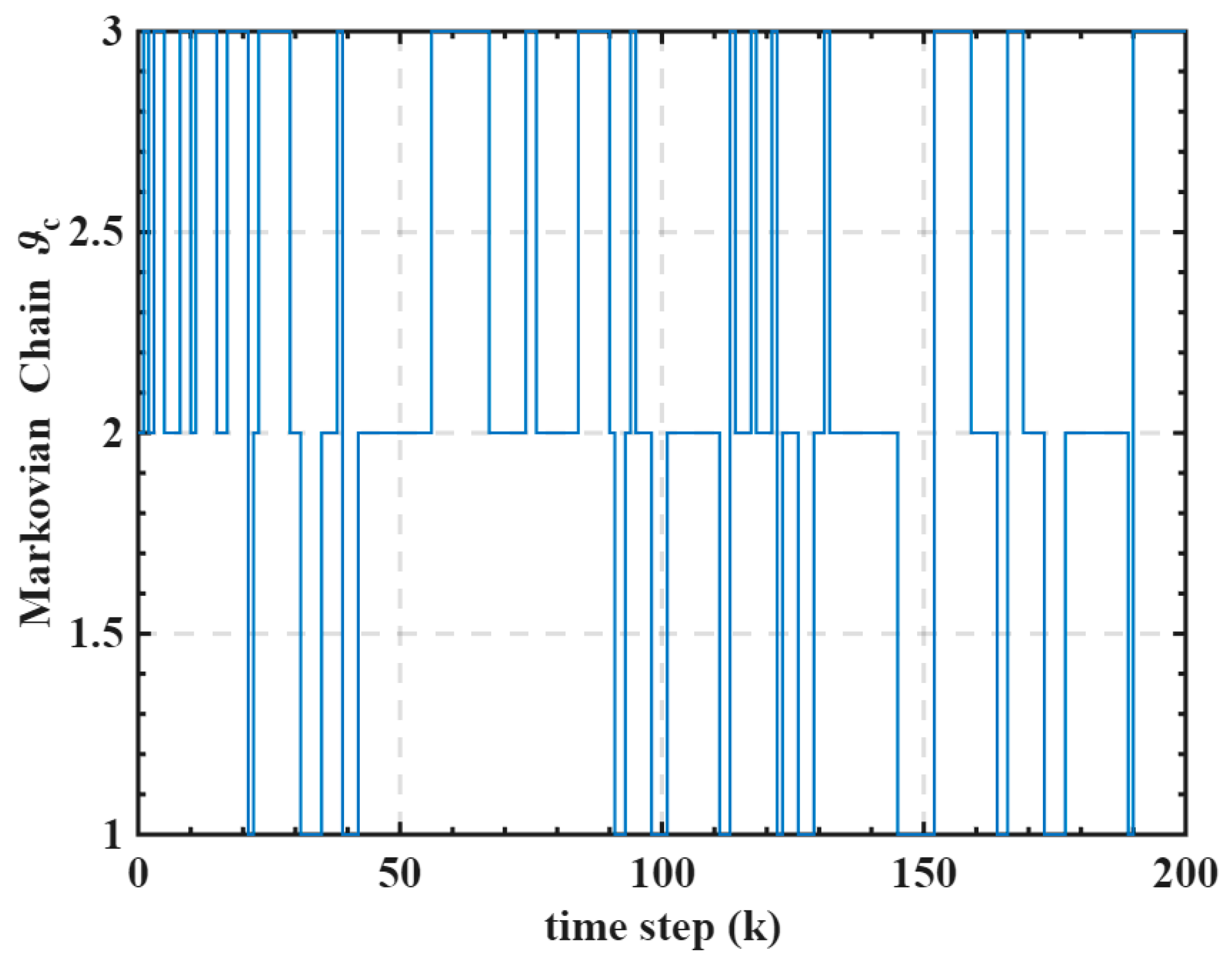
The Markovian channel fading model is assumed to have three states, ${\vartheta }_c\in \left\{1,2,3\right\}$ with $n_c=3$. The state transition probability matrix of the Markovian chain is given by,

$$\mathit{\pi }=\left(\begin{array}{ccc}0.7& 0.2& 0.1\\ 0.1& 0.8& 0.1\\ 0.05& 0.15& 0.8\end{array}\right)$$

Figure 6 depicts the jumping process of the Markovian chain for the channel fading state. States 1, 2, and 3 represent the three channel states corresponding to distinct fading gains, respectively. The statistical characteristics of the channel fading gain, including expectations and variances, under each channel state ${\vartheta }_c$ are defined

$$\begin{array}{c}{\overline{\mathit{\zeta }}}_1=\mathrm{diag}\left\{0.8,0.8,0.8\right\}\\ {\overline{\mathit{\zeta }}}_2=\mathrm{diag}\left\{0.75,0.75,0.75\right\}\\ {\overline{\mathit{\zeta }}}_3=\mathrm{diag}\left\{0.85,0.85,0.85\right\}\\ {\mathit{S}}_1={\mathit{S}}_2={\mathit{S}}_3=\mathrm{diag}\left\{0.0001,0.0001,0.0001\right\}\end{array}$$

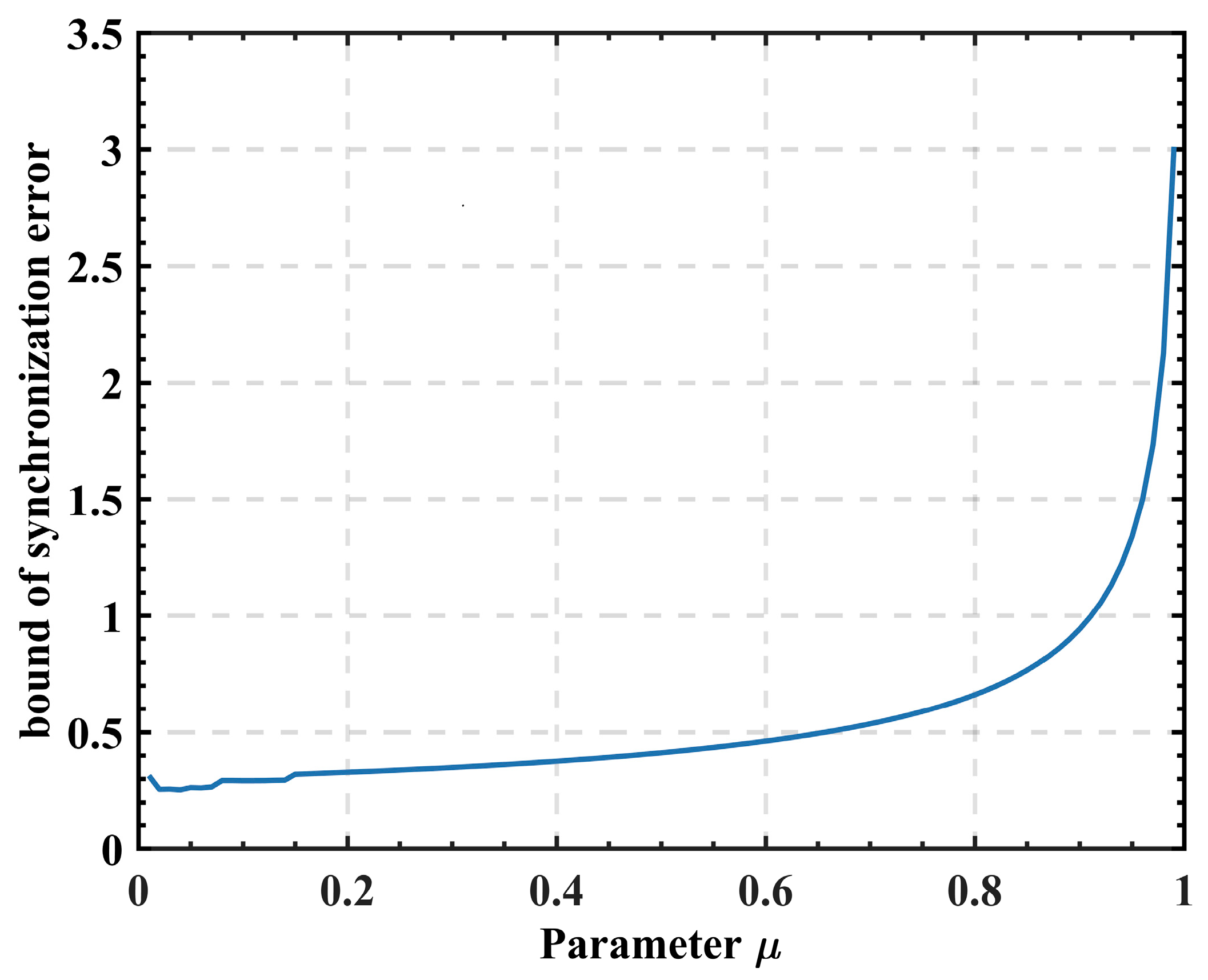
The setting value of the parameter $\mu$ has an impact on stability, error bound, and dynamic performance. The detailed optimization method to determine its value is beyond the scope of this paper. For the current simulation study, the bound of the synchronization error computed by Equation (30) under different values of $\mu$ is depicted in Figure 7. Setting $\mu$ to 0.4 in this paper, the bound of the synchronization error is 0.3762. With the impulse activation interval step set to 2, the impulse control gains under each channel state ${\vartheta }_c$ are obtained

$$\begin{array}{l}{\mathit{K}}_{{\vartheta }_c=1}=\left[\begin{array}{ccc}-0.7576& 0.0021& 0.0076\\ 0.0028& -0.6472& 0.0072\\ 0.0079& 0.0065& -0.4547\end{array}\right]\\ {\mathit{K}}_{{\vartheta }_c=2}=\left[\begin{array}{ccc}-0.8081& 0.0022& 0.0081\\ 0.0030& -0.6903& -0.0077\\ 0.0084& 0.0069& -0.4850\end{array}\right]\\ {\mathit{K}}_{{\vartheta }_c=3}=\left[\begin{array}{ccc}-0.7131& 0.0020& 0.0072\\ 0.0027& -0.6091& 0.0068\\ 0.0074& 0.0061& -0.4279\end{array}\right]\end{array}$$

.

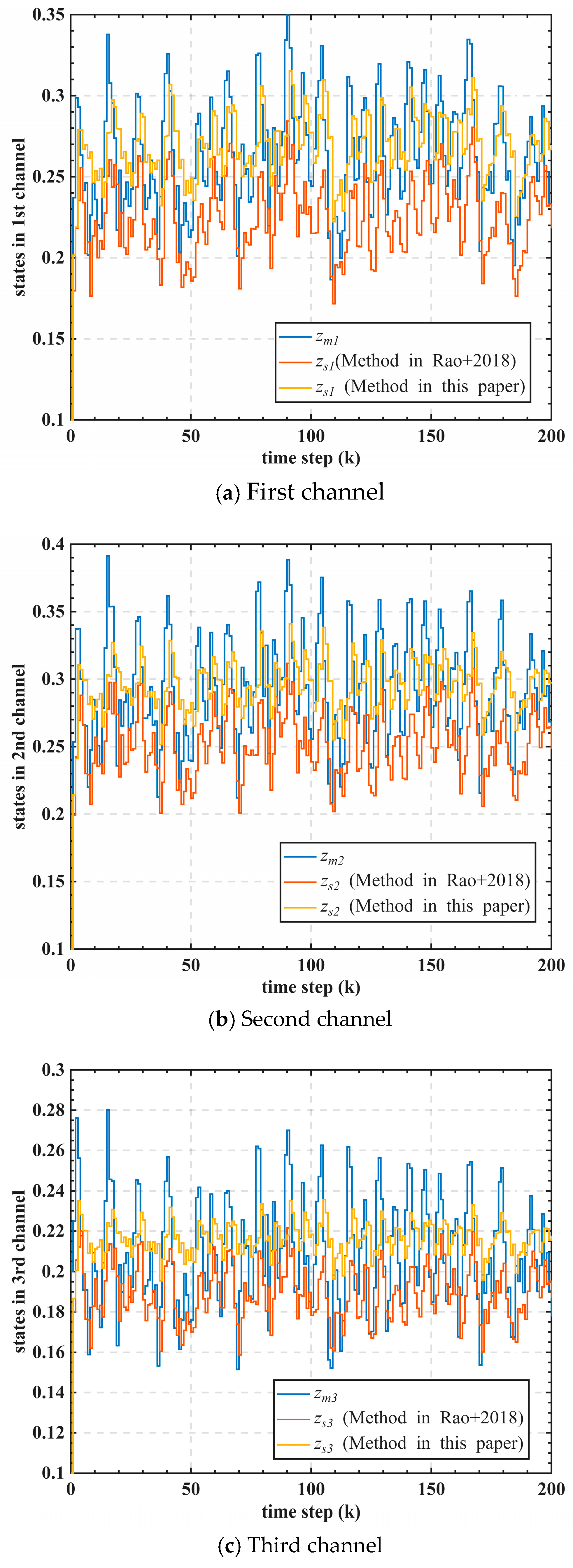
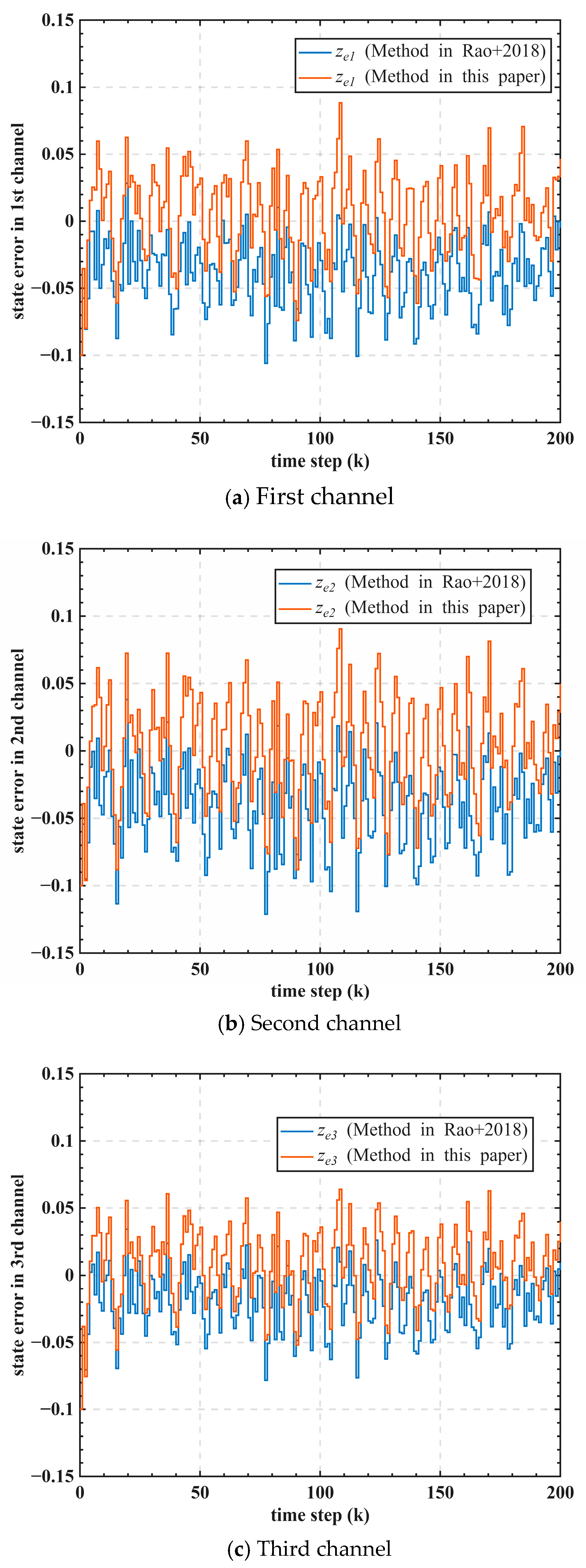
Detailed comparisons on control performance between the method in [17] and the method in this paper are shown in Figure 8, Figure 9, Figure 10 and Figure 11. As shown in Figure 8 and Figure 9, a steady-state tracking error in each channel is observed for the method in [17] because it does not consider the Markovian jumping fading effect. By adaptively adjusting the control gain according to the detected Markovian fading state, the approach proposed in this paper effectively eliminates the steady tracking error caused by the time-varying fading gains. 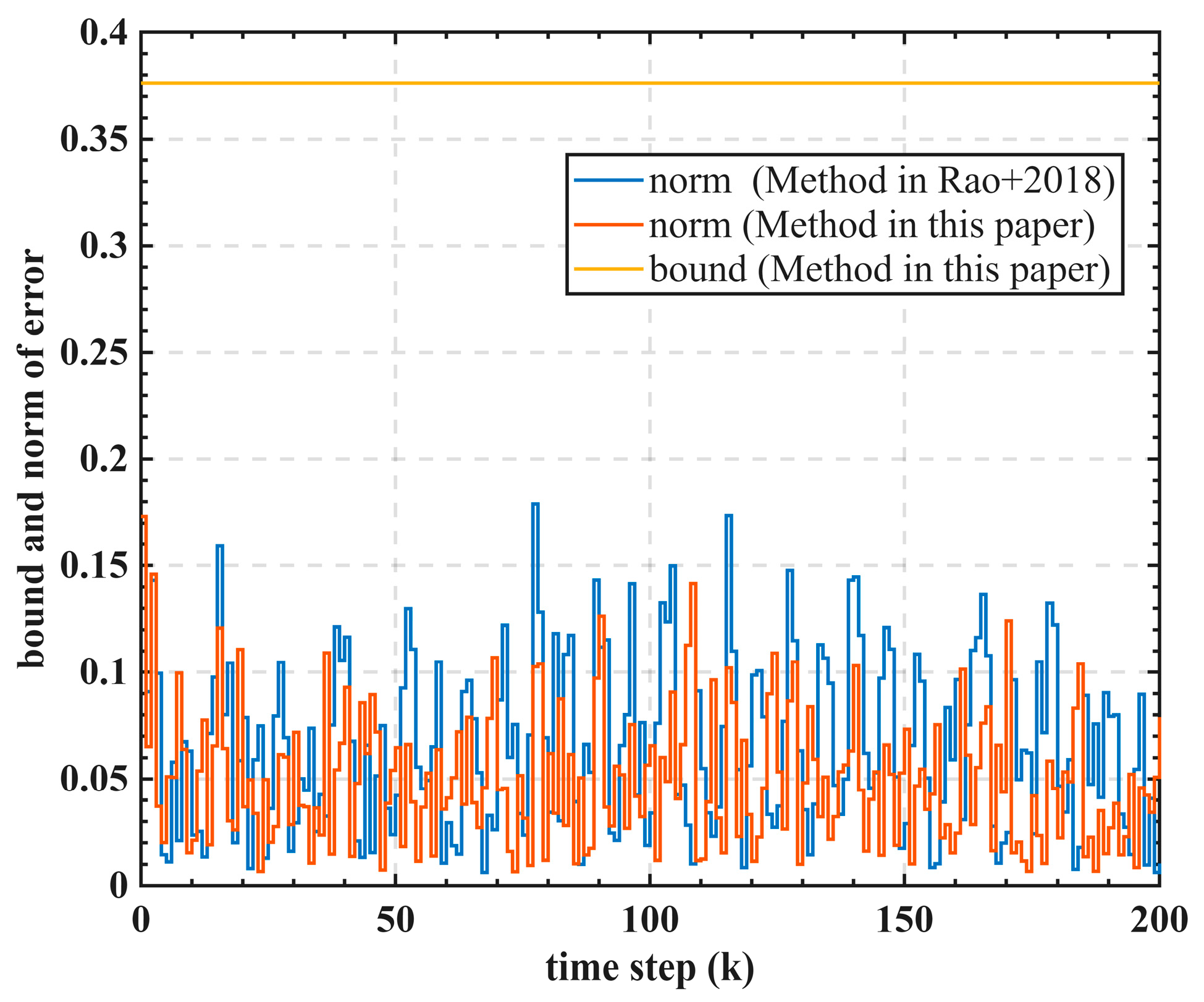Figure 10 presents the bound of the synchronization error and its norm considering all three channels. It is evident that the synchronization error for each communication channel is controlled within 0.1. The error vector bound is computed as 0.3762, and its norm consistently remains within this bound, demonstrating that the proposed impulse control algorithm achieves quasi-synchronization for the leader–follower states. The norm of the synchronization error using the present method is generally lower than that of the method in [17]. 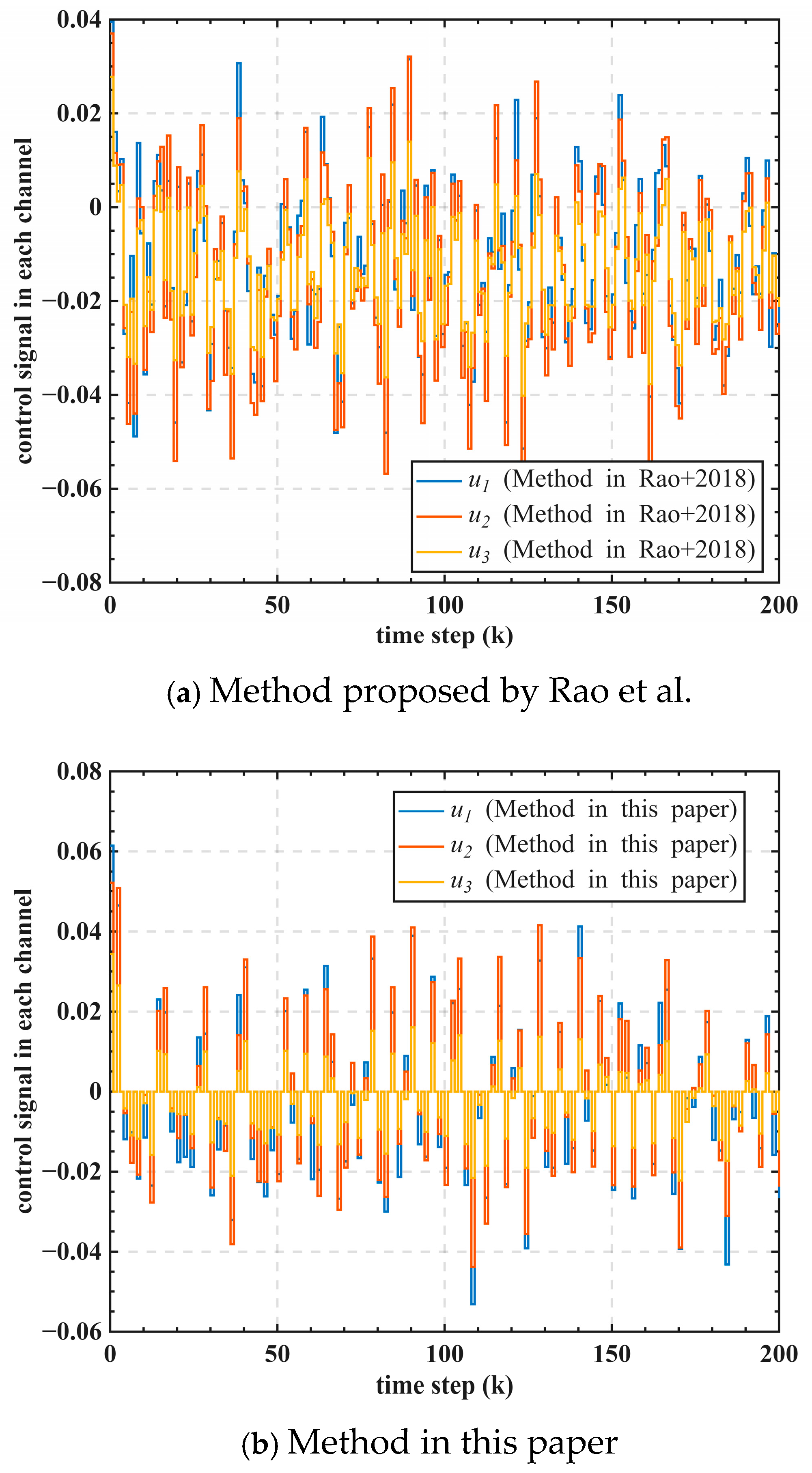Figure 11 illustrates the control signals for each communication channel in the follower neural networks. The average norms of the synchronization error and control input signals are summarized in

Table 1. The average norms of synchronization error and control input signals compared with the method proposed by Rao et al. [17].

	Method in [17]	Method in This Paper
The average norm of synchronization error	0.0650	0.0494 (−24.00%)
The average norm of control input signal u1	4.4367 × 10−4	2.4884 × 10−4 (−43.91%)
The average norm of control input signal u2	5.7378 × 10−4	2.4008 × 10−4 (−58.16%)
The average norm of control input signal u3	3.1088 × 10−4	6.0495 × 10−5 (−80.54%)
The average norm of control input signal u	4.4278 × 10−4	1.8314 × 10−4 (−58.64%)

. Compared with an existing method [17], the proposed approach consumes less control energy but achieves better performance in terms of synchronization error. The average norms of the synchronization error and the control input signal are reduced by 24.00% and 58.64%, respectively.

6. Conclusions

This paper deeply investigates the quasi-synchronization control problem for the discrete-time leader–follower neural networks subject to randomly occurring parameter uncertainties and stochastic channel fading. Discrete leader–follower neural networks are constructed using the state-space method. A finite-state Markovian channel model is used to describe the transitions among communication channel fading states, and a Bernoulli process is employed to depict the randomly occurring parameter uncertainties. Based on linear matrix inequalities and the Lyapunov stability principle, an intermittent impulsive control strategy is designed for the follower neural networks. Crucially, the impulsive control gain is automatically adjusted according to the channel fading states. Furthermore, the bound of the synchronization error is rigorously derived as well. Through modeling and simulation of leader–follower neural networks with three communication channels, it is verified that the proposed impulse control strategy can effectively suppress the synchronization error caused by parameter uncertainties and Markovian channel fading, therefore ensuring mean-square boundedness.

The proposed method based on linear matrix inequalities and the Lyapunov stability principle can be extended to coupled nonlinear systems and ensure the complete state quasi-synchronization. If the coupling gain in coupled nonlinear systems is a controllable parameter, the linear matrix inequalities in this paper can be solved to design the coupling gain for the desired synchronization. For phase/frequency synchronization, defining the output as a phase map rather than the full state enables practical phase/frequency tracking with a computable mean-square error bound.

However, several aspects require further improvement in future work. First, the influences of the impulse activation interval step and the Lyapunov parameter $\mu$ on quasi-synchronization performance, error bound, and control energy consumption should be investigated and optimized. Moreover, the present approach relies on a known model structure and parameters. In addition, the Lyapunov stability principle is a little conservative. Therefore, developing a less conservative data-driven control method for leader–follower neural networks is a promising direction.