Hybrid Deep-Ensemble Network with VAE-Based Augmentation for Imbalanced Tabular Data Classification
Abstract
1. Introduction
- Cross-domain imbalance handling. We investigated the effectiveness of VAE-based minority synthesis and hybrid ensemble learning across manufacturing, finance, and healthcare using publicly available imbalanced datasets.
- VAE-based synthetic NG generation. For each dataset, we trained a variational autoencoder on minority (NG) samples to generate additional synthetic data, enhancing class balance and improving rare-class recall.
- Comprehensive evaluation and ablation. Beyond standard metrics, we conducted focal-loss [25] ablations, and ensemble-weight sensitivity analyses, and we further contrasted VAE with SMOTE/ADASYN under identical protocols, quantified synthetic-data fidelity (TSTR, two-sample discriminability ROC AUC [26], MMD), ablated correlation-aware seriation and positional embeddings (PE), and profiled efficiency/latency to guide deployment.
Related Works
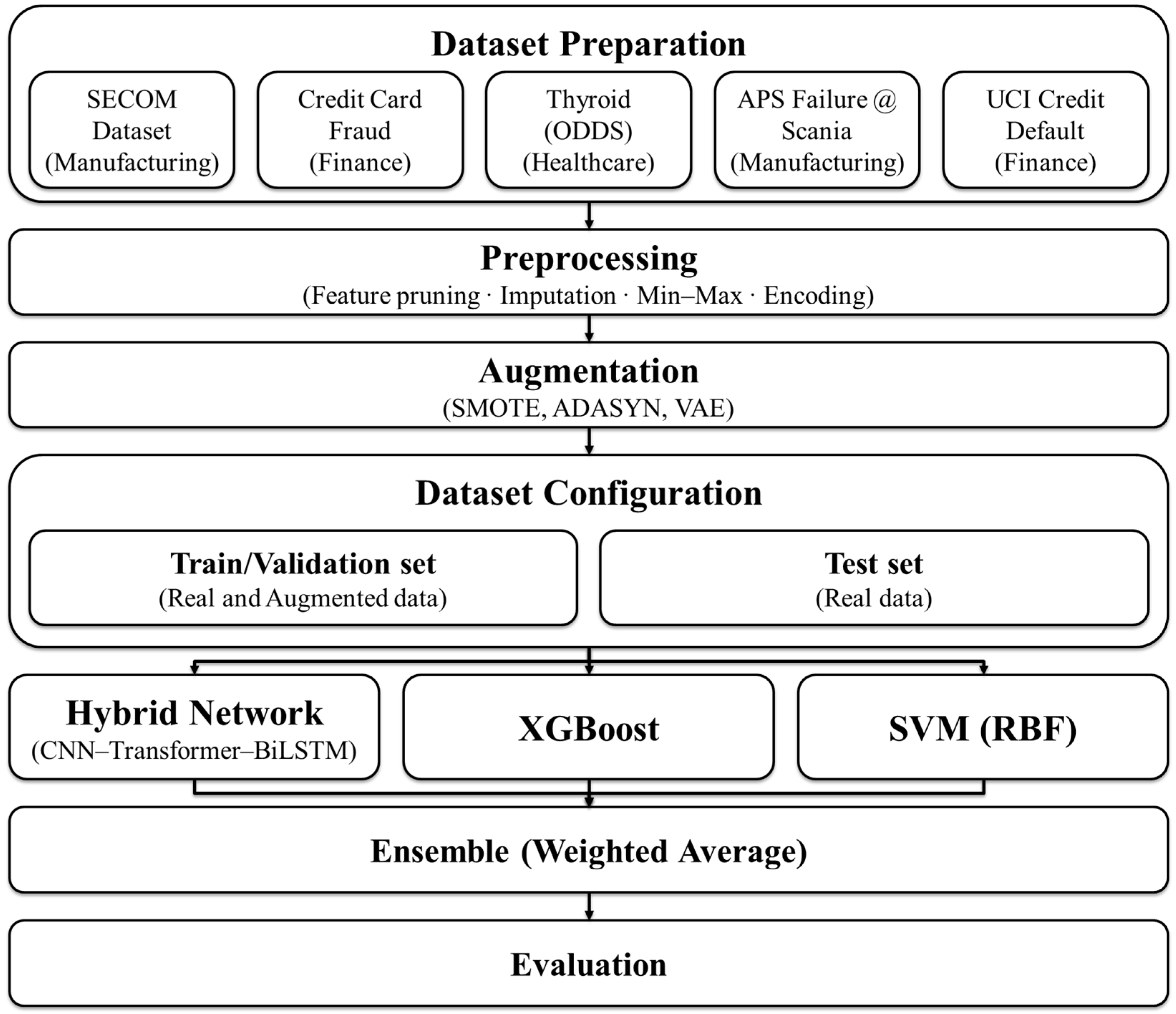
2. Materials and Methods
2.1. Dataset Description and Preprocessing
- SECOM [17] (manufacturing): A high-dimensional dataset from a semiconductor manufacturing process, containing 1563 samples and 590 sensor features. After preprocessing (feature pruning, missing value imputation, and min–max normalization), 25 features were retained. The dataset is highly imbalanced, with only ~6.6% defective (“NG”) samples.
- Credit Card Fraud [18] Detection (CREDIT, finance): Originally comprising over 280,000 transactions, we sampled 20,000 normal and 1000 fraud (NG) instances to simulate a manageable but still imbalanced scenario. The 21k-row scale preserved rare-event conditions (positivity ≈ 4.76%) while keeping repeated ablations and grid searches (augmentation × focal loss [25] × ensemble weights) tractable. Specifically, equalizing effective training size across domains prevented the Credit Card set from dominating hyperparameter selection and enabled methodologically symmetric comparisons with other datasets. The dataset includes 30 numerical features (V1–V28 PCA components, amount, and time) and a binary target column (“Label”).
- Thyroid [19] Disease (THYROID, healthcare): The dataset includes 3772 patient records with 21 physiological features. Anomalous (outlier) instances—based on diagnosis—are labeled as “NG” (1), while normal patients are labeled as “OK” (0). All features were normalized to the {0, 1} range.
- APS Failure at Scania Trucks [20] (APS, manufacturing): We included the APS dataset, a heavily imbalanced predictive maintenance [34,35] benchmark focusing on air pressure system (APS) failures in heavy-duty trucks. The official training set contained 60,000 examples (1000 positives; 59,000 negatives) with 171 anonymized numeric features; the test set contained 16,000 examples. Missing values were encoded as the string “na” in the raw CSV files. We converted “na” to NaN, fit median imputation and standardization on the training split only and mapped the positive label to y = 1 (= APS failure).
- Default of Credit Card Clients [21] (UCI, finance): We also added the UCI Credit Default dataset containing 30,000 clients and 23 features (demographics, repayment history, bill statements, previous payments). The binary response was default payment next month, with coding Yes = 1, No = 0. We dropped the identifier (ID), one-hot encoded low-cardinality categorical variables as needed, and standardized continuous features using training-split statistics. All preprocessing, augmentation, and model selection were confined to the training/validation data; the test set remained untouched.
- Missing value handling: feature-wise mean imputation for datasets with NaNs.
- Normalization: min–max scaling was applied to standardize feature ranges.
- Label mapping: all datasets were binarized, with 0 = OK, 1 = NG.
- Train/test split: a stratified 80/20 split ensured class distribution was preserved in both training and testing subsets.
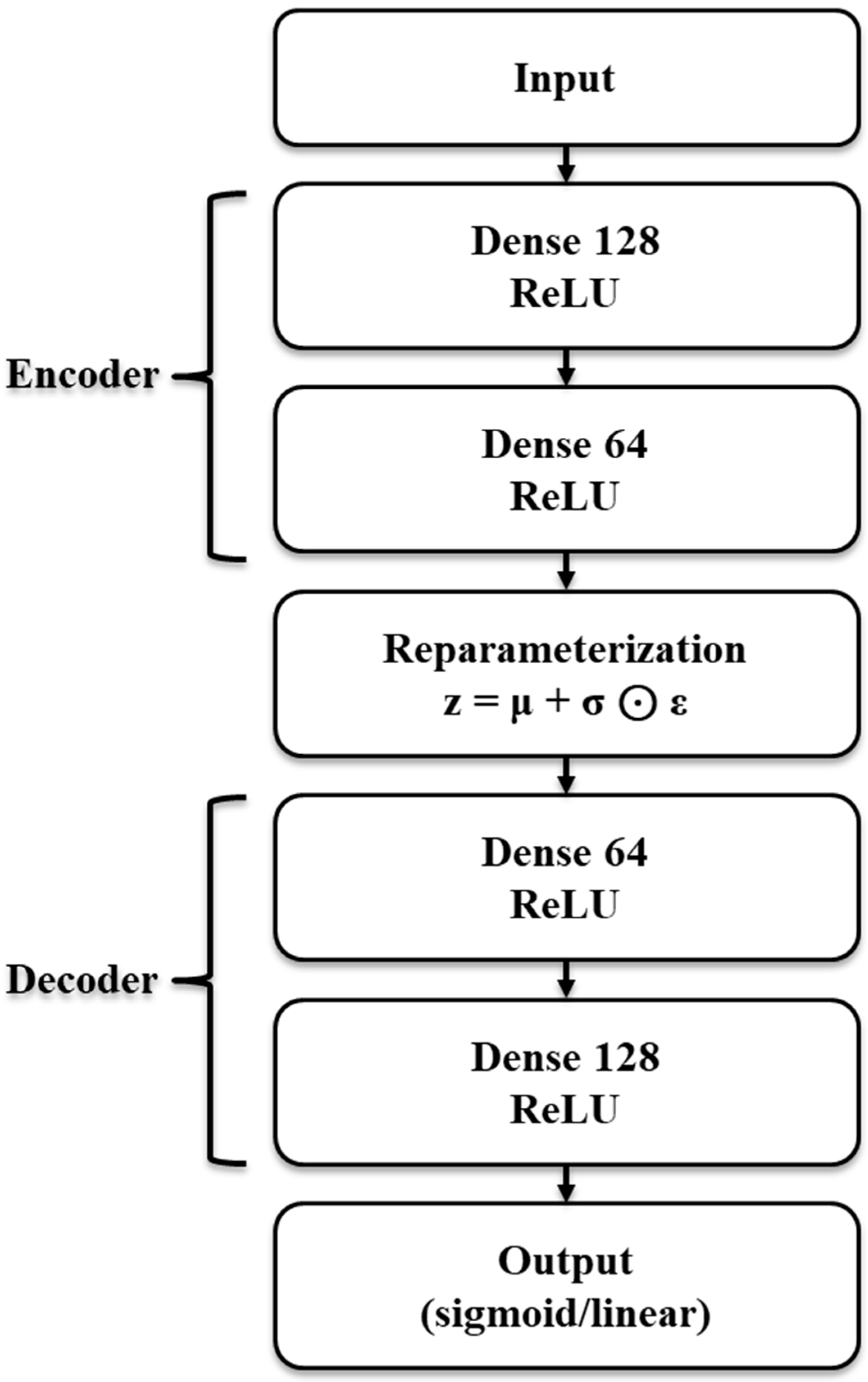
2.2. VAE-Based Augmentation and Interpolative Baselines
2.3. Correlation-Aware Seriation
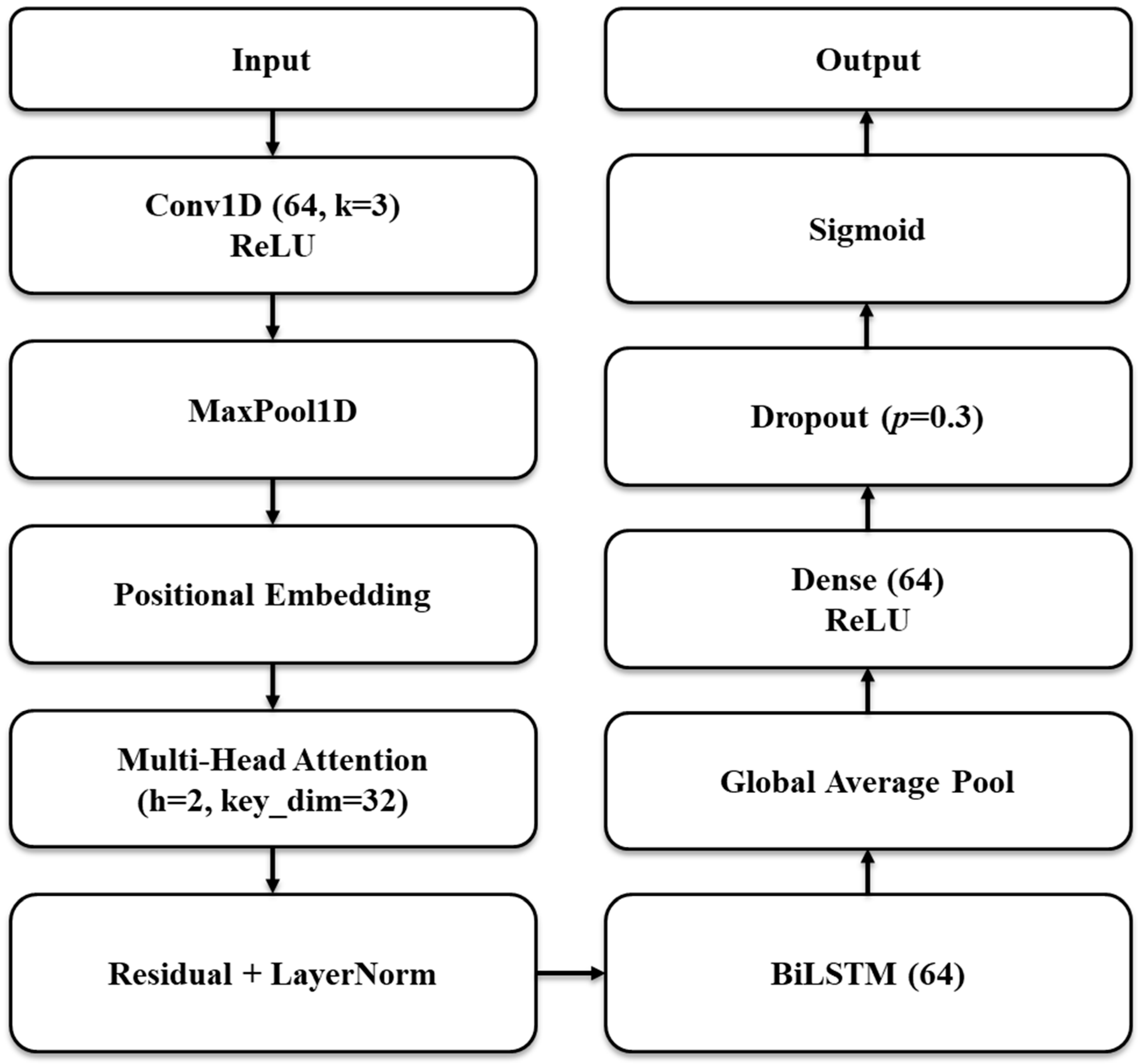
2.4. Model Architecture: CNN–Transformer–BiLSTM–Hybrid Network (DNN)
- Input layer: the normalized inputs were reshaped to an appropriate sequence-like layout for each dataset to enable convolution and attention.
- Convolutional module: A 1D convolutional layer with 64 filters (kernel size = 3) and ReLU activation was used to capture local dependencies and micro-patterns across adjacent features. This was followed by max pooling to reduce spatial dimensionality.
- Positional embedding (PE): Given the lack of inherent temporal structure in the data, learnable positional embeddings were added to introduce ordering and location-specific inductive bias. We therefore evaluated PE on/off cases.
- BiLSTM layer: a bidirectional LSTM [15] with 64 units was stacked on top to further capture sequential dynamics from both directions.
- Output layer: after a fully connected layer and dropout (p = 0.3), a sigmoid output unit was used to perform binary classification.
- Channel width (64), transformer hidden size (64), and BiLSTM units (64) were selected from {32, 64, 128} by maximizing validation AUPRC under a fixed FLOPs budget; this struck a stable accuracy–latency balance.
2.5. Training Procedure with Focal Loss
2.6. Ensemble Learning with XGBoost and SVM
2.7. Evaluation, Visualization, and Synthetic-Sample Fidelity Analysis
- Train-on-synthetic, test-on-real (TSTR): we trained a simple classifier on the synthetic minority + real majority from the training split and evaluated on real held-out data.
- Two-sample discriminability area under the curve (AUC): we trained a binary discriminator to distinguish real vs. synthetic minority samples from the training split and measured ROC AUC on a held-out validation fold. Values near 0.5 indicate the discriminator could not tell them apart, suggesting higher fidelity.
- Maximum Mean Discrepancy (MMD2): we computed the squared kernel MMD2 between real and synthetic minority sets.
3. Results
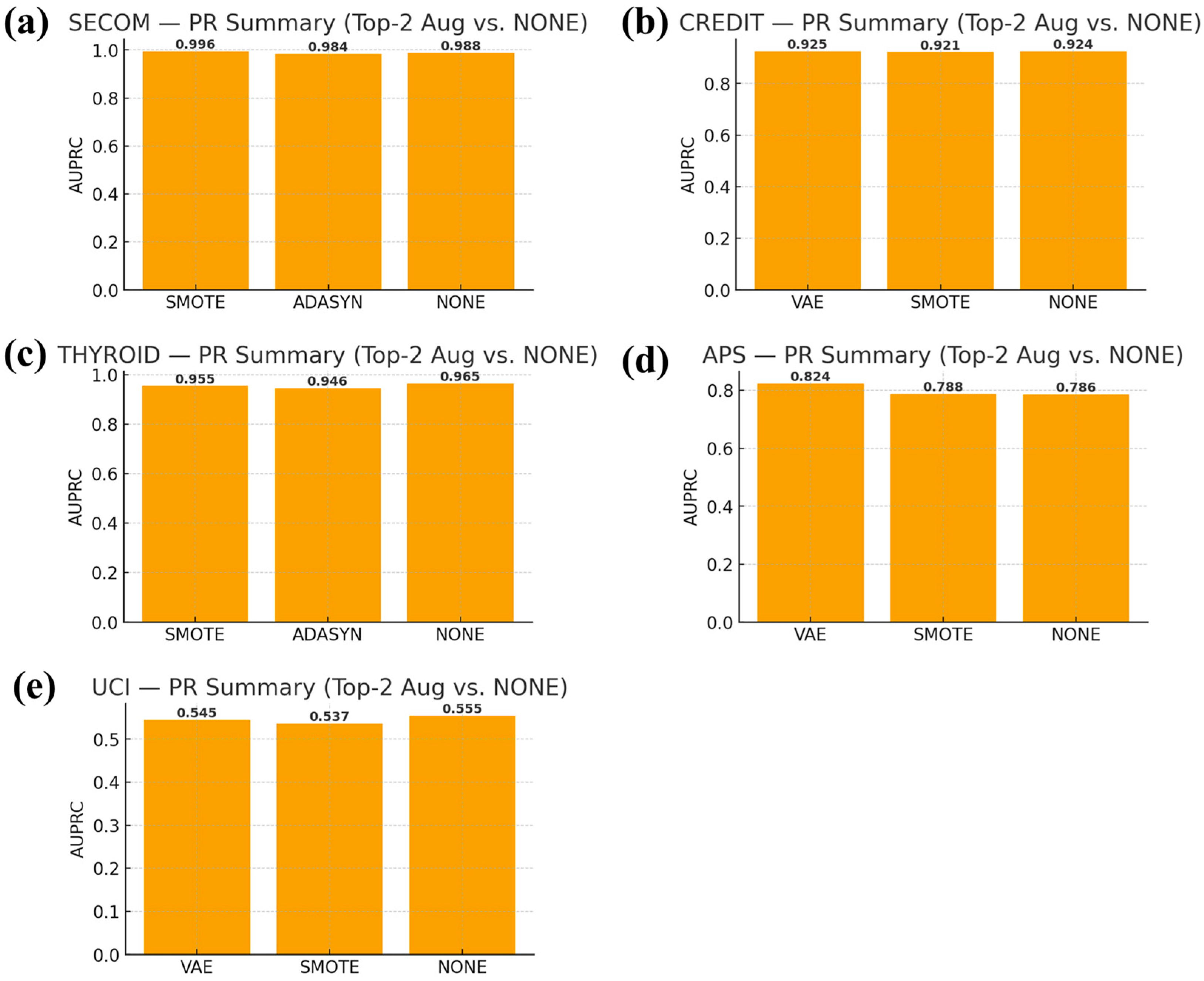
3.1. Main Comparison with Augmentation
- APS (manufacturing): VAE achieved the best AUPRC (0.824), outperforming SMOTE by +3.66 pp.
- CREDIT (finance): VAE was competitive, with +0.10 pp AUPRC over None.
- SECOM [17] (manufacturing): SMOTE dominated (AUPRC 0.996), consistent with its stability on smoother manifolds.
- THYROID (healthcare) and UCI (finance): no augmentation (None) was preferable, suggesting that interpolation or generation did not improve already strong baselines.
3.2. Positional Embedding and Seriation Ablation
- Gains were largest on APS (+6.56 pp) and modest on CREDIT/THYROID/UCI (+0.6–1.4 pp).
- SECOM [17] showed a slight decrease (−0.30 pp) with PE, indicating that sequence inductive bias is not universally beneficial on all tabular structures.
3.3. Quantitative Synthetic-Data Fidelity
- TSTR (train-on-synthetic, test-on-real) AUPRC. Higher values indicate synthetic samples supported downstream discrimination.
- Two-sample discriminability ROC AUC. Values near 0.5 imply that the discriminator could not tell real from synthetic samples (indicating higher fidelity).
- Kernel MMD2. Lower values indicate closer distributions.
3.4. Local Hyperparameter Selection
3.5. Ensemble Weight Optimization Across Datasets
3.6. Threshold-Dependent Evaluation
3.7. Efficiency and Deployability
- THYROID 5.1 ms;
- UCI 8.1 ms;
- CREDIT 8.3 ms;
- SECOM 33 ms;
- APS 66 ms.
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Definition |
| BiLSTM | Bidirectional Long Short-Term Memory |
| CNN | Convolutional neural network |
| CREDIT | Credit Card Fraud dataset |
| F1 | F1-score (harmonic mean of precision and recall) |
| FL | Focal Loss |
| KL (KLD) | Kullback–Leibler Divergence |
| NG | Not Good (defective class) |
| OK | Normal/acceptable class |
| ReLU | Rectified Linear Unit |
| SECOM | Semiconductor manufacturing dataset (UCI) |
| SVM | Support Vector Machine |
| THYROID | Thyroid disease dataset (UCI) |
| VAE | Variational Autoencoder |
| XGB (XGBoost) | Extreme Gradient Boosting |
| AUPRC | Area Under the Precision–Recall Curve |
| ROC AUC | Area Under the Receiver Operating Characteristic Curve |
| PR | Precision Recall |
| PE | Positional embedding |
| TSTR | Train-on-synthetic, test-on-real |
| MMD2 | Squared Maximum Mean Discrepancy |
| APS | Air Pressure System failure dataset (Scania Trucks) |
| UCI | University of California, Irvine Machine Learning Repository |
| SMOTE | Synthetic Minority Over-sampling Technique |
| ADASYN | Adaptive Synthetic Sampling |
| CI | Confidence Interval |
| pp | Percentage point |
| RBF | Radial Basis Function (kernel) |
References
- He, H.; Garcia, E.A. Learning from Imbalanced Data. IEEE Trans. Knowl. Data Eng. 2009, 21, 1263–1284. [Google Scholar] [CrossRef]
- Johnson, J.M.; Khoshgoftaar, T.M. Survey on Deep Learning with Class Imbalance. J. Big Data 2019, 6, 27. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-Sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive Synthetic Sampling Approach for Imbalanced Learning. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IJCNN), Hong Kong, China, 1–8 June 2008; pp. 1322–1328. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-encoding Variational Bayes. arXiv 2014, arXiv:1312.6114. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the Advances in Neural Information Processing Systems 27 (NeurIPS 2014), Montreal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Esteban, C.; Hyland, S.L.; Rätsch, G. Real-Valued (Medical) Time Series Generation with Recurrent Conditional GANs. arXiv 2017, arXiv:1706.02633. [Google Scholar] [CrossRef]
- Xu, L.; Skoularidou, M.; Cuesta-Infante, A.; Veeramachaneni, K. Modeling Tabular Data Using Conditional GAN. arXiv 2019, arXiv:1907.00503. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Kotelnikov, A.; Baranchuk, D.; Rubachev, I.; Babenko, A. TabDDPM: Modeling Tabular Data with Diffusion Models. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS 2023), New Orleans, LA, USA, 10–16 December 2023. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-Based Learning Applied to Document Recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Proceedings of the Advances in Neural Information Processing Systems 30 (NeurIPS 2017), Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’16), San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Gretton, A.; Borgwardt, K.M.; Rasch, M.J.; Schölkopf, B.; Smola, A.J. A Kernel Two-Sample Test. J. Mach. Learn. Res. 2012, 13, 723–773. [Google Scholar]
- UCI—SECOM Dataset. UCI Machine Learning Repository. 2008. Dataset. Available online: https://archive.ics.uci.edu/dataset/179/secom (accessed on 18 September 2025).
- Kaggle. Credit Card Fraud Detection Dataset. Available online: https://www.kaggle.com/mlg-ulb/creditcardfraud (accessed on 18 September 2025).
- Rayana, S. Thyroid Disease (ODDS). In Outlier Detection DataSets (ODDS); Stony Brook University: New York, NY, USA, 2016; Dataset; Available online: https://shebuti.com/thyroid-disease-dataset/ (accessed on 18 September 2025).
- UCI—APS Failure at Scania Trucks. UCI Machine Learning Repository. 2016. Dataset. Available online: https://www.kaggle.com/datasets/uciml/aps-failure-at-scania-trucks-data-set (accessed on 18 September 2025).
- UCI—Default of Credit Card Clients. UCI Machine Learning Repository. 2016. Dataset. Available online: https://archive.ics.uci.edu/dataset/350/default+of+credit+card+clients (accessed on 18 September 2025).
- Huang, X.; Khetan, A.; Cvitkovic, M.; Karnin, Z. TabTransformer: Tabular Data Modeling Using Contextual Embeddings. arXiv 2020, arXiv:2012.06678. [Google Scholar] [CrossRef]
- Schuster, M.; Paliwal, K.K. Bidirectional Recurrent Neural Networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Gorishniy, Y.; Rubachev, I.; Khrulkov, V.; Babenko, A. Revisiting Deep Learning Models for Tabular Data. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS 2021), Virtual, 6–14 December 2021. [Google Scholar]
- Lin, T.-Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal Loss for Dense Object Detection. In Proceedings of the IEEE International Conference on Computer Vision (ICCV 2017), Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar] [CrossRef]
- Saito, T.; Rehmsmeier, M. The Precision–Recall Plot Is More Informative than the ROC Plot When Evaluating Binary Classifiers on Imbalanced Datasets. PLoS ONE 2015, 10, e0118432. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Cisse, M.; Dauphin, Y.N.; Lopez-Paz, D. mixup: Beyond Empirical Risk Minimization. In Proceedings of the International Conference on Learning Representations (ICLR 2018), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Yun, S.; Han, D.; Oh, S.J.; Chun, S.; Choe, J.; Yoo, Y. CutMix: Regularization Strategy to Train Strong Classifiers with Localizable Features. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV 2019), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 6023–6032. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, H.; Da, F.; Bai, L.; Wu, G. PointCutMix: Regularization Strategy for Point Clouds. Neurocomputing 2022, 488, 11–24. [Google Scholar] [CrossRef]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased Boosting with Categorical Features. In Proceedings of the 2018 Conference on Neural Information Processing Systems (NeurIPS 2018), Montreal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Arik, S.Ö.; Pfister, T. TabNet: Attentive Interpretable Tabular Learning. Proc. AAAI Conf. Artif. Intell. 2021, 35, 6679–6687. [Google Scholar] [CrossRef]
- Somepalli, G.; Goldblum, M.; Schwarzschild, A.; Bruss, C.B.; Goldstein, T. SAINT: Improved Neural Networks for Tabular Data via Row Attention and Contrastive Pre-Training. arXiv 2021, arXiv:2106.01342. [Google Scholar] [CrossRef]
- Hollmann, N.; Müller, S.; Eggensperger, K.; Hutter, F. TabPFN: A Transformer That Solves Small Tabular Classification Problems in a Second. In Proceedings of the 2022 Conference on Neural Information Processing Systems (NeurIPS 2022), New Orleans, LA, USA, 28 November–9 December 2022. [Google Scholar]
- Radicioni, L.; Bono, F.M.; Cinquemani, S. Vibration-Based Anomaly Detection in Industrial Machines: A Comparison of Autoencoders and Latent Spaces. Machines 2025, 13, 139. [Google Scholar] [CrossRef]
- Alsaif, M.; Alaqel, H.; Almalaq, A.; Alharbi, R.; Alshahrani, M.; Pasha, M. A Novel Data Augmentation-Based Brain Tumor Detection Using Convolutional Neural Network. Appl. Sci. 2022, 12, 3773. [Google Scholar] [CrossRef]
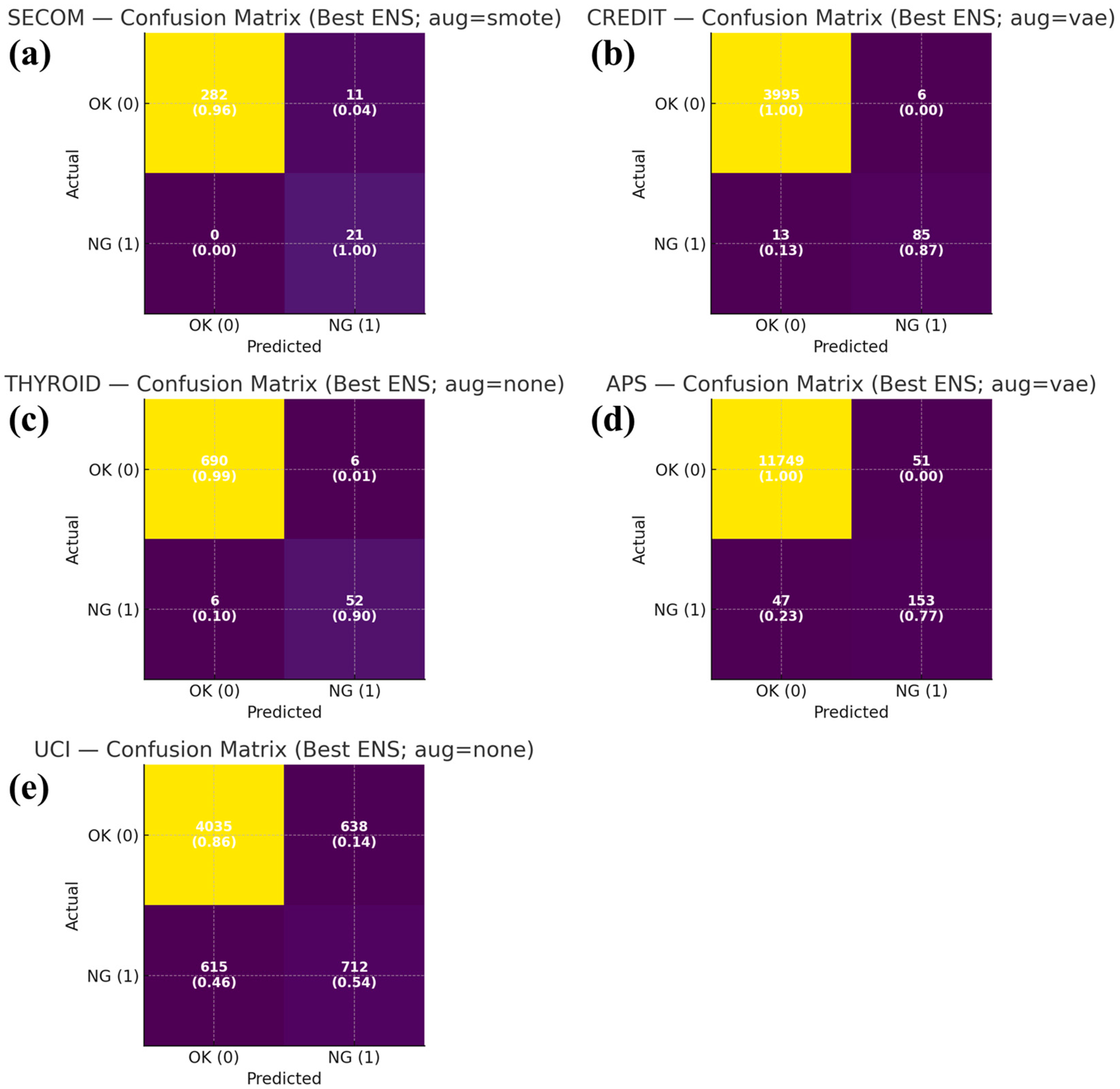
| Dataset | Augmentation | AUPRC | F1 (NG) | TN | FP | FN | TP | Selected Weights (XGB, SVM, DNN) |
|---|---|---|---|---|---|---|---|---|
| SECOM | None | 0.99 | 0.00 | 293 | 0 | 21 | 0 | (0.00, 0.00, 1.00) |
| SECOM | SMOTE | 1.00 | 0.79 | 282 | 11 | 0 | 21 | (0.00, 0.00, 1.00) |
| SECOM | ADASYN | 0.98 | 0.79 | 282 | 11 | 0 | 21 | (0.00, 0.00, 1.00) |
| SECOM | VAE | 0.97 | 0.00 | 293 | 0 | 21 | 0 | (0.00, 0.10, 0.90) |
| SECOM | Best vs. Runner-up ΔAUPRC (pp) | 0.75 | ||||||
| CREDIT | None | 0.92 | 0.92 | 3998 | 3 | 12 | 86 | (0.00, 0.00, 1.00) |
| CREDIT | SMOTE | 0.92 | 0.74 | 3948 | 53 | 9 | 89 | (0.00, 0.00, 1.00) |
| CREDIT | ADASYN | 0.92 | 0.89 | 3991 | 10 | 11 | 87 | (0.00, 0.95, 0.05) |
| CREDIT | VAE | 0.93 | 0.90 | 3995 | 6 | 13 | 85 | (0.00, 0.00, 1.00) |
| CREDIT | Best vs. Runner-up ΔAUPRC (pp) | 0.10 | ||||||
| THYROID | None | 0.96 | 0.90 | 690 | 6 | 6 | 52 | (0.80, 0.00, 0.20) |
| THYROID | SMOTE | 0.96 | 0.86 | 681 | 15 | 3 | 55 | (0.00, 0.00, 1.00) |
| THYROID | ADASYN | 0.95 | 0.85 | 687 | 9 | 8 | 50 | (0.50, 0.50, 0.00) |
| THYROID | VAE | 0.94 | 0.89 | 689 | 7 | 6 | 52 | (1.00, 0.00, 0.00) |
| THYROID | Best vs. Runner-up ΔAUPRC (pp) | 0.97 | ||||||
| APS | None | 0.79 | 0.74 | 11,763 | 37 | 62 | 138 | (0.10, 0.00, 0.90) |
| APS | SMOTE | 0.79 | 0.76 | 11,746 | 54 | 45 | 155 | (0.65, 0.00, 0.35) |
| APS | ADASYN | 0.78 | 0.55 | 11,511 | 289 | 16 | 184 | (0.15, 0.05, 0.80) |
| APS | VAE | 0.82 | 0.76 | 11,749 | 51 | 47 | 153 | (0.20, 0.00, 0.80) |
| APS | Best vs. Runner-up ΔAUPRC (pp) | 3.66 | ||||||
| UCI | None | 0.55 | 0.53 | 4035 | 638 | 615 | 712 | (0.05, 0.15, 0.80) |
| UCI | SMOTE | 0.54 | 0.46 | 2349 | 2324 | 243 | 1084 | (0.00, 0.05, 0.95) |
| UCI | ADASYN | 0.53 | 0.47 | 2720 | 1953 | 310 | 1017 | (0.00, 0.10, 0.90) |
| UCI | VAE | 0.54 | 0.45 | 4438 | 235 | 872 | 455 | (0.05, 0.05, 0.90) |
| UCI | Best vs. Runner-up ΔAUPRC (pp) | 1.01 | ||||||
| Dataset | PE = On Mean AUPRC | PE = Off Mean AUPRC | Δ (pp) On−Off |
|---|---|---|---|
| SECOM | 0.98 | 0.98 | −0.30 |
| CREDIT | 0.92 | 0.92 | 0.61 |
| THYROID | 0.95 | 0.94 | 1.39 |
| APS | 0.80 | 0.73 | 6.56 |
| UCI | 0.54 | 0.53 | 0.93 |
| Dataset | TSTR AUPRC | Two-Sample ROC AUC | MMD2 |
|---|---|---|---|
| SECOM | 0.07 | 1.00 | 0.41 |
| CREDIT | 0.92 | 0.67 | 0.06 |
| THYROID | 0.85 | 0.58 | 0.16 |
| APS | 0.44 | 0.98 | 0.08 |
| UCI | 0.39 | 0.58 | 0.03 |
| Dataset | Best Augmentation | Selected (γ, α) | Ensemble Weights (XGB, SVM, DNN) | AUPRC (Test) | F1 (NG, Test) | PE |
|---|---|---|---|---|---|---|
| SECOM | SMOTE | (3.00, 0.50) | (0.00, 0.00, 1.00) | 1.00 | 0.79 | Off |
| CREDIT | VAE | (2.50, 0.60) | (0.00, 0.00, 1.00) | 0.93 | 0.90 | On |
| THYROID | None | (2.50, 0.70) | (0.80, 0.00, 0.20) | 0.96 | 0.90 | On |
| APS | VAE | (2.50, 0.60) | (0.20, 0.00, 0.80) | 0.82 | 0.76 | On |
| UCI | None | (1.50, 0.75) | (0.05, 0.15, 0.80) | 0.55 | 0.53 | On |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.-J.; Bae, Y.-S. Hybrid Deep-Ensemble Network with VAE-Based Augmentation for Imbalanced Tabular Data Classification. Appl. Sci. 2025, 15, 10360. https://doi.org/10.3390/app151910360
Lee S-J, Bae Y-S. Hybrid Deep-Ensemble Network with VAE-Based Augmentation for Imbalanced Tabular Data Classification. Applied Sciences. 2025; 15(19):10360. https://doi.org/10.3390/app151910360
Chicago/Turabian StyleLee, Sang-Jeong, and You-Suk Bae. 2025. "Hybrid Deep-Ensemble Network with VAE-Based Augmentation for Imbalanced Tabular Data Classification" Applied Sciences 15, no. 19: 10360. https://doi.org/10.3390/app151910360
APA StyleLee, S.-J., & Bae, Y.-S. (2025). Hybrid Deep-Ensemble Network with VAE-Based Augmentation for Imbalanced Tabular Data Classification. Applied Sciences, 15(19), 10360. https://doi.org/10.3390/app151910360






