Abstract
Security systems are essential for maintaining public safety and protecting critical assets, yet most existing evaluation approaches remain static, capture only partial interactions among assets, security systems, and offenders, and lack qualitative analyses of long-term stability. To address these limitations, this study introduces an integrated Petri net–ordinary differential equation framework that combines the discrete-event modeling strength of Petri nets with the continuous-time analysis capability of ordinary differential equations, thereby capturing the dynamic interplay among assets, security systems, and offenders and enabling equilibrium and stability analysis. Numerical simulations are conducted under different parameter settings to validate both the stability of the framework and the role of the security effectiveness parameter. The results demonstrate that enhancing this parameter improves protection capability, suppresses offender activity, reduces asset losses and promotes long-term system stability. By capturing interdependent dynamics within a unified model, the proposed approach advances beyond traditional methods and provides both a theoretical foundation and practical guidance for optimizing resource allocation and designing protection strategies.
1. Introduction
Security systems are essential for safeguarding public safety and protecting personal property. The failure of such systems can lead to severe consequences, including property loss, social instability, and even threats to human life [1]. Although numerous evaluation methods have been proposed, most remain static, capture only partial aspects of the interactions among assets, security systems, and offenders, and rarely provide qualitative analyses of long-term stability.To address this gap, the present study develops a dynamic evaluation approach that investigates how protection effectiveness influences the long-term behavior of security systems.
The proposed framework integrates Petri nets (PN) [2,3] with ordinary differential equations (ODEs) [4] to analyze the dynamic interactions among assets, security systems, and offenders. It captures key processes such as asset investment in security systems, the attractiveness of assets to offenders, the defensive actions of security systems, and the intrusions and damage caused by offenders. Within this integration, Petri nets provide a modular and visual structure for modeling discrete protection processes, while ODEs translate these processes into continuous-time state equations that enable rigorous equilibrium and stability analysis. By ensuring that both representations describe the same state transitions and feedback loops, the framework maintains internal consistency and delivers a unified description that is both intuitively interpretable and analytically robust.
Among existing modeling techniques, Petri nets are particularly well suited for representing concurrency, feedback, and resource flows that are intrinsic to security processes. They can also be systematically transformed into ODEs, since places correspond to state variables, transitions describe dynamic processes, and arc weights define interaction rates. Through this natural correspondence, discrete token flows are translated into continuous-time equations, which makes it possible to conduct rigorous analyses of equilibrium, stability, and long-term dynamics. This dual capability renders the Petri net–ODE framework especially appropriate for advancing beyond traditional static or pairwise methods, thereby enabling a dynamic evaluation of how protection effectiveness shapes system performance over time.
In recent years, many studies have explored the integration of Petri nets and ODEs to leverage the complementary strengths of the two methods, particularly in areas such as process control, industrial safety, and reliability engineering [5,6,7]. These studies generally follow a procedure of modeling system behavior with Petri nets, transforming the models into ODEs, and then conducting quantitative evaluation of performance, reliability, or availability. Despite these advances, the integration of Petri nets and ODEs has not been applied to the evaluation of security system effectiveness, and it has not addressed qualitative analysis such as equilibrium identification and stability assessment. Building on this gap, the present study develops an integrated framework to model the dynamic relationships among assets, security systems, and offenders. The framework thus enables both qualitative and quantitative analysis of dynamic effectiveness and provides a basis for rigorous evaluation of equilibrium and stability in security systems.
The main contributions of this study are as follows:
- Unified dynamic modeling of assets, security systems and offenders: Most existing studies model only partial aspects of protection processes and fail to capture the joint dynamics of assets, security systems, and offenders. To overcome this limitation, the present study develops an integrated Petri net–ODE model that explicitly represents their interdependent and evolving interactions within a unified dynamic framework.
- Qualitative stability analysis: Prior research that combined Petri nets and ODEs seldom offered qualitative proofs of long-term stability. This study conducts equilibrium and stability analysis of the ODE model, thereby providing formal conditions under which the system can maintain dynamic balance across different parameter settings.
- Comprehensive simulation of protection effectiveness: Prior work has largely assessed effectiveness through the protection capability of security systems alone. In contrast, this study conducts numerical simulations grounded in practical scenarios to predict how variations in the security effectiveness parameter affect the long-term stability of the asset–system–offender triad, thereby offering a more comprehensive and forward-looking evaluation of security system performance.
To systematically investigate the dynamic performance of security prevention systems, this paper is organized as follows. Section 2 reviews existing approaches for evaluating the effectiveness of security systems and presents a structured comparison across modeling dynamics, relational representation and application scenarios. Section 3 introduces the basic theories of Petri nets and ODEs, which provide the foundation for the modeling process. Section 4 develops a dynamic performance evaluation framework that integrates Petri nets and ODEs, and describes the system model and its dynamic interactions. Section 5 analyzes the equilibrium and stability of the proposed model to verify its ability to capture system dynamics. Section 6 conducts numerical simulations to verify the stability of the PN–ODE model under multiple initial conditions, to evaluate the robustness of system behavior through global sensitivity analysis of model parameters, and to examine in detail the effects of the security effectiveness parameter on the dynamic interactions among assets, security systems, and offenders. Finally, Section 7 summarizes the main findings and discusses future research directions.
2. Related Work
In the 1970s, with the widespread use of nuclear technology, Sandia National Laboratories in the United States, part of the Department of Energy, pioneered the research, development, and evaluation of physical protection systems (PPSs). Since then, many methods have been proposed to evaluate the effectiveness of safety systems. These methods aim to assess protection capabilities, resource allocation, and system responsiveness under specific threat scenarios. Common approaches include path analysis algorithms, cloud models, structural hierarchy analysis, and Estimate of Adversary Sequence Interruption (EASI) models.
R.A. Al-Ayat et al. [8] developed the Analytic System and Software for Evaluating Safeguards and Security (ASSESS) system, which uses a modular approach to assess the threat of nuclear material theft. The system integrates a path analysis algorithm and the Brief Adversary Threat Loss Estimator (BATLE) model to assess risks from internal, external, and collusion scenarios. It also supports weighted average analysis and defense-in-depth assessments. Although comprehensive and flexible, ASSESS has limitations in analyzing violent threats and in adapting to highly complex scenarios.
In a related study, Ke Yin [9] proposed a cloud model to assess the effectiveness of physical protection systems in high-security prisons. The model integrates fuzzy mathematics and probabilistic statistics to combine qualitative descriptions with quantitative data. This approach helps to reduce the impact of subjective judgments on evaluation results.
Similarly, Bowen Zou et al. [10] introduced a method for evaluating the effectiveness of physical protection systems based on Structural Hierarchical Analysis (SAHA). This method applies a community detection algorithm to hierarchically clustered protection units. It also uses the EASI method to quantitatively assess the protection effectiveness of critical assets.
In addition, Ahmad Ciptadi Syuryavin et al. [11] proposed an evaluation methodology for nuclear security systems based on the EASI and Bounded Adversary Assessment (BAA) models. This method quantifies the interruption probability of physical protection systems and assesses the overall effectiveness of integrated physical–cyber security systems under three hostile path scenarios. Specifically, the EASI model estimates interruption probabilities at each protection level, and the BAA method analyzes the combined effects of physical and cyber security measures under cyber attack conditions.
In a pioneering study, Jiwei Zhang et al. [12] proposed a method for optimizing the communication probability in physical protection systems for nuclear facilities. Unlike traditional models that use fixed communication probabilities, this method incorporates human and equipment factors to dynamically evaluate the impact of communication delays on system interruption probabilities. The results show that consideration of dynamic communication probabilities improves the accuracy of effectiveness assessments.
In addition, I. Cheikh El Wely and A. Chetaine [13] presented a performance-based model for assessing the effectiveness of physical protection systems in nuclear power plants. This model combines the EASI model, which quantifies probabilities of interruption, with the Adversary Sequence Diagram (ASD), which maps threat pathways. It systematically analyzes both internal and external threat scenarios.
Arafat H. Hamadah et al. [14] also proposed an integrated design and assessment model for physical protection systems in nuclear power plants. Their method uses the EASI and ASSESS tools to evaluate system effectiveness against external intrusion scenarios.
At a broader level, advances in AI and ML shift security from static rules to data-driven, adaptive defense. Geeta Sandeep Nadella et al. [15] propose a generative-AI-enhanced framework that leverages Generative adversarial network (GAN)- and variational autoencoder (VAE)-generated synthetic data together with anomaly detectors such as Random Forest, support vector machine (SVM), and long short-term memory (LSTM) to enhance enterprise security.
By contrast, at the system-architecture level in security engineering, Si Chen et al. [16] propose a vulnerability-assessment framework that couples complex-network modeling with fuzzy Petri nets (FPNs). It models protection zones and routes as a directed network to capture dependencies and rank node/edge importance, while fuzzy rules in a Petri net propagate vulnerability and quantify system-level risk.
Building on the above review, Table 1 organizes traditional security system evaluation approaches by model type and dynamic capability, shows whether and how assets, security systems, and offenders are related in the modeling, and summarizes the scenarios in which these approaches are typically applied.

Table 1.
Comparison of representative approaches for evaluating security systems.
As seen in Table 1, most existing evaluation methods for security protection systems have provided valuable tools for path analysis, risk quantification, and subsystem assessment, but they remain constrained in three key respects: most are static or only partially dynamic, they largely describe two-way relations among assets, security systems, and offenders, and they provide no qualitative proofs or analyses to establish long-run system stability. To address these gaps, this study develops an integrated Petri net–ODE framework [17] that combines discrete event representation with continuous-time dynamics, captures the triadic interactions of assets, security systems, and offenders within a single model, and supports equilibrium and stability analysis. This comparison underscores the advancement of our approach beyond earlier techniques.
3. Preliminary Concepts and Definitions
3.1. Petri Net Basics
A Petri net is a mathematical formalism for modeling dynamic systems with discrete events. It describes the relationships between system states and events, as well as the dynamic behavior of these systems. Formally, a Petri net [18] is defined as a five-tuple:
where each component is defined as follows:
- P: A finite set of places that represent system states or resource distributions. Each place may contain tokens and is usually depicted as a circle.
- T: A finite set of transitions that represent events or actions in the system. Transitions are typically shown as rectangles or boxes and are distinct from places.
- F: A set of directed arcs that connect places and transitions. Arcs may point from a place to a transition (input arcs) or from a transition to a place (output arcs), defining the relationships between states and events.
- W: An arc weight function that assigns a non-negative integer weight to each arc. The weights and represent the input and output arc weights, indicating the number of tokens consumed or produced when a transition fires.
- : The initial marking that specifies the initial distribution of tokens across places. It defines the system’s initial state.
3.2. Constant Transition Definition
A Constant Transition represents a distinct type of transition within a Petri net. Unlike standard transitions, the firing of a Constant Transition does not consume tokens from its input places. Instead, through a dynamic feedback mechanism, it adjusts the number of tokens in the output places based on a specific weighting scheme. The key characteristics of a Constant Transition are as follows:
- Non-consumptive input places : The number of tokens in each input place remains unchanged when transition t fires, ensuring that input resources are unaffected. This condition is formally expressed as follows:Here, denotes the updated marking of place p after the firing of transition t, represents the set of input places for transition t that provide tokens when t fires, and indicates the current number of tokens in place p.
- Dynamically adjusted output places : The number of tokens in each output place is dynamically increased or decreased based on the tokens in input places and a dynamic weighting function. The change in tokens is given byHere, denotes the change in the number of tokens in the output place p, representing the increase or decrease in its marking when transition t fires. The term specifies the weight of the arc from place q to transition t, indicating how many tokens are consumed from q when t fires, while represents the weight of the arc from transition t to place p, describing the number of tokens allocated to p after firing. Finally, denotes the set of output places for transition t, indicating the destinations where tokens are distributed.
3.3. ODE Modeling of Petri Nets
The discrete dynamic behavior of Petri nets can be transformed into a continuous dynamic representation using an ODE model. This approach allows the analysis of discrete-event systems within a continuous framework. The transformation is achieved by constructing differential equations that describe the evolution of system states over time. Specifically, the number of tokens at each location is expressed as a continuous function of time, denoted , and the effects of transition firing rates are incorporated into the model.
Consider a Petri net consisting of n places, denoted by , and m transitions, denoted by . The continuous state variables are defined as follows:
where represents the continuous state variable corresponding to place .
The dynamic evolution of state variables is governed by time t and the rates associated with input and output arcs. These arc rates determine the temporal changes of the state variables .
In the context of ODE modeling, the arc weighting functions and are no longer fixed quantities merely representing discrete token transfers. Instead, they are transformed into dynamic functions of the state variables and time, thereby characterizing the continuous flow rates of resources within the system over time. This transformation can be expressed as follows:
where is a function of the place state variable and time t, describing the rate of resource consumption along the input arc from place to transition , and is a function of and t, representing the rate of resource generation along the output arc from transition to place .
In a Petri net, the firing of a transition involves the removal of tokens from its input places and the addition of tokens to its output places. Accordingly, the dynamic change of the state variable associated with place can be described by the following ordinary differential equation:
where the first term represents the total rate at which tokens are added to place by all transitions , with indicating that q belongs to the set of input places of transition . The second term denotes the total rate at which tokens are consumed from place as input to all transitions .
3.4. Causal Relations in the PN–ODE Model
In the ODE-based transformation of Petri nets, the dynamic changes of state variables are determined not only by weight functions and transition firing rates, but also by interaction patterns and feedback mechanisms. These mechanisms can be analyzed by means of causal relationships. Within the PN–ODE model, causal relationships describe the dynamic interdependencies between state variables and explain how changes in one variable affect the direction and magnitude of changes in others through transitions.
According to the nature of the interactions among variables, causal relationships can be classified into two categories: positive causality and negative causality. These are formally defined as follows:
- Positive polarity of a cause–effect relationship: A causal relationship is said to have positive polarity when an increase in one variable leads to an increase in another variable, or when both variables change in the same direction. For instance, as illustrated in Figure 1, indicates that an increase in A results in an increase in B, thereby representing a positive cause–effect relationship.
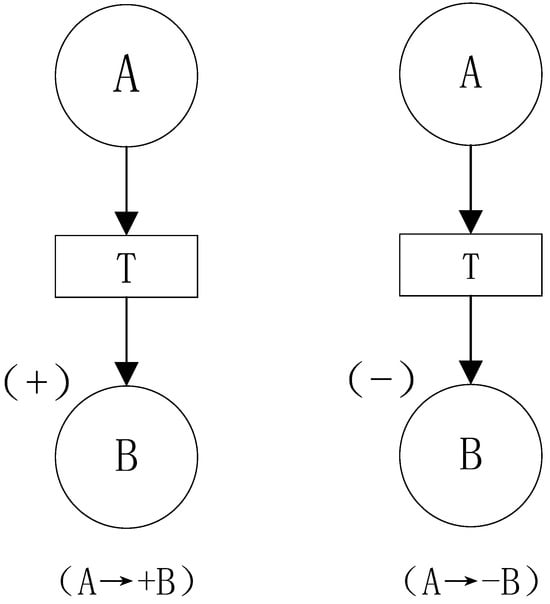 Figure 1. Illustration of positive and negative causal relationships.
Figure 1. Illustration of positive and negative causal relationships. - Negative polarity of a cause–effect relationship: A causal relationship is said to have negative polarity when an increase in one variable leads to a decrease in another variable, or when the two variables change in opposite directions. As illustrated in Figure 1, signifies that an increase in A results in a decrease in B, thereby representing a negative cause–effect relationship.
4. Security System Models
4.1. System Description
The dynamic interaction between assets, security systems, and offenders is complex and intense. Assets are critical resources whose value increases with continued use. Their high value inevitably attracts offenders, making them prime targets for attack. At the same time, assets provide the financial basis for building security systems designed to enhance protection capabilities. Security systems, in turn, deter criminal activity by improving the effectiveness of protection. However, their effectiveness naturally diminishes over time due to continuous operation, a phenomenon known as self-depletion.
Rational choice theory [19] in criminology suggests that offenders may choose to damage the security system or attack the asset directly after weighing the potential benefits and risks. This dynamic forms a complex system of interdependencies in which assets, security systems, and offenders interact in mutually reinforcing and counterbalancing ways. The interplay between asset value growth, security system effectiveness and perpetrator behavior together determine the overall stability and dynamic equilibrium of the system. Such interdependent and evolving interactions exemplify the essence of threat analysis [20] in protection research, highlighting the need to move beyond static evaluations toward dynamic approaches capable of capturing feedback loops and long-term system behavior.
4.2. Petri Net Models
The dynamic relationships among assets, security systems, and offenders form the foundation of this study. In the modeling process, these entities are abstracted within a Petri net framework, where the asset value is represented by , the protection capacity of the security system by , and the population of offenders by . The asset value naturally increases through its own growth (), but decreases when part of it is allocated to the security system () or lost due to offender intrusions (). The protection capacity of the security system is enhanced by investment from assets (), but it degrades during continuous operation () and can also be weakened by offender attacks (). The population of offenders expands as the asset value becomes more attractive (), but it is reduced through the defensive actions of the security system (). Taken together, these interactions establish feedback loops: assets provide resources that strengthen the security system, the security system suppresses offenders while being subject to their attacks, and offenders are attracted to assets while simultaneously diminishing them through intrusions. As summarized in Table 2 and Table 3, these places and transitions collectively characterize the flows of resources, protective actions, and attacks, thereby establishing the structural foundation of the Petri net model, as illustrated in Figure 2.

Table 2.
Description of places in the Petri net model.

Table 3.
Description of transitions in the Petri net model.
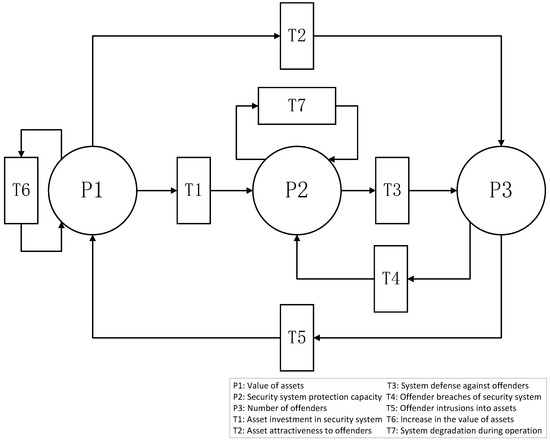
Figure 2.
Petri net model of assets, security systems, and offenders. P1–P3 denote the places and T1–T7 denote the transitions.
4.3. ODE Modeling
To quantitatively analyze the dynamic interactions among assets, offenders, and the security system, the Petri net model is transformed into an ODE model. In this formulation, the places in the Petri net are mapped to state variables that characterize the evolving states of the system: denotes the value of assets, represents the protection capability of the security system, and indicates the number of offenders.
Transitions in the Petri net correspond to dynamic processes that govern the interactions among these state variables. The intensity of these interactions within the ODE framework is directly influenced by the weights of the input and output arcs as defined in the Petri net structure. Table 4 presents the mapping between arc weights in the Petri net and their corresponding parameters in the ODE model.

Table 4.
Mapping between arc weights in the Petri net and parameters in the ODE model.
In translating Petri net transitions into the ODE framework, we assume that the discrete markings of places can be approximated by continuous state variables, that transition firings can be represented as rate processes with arc weights mapped to interaction parameters, and that all output arc weights are normalized to so that process magnitudes are fully determined by these parameters.
Building on these assumptions, the arc weights in Table 4 are specified with particular functional forms. Asset growth is modeled by a constant rate , normalized by the current asset level, while asset investment into the security system is captured by a fixed proportion , reflecting the allocation of a share of asset value to protection. The impact of offenders on assets (), the damage they cause to the security system (), and the attractiveness of assets to offenders () are all represented by constant coefficients, describing their average interaction intensities. The degradation of the security system is similarly represented by a constant rate . By contrast, defensive effectiveness is expressed through the nonlinear saturating function , which captures diminishing returns: defensive capability increases nearly linearly when resources are limited, but gradually approaches an upper bound a as resources increase. This choice prevents the defensive process from unrealistically growing without limit and better reflects real-world constraints.
The present study proposes a novel methodology that integrates the graphical representation of a Petri net with the mathematical formulation of an ODE model. Based on this integration, the following ODE system is established:
where all parameters are positive constants, as defined in Table 4. The state variables , , and represent, respectively, the value of assets, the protection capability of the security system, and the number of offenders.
The parameter space is defined as
and the state space is given by
Clearly, the initial conditions of system (7) belong to , and it can be deduced that is a positively invariant set of the system.
To ensure that system (7) is dissipative, the following condition is assumed to hold
5. Existence and Stability Analysis of Equilibrium Points
This section focuses on establishing the mathematical soundness and stability of the proposed Petri net and ODE model. By analyzing key mathematical properties of the system, such as the existence of equilibrium points, stability, and dynamic behavior, the validity of the model in describing the interactions among assets, offenders, and protection capacity can be rigorously demonstrated. Furthermore, these analyses provide theoretical foundations for optimizing system performance and guiding practical applications.
5.1. Existence, Uniqueness, and Boundedness of Solutions
Theorem 1.
The system (7) admits a unique solution for any initial condition on the interval . Moreover, this solution remains ultimately bounded in for all .
Proof of Theorem 1.
In accordance with the existence and uniqueness theorem for solutions of ordinary differential equations, the solution of the model with initial value is unique within its maximal existence interval , where .
To facilitate the analysis of the system’s boundedness, we introduce the following auxiliary variable:
where the constants and are defined as
According to the differential inequality (14) and applying Gronwall’s inequality, we obtain
Hence, the auxiliary function is ultimately bounded. Consequently, the solution of system (7) is bounded on . According to the continuation theorem for solutions of ordinary differential equations, it follows that .
Thus, the proof of Theorem 1 is complete. □
5.2. Existence Analysis of the Equilibrium Point
Theorem 2.
The existence of positive equilibrium points of system (7) depends on the threshold parameter , defined as
The system exhibits the following scenarios:
- If , the system admits at least one positive equilibrium point. In particular, when , the system admits a unique positive equilibrium point ; whereas when , the system admits two distinct positive equilibrium points and .
- If , the system admits no positive equilibrium point.
Proof of Theorem 2.
Assume that is an arbitrary equilibrium point of system (7). To satisfy the system of nonlinear algebraic equations, the following relations must hold:
From the first and third equations, by expressing x and z in terms of y, and substituting into the second equation, we obtain a quadratic equation in y:
Define the discriminant as
If , two equilibrium points and exist, explicitly given by
Thus, Theorem 2 is proven. □
5.3. Stability Analysis of Equilibrium Points
Theorem 3.
Assume that . Then, the local stability of equilibrium points can be characterized as follows:
- If , the equilibrium point is locally asymptotically stable, whereas the equilibrium point is unstable.
- If , the unique equilibrium point is linearly stable.
Proof of Theorem 3.
The local stability of equilibrium points is analyzed via the eigenvalues of the Jacobian matrix. The Jacobian matrix J of system (7) evaluated at an equilibrium point is given by
The eigenvalues of J satisfy the characteristic equation:
that is,
Thus, the characteristic equation can be expressed in the standard cubic form:
where the coefficients of the characteristic equation are given by
Furthermore, the coefficient can be equivalently expressed to highlight its dependence on the discriminant as follows:
where
At the equilibrium point , when , the following inequalities hold:
Moreover, we have
According to the Routh–Hurwitz criterion, since all the following conditions are satisfied at :
the real parts of all eigenvalues are negative. Therefore, is locally asymptotically stable.
In contrast, at , we have
To analyze the sign of , note that
since
Hence, , and thus . It follows that the term in the parentheses of is greater than 1, making .
Therefore, the Routh–Hurwitz conditions are violated at , implying that this equilibrium point is unstable. Furthermore, since , the negativity of is confirmed, and by Routh–Hurwitz criterion, there exists at least one eigenvalue with positive real part, indicating instability of .
Finally, when , at , the following relations hold:
Therefore, the characteristic equation admits a zero eigenvalue , and the remaining eigenvalues have negative real parts. According to the definition of linear stability, the equilibrium point is linearly stable. □
6. Numerical Modeling
This section presents numerical simulations based on the proposed PN-ODE model to validate the theoretical analysis and assess the dynamic behavior and stability of the system. Through numerical integration of the model equations, the dynamic interactions among assets, security systems, and offenders are systematically investigated. Simulations are also performed to analyze the equilibrium states and stability of the system under different initial conditions and security performance parameters. These results verify the feasibility and robustness of the proposed modeling framework.
6.1. Verification of the Stability of the Model
In order to perform numerical simulations and validate the stability of the proposed model, this study collected relevant data, including asset value distributions, security system effectiveness, security investment ratios, and offender statistics. These data were obtained through structured interviews with security companies, public security management departments, and industry associations. Historical records and industry reports were also reviewed to cross-check typical ranges of system parameters. This information was used to determine the initial conditions and to calibrate the parameter values employed in the model simulations.
In this study, the concept of protection value is used as a key indicator to quantify the protection capability of the security system. The protection value reflects the level of asset protection provided by the system within a given unit of time. This metric allows for a dynamic assessment of how resource allocation and offender activities affect the level of protection provided by the system over time.
The numerical values of the key model parameters are summarized in Table 5. Their determination combined empirical data with expert and institutional input. Specifically, the asset growth rate () and the investment ratio () were derived from historical operational and financial records. Parameters including the degradation rate of the security system (), its performance coefficient (a), the intensity of offenders’ intrusion into assets (), the attractiveness of assets to offenders (), and the impact of offender attacks on the security system () were determined through structured interviews and consultations with industry experts and security practitioners. In addition, the competition parameter among offenders () was obtained through consultation with public security departments, reflecting their assessment of rivalry among offenders in practice.

Table 5.
Initial values and key parameters of the model.
To investigate the stability of the proposed model and to verify the existence of equilibrium points, five sets of initial conditions were considered: , , , , and . The baseline configuration is defined using operational data from a case organization combined with local crime statistics and calibrated through expert review. In this baseline, the asset value reflects the initial investment, the protection capacity is set to zero to reflect the absence of early defensive measures, and the offender population corresponds to the average local threat level over a recent observation window. For comparability across scenarios, the raw quantities are normalized to dimensionless units with the reference level set to 100. On this basis, serves as the control case, against which the other scenarios can be compared. The configuration reduces the initial asset value while keeping protection and offenders unchanged, enabling an assessment of whether trajectories scale proportionally and whether low-asset states affect the short-term adjustment process. The configuration introduces a small amount of initial protection to examine how early defensive capacity modifies system interactions and whether it accelerates or delays convergence. The configuration doubles the initial number of offenders, thereby testing the system’s resilience under heightened threat conditions when protection is absent. Finally, the configuration perturbs all three variables simultaneously—moderate assets, substantial protection, and elevated offenders—representing a complex operating condition used to verify that stability persists under mixed stress. These settings together allow for a systematic examination of equilibrium behavior and stability under varied conditions.
Numerical simulations were conducted using the PyCharm 2024.2 (JetBrains) platform to solve the system of ODEs derived from the Petri net model. The dynamic evolution trajectories of the state variables , , and under different initial conditions are illustrated in Figure 3 and Figure 4.
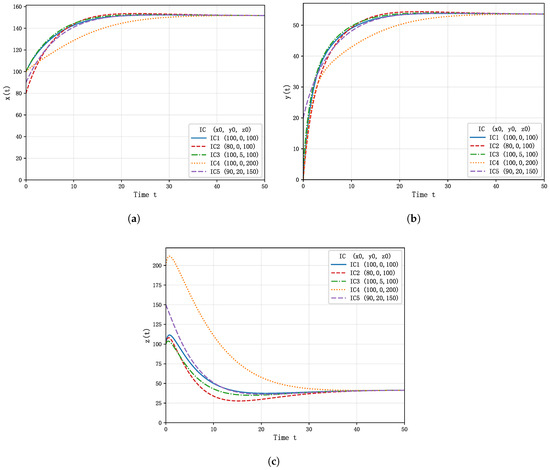
Figure 3.
Time evolution of the system variables under different initial conditions: (a) Asset value . (b) Protection capability of the security system . (c) Number of offenders .
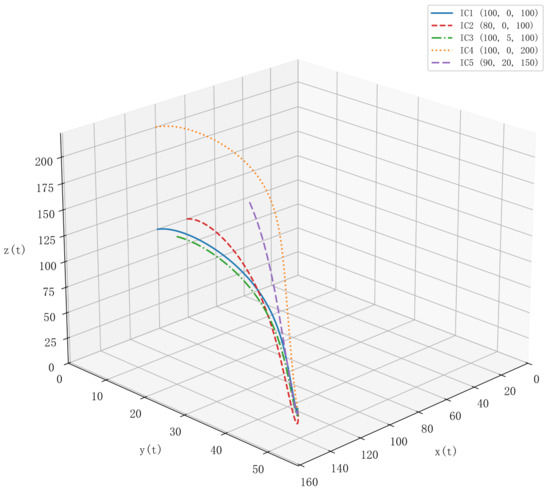
Figure 4.
Three-dimensional trajectories of asset value , protection capability of the security system , and number of offenders under different initial conditions.
As shown in Figure 3 and Figure 4, the system converges to a dynamic equilibrium under all initial conditions, confirming both the stability and the validity of the proposed model. In the early stages of system evolution, the initially low level of protection allows offenders to threaten asset growth, leading to sharp fluctuations and temporary declines in asset value. As asset resources are gradually allocated to the security system, protection capability improves and the number of offenders decreases. This process reduces the threat to assets and facilitates the recovery and stabilization of asset value over time.
At the same time, protection capacity increases rapidly in the early stages due to continuous investment from asset resources. As the system operates, this growth slows because of natural degradation and attacks from offenders, eventually stabilizing at a dynamic equilibrium. The high attractiveness of assets also triggers a temporary rise in offender activity at the beginning; however, as the security system strengthens, such activity is gradually suppressed and the number of offenders falls to a stable low level.
Comparative analysis across the five sets of initial conditions further illustrates these dynamics. Specifically, lowering the initial asset level slows the recovery process, introducing early protection moderates fluctuations, and a surge in offenders intensifies short-term volatility. Even under the most stressed scenario, where assets, protection, and offenders are simultaneously perturbed, the trajectories still converge to equilibrium. These results indicate that although different initializations produce distinct short-term behaviors, the long-term outcome is consistent: the system’s state variables evolve toward a stable equilibrium. This highlights both the robustness of the modeled security prevention system and the effectiveness of the dynamic interactions among assets, security systems, and offender behavior.
6.2. Global Sensitivity Analysis
While the simulations under multiple initial conditions in Section 6.1 confirmed the stability of the PN–ODE model, real-world systems are inevitably subject to uncertainty in parameter estimation. Coefficients such as asset growth rates, investment ratios, security system degradation rates, and offender behavioral parameters are typically obtained from empirical data or expert judgement, and therefore cannot be treated as fixed values. To ensure that the stability conclusions remain valid under such uncertainty, a global sensitivity analysis (GSA) was conducted.
As an initial step, Morris screening was applied by simultaneously perturbing all eight parameters within a range around their baseline values. The analysis focused on three steady-state indicators: the asset value , the protection capacity of the security system , and the offender population . The ranking of parameter importance, based on the mean absolute elementary effects (), is reported in Table 6.

Table 6.
Morris screening results: parameter ranking based on values for each steady-state indicator.
The Morris results in Table 6 indicate that the performance coefficient of the security system a, the asset attractiveness coefficient , the investment ratio , and the asset growth rate consistently exert the strongest influence on all three steady-state indicators. In contrast, parameters such as the degradation rate , the competition coefficient , the effect of offender behavior , and the intrusion intensity have only marginal impacts within the tested range.
To obtain a more detailed quantification of parameter importance and to assess potential interaction effects, the five most influential parameters identified by Morris screening—namely the performance coefficient of the security system a, the asset attractiveness coefficient , the investment ratio , the asset growth rate , and the degradation rate —were further analyzed using Sobol variance decomposition. Figure 5 present the first-order () and total-order () indices for , , and , respectively.
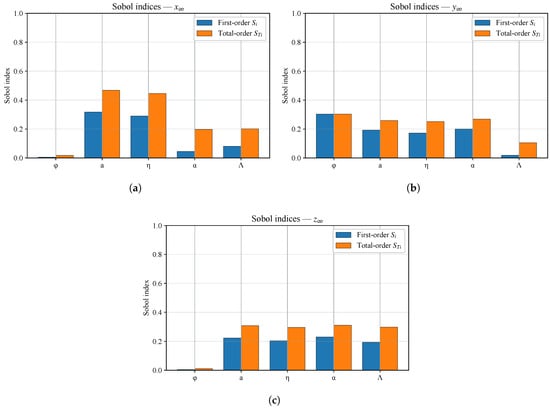
Figure 5.
Sobol variance decomposition results for the PN–ODE model: (a) Sobol indices for steady-state asset value . (b) Sobol indices for steady-state protection capacity of the security system . (c) Sobol indices for steady-state offender population .
As shown in Figure 5, the Sobol indices reveal that a and dominate the variance of , while has the strongest effect on , and the combined influence of a, , and largely determines . Overall, these results confirm that the PN–ODE model converges to a stable equilibrium under parameter perturbations, with stability being most sensitive to the effectiveness of the security system, the attractiveness of assets, and the allocation of resources to protection.
6.3. Impact of Security Effectiveness Parameter a on System Dynamics
To further examine the determinants of system behavior, this study focuses on the role of the security effectiveness parameter a in shaping system dynamics. The parameter a reflects the level of protection that the security system can deliver per unit of resource input, thereby directly influencing the system’s ability to safeguard assets and suppress offender activities.
To assess its impact, numerical simulations were conducted by varying a across six representative values (80, 82.5, 85, 87.5, 90, and 92.5), while keeping all other parameters constant. The resulting trajectories of asset value , protection capability , and offender population are presented in Figure 6, and their final values at are summarized in Table 7.
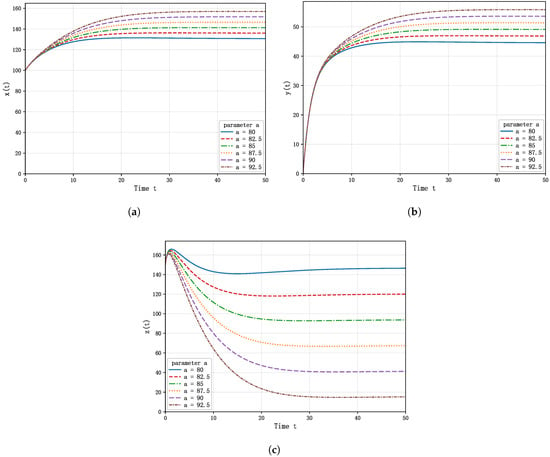
Figure 6.
Time evolution of the system variables under different values of the effectiveness parameter a: (a) Asset value . (b) Protection capability of the security system . (c) Number of offenders .

Table 7.
Final values of asset value , security system protection capability , and offender population at under different values of the effectiveness parameter a.
As shown in Figure 5 and Table 6, increasing the security effectiveness parameter a significantly improves the dynamic performance of the system. A larger value of a reduces asset losses in the initial phase, accelerates asset recovery, and leads to a higher equilibrium value of asset value , indicating stronger protection of assets against offenders. For the protection capability of the security system , a higher a results in a steeper initial rise and a higher steady-state level, reflecting a significant improvement in protective capacity. Meanwhile, the offender population decreases more rapidly when a is larger, reaching a substantially lower equilibrium level, which demonstrates stronger system deterrence and sustained suppression of offender activity. Collectively, these results underscore the critical role of the security effectiveness in stabilizing the system and mitigating risks to protected assets.
7. Conclusions
This study presents a novel methodology for evaluating the effectiveness of security systems by integrating Petri nets and ODEs. The proposed approach aims to overcome the limitations of traditional static analysis methods, which fail to capture the complex dynamic interactions between assets, the security system, and offenders. By constructing a Petri net model to characterise system interactions and using ODEs for quantitative analysis, the study investigates the existence and stability of equilibrium points. The rationality and stability of the proposed model are further validated through numerical simulations under different initial conditions and parameter settings. The analysis confirms that increasing the security effectiveness parameter a significantly increases the protection capability of the system, reduces asset losses, and improves the long-term stability of the security system in dynamic environments. These results demonstrate that, through appropriate parameter configuration, a dynamic balance can be achieved between asset protection, security system performance, and offender suppression, thereby improving overall system effectiveness.
This research provides a theoretical framework and technical basis for dynamic modeling and performance evaluation of security systems. It offers scientific guidance for optimizing resource allocation and designing adaptive security strategies. However, the current model has limitations, such as not fully capturing multi-dimensional offender behaviors and lacking adaptability to highly dynamic environments.
To address these limitations, the framework may be advanced in several directions. Incorporating multiple asset types with different values and vulnerabilities would enable a more comprehensive analysis of protection trade-offs; modeling offenders with heterogeneous strategies and adaptive behaviors would enhance the fidelity of threat representation; and allowing parameters such as resource allocation ratios or offender learning effects to vary dynamically would improve adaptability to highly dynamic environments. Advancing the framework along these lines would overcome current shortcomings and further strengthen its value as a tool for evaluating and optimising complex security systems.
Author Contributions
Y.C. was the lead author of this study. He developed the theoretical framework, designed and implemented the Petri net model, constructed the ODE system, and conducted the simulations. H.J. initiated and supervised the entire research project, provided key methodological guidance, and extensively revised the manuscript. T.W. provided assistance in mathematical formulation and participated in the validation of simulation results. W.C. supported the literature survey and contributed to figure generation and manuscript polishing. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by “Security Engineering Double First-Class Special Project of People’s Public Security University of China” No. 2023SYL08 and “Theoretical and Practical Research on Virtual Reality Technology in Public Safety Education and Training” No. 20230086.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available within the article.
Acknowledgments
The authors wish to express their appreciation to Chen for his valuable experience and advice.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yao, Y.; Chen, W. Security risk assessment of projects in high-risk areas based on attack-defense game model. Sci. Rep. 2023, 13, 13293. [Google Scholar] [CrossRef] [PubMed]
- Petri, C.A. Kommunikation mit Automaten; Schriften des Rheinisch-Westfälischen Instituts für Instrumentelle Mathematik an der Universität Bonn, Nr. 2; Universität Bonn: Bonn, Germany, 1962. [Google Scholar]
- Gu, Y.; He, L.; Bi, Q. A hierarchical fuzzy Petri net risk assessment method. J. Mech. Des. Manuf. 2024, 2, 369–372, 379. [Google Scholar]
- Qiang, R.; Ma, W.; Guo, K.; Du, H. The differential equation model of pathogenesis of Kawasaki disease with theoretical analysis. Math. Biosci. Eng. 2019, 16, 3488–3511. [Google Scholar] [CrossRef] [PubMed]
- Jyotish, N.K.; Singh, L.K.; Kumar, C. Availability analysis of safety-critical systems of nuclear power plant using ordinary differential equations and reachability graph. Prog. Nucl. Energy 2023, 159, 104624. [Google Scholar] [CrossRef]
- Jyotish, N.K.; Singh, L.K.; Kumar, C. Reliability assessment of safety-critical systems of nuclear power plant using ordinary differential equations and reachability graph. Nucl. Eng. Des. 2023, 412, 112469. [Google Scholar] [CrossRef]
- Jyotish, N.K.; Singh, L.K.; Kumar, C. Performance measurement of safety-critical systems based on ordinary differential equations and Petri nets: A case study of nuclear power plant. Nucl. Eng. Technol. 2023, 55, 861–869. [Google Scholar] [CrossRef]
- Al-Ayat, R.A.; Cousins, T.D.; Hoover, E.R. ASSESS (Analytic System and Software for Evaluating Safeguards and Security) Update: Current Status and Future Developments; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1990; UCRL-JC-104360. [Google Scholar]
- Yin, K. A study on effectiveness evaluation for the physical protection system of a high security prison based on the cloud model. Secur. Commun. Netw. 2018, 2018, 9583982. [Google Scholar] [CrossRef]
- Zou, B.; Wang, W.; Liu, J.; Yan, Z.; Liu, G.; Wang, J.; Wei, G. Development of a structure analytic hierarchy approach for the evaluation of the physical protection system effectiveness. Nucl. Eng. Technol. 2020, 52, 1661–1668. [Google Scholar] [CrossRef]
- Syuryavin, A.C.; Lee, S.H.; Syam, N.S. Nuclear security system effectiveness assessment using bounded analysis approach: A case study of different adversary scenarios. J. Nucl. Sci. Technol. 2020, 57, 1131–1139. [Google Scholar] [CrossRef]
- Zhang, J.; Jiang, S.; Liu, J.; Zhang, L.; Chen, H.; Li, X. Optimization of communication probability in effectiveness evaluation of physical protection system. IEEE Access 2020, 8, 228199–228205. [Google Scholar] [CrossRef]
- Cheikh El Wely, I.; Chetaine, A. Analysis of physical protection system effectiveness of nuclear power plants based on performance approach. Ann. Nucl. Energy 2021, 152, 107980. [Google Scholar] [CrossRef]
- Hamadah, A.H.; Nagy, M.S.; Abou-Gabal, H.; El Mongy, S.A. Integrated security system (ISS) design and evaluation for commercial nuclear power plant. Sci. Technol. Nucl. Install. 2021, 2021, 4092760. [Google Scholar] [CrossRef]
- Nadella, G.S.; Addula, S.R.; Yadulla, A.R.; Sajja, G.S.; Meesala, M.; Maturi, M.H.; Meduri, K.; Gonaygunta, H. Generative AI-Enhanced Cybersecurity Framework for Enterprise Data Privacy Management. Computers 2025, 14, 55. [Google Scholar] [CrossRef]
- Chen, S.; Wang, Z.; Jin, B.; Tong, X.; Jin, H. Vulnerability Assessment Framework for Physical Protection Systems Integrating Complex Networks and Fuzzy Petri Nets. Appl. Sci. 2025, 15, 7062. [Google Scholar] [CrossRef]
- Gutowska, K.; Kogut, D.; Kardynska, M.; Formanowicz, P.; Smieja, J.; Puszynski, K. Petri Nets and ODEs as Complementary Methods for Comprehensive Analysis on an Example of the ATM–p53–NF-κB Signaling Pathways. Sci. Rep. 2022, 12, 1135. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.; Ding, Z.; Liu, L.; Wang, X.; Crossley, R.D. Petri net-based methods for analyzing structural security in e-commerce business processes. Future Gener. Comput. Syst. 2020, 109, 611–620. [Google Scholar] [CrossRef]
- Hofer, J. Red light game identifies ineffective criminal deterrence. Am. J. Econ. Sociol. 2024, 83, 673–682. [Google Scholar] [CrossRef]
- Tyagi, A.K.; Addula, S.R. Artificial Intelligence for Malware Analysis: A Systematic Study. Artificial Intelligence-Enabled Digital Twin for Smart Manufacturing; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2024; pp. 359–390. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).