A Novel Recognition-Before-Tracking Method Based on a Beam Constraint in Passive Radars for Low-Altitude Target Surveillance
Abstract
1. Introduction
- (1)
- We propose a new method for feature vector extraction and construction based on a beam constraint. It extracts biased RCS from the detected peak on the range-Doppler (RD) map and takes targets from a short period of time in the same beam as the same target and constructs feature vectors accordingly. In this way, the target tracking is no longer needed for feature vector construction. Thus, it can sufficiently eliminate the side effects of tracking error imposed on the feature vector construction.
- (2)
- We propose a light-weight metric for measuring the similarity of feature vectors between the unknown target and standard targets. The metric is proposed based on the Euclidean distance (ED), trend consistency (TC), and volatility consistency (VC) of the feature vectors. Experimental results based on the simulated and synthetic data both validate its feasibility and effectiveness for recognizing targets with different feature sizes.
- (3)
- We propose a novel RBT method for passive radars. It utilizes the time sequence, extracted before target tracking from the biased RCS, to construct the feature vector of the unknown target. Meanwhile, the feature vectors of standard targets are dynamically constructed based on the attitude information of the unknown target. By measuring the similarity of feature vectors between the unknown target and standard targets, target recognition is realized. Experimental results show that the proposed method can make good use of the local scattering characteristics for effective target recognition.
2. Design of the Proposed Method
2.1. Block Diagram of the Proposed Method
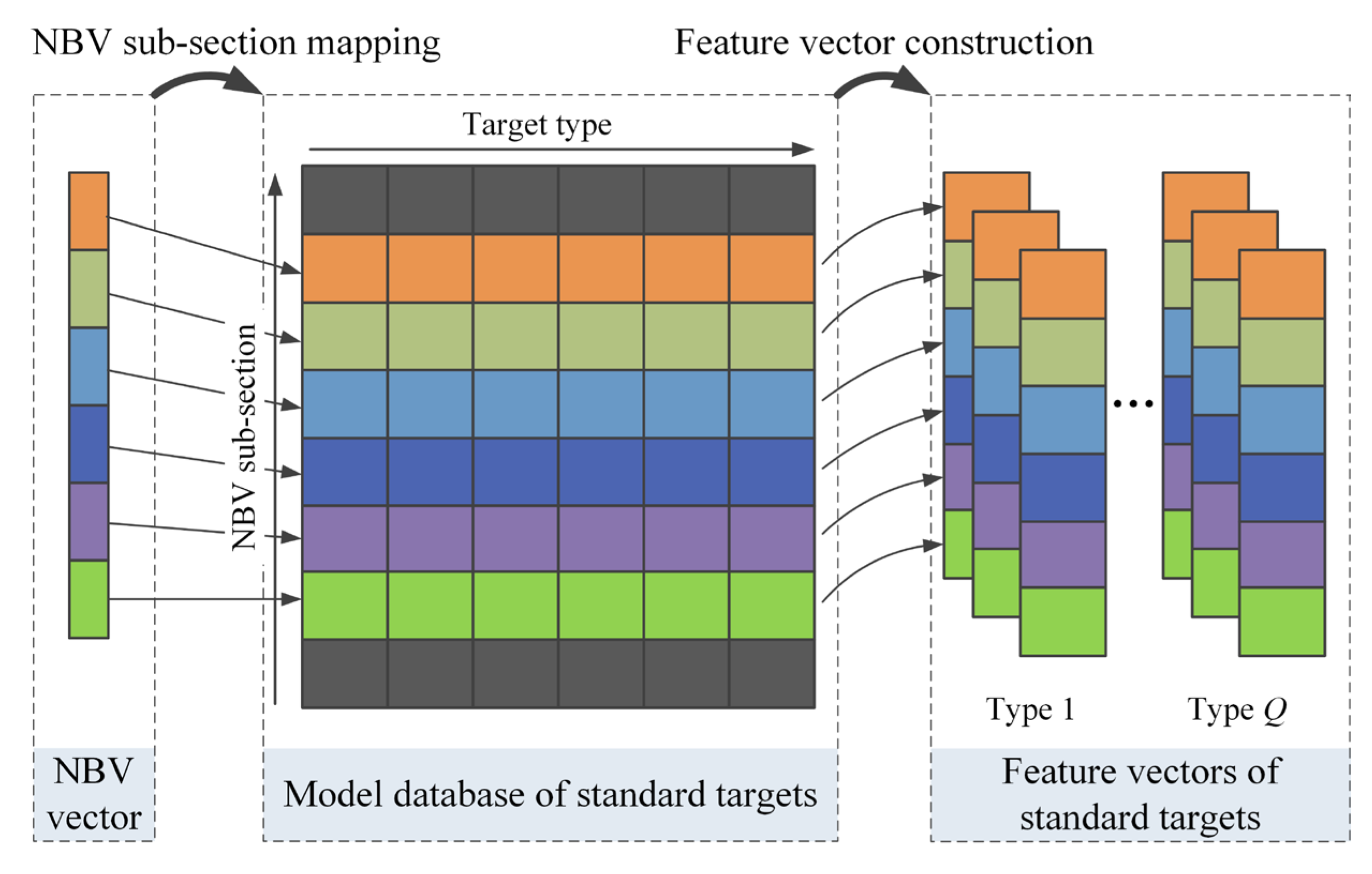
2.2. Acquisition of Data and Construction of Standard Target Model
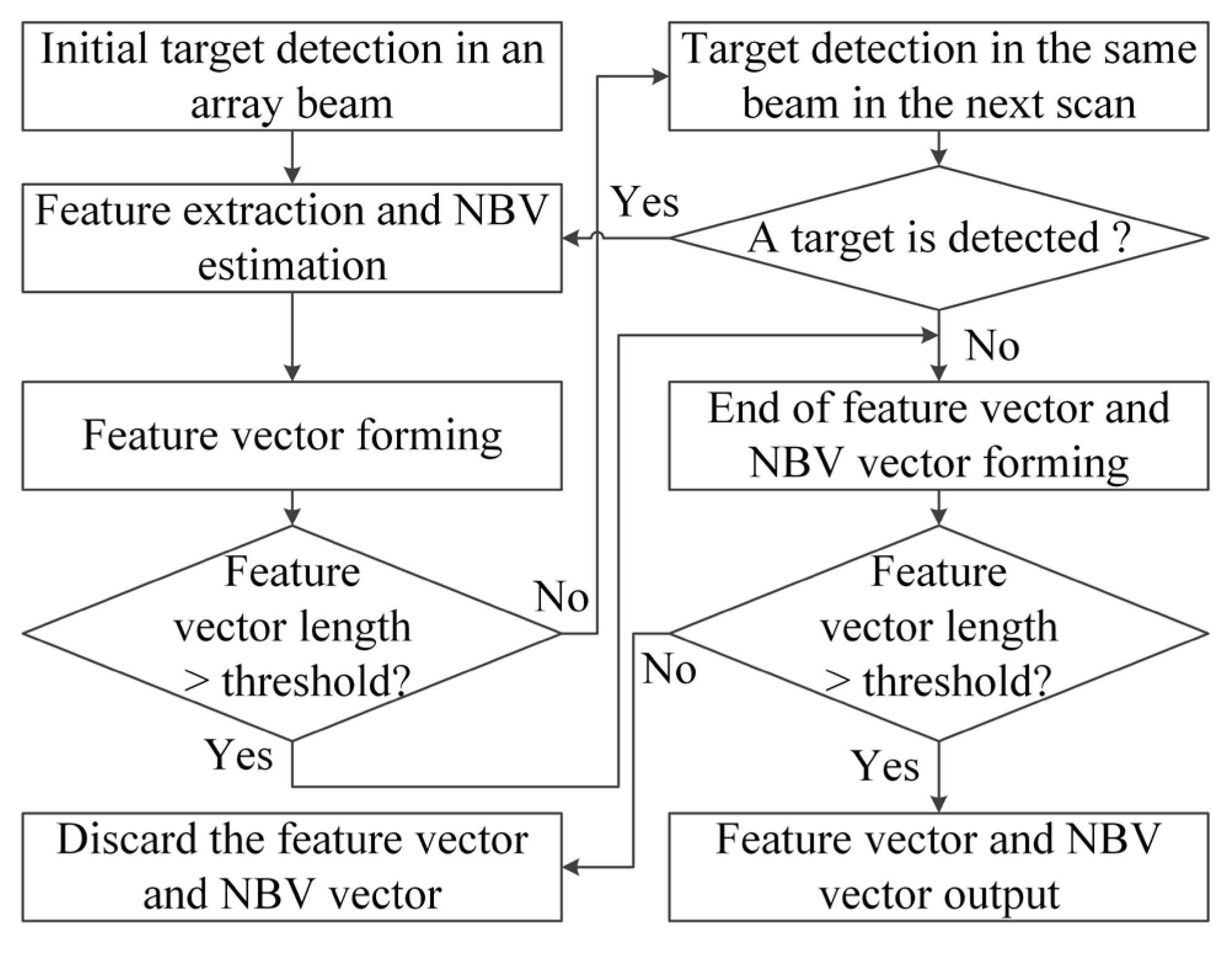
2.3. Construction of Feature Vector of Unknown Targets Under Beam Constraint
2.4. Dynamic Recognition with Time-Varying Feature Vector
3. Simulation and Measured Data Results
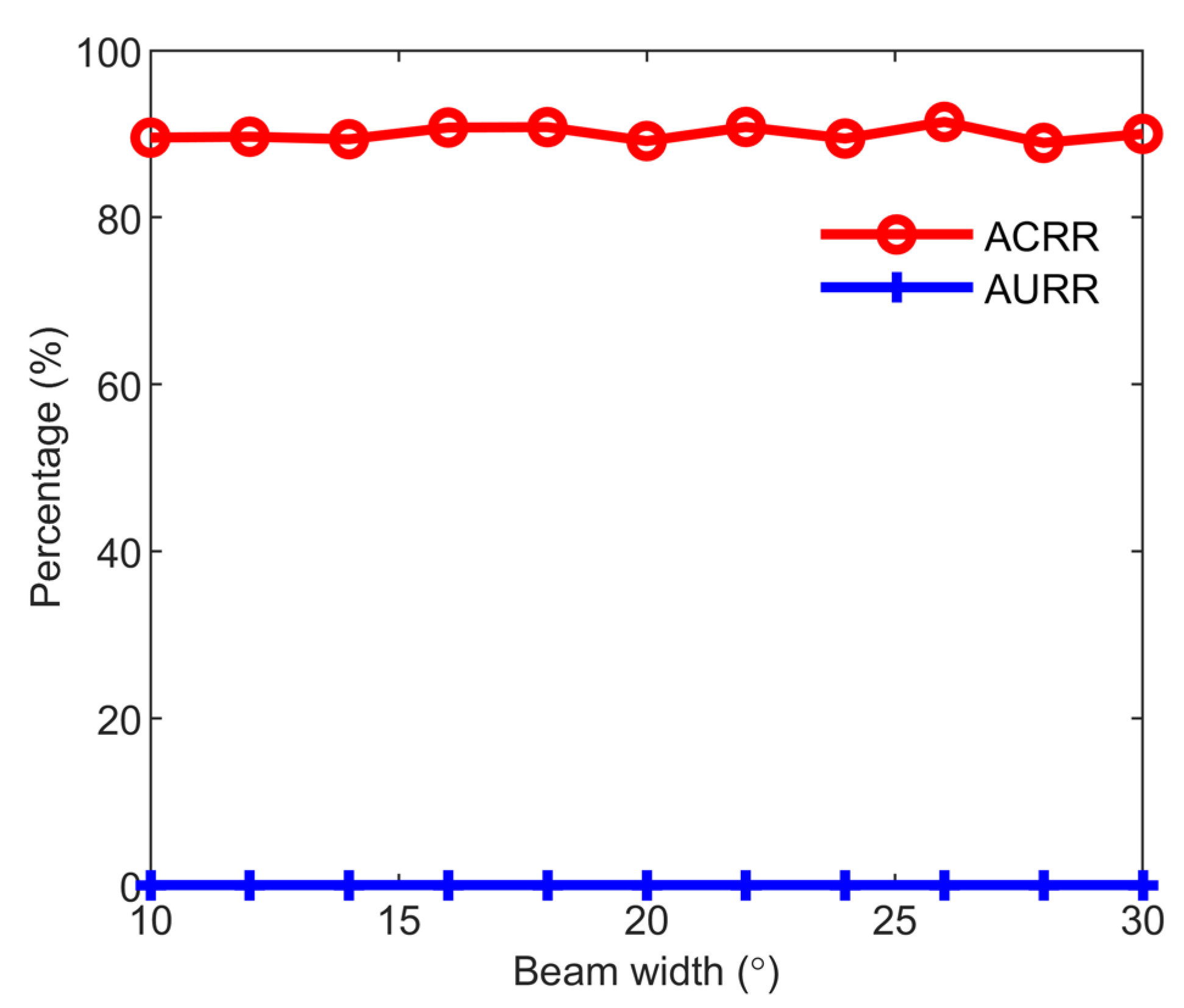
3.1. Performance Evaluation of the Proposed Method Under Different Beam Widths
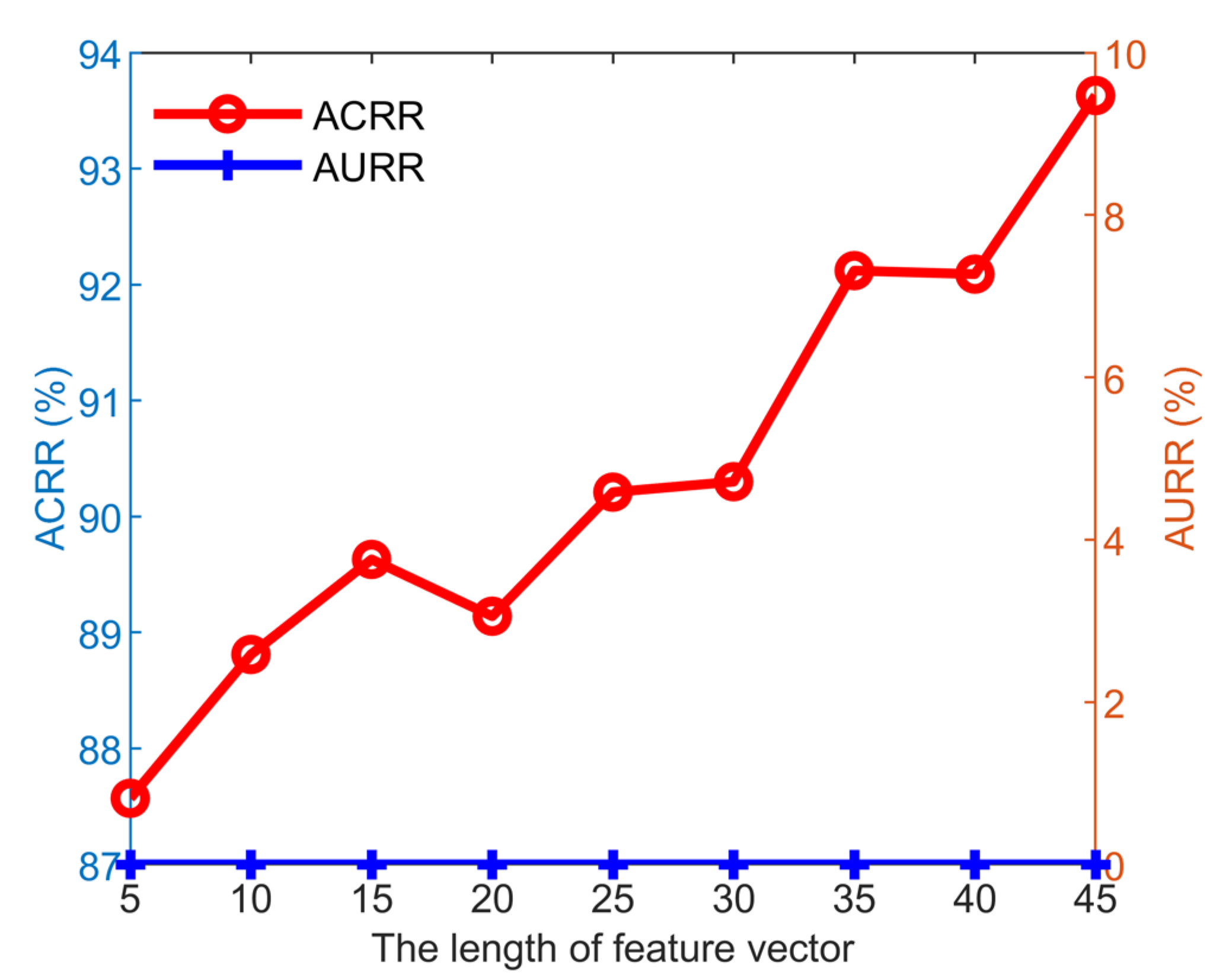
3.2. Performance Evaluation of the Proposed Method Under Different Lengths of Feature Vectors
3.3. Performance Evaluation with Measured Data
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| UAV | Unmanned Aviation Vehicle |
| ADS-B | Automatic Dependent Surveillance Broadcast |
| HRRP | High-Resolution Range Profile |
| IO | Illuminator of Opportunity |
| ISAR | Inverse Synthetic Aperture Radar |
| DTMB | Digital Television Terrestrial Multimedia Broadcasting |
| RCS | Radar Cross-Section |
| TBD | Tracking Before Detection |
| JTC | Joint Tracking and Classification |
| RBT | Recognition Before Tracking |
| RD | Range-Doppler |
| ED | Euclidean Distance |
| TC | Trend Consistency |
| VC | Volatility Consistency |
| NBV | Normalized Bistatic Velocity |
| MIVS | Minimum Value Sequence |
| MEVS | Mean Value Sequence |
| MAVS | Maximum Value Sequence |
| FRS | Final Recognition Score |
| DOA | Direction of Arrival |
| GAA | General Aviation Aircraft |
| CAA | Civil Aviation Aircraft |
| DTW | Dynamic Time Warping |
| DRS | Distance Recognition Score |
| TCS | TC Score |
| VCS | VC Score |
| PSO | Particle Swarm Optimization |
| ACRR | Average Correct Recognition Rate |
| AURR | Average Unknown Recognition Rate |
| CRR | Correct Recognition Rate |
References
- Ma, B.; Egiazarian, K.O.; Chen, B. Low-resolution radar target classification using vision transformer based on micro-Doppler signatures. IEEE Sens. J. 2023, 23, 28474–28485. [Google Scholar] [CrossRef]
- Du, L.; He, H.; Zhao, L.; Wang, P. Noise robust radar HRRP target recognition based on scatterer matching algorithm. IEEE Sens. J. 2016, 16, 1743–1753. [Google Scholar] [CrossRef]
- Guo, P.; Liu, Z.; Wang, J. Radar group target recognition based on HRRPs and weighted mean shift clustering. J. Syst. Eng. Electron. 2020, 31, 1152–1159. [Google Scholar] [CrossRef]
- Shu, K.; Yi, J.X.; Wan, X.R.; Cheng, F. A hybrid tracking algorithm for multistatic passive radar. IEEE Syst. J. 2021, 15, 2024–2034. [Google Scholar] [CrossRef]
- Colone, F.; Filippini, F.; Pastina, D. Passive radar: Past, present, and future challenges. IEEE Trans. Aerosp. Electron. Syst. Mag. 2022, 38, 54–69. [Google Scholar] [CrossRef]
- Del-Rey-Maestre, N.; Jarabo-Amores, M.-P.; Mata-Moya, D.; Almodovar-Hernandez, A.; Gomez-del-Hoyo, P.J. A DVB-T passive radar 3D-detection approach based on non-coherent spatial integration. In Proceedings of the 2020 17th European Radar Conference (EuRAD), Utrecht, The Netherlands, 10–15 January 2021. [Google Scholar]
- Azimifar, M.; Sebt, M.A. Clutter suppression in passive ISAR using compressive sensing. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 2210–2223. [Google Scholar] [CrossRef]
- Mahfoudia, O.; Horlin, F.; Neyt, X. Pilot-based detection for DVB-T passive coherent location radars. IET Radar Sonar Navig. 2020, 14, 845–851. [Google Scholar] [CrossRef]
- Wang, T.; Liu, B.; Wang, X.; Xu, X.; Wei, Q. Passive radar analysis using DTMB signal. In Proceedings of the 19th International Conference on Optical Communications and Networks (ICOCN), Qufu, China, 23–27 August 2021. [Google Scholar]
- Kulpa, K.; Malanowski, M.; Baczyk, M. Passive radar for drone detection and classification. In Proceedings of the 2025 26th International Radar Symposium (IRS), Hamburg, Germany, 21–23 May 2025. [Google Scholar]
- Dong, H.; Shan, T.; Feng, Y. Noise suppression and ridge extraction based on squeezing bandwidth for micro-Doppler feature extraction. IEEE Trans. Instrum. Meas. 2025, 74, 8509113. [Google Scholar] [CrossRef]
- Santi, F.; Pisciottano, I.; Pastina, D.; Cristallini, D. Multi-angle DVB-S based passive ISAR sensitivity to target motion estimation errors. In Proceedings of the 2023 IEEE Radar Conference (RadarConf23), San Antonio, TX, USA, 1–5 May 2023. [Google Scholar]
- Manno-Kovacs, A.; Giusti, E.; Berizzi, F.; Kovacs, F. Image based robust target classification for passive ISAR. IEEE Sens. J. 2019, 19, 268–276. [Google Scholar] [CrossRef]
- Ehrman, L.M.; Lanterman, A.D. Incorporation of aircraft orientation into automatic target recognition using passive radar. IET Radar Sonar Navig. 2020, 14, 1079–1087. [Google Scholar] [CrossRef]
- Fix, J.; Ren, C.F.; Lopes, A.C.; Morice, G.; Kobayashi, S.; Letertre, T.; Hinostroza, I. Deep learning for aircraft classification from VHF radar signatures. IET Radar Sonar Navig. 2021, 15, 697–707. [Google Scholar] [CrossRef]
- Pisane, J.; Azarian, S.; Lesturgie, M.; Verly, J. Automatic target recognition for passive radar. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 371–392. [Google Scholar] [CrossRef]
- Cao, X.; Yi, J.; Gong, Z.; Wan, X. Automatic target recognition based on RCS and angular diversity for multistatic passive radar. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 4226–4240. [Google Scholar] [CrossRef]
- Zhan, W.J.; Yi, J.X.; Wan, X.R.; Rao, Y.H. Track-feature-based target classification in passive radar for low-altitude airspace surveillance. IEEE Sens. J. 2021, 21, 10017–10028. [Google Scholar] [CrossRef]
- Tang, T.; Wang, P.B.; Zhao, P.; Zeng, H.C.; Chen, J. A novel multi-target TBD scheme for GNSS-based passive bistatic radar. IET Radar Sonar Navig. 2024, 18, 2497–2512. [Google Scholar] [CrossRef]
- Zhang, C.; Shi, S.; Gong, J.; Li, R. A coherent TBD algorithm for remote sensing of weak targets using GNSS reflected signals. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2024, 17, 11485–11502. [Google Scholar] [CrossRef]
- Xu, L.; Zhan, K.; Jiang, H.; Bai, L.; Wu, M. Joint tracking and classification on aerodynamic model and RCS by ground-based passive radar. In Proceedings of the 2014 IEEE Chinese Guidance, Navigation and Control Conference, Yantai, China, 8–10 August 2014. [Google Scholar]
- Faloutsos, C.; Ranganathan, M.; Manolopoulos, Y. Fast subsequence matching in time-series database. ACG SIGMOD Rec. 1994, 23, 419–429. [Google Scholar] [CrossRef]
- Schafer, P.; Brand, J.; Leser, U.; Peng, B.; Palpanas, T. Fast and exact similarity search in less than a blink of an eye. In Proceedings of the IEEE 41st International Conference on Data Engineering (ICDE), Hong Kong, China, 19–23 May 2025. [Google Scholar]
- Zhang, H.; Dong, Y.; Li, J.; Xu, D. Dynamic time warping under product quantization, with applications to time-series data similarity search. IEEE Internet Things J. 2022, 9, 11814–11826. [Google Scholar] [CrossRef]
- Teng, Y.; Wang, G.; He, C.; Wu, Y.; Li, C. Optimization of dynamic time warping algorithm for abnormal signal detection. Int. J. Data Sci. Anal. 2025, 19, 115–127. [Google Scholar] [CrossRef]
- Belkhouja, T.; Yan, Y.; Doppa, J.R. Dynamic time warping based adversarial framework for time-series domain. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 7353–7366. [Google Scholar] [CrossRef]
- Li, W.; He, R.; Liang, B.; Yang, F.; Han, S. Similarity measure of time series with different sampling frequencies based on context density consistency and dynamic time warping. IEEE Signal Process. Lett. 2023, 30, 1417–1421. [Google Scholar] [CrossRef]
- Liu, C.; Zeng, Q.; Cheng, L.; Duan, H.; Cheng, J. Measuring similarity for data-aware business processes. IEEE Trans. Autom. Sci. Eng. 2022, 19, 1070–1082. [Google Scholar] [CrossRef]

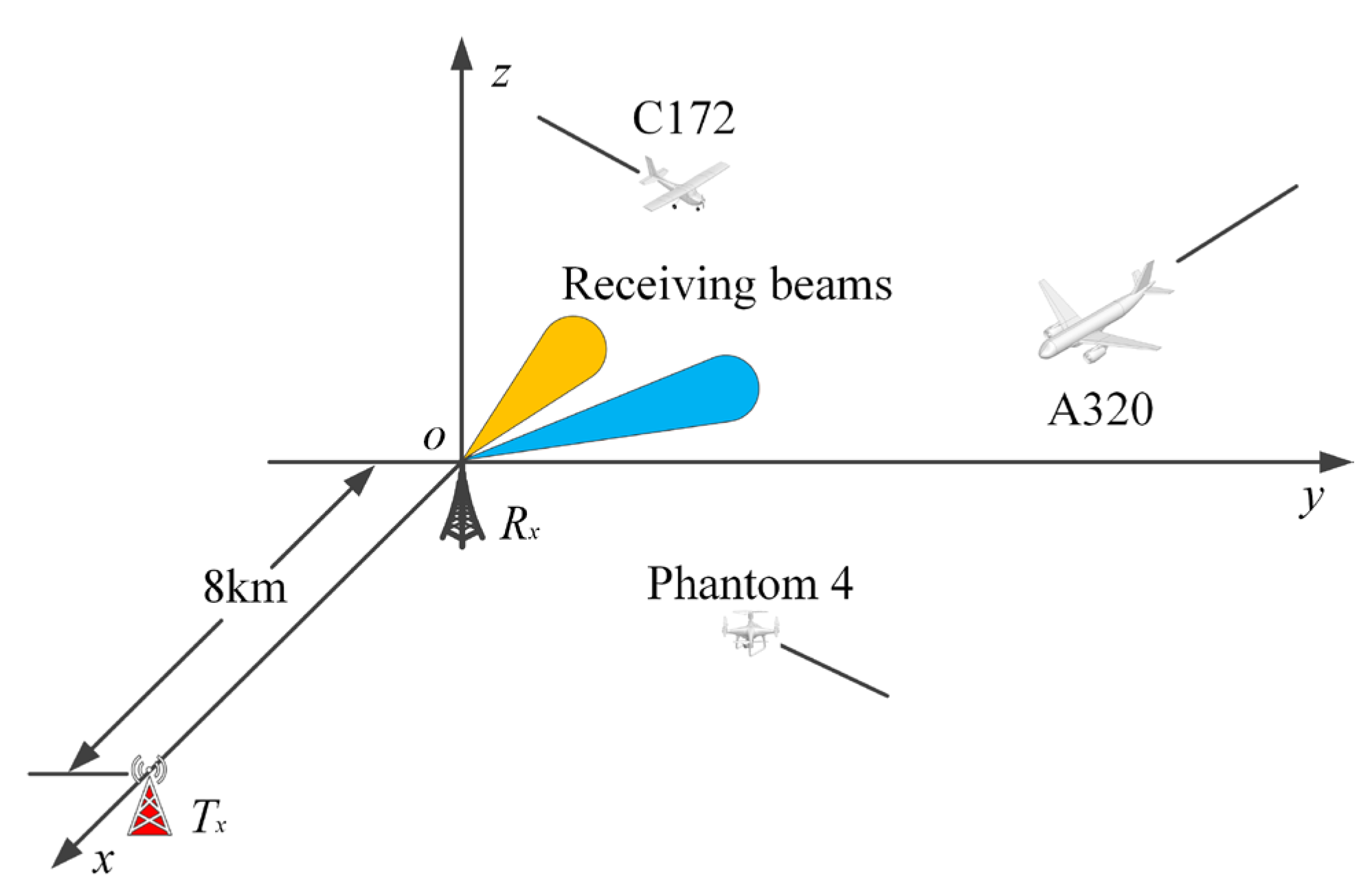
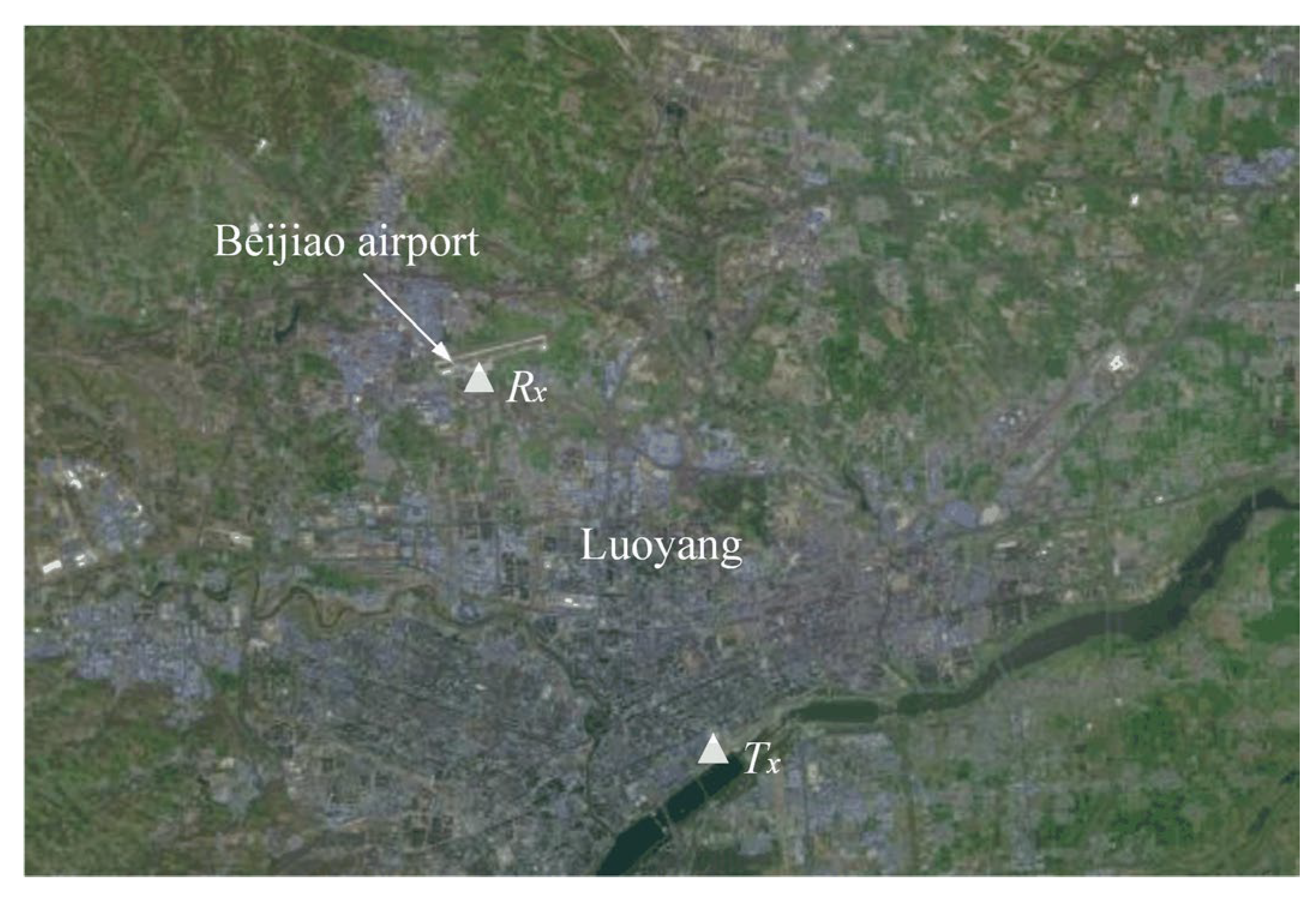
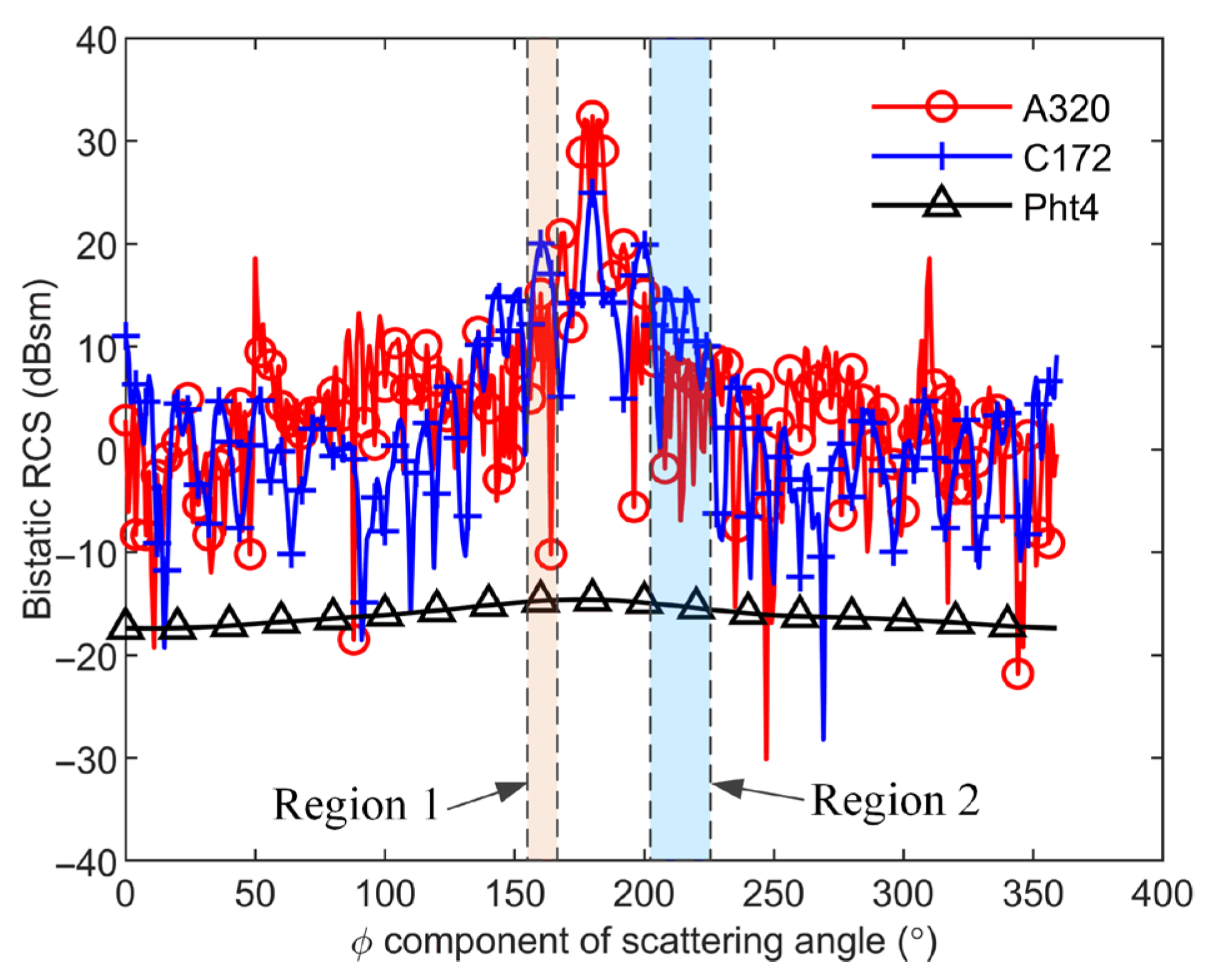
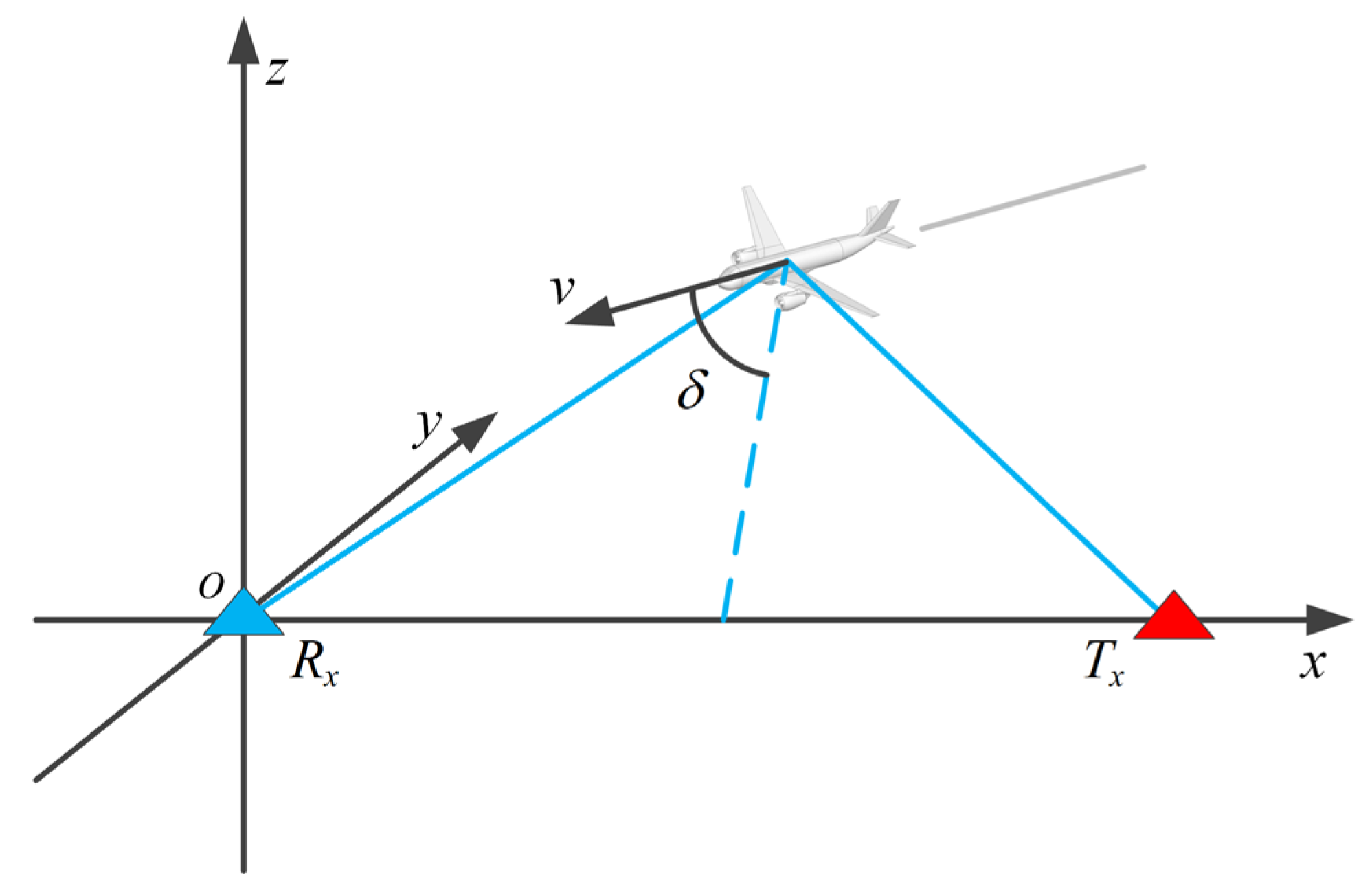
| Standard Targets | CRR | URR | |||||
|---|---|---|---|---|---|---|---|
| Pht4 | SR20 | A320 | Unknown | ||||
| Testing targets | Pht4 | 109 | 0 | 0 | 0 | 100% | 0% |
| SR20 | 1 | 72 | 16 | 0 | 80.90% | 0% | |
| A320 | 0 | 29 | 83 | 0 | 74.11% | 0% | |
| Total | 110 | 101 | 99 | 0 | 85.16% | 0% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, X.; Ma, H.; Jin, J.; Wan, X.; Yi, J. A Novel Recognition-Before-Tracking Method Based on a Beam Constraint in Passive Radars for Low-Altitude Target Surveillance. Appl. Sci. 2025, 15, 9957. https://doi.org/10.3390/app15189957
Cao X, Ma H, Jin J, Wan X, Yi J. A Novel Recognition-Before-Tracking Method Based on a Beam Constraint in Passive Radars for Low-Altitude Target Surveillance. Applied Sciences. 2025; 15(18):9957. https://doi.org/10.3390/app15189957
Chicago/Turabian StyleCao, Xiaomao, Hong Ma, Jiang Jin, Xianrong Wan, and Jianxin Yi. 2025. "A Novel Recognition-Before-Tracking Method Based on a Beam Constraint in Passive Radars for Low-Altitude Target Surveillance" Applied Sciences 15, no. 18: 9957. https://doi.org/10.3390/app15189957
APA StyleCao, X., Ma, H., Jin, J., Wan, X., & Yi, J. (2025). A Novel Recognition-Before-Tracking Method Based on a Beam Constraint in Passive Radars for Low-Altitude Target Surveillance. Applied Sciences, 15(18), 9957. https://doi.org/10.3390/app15189957





