Characteristics of Mining-Induced Stress Rotation Due to Unloading in Deep Roadway Excavation and Surrounding Rock Control Countermeasures
Abstract
1. Introduction
2. Engineering Background and Numerical Simulation
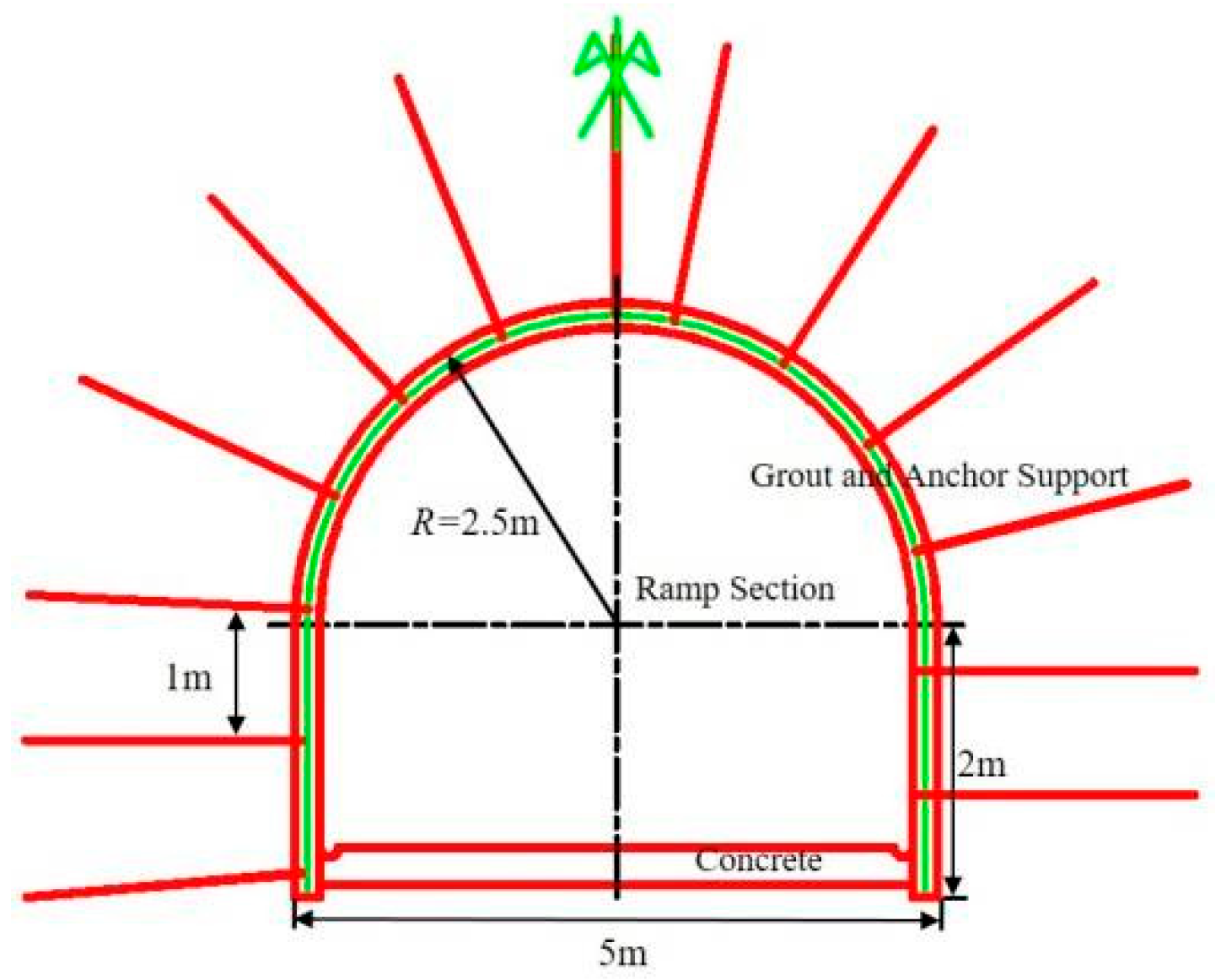
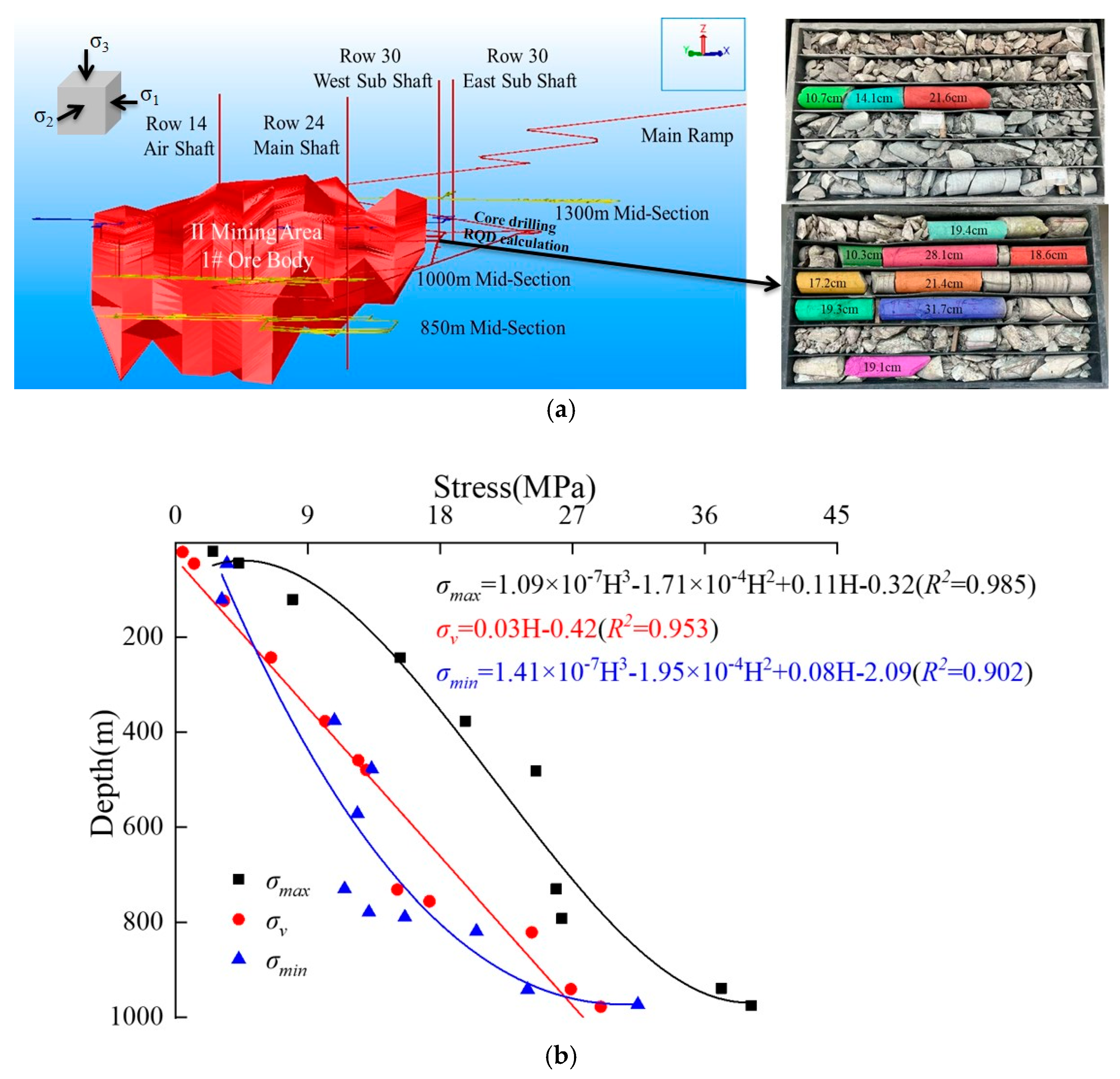
2.1. Engineering Background
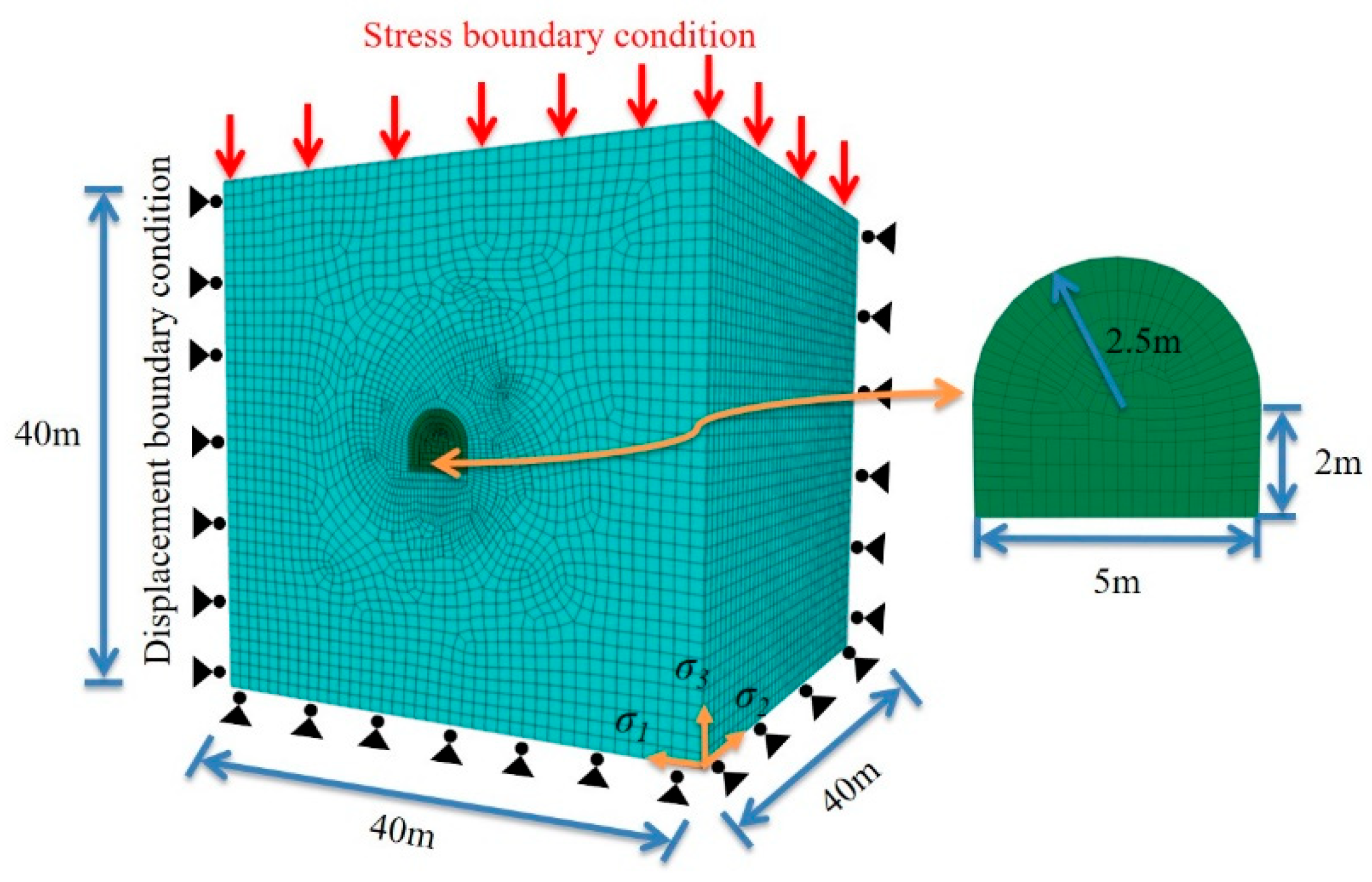
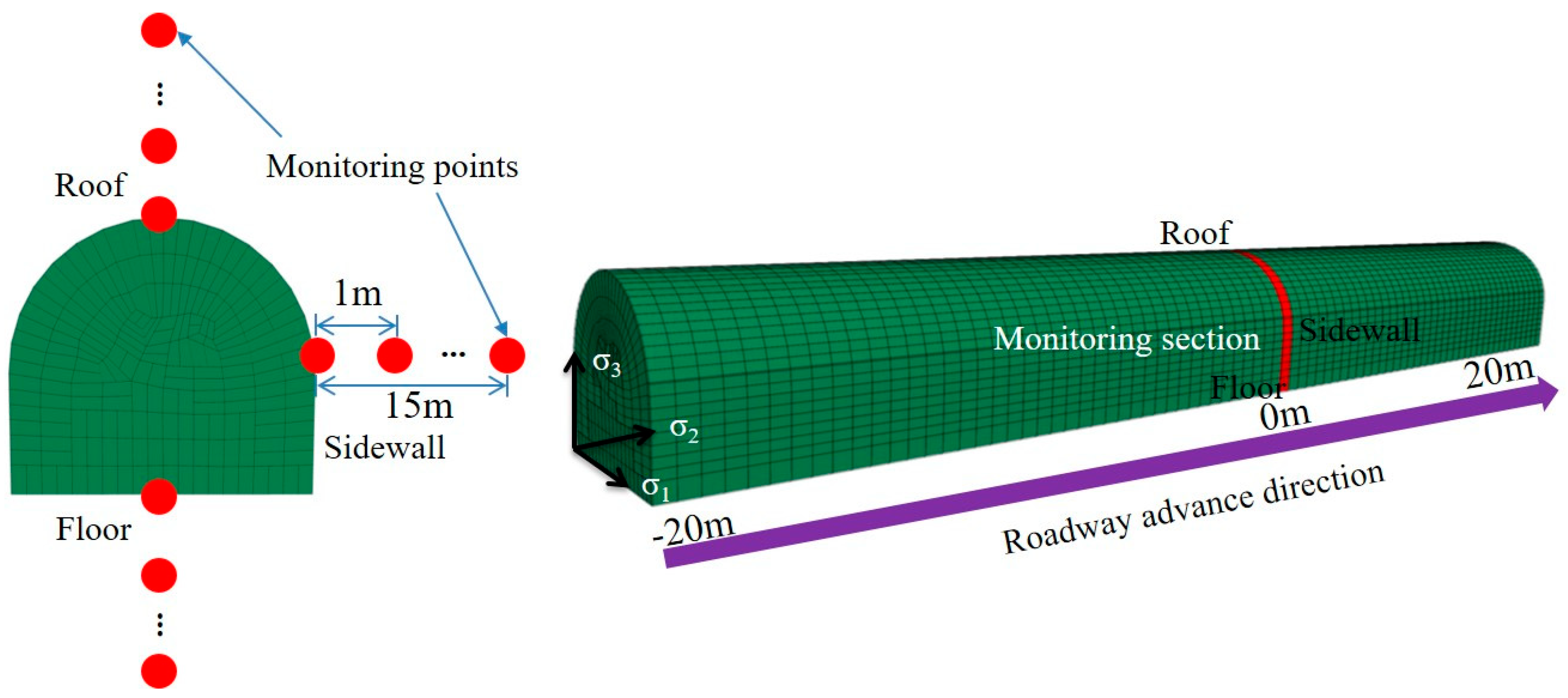
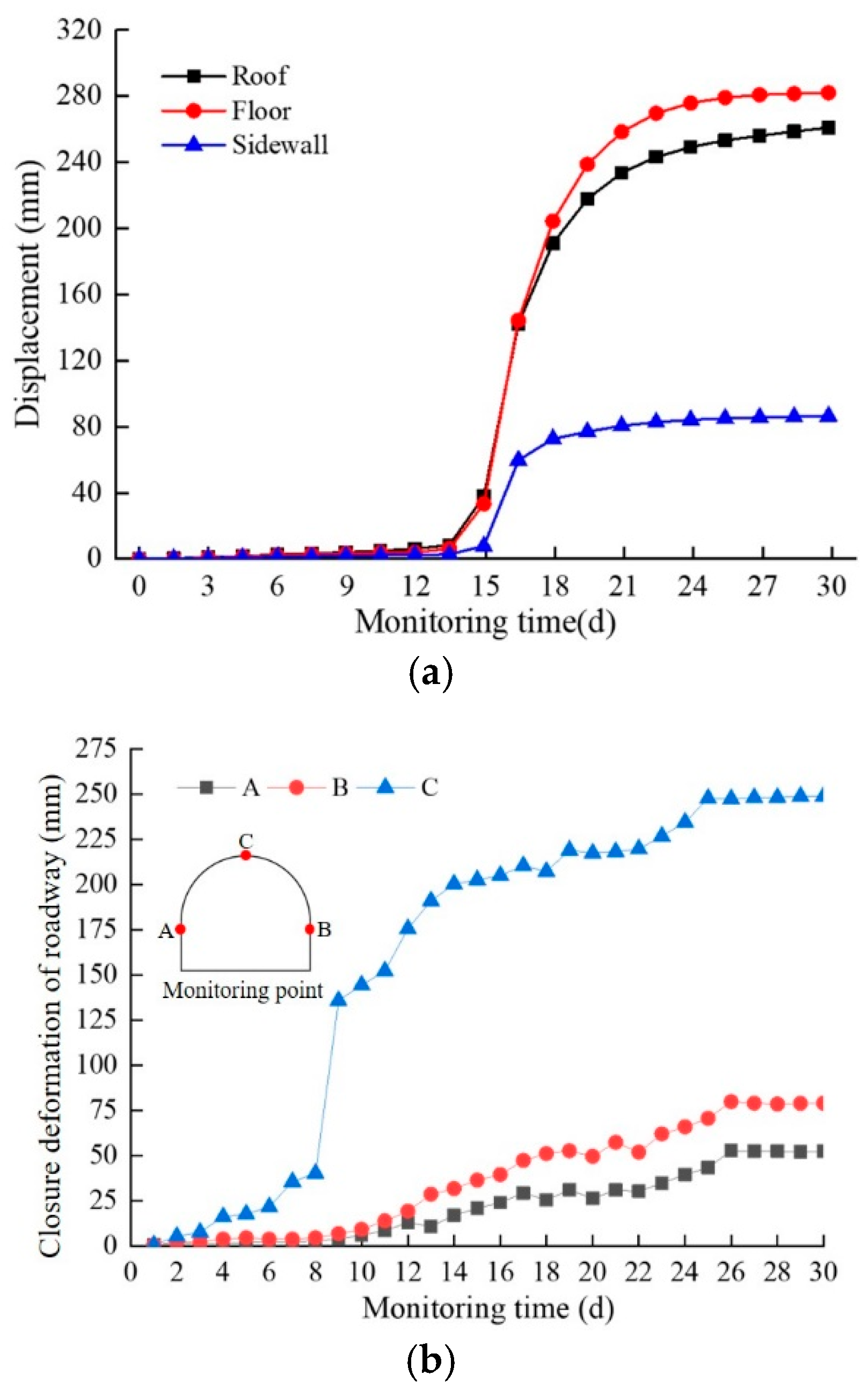
2.2. Construction and Reliability Verification of Numerical Model
3. Evolution Characteristics of Mining-Induced Stress in Surrounding Rock During Excavation and Unloading of Deep Roadways
3.1. Mechanism of Principal Stress Rotation in Surrounding Rock
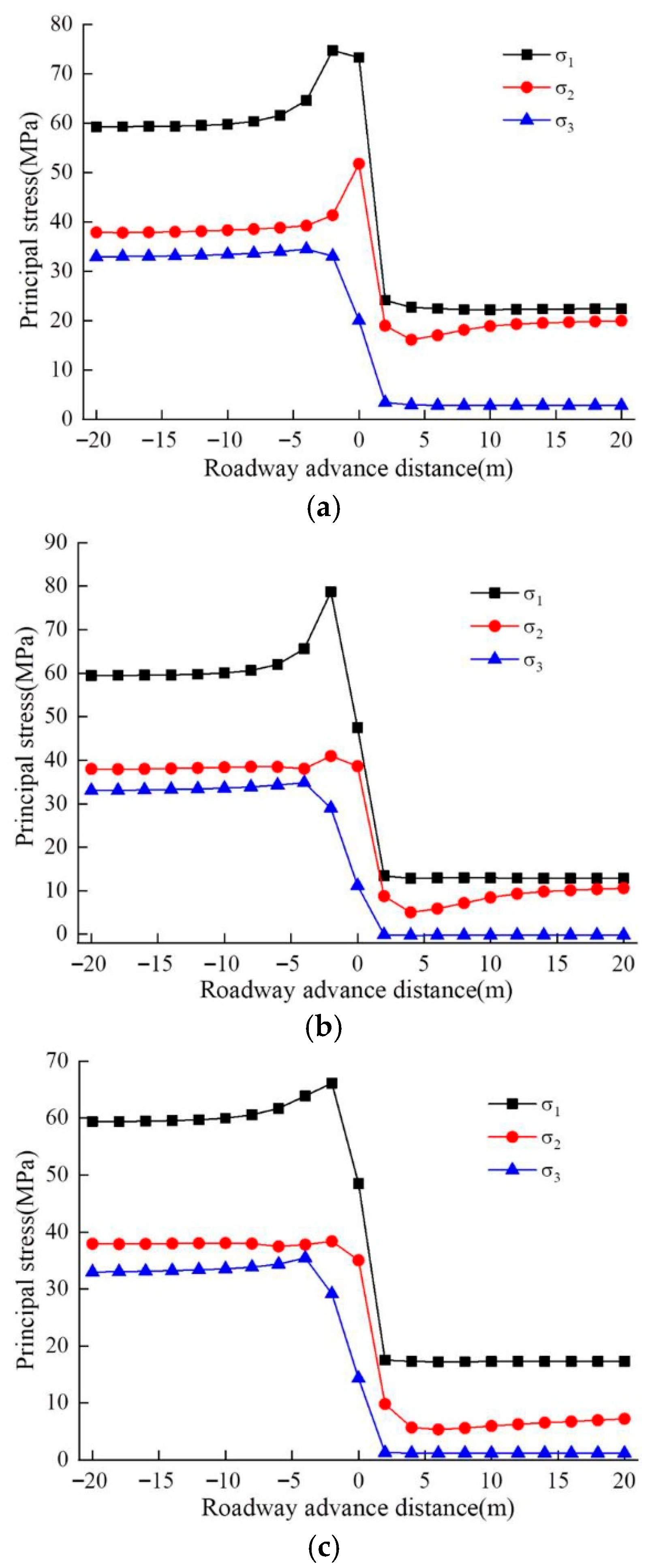
3.2. Variation Process of the Principal Stress Magnitude in the Surrounding Rock
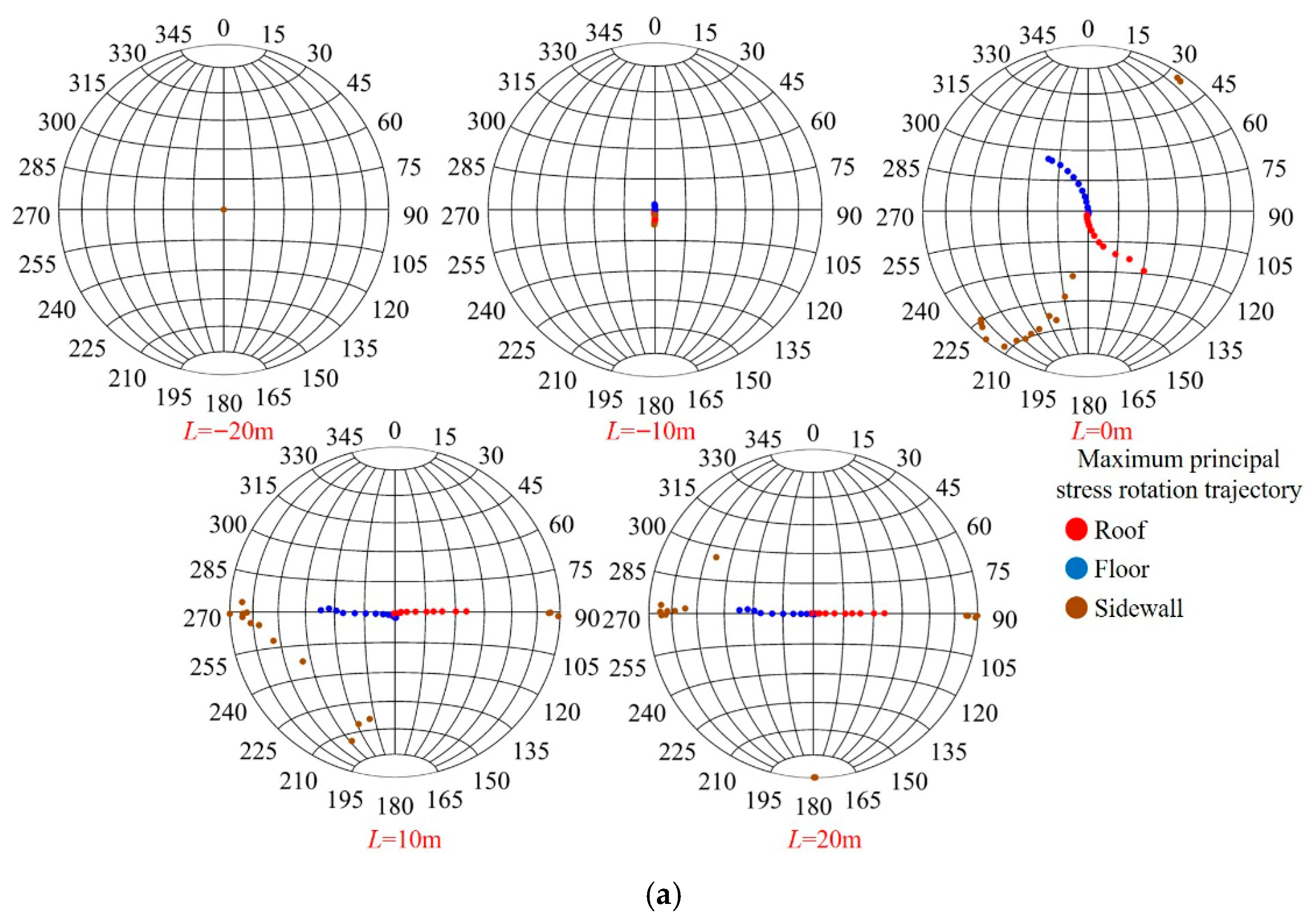
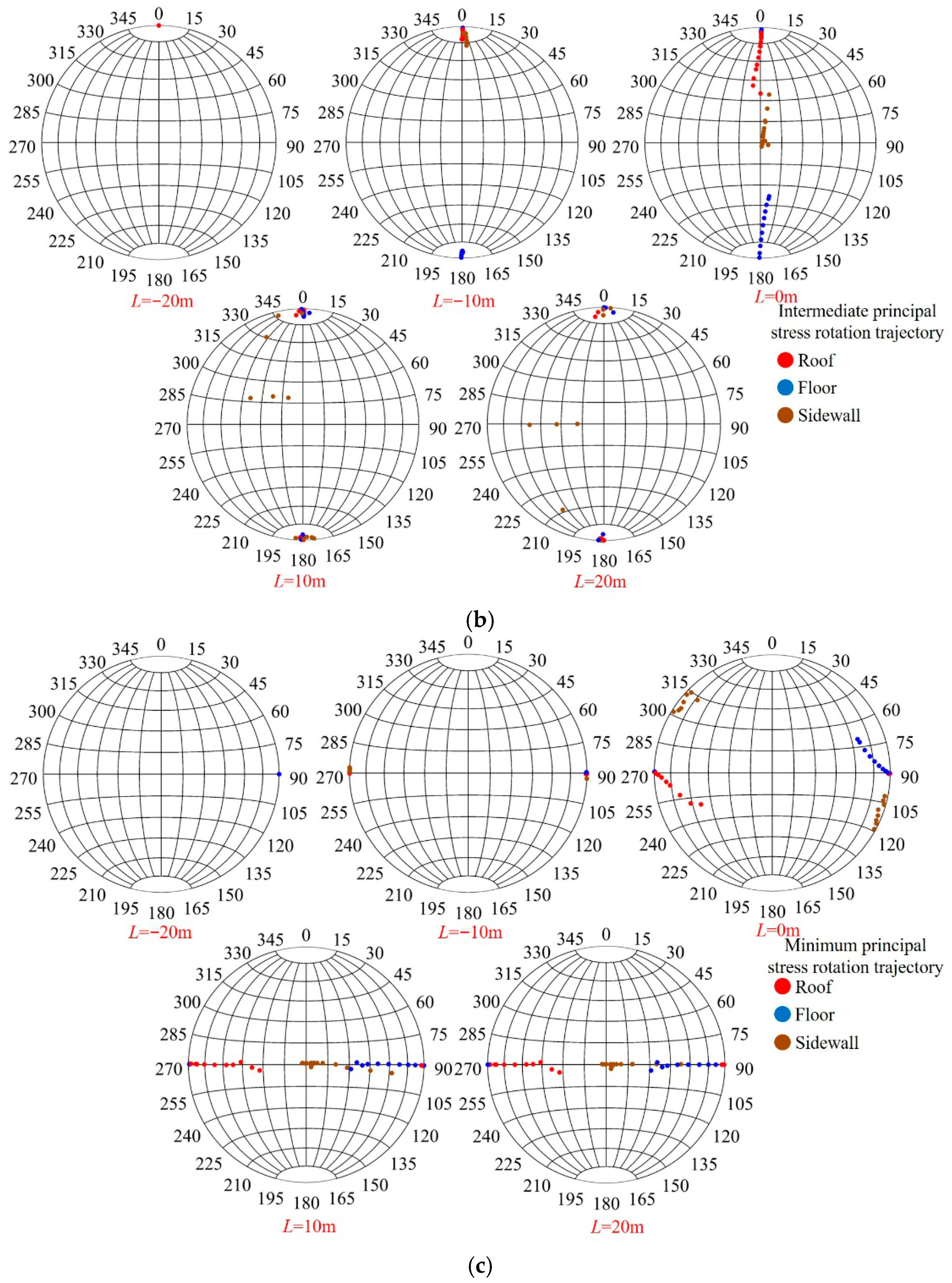
3.3. Evolution Law of Principal Stress Direction in Surrounding Rock
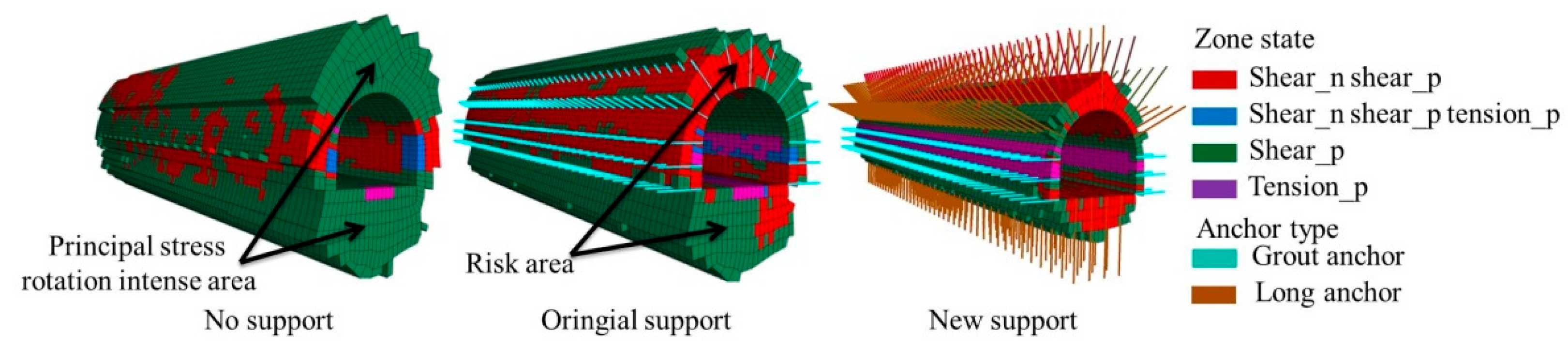
4. Mining-Induced Stress Rotation Guiding Roadway Surrounding Rock Control
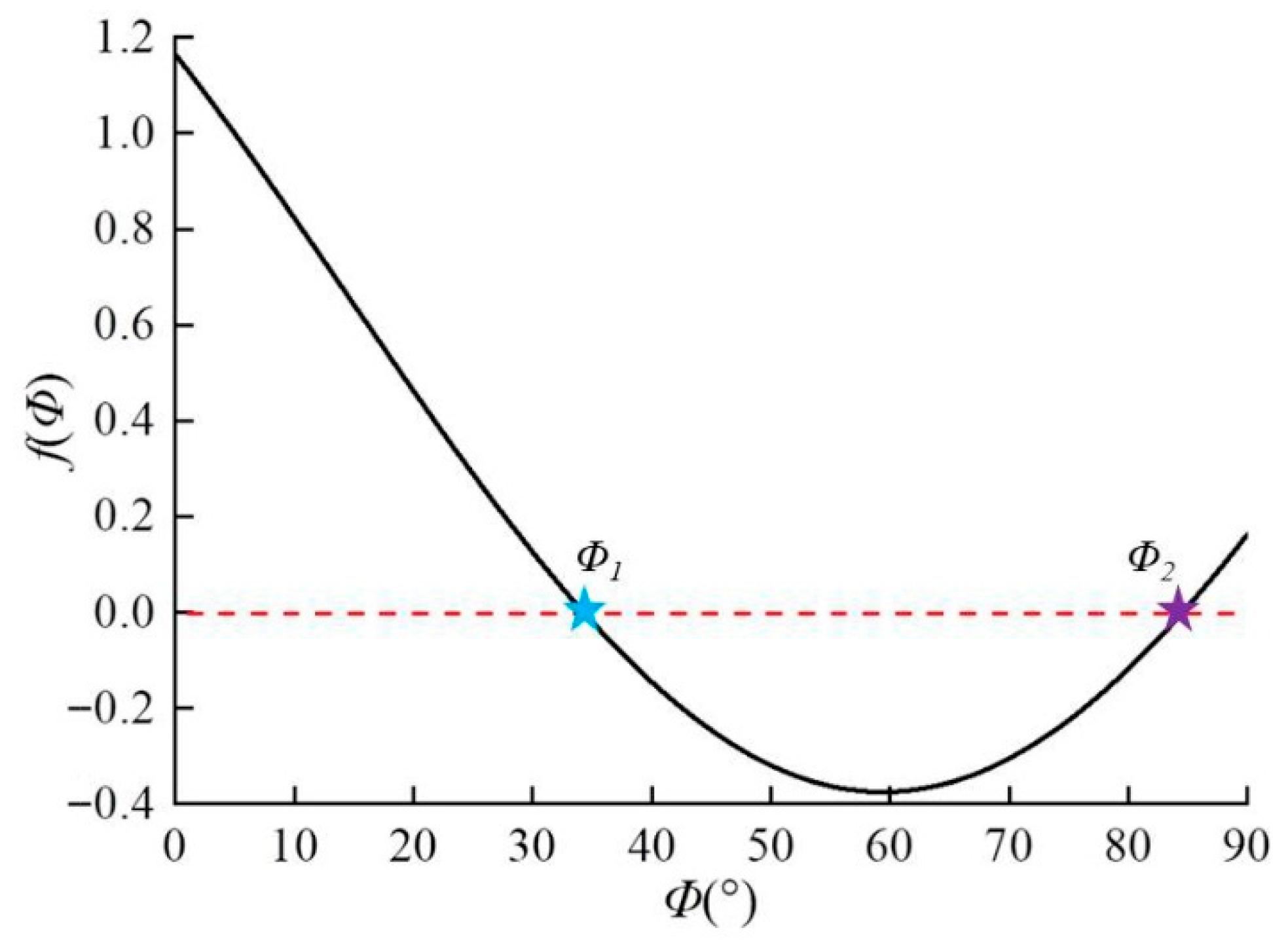
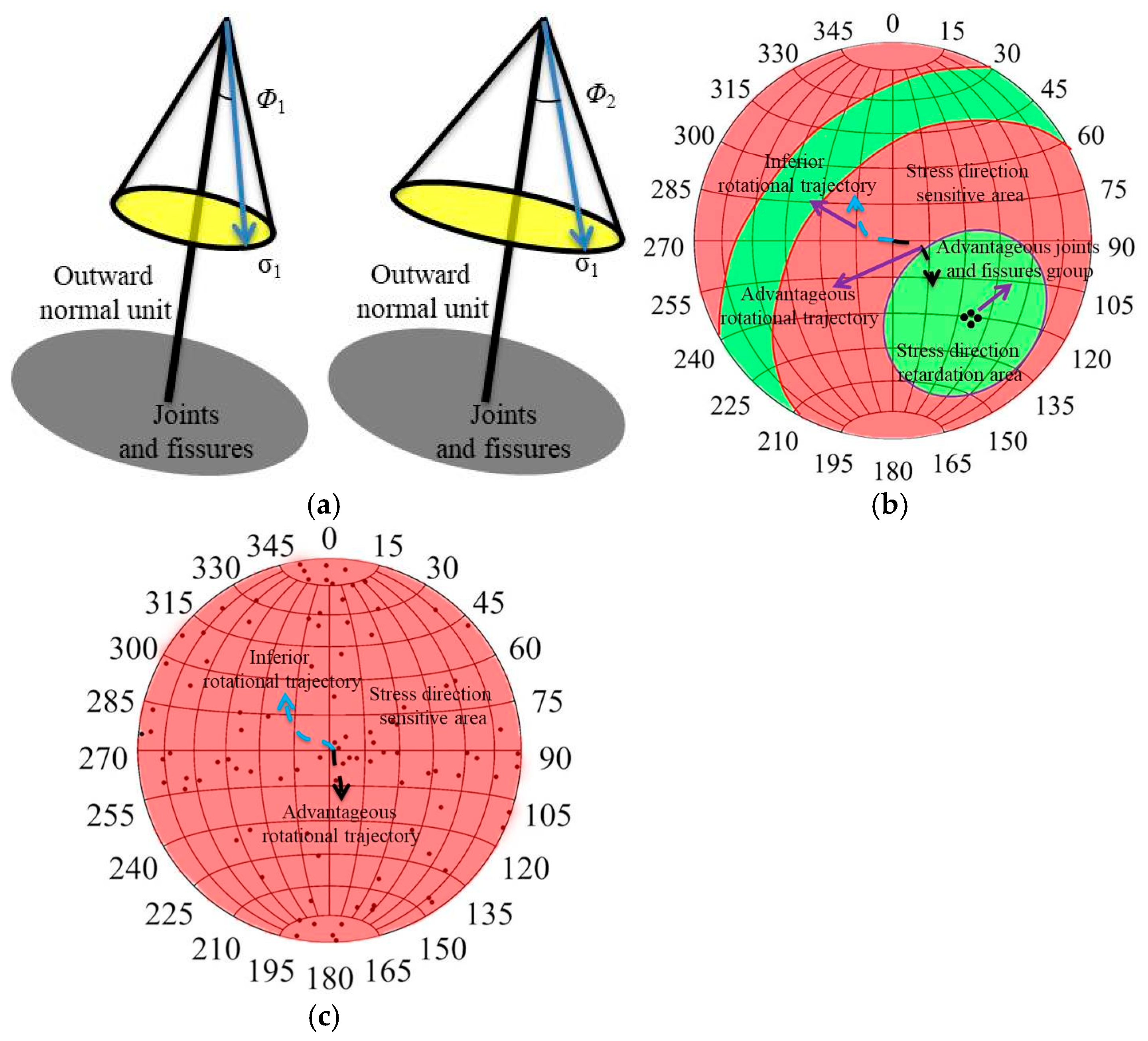
4.1. Determination of Dominant Rotation Trajectory of Mining-Induced Stress
4.2. Asymmetric Coupling Support Scheme
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dai, L.; Feng, D.; Pan, Y.; Wang, A.; Ma, Y.; Xiao, Y.; Zhang, J. Quantitative principles of dynamic interaction between rock support and surrounding rock in rockburst roadways. Int. J. Min. Sci. Technol. 2025, 35, 41–55. [Google Scholar] [CrossRef]
- Zhang, C.; Li, D.; Su, X.; Luo, P.; Ma, J.; Zhu, Q. Fracture behavior of thermally treated granite under compression-shear loading. Int. J. Rock. Mech. Min. Sci. Géoméch. Abstr. 2024, 184, 105966. [Google Scholar] [CrossRef]
- Si, X.; Zhang, Z.; Li, X.; Yi, G.; Luo, Y.; Tan, L.; Han, K. Influences of maximum principal stress direction and cross-section shape on tunnel stability. J. Rock. Mech. Geotech. Eng. 2025, 17, 2159–2180. [Google Scholar] [CrossRef]
- Han, Z.; Li, D.; Li, X. Dynamic mechanical properties and wave propagation of composite rock-mortar specimens based on SHPB tests. Int. J. Min. Sci. Technol. 2022, 32, 793–806. [Google Scholar] [CrossRef]
- Gong, H.; Li, D.; Luo, P.; Ru, W.; Zhang, G.; Liu, Y. Floor heave mechanism and stiff control technology by I-beam for deep mine roadway. Eng. Fail. Anal. 2025, 175, 109600. [Google Scholar] [CrossRef]
- Zhao, C.; Li, Y.; Liu, G.; Meng, X. Mechanism analysis and control technology of surrounding rock failure in deep soft rock roadway. Eng. Fail. Anal. 2020, 115, 104611. [Google Scholar] [CrossRef]
- Yang, Z.; Tao, M.; Ranjith, P. Novel insights into grain size effect of stressed crystalline rock using weakened grain boundary model. Int. J. Rock. Mech. Min. Sci. Géoméch. Abstr. 2025, 189, 106098. [Google Scholar] [CrossRef]
- Li, G.; Ma, F.; Guo, J.; Zhao, H.; Liu, G. Study on deformation failure mechanism and support technology of deep soft rock roadway. Eng. Geol. 2020, 264, 105262. [Google Scholar] [CrossRef]
- Jing, H.; Wu, J.; Yin, Q.; Wang, K. Deformation and failure characteristics of anchorage structure of surrounding rock in deep roadway. Int. J. Min. Sci. Technol. 2020, 30, 593–604. [Google Scholar] [CrossRef]
- Han, Z.; Li, J.; Wang, H.; Zhao, J. Initiation and propagation of a single internal 3D crack in brittle material under dynamic loads. Eng. Fract. Mech. 2023, 285, 109299. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, W.; Shui, Y.; Liu, P. Mining-induced stress rotation trace and its sensitivity to face advance direction in kilometer deep longwall panel with large face length. J. China Coal Soc. 2022, 47, 634–650. [Google Scholar]
- Liu, J.; Zhu, K.; Zuo, J.; Sun, K.; Sheng, Y.; Jia, B. Soft rock deformation and failure modes under principal stress rotation from roadway excavation. Bull. Eng. Geol. Environ. 2024, 83, 83. [Google Scholar] [CrossRef]
- Diederichs, M.; Kaiser, P.; Eberhardt, E. Damage initiation and propagation in hard rock during tunnelling and the influence of near-face stress rotation. Int. J. Rock. Mech. Min. Sci. Géoméch. Abstr. 2004, 41, 785–812. [Google Scholar] [CrossRef]
- Kaiser, P.; Yazici, S.; Maloney, S. Mining-induced stress change and consequences of stress path on excavation stability—A case study. Int. J. Rock. Mech. Min. Sci. Géoméch. Abstr. 2001, 38, 167–180. [Google Scholar] [CrossRef]
- Eberhardt, E. Numerical modelling of three-dimension stress rotation ahead of an advancing tunnel face. Int. J. Rock. Mech. Min. Sci. Géoméch. Abstr. 2001, 38, 499–518. [Google Scholar] [CrossRef]
- Du, S.; Wu, G.; Zhao, Y.; Ma, L. Re-orientation of principal stresses during tunnel excavation: Model development and support strategy. Alex. Eng. J. 2024, 107, 591–613. [Google Scholar] [CrossRef]
- Ma, J.; Li, D.; Du, S.; Han, Z.; Luo, P.; Zhao, J. Comparison of subcritical crack growth and dynamic fracture propagation in rocks under double-torsion tests. Int. J. Rock. Mech. Min. Sci. Géoméch. Abstr. 2023, 56, 7905–7922. [Google Scholar] [CrossRef]
- Colwell, M.; Frith, R. Why uniaxial compressive strength and Young’s modulus are commonly poor indicators of roadway roof stability-except in the tailgate. In Proceedings of the International Conference on Ground Control in Mining, Morgantown, WV, USA, 1–3 August 2006. [Google Scholar]
- Li, K.-S.; Luan, Y.-Q.; Zhang, J.-P.; Liu, C.-X. Experimental study on mechanical behavior, AE response and energy evolution of fissure-filled sandstone from mine roadway under conventional triaxial compression. Theor. Appl. Fract. Mech. 2024, 130, 104334. [Google Scholar] [CrossRef]
- Kong, P.; Jiang, L.; Jiang, J.; Wu, Y.; Chen, L.; Ning, J. Numerical analysis of roadway rock-burst hazard under superposed dynamic and static loads. Energies 2019, 12, 3761. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, D.; Nowamooz, H.; Jiang, C.; Ye, C. Investigation on damage and failure mechanisms of roadway surrounding rock triggered by dynamic–static combined loads. Rock. Mech. Rock. Eng. 2022, 55, 5639–5657. [Google Scholar] [CrossRef]
- Han, Z.; Yan, Z.; Li, D.; Wang, H.; Wang, H. Dynamic fracture mechanism from a pre-existing flaw in granite: Insights from grain-based modelling. Soil. Dyn. Earthq. Eng. 2024, 184, 108810. [Google Scholar] [CrossRef]
- Ma, Q.; He, X.; Zhou, Y.-G.; Chen, Y.-M.; Han, Y.-S. An approach to DEM simulation of hollow torsional shear tests for achieving general loading paths. Comput. Geotech. 2024, 172, 106402. [Google Scholar] [CrossRef]
- Zhou, H.; Jiang, Y.; Lu, J.; Gao, Y.; Chen, J. Development of a hollow cylinder torsional apparatus for rock. Rock. Mech. Rock. Eng. 2018, 51, 3845–3852. [Google Scholar] [CrossRef]
- Zuo, J.; Ma, Z.; Xu, C.; Zhan, S.; Liu, H. Mechanism of principal stress rotation and deformation failure behavior induced by excavation in roadways. J. Rock. Mech. Geotech. Eng. 2024, 16, 4605–4624. [Google Scholar] [CrossRef]
- Xiong, X.; Nie, W.; Ouyang, Y.; Dai, J.; Huang, Y. Principal stress rotation effect and multi-factor coupling support optimization in roadways of inclined coal seams. Sci. Rep. 2025, 15, 25628. [Google Scholar] [CrossRef]
- Wang, J.C.; Wang, Z.H.; Yang, S.L. Stress analysis of longwall top-coal caving face adjacent to the gob. Int. J. Min. Reclam. Environ. 2020, 34, 476–497. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Z.; Yang, S. A coupled macro- and meso-mechanical model for heterogeneous coal. Int. J. Rock. Mech. Min. Sci. Géoméch. Abstr. 2017, 94, 64–81. [Google Scholar] [CrossRef]
- Lu, Z.; Ju, W.; Zhao, Y.; Wang, H.; Zheng, J.; Liu, A. Analysis of the mining induced stress rotation influence on fault stability. Rock Soil Mech. 2019, 40, 4459–4466. [Google Scholar]
- Oliva, S.J.; Ebinger, C.J.; Rivalta, E.; Williams, C.A.; Wauthier, C.; Currie, C.A. State of stress and stress rotations: Quantifying the role of surface topography and subsurface density contrasts in magmatic rift zones (Eastern Rift, Africa). Earth Planet. Sci. Lett. 2022, 584, 117478. [Google Scholar] [CrossRef]
- Zheng, Z.; Feng, X.-T.; Zhang, X.; Zhao, J.; Yang, C.-X. Residual strength characteristics of cjpl marble under true triaxial compression. Rock. Mech. Rock. Eng. 2019, 52, 1247–1256. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Z.; Tang, Y.; Sun, W.; Feng, Y. Regional failure mechanism of main roof and zonal method for ground control inkilometer-deep longwall panel with large face length. J. China Coal Soc. 2023, 48, 3615–3627. [Google Scholar]
- Jaeger, J.C. Shear failure of anistropic rocks. Geol. Mag. 1960, 97, 65–72. [Google Scholar] [CrossRef]
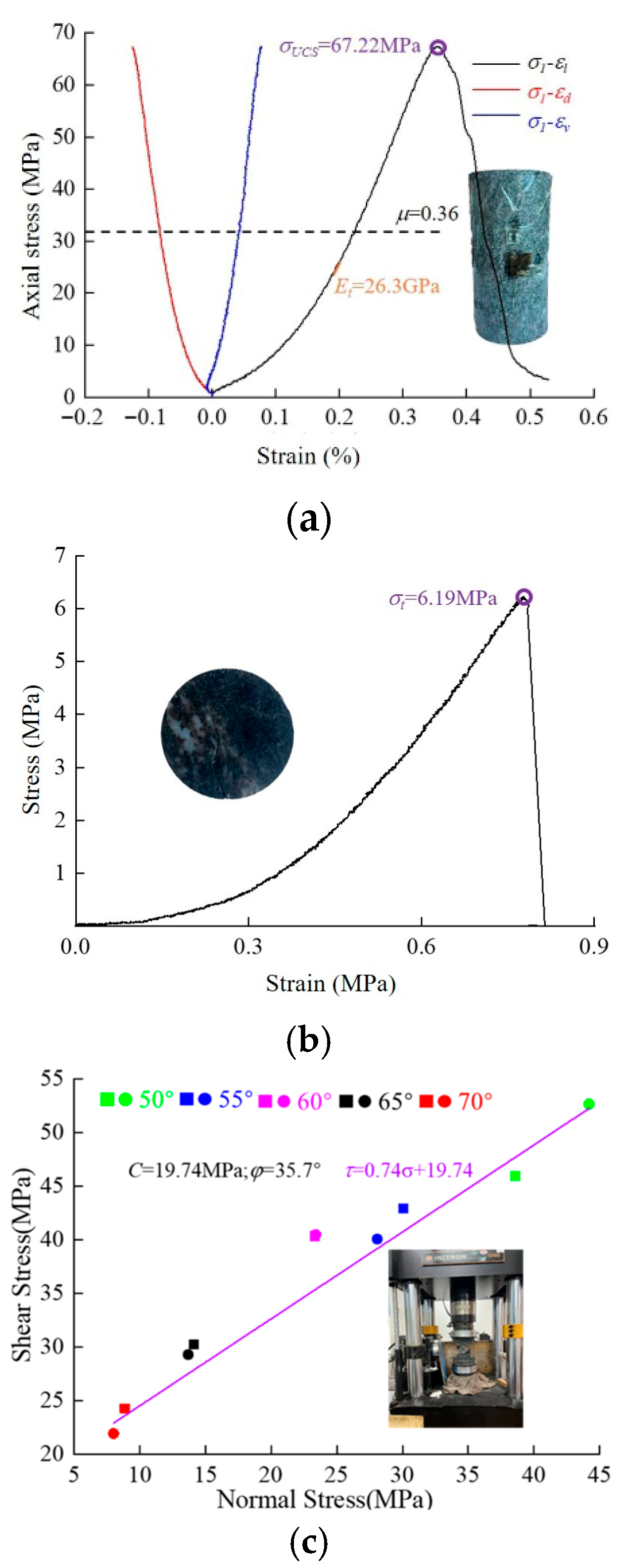
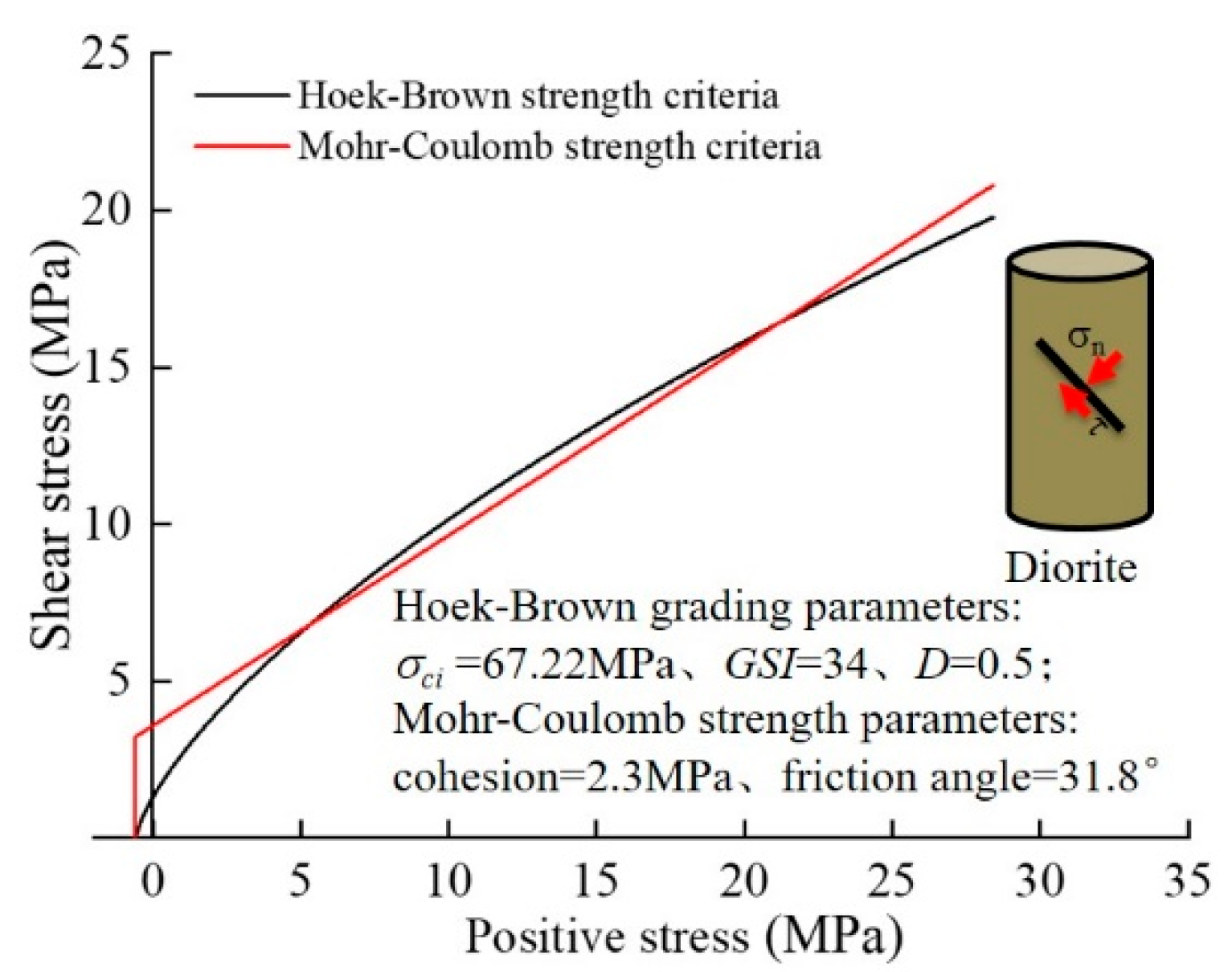




| Lithology | σc (MPa) | σt (MPa) | Cohesion (MPa) | Friction Angle (°) | Elastic Modulus (GPa) | Poisson’s Ratio | Density (g/cm3) |
|---|---|---|---|---|---|---|---|
| Diorite | 67.22 | 6.19 | 19.74 | 35.7 | 26.3 | 0.36 | 2.84 |
| Lithology | Cohesion (MPa) | Friction Angle (°) | Elastic Modulus (GPa) | Poisson’s Ratio | Tension Strength (MPa) |
|---|---|---|---|---|---|
| Diorite | 2.3 | 31.8 | 2.63 | 0.32 | 1.17 |
| Structural Type | Yong Modulus (GPa) | Poisson’s Ratio | Cross-Sectional Area (m2) | Yield Tension (GPa) | Grout Cohesion (GPa) |
|---|---|---|---|---|---|
| Anchor | 73.9 | 0.21 | 6 × 10−3 | 5.12 | 1.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Gong, H.; Han, Z.; Ru, W.; Luo, P. Characteristics of Mining-Induced Stress Rotation Due to Unloading in Deep Roadway Excavation and Surrounding Rock Control Countermeasures. Appl. Sci. 2025, 15, 9950. https://doi.org/10.3390/app15189950
Li D, Gong H, Han Z, Ru W, Luo P. Characteristics of Mining-Induced Stress Rotation Due to Unloading in Deep Roadway Excavation and Surrounding Rock Control Countermeasures. Applied Sciences. 2025; 15(18):9950. https://doi.org/10.3390/app15189950
Chicago/Turabian StyleLi, Diyuan, Hao Gong, Zhenyu Han, Wenkai Ru, and Pingkuang Luo. 2025. "Characteristics of Mining-Induced Stress Rotation Due to Unloading in Deep Roadway Excavation and Surrounding Rock Control Countermeasures" Applied Sciences 15, no. 18: 9950. https://doi.org/10.3390/app15189950
APA StyleLi, D., Gong, H., Han, Z., Ru, W., & Luo, P. (2025). Characteristics of Mining-Induced Stress Rotation Due to Unloading in Deep Roadway Excavation and Surrounding Rock Control Countermeasures. Applied Sciences, 15(18), 9950. https://doi.org/10.3390/app15189950








