Abstract
Compared to traditional algorithms that rely exclusively on user–item correlations, recommendation algorithms based on social networks, which incorporate users’ social data, can provide a more balanced approach to improving the precision of recommendations. This research introduces a trust-enhanced recommendation algorithm, called TECosRA, which integrates users’ historical behavior records with adjustable-weight social relationships by amplifying users’ social influence to enhance recommendation efficiency. Empirical results demonstrate that strengthening social connections and their positive impact on user decisions can broaden users’ choice channels and improve the accuracy of recommendation algorithms.
1. Introduction
Today’s social media platforms—such as TikTok [1], which blends content sharing with social features—produce enormous data while growing rapidly in user adoption. This platform faces challenges from information overload, which recommendation systems effectively mitigate. Recommendation systems analyze users’ information to construct personalized recommendations. While existing research predominantly focuses on recommendation accuracy, the lack of diversity often traps users in “information cocoon”. Recent approaches attempt to enhance algorithm performance by incorporating users’ auxiliary data (e.g., social relationships [2], tags [3], and locations [4]). However, how to utilize this auxiliary information can greatly impact the recommendation effectiveness.
It has been shown that users’ social relationships have an important impact on recommendation algorithms [5]. This article proposes a recommendation algorithm called TECosRA, which can enhance trust relationships to enhance accuracy in recommendation algorithms. The algorithm integrates the fundamental CosRA algorithm [6] and acquires the item resource values of all users using the CosRA similarity index. It highlights the positive impact of a user’s social connections on their decision-making process. In cases where users have established trust relationships, it computes the mean value of the item resource value of all their trusted users, augments the item resource value of the focal user, and enhances the similarity in preferences to those of the trusted user. The ultimate resource of the target user is determined by amalgamating the resource values of users with akin tastes and trusted users via a modifiable parameter. Experimental results demonstrate that enhanced social connectivity expands users’ domains, which significantly magnifies the positive impact of social relationships on behavioral decision-making.
The algorithm broadens users’ selection channels by strengthening their social relationships, enhancing the positive impact of social relationships on users’ choices, strengthening users’ social influence, social relationships expanding users’ choices, and improving the accuracy of recommendations. Meanwhile, users’ diversity is also affected to some extent.
The rest of this article is structured as follows. Section 2 reviews some related work and its limitations, Section 3 introduces the principle of recommendation algorithms for strengthening trust relationships, Section 4 introduces the dataset, evaluation indicators, and experimental result analysis of the experimental design, and it is followed by the conclusion in Section 5.
2. Related Work
Recommendation systems alleviate information overload by utilizing personalized algorithms to analyze user behavior data, efficiently presenting related content. For instance, e-commerce platforms can use recommendation systems to predict users’ purchasing behavior, thereby accurately recommending products to users [7]. The recommendation algorithm serves as the foundational core of recommendation systems. Collaborative filtering (CF) [8], a widely fundamental and extensively adopted algorithm in recommendation systems, comprises two dominant approaches: user-based CF (UCF) [9] and item-based CF (ICF) [10], which recommend items to users based on similarities to other users or items, respectively. The integration of physics and statistics into recommendation algorithms has facilitated the creation of diffusion-based recommendation algorithms, which model the diffusion process within a bipartite network connecting users and items. Notable examples of these algorithms include mass diffusion (MD) [11] and heat conduction (HC) [12]. Zhou et al. [13] proposed the resource allocation (RA) algorithm, which employs heat conduction principles to compute item similarity and generate recommendations based on these similarities. Lü et al. [14] introduced a method that combines priority diffusion and filtering techniques to enhance recommendation accuracy through diffusion-based approaches. Additionally, Chen et al. [5] combined cosine similarity from ICF algorithms with the similarity metric of the RA algorithm to introduce a new node similarity metric known as CosRA, which has shown some improvement in the precision of recommendation algorithms.
Nevertheless, the previously discussed algorithms focus solely on the interaction data between users and items, failing to consider the influence of social factors on recommendation systems. Due to the rapid development of social networks [15], Schroeder et al. [16] suggest that behind individual-based platforms lies a social network. Users are inclined to engage with reliable individuals with whom they have had favorable encounters [17]. Gao et al. [18], through analysis of social media, indicate that users aggregating into homogeneous groups dominate the online interaction of certain social media platforms. Choudhury et al. [19] propose trust matrix measure, which combines user similarity with weighted trust propagation, to address cold start problems, data sparsity, and malicious attacks. Liu et al. [20] proposed a recommendation algorithm that combines trust and ratings, in which user and item preferences and user implicit feedback are considered simultaneously in the algorithm, which partially alleviates the data sparsity and cold start problems. Zarzour et al. [21] proposed an innovative model-based interpretable CF method to support recommendation algorithms based on trust relations and make trust-based recommendation systems more interpretable. Wang et al. [22] found through research on social recommendation systems that social networks have been used as a good source of information to determine user preferences and alleviate cold start problems. Wahab et al. [23] propose a federated learning-based approach with a trust mechanism and double deep Q learning scheduling to address cold start items in recommendation systems. Wang et al. [24] introduced a mixed CF recommendation method based on user–item trust records. This method integrates user trust into established CF recommendation techniques to enhance the information provided by ratings. Lee et al. [25] propose a federated learning-based approach with a trust mechanism and double deep Q learning scheduling to address cold start items in recommendation systems.
In summary, these methods demonstrate that introducing social relationships between users to provide them with recommendation lists improves the accuracy of the algorithms.
3. Weighted Trust-Enhanced Recommendation Algorithm
To further explore the role of trust relationships in recommendation algorithms, this experiment considers users who not only interact with items but also establish mutual trust relationships. First, the interaction objects of users are initialized on the “user–object” bipartite graph. Then, a conventional node similarity metric called CosRA is utilized for resource diffusion. Subsequently, the user’s trust relationship is established prior to the final resource allocation, and adjustable parameters are utilized to assign weight to the trust relationship. The impact of trust relationships on the recommendation algorithm is controlled through the scaling operation of adjustable parameters. Finally, a personalized recommendation list is generated, establishing a trust-enhanced weighted recommendation algorithm.
The principle of the TECosRA algorithm is as follows: if there is a directed edge between users, it signifies a trust relationship between them. This indicates that the target user recognizes to some extent the preferred behavior of the trusted user, and this trust relationship may influence the decision-making of the target user. When the algorithm identifies a trust relationship between users, it locates the trusted user and the shared interaction object through the user’s social network. It incorporates the user’s trust relationship into the algorithm, manages the trust relationship using adjustable parameters, and enhances the value of the user’s resources with a trust relationship. If a user does not have a trust relationship, the trust relationship will not have any effect on the resource diffusion process. In this algorithm, by incorporating the social relationships of the user, the positive impact of these relationships on the user’s choices is enhanced to expand the user’s range of options.
3.1. Similarity Metrics
Formally, a recommendation system is defined as a bipartite graph , where adjacency matrix A encodes user–item ratings ( = 1 if user i select item , = 0 otherwise). Let denote the set of users, denote the set of items, and represent the rating links between them. Where m, n, and l are the total number of objects, products, and ratings. User–user trust relations are similarly represented by matrix B, where = 1 if user i trusts user j, and 0 otherwise. The recommendation algorithm generates a ranked list of length L for each target user, consisting of the top L recommended items.
The CosRA similarity metric, utilized in the recommendation algorithm centered on weighted trust enhancement, is introduced as a measure of similarity. This metric, known as CosRA similarity, is derived from the notion of node similarity introduced by scholars. It integrates the cosine similarity and the RA similarity metric, thereby incorporating the advantages of both metrics. Specifically, it capitalizes on the extensive influence of high-degree nodes while also amplifying the significance of low-degree nodes. The CosRA similarity between two items, denoted as item α and item β, is mathematically expressed in Equation (1):
where α and β denote items and , and and represent the ratings of items and by user , respectively. , , and represent the degrees of items , , and user , respectively.
3.2. Trust-Based Recommendation Method
In this study, we introduce a recommendation algorithm that incorporates trust elements through the utilization of weighted trust, aiming to explore the influence of trust connections on recommendation systems. The algorithm is structured around four primary stages.
The first step is to initialize an n-dimensional initial resource matrix for the selected item α by target user i using Equation (2):
where denotes the resource value of item α that user i interacts with. When , it means that user i has selected item α, otherwise .
The second step is the initial resource diffusion, which is calculated based on the CosRA similarity index. The initial resources are allocated from items to users through solid edges between items and users. During this resource diffusion process, the resource value obtained by user from item allocation is calculated using Equation (3), resulting in an n-dimensional resource matrix .
where denotes the CosRA similarity index, as mentioned in Equation (1). denotes the initial resource value matrix of the items interacted by the user i.
In the third step, based on the user’s social network, if there exists a trust relationship in the social network of the target user i, after introducing the social relationships of the target user, we look for user j, whom user i trusts, and the objects α that they both interact with. The resource allocation of user i for items will receive a bonus effect based on the social similarity. This is represented by Equation (4).
where represents the mean rating value of the items α by the users j, trusted by the user i. is indicative of the resource value of the item α selected by user j, calculated using Equation (3), m represents the aggregate number of users in the network, and is the trust degree of the target user i in the social network.
In the fourth step, if the target user i trusts user j, during the final resource allocation for items, the impact of the introduced trust relationship on recommendation performance is adjusted through a scaling parameter λ. The parameter λ is used to adjust the influence degree of trust relationship to weigh the item resource values, as represented by Equation (5).
where λ is a tunable parameter, is the trust matrix of the target user i. If there is no trust relationship, it does not affect the process of resource reallocation. The trust relationships in users’ social information are represented by a trust matrix, which models the mutual interactions among users. The trust matrix is represented by Equation (6).
If the user i trusts the user j, then , otherwise .
After the final resource diffusion, the items’ final resource values are ranked in descending order. Items that have already been selected by the target user will be filtered out, and a recommendation list will be recommended to the target user i, calculated using Equation (5). After the final resource diffusion, the items’ final resource values are ranked in descending order. Items that have previously been chosen by the target user will be excluded, resulting in a recommendation list of a specified length being presented to the target user i.
An example of the algorithm process is shown in Figure 1. The relations between users and items are represented by solid lines, while the relations between users are represented by directed edges with dashed arrows. The orange characters in the diagram denote the target users, and the orange squares represent the items selected by the target users. The green characters denote the users who have a trust relationship with the target users. The relationship between users and items is represented by solid lines, while the relations between users are represented by directed edges with dashed arrowheads. The numerical values represent the resource values obtained by the users or items.
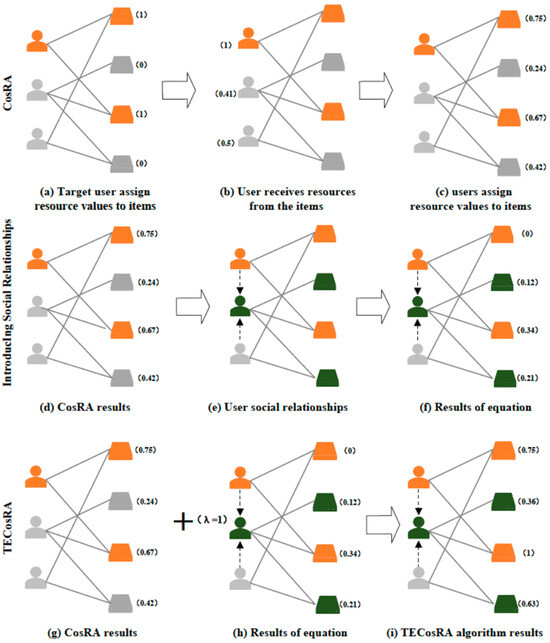
Figure 1.
Diagram of resource diffusion based on the weighted trust-enhanced algorithm. Source: author’s contribution. Source: J.C.’s contribution.
The CosRA algorithm consists of three steps: First, users assign resource values to items, as illustrated in Figure 1a and Equation (2). Second, these values are then propagated through user–item edges to users, as shown in Figure 1b. Third, users subsequently retransmit the propagated values to items, depicted in Figure 1c. Steps 2 and 3 are governed by Equation (3).
The CosRA+T algorithm follows the same three-step procedure as the CosRA algorithm, with one key distinction: In Step 3, when resources are transferred from users to items, the values propagated by the target user’s trusted users are assigned distinct weights, while untrusted users retain the original Step 3 mechanism of the CosRA algorithm. Consequently, the final resource values assigned to items are governed by Equation (7).
The TECosRA algorithm shares the same first two steps as the CosRA algorithm, but diverges in Step 3; the resources received by an item are divided into two parts, one derived from the CosRA algorithm in Figure 1g, and another redistributed by trusted users as a new resource value , as specified in Equation (4) and illustrated in Figure 1d–f. Ultimately, the item accumulates a combined resource value from both components, as defined by Equation (5) and depicted in Figure 1i. If λ = 0, the TECosRA algorithm degenerates into the CosRA algorithm.
4. Experiments and Analysis
To further explore the role of trust relationships in recommendation algorithms, this experiment considers users who not only have connections with items but also establish trust relationships with each other. Firstly, the interaction objects of users are initialized on the “user–object” bipartite graph. Then, a conventional algorithm CosRA is utilized for resource diffusion. Next, the user’s trust relationship is established prior to the final resource allocation, and adjustable parameters are utilized to assign weight to the trust relationship. The impact of trust relationships on the recommendation algorithm is controlled through the scaling operation of adjustable parameters. Finally, a personalized recommendations list is generated for the user. Thus, a weighted trust-enhanced recommendation algorithm is established.
4.1. Datasets
This research utilized the publicly accessible FriendFeed, Epinions, and FilmTrust datasets to evaluate recommendation performance. Prior to experimentation, both datasets underwent preprocessing procedures. The k-fold cross-validation method [26] employs a k value of 10. This method involves dividing the datasets into k equal segments, with one segment designated as the test dataset in each iteration while the remaining segments serve as the train dataset. This process yields k distinct training–testing pairs, making sure that each subsample serves as the testing set once. The outcomes of the experiments, repeated k times, were subsequently averaged to derive the final experimental results.
This research primarily employed datasets from FriendFeed, Epinions, and FilmTrust for experimentation purposes. FriendFeed is a platform that consolidates personal data from various sources such as social networking services, blogs, and community media. On the other hand, Epinions and FilmTrust are review sites where users can express subjective evaluations of products. Both datasets feature a 5-point rating system, with ratings ranging from 1 to 5. A rating of 1 signifies the lowest quality, while a rating of 5 indicates the highest quality. During preprocessing, the dataset used to develop the resource diffusion model underwent a filtration process where ratings below 3 were eliminated, and both users and objects were required to have a minimum degree of 2. The purpose of this approach is to ensure that each user is present in both the training and test sets to maintain the user–item bipartite graph’s connectivity, thereby preventing the formation of isolated network nodes. Following data processing, Table 1 presents the core characteristics of the benchmark datasets (FriendFeed, Epinions, and FilmTrust), including users, items, ratings, and network (user–item) sparsity metrics Sl.

Table 1.
Summary basic content of three datasets. Source: J.C.’s contribution.
Furthermore, apart from the connections between users and items, datasets incorporate social network data to depict trust relationships among users. A “user–user” trust network is established within the social network, where if user i trusts user j, a directed edge from user i to user j is assigned a value of 1; otherwise, the edge is assigned a value of 0. The weights in this trust network are directional and weighted, represented as in the formula (see Equation (5)). All datasets contain trust edges. Table 1 presents the edge counts and sparsity metrics (St) of trust networks across three benchmark datasets.
4.2. Evaluation Metrics
To evaluate the effectiveness of the recommender algorithms employed in this experiment, eight evaluation metrics will be used to assess their performance. The evaluation metrics are mainly divided into accuracy metrics and diversity metrics of eight evaluation metrics. Additionally, a quantitative evaluation is performed by comparing the performance of the benchmark algorithms with the performance of the new algorithm.
AUC [27] metric is used to test the accuracy of the recommender algorithm in globally predicting items. For the randomly sorted recommendation list, the AUC is generally 0.5. An elevated Area Under the Curve value signifies an increased accuracy in the predictive capabilities of the algorithm, and the maximum AUC is 1. The AUC value is calculated as follows:
where m represents the total number of users, N signifies the number of independent comparisons, N1 represents the number of instances that the resource value of the object selected by the user is greater than the resource value of the unselected object, while N2 denotes the number of instances that the resource value of the object selected by the user is the same as the resource value of the unselected object.
Precision (P) [28] is used to measure the proportion of correctly predicted items in the recommendation list for the target user. When none of the items in the target user’s recommendation list are predicted correctly, P(L) = 0. When all the predictions are correct, P(L) = 1. Therefore, a higher precision indicates the more in line with the user’s actual preferences by the prediction of the algorithm. The P(L) value is determined through the following calculation:
where denotes the quantity of identical items present in both the test set and the recommendation list, which has a length of L.
Recall (R) [29] is used to measure the proportion of correctly predicted items in the test set for the target user. When none of the items in the target user’s test set are predicted correctly, R(L) = 0. When all the items in the target user’s test set are predicted correctly, R(L) = 1. Therefore, a higher recall indicates a better alignment between the algorithm’s predictions and the user’s interests. The R(L) value is determined through the following calculation:
where denotes the number of objects in the test set.
F1 score [28] is a metric that balances precision and recall to comprehensively evaluate the performance of an algorithm. The F1 score is directly proportional to the recommendation accuracy. The F1 value is calculated as follows:
where and are the Precision and Recall values of user i, respectively.
Ranking Score (RS) [28] is a ranking evaluation metric similar to the AUC score. It measures the relative ranking of items in the test set of a target user in the recommendation list. The lower the RS, the more accurate the ranking of the predicted items in the recommendation list. The RS value is determined through the following calculation:
where denotes the size of the test dataset, denotes the location of the target item within the recommendation list, and denotes the number of items that remain uncollected by the user within the training dataset.
Intra-similarity (I) [29] is used to evaluate the diversity of items in the user’s recommendation list. A lower value of I(L) indicates that the algorithm recommends a more diverse set of items to the target user. The I(L) value is determined through the following calculation:
where represents the cosine similarity between the recommended items α and β in user i’s recommendation list.
Hamming Distance (H) [29] evaluates the diversity of the recommended items in the lists of different users. When the recommended items in the lists of two different users are exactly the same, H(L) = 0, and when they are completely different, H(L) = 1. The larger the H(L) value indicates better algorithm diversity. The mean value of H(L) is determined through the following calculation:
where represents the number of common items in the recommendation lists of users i and j, with a length of L.
Novelty (N) [29] evaluates the “popularity” of the recommended items in the user’s recommendation list. The larger the N(L) value, the higher the popularity of the recommended items, and the smaller the N(L) value, t indicating higher algorithm novelty. The mean value of N(L) is determined through the following calculation:
where denotes the degree of object α in the target user’s recommendation list.
4.3. The Impact of Adjustable Parameter Scaling
In the recommendation algorithm based on enhanced social relationships proposed in this chapter, a tunable parameter λ is used to adjust the resources received by target users. To explore the effect of the tunable parameter on the performance of the proposed recommendation algorithm, this experiment will increase λ from 0 to 1, and evaluate it on the FriendFeed dataset, Epinions dataset, and FilmTrust dataset through three recommendation algorithm evaluation metrics: AUC, RS, and F1. Figure 2 shows the evaluation results. Figure 2a–i represent FriendFeed, Epinions, and FilmTrust datasets, respectively. Three precision metrics, including AUC, RS, and F1(L), are used on the vertical axis. The adjustable parameter λ increases from 0 to 1 along the horizontal axis. The vertical dashed red line represents the optimal value of the parameter , where the precision metric reaches the optimal value. When calculating the F1(L) measure, L has been established at L = 10. The results were obtained through 10-fold cross-validation and 40 parameter values.
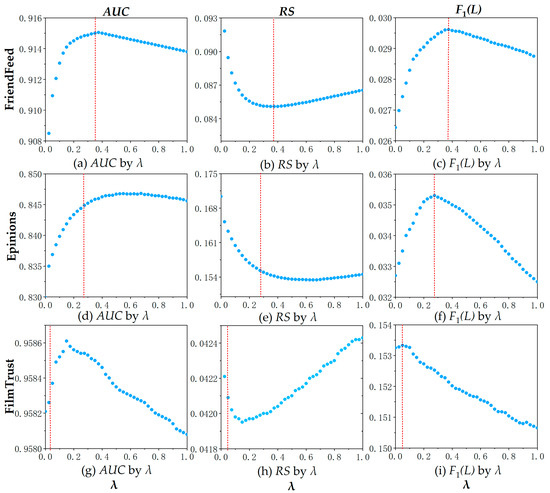
Figure 2.
The impact of adjustable parameter scaling. Source: L.C.’s contribution.
It can be observed from Figure 2 that as the tunable parameter λ increases from 0 to 1, the influence of user trust relationships on the resource allocation process exhibits a curvilinear effect. Through observation of the evaluation results, there appears to be an optimal value for the tunable parameter λ regarding the best recommendation accuracy. When evaluating with the three accuracy metrics on the FriendFeed, Epinions, and FilmTrust datasets, the accuracy shows peaks with changes in λ. On the FriendFeed dataset, the best global accuracy results for AUC and RS are achieved when λ = 0.375. On the Epinions dataset, the best AUC is achieved when λ = 0.575. On the FilmTrust dataset, the best AUC is achieved when λ = 0.15.
After this point, the algorithm’s accuracy gradually declines. However, from the trend in Figure 2f, the F1(L) value on the Epinions dataset peaks at approximately λ = 0.275 and begins to decrease when λ exceeds 0.275. From the trend in Figure 2i, the F1(L) value on the FilmTrust dataset peaks at approximately λ = 0.05 and begins to decrease when λ exceeds 0.05, which differs from the performance on the FriendFeed dataset. Based on a comprehensive consideration of the experimental results, the optimal parameters for the TECosRA algorithm are λ = 0.375 on the FriendFeed, λ = 0.275 on the Epinions dataset, and λ = 0.05 on the FilmTrust dataset when L = 10.
After determining the algorithm’s optimal parameter, subsequent experiments investigated the dependence and sensitivity of the accuracy metrics P, R, and F1 on the recommendation list length L by varying L. In Figure 3a,d,g, the Y-axis is used to represent the accuracy metrics P and R based on L. In Figure 3b,e,h, the Y-axis represents the F1 value. In Figure 3c,f,i, the parameter values λ corresponding to the optimal values for each accuracy metrics are given. The results of P, R, and F1 on both datasets are studied by manipulating the L.
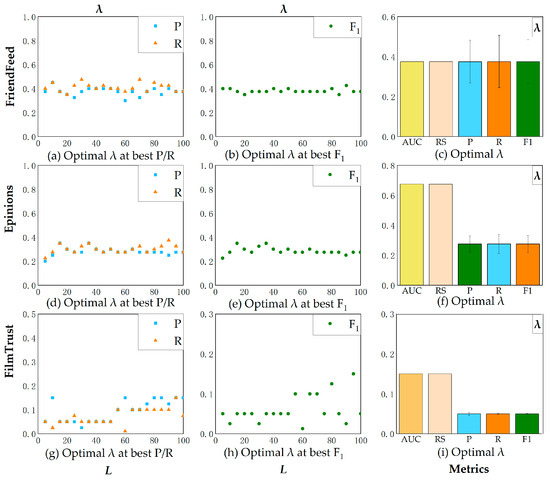
Figure 3.
Optimal values of adjustable parameters. Source: J.L.’s contribution.
The experimental results in Figure 3a,b,d,e,g,h demonstrate that when the recommendation list changes, the accuracy metrics maintain stability under the optimal parameter λ, indicating minimal dependence and sensitivity of λ to L.
For the P and R metrics: The optimal parameter on the FriendFeed dataset is 0.40 (Figure 3a), achieving metric variances of 1.06 × 10−3 (Precision) and 1.15 × 10−3 (Recall). The optimal parameter on the Epinions dataset is 0.275 (Figure 3d), achieving metric variances of 9.92 × 10−4 and 1.15 × 10−3. The optimal parameter on the FilmTrust dataset is 0.05 (Figure 3g), achieving metric variances of 2.05 × 10−3 and 1.08 × 10−3. The same trend is observed for the F1 metric (Figure 3b,e,h), achieving metric variances of 3.05 × 10−4, 8.42 × 10−4 and 1.21 × 10−3. Additionally, Figure 3a,d,g show that the optimal parameter values of P, R, and F1 were determined through experiments. Extensive parameter testing confirms the following globally optimal parameters: Epinions⟨λ⟩ ≈ 0.275, FriendFeed⟨λ⟩ ≈ 0.375, FilmTrust⟨λ⟩ ≈ 0.05.
It can be observed from Figure 3 that the optimal parameter values for the five accuracy metrics on the FriendFeed dataset are consistent. On the Epinions and FilmTrust datasets, the λ values corresponding to the best AUC and RS values are consistent, and the λ values corresponding to the best P(L), R(L), and F1(L) values are also consistent, demonstrating the stability of λ.
4.4. Recommended Performance
To comprehensively evaluate the TECosRA algorithm, we compare its performance with five benchmark algorithms (MD, HC, UCF, CosRA, and CosRA+T) on the same dataset. Eight evaluate metrics are used in this experiment, including two metrics (AUC and RS) that are independent of L, three metrics (P, R, and F1) that depend on L, Hamming Distance and intra-similarity both depend on L, and novelty depends on L. The base recommendation list length L is set to 10, while additional tests analyze performance variations across different L values to examine its influence on recommendation quality. Compared with the benchmark methods, the weighted trust-enhanced recommendation algorithm uses the optimal parameter value for each dataset ( = 0.275 for Epinions, = 0.375 for FriendFeed, and = 0.05 for FilmTrust) in all the evaluation metrics, and the findings presented are derived from the average of ten independent trials. For further information, please consult Table 2.

Table 2.
Outcomes of the performance evaluation metrics. The results are achieved at λ = 0.275 for Epinions, λ = 0.375 for FriendFeed, and λ = 0.05 for FilmTrust. Source: J.L.’s contribution.
The performance of the recommendation algorithm is shown in Table 2. Columns 1–5 of Table 2 demonstrate that the weighted trust-enhanced recommendation algorithm outperforms all benchmark algorithms on the FriendFeed and Epinions datasets. The AUC values of this algorithm are 0.9151, 0.8449, and 0.9584 on the FriendFeed, Epinions, and FilmTrust datasets, respectively. In terms of accuracy metrics, this algorithm performs better than the benchmark algorithms. For example, the P(L), R(L), and F1(L) values of this algorithm on the FriendFeed, Epinions, and FilmTrust datasets are the highest among all algorithms. Furthermore, in terms of the rank-based accuracy metric RS, the proposed algorithm achieves an RS value second only to the CosRA algorithm, indicating that the new algorithm performs well in ranking accuracy among all benchmark algorithms. In terms of diversity metrics, on one hand, the HC algorithm outperforms other algorithms by a large margin. On the other hand, the performance of the new algorithm is better than the UCF algorithm and similar to the MD algorithm. For example, the I(L) value of this algorithm on FriendFeed, Epinions, and FilmTrust datasets is much lower than the UCF algorithm, and the H(L) value is much higher than the UCF algorithm. The N(L) value is in a moderate position among the benchmark algorithms. In general, due to the reinforcement of trust relationships, the proposed algorithm shows weaker performance in diversity metrics but outperforms the UCF algorithm.
4.5. The Impact of the Recommended List Length L on Algorithm Performance
The evaluation of recommendation performance under the evaluation metrics (P(L), R(L), F1(L), H(L), I(L), and N(L)) is inherently influenced by variations in L∈[0, 100], by comparing the performance of the TECosRA algorithm with five other benchmark methods over a range of L from 0 to 100. The experimental results are presented in Figure 4 and Figure 5, showing the outcomes for the three datasets. The parameter λ in the weighted trust-enhanced recommendation algorithm is set to the ideal value for both datasets. The outcomes are obtained through 10-fold cross-validation and averaging 40 parameters.

Figure 4.
The accuracy of the recommendation results is influenced by L. Source: L.C.’s contribution.
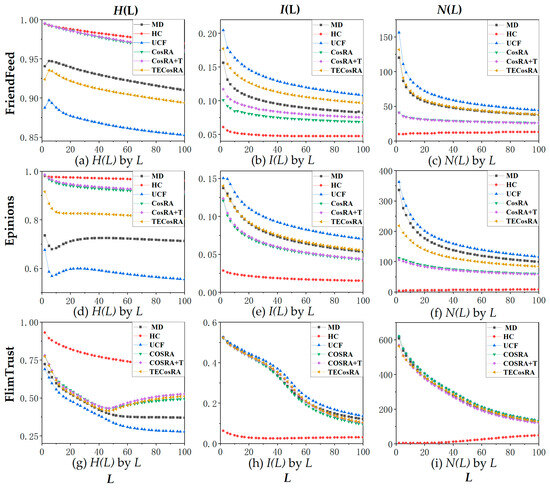
Figure 5.
The diversity and novelty of recommendation results are influenced by L. Source: L.C.’s contribution.
Figure 4 presents the results of P(L), R(L), and F1(L) metrics of the recommendation algorithm on the FriendFeed, Epinions, and FilmTrust datasets as the recommendation list length varies. From the results, we observe that for all benchmark methods selected in the experiment, as the L increases, there is a noted decline in performance in P(L) (refer to Figure 4a,d,g, while performance in R(L) exhibits an upward trend (refer to Figure 4b–h). As L increases, the F1(L) value initially exhibits an increase followed by a subsequent decrease, and F1(L) reaches its maximum value at L ≈ 5 on FriendFeed, Epinions, and FilmTrust. Furthermore, the performance of the weighted trust-enhanced recommendation algorithm demonstrates superior efficacy compared to various benchmark methods across different lengths of recommendation lists. The weighted trust-enhanced algorithm outperforms benchmarks throughout, with maximal efficacy near its parameter-optimized L values. It achieves significant accuracy improvements over CosRA+T, while competing with MD, UCF, and surpassing HC (lowest accuracy).
Figure 5 presents the diversity and novelty metrics analysis. Figure 5a–f represent the results on the FriendFeed, Epinions, and FilmTrust datasets, respectively. The L ranges from 1 to 100. The parameter λ of the weighted trust-enhanced recommendation algorithm is set to the ideal value for both datasets. The findings were derived through the application of 10-fold cross-validation. The value of H(L) decreases with the increase in the length of the recommendation list, as shown in Figure 5a,d,g. HC algorithm performs the best. The performance of the new algorithm is close to that of the MD algorithm in terms of H(L), whereas the UCF algorithm exhibits the least favorable performance. The value of I(L) initially experiences a swift escalation and then slowly decreases as the L increases (refer to Figure 5b,e,h). The maximum I(L) value of UCF indicates its worst performance on this evaluation metric. The improved new algorithm performs better than the UCF algorithm and is close in performance to the MD algorithm. The HC algorithm demonstrates superior performance compared to all other methodologies across both datasets, as evidenced by its minimal I(L) value. As for the N(L), the value of N(L) initially decreases rapidly with the increase in the L and then shows a slow decreasing trend (refer to Figure 5c,f,i). After the recommendation list exceeds approximately 50, the algorithm’s results start to become less sensitive to changes in L.
From the results, the HC algorithm performs the best; except for HC, the improved new algorithm performs better than the UCF algorithm. The new algorithm performs poorly in terms of diversity and novelty.
In summary, this study builds upon the CosRA algorithm and primarily compares it with both the original CosRA and CosRA+T algorithms. Compared to the standard CosRA approach, the proposed TECosRA algorithm divides the predicted resource values for items (ranked in descending order for recommendations) into two components: one derived from the base CosRA algorithm, and the other allocated as additional resources to items selected by trusted users based on social relationships, with the allocation controlled by parameter λ. This supplementary resource allocation mechanism differs from that of the CosRA+T algorithm, which linearly combines the base CosRA values with social relationship-based values using a single parameter. While both CosRA+T and TECosRA algorithms leverage users’ social relationships, their recommendation performance exhibits distinct characteristics. A comprehensive comparison of these algorithms’ accuracy and diversity metrics is presented in Table 3.

Table 3.
Accuracy and diversity results.
As shown in Table 3, the TECosRA algorithm demonstrates superior performance in terms of the global accuracy metric AUC. For F1 score metrics that depend on recommendation list length, three F1 results are presented (for list lengths L = 10, 20, 30). Experimental results on Friendfeed and Epinions datasets indicate that TECosRA outperforms both the original CosRA algorithm and slightly surpasses CosRA+T. On the FilmTrust dataset, it shows marginal inferiority to CosRA+T, a trend that remains consistent across different values of L. However, in terms of diversity metrics (as illustrated in Figure 5), TECosRA generally underperforms both CosRA and CosRA+T algorithms. Table 3 presents diversity metric results for H and N (with L = 10, 20, 30), where CosRA+T achieves optimal diversity performance. This superiority stems from its mechanism of expanding user choice scope through social relationships, thereby enhancing diversity. In contrast, TECosRA’s stronger emphasis on social influence ends up limiting diversity compared to CosRA+T.
5. Conclusions
Current research frontiers in personalized recommendations focus on social recommendation algorithms leveraging network structures. While utilizing social networks to optimize recommendation algorithms presents a significant challenge, this research investigates how trust relationships enhance performance during social network-based resource diffusion. The introduction of trust relations during resource allocation is achieved through the combined CosRA similarity, which merges RA similarity and cosine similarity. An advanced recommendation algorithm is proposed based on weighted trust social networks, where adjustable parameters regulate the resources allocated to the target user upon the inclusion of trust relations. These resources are subsequently redistributed to the collected objects during the resource reallocation process. Experimental findings demonstrate that integrating trust relationships in social networks is beneficial for improving the performance of socialized recommendation algorithms. In summary, the improved recommendation algorithm amplifies the positive impact of trust relationships on recommendation algorithms by assigning weights to effective trust relationships, thereby achieving high accuracy but poor performance in diversity.
However, the proposed results exhibit limitations in both the dataset and the modeling process, requiring further enhancements to develop more accurate, diverse, and novel methods. Additionally, factors beyond social relationships, such as user timing and community, also significantly influence recommendation systems. Future advancements may involve integrating social trust information, timing, and user community [30] to mitigate the cold start problem that arises when new users join the network [31] and enhance the performance of personalized recommendation algorithms in practical scenarios.
Author Contributions
Conceptualization, L.C. and Z.W.; Methodology, L.C. and Y.W.; Software, J.C.; Validation, J.C.; Formal analysis X.C.; Investigation, X.C.; Data curation, L.C.; Writing—original draft, J.C. and L.C.; Writing—review and editing, J.C. and L.C.; Visualization, J.C.; Supervision, Z.W.; Project administration, Y.W.; Funding acquisition, L.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grant Nos. 62106074, 62303177), in part by the Natural Science Foundation of Hunan Province (Grant No. 2025JJ70057), in part by the open project initiative of the Hunan Key Laboratory for Intelligent Information Perception and Processing Technology (Grant No. 2024KF03), in part by the Hunan Provincial Natural Science Foundation (Grant No. 2025JJ50420), and in part by the Key Project of Hunan Provincial Education Department (Grant No. 23A0440).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. http://konect.cc/networks/epinions/ accessed on 11 May 2018; http://multilayer.it.uu.se/datasets.html accessed on 11 May 2018; https://guoguibing.github.io/librec/datasets.html accessed on 1 January 2023.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wang, P. Recommendation Algorithm in TikTok: Strengths, Dilemmas, and Possible Directions. Int. J. Soc. Sci. Stud. 2022, 10, 6066. [Google Scholar] [CrossRef]
- Shokeen, J.; Rana, C. A study on features of social recommender systems. Artif. Intell. Rev. 2020, 53, 965–988. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, R.; Liang, Y.; Liang, A.; Liu, W. Metric learning for tag recommendation: Tackling data sparsity and cold start issues. In Proceedings of the 2024 5th International Symposium on Computer Engineering and Intelligent Communications (ISCEIC), Wuhan, China, 8–10 November 2024; IEEE: New York, NY, USA, 2024; pp. 99–103. [Google Scholar]
- Sánchez, P.; Bellogín, A. Point-of-interest recommender systems based on location-based social networks: A survey from an experimental perspective. ACM Comput. Surv. 2022, 54, 1–37. [Google Scholar] [CrossRef]
- Chen, L.J.; Gao, J. A trust-based recommendation method using network diffusion processes. Phys. A Stat. Mech. Its Appl. 2018, 506, 679–691. [Google Scholar] [CrossRef]
- Chen, L.J.; Zhang, Z.K.; Liu, J.H.; Gao, J.; Zhou, T. A vertex similarity index for better personalized recommendation. Phys. A Stat. Mech. Its Appl. 2017, 466, 607–615. [Google Scholar] [CrossRef]
- Lee, H. Interest-based e-commerce and users’ purchase intention on social network platforms. IEEE Access 2024, 12, 87451–87466. [Google Scholar] [CrossRef]
- Ekstrand, M.D.; Riedl, J.T.; Konstan, J.A. Collaborative filtering recommender systems. Found. Trends® Hum.–Comput. Interact. 2011, 5, 81–175. [Google Scholar] [CrossRef]
- Goldberg, D.; Nichols, D.; Oki, B.M.; Terry, D. Using collaborative filtering to weave an information tapestry. Commun. ACM 1992, 55, 61–70. [Google Scholar] [CrossRef]
- Sarwar, B.; Karypis, G.; Konstan, J.; Riedl, J. Item-based collaborative filtering recommendation algorithms. In Proceedings of the 10th International Conference on World Wide Web, Hong Kong, China, 1–5 May 2001; pp. 285–295. [Google Scholar]
- Zhou, T.; Ren, J.; Medo, M.; Zhang, Y.-C. Bipartite network projection and personal recommendation. Phys. Rev. E 2007, 76, 056115. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.C.; Blattner, M.; Yu, Y.K. Heat conduction process on community networks as a recommendation model. Phys. Rev. Lett. 2007, 99, 155501. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Lü, L.; Zhang, Y.C. Predicting missing links via local information. Eur. Phys. J. B 2009, 71, 625–650. [Google Scholar] [CrossRef]
- Lü, L.; Liu, W. Information filtering via preferential diffusion. Phys. Rev. E 2011, 85, 066119. [Google Scholar] [CrossRef]
- Wu, W.; Ghazali, M.; Huspi, S.H. A review of user profiling based on social networks. IEEE Access 2024, 12, 122642–122670. [Google Scholar] [CrossRef]
- Schroeder, D.T.; Langguth, J.; Burchard, L.; Pogorelov, K.; Lind, P.G. The connectivity network underlying the German’s Twittersphere: A testbed for investigating information spreading phenomena. Sci. Rep. 2022, 12, 4085. [Google Scholar] [CrossRef]
- Ghavipour, M.; Meybodi, M.R.A. dynamic sampling algorithm based on learning automata for stochastic trust networks. Knowl.-Based Syst. 2021, 212, 106620. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, F.; Gao, L. Echo chamber effects on short video platforms. Sci. Rep. 2023, 13, 6282. [Google Scholar] [CrossRef]
- Choudhury, S.S.; Mohanty, S.N.; Jagadev, A.K. Multimodal trust based recommender system with machine learning approaches for movie recommendation. Int. J. Inf. Technol. 2021, 13, 475–482. [Google Scholar] [CrossRef]
- Liu, Z.H.; Xiong, H.L.; Liu, J. Recommendation algorithm fusing implicit similarity of users and trust. In Proceedings of the 2019 IEEE 21st International Conference on High Performance Computing and Communications; IEEE 17th International Conference on Smart City; IEEE 5th International Conference on Data Science and Systems (HPCC/SmartCity/DSS), Zhangjiajie, China, 10–12 August 2019; IEEE: New York, NY, USA, 2019; pp. 2084–2092. [Google Scholar]
- Zarzour, H.; Jararweh, Y.; Al-Sharif, Z.A. An effective model-based trust collaborative filtering for explainable recommendations. In Proceedings of the 2020 11th International Conference on Information and Communication Systems (ICICS), Online, 7–9 April 2020; IEEE: New York, NY, USA, 2020; pp. 238–242. [Google Scholar]
- Wang, F.; Zhu, H.; Srivastava, G.; Li, S.; Khosravi, M.R.; Qi, L. Robust collaborative filtering recommendation with user-item-trust records. IEEE Trans. Comput. Soc. Syst. 2021, 9, 986–996. [Google Scholar] [CrossRef]
- Wahab, O.A.; Rjoub, G.; Bentahar, J.; Cohen, R. Federated against the cold: A trust-based federated learning approach to counter the cold start problem in recommendation systems. Inf. Sci. 2022, 601, 189–206. [Google Scholar] [CrossRef]
- Weng, L.; Zhang, Q.; Lin, Z.; Wu, L. Harnessing heterogeneous social networks for better recommendations: A grey relational analysis approach. Expert Syst. Appl. 2021, 174, 114771. [Google Scholar] [CrossRef]
- Lee, Y.L.; Zhou, T.; Yang, K.; Du, Y.; Pan, L. Personalized recommender systems based on social relationships and historical behaviors. Appl. Math. Comput. 2023, 437, 127549. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Liu, C.A. Model averaging prediction by K-fold cross-validation. J. Econom. 2023, 235, 280–301. [Google Scholar] [CrossRef]
- Yang, T.; Ying, Y. AUC maximization in the era of big data and AI: A survey. ACM Comput. Surv. 2022, 55, 1–37. [Google Scholar] [CrossRef]
- Fayyaz, Z.; Ebrahimian, M.; Nawara, D.; Ibrahim, A.; Kashef, R. Recommendation systems: Algorithms, challenges, metrics, and business opportunities. Appl. Sci. 2020, 10, 7758. [Google Scholar] [CrossRef]
- Lü, L.; Medo, M.; Yeung, C.H.; Zhang, Y.C.; Zhang, Z.K.; Zhou, T. Recommender systems. Phys. Rep. A Rev. Sect. Phys. Lett. (Sect. C) 2012, 519, 1–49. [Google Scholar] [CrossRef]
- Shirzadian, P.; Antony, B.; Gattani, A.G.; Tasnina, N.; Heath, L.S. A time evolving online social network generation algorithm. Sci. Rep. 2023, 13, 2395. [Google Scholar] [CrossRef] [PubMed]
- Yuliansyah, H.; Othman, Z.A.; Bakar, A.A. A new link prediction method to alleviate the cold-start problem based on extending common neighbor and degree centrality. Phys. A Stat. Mech. Its Appl. 2023, 616, 128546. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).