Experiment of Suppressing Atmospheric Turbulence by Using Fast-Steering Mirror
Abstract
1. Introduction
2. Theoretical Analysis
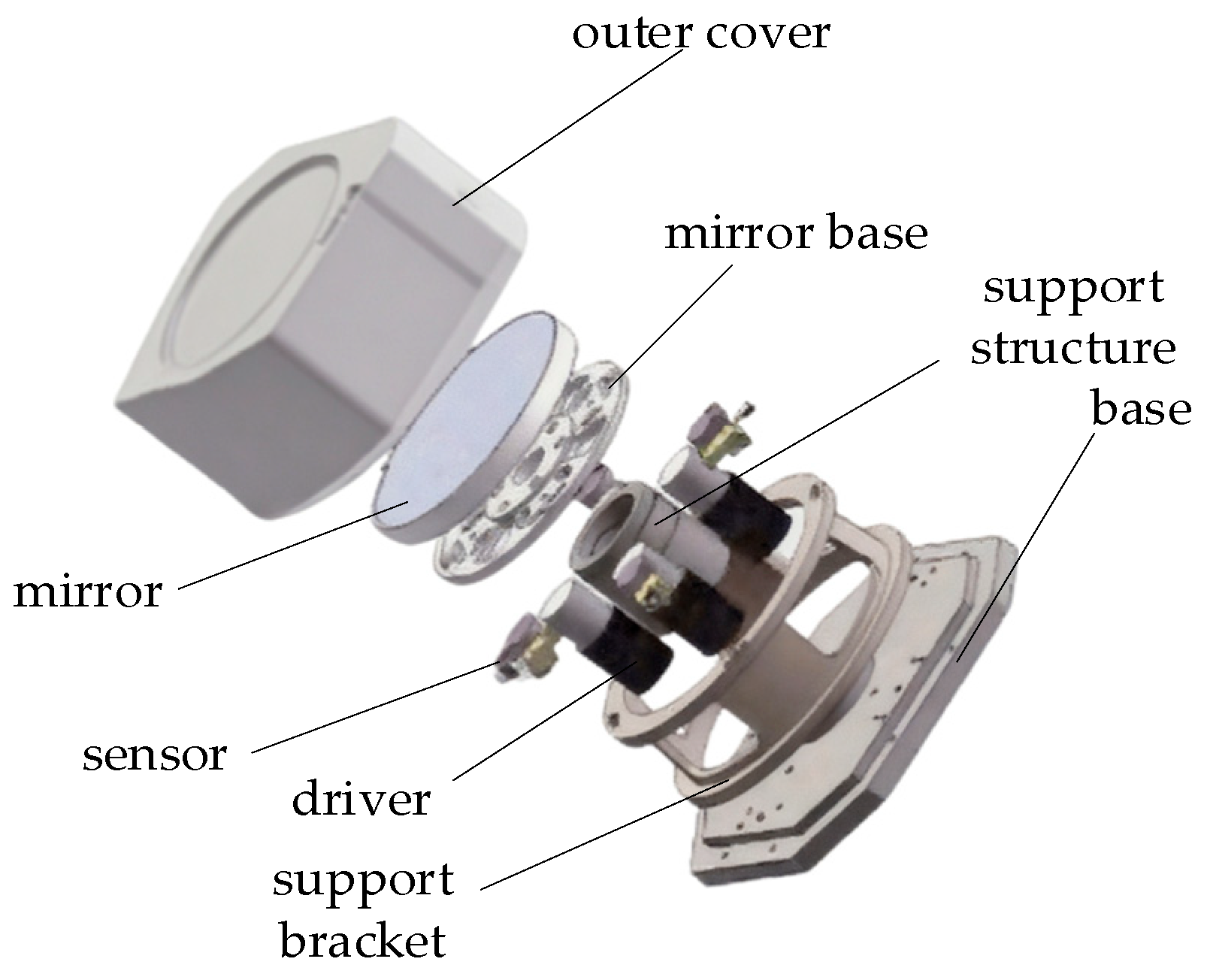
2.1. Operating Principle of the FSM
2.1.1. Composition of the FSM
2.1.2. Dynamic Analysis of the FSM
2.2. Atmospheric Turbulence
2.2.1. The Formation of Turbulence and Its Influence Mechanism on the Beam
2.2.2. Quantitative Analysis of Turbulence’s Cumulative Effect
2.2.3. Discussion of Factors Affecting the Effectiveness of Drift Suppression
3. Experimental Measurement
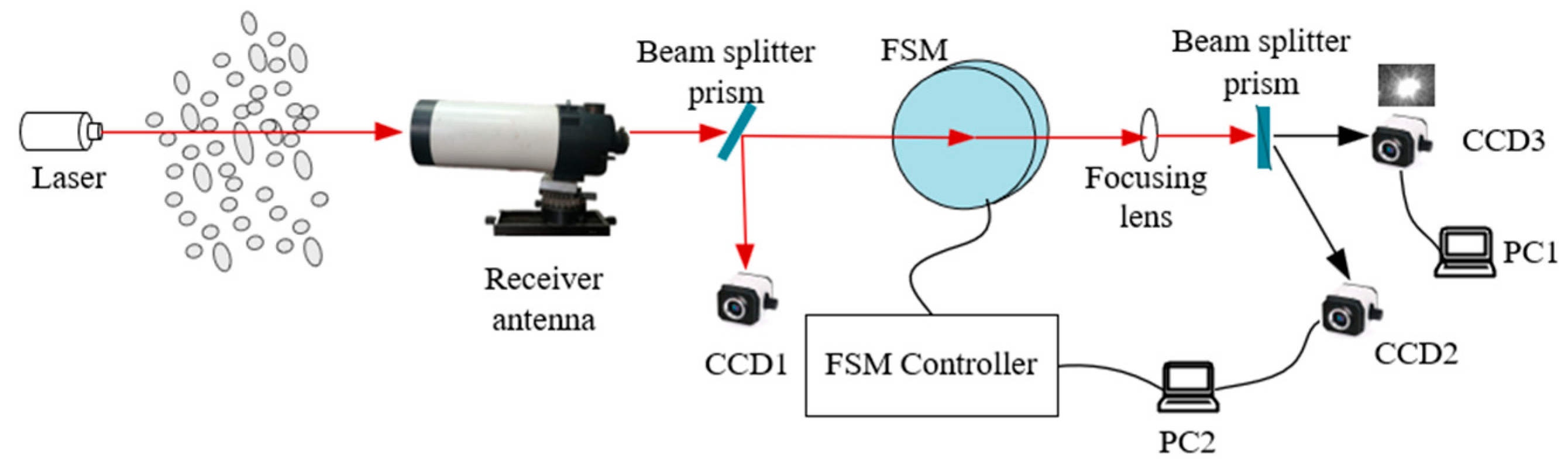
3.1. Experiment on FSM Suppressing Atmospheric Turbulence
3.2. Field Experiment
4. Data Analysis
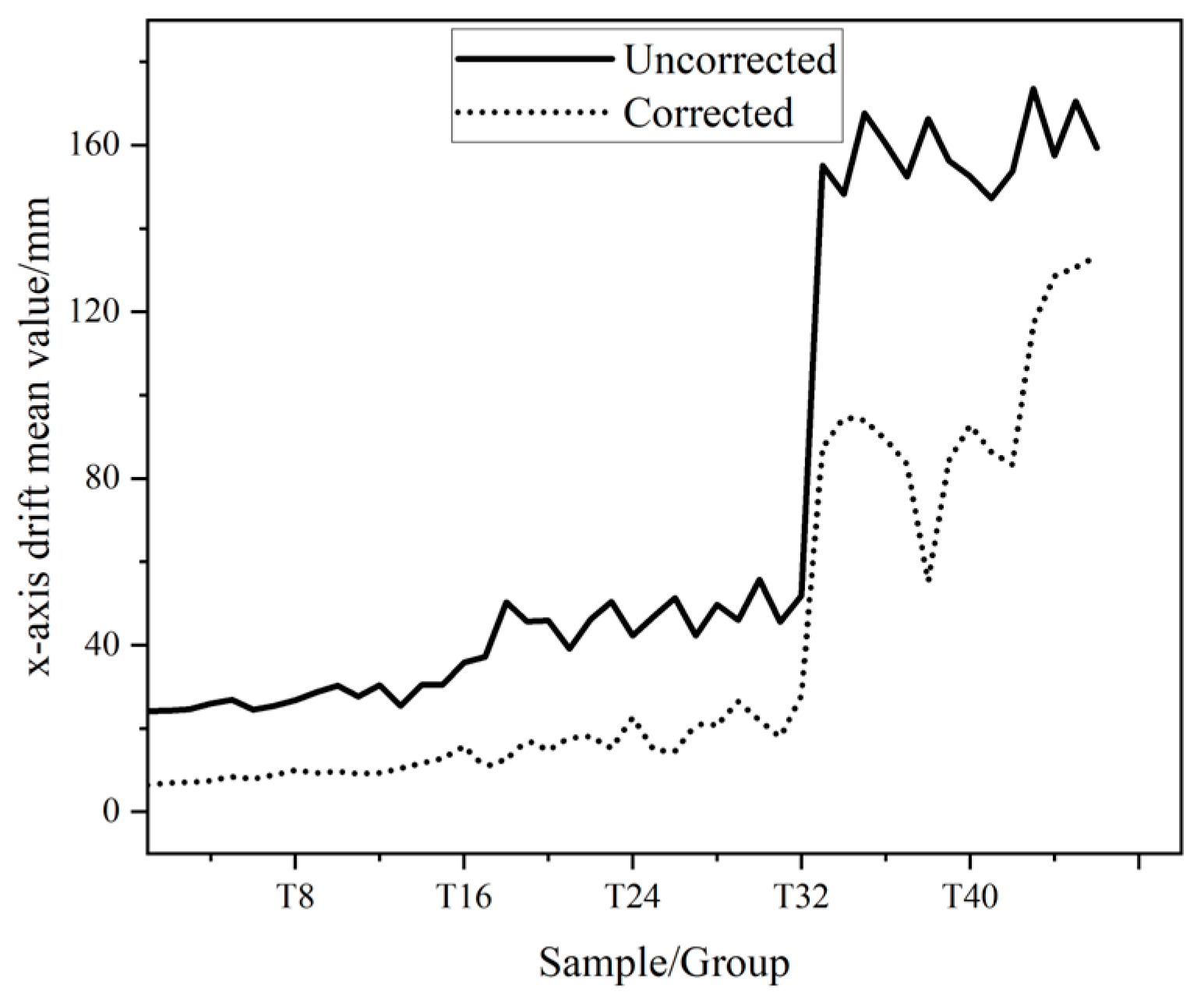
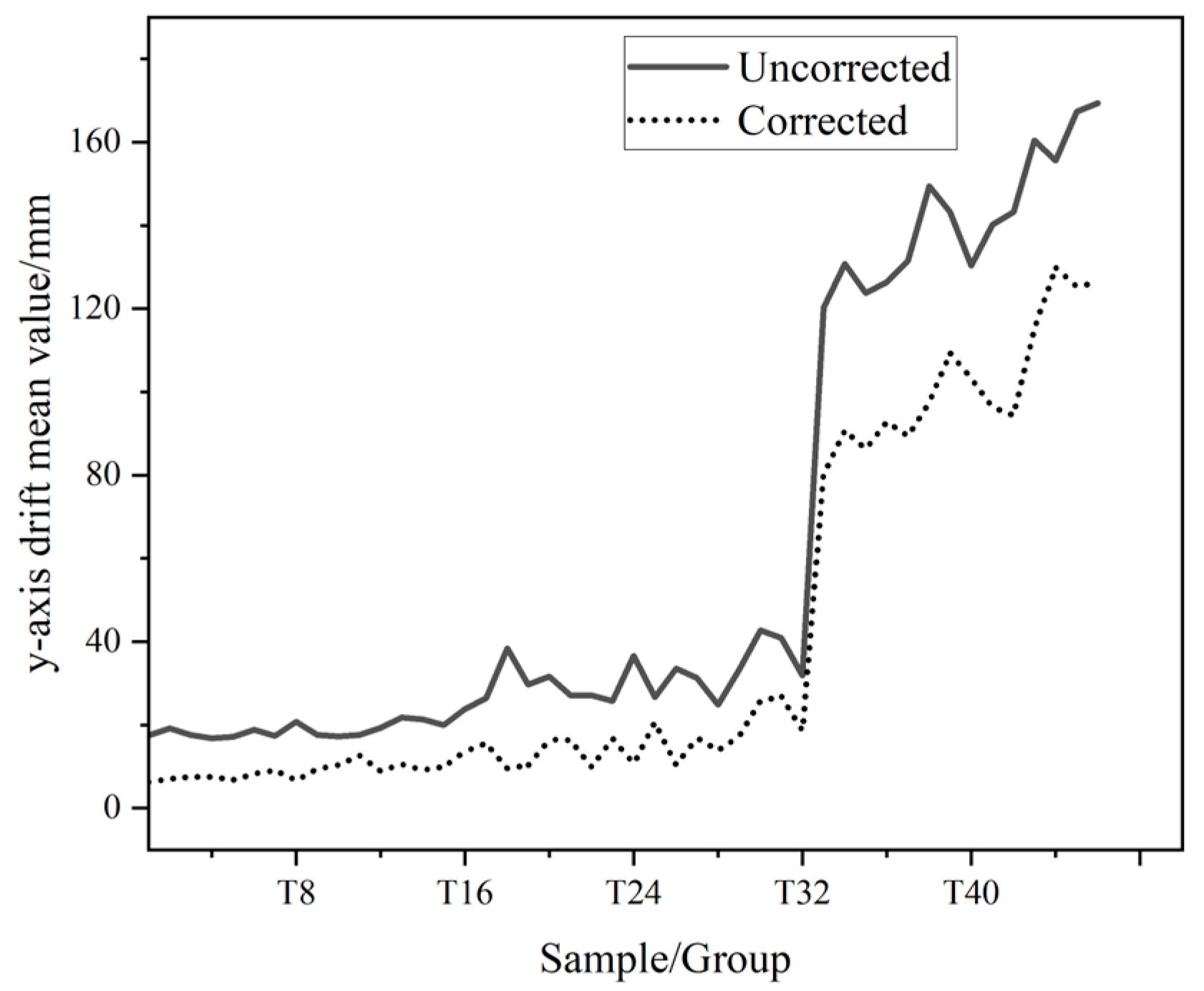
4.1. Mean Beam Drift
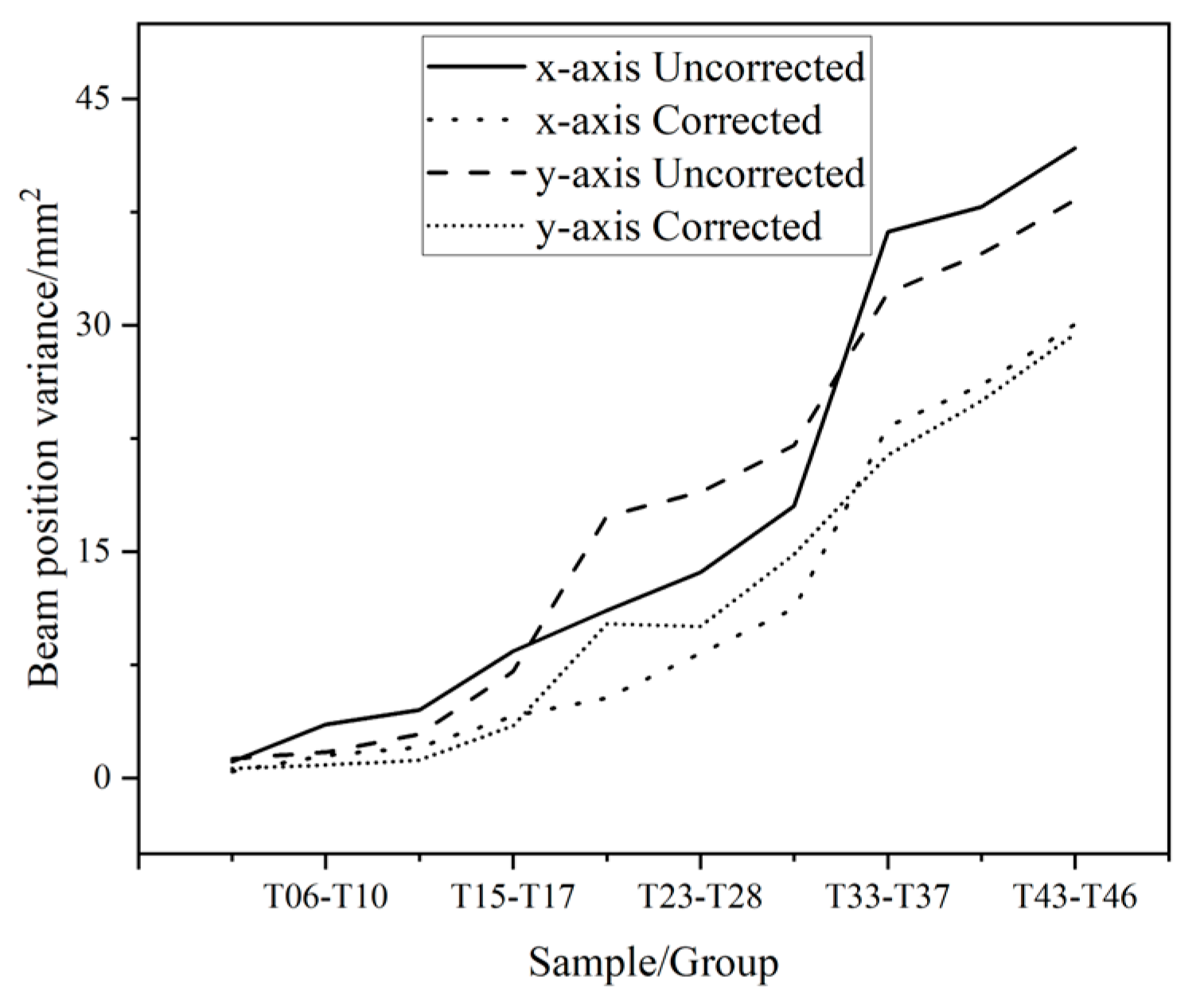
4.2. Beam Position Drift Variance
5. Conclusions
- (1)
- Under the same transmission distance, the samples under sunny, cloudy, rainy and dust-storm weather conditions are analyzed. It is found that with the deterioration of weather conditions, the mean and variance of spot drift gradually increase. This shows that the intensity of atmospheric disturbance increases with the severity of the weather, which has a more significant impact on the stability of the spot.
- (2)
- Under the same weather conditions, the measurement samples under three transmission distances of 0.42 km, 1.3 km and 10 km are analyzed. It is found that the mean and variance of spot drift increase gradually with the increase in link distance. This shows that the longer the transmission distance, the more significant the disturbance of atmospheric turbulence to the beam, resulting in a decrease in system stability.
- (3)
- At the same transmission distance, the FSM has a significant effect on the correction of low-frequency spot drift in weakly turbulent environments such as on sunny and cloudy days, which can effectively reduce the mean and variance of drift. Under strong-turbulence conditions such as rainy days and dust storms, the high-frequency disturbance is enhanced, the ability of the FSM to suppress the spot drift of high-frequency rapid change is weakened, and the correction effect is reduced.
- (4)
- Under the same weather conditions, with the increase in transmission distance, the amplitude and frequency characteristics of spot drift change, and the correction performance of the FSM shows obvious difference. For a short distance, the spot drift is mainly characterized by low-frequency and low-amplitude disturbance. The FSM can effectively compensate and achieve a better correction effect. As the distance increases, the high-frequency and high-amplitude disturbances caused by atmospheric turbulence increase, and the FSM’s ability to suppress these rapidly changing high-frequency components is weakened, resulting in a decrease in the correction effect. In general, the FSM is suitable for compensating for low-frequency drift. The farther the distance is, the more limited its ability to correct high-frequency disturbances is.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khalghi, M.A.; Uysal, M. Survey on free space optical communication: A communication theory perspective. IEEE Commun. Surv. Tutor. 2014, 16, 2231–2258. [Google Scholar] [CrossRef]
- Li, M.; Wu, Z.; Wang, Y.; Feng, Y.; Zhang, C.; Su, Z.; Feng, Z.; Jiang, Y. BER for a space uplink laser communication system under an actual optical distortion with a cake-cutting method. Opt. Lett. 2023, 48, 5992–5995. [Google Scholar] [CrossRef] [PubMed]
- Hayal, M.R.; Yousif, B.B.; Azim, M.A. Performance enhancement of DWDM FSO optical fiber communication systems based on hybrid modulation techniques under atmospheric turbulence channel. Photonics 2021, 8, 464. [Google Scholar] [CrossRef]
- Wang, J. Research on Adaptive Receiving Technology of Optical Wireless Communication; Huazhong University of Science and Technology: Wuhan, China, 2006. [Google Scholar]
- Ke, X.; Liao, Z.; Liang, J.; Wang, R.; Ding, D. Research on atmospheric turbulence noise measurement in wireless optical communication. J. Radio Wave Sci. 2024, 39, 225–236. [Google Scholar]
- Mo, J.; Feng, X.; Pan, X. Research on laser spot position drift correction of stereolithography system. J. Laser 2007, 4, 77–78. [Google Scholar]
- Zhang, L.; Lin, W.; Liao, Z.; Wang, R. Research of algorithm to correct direction drifts of laser beam. Laser Technol. 2012, 36, 386–389. [Google Scholar]
- Ren, X.; Fan, J.; Pan, R.; Sun, K. Beam Pointing Deviation Correction System Based on FSMs. Chin. J. Lasers 2023, 50, 110–120. [Google Scholar]
- Liu, W.; Yao, K.; Huang, D.; Lin, X.; Wang, L.; Lv, Y. Performance evaluation of coherent free space optical communications with a double-stage fast-steering-mirror adaptive optics system depending on the Greenwood frequency. Opt. Express 2016, 24, 13288–13302. [Google Scholar] [CrossRef]
- Poliak, J.; Calvo, R.M.; Rein, F. Demonstration of 1.72 Tbit/s Optical Data Transmission Under Worst-Case Turbulence Conditions for Ground-to-Geostationary Satellite Communications. IEEE Commun. Lett. 2018, 22, 1818–1821. [Google Scholar] [CrossRef]
- Kaymak, Y.; Rojas-Cessa, R.; Feng, J.H.; Ansari, N.; Zhou, M.C.; Zhang, T. A Survey on Acquisition, Tracking, and Pointing Mechanisms for Mobile Free-Space Optical Communications. IEEE Commun. Surv. Tutor. 2018, 20, 1104–1123. [Google Scholar] [CrossRef]
- Walsh, S.M.; Karpathakis, S.F.E.; McCann, A.S.; Dix-Matthews, B.P.; Frost, A.M.; Gozzard, D.R.; Gravestock, C.T.; Schediwy, S.W. Demonstration of 100 Gbps coherent free-space optical communications at LEO tracking rates. Sci. Rep. 2022, 12, 18345. [Google Scholar] [CrossRef] [PubMed]
- Ke, X.; Zhao, J. Beam alignment of wireless optical communication using dual-mirror control. J. Opt. Sci. 2023, 43, 169–178. [Google Scholar]
- Zhao, Q.; Zhong, M.; Lv, B. Experimental study on atmospheric laser beam drift. Laser Technol. 2010, 34, 532–534. [Google Scholar]
- Ai, Z.; Chen, J.; Ji, J. FSM assembly error disturbance rejection method. Prog. Laser Optoelectron. 2024, 61, 283–290. [Google Scholar]
- Yang, S.; Ke, X.; Wu, J.; Liu, X. Fast alignment of wireless optical communication using two-dimensional mirrors. China Laser 2022, 49, 101–114. [Google Scholar]
- Xie, N.; Du, Y.; Jiang, S.; Gong, Q.; Wang, M.; Xu, F.; Wang, X.; Qi, Y. Theoretical modeling and simulation analysis of FSM. Appl. Opt. 2023, 44, 513–522+585. [Google Scholar]
- Kang, D.; Jiang, C.; Liu, L.; Zhao, J.; Yu, B.; Chen, Q.; Wang, S.; Wang, N.; Chen, J.; Zhang, Y.; et al. Design of two-dimensional fast control plane mirror system with large aperture and high precision. Appl. Opt. 2022, 43, 661–668. [Google Scholar]
- Jia, G.; Hou, L.; Hong, P. Research on image rotation model of reflective two-dimensional fast control mirror. Opt. Optoelectron. Technol. 2021, 19, 86–92. [Google Scholar]
- Huang, Z.; Li, Y.; Xie, H.; Yang, R.; Gu, J.; Xie, X. Fast calculation method of deflection angle of double FSM for beam pointing control. Infrared Laser Eng. 2024, 53, 147–156. [Google Scholar]
- Zhang, Q.; Gu, W.; Ming, K. Research on driving characteristics of two-axis reluctance FSM with large rotation angle. Mach. Hydraul. 2025, 53, 190–194+220. [Google Scholar]
- Ji, J.; Liu, Y. Bilinear interpolation fitting calibration method for two-dimensional large-angle FSM. Laser Infrared 2024, 54, 1737–1743. [Google Scholar]
- Wang, M.; Xi, J.; Wang, W. Analysis of the influence of acoustic wave disturbance on the internal and external scales of atmospheric turbulence and the refractive index power spectrum function. Physics 2023, 72, 165–175. [Google Scholar] [CrossRef]
| Weather | Sample | Date | Temperature | Wind | AQI |
|---|---|---|---|---|---|
| Sunny | T1 | 27 November 2024 | 1–12 | West wind level 3 | 70 |
| T2 | 17 December 2024 | −2–11 | Northwest wind level 1 | 80 | |
| T3 | 1 December 2024 | 1–17 | North wind level 1 | 72 | |
| T4 | 21 March 2025 | 9–23 | Northeast wind level 1 | 65 | |
| T5 | 24 March 2025 | 12–30 | Northwest wind level 1 | 74 | |
| Overcast | T6 | 12 December 2024 | 0–6 | West wind level 3 | 63 |
| T7 | 26 December 2024 | 0–8 | Northeast wind level 2 | 66 | |
| T8 | 17 March 2025 | 2–15 | Southwest wind level 3 | 52 | |
| T9 | 28 March 2025 | 6–11 | Northwest wind level 3 | 127 | |
| T10 | 3 April 2025 | 11–18 | Northeast wind level 2 | 92 | |
| Rain | T11 | 1 March 2025 | 6–15 | North wind level 2 | 172 |
| T12 | 2 March 2025 | 6–11 | Southwest wind level 4 | 68 | |
| T13 | 13 March 2025 | 11–20 | Southeast wind level 4 | 90 | |
| T14 | 14 March 2025 | 9–11 | West wind level 3 | 63 | |
| Sandstorm | T15 | 26 March 2025 | 14–27 | West wind level 2 | 185 |
| T16 | 11 April 2025 | 10–26 | Northwest wind level 3 | 117 | |
| T17 | 22 March 2025 | 9–24 | Southwest wind level 4 | 69 |
| Weather | Sample | Date | Temperature | Wind | AQI |
|---|---|---|---|---|---|
| Sunny | T18 | 5 November 2024 | 8–18 | Northeast wind level 1 | 79 |
| T19 | 28 November 2024 | 1–13 | West wind level 1 | 72 | |
| T20 | 20 December 2024 | −1–8 | Northeast wind level 1 | 76 | |
| T21 | 9 March 2025 | 05–19 | Northeast wind level 2 | 75 | |
| T22 | 10 April 2025 | 15–27 | Northeast wind level 2 | 107 | |
| Overcast | T23 | 18 December 2024 | 0–6 | Northeast wind level 2 | 90 |
| T24 | 13 December 2024 | 0–6 | Northwest wind level 3 | 105 | |
| T25 | 5 December 2024 | 0–10 | Southwest wind level 1 | 98 | |
| T26 | 14 December 2024 | −1–7 | Southwest wind level 3 | 81 | |
| T27 | 4 April 2025 | 9–25 | Northwest wind level 2 | 107 | |
| T28 | 7 April 2025 | 15–31 | Southeast wind level 2 | 78 | |
| Rain | T29 | 21 April 2025 | 11–22 | Southwest wind level 4 | 75 |
| T30 | 3 May 2025 | 17–25 | Northeast wind level 3 | 77 | |
| T31 | 7 May 2025 | 20–31 | Northeast wind level 3 | 198 | |
| T32 | 9 May 2025 | 13–25 | Northwest wind level 5 | 85 |
| Weather | Sample | Date | Temperature | Wind | AQI |
|---|---|---|---|---|---|
| Sunny | T33 | 25 November 2024 | −2–10 | West wind level 2 | 37 |
| T34 | 2 April 2025 | 9–18 | Northwest wind level 2 | 98 | |
| T35 | 14 April 2024 | 12–28 | Northwest wind level 2 | 92 | |
| T36 | 11 May 2025 | 15–31 | Northeast wind level 1 | 44 | |
| T37 | 12 June 2025 | 26–39 | Southeast wind level 1 | 48 | |
| Overcast | T38 | 20 November 2024 | 5–14 | Southwest wind level 1 | 49 |
| T39 | 5 May 2024 | 14–28 | Southwest wind level 3 | 111 | |
| T40 | 18 May 2024 | 20–36 | Southwest wind level 3 | 120 | |
| T41 | 6 June 2024 | 25–35 | Southwest wind level 2 | 44 | |
| T42 | 17 June 2025 | 27–38 | Northeast wind level 2 | 72 | |
| Rain | T43 | 17 November 2024 | 8–10 | Northeast wind level 1 | 23 |
| T44 | 14 May 2025 | 16–29 | Northwest wind level 3 | 62 | |
| T45 | 25 May 2025 | 16–26 | Northwest wind level 1 | 57 | |
| T46 | 14 June 2025 | 20–31 | Southwest wind level 3 | 47 |
| Sample | x/Uncorrected | x/Corrected | y/Uncorrected | y/Corrected |
|---|---|---|---|---|
| T1 | 24.17 | 6.34 | 6.34 | 6.27 |
| T2 | 24.28 | 6.97 | 6.97 | 7.06 |
| T3 | 24.63 | 7.1 | 7.1 | 7.55 |
| T4 | 25.91 | 7.5 | 7.5 | 7.55 |
| T5 | 26.87 | 8.37 | 8.37 | 6.79 |
| T6 | 24.53 | 7.95 | 7.95 | 8.23 |
| T7 | 25.39 | 8.85 | 8.85 | 9.11 |
| T8 | 26.73 | 9.99 | 9.99 | 6.63 |
| T9 | 28.73 | 9.33 | 9.33 | 9.49 |
| T10 | 30.32 | 9.7 | 9.7 | 10.4 |
| T11 | 27.63 | 9.13 | 9.13 | 12.63 |
| T12 | 30.39 | 9.38 | 9.38 | 8.9 |
| T13 | 25.37 | 10.43 | 10.43 | 10.61 |
| T14 | 30.48 | 11.73 | 11.73 | 9.17 |
| T15 | 30.44 | 12.79 | 12.79 | 9.96 |
| T16 | 35.78 | 15.69 | 15.69 | 13.68 |
| T17 | 37.17 | 10.75 | 10.75 | 15.59 |
| Sample | x/Uncorrected | x/Corrected | y/Uncorrected | y/Corrected |
|---|---|---|---|---|
| T18 | 50.27 | 12.63 | 38.39 | 9.58 |
| T19 | 45.68 | 17.18 | 29.66 | 10.27 |
| T20 | 45.84 | 14.78 | 31.61 | 16.49 |
| T21 | 39.09 | 17.78 | 27.11 | 16.34 |
| T22 | 46.23 | 18.06 | 27.102 | 9.87 |
| T23 | 50.36 | 15.25 | 25.75 | 16.7 |
| T24 | 42.29 | 22.65 | 36.58 | 10.67 |
| T25 | 46.93 | 14.81 | 26.61 | 20.6 |
| T26 | 51.3 | 14.56 | 33.6 | 10.45 |
| T27 | 42.24 | 20.99 | 31.23 | 16.86 |
| T28 | 49.69 | 20.76 | 24.83 | 13.87 |
| T29 | 45.99 | 26.42 | 33.33 | 17.3 |
| T30 | 55.73 | 22 | 42.7 | 25.77 |
| T31 | 45.55 | 17.9 | 40.91 | 26.85 |
| T32 | 51.89 | 27.84 | 31.8 | 18.6 |
| Sample | x/Uncorrected | x/Corrected | y/Uncorrected | y/Corrected |
|---|---|---|---|---|
| T33 | 155.09 | 87.29 | 120.25 | 80.17 |
| T34 | 148.19 | 94.63 | 130.8 | 90.74 |
| T35 | 167.63 | 93.97 | 123.77 | 86.25 |
| T36 | 160.29 | 89.26 | 126.39 | 92.85 |
| T37 | 152.37 | 83.48 | 131.54 | 89.35 |
| T38 | 166.33 | 55.28 | 149.4 | 97.41 |
| T39 | 156.21 | 84.41 | 143.18 | 109.28 |
| T40 | 152.46 | 92.78 | 130.31 | 103.22 |
| T41 | 147.17 | 86.39 | 140.14 | 96.26 |
| T42 | 153.74 | 83.28 | 143.2 | 94.35 |
| T43 | 173.53 | 117.25 | 160.43 | 115.39 |
| T44 | 157.49 | 128.54 | 155.57 | 129.84 |
| T45 | 170.56 | 130.65 | 167.39 | 125.32 |
| T46 | 159.35 | 133.28 | 169.38 | 126.3 |
| Sample | x/Uncorrected | x/Corrected | y/Uncorrected | y/Corrected |
|---|---|---|---|---|
| T01–05 | 1.1 | 0.45 | 1.28 | 0.63 |
| T06–10 | 3.54 | 1.51 | 1.72 | 0.87 |
| T11–14 | 4.51 | 2.05 | 2.9 | 1.19 |
| T15–17 | 8.42 | 4.11 | 7.06 | 3.46 |
| T18–22 | 11.13 | 5.32 | 17.37 | 10.22 |
| T23–28 | 13.63 | 8.26 | 18.95 | 10.05 |
| T29–32 | 18.03 | 11.24 | 22.04 | 14.83 |
| T33–37 | 36.20 | 23.31 | 32.17 | 21.41 |
| T38–42 | 37.85 | 26.03 | 34.75 | 25.01 |
| T43–46 | 41.75 | 30.07 | 38.29 | 29.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, Y.; Ke, X.; Wang, R. Experiment of Suppressing Atmospheric Turbulence by Using Fast-Steering Mirror. Appl. Sci. 2025, 15, 9920. https://doi.org/10.3390/app15189920
Yuan Y, Ke X, Wang R. Experiment of Suppressing Atmospheric Turbulence by Using Fast-Steering Mirror. Applied Sciences. 2025; 15(18):9920. https://doi.org/10.3390/app15189920
Chicago/Turabian StyleYuan, Yingmin, Xizheng Ke, and Rui Wang. 2025. "Experiment of Suppressing Atmospheric Turbulence by Using Fast-Steering Mirror" Applied Sciences 15, no. 18: 9920. https://doi.org/10.3390/app15189920
APA StyleYuan, Y., Ke, X., & Wang, R. (2025). Experiment of Suppressing Atmospheric Turbulence by Using Fast-Steering Mirror. Applied Sciences, 15(18), 9920. https://doi.org/10.3390/app15189920





