Spatiotemporal Evolution of the Failure Process of Sandstone Monitored Using Multi-Point Fiber Bragg Grating

Abstract

Coal-rock dynamic disasters, especially rock bursts, require insight into the spatiotemporal evolution of strain and temperature to clarify failure mechanisms and improve early warning. This study aims to characterize the spatiotemporal evolution of the strain field during brittle rock instability by developing a multi-point Fiber Bragg Grating (FBG) strain–temperature monitoring and inversion method. Multi-directional, multi-location FBG deployment enables real-time reconstruction of strain tensors and temperature at each monitoring point, capturing both surface and internal responses under loading. The strain records resolve four stages—initial smoothing, linear growth, pre-peak nonlinearity, and failure fluctuation—with earlier sensitivity than Linear Variable Differential Transformers (LVDT), enabling finer localization of yielding and microcracking. The FBG sensors capture clear spatial heterogeneity and timing offsets during yielding, supporting instability warning. Temperature results show a slow rise followed by a surge from the end of the elastic stage into the plastic stage, reaching ~1.6 °C before declining; the thermal peak precedes the stress peak by ~0.38 s. Meanwhile, the temperature-field coefficient of variation jumps from <0.15 to >0.25, indicating a transition from diffuse heating to banded localization. Together, these strain–temperature precursors validate the FBG-based method as an effective and reliable approach for early warning of brittle rock instability.

1. Introduction

With the continuous increase in mining depth and the growing intensity of mining activities, dynamic coal-rock disasters, such as rock burst, have become one of the most serious threats to the safe production of coal [1,2]. As the primary carrier of rock burst disasters, studying the mechanisms and evolutionary processes of instability and failure in rock samples under loading is the foundation for the prevention and control of coal-rock dynamic disasters [3]. Strain, as the core parameter characterizing the failure behavior of rock under loading, plays a crucial role. Studying the spatiotemporal evolution characteristics of the strain field and damage localization analysis during rock instability and failure not only helps to reveal the intrinsic mechanisms of rock failure but also provides theoretical support and technical basis for monitoring, early warning, and prevention measures for dynamic disasters [4,5].

The uniaxial compressive strength (UCS) test is one of the most fundamental and widely used experimental methods in rock mechanics [6,7]. In practical engineering for coal–rock dynamic disaster prevention, laboratory testing of field-collected samples remains the primary means for obtaining the fundamental physical and mechanical parameters of coal and rock media. During UCS tests, dynamic measurement of strain parameters is indispensable [8] and plays a crucial role in engineering fields such as oil and gas, aerospace, and structural health monitoring [9,10].

Currently, several strain monitoring techniques are widely employed, including LVDT, ESG, DIC [11], DTP [12], and Industrial CT scanning [13,14], among others [15]. To clearly compare the characteristics of commonly used strain monitoring methods,

Table 1. Comparative summary of strain monitoring technologies.

Technology	Advantages	Disadvantages	Typical Applications	Remarks
Electrical Resistance Strain Gauge	High measurement accuracy; mature technology; low cost	Susceptible to electromagnetic interference; poor long-term stability in harsh environments; single-point measurement	Laboratory material testing, structural health monitoring in stable environments	Requires adhesive bonding; sensitive to temperature variations
LVDT Displacement Transducer	High resolution; robust structure; insensitive to electromagnetic interference	Measures displacement rather than direct strain; bulky; limited to local measurement	Rock mass convergence monitoring, structural deformation measurement	Requires stable installation base; sensitive to alignment errors
Electro-Static Strain meter	Can achieve distributed measurement over long distances; suitable for deep underground stress monitoring	Large size; installation complexity; low temporal resolution	Mine roadway deformation, long-term geomechanical monitoring	Mainly used for long-term, low-frequency monitoring
Fiber Bragg Grating (FBG) Sensor	High precision; immune to electromagnetic interference; capable of multiplexing and distributed sensing; resistant to corrosion; suitable for harsh environments	Higher initial cost; requires specialized demodulation equipment	Real-time strain and temperature monitoring in mining, tunnels, and large structures	Enables multi-parameter monitoring (strain, temperature, vibration); suitable for early warning systems

provides a comprehensive summary of different techniques, outlining the main advantages, limitations, typical application scenarios, and relevant remarks for each. Traditional electrical methods, such as LVDT and ESG, offer high accuracy and ease of use, with strain values indirectly derived from the deformation of internal sensing components. However, signal attenuation, complex wiring, and sensitivity to electromagnetic interference limit their long-term stability, making them more suitable for short-term experimental applications. Noncontact techniques, like DIC, DTP, and Industrial CT, have gained increasing traction with advances in computer vision and image processing [16]. For example, Abdulqader and Rizos applied DIC to UCS tests and confirmed its feasibility as a high-precision surface strain measurement alternative to ESGs [17]; Gao et al. investigated the mechanical behavior of coal at different loading rates using DIC [18]. Nonetheless, DIC is restricted by camera field of view, and full circumferential coverage requires multiple coordinated cameras, which is impractical under dynamic loading or in confined spaces. DTP has been used for rock slope stability analysis [19] but is highly sensitive to lighting and limited in spatial resolution, reducing applicability in complex field scenarios. Combining CT with digital speckle analysis can reconstruct three-dimensional strain fields during loading [20,21], but high equipment costs and static imaging limit its potential for real-time monitoring.

To address these limitations, Fiber Bragg Grating (FBG) sensing technology has attracted increasing attention for both laboratory and in situ strain monitoring [22,23,24,25,26]. FBG sensing technology possesses several notable advantages, including compact size, flexible deployment, high resistance to temperature and pressure, immunity to electromagnetic interference, and excellent linearity [27,28,29]. Compared with traditional electrical and optical measurement methods [30,31,32,33], FBG sensors offer high accuracy and sensitivity, enabling the detection of microstrain changes under low-noise conditions. They maintain stable performance in electrically noisy or underground environments and support multiplexing and distributed sensing, allowing multiple sensing points to be integrated along a single optical fiber for full-field, simultaneous monitoring. Furthermore, FBG sensors can operate reliably in harsh conditions—such as high temperature, high pressure, humidity, and corrosion—while preserving excellent repeatability under both static and dynamic loading, ensuring dependable strain measurements across diverse applications. Previous studies have demonstrated that FBG sensors not only provide high-precision surface strain measurements but are also highly responsive to internal structural changes [34,35,36]. For example, Xie et al. found that internal strains captured by FBG in perforated coal samples were more sensitive to localized instability than surface or axial strain measurements [37]; Sun et al. used a multi-channel FBG array for dynamic strain monitoring in cylindrical specimens under UCS, achieving strong agreement with LVDT results and enabling full-field surface strain sensing [38]; Gage et al. embedded FBG strain sensors in the roof of underground excavations to monitor deformation at varying depths, quantifying stiffness gradients and revealing scale effects in rock mechanical parameters [38]. Landreau et al. demonstrated that under dynamic loading, the strain transfer performance of FBG sensors is highly sensitive to the type of adhesive, and that optimized adhesive selection can achieve dynamic strain measurement performance comparable to conventional strain gauges [39]. Her and Chung validated that FBG-based sensing systems can reliably capture rapid strain changes caused by impact loading in structural health monitoring scenarios, showing good agreement with reference strain gauges [40,41]. These findings underscore FBG’s unique advantages in detecting localized deformation, capturing deep structural responses, and maintaining stability in harsh environments.

To fill this gap, this study proposes a novel strain tensor monitoring and inversion method based on multi-directional, multi-point FBG sensor deployment, aiming to accurately characterize the spatiotemporal evolution of strain and temperature fields during brittle rock instability under loading. The method reconstructs strain tensors and temperatures at each monitoring point, enabling real-time, dynamic tracking of both surface and internal field evolution. This approach facilitates a better understanding of spatiotemporal heterogeneity and its relationship to failure mechanisms, providing valuable theoretical support and practical potential for early warning of dynamic disasters such as rock bursts.

2. Experimental Procedure

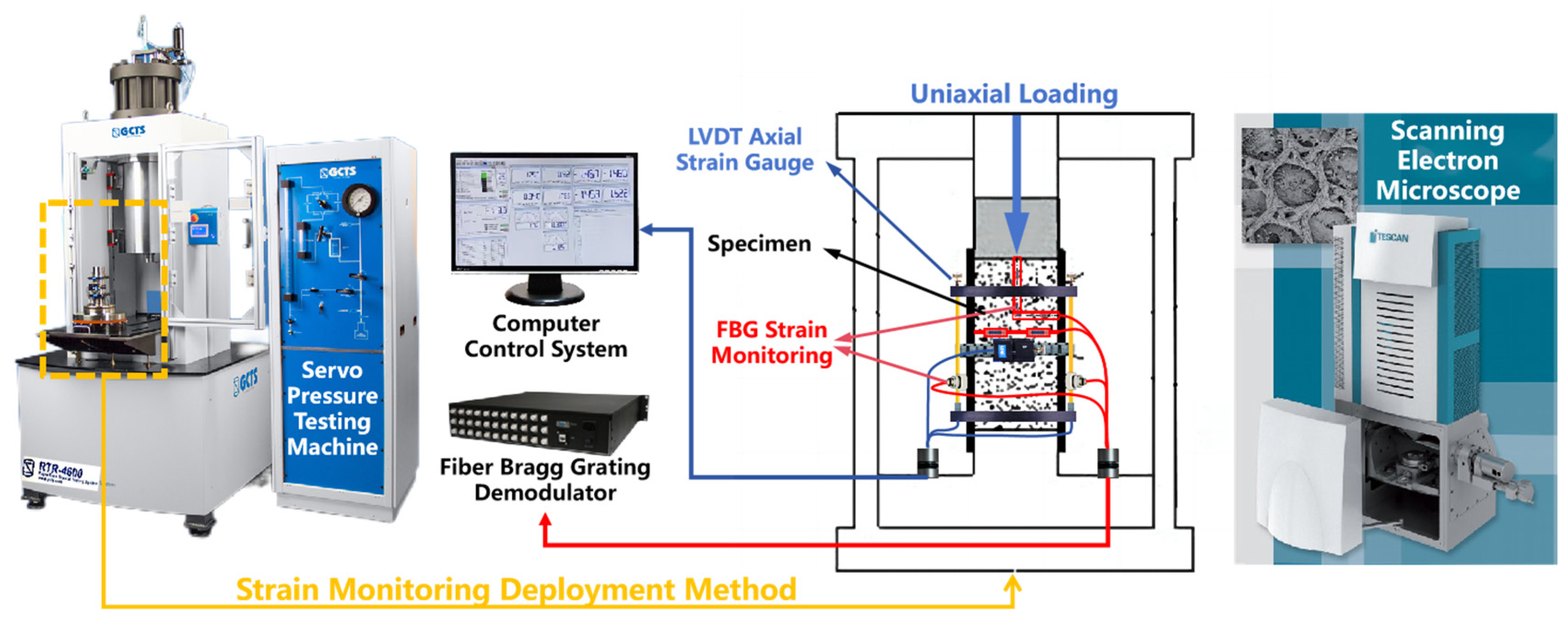
The experimental system consists of a loading system, an optical fiber strain acquisition system (Zhixing, Nantong, China), and a scanning electron microscope (SEM, TESCAN, Brno, Czech Republic) (as shown in Figure 1). The loading control system is the RTR-4600 high-temperature and high-pressure rock testing system (GCTS, Tempe, AZ, USA), which can achieve both stress control and displacement control, with a maximum load capacity of 4600 kN. The system is also equipped with an LVDT (GCTS, Tempe, AZ, USA) for axial deformation measurement, with an accuracy of 0.25% FS and a range of ±6 mm. The optical fiber acquisition system is composed of an optical FBG strain sensor and a modulator–demodulator. The modulator–demodulator uses frequency-sweep laser measurement technology to collect data via full-spectrum scanning. The data acquisition frequency is 2000 Hz, with an accuracy of ±1 pm and a resolution of 0.1 pm. The SEM was used to observe the microstructure at the bonding interface between the FBG sensor and the sample. The resolution of the SEM backscattered electron detector is less than 3.5 nm.

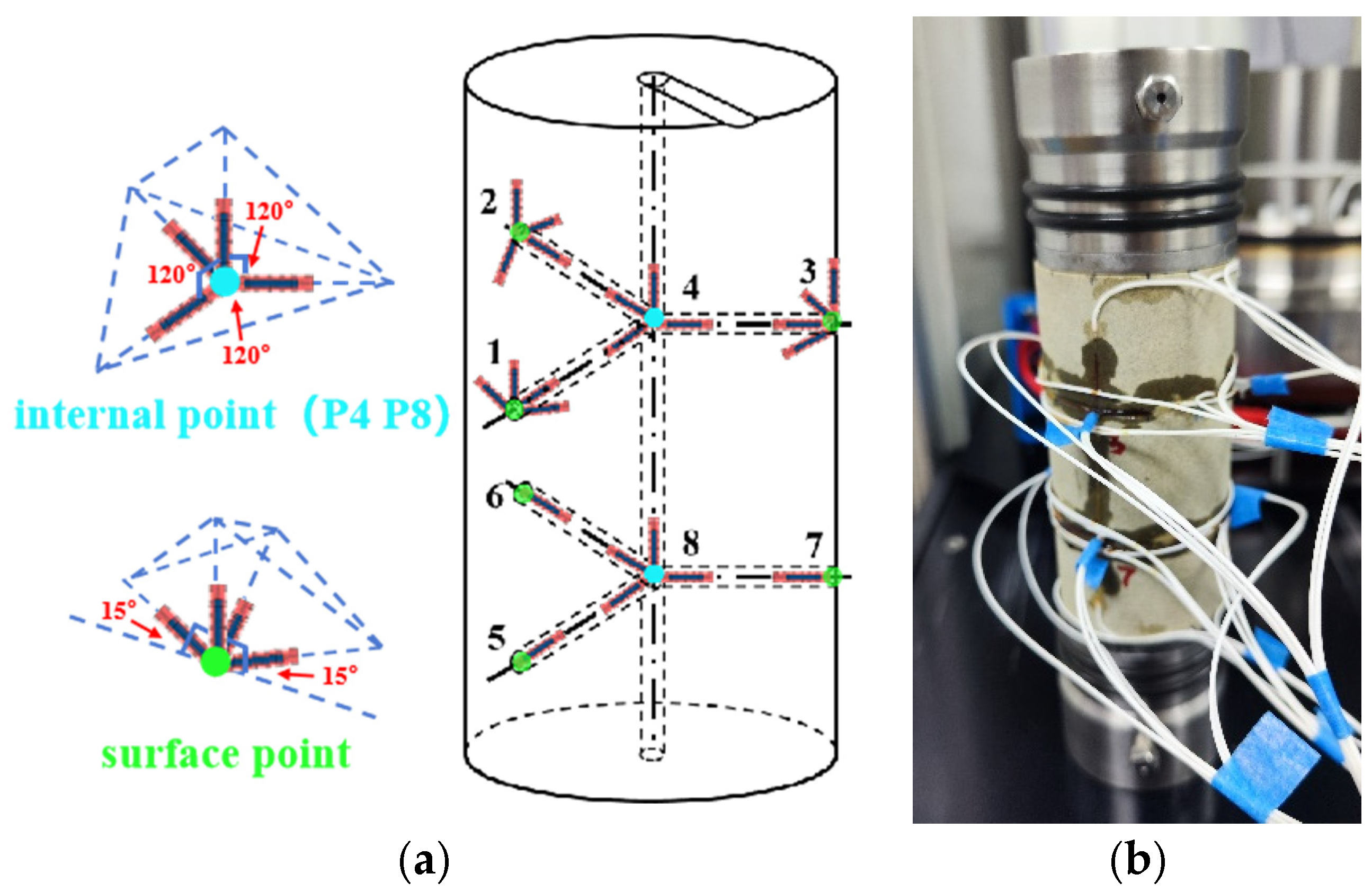
The experimental process followed the standards recommended by the International Society for Rock Mechanics and Rock Engineering. Standard sandstone samples with dimensions of 50 mm × 100 mm (diameter × height) were used, with processing errors of ±0.5 mm for the sides and ±0.02 mm for the end faces. To monitor the multi-directional strain values at multiple points inside and on the surface of the sample in real-time during the experiment, a 3 mm diameter through hole was pre-drilled at the center of the sample. Additionally, three holes, each with a diameter of 2 mm and a length of 25 mm, were drilled at 32.5 mm from the top and bottom end faces, with each pair of holes at a 120° angle to each other. Fixed-angle grooves were pre-formed around these holes to arrange the FBG sensors. Considering the potential influence of such drilling and grooving on specimen integrity, previous studies have shown that when the specimen size-to-bore diameter ratio exceeds 10, pre-drilled holes do not significantly affect the stress level at failure initiation [42]. In the present study, the bore diameters are small relative to the specimen size (ratios > 16), and the grooves are shallow, indicating that the adopted installation approach is unlikely to weaken the overall mechanical properties of the sandstone specimens. To verify this, a pre-test comparative study was conducted on two specimen groups: intact specimens and specimens with boreholes of identical dimensions and placement to those used for sensor installation. Uniaxial compression tests under identical loading conditions showed no significant differences in peak strength (<2% variation) or in the overall stress–strain curve profiles, confirming that such small-diameter boreholes did not measurably affect the global mechanical behavior.

Before the formal tests, a series of preliminary experiments involving more than 30 sandstone samples were conducted to investigate the coupling characteristics between the FBG sensors and the rock material. These included various single-point and multi-directional sensor layouts. The final deployment scheme used in this study was selected based on the performance stability and measurement accuracy observed in the pre-tests. As shown in Figure 2a, to more intuitively describe the different monitoring points, they were labeled as points 1 to 8. Among them, points 4 and 8 were located at the central points inside the sample, with multi-directional strain sensors arranged as one FBG in the vertical direction and three FBGs in the horizontal direction at 120° intervals. The remaining 6 points were surface monitoring points, with one FBG arranged in the vertical direction at each point. Of the three FBGs arranged in the horizontal plane, two were placed with a 150° angle along the surface, and the middle one was placed in the hole, pointing toward the center of the hole. All FBG strain sensors were adhered with epoxy resin, and the coupled sample is shown in Figure 2b.

Before the formal loading of the experiment begins, a 1 kN pre-load was applied to the rock specimen to ensure that the GCTS platen is in close contact with the upper surface of the rock sample. The FBG strain monitoring data were recorded only after the pressure sensor and LVDT readings stabilize. During the experiment, the data acquisition frequency for the stress sensor and LVDT was 10 Hz, while the FBG data acquisition frequency was 2000 Hz. The loading mode was uniaxial displacement control. The experiment was conducted on sandstone specimens under uniaxial compression, with loading rates of 0.1 mm/s.

3. Results

3.1. Calculation of Strain Transfer Rate

As shown in Figure 3, bare FBG sensors were used in this study. The sensing part of the FBG strain sensor typically consists of the grating, protective layer, adhesive layer, and other components. During the strain transfer process, the protective and adhesive layers absorb a portion of the energy, which causes the strain measured by the FBG to differ from the actual strain in the substrate structure. The accuracy of the FBG strain sensor also depends on the physical and mechanical properties of the grating, protective layer, adhesive layer, and the rock mass. To more accurately capture the evolution of the strain field during the loading process of the rock specimen, it is essential to calculate the interface transfer characteristics of the FBG strain sensing.

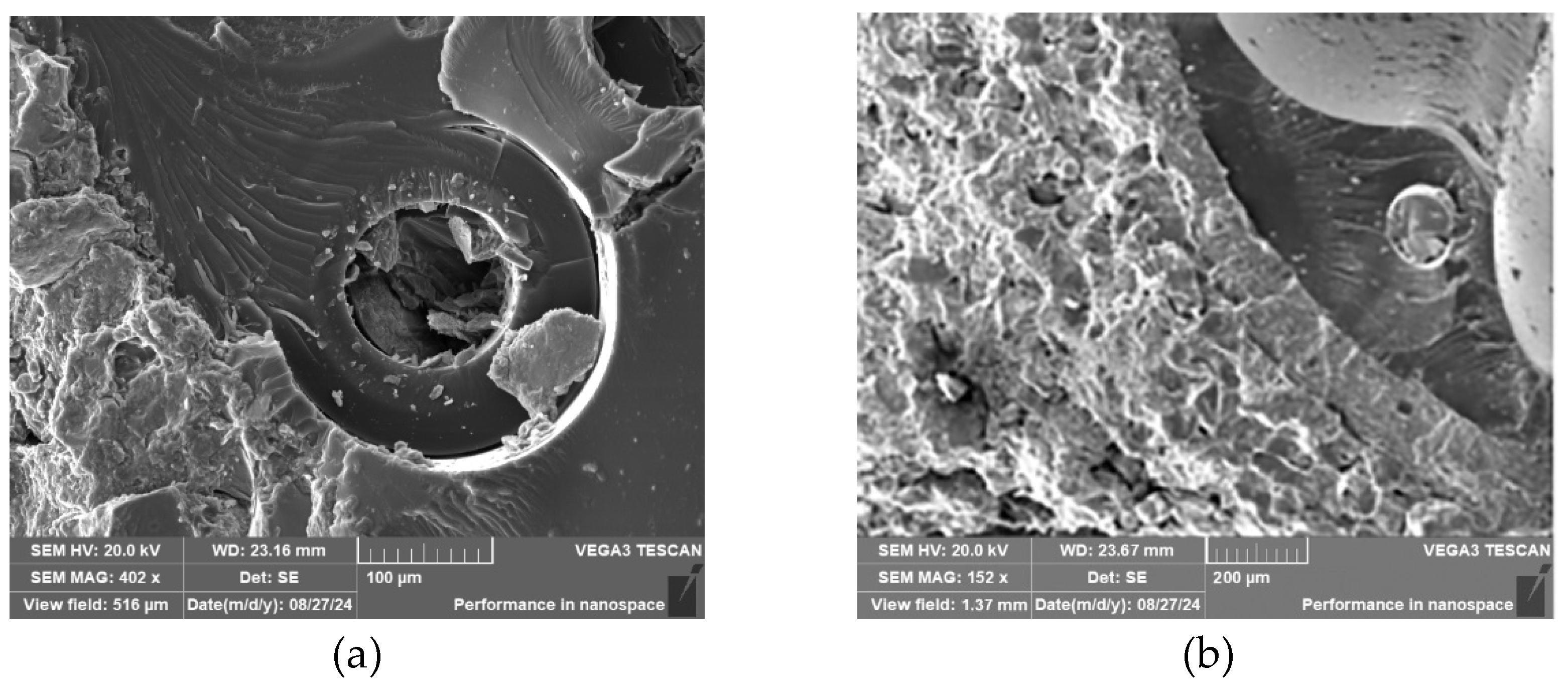
Figure 4 shows electron microscope micrographs of some post-experiment specimen sections observed using SEM. The images display the thickness of the FBG coating layer and the radius size of the optical fiber core, as well as the distribution structure of the FBG with the sandstone specimen. Figure 4a shows the cross-sectional view of the FBG strain sensor attached to the surface groove at a magnification of 402×. The coating area and the optical fiber core area dimensions are clearly visible. Additionally, from the relative positioning of the FBG and the sandstone specimen, it can be observed that the two are almost in tight contact, and the thickness of the adhesive layer is negligible. Figure 4b shows the microscopic structure of the sandstone portion inside the hole at a magnification of 152×. The microstructure of the sandstone indicates that the drilling process has a relatively minor impact on the sample structure. Meanwhile, due to the spatial constraints within the hole, the thickness of the FBG adhesive layer is noticeably increased.

Based on the above SEM micrographs, the following mechanical model is established [43]:

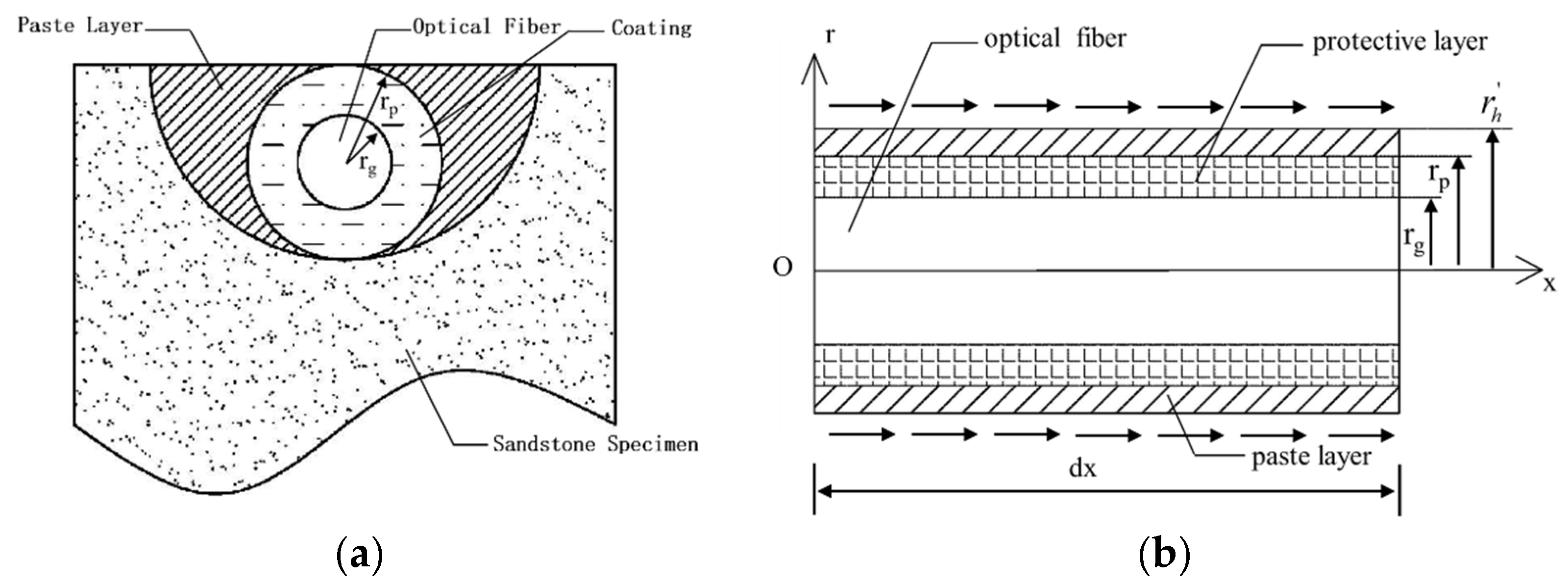
It is assumed that a half-circular groove is carved on the surface of the rock, with a radius $r_h$ equal to the diameter of the optical fiber protective layer, denoted as $r_h=2r_p$. The optical fiber is attached within this groove using an adhesive. The length of the FBG strain sensor is denoted as 2L = 10 mm, and the coupling cross-section schematic is shown in Figure 5a. Additionally, for the adhesive layer, the thickness varies along the circumferential direction of the optical fiber coating. However, since the pre-drilled hole and groove dimensions are relatively small, and epoxy resin is selected as the adhesive layer with a high strain transfer efficiency, it is assumed that the adhesive layer is uniformly distributed around the sensor. The mechanical model for the fiber attached to the surface of the sample is the same as the mechanical transfer model for the fiber placed inside the hole. The stress transfer schematic is shown in Figure 5b. The relationship between the real strain of the specimen ${\overline{\epsilon }}_r$ and the FBG strain ${\overline{\epsilon }}_g$ is defined as the strain transfer rate α, which can be expressed as follows:

$${\displaystyle \frac{{\overline{\epsilon }}_r}{{\overline{\epsilon }}_g}}=\alpha ={\displaystyle \frac{1}{1-\frac{\sinh (kL)}{kL\cosh (kL)}}}$$

(1)

$$k=\sqrt{{\displaystyle \frac{2}{E_g{r}_g^2\left(\frac{1}{G_p}\ln \frac{r_p}{r_g}+\frac{1}{G_h}\ln \frac{r_h}{r_p}\right)}}}$$

(2)

In terms of characteristic parameter selection, the FBG is chosen with a protective coating of acrylic ester on the pure coated fiber. To achieve better coupling between the optical fiber and the rock, the FBG is attached and fixed to the specimen using epoxy resin glue. Since the specimen may experience instability, damage, or some vibration during loading, which could lead to fiber detachment, a high-strength adhesive with strong curing properties is selected to ensure the coupling effect.

From the Figure 4a, it can be seen that the FBG sensor pasted onto the surface groove is almost in close contact with the sample, i.e., $r_h^{\prime }=r_p$, the length of the fiber Bragg grating strain sensor is 2L = 10 mm, and other parameters are shown in

Table 2. Fiber optic mechanical parameters.

Characteristic	Mechanical Parameters	Value
$E_g$	Fiber Elastic Modulus	7.2 × 1010 Pa
$G_p$	Coating Shear Modulus	1 × 108 Pa
$G_h$	Adhesive Layer Shear Modulus	3.5 × 109 Pa
$r_p$	Fiber with Coating Radius	125 μm
$r_g$	Fiber Radius	62.5 μm

. Based on Equation (1), it can be calculated that the strain transfer coefficient for the surface-mounted FBG is ${\alpha }_{surface}=2.34$.

For the FBG sensor set inside the hole, the thickness of the adhesive layer is clearly thicker compared to Figure 4a, as seen in Figure 4b. The thickness of the adhesive layer, measured from the image, is $d=110 \mathsf{\mu }\mathrm{m}$, thus $r_h^{\prime }=r_p+d=235 \mathsf{\mu }\mathrm{m}$. The length of the FBG sensor and other parameters remain unchanged, and based on Equation (1), it can be calculated that ${\alpha }_{hole}=2.34$.

Through calculations, it is easy to see that when the FBG is applied to the surface or inside the hole, although the adhesive thickness differs, the strain transfer rate is the same. This is mainly because the shear modulus of the selected curing adhesive is an order of magnitude larger than that of the coating layer. This also indicates that when selecting an adhesive, one with better curing strength has better strain transfer characteristics and can more accurately reflect the real strain state of the object being measured during the monitoring process.

3.2. Verification of FBG Strain Monitoring Effectiveness

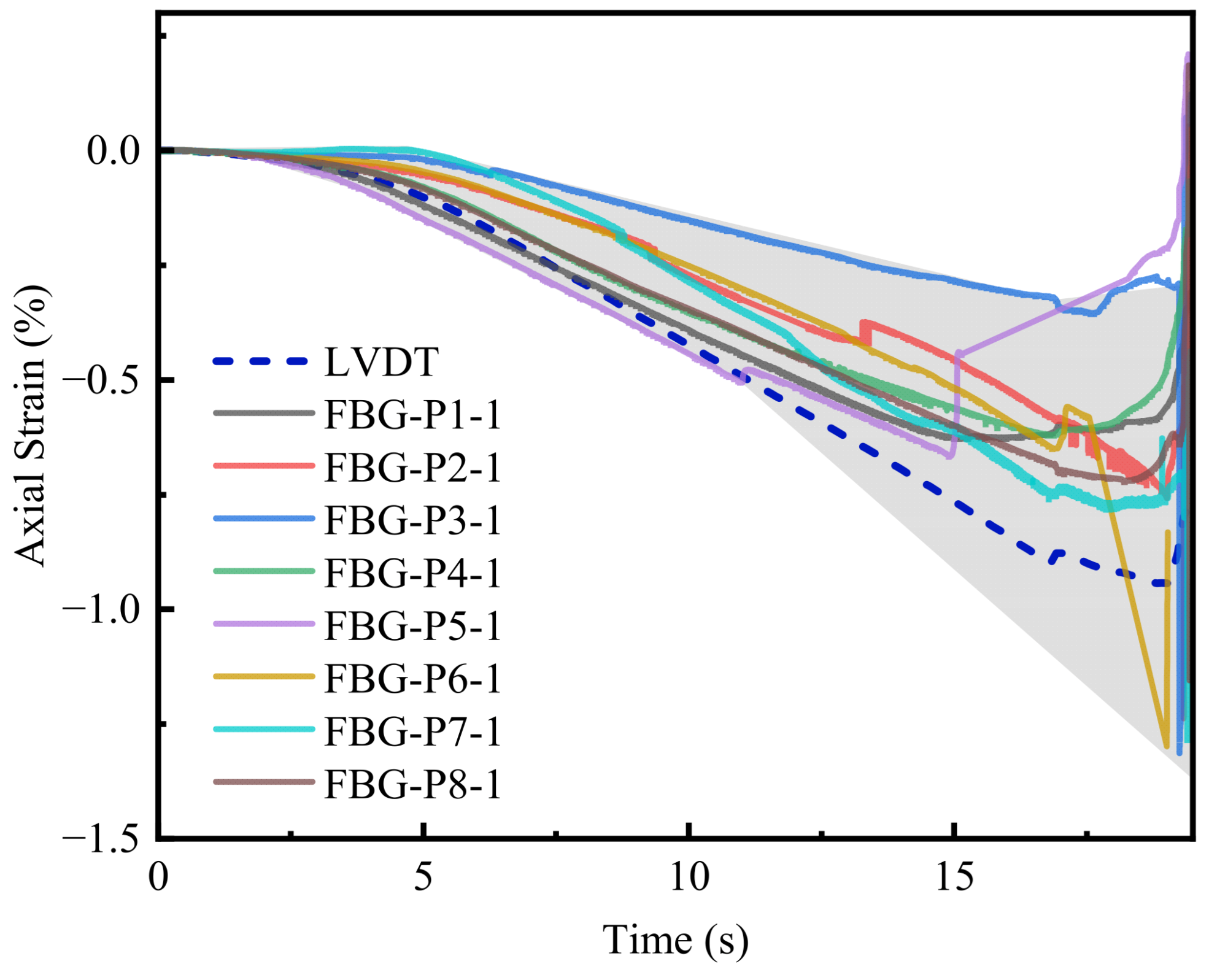
To verify the accuracy of strain measurements based on FBG, the axial (z-axis) strain at each monitoring point was compared with the LVDT data, as shown in Figure 6. During the loading process leading to instability and failure of the sandstone specimen, the axial strain responses from all eight FBG monitoring points exhibited a similar decreasing trend to the LVDT data. Throughout the entire loading range, the strain values measured by the LVDT consistently fell within the shaded envelope formed by the FBG axial strain data, and the maximum difference between the average axial strain values from the eight FBG sensors and the LVDT measurement was 0.23%.

Some fluctuations were observed between the strain curves of different FBG sensors, which can mainly be attributed to the following: (i) the heterogeneity of the sandstone material, including variations in grain structure, cementation strength, and pore distribution, leading to local differences in mechanical properties at each monitoring point; (ii) localized stress concentrations and microcrack initiation, where certain regions may enter the damage stage earlier during the nonlinear phase, causing short-term fluctuations or abrupt changes in the strain curves; and (iii) differences in sensor positioning and bonding quality, such as slight variations in adhesive layer thickness or borehole wall roughness, which can affect strain transfer efficiency. These differences, in fact, reflect the capability of FBG sensors to capture local strain features with high spatial resolution.

For about 35% of the loading process, the strain measured by the LVDT was lower than that measured by the FBG sensors. This is because the LVDT (with a gauge length of approximately 82.5 mm) is a global averaging measurement method, and its sensitivity to local strain variations is lower than that of the FBG sensors (with a gauge length of approximately 10 mm). The larger measurement range of the LVDT may result in certain delays or distortions when capturing localized strain changes, particularly at a lower sampling frequency (10 Hz). In contrast, the FBG sensors, with their higher sampling frequency (2000 Hz), can accurately capture strain fluctuations in small areas. Therefore, during certain time intervals, the LVDT readings were lower than those of the FBG sensors. Overall, the optical strain sensors and the LVDT exhibited good agreement in strain readings within the same measurement range, and the results indicate that the FBG system can be considered an effective tool for strain monitoring. However, it should be noted that the LVDT measures global displacement over a relatively long gauge length, whereas the FBG measures local strain over a short gauge length. For sandstone, a heterogeneous material that exhibits localized deformation, cracking, and transverse expansion due to the Poisson effect, such fundamental differences in measurement principle and spatial scale make it impossible for the two methods to produce identical results throughout the entire loading process. Therefore, the comparison presented here should be regarded as a qualitative assessment of trend consistency rather than a rigorous accuracy validation.

3.3. Characteristics of the Stress–Strain Curve

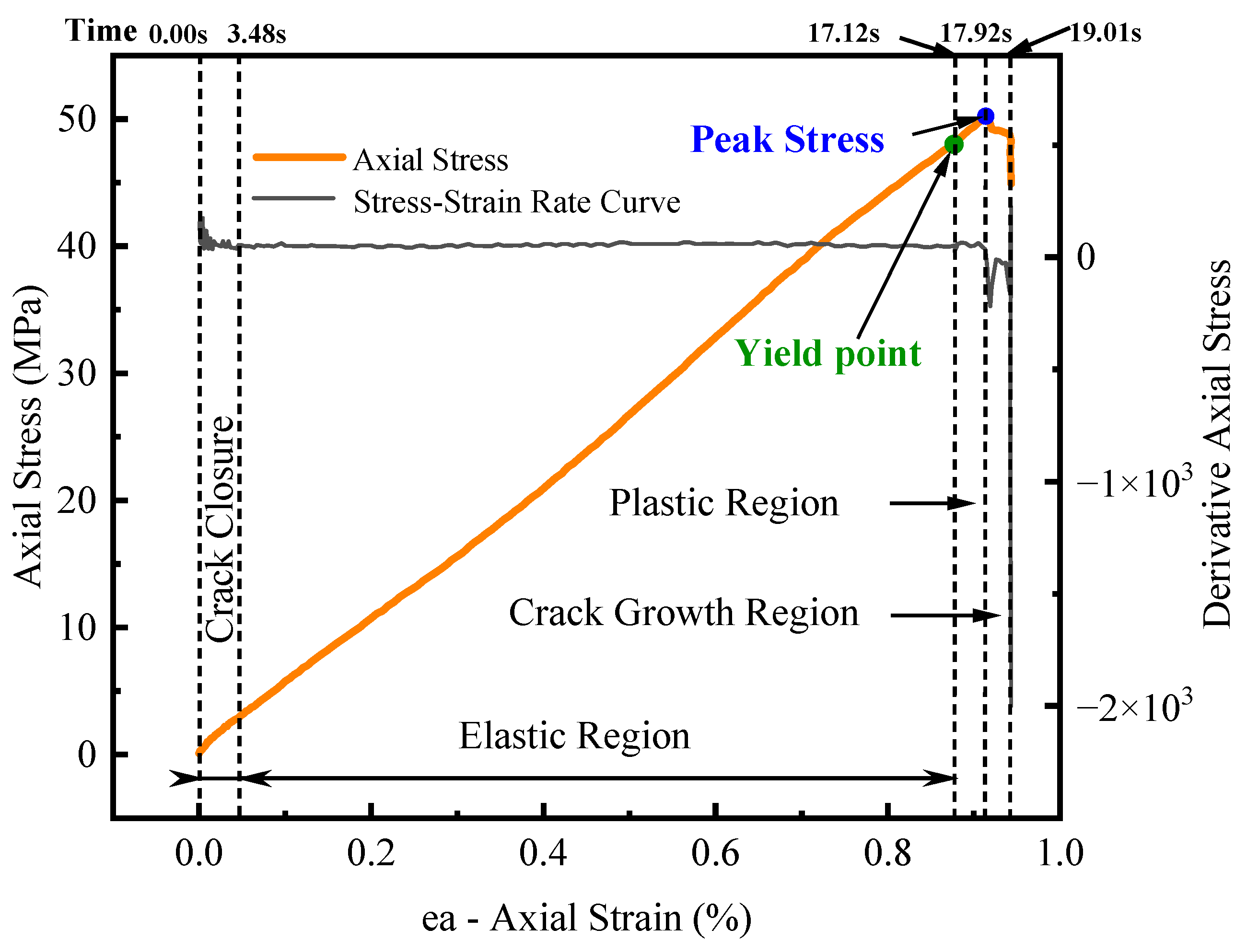
Figure 7 presents the stress–strain curve and the corresponding tangent modulus curve of the sandstone specimen under uniaxial compression at a displacement loading rate of 0.1 mm/s. The tangent modulus curve reflects the instantaneous stiffness of the specimen during loading, and in this study, it is used in combination with the stress–strain curve to qualitatively identify the deformation stages. Based on the overall trends of the two curves, five stages can be distinguished: the compaction phase (Stage I), the elastic phase (Stage II), the plastic phase (Stage III) after the yield point, the crack propagation phase (Stage IV), and the complete failure phase (Stage V). During the initial 3.48 s of loading, fluctuations in the tangent modulus curve indicate the gradual closure of internal pores or microdefects; however, the short duration of this stage may also be influenced by the relatively fast loading rate, initial microcracks introduced during sample preparation, and system-related factors. The specimen then enters the elastic phase, where the stress–strain curve exhibits an almost linear increase, and the tangent modulus remains relatively stable. At approximately 17.12 s, the yield point occurs, and the specimen transitions into the plastic phase. The stress–strain curve changes from linear to nonlinear, and the tangent modulus shows more pronounced fluctuations, which may be associated with the initiation and growth of microcracks within the material. After about 0.8 s, the specimen reaches its ultimate compressive strength (UCS = 50.2 MPa). Beyond the peak stress point, the stress–strain curve drops sharply, indicating strain softening; internal cracks propagate and coalesce, and by 19.01 s the stress has decreased markedly, indicating complete instability and failure of the specimen. Throughout the loading process, the sandstone exhibits pronounced brittle failure characteristics, accompanied by local surface spalling and through-going shear cracks. It should be noted that the stage classification in this study is primarily based on the stress–strain curve in future work, secant modulus analysis will be employed for comparison to further verify the reliability of the stage classification.

3.4. Analysis of the Strain Field Spatiotemporal Evolution

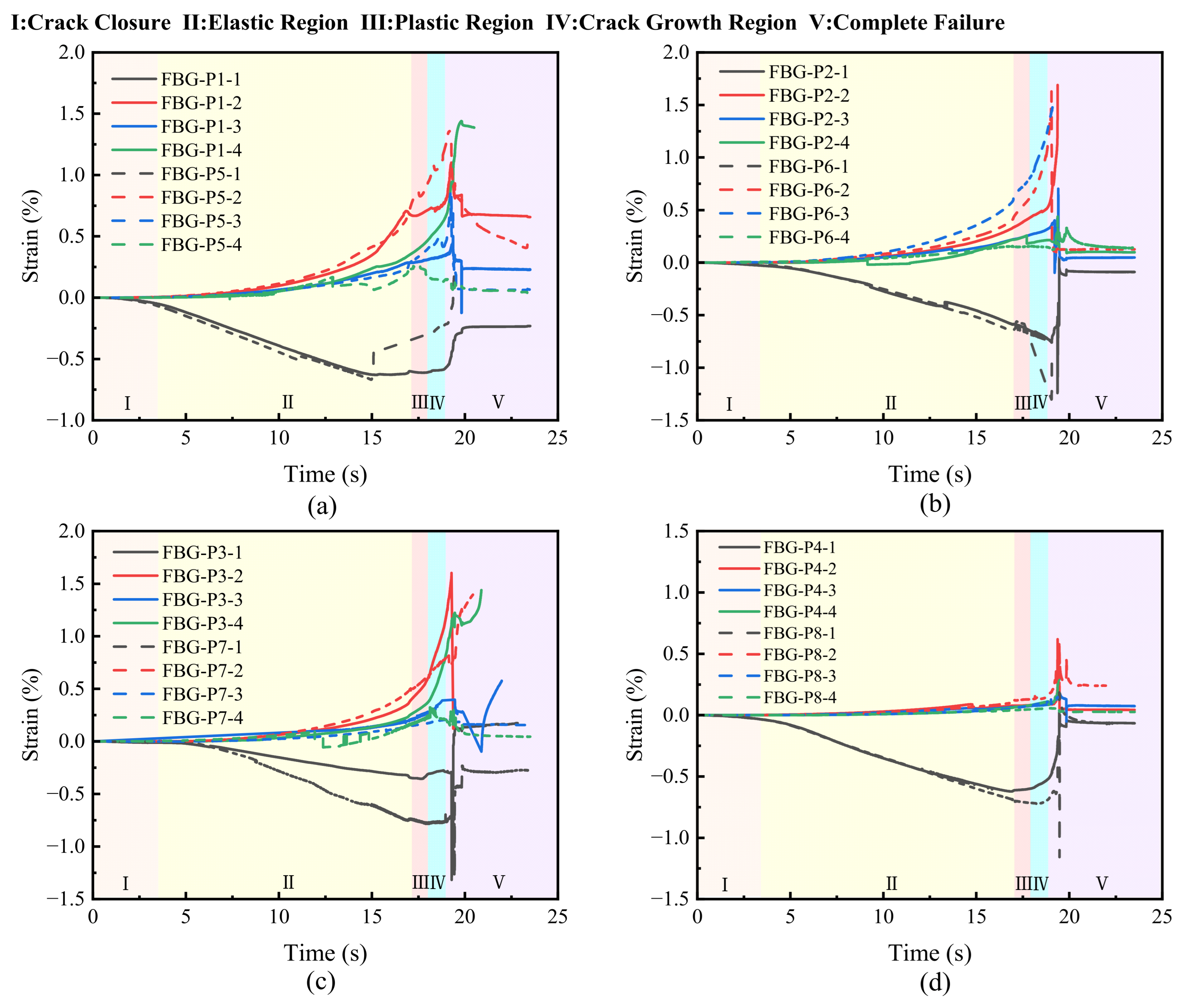
At each monitoring point of the sandstone specimen, the first sensor is arranged along the axial direction, while the second, third, and fourth sensors are arranged along the radial horizontal direction. Figure 8 shows the strain monitoring values from the FBG sensors at all monitoring points in the four directions mentioned above, with the curves representing the variation of strain over time. The five time periods divided by the background correspond to the five stages in the stress–strain curve during the loading process (as shown in Figure 7).

Under uniaxial compression, the test is displacement-controlled, applying axial compression to the sandstone specimen. As the specimen height decreases and the radial direction remains unconstrained, lateral expansion occurs. For an FBG sensor under compression, the axial shortening reduces the grating period, causing the reflected Bragg wavelength to shift toward the shorter-wavelength side. The demodulation system interprets this wavelength decrease as a negative axial strain change; in this study, strain is defined such that compression is negative and tension is positive. This explains why, during the initial loading stage, the axial strain values (after conversion using the strain transfer coefficient) measured by the first sensor at all monitoring points exhibit a decreasing trend. Conversely, when the sensor is under tension, the grating period increases, resulting in a Bragg wavelength shift toward the longer-wavelength side, which the demodulation system interprets as a positive strain change. This is reflected in the radial strain measurements at all monitoring points, where values gradually increase over time during the initial loading phase.

As shown in Figure 8, during the initial compaction stage of loading, the strain values obtained by converting the axial and radial FBG monitoring data at each measurement point using the strain transfer coefficient show only small variations, with the radial direction exhibiting an overall stable trend. After entering the elastic stage, the axial sensors at each point first exhibit a gradual decrease, and around 5 s, the axial strain begins to decrease linearly with different rates, continuing until the end of the elastic stage (around 15 s), when the axial strain shows either a leveling off or slight fluctuations. This indicates that local instability or damage begins at these points, which is consistent with the fracture or local yielding phenomenon observed in the sandstone compression experiment.

Meanwhile, the radial strain at each point shows a relatively smooth, near-linear increase during the early part of the elastic stage. In the mid- to late stages, some points (P2-1, P7-1) show slight fluctuations or discontinuities in radial strain, but the overall upward trend remains consistent. Due to the high loading rate, the elastic stage of the sandstone specimen is followed by a short plastic stage before the peak and a post-peak crack propagation stage, with consistent variation patterns. After the yield point and before the specimen fails completely, the axial strain fluctuations increase significantly at each point, and peak values appear sequentially. The radial strain curve shows a sharp nonlinear increase, indicating that microcracks at the monitoring points are further expanding, spreading, and localizing strain, with the material gradually losing its load-bearing capacity. At 19.01 s, the sandstone specimen experiences a stress drop on the stress–strain curve, marking the overall failure of the specimen, and loading is stopped. From the moment of the stress drop at load cessation to the end of strain monitoring, the FBG data continued to show noticeable fluctuations. During this period, axial and radial strain values decreased rapidly until they either vanished or reached a stable plateau. In standard uniaxial tests on brittle rock, however, the machine–specimen system typically undergoes rapid elastic unloading after macroscopic failure. This suggests that the pronounced fluctuations recorded by the FBG sensors after unloading are more likely the result of multiple overlapping mechanisms rather than a single, ongoing “damage” process. Potential contributors include: micro-debonding at the sensor–rock interface, tensile rupture of the grating section, or relative sliding of the coating during specimen disintegration, all of which can cause instantaneous strain release; residual contact among fragmented blocks and intermittent stick–slip friction that generate localized strain pulses; inertial rebound and mechanical ringing of the loading frame and grips, transmitting high-frequency components to the sensors through residual contact points; and frictional heating, thermoelastic coupling, or fluid–vapor phase transitions within pores, which can induce Bragg-wavelength thermal drift superimposed on the mechanical signal. Acting together in both time and space, these mechanisms can produce the apparent short-term post-peak fluctuations observed in the measurements.

3.5. Analysis of the Temperature Field Spatiotemporal Evolution

Temperature change is a direct measure of energy dissipation in rock. It sensitively captures frictional and plastic heating caused by microcrack initiation, grain rearrangement, and shear slip, thus filling the blind spot that traditional stress–strain signals have regarding the “energy pathway.” In engineering practice, multi-point FBG temperature monitoring offers high spatiotemporal resolution, immunity to electromagnetic interference, and in situ embedment capability. It provides real-time, quantitative information on energy–structure coupling throughout loading, supplies reliable evidence for identifying critical states and enabling early warning, and complements stress, strain, and acoustic-emission measurements.

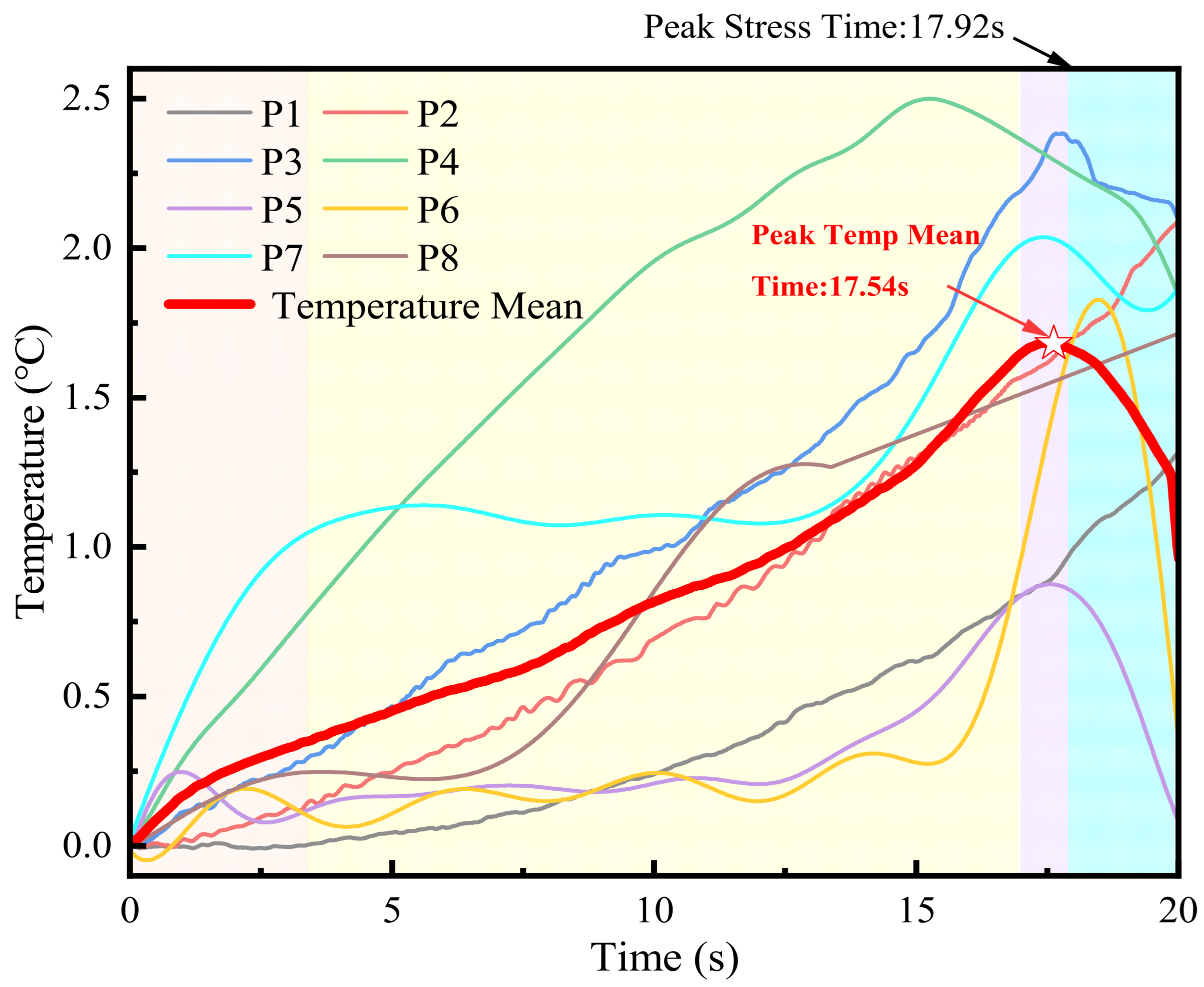
Figure 9 presents the time histories of temperature increments measured by a multi-point FBG array (P1–P8) during a uniaxial compression test, together with their mean curve. The background colors divide the loading process into four mechanical stages: compaction, elastic, plastic, and post-peak. Overall, only slight, short-lived compressive heating appears during compaction. In the elastic stage, the mean temperature increment increases almost linearly with a small slope, from 0.3 °C to 0.8 °C; the traces are smooth with low spatial dispersion, and the mean heating rate is about 0.06–0.08 °C/s. In the late elastic stage, the slope grows to 0.08–0.12 °C/s; minor oscillations and kinks appear at some points, and locations closer to the prospective shear band heat up faster (representative points reach 1.5–2.0 °C before the peak). From the end of the elastic stage into the plastic stage, the mean temperature increment rises rapidly from 1.2 °C to its peak (~1.6–1.7 °C), with instantaneous rates up to 0.4–0.6 °C/s. It then drops quickly to 1.2 °C in the post-peak stage, while local hot spots remain elevated, indicating a spatiotemporal lag in dissipation. Among the points, P4 attains the highest pre-peak temperature; P7 rises rapidly at first and then forms a plateau, followed by a second rise in the post-peak stage, reflecting staged strengthening and migration of heat sources.

4. Discussion

4.1. Early Yielding Revealed by Multi-Point FBG: Staging, Discreteness, and Hysteresis

By analyzing the time-dependent strain variation curves of the axial and radial strain at different monitoring points, it can be observed that the evolution of the FBG strain monitoring values can be divided into four stages: the initial smooth segment, the linear growth segment, the pre-peak nonlinear segment, and the failure fluctuation segment. As shown in Figure 8, the initial smooth segment lasts longer than stage I of the LVDT, typically ending around 5 s into stage II. After this, the strain monitoring values begin to change linearly. When the loading reaches around 15 s in stage II, the linear growth segment ends. The strain monitoring curve then begins to increase significantly in a nonlinear fashion, marking the entry into the pre-peak nonlinear segment. This stage usually lasts from the start of stage II until the inflection point at the peak of stage V, covering four stages of the stress–strain curve. The failure fluctuation segment occurs at the moment when the strain starts to drop suddenly in stage V. During this stage, the strain at the monitoring point undergoes significant oscillations and fluctuations. Eventually, the strain values either stabilize due to the detachment of the sensor or fail completely due to the sensor’s fracture. Compared to the axial sensor, the strain change during the linear growth segment of the radial sensor is smaller and lasts for a shorter time. The linear growth segment usually ends around 10 s into stage II. The variation pattern in other stages is generally consistent with that of the axial sensor.

It is worth noting that the nonlinear responses recorded by different sensors occur within stage II of the stress–strain curve for the sandstone specimen, but the onset times vary among locations, showing a clear spatial discreteness. This temporal offset, or “asynchrony,” means that different regions of the specimen enter the nonlinear, pre-yield stage at different times. Such asynchrony is driven by intrinsic material heterogeneity, including variations in grain structure, cementation, and microdefect distribution, which cause localized stress concentrations and premature microcrack initiation in certain areas. From a failure-mechanism perspective, this indicates that yielding and failure do not develop uniformly across the specimen. Instead, localized zones of early instability emerge first, triggering stress redistribution that activates and progressively links other potential weak zones, ultimately forming dominant fracture surfaces. The spatial multi-point FBG monitoring method effectively captures these spatiotemporal evolution characteristics of the strain field during loading. The discrete responses at each monitoring point thus reveal not only the spatial heterogeneity of the strain distribution but also the asynchronous nature of the deformation-to-yield process, thereby providing a dynamic portrayal of the progressive failure mechanism. In addition, the FBG sensors can monitor strain evolution throughout the entire loading process and record the hysteresis effect of crack propagation after loading stops. This demonstrates that the method offers high temporal and spatial resolution, enabling a detailed depiction of sandstone’s spatiotemporal failure evolution. It should be noted, however, that the present multi-point array contains only eight measurement points, with internal sensors arranged along the central axis and surface sensors distributed around the perimeter. For small-sized standard specimens, this layout essentially covers the effective monitoring region. To further improve spatial resolution and monitoring accuracy, future studies will adopt denser FBG arrays to enhance the capability of capturing detailed spatiotemporal evolution and to ensure that the recorded signals more accurately reflect the true material response rather than local placement effects.

4.2. Thermal Precursors of Failure

In this study, the FBG temperature sensing channel recorded a distinct temperature surge of approximately 1.6–1.7 °C as the specimen transitioned from the end of the elastic stage into the plastic stage, followed by a subsequent decline. This behavior can be attributed to a combination of factors. First, at the onset of yielding, the initiation and propagation of microcracks are accompanied by the rapid release of strain energy, which is partially converted into heat through frictional heating and energy dissipation along microfracture surfaces, leading to a sharp local temperature rise. Second, continued loading in the plastic stage promotes intensified frictional slip within localized shear or fracture zones, further concentrating heat generation. Finally, as failure progresses, the coalescence of fractures facilitates stress relaxation, while crack opening and connectivity enhance heat dissipation through conduction and possible micro-scale convection, causing the recorded temperature to decrease after peaking. Overall, the “temperature surge–decline” process reflects a transition from energy concentration and frictional heating to fracture propagation and thermal dissipation. This strong coupling between thermal response and mechanical behavior indicates that temperature anomalies can serve as a valuable auxiliary precursor for instability warning.

The comparison between temperature increment and stress peaks shows that the mean temperature-increment peak occurs at 17.54 s, whereas the stress peak appears at 17.92 s. The lead time is Δt ≈ 0.38 s, indicating that the thermal peak precedes the strength peak. This implies that, as the system approaches the pre-peak critical regime, dissipation from crack propagation, grain rearrangement, and shear sliding accelerates and reaches a maximum in the temperature field before the macroscopic load-bearing capacity peaks.

The coefficient of variation (CV) is defined from the multi-point FBG temperature series:

$$CV\left(t\right)={\displaystyle \frac{\sqrt{\frac{1}{n-1}{\displaystyle {\sum }_{i=1}^n{\left(T_i-\overline{T}\right)}^2}}}{{\displaystyle \frac{1}{n}}{\displaystyle {\sum }_{i=1}^n{T}_i}}}$$

(3)

Its temporal evolution directly reflects the spatial heterogeneity of heat sources. Experiments show that CV < 0.15 during the elastic stage; it rises markedly after entering the plastic stage and remains high in the post-peak stage (CV > 0.25). This behavior is consistent with rapid heating at individual points (e.g., P4 and P3), indicating a transition from diffuse heating to banded localization and a pronounced jump across the pre- to post-peak transition.

In summary, FBG-based temperature-increment monitoring clearly reveals a four-stage “compaction–elastic–plastic–post-peak” sequence of temperature–damage coupling. The thermal lead relative to the stress peak (Δt ≈ 0.38 s) and the staged jump in CV (from <0.15 to >0.25) jointly delineate the formation and evolution of localization, providing quantitative evidence for identifying imminent instability in sandstone. It should be noted that the identification of thermal precursors in this study is based on the test results of a single specimen, and thus the statistical support for the related conclusions remains limited; their applicability is, therefore, primarily confined to this specific case, and future work will involve multiple tests to further verify and extend these findings.

4.3. Application Prospects and Engineering Challenges

The proposed multi-point FBG sensing network has demonstrated high spatial–temporal resolution and stability under laboratory conditions; however, implementing such a system at the rock-mass scale in the complex underground environments of coal or metal mines will require addressing several engineering challenges, including network deployment strategy, installation adaptability, cost-effectiveness, and long-term durability. Future work will explore a hierarchical and zoned layout in which interrogators are centrally located in easily accessible nodes, with branch optical cables extending to high-risk zones to enable tiered monitoring and priority deployment, thereby reducing both initial and maintenance costs. On the installation side, optimization of cable routing, protective measures, and integration with existing rock-bolt support systems will be carried out to suit the high-humidity, dust-laden, and vibration-prone conditions of mine roadways and stopes. In terms of durability, further enhancements will be made to sensor encapsulation for improved waterproofing, corrosion resistance, and impact protection. We have already developed armored FBG cables for multi-parameter underground monitoring and plan to conduct in situ verification in upcoming field trials. At the operational level, integration with mine communication networks and comprehensive early-warning platforms will be pursued to enable rapid data acquisition, processing, and multi-parameter fusion for hazard prediction. These technological and engineering improvements are expected to facilitate a smooth transition of the FBG sensing network from laboratory research to field-scale deployment, thereby supporting the engineering feasibility of large-scale rock-mass stability monitoring and early warning.

5. Conclusions

To accurately characterize the spatiotemporal evolution of the strain and temperature field during the instability process of coal and rock media, this study proposed a monitoring method using multi-directional FBG sensors to investigate brittle rock failure under uniaxial loading. It enabled real-time monitoring of internal and surface strain and temperature evolution, offering a promising approach for early detection and failure warning in deep coal-rock engineering. The main conclusions are as follows:

(1)

Using multi-directionally arranged FBG sensors, the axial and radial strains at different locations of the sandstone specimen under uniaxial loading were continuously monitored. The strain evolution was clearly divided into four stages: initial smoothing, linear growth, pre-peak nonlinearity, and failure fluctuation, with well-defined phase boundaries.

(2)

Compared with traditional LVDT methods, FBG sensors exhibited longer sensitivity in the early stage and higher resolution, enabling precise identification of local yielding, microcrack initiation, and strain surges, highlighting their advantage in fine-scale deformation detection.

(3)

Temporal analysis of strain responses at different monitoring points confirms that FBG sensors can effectively identify instability timing differences during sandstone failure. Nonlinear responses occurred primarily in stage II of the stress–strain curve and exhibited notable spatial discreteness, reflecting the heterogeneity and asynchrony of the deformation-to-yield process. This demonstrates that a multi-point FBG layout is capable of capturing the dynamic progression of local instabilities, offering reliable support for failure mechanism identification and zonal early warning in heterogeneous rock masses.

(4)

FBG-based multi-point monitoring shows that the mean temperature increment rises slowly, then surges from the end of the elastic stage into the plastic stage to a peak (~1.6–1.7 °C) and subsequently declines. The thermal peak leads the stress peak by ~0.38 s, and the temperature-field CV jumps from <0.15 to >0.25, indicating a transition from diffuse heating to banded localization. Together, the lead time and CV jump provide concise, quantitative criteria for identifying imminent instability in sandstone.

While these results validate the effectiveness of the proposed FBG-based method for capturing fine-scale strain–temperature precursors, certain limitations should be acknowledged. The experiments were performed on standard-sized laboratory specimens, and the monitoring array comprised a limited number of points, which may not fully capture complex field-scale behaviors. Future work will focus on increasing sensor density, incorporating complementary full-field measurement techniques (e.g., digital image correlation), and conducting field-scale trials to further verify the robustness, scalability, and accuracy of the approach in operational early warning systems.