Locations of Non-Cooperative Targets Based on Binocular Vision Intersection and Its Error Analysis

Abstract

The precise locations of unknown non-cooperative targets are a long-standing technical problem that needs to be solved urgently in disaster relief and emergency rescue. An imaging model of photography to a non-cooperative target was established based on the binocular vision forward intersection. The collinear equation representing the spatial position relationship between the target and its two images was obtained through coordinate system transformation, and the system of equations to calculate the geographic coordinates of the target was derived, which realized the geo-location of the unknown non-cooperative target with no control points and no source. The composition and source of the error of this target location method were analyzed, and the equation to calculate the total error of the target location was obtained according to the error synthesis theory. The accuracy of the target location was predicted. When the elevation difference between the camera and the target is 3 km, the location accuracy is 15.5 m. The same ground target was imaged by a certain type of aerial camera at different locations 3097 m above ground, and a target location verification experiment was completed. The longitude and latitude of the target obtained were compared with the true geographic longitude and latitude, and the location error of the verification experiment was calculated to be 16.3 m. The research work of this paper provides a theoretical basis and methods for the precise locations of unknown non-cooperative targets and proposes specific measures to improve the accuracy of target location.

1. Introduction

Precise localization of unknown non-cooperative targets has been widely used in many fields such as reconnaissance, monitoring, emergency rescue, topographic mapping, investigations, etc. [1,2]. The position information of non-cooperative targets can only be obtained by direct measurement through sensors, and it is impossible to obtain it by other cooperative means (such as active feedback of self-position information by the targets, radio navigation auxiliary positioning, equipping the targets with GPS receivers, etc.). In recent years, non-cooperative target location technology is becoming more and more widely used, and the trend is that a location system can simultaneously locate and track multiple targets in real-time; high-precision rapid non-cooperative passive target location without control points; the vision of multi-cameras forward intersect to form a stereo image, and the three-dimensional spatial stereo location of targets can be achieved; the combination of cameras, laser rangefinders, synthetic aperture radars, and other means to achieve high-precision location; rough location of targets first, and high-precision location of key targets in the later stage [3,4,5,6].

Based on the target location by stereo images, multiple non-cooperative passive targets in the stereo images can be precisely located at the same time without control points. The location data can be processed quickly, and real-time location can be achieved. The technology of target location by shooting stereo images with multi-eye vision aerial is developing rapidly, and many models of multi-eye stereo vision aerial cameras have appeared at home and abroad. Among them, the A3 digital aerial photogrammetry system designed and manufactured by the Israeli company VisionMap uses a rigid fixed combination of dual-measurement digital cameras. Through many overlapping sub-images, and utilizing multi-eyes vision, multi-baseline matching technology, it can obtain a large amount of matching data for the same ground target. The triangular network is very dense, and many redundant results can be obtained at the same time. These results are close enough to the true value with a high precision through the least square solution [7,8].

Due to the existence of factors such as platform stability errors, platform pointing errors, Position and Orientation System (POS) measurement errors, calibration errors, and other factors, there will be errors in the obtained image exterior orientation elements. There will also be errors in the calibration of image interior orientation elements and the measurement of image points. These errors in the exterior and interior orientation elements will bring errors to the target location at different levels. To improve the accuracy of target location, it is necessary to analyze the composition of location errors in detail and find out main sources of errors, and this has great significance for improving location accuracy [9,10].

To achieve high-precision target location in long-range oblique photography, a new method of high-precision target location based on multi-perspective observation was introduced by Liu [11]. First, feature matching between the images was used to acquire landmarks. Then, to obtain the geo-locations of these landmarks, a process of map-building is performed. Third, the spatial location of the landmarks and the camera parameters are optimized using bundle adjustment. Last, with the optimization result of camera parameters, the target location is calculated using a location method based on the line-of-sight.

To achieve real-time, high-precision, and long-range target location, a new location method and a set of work patterns were proposed by Zhang [12]. First, using the traditional location method, the rough location of a target is calculated. Then, the target with its rough location is re-imaged. Third, by processing the re-projection error, a weighted filtering algorithm is proposed, and the optimized target location is obtained. Last, the estimation of the target location can converge to the true value after repeating the process mentioned above several times.

In this paper, based on the binocular vision forward intersection to image a non-cooperative target, the target location model was established with no control point, two groups of photographic imaging collinear equations were obtained, and the calculation method of the geographical coordinates of the target was analyzed [13]. The constitution and source of the target location error were analyzed, and the accuracy of the target location was predicted by the error synthesis theory. A verification experiment of the target location method was completed based on the image obtained by a certain aerial camera in a flight experiment and the measurement information of the POS at the time of shooting. The longitude and latitude of geographical target A, located in the overlapping area of two images, were calculated, and the location accuracy of the verification experiment was obtained by comparing with the true longitude and latitude of geographical target A.

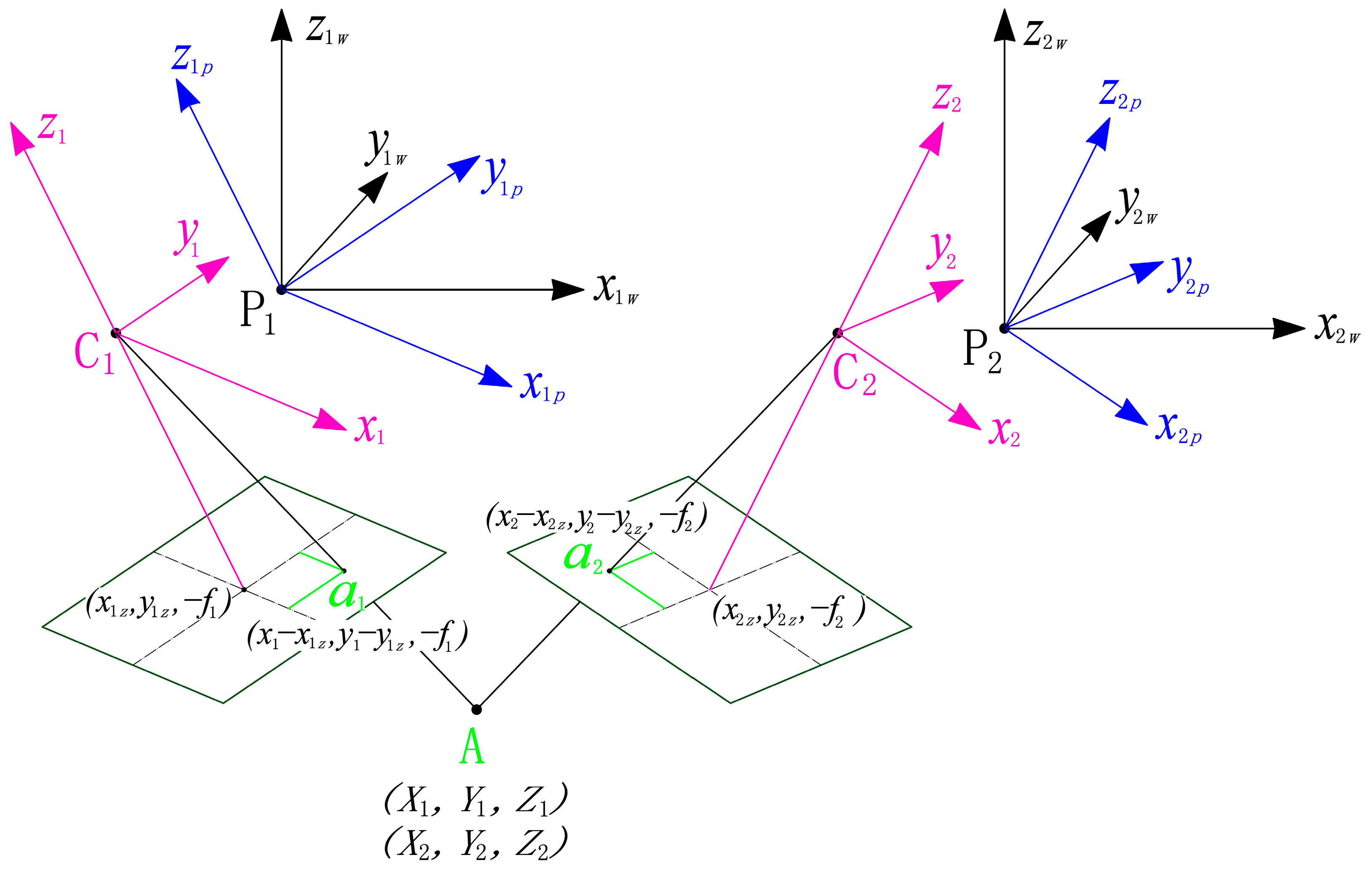
2. Establishment of Target Location Model

2.1. Establishment of Coordinate System and Definition of Internal and External Orientation Elements

2.1.1. Camera Coordinate System

For camera 1, the camera coordinate system C₁-x₁y₁z₁ is a three-dimensional rectangular coordinate system established by taking the photographic center C₁ as the coordinate origin and the main optical axis of the camera as the z₁-axis. The x₁- and y₁-axes are parallel to the transverse and longitudinal directions of the imaging detector of camera 1, respectively. The x₁-, y₁-, and z₁-axes of the camera coordinate system C₁-x₁y₁z₁ conform to the right-hand rule, and the z₁-axis points to camera 1 from the target area and passes through the main point of the imaging detector. Taking center O₁ of the imaging detector as the origin and the transverse and longitudinal directions of the imaging detector as the x- and y-axes, the image 1 two-dimensional coordinate system is established. So, the x- and y-axes of the image 1 coordinate system are parallel and in the same direction as the x₁- and y₁-axes of the camera 1 coordinate system. In image 1, the image $a_1$ of the geographic target A has the coordinates (x₁, y₁) in the image 1 coordinate system. The coordinates of the main point of camera 1 in the image 1 coordinate system are (x_1z, y_1z); then, the image point $a_1$ has the coordinates (x₁−x_1z, y₁−y_1z, −f₁) in the camera 1 coordinate system, where f₁ is the focal length of camera 1 [14].

Similarly, for camera 2, the camera 2 coordinate system C₂-x₂y₂z₂ and the two-dimensional coordinate system of image 2 (x₂, y₂) can be established, and the coordinates of the image point $a_2$ of geographical target A in the camera 2 coordinate system are (x₂−x_2z, y₂−y_2z, −f₂), where f₂ is the focal length of camera 2.

2.1.2. POS Measurement Coordinate System

To achieve the goal of target location, it is necessary to obtain exterior orientation elements at the time of imaging, and a POS is usually installed fixedly with the camera to measure the exterior orientation elements at the time of imaging. The POS measurement system mainly consists of two parts: a Global Positioning System (GPS) receiver and an Inertial Measurement Unit (IMU).

For camera 1, the POS 1 measurement coordinate system is P₁-x_1py_1pz_1p, and the directions of the coordinate axes are defined on the top surface of the IMU 1, as shown in the structure dimension diagram in the IMU manual. The origin of the coordinates is point P₁, which is the measurement center of the POS 1. It can be seen from the actual installation position and direction of the POS that, without considering the IMU installation errors, the x₁-, y₁-, and z₁-axes of the camera 1 coordinate system C₁-x₁y₁z₁ are parallel and in the same direction as the x_1p-, y_1p-, and z_1p axes of the POS 1 measurement coordinate system. The coordinates of the image point $a_1$ in the POS 1 measurement coordinate system (P₁-x_1py_1pz_1p) are (X_1ap, Y_1ap, Z_1ap).

For camera 2, the POS 2 measurement coordinate system P₂-x_2py_2pz_2p can be similarly established, where the coordinate origin is the measurement center point P₂ of POS 2, and the coordinates of the image point $a_2$ in the POS 2 measurement coordinate system P₂-x_2py_2pz_2p are (X_2ap, Y_2ap, Z_2ap).

2.1.3. POS Navigation Coordinate System

The POS 1 navigation coordinate system W₁-x_1wy_1wz_1w is the geographical coordinate system of camera 1, where the x_1w-axis points to the east, the y_1w-axis points to the north, and the z_1w-axis points to the sky. The origin of the POS 1 navigation coordinate system is P₁, the measurement center of POS 1, which is the same as the origin of the POS 1 measurement coordinate system P₁-x_1py_1pz_1p. Geographical target A has the coordinates (X₁, Y₁, Z₁) in the POS 1 navigation coordinate system W₁-x_1wy_1wz_1w, and the image point $a_1$ has the coordinates (X_1aw, Y_1aw, Z_1aw) in the POS 1 navigation coordinate system W₁-x_1wy_1wz_1w.

For camera 2, the POS 2 navigation coordinate system W₂-x_2wy_2wz_2w can be established in the same way. Coordinates of geographical target A are (X₂, Y₂, Z₂) in the POS 2 navigation coordinate system W₂-x_2wy_2wz_2w, and coordinates of image point $a_2$ are (X_2aw, Y_2aw, Z_2aw) in the POS 2 navigation coordinate system W₂-x_2wy_2wz_2w.

From the imaging principle of binocular vision forward intersection, it can be found that there are two sets of photographic imaging coordinate system transformation models. In the target location model established in this paper, the coordinate systems involved are the camera 1 coordinate system (C₁-x₁y₁z₁), camera 2 coordinate system (C₂-x₂y₂z₂), image 1 coordinate system (x₁, y₁), image 2 coordinate system (x₂, y₂), POS 1 measurement coordinate system (P₁-x_1py_1pz_1p), POS 2 measurement coordinate system (P₂-x_2py_2pz_2p), POS 1 navigation coordinate system (W₁-x_1wy_1wz_1w), and POS 2 navigation coordinate system (W₂-x_2wy_2wz_2w).

2.2. Establishment of Coordinate Systems Transformation Relations

2.2.1. Transformation Between POS Measurement Coordinate System and Camera Coordinate System

The IMU in the POS is usually rigidly connected to the camera, so the distance between the origin of the POS measurement coordinate system and the origin of the camera coordinate system is less than 0.1 m, which is much less than the errors of the GPS of the POS, and the geographical location of the origin of the POS measurement coordinate system can be approximately considered the same as that of the origin of the camera coordinate system.

The three coordinate axes of the POS measurement coordinate system are parallel to the three coordinate axes of the camera coordinate system in the absence of installation errors, but due to the existence of actual assembly errors, there is a small assembly error angle between each of the three coordinate axes of the POS measurement coordinate system and the corresponding coordinate axis of the camera coordinate system. By calibrating the IMU assembly errors, the assembly error angles between the POS measurement coordinate system and the camera coordinate system can be measured [15].

For camera 1, the assembly error angles of IMU 1 are (Ψ_1M, θ_1M, γ_1M). After the camera 1 coordinate system C₁-x₁y₁z₁ is rotated by the Ψ_1M, θ_1M, and γ_1M angles in counterclockwise directions around the z₁-, x₁- and y₁-axes in turn, the POS 1 measurement coordinate system P₁-x_1py_1pz_1p can be obtained.

Then, in the POS 1 measurement coordinate system P₁-x_1py_1pz_1p, the coordinates (X_1ap, Y_1ap, Z_1ap) of point $a_1$ can be concluded as the following:

$$\begin{array}{c} \left(\begin{array}{c}{X}_{1ap}\\ Y_{1ap}\\ Z_{1ap}\end{array}\right)=\left[\begin{array}{ccc}\mathit{cos}{\psi }_{1M}& -\mathit{sin}{\psi }_{1M}& 0\\ \mathit{sin}{\psi }_{1M}& \mathit{cos}{\psi }_{1M}& 0\\ 0& 0& 1\end{array}\right]•\left[\begin{array}{ccc}1& 0& 0\\ 0& \mathit{cos}{\theta }_{1M}& -\mathit{sin}{\theta }_{1M}\\ 0& \mathit{sin}{\theta }_{1M}& \mathit{cos}{\theta }_{1M}\end{array}\right]•\left[\begin{array}{ccc}\mathit{cos}{\gamma }_{1M}& 0& \mathit{sin}{\gamma }_{1M}\\ 0& 1& 0\\ -\mathit{sin}{\gamma }_{1M}& 0& \mathit{cos}{\gamma }_{1M}\end{array}\right]•\left(\begin{array}{c}{x}_1-x_{1z}\\ y_1-y_{1z}\\ -f_1\end{array}\right)\\ =\left[\begin{array}{ccc}\cos {\psi }_{1M}\cos {\gamma }_{1M}-\sin {\psi }_{1M}\sin {\theta }_{1M}\sin {\gamma }_{1M}& -\sin {\psi }_{1M}\cos {\theta }_{1M}& \cos {\psi }_{1M}\sin {\gamma }_{1M}+\sin {\psi }_{1M}\sin {\theta }_{1M}\cos {\gamma }_{1M}\\ \sin {\psi }_{1M}\cos {\gamma }_{1M}+\cos {\psi }_{1M}\sin {\theta }_{1M}\sin {\gamma }_{1M}& \cos {\psi }_{1M}\cos {\theta }_{1M}& \sin {\psi }_{1M}\sin {\gamma }_{1M}-\cos {\psi }_{1M}\sin {\theta }_{1M}\cos {\gamma }_{1M}\\ -\cos {\theta }_{1M}\sin {\gamma }_{1M}& \sin {\theta }_{1M}& \cos {\theta }_{1M}\cos {\gamma }_{1M}\end{array}\right]•\left(\begin{array}{c}{x}_1-x_{1z}\\ y_1-y_{1z}\\ -f_1\end{array}\right)\end{array}$$

(1)

Similarly, for camera 2, the coordinates of the image point $a_2$ in the POS 2 measurement coordinate system P₂-x_2py_2pz_2p can be concluded as the following:

$$\left(\begin{array}{c}{X}_{2ap}\\ Y_{2ap}\\ Z_{2ap}\end{array}\right)=\left[\begin{array}{ccc}\cos {\psi }_{2M}\cos {\gamma }_{2M}-\sin {\psi }_{2M}\sin {\theta }_{2M}\sin {\gamma }_{2M}& -\sin {\psi }_{2M}\cos {\theta }_{2M}& \cos {\psi }_{2M}\sin {\gamma }_{2M}+\sin {\psi }_{2M}\sin {\theta }_{2M}\cos {\gamma }_{2M}\\ \sin {\psi }_{2M}\cos {\gamma }_{2M}+\cos {\psi }_{2M}\sin {\theta }_{2M}\sin {\gamma }_{2M}& \cos {\psi }_{2M}\cos {\theta }_{2M}& \sin {\psi }_{2M}\sin {\gamma }_{2M}-\cos {\psi }_{2M}\sin {\theta }_{2M}\cos {\gamma }_{2M}\\ -\cos {\theta }_{2M}\sin {\gamma }_{2M}& \sin {\theta }_{2M}& \cos {\theta }_{2M}\cos {\gamma }_{2M}\end{array}\right]•\left(\begin{array}{c}{x}_2-x_{2z}\\ y_2-y_{2z}\\ -f_2\end{array}\right)$$

(2)

In Equation (2), (Ψ_2M, θ_2M, γ_2M) are the assembly error angles of IMU 2.

2.2.2. Transformation Between POS Navigation Coordinate System and POS Measurement Coordinate System

The definition of the POS posture angles and their effective range are defined as follows:

The heading angle Ψ is the angle between the projection of the y-axis of the POS measurement coordinate system on the horizontal plane (x-y plane) of the POS navigation coordinate system and the y-axis of the POS navigation coordinate system, starting from the y-axis of the POS navigation coordinate system. Ψ is positive when it is counted in the “counterclockwise direction”, and the effective range is [0°, 360°].

The pitch angle θ is the angle between the y-axis of the POS measurement coordinate system and the horizontal plane (x-y plane) of the POS navigation coordinate system. When the y-axis of the POS measurement coordinate system points above the horizontal plane, θ is positive, otherwise it is negative, and the effective range is [−90°, 90°].

The roll angle γ is defined as positive when the IMU is right tilted with the y-axis of the POS measurement coordinate system pointing forward and the x-axis of the POS measurement coordinate system pointing right. γ is negative when the IMU is left tilted, and the effective range is [$-$180°, 180°].

The inner orientation elements of camera 1 can be defined as (x_1z, y_1z, f₁); the angular outer orientation elements of camera 1 are (Ψ₁, θ₁, γ₁), where Ψ₁ is heading angle 1, θ₁ is pitch angle 1, and γ₁ is roll angle 1. The inner orientation elements of camera 2 are (x_2z, y_2z, f₂); the angular outer orientation elements of camera 2 are (Ψ₂, θ₂, γ₂), where Ψ₂ is heading angle 2, θ₂ is pitch angle 2, and γ₂ is roll angle 2 [16].

For camera 1, after the POS 1 navigation coordinate system (W₁-x_1wy_1wz_1w) is successively rotated by Ψ₁, θ₁, and γ₁ with the z_1w-, x_1w-, and y_1w-axes in the counterclockwise direction, the POS 1 measurement coordinate system P₁-x_1py_1pz_1p is obtained. Thus, the transformation relationship between the coordinates of image point $a_1$ in the POS 1 navigation coordinate system as (X_1aw, Y_1aw, Z_1aw) and the coordinates of image point $a_1$ in the POS 1 measurement coordinate system as (X_1ap, Y_1ap, Z_1ap) is as follows [17,18]:

$$\begin{array}{c}\left(\begin{array}{c}{X}_{1aw}\\ Y_{1aw}\\ Z_{1aw}\end{array}\right)=\left[\begin{array}{ccc}\mathit{cos}{\psi }_1& -\mathit{sin}{\psi }_1& 0\\ \mathit{sin}{\psi }_1& \mathit{cos}{\psi }_1& 0\\ 0& 0& 1\end{array}\right]•\left[\begin{array}{ccc}1& 0& 0\\ 0& \mathit{cos}{\theta }_1& -\mathit{sin}{\theta }_1\\ 0& \mathit{sin}{\theta }_1& \mathit{cos}{\theta }_1\end{array}\right]•\left[\begin{array}{ccc}\mathit{cos}{\gamma }_1& 0& \mathit{sin}{\gamma }_1\\ 0& 1& 0\\ -\mathit{sin}{\gamma }_1& 0& \mathit{cos}{\gamma }_1\end{array}\right]•\left(\begin{array}{c}{X}_{1ap}\\ Y_{1ap}\\ Z_{1ap}\end{array}\right)\\ =\left[\begin{array}{ccc}\mathit{cos}{\psi }_1\mathit{cos}{\gamma }_1-\mathit{sin}{\psi }_1\mathit{sin}{\theta }_1\mathit{sin}{\gamma }_1& -\mathit{sin}{\psi }_1\mathit{cos}{\theta }_1& \mathit{cos}{\psi }_1\mathit{sin}{\gamma }_1+\mathit{sin}{\psi }_1\mathit{sin}{\theta }_1\mathit{cos}{\gamma }_1\\ \mathit{sin}{\psi }_1\mathit{cos}{\gamma }_1+\mathit{cos}{\psi }_1\mathit{sin}{\theta }_1\mathit{sin}{\gamma }_1& \mathit{cos}{\psi }_1\mathit{cos}{\theta }_1& \mathit{sin}{\psi }_1\mathit{sin}{\gamma }_1-\mathit{cos}{\psi }_1\mathit{sin}{\theta }_1\mathit{cos}{\gamma }_1\\ -\mathit{cos}{\theta }_1\mathit{sin}{\gamma }_1& \mathit{sin}{\theta }_1& \mathit{cos}{\theta }_1\mathit{cos}{\gamma }_1\end{array}\right]•\left(\begin{array}{c}{X}_{1ap}\\ Y_{1ap}\\ Z_{1ap}\end{array}\right)\\ =\left[\begin{array}{ccc}{a}_{11}^1& a_{12}^1& a_{13}^1\\ a_{21}^1& a_{22}^1& a_{23}^1\\ a_{31}^1& a_{32}^1& a_{33}^1\end{array}\right]•\left(\begin{array}{c}{X}_{1ap}\\ Y_{1ap}\\ Z_{1ap}\end{array}\right)\end{array}$$

(3)

where

$$\left\{\begin{array}{l}{a}_{11}^1=\mathit{cos}{\psi }_1\mathit{cos}{\gamma }_1-\mathit{sin}{\psi }_1\mathit{sin}{\theta }_1\mathit{sin}{\gamma }_1\\ a_{21}^1=\mathit{sin}{\psi }_1\mathit{cos}{\gamma }_1+\mathit{cos}{\psi }_1\mathit{sin}{\theta }_1\mathit{sin}{\gamma }_1\\ a_{31}^1=-\mathit{cos}{\theta }_1\mathit{sin}{\gamma }_1\\ a_{12}^1=-\mathit{sin}{\psi }_1\mathit{cos}{\theta }_1\\ a_{22}^1=\mathit{cos}{\psi }_1\mathit{cos}{\theta }_1\\ a_{32}^1=\mathit{sin}{\theta }_1\\ a_{13}^1=\mathit{cos}{\psi }_1\mathit{sin}{\gamma }_1+\mathit{sin}{\psi }_1\mathit{sin}{\theta }_1\mathit{cos}{\gamma }_1\\ a_{23}^1=\mathit{sin}{\psi }_1\mathit{sin}{\gamma }_1-\mathit{cos}{\psi }_1\mathit{sin}{\theta }_1\mathit{cos}{\gamma }_1\\ a_{33}^1=\mathit{cos}{\theta }_1\mathit{cos}{\gamma }_1\end{array}\right.$$

(4)

Similarly, for camera 2, the coordinates (X_2aw, Y_2aw, Z_2aw) of the image point $a_2$ in the POS 2 navigation coordinate system W₂-x_2wy_2wz_2w can be concluded as follows:

$$\begin{array}{c}\left(\begin{array}{c}{X}_{2aw}\\ Y_{2aw}\\ Z_{2aw}\end{array}\right)=\left[\begin{array}{ccc}\mathit{cos}{\psi }_2\mathit{cos}{\gamma }_2-\mathit{sin}{\psi }_2\mathit{sin}{\theta }_2\mathit{sin}{\gamma }_2& -\mathit{sin}{\psi }_2\mathit{cos}{\theta }_2& \mathit{cos}{\psi }_2\mathit{sin}{\gamma }_2+\mathit{sin}{\psi }_2\mathit{sin}{\theta }_2\mathit{cos}{\gamma }_2\\ \mathit{sin}{\psi }_2\mathit{cos}{\gamma }_2+\mathit{cos}{\psi }_2\mathit{sin}{\theta }_2\mathit{sin}{\gamma }_2& \mathit{cos}{\psi }_2\mathit{cos}{\theta }_2& \mathit{sin}{\psi }_2\mathit{sin}{\gamma }_2-\mathit{cos}{\psi }_2\mathit{sin}{\theta }_2\mathit{cos}{\gamma }_2\\ -\mathit{cos}{\theta }_2\mathit{sin}{\gamma }_2& \mathit{sin}{\theta }_2& \mathit{cos}{\theta }_2\mathit{cos}{\gamma }_2\end{array}\right]•\left(\begin{array}{c}{X}_{2ap}\\ Y_{2ap}\\ Z_{2ap}\end{array}\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\left[\begin{array}{ccc}{a}_{11}^2& a_{12}^2& a_{13}^2\\ a_{21}^2& a_{22}^2& a_{23}^2\\ a_{31}^2& a_{32}^2& a_{33}^2\end{array}\right]•\left(\begin{array}{c}{X}_{1ap}\\ Y_{1ap}\\ Z_{1ap}\end{array}\right)\end{array}$$

(5)

where

$$\left\{\begin{array}{l}{a}_{11}^2=\mathit{cos}{\psi }_2\mathit{cos}{\gamma }_2-\mathit{sin}{\psi }_2\mathit{sin}{\theta }_2\mathit{sin}{\gamma }_2\\ a_{21}^2=\mathit{sin}{\psi }_2\mathit{cos}{\gamma }_2+\mathit{cos}{\psi }_2\mathit{sin}{\theta }_2\mathit{sin}{\gamma }_2\\ a_{31}^2=-\mathit{cos}{\theta }_2\mathit{sin}{\gamma }_2\\ a_{12}^2=-\mathit{sin}{\psi }_2\mathit{cos}{\theta }_2\\ a_{22}^2=\mathit{cos}{\psi }_2\mathit{cos}{\theta }_2\\ a_{32}^2=\mathit{sin}{\theta }_2\\ a_{13}^2=\mathit{cos}{\psi }_2\mathit{sin}{\gamma }_2+\mathit{sin}{\psi }_2\mathit{sin}{\theta }_2\mathit{cos}{\gamma }_2\\ a_{23}^2=\mathit{sin}{\psi }_2\mathit{sin}{\gamma }_2-\mathit{cos}{\psi }_2\mathit{sin}{\theta }_2\mathit{cos}{\gamma }_2\\ a_{33}^2=\mathit{cos}{\theta }_2\mathit{cos}{\gamma }_2\end{array}\right.$$

(6)

3. Principle of Forward Intersection of Binocular Vision

The schematic diagram of the forward intersection of a binocular vision is shown in Figure 1, where a target A appears in two images of camera 1 and camera 2, and the two images will present a pair of stereo images. For camera 1, in the POS 1 navigation coordinate system W₁-x_1wy_1wz_1w, the coordinates (X₁, Y₁, Z₁) of geographical target A can be derived from the similar triangle geometry relationship of photographic imaging in the spatial rectangular coordinate system, and the following equation of proportional relationship is satisfied:

$${\displaystyle \frac{X_1}{X_{1aw}}}={\displaystyle \frac{Y_1}{Y_{1aw}}}={\displaystyle \frac{Z_1}{Z_{1aw}}}$$

(7)

The classical collinear equation for photogrammetry obtained by combining Equations (3) and (7) is as follows [19]:

$$\left\{\begin{array}{l}{\displaystyle \frac{X_1}{Z_1}}={\displaystyle \frac{a_{11}^1{X}_{1ap}+a_{12}^1{Y}_{1ap}+a_{13}^1{Z}_{1ap}}{a_{31}^1{X}_{1ap}+a_{32}^1{Y}_{1ap}+a_{33}^1{Z}_{1ap}}}\\ {\displaystyle \frac{Y_1}{Z_1}}={\displaystyle \frac{a_{21}^1{X}_{1ap}+a_{22}^1{Y}_{1ap}+a_{23}^1{Z}_{1ap}}{a_{31}^1{X}_{1ap}+a_{32}^1{Y}_{1ap}+a_{33}^1{Z}_{1ap}}}\end{array}\right.$$

(8)

From the above collinear equation, it is known that image 1 and image 2 can produce four equations as shown in Equation (9), and the position coordinates of target A containing three unknown values need to be solved.

$$\left\{\begin{array}{c}{\displaystyle \frac{X_1}{Z_1}}={\displaystyle \frac{a_{11}^1{X}_{1ap}+a_{12}^1{Y}_{1ap}+a_{13}^1{Z}_{1ap}}{a_{31}^1{X}_{1ap}+a_{32}^1{Y}_{1ap}+a_{33}^1{Z}_{1ap}}}\\ {\displaystyle \frac{Y_1}{Z_1}}={\displaystyle \frac{a_{21}^1{X}_{1ap}+a_{22}^1{Y}_{1ap}+a_{23}^1{Z}_{1ap}}{a_{31}^1{X}_{1ap}+a_{32}^1{Y}_{1ap}+a_{33}^1{Z}_{1ap}}}\\ {\displaystyle \frac{X_2}{Z_2}}={\displaystyle \frac{a_{11}^2{X}_{2ap}+a_{12}^2{Y}_{2ap}+a_{13}^2{Z}_{2ap}}{a_{31}^2{X}_{2ap}+a_{32}^2{Y}_{2ap}+a_{33}^2{Z}_{2ap}}}\\ {\displaystyle \frac{Y_2}{Z_2}}={\displaystyle \frac{a_{21}^2{X}_{2ap}+a_{22}^2{Y}_{2ap}+a_{23}^2{Z}_{2ap}}{a_{31}^2{X}_{2ap}+a_{32}^2{Y}_{2ap}+a_{33}^2{Z}_{2ap}}}\end{array}\right.$$

(9)

In the POS 1 navigation coordinate system W₁-x_1wy_1wz_1w and POS 2 navigation coordinate system W₂-x_2wy_2wz_2w, the x_1w- and x_2w-axes point east, y_1w- and y_2w-axes point north, and z_1w- and z_2w-axes point to the sky, so the three coordinate axes of the POS 1 navigation coordinate system W₁-x_1wy_1wz_1w are parallel to the three coordinate axes of the POS 2 navigation coordinate system W₂-x_2wy_2wz_2w. P₂ is the coordinate origin of the POS 2 navigation coordinate system W₂-x_2wy_2wz_2w, and the coordinates of P₂ in the POS 1 navigation coordinate system W₁-x_1wy_1wz_1w is (X_P12, Y_P12, Z_P12); thus,

$$\left\{\begin{array}{l}{X}_2=X_1-X_{P12}\\ Y_2=Y_1-Y_{P12}\\ Z_2=Z_1-Z_{P12}\end{array}\right.$$

(10)

The following equations can be concluded by combining Equations (9) and (10):

$$\left\{\begin{array}{c}{\displaystyle \frac{X_1}{Z_1}}={\displaystyle \frac{a_{11}^1{X}_{1ap}+a_{12}^1{Y}_{1ap}+a_{13}^1{Z}_{1ap}}{a_{31}^1{X}_{1ap}+a_{32}^1{Y}_{1ap}+a_{33}^1{Z}_{1ap}}}\\ {\displaystyle \frac{Y_1}{Z_1}}={\displaystyle \frac{a_{21}^1{X}_{1ap}+a_{22}^1{Y}_{1ap}+a_{23}^1{Z}_{1ap}}{a_{31}^1{X}_{1ap}+a_{32}^1{Y}_{1ap}+a_{33}^1{Z}_{1ap}}}\\ {\displaystyle \frac{X_1-X_{P12}}{Z_1-Z_{P12}}}={\displaystyle \frac{a_{11}^2{X}_{2ap}+a_{12}^2{Y}_{2ap}+a_{13}^2{Z}_{2ap}}{a_{31}^2{X}_{2ap}+a_{32}^2{Y}_{2ap}+a_{33}^2{Z}_{2ap}}}\\ {\displaystyle \frac{Y_1-Y_{P12}}{Z_1-Z_{P12}}}={\displaystyle \frac{a_{21}^2{X}_{2ap}+a_{22}^2{Y}_{2ap}+a_{23}^2{Z}_{2ap}}{a_{31}^2{X}_{2ap}+a_{32}^2{Y}_{2ap}+a_{33}^2{Z}_{2ap}}}\end{array}\right.$$

(11)

Equation (11) is a system of ternary quartic equations. First, the first and third equations are combined to obtain the first solution of Z₁, and then the second and fourth equations are combined to obtain the second solution of Z₁. The average of the two solutions of Z₁ is used as the final solution of the geographical location coordinate value Z₁ of target A, and then, the final solution of Z₁ is substituted into the first and second equations to obtain the final solution of X₁ and Y₁. In this way, the accuracy of the location of target A can be improved.

Thereby, the coordinate values (X₁, Y₁, Z₁) of geographic target A in the POS 1 navigation coordinate system W₁-x_1wy_1wz_1w are obtained, and the geographic location of target A is obtained.

4. Analysis and Estimation of Location Error

4.1. Analysis of Location Error

Since the IMU assembly angle errors are systematic errors, the precise values of the IMU assembly angle errors can be obtained after ground calibration. In the process of calculating the target position, the location error caused by the IMU assembly angle errors can be eliminated by modifying the angular outer orientation elements. Therefore, the IMU assembly angle errors will not bring a large target location error. Since the IMU assembly angle errors are extremely small angle values, in the error analysis of target location, the three IMU assembly angle errors (Ψ_1M, θ_1M, γ_1M) can be approximately zero to simplify the calculation process. At this time, Equation (1) can be simplified as follows [20]:

$$\left(\begin{array}{c}{X}_{1ap}\\ Y_{1ap}\\ Z_{1ap}\end{array}\right)=\left(\begin{array}{c}{x}_1-x_{1z}\\ y_1-y_{1z}\\ -f_1\end{array}\right)$$

(12)

The following equation can be concluded by combining Equations (8) and (12):

$$\left\{\begin{array}{l}{X}_1=\left[{\displaystyle \frac{a_{11}^1\left(x_1-x_{1z}\right)+a_{12}^1\left(y_1-y_{1z}\right)-a_{13}^1{f}_1}{a_{31}^1\left(x_1-x_{1z}\right)+a_{32}^1\left(y_1-y_{1z}\right)-a_{33}^1{f}_1}}\right]Z_1\\ Y_1=\left[{\displaystyle \frac{a_{21}^1\left(x_1-x_{1z}\right)+a_{22}^1\left(y_1-y_{1z}\right)-a_{23}^1{f}_1}{a_{31}^1\left(x_1-x_{1z}\right)+a_{32}^1\left(y_1-y_{1z}\right)-a_{33}^1{f}_1}}\right]Z_1\end{array}\right.$$

(13)

Z₁ = H_A − H₁, where H_A is the elevation of geographical target A, and H₁ is the elevation of P_1, the measurement center of POS 1. The errors of the target location are generated in both the x_1w- and y_1w-axis directions. The error of the target location in the x_1w-axis direction is first determined, and it can be concluded from Equation (13) as follows:

$$X_1=\left[{\displaystyle \frac{a_{11}^1\left(x_1-x_{1z}\right)+a_{12}^1\left(y_1-y_{1z}\right)-a_{13}^1{f}_1}{a_{31}^1\left(x_1-x_{1z}\right)+a_{32}^1\left(y_1-y_{1z}\right)-a_{33}^1{f}_1}}\right](H_A-H_1)$$

(14)

Based on Equation (14), the error of the target location in the x_1w-axis direction of the POS 1 navigation coordinate system can be used by finding the partial differential of X₁:

$$M_{X1}=\sqrt{\begin{array}{c}{\left(\delta X_{P1}\right)}^2+{\left({\displaystyle \frac{\partial X_1}{\partial H_1}}\delta H_1\right)}^2+{\left({\displaystyle \frac{\partial X_1}{\partial {\psi }_1}}\delta {\psi }_1\right)}^2+{\left({\displaystyle \frac{\partial X_1}{\partial {\theta }_1}}\delta {\theta }_1\right)}^2+{\left({\displaystyle \frac{\partial X_1}{\partial {\gamma }_1}}\delta {\gamma }_1\right)}^2\\ +{\left({\displaystyle \frac{\partial X_1}{\partial f_1}}\delta f_1\right)}^2+{\left({\displaystyle \frac{\partial X_1}{\partial x_1}}\delta x_1\right)}^2+{\left({\displaystyle \frac{\partial X_1}{\partial y_1}}\delta y_1\right)}^2+{\left({\displaystyle \frac{\partial X_1}{\partial x_{1z}}}\delta x_{1z}\right)}^2+{\left({\displaystyle \frac{\partial X_1}{\partial y_{1z}}}\delta y_{1z}\right)}^2\\ \end{array}}$$

(15)

where $\delta X_{P1}$ is the location error of $P_1$, the measurement center of POS 1 in the x_1w-axis direction, which is determined by the location accuracy of the GPS.

Set up $M_{XP1}=\left|\delta X_{P1}\right|$, $M_{YP1}=\left|\delta Y_{P1}\right|$, $M_{H1}=\left|{\displaystyle \frac{\partial X_1}{\partial H_1}}\delta H_1\right|$, $M_{\psi 1}=\left|{\displaystyle \frac{\partial X_1}{\partial {\psi }_1}}\delta {\psi }_1\right|$, $M_{\theta 1}=\left|{\displaystyle \frac{\partial X_1}{\partial {\theta }_1}}\delta {\theta }_1\right|$, $M_{\gamma 1}=\left|{\displaystyle \frac{\partial X_1}{\partial {\gamma }_1}}\delta {\gamma }_1\right|$, $M_{f1}=\left|{\displaystyle \frac{\partial X_1}{\partial f_1}}\delta f_1\right|$, $M_{x1}=\left|{\displaystyle \frac{\partial X_1}{\partial x_1}}\delta x_1\right|$, $M_{y1}=\left|{\displaystyle \frac{\partial X_1}{\partial y_1}}\delta y_1\right|$, $M_{x1z}=\left|{\displaystyle \frac{\partial X_1}{\partial x_{1z}}}\delta x_{1z}\right|$, $M_{y1z}=\left|{\displaystyle \frac{\partial X_1}{\partial y_{1z}}}\delta y_{1z}\right|$, Equation (15) can be simplified as follows:

$$M_{X1}=\sqrt{{M_{XP1}}^2+{M_{H1}}^2+{M_{\psi 1}}^2+{M_{\theta 1}}^2+{M_{\gamma 1}}^2+{M_{f1}}^2+{M_{x1}}^2+{M_{y1}}^2+{M_{X1z}}^2+{M_{y1z}}^2 }$$

(16)

Similarly, the target location error in the y_1w-axis direction of the POS 1 navigation coordinate system is M_Y1.

The total error of this target location method is calculated as follows:

$$M=\sqrt{M_{X1}^2+M_{Y1}^2}$$

(17)

4.2. Estimation of Location Error

The input parameters for calculating the target location accuracy are obtained by analyzing the error sources given by Equation (15), and combining the actual parameters of the camera, they are as follows [21]:

• $\delta X_{P1}$, $\delta Y_{P1}$, and $\delta H_1:$ the location errors of P₁—the measurement center of POS 1—are caused by the errors of the position measurement system (such as the GPS of POS 1). $\delta X_{P1}$ and $\delta Y_{P1}$ are taken to be 3 m, and $\delta H_1$ is taken to be 5 m.
• $H_A-H_1$: The elevation difference between camera 1 and target A is represented by $H_A-H_1$. When calculating the location error, $H_A-H_1$ is taken to be 2000 m, 3000 m, and 5000 m, respectively.
• $\delta {\psi }_1$, $\delta {\theta }_1$, and $\delta {\gamma }_1$: The IMU drift error is a random error, which cannot be corrected and will bring a large target location error. When calculating the target location error, the main error source of the errors of the attitude angles measurement $\delta {\psi }_1$, $\delta {\theta }_1$, and $\delta {\gamma }_1$ is the IMU drift error. The measurement errors for the heading, pitch, and roll angles can be estimated based on the specification of the IMU of the POS. In the target location method, the real-time measurement accuracy of the IMU and the calibration accuracy of the IMU installation are considered comprehensively; the heading angle measurement error $\delta {\psi }_1$ is taken to be 0.08° and the pitch angle measurement error $\delta {\theta }_1$ and the roll angle measurement error $\delta {\gamma }_1$ are both taken to be 0.04°.
• ${\psi }_1$, ${\theta }_1$, and ${\gamma }_1$: for camera photography imaging, the average values of the angles between its principal ray and the three coordinate axes of the POS 1 navigation coordinate system is 45°, and the three posture angles-heading angle ${\psi }_1$, pitch angle ${\theta }_1$, and roll angle ${\gamma }_1$—are all set to be 45° when calculating the location accuracy.
• $f_1$ and $\delta f_1$: The focal length of the camera 1 is represented by $f_1$, and the value of $f_1$ is 129.4 mm. The calibration error of the focal length is represented by$\delta f_1$, and the value of $\delta f_1$ is 9 µm.
• $x_1{-x}_{1z}$ and $y_1{-y}_{1z}$: In the image 1 coordinate system, the coordinate values of image point $a_1$ are $x_1$ and $y_1$. Based on the size of the photosensitive surface of the imaging detector, the maximum value of $x_1{-x}_{1z}$ is determined to be 8.3 mm, and $y_1{-y}_{1z}$ is determined to be 7 mm.
• $\delta x_1$ and $\delta y_1$: The measurement errors of image point $a_1$ are represented by $\delta x_1$ and $\delta y_1$, and their generation stem from factors such as image distortion and target identification errors. The distortion of the camera optical lens is less than 0.4%, and after the image is processed by the distortion correction software, the distortion of the final image is less than 0.1%. The main error sources of the measurement errors of the image point are the misidentification and errors in image registration. $\delta x_1$ and $\delta y_1$ are determined to all be 26 µm (4 pixels) after comprehensive consideration.
• $\delta x_{1z}$ and $\delta y_{1z}$: The calibration errors of the main point of the internal orientation elements are represented by $\delta x_{1z}$ and $\delta y_{1z}$, which are determined to all be 3 µm.

After substituting the above parameters into Equations (15)–(17), the target location accuracy can be calculated using the MATLAB 2020a calculation software.

Table 1. Summary of location errors (unit: m).

HA − H1	2000		3000		5000
	x1w	y1w	x1w	y1w	x1w	y1w
$M_{XP1}$	3	0	3	0	3	0
$M_{YP1}$	0	3	0	3	0	3
$M_{H1}$	6.13	10.12	6.13	10.12	6.13	10.12
$M_{\psi 1}$	0.73	0.54	1.10	0.81	1.83	1.36
$M_{\theta 1}$	2.85	2.41	4.28	3.61	7.13	6.01
$M_{\gamma 1}$	0.04	4.17	0.06	6.25	0.09	10.42
$M_{f1}$	0	0.04	0.01	0.06	0.01	0.10
$M_{x1}$	0.90	1.71	1.35	2.57	2.25	4.28
$M_{y1}$	0.88	0.22	1.33	0.34	2.21	0.56
$M_{x1z}$	0.10	0.20	0.16	0.30	0.26	0.49
$M_{y1z}$	0.10	0.03	0.15	0.04	0.25	0.06
$M_{X1}$$\mathrm{or} M_{Y1}$	7.54	11.75	8.35	13.08	10.52	16.64
$M$	14.0		15.5		19.7

shows the summarized data of location errors.

It can be seen from Table 1 that the percentages of the location errors ($M_{x1z}$, $M_{y1z}$, $M_{f1}$, $M_{x1}$, $M_{y1}$) caused by the calibration errors of the internal orientation elements of the camera, the calibration errors of the principal distance (focal length), and the measurement errors of the image points are all less than 22%, and they account for a small proportion of the total location error, and they have little effect on the total location error. When shooting at different heights, the main component of the total error is the location error $M_{H1}$ which is caused by $\delta H_1$ (the height location error of point P₁ which is the measurement center of the POS).

When the elevation difference between camera 1 and target A is 2000 m; the pitch angle measurement error $\delta {\theta }_1$ and the roll angle measurement error $\delta {\gamma }_1$ of the camera posture have little effect on the location accuracy. When the elevation difference between the camera and target A is 5000 m, the pitch angle measurement error $\delta {\theta }_1$ and the roll angle measurement error $\delta {\gamma }_1$ of the camera posture have a greater effect on the location accuracy. The location errors caused by the measurement error of the camera heading angle $\delta {\psi }_1$ are all less than 2 m, and its impact on the location accuracy is small.

According to the data in Table 1, when the elevation difference between the camera and target A is 3000 m, the accuracy of the target location method is 15.5 m.

When the elevation difference between the camera and the target is small (less than 3000 m), the main method to improve the target location accuracy is to improve the elevation accuracy of the camera itself. When the elevation difference between the camera and the target is large (greater than 5000 m), the main method to improve the target location accuracy is to improve the pitch and roll angle measurement accuracy of the POS.

5. Verification Experiment of Target Location Based on Binocular Vision

A certain aerial camera has obtained a large number of ground images in a flight experiment, some of which have 20% overlapping areas. Two images with overlapping areas were selected, and the longitude and latitude of geographical target A in the image overlapping area can be solved using the target location method, based on the POS measurement information at the time of image shooting. The calculation results of the longitude and latitude of target A are compared with the true longitude and latitude of target A; the location accuracy can be obtained, and thus, the feasibility of the target location method studied in this paper is verified.

5.1. Coordinate Extraction of the Image Point

Ground image 1 captured by the camera during the flight experiment is shown in Figure 2. Ground image 2 captured by the camera during the flight experiment is shown in Figure 3.

The images were taken by a black and white camera on an aircraft flying at an altitude of about 3000 m. The detailed parameters of the camera are the same as the input parameters for calculating the target location accuracy in Section 4.2. The target area in the images of Figure 2 and Figure 3 is the People’s Square in Shahe City of Xingtai City, Hebei Province, China. The distinctive diamond-shaped building of the People’s Square and the sculpture in front of the building are clearly visible in the images. The left side of Figure 2 and the right side of Figure 3 have an overlapping area of about 20%.

5.1.1. Coordinate Extraction of the Image Point in Image 1

In Figure 2, at the moment of shooting the target image, the heading, pitch, and roll angles output by the POS were (272.2932781°, −0.0020300°, 15.5612191°), and the longitude, latitude, and altitude of the measurement center point $P_1$ were (114.5147927°, 36.8630194°, 3097 m). The focal length $f_1$ of the camera at the shooting moment was 129.4 mm.

As shown in Figure 2, geographic target A is set as the center position of a square sculpture on the left side of image 1. In image 1, the image point position of geographic target A is shown as point $a_1$ in Figure 2. According to the actual geographic direction of the target area, the north direction of the actual geography is the left direction of image 1, and the heading angle output by the POS at the shooting moment is 272.2932781°; thus, the x-axis direction of image 1 is the right direction, and the y-axis direction is the up direction.

The parameters of the image detector are shown in

Table 2. Parameters of the image detector.

Parameters	Values
Detector pixel	2560 (H 1) × 2160 (V 2)
Pixel size	6.5 μm × 6.5 μm
Size of the photosensitive surface	16.64 mm × 14.04 mm

¹ H represents the horizontal. ² V represents the vertical.

. According to the pixel position of point $a_1$ in image 1, the coordinate values of point $a_1$ in the image 1 coordinate system can be calculated as ($-7.4816\times {10}^{-3} \mathrm{m}$, $0.2137\times {10}^{-3} \mathrm{m}$); thus [22],

$$\left\{\begin{array}{l}{x}_1=-7.4816\times {10}^{-3} \mathrm{m}\\ y_1=0.2137\times {10}^{-3} \mathrm{m}\end{array}\right.$$

(18)

5.1.2. Coordinate Extraction of the Image Point in Image 2

In Figure 3, at the moment of shooting the target image, the heading, pitch, and roll angles output by the POS were (272.2898266°, −0.0123494°, 21.8834031°), and the longitude, latitude, and altitude of the measurement center point $P_2$ were (114.5147249°, 36.8630363°, 3097 m). The focal length $f_2$ of the camera at the shooting moment was 129.4 mm.

As shown in Figure 3, geographic target A is set as the center position of the square sculpture on the right side of image 2. In image 2, the image point position of geographic target A is shown as point $a_2$ in Figure 3. According to the actual geographic direction of the target area, the north direction of the actual geography is the left direction of image 2, and the heading angle output by the POS at the shooting moment is 272.2898266°; thus, the x-axis direction of image 2 is the right direction, and the y-axis direction is the up direction.

According to the pixel position of point $a_2$ in image 2, the coordinate values of point $a_2$ in the image 2 coordinate system can be calculated as ($6.9178\times {10}^{-3} \mathrm{m}$, $0.4293\times {10}^{-3} \mathrm{m}$); thus,

$$\left\{\begin{array}{c}{x}_2=6.9178\times {10}^{-3} \mathrm{m}\\ y_2=0.4293\times {10}^{-3} \mathrm{m}\end{array}\right.$$

(19)

5.2. Calculation of Target Coordinate

It can be seen from the calibration results of the internal orientation elements of this camera that the coordinates of its principal point in the image coordinate system are ($-2.8\times {10}^{-5} \mathrm{m}$, $2.34\times {10}^{-5} \mathrm{m}$). Since image 1 and image 2 were shot by the same camera, and the focal length of the camera at both shooting moments was 129.4 mm, and the coordinates of the principal point of camera 1 in the image 1 coordinate system ($x_{1z}$, $y_{1z}$) are the same as the coordinates of the principal point of camera 2 in the image 2 coordinate system ($x_{2z}$, $y_{2z}$), the relevant parameters are shown as follows:

$$\left\{\begin{array}{l}{x}_{1z}=x_{2z}=-2.8\times {10}^{-5} \mathrm{m}\\ y_{1z}=y_{2z}=2.34\times {10}^{-5} \mathrm{m}\\ f_1=f_2=0.1294 \mathrm{m}\end{array}\right.$$

(20)

According to the calibration results of the installation errors between the IMU and the camera, the error angles of the IMU installation are (−0.0494°, 0.0549°, 0.0346°) and they can be obtained as follows:

$$\left\{\begin{array}{l}{\Psi }_{1M}={\Psi }_{2M}=-0.0494°\\ {\theta }_{1M}={\theta }_{2M}=0.0549°\\ {\gamma }_{1M}={\gamma }_{2M}=0.0346°\end{array}\right.$$

(21)

Substituting the data in Equations (18), (20), and (21) into Equation (1), the following can be obtained:

$$\left\{\begin{array}{l}{X}_{1ap}=\left(-7.4816\times {10}^{-3}+2.80\times {10}^{-5}\right)+0.0009\left(0.2137\times {10}^{-3}-2.34\times {10}^{-5}\right)-0.0776\times {10}^{-3}\\ Y_{1ap}=-0.0009\left(-7.4816\times {10}^{-3}+2.80\times {10}^{-5}\right)+\left(0.2137\times {10}^{-3}-2.34\times {10}^{-5}\right)+0.1165\times {10}^{-3}\\ Z_{1ap}=-0.0006\left(-7.4816\times {10}^{-3}+2.80\times {10}^{-5}\right)+0.0009\left(0.2137\times {10}^{-3}-2.34\times {10}^{-5}\right)-0.1294\end{array}\right.$$

(22)

The solution of Equation (22) can be obtained as follows:

$$\left\{\begin{array}{l}{X}_{1ap}=-0.007531 \mathrm{m}\\ Y_{1ap}=0.000321 \mathrm{m}\\ Z_{1ap}=-0.129395 \mathrm{m}\end{array}\right.$$

(23)

Substituting the data in Equations (19)–(21) into Equation (2), the following can be obtained:

$$\left\{\begin{array}{l}{X}_{2ap}=\left(6.9178\times {10}^{-3}+2.80\times {10}^{-5}\right)+0.0009\left(0.4293\times {10}^{-3}-2.34\times {10}^{-5}\right)-0.0776\times {10}^{-3}\\ Y_{2ap}=-0.0009\left(6.9178\times {10}^{-3}+2.80\times {10}^{-5}\right)+\left(0.4293\times {10}^{-3}-2.34\times {10}^{-5}\right)+0.1165\times {10}^{-3}\\ Z_{2ap}=-0.0006\left(6.9178\times {10}^{-3}+2.80\times {10}^{-5}\right)+0.0009\left(0.4293\times {10}^{-3}-2.34\times {10}^{-5}\right)-0.1294\end{array}\right.$$

(24)

The solution of Equation (24) can be obtained as follows:

$$\left\{\begin{array}{l}{X}_{2ap}=0.006868 \mathrm{m}\\ Y_{2ap}=0.000524 \mathrm{m}\\ Z_{2ap}=-0.129404 \mathrm{m}\end{array}\right.$$

(25)

The posture angles of image 1 can be obtained from the information output by the POS at the shooting moment of image 1 as follows:

$$\left\{\begin{array}{l}{\Psi }_1=272.2932781°\\ {\theta }_1=-0.0020300°\\ {\gamma }_1=15.5612191°\end{array}\right.$$

(26)

The posture angles of image 2 can be obtained from the information output by the POS at the shooting moment of image 2 as follows:

$$\left\{\begin{array}{l}{\Psi }_2=272.2898266°\\ {\theta }_2=-0.0123494°\\ {\gamma }_2=21.8834031°\end{array}\right.$$

(27)

Substituting the values of the parameters in Equation (26) into Equation (4), the following can be obtained:

$$\left\{\begin{array}{l}{a}_{11}^1= 0.0362\\ a_{21}^1=-0.9627\\ a_{31}^1=-0.2681\\ a_{12}^1= 0.9993\\ a_{22}^1= 0.0376\\ a_{32}^1=-3.5412\times {10}^{-5}\\ a_{13}^1=0.0101\\ a_{23}^1=-0.2679\\ a_{33}^1=0.9634\end{array}\right.$$

(28)

Substituting the values of the parameters in Equation (27) into Equation (6the following can be obtained:

$$\left\{\begin{array}{l}{a}_{11}^2= 0.0348\\ a_{21}^2= -0.9274\\ a_{31}^2=-0.3725\\ a_{12}^2= 0.9993\\ a_{22}^2= 0.0375\\ a_{32}^2= -2.1543\times {10}^{-4}\\ a_{13}^2=0.0142\\ a_{23}^2=-0.3723\\ a_{33}^2=0.9280\end{array}\right.$$

(29)

Substituting the data in Equations (23), (25), (28), and (29) into Equation (11), the following can be obtained:

$$\left\{\begin{array}{c}{\displaystyle \frac{X_1}{Z_1}}=0.0103\\ {\displaystyle \frac{Y_1}{Z_1}}=-0.3419\\ {\displaystyle \frac{X_1-X_{P12}}{Z_1-Z_{P12}}}=0.0088\\ {\displaystyle \frac{Y_1-Y_{P12}}{Z_1-Z_{P12}}}=-0.3410\end{array}\right.$$

(30)

Since the longitude $J_1$ (the eastern hemisphere of Earth is positive), latitude $W_1$ (the northern hemisphere of Earth is positive), and elevation $H_1$ of point $P_1$ are (114.5147927°, 36.8630194°, 3097 m), and the longitude $J_2$, latitude $W_2$, and elevation $H_2$ of point $P_2$ are (114.5147249°, 36.8630363°, 3097 m), the increases in longitude and latitude ($∆J_{P12}$, $∆W_{P12}$) from point $P_1$ to point $P_2$ are (−0.0000145°, 0.0001465°), and the increase in elevation is 0 m.

The Earth is approximately a rotational ellipsoid with a small flattening, and the maximum height difference between the geoid and the surface of the Earth ellipsoid is about 110 m. The surface of the Earth ellipsoid can be used instead of the geoid. The rotational ellipsoid is a collection formed by rotating the meridian ellipse around its minor axis. The length of the major semi-axis is $a=\mathrm{6,378,137} \mathrm{m}$, and the length of the minor semi-axis is $b=\mathrm{6,356,752} \mathrm{m}$ [23]. The points on the surface of the Earth approximately satisfy the ellipsoid surface equation as shown in Equation (31), and ($X_E$, $Y_E$, $Z_E$) is the coordinate values of the point on the surface of the Earth in the Earth-Centered Earth-Fixed (ECEF) coordinate system [24].

$${\displaystyle \frac{{X_E}^2+{Y_E}^2}{a^2}}+{\displaystyle \frac{{Z_E}^2}{b^2}}=1$$

(31)

Since the $x_{1w}$, $y_{1w}$, and $z_{1w}$ axes of the POS 1 navigation coordinate system are defined as the east, north, and sky directions of point $P_1$, based on the longitude and latitude of the origin $P_1$ of the POS 1 navigation coordinate system and the conversion relationship between the ECEF coordinate system and the POS 1 navigation coordinate system, the position difference on the surface of the Earth (in the POS 1 navigation coordinate system) corresponding to the longitude and latitude difference from point $P_1$ to point $P_2$ can be obtained as follows [25]:

$$\left\{\begin{array}{l}\begin{array}{c}{X}_{P12}={\displaystyle \frac{\pi a\sqrt{\frac{b^2}{a^2{\mathit{tan}}^2{w}_1+b^2}}}{{180}^{°}}}\Delta J_{P12}\\ Y_{P12}={\displaystyle \frac{\pi \sqrt{b^2+\left(a^2-b^2\right)\frac{b^2}{a^2{\mathit{tan}}^2{w}_1+b^2}}}{{180}^{°}}}\Delta W_{P12}\end{array}\\ Z_{P12}=H_2-H_1\end{array}\right.$$

(32)

After substituting the values of $∆J_{P12}$, $∆W_{P12}$, $W_1$, $a$, $b$, $H_1$, $H_2$ into Equation (32), the following can be obtained after calculation:

$$\left\{\begin{array}{l}{X}_{P12}=-6.03 \mathrm{m}\\ Y_{P12}=1.88 \mathrm{m}\\ Z_{P12}=0 \mathrm{m}\end{array}\right.$$

(33)

The following equation can be calculated by combining Equations (30) and (33):

$$\left\{\begin{array}{c}{\displaystyle \frac{X_1}{Z_1}}=0.0103\\ {\displaystyle \frac{Y_1}{Z_1}}=-0.3419\\ {\displaystyle \frac{X_1+6.03}{Z_1}}=0.0088\\ {\displaystyle \frac{Y_1-1.88}{Z_1}}=-0.3410\end{array}\right.$$

(34)

Equation (34) is a system of ternary quartic equations. First, the first and third equations are combined to obtain the first solution: $X_{11}$ is −41.41 m and $Z_{11}$ is −4020 m. Then, the second and fourth equations are combined to obtain the second solution: $Y_{12}$ is 714.2 m and $Z_{12}$ is −2089 m. The average of the two solutions of $Z_1$ is used as the final solution of $Z_1$—the geographical location coordinate of target point A—so $Z_1$ is −3055 m.

The final solution of $Z_1$ is substituted into the first and second equations of Equation (34) to obtain the final solutions of $X_1$ and $Y_1$.

$$\left\{\begin{array}{l}{X}_1=-31.5 \mathrm{m}\mathrm{m}\\ Y_1=1044.5 \mathrm{m}\mathrm{m}\\ Z_1=-3055 \mathrm{m}\end{array}\right.$$

(35)

5.3. Calculation of the Latitude and Longitude of Target

Similar to Equation (32), the longitude, latitude, and altitude of geographic target A can be calculated as follows [26]:

$$\left\{\begin{array}{l}{J}_A=J_1+{\displaystyle \frac{X_1}{\pi a\sqrt{\frac{b^2}{a^2{\mathit{tan}}^2{w}_1+b^2}}}}•180^{°}\\ W_A=W_1+{\displaystyle \frac{Y_1}{\pi \sqrt{b^2+\left(a^2-b^2\right)\frac{b^2}{a^2{\mathit{tan}}^2{w}_1+b^2}}}}•180^{°}\\ H_A=Z_1+H_1\end{array}\right.$$

(36)

After substituting the values of $X_1$, $Y_1$, $Z_1$, $J_1$, $W_1$, $a$, $b$, and $H_1$ into Equation (36) for calculation, the longitude, latitude and altitude of geographical target A can be obtained as follows:

$$\left\{\begin{array}{l}{J}_A=114.5143698°\\ W_A=36.8724197°\\ H_A=42 \mathrm{m}\end{array}\right.$$

(37)

Thus, the geographic location of target A is achieved by the method of target location in this paper. The longitude, latitude, and elevation of A, the center position of the square sculpture in the image, are (114.5143698°, 36.8724197°, 42 m).

5.4. Calculation of the Target Location Error in Experiment

The errors of the target coordinates obtained from the GPS map are less than 3 m, far less than the target location error obtained in this study, so it can be considered that the coordinates obtained from the GPS map are approximately the true coordinates of the target. The link of the website of the GPS map is https://www.whatsmygps.com, accessed on 8 July 2025. As shown in Figure 4, the true longitude and latitude ($J_{Ar}$, $W_{Ar}$) of the ground target A are (114°30′51.78″, 36°52′20.18″) or (114.5143843°, 36.8722732°), which are obtained by searching in the GPS map. Compared with the true longitude and latitude of target A, there are errors in the longitude and latitude obtained by the location method based on binocular vision intersection, which are as follows:

$$\left\{\begin{array}{l}{\delta J}_A={-0.0000145}^{°}\\ {\delta W}_A={0.0001465}^{°}\end{array}\right.$$

(38)

Similar to Equation (32), the horizontal location errors on the ground surface (in the POS 1 navigation coordinate system) corresponding to the longitude error and latitude error of target A are calculated as follows:

$$\left\{\begin{array}{l}\begin{array}{c}{\delta X}_A={\displaystyle \frac{\pi a\sqrt{\frac{b^2}{a^2{\mathit{tan}}^2{W}_{Ar}+b^2}}}{{180}^{°}}}\\ \end{array}{\delta J}_A\\ {\delta Y}_A={\displaystyle \frac{\pi \sqrt{b^2+\left(a^2-b^2\right)\frac{b^2}{a^2{\mathit{tan}}^2{W}_{Ar}+b^2}}}{{180}^{°}}}{\delta W}_A\end{array}\right.$$

(39)

The following result can be calculated by combining Equations (38) and (39):

$$\left\{\begin{array}{l}{\delta X}_A=-1.1 \mathrm{m}\\ {\delta Y}_A=16.3 \mathrm{m}\end{array}\right.$$

(40)

The location error of geographic target A by using the location method based on binocular vision intersection is as follows:

$${\delta L}_A=\sqrt{{{\delta X}_A}^2+{{\delta Y}_A}^2}\approx 16.3 \mathrm{m}$$

(41)

5.5. Analysis of the Target Location Experiment Result

In this target location verification experiment, the location error is 16.3 m, and the target location accuracy is high, which verifies the feasibility and correctness of the target location method studied in this paper and can meet the actual application requirements.

However, in this location verification experiment, because the two positions of the camera at the two shooting moments are too close, the flight baseline of the forward intersection imaging is too short, which leads to a large error of $Z_1$, the height of the target location. The flight baseline is too short so the location error of the verification experiment is larger than prediction, and it is the deficiency of this target location verification experiment.

6. Conclusions

Based on binocular vision forward intersection to image non-cooperative targets, this paper established the model of photographic imaging and the model of target location. The collinear equations which represent the spatial position relationship between the target and its two image points were obtained through coordinate system transformation, and the system of equations for calculating the geographical coordinates of the target was derived, which realized the geo-location of unknown non-cooperative targets with no control point and no source.

The error composition and source of the target location method were analyzed, and the calculation equation of the total error of target location was obtained based on the error synthesis theory. The target location accuracy under the three elevation difference conditions between the camera and the target was predicted by substituting specific parameters such as the errors of the internal and external orientation elements and the calibration errors of the camera into the calculation equation of the total error. When the elevation difference of the camera and the target is 3 km, the location accuracy is 15.5 m. Through the composition, source, and weight analysis of the location error, specific measures to improve the target location accuracy were proposed.

Based on the images acquired by a certain aerial camera and the POS measurement information at the shooting moments during a flight experiment, a location verification experiment was completed, and the feasibility and correctness of the location method studied in this paper were verified. In the flight experiment, the aerial camera was 3097 m above ground, the longitude and latitude of geographical target A located in the overlapping area of the two images were calculated, and the location error of the verification experiment was obtained as 16.3 m.

In the verification experiment, due to the overly short baseline between the two positions of the camera, a large elevation error was produced in the target location experiment. The target location accuracy will be significantly different under the conditions of different baseline lengths and different camera tilt angles. In the following research work, the flight routes and camera tilt angles will be further planned, and the target location accuracy under different baseline lengths and camera tilt angles will be verified. Finally, the baseline length and camera tilt angle corresponding to the highest target location accuracy will be found.

The target location method studied in this paper has high location accuracy and can better meet the actual demand for unknown target location in emergency rescue. The research work of this paper gives a method for the accurate location of unknown non-cooperative targets without control points, involving the establishment of the calculation model, the calculation results, the errors analysis and the rules of errors, the verification experiment, and the conclusion. Through the error analysis of the target location method, the rules of the error composition were found, the weight ratio of each error source was obtained, and some methods to improve the target location accuracy were given. In the verification experiment of target location, the actual method and process of location accuracy calculation in the experiment was given. The research work of this paper has certain reference significance for many actual application needs related to target location.