Adaptive Optimization of Traffic Sensor Locations Under Uncertainty Using Flow-Constrained Inference
Abstract
1. Introduction
2. State of the Art
2.1. TSLP for the Observability Problem
2.2. Sensor Location Problem with Uncertainties
2.3. Main Contribution
3. Problem Formulation
4. Problem Complexity
- The maximum error or dependency in inference (min–max);
- The cumulative error across the entire network (min–sum).
- Matrix inversion operations ;
- Absolute values of error coefficients (e.g., );
- Nested aggregations, such as max or ∑ over the inferred error terms.
5. Methodology
5.1. Binary Bat Algorithm (BBA)
5.2. LU Decomposition for Matrix Inversion
| Algorithm 1 LU Decomposition for Matrix Inversion |
|
5.3. Binary Bat Algorithm for Network Optimization
- Echolocation: For detecting distance, all bats utilize echolocation, and they can distinguish between food and obstacles according to the echoes they receive. This remarkable ability allows them to navigate in complete darkness.
- Flying Velocity: To search for prey, each bat flies with a velocity in position , with a fixed frequency and a loudness . Depending on the proximity of the target, they can adjust their frequency and pulse rate.
- Loudness Adjustment The loudness of pulses emitted for each bat changes dynamically. The loudness decreases as the bat approaches the target, while the pulse emission rate increases in response to the closer proximity to the prey.
- Chromosome Generation: For each bat in the population, unobserved links are selected from the set of possible new links corresponding to each node.
- Binary Representation: These unobserved links are represented as binary values (0 or 1), where
- -
- A value of 1 indicates that the link is selected as unobserved (active);
- -
- A value of 0 indicates that the link is not selected (inactive).
- Network-Specific Selection: The initial population is constructed such that the chromosomes reflect potential solutions in terms of the unobserved links across the network. This ensures that each bat represents a feasible sensor placement configuration based on the available new link sets.
| Algorithm 2 Binary Bat Algorithm for Network Optimization |
|
6. Case Studies
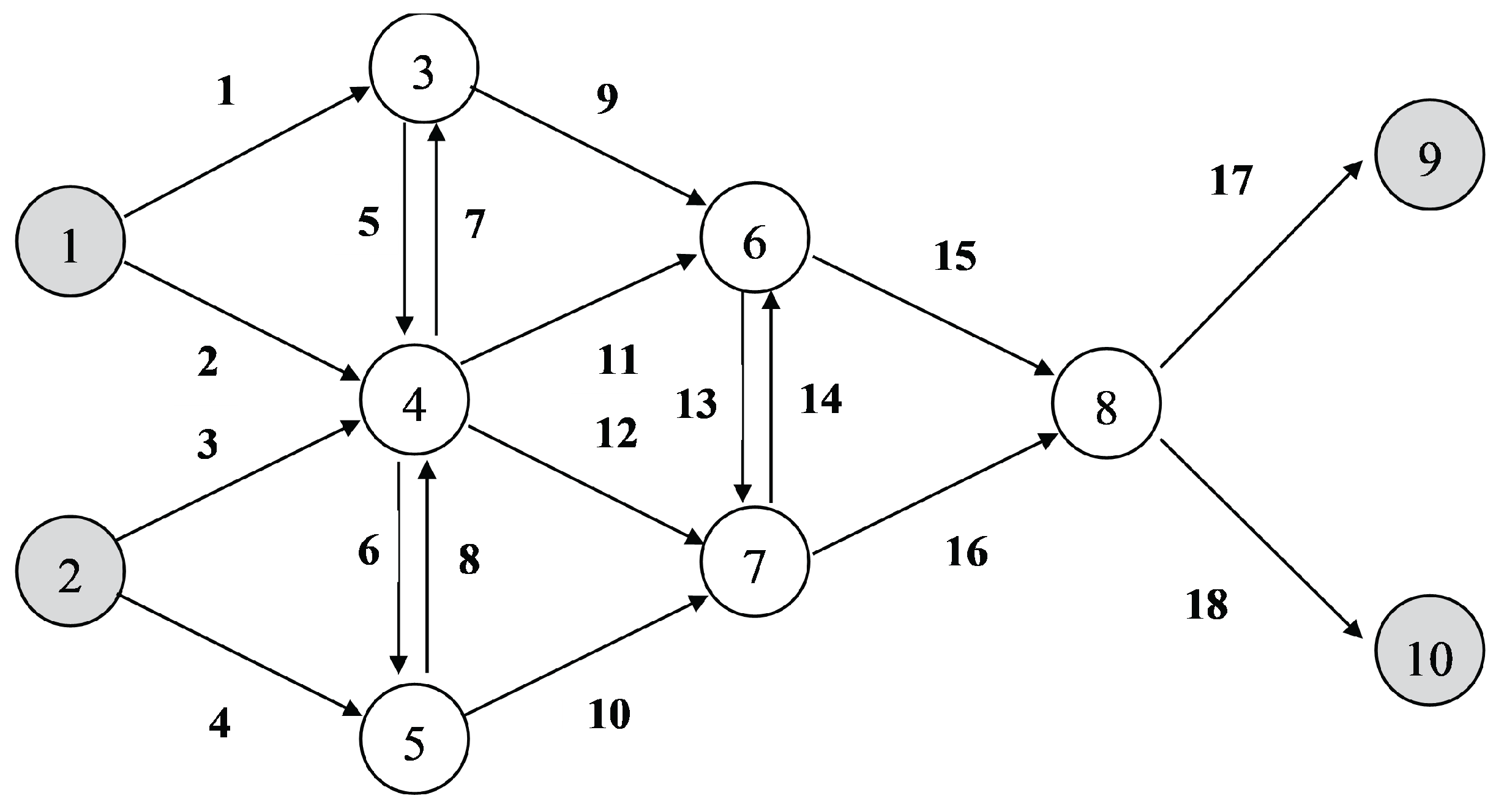
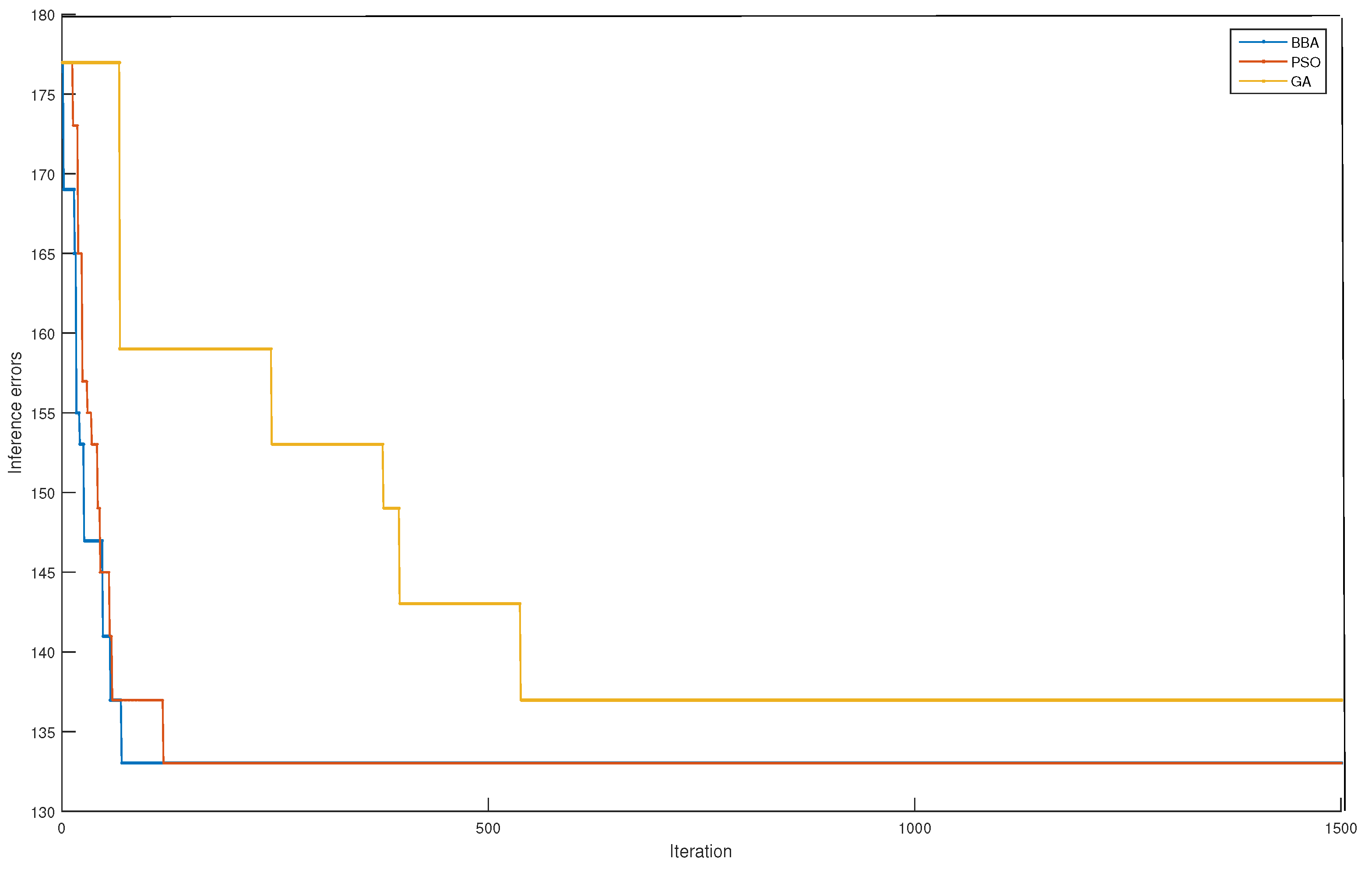
6.1. Fishbone Network
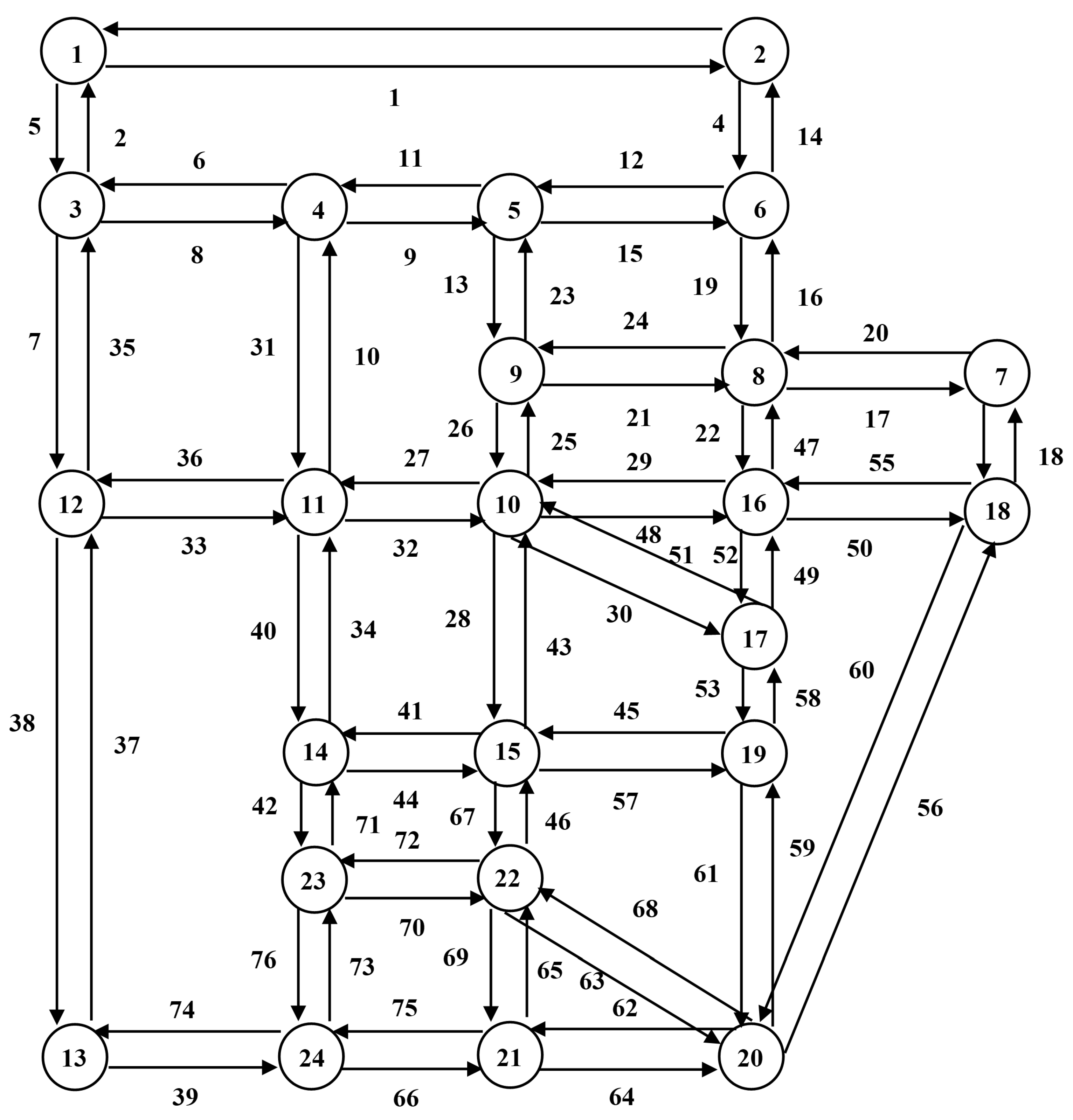
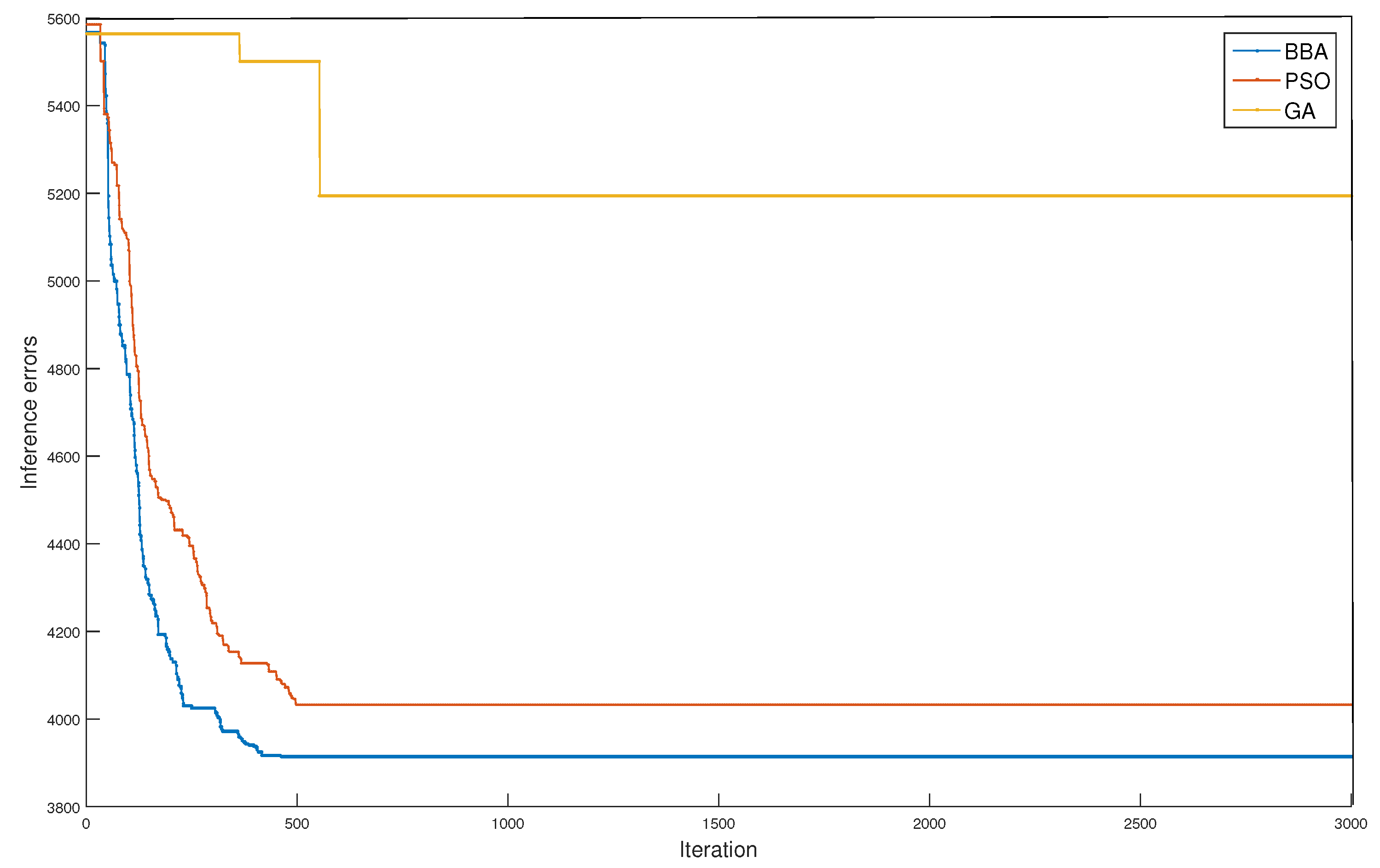
6.2. Sioux Falls Network
6.3. Barcelona Network
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Owais, M. Deep learning for integrated origin–destination estimation and traffic sensor location problems. IEEE Trans. Intell. Transp. Syst. 2024, 25, 6501–6513. [Google Scholar] [CrossRef]
- Mehr, N.; Horowitz, R. A submodular approach for optimal sensor placement in traffic networks. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; IEEE: New York, NY, USA, 2018; pp. 6353–6358. [Google Scholar]
- Li, R.; Mehr, N.; Horowitz, R. Submodularity of optimal sensor placement for traffic networks. Transp. Res. Part B Methodol. 2023, 171, 29–43. [Google Scholar] [CrossRef]
- Bianco, L.; Confessore, G.; Gentili, M. Combinatorial aspects of the sensor location problem. Ann. Oper. Res. 2006, 144, 201–234. [Google Scholar] [CrossRef]
- Castillo, E.; Grande, Z.; Calviño, A.; Szeto, W.Y.; Lo, H.K. A state-of-the-art review of the sensor location, flow observability, estimation, and prediction problems in traffic networks. J. Sens. 2015, 2015, 903563. [Google Scholar] [CrossRef]
- Gentili, M.; Mirchandani, P.B. Locating sensors on traffic networks: Models, challenges and research opportunities. Transp. Res. Part C Emerg. Technol. 2012, 24, 227–255. [Google Scholar] [CrossRef]
- Owais, M. Traffic sensor location problem: Three decades of research. Expert Syst. Appl. 2022, 208, 118134. [Google Scholar] [CrossRef]
- Owais, M.; Moussa, G.S.; Hussain, K.F. Sensor location model for O/D estimation: Multi-criteria meta-heuristics approach. Oper. Res. Perspect. 2019, 6, 100100. [Google Scholar] [CrossRef]
- Yang, H.; Zhou, J. Optimal traffic counting locations for origin–destination matrix estimation. Transp. Res. Part B Methodol. 1998, 32, 109–126. [Google Scholar] [CrossRef]
- Ng, M. Partial link flow observability in the presence of initial sensors: Solution without path enumeration. Transp. Res. Part E Logist. Transp. Rev. 2013, 51, 62–66. [Google Scholar] [CrossRef]
- Owais, M.; Moussa, G.S.; Hussain, K.F. Robust deep learning architecture for traffic flow estimation from a subset of link sensors. J. Transp. Eng. Part A Syst. 2020, 146, 04019055. [Google Scholar] [CrossRef]
- Danczyk, A.; Liu, H.X. A mixed-integer linear program for optimizing sensor locations along freeway corridors. Transp. Res. Part B Methodol. 2011, 45, 208–217. [Google Scholar] [CrossRef]
- Owais, M.; Shahin, A.I. Exact and heuristics algorithms for screen line problem in large size networks: Shortest path-based column generation approach. IEEE Trans. Intell. Transp. Syst. 2022, 23, 24829–24840. [Google Scholar] [CrossRef]
- Yang, H.; Gan, L.; Tang, W. Determing cordons and screen lines for origin-destination trip studies. In Proceedings of the Eastern Asia Society for Transportation Studies, Hanoi, Vietnam, 24–27 October 2001; Volume 3. [Google Scholar]
- Gentili, M.; Mirchandani, P.B. Locating active sensors on traffic networks. Ann. Oper. Res. 2005, 136, 229–257. [Google Scholar] [CrossRef]
- Hu, S.R.; Peeta, S.; Chu, C.H. Identification of vehicle sensor locations for link-based network traffic applications. Transp. Res. Part B Methodol. 2009, 43, 873–894. [Google Scholar] [CrossRef]
- Salari, M.; Kattan, L.; Lam, W.H.; Lo, H.; Esfeh, M.A. Optimization of traffic sensor location for complete link flow observability in traffic network considering sensor failure. Transp. Res. Part B Methodol. 2019, 121, 216–251. [Google Scholar] [CrossRef]
- Shao, M.; Sun, L.; Shao, X. Sensor location problem for network traffic flow derivation based on turning ratios at intersection. Math. Probl. Eng. 2016, 2016, 9012724. [Google Scholar] [CrossRef]
- Xie, C.; Shao, M.; Sun, L. Superiority proof of “incoming layout” for full link flow observability under uncertainty. Transp. Res. Part B Methodol. 2024, 190, 103090. [Google Scholar] [CrossRef]
- Xu, X.; Lo, H.K.; Chen, A.; Castillo, E. Robust network sensor location for complete link flow observability under uncertainty. Transp. Res. Part B Methodol. 2016, 88, 1–20. [Google Scholar] [CrossRef]
- Owais, M.; Matouk, A.E. A factorization scheme for observability analysis in transportation networks. Expert Syst. Appl. 2021, 174, 114727. [Google Scholar] [CrossRef]
- Contreras, S.; Kachroo, P.; Agarwal, S. Observability and sensor placement problem on highway segments: A traffic dynamics-based approach. IEEE Trans. Intell. Transp. Syst. 2015, 17, 848–858. [Google Scholar] [CrossRef]
- Yu, X.; Ma, S.; Zhu, N.; Lam, W.H.; Fu, H. Ensuring the robustness of link flow observation systems in sensor failure events. Transp. Res. Part B Methodol. 2023, 178, 102849. [Google Scholar] [CrossRef]
- Hu, X.; Fan, Y. Sensor placement considering the observability of traffic dynamics: On the algebraic and graphical perspectives. Transp. Res. Part B Methodol. 2024, 189, 103057. [Google Scholar] [CrossRef]
- Castro-Triguero, R.; Murugan, S.; Gallego, R.; Friswell, M.I. Robustness of optimal sensor placement under parametric uncertainty. Mech. Syst. Signal Process. 2013, 41, 268–287. [Google Scholar] [CrossRef]
- Houssein, E.H.; Saad, M.R.; Djenouri, Y.; Hu, G.; Ali, A.A.; Shaban, H. Metaheuristic algorithms and their applications in wireless sensor networks: Review, open issues, and challenges. Clust. Comput. 2024, 27, 13643–13673. [Google Scholar] [CrossRef]
- Almutairi, A.; Owais, M. Active traffic sensor location problem for the uniqueness of path flow identification in large-scale networks. IEEE Access 2024, 12, 180385–180403. [Google Scholar] [CrossRef]
- Almutairi, A.; Yi, P.; Owais, M. New approach for estimating intersection control delay from passive traffic sensors at network level. IEEE Access 2024, 12, 2882–2900. [Google Scholar] [CrossRef]
- Fakhouri, A.A.; Soltani, R. Multi-objective robust optimization for the traffic sensors location problem. IEEE Access 2020, 9, 6225–6238. [Google Scholar] [CrossRef]
- Mitsakis, E.; Chrysohoou, E.; Salanova Grau, J.M.; Iordanopoulos, P.; Aifadopoulou, G. The sensor location problem: Methodological approach and application. Transport 2017, 32, 113–119. [Google Scholar] [CrossRef]
- Owais, M.; El Deeb, M.; Abbas, Y.A. Distributing portable excess speed detectors in AL Riyadh city. Int. J. Civ. Eng. 2020, 18, 1301–1314. [Google Scholar] [CrossRef]
- Shao, M.; Xie, C.; Sun, L. Optimization of network sensor location for full link flow observability considering sensor measurement error. Transp. Res. Part C Emerg. Technol. 2021, 133, 103460. [Google Scholar] [CrossRef]
- Gentili, M.; Mirchandani, P.B. Review of optimal sensor location models for travel time estimation. Transp. Res. Part C Emerg. Technol. 2018, 90, 74–96. [Google Scholar] [CrossRef]
- Castillo, E.; Nogal, M.; Rivas, A.; Sánchez-Cambronero, S. Observability of traffic networks. Optimal location of counting and scanning devices. Transp. B Transp. Dyn. 2013, 1, 68–102. [Google Scholar] [CrossRef]
- Castillo, E.; Gallego, I.; Sanchez-Cambronero, S.; Rivas, A. Matrix tools for general observability analysis in traffic networks. IEEE Trans. Intell. Transp. Syst. 2010, 11, 799–813. [Google Scholar] [CrossRef]
- Castillo, E.; Conejo, A.J.; Pruneda, R.E.; Solares, C. Observability in linear systems of equations and inequalities: Applications. Comput. Oper. Res. 2007, 34, 1708–1720. [Google Scholar] [CrossRef]
- Castillo, E.; Jimenez, P.; Menendez, J.M.; Conejo, A.J. The observability problem in traffic models: Algebraic and topological methods. IEEE Trans. Intell. Transp. Syst. 2008, 9, 275–287. [Google Scholar] [CrossRef]
- Castillo, E.; Rivas, A.; Jiménez, P.; Menéndez, J.M. Observability in traffic networks. Plate scanning added by counting information. Transportation 2012, 39, 1301–1333. [Google Scholar] [CrossRef]
- Ng, M. Synergistic sensor location for link flow inference without path enumeration: A node-based approach. Transp. Res. Part B Methodol. 2012, 46, 781–788. [Google Scholar] [CrossRef]
- He, S.X. A graphical approach to identify sensor locations for link flow inference. Transp. Res. Part B Methodol. 2013, 51, 65–76. [Google Scholar] [CrossRef]
- Bianco, L.; Cerrone, C.; Cerulli, R.; Gentili, M. Locating sensors to observe network arc flows: Exact and heuristic approaches. Comput. Oper. Res. 2014, 46, 12–22. [Google Scholar] [CrossRef]
- Zhou, X.; List, G.F. An information-theoretic sensor location model for traffic origin-destination demand estimation applications. Transp. Sci. 2010, 44, 254–273. [Google Scholar] [CrossRef]
- Fei, X.; Mahmassani, H.S. Structural analysis of near-optimal sensor locations for a stochastic large-scale network. Transp. Res. Part C Emerg. Technol. 2011, 19, 440–453. [Google Scholar] [CrossRef]
- Xing, T.; Zhou, X.; Taylor, J. Designing heterogeneous sensor networks for estimating and predicting path travel time dynamics: An information-theoretic modeling approach. Transp. Res. Part B Methodol. 2013, 57, 66–90. [Google Scholar] [CrossRef]
- Zhu, N.; Fu, C.; Ma, S. Data-driven distributionally robust optimization approach for reliable travel-time-information-gain-oriented traffic sensor location model. Transp. Res. Part B Methodol. 2018, 113, 91–120. [Google Scholar] [CrossRef]
- Fu, H.; Lam, W.H.; Shao, H.; Kattan, L.; Salari, M. Optimization of multi-type traffic sensor locations for estimation of multi-period origin-destination demands with covariance effects. Transp. Res. Part E Logist. Transp. Rev. 2022, 157, 102555. [Google Scholar] [CrossRef]
- Danczyk, A.; Di, X.; Liu, H.X. A probabilistic optimization model for allocating freeway sensors. Transp. Res. Part C Emerg. Technol. 2016, 67, 378–398. [Google Scholar] [CrossRef]
- Zhu, N.; Ma, S.; Zheng, L. Travel time estimation oriented freeway sensor placement problem considering sensor failure. J. Intell. Transp. Syst. 2017, 21, 26–40. [Google Scholar] [CrossRef]
- Yang, X.S.; Hossein Gandomi, A. Bat algorithm: A novel approach for global engineering optimization. Eng. Comput. 2012, 29, 464–483. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.S.; Alavi, A.H.; Talatahari, S. Bat algorithm for constrained optimization tasks. Neural Comput. Appl. 2013, 22, 1239–1255. [Google Scholar] [CrossRef]
- Umar, S.U.; Rashid, T.A.; Ahmed, A.M.; Hassan, B.A.; Baker, M.R. Modified Bat Algorithm: A newly proposed approach for solving complex and real-world problems. Soft Comput. 2024, 28, 7983–7998. [Google Scholar] [CrossRef]
- Arbelaez, A.; Mehta, D.; O’Sullivan, B.; Quesada, L. A constraint-based parallel local search for the edge-disjoint rooted distance-constrained minimum spanning tree problem. J. Heuristics 2018, 24, 359–394. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Yang, X.S. Binary bat algorithm. Neural Comput. Appl. 2014, 25, 663–681. [Google Scholar] [CrossRef]
- Yang, X.S. A new metaheuristic bat-inspired algorithm. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2010); Springer: Berlin/Heidelberg, Germany, 2010; pp. 65–74. [Google Scholar]
- Golberg, D.E. Genetic algorithms in search, optimization, and machine learning. Addion Wesley 1989, 1989, 36. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the Proceedings of ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: New York, NY, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Fierro, R.D. Numerical Linear Algebra; University of Chicago Department of Statistics: Chicago, IL, USA, 1998. [Google Scholar]
- Golub, G.H.; Van Loan, C.F. Matrix Computations, 4th ed.; Johns Hopkins University Press: Baltimore, MD, USA, 2013. [Google Scholar]
- Higham, N.J. Accuracy and Stability of Numerical Algorithms; SIAM: Philadelphia, PA, USA, 2002. [Google Scholar]


| Algorithm | Parameters | Values |
|---|---|---|
| BBA | Number of artificial bats | depends on the network’s dimension |
| 0 | ||
| 2 | ||
| A | 0.25 | |
| r | 0.5 | |
| 0.9 | ||
| a | 0.9 | |
| 0.9 | ||
| Stopping criterion | Max iteration | |
| PSO | Number of particles | depends on the network’s dimension |
| 2.2 | ||
| W | Is decreased linearly from 0.9 to 0.4 | |
| Max iterations | 500 | |
| Max velocity | 6 | |
| Stopping criterion | Max iteration | |
| GA | Number of individuals | depends on the network’s dimension |
| Selection | Roulette wheel | |
| Crossover (probability) | One-point (0.9) | |
| Mutation (probability) | Uniform (0.005) | |
| Max generation | depends on the network’s dimension | |
| Stopping criterion | Max generation |
| Node | Connected Links | New Links |
|---|---|---|
| 3 | {1, 5, 7, 9} | {1, 5, 7, 9} |
| 4 | {2, 3, 5, 6, 7, 8, 11, 12} | {2, 3, 6, 8, 11, 12} |
| 5 | {4, 6, 8, 10} | {4, 10} |
| 6 | {9, 11, 13, 14, 15} | {13, 14, 15} |
| 7 | {10, 12, 13, 14, 16} | {16} |
| 8 | {15, 16, 17, 18} | {17, 18} |
| Layout of Sensors | Link Flow Inference Equations | Error | |
|---|---|---|---|
| A | 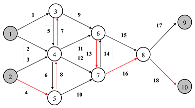 | node 3: node 4: node 5: node 6: node 7: node 8: | 31 |
| B | 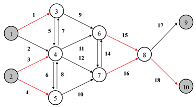 | node 3: node 4: node 5: node 6: node 7: node 8: | 26 |
| Layout of Sensors | Link Flow Inference Equations | Error | |
|---|---|---|---|
| GA |  | node 3: node 4: node 5: node 6: node 7: node 8: | 22 |
| PSO | 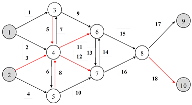 | node 3: node 4: node 5: node 6: node 7: node 8: | 22 |
| BBA | 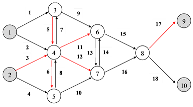 | node 3: node 4: node 5: node 6: node 7: node 8: | 22 |
| Algorithm | Node | Connected Links | New Links | Unobserved Link |
|---|---|---|---|---|
| GA | 3 | {1, 5, 7, 9} | {1, 5, 7, 9} | 7 |
| 5 | {4, 6, 8, 10} | {4, 6, 8, 10} | 6 | |
| 6 | {9, 11, 12, 13, 14, 15} | {11, 13, 14, 15} | 11 | |
| 7 | {10, 12, 13, 14, 16} | {12, 16} | 12 | |
| 4 | {2, 3, 5, 6, 7, 8, 11, 12} | {2, 3} | 3 | |
| 8 | {15, 16, 17, 18} | {17, 18} | 18 | |
| PSO | 3 | {1, 5, 7, 9} | {1, 5, 7, 9} | 5 |
| 5 | {4, 6, 8, 10} | {4, 6, 8, 10} | 8 | |
| 7 | {10, 12, 13, 14, 16} | {12, 13, 14, 16} | 12 | |
| 6 | {9, 11, 12, 13, 14, 15} | {11,15} | 11 | |
| 4 | {2, 3, 5, 6, 7, 8, 11, 12} | {2, 3} | 3 | |
| 8 | {15, 16, 17, 18} | {17, 18} | 18 | |
| BBA | 3 | {1, 5, 7, 9} | {1, 5, 7, 9} | 5 |
| 5 | {4, 6, 8, 10} | {4, 6, 8, 10} | 6 | |
| 6 | {9, 11, 12, 13, 14, 15} | {11, 13, 14, 15} | 11 | |
| 7 | {10, 12, 13, 14, 16} | {12, 16} | 12 | |
| 4 | {2, 3, 5, 6, 7, 8, 11, 12} | {2, 3} | 3 | |
| 8 | {15, 16, 17, 18} | {17, 18} | 17 |
| Node | Links | Set of New Links |
|---|---|---|
| 1 | {1, 2, 3, 5} | {1, 2, 3, 5} |
| 2 | {1, 3, 4, 14} | {4, 14} |
| 3 | {2, 5, 6, 7, 8, 35} | {6, 7, 8, 35} |
| 4 | {6, 8, 9, 10, 11, 31} | {9, 10, 11, 31} |
| 5 | {9, 11, 12, 13, 15, 23} | {12, 13, 15, 23} |
| 6 | {4, 12, 15, 16, 19} | {16, 19} |
| 7 | {17, 18, 20, 54} | {17, 18, 20, 54} |
| 8 | {16, 17, 19, 20, 21, 22, 24, 47} | {21, 22, 24, 47} |
| 9 | {13, 21, 23, 24, 25, 26} | {25, 26} |
| 10 | {25, 26, 27, 28, 29, 30, 32, 43, 48, 51} | {27, 28, 29, 30, 32, 43, 48, 51} |
| 11 | {10, 27, 31, 32, 33, 34, 36, 40} | {33, 34, 36, 40} |
| 12 | {7, 33, 35, 36, 37, 38} | {37, 38} |
| 13 | {37, 38, 39, 74} | {39, 74} |
| 14 | {34, 40, 41, 42, 44, 71} | {41, 42, 44, 71} |
| 15 | {28, 41, 43, 44, 45, 46, 57, 67} | {45, 46, 57, 67} |
| 16 | {22, 29, 47, 48, 49, 50, 52, 55} | {49, 50, 52, 55} |
| 17 | {30, 49, 51, 52, 53, 58} | {53, 58} |
| 18 | {18, 50, 54, 55, 56, 60} | {56, 60} |
| 19 | {45, 53, 57, 58, 59, 61} | {59, 61} |
| 20 | {56, 59, 60, 61, 62, 63, 64, 68} | {62, 63, 64, 68} |
| 21 | {62, 64, 65, 66, 69, 75} | {65, 66, 69, 75} |
| 22 | {46, 63, 65, 67, 68, 69, 70, 72} | {70, 72} |
| 23 | {42, 70, 71, 72, 73, 76} | {73, 76} |
| 24 | {39, 66, 73, 74, 75, 76} | {} |
| Layout of Sensors | Link Flow Inference Equations | Error | |
|---|---|---|---|
| GA | 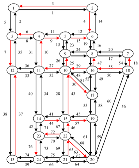 | node 1: node 2: node 3: node 4: node 5: node 6: node 7: node 8: node 9: node 10: node 11: node 12: node 13: node 14: node 15: node 16: node 17: node 18: node 19: node 20: node 21: node 22: node 23: | 137 |
| PSO |  | node 1: node 2: node 3: node 4: node 5: node 6: node 7: node 8: node 9: node 10: node 11: node 12: node 13: node 14: node 15: node 16: node 17: node 18: node 19: node 20: node 21: node 22: node 23: | 133 |
| BBA | 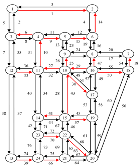 | node 1: node 2: node 3: node 4: node 5: node 6: node 7: node 8: node 9: node 10: node 11: node 12: node 13: node 14: node 15: node 16: node 17: node 18: node 19: node 20: node 21: node 22: node 23: | 133 |
| Unobserved Links per Node | GA | PSO | BBA |
|---|---|---|---|
| 1 | 425 | 436 | 426 |
| 2 | 304 | 317 | 331 |
| 3 | 161 | 140 | 137 |
| 4 | 27 | 29 | 30 |
| 5 | 2 | 5 | 3 |
| 6 | 1 | 1 | 1 |
| 7 | 0 | 0 | 0 |
| 8 | 2 | 0 | 2 |
| 9 | 0 | 1 | 0 |
| 10 | 0 | 1 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Owais, M.; Allam, A.A. Adaptive Optimization of Traffic Sensor Locations Under Uncertainty Using Flow-Constrained Inference. Appl. Sci. 2025, 15, 10257. https://doi.org/10.3390/app151810257
Owais M, Allam AA. Adaptive Optimization of Traffic Sensor Locations Under Uncertainty Using Flow-Constrained Inference. Applied Sciences. 2025; 15(18):10257. https://doi.org/10.3390/app151810257
Chicago/Turabian StyleOwais, Mahmoud, and Amira A. Allam. 2025. "Adaptive Optimization of Traffic Sensor Locations Under Uncertainty Using Flow-Constrained Inference" Applied Sciences 15, no. 18: 10257. https://doi.org/10.3390/app151810257
APA StyleOwais, M., & Allam, A. A. (2025). Adaptive Optimization of Traffic Sensor Locations Under Uncertainty Using Flow-Constrained Inference. Applied Sciences, 15(18), 10257. https://doi.org/10.3390/app151810257





