State-of-the-Art and Future Trends in Deformation Response of Tunnel Intersection Construction Zones

Abstract

The construction of urban underground space develops very fast, and tunnel intersection construction has become a common practice, attracting significant attention due to the associated deformation responses and risk control challenges. To systematically review the research landscape and cutting-edge developments in this field, this study conducts a comprehensive analysis based on 744 publications (1994–2025) from the Web of Science Core Collection using bibliometric methods. Firstly, through visual analyses of annual publication trends, journal distributions, and keyword co-occurrences, the study reveals the evolution and research hotspots of the past three decades. Subsequently, three core dimensions are explored in depth: deformation mechanisms and patterns, deformation analysis methods for ground and existing structures, and ground control and reinforcement techniques. The review highlights the following: (1) Research focus has shifted from single construction scenarios to the complex interactions among multiple tunnels, yet the cumulative deformation effects caused by repeated soil disturbances during sequential excavation remain inadequately understood. (2) The bidirectional coupling between existing tunnels and surrounding soil has become a major research focus and challenge. Particularly in the presence of high-stiffness structures, the “free-field” assumption in the commonly used two-stage method is being questioned, necessitating the development of more refined computational theories. (3) Optimization of construction schemes under complex conditions is key to disturbance control, but current research still lacks systematic multi-objective optimization approaches. In addition, this paper analyzes the current research status and future directions to enhance the deformation perception capability and control technologies in tunnel construction influence zones, thereby further improving the safety and intelligence level of tunnel construction.

1. Introduction

With the continuous advancement of urbanization, both the population and vehicles in the central areas of Chinese cities have steadily increased, placing a growing strain on road traffic. Developing a multi-level, three-dimensional urban transportation system has become an inevitable choice to alleviate congestion and improve travel efficiency. Urban rail transit, with its advantages of high capacity, high speed, and low energy consumption, has been developing rapidly over the past decade. By the end of December 2024, 54 cities across China had opened a total of 325 urban rail transit lines, with an operating mileage of 10,945.6 km [1]. This large-scale expansion of underground space has made overlapping and intersecting construction scenarios increasingly common within the same city or transit line, reflecting a transition in network configuration from planar layouts to fully three-dimensional arrangements and from isolated single-line systems to integrated multi-line networks.

During excavation, underground tunnels, such as those constructed using the New Austrian Tunnelling Method (NATM), inevitably disturb the surrounding strata, inducing stress unloading-reloading cycles and subsequently triggering spatially heterogeneous, three-dimensional deformation. When tunnels intersect, overlap, or pass beneath existing operational lines within constrained urban spaces, these disturbance effects can be superimposed, coupled, and potentially amplified [2,3,4,5,6,7]. This escalation poses more stringent deformation-control challenges for adjacent ground surface structures, underground utilities, and existing tunnel systems. Suppose ground settlement or lateral displacement exceeds acceptable limits. In that case, it may cause differential settlement of ground surface buildings, bending and cracking of foundation piles, misalignment or rupture of the pipelines, and even compromise the operational safety of existing metro lines. Consequently, both engineering risks and public concerns are significantly heightened.

In light of these challenges, a systematic review of deformation mechanisms, predictive methods, and control technologies associated with tunnel intersection influence zones is of significant practical and theoretical value. Such work not only contributes to safeguarding the existing urban environment but also supports the sustainable development of ultra-dense underground spaces. Drawing on a systematic and reproducible literature retrieval strategy, this study synthesizes research findings from the past three decades. It provides a comprehensive review with exploratory insights, focusing on four key areas:

(1)

Understanding deformation mechanisms and patterns in tunnel intersection influence zones;

(2)

Developing analytical and numerical approaches for ground deformation prediction;

(3)

Evaluating the response of existing structures;

(4)

Implementing ground control and reinforcement measures, along with their applicability.

Through a systematic comparison of the applicability and limitations of different research methodologies, this study identifies critical knowledge gaps, pinpoints key scientific issues that remain unresolved, and outlines prospective technical pathways. The overarching objective is to establish a coherent research framework and provide a solid basis for informed decision-making in both academic research and engineering practice.

2. Literature Research and Statistical Analysis

2.1. Analysis of Publication Volume and Citation Frequency

In this study, a topic search was conducted on 17 July 2025, using the Web of Science Core Collection database. The search query was set as TS = (“tunnel excavation” AND “deformation response”), with the document types restricted to Article and Review, and the language limited to English. After duplicate removal and manual screening, a total of 744 records form 1994 to 2025 were included for analysis.

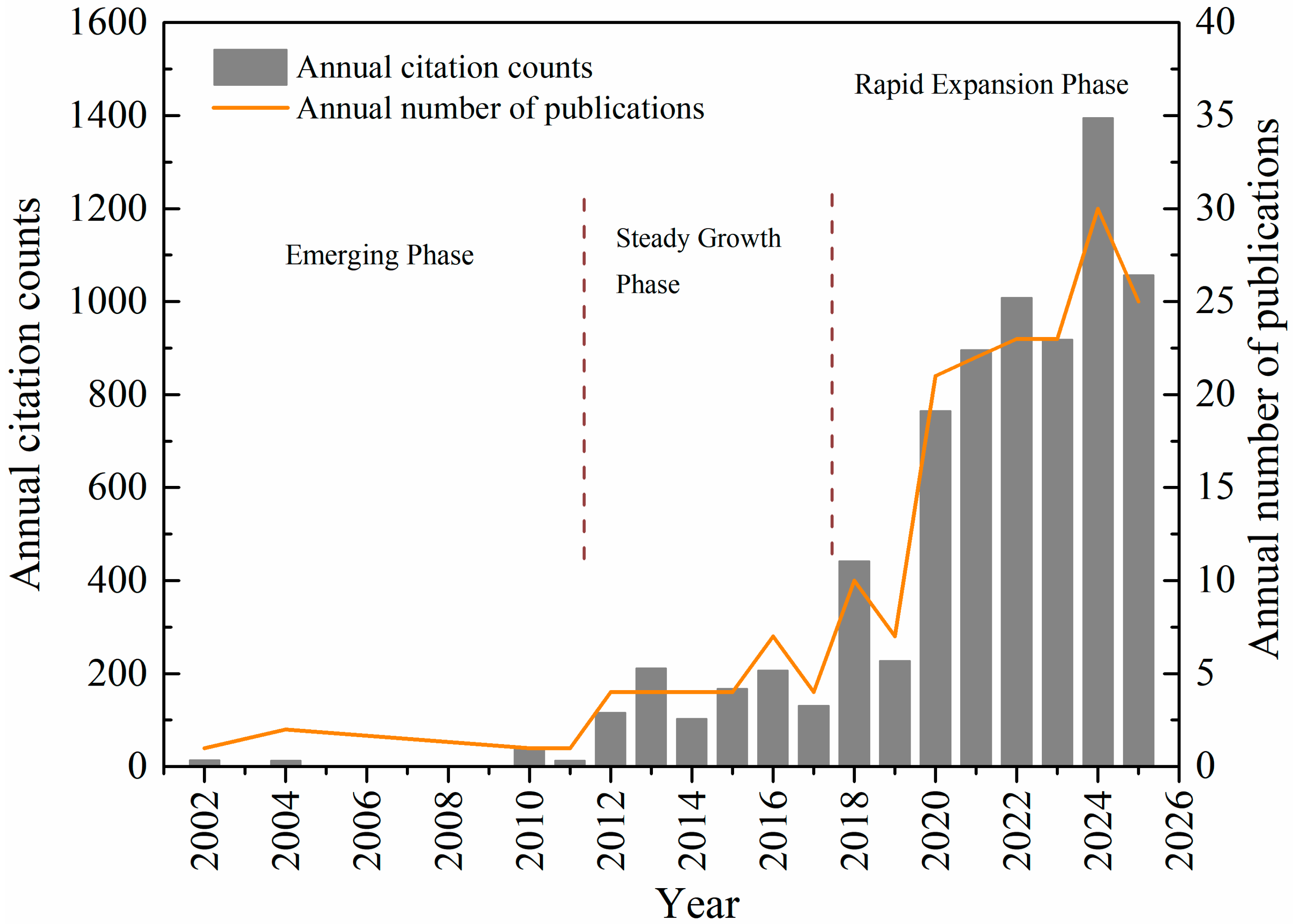
Figure 1 presents the annual number of publications (orange line, left axis) and annual citation counts (blue bars, right axis) from 1994 to 2025. An analysis of the overall trends indicates an initial period of growth followed by a subsequent decline in recent years, which can be broadly categorized into three distinct phases:

Emerging Phase (1994–2006): Fewer than 10 papers were published per year, with annual citation counts remaining below 50. Project-specific case studies dominated research during this phase.

Steady Growth Phase (2007–2013): The number of publications rose from 12 to 42 per year (CAGR ≈ 18%), while citation counts also increased proportionally, indicating growing research demand driven mainly by the rapid acceleration of metro construction.

Rapid Expansion Phase (2014–2024): Research activity expanded substantially, with annual publications peaking at approximately 150 per year in 2024; the highest annual citation count was recorded in 2020, reaching about 1600 citations, reflecting the significant impact of earlier publications during this period.

The search strategy was further refined, and a topic search was conducted in the Web of Science Core Collection with the search query set as TS = (“tunnel excavation” AND “deformation response” AND (“intersection” OR “crossing” OR “overlapping”)). The document types were limited to Article and Review, and the language was restricted to English. After deduplication and manual screening, a total of 193 records were included.

Figure 2 shows the annual number of publications (orange line, left axis) and annual citation frequency (grey bars, right axis) from 2002 to 2025. Analysis of the overall trend in Figure 2 reveals a pattern similar to that in Figure 1, with both exhibiting a rise-then-slight decline trajectory. The development can be divided into three stages: the emergence stage (2002–2011), the steady growth stage (2012–2017), and the rapid expansion stage (2018–2024). The growth characteristics of each stage are also consistent with those in Figure 1. Comparing the two, it can be observed that due to the development of tunnel construction, research related to tunnel crossings and intersecting construction has lagged behind studies on deformation in the influence zones caused by tunnel excavation. In the early stages of tunnel engineering, the primary focus was on solving fundamental issues associated with initial construction. As the density of tunnel networks increased, the research focus gradually shifted toward multi-line tunnel intersections and crossing construction.

The temporary decline in citation counts observed in 2025 can be attributed to the well-recognized citation lag effect and should not be interpreted as a decline in the actual research impact.

Furthermore, a refined search was conducted using the query TS = (“tunnel excavation” AND “deformation response” AND “intersection”), which yielded a total of 11 publications. These studies were primarily published between 2018 and 2025, with a relatively balanced temporal distribution. The total citation frequency reached 533, indicating that research in this field is still in its early stages but has already attracted a certain degree of attention.

Overall, deformation issues in strata-structure systems induced by tunnel intersection construction have emerged as a critical research frontier and hotspot within the field of underground space engineering.

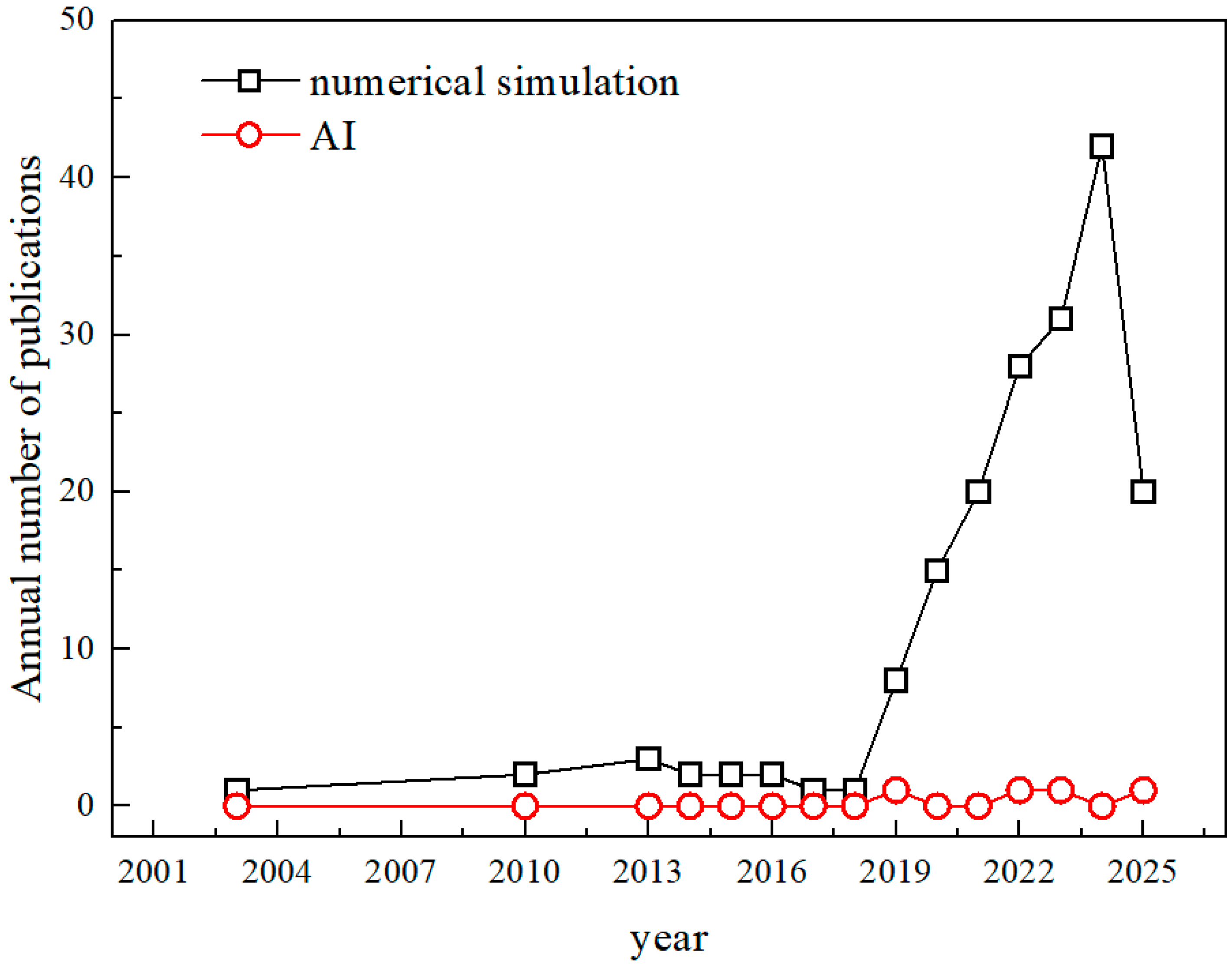
Considering the development of computer technology, searches were conducted using the queries TS = (“tunnel excavation” AND “deformation response” AND “numerical simulation”) and TS = (“tunnel excavation” AND “deformation response” AND “AI”), respectively. The annual publication counts obtained from these searches are shown in Figure 3.

As shown in the Figure 3, numerical simulation techniques have been applied to tunnel construction and deformation studies relatively early, entering a rapid expansion phase around 2019. At present, their application in research has become relatively mature. In recent years, with the advancement of AI technologies, methods such as machine learning have begun to attract increasing attention from researchers. Tree-based models, neural network models, and linear models are gradually being applied to studies related to tunnel construction and deformation problems.

The number of publication data indicate that research involving AI is still in its early stage. However, analysis of citation frequency shows a total of 490 citations, suggesting that this research direction has already attracted significant academic interest. With the continuous development of artificial intelligence, more sophisticated machine learning methods are expected to be further applied and integrated into tunnel construction and deformation analysis in the future.

2.2. Journal Distribution Analysis

The 744 retrieved documents were used as samples, classified and counted by journal source, and the top 10 journals were listed from high to low by the number of publications. The results are shown in

Table 1. Ranking of journals by number of publications.

Ranking	Journal	Number of Article Publications	Proportion (%)
1	Tunnelling and Underground Space Technology	152	20.4
2	Computers and Geotechnics	68	9.1
3	Applied Sciences	45	6.0
4	International Journal of Rock Mechanics and Mining Sciences	38	5.1
5	Rock Mechanics and Rock Engineering	36	4.8
6	Engineering Failure Analysis	30	4.0
7	International Journal of Geomechanics	28	3.8
8	Advances in Civil Engineering	26	3.5
9	Canadian Geotechnical Journal	24	3.2
10	Bulletin of Engineering Geology and the Environment	22	3.0

.

As shown in Table 1, the top 10 journals published 469 articles, accounting for approximately 63% of the overall sample, demonstrating a pronounced core concentration pattern in a limited number of specialized journals. Among them, Tunnelling and Underground Space Technology (TUST) and Computers and Geotechnics are widely recognized as leading journals in tunneling and geotechnical engineering, reflecting the strong engineering orientation of research in this domain. The inclusion of the multidisciplinary journal Applied Sciences indicates that the field is beginning to expand across disciplinary boundaries, particularly into materials science and computational methods. Except Applied Sciences and Advances in Civil Engineering (IF ≈ 2), the remaining eight journals have impact factors in the range of 3 to 7, suggesting that most research outputs in this area are published in medium to high impact journals.

The retrieved results on the integrated application of numerical simulation and AI technologies to deformation responses induced by tunnel excavation were summarized, and the journal distribution of the publications is presented in

Table 2. Ranking of journals by number of publications.

Ranking	Journal	Number of Article Publications	Proportion (%)
1	Tunnelling and Underground Space Technology	22	23
2	Applied Sciences	15	16
3	Engineering Failure Analysis	10	10
4	Advances in Civil Engineering	9	9
5	Rock Mechanics and Rock Engineering	8	8
6	Buildings	7	7
7	Scientific Reports	7	7
8	Computers and Geotechnics	7	7
9	KSCE Journal of Civil Engineering	6	6
10	International Journal of Geomechanics	5	5

.

Analysis of the data in Table 2 shows that the top 10 journals have published a total of 96 articles, indicating a clear concentration effect. The leading journal, Tunnelling and Underground Space Technology (TUST), is a top-tier journal in tunnel and geotechnical engineering, reflecting the high level of attention to this research direction. The second-ranked journal, Applied Sciences, covers multiple research fields, suggesting that studies on the integration of tunnel excavation-induced deformation responses with numerical simulation and AI techniques have become one of the key research focuses. In addition, except for the KSCE Journal of Civil Engineering and the International Journal of Geomechanics, the publication volumes of journals ranked 3rd to 8th are relatively close, indicating a consistent level of attention to this research direction across the industry.

2.3. Keyword Co-Occurrence Analysis

During the research process, the collected literature was subjected to keyword co-occurrence analysis, and the results shown in Figure 4 were obtained.

Analysis of the keyword co-occurrence network in Figure 4 reveals that current research hotspots are primarily concentrated on topics such as tunnels, deformation, shield tunnels, failure, rock, stability, soil, prediction, adjacent excavation, numerical simulation, analytical solutions, and existing tunnels. Among these, shield tunneling has emerged as a significant focus of attention. Increasing interest is being directed toward the deformation of existing tunnels and the surrounding stratum induced by adjacent excavations. Additionally, issues related to the stability of soil and rock deformation prediction have become central research concerns. Numerical simulation and analytical methods remain widely adopted and effective tools in this field.

To further analyze the research progress in this area, a search was conducted in the CNKI database using the query TS = (“tunnel excavation” AND “deformation response” AND (“intersection” OR “crossing” OR “overlapping”)). To ensure the representativeness of the retrieved results, the literature source was limited to EI-indexed. The co-occurrence analysis results are presented in Figure 5.

Analysis of the keyword co-occurrence network in the Figure 5 indicates that current research focuses primarily on tunnel engineering, numerical simulation, shield tunnels, composite strata, deformation control, and longitudinal deformation. The distribution of research hotspots is largely consistent with the results obtained from the Web of Science search. Moreover, many scholars have conducted in-depth studies on longitudinal deformation of tunnels induced by adjacent construction and its control techniques, further steering research in this field toward tunnel deformation responses and control strategies under complex construction conditions.

3. Study on Deformation Mechanism and Deformation Law of Tunnel Excavation Affected Area

3.1. Research Progress Based on Numerical Simulation Analysis Methods

With the rapid advancement of computational technologies and construction techniques, numerical simulation has become an indispensable tool in tunnel engineering research. It enables the effective investigation of interaction mechanisms among various influencing factors under complex construction conditions, variable geological conditions, and refined excavation sequences. Through parametric analysis, researchers can systematically explore the effects of individual or combined factors on the stress-strain behavior of strata and supporting structures. On this basis, scholars have conducted extensive and in-depth studies on the deformation patterns and underlying mechanisms induced by tunnel excavation using numerical methods.

In terms of deformation patterns, early studies often focused on typical stratum conditions and basic tunnel configurations. The deformation behavior in soft clay is particularly complex due to its unique geotechnical properties. Lee and Rowe [2] developed a finite element model considering the three-dimensional elasto-plastic behavior of soil, revealing fundamental patterns of ground settlement and structural stress during single-track tunnel excavation. Building upon this, research expanded to more common double-track parallel tunnels. E. Soliman et al. [3] clarified the stress redistribution and deformation behavior induced by interaction effects during closely spaced tunnel construction. Ng et al. [4] further modeled tunnel excavation using the NATM and revealed the load transfer mechanism in offset tunnel sequences, where excavation of the subsequent tunnel can cause partial load transfer to the preceding tunnel, thereby decreasing the bending moment in the former and increasing it in the latter. Beyond soil constitutive models, differences in geological media also play a critical role. For instance, He et al. [5] utilized the discrete element method to analyze sandy gravel formations and identified tunnel depth and spacing between twin tunnels as key geometric parameters governing the formation of the “soil arching effect.” In addition, construction dewatering, a commonly employed auxiliary measure, cannot be overlooked. Some studies have shown that in water-rich, weak strata, settlement caused by dewatering can even exceed that caused by excavation itself, contributing up to 50–60% of total settlement [6], highlighting the necessity of coupled hydro-mechanical (fluid-structure) analysis.

As research has progressed, the focus has gradually shifted toward the refined influence of procedural factors such as construction methods and excavation sequencing. Different excavation techniques and construction sequences significantly affect the rate and magnitude of ground settlement. Kong [7], Wang and Yang [8] employed numerical simulations to compare the performance of shield tunneling and the CRD method, as well as various NATM techniques, analyzing their advantages, limitations, and applicability in controlling ground surface settlement. They also explored the interactive effects of differing construction sequences. Beyond the choice of methods, optimization of excavation sequencing has become a research hotspot. Wang et al. [9], using a single-bore double-layer tunnel as the study context, analyzed the ground surface and crown settlement patterns under different excavation sequences. Liu et al. [10] systematically investigated more complex underground station structures, examining factors such as pilot tunnel offsets, lining sequences, lower excavation orders, and single excavation advance lengths, thereby providing theoretical guidance for optimizing construction procedures and controlling soil disturbance.

In recent years, with intensified urban underground space development, research focus has further expanded to complex three-dimensional tunnel group relationships. Tunnel positional relationships have evolved from traditional planar parallelism to spatial stacking and intersection. Regarding stacked tunnels, Tai et al. [11], Song and Zhang [12] focused on Beijing’s geological conditions, modeling the effects of various excavation sequences and spatial layouts on ground surface and deep soil deformation, and quantifying soil loss rates. Tang et al. [13], Huang and Zhang [14], who focus on Shenzhen’s geological conditions, further incorporated seepage effects to derive more engineering-relevant settlement prediction models, which were validated against field measurements. For more complex spatial intersections, particularly scenarios where new tunnels pass beneath existing operational lines, Wang et al. [15], Huang and Gao [16] included the influence of existing line loads in their analysis of multi-factor-induced stratum responses. Additionally, Ma [17], Wu and Gao [18] revealed settlement mechanisms under coupled effects of grouting pressure, tunnel depth, geological heterogeneity, and dewatering. Considering unloading effects from adjacent construction and the interaction between strata and tunnel structures, Lai et al. [19] developed numerical models based on in-situ test parameters to analyze tunnel deformation responses during construction. These studies increasingly emphasize the dynamic interactions among strata, new structures, and existing structures under construction disturbances. Mei et al. [20] developed a numerical simulation model for the construction process using the freezing method in saturated sandy layers in collapsible loess regions. They analyzed the temperature evolution, frost heave, and thaw settlement distribution and variation patterns during construction, and revealed the mechanism of displacement changes induced by frost heave.

In summary, previous studies have made significant progress in exploring construction-induced deformation patterns of single, double, and spatially intersecting tunnels through numerical simulation methods, considering geological conditions, construction techniques, and tunnel configurations. Valuable insights have been accumulated. However, most research focuses on specific engineering cases or relatively simplified spatial relationships. Systematic comparisons and generalized conclusions on the interaction mechanisms of multiple tunnels (e.g., parallel, stacked, intersecting) under complex spatial configurations, particularly regarding the intrinsic coupling between structural forces and ground deformation under varying geological conditions, remain insufficient. Therefore, this paper aims to further analyze the research progress on the stress-deformation behavior and underlying mechanisms of ground and existing structures during multi-tunnel construction in complex spatial arrangements.

3.2. Research Progress Based on Model Experiments

Physical model testing is another essential method for investigating the deformation mechanisms associated with tunnel excavation. It provides an intuitive means to replicate the complex interactions and deformation behaviors between the structure and the stratum during construction. This approach offers critical support for validating theoretical analyses and optimizing construction schemes. Based on the simulation of gravity fields, physical model tests can be broadly categorized into two types: similar-material model tests conducted under normal gravity conditions, and centrifuge model tests performed under enhanced gravity fields.

Similar-material model tests, conducted under 1 g gravity conditions (natural gravity conditions), simulate the properties of real strata by carefully testing and adjusting the mechanical parameters of model materials.

While similar-material model tests (1 g model tests) offer advantages in terms of cost and operational simplicity, their primary limitation lies in the inability to accurately replicate the in-situ stress conditions of the prototype, especially for deep-buried tunnels. These tests are conducted under natural gravity (1 g), and thus cannot simulate the high stress field that significantly influences the mechanical behavior of the surrounding geomaterials in deep underground engineering. This can lead to discrepancies between the model’s behavior and the actual in-situ response.

In contrast, centrifuge model tests can reproduce the true in-situ stress field by creating a high-gravity environment, making them more suitable for simulating deep-buried tunnel construction where gravity effects are significant. We have clarified this distinction in the revised manuscript to provide a more balanced view of different experimental methods.

This method is widely used to investigate the influence of construction parameters and to reproduce specific engineering scenarios. In terms of construction parameter optimization, Wang et al. [21] demonstrated how two key factors-advanced support strength and excavation step length-significantly influence ground surface settlement and soil displacement, providing direct guidance for construction control. In reproducing specific engineering conditions, this method has also shown strong applicability. For instance, Zhu et al. [22] uses the Dalian metro project as a case study, successfully replicating the time-dependent evolution of ground surface settlement. Zhang [23], addressing the challenges of tunneling in weak and water-rich strata, experimentally obtained the settlement behavior under pre-grouting conditions. Moreover, large-scale model tests have been employed to study the stability of shield excavation faces in greater depth. These studies clarified the intrinsic relationship between support pressure and ground surface settlement. They captured the incremental displacement field during the failure process [24], offering experimental support for determining appropriate support pressures.

Centrifuge model testing creates a stress field in scaled-down physical models that closely replicates the prototype by applying high gravitational acceleration through rapid rotation. This technique is particularly well-suited for studying geotechnical problems with strong stress-path dependency. Early studies utilized centrifuge testing to examine the influence of basic parameters; for example, Imamura et al. [25] systematically investigated the ground surface settlement patterns associated with varying tunnel depths. With advances in experimental techniques, centrifuge tests have been applied to more complex excavation scenarios. Wu et al. [26] conducted comparative tests in clayey soils to explore the differences between single and twin tunnel excavations. The results confirmed that the closer the spacing between twin tunnels, the stronger the interaction effects—an issue that becomes especially critical under high-stress conditions. In urban tunneling contexts, centrifuge testing offers unique advantages in assessing the impact on nearby infrastructure. Wu et al. [27], Ma and Gao [28], using the Shenzhen Metro project as a case study, analyzed the deformation behavior of both the ground and nearby structures during tunnel excavation. Other studies [29,30,31,32] have focused on the effects of tunneling on existing pipelines, surrounding strata, and tunnel structures themselves. By comparing test results with field monitoring data, these studies have provided valuable insights for assessing construction risks and supporting informed engineering decisions.

Meanwhile, advances in model testing techniques themselves have further propelled research in this field, particularly in two aspects: the development of experimental apparatus and the refinement of analog materials. To enhance testing precision and operability, Qin et al. [33] developed a medium-scale tunnel excavation test apparatus and systematized the formulation process of similarity materials. Berthoz et al. [34] introduced an advanced scaled tunnel boring machine (TBM) model, aiming to investigate the complex interaction mechanisms between the TBM and surrounding soil. In addition, numerous studies have focused on improving analog materials, such as using specific clays and uniformly graded sands to simulate various ground conditions [35,36,37,38], in order to explore soil deformation behaviors in challenging scenarios such as closely spaced tunnel construction.

In summary, physical model testing—whether using similarity materials or centrifuge techniques—has become a powerful tool for simulating tunnel construction processes and revealing the deformation mechanisms of structures and surrounding soil.

Similarity model tests offer advantages such as low cost, simple operation, the ability to simulate large-scale and complex structures, and intuitive visualization of test results. However, they are less suitable for construction processes where gravity effects are significant, such as deep-buried tunnels. In contrast, centrifuge model tests can use prototype geotechnical materials and reproduce the true in-situ stress field, making them suitable for simulating deep-buried tunnel construction. Nevertheless, they are limited in applicability to large-scale structures due to equipment constraints, and involve more complex operations and higher costs.

Notably, substantial achievements have been made in simulating shield tunneling operations. However, certain limitations and areas for further exploration remain. First, current studies predominantly focus on shield tunnels, while research on NATM tunnels—characterized by fundamentally different cross-sectional geometries, dimensions, and construction methods—is relatively scarce. These tunnels often induce more complex ground disturbances, which remain insufficiently addressed in existing model experiments. Second, although the formulation techniques of analog materials have seen continuous refinement, achieving high fidelity in replicating the complex physical and mechanical behaviors of natural geomaterials remains an ongoing challenge. This necessitates not only in-depth investigation into how different material ratios affect target properties but also leveraging advancements in material science to improve simulation accuracy. Therefore, future research should focus on model testing of NATM tunnels under specific regional geological conditions, and on enhancing material similarity to better capture the true behavior of complex ground-structure systems.

4. Study on Calculation Method of Stratum Deformation in Tunnel Excavation Affected Area

Prior to tunnel design and construction, predicting the potential ground deformation induced by excavation is a critical step for assessing the impact on adjacent buildings and structures, as well as for formulating targeted protection measures. Based on extensive research and engineering practice over the years, several mature prediction methods have been developed. Among them, the Peck empirical method, stochastic medium theory, and analytical approaches are the most widely adopted.

4.1. Peck Empirical Method

The Peck formula is an empirical method based on a large amount of measured data. It has been widely used in the engineering community due to its simple form and clear parameters.

(1)

Core theory and early development

The core idea of this method originated from the pioneering work of Peck [39], who found that the morphology of the transverse ground surface settlement trough caused by tunnel excavation is highly consistent with the Gaussian distribution curve, and further developed it into a settlement calculation formula:

$$S(x)=S_{\max }\exp (-{\displaystyle \frac{x^2}{2i^2}})$$

(1)

where S(x) is the ground surface settlement at a horizontal distance x from the tunnel axis; S_max is the maximum ground surface settlement, located directly above the tunnel axis; and i is the settlement trough width coefficient, which is the horizontal distance from the tunnel axis to the inflection point of the settlement curve (the point with the maximum settlement change rate).

These two core parameters, S_max and i, directly determine the depth and width of the settlement trough. To determine parameter i, O’Reilly and New [40] proposed a linear relationship between it and the tunnel depth Z₀ based on engineering experience in the London area, as shown in Equation (2).

$$i=K{Z}_0$$

(2)

Here, Z₀ represents the depth of the tunnel axis, and K is the ground surface settlement trough width parameter, which primarily depends on the geological properties of the stratum. Building upon this foundation, Attewell and Woodman [41] extended the original two-dimensional model into three-dimensional space. They proposed that the longitudinal settlement pattern could be described using a cumulative probability curve and derived a three-dimensional expression for ground settlement at any given point. This effectively captures the dynamic settlement process as the tunnel excavation face approaches and moves away, as shown in Equation (3).

$$S={\displaystyle \frac{V_l}{\sqrt{2\pi }{i}^2}}\exp \left[{\displaystyle \frac{-y^2}{2i^2}}\right]\left\{G\left({\displaystyle \frac{x-x_i}{i}}\right)-G\left({\displaystyle \frac{x-x_f}{i}}\right)\right\}$$

(3)

where, G represents the normal distribution function, V_l intuitively reflects the volume of soil lost during the construction process, i denotes the inflection point of the settlement trough curve, y represents the horizontal distance between the settlement point and the tunnel axis, x_i is the starting position of tunnel excavation, and x_f indicates the current position of the tunnel excavation face.

(2)

Deepening of the theory and interpretation of the physical meaning of parameters

With the advancement of research, scholars have aimed to assign clearer physical interpretations to this empirical formula. Based on the Peck equation, Fujita [42] systematically studied and summarized the predicted values of maximum settlement (S_max) under different tunneling methods. In China, Han [43] directly correlated the “ground loss ratio” with S_max, as shown in Equation (4):

$$V_l={\displaystyle \frac{\sqrt{2\pi }i{S}_{max}}{A}}$$

(4)

In this formula, A represents the excavation cross-sectional area of the tunnel. The ground loss ratio V_l intuitively reflects the volume of soil lost during the construction process, making it a core parameter with more physical significance than S_max. Meanwhile, Liu and Hou [44] incorporated the concept of negative ground loss to optimize the longitudinal settlement prediction formula, enabling it to better represent the actual tunneling process of shield construction.

(3)

Verification and expansion of engineering applications

The effectiveness of the Peck formula has been widely validated across diverse engineering practices. Studies have shown that the ground surface settlement patterns induced by both shield tunneling and NATM can be well described by the Peck formula [45,46]. Its applicability has also been confirmed under complex conditions such as sandy gravel strata [47] and twin circular shield tunnels [48], with calculated results aligning closely with measured data and numerical simulations. Furthermore, Liu [49], based on the Poussin theory, investigated the influence of the “no-pressure arch” effect on ground surface settlement, finding that the formation of an effective soil arch is critical in determining the magnitude of settlement. He further established a relationship between S_max and soil parameters by numerical simulation test, The factors influencing S_max primarily include the ratio of the elastic modulus of the upper soil layer to the tunnel formation pressure, the ratio of the equivalent layer thickness to the burial depth at the tunnel invert, and the ratio of the tunnel excavation diameter to the burial depth at the tunnel invert. Among these factors, the ratio of the elastic modulus of the upper soil layer to the tunnel formation pressure exerts the most significant influence on ground surface settlement, further indicating that the mechanical properties of the surrounding strata play a dominant role in determining the final settlement, that work deepen the understanding of the settlement mechanism.

(4)

Core Challenge: Parameter Selection and Calibration

Although the Peck formula is simple in form, its predictive accuracy entirely depends on the precise selection of key parameters (V_l and K or S_max and i), which exhibit substantial regional and project-specific variability. To address this, numerous studies have focused on parameter statistical analysis and calibration based on measured data, which can be summarized into three aspects: (1) parameter statistics and regionalization recommendations; (2) analysis of influencing factors; (3) determination of parameters under complex excavation conditions.

For example, Wei [50], Han and Li [51] conducted statistical analyses of numerous Chinese engineering cases and proposed recommended ranges for the soil loss rate V_l under different regional and construction quality conditions. Meng et al. [52] and Yang et al. [53], based respectively on subway monitoring data from Qingdao and Beijing, inverted and provided average settlement parameters for their local areas.

Regarding influencing factors, some research has found that the settlement trough width parameter is significantly correlated with the soil grain composition, specifically the ratio of coarse to fine grains [54]. Meanwhile, operational parameters of the shield machine, such as face pressure, grouting pressure, and machine thrust, directly affect the soil loss rate [55]. For large-diameter shield tunnels [56], studies have indicated considerable deviations in the traditional prediction formulas for the parameter i, and proposed recommended correction ranges.

For parameter determination under complex conditions, such as twin tunnels, Han et al. [57] research demonstrated that the overall settlement trough can be approximated by the superposition of the settlement curves of two single tunnels; however, the shape of the trough is jointly influenced by the spacing between the tunnels and their burial depth. Fang et al. [58] provided a recommended soil loss rate range of 0.23% to 1.3% for twin circular shield tunnel construction.

(5)

Improvements to Formulas for Complex Conditions

To address the increasing complexity of tunnel engineering, researchers have proposed various modifications to the classical Peck formula. For instance, She et al. [59] improved the longitudinal settlement prediction formula by incorporating parameters such as displacement release rate, specifically tailored to the characteristics of loess strata. Gan [60] introduced a revised Peck formula to enhance settlement prediction accuracy for underground excavations in water-rich strata, achieving better predictive performance. For multi-line tunnels, Chen et al. [61] and Gong et al. [62] extended the application of the Peck formula to settlement prediction for double and even quadruple tunnels by employing superposition principles and introducing correction factors. Regarding specialized construction methods, Yang and Li [63] investigated the settlement characteristics of pipe-roof pre-reinforced stations and accordingly modified the formula, thereby improving its applicability to such engineering scenarios.

(6)

Summary

In summary, the Peck formula, as a classical settlement prediction method, has been extensively and consistently applied in engineering practice due to its computational simplicity and clearly defined parameters. However, as an empirical model, its successful application is highly dependent on regional construction experience and abundant monitoring data. For new projects lacking similar engineering precedents, the accurate selection of parameters remains a significant challenge.

Currently, several challenges remain: First, for double or multi-line tunnels, the mechanism underlying the determination of the settlement trough width coefficient is not yet fully understood. It is still unclear whether different width coefficients should be assigned to the preceding and succeeding tunnels, and how to systematically incorporate the combined effects of geological conditions, burial depth, and tunnel spacing requires further investigation. Second, with increasingly complex spatial tunnel configurations, effectively extending the classical Peck formula to multi-tunnel three-dimensional intersection scenarios, while coupling the influence of existing tunnels, remains a research gap.

4.2. Stochastic Medium Theory

The stochastic medium method is a settlement prediction approach grounded in solid theoretical foundations. It was initially proposed by Polish scholar Litwiniszyn [64] for analyzing ground surface displacements caused by mining activities. Later, Chinese scholars such as Liu and Zhang [65], Yang and Liu [66] introduced and successfully applied this method to the field of tunneling. As a result, it has provided an effective alternative to purely empirical formulas for predicting ground settlement induced by tunnel excavation.

(1)

Basic theories and core ideas

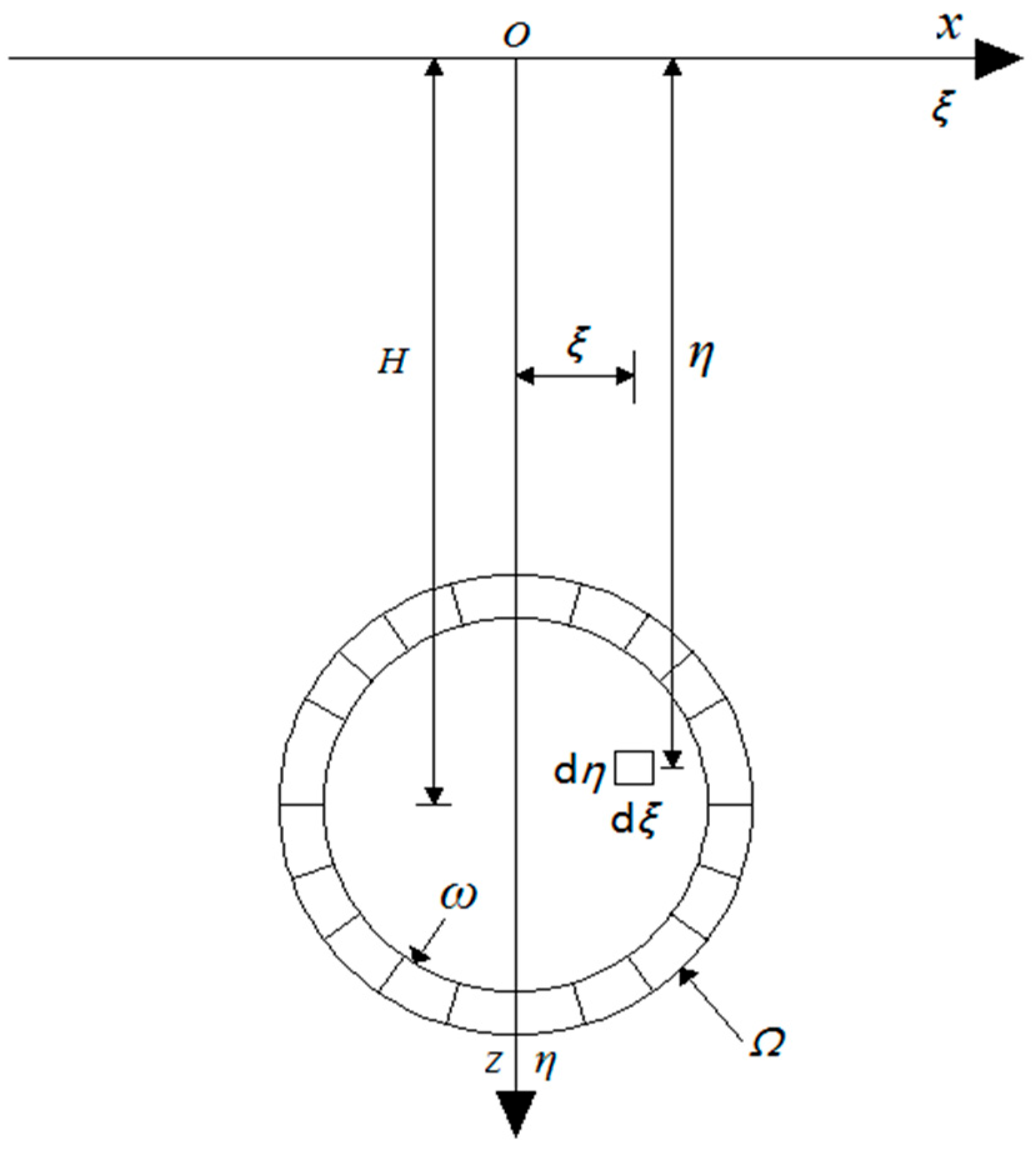
The core concept of this method is to idealize the geomaterial as a “stochastic medium”, wherein tunnel excavation is treated as a stochastic process. The total ground settlement is interpreted as the linear superposition of settlement fields induced by the excavation of numerous infinitesimal elements. As illustrated in Figure 6, the excavation of a single elemental volume generates a minor settlement trough at the ground surface.

In the Figure 6, H is the buried depth of the tunnel axis, dη and dξ are the excavation dimensions of the microelement, ξ is the horizontal coordinate of the microelement, Ω is the tunnel excavation area, and ω is the area of the tunnel after collapse and deformation.

The ground surface settlement at x caused by unit excavation is shown in Equation (5).

$$W_{\mathrm{e}}(x)={\displaystyle \frac{1}{r\left(z\right)}}\exp \left[-{\displaystyle \frac{\pi }{r^2\left(z\right)}}{x}^2\right]\mathrm{d}\xi \mathrm{d}\eta$$

(5)

In which r(z) stands for radius of influence zone.

The relationship between the influence range and the influence angle of the settlement curve obtained based on the experience summarized by Knothe [67] is shown in Equation (6).

$$r(z)=z/\tan \beta$$

(6)

In which z stands for tunnel axis burial depth, and β stands for angle of influence zone of ground settlement.

By integrating Equation (5) and applying the principle of superposition, the ground surface settlement induced by tunnel excavation based on the stochastic medium method can be expressed as shown in Equation (7) [68].

$$W(x)={\displaystyle \underset{\mathsf{\Omega }-\omega }{\iint }\frac{\tan \beta }{\eta }} \exp \left[-{\displaystyle \frac{{\pi }^2{\tan }^2\beta }{{\eta }^2}}\left(x-\xi \right)\right]\mathrm{d}\xi \mathrm{d}\eta$$

(7)

This equation establishes the theoretical foundation of the stochastic medium method. Its greatest advantage lies in its ability to theoretically accommodate excavation cross-sections of arbitrary shapes, rather than being restricted to specific geometries.

(2)

Adaptive expansion and deepening of theory

To enhance the applicability of the stochastic medium method in tunnel engineering, researchers have extended and refined the theory in several key areas, including: (1) simplification and application for typical cross-sections, (2) consideration of non-uniform convergence patterns, and (3) integration with geomechanical theories.

In the first aspect, Qiao et al. [69], Yang and Wang [70], derived simplified analytical expressions for circular tunnel sections under both uniform and non-uniform convergence conditions, significantly improving computational efficiency. Based on this, the method has been successfully extended to more complex configurations such as twin parallel tunnels [71] and dual circular shield tunnels [72].

Secondly, acknowledging the non-uniform nature of deformation in practical tunneling, Wu [73] developed predictive formulas tailored for non-uniform convergence scenarios, thereby enabling more accurate representation of the interaction between surrounding rock and tunnel support systems.

Thirdly, to address the limitation of the stochastic medium method as a purely kinematic approach—namely, its lack of direct consideration for stress-strain behavior. Zhang [74] explored its integration with elasto-plastic theory. They proposed a hybrid prediction model capable of incorporating the elasto-plastic deformation characteristics of stratum, marking a meaningful step toward enhancing the method’s practical applicability.

(3)

Theoretical improvements for complex construction conditions

To address the complexity of real construction environments, extensive research has been conducted to incorporate various key influencing factors into the theoretical framework of the stochastic medium method. These advancements include:

(1) Coupling of spatiotemporal effects: Significant contributions have been made by Shi’s research team [75,76,77,78], who systematically incorporated dynamic factors encountered during tunneling—such as variations in excavation speed, construction delays, staged excavation, and counter-excavation—as well as environmental influences like groundwater drawdown and stratigraphic changes. These elements were integrated into the stochastic medium model through rigorous theoretical derivation, substantially enhancing its predictive capability in real-world applications.

(2) Adaptation to special construction methods and environments: Shi et al. [79] improved the stochastic medium formulation to account for staged excavation in large-section tunnels, yielding results that closely matched field measurements. Cai et al. [80,81] innovatively applied the method to frozen ground tunneling, developing a theoretical model for predicting ground deformation caused by frost heave. Wang et al. [82] derived corresponding predictive formulas for support structure deformation in weak strata, addressing specific challenges related to ground-structure interaction in such environments. Zhang et al. [83] and Hong et al. [84] considered the tunnel construction process using the freezing method and established computational models based on stochastic medium theory. Their work enabled the calculation and prediction of ground surface deformation, addressing soil deformation induced by temperature changes while also extending the application scenarios of the computational theory.

(4)

Inversion and determination of key parameters

The predictive accuracy of the stochastic medium method is also highly dependent on the precise determination of key parameters, primarily the tangent of the angle β (tan β) and the convergence coefficient. Since these parameters are difficult to obtain directly through laboratory testing, inverse analysis based on field monitoring data has become the principal approach. Several researchers have conducted targeted investigations in this area.

For example, in response to the complexity of multi-parameter inversion under conditions such as twin-tunnel construction, Zhu et al. [85] introduced a hybrid simplex-accelerated genetic algorithm, effectively overcoming the limitations of traditional search algorithms. This optimization of the inversion process significantly improved both its efficiency and reliability.

In addition, numerous scholars have explored parameter correction strategies. Wei and Zhou [86] studied closely spaced twin shield tunnels, considering the influence of the first (preceding) tunnel on the second (following) tunnel. By modifying the model to reflect the asymmetry of the ground surface settlement trough, he conducted an in-depth analysis of the relevant parameter adjustments. Similarly, Hu et al. [87] and Yang et al. [88] performed inversion analysis using extensive monitoring data from metro projects in Wuhan, Beijing, and Barcelona, proposing recommended parameter values under specific geological conditions, thereby offering valuable references for similar projects.

(5)

Summary

The stochastic medium method, grounded in rigorous theoretical derivation, is capable of accommodating various tunnel cross-sectional shapes and construction techniques, and can also compute internal ground displacements. These features give it a distinct theoretical advantage and a broader range of applicability compared to purely empirical methods such as the Peck formula.

However, the method also presents inherent limitations. First, its general formulation involves complex integral operations. For circular and other regular cross-sections, engineers can obtain analytical results through rapid integral calculations. However, for irregular cross-sections such as horseshoe-shaped or quasi-rectangular sections, performing manual integral calculations presents certain difficulties. Which may hinder direct application by engineering practitioners-this is one of the primary reasons for its limited adoption relative to the Peck formula. Second, although the theoretical framework is robust, it is essentially a kinematic model that does not directly capture the stress-strain behavior of stratum. As a result, the determination of key parameters still heavily relies on empirical data and inverse analysis from field measurements.

Above all, future research should focus on two main directions:

(1) Simplification for non-circular tunnel sections: Continued efforts are needed to develop simplified calculation formulas for commonly encountered non-circular tunnel sections, such as horseshoe-shaped and quasi-rectangular profiles often used in NATM tunnels. The goal is to create user-friendly calculation charts or software tools to reduce the application threshold and promote wider use in engineering practice.

(2) Integration with geomechanical theory: A deeper investigation into the intrinsic relationship between stochastic medium theory and geomechanics is essential. The objective is to establish semi-theoretical, semi-empirical approaches that enable the direct estimation of model parameters from physical and mechanical properties of stratum, thereby reducing dependence on inverse analysis. This would significantly improve both the generality and reliability of settlement predictions across different geological and engineering conditions.

4.3. Analytical Method

The analytical method, through rigorous mathematical derivation and computation, establishes precise mathematical models to calculate ground deformation induced by tunnel excavation. Compared with empirical methods and the stochastic medium method, the analytical approach offers several notable advantages, including clear mathematical formulation, strong logical consistency, and independence from regional empirical data. It is particularly well-suited for parameter sensitivity analysis, enabling a deeper understanding of the underlying mechanisms by which various factors influence ground deformation.

(1)

Analytical theory based on elasticity theory

Elastic theory forms the foundation of analytical research on tunnel-induced ground deformation. Early studies were mostly conducted under the assumption of an elastic semi-infinite space and gradually developed into two main technical approaches: one based on kinematics, centered on the concept of “equivalent ground loss” for solution; the other based on load effects, solving through stress superposition.

Regarding the approach based on the “equivalent ground loss” concept, Sagaseta [89] pioneered the “method of images”, which simulates the ground surface boundary condition by placing a dilatation source in a virtual upper half-space, thereby ingeniously solving the strain field caused by ground loss in a homogeneous elastic medium. Verruijt and Booker [90] further refined this method by incorporating the soil’s Poisson ratio and the tunnel’s elliptical deformation pattern, enhancing the prediction accuracy. The vertical displacement solution they derived can be expressed as Equation (8).

$$U_{\mathrm{z}}={\displaystyle \frac{2\epsilon R^2}{m}}\left({\displaystyle \frac{\left(m+1\right)z_2}{r_2^2}}-{\displaystyle \frac{mz\left(x^2-z_2^2\right)}{r_2^4}}\right)-2\delta R^{2}h\left({\displaystyle \frac{x^2-z_2^2}{r_2^4}}+{\displaystyle \frac{m}{m+1}}{\displaystyle \frac{2z{z}_2\left(3x^2-z_2^2\right)}{r_2^6}}\right)$$

(8)

In the above equation, ε represents the uniform radial ground loss, δ denotes the tunnel lining deformation, R is the tunnel radius, h is the depth from ground surface to the tunnel axis. The r₂ is the distance from the vertical displacement position to the excavation projection position. The v is the Poisson ratio of the soil and m is a parameter related to Poisson’s ratio ν (m = 1/(1 − 2ν)). The variables z₂ is the vertical distance between the tunnel axis and the vertical displacement position of the soil (z₂ = z + h), z represents the vertical displacement position coordinates of the soil.

This class of methods laid the foundation for subsequent studies. For instance, Park [91] systematically investigated the influence of different tunnel convergence patterns (uniform radial and elliptical deformation) on ground surface settlement based on elastic solutions.

Another important analytical approach grounded in elasticity is the use of Mindlin’s solution [92]. Mindlin’s solution provides the stress and displacement fields within an elastic half-space resulting from a point load applied at any interior location. Building upon this, Wei et al. [93,94] ingeniously applied distributed load integrations along the tunnel excavation face and perimeter using Mindlin’s solution, decomposing complex construction loads such as excavation face pressure, shield friction, and synchronous grouting pressure. Through linear superposition, he derived analytical solutions for ground surface settlement induced by circular and quasi-rectangular shield tunnels under combined loading conditions. This approach successfully extended fundamental elastic theory to simulate complex tunneling processes.

(2)

Development of elastic-plastic and multi-physics coupling analysis

To more accurately reflect the mechanical behavior of stratum, researchers have made significant efforts to incorporate more complex constitutive relationships and physical processes into analytical models. The first and foremost step in this progression has been the introduction of irrecoverable plastic deformation in soils and rocks. For example, Hisatake [95] conducted in-depth studies on elastoplastic and visco-elastoplastic nonlinear theories for circular tunnel excavations, providing corresponding analytical solutions. This marked a critical advancement toward realistically simulating permanent deformations in stratum.

Building upon this foundation, scholars have further recognized the importance of the dynamic evolution of geotechnical parameters during the construction process. For instance, Nordas et al. [96] focused on the unloading effects induced by tunnel excavation and established a quantitative relationship model between deformation modulus, cohesion, and the degree of unloading. This allowed for a more refined simulation of the progressive behavior of rock, from elastic deformation through yielding and eventual failure.

In addition to the enhanced modeling of the soil skeleton’s constitutive behavior, another major advancement has been the incorporation of fluid-solid coupling effects into the analytical framework. This is particularly crucial in saturated or water-rich strata, where variations in pore water pressure play a dominant role. In this regard, Bobet [97] investigated the instantaneous settlement in saturated soils caused by tunnel excavation, while Liu et al. [98] developed analytical solutions under undrained conditions that account for negative pore water pressure and partial soil desaturation due to tunnel advance. These studies offer new theoretical perspectives for settlement prediction in water-bearing ground conditions.

(3)

The transition from theoretical analysis to engineering practice

The value of analytical methods lies not only in theoretical exploration but also in their ability to address practical engineering challenges and ultimately validate their reliability through comparison with real-world observations. In terms of application, researchers have successfully applied analytical theories to complex engineering scenarios. For instance, Zhang et al. [99] based on elastic thin plate and beam theory, developed an analytical method to evaluate the deformation response of pipe-roof support systems used in the construction of ultra-shallow underground stations. The model’s accuracy was validated against field measurements, demonstrating the potential of analytical methods in handling complex structural interaction problems.

Naturally, the vitality of any theory ultimately depends on its predictive capabilities and its relevance in practical engineering. In this regard, scholars have conducted systematic validation and evaluation efforts. Chou and Bobet [100] performed analysis using a specific analytical solution on 28 engineering case studies, revealing that the discrepancies between predicted and observed values were generally within 15%, thereby providing strong evidence for the model’s applicability under specific conditions. Going a step further, to clarify the role of analytical methods within the broader framework of predictive approaches, Migliazza et al. [101] conducted a comprehensive comparative study of empirical methods, analytical models, and numerical simulations. This evaluation systematically assessed the predictive capabilities and applicability of each technique, offering valuable guidance for engineers in selecting the most suitable approach based on project-specific requirements.

(4)

Summary

Analytical methods, with their theoretical rigor and logical clarity, offer irreplaceable advantages in elucidating the mechanisms of tunnel-induced ground deformation and conducting parametric studies. They provide a valuable theoretical foundation for understanding complex stratum-structure interaction problems.

However, the precision of analytical methods often comes at the cost of idealization. To obtain mathematically closed-form solutions, most analytical models must rely on assumptions such as homogeneous stratum conditions, regular geometries, and simplified constitutive relationships. These assumptions limit their applicability when confronted with the complexities of real-world engineering scenarios, such as geological heterogeneity, construction-induced time-dependent effects, and the pronounced nonlinearity of geomaterial behavior.

Therefore, future development of analytical methods should focus on two key directions: first, moving beyond idealized assumptions by developing semi-analytical or novel analytical models capable of incorporating complex conditions such as stratified soils, nonlinear constitutive behavior, and hydro-mechanical coupling; second, strengthening the integration with engineering practice by transforming sophisticated theoretical results into engineer-friendly tools. At present, extensive research has been conducted on various calculation methods, and by integrating computer programming techniques, corresponding programs can be developed to achieve automation of the calculation process, such as calculation charts or simplified algorithms. Moreover, tailored analytical models should be developed for specific engineering problems-such as tunnel crossings or the influence on existing lines-to fully leverage the theoretical strengths of analytical approaches and enhance their practical value.

4.4. Comparative Review and Selection Principles of Different Calculation Methods

Based on the preceding discussions of the Peck empirical method, the stochastic medium method, and analytical methods, it is evident that these three approaches are founded on distinct theoretical principles and exhibit unique advantages, characteristics, and applicable scopes. In both engineering practice and theoretical research, the selection of an appropriate prediction method is of critical importance. This section provides a comparative evaluation of these three categories of methods and, on this basis, proposes guiding principles for their selection.

(1)

Comparison of methods

In terms of theoretical foundations, the three methods represent a progressive hierarchy from “empirical” to “kinematic” and ultimately to “mechanistic” approaches. The Peck empirical method is a purely empirical model; it does not delve into the intrinsic mechanisms of ground deformation but rather summarizes patterns observed from extensive engineering data, with its foundation rooted in engineering statistics. When applying this method, it is necessary to obtain the prediction results through manual calculations based on regional experience and statistical data from similar projects. The stochastic medium method is a semi-theoretical, semi-empirical kinematic model that idealizes the geomaterial as a probabilistic medium and describes the displacement field through geometric superposition. Compared to the empirical method, it offers stronger theoretical grounding and broader applicability, yet still does not directly address the stress-strain relationship. When applying this method, it is necessary to perform integral calculations based on the actual deformation of the tunnel to obtain the prediction results, and for irregular cross-sections, computer assistance may be required to complete the complex integral computations. In contrast, analytical methods are strictly mechanistic models based on elastic and elastoplastic theories. They establish causal relationships between loading, boundary conditions, and deformation through rigorous mathematical derivation, making them the most theoretically sound among the three. When applying this method, the prediction results can be obtained either through manual calculations or with the aid of computer programs, depending on the tunnel deformation conditions. The three methods differ in their computational requirements: the Peck empirical formula method has the lowest demand for computational capability, while the stochastic medium method and the analytical method require relatively higher computational capacity.

In terms of ease of application and parameter acquisition, the three methods differ significantly in complexity. The Peck empirical method is undoubtedly the most convenient: it features a simple formulation with only a few parameters (such as S_max, i), making it highly suitable for rapid estimations. However, its parameters are heavily dependent on regional experience and statistical data from similar projects. The stochastic medium method offers moderate convenience. While its theoretical model is relatively universal, the general formulation involves complex integral operations, and its key parameters (e.g., the convergence coefficient) also require back-analysis based on field measurements, making the process comparatively more intricate. Analytical methods have the highest “entry threshold.” Their mathematical derivations are sophisticated, and to obtain closed-form solutions, numerous idealized assumptions-such as homogeneous strata and regular geometry-are often required. This makes their direct application to complex engineering scenarios the most challenging. Although their parameters (e.g., elastic modulus E and Poisson ratio ν) have clear physical interpretations, accurately determining these values in heterogeneous geomaterials remains a major challenge in practice.

In terms of applicability and limitations, the three methods each have distinct focuses and are mutually complementary. The core advantage of the Peck empirical method lies in its ability to provide fast and reliable predictions of ground surface settlement troughs in regions with extensive existing monitoring data. Its limitations include the inability to estimate ground settlement accurately and reduced applicability in new areas, under novel construction techniques, or in complex geological conditions. The stochastic medium method excels in its capacity to handle arbitrary excavation cross-sectional shapes and to predict ground displacements, thus addressing the shortcomings of the Peck method. However, it is constrained by the complexity of integral calculations and a continued reliance on empirically derived parameters. The analytical method offers unique value in uncovering deformation mechanisms and conducting parameter sensitivity analyses. For example, it can explicitly reveal how a given parameter (e.g., Poisson ratio) theoretically influences settlement. Its limitation lies in the discrepancy between idealized assumptions and the inherent complexity of real-world engineering conditions, which sometimes results in its absolute predictive accuracy being inferior to that of empirical or semi-empirical methods that have been calibrated under specific conditions.

(2)

Principles for selecting methods

Based on the above comparison, the selection of the most appropriate method in engineering practice and academic research should follow certain principles, considering the project stage, objectives, and available resources:

During the preliminary design phase, when rapid estimation of ground surface settlement is needed to assess potential impacts on surrounding infrastructure, and sufficient local experience and monitoring data from similar projects are available, the Peck empirical method is the preferred tool due to its efficiency, simplicity, and reliable results.

When the tunnel has an irregular cross-sectional shape (e.g., horseshoe or quasi-rectangular), or when displacement predictions are required at specific subsurface locations-such as adjacent utility lines or pile foundations-the Peck method becomes inadequate. In such cases, the stochastic medium method should be adopted. It can provide more comprehensive spatial displacement information, serving as a foundation for refined design and construction control.

When the focus is on exploring the deformation mechanisms of specific factors (e.g., grouting pressure, support stiffness), performing parameter sensitivity analyses, or establishing a theoretical benchmark for complex numerical models, the analytical method offers irreplaceable advantages. Its rigorous logical framework allows for deeper insight into the underlying mechanical behavior.

In modern engineering practice, a combined application of multiple methods is increasingly advocated. For example, the Peck method can be used for initial estimation, followed by the stochastic medium method or simplified analytical approaches for more detailed analysis. These results can then serve as references or validation for numerical simulations (e.g., finite element models), forming a multi-level and multi-perspective integrated prediction framework—from empirical estimation, to theoretical analysis, to refined simulation—thereby maximizing the reliability of deformation predictions.

5. Research on Calculation Method of Deformation of Existing Structures

In multi-line crossing or closely spaced tunneling projects, the control and prediction of deformations in existing structures is a core issue equally as crucial as ground surface settlement. At present, a well-established analytical framework—known as the “two-stage method”-has been developed, particularly at the analytical and semi-analytical levels, to address such challenges.

The fundamental concept of this method is as follows: first, the influence of the existing structure is temporarily neglected, and the “free-field” ground displacement at the location of the existing structure induced by the construction of the new tunnel is calculated (i.e., the additional loading effect). Then, this displacement field or its equivalent load is applied to the existing structure to determine its final deformation and internal force response.

5.1. Core Application of the “Two-Stage Method”: Interaction Between Tunnels and Underground Pipelines

The two-stage method is the most widely applied and well-developed approach for predicting the impact of newly constructed tunnels on existing tunnels and underground utilities. Its analytical framework primarily consists of three core components: the mechanical idealization of the existing structure, the ground-structure interaction model, and the calculation of free-field ground displacements.

(1)

Mechanical simplification of the structure

In the analysis of longitudinal deformation, existing tunnels or pipelines are typically idealized as one-dimensional beams. Early studies predominantly employed the classical Euler-Bernoulli beam model, which assumes that cross-sections remain plane and perpendicular to the neutral axis during deformation [102,103,104,105,106,107]. To more accurately account for shear deformation—particularly relevant for short and stocky beams such as shield tunnel segments—subsequent research introduced the use of the Timoshenko beam model [106,107].

(2)

Foundation Model for Soil–Structure Interaction

To investigate the relationship between “free-field displacement” and “structural response”, researchers have adopted foundation models of varying complexity. Among them, the most classical is the Winkler foundation model, which simplifies the foundation as a series of independent elastic springs and offers straightforward computation [108,109,110,111]. To further account for shear transfer between soil elements, the Pasternak foundation model introduces a shear layer atop the spring bed, enabling a more realistic simulation [112,113]. In addition, the Kerr foundation model, a more refined three-parameter model, offers enhanced capability to distinguish between the compressive behavior of the upper soil layer and the tensile response of the lower layer [106,107,114].

(3)

Calculation of free-field displacement

Free-field displacement serves as the input condition in the two-stage method. Researchers commonly adopt the calculation approaches discussed in previous sections, such as the Peck empirical formula [108] or analytical methods based on Mindlin’s elastic solution [111,115], to obtain the soil displacement field induced by the construction of a new tunnel.

Systematic studies by scholars such as Zhang et al. [102,103,104,105] and Zhang et al. [106,107] have combined various beam models with foundation models to establish analytical methods for computing the longitudinal deformation of existing tunnels and pipelines under different construction scenarios (e.g., undercrossing and overcrossing). The accuracy of these methods has been validated through comparisons with field measurements, numerical simulations, and model test results.

To intuitively demonstrate the model selection and characteristics of each core element in this analysis method, a summary is shown in

Table 3. Model selection and characteristics of each core element in the analysis method.

Core Elements	Model Category	Main Features	Representative Literature
Structural simplified model	Euler-Bernoulli beam model	Classical theory, ignoring shear deformation, is applicable to structures with large span ratios	Zhang et al. [102,103,104,105]
	Timoshenko Beam model	Considering shear deformation, it is suitable for short and thick structures (such as shield segments)	Zhang et al. [106,107]
Soil–Structure Interaction (Foundation Model)	Winkler foundation model	Independent spring, the easiest to calculate, ignoring soil continuity	Klar et al. [108], Wei et al. [109]
	Pasternak foundation model	Spring + shear layer, considering shear transfer, a more realistic simulation	[112,113]
	Kerr foundation model	The three-parameter model can distinguish the effects of upper and lower soil layers, making it more precise.	Zhang et al. [106,107]
Free-field displacement calculation (load input)	Empirical formula	Based on Peck formula, simple and fast, relying on regional experience	Klar et al. [108]
	Analytical Theory	Based on Mindlin solution, etc., it has strong theoretical basis and can consider various loads.	Liang et al. [109], Zhang et al. [113]

.

5.2. Other Applications of the “Two-Stage Method”: Interaction with Other Buildings (Structures)

Based on the same core idea, the research scope of this part has been expanded to a wider range of soil–structure interaction problems.

(1)

Foundation pit excavation and adjacent tunnels

In increasingly congested urban environments, the impact of excavation-induced ground movements on adjacent tunnels has become a growing concern. Related studies have similarly employed the beam-on-foundation modeling approach, while further incorporating complex factors such as transverse deformation of the tunnel cross-section [116] and the effects of dewatering and recharge [117,118]. Guo et al. [119] and Peng et al. [120] have extended the analysis to investigate the influence and vulnerability of tunnels under partial or complete excavations of adjacent deep excavations, providing valuable insights into the longitudinal deformation behavior of affected tunnels.

(2)

Tunnel through pile foundation

Tunnel crossing beneath pile foundations represents another typical case of strong three-dimensional soil–structure interaction. Due to the high geometric and mechanical complexity involved, purely analytical solutions are highly challenging. As a result, research in this area relies primarily on physical model tests [121] and refined numerical simulations [122] to investigate the soil-pile response during the crossing process, and to evaluate the effects of parameters such as pile length, pile spacing, and groundwater conditions. Meanwhile, some scholars have attempted to develop improved semi-analytical models [116] to provide convenient tools for preliminary engineering assessments.

(3)

Tunnels and ground surface or shallow infrastructure

Moreover, this analytical framework has also been applied to evaluate the impact of tunnel construction on other critical infrastructure, such as adjacent buildings [123] and high-speed railway subgrades and tracks [124]. These applications provide theoretical support for construction risk assessment and control.

5.3. Research on Tunnel Structure Deformation Calculation Based on Refined Modeling

Wei Gang [125] considered the stiffness differences between tunnels and station structures and developed a shield tunnel segment model that accounts for station constraints, rotation, and misalignment. Based on this model, they derived and established a calculation formula for the horizontal displacement of tunnels adjacent to stations, enabling a quantitative analysis of the deformation response differences between structures with varying stiffness during adjacent construction processes.

The study demonstrated that for structures with different stiffness, there are notable differences in the interaction between the structure and surrounding soil as well as in their deformation responses during adjacent construction. Therefore, when applying the two-stage method for analysis, it is essential to consider the stiffness differences between existing structures and new construction projects when simplifying the soil into a free-field in the first stage, so as to avoid computational bias.

5.4. Summary

In summary, the two-stage method, combined with various beam-foundation models, has become the mainstream analytical and semi-analytical approach for evaluating the longitudinal deformation of existing structures induced by new tunnel construction. This framework provides a valuable theoretical tool for understanding such soil–structure interaction problems. However, the convenience of this prevailing approach is fundamentally based on the key assumption of decoupling ground deformation from structural response—namely, the “free-field” assumption. While this assumption is both reasonable and efficient when the existing structure has relatively low stiffness or is small compared to the newly constructed tunnel, it becomes less valid when the existing structure is a high-stiffness system, such as a large-diameter tunnel or a massive pile cap. In such cases, the presence of the existing structure significantly alters the local stress paths and deformation patterns around the excavation, causing the actual ground displacement field to deviate from the assumed free-field condition. This may result in reduced prediction accuracy. In contrast, the theoretically more rigorous “fully coupled” approach does not rely on this assumption. Although its implementation currently depends primarily on refined numerical simulations, a clear theoretical understanding of the differences and applicable boundaries between these two methods is essential for deep insights into soil–structure interaction problems.

Against this backdrop, the future directions for research in this field are becoming increasingly apparent. Most existing analytical models have been developed for relatively simplified scenarios, primarily single new tunnels crossing existing lines at perpendicular or near-perpendicular angles. However, more complex spatial crossing conditions, such as multi-line tunnel construction, oblique intersections at small angles, and parallel tunneling, introduce pronounced load superposition effects and three-dimensional spatial interactions that pose significant challenges to current analytical methods. Furthermore, how the presence of existing structures in turn influences the final ground surface settlement profile(the coupled relationship between structural deformation and ground settlement), remains insufficiently explored from a theoretical perspective. Therefore, developing analytical or semi-analytical frameworks that can rigorously account for complex spatial configurations, construction sequencing in multi-line tunneling, and the fully coupled interaction between new tunnels, surrounding ground, and existing structures represents a highly valuable and promising direction for future research in this domain.

6. Research on Stratum Control and Reinforcement Measures

In the construction of metro tunnels, particularly those employing the NATM, risk control is a decisive factor for project success. Effective ground control and reinforcement not only serve as critical safeguards for construction safety but also play a vital role in protecting the surrounding environment and existing structures. At present, related research and engineering practice mainly follow two technical pathways: (1) the implementation of proactive engineering interventions, such as optimized construction methods and ground improvement techniques; and (2) the application of advanced monitoring technologies and digital platforms to enable dynamic feedback and intelligent early-warning systems.

6.1. Active Intervention: Construction Method Optimization and Ground Reinforcement

Proactive engineering interventions aim to control ground deformation at its source by directly improving the geotechnical properties or optimizing construction-induced disturbances. At the level of construction method and scheme optimization, researchers have focused on comparative analyses and innovations to identify tunneling approaches that minimize environmental impact. For instance, Zhao [126] conducted a comparative study on three tunnel excavation methods and ground pre-reinforcement techniques in the Chongqing area, quantitatively evaluating their effectiveness in controlling ground deformation. In addressing specific challenges related to tunnel crossings, Wu [127] and Shen et al. [128] analyzed various construction schemes. They respectively proposed optimized excavation sequences and safe construction methods for closely spaced and overlapping tunnels.

Secondly, in the domain of ground reinforcement and support technologies, researchers have developed a variety of direct and effective control measures. The main research focuses can be categorized into the refined application of existing technologies, the exploration of novel support systems, and the formulation of integrated solutions for specific engineering challenges.

In terms of refined application of classical grouting techniques, the trend has shifted from basic filling reinforcement to more differentiated and precise approaches. For example, Pan [129] investigated the application of unequal-strength grouting in undercrossing projects to achieve more cost-effective deformation control. Ren et al. [130], focusing on construction near bridge piles, analyzed the application of sleeve-valve-pipe grouting to attain more precise reinforcement zones. Meanwhile, for high-risk sections, the development of innovative support systems is ongoing. For instance, Huo et al. [131] successfully validated the effectiveness of the NPR support method through model testing, demonstrating its superior reinforcement performance when tunnels pass through fault-fractured zones, thus offering a new perspective for construction safety in extremely adverse geological conditions.

More notably, a growing body of research has focused on integrating multiple techniques to develop comprehensive solutions tailored to specific engineering challenges. For example, Chen et al. [132] proposed a systematic approach combining block excavation and ground improvement to address large-scale excavations in soft soil areas. Pu et al. [133] and Guo et al. [134] respectively tackled the typical problems of pile and pipeline protection, validating the effectiveness of the New Sidewall Method and innovatively introducing a pipeline suspension protection method based on excavation support systems. These studies exemplify the modern tunnel engineering philosophy of multi-technique synergistic control.

6.2. Dynamic Feedback Control: Monitoring, Measurement and Intelligent Early Warning

Suppose active intervention represents a “targeted strategy” for risk control. In that case, dynamic feedback mechanisms serve as the foundation for “real-time perception” and “precise response”, ensuring that the deformations generated during the construction process remains continuously observable and controllable.

Recent research in this domain has shifted from traditional monitoring point layout and data acquisition toward digitalization, networking, and intelligentization. On one hand, scholars have focused on developing integrated safety risk assessment and monitoring-early warning systems that incorporate computer networks, databases, and evaluation models [135,136,137,138,139], enabling comprehensive analysis of massive monitoring datasets and early risk prediction. On the other hand, in terms of sensing and transmission technologies, Zhang [140] combined ZigBee wireless sensor networks with GPRS transmission to develop an automated monitoring system for metro tunnel construction, significantly enhancing the real-time performance and reliability of data acquisition.

In the integrated application of machine learning to tunnel structure deformation prediction, tree-based models, neural networks, and support vector machines (SVM) are primarily used to develop predictive models. These models leverage existing data to capture the nonlinear relationships between various parameters and deformation, thereby enabling accurate deformation prediction.

In terms of tree-based model applications, Kim et al. [141] addressed the issue of pile foundation deformation response induced by tunnel construction by developing a prediction model using the random forest method. Their study identified the key factors influencing pile settlement during the construction process and further analyzed the relationship between the number of piles and ground settlement, providing an effective method for predicting deformation during tunnel construction. For the random forest method, the quality and quantity of the dataset are particularly critical. To address this issue, Bahri et al. [142] combined the random forest approach with numerical simulation techniques to enhance both the volume and quality of the training dataset. Using the improved dataset, they trained a predictive model and conducted feature importance analysis, revealing that soil properties are the most significant factors influencing deformation. Furthermore, they validated and further assessed the accuracy and reliability of the model through engineering case studies.

In terms of neural network applications, artificial neural networks (ANN), as a vital component of machine learning, play a particularly important role in predicting settlement and deformation induced by tunnel construction due to their strong self-learning capabilities. However, during the training process, neural networks typically require large amounts of high-quality and precise data. When the dataset is relatively small, the model may exhibit low robustness. To address this issue, Zhang et al. [143] integrated physical information into the development of a novel neural network model that is suitable for small-sample data training. By comparing the proposed model with conventional neural networks, they demonstrated its superior performance and applicability in deformation prediction tasks.

In terms of support vector machine (SVM) applications, Huang et al. [144] integrated the strengths of both the SVM and BP models to develop a hybrid SVM-BP model for predicting tunnel deformation caused by surrounding rock extrusion. By comparing it with individual SVM and BP models, they validated the superiority and reliability of the hybrid model, contributing to the evolution of machine learning from single models to integrated modeling approaches.

Furthermore, Zheng et al. [145] combined SVM models, ANN models, and numerical simulation methods to achieve more accurate tunnel deformation prediction. Building upon this, Lai et al. [146] further integrated field test methods, enabling a comprehensive comparison and analysis of the prediction performance of different machine learning models(ANN, SVM, and random forest, etc.) for tunnel and soil deformation. These studies have advanced the integrated application of machine learning in tunnel deformation prediction and significantly improved prediction accuracy.

For AI technology practical engineering application, Zhang et al. [147] developed a real-time monitoring system for tunnel construction based on artificial intelligence and Internet of Things (AIoT) technologies. This system integrates machine learning prediction models to forecast shield machine parameters and construction-induced settlement, thereby supporting shield machine control and construction decision-making in actual engineering projects and enhancing the intelligence level of the construction process. Furthermore, Paul et al. [148] reviewed the current applications of AI technologies in tunnel construction and control, analyzing key aspects such as data quality, model computational efficiency, and integration with practical engineering. Their work provides valuable insights and guidance for the future deep integration of AI technologies in the field of tunnel construction.

The development of these technologies enables automatic risk identification, analysis, and prediction during the construction process, thereby reducing the manpower required for construction monitoring and data analysis. Meanwhile, the integration of high-precision sensors and models trained on big data significantly improves the efficiency and accuracy of deformation prediction, providing stronger support for deformation control decision-making and enhancing both the intelligence and safety levels of the construction process. This trend toward informatization aims to transform “post-event analysis” into “real-time warning” and “proactive prediction”, providing construction decision-making with sharper “eyes” and a more intelligent “brain”.

6.3. Summary

In summary, significant progress has been made in the study of ground control and reinforcement measures across multiple dimensions, including construction method optimization, ground improvement, and dynamic monitoring. These efforts have led to the development of an integrated technical system that combines active intervention with dynamic feedback.

However, as tunnel crossing construction environments grow increasingly complex, current research still requires further advancement. On the active intervention front, the extremely confined construction space in crossover zones often renders conventional reinforcement measures difficult to implement. This highlights the urgent need for the development of more precise, minimally invasive, and efficient reinforcement technologies and materials. On the dynamic feedback front, the vast amounts of monitoring data contain rich information on deformation patterns and underlying mechanisms. Leveraging artificial intelligence and big data techniques to deeply learn from and mine these multi-source heterogeneous datasets, thereby enabling a transition from “data monitoring” to “knowledge discovery” and ultimately to “intelligent decision-making” is key to enhancing the intelligence level of monitoring systems.

Therefore, the ultimate development direction in this field is to establish an intelligent construction closed-loop system that deeply integrates active intervention and dynamic feedback. Within this system, real-time perception of construction status is achieved through intelligent monitoring; accurate prediction and risk assessment are conducted using big data and AI algorithms—for example, employing artificial neural networks (ANN) to predict settlement trends, or applying support vector machines (SVM) to classify risk levels. Based on the predictive results, dynamic decision-making and optimization of construction strategies are carried out, which are ultimately implemented through automated equipment to execute precise ground reinforcement and support adjustments.

This will form a complete closed loop of perception-analysis-decision-execution, thereby laying the foundation for truly intelligent construction in complex tunneling projects. The schematic diagram of the perception-analysis-decision-execution cycle is shown in Figure 7.

7. Internal Correlation and Comprehensive Analysis of Various Research Directions

Building upon the previous discussions on four core research areas—namely, the deformation mechanisms in tunnel excavation-affected zones, predictive calculation methods, the response of existing structures, and ground control measures—this paper has provided a comprehensive overview of the current state of research in this field. However, these research areas are not isolated domains; instead, they constitute an integrated, logically cohesive system characterized by mutual reinforcement and coordinated development. This section aims to synthesize the intrinsic interconnections among these directions to reveal the holistic structure of the research landscape and identify emerging trends in the field of tunneling engineering.

7.1. The Logic and Relationship of Research Directions

Throughout the entire research framework, a clear logical progression can be observed—from mechanism understanding to quantitative prediction, and ultimately to engineering control—with various research methods playing indispensable and complementary roles along this continuum.

First and foremost, mechanism understanding serves as the logical foundation and physical basis for all subsequent research. Deformation mechanism and behavior studies—primarily based on numerical simulations and physical model tests, as discussed in Section 3—offer critical value by “reproducing processes and uncovering physical insights”. Through the simulation of complex construction conditions and ground responses, these studies reveal underlying physical phenomena such as the “soil arching effect”, “load transfer” and “hydro-mechanical coupling” which are otherwise invisible to direct observation. Importantly, beyond providing qualitative insights for engineering practice, such research also supplies validated physical models, essential input parameters, and reliable benchmarks that underpin and support other areas of study.

Secondly, predictive computation serves as the critical bridge that transforms qualitative understanding of mechanisms into quantitative indicators. Building upon insights into underlying physical behavior, deformation prediction studies—represented by the Peck empirical method, stochastic medium theory, and analytical approaches (Section 4 and Section 5)—seek to establish mathematical models aimed at “quantifying outcomes and forecasting future behavior”. This stage reflects varying levels of engineering demand, primarily encompassing:

(1) Direct correlation: The “two-stage method” for predicting deformation of existing structures, discussed in Section 5, relies on the “free-field ground displacement” calculated in the first stage—an output directly derived from the deformation prediction methods presented in Section 4. This demonstrates the most explicit “input-output” relationship between research directions.

(2) Data support: Empirical parameters in the Peck empirical method and influence angles in stochastic medium theory, as covered in Section 4, often require calibration and validation using results from numerical simulations or model tests presented in Section 3.

(3) Theoretical validation: The rigorous derivation of analytical methods (Section 4.3) is frequently used to verify the accuracy of more complex numerical models (Section 3.1) under idealized conditions.

Ultimately, engineering control represents the practical implementation and ultimate goal of the aforementioned understanding and predictions. The study of ground control and reinforcement measures (Section 6), whether through “proactive intervention” or “dynamic feedback”, relies heavily on the support of previous research. On one hand, the design and performance assessment of any reinforcement technique (e.g., grouting, pipe-roofing) depend critically on deformation predictions made using the methods outlined in Section 4 and Section 5. On the other hand, the core of dynamic feedback control—namely, “intelligent monitoring and early warning”—requires reliable forecast models for setting warning thresholds and performing proactive risk prediction. The development of such models, in turn, stems from a deep understanding of deformation mechanisms as discussed in Section 3.

7.2. Comprehensive Review and Outlook

The above analysis reveals a clear developmental trajectory within the field of deformation control in tunnel engineering: a progression from empirical summarization (e.g., the Peck method), through mechanism-based analysis (e.g., numerical simulations and analytical solutions), and ultimately toward system-level control (e.g., intelligent construction systems). Rather than a linear sequence, these research directions form a dynamic cycle of mutual verification, mutual promotion, and data-driven.

Looking ahead, the field is expected to evolve toward a deep integration of all aforementioned research components. This integrated approach is exemplified by the intelligent construction framework based on artificial intelligence technologies proposed after Section 6. Within this ultimate ideal system:

Mechanism-based models (Section 3) serve as the physical engine of the digital platform, the actual stress and deformation behavior of the soil and tunnel structure during construction can be obtained through numerical simulations and physical model tests. That ensuring the realism and reliability of model behavior.

Predictive computation methods (Section 4 and Section 5) function as fast algorithms, enabling real-time “what-if” simulations to rapidly forecast the consequences of various construction decisions under multiple engineering conditions.

The intelligent monitoring system (Section 6) acts as the neural system that links the physical and virtual worlds, continuously feeding real-time data into the model to drive synchronized evolution and self-calibration.

Control and reinforcement measures (Section 6) transition from relying solely on engineer experience to being guided by optimal recommendations derived from large-scale, data-driven simulations within the digital system.

In summary, the integration of discrete mechanism studies, stand-alone predictive models, and isolated control technologies into a unified, intelligent platform—capable of real-time perception, scientific decision-making, precise execution, and dynamic feedback—represents the future research direction of the field. This platform enables seamless integration between the physical and digital worlds, forming a closed-loop control system. Once deployed in construction projects, it can aggregate large amounts of monitoring, inspection, video, and image data generated during the construction process. By embedding machine learning models, the platform can perform risk prediction and analysis during tunnel construction, thereby supporting the precise formulation of preventive measures. Furthermore, learning from extensive multi-source heterogeneous data can enhance the generalization capability of the models, improving risk perception and control throughout the construction process. This is crucial for achieving truly safe, efficient, sustainable, and intelligent tunnel construction.

8. Conclusions and Outlook

Based on a systematic review of literature and an in-depth analytical investigation, this study provides a comprehensive evaluation of the deformation-related challenges induced by tunnel construction in complex urban environments. The review addresses multiple dimensions—including deformation mechanisms and patterns, deformation prediction methods for ground and existing structures, and ground control and reinforcement techniques—offering insights into the current state of research, intrinsic interconnections, and emerging trends. The main conclusions are as follows:

(1) Evolution of Research Paradigms: The field demonstrates a clear developmental trajectory characterized by a shift from “shallow to deep” and “localized to holistic” approaches. In terms of research subjects, studies have progressed from early investigations of single-track or twin-tunnel configurations in two-dimensional or quasi-three-dimensional settings to more complex three-dimensional coupled problems involving overlapped, intersecting, or closely spaced tunnels. Methodologically, the research has evolved from reliance on empirical formulas and simplified models for preliminary predictions to more refined mechanistic insights via advanced numerical simulations and physical model testing, as well as theoretical exploration grounded in rigorous mathematical derivation.

(2) Prediction and Computational Theories: A three-tiered system of computational methods—empirical, kinematic, and mechanistic—has emerged. The classical Peck method, as an empirical model, remains an efficient preliminary evaluation tool in data-rich environments. The stochastic medium method, representing the kinematic level, offers advantages in handling irregular tunnel geometries and internal ground displacements. Analytical methods contribute uniquely to the understanding of underlying mechanical mechanisms. For assessing the response of existing structures, the “two-stage method” combined with various “beam-foundation models” represents the mainstream semi-analytical paradigm. Nevertheless, all prediction methods face common challenges, including dependence on empirically derived parameters and the idealization of complex real-world conditions. The rationality of parameter selection in the Peck empirical method and the stochastic medium method determines the accuracy of prediction results. The calculation parameters need to be further analyzed and validated using actual construction monitoring data to enrich engineering experience across different regions. In analytical methods and existing structural calculation approaches, the relationship between the simplifications made and the accuracy of the results is closely linked. The reasonableness of these simplifications depends on validation through actual construction monitoring, as well as simulation and experimental data.

(3) Ground Control and Reinforcement Technologies: A dual-track approach featuring active engineering intervention and dynamic feedback control has become the dominant development model. The former focuses on disturbance mitigation at the source through construction method optimization, targeted grouting, and innovative support techniques. The latter leverages digitalized and networked monitoring systems, integrated with intelligent early-warning models, to enable real-time “health monitoring” of the construction process. The synergy between these two approaches is driving a paradigm shift in tunnel construction—from passive risk response toward proactive prediction and intelligent decision-making.

(4) Intrinsic Interconnections: The various research directions are not isolated endeavors but rather components of a dynamic feedback loop encompassing mechanism cognition, quantitative prediction, engineering control, and real-time monitoring. Mechanistic studies form the foundational basis for both prediction and control strategies; predictive modeling serves as the critical bridge linking fundamental understanding with practical application, and in turn, engineering practices and monitoring data provide invaluable feedback for the calibration, validation, and refinement of both mechanistic insights and predictive models. This cyclical interplay fosters a continuous and synergistic advancement of the entire research framework.

Despite the considerable progress achieved in recent years, several critical scientific questions and technical questions remain to be addressed in light of the increasingly complex demands of urban underground space development:

(1) Insufficient refined characterization of complex spatial coupling mechanisms. Most existing studies focus on simplified two-dimensional or quasi-three-dimensional scenarios. There remains a lack of systematic theoretical description and fine-scale modeling of key mechanisms such as three-dimensional stress redistribution, load transfer paths, and multi-field (soil-water-load) coupling effects under complex conditions—such as multi-line tunneling, small-angle intersection, and dynamic construction sequencing.

(2) A persistent gap between predictive theories and engineering reality. A major challenge for all predictive methods lies in balancing theoretical rigor with the practical need to account for the inherent heterogeneity, anisotropy, and high uncertainty of geotechnical media and construction processes. In particular, the physical significance of key computational parameters and their intrinsic links to fundamental geomechanical properties still require in-depth investigation to reduce dependence on empirical assumptions and inverse calibration.

(3) Limited integration of precise control and intelligent feedback. Within the confined spaces of intersecting tunnel construction, developing minimally invasive, efficient, and precise ground improvement technologies remains a pressing need. Simultaneously, how to use artificial intelligence and other means to deeply explore the nonlinear correlations between deformation mechanisms and construction parameters from massive amounts of multi-source heterogeneous monitoring data and achieve the transition from “data” to “knowledge” and then to “intelligent decision-making” is the key to the practical application of intelligent early warning and feedback control.

Looking ahead, addressing these challenges requires deepening research in various areas while focusing on cross-cutting and system integration. A promising development direction is to build an integrated intelligent construction and maintenance system centered on digital concepts. This system, based on high-fidelity physical and mechanical models, integrates efficient predictive calculation methods for multi-condition simulation and risk assessment. Through dynamic assimilation with real-time on-site monitoring data, it accurately predicts the “stratum + structure” response, providing scientific decision-making support for the dynamic optimization of active control and reinforcement measures. This system aims to integrate the currently relatively separate mechanisms of understanding, predictive calculations, and control measures into a closed-loop framework driven by virtual-reality mapping. Through this framework, it is expected to achieve advanced prediction, real-time perception, and precise control of deformation risks throughout the life cycle of complex tunnel projects, thereby improving the safety, resilience, and sustainability of the projects.