Research on the Indirect Solution Optimization Regularization Method for Ship Mechanical Excitation Force
Abstract
Featured Application
Abstract
1. Introduction
- (a)
- Quasi-optimal (Q-O) refinement: Conduct grid search within the stable region of the L curve. Optimize the division of regions through Hausdorff distance to ensure stability.
- (b)
- Weighted B-spline Stabilization (BL-curve): Embeds residual confidence-weighted B-spline interpolation, reducing curvature calculation error from ±18.6% to ±4.9% under SNR < 15 dB.
2. Analysis of Limitations in Traditional Regularization Methods
2.1. Truncated Singular Value Decomposition
- (a)
- Signal-Fidelity Paradox:
- (b)
- Transfer Matrix Distortion:
2.2. Tikhonov Regularization Method
- (1)
- GCV
- (a)
- At : ,the degree of freedom of the model is close to the number of parameters;
- (b)
- At : , the model degenerates to constants.
- (2)
- L-curve
3. Study of Regularization Methods Based on Optimal Regularization Parameter Solving
3.1. The Quasi-Optimal Discriminant Criterion
3.2. B-Spline Interpolation Function Method
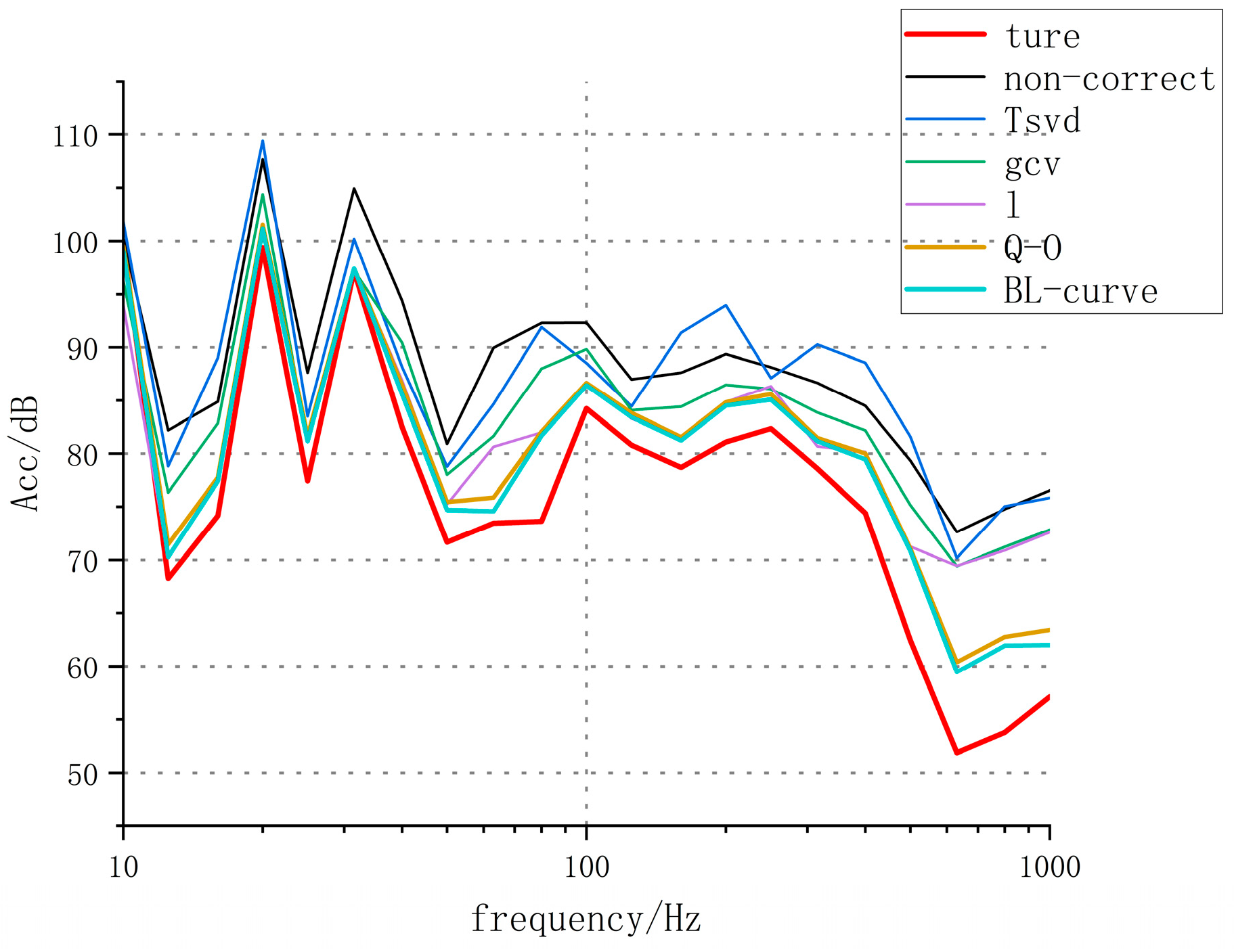
4. Simulation
5. Experimental Validation
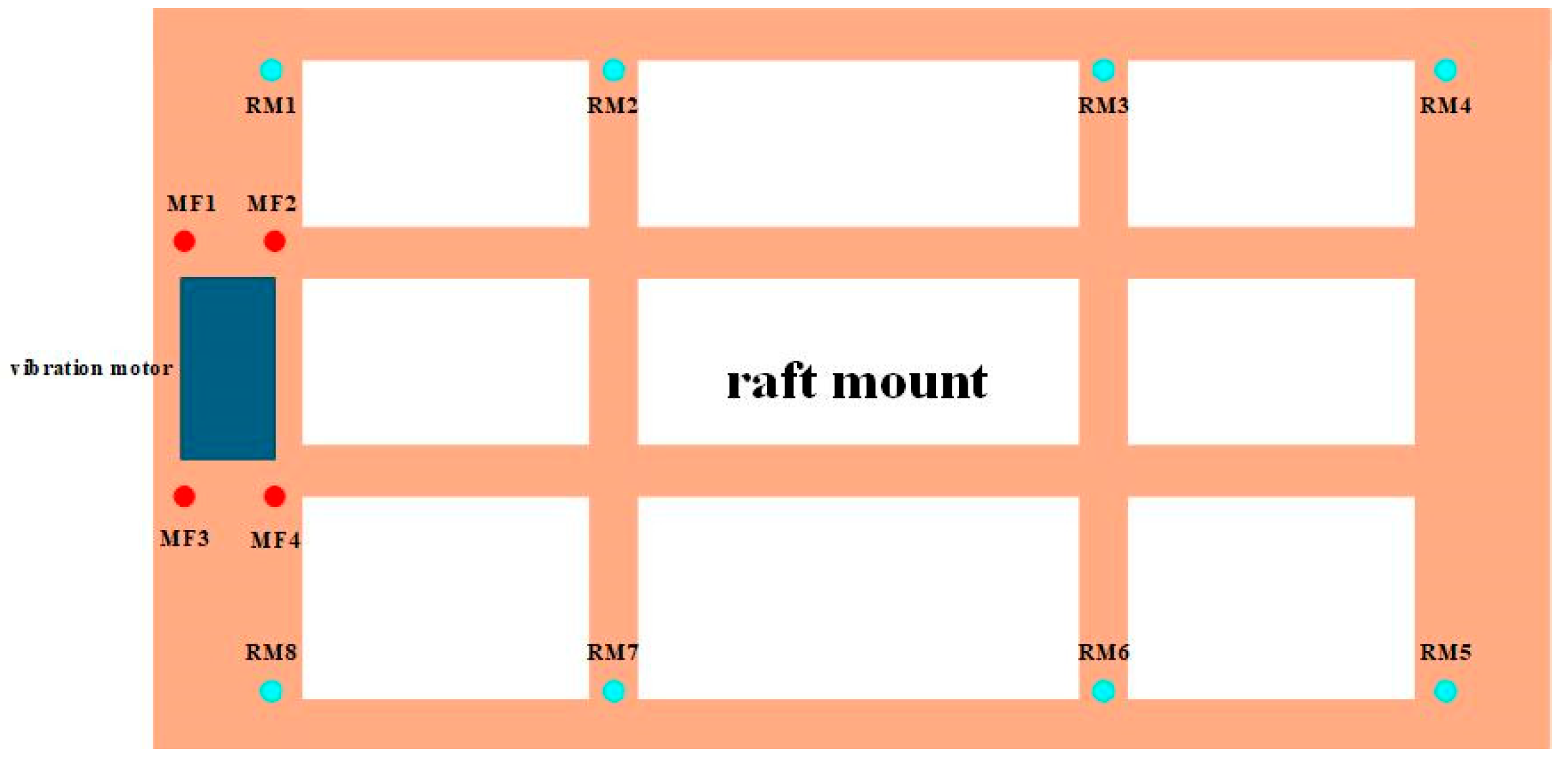
5.1. Experiment Settings
- (a)
- Measurement of the acceleration structural transfer function matrix between the exciting force points and the structural response points: By adopting the impact hammer excitation method, MF1-MF4 were excited sequentially, and the response data of RM1-RM8 were measured synchronously. After screening and averaging processing, the transfer characteristic matrix H was calculated.
- (b)
- Solution and verification of the exciting force: After starting the motor, measure the real response signal at the structural response points, and calculate the exciting force through the equation . Meanwhile, to verify the accuracy of the excitation force solution and measure the error value, analysis and calculation were conducted through indirect verification. By selecting point RM5 as the verification point for acceleration field reconstruction, the acceleration field during the actual operation of the motor was compared with the reconstructed acceleration field, and the magnitude of the error value was calculated.
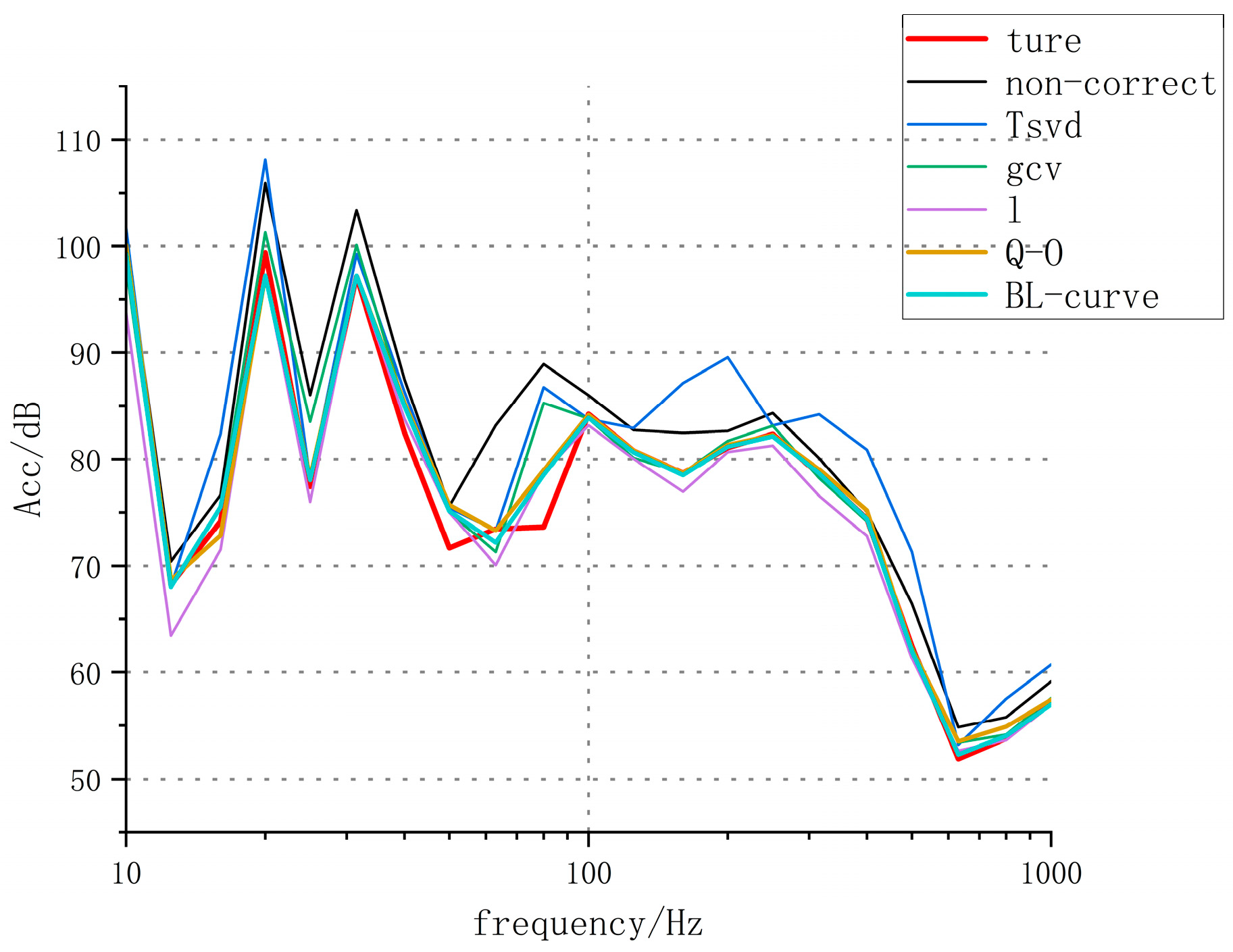
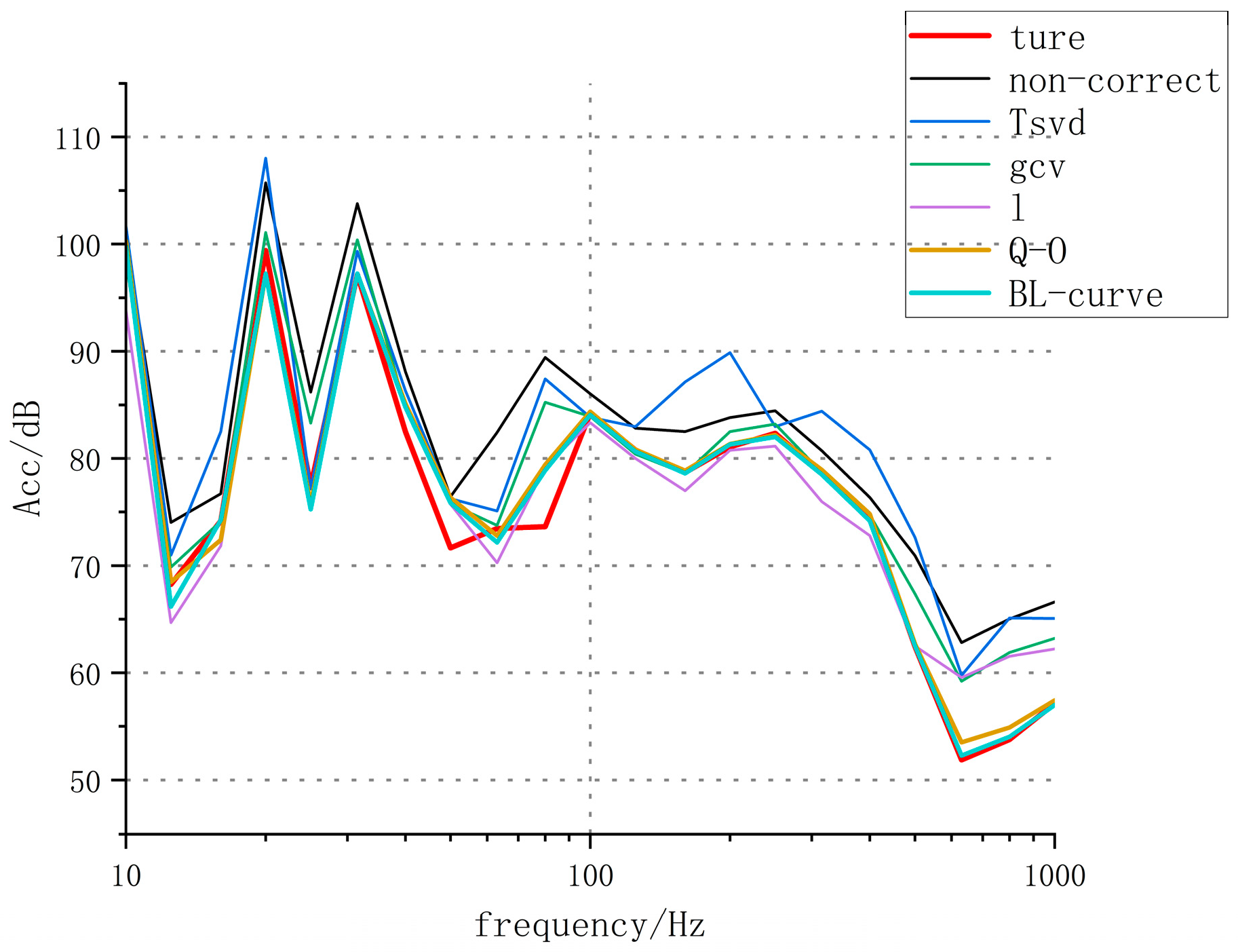
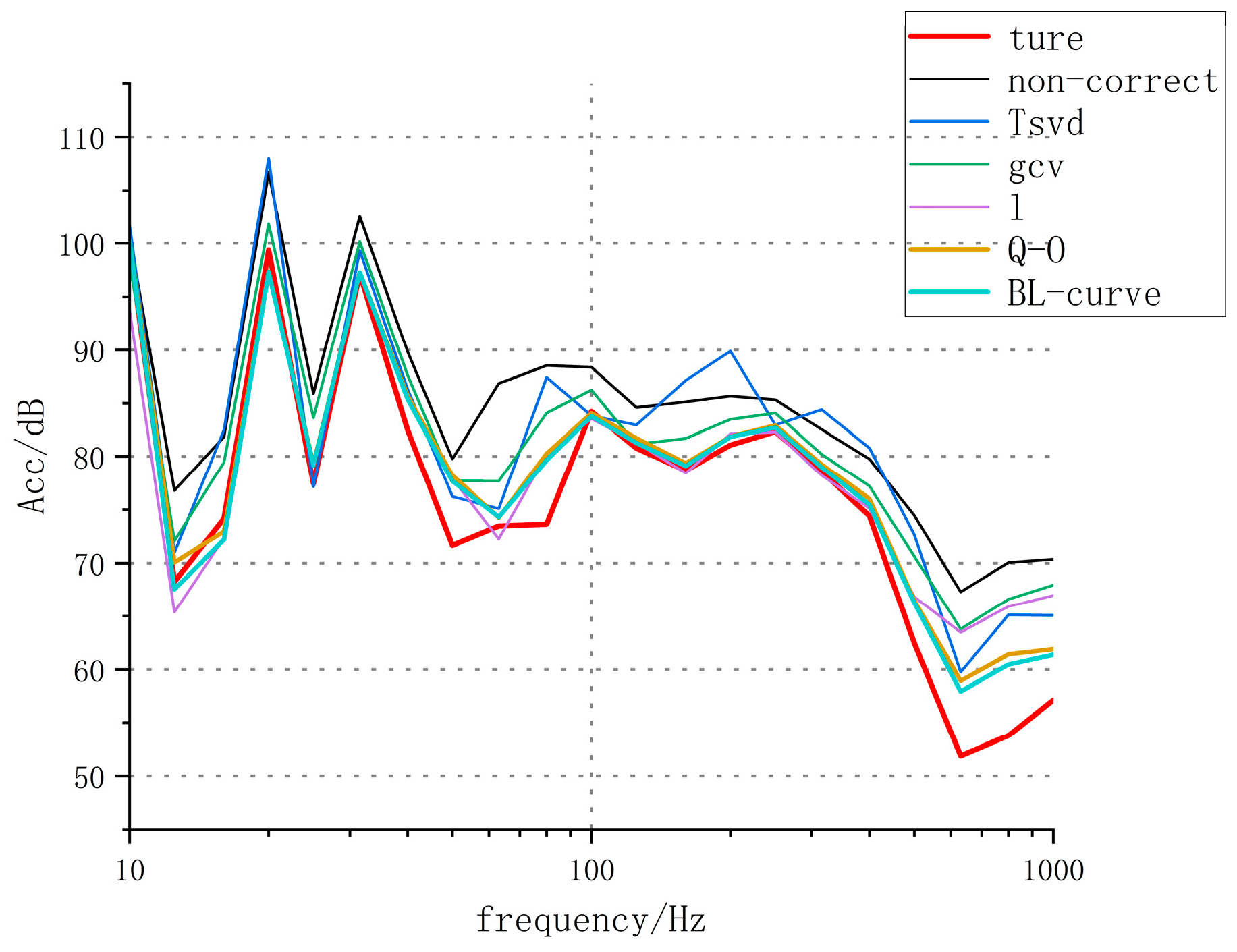
5.2. Test Results Analysis
6. Conclusions
- (1)
- This paper conducts research on the indirect solution process of excitation forces of marine mechanical equipment. Aiming at the ill-posed problem encountered in the solution of inverse problems, it points out the limitations of traditional regularization methods in application and solution under ships with complex acoustic environments. On this basis, optimized Q-O and BL-curve regularization parameter solution methods are proposed. The feasibility of the methods is verified through simulations and experiments, and the robustness of the regularization methods is improved.
- (2)
- This paper optimizes the indirect solution method for the excitation force of ship mechanical equipment and verifies it through scaled cabin section experiments. It provides guidance for the subsequent practical application of ships, which can be further implemented in engineering, and helps with ship structural design, acoustic design, radiated noise prediction, etc.
- (3)
- Meanwhile, further analysis of the experimental results shows that the Q-O regularization method is less effective than the BL-curve method. The reason is that Q-O is improved on the basis of the L-curve. Firstly, it is necessary to roughly estimate the possible value range of the regularization parameter through the L-curve method and then apply the fine-tuning criterion on this basis. However, due to noise interference, the L-curve tends to show local fluctuations. If the initial interval determined by the L-curve method has significant oscillations, the accuracy of the quasi-optimality criterion will also be affected. Therefore, the Q-O regularization method is not perfect and needs to be improved in the future.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, H.H.; Bao, M. Force identify-cation for mechanical vibration: State-of-the-art and prospect. China Mech. Eng. 2002, 13, 526–531. [Google Scholar]
- Jiang, J.H.; Zhang, F. Research Progress on Structural Dynamic Load Identification. J. Vib. Eng. 2024, 37, 1625–1650. [Google Scholar]
- Liu, R.X.; Dobrlban, E.; Hou, Z.C.; Qian, K. Dynamic Load Identification for Mechanical Systems: A Review. Arch. Comput. Methods Eng. 2022, 29, 831–863. [Google Scholar] [CrossRef]
- Mao, Y.M.; Lin, J.F.; Liu, J.H.; Di, W.B. Recent Advances of Dynamic Force Estimation Techniques. J. Dyn. Control 2014, 12, 97–104. [Google Scholar]
- Wei, Y.; Xie, P.; Zhang, L. Tikhonov regularization and randomized GSVD. SIAM J. Matrix Analy. Appl. 2016, 37, 649. [Google Scholar] [CrossRef]
- Chen, Z.; Qin, L.; Zhao, S.; Chan, T.H.; Nguyen, A. Toward efficacy of piecewise polynomial truncated singular value decomposition algorithm in moving force identification. Adv. Struct. Eng. 2019, 22, 2687. [Google Scholar] [CrossRef]
- Jiang, W.S.; Wang, Z.Y.; Lv, J. A fractional-order accumulative regularization filter for force reconstruction. Mech. Syst. Signal Process 2018, 101, 405. [Google Scholar]
- Wang, L.; Liu, J.; Lu, Z.R. Bandlimited force identification based on sinc-dictionaries and Tikhonov regularization. J. Sound Vib. 2020, 464, 114988. [Google Scholar] [CrossRef]
- Choi, H.G.; Thite, A.N.; Thompson, D.J. Comparison of methods for parameter selection in Tikhonov regularization with application to inverse force determination. J. Sound. Vib. 2007, 304, 894–917. [Google Scholar] [CrossRef]
- Chen, Z.; Chan, T.H.T. A truncated generalized singular value decomposition algorithm for moving force identification with ill-posed problems. J. Sound. Vib. 2017, 401, 297–310. [Google Scholar] [CrossRef]
- Hansen, P.C. Truncated singular value decomposition solutions to discrete ill-posed problems with ill-determined numerical rank. SIAM J. Sci. Stat. Comput. 1990, 11, 503. [Google Scholar] [CrossRef]
- Powell, R.E.; Seering, M. Multichannel structural inverse filtering. J. Vib. Acoust. Stress. Reliab. Des. 1984, 106, 22–28. [Google Scholar] [CrossRef]
- Romano, J.; Lodpez, J.A. Practical application of transfer path analysis to resolve structure-borne noise problems in vehicle design. In Proceedings of the 21st International Seminar on Modal Analysis, Kissimmee, FL, USA, 3–6 February 1996; pp. 527–536. [Google Scholar]
- Hansen, P.C.; Jensen, T.K.; Rodriguez, G. An adaptive pruning algorithm for the discrete L-curve criterion. J. Comput. Appl. Math. 2007, 198, 483. [Google Scholar] [CrossRef]
- Qiu, B.B.; Zhang, M.; Li, X.; Qu, X.; Tong, F. Unknown impact force localisation and reconstruction in experimental plate structure using time-series analysis and pattern recognition. Int. J. Mech. Sci. 2020, 166, 105231. [Google Scholar] [CrossRef]
- Hansen, P.C. The L-curve and its use in the numerical treatment of inverse problems. In Computational Inverse Problems in Electrocardiology; WIT Press: Billerica, MA, USA, 1999; pp. 119–142. [Google Scholar]
- He, Z.; Zhang, Z.; Li, E. Multi-source random excitation identification for stochastic structures based on matrix perturbation and modified regularization method. Mech. Syst. Signal Process. 2019, 119, 266. [Google Scholar] [CrossRef]
- He, Z.; Zhang, Z.; Li, E. Random dynamic load identification for stochastic structural-acoustic system using an adaptive regularization parameter and evidence theory. J. Sound Vib. 2020, 471, 115188. [Google Scholar] [CrossRef]
- Chen, H.; Miao, B.R.; Zhao, L.T.; Zhang, Y.; Jiang, C.Y.; Zhou, F. Research on impact load identification based on L1-norm regularization and least squares optimization. Noise Vib. Control 2023, 43, 62–67. [Google Scholar]
- Huang, C.; Wang, L.; Fu, M.; Lu, Z.R.; Chen, Y. A novel iterative integration regularization method for ill-posed inverse problems. Eng. Comput. 2020, 37, 1921–1941. [Google Scholar] [CrossRef]
- Golub, G.H.; Hansen, P.C.; O’Leary, D.P. Tikhonov regularization and total least squares. SIAM J. Matrix Anal. Appl. 1999, 21, 185–194. [Google Scholar] [CrossRef]
- Fenu, C.; Reichel, L.; Rodriguez, G.; Sadok, H. GCV for Tikhonov regularization by partial SVD. BIT Numer. Math. 2017, 57, 1019–1039. [Google Scholar] [CrossRef]
- Wang, L.; Peng, Y.; Xie, Y.; Chen, B.; Du, Y. A new iteration regularization method for dynamic load identification of stochastic structures. Mech. Syst. Signal Process. 2021, 156, 107586. [Google Scholar] [CrossRef]
- Li, X.; Zhao, H.; Chen, Z.; Wang, Q.; Chen, J.; Duan, D. Force identification based on a comprehensive approach combining Taylor formula and acceleration transmissibility. Inverse Probl. Sci. Eng. 2018, 26, 1612. [Google Scholar] [CrossRef]
- Ruibiao, L.I.; Lin, H.E.; Wenjun, B.U.; Rongwu, X.U. Comparison and experimental study of different regularization methods in ship radiated noise calculation. Vib. Shock. 2021, 40, 151–158. [Google Scholar]
- Gordon, W.J.; Riesenfeld, R.F. B-spline curves and surfaces. In Computer Aided Geometric Design; Academic Press: Salt Lake City, UT, USA, 1974; pp. 95–126. [Google Scholar]
- Gunawan, F.E.; Homma, H.; Kanto, Y. Two-step B-splines regularization method for solving an ill-posed problem of impact-force reconstruction. J. Sound Vib. 2006, 297, 200–214. [Google Scholar] [CrossRef]
- Regińska, T. Two-parameter discrepancy principle for combined projection and Tikhonov regularization of ill-posed problems. J. Inverse III-Posed Probl. 2013, 21, 561–577. [Google Scholar] [CrossRef]

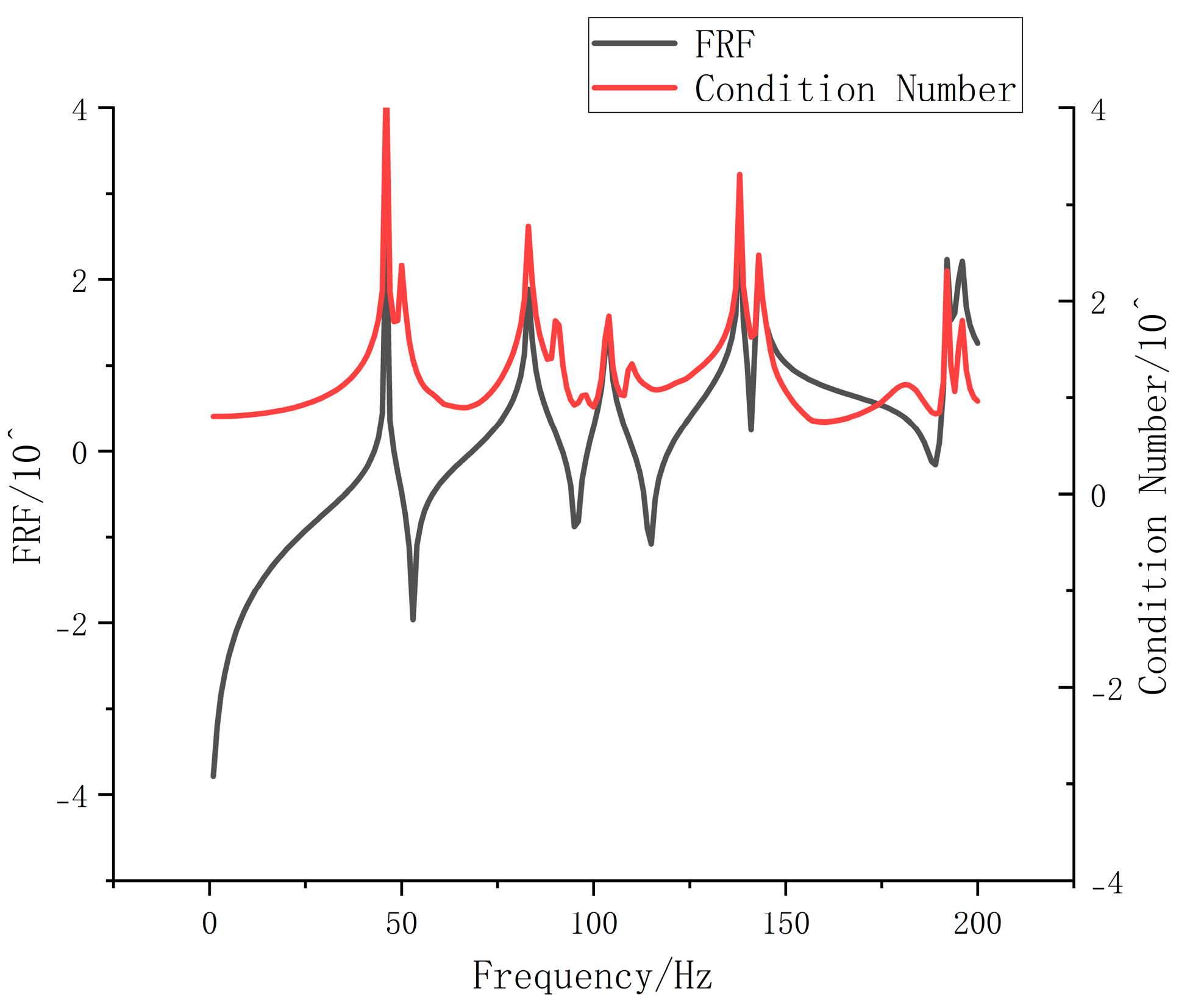



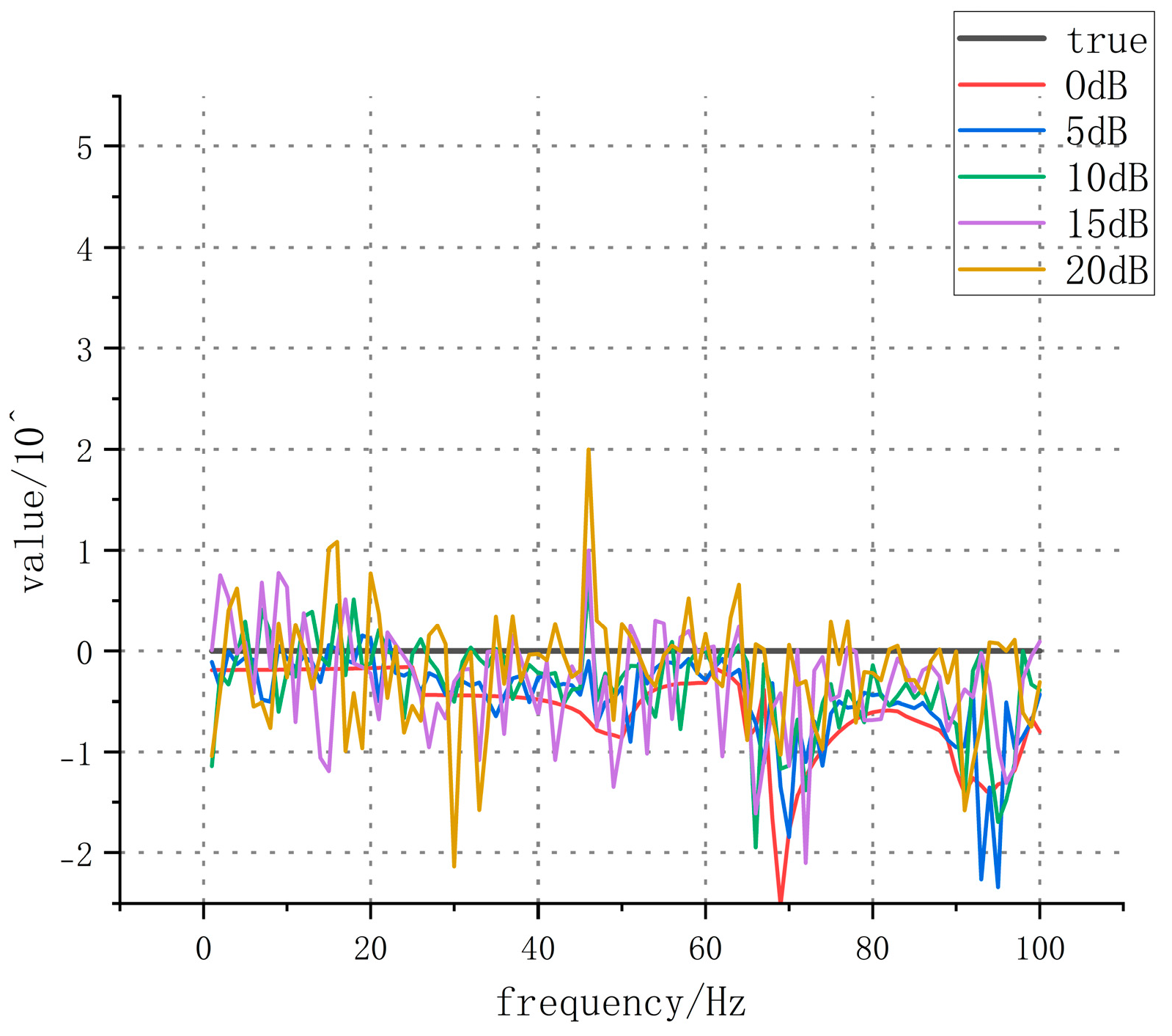
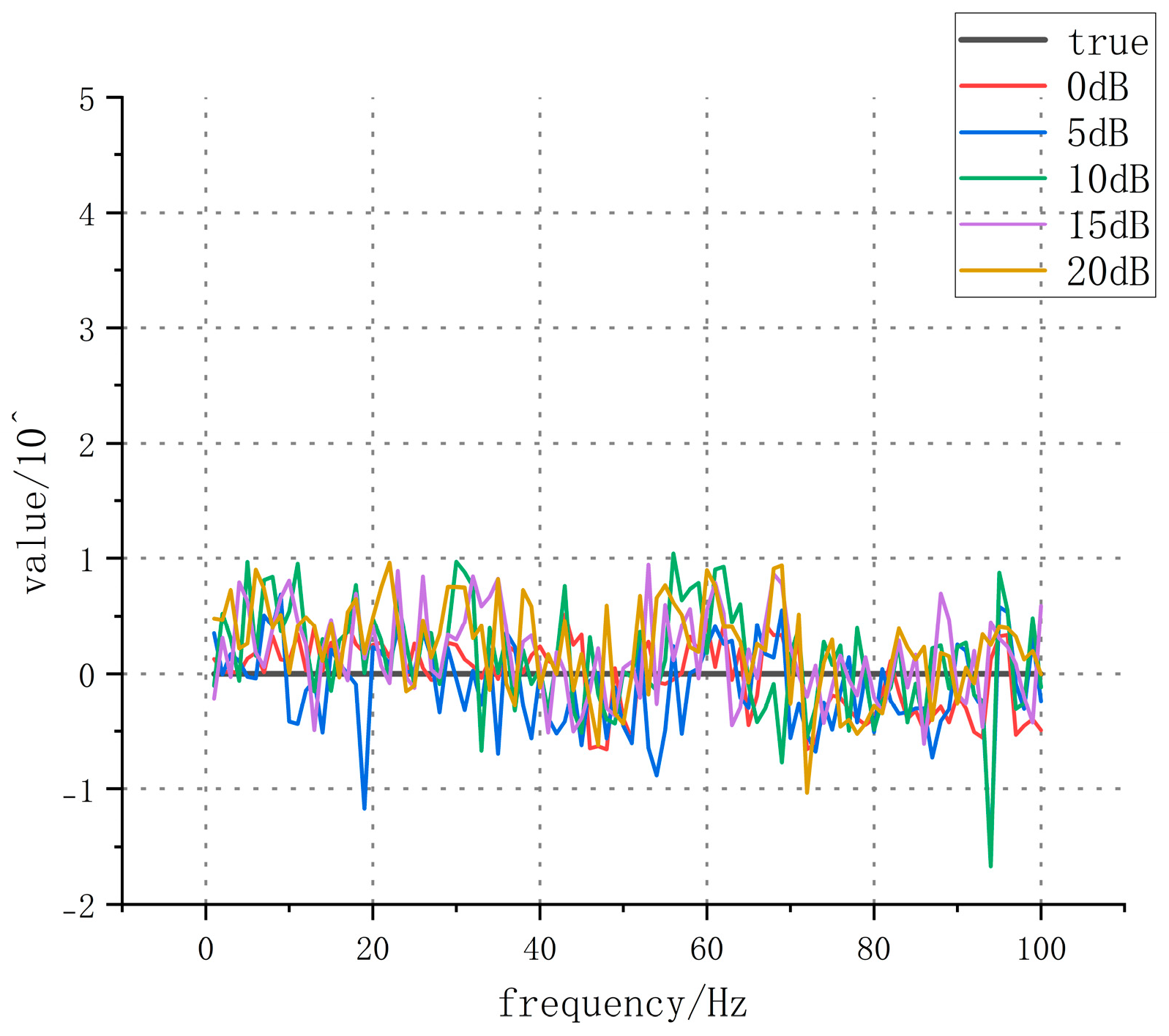
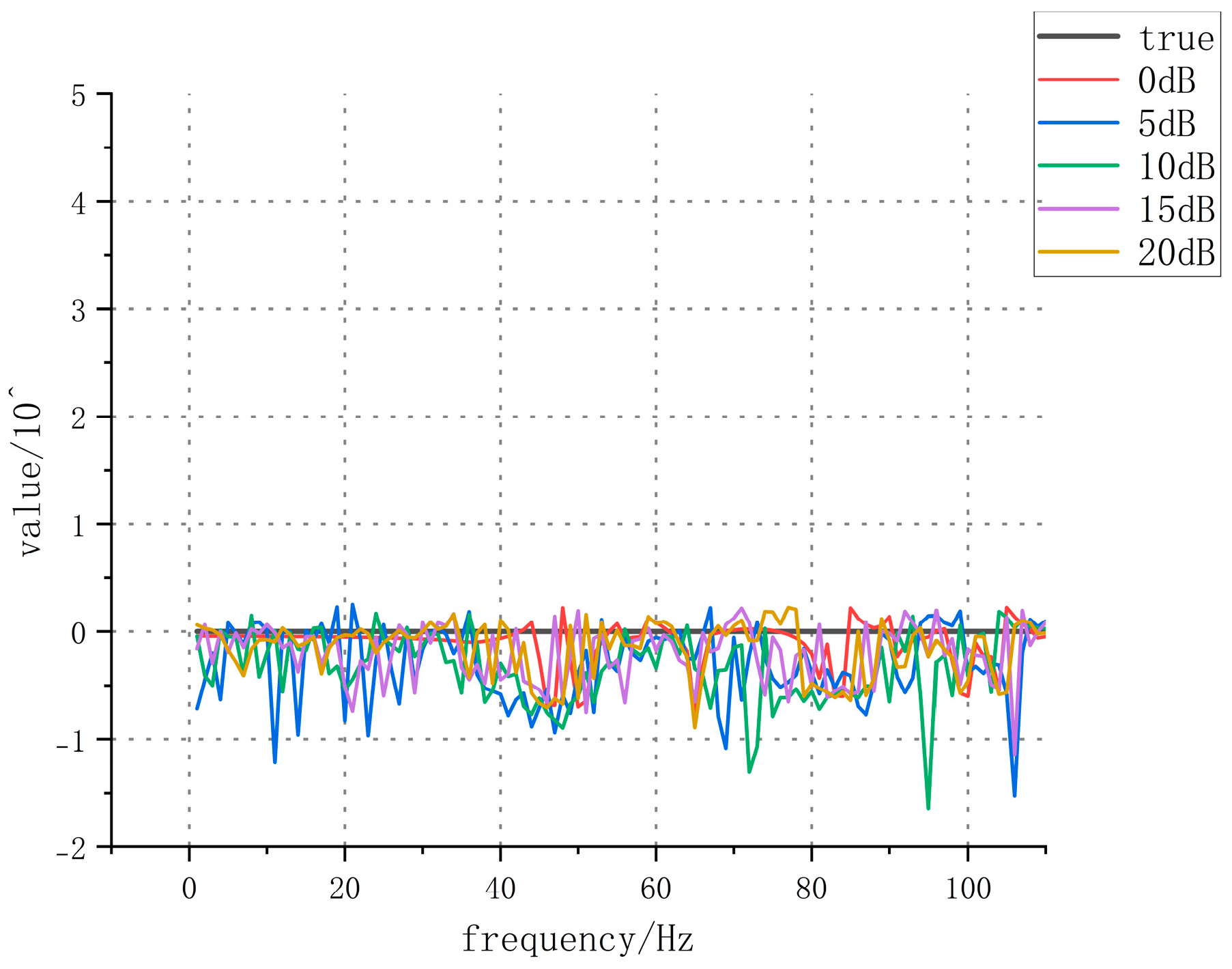



| The First Order | The Second Order | The Third Order | The Fourth Order |
|---|---|---|---|
| 45.994 | 83.21 | 103.61 | 138.07 |
| F1 | F2 | F3 | v1 |
| (0.1, 0.1) | (0.4, 0.3) | (0.5, 0.4) | (0.15, 0.2) |
| v2 | v3 | v4 | v5 |
| (0.15, 0.4) | (0.3, 0.25) | (0.45, 0.2) | (0.45, 0.4) |
| 1/3-Octave Spectral Density Error | ||||
|---|---|---|---|---|
| 0 dB | 5 dB | 10 dB | 15 dB | |
| No amendment | 4.023 | 5.836 | 8.098 | 11.482 |
| TSVD | 4.405 | 5.607 | 5.607 | 10.968 |
| GCV | 1.882 | 2.954 | 5.041 | 7.910 |
| L-curve | 1.962 | 2.931 | 3.507 | 5.896 |
| Q-O | 1.074 | 1.187 | 2.551 | 4.210 |
| BL-curve | 0.923 | 1.036 | 2.264 | 3.676 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, Z.; Xu, R.; Zhang, J.; Peng, T.; Li, R. Research on the Indirect Solution Optimization Regularization Method for Ship Mechanical Excitation Force. Appl. Sci. 2025, 15, 10238. https://doi.org/10.3390/app151810238
Yao Z, Xu R, Zhang J, Peng T, Li R. Research on the Indirect Solution Optimization Regularization Method for Ship Mechanical Excitation Force. Applied Sciences. 2025; 15(18):10238. https://doi.org/10.3390/app151810238
Chicago/Turabian StyleYao, Zhenyu, Rongwu Xu, Jiarui Zhang, Tao Peng, and Ruibiao Li. 2025. "Research on the Indirect Solution Optimization Regularization Method for Ship Mechanical Excitation Force" Applied Sciences 15, no. 18: 10238. https://doi.org/10.3390/app151810238
APA StyleYao, Z., Xu, R., Zhang, J., Peng, T., & Li, R. (2025). Research on the Indirect Solution Optimization Regularization Method for Ship Mechanical Excitation Force. Applied Sciences, 15(18), 10238. https://doi.org/10.3390/app151810238







