A Study on the Soil Seismic Liquefaction Artificial Neural Network Probabilistic Assessment Method Based on Standard Penetration Test Data
Abstract
1. Introduction
2. Comparative Analysis of Existing Liquefaction Assessment Methods
2.1. Liquefaction Assessment Method Based on Critical Standard Penetration Test Blow Number Criteria
2.2. Liquefaction Assessment Method Based on CSR Criteria
2.3. Liquefaction Assessment Method Based on Probability Criteria
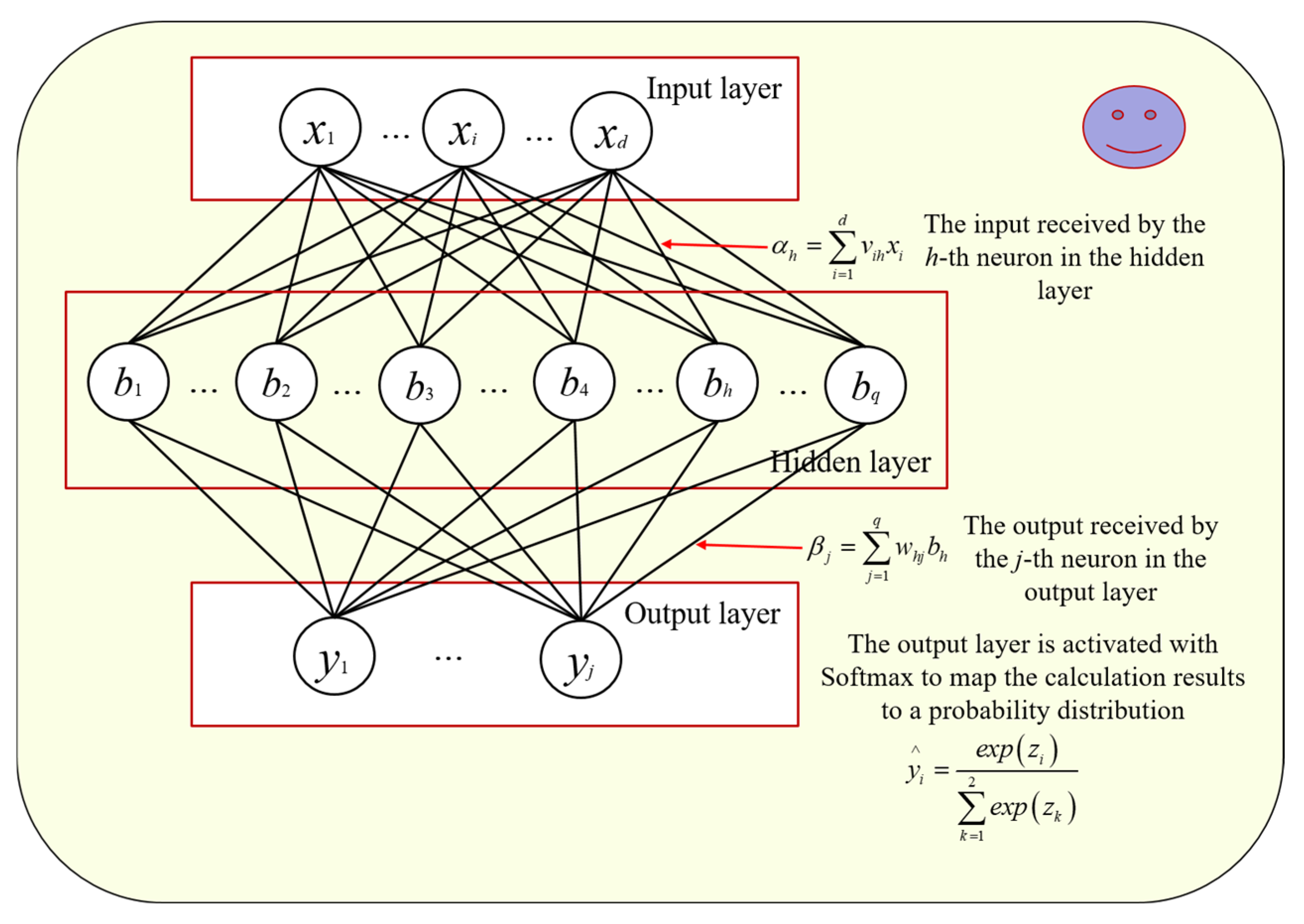
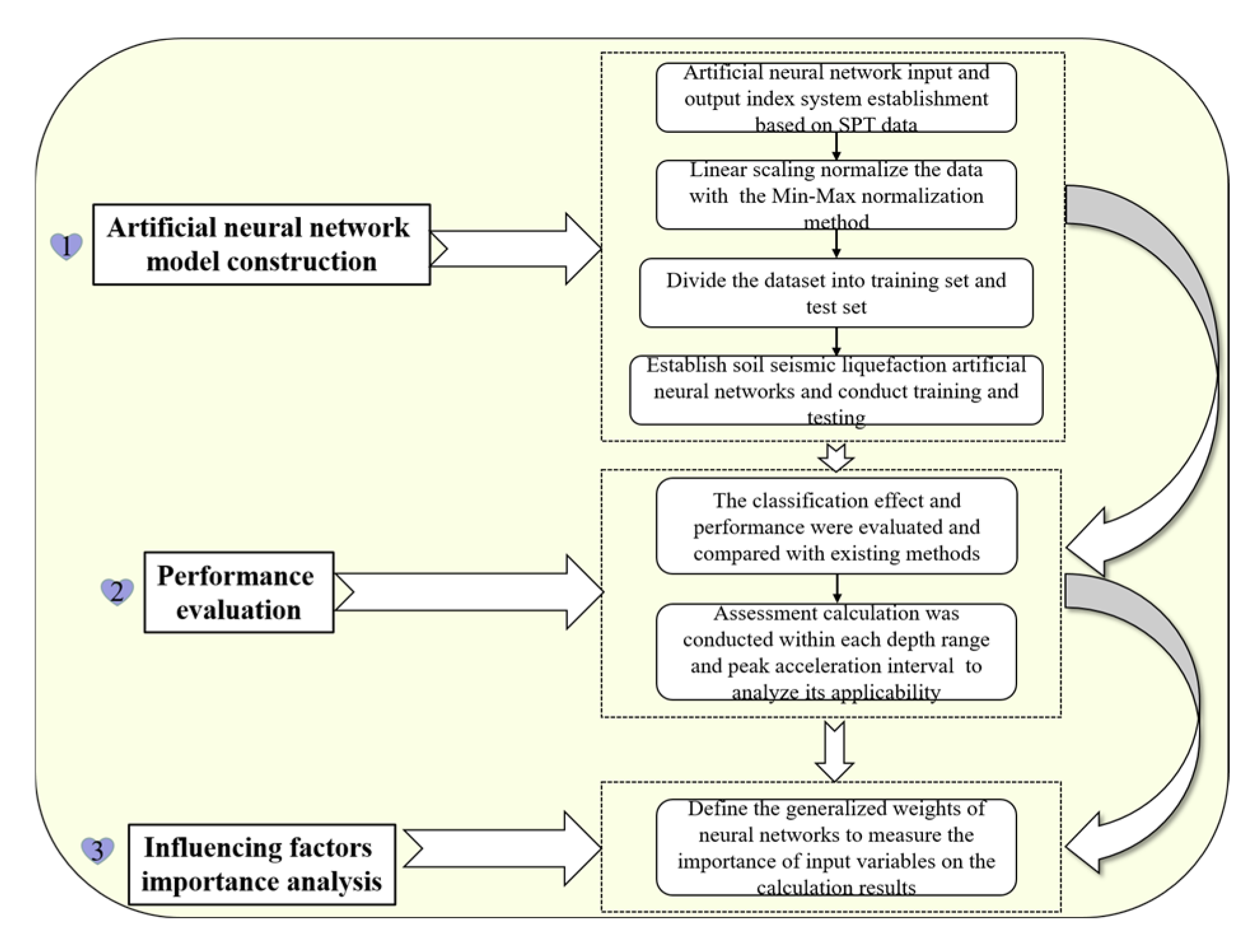
3. Liquefaction Probability Assessment Model Based on Artificial Neural Network
3.1. Collection and Organization of Liquefaction Cases
3.2. Analysis of Liquefaction’s Influencing Factors and Determination of Modeling Variables
3.3. Model Establishment Process and Principles
3.4. Overall Implementation Process of the Model
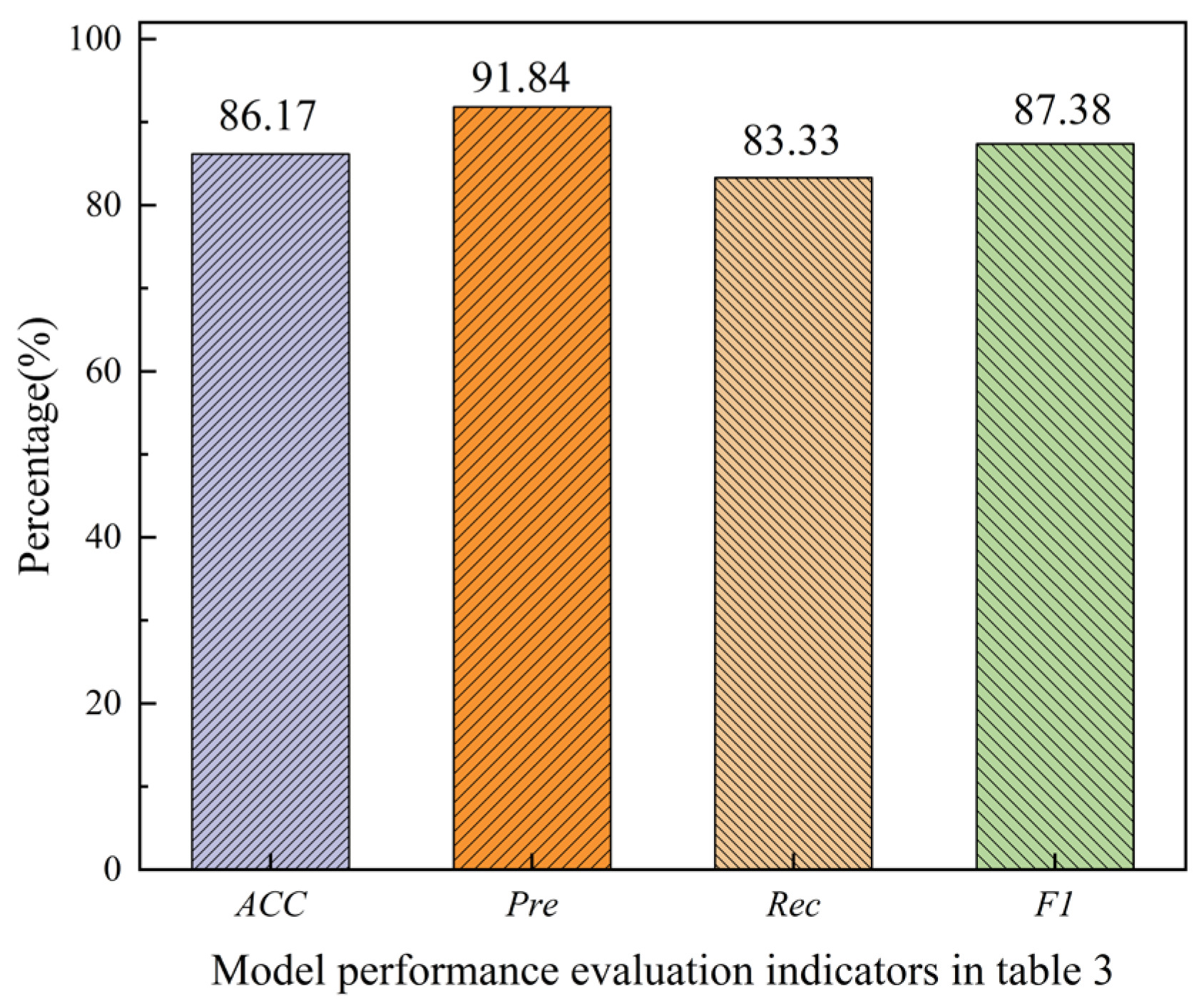
3.5. Calculation of Model Performance Evaluation Indicators
4. Research Results
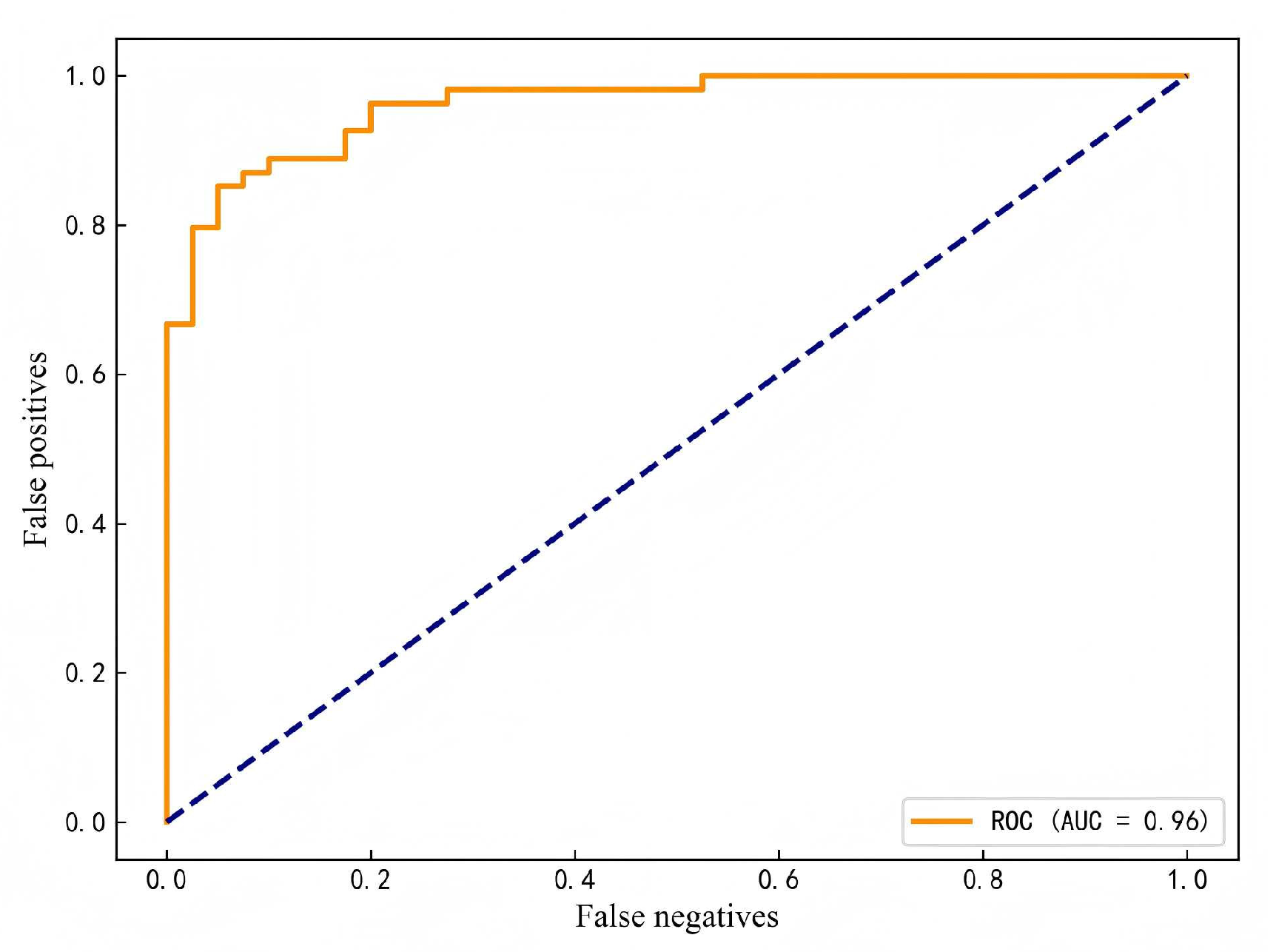
4.1. Evaluation of the Model’s Discrimination Performance on Test Set Samples
4.2. Comparison of the Model with Previous Methods
4.3. Liquefaction Influence Factor Analysis
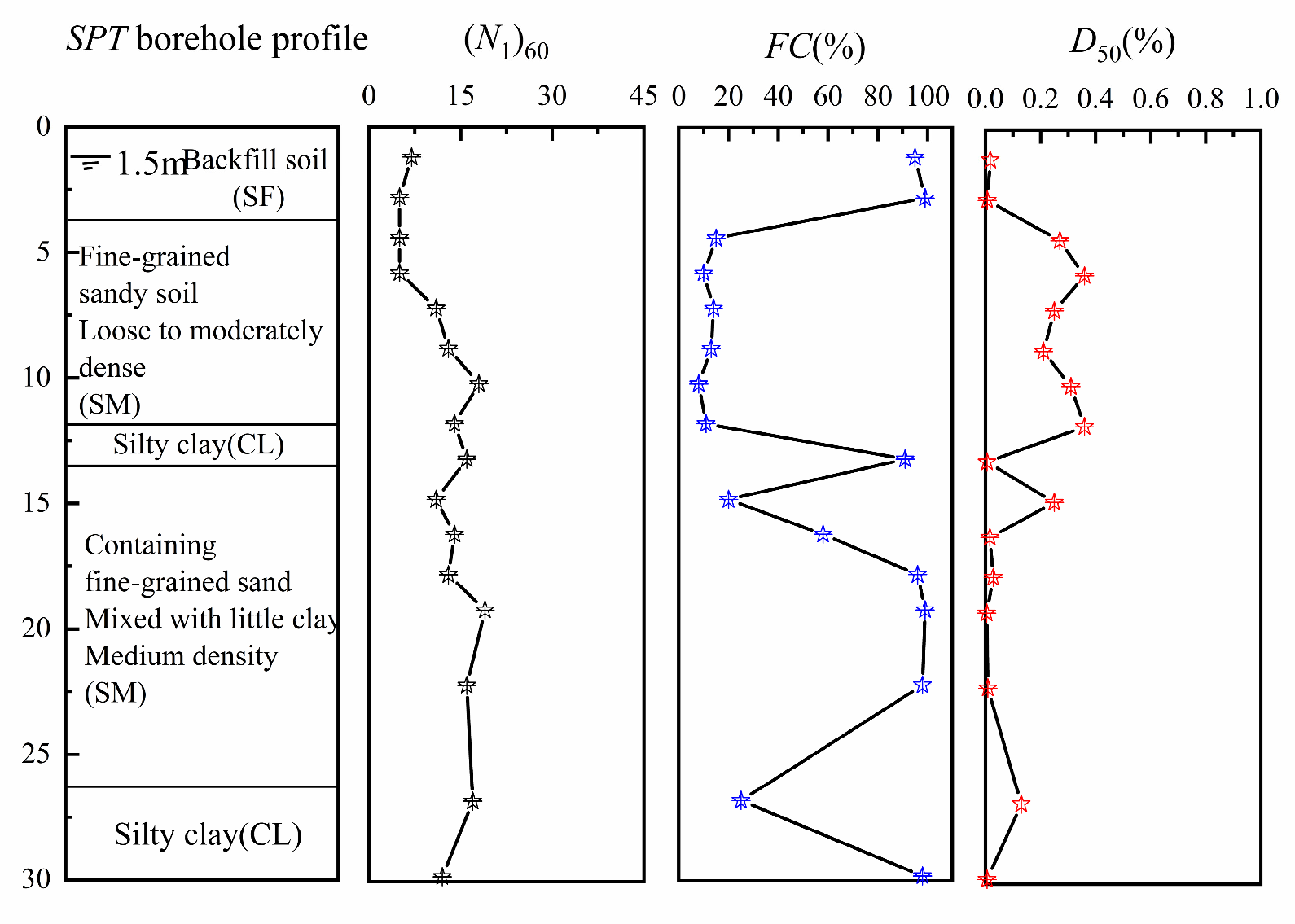
4.4. Engineering Application
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kayen, R.; Moss, R.E.S.; Thompson, E.M.; Seed, R.B.; Cetin, K.O.; Kiureghian, A.D.; Tanaka, Y.; Tokimatsu, K. Shear-Wave Velocity–Based Probabilistic and Deterministic Assessment of Seismic Soil Liquefaction Potential. J. Geotech. Geoenviron. Eng. 2013, 1393, 407–419. [Google Scholar] [CrossRef]
- Cetin, K.O.; Seed, R.B.; Der Kiureghian, A.; Tokimatsu, K.; Harder, L.F., Jr.; Kayen, R.E.; Moss, R.E.S. Standard Penetration Test-Based Probabilistic and Deterministic Assessment of Seismic Soil Liquefaction Potential. J. Geotech. Geoenviron. Eng. 2004, 13012, 1314–1340. [Google Scholar] [CrossRef]
- Youd, T.L.; Idriss, I.M. Liquefaction Resistance of Soils: Summary Report from the 1996 NCEER and 1998 NCEER/NSF Workshops on Evaluation of Liquefaction Resistance of Soils. J. Geotech. Geoenviron. Eng. 2001, 12710, 817–833. [Google Scholar] [CrossRef]
- Boulanger, R.W.; Idriss, I.M. Probabilistic Standard Penetration Test–Based Liquefaction–Triggering Procedure. J. Geotech. Geoenviron. Eng. 2012, 13810, 1185–1195. [Google Scholar] [CrossRef]
- Cetin, K.O.; Seed, R.B.; Kayen, R.E.; Moss, R.E.S.; Bilge, H.T.; Ilgac, M.; Chowdhury, K. SPT-based probabilistic and deterministic assessment of seismic soil liquefaction triggering hazard. Soil Dyn. Earthq. Eng. 2018, 115, 698–709. [Google Scholar] [CrossRef]
- Hu, J.; Wang, J. Prediction of liquefaction of gravelly soils based on a cost-sensitive Bayesian network combined with rough set weighting. Gondwana Res. 2024, 131, 57–68. [Google Scholar] [CrossRef]
- Wang, J.; Hu, J. A new method of interval Bayesian penalized network for gravelly soil seismic liquefaction prediction considering parameter confidence and model flaws uncertainties. Reliab. Eng. Syst. Saf. 2025, 264, 111383. [Google Scholar] [CrossRef]
- Liao, S.S.C.; Whitman, R.V. Overburden Correction Factors for SPT in Sand. J. Geotech. Eng. 1986, 1123, 373–377. [Google Scholar] [CrossRef]
- Idriss, I.M.; Boulanger, R.W. Semi-empirical procedures for evaluating liquefaction potential during earthquakes. Soil Dyn. Earthq. Eng. 2006, 262, 115–130. [Google Scholar] [CrossRef]
- Yang, H.; Liu, Z.; Xie, Y. Probabilistic Liquefaction Assessment Based on an In-situ State Parameter Considering Soil Spatial Variability and Various Uncertainties. KSCE J. Civ. Eng. 2023, 2710, 4228–4239. [Google Scholar] [CrossRef]
- Young, S.K.; Byung, T.K. Use of Artificial Neural Networks in the Prediction of Liquefaction Resistance of Sands. J. Geotech. Geoenviron. Eng. 2006, 13211, 1502–1504. [Google Scholar] [CrossRef]
- Bradley, B.A.; Cubrinovski, M. Simplified probabilistic state concept characterization of sandy soils and application to liquefaction resistance assessment. Soil Dyn. Earthq. Eng. 2013, 48, 104–118. [Google Scholar] [CrossRef]
- Wang, J.; Hu, J. A GLPI framework for gravelly soil liquefaction hazard assessment based on fuzzy mathematics. Eng. Geol. 2025, 353, 108134. [Google Scholar] [CrossRef]
- Duan, W.; Congress, S.S.C.; Cai, G.; Liu, S.; Dong, X.; Chen, R.; Liu, X. A hybrid GMDH neural network and logistic regression framework for state parameter–based liquefaction evaluation. Can. Geotech. J. 2021, 99999, 1801–1811. [Google Scholar] [CrossRef]
- Jas, K.; Mangalathu, S.; Dodagoudar, G.R. Evaluation and analysis of liquefaction potential of gravelly soils using explainable probabilistic machine learning model. Comput. Geotech. 2024, 167, 106051. [Google Scholar] [CrossRef]
- Ordaz, M.; Salgado-Gálvez, M.A.; Mánica, M.A.; Ovando-Shelley, E.; Faccioli, E.; Osorio, L.; Madrigal, M.C. Event-based probabilistic liquefaction hazard analysis for defining soil acceptance criteria. Soil Dyn. Earthq. Eng. 2023, 166, 107781. [Google Scholar] [CrossRef]
- Muftuoglu, G.M.; Dehghanian, K. Soil liquefaction assessment using machine learning. Artif. Intell. Geosci. 2025, 61, 100122. [Google Scholar] [CrossRef]
- Juang, C.H.; Yuan, H.; Lee, D.H.; Ku, C.S. Assessing CPT-based methods for liquefaction evaluation with emphasis on the cases from the Chi-Chi, Taiwan, earthquake. Soil Dyn. Earthq. Eng. 2002, 223, 241–258. [Google Scholar] [CrossRef]
- Juang, C.H.; Yuan, H.; Lee, D.H.; Lin, P.S. Simplified Cone Penetration Test-based Method for Evaluating Liquefaction Resistance of Soils. J. Geotech. Geoenviron. Eng. 2002, 129, 66. [Google Scholar] [CrossRef]
- Fan, M.; Li, J.J.; Yang, Z.Q.; Liu, X.S.; Zhu, K.B.; Zhao, J.M. Applicability of standard penetration test based liquefaction assessment methods for sandy soil in deep layer. Rock Soil Mech. 2025, 46, 2085–2094. [Google Scholar] [CrossRef]
- Han, X.; Gong, W.; Juang, C.H. Probabilistic evaluation of earthquake-induced liquefaction using Bayesian network based on a side-by-side SPT–CPT database. Can. Geotech. J. 2024, 6112, 2653–2666. [Google Scholar] [CrossRef]
- Kurnaz, T.F.; Erden, C.; Kökçam, A.H.; Dağdeviren, U.; Demir, A.S. A hyper parameterized artificial neural network approach for prediction of the factor of safety against liquefaction. Eng. Geol. 2023, 319, 107109. [Google Scholar] [CrossRef]
- Das, R.; Das, A. Limitations of Mw and M Scales: Compelling Evidence Advocating for the Das Magnitude Scale (Mwg)—A Critical Review and Analysis. Indian Geotech. J. 2025. [Google Scholar] [CrossRef]
- Das, R.; Sharma, M.L.; Wason, H.R.; Choudhury, D.; Gonzalez, G. A Seismic Moment Magnitude Scale. Bull. Seismol. Soc. Am. Dropdown Menu 2019, 109, 1542–1555. [Google Scholar] [CrossRef]
- Kishida, T.; Tsai, C.C. Seismic Demand of the Liquefaction Potential with Equivalent Number of Cycles for Probabilistic Seismic Hazard Analysis. J. Geotech. Geoenviron. Eng. 2014, 1403, 04013023. [Google Scholar] [CrossRef]
- Zhao, Z.; Duan, W.; Cai, G.; Wu, M.; Liu, S. CPT-based fully probabilistic seismic liquefaction potential assessment to reduce uncertainty: Integrating XGBoost algorithm with Bayesian theorem. Comput. Geotech. 2022, 149, 104868. [Google Scholar] [CrossRef]
- Kamura, A.; Kurihara, G.; Mori, T.; Kazama, M.; Kwon, Y.; Kim, J.; Han, J.T. Exploring the possibility of assessing the damage degree of liquefaction based only on seismic records by artificial neural networks. Soils Found. 2021, 613, 658–674. [Google Scholar] [CrossRef]
- Xu, T.; Wang, Y.; Qin, G.; Qin, J. Probabilistic Performance Evaluation of Buried Onshore and Offshore Pipelines Subjected to Earthquakes: Perspectives on Uncertainties. J. Pipeline Syst. Eng. Pract. 2025, 163, 04025024. [Google Scholar] [CrossRef]
- Guan, Z.; Wang, Y. SPT-based probabilistic evaluation of soil liquefaction potential considering design life of civil infrastructures. Comput. Geotech. 2022, 148, 104807. [Google Scholar] [CrossRef]
- Yuan, X.M.; Fei, Y.; Chen, L. An unified formula for predicting sand liquefaction in different buried depths under severe seismic ground motionAn unified formula for predicting sand liquefaction in different buried depths under severe seismic ground motion. Chin. J. Rock Mech. Eng. 2021, 40, 2101–2112. [Google Scholar]
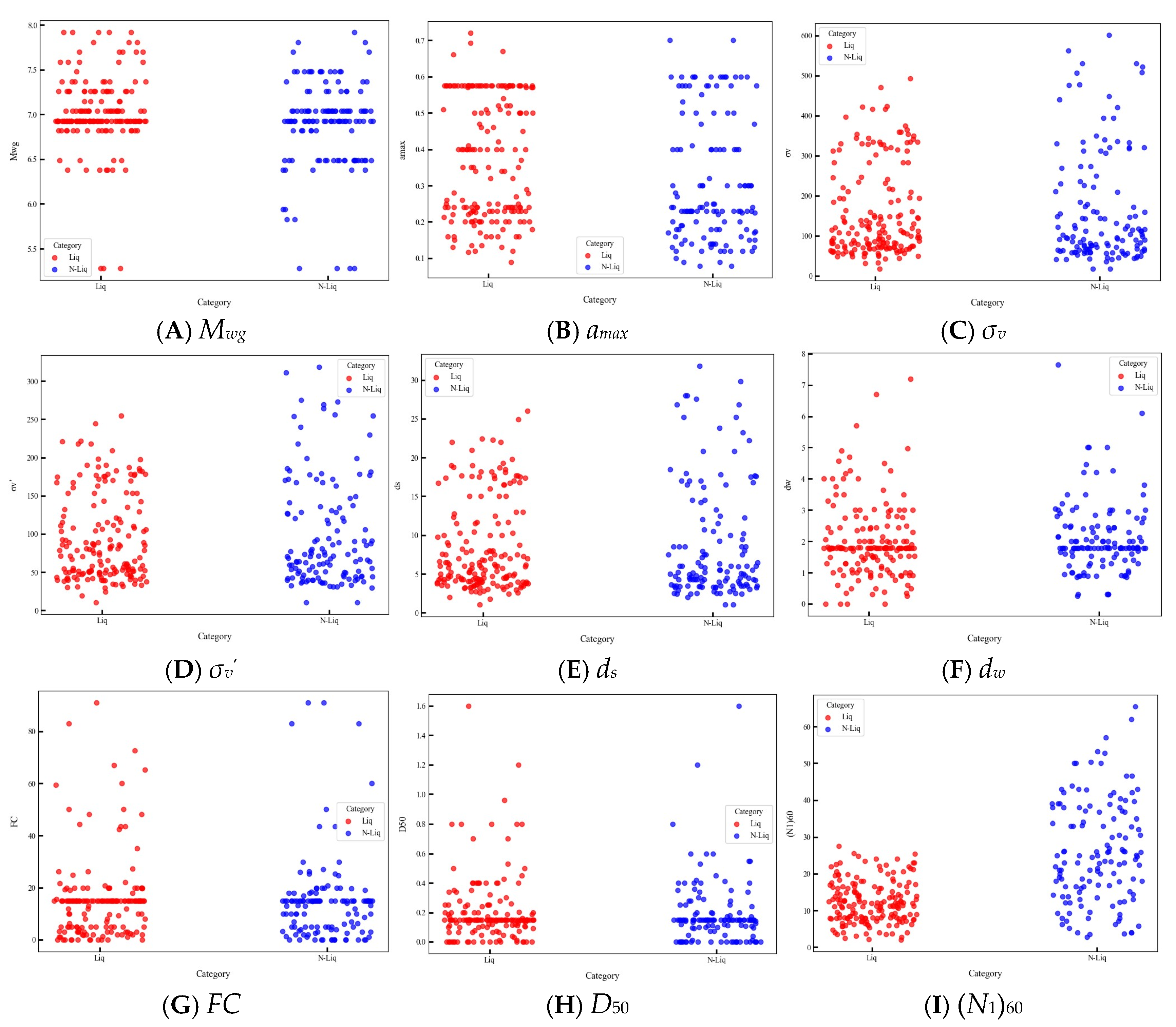
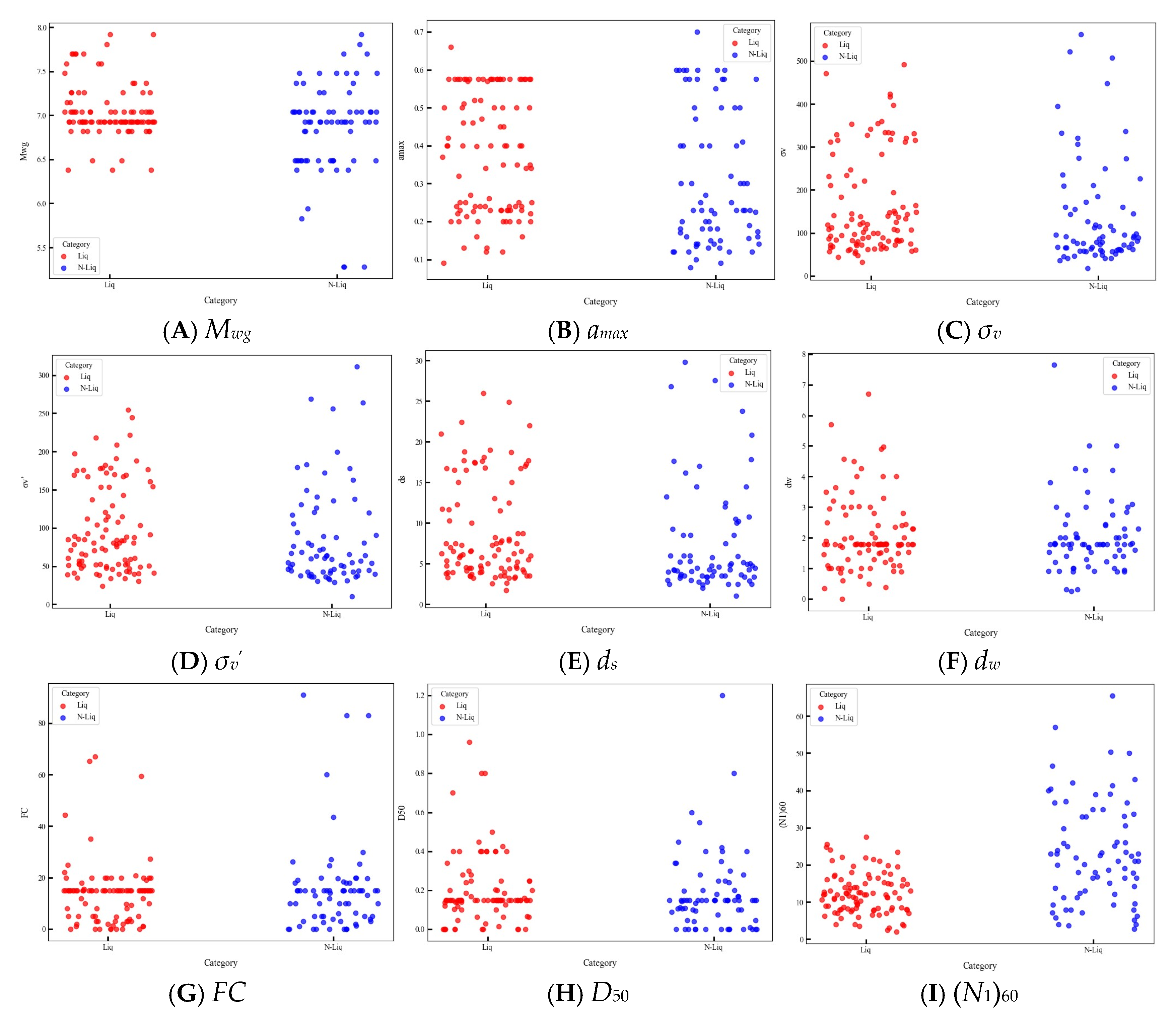

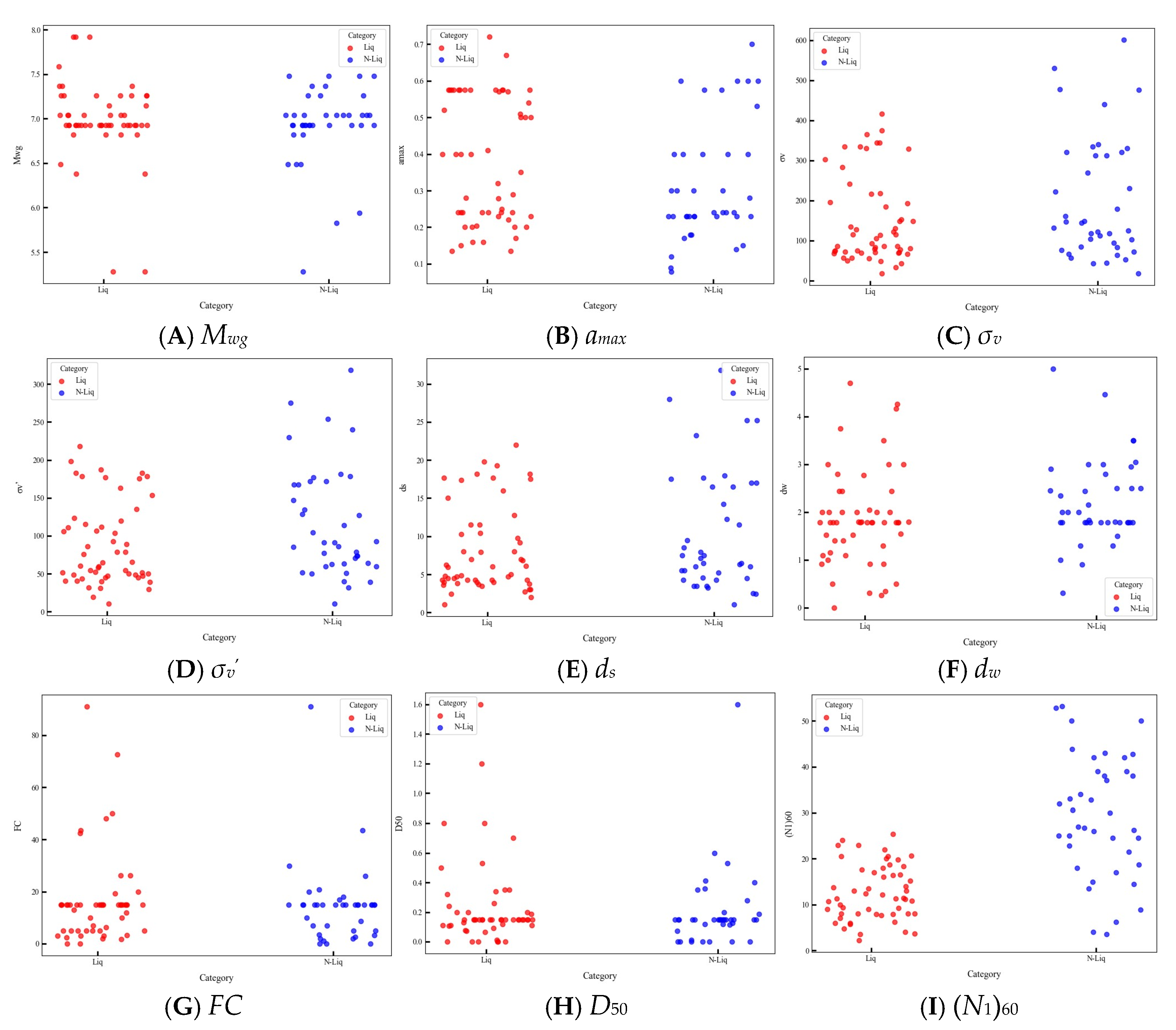


| Factors | Mwg | amax (g) | σv (kPa) | σv’ (kPa) | ds (m) | dw (m) | FC (%) | D50 (mm) | (N1)60 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Cases | ||||||||||
| Liquefaction cases | Minimum | 5.17 | 0.08 | 28.8 | 4.15 | 0.50 | 0.00 | 0.00 | 0.04 | 1.10 |
| Maximum | 8.36 | 1.00 | 492.22 | 316.14 | 26.00 | 16.74 | 99.00 | 1.60 | 42.70 | |
| Mean | 7.19 | 0.35 | 142.13 | 74.55 | 6.27 | 1.80 | 21.61 | 0.24 | 12.04 | |
| Standard deviation | 0.38 | 0.17 | 111.76 | 56.09 | 5.83 | 1.16 | 15.18 | 0.22 | 5.70 | |
| Non-liquefaction cases | Minimum | 5.61 | 0.05 | 35.00 | 5.34 | 0.30 | 0.00 | 0.00 | 0.04 | 2.50 |
| Maximum | 8.36 | 0.78 | 363.30 | 257.00 | 31.80 | 9.60 | 92.00 | 1.60 | 70.50 | |
| Mean | 7.11 | 0.27 | 114.10 | 68.13 | 7.83 | 2.06 | 16.26 | 0.25 | 21.17 | |
| Standard deviation | 0.48 | 0.17 | 140.37 | 69.89 | 7.36 | 1.11 | 16.14 | 0.21 | 13.83 |
| Evaluation Indicators | Computing Equations | Performance Evaluation |
|---|---|---|
| Accuracy (ACC) | ACC = (TP + TN)/(TP + FN + FP + TN) | A larger number indicates higher accuracy in prediction |
| Precision (Pre) | Pre = TP/(TP + FP) | Restrict each other with Rec |
| Recall (Rec) | Rec = TP/(TP + FN) | Restrict each other with Pre |
| F1 | F1 = 2Prex × Rec/(Prex + Rec) | A larger number indicates that Pre and Rec are better |
| ds (m) | Liq (%) | N-Liq (%) | amax (g) | Liq (%) | N-Liq (%) | (N1)60 | Liq (%) | N-Liq (%) |
|---|---|---|---|---|---|---|---|---|
| 0–10 | 76.32 | 84.00 | 0.07–0.13 | / | 100.00 | ≤10 | 86.36 | 100.00 |
| 10–20 | 100.00 | 100.00 | 0.13–0.24 | 66.67 | 84.21 | 10–15 | 84.62 | 66.67 |
| >20 | / | 100.00 | 0.24–0.44 | 81.82 | 90.00 | 15–30 | 78.95 | 85.71 |
| / | / | / | 0.44–0.83 | 100.00 | 100.00 | >30 | / | 100 |
| Variables | Mwg | amax (g) | σv (kPa) | σv’ (kPa) | ds (m) | dw (m) | FC (%) | D50 (mm) | (N1)60 | Liq | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Number | |||||||||||
| 1 | 6.82 | 0.15 | 79.13 | 65.44 | 4.90 | 3.50 | 50.00 | 0.09 | 3.51 | Yes | |
| 2 | 5.28 | 0.23 | 86.22 | 48.86 | 4.72 | 0.91 | 26.20 | 0.11 | 11.28 | Yes | |
| 3 | 6.82 | 0.41 | 133.82 | 111.26 | 7.00 | 4.70 | 13.00 | 0.19 | 20.63 | Yes | |
| 4 | 7.26 | 0.24 | 42.79 | 31.63 | 2.44 | 1.30 | 7.00 | 1.60 | 18.69 | Yes | |
| 5 | 6.82 | 0.22 | 115.51 | 86.09 | 6.00 | 3.00 | 5.00 | 0.32 | 16.38 | Yes | |
| 6 | 6.38 | 0.16 | 17.71 | 10.38 | 1.05 | 0.30 | 91.00 | 0.01 | 3.98 | Yes | |
| 7 | 6.38 | 0.20 | 86.22 | 48.86 | 4.72 | 0.91 | 26.20 | 0.11 | 11.28 | Yes | |
| 8 | 7.37 | 0.14 | 48.86 | 30.92 | 4.27 | 2.44 | 3.00 | 0.80 | 9.31 | Yes | |
| 9 | 7.15 | 0.35 | 147.74 | 106.34 | 7.97 | 3.75 | 3.29 | 0.50 | 20.56 | Yes | |
| 10 | 6.93 | 0.23 | 112.22 | 70.88 | 6.00 | 1.78 | 15.00 | 0.15 | 17.00 | No | |
| 11 | 7.37 | 0.18 | 117.86 | 78.64 | 6.50 | 2.50 | 0.00 | 0.36 | 14.40 | No | |
| 12 | 7.26 | 0.28 | 75.81 | 63.79 | 4.27 | 3.05 | 0.00 | 0.41 | 17.96 | No | |
| 13 | 7.26 | 0.24 | 84.06 | 63.14 | 4.57 | 2.44 | 26.00 | 0.12 | 14.92 | No | |
| Indicator | ACC (%) | Pre (%) | Rec (%) | F1 (%) | |
|---|---|---|---|---|---|
| Method | |||||
| ANN | 86.17 | 91.84 | 83.33 | 87.38 | |
| SVM | 85.11 | 81.25 | 96.30 | 88.14 | |
| LRM | 70.74 | 66.80 | 97.19 | 79.18 | |
| R.B. Seed | 83.92 | 81.37 | 93.26 | 86.91 | |
| NCEER | 71.06 | 67.05 | 97.19 | 79.36 | |
| Idriss | 81.35 | 90.54 | 75.28 | 82.21 | |
| Code method | 66.56 | 64.80 | 91.01 | 75.70 | |
| Principle method | 79.42 | 89.58 | 72.47 | 80.12 | |
| Depth | All Samples | 0–20 m | >20 m | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Method | ACC (%) | Liq (%) | N-Liq (%) | ACC (%) | Liq (%) | N-Liq (%) | ACC (%) | Liq (%) | N-Liq (%) | |
| ANN | 86.17 | 83.33 | 90.00 | 85.23 | 83.02 | 88.57 | 100.00 | 100.00 | 100.00 | |
| SVM | 85.11 | 96.30 | 70.00 | 83.91 | 96.23 | 64.71 | 100.00 | 100.00 | 100.00 | |
| LRM | 70.74 | 97.19 | 35.34 | 70.69 | 97.08 | 32.77 | 71.43 | 100.00 | 57.14 | |
| R.B. Seed | 83.92 | 83.26 | 71.43 | 85.17 | 92.40 | 74.79 | 66.67 | 100.00 | 50.00 | |
| NCEER | 71.06 | 97.19 | 36.09 | 64.83 | 97.08 | 18.49 | 61.90 | 100.00 | 42.86 | |
| Idriss | 81.35 | 75.28 | 89.47 | 80.69 | 74.85 | 89.08 | 90.48 | 85.71 | 92.86 | |
| Code Method | 66.56 | 91.01 | 66.17 | 83.45 | 90.64 | 73.10 | 38.10 | 100.00 | 7.14 | |
| Principle Method | 79.42 | 72.47 | 88.72 | 79.66 | 71.35 | 91.60 | 76.19 | 100.00 | 64.29 | |
| Case | ds (m) | Observed Result | Predicted Result | Probability (%) |
|---|---|---|---|---|
| 1 | 19.3 | Liq | Liq | 94.93 |
| 2 | 8 | Liq | Liq | 98.18 |
| 3 | 4.5 | Liq | Liq | 99.29 |
| 4 | 4.9 | Liq | N-Liq | 9.81 |
| 5 | 10.3 | Liq | Liq | 87.00 |
| 6 | 10.4 | Liq | Liq | 99.84 |
| 7 | 3 | Liq | Liq | 99.10 |
| 8 | 3 | Liq | Liq | 99.60 |
| 9 | 4.7 | Liq | N-Liq | 48.84 |
| 10 | 4.3 | Liq | Liq | 82.40 |
| 11 | 7 | Liq | N-Liq | 10.07 |
| 12 | 4 | Liq | Liq | 96.90 |
| 13 | 12.8 | Liq | Liq | 79.06 |
| 14 | 11.5 | Liq | Liq | 65.79 |
| 15 | 6.3 | Liq | Liq | 95.58 |
| … | … | … | … | … |
| 80 | 2.5 | N-Liq | N-Liq | |
| 81 | 6.0 | N-Liq | N-Liq | |
| 82 | 25.2 | N-Liq | N-Liq | 0.00 |
| 83 | 6.3 | N-Liq | N-Liq | 0.00 |
| 84 | 5.2 | N-Liq | N-Liq | 11.05 |
| 85 | 6.5 | N-Liq | Liq | 67.58 |
| 86 | 3.5 | N-Liq | N-Liq | 0.22 |
| 87 | 28.0 | N-Liq | N-Liq | 0.01 |
| 88 | 16.5 | N-Liq | N-Liq | 0.00 |
| 89 | 14.3 | N-Liq | N-Liq | 0.00 |
| 90 | 16.5 | N-Liq | N-Liq | 0.03 |
| 91 | 7.5 | N-Liq | N-Liq | 7.93 |
| 92 | 6.5 | N-Liq | N-Liq | 0.00 |
| 93 | 5.5 | N-Liq | N-Liq | 0.00 |
| 94 | 25.2 | N-Liq | N-Liq | 0.01 |
| Factor | Seismic Load | Soil Environment | Soil Properties | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mwg | amax | σv | σv’ | ds | dw | FC | D50 | (N1)60 | |
| Percentage (%) | 13.84 | 14.37 | 14.17 | 13.94 | 13.29 | 13.40 | 13.91 | 12.69 | 20.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Fan, M.; Yang, Z.; Liu, X.; Zhao, J. A Study on the Soil Seismic Liquefaction Artificial Neural Network Probabilistic Assessment Method Based on Standard Penetration Test Data. Appl. Sci. 2025, 15, 10229. https://doi.org/10.3390/app151810229
Li J, Fan M, Yang Z, Liu X, Zhao J. A Study on the Soil Seismic Liquefaction Artificial Neural Network Probabilistic Assessment Method Based on Standard Penetration Test Data. Applied Sciences. 2025; 15(18):10229. https://doi.org/10.3390/app151810229
Chicago/Turabian StyleLi, Jingjun, Meng Fan, Zhengquan Yang, Xiaosheng Liu, and Jianming Zhao. 2025. "A Study on the Soil Seismic Liquefaction Artificial Neural Network Probabilistic Assessment Method Based on Standard Penetration Test Data" Applied Sciences 15, no. 18: 10229. https://doi.org/10.3390/app151810229
APA StyleLi, J., Fan, M., Yang, Z., Liu, X., & Zhao, J. (2025). A Study on the Soil Seismic Liquefaction Artificial Neural Network Probabilistic Assessment Method Based on Standard Penetration Test Data. Applied Sciences, 15(18), 10229. https://doi.org/10.3390/app151810229






