Toppling Deformed Rock Mass Hydraulic Fracturing Analysis Based on Extended Finite Elements
Abstract
1. Introduction
2. Basic Theory
2.1. Extended Finite Element Method Displacement Equation
2.2. Control Equation
2.3. Crack Propagation Criteria
2.4. Stress Intensity Factor
3. Computational Model and Parameters
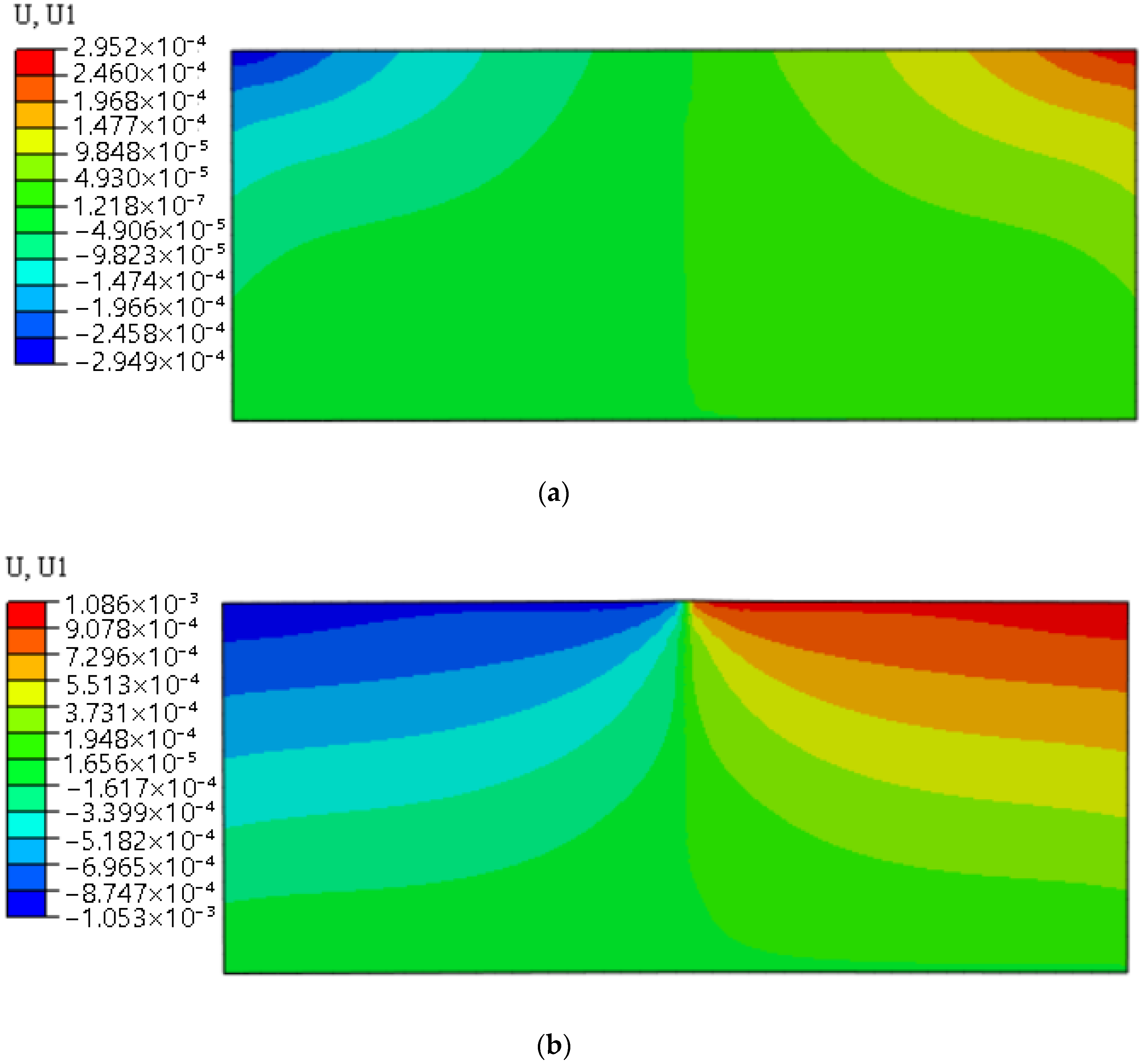
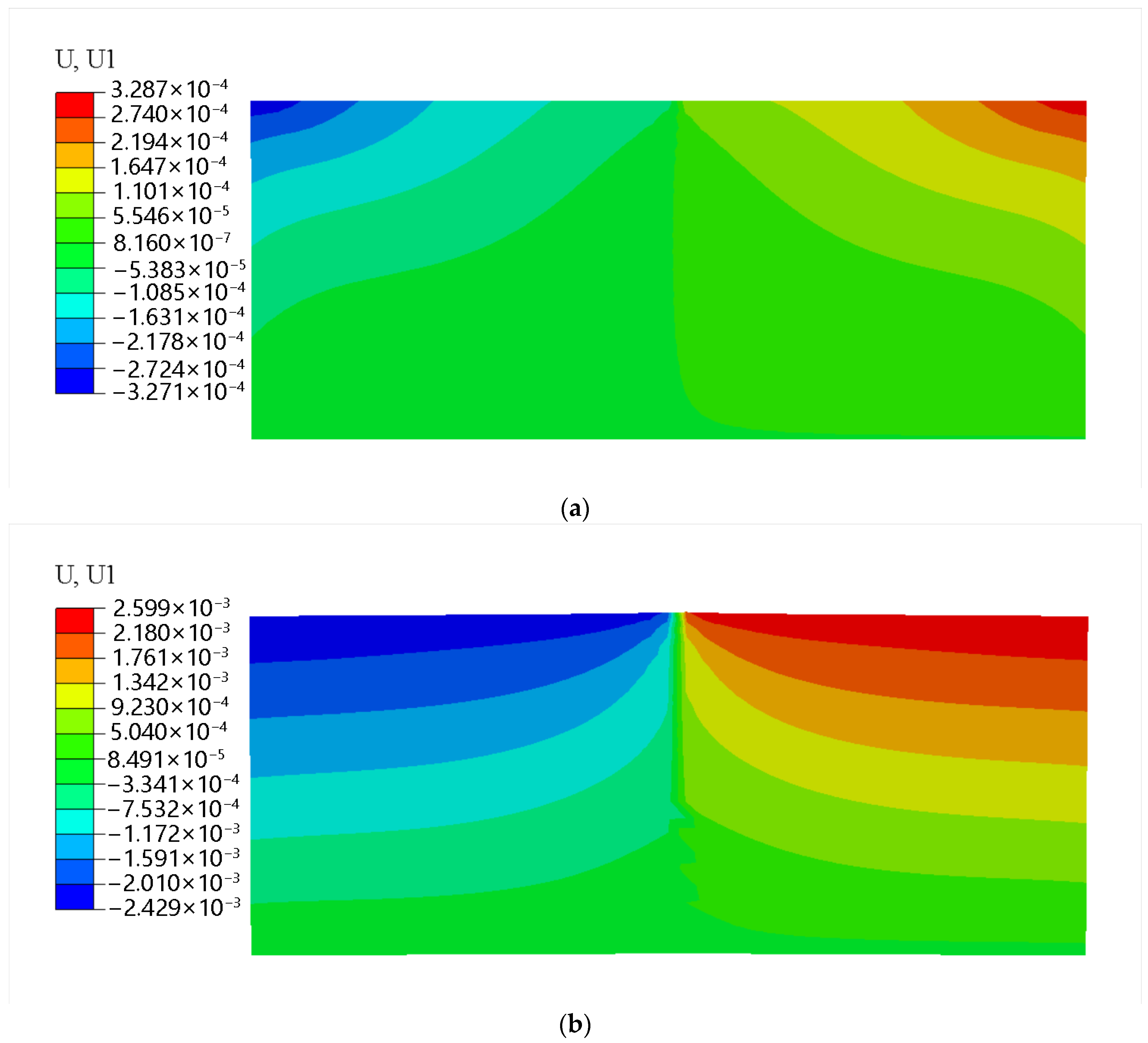
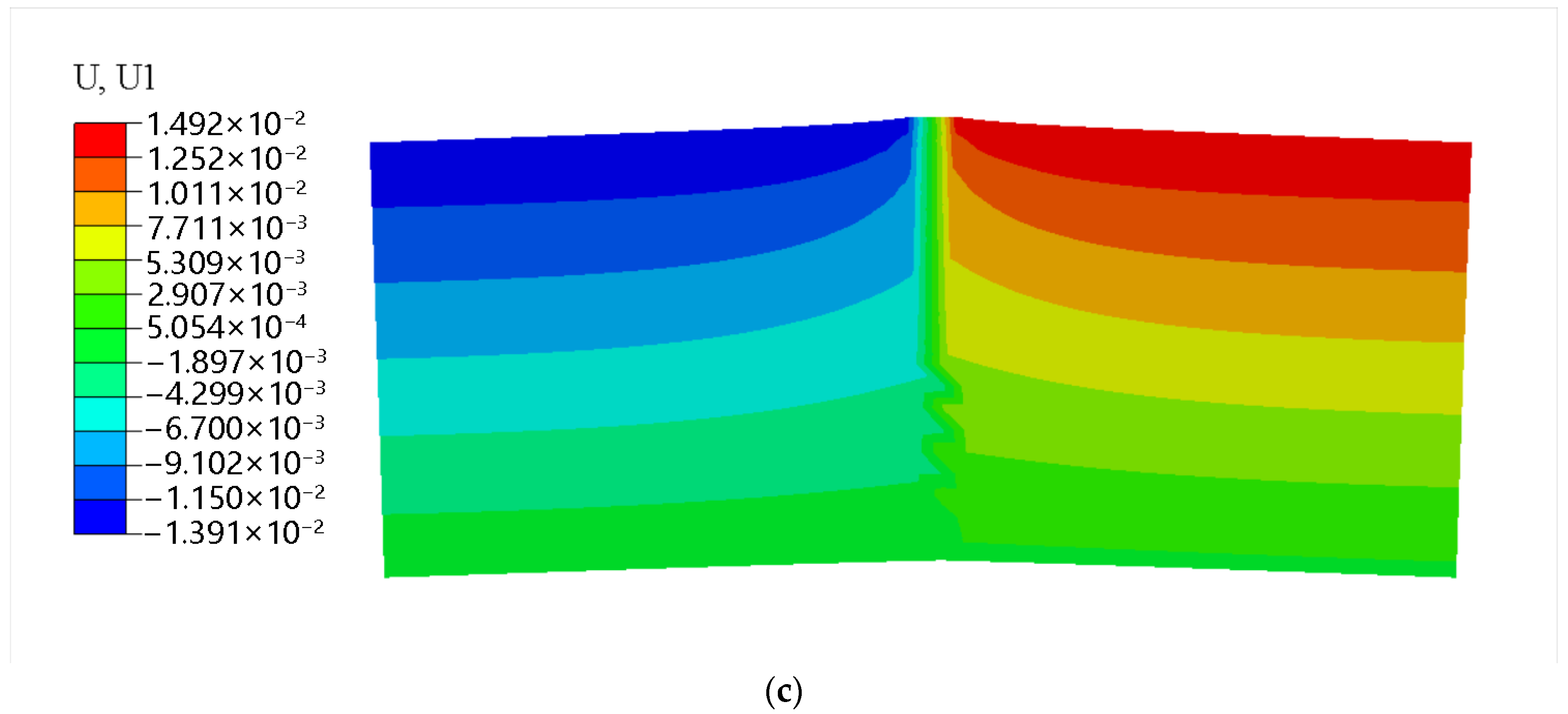
4. Results
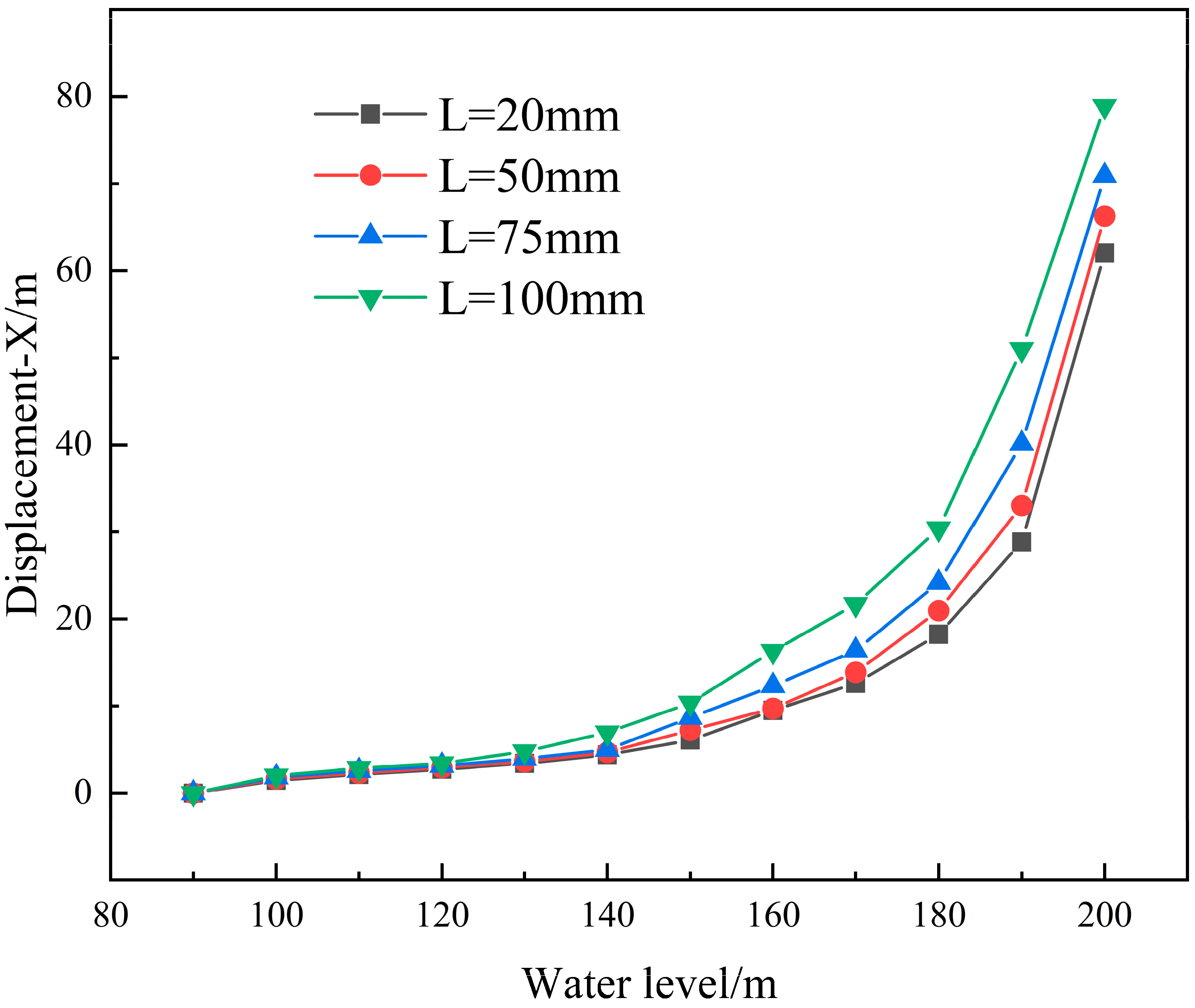
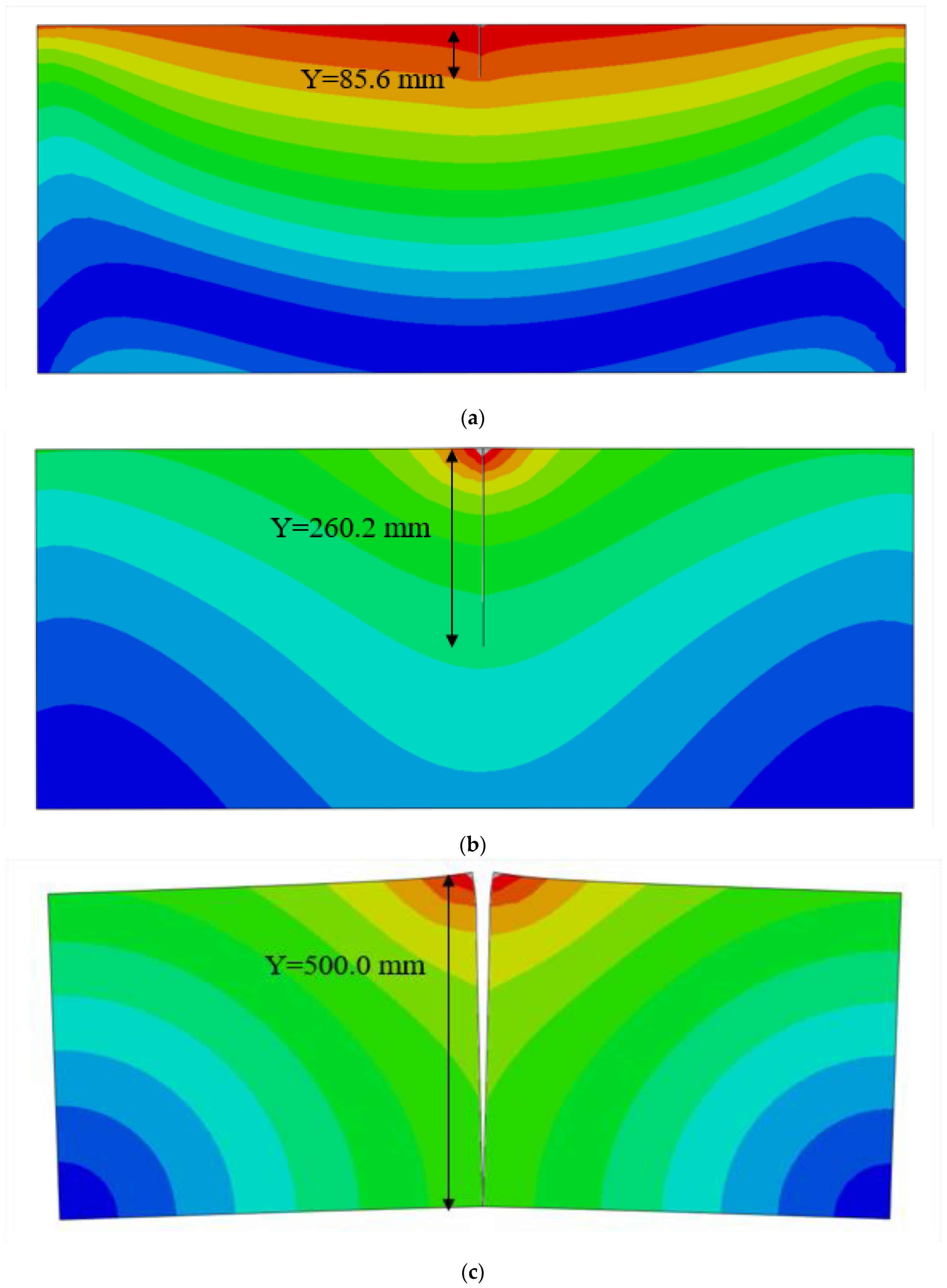
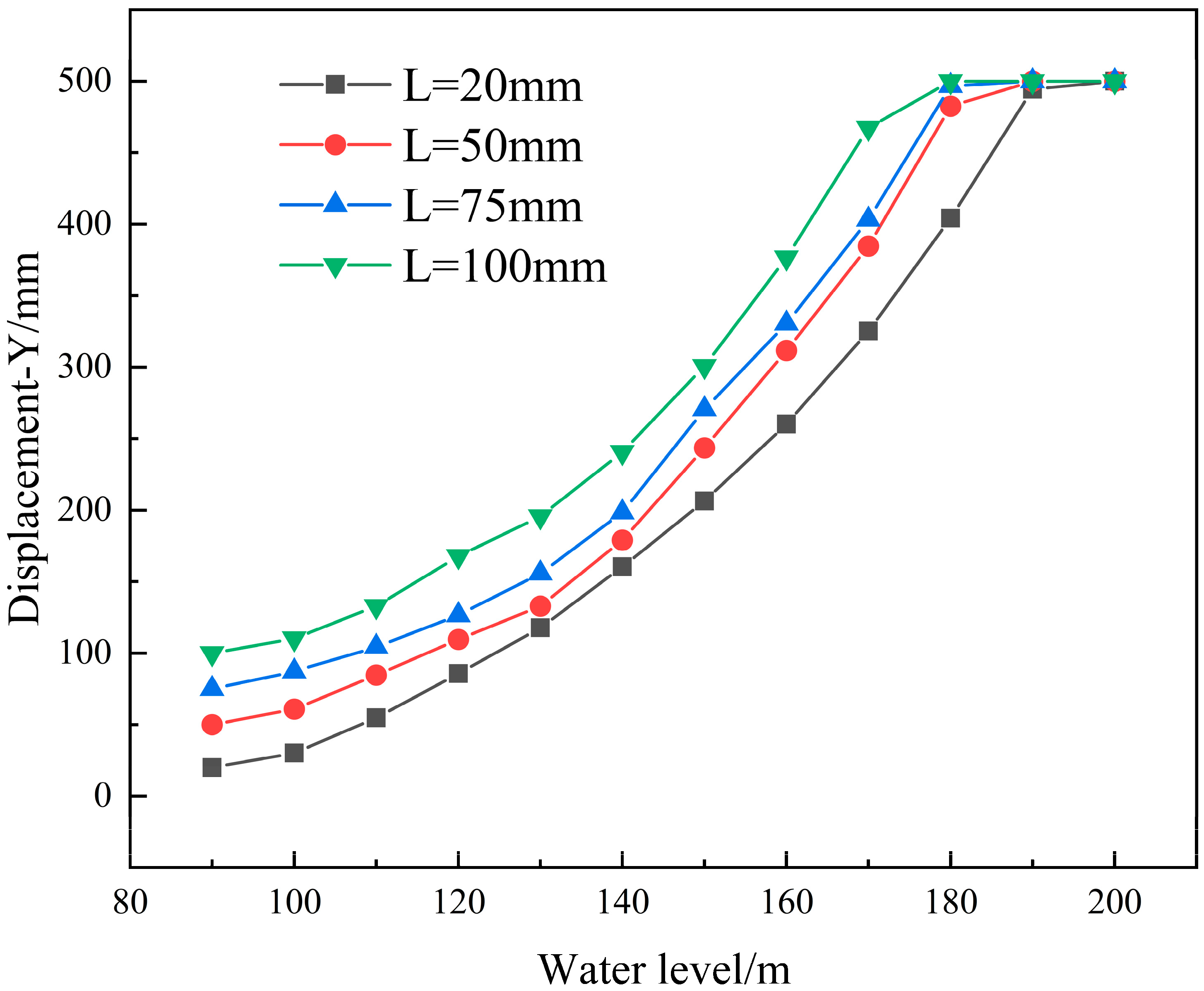
4.1. Different Initial Crack Lengths
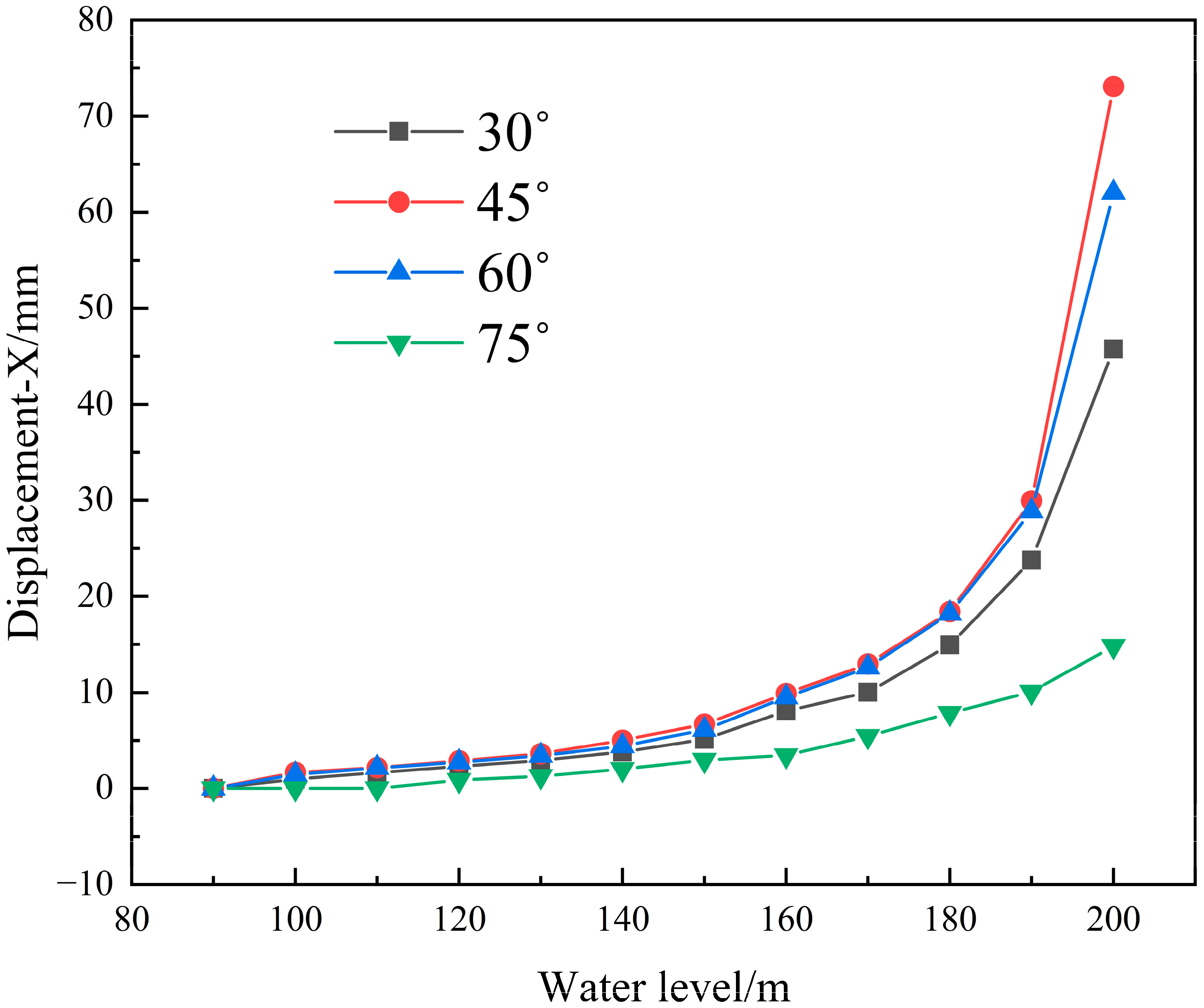
4.2. Different Rock Formation Dips
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yu, P.; Zhang, Y.; Peng, X. Evaluation of impact force of rock landslides acting on structures using discontinuous deformation analysis. Comput. Geotech. 2019, 114, 103137. [Google Scholar] [CrossRef]
- Chen, B.; Barboza, B.R.; Sun, Y.; Bai, J.; Thomas, H.R.; Dutko, M.; Cottrell, M.; Li, C. A review of hydraulic fracturing simulation. Arch. Comput. Methods Eng. 2022, 29, 1–58. [Google Scholar] [CrossRef]
- Ismail, A.; Azadbakht, S. A comprehensive review of numerical simulation methods for hydraulic fracturing. Int. J. Numer. Anal. Methods Geomech. 2024, 48, 1433–1459. [Google Scholar]
- Liu, X.; Hao, Z.; Liu, S.; Zhang, P.; Pan, Y. Study of fracture behavior in three-dimensional Brazilian disk based on phase field method. J. Dalian Univ. Technol. 2025, 65, 181–190. [Google Scholar]
- Zhan, M.L.; Cen, J. Experimental and analytical study on hydraulic fracturing of cylinder sample. Chin. J. Rock Mech. Eng. 2007, 6, 1181–1193. [Google Scholar]
- Wang, S.; Li, D.Y.; Mitri, H. Numerical simulation of hydraulic fracture deflection influenced by slotted directional boreholes using XFEM with a modified rock fracture energy. J. Pet. Sci. Eng. 2020, 193, 107375. [Google Scholar] [CrossRef]
- Lu, S.F.; Wang, S.W.; Chen, X.J. Natural fractures in soft coal seams and their effect on hydraulic fracture propagation: A field study. J. Pet. Sci. Eng. 2020, 192, 107255. [Google Scholar] [CrossRef]
- Ying, Y.; Huang, W.; Ma, Y.; Peng, F. Fracture behavior of periodic porous structures by phase field method. Chin. J. Theor. Appl. Mech. 2022, 54, 3430–3443. [Google Scholar]
- Park, B.Y.; Kim, K.S.; Kwon, S. Determination of the hydraulic conductivity components using a there–dimensional fracture network model in volcanic rock. Eng. Geol. 2002, 66, 127–141. [Google Scholar]
- Azarov, A.; Patutin, A.; Serdyukov, S. Hydraulic fracture propagation near the cavity in a poroelastic media. Appl. Sci. 2021, 11, 11004. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, Y.; Kang, Y. The propagation of hydraulic fractures in a natural fracture network: A numerical study and its implications. Appl. Sci. 2022, 12, 4738. [Google Scholar] [CrossRef]
- Tang, X.; Wan, W.; Lu, Z.; Chen, W. Study on composite fracture characteristics and hydraulic fracturing behavior of hard rock. Appl. Sci. 2024, 14, 2585. [Google Scholar] [CrossRef]
- Liu, T.; Sheng, Y.; Li, Q.; Zhang, C.; Cui, M.; Yu, Z.; Cao, P. Hydraulic fracture propagation in fractured rock mass. Appl. Sci. 2022, 12, 5846. [Google Scholar] [CrossRef]
- Huang, Y.; Zhou, L.T.; Zhou, Z.F. Equations for permeability variation of fractured rock mass under high water pressure. J. Eng. Geol. 2018, 26, 1433–1438. [Google Scholar]
- Li, D.Q.; Li, Z.L.; Lv, C.C. Analysis of fracture strength of rock mass considering fissure additional water pressure. Rock Soil Mech. 2018, 39, 3174–3180. [Google Scholar]
- Zhang, J.; Qin, G.; Wang, B. Study on elastoplastic damage and crack propagation mechanisms in rock based on the phase field method. Appl. Sci. 2025, 15, 6206. [Google Scholar] [CrossRef]
- Hu, S.W.; Wang, Y.; Sun, Y.Y.; Lu, J. Analysis of structure deformation of gravity dam under hydraulic fracturing. J. Water Resour. Archit. 2020, 18, 234–241. [Google Scholar]
- Liu, B.; Jin, Y.; Chen, M. Influence of vugs in fractured–vuggy carbonate reservoirs on hydraulic fracture propagation based on laboratory experiments. J. Struct. Geol. 2019, 124, 143–150. [Google Scholar] [CrossRef]
- Huang, W.; Wang, H.; Zhang, T.; He, M.; Yan, L. Hydraulic pressure effect on mechanical properties and permeabilities of layered rock mass: An experimental study. Eur. J. Environ. Civ. Eng. 2020, 27, 2422–2433. [Google Scholar] [CrossRef]
- Liu, W.; Liu, Y.; Yao, X.; Chu, J.; Chen, X.; Tan, Z. Study on breakdown pressure in hydraulic fracturing process of hard rock based on numerical simulation. Geotech. Geol. Eng. 2021, 39, 909–917. [Google Scholar] [CrossRef]
- Zhang, W.; Shen, Z.; Xu, L.; Zhang, H.; Gan, L.; Li, G. A phase-field fracture model for brittle materials based on COMSOL. Chin. J. Comput. Mech. 2023, 40, 273–280. [Google Scholar]
- Liu, J.; Xue, Y.; Gao, F.; Teng, T.; Liang, X. Propagation of hydraulic fractures in bedded shale based on phase-field method. Chin. J. Geotech. Eng. 2022, 44, 464–473. [Google Scholar]
- Zhao, H.J.; Ma, F.S.; Guo, J. Investigation of hydraulic fracturing mechanism by using a coupled continuous–discontinuous hydromechanical model. IOP Conf. Ser. Earth Environ. Sci. 2020, 570, 042042. [Google Scholar] [CrossRef]
- Cao, Z.; Wang, Y.; Lin, H.; Sun, Q.; Wu, X.; Yang, X. Hydraulic fracturing mechanism of rock mass under stress-damage-seepage coupling effect. Geofluids 2022, 2022, 5241708. [Google Scholar]
- Mao, S.; Li, G.S. Extended finite element modeling of hydraulic fracture propagation. Eng. Mech. 2014, 31, 123–125. [Google Scholar]
- Yu, Y.; Liu, J.; Li, B.; Sun, Y. Analysis of the hydraulic fracturing mechanism and fracture propagation law with a new extended finite element model for the silty hydrate reservoir in the South China Sea. J. Nat. Gas Sci. Eng. 2022, 101, 104535. [Google Scholar] [CrossRef]
- Zheng, A.X.; Luo, X.Q.; Chen, Z.H. Hydraulic fracturing coupling model of rock mass based on extended finite element method. Rock Soil Mech. 2019, 40, 799–808. [Google Scholar]
- Zheng, A.X.; Luo, X.Q. An extended finite element method for modeling hydraulic fracturing in perilous rock. Rock Soil Mech. 2018, 39, 3461–3468. [Google Scholar]
- Shi, Y.K.; Huo, J.Y.; Zhang, D.X. Hydraulic fracturing analysis of concrete gravity dam based on extend finite element method. Sci. Technol. Eng. 2022, 22, 2069–2075. [Google Scholar]
- Hu, Y.F. Hydraulic fracturing analysis of hydraulic pressure tunnel based on extended finite element method. Adhesion 2024, 51, 160–164. [Google Scholar]
- Gao, J.Q.; Zheng, A.X.; Mao, Q. Hydraulic fracturing analysis of gravity dam based on extended finite element method. Water Resour. Power 2018, 36, 95–97. [Google Scholar]
- Li, S.Y.; He, T.M.; Yin, X.C. Introduction to Rock Fracture Mechanics; University of Science and Technology of China Press: Hefei, China, 2010. [Google Scholar]
- Fleming, M.; Chu, Y.A.; Moran, B. Enriched element free Galerkin Methods for crack tip fields. Int. J. Numer. Methods Eng. 1997, 40, 1483–1504. [Google Scholar] [CrossRef]
- Waltersalters, M.C.; Paulino, G.H.; Dodds, R.H. Interaction integral procedures for 3-D curved cracks including surface tractions. Eng. Fract. Mech. 2005, 72, 1635–1663. [Google Scholar] [CrossRef]
- Liu, D.T.; Shen, Z.Z. Experimental study on critical internal water pressure of hydraulic fractured rock mass. South North Water Transf. Water Sci. Technol. 2018, 16, 140–145. [Google Scholar]

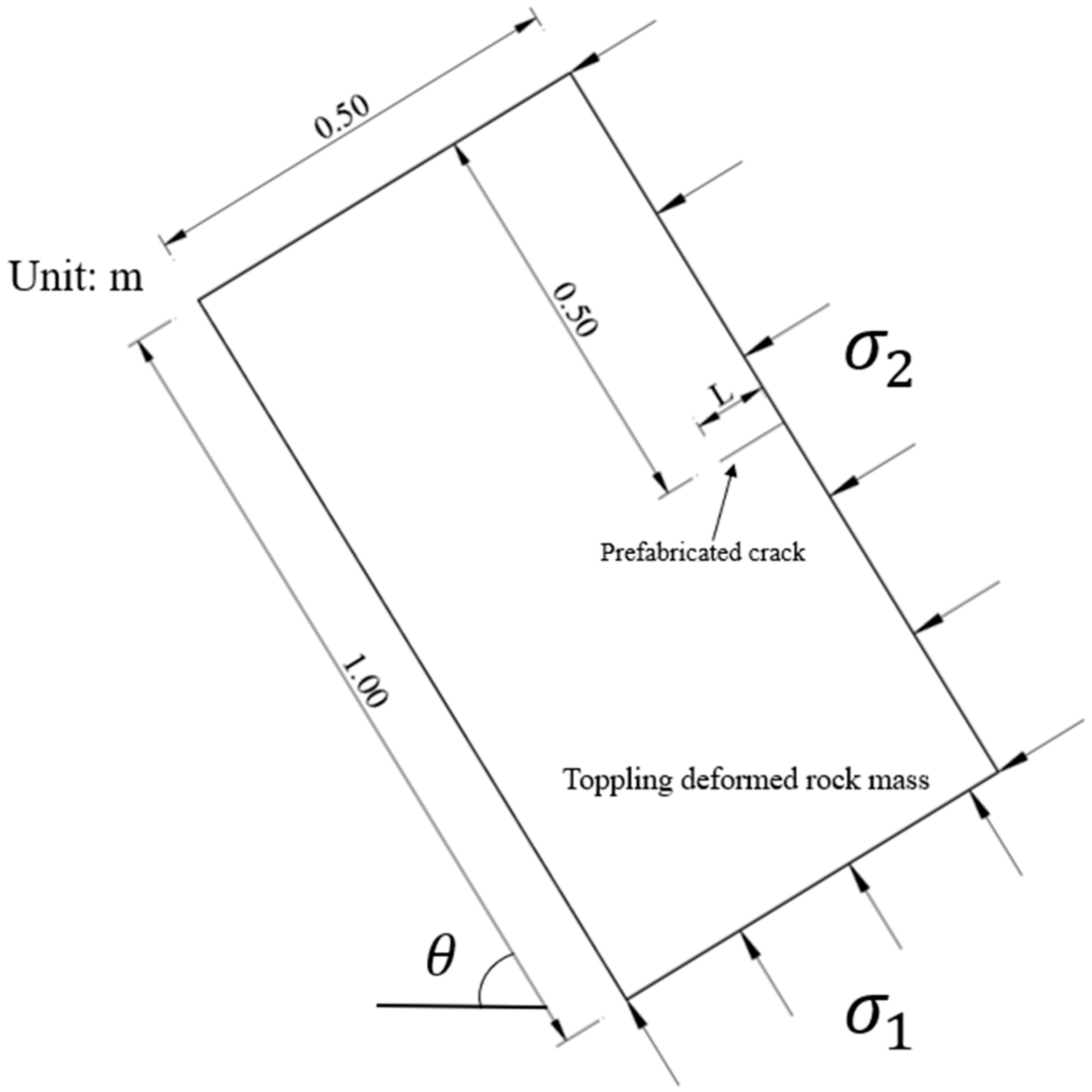

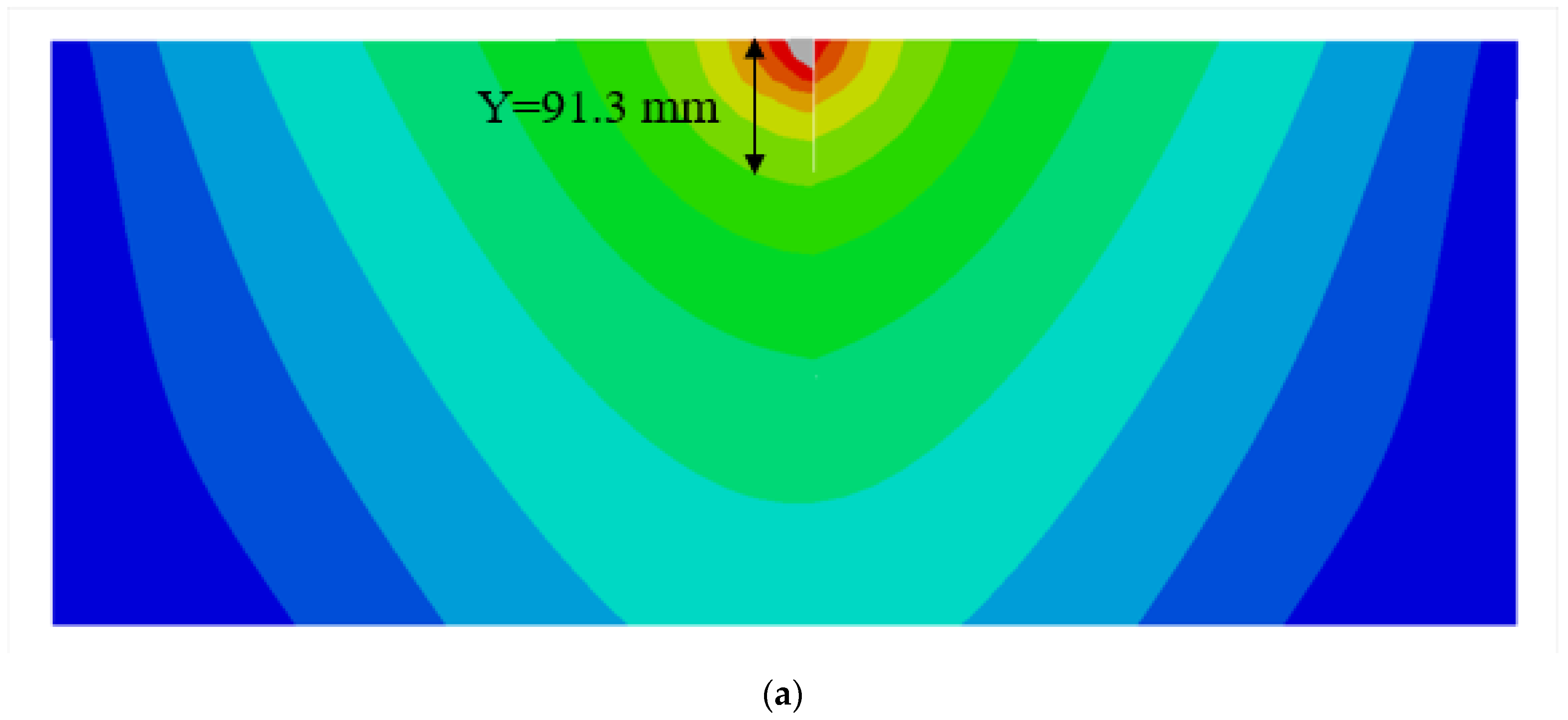
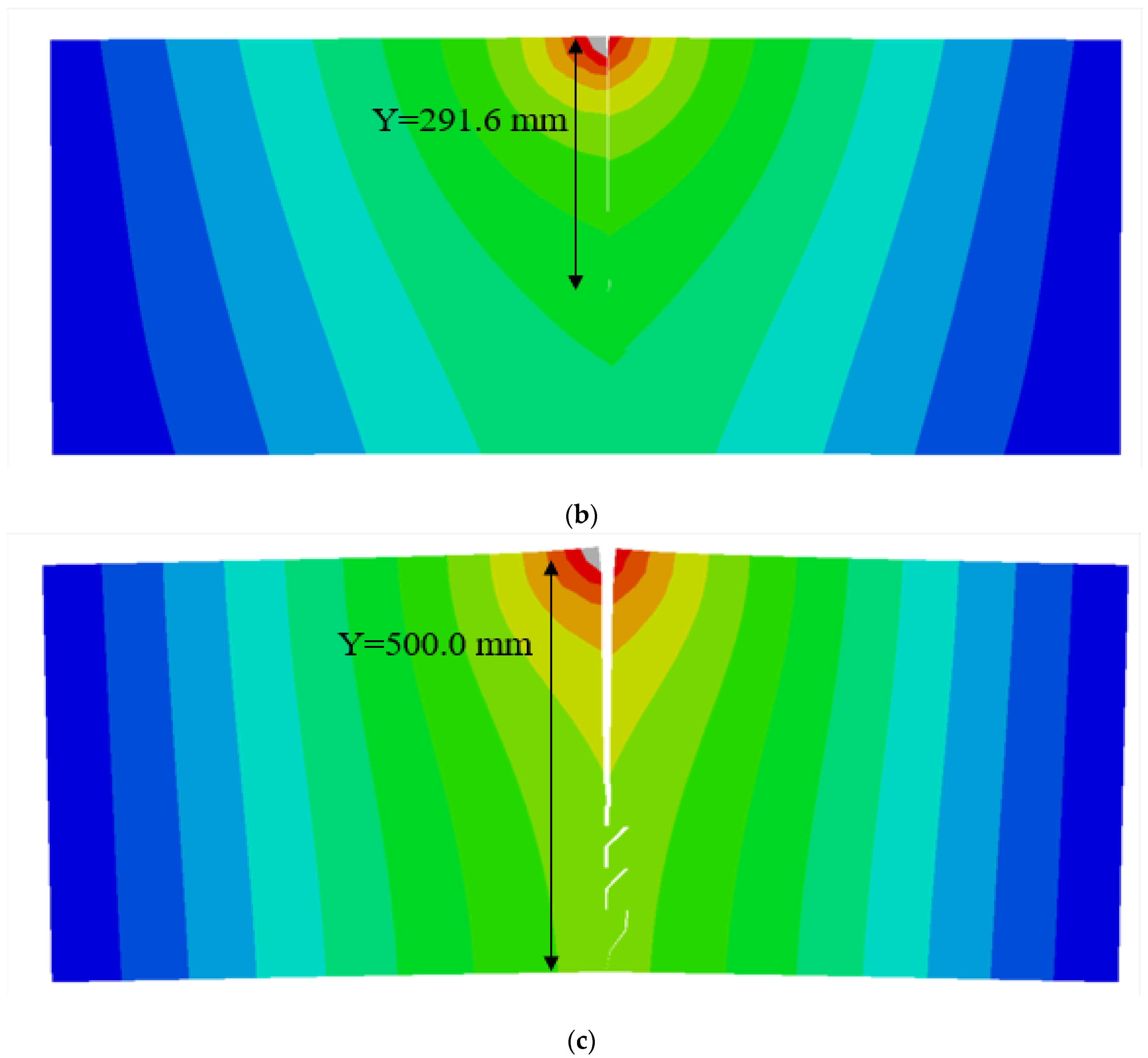
| Permeability Coefficient (m∙s−1) | Fluid Specific Weight (N∙m−3) | Porosity Ratio | Fracture Energy (N∙m−1) | Tensile Strength (MPa) | Elastic Modulus (GPa) | Poisson’s Ratio | Volumetric Weight (KN∙m−3) |
| 1 × 10−8 | 9800 | 0.1 | 8000 | 1.5 | 18.5 | 0.3 | 2.5 × 104 |
| H/m | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L/mm | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 | |
| 20 | X/mm | 0 | 1.45 | 2.14 | 2.73 | 3.42 | 4.41 | 6.11 | 9.50 | 12.62 | 18.23 | 28.85 | 62.04 |
| 50 | X/mm | 0 | 1.62 | 2.31 | 2.94 | 3.63 | 4.70 | 7.22 | 9.71 | 13.89 | 20.96 | 33.03 | 66.30 |
| 75 | X/mm | 0 | 1.83 | 2.55 | 3.15 | 3.95 | 5.00 | 8.67 | 12.32 | 16.39 | 24.17 | 40.15 | 70.91 |
| 100 | X/mm | 0 | 2.01 | 2.87 | 3.40 | 4.81 | 6.95 | 10.37 | 16.31 | 21.70 | 30.37 | 50.99 | 78.94 |
| H/m | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L/mm | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 | |
| 20 | X/mm | 1.45 | 2.14 | 2.73 | 3.42 | 4.41 | 6.11 | 9.50 | 12.62 | 18.23 | 28.85 | 62.04 |
| y | 0.37 | 0.76 | 1.00 | 1.23 | 1.48 | 1.81 | 2.25 | 2.54 | 2.90 | 3.36 | 4.13 | |
| 50 | X/mm | 1.62 | 2.31 | 2.94 | 3.63 | 4.70 | 7.22 | 9.71 | 13.89 | 20.96 | 33.03 | 66.30 |
| y | 0.48 | 0.83 | 1.08 | 1.29 | 1.55 | 1.98 | 2.27 | 2.63 | 3.04 | 3.50 | 4.19 | |
| 75 | X/mm | 1.83 | 2.55 | 3.15 | 3.95 | 5.00 | 8.67 | 12.32 | 16.39 | 24.17 | 40.15 | 70.91 |
| y | 0.60 | 0.94 | 1.15 | 1.37 | 1.61 | 2.16 | 2.51 | 2.80 | 3.19 | 3.69 | 4.26 | |
| 100 | X/mm | 2.01 | 2.87 | 3.40 | 4.81 | 6.95 | 10.37 | 16.31 | 21.70 | 30.37 | 50.99 | 78.94 |
| y | 0.70 | 1.05 | 1.22 | 1.57 | 1.94 | 2.34 | 2.79 | 3.08 | 3.41 | 3.93 | 4.37 | |
| H/m | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L/mm | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 | |
| 20 | Y/mm | 20.0 | 30.1 | 54.7 | 85.6 | 117.7 | 160.3 | 206.3 | 260.2 | 325.2 | 404.2 | 494.3 | 500.0 |
| 50 | Y/mm | 50.0 | 60.8 | 84.6 | 109.6 | 132.8 | 179.1 | 243.5 | 311.6 | 384.7 | 482.5 | 500.0 | 500.0 |
| 75 | Y/mm | 75.0 | 87.1 | 104.3 | 126.6 | 155.8 | 198.4 | 270.6 | 330.4 | 403.1 | 496.7 | 500.0 | 500.0 |
| 100 | Y/mm | 100.0 | 110.2 | 132.9 | 167.8 | 195.7 | 240.6 | 300.8 | 376.7 | 467.3 | 500.0 | 500.0 | 500.0 |
| H/m | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| θ | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 | |
| 30° | X/mm | 0 | 0.97 | 1.67 | 2.31 | 2.93 | 3.81 | 5.14 | 8.09 | 10.01 | 14.96 | 23.76 | 45.77 |
| 45° | X/mm | 0 | 1.69 | 2.18 | 2.89 | 3.62 | 5.03 | 6.70 | 9.89 | 12.97 | 18.41 | 29.97 | 73.11 |
| 60° | X/mm | 0 | 1.45 | 2.14 | 2.73 | 3.42 | 4.41 | 6.11 | 9.50 | 12.62 | 18.23 | 28.85 | 62.04 |
| 75° | X/mm | 0 | 0 | 0 | 0.88 | 1.27 | 2.01 | 2.97 | 3.45 | 5.47 | 7.86 | 10.08 | 14.82 |
| H/m | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| θ | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 | |
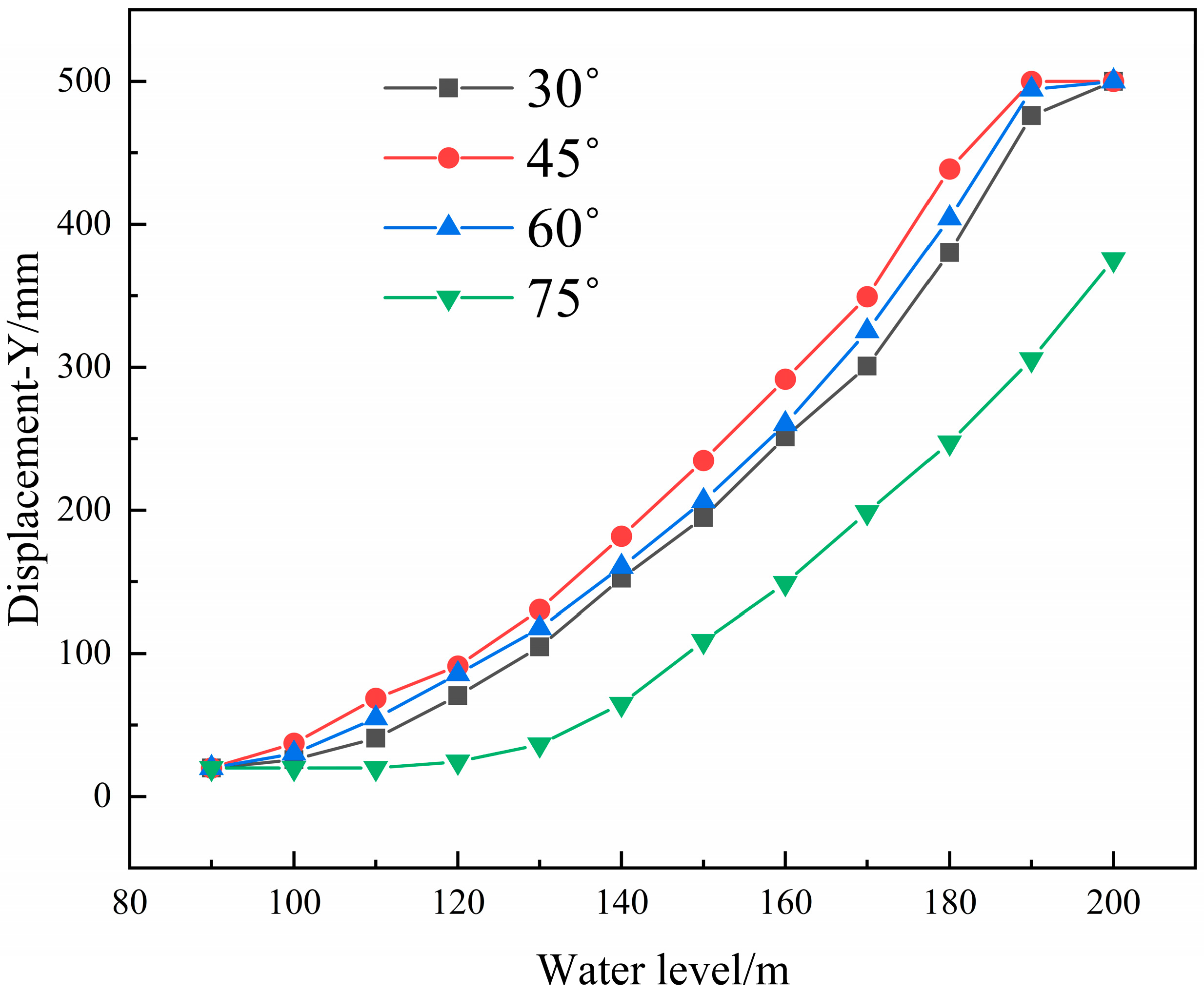
| 30° | Y/mm | 20.0 | 25.8 | 40.9 | 70.6 | 104.6 | 152.3 | 194.8 | 251.2 | 300.8 | 380.3 | 475.9 | 500.0 |
| 45° | Y/mm | 20.0 | 37.2 | 68.6 | 91.3 | 130.6 | 181.7 | 234.8 | 291.6 | 349.3 | 438.6 | 500.0 | 500.0 |
| 60° | Y/mm | 20.0 | 30.1 | 54.7 | 85.6 | 117.7 | 160.3 | 206.3 | 260.2 | 325.2 | 404.2 | 494.3 | 500.0 |
| 75° | Y/mm | 20.0 | 20.0 | 20.0 | 24.3 | 36.4 | 64.8 | 108.7 | 148.9 | 198.6 | 247.3 | 305.6 | 375.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, H.; Dong, M. Toppling Deformed Rock Mass Hydraulic Fracturing Analysis Based on Extended Finite Elements. Appl. Sci. 2025, 15, 10177. https://doi.org/10.3390/app151810177
Pan H, Dong M. Toppling Deformed Rock Mass Hydraulic Fracturing Analysis Based on Extended Finite Elements. Applied Sciences. 2025; 15(18):10177. https://doi.org/10.3390/app151810177
Chicago/Turabian StylePan, Haibin, and Menglong Dong. 2025. "Toppling Deformed Rock Mass Hydraulic Fracturing Analysis Based on Extended Finite Elements" Applied Sciences 15, no. 18: 10177. https://doi.org/10.3390/app151810177
APA StylePan, H., & Dong, M. (2025). Toppling Deformed Rock Mass Hydraulic Fracturing Analysis Based on Extended Finite Elements. Applied Sciences, 15(18), 10177. https://doi.org/10.3390/app151810177






