Experimental Study on Mechanical Specific Energy Optimization in Axial–Torsional Coupled Impact Drilling

Abstract

Axial–torsional coupled impact drilling (ATCID) technology represents a promising solution for overcoming the drilling challenges posed by conglomerate formations, which are characterized by strong heterogeneity, high abrasiveness, and poor drillability. However, the optimal parameter matching relationships and their influence patterns on mechanical specific energy (MSE) remain unclear. This study employed self-developed true triaxial impact rotary rock breaking equipment with conglomerate cores from the Junggar Basin to systematically investigate the effects of weight on bit (WOB), rotational speed (RPM), axial impact frequency, and torsional impact frequency on MSE through orthogonal experimental design. The results demonstrate that the parameter influence ranking on MSE is as follows: torsional impact frequency > WOB > RPM > axial impact frequency, with torsional impact frequency exhibiting the largest range value (87.5 MPa). ANOVA reveals that the interaction between axial and torsional impact frequencies is the dominant controlling factor, contributing 22.8% to MSE variation with high statistical significance. The optimal parameter combination yields the minimum MSE (103 MPa): 19 kN WOB, 20 r/min RPM, 20 Hz axial impact frequency, and 20 Hz torsional impact frequency, representing a 69.1% reduction compared to the maximum value. Response surface analysis revealed that increasing WOB significantly reduces MSE, RPM exhibits positive correlation with MSE, and synergistic effects occur when both impact frequencies reach high values simultaneously. A nonlinear MSE prediction model incorporating main effects, quadratic terms, and interaction effects was established with R² = 0.8240 and a mean absolute percentage error of 9.26%. The research findings provide an essential theoretical foundation for parameter optimization and engineering applications of ATCID technology, offering significant implications for enhancing drilling efficiency in conglomerate and other challenging hard rock formations.

1. Introduction

Deep and ultra-deep well drilling represents a crucial development direction in contemporary energy exploration, yet faces unprecedented technical challenges when encountering hard rock formations. Conglomerate formations, as extensively distributed challenging formations in deep drilling operations, pose significant obstacles to drilling efficiency due to their pronounced heterogeneity, high abrasiveness, and poor drillability characteristics [1,2,3]. Within the Tarim Basin’s deep hydrocarbon resources, 83.2% of petroleum reserves and 63.9% of natural gas reserves are situated at depths exceeding 6000 m, where conglomerate formations are routinely encountered during resource development [4]. Studies demonstrate that conglomerate drilling operations exhibit extremely low rates of penetration (ROP), with drilling speeds of merely 0.5–3.5 m/h recorded in the Luno field conglomerate reservoir in the Norwegian North Sea—substantially lower than conventional formation drilling rates [5]. Conventional drilling technologies typically encounter severe bit wear, wellbore instability, and diminished drilling efficiency when addressing the high hardness and pronounced heterogeneity characteristic of conglomerate formations [6].

Impact drilling technology, as an efficient non-contact rock fragmentation method, demonstrates considerable potential for overcoming penetration rate limitations in conglomerate and other challenging rock formations [7,8]. Axial–torsional coupled impact drilling (ATCID), as an innovative composite impact technology, achieves three-dimensional rock fragmentation by simultaneously applying axial and torsional impact loads to the drill bit, offering substantial advantages for efficient rock destruction in conglomerate and other deep hard rock formations. Experimental investigations by Mu revealed that coupled impact increased penetration depth and drilling rate by 173.38% and 182.74% [9], respectively, compared to axial impact alone. Numerical simulation studies by Song demonstrated that increasing impact velocity from 4 m/s to 16 m/s resulted in a 62.8% improvement in total energy transfer efficiency [10]. Nevertheless, the application of this technology in conglomerate formations continues to face challenges including suboptimal efficiency and unclear relationships among critical drilling parameters, with the optimal matching ratio between axial and torsional impact frequencies remaining a fundamental engineering problem requiring comprehensive investigation [11]. Building upon foundational work by Mu [9] and Shi et al. [11], this study addresses a critical gap concerning the complex, higher-order effects of drilling parameters in ATCID. We advance the understanding of this process by leveraging a novel, patented true triaxial drilling simulator that enables unprecedented control over synchronized impacts. This unique experimental platform allows us to move beyond main-effects analysis to systematically quantify the dominant influence of the axial–torsional frequency interaction (AF-TF) and the significant nonlinear effect of torsional frequency on mechanical specific energy (MSE). Ultimately, these findings are integrated into a robust predictive model that incorporates these critical higher-order terms, providing a more mechanistic basis and a practical tool for optimizing drilling efficiency in challenging formations.

Mechanical specific energy (MSE), as a key indicator for quantifying drilling efficiency and optimizing rate of penetration, has experienced rapid development in drilling engineering applications in recent years. MSE is defined as the mechanical work required to fracture a unit volume of rock and has been widely applied in drilling parameter optimization, performance evaluation, and real-time monitoring [12]. Recently, MSE optimization methods based on experimental design have gained widespread application in drilling engineering. In drilling parameter optimization research, Derdour applied the Taguchi method and response surface methodology to optimize penetration rates in rotary impact drilling, with experimental results showing that air pressure is the most significant factor affecting penetration rate, contributing 59.90% [13]. Chen utilized response surface methodology and multi-objective optimization techniques to study the relationship between penetration rate and MSE, establishing a statistical model with an R² of 96.19% [14]. Mafazy employed response surface methodology and analysis of variance to investigate the effects of weight on bit, RPM (revolutions per minute), cutting angle, and rock resistance on penetration rate during drilling, achieving a model correlation coefficient of 96.19% [15]. In composite material drilling optimization, Yarar used response surface methodology to optimize drilling parameters for Nomex aramid fiber composites, determining optimal drilling conditions through Box–Behnken design and ANOVA analysis [16]. Tzotzis combined artificial neural networks and response surface methodology to optimize composite material drilling processes, demonstrating RSM effectiveness in multi-factor optimization [17]. In impact drilling applications, Chen developed drilling parameter optimization technology for extended reach wells based on MSE and machine learning methods [18]. Song proposed an improved rock breaking specific energy model for real-time drilling efficiency evaluation [19]. Qin established a novel MSE model for composite impact drilling, considering the effects of composite impactors on axial and torsional impact forces applied to the drill bit [20]. However, research on MSE models specifically for axial–torsional coupled impact drilling remains relatively limited, particularly regarding MSE influence mechanisms under complex parameter coupling effects, which has become a key bottleneck constraining further development of this technology. Additionally, recent developments in vibration management technologies have advanced smart controllers for vibration assessment and analytical models for shock absorption mechanisms, providing potential integration pathways for emerging drilling optimization techniques [21,22,23].

Based on the current research status, this study conducts axial–torsional coupled impact rock breaking experiments and systematically investigates the influence patterns of weight on bit, RPM, axial impact frequency, and torsional impact frequency on mechanical specific energy using orthogonal experimental design methods. The study identifies key controlling factors of mechanical specific energy through analysis of variance (ANOVA) and response surface methodology, and establishes an MSE prediction model to provide theoretical foundation for parameter optimization of axial–torsional coupled impact drilling technology. The research findings have significant theoretical importance and practical value for improving drilling efficiency in deep hard rock formations and reducing drilling costs.

2. Materials and Methods

2.1. Experimental Equipment

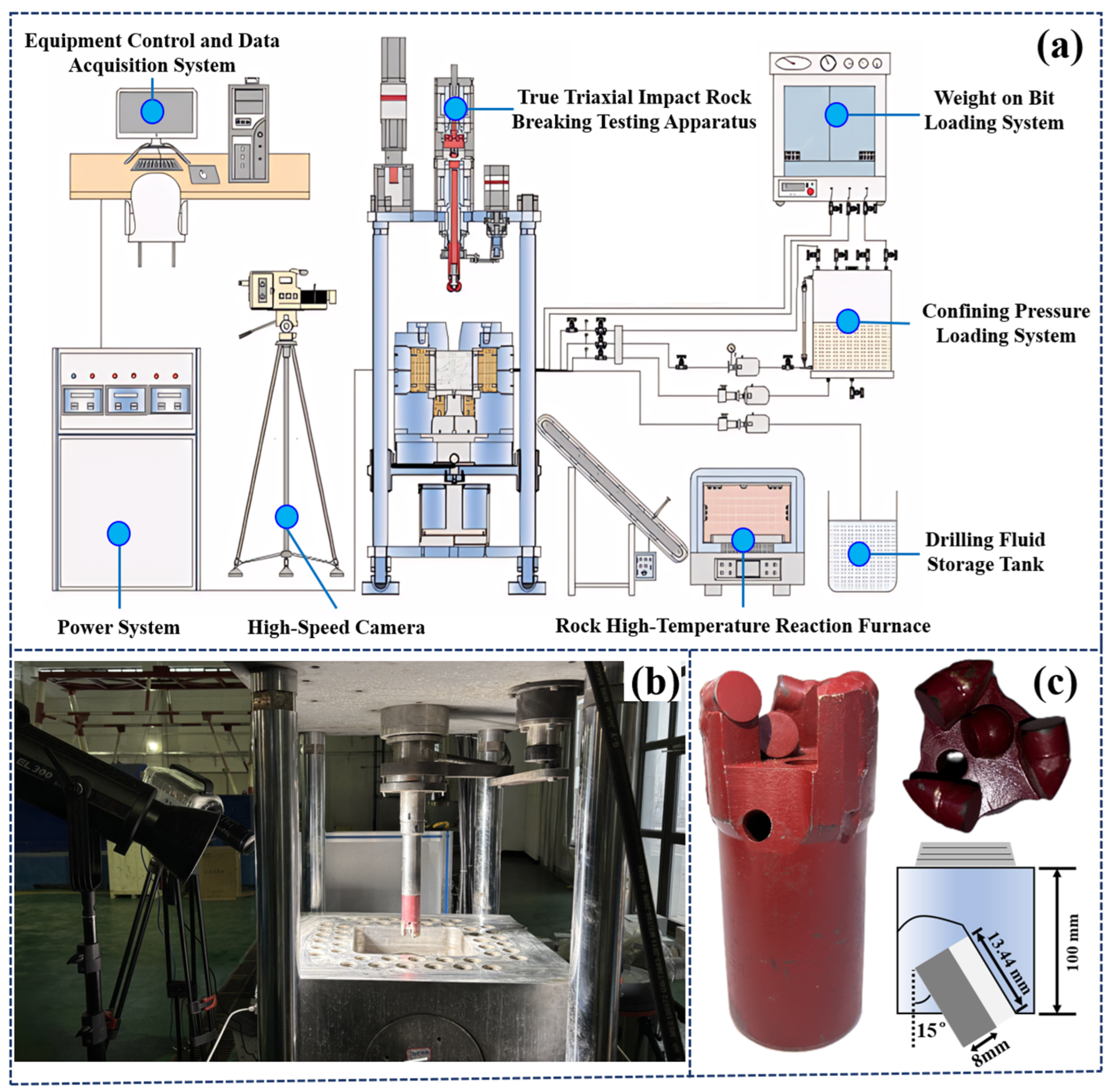
This study employed a self-developed true triaxial impact rotary rock breaking apparatus to conduct axial–torsional coupled impact drilling experiments. The overall configuration of the experimental equipment is shown in Figure 1, which primarily comprises key modules including the true triaxial rock breaking test platform, confining pressure regulation system, drilling fluid storage unit, power transmission system, axial impact control system, and torsional impact control system.

As shown in Figure 1a, this diagram illustrates the axial–torsional coupled impact drilling system, where the load-bearing frame serves as the fundamental structure supporting all components of the high-temperature, high-pressure impact rock breaking apparatus. The rotation system is integrated within the axial impact system and is equipped with servo motors that transmit power through synchronous belts, as depicted in Figure 1b. The torsional impact system is positioned on the upper plate of the load-bearing frame, arranged parallel to the axial impact system. It employs motor-controlled eccentric wheels that drive connecting rods to generate periodic torsional impact forces applied to the drill bit. Each torsional impact cycle consists of approximately 20–30% active loading phase during which the eccentric wheel-connecting rod assembly applies impact force to the drill string, followed by a 70–80% release phase. This intermittent loading mechanism ensures consistent frequency maintenance even during PDC cutter–rock contact, with the temporal coordination between axial and torsional impacts precisely controlled through the PLC system. The axial impact system is similarly located on the upper plate and utilizes motor-driven transmission belts to actuate impact components, thereby delivering axial impacts to the drill bit.

The synchronization of axial and torsional impacts is achieved through a sophisticated PLC multi-directional control system. This master controller coordinates three independent servo motors through high-precision timing signals with microsecond-level accuracy. The system employs a master–slave control architecture where the PLC simultaneously sends synchronized command signals to the axial impact servo motor, torsional impact servo motor, and rotation servo motor. Each impact mode operates independently while maintaining precise phase relationships through the centralized control system, enabling flexible frequency combinations ranging from 5–20 Hz for both axial and torsional impacts. Real-time feedback from load sensors and torque sensors ensures continuous monitoring and adjustment of impact parameters during operation. The control system allows for independent adjustment of impact amplitudes and frequencies, while maintaining synchronization accuracy within ±0.1 Hz for both impact modes.

Prior to conducting the orthogonal experiments, the apparatus underwent comprehensive validation procedures to ensure measurement accuracy and reliability. All sensors were calibrated using certified reference standards with traceability to national measurement standards, achieving calibration accuracy within ±1% for all key parameters. Baseline validation experiments using conventional rotary drilling confirmed the consistency of measured parameters (WOB, torque, ROP) with established drilling relationships. Repeatability tests under identical parameter settings demonstrated measurement consistency with coefficients of variation below 5% for all critical parameters. The impact frequency accuracy was verified using high-speed data acquisition systems, confirming that both axial and torsional frequencies were maintained within ±0.1 Hz of target values throughout experimental duration.

This system can independently execute either torsional or axial impact according to experimental requirements and supports multi-directional impact drilling tests in both two-dimensional and three-dimensional (X-, Y-, and Z-axis loading) configurations. The impact system and rock core holder are connected to a PLC multi-directional controller via cables, which regulates parameters such as WOB and RPM required for different tests. The experiments utilize a 50 mm diameter diamond drill bit (Figure 1c) with a cutter diameter of 13.44 mm, PDC cutter thickness of 8 mm, and cutter rake angle of 15°. The specific parameters of the apparatus are presented in

Table 1. Technical parameters of experimental equipment.

RPM	WOB	Torque Sensor	Axial Impact Force	Pressure Sensor	Load Sensor	AF	TF
0–60 r/min	0–20 kN	500 N·m	0–6 kN	1 MPa	15,000 Kg	20 Hz	20 Hz

.

Prior to testing, appropriate loading rate parameters, target values, dwell time, rotational speed, and displacement limits must be configured according to experimental objectives. The rock breaking test procedure is divided into two operational phases: preliminary drilling and impact rock breaking. During the preliminary drilling phase, the rock sample height is adjusted to establish slight contact between its upper surface and the drill bit. Subsequently, the rotation function is activated to slowly penetrate to a depth of 5 mm before operation is paused. This phase effectively prevents damage to both the drill bit and rock sample. Once the WOB reaches the preset target value and stabilizes, both rotation and impact loading functions are simultaneously activated to formally commence the impact rock breaking test. Upon reaching the predetermined drilling depth, the system automatically terminates operation.

2.2. Experimental Material

This study utilized actual rock cores from the Junggar Basin as the primary research specimens. The rock cores were processed using wire saw cutting and polished to ensure parallel end surfaces, then embedded in C60 grade concrete and sectioned into cubic rock samples measuring 150 mm × 150 mm × 150 mm, as illustrated in Figure 2b. The concrete embedding approach was designed to provide controlled triaxial stress conditions while minimizing boundary effects on the drilling process. The C60 concrete shell serves as a confining medium similar to surrounding formations in actual drilling conditions. The rock specimen dimensions (approximately 100 mm diameter) within the 150 mm concrete shell are significantly larger than the drill bit diameter (50 mm), maintaining a 2:1 size ratio that minimizes boundary effects on the immediate drilling zone. The impact frequencies used (5–20 Hz) generate wavelengths in rock that are much larger than the specimen dimensions, reducing the influence of boundary reflections in the frequency domain of interest. While the concrete shell may introduce some boundary condition differences compared to infinite rock formations, the focus on steady-state mechanical specific energy calculations, rather than transient wave effects, minimizes the sensitivity to these boundary conditions.

To determine the rock mechanical properties, triaxial compression tests were performed on cylindrical specimens using an RTR-1000 testing machine (GCTS Testing Systems, Tempe, AZ, USA) shown in Figure 2a in accordance with ISRM (International Society for Rock Mechanics) standards. The cylindrical specimens had dimensions of Ø25 mm × 50 mm, as depicted in Figure 2c, with experimental results presented in

Table 2. Rock physical and mechanical properties.

No.	Confining Pressure (MPa)	Compressive Strength (MPa)	Elastic Modlus (GPa)	Poisson’s Ratio	Desity (g/cm3)
Sandstone #1	15	114.51	13.20	0.16	2.472
Sandstone #2	30	121.82	26.52	0.17	2.476

.

2.3. Experimental Design

This study primarily employs orthogonal rock breaking experiments combined with analysis of variance (ANOVA) and response surface methodology (RSM) to investigate the effects of impact approach, weight on bit, RPM, axial impact frequency, and torsional impact frequency on drilling performance, and to identify key influencing factors.

Orthogonal experimental design was first introduced by Fisher [24], with Taguchi further advancing this methodology to enable acquisition of main effects and interactive effects information for various factors using fewer experimental trials [25,26]. Analysis of variance (ANOVA) quantitatively evaluates each factor’s contribution to response variables, determining significant factors and their influence ranking [27,28]. RSM constructs mathematical models to describe functional relationships between factors and responses, facilitating parameter optimization and prediction [29,30].

The experimental conditions simulate downhole conditions at a well depth of 4000 m and temperature of 110 °C. To replicate realistic in situ stress conditions, the experimental design was based on actual field data from the wellsite where the rock cores were obtained. At 4000 m depth, field measurements indicate formation temperature of 107.4 °C, overburden pressure of 92 MPa, maximum horizontal principal stress of 76 MPa, and minimum horizontal principal stress of 63 MPa. The stress coefficient is calculated as (σH − σh)/σH = (76 − 63)/76 ≈ 0.17. Using a scaling approach to maintain identical stress ratios, the experiment maintained a maximum horizontal stress (σH) of 20 MPa, minimum horizontal stress (σh) of 16.6 MPa, and overburden stress of 23 MPa, preserving the same relative stress state as field conditions. The experimental temperature of 110 °C closely matches the actual formation temperature of 107.4 °C. Throughout the experimental process, parameters including weight on bit, drilling depth, torque, and rate of penetration were continuously monitored and recorded. Based on the fundamental performance parameters of the axial–torsional coupled impact drilling system and impact energy calibration test data, combined with conventional rotary drilling field data and previous research findings, the orthogonal experimental factor levels were established, as presented in

Table 3. Factor level settings for orthogonal experiments.

Factor	A:WOB (kN)	B:RPM (r/min)	C:AF (Hz)	D:TF (Hz)
Level 1	10	20	5	5
Level 2	13	30	10	10
Level 3	16	40	15	15
Level 4	19	50	20	20

.

Based on the aforementioned factors and level configurations, 16 parameter combinations were designed for the experiments, with each test conducted to a penetration depth of 30 mm. The experimental parameter combinations are presented in

Table 4. Orthogonal experimental parameter combinations.

No	WOB (kN)	RPM (r/min)	AF (Hz)	TF (Hz)	MSEtea (MPa)	MSEdup (MPa)
C1	10	20	5	5	177	62.2
C2	13	30	10	10	243	85.1
C3	19	50	20	20	103	37.4
C4	16	40	15	15	276	96.7
C5	10	30	15	20	131	45.8
C6	16	50	5	10	286	100
C7	13	20	20	15	165	57.9
C8	19	40	10	5	216	76.1
C9	16	20	10	20	193	67.7
C10	19	30	5	15	221	77.8
C11	10	40	20	10	239	83.5
C12	13	50	15	5	273	95.7
C13	13	40	5	20	218	76.4
C14	19	20	15	10	208	72.8
C15	16	30	20	5	261	91.3
C16	10	50	10	15	333	116

.

2.4. Mechanical Specific Energy Calculation Method

Based on precisely measured key parameters including torque, rate of penetration, weight on bit, and RPM from the experiments, MSE values were systematically calculated under different experimental conditions. To comprehensively evaluate rock breaking efficiency, typical vertical drilling MSE models were adopted. The mathematical expressions of these models originate from the classic studies of Teale and Dupriest and Koederitz [12,31]. These models were used to calculate MSE under various experimental conditions and evaluate rock breaking efficiency under different axial–torsional impact frequency combinations. The MSE calculation formulas are as follows:

$$MS{E}_{tea}={\displaystyle \frac{WOB}{A_b}}+{\displaystyle \frac{480·RPM·TOB}{D_b^2·ROP}}$$

(1)

$$MS{E}_{dup}=0.35·\left({\displaystyle \frac{WOB}{A_b}}+{\displaystyle \frac{120\pi ·RPM·TOB}{A_b·ROP}}\right)$$

(2)

where MSE is mechanical specific energy (psi); WOB is weight on bit (lbf); A_b is drill bit cross-sectional area (in²); RPM is revolutions per minute (r/min); TOB is torque on bit (ft·lbs); D_b is drill bit diameter (ft); ROP is rate of penetration (ft/h); μ is friction coefficient (dimensionless); and 0.35 is the correction coefficient in the Dupriest model.

3. Results

3.1. Experimental Results

Mechanical specific energy, as a critical indicator for evaluating drilling efficiency, directly reflects the energy consumption required to fracture a unit volume of rock. Figure 3 presents a comparison of MSE calculation results from 16 orthogonal experimental runs using both the Teale and Dupriest models: (a) shows results from the Teale model and (b) shows results from the Dupriest model. where upward triangles indicate maximum MSE values and downward triangles indicate minimum MSE values for each experimental condition. The figure demonstrates that while absolute values differ between the two models, their trends exhibit high consistency. Due to the widespread application of the Teale model in engineering practice, the subsequent analysis is primarily based on results from this model.

Table 4 presents detailed MSE data means for each experimental group. Statistical analysis reveals coefficients of variation for the rock breaking parameters as follows: WOB (23.13%), RPM (31.94%), axial impact frequency (44.72%), and torsional impact frequency (44.72%), with an overall MSE coefficient of variation of 25.99%. The experimental results demonstrate that the parameter combination of 19 kN weight on bit, 50 r/min RPM, 20 Hz axial impact frequency, and 20 Hz torsional impact frequency achieved the minimum MSE value (103 MPa), indicating optimal energy efficiency for this configuration. Group analysis revealed the influence patterns of individual parameter levels on MSE: the 19 kN WOB group averaged 187 MPa, the 20 r/min RPM group averaged 185.75 MPa, the 20 Hz axial impact frequency group averaged 192 MPa, and the 20 Hz torsional impact frequency group achieved the lowest average MSE (161.25 MPa). These data indicate that high WOB and high torsional impact frequency conditions enable lower MSE values, thereby achieving superior drilling efficiency.

Figure 4 illustrates the variation trends of mechanical specific energy (MSE) under different parameter combinations using cubic interpolation. The study determined that optimal drilling efficiency (minimum MSE value of 103 MPa) occurred under the combination of high WOB (19 kN), high RPM (50 r/min), high axial impact frequency (20 Hz), and high torsional impact frequency (20 Hz). Conversely, the maximum MSE value (333 MPa) corresponded to low WOB (10 kN), high RPM (50 r/min), moderate axial impact frequency (10 Hz), and moderate torsional impact frequency (15 Hz). Analysis of parameter interaction effects reveals significant interactions between WOB and other parameters. Particularly under high torsional impact frequency conditions, appropriately increasing WOB effectively reduces MSE values and enhances energy efficiency.

3.2. Range Analysis

To further quantify the influence of each rock breaking parameter on mechanical specific energy,

Table 5. Range analysis results of mechanical specific energy.

Factor	WOB (kN)	RPM (r/min)	AF (Hz)	TF (Hz)
K1	880	743	902	927
K2	899	856	985	976
K3	1016	949	888	995
K4	748	995	768	645
k1	220.00	185.75	225.50	231.75
k2	224.75	214.00	246.25	244.00
k3	254.00	237.25	222.00	248.75
k4	187.00	248.75	192.00	161.25
Rang R	67.00	63.00	54.25	87.50

presents the range analysis results. The study revealed that torsional impact frequency exhibits the largest range (R = 87.5 MPa), indicating this parameter has the most significant effect on MSE, followed by WOB (R = 67 MPa), RPM (R = 63 MPa), and axial impact frequency (R = 54.25 MPa).

Based on the range analysis results, the ranking of parameter influence on MSE is established as follows: torsional impact frequency > WOB > RPM > axial impact frequency. Through comparison of average MSE values (ki) at each level, the optimal parameter combination A4B1C4D4 was identified, corresponding to 19 kN weight on bit, 20 r/min RPM, 20 Hz axial impact frequency, and 20 Hz torsional impact frequency.

As illustrated in Figure 5, mechanical specific energy exhibits a nonlinear response to increasing weight on bit, initially rising then decreasing to reach its minimum value (187.00 MPa) at the maximum WOB level (19 kN). The effect of RPM on MSE demonstrates a clear positive correlation, with MSE increasing as RPM rises, and the minimum MSE value (185.75 MPa) occurring at the lowest RPM level (20 r/min). The influence of axial impact frequency on MSE follows a U-shaped curve, achieving optimal performance (192.00 MPa) at the high frequency condition of 20 Hz. The effect of torsional impact frequency is more pronounced, also exhibiting nonlinear characteristics, and achieving the lowest MSE value (161.25 MPa) among all rock breaking parameter combinations at the maximum frequency (20 Hz).

3.3. Variance Analysis

To quantify the significance of influence of each rock breaking parameter on mechanical specific energy, nonlinear analysis of variance was conducted on the experimental data, constructing a comprehensive mathematical model incorporating main effects, quadratic terms, and interaction effects. The statistical evaluation metrics of the model are presented in

Table 6. Statistical measures of nonlinear ANOVA model for MSE.

Statistical Type	R2	Adjusted R2	Predicted R2	RMSE	Coefficient of Variation
Statistical Value	0.8240	0.7067	0.4256	32.19	14.54%

.

The established model achieves an R² of 0.8240, indicating that the model explains over 82% of MSE data variability, which represents satisfactory fitting performance under complex formation conditions with multi-parameter interactions. The adjusted R² of 0.7067 accounts for the number of independent variables in the model and also reaches a high level. The predicted R² is relatively low (0.4256), primarily attributed to the complex multi-factor influences on mechanical specific energy and its nonlinear characteristics, where strong parameter interactions cause single parameter changes to significantly affect overall model response.

The model’s root mean square error (RMSE) is 32.19 MPa. Relative to the mean MSE value (approximately 201.25 MPa), the error rate is approximately 16%, which falls within acceptable limits. The coefficient of variation (CV) of 14.54% is significantly lower than the overall coefficient of variation of experimental data (25.99%), demonstrating that the established ANOVA model successfully captures the primary sources of MSE data variation and effectively reflects the influence patterns of rock breaking parameters on MSE. Based on these statistical indicators, the model exhibits good stability and reliability, making it suitable for subsequent parameter optimization analysis.

Table 7. ANOVA results and significance test for MSE.

Factor	Sum of Squares (SS)	df	MS	F Value	p Value	Significance	Contribution
WOB	973.01	1	973.01	0.939	0.357	Not significant	1.80%
RPM	9010.01	1	9010.01	8.700	0.016	*	17.0%
AF	3112.51	1	3112.51	3.00	0.117	Not significant	5.90%
TF	8549.11	1	8549.11	8.250	0.018	*	16.1%
TF2	9950.06	1	9950.06	9.600	0.012	*	18.8%
AF-TF	12,067.02	1	12,067.02	11.65	0.007	**	22.8%
Residual	9324.2	9	1036.02	-	-	-	17.6%
Total	52,985.9	15	-	-	-	-	100%

Note: * indicates p < 0.05, significant; ** indicates p < 0.01, highly significant.

presents the ANOVA results with significance testing conducted at α = 0.05. The analysis reveals that the interaction between axial and torsional impact frequencies (22.8% contribution) is the dominant factor influencing MSE, achieving high statistical significance (p = 0.0077 < 0.01). This is followed by the quadratic term of torsional impact frequency (18.8%), RPM (17.0%), and the linear term of torsional impact frequency (16.1%), all reaching significance levels (p < 0.05). The main effects of WOB and axial impact frequency contributed only 1.8% and 5.9% of total variation, respectively, and neither achieved statistical significance (p > 0.05).

Additionally, the ANOVA results differ from the influence ranking obtained through range analysis (torsional impact frequency > WOB > RPM > axial impact frequency). This discrepancy primarily arises from fundamental differences between the two analytical methods: range analysis considers only single-factor main effects and cannot distinguish interaction effects between different factors, whereas ANOVA simultaneously evaluates main effects, nonlinear effects, and interaction effects, providing more comprehensive analytical results.

3.4. Response Surface Methodology and Regression Analysis

Based on the ANOVA results and considering the strong interaction between torsional and axial impact frequencies, a comprehensive response surface model was constructed, as illustrated in Figure 6. Response surface analysis reveals the influence patterns of each parameter on MSE: increasing weight on bit significantly reduces MSE, with the high weight on bit region (19 kN) achieving minimum MSE values; RPM exhibits positive correlation with MSE, where low RPM (20 r/min) produces lower MSE values; and increasing impact frequency promotes MSE reduction, with torsional impact frequency demonstrating more pronounced effects. When both axial and torsional impact frequencies reach high values (20 Hz), a strong combined effect occurs, reducing MSE to its minimum level.

Parameter interaction patterns are evident from the response surface characteristics. The weight on bit versus RPM surface exhibits a saddle shape, with the low RPM and high weight on bit region forming an MSE minimum zone. The weight on bit versus impact frequency surface shows significant concavity in the high weight on bit and high frequency region. The axial versus torsional impact frequency response surface forms the deepest basin in the high frequency combination region, corresponding to optimal drilling efficiency. The RPM versus impact frequency surface demonstrates a contrasting relationship, indicating that lower RPM should be employed under high impact frequency conditions to minimize MSE.

Comprehensive analysis indicates that the optimal parameter combination consists of high weight on bit (19 kN), low RPM (20 r/min), and high impact frequencies (axial impact 20 Hz, torsional impact 20 Hz). Regression analysis was conducted on the mechanical specific energy orthogonal experimental results using nonlinear models to develop quantitative prediction models. The analysis results are presented in

Table 8. Coefficients and statistical tests of MSE nonlinear regression model.

Model	Coefficient Estimate	Standard Error	95% CI Low	95% CI High	VIF
Intercept	252.61	12.88	223.47	281.75	-
x1	−10.46	10.8	−34.88	13.96	1
x2	31.84	10.8	7.42	56.26	1
x3	−18.71	10.8	−43.13	5.71	1
x4	−31.01	10.8	−55.43	−6.59	1
x3x4	−49.43	14.48	−82.2	−16.67	1
x42	−56.11	18.11	−97.07	−15.15	1

, including model regression coefficients, standard errors, confidence intervals, and VIF values.

In this model, x₁, x₂, x₃, and x₄ represent weight on bit, RPM, axial impact frequency, and torsional impact frequency, respectively, while x₄² denotes the quadratic term of torsional impact frequency, and x₃x₄ represents the interaction between axial and torsional impact frequencies. The regression equation reveals the influence mechanisms of each parameter on MSE: weight on bit exhibits a negative effect (coefficient −10.46), indicating that increasing weight on bit effectively reduces MSE; RPM shows a positive effect (coefficient 31.84), meaning that increasing RPM leads to higher MSE; and both axial impact frequency (coefficient −18.71) and torsional impact frequency (coefficient −31.01) demonstrate negative effects, confirming that increasing impact frequencies reduces MSE. Furthermore, the interaction term between axial and torsional impact frequencies (coefficient −49.43) and the quadratic term of torsional impact frequency (coefficient −56.11) both exhibit strong negative effects, with absolute values significantly exceeding those of individual factor coefficients. Pronounced interaction effects exist between the two impact modes, where simultaneously increasing both frequencies produces effects surpassing those achieved by increasing either frequency independently. The quadratic term of torsional impact frequency demonstrates nonlinear influence on MSE, with reduction effects becoming more pronounced as torsional impact frequency increases.

Based on the regression coefficients of the nonlinear model, the mechanical specific energy prediction equation is as follows:

$$\begin{array}{c}MSE=252.61-7.80x_1+23.73x_2-13.95x_3-23.12x_4-27.46x_3{x}_4-31.7x_4^2\end{array}$$

(3)

where $x_1={\displaystyle \frac{\mathrm{WOB}-14.5}{4.5}}$, $x_2={\displaystyle \frac{\mathrm{RPM}-35}{15}}$, $x_3={\displaystyle \frac{\mathrm{AF}-12.5}{7.5}}$, and $x_4={\displaystyle \frac{\mathrm{TF}-12.5}{7.5}}$. Therefore, the final mechanical specific energy prediction equation is

$$MSE=1.7375-2.325WOB+2.21225RPM+8.4900\mathrm{AF}+31.7875\mathrm{TF}-0.8788AF*TF-0.9975T{F}^2$$

(4)

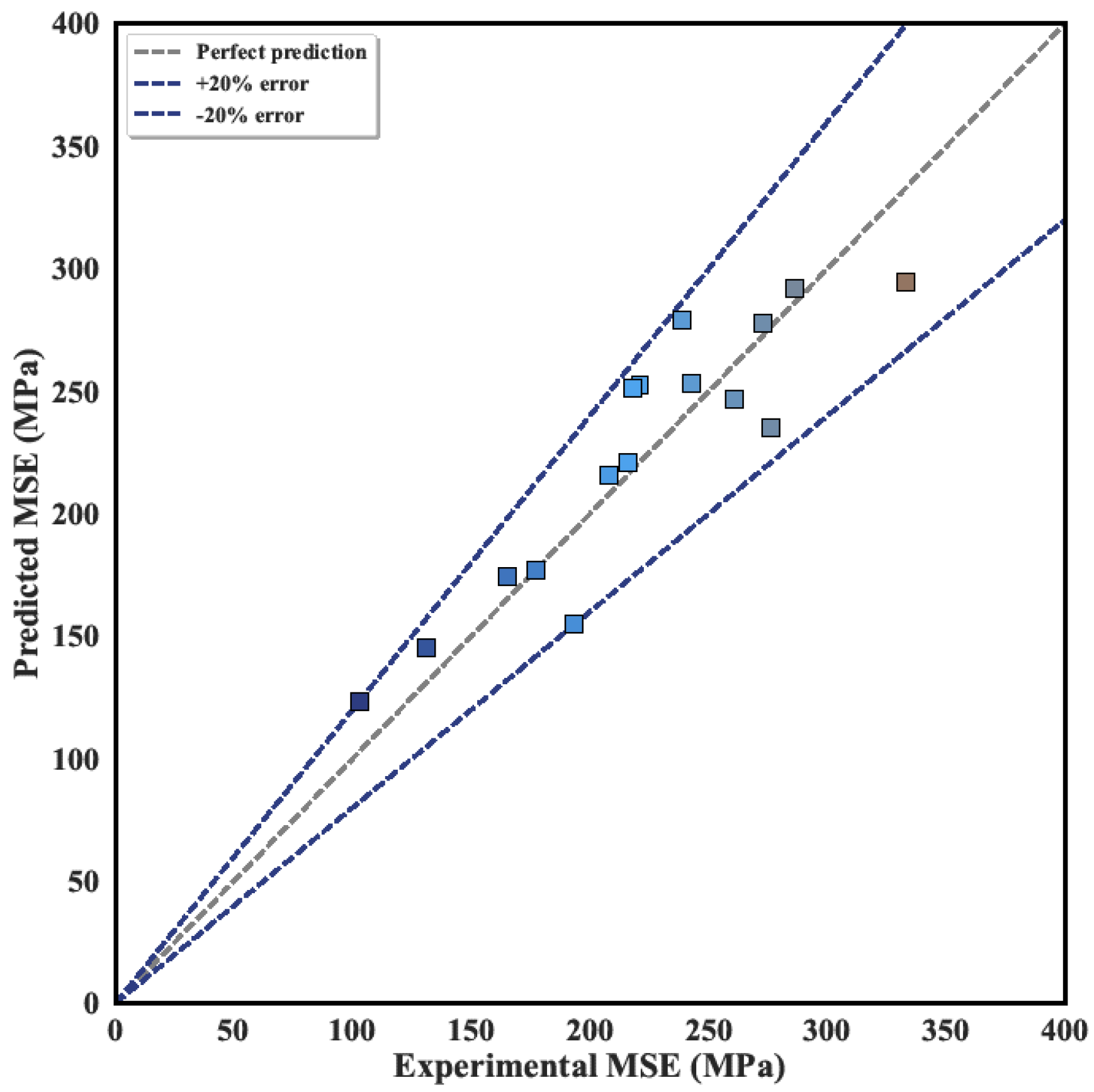
The comparison between the mechanical specific energy prediction model and experimental data is presented in Figure 7. Analysis demonstrates that the model accurately reflects the relationship between rock breaking parameters and MSE under most operational conditions, with a mean absolute percentage error of 9.26%. Although prediction errors are relatively large under specific parameter combinations, such as high axial and high torsional impact frequency combination (C3) and moderate weight on bit with high torsional impact frequency combination (C9), reaching approximately ±19%, these errors must be considered within the context of MSE’s complex multi-factor influences and inherent parameter correlations.

Mechanical specific energy, as a comprehensive drilling efficiency indicator, is influenced by multiple factors including rock physical and mechanical properties, drill bit type, drilling parameters, and formation conditions. For instance, changes in weight on bit not only directly affect MSE but also alter the rate of penetration, indirectly influencing MSE. These complex factor interactions contribute to MSE’s inherent variability. Therefore, while the established prediction model exhibits certain errors, considering MSE’s inherent variability, this error level is entirely acceptable for engineering applications and the model remains effective for guiding practical drilling parameter optimization.

4. Discussion

Recent advances in multi-dimensional impact drilling research have demonstrated that coupled axial–torsional impact enhances brittle–ductile mixed failure modes in hard rock formations, with granite showing transgranular, intergranular, and mixed transgranular–intergranular fracture patterns under multi-dimensional impact conditions [32]. These findings are consistent with our observed synergistic effects between axial and torsional impact frequencies, where the 22.8% contribution of the AF-TF interaction to MSE variation suggests enhanced energy transfer efficiency through complex fracture network development in conglomerate formations.

Experimental results demonstrate that the interaction between axial and torsional impact frequencies (AF-TF) represents the most critical factor influencing MSE, contributing 22.8% to total variance. This interaction mechanism provides essential theoretical foundation for understanding energy transfer efficiency in coupled impact drilling systems. When both axial and torsional impact frequencies simultaneously reach high values (20 Hz), their synergistic effects create optimal conditions for efficient rock fragmentation. This occurs primarily because the composite stress field generated by dual-mode impacts exhibits synergistic effects that substantially exceed simple additive contributions from individual impact modes. From a physical mechanism perspective, this phenomenon results from coherent superposition of stress waves in the spatiotemporal domain, effectively enhancing microcrack initiation rates and macrocrack propagation efficiency within heterogeneous conglomerate formations. Furthermore, the nonlinear relationship between torsional impact frequency and MSE has been quantitatively validated through a significant quadratic term coefficient (TF² = −56.11), indicating the existence of a distinct optimal frequency threshold in engineering applications. Beyond this threshold, continued increases in impact frequency may yield diminishing marginal returns or adverse effects. This finding provides crucial guidance for field drilling parameter optimization, demonstrating that efficient, energy-saving drilling requires precise frequency matching optimization rather than indiscriminate maximization of impact parameters.

From a rock mechanics perspective, the synergistic effects of coupled axial–torsional impacts can be attributed to the coherent superposition of stress waves generated by dual-mode loading. The temporal and spatial coordination of axial and torsional impacts creates a complex three-dimensional stress field that promotes more efficient crack initiation and propagation in the heterogeneous conglomerate matrix. This mechanism differs fundamentally from single-mode impacts, where stress concentrations are primarily uniaxial or purely torsional. The enhanced microcrack density and connectivity under coupled loading conditions likely contribute to the observed 69.1% MSE reduction. However, direct microscopic evidence through advanced diagnostic techniques such as micro-CT scanning, acoustic emission monitoring, or post-test fracture mapping would provide more definitive validation of these proposed mechanisms and represents a crucial direction for future research.

This study acknowledges several inherent limitations. First, experiments utilized regular cubic specimens under controlled laboratory conditions, which inadequately simulate the complex heterogeneous characteristics of actual conglomerate formations, including random variations in gravel size distribution, cement strength, and structural anisotropy. Second, the research focused exclusively on specific conglomerate types from the Junggar Basin, encompassing relatively narrow ranges of rock mechanical properties. Consequently, the established MSE prediction model may require recalibration when applied to different geological settings. Additionally, the 30 mm drilling depth and limited experimental duration differ substantially from actual drilling operations. The influence mechanisms of long-term effects—including bit wear, elevated temperature and pressure conditions, and cumulative rock damage—remain inadequately characterized, yet these factors may significantly influence MSE dynamic behavior during actual drilling processes. Despite these limitations, ATCID technology demonstrates considerable potential for addressing drilling challenges in hard rock formations beyond conglomerates. The 69.1% MSE reduction achieved through optimal parameter combinations represents substantial advancement in drilling efficiency. However, field implementation requires careful consideration of operational risks associated with the recommended low rotation speed (20 r/min) combined with high impact frequencies (20 Hz), which may increase the likelihood of hole cleaning issues, stick–slip phenomena, and equipment fatigue under certain drilling conditions. Therefore, the recommended parameters should be applied selectively based on formation characteristics and drilling system capabilities, with modified parameter sets using moderate impact frequencies potentially more appropriate for challenging drilling environments to balance efficiency gains with operational safety and equipment longevity. The 69.1% MSE reduction achieved through optimal parameter combinations represents substantial advancement in drilling efficiency, translating to significant cost reductions for deep and ultra-deep well operations. The established nonlinear prediction model provides a practical framework for real-time drilling optimization. Integration of this model into automated drilling systems enables adaptive parameter adjustment based on formation characteristics and drilling performance feedback.

To enhance field applicability, future research must address several critical aspects. First, scaled investigations are essential to evaluate ATCID technology performance under full-scale drilling equipment and extended drilling depths. Factors including drill string dynamics, wellbore pressure effects, and formation fluid interactions may necessitate modifications to energy transfer efficiency relationships and optimal parameters established at laboratory scale. Second, comprehensive wear characterization of PDC cutters under coupled impact conditions is crucial for determining economic viability. While current research demonstrates excellent drilling efficiency, systematic investigation of drilling tool durability under sustained high-frequency impact loading remains essential for practical implementation.

5. Conclusions

This study systematically investigated the influence patterns of weight on bit, RPM, axial impact frequency, and torsional impact frequency on mechanical specific energy in axial–torsional coupled impact drilling using self-developed true triaxial impact rotary rock breaking equipment and employing orthogonal experimental design, analysis of variance, and response surface methodology. The main conclusions are as follows:

(1)

Through analysis of 16 orthogonal experiments, the ranking of parameter influence on MSE was established: torsional impact frequency > weight on bit > RPM > axial impact frequency. Torsional impact frequency exhibited the largest range value (R = 87.5 MPa), representing the most critical factor affecting MSE. The optimal parameter combination consists of 19 kN weight on bit, 20 r/min RPM, 20 Hz axial impact frequency, and 20 Hz torsional impact frequency, achieving the minimum MSE value (103 MPa).

(2)

ANOVA results demonstrate that the interaction between axial and torsional impact frequencies is the dominant factor influencing MSE, contributing 22.8% and reaching high statistical significance (p = 0.0077 < 0.01). The quadratic term of torsional impact frequency (18.8%), RPM (17.0%), and the linear term of torsional impact frequency (16.1%) all achieved significance levels (p < 0.05), while the main effects of weight on bit and axial impact frequency did not reach statistical significance.

(3)

Response surface analysis revealed parameter influence patterns on MSE: increasing weight on bit significantly reduces MSE; RPM exhibits positive correlation with MSE; and simultaneous high values of axial and torsional impact frequencies produce strong interaction effects, minimizing MSE. The interaction mechanism of axial–torsional coupled impact mode is key to enhancing rock breaking efficiency.

(4)

A nonlinear MSE prediction model incorporating main effects, quadratic terms, and interaction effects was established with R² = 0.8240, explaining over 82% of MSE data variability. The model achieved a mean absolute percentage error of 9.26% and RMSE = 32.19 MPa, satisfying engineering application accuracy requirements.