Fuzzy Rule-Based Optimal Direct Yaw Moment Allocation for Stability Control of Four-Wheel Steering Mining Trucks
Abstract
1. Introduction
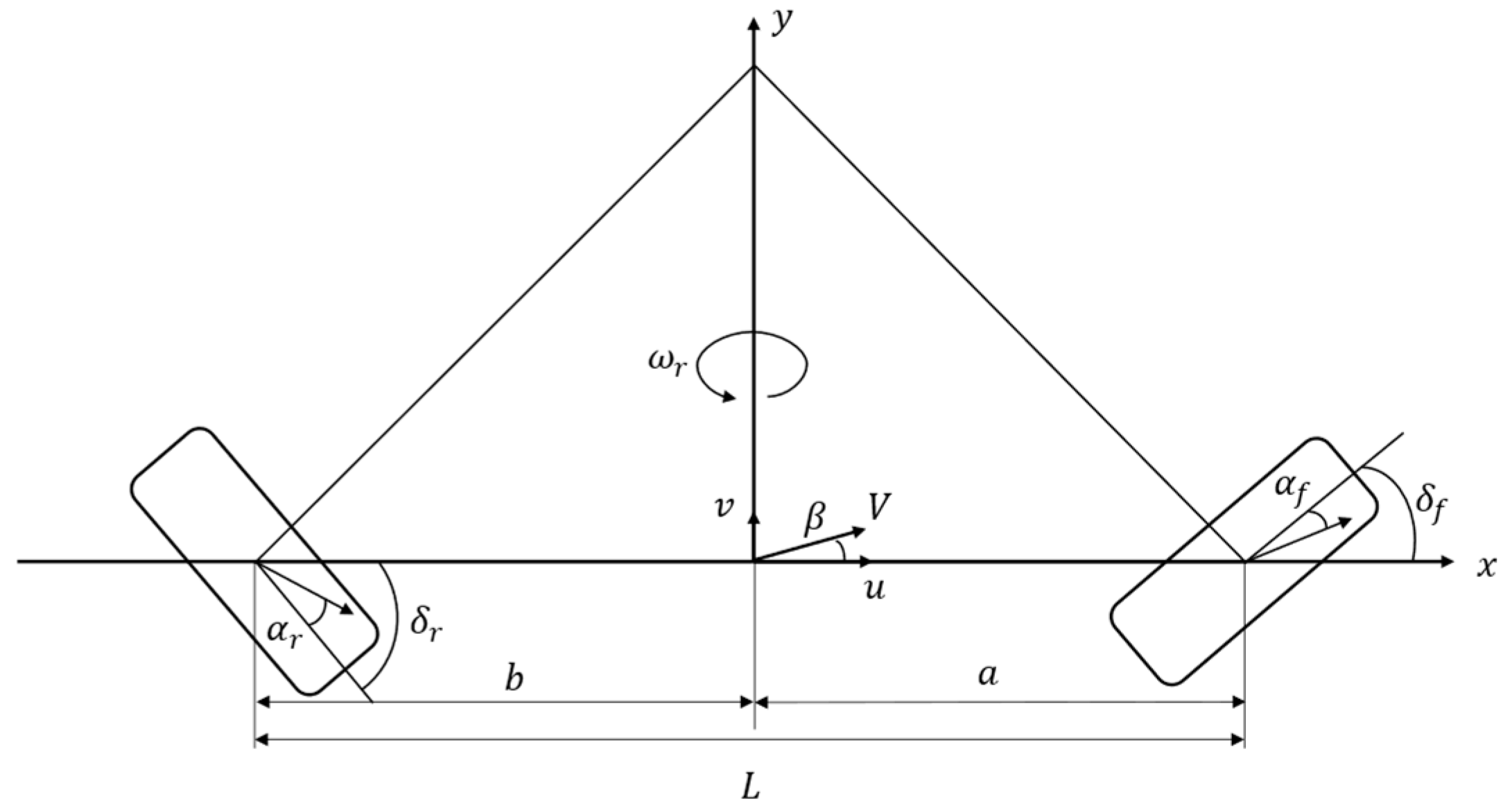
2. Dynamic Model of the Vehicle
Four-Wheel Steering Two-Degree-of-Freedom Vehicle Dynamics Modeling
- (1)
- The influence of suspension vibration on vehicle handling stability is neglected. The vehicle is assumed to have zero displacement along the Z-axis and only perform planar motion.
- (2)
- The front and rear wheel steering angles are considered as system inputs, while dynamic lag in the steering system is neglected.
- (3)
- Uneven load distribution between left and right wheels is disregarded.
- (4)
- Aerodynamic forces and lateral wind effects are excluded from consideration.
- (5)
- Nonlinear tire characteristics and aligning moments are not accounted for in the model.
- (6)
- The road surface is presumed to be flat and even, with exclusion of load variations induced by road irregularities.
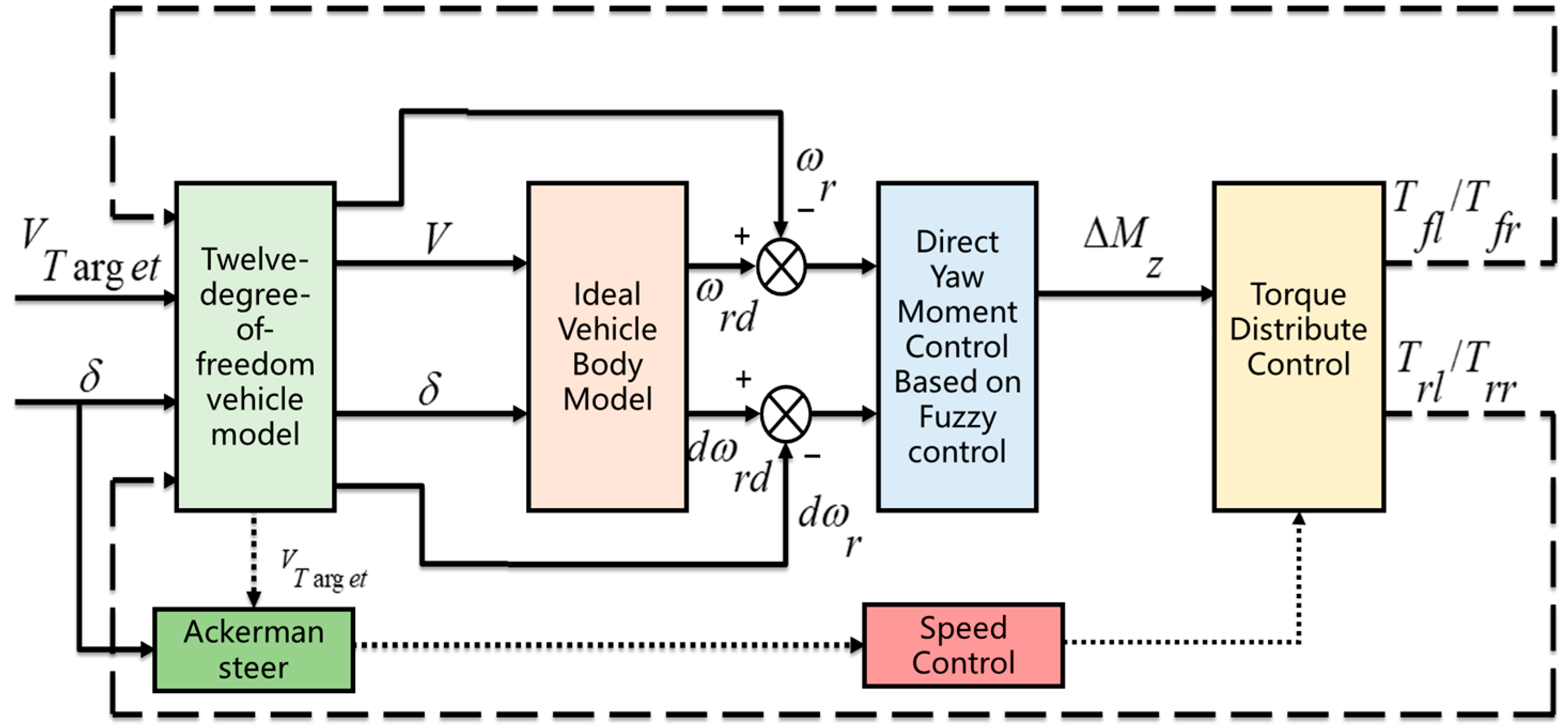
3. Design of Direct Yaw Moment Control Strategy
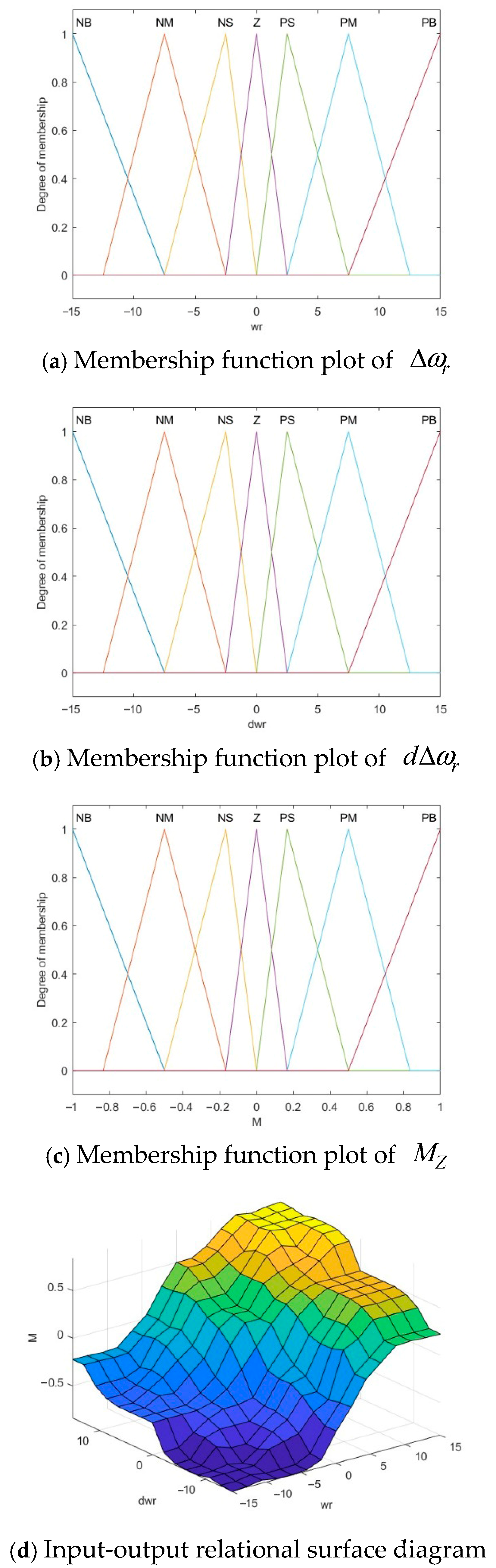
3.1. Design of Yaw Moment-Based Upper-Layer Controller
3.2. Design of Optimal Torque Distribution-Based Controller
4. Simulation Experiments and Results Analysis
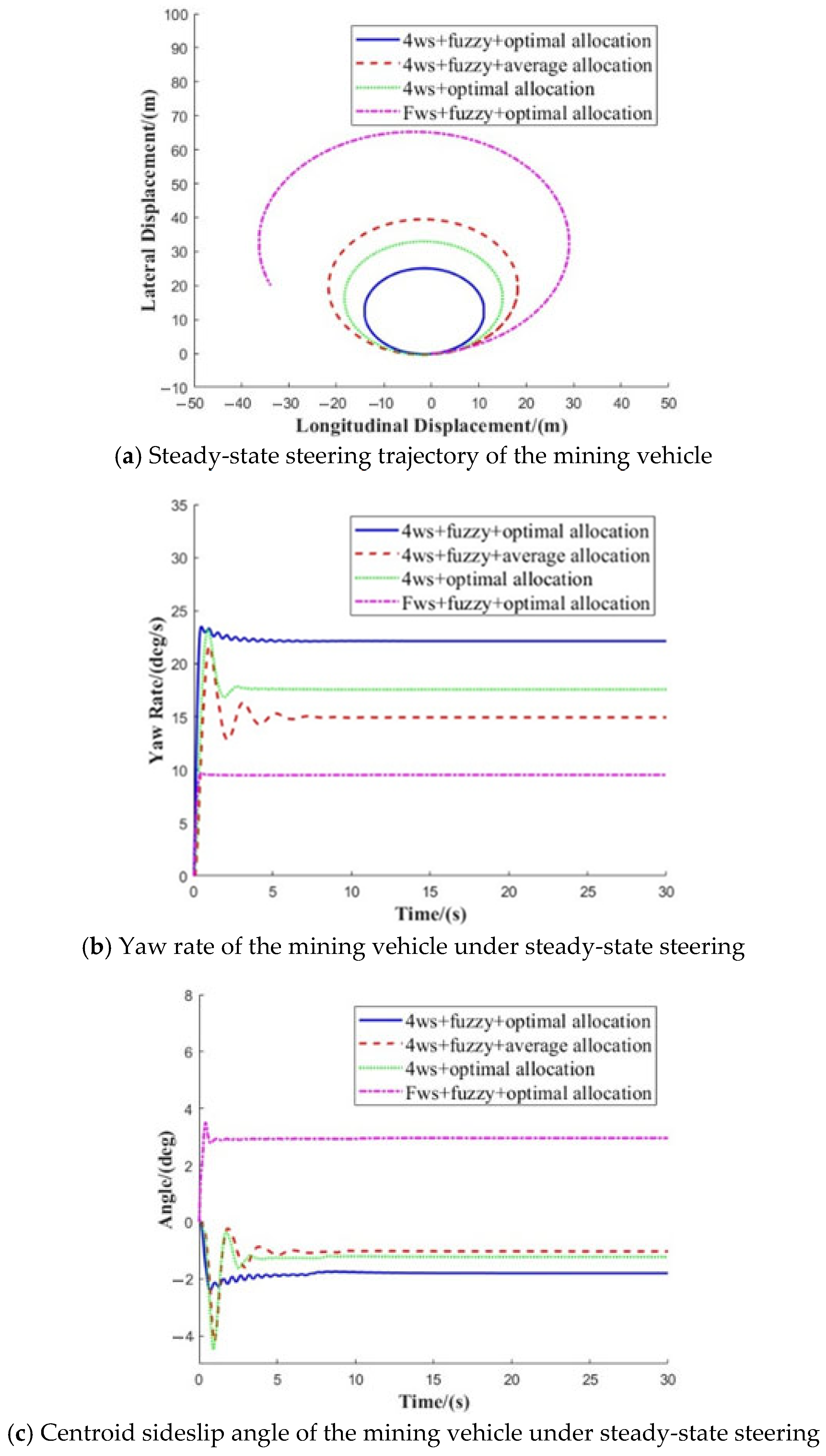
4.1. Steady-State Steering Simulation Experiment
4.2. Double Lane Change Simulation Experiment
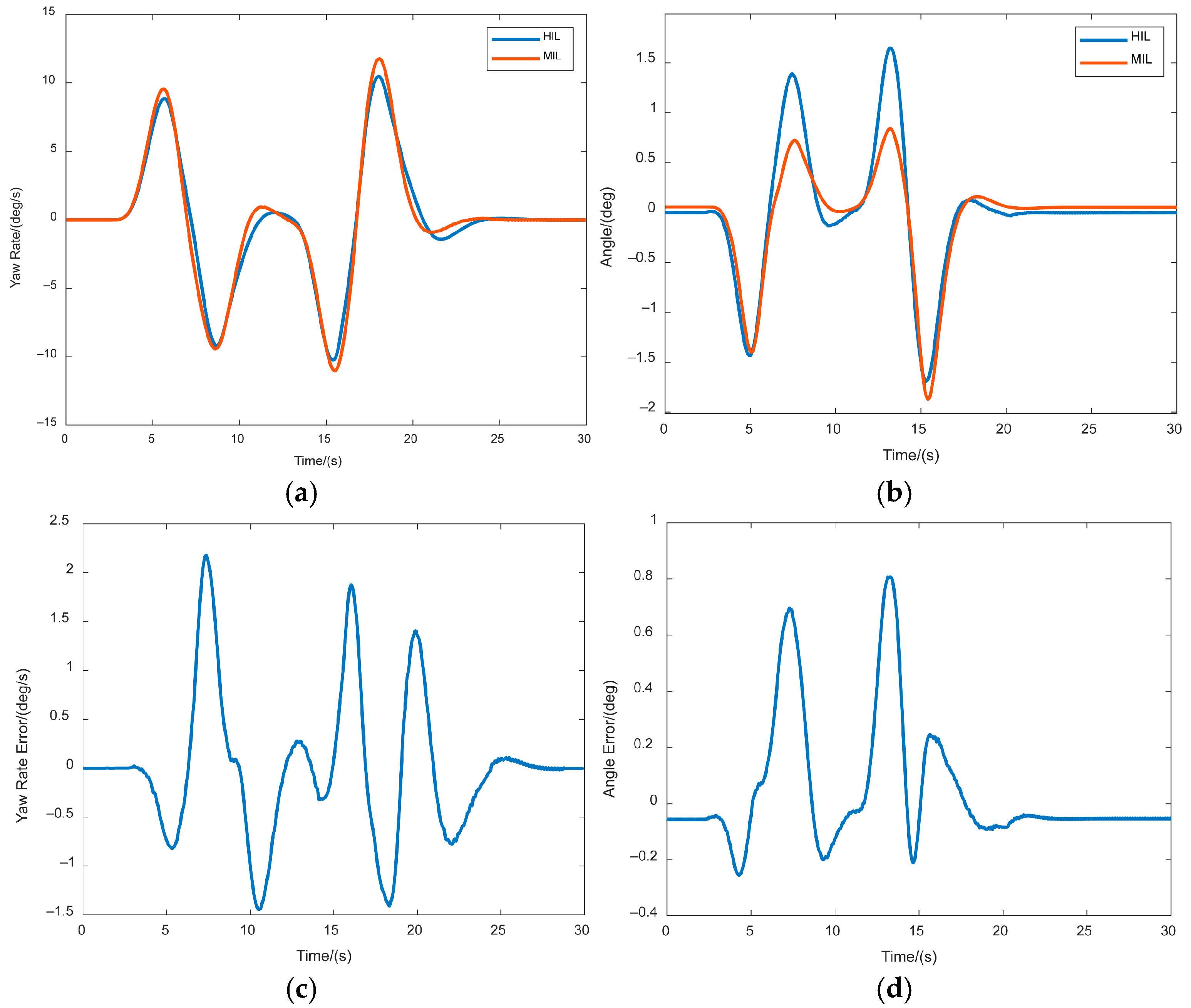
4.3. HIL Test
5. Conclusions
- (1)
- Compared to conventional front-wheel-steering (FWS) mining trucks, the four-wheel-steering (4WS) configuration with counter-phase Ackermann geometry significantly enhances maneuverability in tight, high-curvature bends. Under extreme conditions, the 4WS system effectively overcomes the poor trajectory tracking and limited stability inherent in FWS vehicles.
- (2)
- A 4WS mining vehicle equipped with a fuzzy logic-based direct yaw moment control (DYC) system, utilizing dual inputs (yaw rate and yaw angular acceleration) and a single output (compensatory yaw moment), achieves a smaller turning radius, improved maneuverability, and enhanced stability during steady-state steering compared to conventional 4WS vehicles without DYC.
- (3)
- The 4WS mining truck with optimal torque distribution control accounts for the physical constraints of electric motors and road adhesion. By dynamically allocating wheel-specific torque based on friction circle theory, this approach markedly improves trajectory tracking accuracy and vehicle stability compared to conventional equal torque distribution methods.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 4WS | Four Wheel Steering |
| DISO | dual-input single-output |
| DYC | Direct Yaw Moment Control |
| AFS | Active Front Steering |
| FWS | Front-Wheel Steering |
| PID | Proportional-Integral-Derivative |
| MPC | model predictive control |
| MDOF | multi-degree-of-freedom |
References
- Yu, Z.P.; Feng, Y.; Xiong, L. Review on the Development Status of Dynamic Control for Distributed Drive Electric Vehicles. J. Mech. Eng. 2013, 49, 105–114. [Google Scholar] [CrossRef]
- Sun, P.K.; Trigell, A.S.; Drugge, L.; Jerrelind, J. Energy efficiency and stability of electric vehicles utilising direct yaw moment control. Veh. Syst. Dyn. 2022, 60, 930–950. [Google Scholar] [CrossRef]
- Ye, Z.M.; Yao, C.Y.; Fu, C.Y. Adaptive Cruise Control with Integrated Active Front Steering and Direct Yaw Moment Control. J. Chongqing Univ. 2024, 1–22. [Google Scholar]
- Zhao, S.; Hu, H.; Jing, D. Stability Control for Distributed Drive Electric Vehicles with Coordinated Active Front Steering and Direct Yaw Moment Control. J. Huaqiao Univ. (Nat. Sci. Ed.) 2021, 42, 571–579. [Google Scholar]
- Lin, J.; Zou, T.; Zhang, F.; Zhang, Y. Yaw Stability Research of the Distributed Drive Electric Bus by Adaptive Fuzzy Sliding Mode Control. Energies 2022, 15, 1280. [Google Scholar] [CrossRef]
- Sun, X.Q.; Wang, Y.; Cai, Y.; Wong, P.K.; Chen, L.; Bei, S. Nonsingular Terminal Sliding Mode-Based Direct Yaw Moment Control for Four-Wheel Independently Actuated Autonomous Vehicles. IEEE Trans. Transp. Electrif. 2023, 9, 2568–2582. [Google Scholar] [CrossRef]
- Wang, Z.P.; Ding, X.L.; Zhang, L. Chassis Coordinated Control for Full X-by-Wire Four-Wheel-Independent-Drive Electric Vehicles. IEEE Trans. Veh. Technol. 2023, 72, 4394–4410. [Google Scholar] [CrossRef]
- Chen, L.-D. Simulation Research on Four-wheel Independent Steering System of Coal Mine Anchor Vehicle. Chin. Hydraul. Pneum. 2020, 7, 106–111. [Google Scholar]
- Zhao, J.; Zhu, L.; Liu, C. Research on Path Tracking Control Strategy of Four-wheel Steering Intelligent Vehicle. J. Syst. Simul. 2021, 33, 2390–2398. [Google Scholar]
- Zhang, B.J. Lateral Dynamic Characteristics and Control of Four-Wheel Steering Vehicles. Ph.D. Thesis, Tianjin University, Tianjin, China, 2006. [Google Scholar]
- Tu, Q.M.; Sun, F.L.; Xin, Q.F.; Mei, G.H. Research Status and Prospects on Driving Stability of Four-Wheel Steering (4WS) Vehicles. Small Intern. Combust. Engines Automot. Technol. 2025, 54, 93–96. [Google Scholar]
- Zhao, W.; Qin, X.; Wang, C. Yaw and Lateral Stability Control for Four-Wheel Steer-by-Wire System. IEEE/ASME Trans. Mechatron. 2018, 23, 2628–2637. [Google Scholar] [CrossRef]
- Chu, Y.; Wang, C.; Zhou, X.; Zhang, Z.; Zhao, W. Instantaneous Center of Rotation Tracking Control of Four-Wheel Independent Steering Vehicles Under Large-Curvature Turning Conditions. IEEE Trans. Intell. Transp. Syst. 2024, 25, 17965–17978. [Google Scholar] [CrossRef]
- Fu, X.W.; Fu, L.; Kong, F. Research of Automotive Steer-by-wire Control Based on Integral Partition PID Control. In Proceedings of the Third International Conference on Genetic and Evolutionary Computing, Guilin, China, 14–17 October 2009; Huang, T.L., Li, L.F., Zhao, M., Huang, T.L., Li, L.F., Zhao, M., Eds.; p. 561. [Google Scholar]
- Krishna, S.; Narayanan, S.; Denis Ashok, S. Fuzzy logic based yaw stability control for active front steering of a vehicle. J. Mech. Sci. Technol. 2014, 28, 5169–5174. [Google Scholar] [CrossRef]
- Ghosh, S.; Deb, A.; Mahala, M.; Tanbakuchi, M.; Makowski, M. Active Yaw Control of a Vehicle using a Fuzzy Logic Algorithm. In Proceedings of the SAE 2012 World Congress & Exhibition, Detroit, MI, USA, 24–26 April 2012. [Google Scholar]
- Nwagboso, C.O.; Ouyang, X.; Morgan, C. Development of neural-network control of steer-by-wire system for intelligent vehicles. Heavy Veh. Syst.-Int. J. Veh. Des. 2002, 9, 1–26. [Google Scholar] [CrossRef]
- Han, Z.; Ruan, J.; Li, Y.; Wan, H.; Xue, Z.; Zhang, J. Active Collision-Avoidance Control Based on Emergency Decisions and Planning for Vehicle–Pedestrian Interaction Scenarios. Sustainability 2025, 17, 2016. [Google Scholar] [CrossRef]
- Zhao, L.; Chen, W.; Wang, J.; Cong, G.; Xie, Y. Research on Steering-by-wire Control Strategy Based on Extension Sliding Mode Control. J. Mech. Eng. 2019, 55, 126–134. [Google Scholar] [CrossRef]
- Liu, H. Research on Sliding Mode Control Strategy for Multi-agent-based Steer-by-Wire Four-Wheel Active Steering Vehicles. Mater’s Thesis, Changchun University of Technology, Changchun, China, 2023. [Google Scholar]
- Shi, Q.; Wei, Y.; Xie, D.; Li, F.; Song, K.; He, L. A model predictive control approach for angle tracking of steer-by-wire system with nonlinear transmission ratio. Asian J. Control 2023, 25, 1156–1166. [Google Scholar] [CrossRef]
- Xu, Z.; He, L.; Huang, C.; Zheng, X.; Li, S.; Shi, Q. A model-tuned predictive sliding control approach for steering angle following of full self-driving vehicles. Proc. Inst. Mech. Eng. Part C-J. Mech. Eng. Sci. 2024, 238, 7399–7409. [Google Scholar] [CrossRef]
- Hu, J.J.; Xiao, F.; Lin, Z.Q.; Huang, J.; Deng, C.H. Vehicle Yaw Stability Control Based on Fuzzy Sliding Mode Direct Yaw Moment. J. Tongji Univ. Nat. Sci. 2023, 51, 954–962. [Google Scholar]
- Wu, L.; Wang, Q.; Zhang, P. Research on Vehicle Stability Based on Four-Wheel Steering and Direct Yaw Moment. Mech. Des. Manuf. 2023, 384, 32–36. [Google Scholar]
- Yan, Y.B.; Yi, Z.Y.; Yang, Y. Stability Control of Distributed Drive Electric Vehicles on Low-Adhesion Surfaces. Mech. Des. Manuf. 2022, 379, 175–179+184. [Google Scholar]
- Wang, T.; Qu, D.; Song, H.; Dai, S. A Hierarchical Framework of Decision Making and Trajectory Tracking Control for Autonomous Vehicles. Sustainability 2023, 15, 6375. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, X.-J.; Liu, C.-G.; Wei, S.-G. Dual-steering mode based on direct yaw moment control for multi-wheel hub motor driven vehicles: Theoretical design and experimental assessment. Def. Technol. 2022, 18, 49–61. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, B.; Deng, Z.; Wu, H.; Zhu, Y. Research on stability of four-wheel independent electric drive vehicle based on sliding mode coordinated control. Mod. Manuf. Eng. 2024, 520, 51–57. [Google Scholar]
- Li, Q.; Tang, J.; Zhang, B.; Chen, Y.; Wang, Y. Research on Fault-Tolerant Control of Multi-Actuator for Distributed Drive Electric Vehicles. Automot. Eng. 2023, 45, 2251–2259. [Google Scholar]
- Gao, B.; Yan, Y.; Chu, H.; Chen, H.; Xu, N. Torque allocation of four-wheel drive EVs considering tire slip energy. Sci. China Inf. Sci. 2022, 65, 122202. [Google Scholar] [CrossRef]
- Meng, X.; Zhou, Z.; Yang, W. Controlling Yaw Stability of Hub Motor Electric Vehicle Based on Unscented Kalman Filtering. J. Highw. Transp. Res. Dev. 2023, 40, 207–215. [Google Scholar]
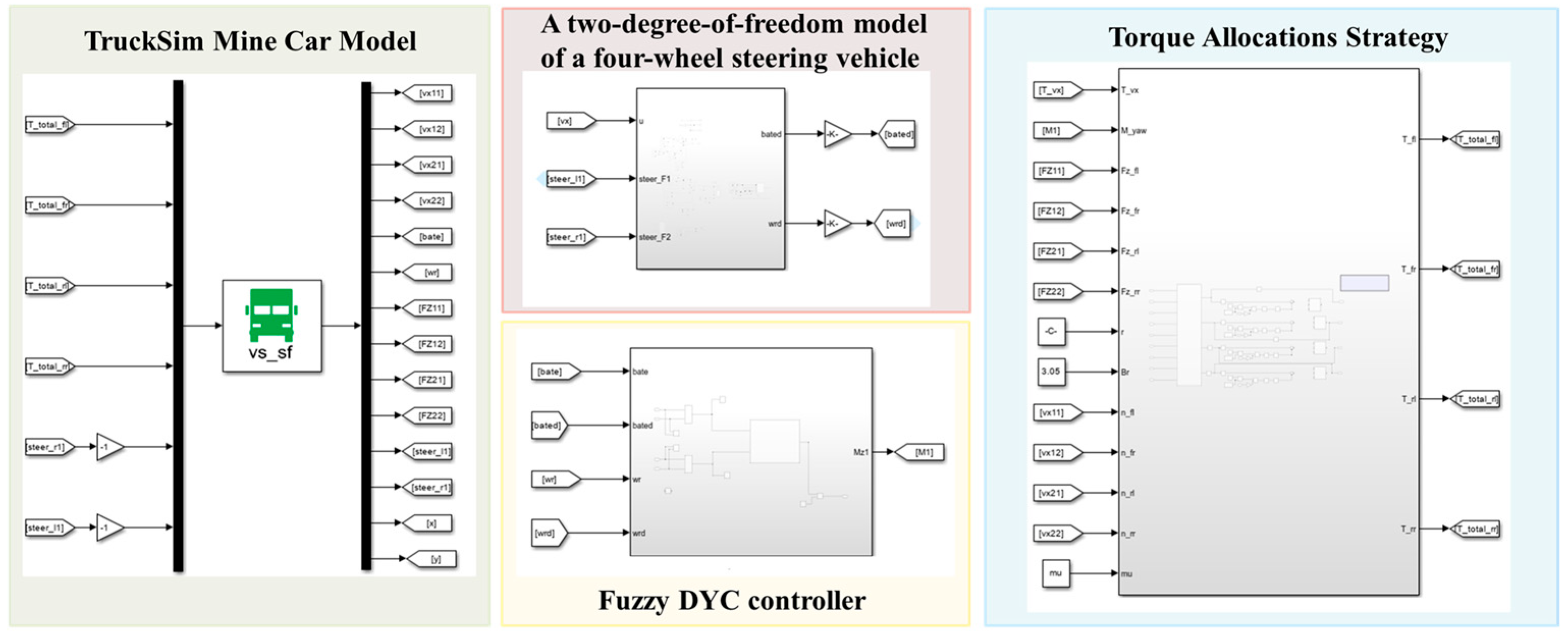



| Parameters | Data (m) |
|---|---|
| Sprung mass m/ | 91,300 |
| Distance from centroid to front axles | 2.8 |
| Distance from centroid to rear axles | 2.8 |
| Wheelbase | 6.1 |
| Centroid height | 2.9 |
| Wheel track | 8.0 |
| Wheel center height | 1.8 |
| Moment of inertia about the vertical-axis | 1,050,548 |
| NB | NM | NS | ZE | PS | PM | PB | |
| NB | PB | PB | PM | PM | PS | NS | NS |
| NM | PB | PB | PS | PS | PS | NS | NM |
| NS | PB | PM | PS | PS | Z | NM | NM |
| Z | PM | PM | PS | Z | NS | NM | NM |
| PS | PM | PM | Z | NS | NM | NM | NB |
| PM | PM | PM | NS | NS | NM | NB | NB |
| PB | PS | PS | NS | NM | NB | NB | NB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Liu, J.; Li, J.; Zhao, X. Fuzzy Rule-Based Optimal Direct Yaw Moment Allocation for Stability Control of Four-Wheel Steering Mining Trucks. Appl. Sci. 2025, 15, 10155. https://doi.org/10.3390/app151810155
Wang F, Liu J, Li J, Zhao X. Fuzzy Rule-Based Optimal Direct Yaw Moment Allocation for Stability Control of Four-Wheel Steering Mining Trucks. Applied Sciences. 2025; 15(18):10155. https://doi.org/10.3390/app151810155
Chicago/Turabian StyleWang, Feiyu, Jiadian Liu, Jiaqi Li, and Xinxin Zhao. 2025. "Fuzzy Rule-Based Optimal Direct Yaw Moment Allocation for Stability Control of Four-Wheel Steering Mining Trucks" Applied Sciences 15, no. 18: 10155. https://doi.org/10.3390/app151810155
APA StyleWang, F., Liu, J., Li, J., & Zhao, X. (2025). Fuzzy Rule-Based Optimal Direct Yaw Moment Allocation for Stability Control of Four-Wheel Steering Mining Trucks. Applied Sciences, 15(18), 10155. https://doi.org/10.3390/app151810155






