Study on Simplified Model of Pressure Loading in Adjacent Cabin with Internal Explosions in Cabin
Abstract
1. Introduction
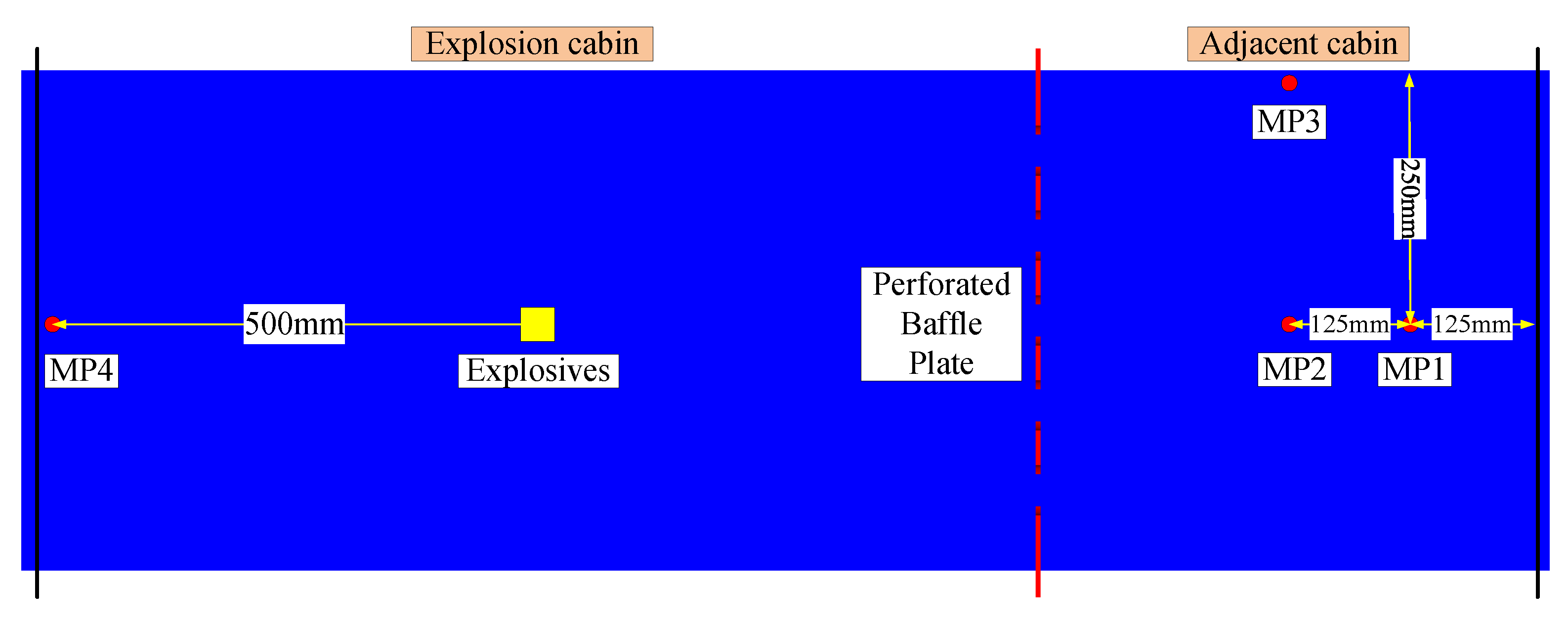
2. Experimental Design
2.1. Cabin Structure Design
2.2. Charging Parameters and Structure
2.3. Test Methods
2.4. Test Condition Design
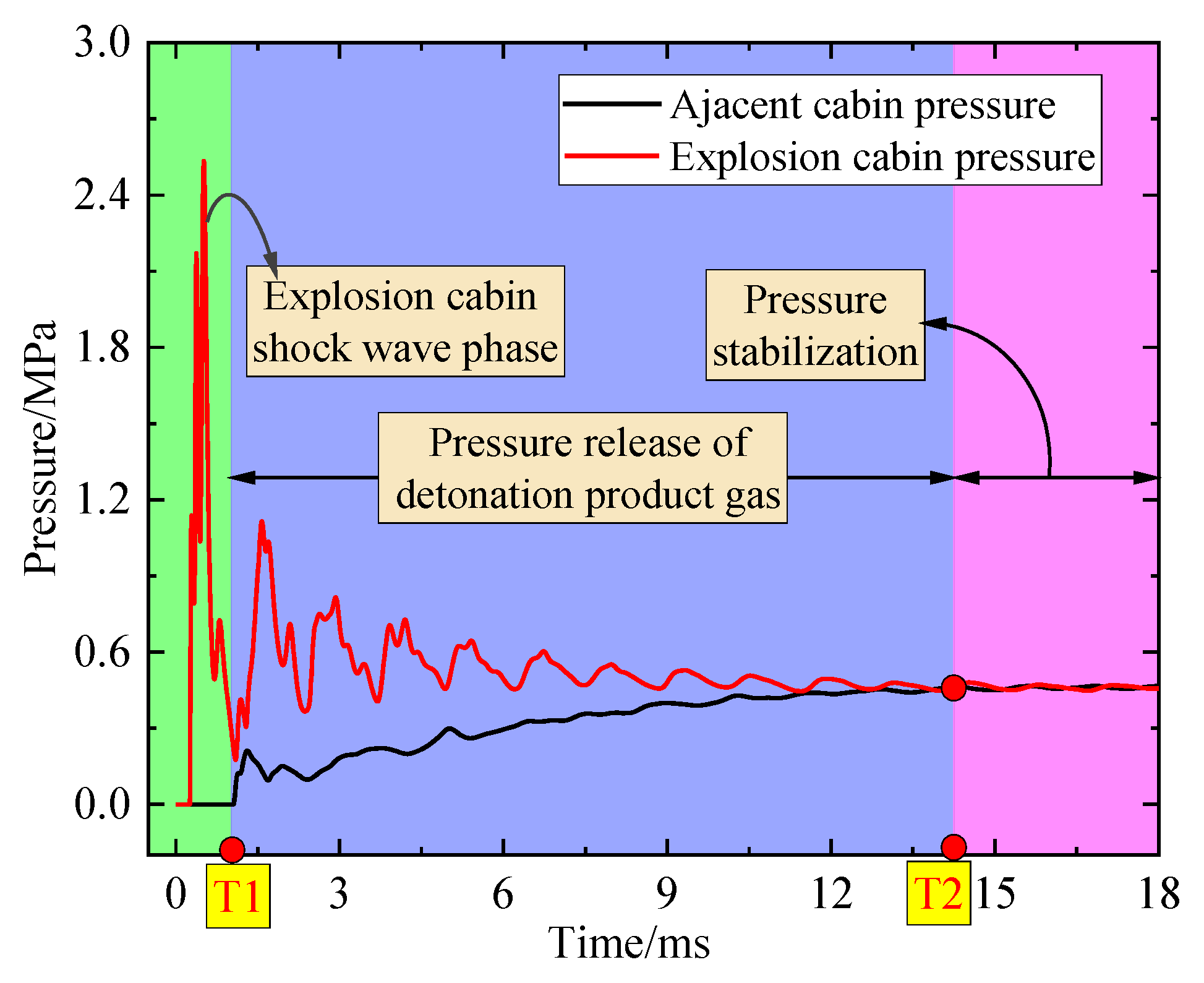
2.5. Analysis of Experimental Results
3. Finite Element Simulation
3.1. Simulation Model Introduction
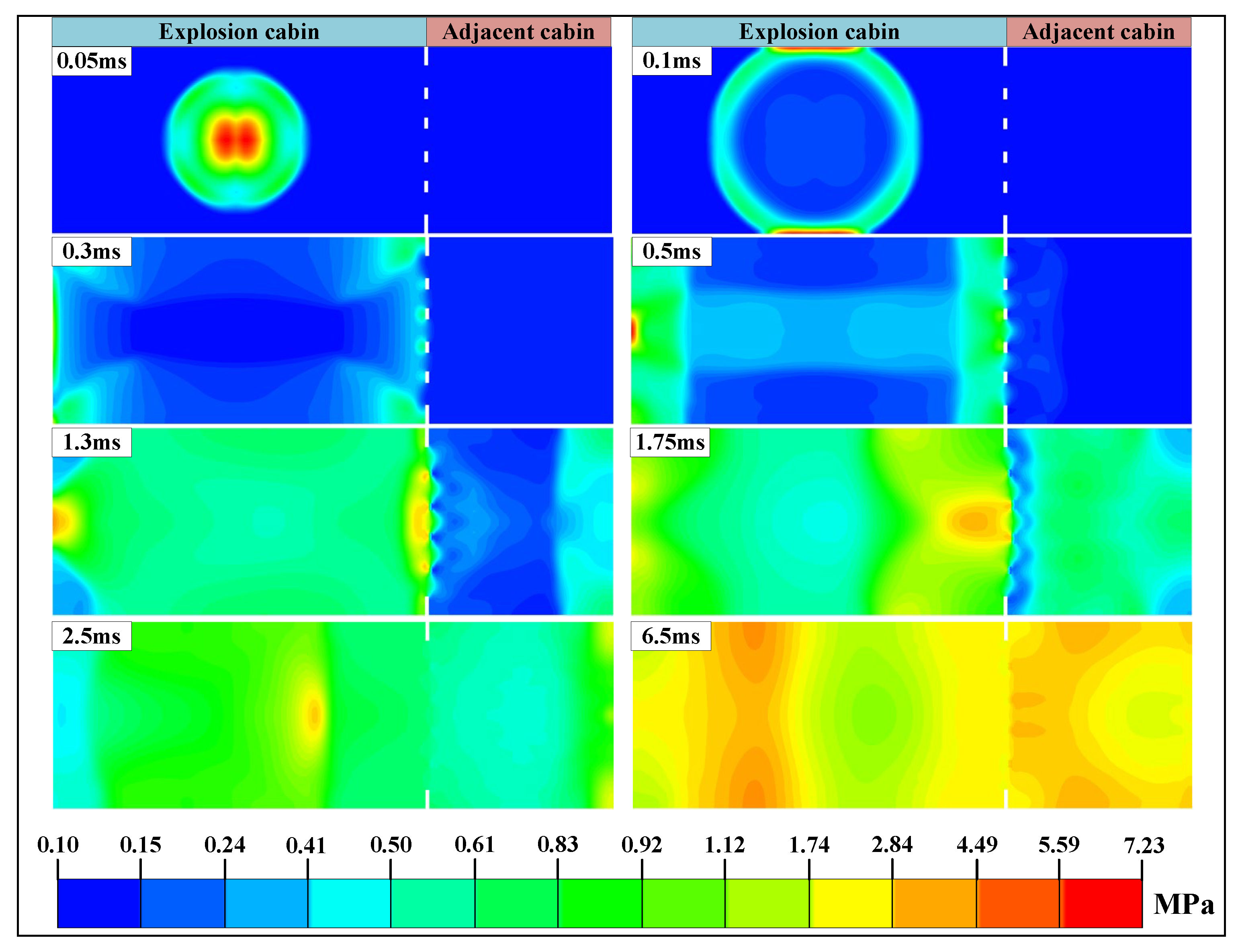
3.2. Analysis of Simulation Results
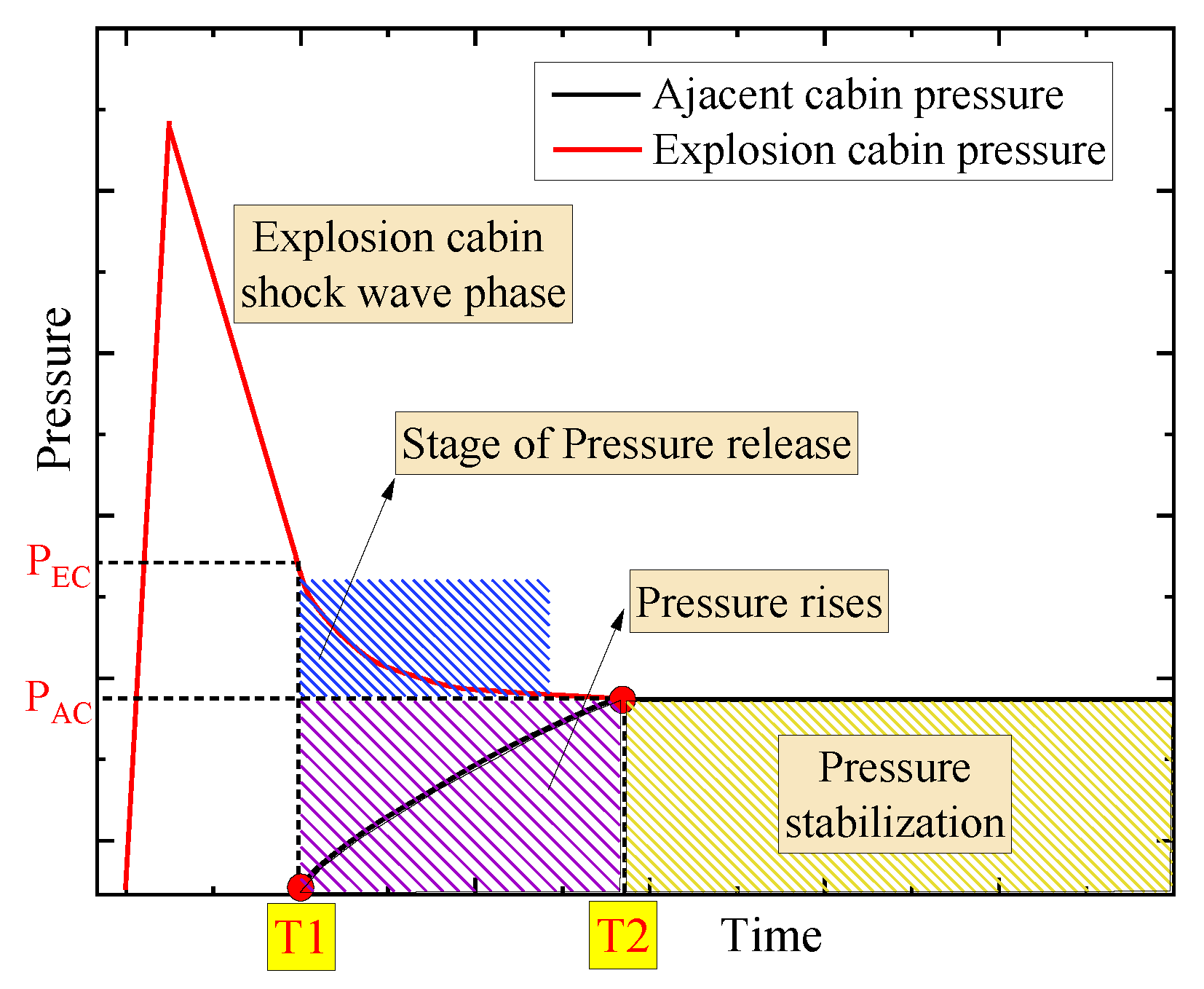
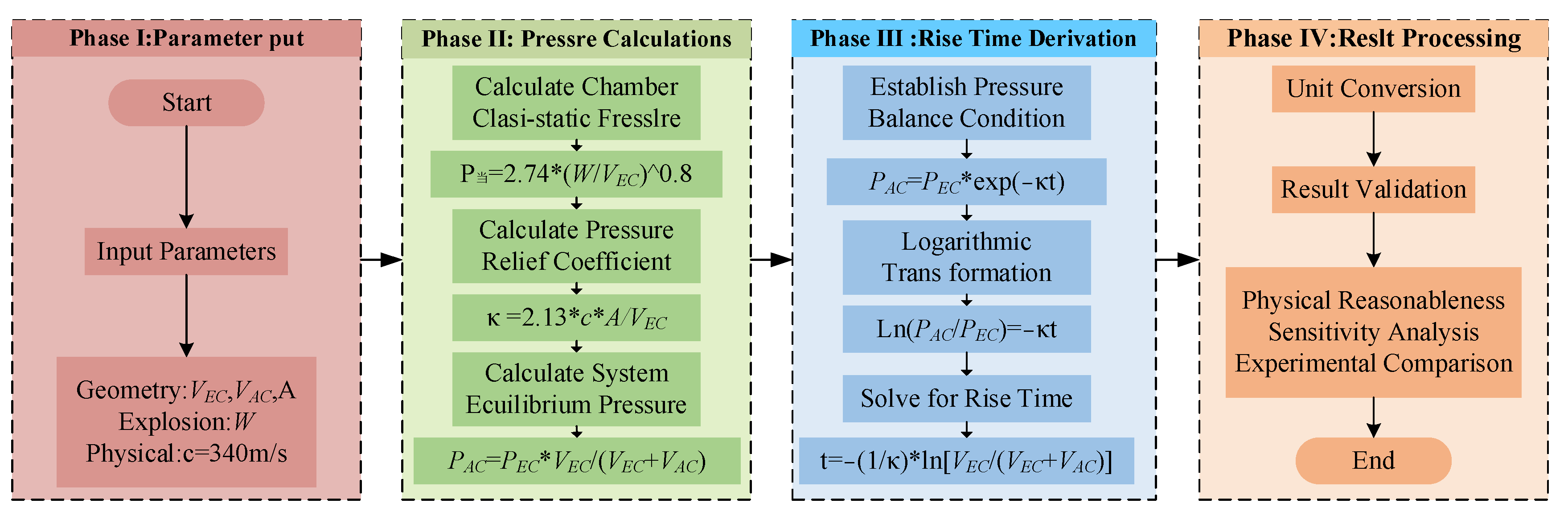
4. Simplified Model of Pressure Loading in the Adjacent Cabin of the Explosion
5. Conclusions
- (1)
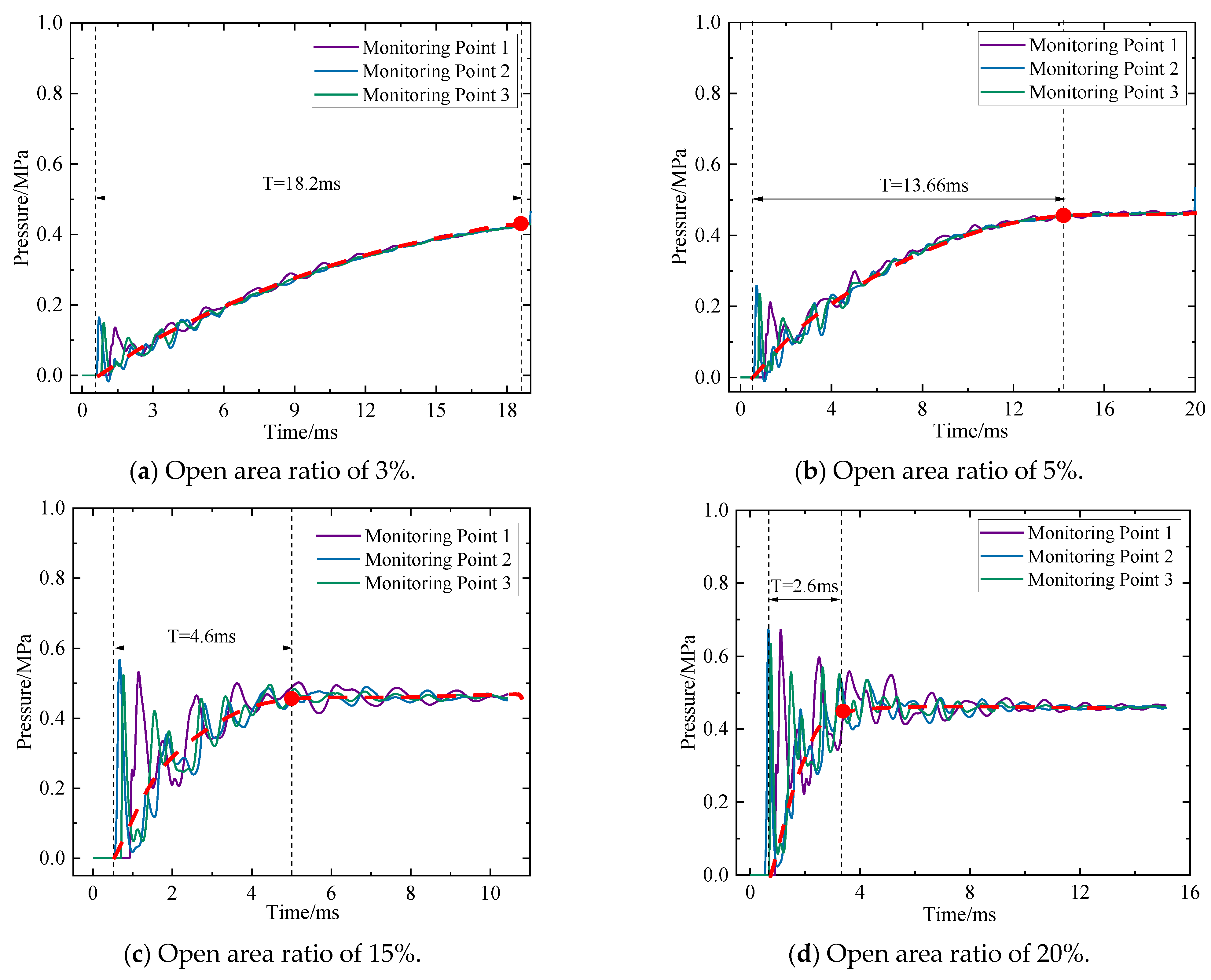
- Pressure measurements in the adjacent cabin exhibit characteristic quasi-static loading profiles, consisting of a pressure rise phase followed by stabilization. The pressure rise time decreases exponentially with an increasing open area ratio.
- (2)
- Finite element simulations replicated experimental conditions, obtaining pressure curves for both the explosion and adjacent cabins, along with pressure contours and the propagation process of detonation products at various time intervals. Analysis demonstrates the following: During the initial phase, adjacent cabin loading experiences disturbances from the explosion cabin’s shock wave, with disturbance intensity proportional to vent area. In the intermediate phase, venting of detonation products from the explosion cabin induces a gradual pressure rise in the adjacent cabin. Ultimately, the pressures equilibrate between cabins. Pressure curves at all adjacent cabin locations essentially coincide, exhibiting deviations only during the initial shock wave disturbance phase.
- (3)
- Based on the assumption that the venting process is an exponential decay, the computational model of the pressure loading rise time of adjacent cabins for internal explosions in the cabin is established. A simplified workflow for estimating the adjacent cabin load is provided. The model predicts pressure rise times with relatively small error compared to experimental values, demonstrating its suitability for engineering applications.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, C.; Lukaszewicz, M.; Schebella, K.; Antanovskii, L. Experimental and numerical investigation of confined explosion in a blast chamber. J. Loss Prev. Process. Ind. 2013, 26, 737–750. [Google Scholar] [CrossRef]
- Kong, X.; Zhou, H.; Xu, J.; Zheng, C.; Lu, A.; Wu, W. Scaling of confined explosion and structural response. Thin-Walled Struct. 2023, 186, 110656. [Google Scholar] [CrossRef]
- Edri, I.; Feldgun, V.; Karinski, Y.; Yankelevsky, D. On Blast Pressure Analysis Due to a Partially Confined Explosion: III. Afterburning Effect. Int. J. Prot. Struct. 2012, 3, 311–331. [Google Scholar] [CrossRef]
- Ames, R.G.; Drotar, J.T.; Silber, J.; Sambrook, J. Quantitative distinction between detonation and afterburn energy deposition using pressure-time histories in enclosed explosions. In Proceedings of the 13th International Detonation Symposium, Norfolk, VA, USA, 23–28 July 2006. [Google Scholar]
- Baker, W.E. Explosion Hazard Sand Evaluation; Elsevier Publishing Company: New York, NY, USA, 1983. [Google Scholar]
- U.S. Department of Defense. Structures to Resist the Effects of Accidental Explosions (UFC 3-340-02); U.S. Department of Defense: Washington, DC, USA, 2023. [Google Scholar]
- Lin, X.; Wang, S.; Zhang, L.; Xu, S.; Hu, Y. Study on load characteristics and structural impact response propagation law of cabin internal explosion. Ocean Eng. 2024, 301, 117582. [Google Scholar] [CrossRef]
- Kong, X.; Zhu, Z.; Zheng, C.; Zhou, H.; Wu, W. Numerical investigation on the dynamic behavior of thermoplastic fiber-metal laminates subject to confined explosion loading. Thin-Walled Struct. 2025, 214, 113354. [Google Scholar] [CrossRef]
- Salvado, F.C.; Tavares, A.J.; Teixeira-Dias, F.; Cardoso, J.B. Confined explosions: The effect of compartment geometry. J. Loss Prev. Process. Ind. 2017, 48, 126–144. [Google Scholar] [CrossRef]
- Grisaro, H.Y. Pressure-Impulse diagrams for assessment of structural response due to a fully confined explosion. Eng. Fail. Anal. 2023, 146, 107103. [Google Scholar] [CrossRef]
- Chang, W.; Choung, J. Sensitivity analysis of damage extent in naval ship compartments due to internal airborne explosions. Int. J. Nav. Arch. Ocean Eng. 2024, 16, 100622. [Google Scholar] [CrossRef]
- Zhang, Y.-L.; Liu, Y.; Song, P.; Liang, H.-Z.; Yang, D.; Han, L.; Jiang, H.-Y.; Zhong, K. Experimental study on the TNT equivalence for blast parameters in a confined space. Def. Technol. 2025, 48, 238–249. [Google Scholar] [CrossRef]
- Guo, X.; Li, Y.; McCrum, D.P.; Hu, Y.; Bai, Z.; Zhang, H.; Li, Z.; Wang, X. A reinforced concrete shear wall building structure subjected to internal TNT explosions: Test results and numerical validation. Int. J. Impact Eng. 2024, 190, 104950. [Google Scholar] [CrossRef]
- Li, S.; Ma, J.; Zhao, K.; Xiu, Z.; Li, R.; Liu, Z.; Zhao, Y.; Li, M.; Liu, Q. Experimental study on the effects of equivalence ratio on vented methane-hydrogen mixture explosion in confined area. Energy 2025, 322, 135646. [Google Scholar] [CrossRef]
- Choubey, B.; Dutta, S.C.; Prakhya, G.K.V.; Mandal, P.; Tanwar, R.K. Blast pressure analysis due to confined explosion-after effects. Structures 2020, 28, 521–536. [Google Scholar] [CrossRef]
- Guo, B.; Liang, W.; Xu, X.; Song, S.; Fu, Q.; Liu, S. Study on the characteristics of internal explosion loads in masonry-infilled reinforced concrete frame structures. J. Build. Eng. 2025, 111, 113243. [Google Scholar] [CrossRef]
- Zhong, Q.; Zhong, X.; Liu, Z.; Lu, Y.; Chen, T. Impact of the blockage ratio and void fraction of porous obstacle on gas explosion characteristics in semi-confined channel. Int. J. Hydrogen Energy 2024, 77, 253–264. [Google Scholar] [CrossRef]
- Li, R.; Xiu, Z.; Liu, Z.; Liu, Q.; Li, M. Simulation of obstacle spacing effects on premixed hydrogen-air explosion dynamics in semi-confined spaces. Int. J. Hydrogen Energy 2025, 105, 735–747. [Google Scholar] [CrossRef]
- Tang, J.; Chen, C.; Wang, B.; Zhang, S.; Mo, L.; Li, C. Whether hydrogen blending in natural gas pipelines induce detonation? A numerical investigation of explosions in confined pipeline compressor plants. Int. J. Hydrogen Energy 2025, 133, 247–260. [Google Scholar] [CrossRef]
- Xu, L.; Chen, L.; Feng, B.; Zhou, D. Research on internal explosion loads in folded arch tunnels: A theoretical approach. Tunn. Undergr. Space Technol. 2024, 147, 105731. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, H.; Wang, Z.; Tian, W.; Wang, Z. The effect of orifice plates with different shapes on explosion propagation of premixed methane–air in a semi-confined pipeline. J. Loss Prev. Process. Ind. 2021, 71, 104498. [Google Scholar] [CrossRef]
- Cheng, R.; Chen, W.; Hao, H.; Li, J. Effect of internal explosion on tunnel secondary and adjacent structures: A review. Tunn. Undergr. Space Technol. 2022, 126, 104536. [Google Scholar] [CrossRef]
- Weibull, H.R.W. Pressures recorded in partially closed compartments at explosion of TNT charges. Ann. N. Y. Acad. Sci. 1968, 152, 357–361. [Google Scholar] [CrossRef]
- Hou, H.L.; Zhu, X. Experimental studies on characteristics of blast loading when exploded inside ship cabin. J. Ship Mech. 2010, 14, 901–907. [Google Scholar]
- Hu, Y.; Wu, C.; Lukaszewicz, M.; Dragos, J.; Ren, J.; Haskett, M. Characteristics of confined blast loading in unvented structures. Int. J. Prot. Struct. 2011, 2, 21–43. [Google Scholar] [CrossRef]
- Zyskowski, A.; Sochet, I.; Mavrot, G.; Bailly, P.; Renard, J. Study of the explosion process in a small scale experiment—structural loading. J. Loss Prev. Process. Ind. 2004, 17, 291–299. [Google Scholar] [CrossRef]
- Anderson, C.E.; Baker, W.E.; Wauters, D.K.; Morris, B.L. Quasi-static pressure, duration, and impulse for explosions in structures. Int. J. Mech. Sci. 1983, 25, 455–464. [Google Scholar] [CrossRef]
- Kingery, C.N.; Schumacher, R.N.; Ewing, W.O. Internal Pressures from Explosions in Suppressive Structures; BRL Memorandum Report ARBRL-MR-02848; USA Ballistic Research Laboratory: Aberdeen Proving Ground, MD, USA, 1978. [Google Scholar]
- Proctor, J.F.; Filler, W.S. A computerized technique for blast loads from confined explosions. In Proceedings of the 14th Annual Explosives Safety Seminar, New Orleans, LA, USA, 8–10 November 1972; Volume 10, pp. 99–124. [Google Scholar]
- Kinney, G.F.; Sewell, R.G.S. Venting of Explosions; NWC Tech. Mem. 2448; Naval Weapons Center: China Lake, CA, USA, 1974. [Google Scholar]
- Carlson, R.W. Confinement of an Explosion by a Steel Vessel; LANL: Los Alamos, NM, USA, 1945. [Google Scholar]
- Moir, D.C. Safety Analysis of the M-2 Comfinement Systems; LANL: Los Alamos, NM, USA, 1979. [Google Scholar]
- Baker, W.E.; Hokanson, J.C.; Esparza, E.D.; Sandoval, N.R. Gas Pressure Loads with Invented and Unvented Structures; Southwest Research Institute: San Antonio, TX, USA, 1983. [Google Scholar]
- Lloyd’s Register. Rules and Regulations for the Classification of Naval Ships: Naval Ship Code (NSC); Lloyd’s Register Group Limited: London, UK, 2020. [Google Scholar]
- TM5-1300; Structures to Resist the Effects of Accidental Explosions. Departments of the Army, the Navy and the Airforce: Washington, DC, USA, 1990.
- Wang, Y.; Li, W.; Zhu, W.; Zhang, Q.; Li, W.; Wang, X. Dynamic response of steel cabin structure under blast loading from adjacent cabin. Eng. Struct. 2024, 311, 118213. [Google Scholar] [CrossRef]

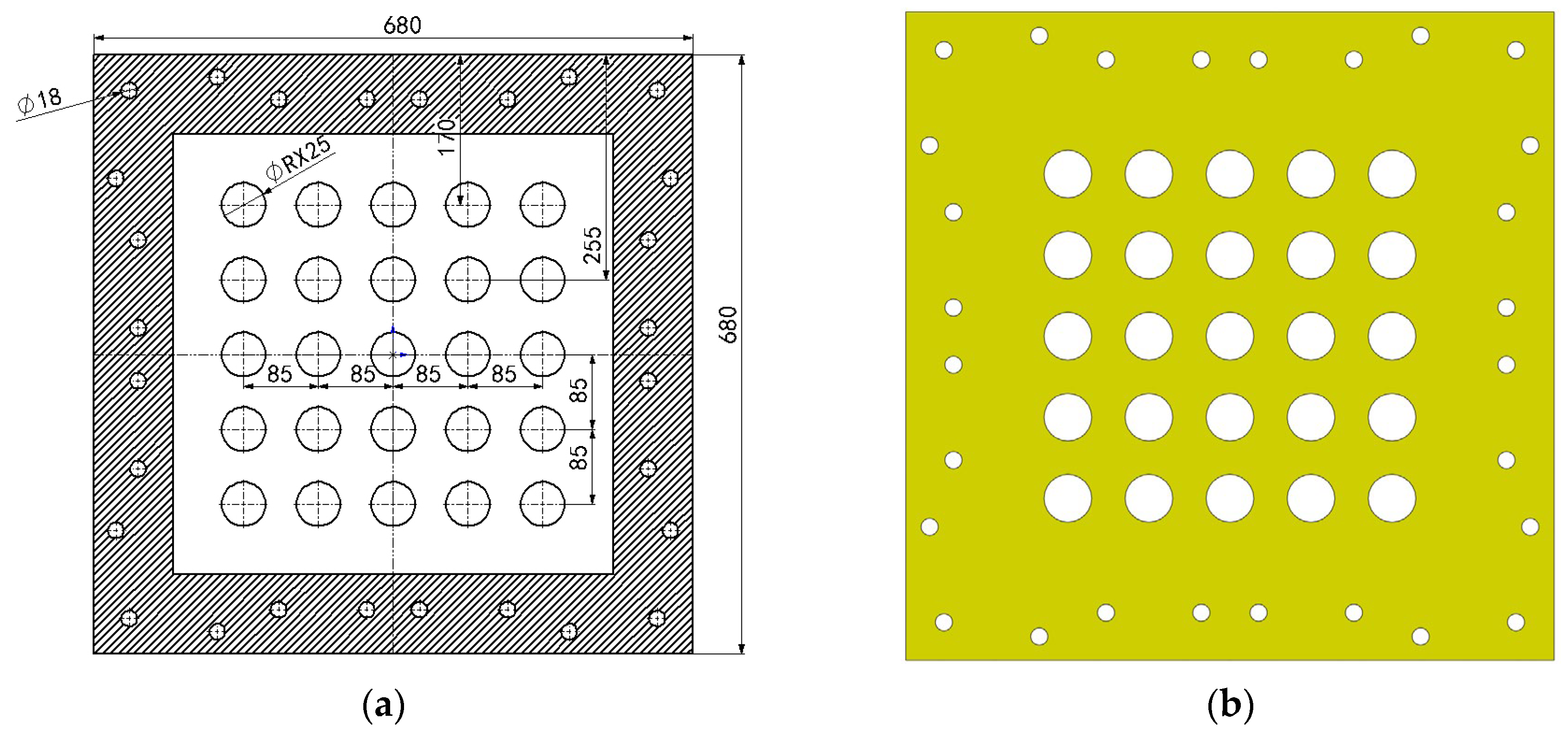


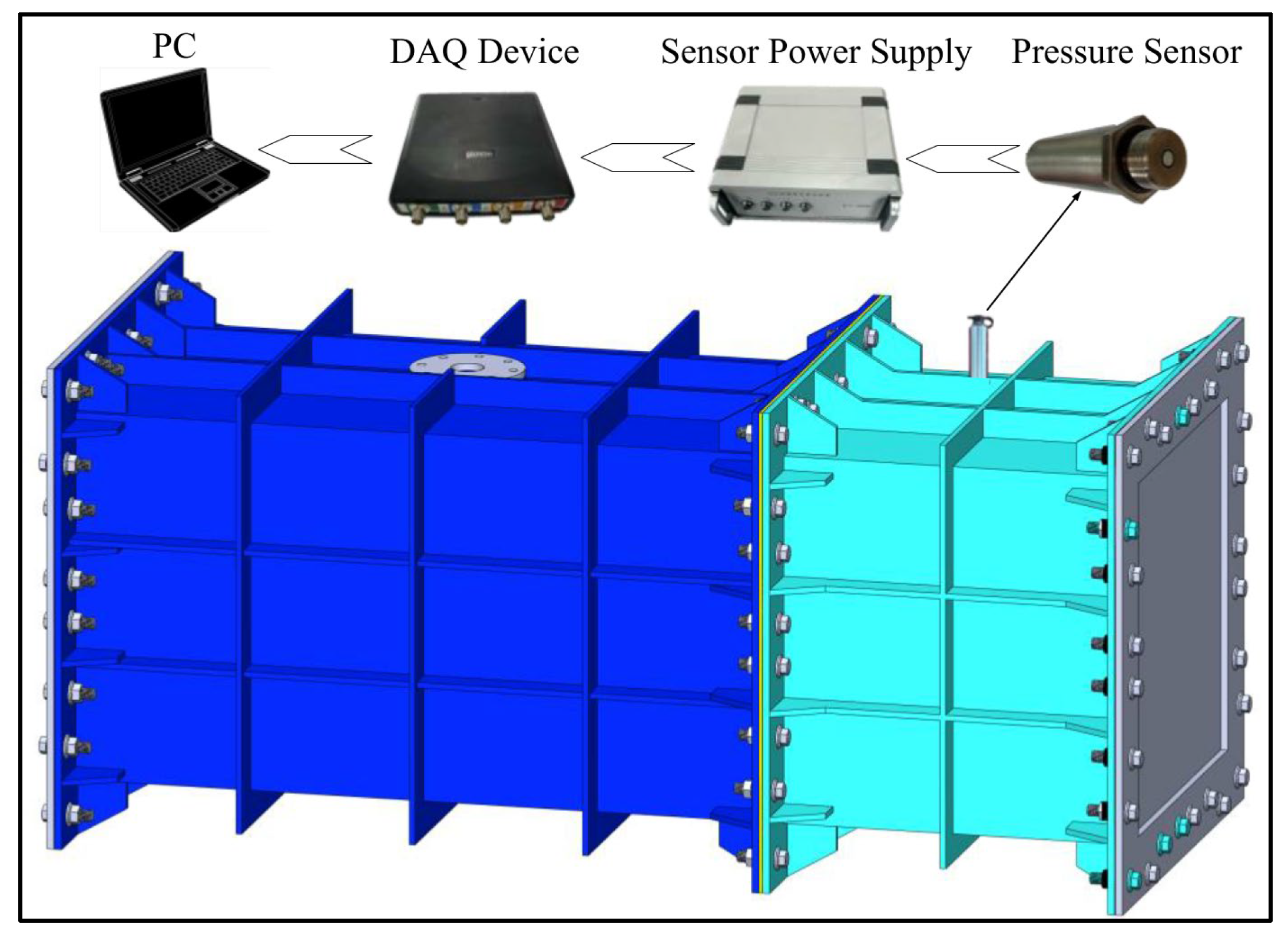



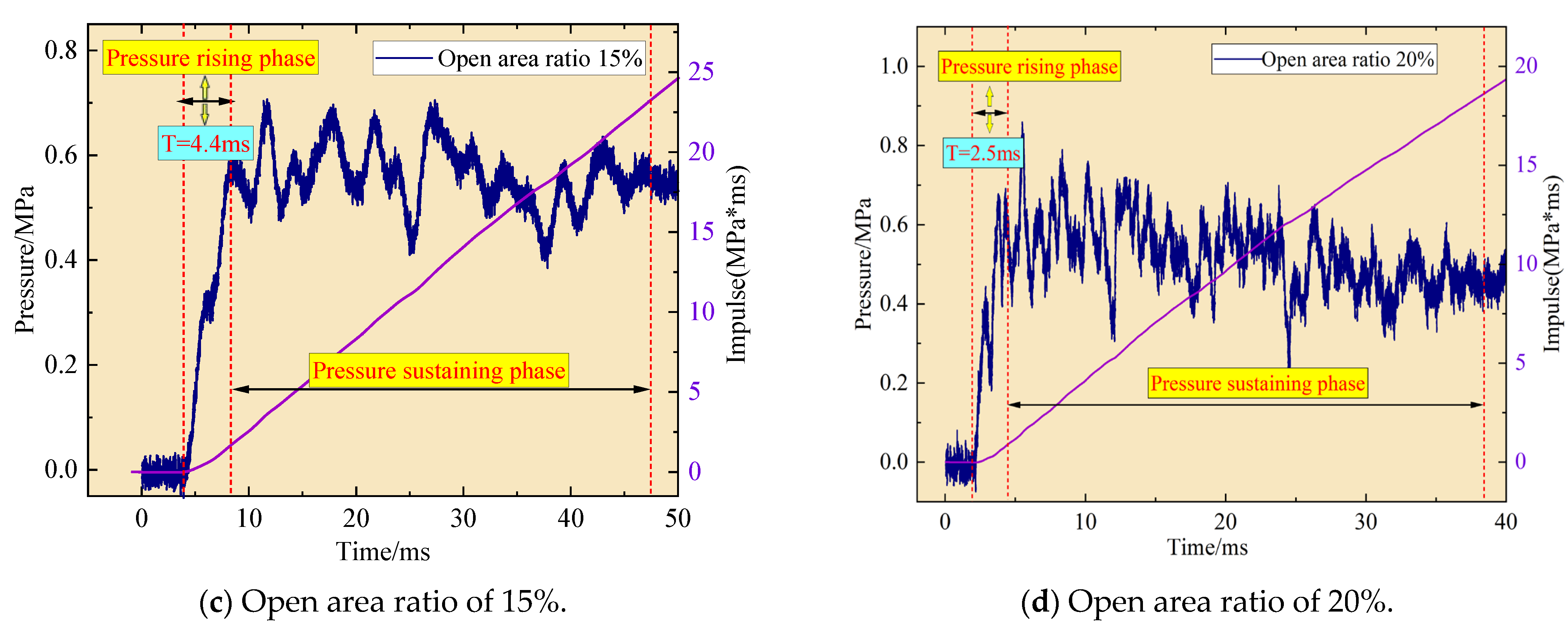
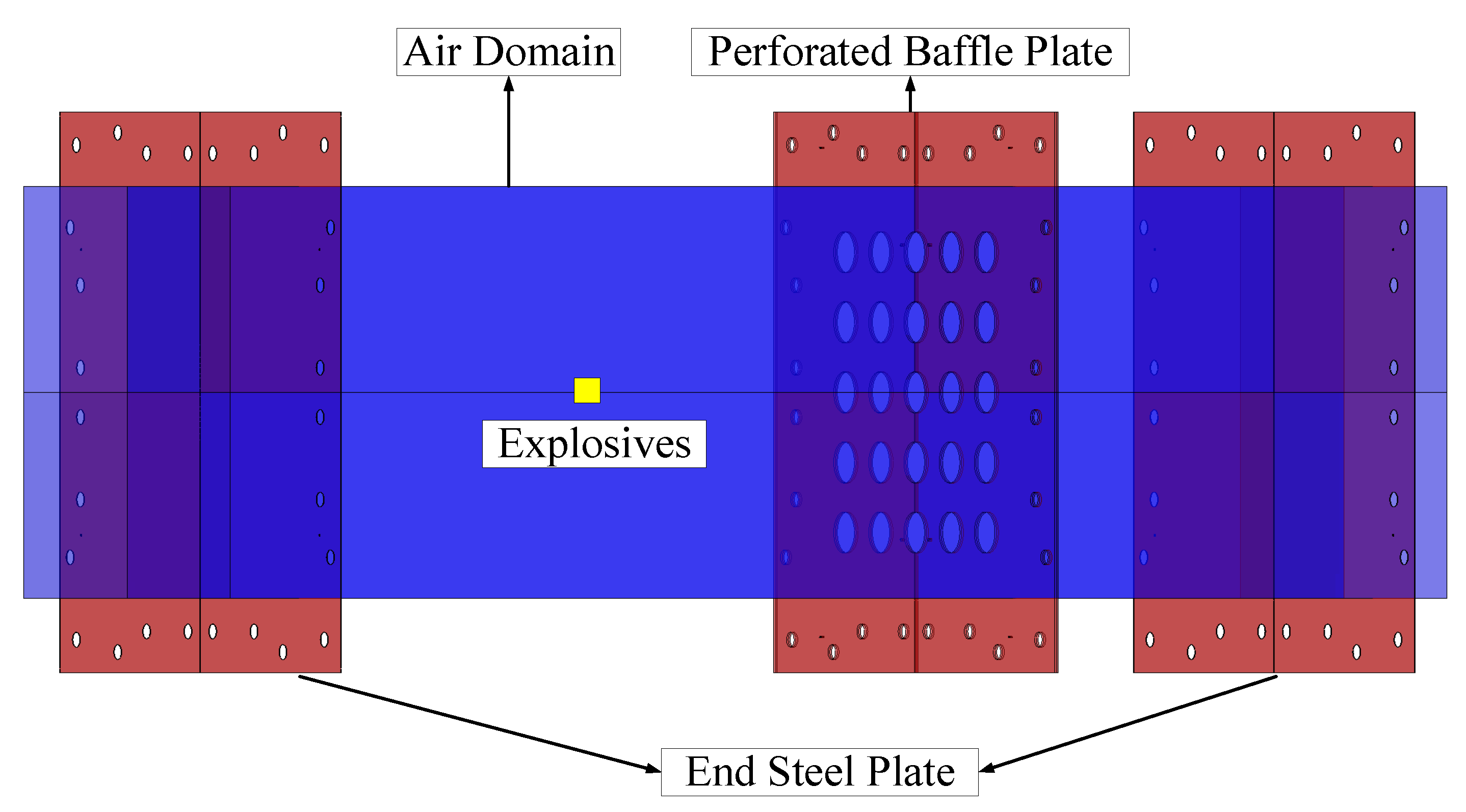





| Test | Charge Mass (g) | Open Area Ratio | Hole Radius (mm) | Schematic |
|---|---|---|---|---|
| 1 | 59.35 | 3% | 10 |  |
| 2 | 59.46 | 5% | 13 |  |
| 3 | 60.41 | 15% | 22 |  |
| 4 | 59.68 | 20% | 25 |  |
| Density ρ/(kg/m3) | /(Mpa) | B/(Mpa) | n | C | m |
|---|---|---|---|---|---|
| 7800 | 268 | 889 | 0.746 | 0.058 | 0.94 |
| Density ρ/(kg/m3) | Detonation Velocity/D(m/s) | C-J Pressure/(Pa) | C1/(Pa) |
|---|---|---|---|
| 1630 | 6800 | 2.1 × 1010 | 3.74 × 1011 |
| C2 | r1 | r2 | ω |
| 3.75 × 109 | 4.15 | 0.9 | 0.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Fan, Z.; Zhang, X.; Yi, J. Study on Simplified Model of Pressure Loading in Adjacent Cabin with Internal Explosions in Cabin. Appl. Sci. 2025, 15, 10140. https://doi.org/10.3390/app151810140
Li X, Fan Z, Zhang X, Yi J. Study on Simplified Model of Pressure Loading in Adjacent Cabin with Internal Explosions in Cabin. Applied Sciences. 2025; 15(18):10140. https://doi.org/10.3390/app151810140
Chicago/Turabian StyleLi, Xudong, Zirui Fan, Xuepeng Zhang, and Jianya Yi. 2025. "Study on Simplified Model of Pressure Loading in Adjacent Cabin with Internal Explosions in Cabin" Applied Sciences 15, no. 18: 10140. https://doi.org/10.3390/app151810140
APA StyleLi, X., Fan, Z., Zhang, X., & Yi, J. (2025). Study on Simplified Model of Pressure Loading in Adjacent Cabin with Internal Explosions in Cabin. Applied Sciences, 15(18), 10140. https://doi.org/10.3390/app151810140






