LLM-Assisted Non-Dominated Sorting Genetic Algorithm for Solving Distributed Heterogeneous No-Wait Permutation Flowshop Scheduling
Abstract
1. Introduction
- (1)
- A multi-objective optimization framework is developed for the distributed heterogeneous no-wait permutation flowshop scheduling problem with sequence-dependent setup times (DHNPFSP-SDST), explicitly minimizing both Cmax and Ttot, which extends the single-objective optimization paradigm from prior work and addresses practical production scenarios where decision-makers must balance operational efficiency.
- (2)
- We propose the LLM-NSGAII that integrates LLM into the traditional NSGAII framework to solve DHNPFSP-SDST. By designing a structured prompt system to guide evolutionary operations via in-context learning, it introduces natural language-based intelligence into multi-objective optimization. This innovation demonstrates LLMs’ potential to enhance evolutionary algorithms, offering a new paradigm for algorithm design in complex combinatorial optimization.
- (3)
- Experiments on extended benchmark examples show that the LLM-assisted method achieves competitive results equivalent to the most advanced algorithm on different problem scales, which verifies the feasibility of integrating LLMs into evolutionary computation of complex scheduling optimization.
2. Problem Formulation of the DHNPFSP-SDST
2.1. Problem Definition
- A job can only be processed completely in a shop and cannot be transferred to another shop during processing.
- There are no considerations on transportation in a factory and between factories, and transportation times are included in processing time.
- Machines can process jobs continuously and do not experience facility malfunctions or maintenance issues.
2.2. Mathematical Model
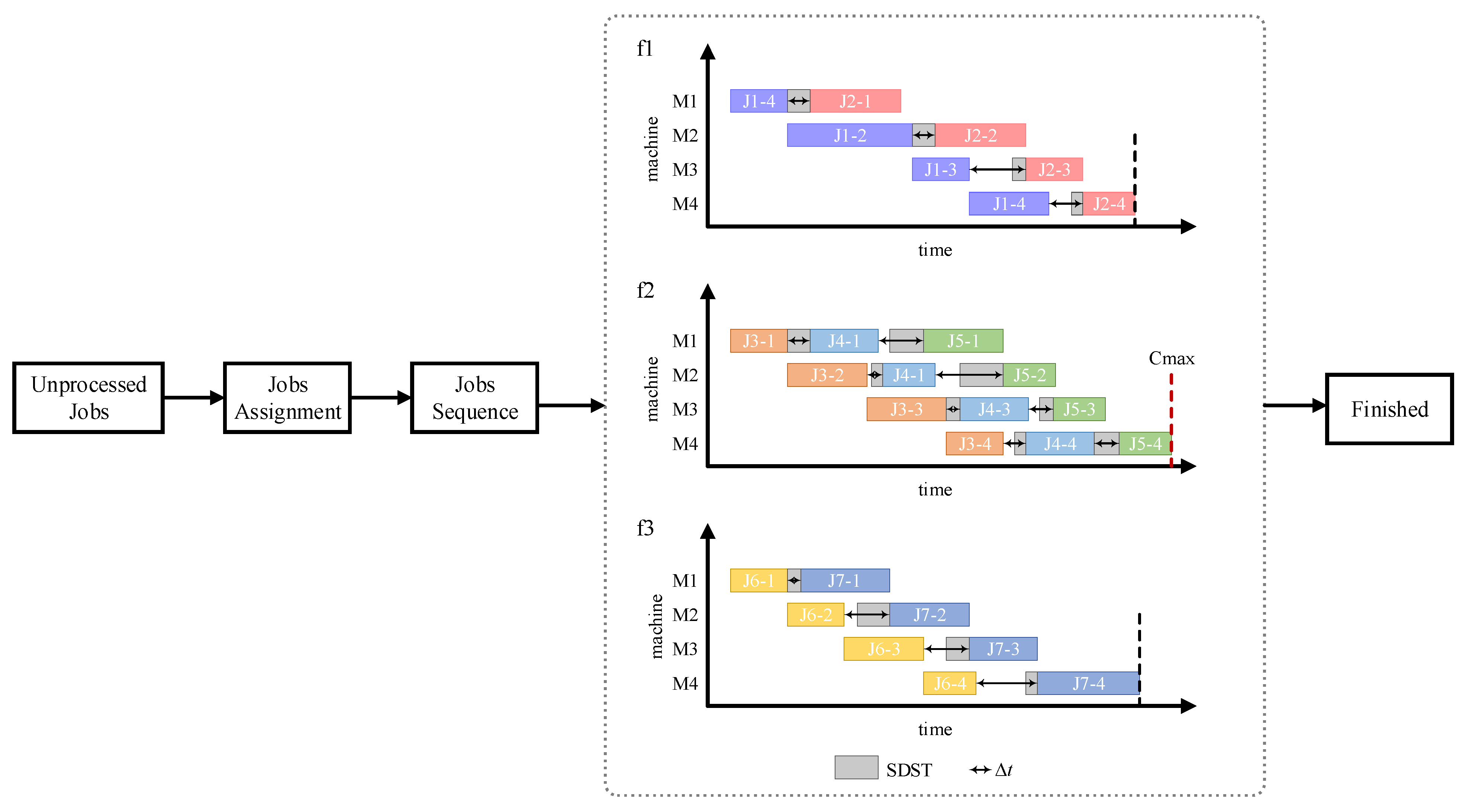
2.3. Illustrative Example
2.4. Problem Complexity Analysis
3. Proposed LLM-NSGAII for the DHNPFSP-SDST
3.1. Framework of Proposed LLM-NSGAII
3.2. Solution Representation and Initialization
- Cmax-Greedy Initialization
- SDST-Greedy Initialization
3.3. LLM-Assisted Evolution Operation
- (1)
- Problem definition and solution representation: This section outlines the DHNPFSP-SDST, including the number of factories and jobs. And it specifies the input format of solution, which is encoded as a one-dimensional integer array with delimiters separating factory-specific job sequences; each solution has corresponding attributes to help make decision. The optimization objectives are clearly defined.
- (2)
- Input solutions: A set of solutions from the current population is provided, each formatted as an integer array and accompanied by attributes values reflecting their performance against the defined objectives. These examples serve as in-context learning material for the LLM, illustrating the relationship between solution structures and their optimization outcomes.
- (3)
- Evolutionary operation instructions: Explicit instructions guide the LLM to perform parent selection, crossover, and mutation. Selection involves randomly choosing diverse parent solutions. Crossover operators (CrO1, CrO2, CrO3) and mutation operators (M1, M2, M3) are described, with parameters such as the number of crossover points or mutation sites specified. The LLM is tasked with generating new solutions by applying these operations in a zero-shot manner.
- (4)
- Output legalization: The output is required to verify that generated solutions adhere to the specified encoding format, contain no duplicate jobs, and satisfy problem constraints. It must return a predefined number of valid solutions, formatted as integer arrays, suitable for direct integration into the next generation of the NSGAII population.
4. Experiment Results and Analysis
4.1. Dataset and Metrics
4.2. Comparison Experiment
4.3. Results and Analysis
4.3.1. Comparison Between LLM-NSGAII and NSGAII
4.3.2. Comparison Between LLM-NSGAII and Other Multi-Objective Algorithms
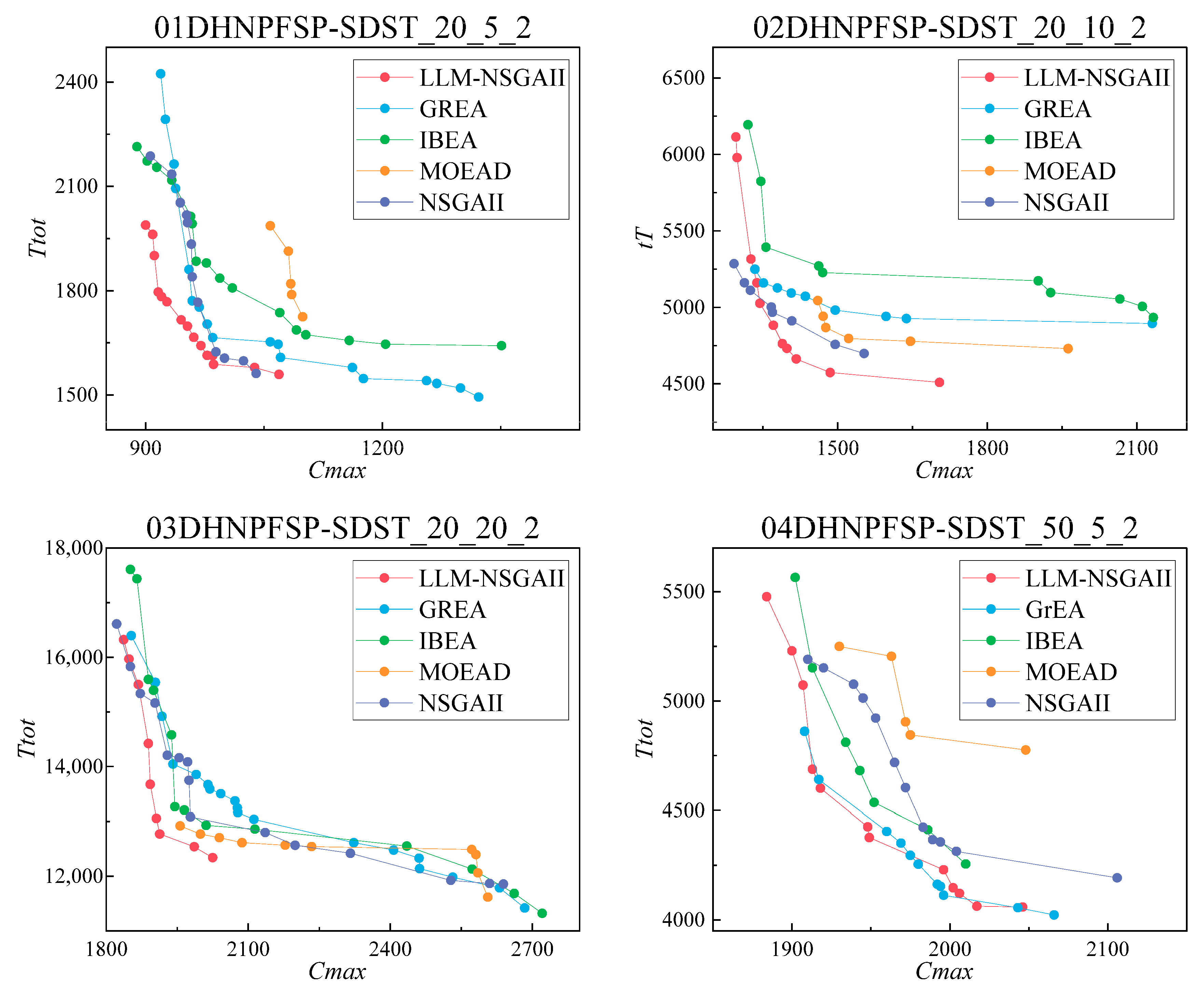
4.3.3. Pareto Front Analysis
4.3.4. Statistical Significance Testing
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Notation | Description |
| Indices | |
| i | machine index, i ∈ {1,2,…,m} |
| j, v | job index, j,v ∈ {1,2,…,n} |
| l | factory index, l ∈ {1,2,…,f} |
| k | position index, k ∈ {1,2,…,n} |
| Parameters | |
| f | the total number of factories |
| n | the total number of jobs |
| m | the total number of machines in a factory |
| F | {F1, F2, …, Ff}, factory set |
| N | {J1, J2, …, Jn}, job set |
| M | {M1, M2, …, Mm}, machine set in a factory |
| pl,i,j | processing time of Jj on Mi in Fl |
| sdstl,i,j,v | setup time of processing Jv after Jj on Mi in Fl |
| Decision Variable | |
| Xl,k,j | binary value that is set to 1 when Jj is processed at position k and assigned to Fl, otherwise set to 0 |
| Cl,i,k | completion time of job at position k in Fl on Mi |
| Cmax | the makespan |
| Ttot | the total non-working time of machines in all factories |
References
- Soori, M.; Arezoo, B.; Dastres, R. Digital twin for smart manufacturing. A review. Sustain. Manuf. Serv. Econ. 2023, 62, 100017. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, L. Differential evolution algorithm for hybrid flow-shop scheduling problems. Syst. Eng. Electron. 2011, 22, 794–798. [Google Scholar] [CrossRef]
- Jiang, E.; Wang, L.; Wang, J. Decomposition-based multi-objective optimization for energy-aware distributed hybrid flowshop scheduling with multiprocessor tasks. Tsinghua Sci. Technol. 2021, 26, 646–663. [Google Scholar] [CrossRef]
- Yuan, Y.; Xu, H. Multiobjective flexible job shop scheduling using memetic algorithms. IEEE Trans. Autom. Sci. Eng. 2015, 12, 336–353. [Google Scholar] [CrossRef]
- Men, T.; Pan, Q.K. A distributed heterogeneous permutation flowshop scheduling problem with lot-streaming and carryover sequence-dependent setup time. Swarm Evol. Comput. 2021, 60, 100804. [Google Scholar]
- Wang, K.; Luo, H.; Liu, F.; Yue, X. Permutation flowshop scheduling with batch delivery to multiple customers in supply chains. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 1826–1837. [Google Scholar] [CrossRef]
- Li, X.; Li, M. Multiobjective local search algorithm-based decomposition for multiobjective permutation flowshop scheduling problem. IEEE Trans. Eng. Manag. 2015, 62, 544–557. [Google Scholar] [CrossRef]
- Li, H.; Gao, K.; Duan, P.Y.; Li, J.Q.; Zhang, L. An improved artificial bee colony algorithm with q-learning for solving permutation flow-shop scheduling problems. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 2684–2693. [Google Scholar] [CrossRef]
- Chen, S.Y.; Wang, X.W.; Wang, Y.; Gu, X.S. A modified adaptive switching-based many-objective evolutionary algorithm for distributed heterogeneous flowshop scheduling with lot-streaming. Swarm Evol. Comput. 2023, 81, 101353. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, B.; Wang, L.; Xing, K. Distributed heterogeneous co-evolutionary algorithm for scheduling a multistage fine-manufacturing system with setup constraints. IEEE Trans. Cybern. 2024, 54, 1497–1510. [Google Scholar] [CrossRef]
- Shao, W.; Shao, Z.; Pi, D. An ant colony optimization behavior-based moea/d for distributed heterogeneous hybrid flowshop scheduling problem under nonidentical time-of-use electricity tariffs. IEEE Trans. Autom. Sci. Eng. 2022, 19, 3379–3394. [Google Scholar] [CrossRef]
- Li, R.; Gong, W.; Wang, L.; Lu, C.; Pan, Z.; Zhuang, X. Double DQN-based coevolution for green distributed heterogeneous hybrid flowshop scheduling with multiple priorities of jobs. IEEE Trans. Autom. Sci. Eng. 2024, 21, 6550–6562. [Google Scholar] [CrossRef]
- Zhao, F.; Jiang, T.; Wang, L. A reinforcement learning driven cooperative meta-heuristic algorithm for energy-efficient distributed no-wait flow-shop scheduling with sequence-dependent setup time. IEEE Trans. Ind. Inform. 2023, 19, 8427–8440. [Google Scholar] [CrossRef]
- Fu, Y.; Hou, Y.; Wang, Z.; Wu, X.; Gao, K.; Wang, L. Distributed scheduling problems in intelligent manufacturing systems. Tsinghua Sci. Technol. 2021, 26, 625–645. [Google Scholar] [CrossRef]
- Li, H.R.; Li, X.Y.; Gao, L. A discrete artificial bee colony algorithm for the distributed heterogeneous no-wait flowshop scheduling problem. Appl. Soft Comput. 2021, 100, 106946. [Google Scholar] [CrossRef]
- Liu, S.; Chen, C.; Qu, X.; Tang, K.; Ong, Y.S. Large language models as evolutionary optimizers. In Proceedings of the IEEE Congress on Evolutionary Computation, Yokohama, Japan, 30 June–5 July 2024; pp. 1–8. [Google Scholar]
- Huang, Y.; Zhang, W.; Feng, L.; Wu, X.; Tan, K.C. How multimodal integration boost the performance of LLM for optimization: Case study on capacitated vehicle routing problems. arXiv 2024, arXiv:2403.01757. [Google Scholar] [CrossRef]
- Wu, X.; Wu, S.H.; Wu, J.; Feng, L.; Tan, K.C. Evolutionary computation in the era of large language model: Survey and roadmap. IEEE Trans. Evol. Comput. 2025, 29, 534–554. [Google Scholar] [CrossRef]
- Brahmachary, S.; Joshi, S.M.; Panda, A.; Koneripalli, K.; Sagotra, A.K.; Patel, H.; Sharma, A.; Jagtap, A.D.; Kalyanaraman, K. Large language model-based evolutionary optimizer: Reasoning with elitism. arXiv 2024, arXiv:2403.02054. [Google Scholar] [CrossRef]
- Chiquier, M.; Mall, U.; Vondrick, C. Evolving interpretable visual classifiers with large language models. arXiv 2024, arXiv:2404.09941. [Google Scholar] [CrossRef]
- Leung, J.; Shen, Z. Prompt Engineering for Curriculum Design. In Proceedings of the International Conference on Educational Technology, Wuhan, China, 13–15 September 2024; pp. 97–101. [Google Scholar]
- Haneef, F.; Varalakshmi, M.; P U, P.M. Leveraging RAG for Effective Prompt Engineering in Job Portals. In Proceedings of the International Conference on Computational Intelligence, Okayama, Japan, 21–23 November 2025; pp. 717–721. [Google Scholar]
- Loss, L.A.; Dhuvad, P. From Manual to Automated Prompt Engineering: Evolving LLM Prompts with Genetic Algorithms. In Proceedings of the IEEE Congress on Evolutionary Computation, Hangzhou, China, 8–12 June 2025; pp. 1–8. [Google Scholar]
- Li, Y.; Zhang, R.; Liu, J.; Lei, Q. A Semantic Controllable Long Text Steganography Framework Based on LLM Prompt Engineering and Knowledge Graph. IEEE Signal Process. Lett. 2024, 31, 2610–2614. [Google Scholar] [CrossRef]
- Petke, J.; Haraldsson, S.O.; Harman, M.; Langdon, W.B.; White, D.R.; Woodward, J.R. Genetic improvement of software: A comprehensive survey. IEEE Trans. Evol. Comput. 2017, 22, 415–432. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zhao, F.; Hu, X.; Wang, L.; Zhao, J.; Tang, J. A reinforcement learning brain storm optimization algorithm (BSO) with learning mechanism. Knowl.-Based Syst. 2022, 235, 107645. [Google Scholar] [CrossRef]
- Zhao, F.; Wang, Z.; Wang, L. A reinforcement learning driven artificial bee colony algorithm for distributed heterogeneous no-wait flowshop scheduling problem with sequence-dependent setup times. IEEE Trans. Autom. Sci. Eng. 2023, 20, 2305–2320. [Google Scholar] [CrossRef]
- Ruiz, R.; Pan, Q.K.; Naderi, B. Iterated greedy methods for the distributed permutation flowshop scheduling problem. Omega 2019, 83, 213–222. [Google Scholar] [CrossRef]
- Huang, K.H.; Li, R.; Gong, W.Y.; Wang, R.; Wei, H. BRCE: Bi-roles co-evolution for energy-efficient distributed heterogeneous permutation flowshop scheduling with flexible machine speed. Complex Intell. Syst. 2023, 9, 4805–4816. [Google Scholar] [CrossRef]
- Shang, K.; Ishibuchi, H.; He, L.; Pang, L.M. A survey on the hypervolume indicator in evolutionary multi-objective optimization. IEEE Trans. Evol. Comput. 2021, 25, 1–20. [Google Scholar] [CrossRef]
- Zhang, Q.F.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Zitzler, E.; Künzli, S. Indicator-based selection in multi-objective search. In Proceedings of the Parallel Problem Solving from Nature, Birmingham, UK, 18–22 September 2004; pp. 832–842. [Google Scholar]
- Yang, S.; Li, M.; Liu, X.; Zheng, J. A grid-based evolutionary algorithm for many-objective optimization. IEEE Trans. Evol. Comput. 2013, 17, 721–736. [Google Scholar] [CrossRef]
- Na, S.; Jeong, G.; Ahn, B.H.; Young, J.; Krishna, T.; Kim, H. Understanding Performance Implications of LLM Inference on CPUs. In Proceedings of the IEEE International Symposium on Workload Characterization, Vancouver, BC, Canada, 15–17 September 2024; pp. 169–180. [Google Scholar]
- Shahandashti, K.K.; Sivakumar, M.; Mohajer, M.M.; Belle, A.B.; Wang, S.; Lethbridge, T. Assessing the Impact of GPT-4 Turbo in Generating Defeaters for Assurance Cases. In Proceedings of the IEEE/ACM First International Conference on AI Foundation Models and Software Engineering, Lisbon, Portugal, 14 April 2024; pp. 52–56. [Google Scholar]


| Reference | Problem Type | Key Constraints | Optimization Objective |
|---|---|---|---|
| Johnson [2] | FSP | Idealized scenario, homogeneous machines, fixed process routes | makespan |
| Wang et al. [6] Li et al. [7] Li et al. [8] | PFSP | Sequence consistency of jobs across machines | makespan |
| Zhang et al. [10] | DPFSP | Distributed fabrication–assembly–differentiation process, customized requirements | makespan |
| Shao et al. [11] Li et al. [12] | DHHFSP | Heterogeneous factories, nonidentical electricity costs | makespan |
| Zhao et al. [13] | DNW-FSP | Distributed factories, no-wait constraint, sequence-dependent setup time (SDST), energy efficiency | makespan energy consumption |
| This study | DHNWPFSP-SDST | Distributed heterogeneous factories, no-wait constraint, SDST | makespan idle time |
| Instance | HV | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| n_m_f | LLM-NSGAII | NSGAII | MOEAD | IBEA | GREA | |||||
| mean | std | mean | std | mean | std | mean | std | mean | std | |
| 20_5_2 | 0.539 | 0.006 | 0.541 | 0.003 | 0.491 | 0.003 | 0.484 | 0.004 | 0.515 | 0.002 |
| 20_10_2 | 0.525 | 0.012 | 0.525 | 0.004 | 0.514 | 0.003 | 0.521 | 0.002 | 0.523 | 0.005 |
| 20_20_2 | 0.527 | 0.008 | 0.531 | 0.003 | 0.522 | 0.003 | 0.532 | 0.005 | 0.526 | 0.003 |
| 50_5_2 | 0.431 | 0.008 | 0.428 | 0.004 | 0.414 | 0.004 | 0.443 | 0.002 | 0.444 | 0.003 |
| 50_10_2 | 0.547 | 0.007 | 0.530 | 0.004 | 0.544 | 0.002 | 0.545 | 0.004 | 0.541 | 0.004 |
| 50_20_2 | 0.523 | 0.008 | 0.507 | 0.004 | 0.525 | 0.004 | 0.527 | 0.003 | 0.514 | 0.003 |
| 100_5_2 | 0.416 | 0.005 | 0.395 | 0.002 | 0.399 | 0.004 | 0.415 | 0.004 | 0.406 | 0.004 |
| 100_10_2 | 0.533 | 0.005 | 0.516 | 0.003 | 0.531 | 0.002 | 0.540 | 0.002 | 0.527 | 0.004 |
| 100_20_2 | 0.521 | 0.006 | 0.524 | 0.006 | 0.513 | 0.005 | 0.517 | 0.004 | 0.519 | 0.004 |
| 200_10_2 | 0.406 | 0.007 | 0.403 | 0.005 | 0.396 | 0.004 | 0.394 | 0.005 | 0.393 | 0.003 |
| 200_20_2 | 0.525 | 0.006 | 0.516 | 0.006 | 0.504 | 0.006 | 0.507 | 0.006 | 0.511 | 0.005 |
| 500_20_2 | 0.510 | 0.009 | 0.502 | 0.005 | 0.510 | 0.004 | 0.527 | 0.005 | 0.506 | 0.005 |
| 20_5_3 | 0.568 | 0.010 | 0.564 | 0.003 | 0.565 | 0.005 | 0.562 | 0.004 | 0.556 | 0.003 |
| 20_10_3 | 0.573 | 0.009 | 0.565 | 0.002 | 0.565 | 0.002 | 0.560 | 0.003 | 0.564 | 0.005 |
| 20_20_3 | 0.576 | 0.007 | 0.578 | 0.003 | 0.574 | 0.003 | 0.540 | 0.002 | 0.563 | 0.004 |
| 50_5_3 | 0.465 | 0.009 | 0.458 | 0.003 | 0.452 | 0.002 | 0.455 | 0.004 | 0.462 | 0.005 |
| 50_10_3 | 0.592 | 0.008 | 0.597 | 0.006 | 0.592 | 0.005 | 0.601 | 0.003 | 0.596 | 0.006 |
| 50_20_3 | 0.574 | 0.008 | 0.557 | 0.005 | 0.572 | 0.006 | 0.547 | 0.003 | 0.566 | 0.005 |
| 100_5_3 | 0.497 | 0.008 | 0.481 | 0.007 | 0.504 | 0.003 | 0.517 | 0.005 | 0.493 | 0.006 |
| 100_10_3 | 0.551 | 0.012 | 0.542 | 0.004 | 0.550 | 0.005 | 0.583 | 0.006 | 0.552 | 0.008 |
| 100_20_3 | 0.578 | 0.015 | 0.575 | 0.005 | 0.571 | 0.007 | 0.562 | 0.005 | 0.581 | 0.008 |
| 200_10_3 | 0.466 | 0.014 | 0.465 | 0.007 | 0.469 | 0.009 | 0.487 | 0.008 | 0.468 | 0.009 |
| −/=/+ | 16/1/5 | 17/0/5 | 13/0/9 | 17/0/5 | ||||||
| p-Value Based on the Rank-Sum Test of Wilcoxon | ||||||
|---|---|---|---|---|---|---|
| LLM-NSGAII vs. the compared algorithms | + | − | ≈ | Z | p-value | A = 0.05 |
| NSGAII | 16 | 5 | 1 | −3.872 | 0.0001 | significant |
| MOEAD | 17 | 5 | 0 | −3.215 | 0.0013 | significant |
| IBEA | 13 | 9 | 0 | −1.264 | 0.2076 | not significant |
| GREA | 17 | 5 | 0 | −2.941 | 0.0034 | significant |
| Algorithm | Total Rank Sum | Average Rank |
|---|---|---|
| LLM-NSGAII | 38.8 | 1.72 |
| IBEA | 47.30 | 2.15 |
| GREA | 67.76 | 3.08 |
| NSGAII | 78.32 | 3.56 |
| MOEAD | 98.78 | 4.49 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Zhao, H.; Zhao, W.; Bian, X.; Yun, X. LLM-Assisted Non-Dominated Sorting Genetic Algorithm for Solving Distributed Heterogeneous No-Wait Permutation Flowshop Scheduling. Appl. Sci. 2025, 15, 10131. https://doi.org/10.3390/app151810131
Zhang Z, Zhao H, Zhao W, Bian X, Yun X. LLM-Assisted Non-Dominated Sorting Genetic Algorithm for Solving Distributed Heterogeneous No-Wait Permutation Flowshop Scheduling. Applied Sciences. 2025; 15(18):10131. https://doi.org/10.3390/app151810131
Chicago/Turabian StyleZhang, ZhaoHui, Hong Zhao, Wanqiu Zhao, Xu Bian, and Xialun Yun. 2025. "LLM-Assisted Non-Dominated Sorting Genetic Algorithm for Solving Distributed Heterogeneous No-Wait Permutation Flowshop Scheduling" Applied Sciences 15, no. 18: 10131. https://doi.org/10.3390/app151810131
APA StyleZhang, Z., Zhao, H., Zhao, W., Bian, X., & Yun, X. (2025). LLM-Assisted Non-Dominated Sorting Genetic Algorithm for Solving Distributed Heterogeneous No-Wait Permutation Flowshop Scheduling. Applied Sciences, 15(18), 10131. https://doi.org/10.3390/app151810131






