Abstract
This paper presents a practical experiment for estimating the state-of-charge (SOC) of individual cells in a series-connected heterogeneous lithium-ion battery pack, where only the terminal voltage of the battery pack is measured. To deal with real-time computation constraints, the dense extended Kalman filter (DEKF) algorithm has been proposed in the literature, which has a significantly lower computational complexity compared to the regular extended Kalman filter for this specific estimation problem. This work supplements the existing work by conducting a real-world experiment to validate the performance of the DEKF. Specifically, experiments involving a battery pack of three cells connected in series were conducted, where the battery pack was discharged under a constant current load. A genetic algorithm was applied to identify missing model parameters, as well as tuning the DEKF for optimal convergence and accurate SOC estimation. Our experimental results confirm that the proposed DEKF accurately estimates the SOC of each cell regardless of the hardware limitations and uncertainty, making it suitable for low-cost, real-time battery management systems. In particular, the SOC estimation error can be kept well under 1% even if the initial estimate is far from the true SOC.
1. Introduction
The need to store energy efficiently using batteries has increased significantly in recent decades and has become essential in many industries. Today, electric vehicles (EVs) rely heavily on batteries [1,2], and large-scale battery storage systems are widely deployed alongside renewable energy plants and grids [3,4]. This growing reliance is also driven by global efforts to reduce greenhouse gas emissions and combat climate change. As nations commit to decarbonization targets and adopt stricter environmental regulations, interest in EVs and renewable energy has surged, positioning battery technologies as key enablers in the transition to a low-carbon future [5,6,7].
Because of the unavoidable manufacturing inconsistencies, individual battery cells often experience variations in voltage and state-of-charge (SOC), which, in turn, negatively impact both performance and lifespan, eventually affecting the performance of the EVs [8,9]. To address this issue, balancing circuits are commonly paired with advanced control algorithms such as model predictive control [10,11], which requires accurate estimation of the SOC for each individual cell. Reliable SOC estimation becomes essential, since inaccurate estimations can mislead balancing controllers into overcharging or overdischarging multiple cells, accelerating pack degradation. Unfortunately, accurately estimating the SOC remains a fundamental challenge due to the highly nonlinear nature of battery dynamics and the complex internal electrochemical behavior of the cells [12,13].
Although traditional Coulomb counting methods are computationally simple, they are significantly affected by cumulative integration errors, which degrade SOC estimation accuracy over time [14,15]. In contrast, the extended Kalman filter (EKF) offers a more robust solution by combining a mathematical model of the nonlinear cell dynamic with real-time terminal voltage measurements, thus reducing the drift issues seen in Coulomb counting [16,17,18]. The EKF has been extensively studied for its ability to improve SOC estimation accuracy [19,20,21]. The extension of the EKF to estimating the SOC of multiple cells, especially when the cells have heterogeneous characteristics and only the battery pack terminal voltage is measured, is considered challenging due to significant computational delays and the requirement of large memory resources [22,23,24]. This makes full-scale Kalman filtering across a large number of cells unsuitable for resource-constrained environments, where both processing power and memory are severely limited. While some research has explored data-driven approaches for estimating the overall pack SOC [25,26], these methods lack transparency and predictability, which is unfavorable in the context of deterministic estimation. Finally, data-driven SOC estimation has been recently studied in [27,28,29].
To enable cell SOC estimation in a heterogeneous battery pack, ref. [30] introduced a novel approach, termed as the dense extended Kalman filter (DEKF). Unlike the traditional EKF, which handles each cell’s dynamics individually using sparse state-space representations, the DEKF reformulates the entire battery pack as a single “average” cell and conducts state estimation on this unified representation. Importantly, this average cell model retains fixed dimensions that do not change with respect to the number of cells in the series string. To capture individual cell differences, a relative fitness factor (RFF) is assigned to each cell, which reflects how a particular cell’s SOC deviates from that of the average cell and is primarily governed by the cell’s physical parameters. These RFFs enable the reconstruction of each individual cell’s SOC from the average state, effectively simplifying the problem to estimating a single fixed-size state. Similar to the interval estimation strategy in [24], the size of the DEKF’s state vector remains constant regardless of how many cells are present. The simulation results reported in [30] show that for a 100-cell battery system the proposed DEKF can reduce computational demands by over 16 million floating-point operations (FLOPs) compared to the sparse EKF, while maintaining nearly equivalent estimation accuracy. Moreover, performance improves as the number of cells increases. For example, the average SOC estimation RMSE decreases from approximately 0.0055 with 2 cells to about 0.0040 with 200 cells. Likewise, the predicted measurement RMSE drops more significantly, from nearly 0.0095 to below 0.0030 as the number of cells increases. This improvement results from the averaging effect across more cells, which reduces measurement noise and enables the adaptive DEKF to rely more confidently on sensor data to refine model predictions.
However, although ref. [30] provides a rigorous theoretical analysis of the properties of the proposed DEKF, accompanied by simulation validation, its performance in a real-world setting has yet to be confirmed. Therefore, this paper focused on demonstrating the DEKF’s computational efficiency and SOC estimation accuracy through real-world experiments. More specifically, a physical battery pack was built using lithium-ion cells arranged in different groups to intentionally make them behave differently from each other. Arduino microcontrollers, together with voltage sensors, were used to record the battery pack terminal voltage for the SOC estimation. The experimental setup allowed logging voltages at 1 Hz frequency and provided a large dataset that closely represented actual battery operation.
To test the efficiency of the DEKF, the battery was operated in discharge mode, with a constant discharging current of 1 A. The collected data was first utilized to identify battery parameters such as internal resistance, by utilizing genetic algorithms. Note that each individual cell’s voltage was also measured and recorded for parameter identification. However, for evaluating the DEKF performance, only the pack terminal voltage data was used. The key parameters for the DEKF, including the process noise covariance matrix and the measurement noise covariance matrix, were manually tuned to achieve the best SOC estimation accuracy. Note that the Coulomb counting approach was used to compute the referenced SOC, as the battery was operated with a constant discharge current. Moreover, an auto-tuning approach utilizing genetic algorithms to optimize noise covariance matrices was also explored, which significantly enhanced the DEKF’s accuracy and enabled it to quickly converge to correct SOC estimates even under uncertain initial conditions. The contribution of this paper is summarized as follows:
- A heterogeneous battery pack was constructed for real-world validation of DEKF-based SOC estimation.
- A thorough validation of DEKF was performed, where only battery pack terminal voltage was used as input to the estimation algorithm for estimating the SOC for each single cell. By validating the DEKF performance under realistic conditions, this study demonstrates its potential for scalable deployment in real-world battery packs. The findings contribute to the greater goal of developing efficient and embedding-friendly algorithms for future energy storage and electric mobility systems.
- Our manual tuning results shows that the DEKF, starting from an initial SOC estimate of 98%, converged to accurate SOC values in less than 200 s, achieving an RMSE of under 1%.
- An auto-tuning approach based on genetic algorithms is proposed to tune the DEKF’s noise covariances. Starting from a more uncertain initial SOC estimate of 90%, the filter achieved a SOC RMSE < 1% after 1000 s, highlighting the robustness and practicality of the method while significantly reducing calibration effort.
The remainder of this paper is organized as follows. Section 2 details the mathematical models of battery cell dynamics and presents the foundational theory behind the DEKF. Section 3 describes the design and physical construction of the experimental circuit, while Section 4 presents the main results for the DEKF’s performance and its behavior with different initial SOC estimations. Finally, Section 5 concludes the paper with a summary of our findings and a discussion of avenues for future research.
2. Dense EKF for Cell SOC Estimation
2.1. Cell Dynamics
In this paper, we considered a battery of multiple cells, where each cell’s dynamics were represented by a first-order equivalent circuit model [10,31,32] that described the chemical reaction of the batteries in terms of open-circuit voltage (), open-circuit resistance (), terminal voltage (y), cell current (u), relaxation resistance (), and relaxation capacitance (). Note that an equivalent circuit model was used to model single battery cells [10] or battery packs with multiple cells [33]. As shown in Figure 1, the detailed system dynamics are given as
where is the SOC, is the Coulomb efficiency constant, is the relaxation voltage, is the cell capacity, and is the discharge current.
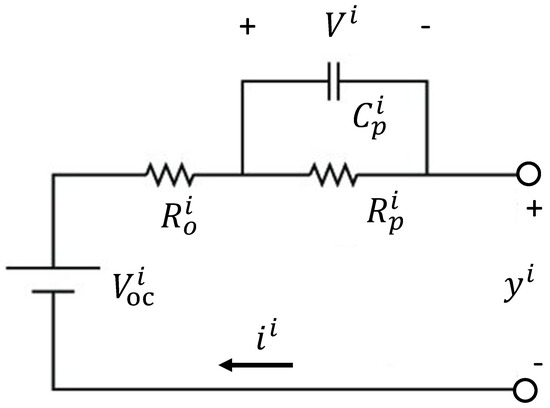
Figure 1.
Equivalent circuit model.
Denoting , the linear behavior of a single cell can be represented in a simplified state equation as
where
Here, is the sampling time. Note that is a nonlinear function of the SOC, which makes the measurement function nonlinear. By combining the state update equations of all the N cells, we define the sparse state vector as follows:
The complete state vector at time step k is given by , and the complete input vector at time step k is given by , allowing the dynamics of the full battery pack to be described as
Note that here we assume can be different for each cell, especially when a balancing circuit is present. In the event that there is no balancing circuit, for serial-connected battery packs all cell currents are equal, making the input of (4) a scalar.
2.2. Dense EKF
This section provides a brief overview of the DEKF algorithm developed in [30]. Readers are referred to [30] for more detail. The DEKF has been proposed to address the computational challenges associated with multi-cell battery state estimation. While the conventional EKF has a computational complexity of , due to the large covariance matrix associated with N series-connected battery cells, the DEKF reduces this burden to by reformulating the estimation problem through a low-rank approximation.
Consider the following model:
Here, represents process noise and represents measurement noise. Since only one terminal voltage is used for the DEKF, here is a scalar.
Now, the dense formulation utilizes the following model:
where and , and where is known as the RFF (relative fitness factor) matrix, which is defined as
Here, is the RFF that is related to the SOC of the cell, and is related to the relaxation voltage of the cell. Now the individual RFF for the SOC and relaxation voltage are explained as
Note that the RFFs introduced above quantify how each cell’s internal state, and , diverges from the dynamics of the average cell. Utilizing these RFFs, the change of each cell’s state can be reconstructed from the change and of the average state, as expressed in the following update equations:
However, to compute the predicted covariance, the DEKF framework establishes a correspondence between the dense covariance matrix and the full sparse covariance matrix . This relationship is expressed as
It is to be observed that in the DEKF algorithm the covariance matrix remains of fixed size regardless of the number of cells N.
3. Experimental Setup
To create a realistic battery pack with cell heterogeneity, a custom circuit was built, which consisted of three series-connected “cells”. To introduce heterogeneity, Cell 1 was formed by connecting two 18650 Sanyo lithium-ion cells in parallel, Cell 2 used two parallel cells, and Cell 3 used three parallel cells (see Figure 2 and Figure 3). Each 18650 cell had a nominal voltage of 3.6 V, a fully charged voltage of 4.2 V, a capacity of 3.5 Ah, and supported a continuous discharge rate of up to 10 A. These cells were rechargeable and were rated for approximately 300 cycles before significant performance degradation occurred. Figure 2 illustrates the circuit diagram and Figure 3 presents the actual experimental setup used for the data collection. Note that the diagram of Figure 2 is used to create heterogeneity between Cell 1 and Cells 2 and 3. Though the DEKF only required the total terminal voltage to be measured, the voltages of each cell group were measured for parameter identification. Due to the use of common ground required by Arduino, the first voltage sensor measured the total voltage across the entire battery pack, the second measured the combined voltage of Cell 1 and Cell 2, and the third measured the voltage across Cell 3. Individual cell voltages could then be calculated.
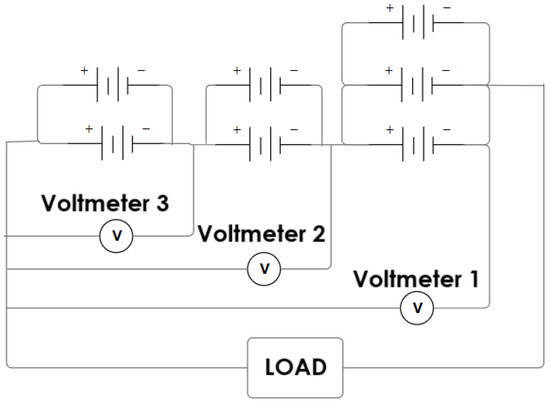
Figure 2.
Diagram for the battery pack with voltmeters and load. Each cell group was formed using multiple cells to create heterogeneity.

Figure 3.
Actual experimental setup for the circuit diagram shown in Figure 2.
An Arduino board was used to record the voltages in real-time, treating each branch of the pack as an individual “cell”. To log the voltage data, PuTTY was used, which is an open-source serial terminal that captures and saves data from Arduino to a text file through serial connection. Once the experiment was complete, the measurement data was imported into Matlab for the DEKF to estimate cell SOC. Note that the DEKF was running on Matlab as opposed to Arduino to reduce the experiment time. A programmable current load was used to draw a steady, user-defined current, effectively replicating real-world discharge conditions in a steady-state condition. Prior to testing, all the cells were fully charged to start from a 100% SOC. Note that this was to ensure the results were repeatable. As the SOC is not measurable, there is always uncertainty about the starting SOC if we do not fully charge the battery. The load was set to a constant discharge current of 1 A. Furthermore, the discharge current was being measured by the load and used in the DEKF for estimation.
4. Results and Discussions
4.1. Parameter Identification
The cell model (1) requires four parameters, namely, , , , and C. The cell capacity C can be obtained from the vendor, while the other three missing parameters need to be estimated. To identify them, we apply a genetic algorithm (GA) from Matlab’s Global Optimization Toolbox. The GA searches for optimal parameter values by minimizing a user-defined cost function, which quantifies the error between the measured battery voltages and those predicted by the model. In our case, the cost function is designed to reduce the root mean square error (RMSE) between the experimental voltage data and the simulated output of the DEKF. The GA is particularly useful for estimating uncertain model parameters, such as , , and . In this paper, the GA was configured with a population size of 50, a maximum of 12,000 generations, and a stall limit of 1500 generations, with parallel computing enabled to reduce optimization time. Algorithm 1 summarizes this process, where the inputs to our GA were the measured battery terminal voltage (), the lookup table, and the initial estimate of the parameters we were trying to optimize. Then, the GA called the cost function and injected our previously defined inputs into it. Finally, the GA kept evolving the population until it found the best fit for the parameters with the lowest cost.
The estimated parameters for each cell group are summarized in Table 1. Moreover, Figure 4, Figure 5 and Figure 6 compare the modeled terminal voltage using the estimated parameters against the measurements. Here, these figures illustrate the comparison between the measured and calculated terminal voltages for all the cells over a 3600 s simulation period. The bold green line represents the voltage calculated using the GA-optimized parameters, while the red dashed line corresponds to the voltage measured using a low-cost voltage sensor. It is evident from the figures that the calculated voltage (the green line) closely followed the central trend of the measured voltage data (the red dashed line). In particular, the reported error value in each simulation was less than 1.5%. This strong agreement indicates that the GA is successful in identifying parameters that yield an accurate model, even in the presence of sensor noise. Please note that there are other methods for estimating cell parameters (see ref. [34], for example). The GA was adopted in this work due to its robustness against noise and its ability to locate the global optimum.
| Algorithm 1 GA for battery parameter optimization. |
|

Table 1.
GA results for , , and .
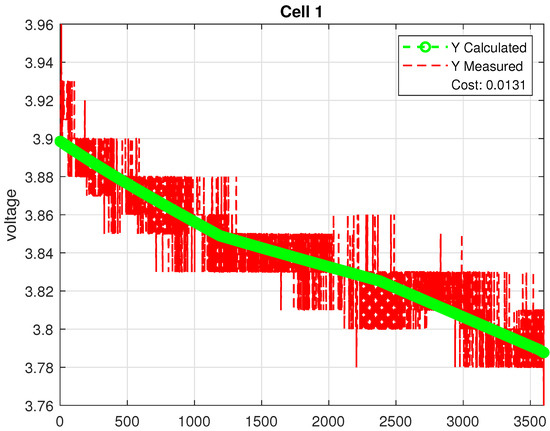
Figure 4.
Measured vs. calculated voltage using GA-optimized parameters (Cell 1).
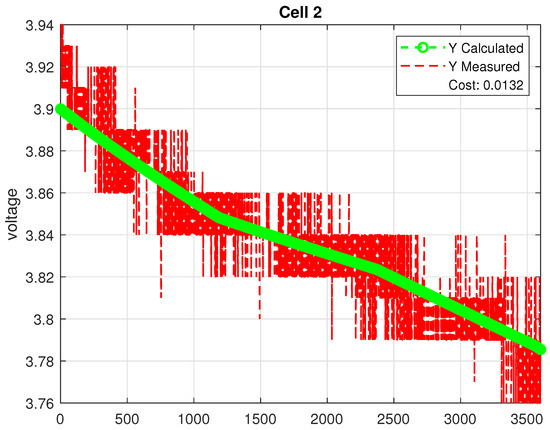
Figure 5.
Measured vs. calculated voltage using GA-optimized parameters (Cell 2).
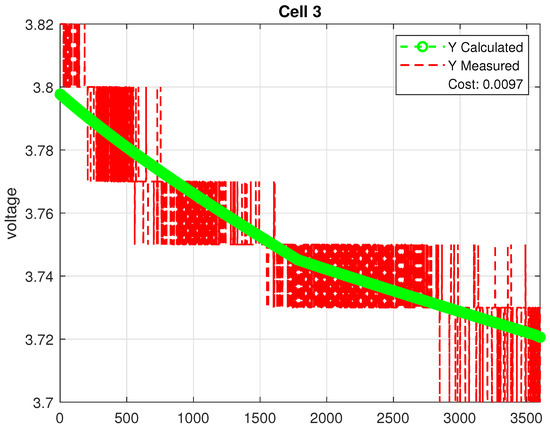
Figure 6.
Measured vs. calculated voltage using GA-optimized parameters (Cell 3).
4.2. DEKF Results with Manual Tuning
This section presents the cell SOC estimation results for the DEKF parameters being manually tuned. As previously discussed, all the missing parameters were identified using appropriate estimation techniques. Additionally, tuning the DEKF’s key parameters—i.e., the process noise covariance and measurement noise covariance —was essential, as these directly influenced the filter’s performance. In the first set of results, with an initial SOC estimate of 98% and a relaxation voltage of 0v, the DEKF performance was excellent. As shown in Figure 7 and Figure 8, the DEKF achieved fast convergence and a predicted SOC closely matching the actual data. In addition, we changed the initial SOC estimation to 90%, which was further away from the true value. The results are shown in Figure 9 and Figure 10. As can be seen, the performance was inferior compared to the case with a 98% initial estimate, indicating room for better DEKF parameter tuning. Therefore, in the sequel we explored the use of the GA for auto-tuning.
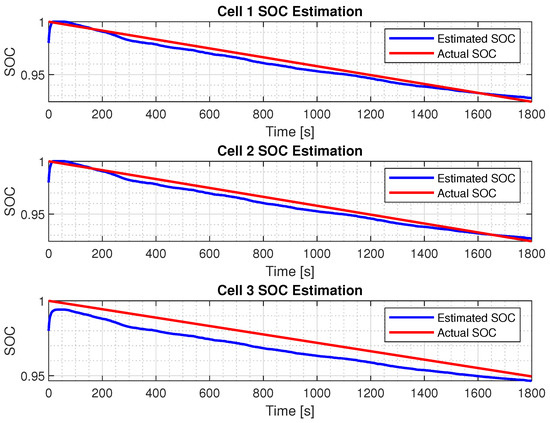
Figure 7.
SOC estimation with initial SOC estimation of 98%.
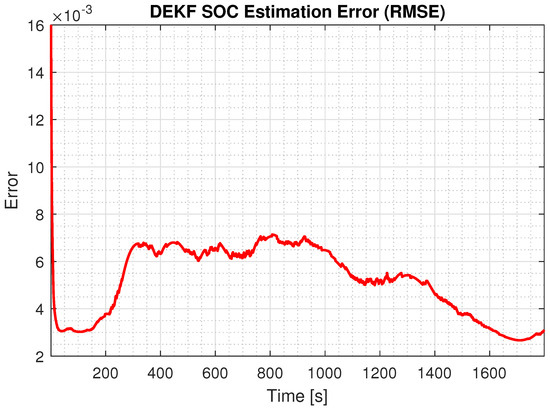
Figure 8.
SOC estimation error with initial SOC estimation of 98%.
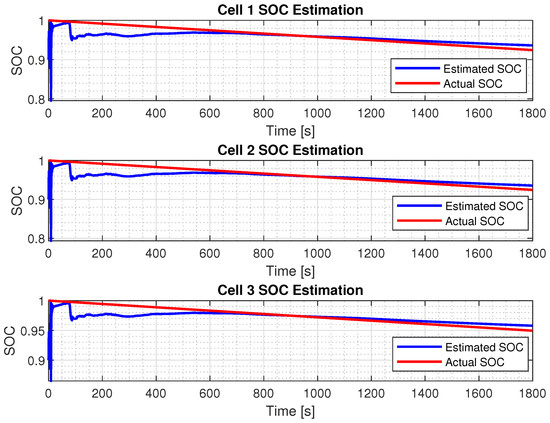
Figure 9.
SOC estimation with initial SOC estimation of 90%.
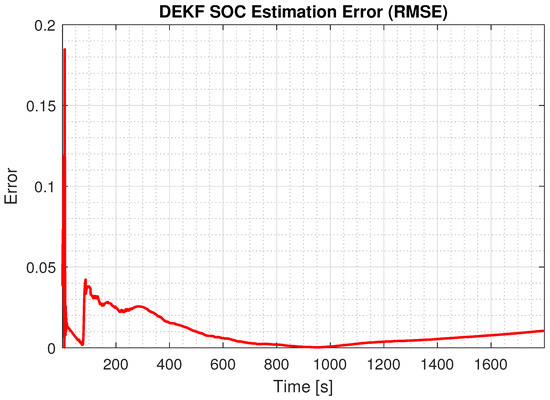
Figure 10.
SOC estimation error with initial SOC estimation of 90%.
4.3. DEKF Results with Automatic Tuning
This section presents the DEKF-based SOC estimation results for automatic tuning. In particular, the two DEKF parameters and were optimized using the GA, as described by Algorithm 2. Applying the GA to optimize the tuning parameters of the DEKF yielded superior performance compared to manual tuning. The results are shown in Figure 11 and Figure 12. As can be seen, the resultant DEKF converged faster than the manually tuned DEKF and closely tracked the actual SOC. Furthermore, the RMSE plot confirms a sharper drop in estimation error and a more stable trajectory over time.
| Algorithm 2 GA for battery parameter optimization. |
|
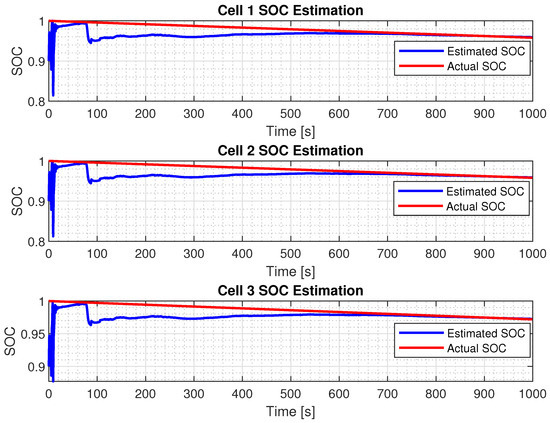
Figure 11.
GA-tuned SOC estimation with initial estimate of 90%.
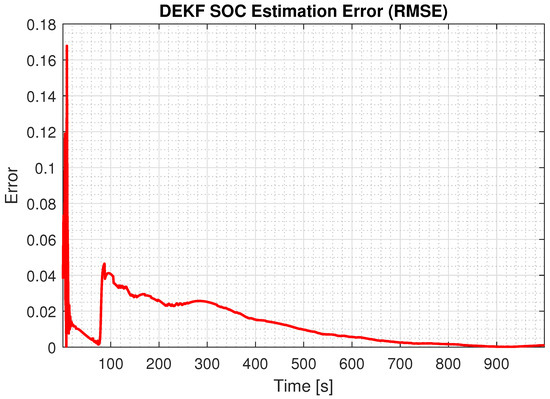
Figure 12.
GA-tuned SOC estimation error with initial estimate of 90%.
5. Conclusions
This work presents an actual implementation of a computationally efficient method for estimating the state-of-charge (SOC) of individual cells in a heterogeneous lithium-ion battery pack. Using an equivalent circuit model to model each cell in the pack, the proposed dense extended Kalman filter (DEKF) was practically implemented to evaluate its viability in a real-world setting. Building upon the theoretical foundation established in [30], a physical battery pack with heterogeneous cells was constructed, and experimental voltage data was collected using a constant current discharge setup. This data was injected into a MATLAB 2024b based DEKF implementation specifically adapted to account for cell-to-cell variations. Our experimental results confirm the effectiveness of the DEKF in terms of convergence speed, accurate SOC estimation, and computational scalability for embedded deployment. Future work will focus on expanding the experiment to include more diverse scenarios, such as degraded or aged cells, as well as more cells. Evaluating the DEKF performance in an embedded environment, similar to that of [35], and considering current deviation will be another work direction. Finally, validating the DEKF performance when the SOC is down to 10%, together with statistical analysis, will also be a future work direction.
Author Contributions
Conceptualization, J.C. and L.N.; methodology, J.C. and L.N.; software, L.N., O.O. and Z.Z.; validation, O.O. and J.C.; formal analysis, O.O. and J.C.; investigation, O.O., L.N., A.I. and J.C.; resources, J.C.; data curation, O.O. and A.I.; writing—original draft preparation, O.O. and L.N.; writing—review and editing, Z.Z. and J.C.; visualization, O.O.; supervision, J.C.; project administration, J.C.; funding acquisition, J.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Science Foundation through Award #2237317 and Award #2430374.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
The data is available upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Dixon, J. Energy storage for electric vehicles. In Proceedings of the 2010 IEEE International Conference on Industrial Technology, Via del Mar, Chile, 14–17 March 2010; pp. 20–26. [Google Scholar] [CrossRef]
- Gao, Z.W.; Lan, T.; Yin, H.; Liu, Y. Development and Commercial Application of Lithium-Ion Batteries in Electric Vehicles: A Review. Processes 2025, 13, 756. [Google Scholar] [CrossRef]
- Denholm, P.; Ela, E.; Kirby, B.; Milligan, M. Role of Energy Storage with Renewable Electricity Generation; Technical Report National Renewable Energy Lab. (NREL): Golden, CO, USA, 2010. [Google Scholar]
- Dehghani-Sanij, A.; Tharumalingam, E.; Dusseault, M.; Fraser, R. Study of energy storage systems and environmental challenges of batteries. Renew. Sustain. Energy Rev. 2019, 104, 192–208. [Google Scholar] [CrossRef]
- Pimm, A.J.; Palczewski, J.; Barbour, E.R.; Cockerill, T.T. Using electricity storage to reduce greenhouse gas emissions. Appl. Energy 2021, 282, 116199. [Google Scholar] [CrossRef]
- Arbabzadeh, M.; Sioshansi, R.; Johnson, J.X.; Keoleian, G.A. The role of energy storage in deep decarbonization of electricity production. Nat. Commun. 2019, 10, 3413. [Google Scholar]
- Jones, C.; Gilbert, P.; Stamford, L. Assessing the climate change mitigation potential of stationary energy storage for electricity grid services. Environ. Sci. Technol. 2019, 54, 67–75. [Google Scholar] [CrossRef]
- Huang, J.; Shi, D.; Chen, T. Event-triggered state estimation with an energy harvesting sensor. IEEE Trans. Autom. Control 2017, 62, 4768–4775. [Google Scholar] [CrossRef]
- Chiasson, J.; Vairamohan, B. Estimating the state of charge of a battery. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; Volume 4, pp. 2863–2868. [Google Scholar]
- Chen, J.; Behal, A.; Li, Z.; Li, C. Active Battery Cell Balancing by Real Time Model Predictive Control for Extending Electric Vehicle Driving Range. IEEE Trans. Auto. Sci. Eng. 2024, 21, 4003–4015. [Google Scholar] [CrossRef]
- Pozzi, A.; Zambelli, M.; Ferrara, A.; Raimondo, D.M. Balancing-aware charging strategy for series-connected lithium-ion cells: A nonlinear model predictive control approach. IEEE Trans. Control Syst. Technol. 2020, 28, 1862–1877. [Google Scholar] [CrossRef]
- Lai, X.; Zheng, Y.; Sun, T. A comparative study of different equivalent circuit models for estimating state-of-charge of lithium-ion batteries. Electrochim. Acta 2018, 259, 566–577. [Google Scholar] [CrossRef]
- Moura, S.J.; Argomedo, F.B.; Klein, R.; Mirtabatabaei, A.; Krstic, M. Battery state estimation for a single particle model with electrolyte dynamics. IEEE Trans. Control Syst. Technol. 2016, 25, 453–468. [Google Scholar]
- Movassagh, K.; Raihan, S.A.; Balasingam, B. Performance analysis of coulomb counting approach for state of charge estimation. In Proceedings of the 2019 IEEE Electrical Power and Energy Conference (EPEC), Montreal, QC, Canada, 16–18 October 2019; pp. 1–6. [Google Scholar]
- Fathoni, G.; Widayat, S.A.; Topan, P.A.; Jalil, A.; Cahyadi, A.I.; Wahyunggoro, O. Comparison of State-of-Charge (SOC) estimation performance based on three popular methods: Coulomb counting, open circuit voltage, and Kalman filter. In Proceedings of the 2017 2nd International Conference on Automation, Cognitive Science, Optics, Micro Electro-Mechanical System, and Information Technology (ICACOMIT), Jakarta, Indonesia, 23–24 October 2017; pp. 70–74. [Google Scholar]
- Kulikov, G.Y.; Kulikova, M.V. Accurate numerical implementation of the continuous-discrete extended Kalman filter. IEEE Trans. Autom. Control 2013, 59, 273–279. [Google Scholar]
- Tsiamis, A.; Pappas, G.J. Online learning of the kalman filter with logarithmic regret. IEEE Trans. Autom. Control 2022, 68, 2774–2789. [Google Scholar]
- Liu, S.; Wang, Z.; Chen, Y.; Wei, G. Protocol-based unscented Kalman filtering in the presence of stochastic uncertainties. IEEE Trans. Autom. Control 2019, 65, 1303–1309. [Google Scholar]
- Xiong, R.; He, H.; Sun, F.; Zhao, K. Evaluation on state of charge estimation of batteries with adaptive extended Kalman filter by experiment approach. IEEE Trans. Veh. Technol. 2012, 62, 108–117. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 3. State and parameter estimation. J. Power Sources 2004, 134, 277–292. [Google Scholar]
- Sun, D.; Yu, X.; Wang, C.; Zhang, C.; Huang, R.; Zhou, Q.; Amietszajew, T.; Bhagat, R. State of charge estimation for lithium-ion battery based on an Intelligent Adaptive Extended Kalman Filter with improved noise estimator. Energy 2021, 214, 119025. [Google Scholar] [CrossRef]
- Valade, A.; Acco, P.; Grabolosa, P.; Fourniols, J.Y. A study about Kalman filters applied to embedded sensors. Sensors 2017, 17, 2810. [Google Scholar] [CrossRef] [PubMed]
- Closas, P.; Vila-Valls, J.; Fernández-Prades, C. Computational complexity reduction techniques for quadrature Kalman filters. In Proceedings of the 2015 IEEE 6th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), Cancun, Mexico, 13–16 December 2015; pp. 485–488. [Google Scholar]
- Zhang, D.; Couto, L.D.; Gill, P.S.; Benjamin, S.; Zeng, W.; Moura, S.J. Thermal-enhanced adaptive interval estimation in battery packs with heterogeneous cells. IEEE Trans. Control Syst. Technol. 2021, 30, 1102–1115. [Google Scholar] [CrossRef]
- Deng, Z.; Hu, X.; Lin, X.; Che, Y.; Xu, L.; Guo, W. Data-driven state of charge estimation for lithium-ion battery packs based on Gaussian process regression. Energy 2020, 205, 118000. [Google Scholar] [CrossRef]
- Song, L.; Zhang, K.; Liang, T.; Han, X.; Zhang, Y. Intelligent state of health estimation for lithium-ion battery pack based on big data analysis. J. Energy Storage 2020, 32, 101836. [Google Scholar] [CrossRef]
- Eleftheriadis, P.; Giazitzis, S.; Leva, S.; Ogliari, E. Data-driven methods for the state of charge estimation of lithium-ion batteries: An overview. Forecasting 2023, 5, 576–599. [Google Scholar] [CrossRef]
- How, D.N.; Hannan, M.; Lipu, M.H.; Ker, P.J. State of charge estimation for lithium-ion batteries using model-based and data-driven methods: A review. IEEE Access 2019, 7, 136116–136136. [Google Scholar] [CrossRef]
- Lipu, M.H.; Hannan, M.; Hussain, A.; Ayob, A.; Saad, M.H.; Karim, T.F.; How, D.N. Data-driven state of charge estimation of lithium-ion batteries: Algorithms, implementation factors, limitations and future trends. J. Clean. Prod. 2020, 277, 124110. [Google Scholar]
- Nuculaj, L.; Chen, J. Simultaneous Cell State Estimation via Dense Adaptive Extended Kalman Filter. IEEE Trans. Control Syst. Technol. 2025. to appear. [Google Scholar] [CrossRef]
- Pei, Z.; Zhao, X.; Yuan, H.; Peng, Z.; Wu, L. An equivalent circuit model for lithium battery of electric vehicle considering self-healing characteristic. J. Control Sci. Eng. 2018, 2018, 5179758. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Zhang, X.; Sun, F.; Fan, J. State-of-Charge Estimation of the Lithium-Ion Battery Using an Adaptive Extended Kalman Filter Based on an Improved Thevenin Model. IEEE Trans. Veh. Technol. 2011, 60, 1461–1469. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Guo, H.; Li, S. Comparison study on the battery state of charge estimation methods for electric vehicles. Energy Procedia 2011, 12, 159–165. [Google Scholar]
- Plett, G.L. Battery Management Systems, Volume II: Equivalent-Circuit Methods; Artech House: London, UK, 2015. [Google Scholar]
- Nuculaj, L.; Kidwell, A.; Homayouni, C.; Fillmore, A.; Hanna, D.; Chen, J. Optimal FPGA Implementation of Dense Extended Kalman Filter for Simultaneous Cell State Estimation. In Proceedings of the IEEE International Midwest Symposium on Circuits and Systems (MWSCAS), Springfield, MA, USA, 11–14 August 2024. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).