Research, Verification and Uncertainty Analysis of Aircraft Structural Load/Strain Testing
Abstract
1. Introduction
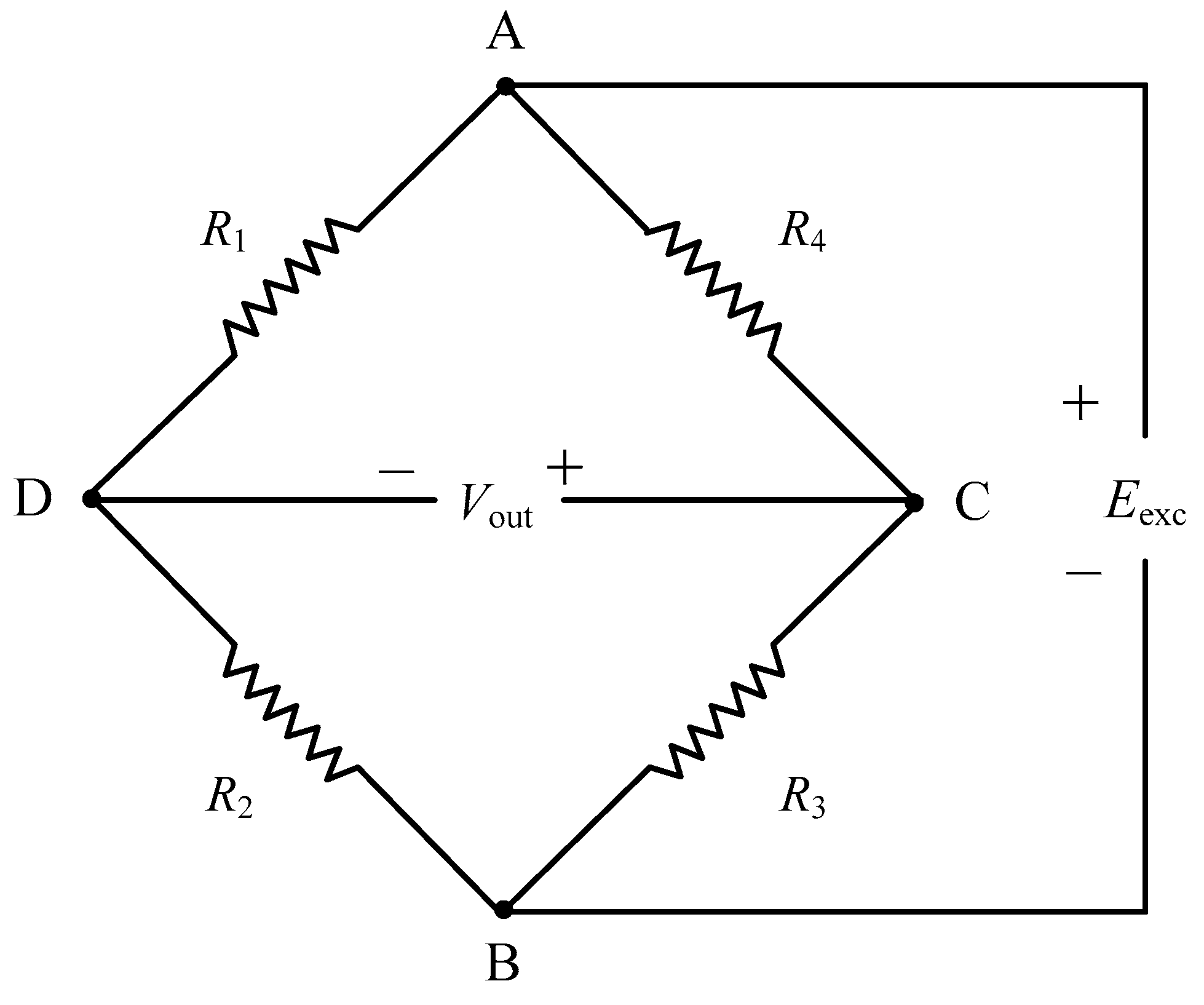
2. Structural Strain Measurement Principle
3. Strain Airborne Measurement Cases and Existing Problems
- (1)
- Due to the resistance temperature effect of the strain gauge’s sensitive grid, the heating of the sensitive grid during normal operation will cause changes in its own resistance value, and real-time effective compensation cannot be performed due to the bridge characteristics;
- (2)
- According to Fourier’s law of heat conduction, the temperature of the sensitive grid will reach dynamic thermal equilibrium with its surrounding environment. Currently, there is a temperature gradient between the sensitive grid and the measured structural part, leading to inconsistent thermal deformation between the two, which causes thermal strain output;
- (3)
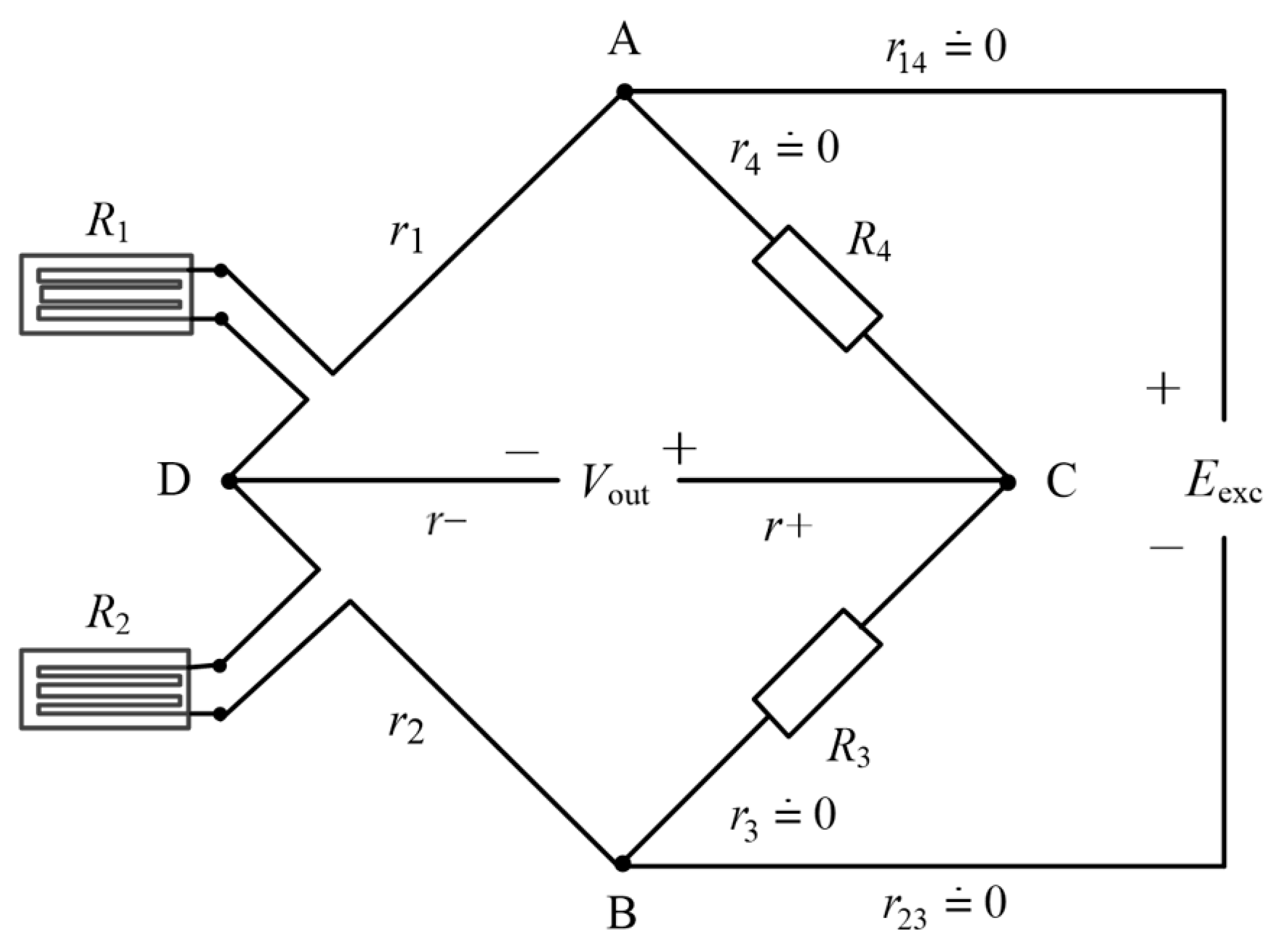
- In Figure 2, due to the resistance of the short-circuit wire, there is always a certain potential difference between point C and the casing, and this potential difference will change with the working state of the bridge and the external environment; that is, the zero point of the output signal will fluctuate during the entire airborne measurement process;
- (4)
- During the flight measurement process, there are differences in specimen materials, strain gauge pasting and protection processes, service environments, etc., between the thermal strain output results of the strain test bridge and the ground thermal output calibration test of the strain gauge. These differences may cause the actual thermal strain output of the strain gauge to deviate from the ground calibration thermal output curve or exceed the expected acceptable range, resulting in a significant increase in thermal strain output.
4. Improved Structural Strain Measurement Method
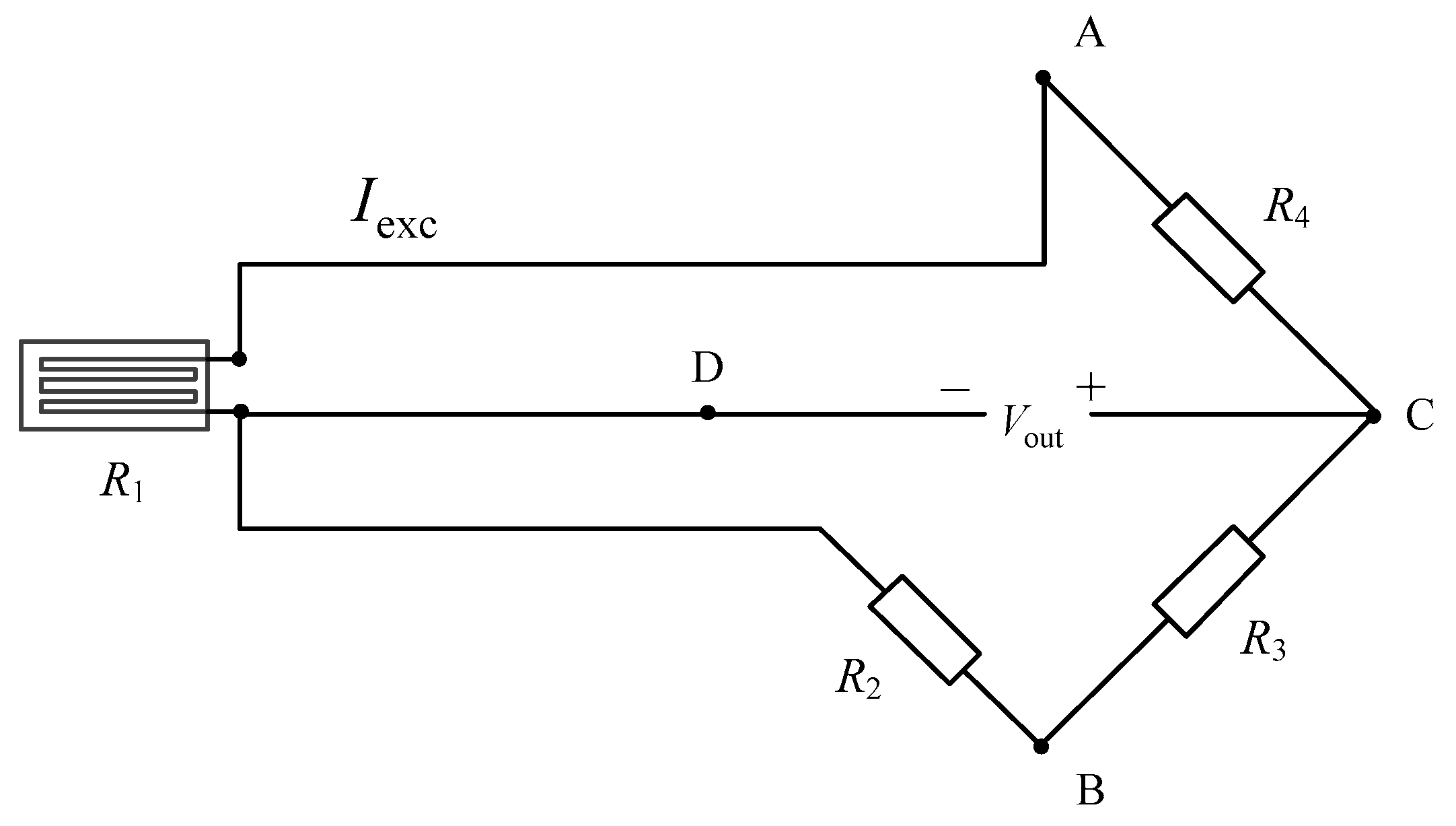
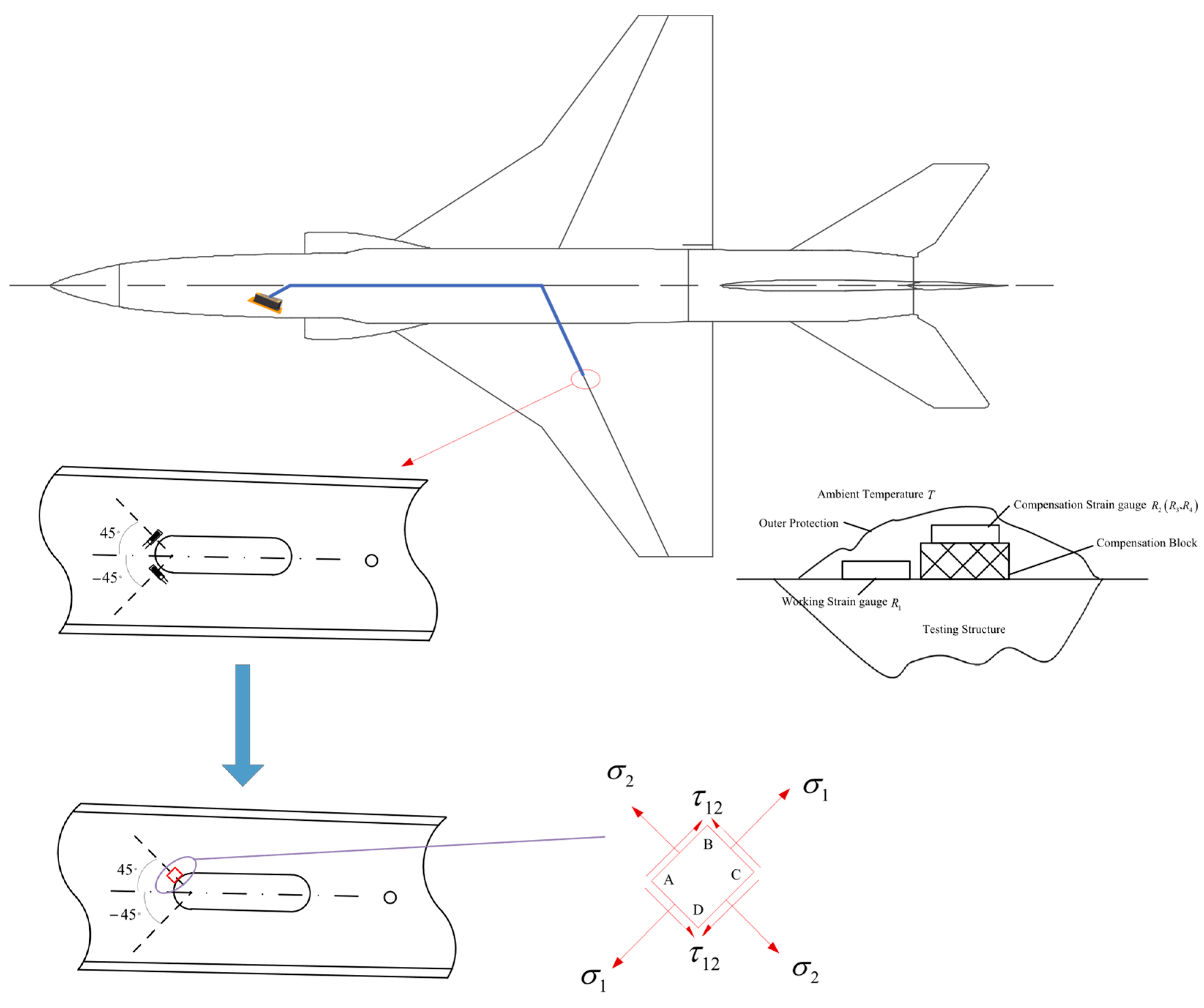
4.1. Structural Strain Measuring Point Location and Bridge Design
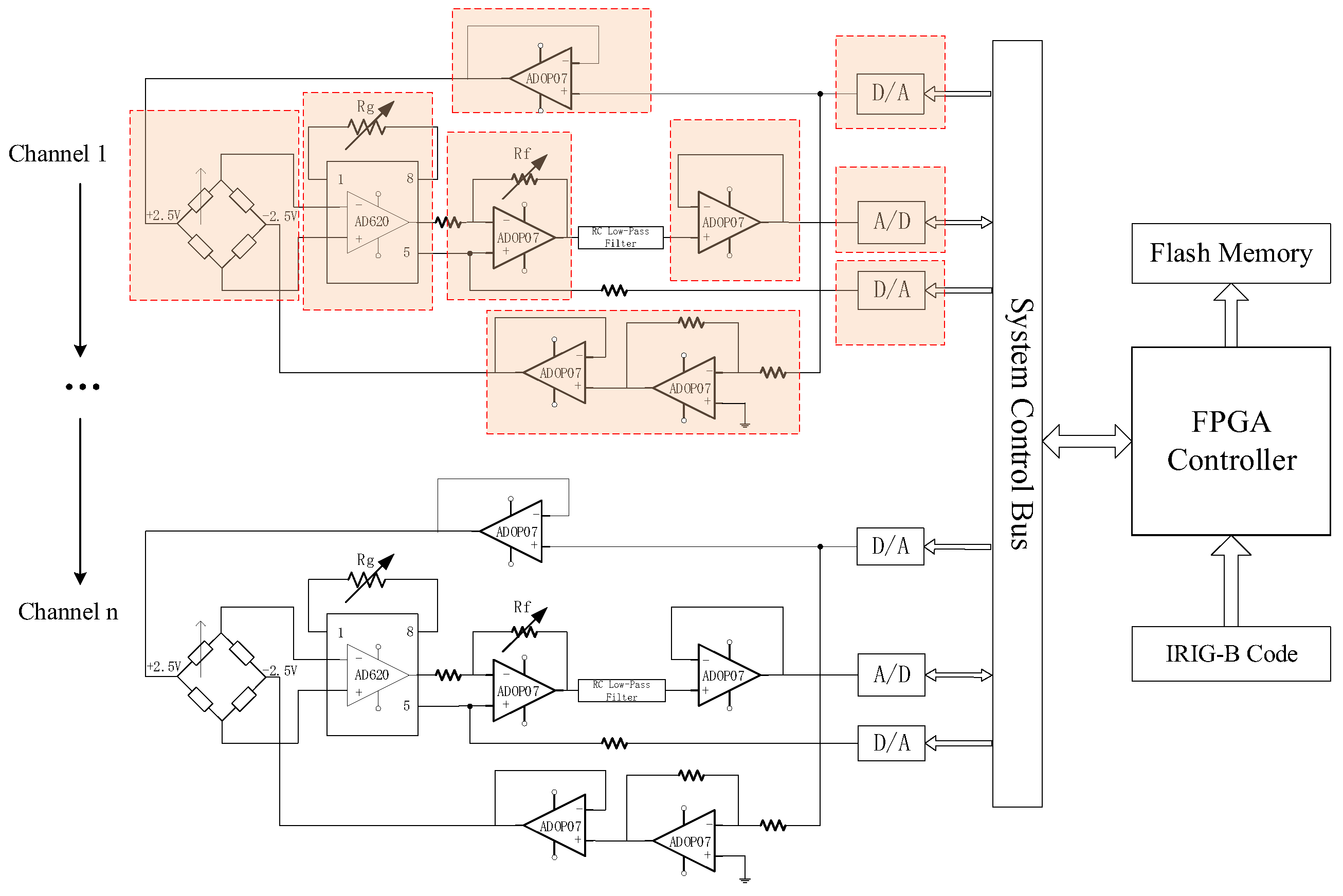
4.2. Multi-Channel Strain Testing System Construction and Calibration
5. Uncertainty Estimation of Strain Airborne Measurement Output
5.1. Influencing Factors of Strain Airborne Measurement Output
- (1)
- Uncertainty of the channel excitation voltage ;
- (2)
- Nonlinearity between the bridge output voltage and strain , especially significant when measuring large strains;
- (3)
- Difference between the strain output by the strain bridge and the strain output by the standard strain source during calibration, affected by factors such as the transverse sensitivity effect of strain gauges, performance, and thickness of strain adhesive layers;
- (4)
- Dispersion of the strain channel calibration coefficient ;
- (5)
- and are affected by environmental temperature T changes, differences between adjacent bridge arm strain gauges and low-temperature drift resistors and or strain gauges and as well as differences in linear expansion coefficients among sensitive grids, strain adhesive layers, and measured structural parts.
5.2. Summary of Influence Factors and Corresponding Variables
- (1)
- Expression of Structural Strain
- (2)
- The expression for the thermal output of the strain gauge bridge arm
- (3)
- Expression for the thermal output of the low-temperature drift resistance bridge arm
- (1)
- Structural Strain Causedby Mechanical Loads
- (2)
- Thermal Output of Strain Measurement Bridge Circuit and
5.3. Uncertainty Measurement Based on Multivariate Fuzzy Comprehensive Evaluation
5.3.1. Establishment of Factor Set
5.3.2. Determine Variable Weights
- (1)
- Variable weights of the structural strain caused by mechanical loads
- (2)
- Variable weights of the thermal output of the strain measurement bridge circuit
5.3.3. Determination of Judgment Set and Membership Degree
5.3.4. Fuzzy Comprehensive Evaluation
6. Flight Test Verification and Statistical Analysis
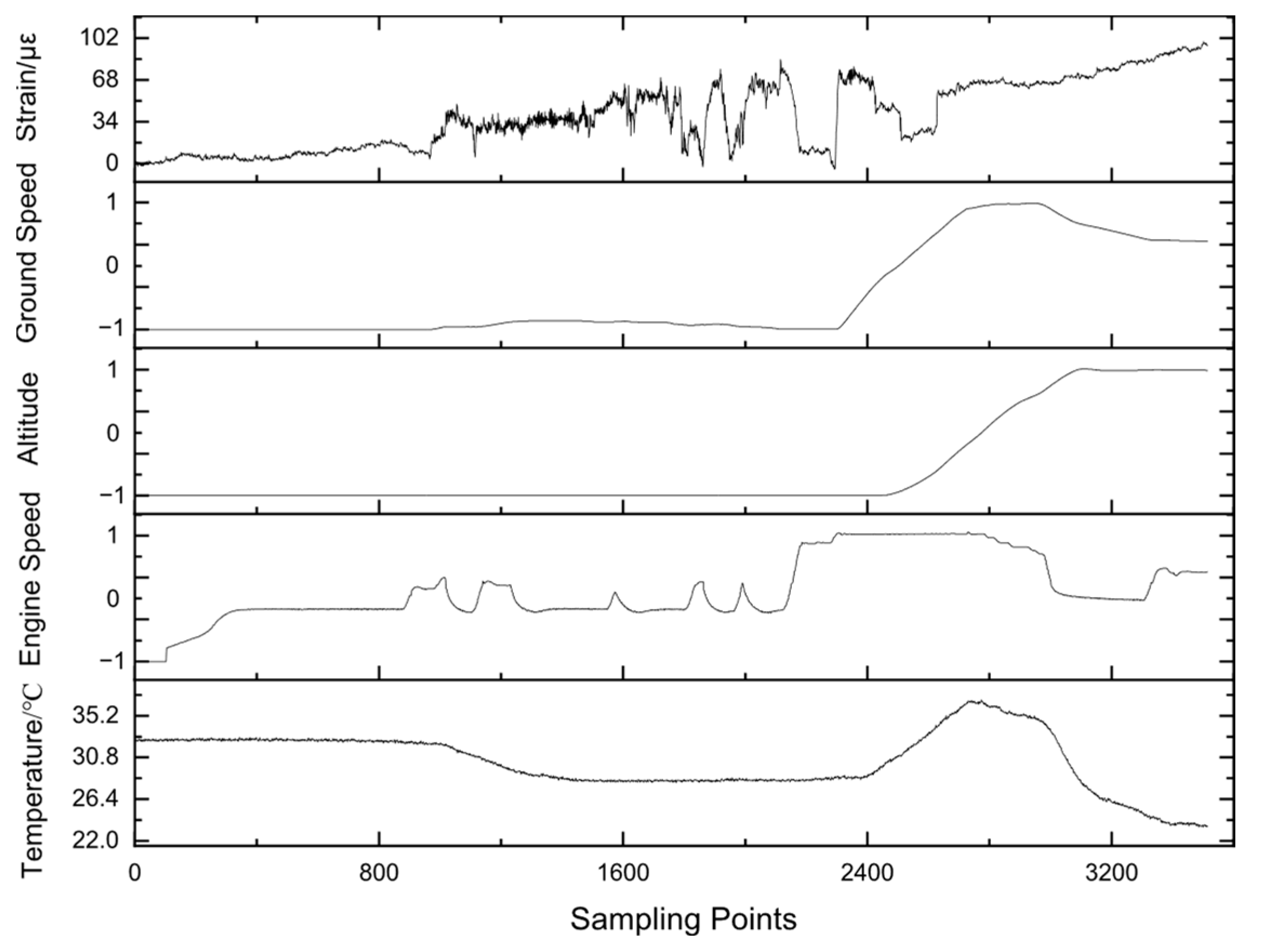
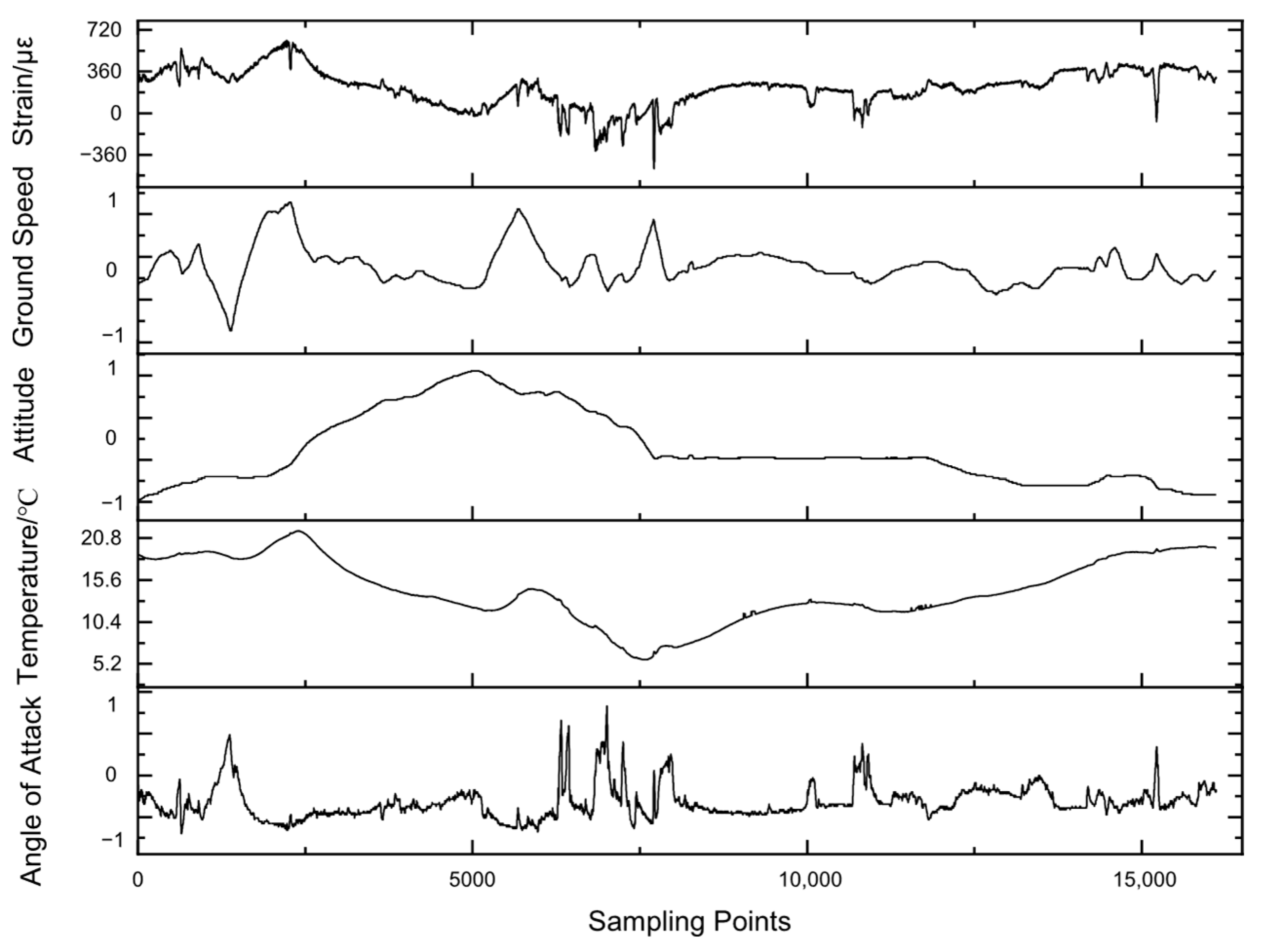
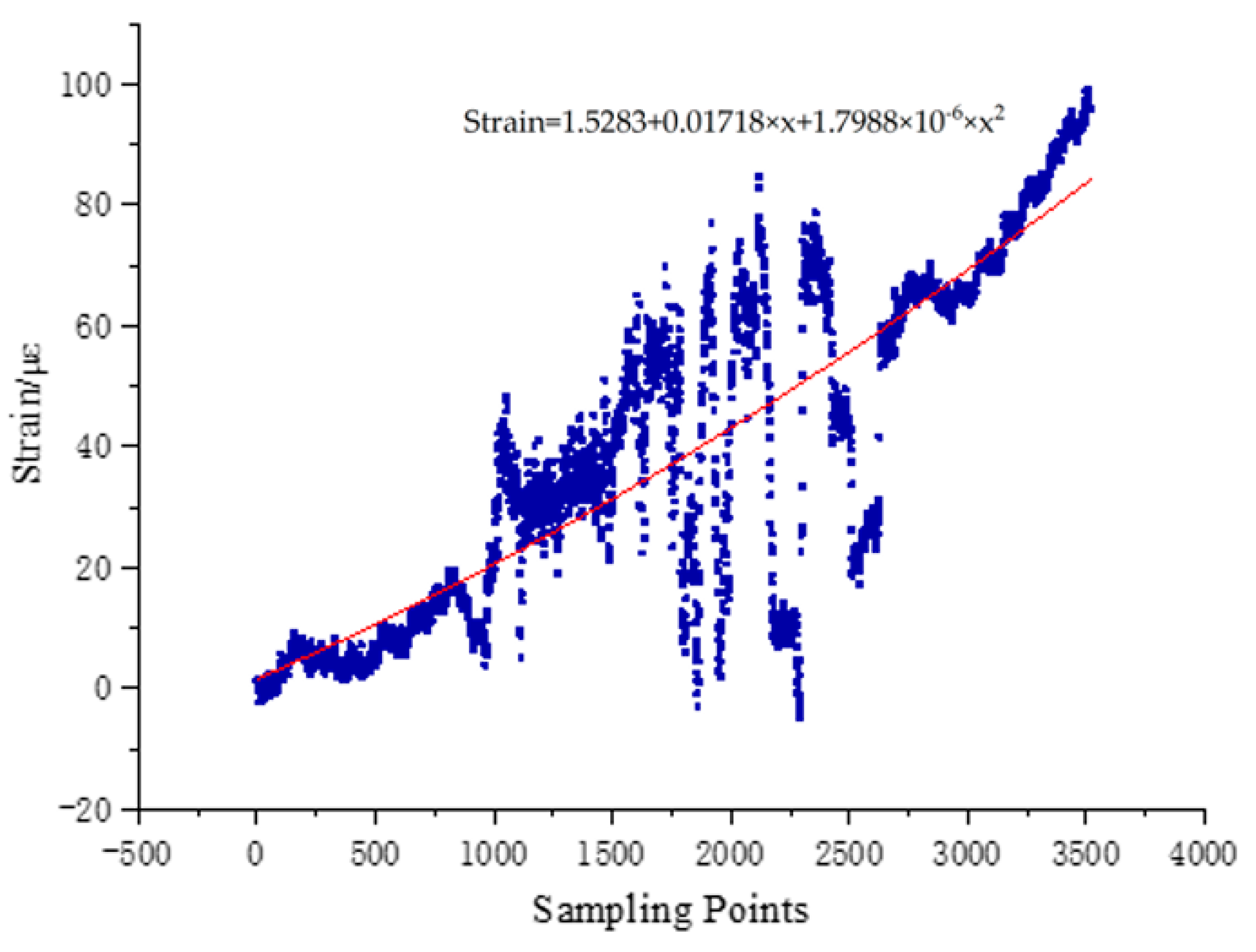
6.1. Measured Strain Time–History
6.2. Strain and Flight Parameters Statistical Analysis
6.2.1. Non-Parametric Partial Correlation Analysis PMIC
6.2.2. Result Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DC | Direct Current |
| V out | Analog Strain Signal |
| E exc | Input Bridge Excitation Voltage |
| E AB | Bridge Excitation Voltage between A and B |
| ŋ | Strain–Analog Strain Signal Coefficient |
| k | Ratio of Cable Resistance to Strain Gauge Resistance |
| F g | Gauge Factor |
| α a | Coefficient of Thermal Expansion of Strain Adhesive Layer |
| α g | Coefficient of Thermal Expansion of Sensitive Grid |
| α s | Coefficient of Thermal Expansion of Tested Structural Part |
| β g | Temperature Coefficient of Resistance of Sensitive Grid |
| β r | Temperature Coefficient of Test Cable |
| H g | Transverse Effect Coefficient of Strain Gauge |
| E | Elastic Modulus of Structural Material |
| ν0 | Poisson’s Ratio of Structural Material |
| λ | Strain Transfer Efficiency of Adhesive Layer |
| ΔTa | Temperature Change in Strain Adhesive Layer |
| ΔTg | Temperature Change in Strain Gauge Sensitive Grid |
| ΔTr | Temperature Change in Test Cable |
| ΔTs | Temperature Change in Tested Structural Part |
| β R | Temperature Coefficient of Low-Drift Resistance |
| ΔTR | Temperature Change in Low-Drift Resistance |
| Ratio of Strain to Strain | |
| R | Strain Gauge Resistance |
| ΔR | Change in Strain Gauge Resistance |
| Nonlinear Coefficient of the Test Bridge | |
| Constant Current of Bridge Circuit | |
| A/D | Analog to Digital |
| PC | Personal Computer |
| FPGA | Field-Programable Gate Array |
| IRIG-B | Inter-Range Instrumentation Group-B |
| PCM | Pulse Code Modulation |
| Mc | Code Value of the Acquisition Channel |
| Strain Code Value Conversion Coefficient | |
| Strain–Analog Strain Signal Coefficient | |
| K | Set Value of the Sensitivity Coefficient of the Standard Strain Source |
| MIC | Maximal Information Coefficient |
| PMIC | Non-parametric Partial Correlation Analysis |
References
- Staszewski, W.; Boller, C.; Tomlinson, G.R. Health Monitoring of Aerospace Structures: Smart Sensor Technologies and Signal Processing; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2003. [Google Scholar]
- Gao, Z.T. Statistics Applied in Fatigue; National Defense Industry Press: Beijing, China, 1986; pp. 169–198. (In Chinese) [Google Scholar]
- Yan, C.L. Measurement Technology and Compilation Theory of Load-Spectrum for Airplane; Aviation Industry Press: Beijing, China, 2010; pp. 1–288. (In Chinese) [Google Scholar]
- Yan, C.L.; Su, K.X. Safety Life and Design with Damage Tolerance of Aircraft Landing Gear; Aviation Industry Press: Beijing, China, 2011; pp. 1–134. (In Chinese) [Google Scholar]
- Yan, C.L.; Zhang, S.M.; Zhuo, N.S.; Gao, Z.T. Mechanical Model and Data Processing of Load Measurement Test for The Air-plane’s Wing Structure. Acta Aeronaut. Astronaut. Sin. 2000, 21, 56–59. (In Chinese) [Google Scholar]
- William, A.L.; Olney, C.D.; Chen, T.; Crawford, N.D.; Stauf, R.; Reichenbach, E.Y.; Bessette, D. Strain-gage loads calibration testing of the active aeroelastic wing f/a-18 airplane. In Proceedings of the 22nd AIAA Aerodynamic Measurement Technology and Ground Testing Conference, St. Louis, MO, USA, 24–26 June 2002. [Google Scholar]
- Conners, T.; Sims, R. Full Flight Envelope Direct Thrust Measurement on a Supersonic Aircraft. In Proceedings of the 34th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Cleveland, OH, USA, 13–15 July 1998; p. 206560. [Google Scholar]
- Guo, L.L.; Liu, L.Q.; Liu, P.X. The application of multi-channel dynamic strain observation sysytem in earthquake simulation experiments. Seismol. Geol. 2014, 36, 929–938. (In Chinese) [Google Scholar]
- Israel, L.; Nesrin, S.-K. A review of uncertainty in flight vehicle structural health monitoring, diagnosis and con-trol: Challenges and opportunities. Prog. Aerosp. Sci. 2010, 46, 247–273. [Google Scholar]
- Motra, H.B.; Hildebrand, J.; Dimmig-Osburg, A. Assessment of strain measurement techniques to characterise mechanical properties of structural steel. Eng. Sci. Technol. Int. J. 2014, 17, 260–269. [Google Scholar] [CrossRef]
- Montero, W.; Farag, R.; Diaz, V.; Ramirez, M.; Boada, B.L. Uncertainties associated with strain-measuring system using resistance strain gauges. J. Strain Anal. Eng. Des. 2010, 46, 1–13. [Google Scholar] [CrossRef]
- Haslbeck, M.; Böttcher, J.; Braml, T. An Uncertainty Model for Strain Gages Using Monte Carlo Methodology. Sensors 2023, 23, 8965. [Google Scholar] [CrossRef] [PubMed]
- Arpin-Pont, J.; Gagnon, M.; Tahan, S.A.; Coutu, A.; Thibault, D. Strain gauge measurement uncertainties on hydraulic tur-bine runner blade. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 062042. [Google Scholar] [CrossRef]
- Arpin-Pont, J.; Gagnon, M.; Tahan, S.A.; Coutu, A.; Thibault, D. Methodology for estimating strain gauge measurement biases and uncertainties on isotropic materials. J. Strain Anal. Eng. Des. 2015, 50, 40–50. [Google Scholar] [CrossRef]
- Ma, L.C.; Feng, R.X.; Xu, D.B. Electrical Measurement for Strain and Technology of Sensing; China Metrology Press: Beijing, China, 2010; pp. 174–195. (In Chinese) [Google Scholar]
- Borko, J.; Dulnik, G.; Grzelka, A.; Luczak, A.; Paszkowski, A. A parametric synthesizer of audio signals on FPGA. Pomiary Autom. Kontrola 2015, 61, 367–369. [Google Scholar]
- Tong, S.B.; Hua, C.Y. Fundamentals of Analog Electronics; Higher Education Press: Beijing, China, 2015; pp. 276–296. (In Chinese) [Google Scholar]
- Richard, W.L. A New Correction Technique for Strain-Gage Measurements Acquired in Transient-Temperature Environments; NASA Technical Memorandum 3593; 1996. Available online: https://ntrs.nasa.gov/api/citations/19960016591/downloads/19960016591.pdf (accessed on 7 September 2025).
- Xie, J.J.; Liu, C.P. Fuzzy Mathematical Method and its Application; Machinery Industry Press: Beijing, China, 2018; pp. 143–156. (In Chinese) [Google Scholar]
- Ma, S.L.; Wang, J. The Fuzzy Method of Risk Analysis in R&D of Air-to-Air Missile. Acta Aeronaut. Astronaut. Sin. 2007, 28, 106–110. (In Chinese) [Google Scholar]
- Sheng, Z.; Xie, S.Q.; Pan, C.Y. Probability Theory and Mathematical Statistics; Higher Education Press: Beijing, China, 2001; pp. 109–143. (In Chinese) [Google Scholar]
- Reshef, D.N.; Reshef, Y.A.; Finucane, H.K.; Grossman, S.R.; McVean, G.; Turnbaugh, P.J.; Lander, E.S.; Mitzenmacher, M.; Sabeti, P.C. Detecting Novel Associations in Large Data Sets. Science 2011, 334, 1518–1524. [Google Scholar] [CrossRef] [PubMed]
- Reshef, Y.A.; Reshef, D.N.; Finucane, H.K.; Sabeti, P.C.; Mitzenmacher, M. Measuring Dependence powerfully and Equitably. J. Mach. Learn. Res. 2016, 17, 1–63. [Google Scholar]
- Tan, Q.H.; Jiang, H.J.; Ding, Y.M. Model Selection Methods Based on Maximum Information Coefficient of Residuals. Acta Math. Sci. 2014, 34B, 579–592. [Google Scholar] [CrossRef]






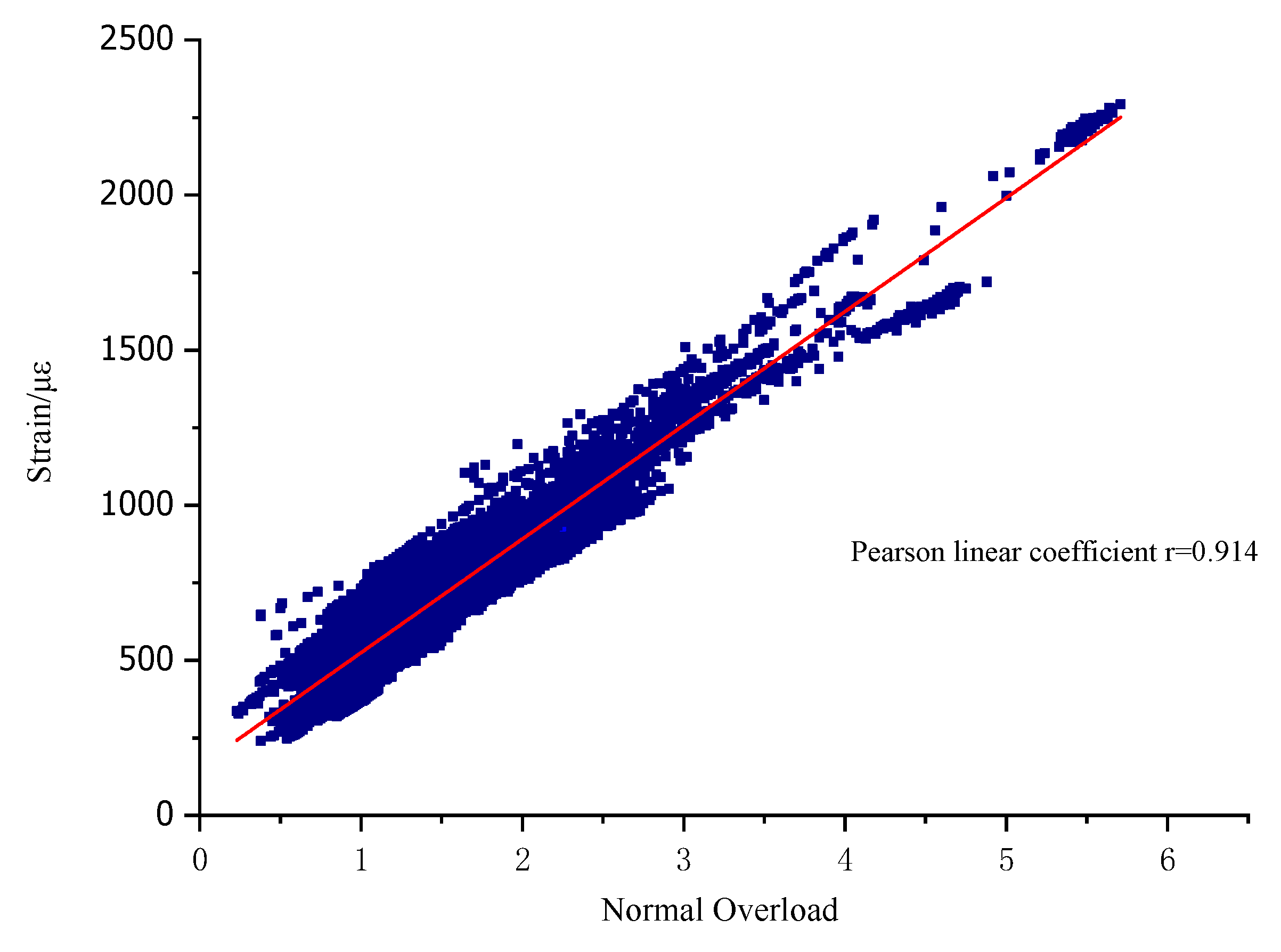
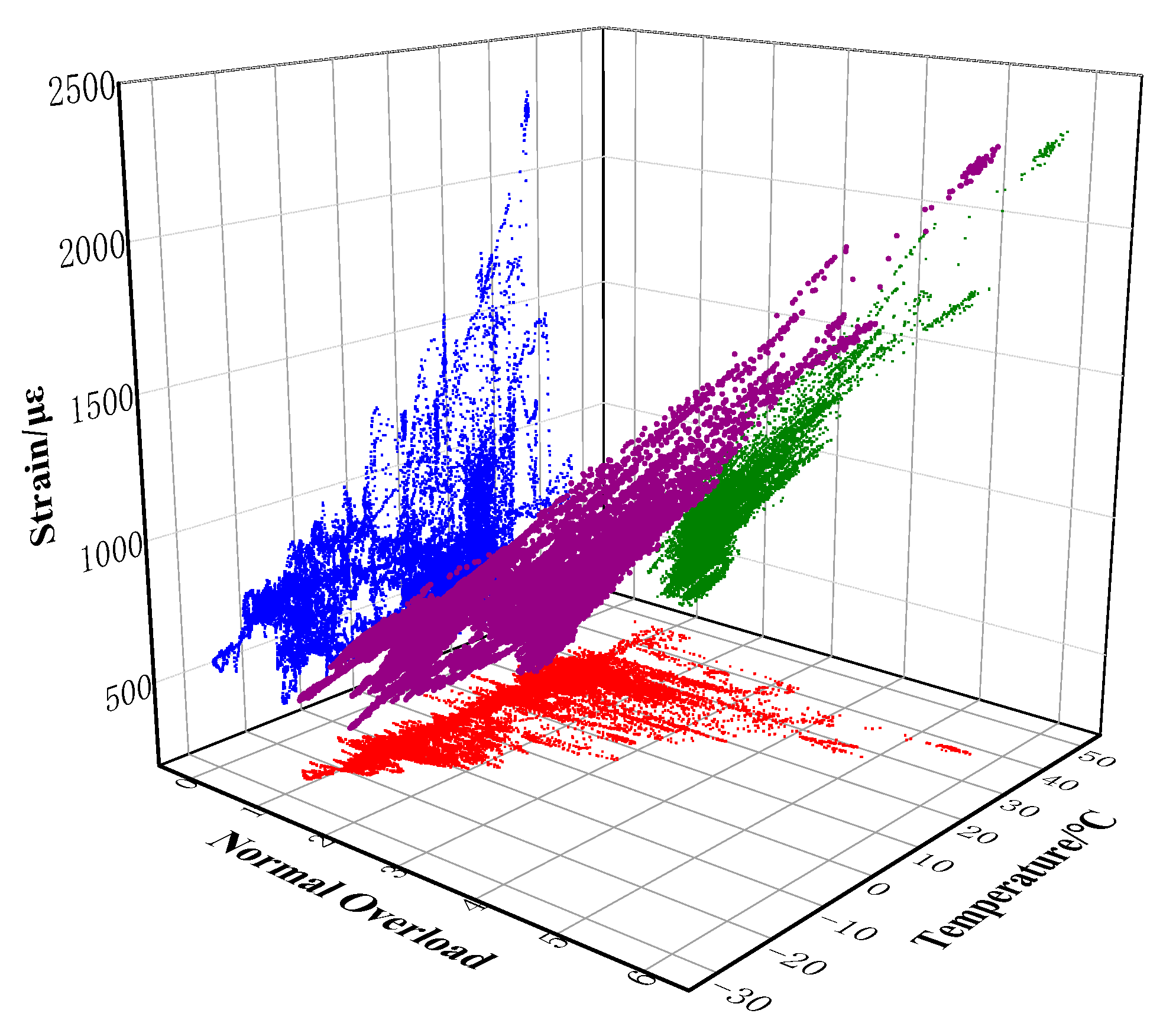
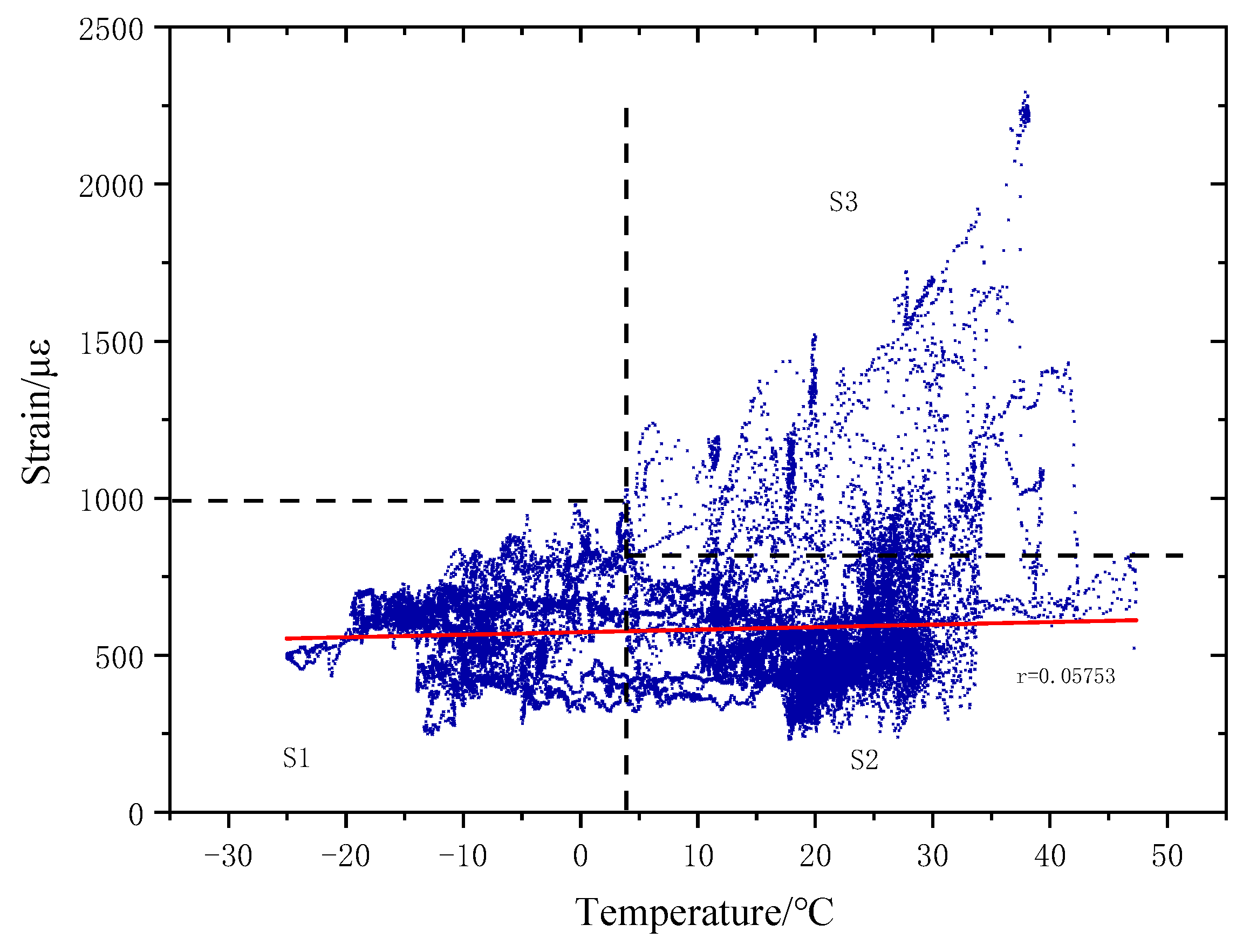
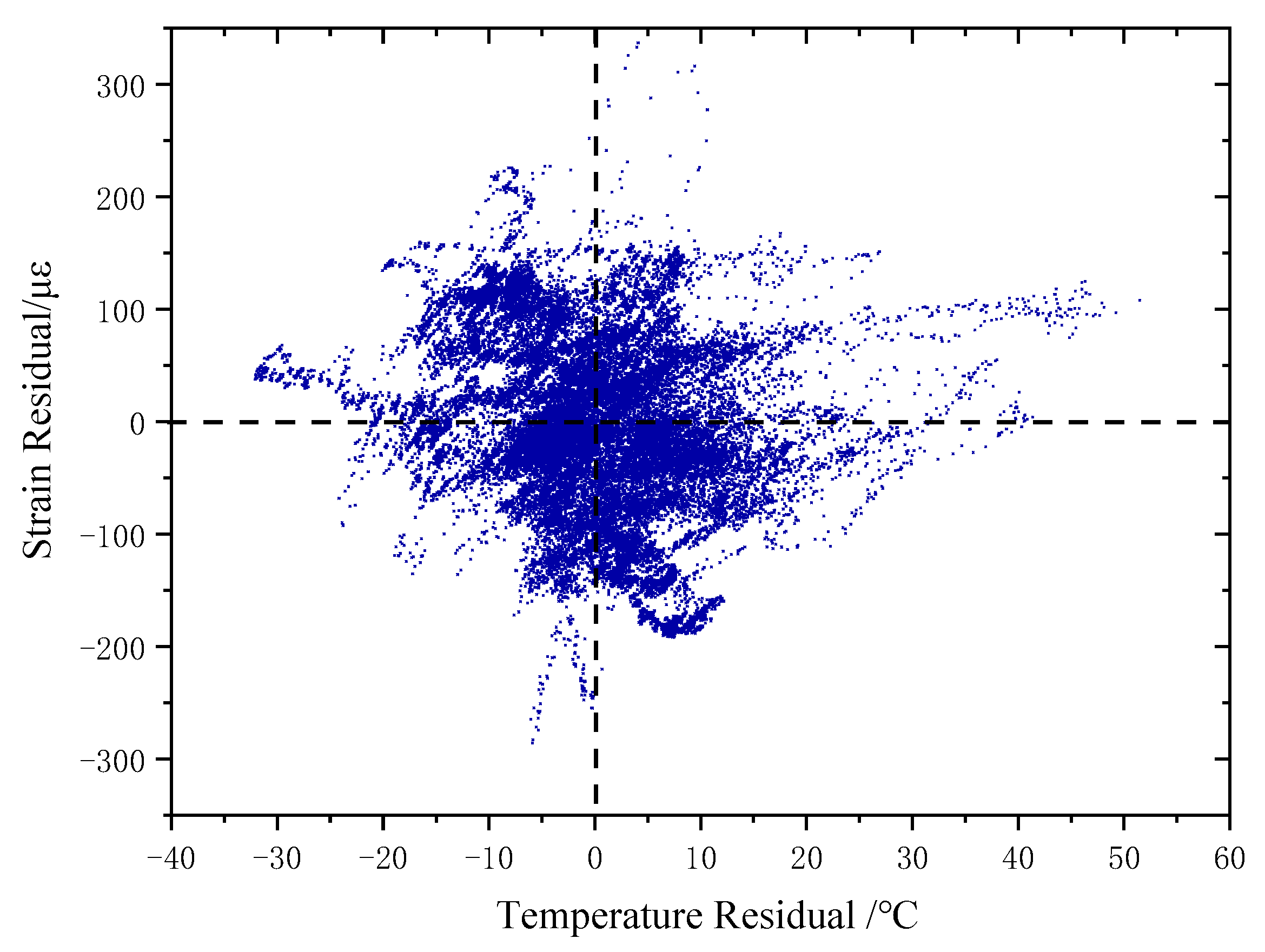
| Serial Number | Variables Corresponding to Influencing Factors | Median Value | Lower Limit Value | Upper Limit Value | Remarks |
|---|---|---|---|---|---|
| 1 | Bridge Excitation Voltage EAB | 4.99 V | 4.99 V | 4.99 V | Corresponds to Figure 9 |
| 4.89 V | 4.95 V | 4.82 V | Corresponds to Figure 10 | ||
| 2 | Strain–Analog Strain Signal Coefficient η | 0.4045 | 0.4018 | 0.4073 | Corresponds to Figure 9 |
| 0.4092 | 0.4043 | 0.4152 | Corresponds to Figure 10 | ||
| 3 | Ratio of Cable Resistance to Strain Gauge Resistance k | 1.143 × 10−2 | 4.571 × 10−3 | 1.829 × 10−2 | Corresponds to Figure 9 |
| 5.714 × 10−4 | 1.143 × 10−4 | 1.029 × 10−3 | Corresponds to Figure 10 | ||
| 4 | Gauge Factor Fg | 2.1 | 2 | 2.2 | |
| 5 | Coefficient of Thermal Expansion of Strain Adhesive Layer αa | 35.0 × 10−6/°C | 25.0 × 10−6/°C | 45.0 × 10−6/°C | |
| 6 | Coefficient of Thermal Expansion of Sensitive Grid αg | 15.2 × 10−6/°C | 10.2 × 10−6/°C | 20.2 × 10−6/°C | |
| 7 | Coefficient of Thermal Expansion of Tested Structural Part αs | 23.4 × 10−6/°C | 20.4 × 10−6/°C | 26.4 × 10−6/°C | |
| 8 | Temperature Coefficient of Resistance of Sensitive Grid βg | −15.6 × 10−6/°C | −20.6 × 10−6/°C | −10.6 × 10−6/°C | |
| 9 | Temperature Coefficient of Test Cable βr | 0.0043/°C | 0.0038/°C | 0.0048/°C | |
| 10 | Transverse Effect Coefficient of Strain Gauge H | 0.3% | 0.10% | 0.50% | |
| 11 | Poisson’s Ratio of Structural Material ν0 | 0.3 | 0.25 | 0.35 | |
| 12 | Strain Transfer Efficiency of Adhesive Layer λ | 0.95 | 0.9 | 1 | |
| 13 | Temperature Change in Strain Adhesive Layer ΔTa | - | - | - | |
| 14 | Temperature Change in Strain Gauge Sensitive Grid ΔTg | - | - | - | |
| 15 | Temperature Change in Test Cable ΔTr | - | - | - | |
| 16 | Temperature Change in Tested Structural Part ΔTs | - | - | - | |
| 17 | Temperature Coefficient of Low-Drift Resistance βR | 0.4 × 10−6/°C | 0.35 × 10−6/°C | 0.45 × 10−6/°C | |
| 18 | Temperature Change in Low-Drift Resistance ΔTR | - | - | - | |
| 19 | −0.3 | −1 | 0.7 | ||
| * | Strain Gauge Resistance R | 350 Ω | 351.8 Ω | 348.2 Ω | Included in k |
| Serial Number | Variable | Strain Bridge in Figure 9 | Strain Bridge in Figure 10 |
|---|---|---|---|
| Weight Value | Weight Value | ||
| 1 | EAB | 0 | 1.2068 × 10−2 |
| 2 | η | 6.5773 × 10−3 | 1.1777 × 10−2 |
| 3 | k | −6.6823 × 10−3 | −3.1799 × 10−3 |
| 4 | Fg | 4.6923 × 10−2 | 4.6834 × 10−2 |
| 5 | H | −1.1102 × 10−19 | 0 |
| 6 | ν0 | 1.4794 × 10−4 | 1.4766 × 10−4 |
| 7 | λ | 5.1862 × 10−2 | 5.1764 × 10−2 |
| 8 | 2.0712 × 10−3 | 2.0672 × 10−3 | |
| 9 | Fg × λ | 2.4696 × 10−3 | 2.4748 × 10−3 |
| 10 | 1.3820 × 10−3 | 1.3849 × 10−3 |
| Serial Number | Variable | Strain Bridge in Figure 9 | Serial Number | Variable | Strain Bridge in Figure 10 |
|---|---|---|---|---|---|
| Weight Value | Weight Value | ||||
| 1 | k | 1.4394 × 10−5 | 1 | α g | 5.2174 × 10−6 |
| 2 | α a | 5.2065 × 10−6 | 2 | α s | 2.9739 × 10−6 |
| 3 | F g | 2.9677 × 10−6 | 3 | β g | 2.4748 × 10−6 |
| 4 | αs*×λ | 2.8228 × 10−6 | 4 | k | 9.7218 × 10−7 |
| 5 | Fg×αg | 2.4696 × 10−6 | 5 | λ | 6.0522 × 10−7 |
| 6 | ν0×λ | 1.6749 × 10−6 | 6 | αa×λ | 5.2174 × 10−7 |
| 7 | k×βr | 6.0395 × 10−7 | 7 | α a | 5.2174 × 10−7 |
| 8 | E AB-ν0 | 5.2065 × 10−7 | 8 | F g | 4.3627 × 10−7 |
| 9 | αa×λ | 5.2064 × 10−7 | 9 | Fg×αg | 2.4845 × 10−7 |
| 10 | λ | 4.3535 × 10−7 | 10 | αs×λ | 1.5652 × 10−7 |
| 11 | k-ν0 | 2.4793 × 10−7 | 11 | Fg×αs | 1.4161 × 10−7 |
| 12 | β g | 1.7481 × 10−7 | 12 | β r | 1.4141 × 10−7 |
| 13 | ΔTa | 1.07 × 10−6 | 13 | ΔTa | 1.0931 × 10−6 |
| 14 | ΔTg | −2.54 × 10−5 | 14 | ΔTg | −2.5752 × 10−5 |
| 15 | ΔTr | 3.34 × 10−5 | 15 | ΔTr | 1.8289 × 10−6 |
| 16 | ΔTs | 2.59 × 10−5 | 16 | ΔTs | 2.6311 × 10−5 |
| Serial Number | Variable | Strain Bridge in Figure 9 |
|---|---|---|
| Weight Value | ||
| 1 | η | 1.3585 × 10−9 |
| 2 | β R | 2.4978 × 10−8 |
| 3 | η-β R | 1.6982 × 10−10 |
| 4 | ΔTR | 2.8228 × 10−6 |
| Serial Number | Factor Set U | Judgment Set V | ||||
|---|---|---|---|---|---|---|
| (Small) | (Relatively Small) | (Medium) | (Relatively Large) | (Large) | ||
| 1 | 2 | 3 | 4 | 5 | ||
| 1 | Bridge excitation voltage ΔEAB,1-0 | 0.8 | 0.2 | 0 | 0 | 0 |
| 2 | Strain-simulated strain signal coefficient Δη,1-0 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
| 3 | Resistance ratio of cable and strain gauge Δk,1-0 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
| 4 | Gauge factor of strain gauge ΔFg,1-0 | 0.5 | 0.2 | 0.2 | 0.1 | 0 |
| 5 | Linear expansion coefficient of strain adhesive layer ΔH,1-0 | 0.5 | 0.2 | 0.2 | 0.1 | 0 |
| 6 | Expansion coefficient of sensitive grid wire Δν0,1-0 | 0.5 | 0.2 | 0.2 | 0.1 | 0 |
| 7 | Strain transfer efficiency of adhesive layer Δλ,1-0 | 0.3 | 0.3 | 0.2 | 0.1 | 0.1 |
| 8 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | |
| Serial Number | Factor Set U | Judgment Set V | ||||
|---|---|---|---|---|---|---|
(Small) | (Relatively Small) | (Medium) | (Relatively Large) | (Large) | ||
| 1 | Bridge excitation voltage ΔEAB,1-2 or ΔEAB,3-4 | 0 | 0 | 0 | 0 | 0 |
| 2 | Strain-simulated strain signal coefficient Δη,1-2 or Δη,3-4 | 0 | 0 | 0 | 0 | 0 |
| 3 | Resistance ratio of cable and strain gauge Δk,1-2 or Δk,3-4 | 0.7 | 0.2 | 0.1 | 0 | 0 |
| 4 | Gauge factor of strain gauge ΔFg,1-2 or ΔFg,3-4 | 0.5 | 0.2 | 0.2 | 0.1 | 0 |
| 5 | Linear expansion coefficient of strain adhesive layer Δαa,1-2 or Δαa,3-4 | 0.5 | 0.2 | 0.2 | 0.1 | 0 |
| 6 | Expansion coefficient of sensitive grid wire Δαg,1-2 or Δαg,3-4 | 0.5 | 0.2 | 0.2 | 0.1 | 0 |
| 7 | Coefficient of linear expansion of the measured structural part Δαs,1-2 | 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
| Coefficient of linear expansion of the measured structural part Δαs,3-4 | 1 | 0 | 0 | 0 | 0 | |
| 8 | Temperature coefficient of the sensitive grid Δβg,1-2 or Δβg,3-4 | 0.5 | 0.2 | 0.2 | 0.1 | 0 |
| 9 | Temperature coefficient of test cable Δβr,1-2 or Δβr,3-4 | 0.7 | 0.2 | 0.1 | 0 | 0 |
| 10 | Transverse effect coefficient of strain gauge ΔH1-2 or ΔH3-4 | 0.5 | 0.2 | 0.2 | 0.1 | 0 |
| 11 | Poisson’s ratio of structural material Δν0,1-2 | 0.7 | 0.2 | 0.1 | 0 | 0 |
| Poisson’s ratio of structural material Δν0,3-4 | 1 | 0 | 0 | 0 | 0 | |
| 12 | Strain transfer efficiency of the adhesive layer Δλ,1-2 or Δλ,3-4 | 0.3 | 0.3 | 0.2 | 0.1 | 0.1 |
| 13 | Temperature change in the strain adhesive layer ΔTa,1-2 | 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
| Temperature change in the strain adhesive layer ΔTa,3-4 | 0.8 | 0.2 | 0 | 0 | 0 | |
| 14 | Temperature change in the strain gauge sensitive grid ΔTg,1-2 | 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
| Temperature change in the strain gauge sensitive grid ΔTg,3-4 | 0.8 | 0.2 | 0 | 0 | 0 | |
| 15 | Temperature change in the test cable ΔTr,1-2 | 0.8 | 0.2 | 0 | 0 | 0 |
| Temperature change in the test cable ΔTr,3-4 | 0.8 | 0.2 | 0 | 0 | 0 | |
| 16 | Temperature variation in the tested structural part ΔTs,1-2 | 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
| Temperature variation in the tested structural part ΔTs,3-4 | 0.8 | 0.2 | 0 | 0 | 0 | |
| 17 | Temperature coefficient of low-drift resistor ΔβR,3-4 | 0.7 | 0.2 | 0.1 | 0 | 0 |
| 18 | Temperature change in low-drift resistor ΔTR,3-4 | 0.8 | 0.2 | 0 | 0 | 0 |
| Serial Number | Evaluation Item | Score S | Remarks | |
|---|---|---|---|---|
| 1 | (0.382, 0.244, 0.195, 0.11, 0.069) | 2.24 | Figure 9 | |
| 2 | (0.425, 0.239, 0.175, 0.099, 0.062) | 2.135 | Figure 10 | |
| 3 | (0.626, 0.194, 0.131, 0.038, 0.011) | 1.596 | Figure 9 | |
| 4 | (0.781, 0.2, 0.009, 0.005, 0.005) | 1.251 | Figure 9 | |
| 5 | (0.7, 0.2, 0.1, 0, 0) | 1.4 | Figure 9 | |
| 6 | (0.8, 0.2, 0, 0, 0) | 1.2 | Figure 9 | |
| 7 | (0.508, 0.202, 0.18, 0.085, 0.025) | 1.861 | Figure 10 | |
| 8 | (0.61, 0.2, 0.095, 0.0475, 0.0475) | 1.722 | Figure 10 | |
| 9 | (0.636, 0.158, 0.138, 0.064, 0.004) | 1.596 | Figure 10 | |
| 10 | (0.8, 0.2, 0, 0, 0) | 1.200 | Figure 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, W.; Pang, X.; Huang, H.; Yan, G. Research, Verification and Uncertainty Analysis of Aircraft Structural Load/Strain Testing. Appl. Sci. 2025, 15, 10116. https://doi.org/10.3390/app151810116
Xue W, Pang X, Huang H, Yan G. Research, Verification and Uncertainty Analysis of Aircraft Structural Load/Strain Testing. Applied Sciences. 2025; 15(18):10116. https://doi.org/10.3390/app151810116
Chicago/Turabian StyleXue, Weijun, Xiwen Pang, Heng Huang, and Guang Yan. 2025. "Research, Verification and Uncertainty Analysis of Aircraft Structural Load/Strain Testing" Applied Sciences 15, no. 18: 10116. https://doi.org/10.3390/app151810116
APA StyleXue, W., Pang, X., Huang, H., & Yan, G. (2025). Research, Verification and Uncertainty Analysis of Aircraft Structural Load/Strain Testing. Applied Sciences, 15(18), 10116. https://doi.org/10.3390/app151810116





