Adaptive Time Delay Impedance Control of Robot Manipulator via Voltage-Based Motor Control
Abstract
1. Introduction
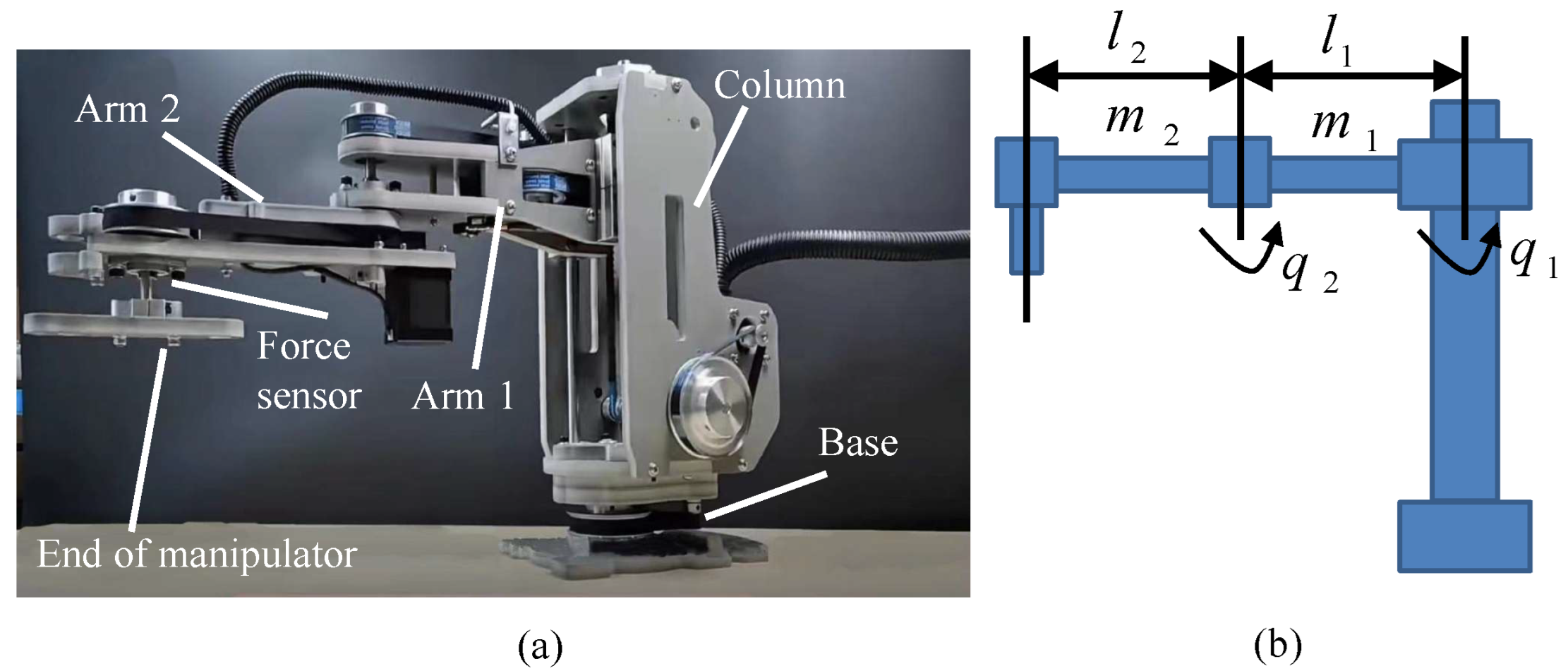
2. Materials and Methods
2.1. Voltage-Based Motor Control
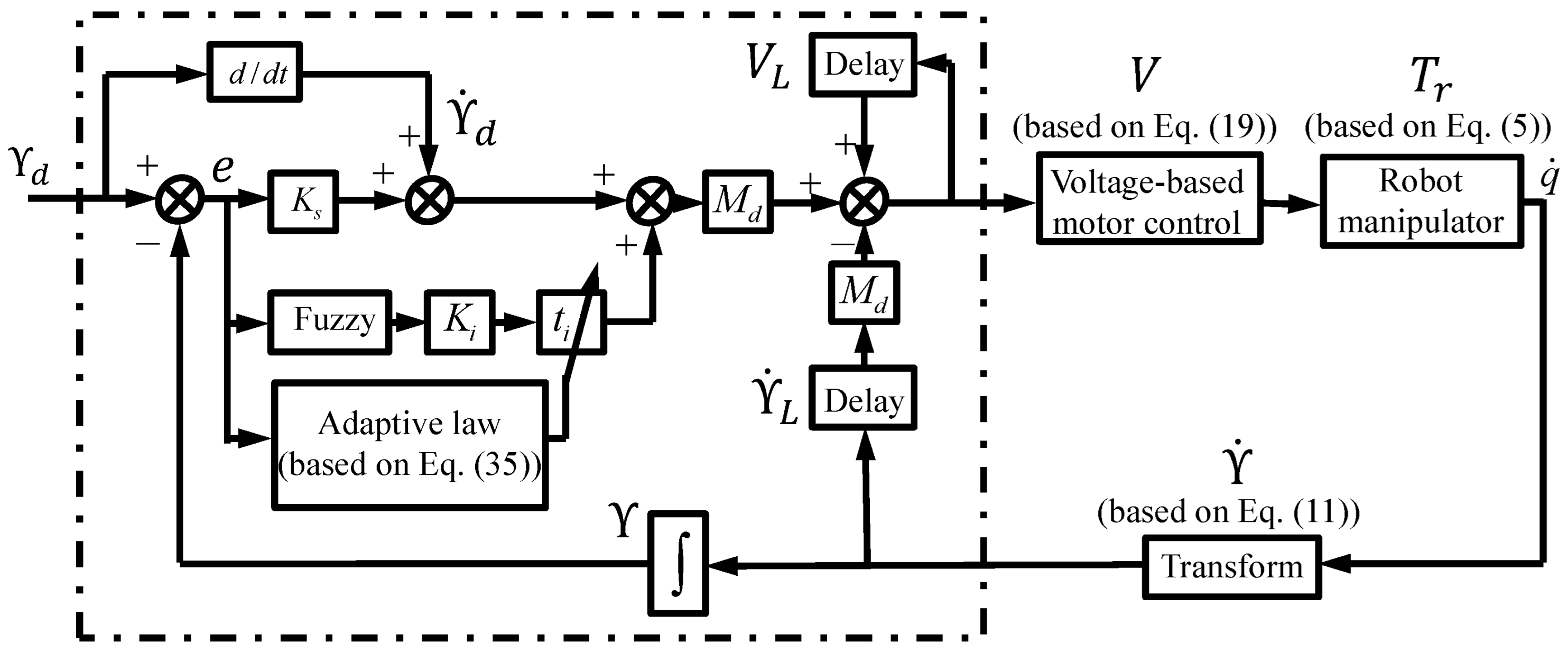
2.2. Impedance Control Design
2.3. Stability Analysis
3. Experiments and Results
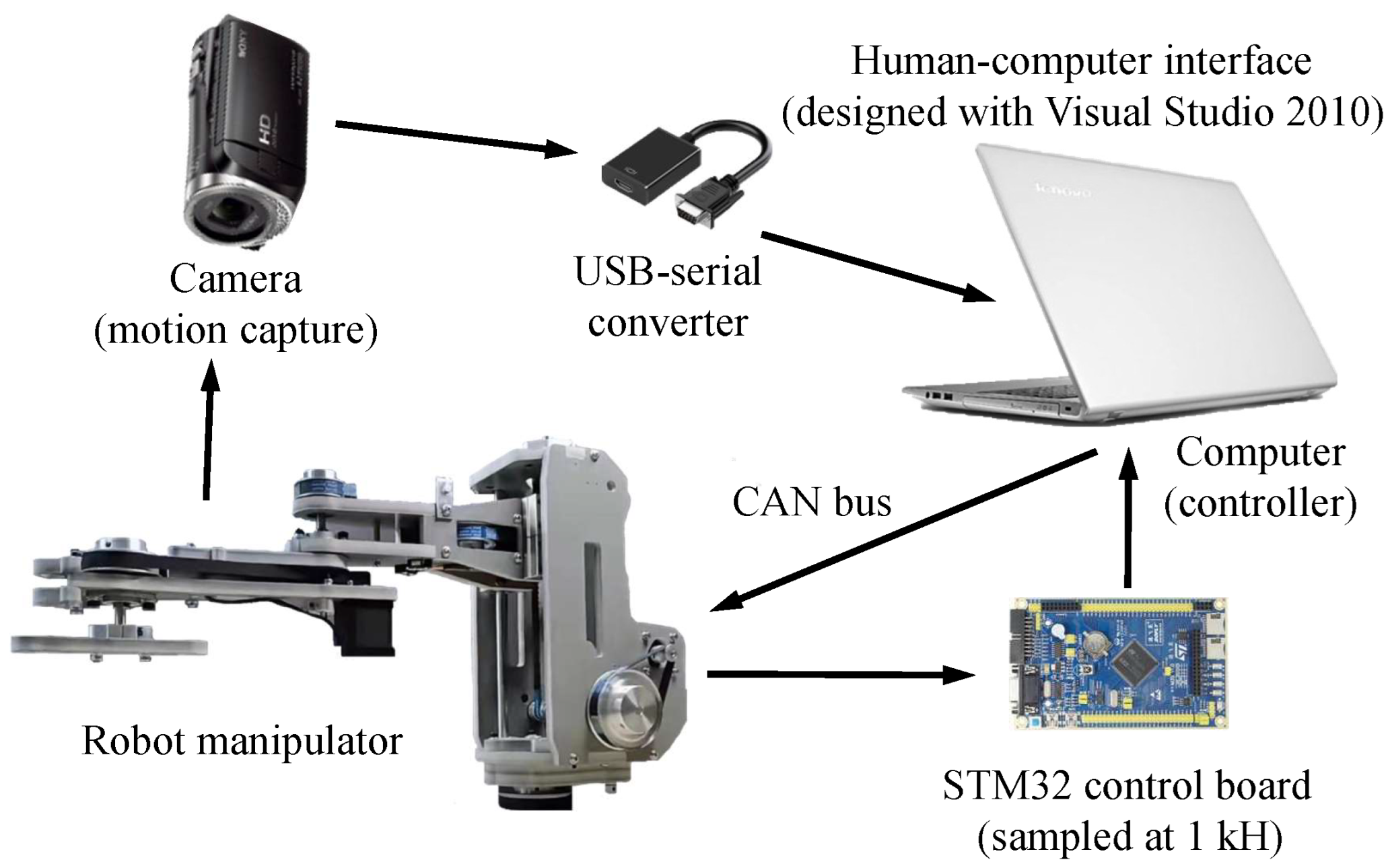
3.1. Experiment Setup
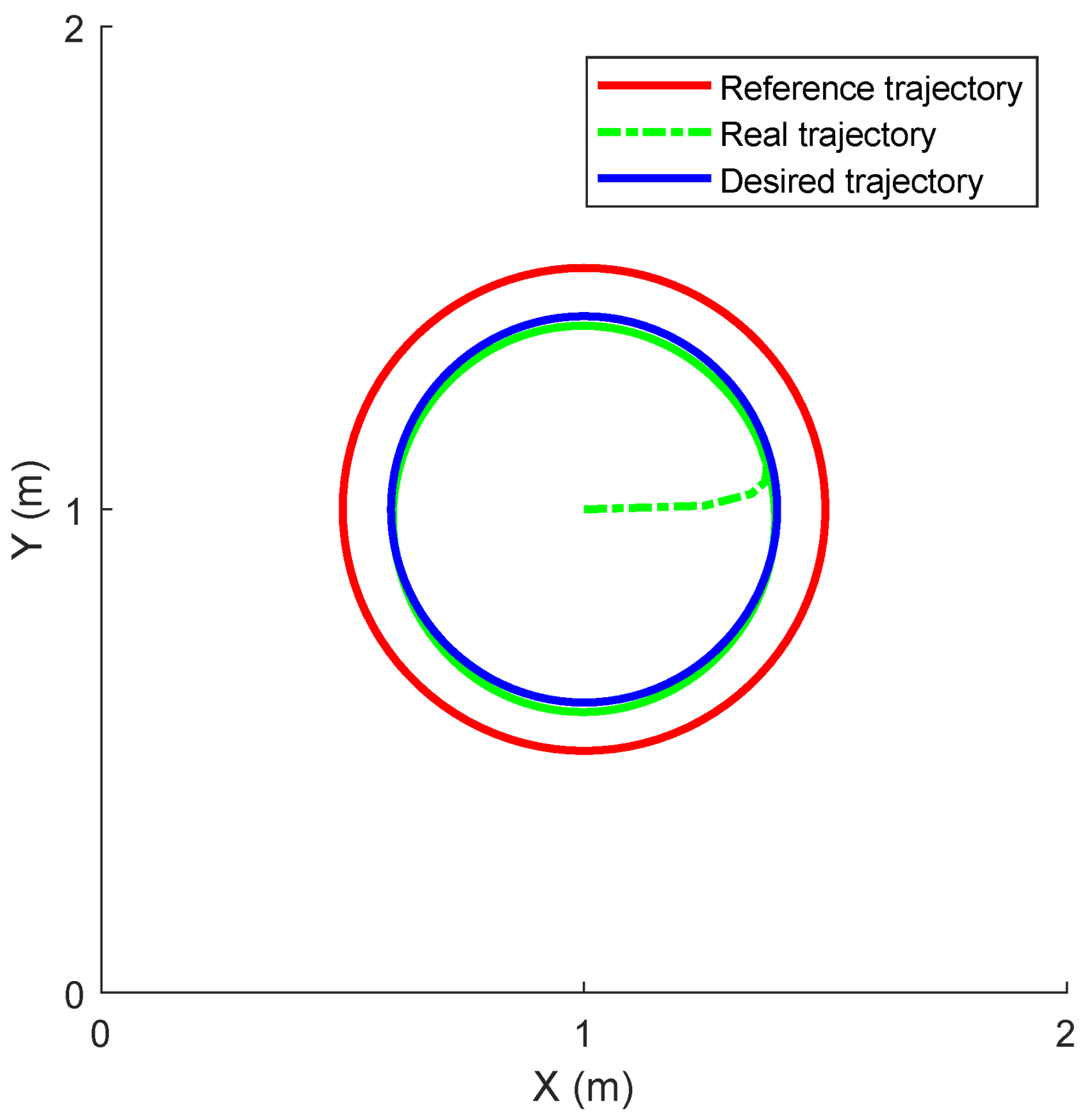
3.2. Case 1: Following a Circular Motion
3.2.1. Experimental Protocol
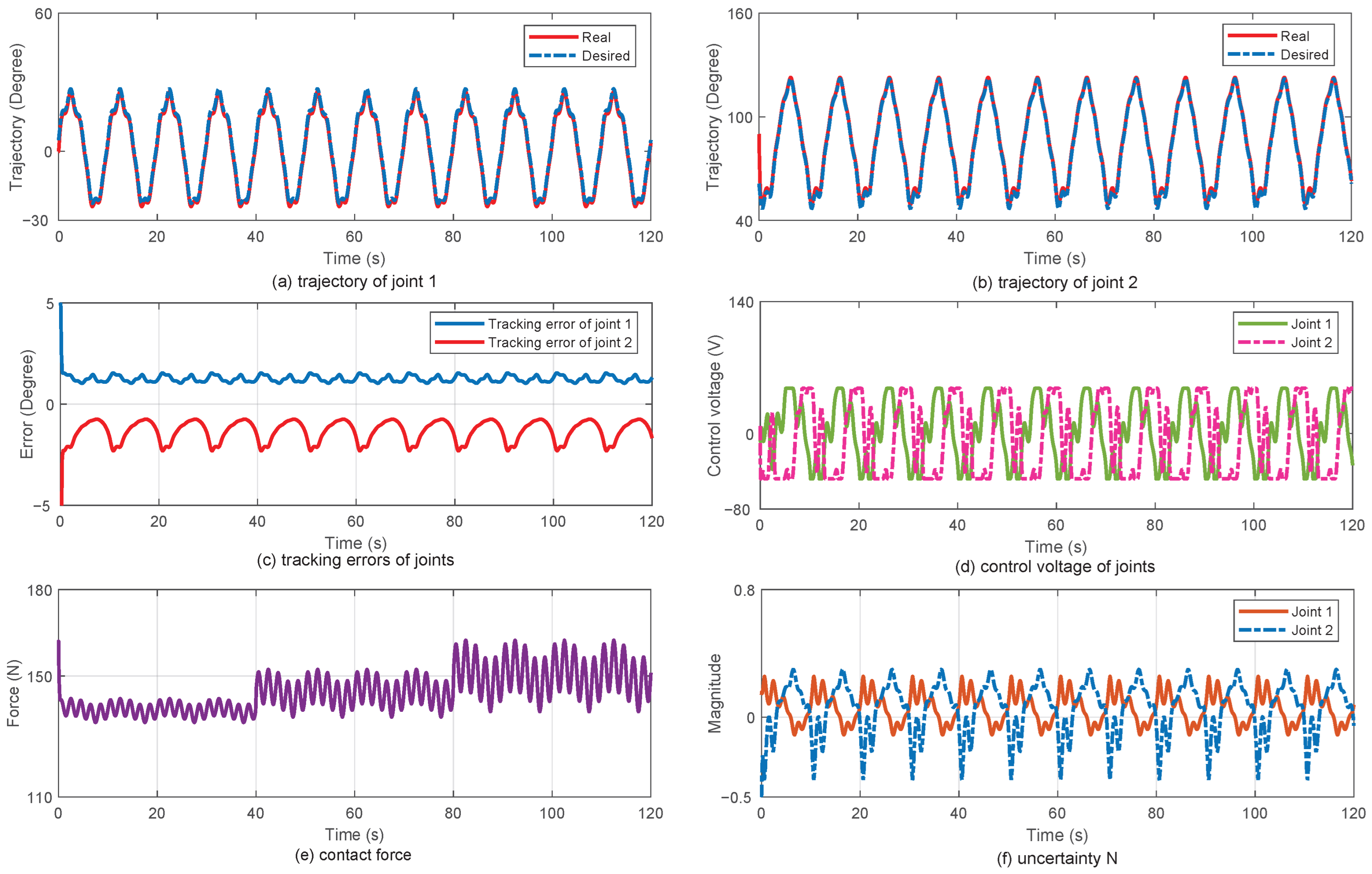
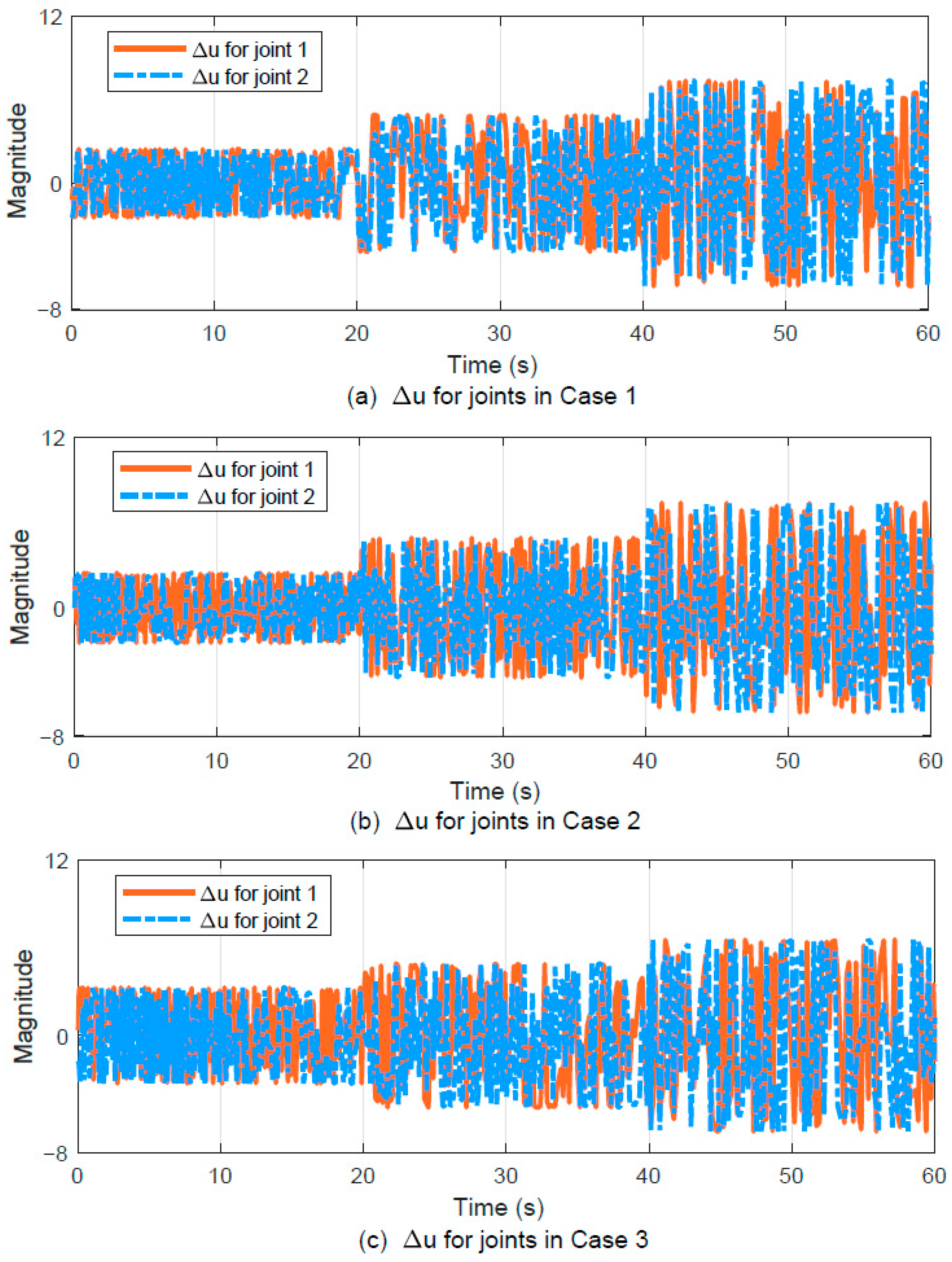
3.2.2. Results
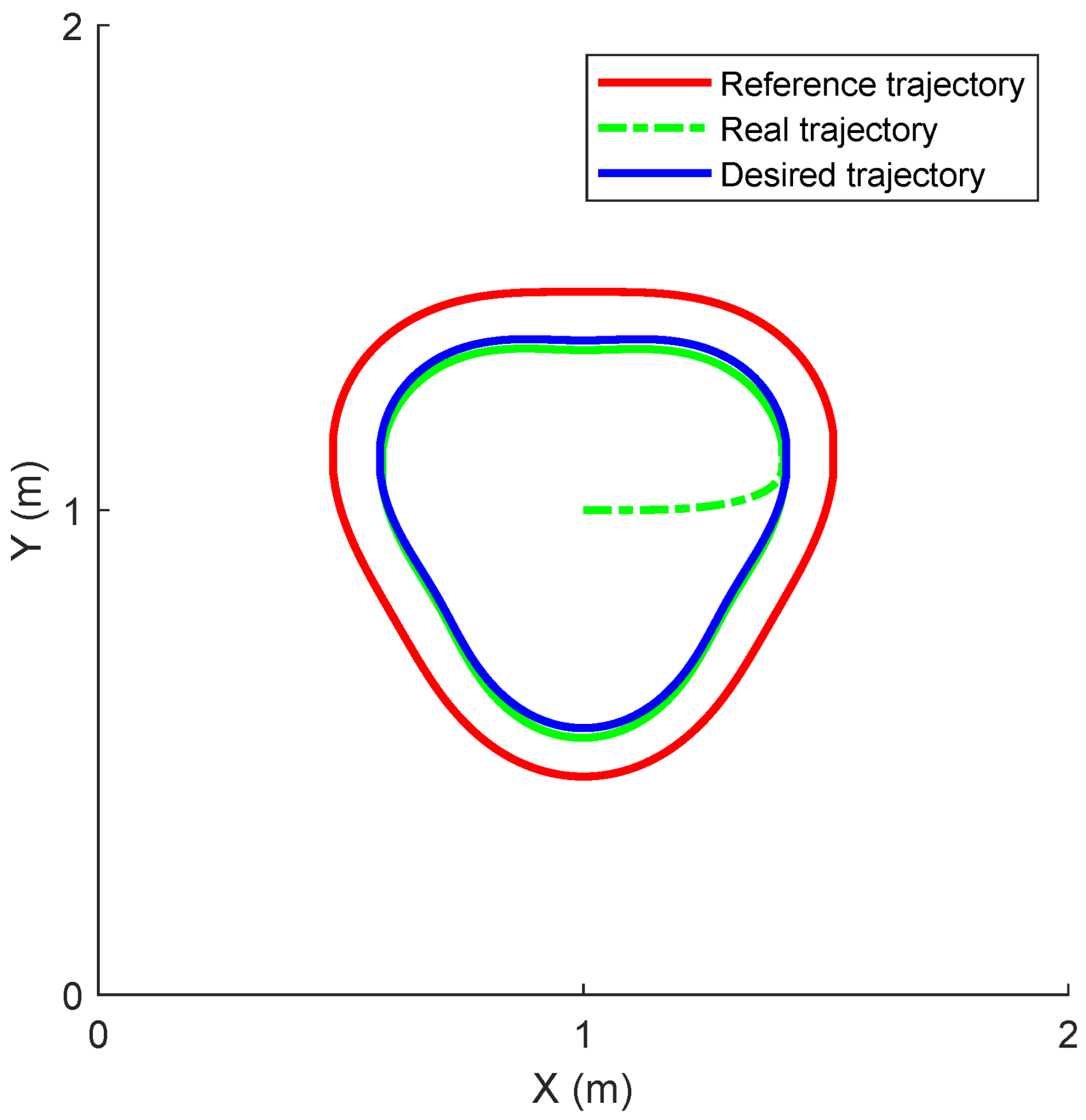
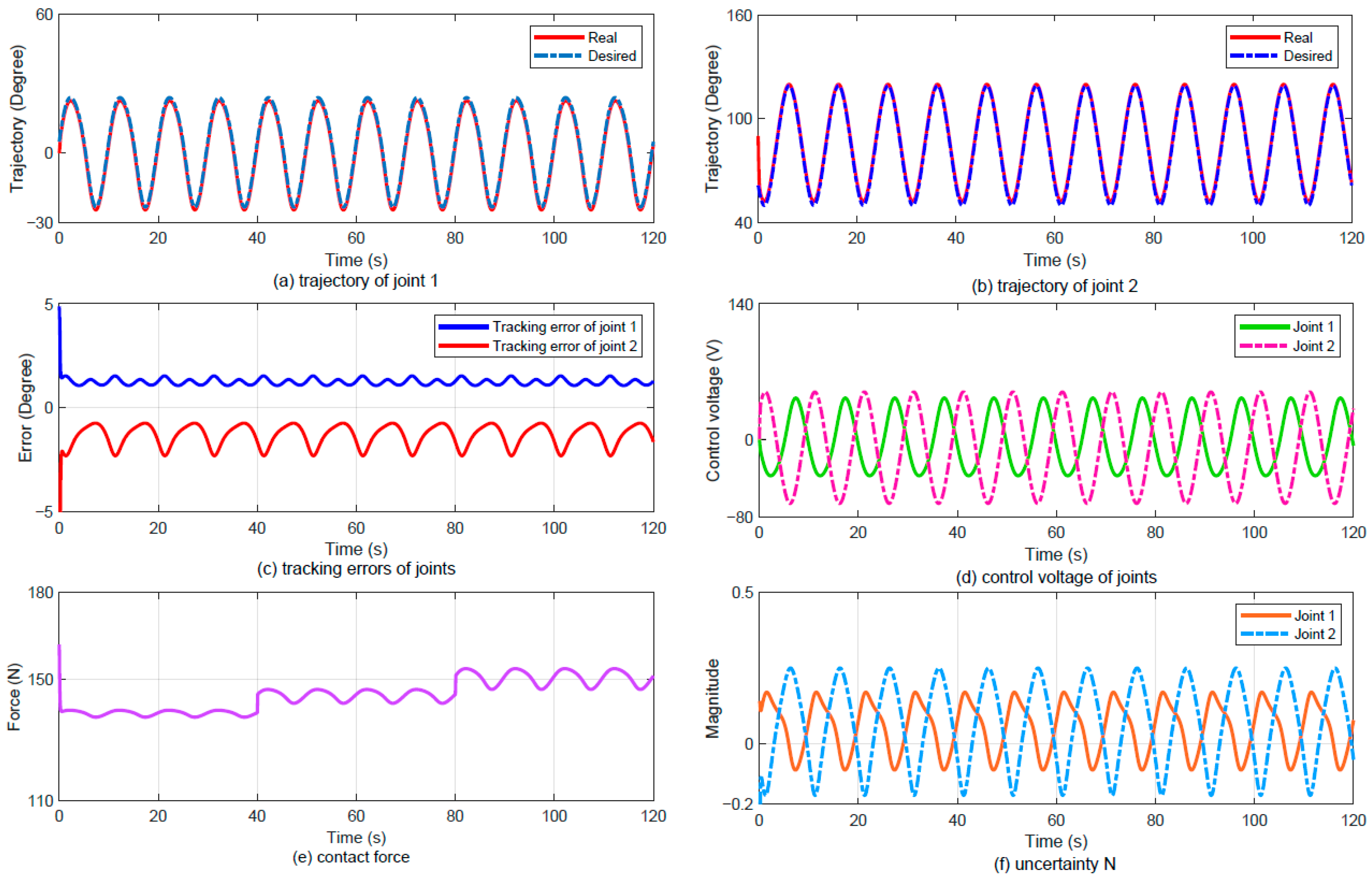
3.3. Case 2: Following a Triangle Circular Motion
3.3.1. Experimental Protocol
3.3.2. Results
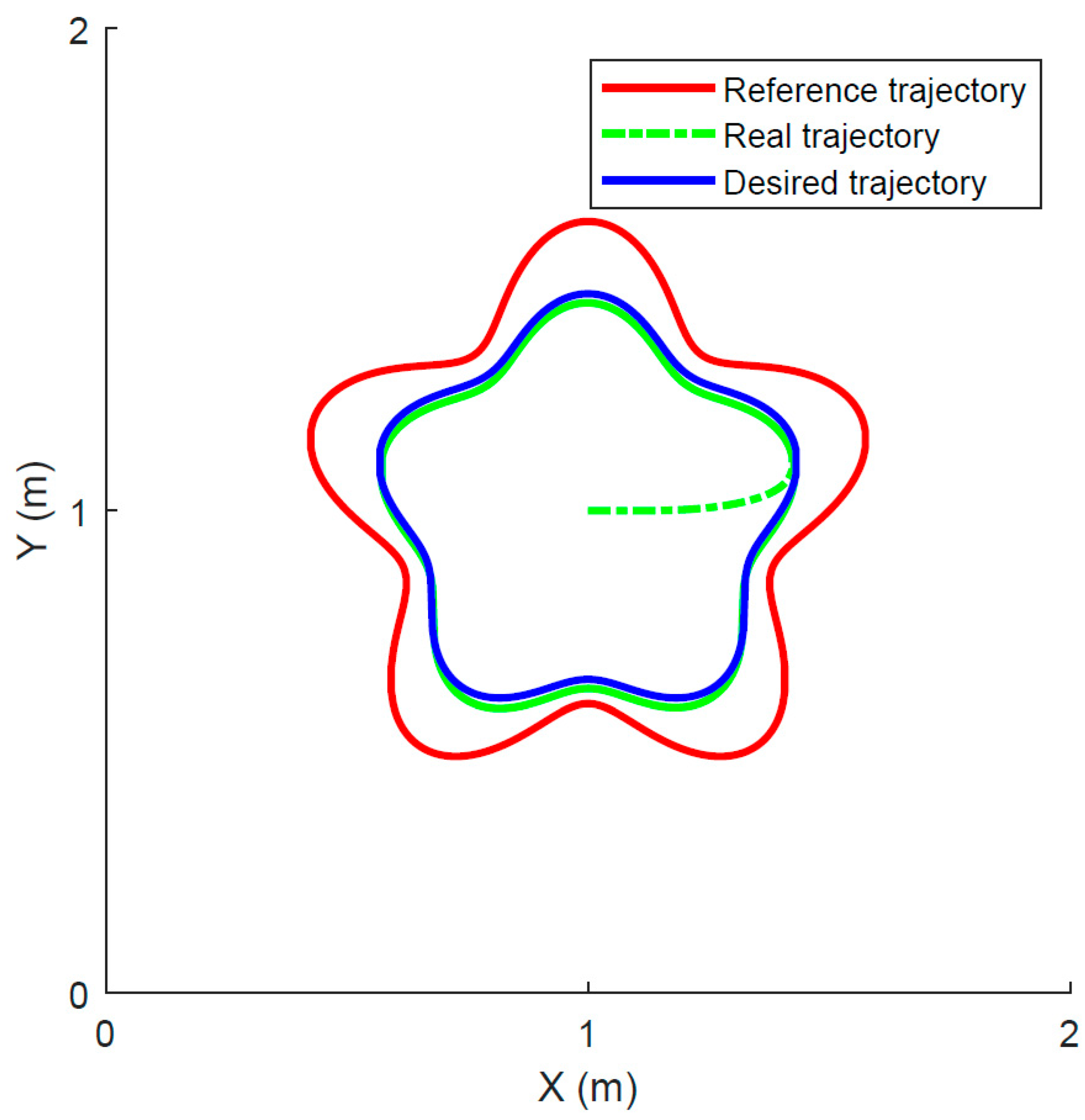
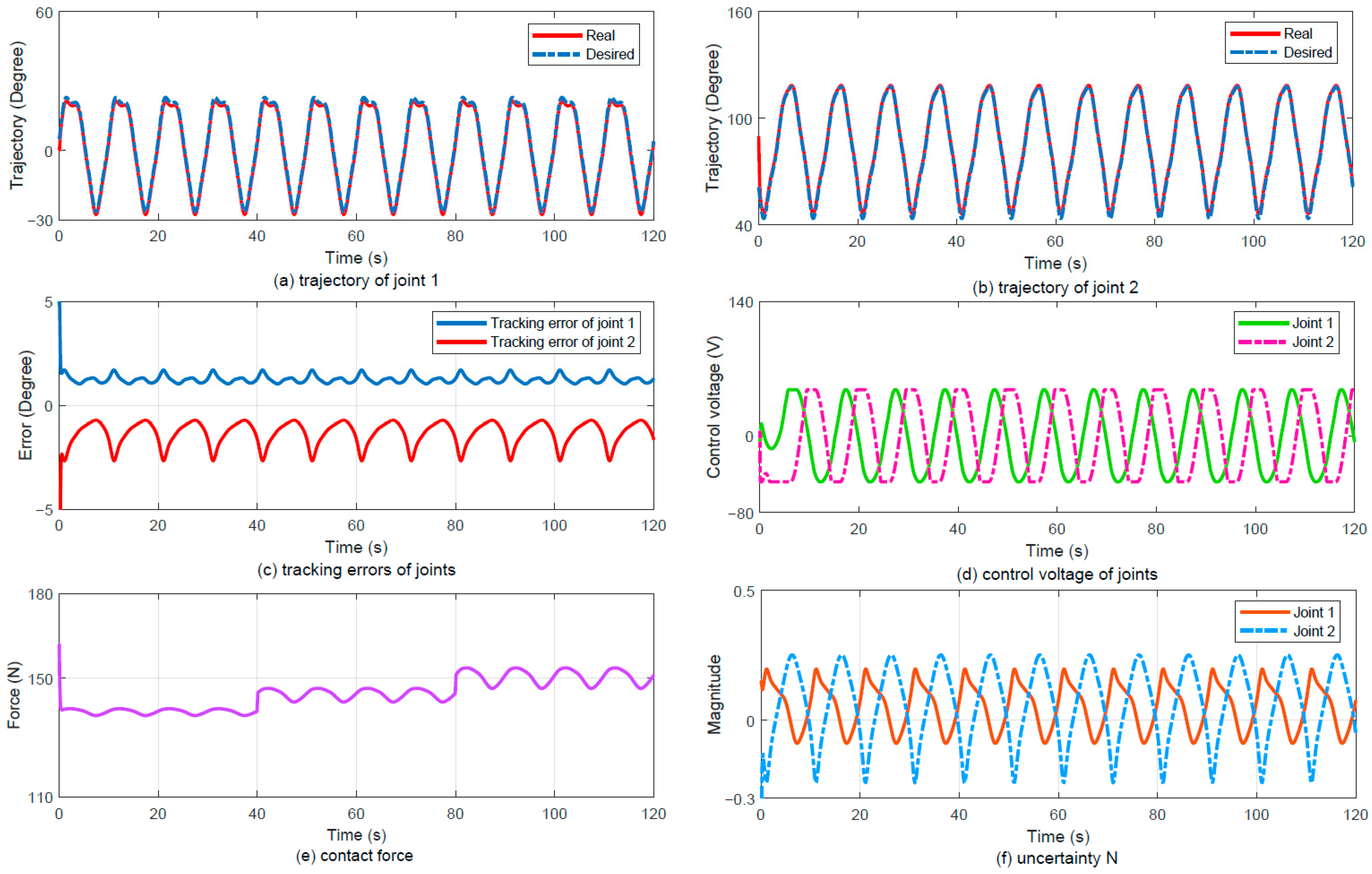
3.4. Case 3: Following a Sine Circular Motion
3.4.1. Experimental Protocol
3.4.2. Results
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Kommuri, S.K.; Han, S.; Lee, S. External torque estimation using higher order sliding-mode observer for robot manipulators. IEEE/ASME Trans. Mechatron. 2022, 27, 513–523. [Google Scholar] [CrossRef]
- Dong, W.; Ma, Z.; Sheng, X.; Zhu, X. Centimeter-level aerial assembly achieved with manipulating condition inference and compliance. IEEE/ASME Trans. Mechatron. 2022, 27, 1660–1671. [Google Scholar] [CrossRef]
- Xie, Z.; Jin, L.; Luo, X. Kinematics-based motion-force control for redundant manipulators with quaternion control. IEEE Trans. Autom. Sci. Eng. 2023, 20, 1815–1828. [Google Scholar] [CrossRef]
- Fan, J.; Jin, L.; Xie, Z.; Li, S.; Zheng, Y. Data-driven motion-force control scheme for redundant manipulators: A kinematic perspective. IEEE Trans. Ind. Inform. 2022, 18, 5338–5347. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, S.; Guidi, G.; Tang, Y.; Suul, J.A. Dynamic improvement of sub-resonant frequency control for inductive power transfer systems by coupling estimation and sending-side gain-scheduled control. IEEE Trans. Ind. Appl. 2024, 60, 3734–3745. [Google Scholar] [CrossRef]
- Shi, H.; Sun, K.; Wu, H.; Li, Y. A unified state-space modeling method for a phase-shift controlled bidirectional dual-active half-bridge converter. IEEE Trans. Power Electron. 2020, 35, 3254–3265. [Google Scholar] [CrossRef]
- Chai, R.; Chen, K.; Hua, B.; Lu, Y.; Xia, Y.; Sun, X.-M. A two phases multiobjective trajectory optimization scheme for multi-UGVs in the sight of the first aid scenario. IEEE Trans. Cybern. 2024, 54, 5078–5091. [Google Scholar] [CrossRef]
- Zhou, Y.; Helian, B.; Chen, Z.; Yao, B. Adaptive robust constrained motion control of an independent metering electro-hydraulic system considering kinematic and dynamic constraints. IEEE Trans. Ind. Inform. 2025, 21, 5943–5953. [Google Scholar] [CrossRef]
- Shen, J.; Zhang, J.; Zong, H.; Cheng, M.; Xu, B. Hierarchical decoupling controller with cylinder separated model of hydraulic manipulators for contact force/motion control. IEEE/ASME Trans. Mechatron. 2023, 28, 1081–1092. [Google Scholar] [CrossRef]
- Jin, X. Formation-based decentralized iterative learning cooperative impedance control for a team of robot manipulators. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 872–881. [Google Scholar] [CrossRef]
- Arefinia, E.; Talebi, H.A.; Doustmohammadi, A. A robust adaptive model reference impedance control of a robotic manipulator with actuator saturation. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 409–420. [Google Scholar] [CrossRef]
- Li, G.; Yu, J.; Chen, X. Adaptive fuzzy neural network command filtered impedance control of constrained robotic manipulators with disturbance observer. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 5171–5180. [Google Scholar] [CrossRef]
- He, X.; Li, X.; Song, S. Nonsingular terminal sliding-mode control of second-order systems subject to hybrid disturbances. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 5019–5023. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, Y.; Gong, D.; Liu, J. Global integral sliding-mode control with improved nonlinear extended state observer for rotary tracking of a hydraulic roofbolter. IEEE/ASME Trans. Mechatron. 2023, 28, 483–494. [Google Scholar] [CrossRef]
- Stefano, M.D.; Balachandran, R.; Secchi, C. A passivity-based approach for simulating satellite dynamics with robots: Discrete-time integration and time-delay compensation. IEEE Trans. Robot. 2020, 36, 189–203. [Google Scholar] [CrossRef]
- Boudjedir, C.E.; Bouri, M.; Boukhetala, D. An enhanced adaptive time delay control-based integral sliding mode for trajectory tracking of robot manipulators. IEEE Trans. Control Syst. Technol. 2023, 31, 1042–1050. [Google Scholar] [CrossRef]
- Sun, W.; Wu, Y.; Lv, X. Adaptive neural network control for full-state constrained robotic manipulator with actuator saturation and time-varying delays. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 3331–3342. [Google Scholar] [CrossRef]
- Zheng, L.; Zhang, Z. Time-varying quadratic-programming-based error redefinition neural network control and its application to mobile redundant manipulators. IEEE Trans. Autom. Control 2022, 67, 6151–6158. [Google Scholar] [CrossRef]
- Li, C.; Zhao, L.; Xu, Z. Finite-time adaptive event-triggered control for robot manipulators with output constraints. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 3824–3828. [Google Scholar] [CrossRef]
- Cornejo, J.; Barrera, S.; Ruiz, C.H.; Gutierrez, F.; Casasnovas, M.O.; Kot, L.; Solis, M.A.; Larenas, R.; Castro-Nieny, F.; Arbulú Saavedra, M.R.; et al. Industrial, collaborative, and mobile robotics in Latin America: Review of mechatronic technologies for advanced automation. Emerg. Sci. J. 2023, 7, 1430–1458. [Google Scholar] [CrossRef]
- Armero, J.A.C.; Quezada, M.T.; Vázquez, L.B.; Rodríguez, R.; Serrezuela; Montiel, J.J.; Hermosilla, D.M.; Zamora, R.S. Digital twin: An option for the integrated design of upper limb robotic exoskeletons for rehabilitation tasks. ARPN J. Eng. Appl. Sci 2021, 16, 686–697. Available online: https://www.semanticscholar.org/paper/DIGITAL-TWIN%3A-AN-OPTION-FOR-THE-INTEGRATED-DESIGN-Armero-Quezada/a081a21f427ae78dde879d99f1311e35a5cf7dce (accessed on 12 September 2025).
- Wan, L.; Pan, Y.J.; Shen, H. Improving synchronization performance of multiple euler–lagrange systems using nonsingular terminal sliding mode control with fuzzy logic. IEEE/ASME Trans. Mechatron. 2022, 27, 2312–2321. [Google Scholar] [CrossRef]
- Lee, S.; Shin, M.; Son, H. Robust predictor-based control for multirotor UAV with various time delays. IEEE Trans. Ind. Electron. 2023, 70, 8151–8162. [Google Scholar] [CrossRef]
- Baek, J.; Kang, M. A synthesized sliding-mode control for attitude trajectory tracking of quadrotor UAV systems. IEEE/ASME Trans. Mechatron. 2023, 28, 2189–2199. [Google Scholar] [CrossRef]
- Park, J.; Kwon, W.; Park, P. An improved adaptive sliding mode control based on time-delay control for robot manipulators. IEEE Trans. Ind. Electron. 2023, 70, 10363–10373. [Google Scholar] [CrossRef]
- Yang, J.; Wang, Y.; Wang, T.; Hu, Z.; Yang, X.; Rodriguez-Andina, J.J. Time-delay sliding mode control for trajectory tracking of robot manipulators. IEEE Trans. Ind. Electron. 2024, 71, 13083–13091. [Google Scholar] [CrossRef]
- Tran, D.T.; Nguyen, X.T.; Nguyen, T.N.; Truong, O.T. Practical synchronous sliding mode control with time delay estimation for a 4-DOF parallel manipulator with unknown dynamics and variable payload. IEEE Access 2025, 13, 102758–102770. [Google Scholar] [CrossRef]
- Zhang, Y.; Niu, B.; Zhao, X.; Duan, P.; Wang, H.; Gao, B. Global predefined-time adaptive neural network control for disturbed pure-feedback nonlinear systems with zero tracking error. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 6328–6338. [Google Scholar] [CrossRef] [PubMed]
- Zhao, R.; Yang, J.; Li, X.; Mo, H. Adaptive variable universe fuzzy sliding-mode control for robot manipulators with model uncertainty. IEEE J. Radio Freq. Identif. 2024, 8, 658–664. [Google Scholar] [CrossRef]
- Hajari, S.; Ray, O. A dynamic voltage-based current estimation technique for DC motor speed control applications. IEEE Sens. Lett. 2024, 8, 6001404. [Google Scholar] [CrossRef]
- Truong, H.T. Adaptive voltage control for DC motors of omnidirectional mobile robot with prevent wheel slippage. IEEE Access 2025, 13, 105220–105230. [Google Scholar] [CrossRef]
- Souzanchi-K, M.; Arab, A.; Akbarzadeh-T, M.R. Robust impedance control of uncertain mobile manipulators using time-delay compensation. IEEE Trans. Control Syst. Technol. 2018, 26, 1942–1953. [Google Scholar] [CrossRef]
| Notation | Definition | Notation | Definition | Notation | Definition |
|---|---|---|---|---|---|
| M | inertia matrix | angle for joint 1 | Y | movement of the end | |
| C | centripetal–Coriolis matrix | angle for joint 2 | Jacobian matrix | ||
| G | gravitational torque | g | the gravity | assistant variable | |
| q | real angle of joints | desired trajectory | assistant variable | ||
| torque for joint | motor moment | assistant variable | |||
| desired contact force | B | motor coefficient | N | assistant variable | |
| mass of 1st limb | motor rotation angle | constant matrix | |||
| mass of 2nd limb | frequency | real contact force | |||
| distance from joint to center of 1st limb | motor torque | desired movement of the end | |||
| distance from joint to center of 2nd limb | V | control voltage | constant matrix | ||
| distance from joint 1 to joint 2 | nonlinear model part | constant matrix | |||
| distance from the end to joint 2 | constant gain | constant matrix | |||
| moment of inertia of 1st limb | K | assistant variable | e | tracking error | |
| moment of inertia of 2nd limb | assistant variable | estimation of N | |||
| X | assistant variable | assistant variable | desired scale factor | ||
| compensation for TDE error | TDE error | control gain | |||
| K | output of control law | R | number of fuzzy rules | constant factor | |
| b | constant gain | c | constant gain | Lyapunov function | |
| Lyapunov function | assistant variable | assistant variable | |||
| t | scale factor | a | constant gain |
| Part | Mass (kg) | Motion Range (°) |
|---|---|---|
| Body Structure | 2.06 | |
| Joint 1 Motor Unit | 2.77 | |
| Joint 2 Motor Unit | 2.59 | |
| Electronics Assembly | 2.38 | |
| Motion Range of Joint 1 | −90° to 90° | |
| Motion Range of Joint 2 | −150° to 150° | |
| Total | 10.8 |
| Controllers | Tracking Error (°) | Contact Force (N) | ||
|---|---|---|---|---|
| MEAN (°) | MSE (°) | MEAN (N) | MSE (N) | |
| Impedance control (torque-based) [11] | 4.4 | 3.2 | 3.3 | 2.5 |
| Impedance control (voltage-based) [32] | 3.5 | 2.4 | 3.2 | 2.6 |
| ATDIC | 2.8 | 1.4 | 2.4 | 1.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pi, M. Adaptive Time Delay Impedance Control of Robot Manipulator via Voltage-Based Motor Control. Appl. Sci. 2025, 15, 10101. https://doi.org/10.3390/app151810101
Pi M. Adaptive Time Delay Impedance Control of Robot Manipulator via Voltage-Based Motor Control. Applied Sciences. 2025; 15(18):10101. https://doi.org/10.3390/app151810101
Chicago/Turabian StylePi, Ming. 2025. "Adaptive Time Delay Impedance Control of Robot Manipulator via Voltage-Based Motor Control" Applied Sciences 15, no. 18: 10101. https://doi.org/10.3390/app151810101
APA StylePi, M. (2025). Adaptive Time Delay Impedance Control of Robot Manipulator via Voltage-Based Motor Control. Applied Sciences, 15(18), 10101. https://doi.org/10.3390/app151810101





