Predictive Models for the Convective Drying Kinetics of Pinus spp. Energy Wood Chips
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Material
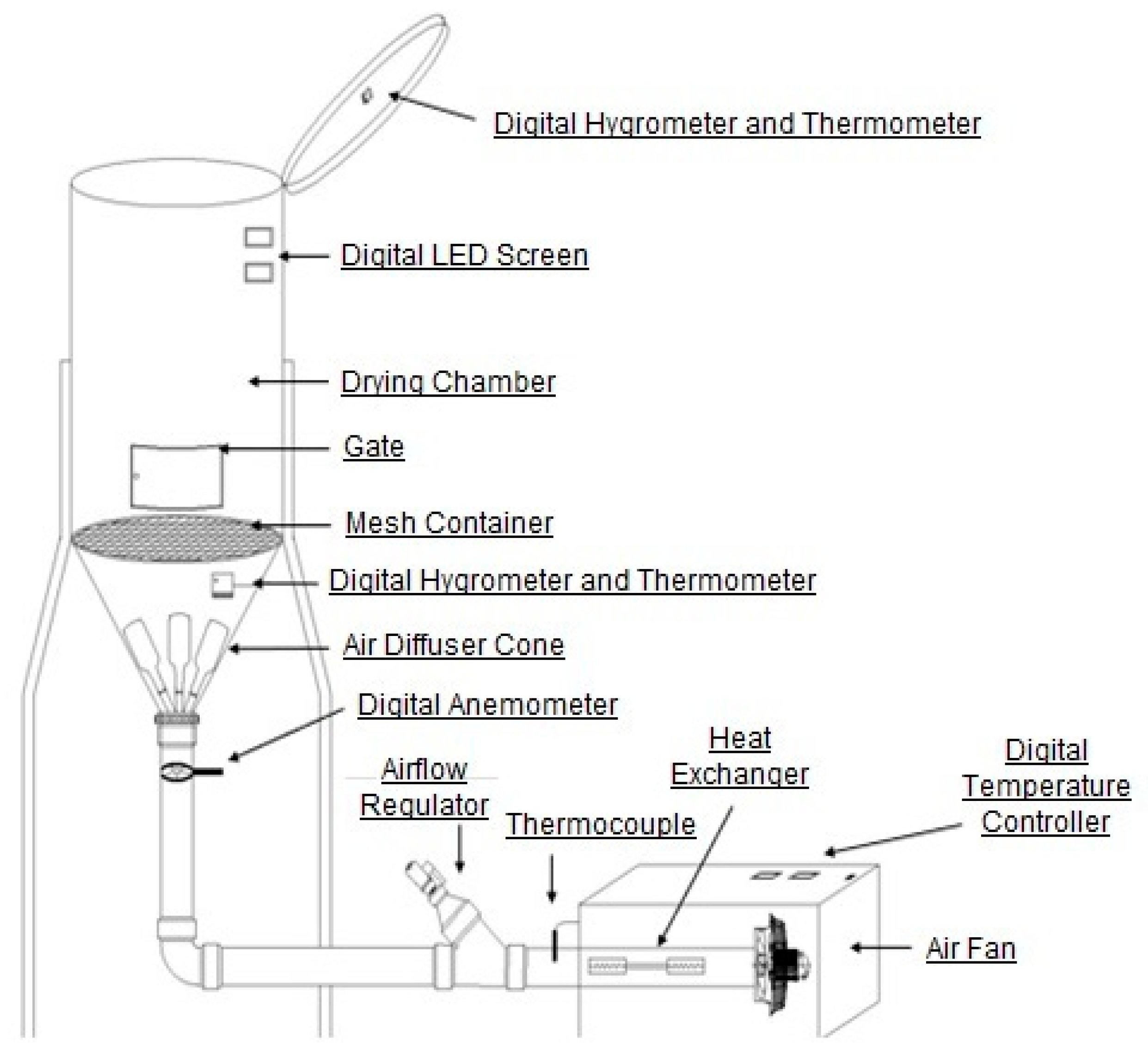
2.2. Experimental Device
2.3. Measurement Procedure
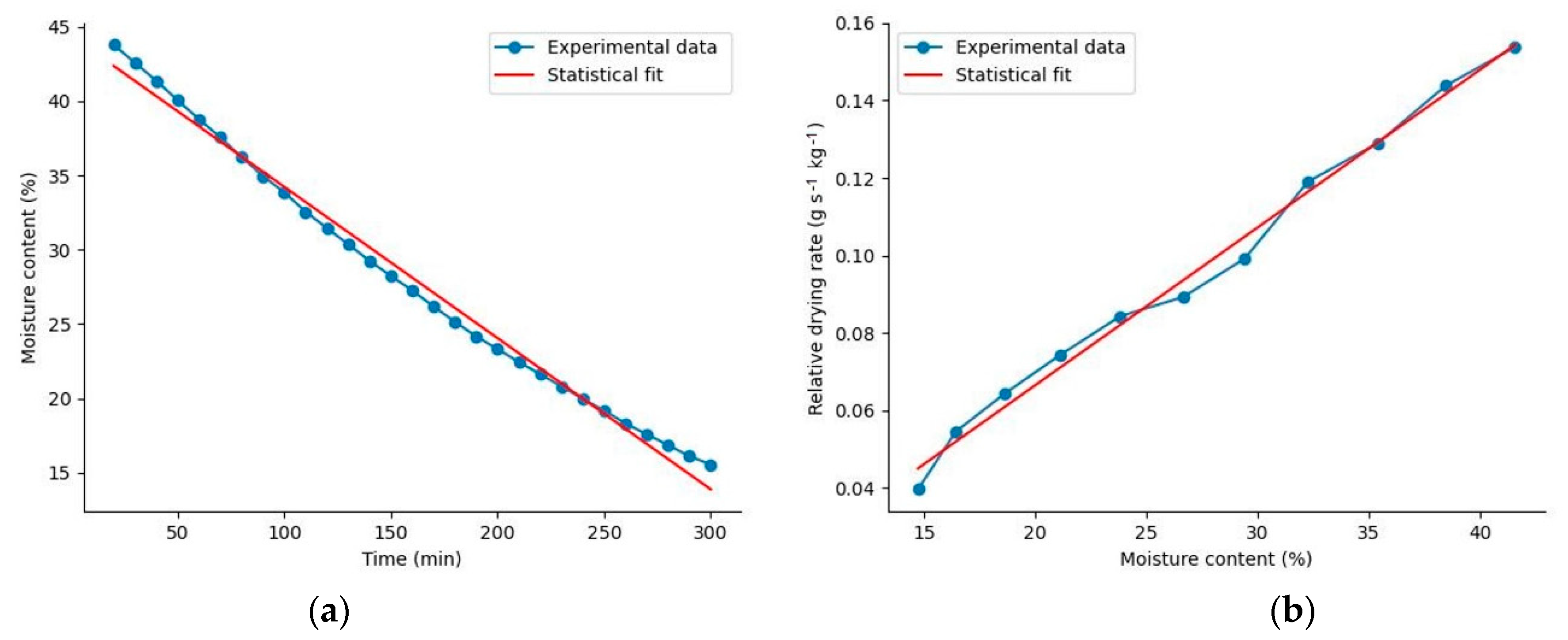
2.4. Characterization of the Drying Process
2.5. Calculation of Convective Mass Transfer
3. Results and Discussion
3.1. Statistical Description of the Measured Variables
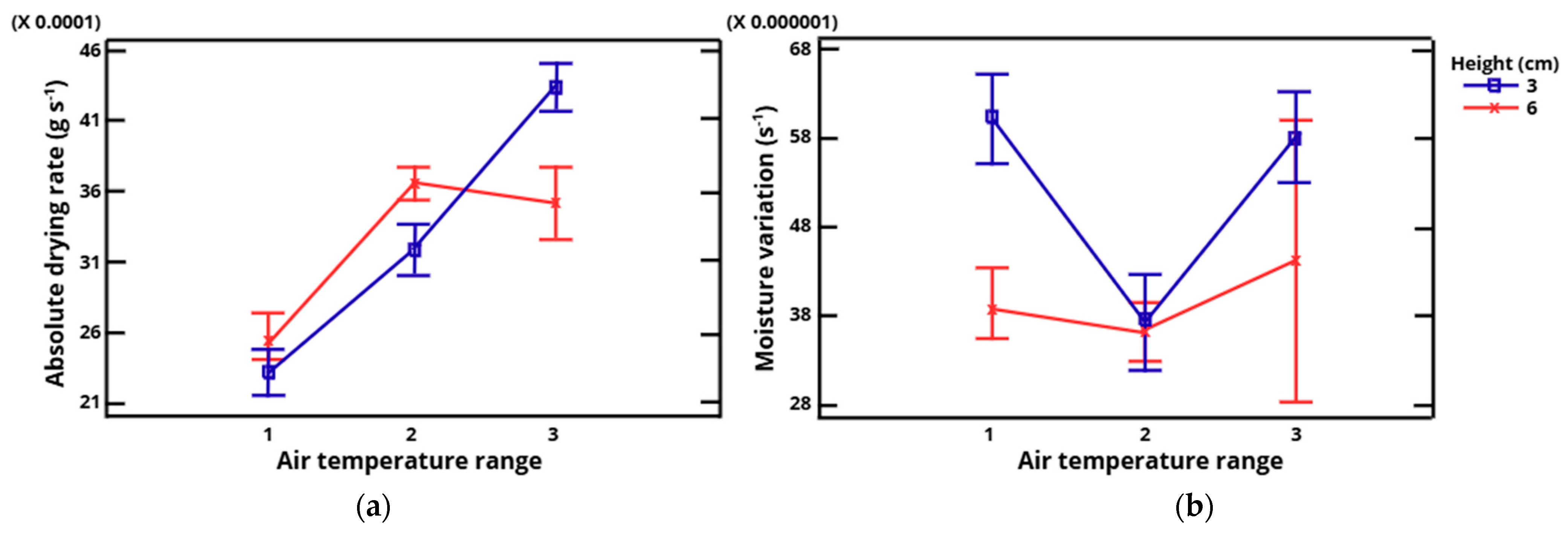
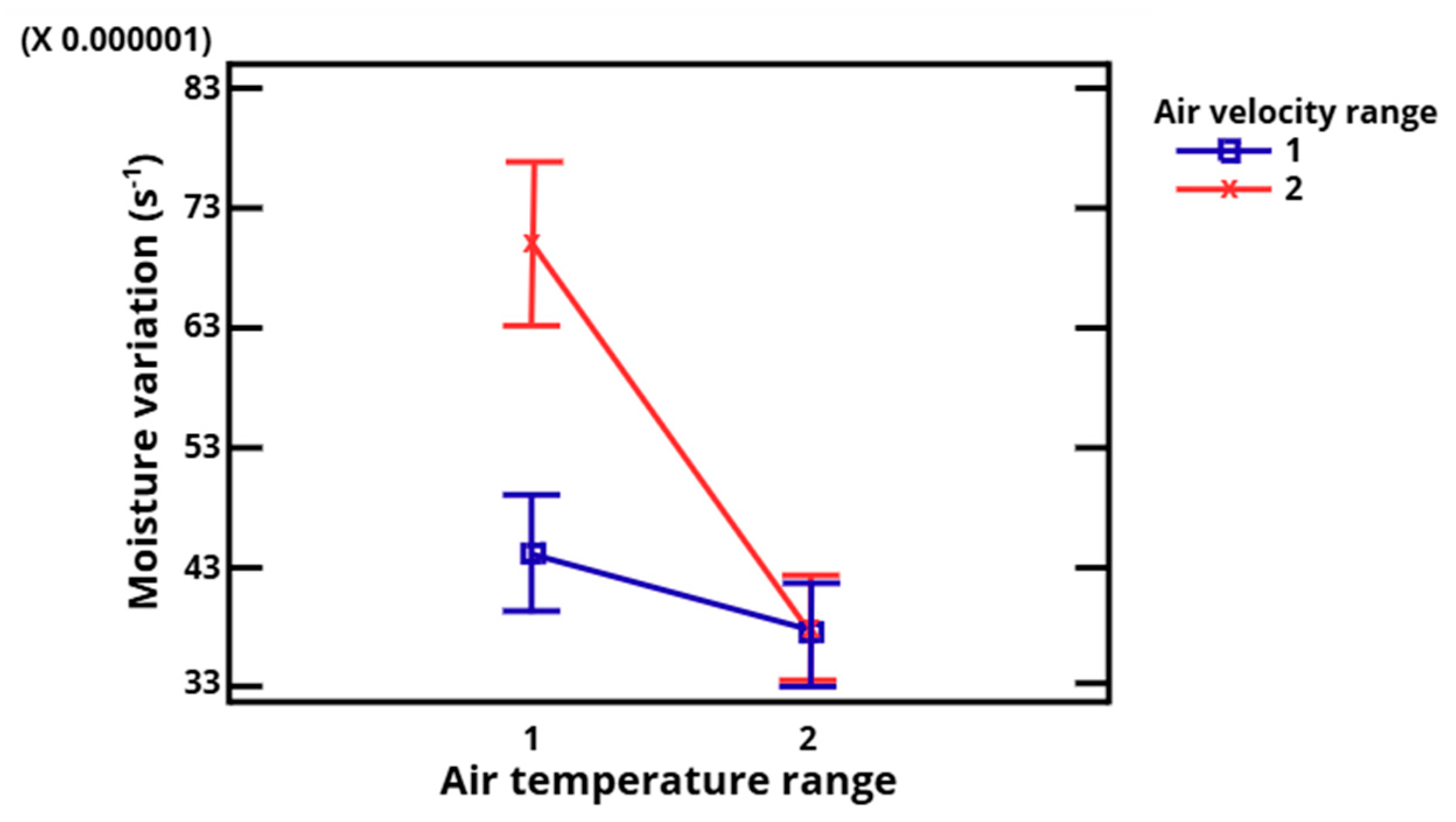
3.2. Analysis of the Interactions
3.3. Mass Transfer Models in the Prediction of Drying Rate
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Transfer area (m2) | Reynolds number | ||
| Biot number of the mass transfer process | Schmidt number | ||
| Mass diffusivity (m−2 s−1) | Schmidt number at the mass transfer surface | ||
| Diameter of the air supply tube before the diffuser cone (m) | Sherwood number | ||
| Diameter of the drying column (m) | Air temperature (°C) | ||
| Convective mass transfer coefficient (m−2 s−1) | Drying process time (s) | ||
| Wood chip column height (cm) | Air velocity (m s−1) | ||
| -Characteristic length (m) | Air velocity measured before its contact with the wood chips (m s−1) | ||
| Mean length of the chip (m) | Air velocity after passing through the bed of wood chips (m s−1) | ||
| Initial mass of the wood chips (g) | Greek symbols | ||
| Final mass of the wood chips (g) | |||
| Mass of the dry wood chips (kg) | Air density (kg m−3) | ||
| Average absolute drying rate (g of water s−1) | Dynamic viscosity (kg m−1 s−1) | ||
| Instantaneous absolute drying rate (g of water s−1) | |||
| Mass of water removed per unit of time (g s−1) | Average moisture variation (% s−1) | ||
| Average relative drying rate (g of water s−1 kg of dry wood chip−1) | Instantaneous moisture variation (% s−1) | ||
| Instantaneous relative drying rate (g of water s−1 kg of dry chip−1) | Absolute air humidity (kg of water kg of dry air−1) | ||
| Mass of wood chips at time (g) | Saturation absolute humidity (kg of water kg of dry air−1) | ||
| Mass of wood chips at time (g) | Air density (kg of dry air m−3) | ||
References
- Khamtree, S.; Ratanawilai, T.; Nuntadusit, C.; Marzbani, H. Experimental study and numerical modeling of heat and mass transfer in rubberwood during kiln drying. Heat Mass Transf. 2020, 57, 453–464. [Google Scholar] [CrossRef]
- Koukouch, A.; Bakhattar, I.; Asbik, M.; Idlimam, A.; Zeghmati, B.; Aharoune, A. Analytical solution of coupled heat and mass transfer equations during convective drying of biomass: Experimental validation. Heat Mass Transf. 2020, 56, 1971–1983. [Google Scholar] [CrossRef]
- Kuznetsov, G.V.; Syrodoy, S.V.; Nigay, N.A.; Maksimov, V.I.; Gutareva, N.Y. Features of the processes of heat and mass transfer when drying a large thickness layer of wood biomass. Renew. Energy 2021, 169, 498–511. [Google Scholar] [CrossRef]
- Sychevskii, V.A. Heat and Mass Transfer in Convective Wood-Drying Plants. J. Eng. Phys. Thermophys. 2018, 91, 705–711. [Google Scholar] [CrossRef]
- Callejón-Ferre, A.J.; Carreño-Sánchez, J.; Suárez-Medina, F.J.; Pérez-Alonso, J.; Velázquez-Martí, B. Prediction models for higher heating value based on the structural analysis of the biomass of plant remains from the greenhouses of Almería (Spain). Fuel 2014, 116, 377–387. [Google Scholar] [CrossRef]
- Velázquez-Martí, B. Aprovechamiento de la Biomasa Para Uso Energético, 2nd ed.; Reverté: Barcelona, Spain, 2017; ISBN 978-84-9048-675-7. [Google Scholar]
- Kamperidou, V. Quality Analysis of Commercially Available Wood Pellets and Correlations between Pellets Characteristics. Energies 2022, 15, 2865. [Google Scholar] [CrossRef]
- Konopka, A.; Barański, J.; Orłowski, K.A.; Mikielewicz, D.; Dzurenda, L. Mathematical model of the energy consumption calculation during the pine sawn wood (Pinus sylvestris L.) drying process. Wood Sci. Technol. 2021, 55, 741–755. [Google Scholar] [CrossRef]
- Mołczan, T.; Cyklis, P. Mathematical Model of Air Dryer Heat Pump Exchangers. Energies 2022, 15, 7092. [Google Scholar] [CrossRef]
- Mołczan, T.; Cyklis, P. Impact of the Evaporation Temperature on the Air Drying Rate for a Finned Heat Exchanger. Energies 2023, 16, 2132. [Google Scholar] [CrossRef]
- Mohan, V.P.C.; Talukdar, P. Design of an experimental set up for convective drying: Experimental studies at different drying temperature. Heat Mass Transf. 2013, 49, 31–40. [Google Scholar] [CrossRef]
- Chávez, C.A.; Moraga, N.O.; Salinas, C.H.; Cabrales, R.C.; Ananías, R.A. Modeling unsteady heat and mass transfer with prediction of mechanical stresses in wood drying. Int. Commun. Heat Mass Transf. 2021, 123, 105230. [Google Scholar] [CrossRef]
- Simo-Tagne, M.; Rémond, R.; Rogaume, Y.; Zoulalian, A.; Bonoma, B. Modeling of coupled heat and mass transfer during drying of tropical woods. Int. J. Therm. Sci. 2016, 109, 299–308. [Google Scholar] [CrossRef]
- Çengel, Y. Transferencia de Calor y Masa; Tercera, Ed.; McGraw-Hill Interamericana: New York, NY, USA, 2007; ISBN 9788578110796. [Google Scholar]
- Jalili, M.; Anca-Couce, A.; Zobel, N. On the uncertainty of a mathematical model for drying of a wood particle. Energy Fuels 2013, 27, 6705–6717. [Google Scholar] [CrossRef]
- Dedic, A.D. Modelling of coupled heat and mass transfer during convective drying of wood. Dry. Technol. 2002, 20, 1299–1301. [Google Scholar] [CrossRef]
- Tremblay, C.; Cloutier, A.; Fortin, Y. Experimental determination of the convective heat and mass transfer coefficients for wood drying. Wood Sci. Technol. 2000, 34, 253–276. [Google Scholar] [CrossRef]
- Skarbalius, G.; Džiugys, A.; Misiulis, E.; Navakas, R. A novel method for convective drying rate estimation in a deep fixed porous material bed. Powder Technol. 2022, 404, 117499. [Google Scholar] [CrossRef]
- Vorotinskienė, L.; Paulauskas, R.; Zakarauskas, K.; Navakas, R.; Skvorčinskienė, R.; Striūgas, N. Parameters influencing wet biofuel drying during combustion in grate furnaces. Fuel 2020, 265, 117013. [Google Scholar] [CrossRef]
- Bajwa, D.S.; Peterson, T.; Sharma, N.; Shojaeiarani, J.; Bajwa, S.G. A review of densified solid biomass for energy production. Renew. Sustain. Energy Rev. 2018, 96, 296–305. [Google Scholar] [CrossRef]
- UNE-EN ISO 17225-4; Especificaciones y Clases de Combustibles. Parte 4: Clases de Astillas de Madera. Spanish Association for Standardization and Certification: Madrid, Spain, 2014.
- UNE-EN ISO 18134-3; Determinación del Contenido de Humedad. Método de Secado en Estufa. Parte 3: Humedad de la Muestra Para Análisis General. Spanish Association for Standardization and Certification: Madrid, Spain, 2016.
- Coumans, W.J. Models for drying kinetics based on drying curves of slabs. Chem. Eng. Process. Process Intensif. 2000, 39, 53–68. [Google Scholar] [CrossRef]
- Kucuk, H.; Midilli, A.; Kilic, A.; Dincer, I. A Review on Thin-Layer Drying-Curve Equations. Dry. Technol. 2014, 32, 757–773. [Google Scholar] [CrossRef]
- Ananias, R.A.; Vallejos, S.; Salinas, C. Estudio de la cinética del secado convencional y bajo vacío del pino radiata. Maderas Cienc. Tecnol. 2005, 7, 37–47. [Google Scholar] [CrossRef]
- Inoue, T.; Iyota, H.; Nishimura, N.; Yoshida, M. Effect of Pore Size Distribution on Heat and Moisture Transfer in Porous Material for High Humidity Hot Air and Superheated Steam Drying. J. Jpn. Soc. Exp. Mech. 2009, 9, 54–59. [Google Scholar]
- Ananias, R.A.; Mougel, E.; Zoulalian, A. Introducing an overall mass-transfer coefficient for prediction of drying curves at low-temperature drying rates. Wood Sci. Technol. 2009, 43, 43–56. [Google Scholar] [CrossRef]
- Arabi, M.; Faezipour, M.M.; Layeghi, M.; Khanali, M.; Zareahosseinabadi, H. Evaluation of thin-layer models for describing drying kinetics of poplar wood particles in a fluidized bed dryer. Part. Sci. Technol. 2017, 35, 723–730. [Google Scholar] [CrossRef]
- Hosseinabadi, H.Z.; Doosthoseini, K.; Layeghi, M. Drying Kinetics of Poplar (Populus deltoides) Wood Particles by a Convective Thin Layer Dryer. Drv. Ind. 2012, 63, 169–176. [Google Scholar] [CrossRef]
- Sridhar, D.; Madhu, G.M. Drying kinetics and mathematical modeling of Casuarina equisetifolia wood chips at various temperatures. Period. Polytech. Chem. Eng. 2015, 59, 288–295. [Google Scholar] [CrossRef]
- Keey, R.; Langrish, T.A.G.; Walker, K.C.F. Kiln-Drying of Lumber, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2000; ISBN 978-3-642-64071-1. [Google Scholar]
- Ozollapins, M.; Kakitis, A.; Nulle, I. Stalk biomass drying rate evaluation. Eng. Rural Dev. 2013, 482–487. [Google Scholar]
- Grubecki, I. Airflow versus pressure drop for a mixture of bulk wood chips and bark at different moisture contents. Biosyst. Eng. 2015, 139, 100–110. [Google Scholar] [CrossRef]
- Kuptz, D.; Hartmann, H. Prediction of air pressure resistance during the ventilation of wood chips as a function of multiple physical fuel parameters. Biomass Bioenergy 2021, 145, 105948. [Google Scholar] [CrossRef]
- Bengtsson, P. Experimental analysis of low-temperature bed drying of wooden biomass particles. Dry. Technol. 2008, 26, 602–610. [Google Scholar] [CrossRef]
- Phanphanich, M.; Mani, S. Drying characteristics of pine forest residues. BioResources 2009, 5, 108–120. [Google Scholar] [CrossRef]
- Cota-Espericueta, A.D.; Ponce-Corral, C. Eliminación de bacterias patógenas en lodos residuales durante el secado solar. Rev. Int. Contam. Ambient. 2008, 24, 161–170. [Google Scholar]
- Ståhl, M.; Granström, K.; Berghel, J.; Renström, R. Industrial processes for biomass drying and their effects on the quality properties of wood pellets. Biomass Bioenergy 2004, 27, 621–628. [Google Scholar] [CrossRef]
- Klavina, K.; Cinis, A.; Zandeckis, A. Experimental Study on the Effects of Air Velocity, Temperature and Depth on Low-temperature Bed Drying of Forest Biomass Residue. Energy Procedia 2015, 72, 42–48. [Google Scholar] [CrossRef]
- Ahmadinia, S.; Palviainen, M.; Kiuru, P.; Routa, J.; Sikanen, L.; Urzainki, I.; Laurén, A. Forest chip drying in self-heating piles during storage as affected by temperature and relative humidity conditions. Fuel 2022, 324, 124419. [Google Scholar] [CrossRef]
- Lerman, P.; Wennberg, O. Experimental method for designing a biomass bed dryer. Biomass Bioenergy 2011, 35, S31–S39. [Google Scholar] [CrossRef]
- Ndukwu, M.C. Effect of Drying Temperature and Drying Air Velocity on the Drying Rate and Drying Constant of Cocoa Bean. Agric. Eng. Int. CIGR J. 2009. [Google Scholar]
- Pari, L.; Brambilla, M.; Bisaglia, C.; Del Giudice, A.; Croce, S.; Salerno, M.; Gallucci, F. Poplar wood chip storage: Effect of particle size and breathable covering on drying dynamics and biofuel quality. Biomass Bioenergy 2015, 81, 282–287. [Google Scholar] [CrossRef]
- Rezaei, H.; Jim Lim, C.; Lau, A.; Bi, X.; Sokhansanj, S. Development of Empirical Drying Correlations for Ground Wood Chip and Ground Wood Pellet Particles. Dry. Technol. 2017, 35, 1423–1432. [Google Scholar] [CrossRef]
- Tenorio, C.; Moya, R.; Cubero, R. Difusión del agua en astillas de madera de diez especies de rápido crecimiento en plantaciones en costa rica. Interciencia 2014, 39, 129–135. [Google Scholar]
- Anerud, E.; Larsson, G.; Eliasson, L. Storage of wood chips: Effect of chip size on storage properties. Croat. J. For. Eng. 2020, 41, 277–286. [Google Scholar] [CrossRef]
- Pecenka, R.; Lenz, H.; Idler, C. Influence of the chip format on the development of mass loss, moisture content and chemical composition of poplar chips during storage and drying in open-air piles. Biomass Bioenergy 2018, 116, 140–150. [Google Scholar] [CrossRef]

| Airflow (m s−1) | Temperature (°C) | Height (cm) | |||
|---|---|---|---|---|---|
| 6.93–8.46 | 40.10–48.84 | 3 | |||
| 48.84–57.58 | |||||
| 8.46–9.99 | 6 | ||||
| 57.58–66.32 | |||||
| Parameter | Factor | Mean | Standard Deviation | Minimum | Maximum | Standardized Skewness | Standardized Kurtosis | |
|---|---|---|---|---|---|---|---|---|
(g of water s−1 kg of dry chip−1) | Height | 0.063 | 0.015 | 0.034 | 0.104 | 0.61 | −1.46 | |
| 0.040 | 0.010 | 0.023 | 0.066 | 1.72 | −1.15 | |||
| Air velocity | 0.046 | 0.010 | 0.023 | 0.066 | 1.29 | −0.38 | ||
| 0.057 | 0.017 | 0.028 | 0.104 | 1.71 | −1.35 | |||
| Air temperature | 0.041 | 0.010 | 0.023 | 0.064 | 0.96 | −1.33 | ||
| 0.058 | 0.012 | 0.034 | 0.084 | 1.62 | −0.09 | |||
| 0.055 | 0.019 | 0.028 | 0.104 | −1.22 | −0.73 | |||
(g of water s−1) | Height | 0.0031 | 0.0009 | 0.0019 | 0.0058 | 2.82 | −0.18 | |
| 0.0032 | 0.0008 | 0.0016 | 0.0055 | 1.65 | −0.48 | |||
| Air velocity | 0.0028 | 0.0005 | 0.001 | 0.004 | 0.83 | −1.75 | ||
| 0.0035 | 0.0008 | 0.002 | 0.005 | 1.41 | −1.17 | |||
| Air temperature | 0.0024 | 0.0003 | 0.0016 | 0.0032 | 0.85 | −0.73 | ||
| 0.0035 | 0.0006 | 0.0022 | 0.0055 | 1.55 | −0.28 | |||
| 0.0036 | 0.0008 | 0.0025 | 0.0058 | 1.03 | −1.01 | |||
(% of water s−1) | Height | 0.0024 | 0.0008 | 0.00013 | 0.0047 | 2.53 | −1.58 | |
| 0.0017 | 0.0004 | 0.0008 | 0.0027 | 0.89 | −1.12 | |||
| Air velocity | 0.0019 | 0.0004 | 0.0008 | 0.0030 | 2.77 | 1.58 | ||
| 0.0022 | 0.0007 | 0.0010 | 0.0041 | 3.58 | 0.04 | |||
| Air temperature | 0.0016 | 0.0004 | 0.0008 | 0.0028 | 1.94 | −0.90 | ||
| 0.0022 | 0.0003 | 0.0011 | 0.0030 | 2.87 | 0.89 | |||
| 0.0024 | 0.0008 | 0.0018 | 0.0041 | 1.46 | −1.76 | |||
(g of water s−1 kg of dry chip−1 %−1) | Height | 0.0028 | 0.0009 | 0.0013 | 0.0051 | 1.24 | −1.75 | |
| 0.0022 | 0.0007 | 0.0011 | 0.0040 | 1.73 | −1.15 | |||
| Air velocity | 0.0021 | 0.0004 | 0.0011 | 0.0031 | 1.45 | −0.57 | ||
| 0.0029 | 0.0008 | 0.0013 | 0.0051 | 1.11 | −0.88 | |||
| Air temperature | 0.0019 | 0.0005 | 0.0011 | 0.0030 | 2.00 | −0.88 | ||
| 0.0027 | 0.0006 | 0.0013 | 0.0042 | 1.64 | −0.79 | |||
| 0.0030 | 0.0008 | 0.0016 | 0.0051 | −0.43 | −0.86 | |||
(g of water s−1 %−1) | Height | 0.00013 | 0.00004 | 0.00005 | 0.00029 | 3.84 | 1.94 | |
| 0.00018 | 0.00006 | 0.00008 | 0.00034 | 2.94 | −0.50 | |||
| Air velocity | 0.00013 | 0.00003 | 0.00005 | 0.00023 | 1.77 | −0.72 | ||
| 0.00018 | 0.00006 | 0.00008 | 0.00034 | 2.28 | −1.19 | |||
| Air temperature | 0.00011 | 0.00002 | 0.00007 | 0.00018 | 1.14 | 0.75 | ||
| 0.00017 | 0.00005 | 0.00005 | 0.00031 | 1.93 | −0.09 | |||
| 0.00019 | 0.00006 | 0.00013 | 0.00034 | 1.46 | −0.35 | |||
(s−1) | Height | 0.000049 | 0.00002 | 0.00002 | 0.00014 | 3.45 | 0.12 | |
| 0.000041 | 0.00001 | 0.00002 | 0.00009 | 4.61 | 2.64 | |||
| Air velocity | 0.000040 | 0.00002 | 0.00002 | 0.00009 | 3.77 | 0.61 | ||
| 0.000049 | 0.00002 | 0.00002 | 0.00011 | 3.58 | 0.10 | |||
| Air temperature | 0.000052 | 0.00002 | 0.00002 | 0.00010 | 0.85 | −1.83 | ||
| 0.000038 | 0.00001 | 0.00002 | 0.00008 | 2.06 | 0.57 | |||
| 0.000043 | 0.00001 | 0.00002 | 0.00009 | 2.01 | 0.87 |
| Parameter | Factors | Interactions | ||||
|---|---|---|---|---|---|---|
| Height | Air Velocity | Air Temperature | ||||
| 0.063 ± 0.015 a 0.040 ± 0.010 b | V1 0.046 ± 0.010 b V2 0.057 ± 0.017 a | T1 0.041 ± 0.010 b T2 0.058 ± 0.012 a T3 0.055 ± 0.019 a | No interaction | No interaction | No interaction | |
| 0.0031 ± 0.0009 a 0.0032 ± 0.0008 a | V1 0.0028 ± 0.0005 b V2 0.0035 ± 0.0008 a | T1 0.0024 ± 0.0003 b T2 0.0035 ± 0.0006 a T3 0.0036 ± 0.0008 a | No interaction | Interaction p = 0.0001 | No interaction | |
| 0.0024 ± 0.0008 a 0.0017 ± 0.0004 b | V1 0.0019 ± 0.0004 b V2 0.0022 ± 0.0007 a | T1 0.0016 ± 0.0004 c T2 0.0022 ± 0.0003 b T3 0.0024 ± 0.0008 a | No interaction | No interaction | No interaction | |
| 0.0028 ± 0.0009 a 0.0022 ± 0.0007 b | V1 0.0021 ± 0.0004 b V2 0.0029 ± 0.0008 a | T1 0.0019 ± 0.0005 c T2 0.0027 ± 0.0006 b T3 0.0030 ± 0.0008 a | No interaction | No interaction | No interaction | |
| 0.00013 ± 0.00004 b 0.00018 ±0.00006 a | V1 0.00013 ± 0.00003 b V2 0.00018 ± 0.00006 a | T1 0.00011 ± 0.00002 c T2 0.00017 ± 0.00005 b T3 0.00019 ± 0.00006 a | No interaction | No interaction | No interaction | |
| 0.000049 ± 0.00002 a 0.000041 ± 0.00001 b | V1 0.000040 ± 0.00002 b V2 0.000049 ± 0.00002 a | T1 0.000052 ± 0.00002 a T2 0.000038 ± 0.00001 b T3 0.000043 ± 0.00001 ab | No interaction | Interaction p = 0.02 | Interaction p = 0.0007 | |
| Parameter | Height | Model | R2 | Adjusted R2 | MAE | RMS |
|---|---|---|---|---|---|---|
| General | 57.11 | 56.87 | 0.0084 | 0.0101 | ||
| 64.03 | 63.51 | 0.0068 | 0.0085 | |||
| 59.87 | 59.43 | 0.0055 | 0.0067 | |||
| General | 80.36 | 80.22 | 0.00031 | 0.00037 | ||
| 86.20 | 86.00 | 0.00030 | 0.00035 | |||
| 71.16 | 70.77 | 0.00031 | 0.00038 | |||
| General | 47.06 | 46.71 | 0.00025 | 0.00029 | ||
| 68.52 | 67.44 | 0.00011 | 0.00013 | |||
| 57.17 | 56.77 | 0.00022 | 0.00026 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Núñez-Retana, V.D.; Carrillo-Parra, A.; Escobar Machado, J.A.; Moposita-Vasquez, D.-D.; Velázquez-Martí, B. Predictive Models for the Convective Drying Kinetics of Pinus spp. Energy Wood Chips. Appl. Sci. 2025, 15, 10081. https://doi.org/10.3390/app151810081
Núñez-Retana VD, Carrillo-Parra A, Escobar Machado JA, Moposita-Vasquez D-D, Velázquez-Martí B. Predictive Models for the Convective Drying Kinetics of Pinus spp. Energy Wood Chips. Applied Sciences. 2025; 15(18):10081. https://doi.org/10.3390/app151810081
Chicago/Turabian StyleNúñez-Retana, Víctor Daniel, Artemio Carrillo-Parra, José Antonio Escobar Machado, Diego-David Moposita-Vasquez, and Borja Velázquez-Martí. 2025. "Predictive Models for the Convective Drying Kinetics of Pinus spp. Energy Wood Chips" Applied Sciences 15, no. 18: 10081. https://doi.org/10.3390/app151810081
APA StyleNúñez-Retana, V. D., Carrillo-Parra, A., Escobar Machado, J. A., Moposita-Vasquez, D.-D., & Velázquez-Martí, B. (2025). Predictive Models for the Convective Drying Kinetics of Pinus spp. Energy Wood Chips. Applied Sciences, 15(18), 10081. https://doi.org/10.3390/app151810081








