A Method for Assessing the Performance of Breaking Hammers Based on Acoustic Signal and Video Analysis

Abstract

Mining is a branch of industry that continuously implements new technologies to optimise processes, in terms of increasing performance and decreasing the negative impact on the environment. To enhance the efficiency of the rock material fragmentation process, it is proposed to replace the existing hydraulic hammer with a fully electric alternative. This study used simple data-acquisition methods, including acoustic signals, vibrations, electric currents, and video recordings, to compare the efficiency of both hammers. Measurements were taken for hydraulic and electric hammers under comparable conditions, using the same boom, operator, and rock material. Two methodologies are proposed: the first one is based on acoustic data measurement and parametrisation, and the second one, for validation purposes, is based on visual (video) data analysis. The acoustic approach analyses the stability parameter ($\alpha$) of the $\alpha$-stable distribution, the shape parameter ($\nu$) of the t Location–Scale distribution that can assess signal impulsiveness, and three additional basic parameters (number of peaks, sum of amplitudes of impulses, and duration of the cycle for each truck/loader). The visual approach, used for validation, detects individual rock sizes and roughly evaluates the number of oversized pieces. However, it is a manual approach, due to challenging conditions. The results of both methods demonstrate that the electric hammer is more than three times more efficient. This increased efficiency is attributable to adaptive impact frequency control, a feature that is unavailable in hydraulic hammers.

1. Introduction

There are many methods of mechanical excavation of rocks, such as excavating using crawler rippers, rotary hammers, vibratory rippers, or grinding heads [1]. Drilling with various methods is used for the exploration and exploitation of deep resources [2] or to prepare holes for explosive charges for the drilling and blasting technique [3]. Machines consisting of a rotating cutting wheel in front, called a cutter head, followed by a main bearing, a thrust system, a system to remove excavated material (muck), and support mechanisms named TBMs (Tunnel-Boring Machines) are used for tunnelling purposes [4]. Rock fragmentation operations are very energy-consuming and produce excessive noise and dust [5,6]. Due to the high energy consumption, opportunities are sought to optimise processes based on the mechanical fragmentation of rocks to ensure better performance in the exploration and exploitation of natural resources. Increasing the performance of rock fragmentation is particularly important when the energy used for this purpose comes from conventional sources. Reducing the level of energy used allows for decreasing the negative impact of mining on the natural environment.

Many examples of studies aimed at optimising rock fragmentation in mining and tunnelling can be found in the literature. In [7], the authors characterised the rock-breaking performance of PDC cutters in FDEM simulations using two metrics: the Stability Index (SI) and Mechanical Specific Energy (MSE). The results show that metrics are crucial in the optimisation of cutter performance; that is, balancing SI and MSE is essential to achieve optimal drilling efficiency and cutter stability. A similar numerical analysis of rock-breaking mechanisms and the factors that influence different PDC cutters is presented in [8]. The results provide insights for optimising drilling cutters and engineering parameters for efficient rotary percussion drilling. In work [9], a study of rock-breaking parameters was carried out on a rotary drilling test rig, which allowed the development of optimal parameters for multi-nozzle jet drill bits and rotational rock breaking. In contrast, a study of rock-breaking parameters for Tunnel-Boring Machines (TBMs) in [10] provided insight into tunnelling efficiency and safety.

Heavy-duty machines such as Load Haul Dump vehicles (LHDs) or Haul Trucks (HTs) are used in underground mining of ores with “room-and-pillar” technology [11]. This technological process includes scheduled ore extraction using the blasting technique, loading, and transportation by LHDs and HTs to the dumping points of belt conveyors for further transportation. As shown in [12,13], under non-stationary rock loading/unloading regimes, diesel-powered vehicles produce large amounts of heat, NOx, and other harmful gases, creating a hazardous environment in the miner’s workplace.

Recent developments and massive production of electric machines have informed a global trend in industrial facilities modernisation toward ubiquitous electrification and digitisation, allowing sustainable development. Changing the drives used so far to electric ones may be beneficial in the mining industry, particularly due to the hazards that occur, but also in terms of process optimisation.

One of the actions taken in this regard is the prospect of replacing the hydraulic hammers used in underground mining to break rocks with fully electric hammers. Ore dumping points are currently equipped with hydraulic manipulators that carry the hydraulic hammers used to break oversized ore pieces and prevent belt conveyor failures. The scheme of this process is shown in Figure 1. A competitive solution was proposed by the Finnish company Lekatech, which has developed the Lekatech Electric Hammer (LEH) based on a linear electric motor [14] with permanent magnets as the hammer drive mechanism [15]. The ECHO project (Electrical Computerised Hammering Operator), funded by EIT RawMaterials, aims to optimise the design and improve the control of the rock-breaking process.

The short time intervals between the arrival of LHDs and HTs at dump points require quick processing of subsequent portions of rock pieces on the grizzly screen. As the change of the working parameters of hydraulic hammers is limited, in some cases, loaders and trucks must wait for unloading. Since almost 15% of the mined material is initially considered too large for further transport [16], increasing the throughput of the ore through a grizzly screen can lead to an improvement in the transportation process. One way to solve the technological bottleneck may be to implement electric hammers, which are declared to operate with lower energy consumption, increased blow impact energy, reduced oil consumption, and the ability to adjust operating parameters [17]. The design and performance analysis of a long-stroke electromagnetic double-reel hammer was fulfilled in [18]. The results indicate greater impact energy and higher speed, lower energy losses, and higher efficiency per cycle for the electric hammer compared to a conventional hydraulic hammer. However, for the specific use case of underground ore mining, the comparison requires additional analysis.

This paper presents the results of the performance investigation of an electric hammer and its existing hydraulic counterpart under real working conditions. Measurements were performed on both hammers installed on the same manipulator under the same conditions. Performance evaluation was based on acquired audio signals. The general performance of the hammer was characterised by the time and the number of impacts per single loader/truck, which were estimated from the obtained audio signals. Then, it was validated by measurements of vibration data, current consumption, and video sequence. In addition, the visual data served the purpose of a rough classification of the size of the processed rock.

The novelty of the paper is related to the methodology of acoustic-based comparison of two machines performing the same process. Simple and objective indicators are proposed, indicating that the introduced modification of the machine (electric instead of hydraulic hammer) may improve the efficiency of the process in terms of duration of the cycle and number of impacts per cycle.

The paper is organised as follows. Firstly, since the research problem is specific, the results of the literature analysis are presented; then, our experiments and the proposed methodology for data processing, with a necessary description of the theoretical aspects, are described. The next section consists of the results of the analysis and validation that finally conclude the paper.

2. State of the Art

Breaking hammers are an example of mining machines that are difficult to automate, as they are characterised by many parameters (frequency, force, and energy of impact), most of which can be optimised in real-time. For comparison purposes, usually a set of factors is defined that has a direct impact on the performance of the rock-breaking process [19]. There are several different approaches to the analysis of the hammer performance. Usually, the proposed parameters are based on a prediction of the net cutting rate (NCR), the net breaking rate (NBR), and the total net excavation (NE), an example of which can be found in the comparative study between the road-header and the breaking hammer, together with the distinction between the drilling and blasting methods [20]. This study was based on data obtained from the case of the excavation of a metro station in Istanbul, with the calculation formulas for the parameters established in [21,22,23]. In addition, machine learning has been extensively researched and applied in the prediction of net excavation parameters. Some examples are adaptive neuro-fuzzy inference system (ANFIS) models [19,24], reinforced learning with Duelling Double Deep-Q Networks [25], multi-layer perceptron (MLP), support vector machine (SVM), and k-nearest neighbours (KNNs) algorithms [26,27].

In [28], the authors applied mathematical models to optimise the performance of the percussive drilling system. Related design variables were identified through simulation, verified by results obtained during specified lab tests, and optimised using the progressive quadratic response surface method (PQRSM). In [29], the authors designed a numerical model of rock breaking performed by a hydraulic splitter to identify factors that influence the crack formation process.

For a direct comparison of two devices (electric and hydraulic hammer), auxiliary parameters can be used that ensure reference to similar quantities of processed material. First, it is worth identifying the need for breaking by detecting oversizes according to the method proposed in [30] and counting the number of pieces necessary to carry out the breaking action, together with the value of the energy used. Since the size of individual oversizes brought by individual LHDs / HTs can be different, this approach may not be sufficient. Another possible approach is to use the volume information on the material unloaded by each of the LHDs/HTs. In the mining industry, LiDAR systems are the technology mainly used in the volume calculations task, where excavated material is scanned before and after ore removal [31].

However, since not all materials require processing with a breaking hammer, only the volume assessment of the oversized rock pieces should be considered. In [32], the authors proposed a methodology for estimating rock volume based on the use of laser scanning data with oversized rock segmentation performed on visual data from cameras. After obtaining the point cloud representing the rock shape, various methods of spatial volume calculation can be applied, such as voxels or slice methods [33]. Laser scanning data are also used in other breaking hammer-related tasks, such as automating the rock-breaking process [34,35].

This paper proposes a method for the performance evaluation of hammer operations using an acoustic signal. It is a contactless measurement method that can be performed from a safe position and does not require the installation of a sensor on the moving part of the hammer or the whole manipulator (boom). Acoustic signals have already been used in the mining industry for different applications—for example, in rotating idlers monitoring on belt conveyors [36,37,38,39] or inspection of roof-bolt housings [40].

Rock breaking produces an impulsive acoustic signal that requires specific parametrisation methods. Simple statistical features can be used (peak amplitude, peak-to-peak, impulse factor, kurtosis, etc.). However, more advanced techniques require the modelling of distributions. The $\alpha$-stable distribution has been used for such purposes [41,42]. Recently, Skowronek et al. [43] also analysed the possibility of using t Location–Scale distribution to describe impulsive noise properties. Both distributions are useful here, as in the presence of non-Gaussian heavy-tailed noise their parameters will indicate the level of impulsiveness. In cases of a lack of impulses, when the signal becomes close to Gaussian, the mathematical description of these distributions also reduces to a Gaussian distribution. The proposed methods can therefore be used for both Gaussian and non-Gaussian signals.

It is worth mentioning that, inspired by [44], the authors compared time series from various sources—namely, the acoustic signal recorded, the vibration signal, and the electric current consumed by the hammer during operation.

3. Data Acquisition

The object of the measurements was a rock-breaking station in an underground mining facility located in Poland. At the site, during the experiments, the material was delivered by HTs and/or LHDs directly onto the grizzly screen. Both hydraulic and electric hammers (Figure 2) were tested at the same dumping point and hydraulic boom.

The main parameters of the hydraulic manipulator, the hydraulic hammer, and the electric hammer are given in

Table 1. Parameters of the hydraulic manipulator [45].

Parameter	Value
Height min	5.0 m
Width min	6.0 m
Length min	10.0 m
Boom reach	4.7 m
Boom turning angle	±40 grad
Total weight (with hammer)	±7000 kg

,

Table 2. Parameters of the hydraulic hammer [45].

Parameter	Value
Total weight	520 kg
Impact rate, constant	4 Hz
Impact energy	400 ÷ 1900 J
Working pressure	10 ÷ 17 MPa
Hydraulic oil flow	20 ÷ 120 L/min

, and

Table 3. Parameters of the electric hammer [46].

Parameter	Value
Total weight (tool and mounting)	540 kg
Impact rate, adjustable	1 ÷ 15 Hz
Impact energy	300 ÷ 1500 J
Input power	18 kW

, respectively.

In the experiments, sets of data from different sources were measured: vibration data from a wireless NG IMU sensor (see Figure 3a and

Table 4. Parameters of NG IMU sensor [47].

Parameter	Value
Triple-axis gyroscope	±2000°/s, 400 Hz sample rate
Triple-axis accelerometer	±16 g, 400 Hz sample rate
Triple-axis magnetometer	±1300 µT
Barometric pressure	300–1100 hPa
Humidity	-
Temperature	-
Battery parameters	-
Analogue inputs	8 channels, 0–3.1 V, 10-bit, 1 kHz sample rate
Auxiliary serial	RS-232 compatible
Real-time clock	-

); acoustic data from a Bruel & Kjaer 4188 microphone with a Type 2671 pre-amplifier for sound recording (see Figure 3b and

Table 5. Parameters of Bruel & Kjaer 4188 microphone with Type 2671 pre-amplifier [48].

Parameter	Value
Frequency range	6.3–20 000 Hz
Dynamic range	14.6–146 dB
Lower limiting frequency -3dB	4 Hz
Sensitivity	50 mV/Pa

); electric current measurement with Fluke i400s AC current clamps (see Figure 4a and

Table 6. Parameters of Fluke i400s AC current clamp on the 400A range [49].

Parameter	Value
Nominal current range	5–400 A
Basic accuracy	2% + 0.04 A
Output level	1 mV/A

); and video data from a GoPro Hero 12 camera (see Figure 4b and

Table 7. GoPro Hero 12 [50] parameters set during measurements.

Parameter	Value
Resolution	3840 × 2160 px A
Frame rate	30 fps
Audio sample rate	48 kHz

).

Current and audio measurements were recorded via the Kistler LabAmp type 5165A charge amplifier with data acquisition software (see Figure 3c). Due to technical limitations (such as accessibility to the power grid), not all types of data were recorded during each of the measurement sessions. Since the audio and video recordings did not fall under any restrictions, the presented methodology focused on audio data analysis. The comparison of additional data between audio and different data sources proved the applicability of the algorithm to vibration and current measurements, while the video data allowed the obtained results to be verified by incorporating the information on the size of the individual rock pieces into the calculations.

The measurement equipment was placed near the operator’s cabin (see Figure 2b). The experiment took place in three measurement sessions (days), two of them with the hydraulic hammer attached to the hydraulic boom placed at the station, and one measurement day on the electric hammer mounted on the same hydraulic boom at the same mining site. The same cutting tools were used for both hammers. Although the same operator was present on the site for all the experiments, his daily physical and psychological capabilities—the so-called human factor—were not measured and were not taken into account in the analysis, which potentially had an impact on the results. The influence of the difference in every transport loading rate was minimised due to the averaging of the results obtained and the approach in the second part of the methodology, where the size of individual oversized rock pieces was taken into account.

4. Methodology

The proposed methodology is based on acoustic signal analysis. M signals are acquired for M cycles. More cycles provide more stable statistical results. Each cycle is analysed separately according to the flowchart presented in Figure 5. The acquired acoustic signal should be parametrised, i.e., some features should be extracted to describe the required information. As impact-related impulses are sought, two paths are proposed. The first one, intuitive, is based on peak detection. Then, two other features are proposed: the number of peaks and the sum of amplitudes of these peaks. A more advanced approach is related to statistical distribution using random processes theory. It is assumed that in a case of the presence of some oversized pieces in the cycle, their fragmentation by hammer will produce mechanical impacts (the hammer chisel will hit the rock), producing impulsive noise. To describe such signal distributions, $\alpha$-stable and t Location–Scale are suitable. The crucial parameters of these distributions are estimated: the stability index $\alpha$ and the number of degrees of freedom $\nu$. Finally, the duration of each cycle is measured, and this is the fifth parameter used for performance measurement and comparison.

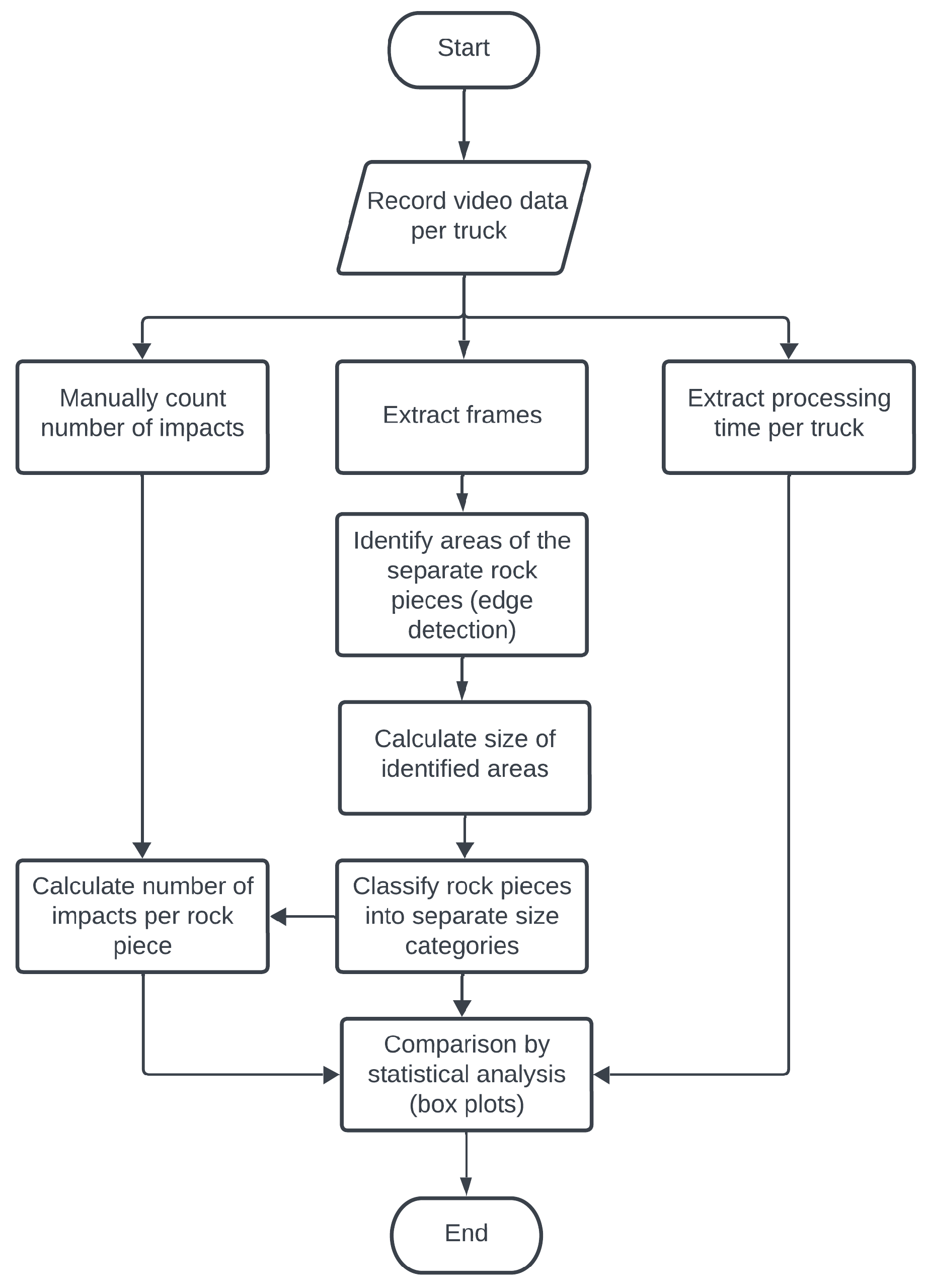
The second procedure is developed additionally to validate the main results and to enhance the results of parameters $P4$ and $P5$, providing a context that describes the granulation of the provided copper ore (Figure 6). A video sequence is used. First, expert manual evaluation is applied to check if the obtained results are the same, in terms of the number of impacts. Second, frames from the video are extracted and, using simple algorithms for object detection and area measurement, the size of the oversized rock pieces is roughly estimated to classify them as small, medium, or large. Such a rough description allows sound-based results presentation in the context of the class of delivered granulation of the ore. In the next section, each step of the methodology is discussed in detail.

4.1. Sound-Based Estimation of Oversized Rock Content in Haulage Truck

This section describes the method used to estimate the amount of oversized rocks in the material hauled to the dumping point. This estimation relies on two key assumptions:

• The volume of the material transported in a haul truck bucket is comparable for every transport (for each truck/loader in the considered shifts). To further reduce the estimation error originating from this assumption, the top surface of the bucket can be scanned and the volume can be precisely calculated, which will serve as a normalisation parameter for the estimation. This is essential if various haul trucks with different payload capacities are used in a given area. The problem does not occur when only one type of hauling machine is used, since the estimation is carried out per machine, not per unit of volume.
• Estimation is made based on the presence of hammer impacts in the acoustic signal. Hence, it is assumed that the loose material falls through the screed by gravity, and even if not, it is enough to sweep it without breaking. Consequently, when impacts are present, this means that the actual oversized rocks are fragmented.
• The number of impacts is proportional to the number and size of oversized rocks (it should be stated that the number of impacts may also depend on other factors, but for simplicity this is neglected).
• An acoustic signal with impulses is characterised by simple measures and later described (modelled) in terms of random processes with heavy tails. For bulk materials, no impacts are expected (i.e., impulses in the signal), so the distribution will be close to Gaussian. In case of oversized blocks, impulses in the acoustic signal will appear, so the distribution of the samples will be far from Gaussian due to the presence of large values. The two most suitable distributions are proposed: $\alpha$-stable and t Location–Scale.

The analysis is conducted using the estimation of several parameters. The first fundamental parameter $P1$ is the stability parameter ($\alpha$) of the $\alpha$-stable distribution [51,52,53]. As a “heavy-tailed” distribution, the $\alpha$-stable distribution suits well for describing processes with a significant content of outliers, understood as observations located further from the mean value. In the special case of $\alpha =2$, this distribution is reduced to Gaussian. With the values of $\alpha <2$, the presence of outliers in the signal becomes more prominent and causes the shape of the density distribution function to diverge from the Gaussian distribution. Hence, estimating the operational parameter $P1=2-\alpha$ is a good way to assess the amount of impulsive behaviour in the signal with a Gaussian noise floor.

The second fundamental parameter $P2$ is based on the shape parameter ($\nu$) of the t Location–Scale distribution (see Section 4.1.2) [54,55]. This distribution is also designed to model heavy-tailed processes, and, similarly to the previous case, this distribution approaches Gaussian when the value of the parameter $\nu$ tends to infinity. Hence, the operational parameter $P2=1/\nu$ is a suitable candidate to estimate the amount of impulsive behaviour in the signal.

The third parameter $P3$ is the sum of the amplitudes of the peaks in the acoustic signal. It is based on the detection and calculation of the number of peaks that constitute the fourth parameter $P4$. The peaks are identified based on the upper envelope of the acoustic signal. The informative peaks are selected on the basis of minimum prominence relative to the variance. In this way, it is possible to designate the actual hammer impacts and omit all minor local maxima of the envelope that occur throughout the entire length of the signal.

Finally, parameter $P5$ is proposed, the most intuitive and important from an operational point of view. It is the duration of the cycle related to processing the material unloaded on the grizzly screen.

4.1.1. The $\alpha$-Stable Distribution

The $\alpha$-stable distribution can be used to describe non-Gaussian (impulsive) behaviour in the data. It is a generalisation of the Gaussian distribution.

Definition 1.

The α-stable distribution of a random variable X can be described by its characteristic function [51]:

$$\begin{array}{c}\hfill E\left[e^{itX}\right]=\left\{\begin{array}{cc}exp\left\{-{\sigma }^{\alpha }{\left|t\right|}^{\alpha }\left\{1-i\beta \mathrm{sign}\left(t\right)tan\left(\pi \alpha /2\right)\right\}+i\mu t\right\}\hfill & \mathrm{for}\alpha \ne 1,\hfill \\ & \\ exp\left\{-\sigma \left|t\right|\{1+i\beta \mathrm{sign}\left(t\right){\displaystyle \frac{2}{\pi }}log\left(\right|t\left|\right\}+i\mu t\right\}\hfill & \mathrm{for}\alpha =1,\hfill \end{array}\right.\end{array}$$

(1)

where $\alpha \in (0,2]$ is the stability parameter, $\beta \in [-1,1]$ is the skewness parameter, $\sigma \in (0,\infty )$ is the scale parameter, and $\mu \in \mathbb{R}$ is the location parameter.

According to Equation (1), if the $\alpha =2$, the $\alpha$-stable distribution reduces to the Gaussian distribution with mean $\mu$ and variance $2{\sigma }^2$. When the stability parameter decreases, the signal X becomes more impulsive.

4.1.2. The t Location–Scale Distribution

The t Location–Scale distribution is useful for modelling data distributions with heavier tails (more prone to outliers) than the normal distribution. It approaches the normal distribution as the scale parameter $\nu$ approaches infinity, and smaller values of $\nu$ produce heavier tails. The probability density function for a random variable X is defined as [56]

$$f_X={\displaystyle \frac{\mathsf{\Gamma }\left(\frac{\nu +1}{2}\right)}{\mathsf{\Gamma }\left(\frac{\nu }{2}\right)\sqrt{\nu \pi }\sigma }}{\left({\displaystyle \frac{\nu +{\left(\frac{X-\mu }{\sigma }\right)}^2}{\nu }}\right)}^{-{\displaystyle \frac{\nu +1}{2}}},$$

(2)

where $\mathsf{\Gamma }(·)$ is the gamma function.

4.2. Discussion on the Methodology

The performance of the rock hammer operation depends on many factors, including the operator’s experience and the technical condition of the hammer-carrying manipulator, which are difficult to analyse quantitatively. Therefore, after preliminary process observations, the influence of the factors mentioned above was neglected. Ultimately, in this research, the following quantitative parameters of hammers were taken into account for analysis:

• Impulsiveness of the acoustic signal using parameters $P1$ and $P2$.
• Number of impacts required per one truck (loader) processing with a hydraulic or electric hammer ($P3$ parameter).
• Number of peaks constituted parameter $P4$.
• The time (duration) required for processing one truck (loader) with a hydraulic or electric hammer formed parameter $P5$.

As the granulation in some extreme cases may have a significant impact on the results, manual analysis of the video sequence was provided. Using image analysis of selected frames, the visible area of the oversized piece was determined and classified for a given rock size category. Then, another parameter could be introduced—namely, the number of impacts required for disintegration per one piece of rock. The three categories of rock size applied (1—small, 2—average, 3—large) will be explained in detail in further paragraphs.

In contrast to work [57], where rock segregation was based on empirical dimension ranges registered by the camera (upper view) in the loader bucket, in this study the rock sizes were classified based on data from video recordings from the measuring station placed in front of the unloaded material. Since the measurements were made without a physical calculation of the distance between the grizzly screen and the camera, the size of the single grizzly screen cell visible on the frame was used as a reference for the surface area calculations. This was necessary, as on different measurement days the measurement station had to be placed at different positions.

The small category (1) meant that the size of the rock was about the size of a cell, but not enough to push the piece through it. The operator could crush such rock by 1–2 impacts or force it to fall through the grizzly screen, which were equal events for a performance analysis. The average category (2) corresponded to the size of a rock that covered more than one grizzly screen cell (350 × 350 mm) and that required more impacts for its disintegration; for this category, there was no guarantee that the resultant smaller parts would appear smaller than the cell size. The large category (3) corresponded to big rocks (occurring 1–2 per bucket), whose size might cover many cells, and which required quite a long time from the operators for their disintegration. The operators tried to obtain small pieces of rock by applying hammer impacts to the nearest edge of big pieces, but this did not guarantee that the new piece could fit the cell size; therefore, it was transferred to the lower categories (1) or (2). These categories were used to normalise the number of hammer impacts per rock-breaking cycle to obtain the appropriate performance values under different working conditions.

The operator spent a certain time on all the categories of rock processing to find rock pieces among the bulk fractions. The content in every loader bucket or truck was estimated to be statistically the same in all the experiments because the rock-blasting technology and geological properties of the rock (copper ore) were stable enough for a long time. In addition, the operators used the hammer chisel to change the rock position on the grizzly screen (rotate, move, or turn over). Since these auxiliary actions were present for both types of hammers, hydraulic and electric, they did not affect the results of their comparison. The obtained values of time (duration) and the impact numbers of separate rock breaking were statistically treated to obtain mean values and standard deviations for every transport (rock portion) processing by both hammers in three series of experiments. The associated graphs were constructed over the whole number of processed cycles (transports), which are given in the next section.

5. Results

The presented results are based on data from three measurement sets, two obtained from the hydraulic hammer and the last one from the electric hammer. For the final performance, the second method (based on visual assessment of granulation) was chosen to extract quantity information, as this approach includes information on the size of individual rocks and provides a context-based analysis of granulation.

5.1. Sound-Based Estimation

Figure 7 and Figure 8 present the acoustic signals registered for the tests performed with a hydraulic and with an electric hammer, respectively. Each signal (truck number) represented a different measurement from a different load of material provided by the loader-truck. Although the amount of material inside each truck was roughly the same the fragmentation of the material could vary, as the load-truck operators waited until the bucket was full, resulting in processing time differences even for measurements from the same hammer. The time between the breaking process, understood as the flat signals between large amplitudes, was a result of moving the small material through the grizzly screen, as it sometimes required only a slight movement to fit through the screen cells. The total length of the signal was from a time taken at the end of the unloading of the material to the point where all of the unloaded material had been moved through the screen. Five parameters were calculated for each signal, according to the description presented in Section 4.1. For parameters $P3$ and $P4$, Figure 9 presents an example of peak detection and estimation of their amplitude. The smoothed upper envelope allowed for obtaining clean features, where individual impacts could be easily identified (the red line), and the identification was performed using a simple gradient-based peak detection procedure (the black circles). In this way, it was possible to determine and aggregate the amplitudes of the peaks. 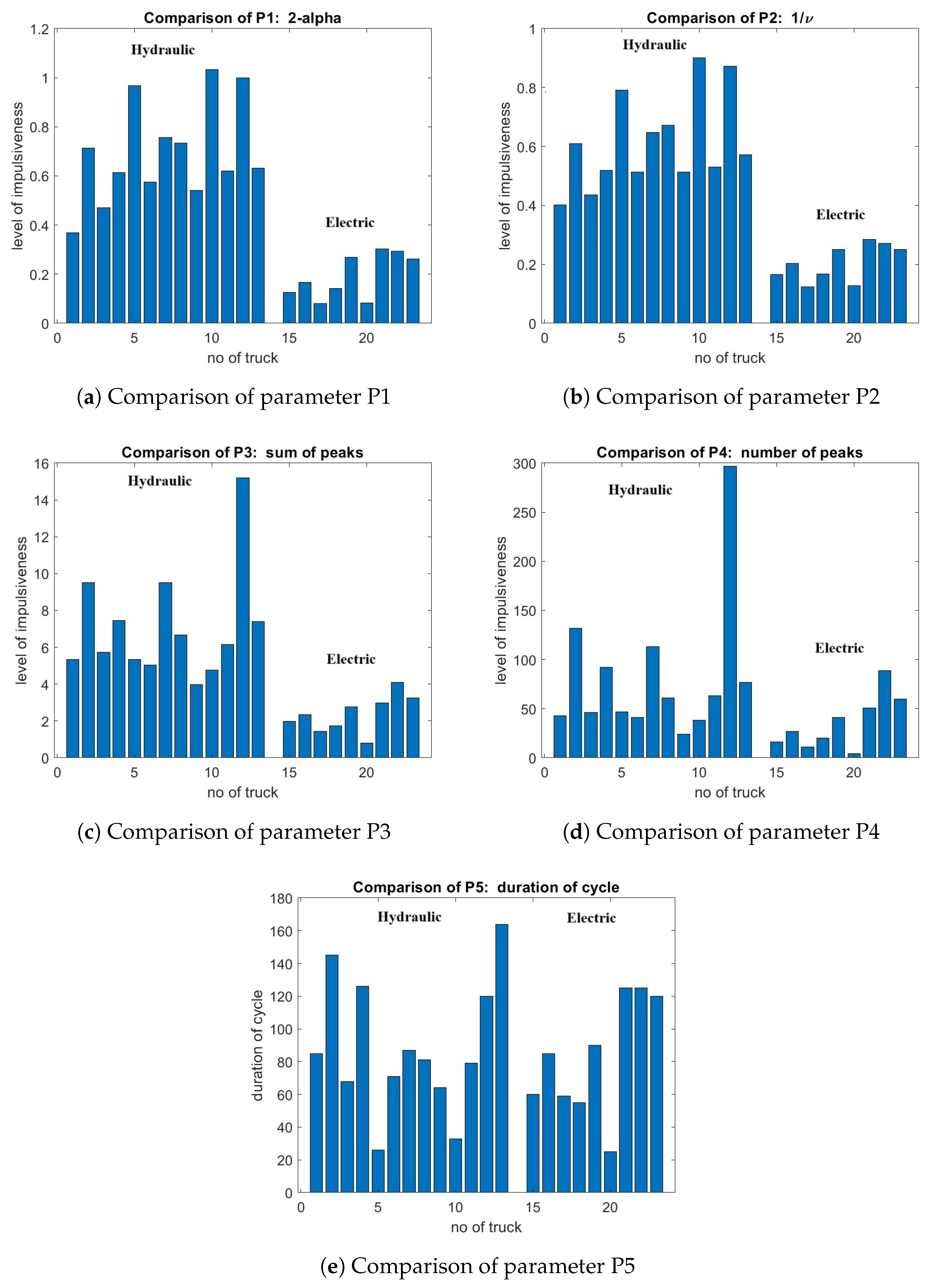The signal recorded as Truck 6 during the electric hammer measurements (Figure 8) was classified as an outlier due to the very long operating time that was related to an instance of a rock piece significantly larger and with greater hardness than in the other measurements. No such instance was observed in the hydraulic hammer measurements; therefore, this measurement was excluded from further analysis.

The results for the two hammers (hydraulic and electric) for all five parameters are presented in the Figures below. Figure 10a–d present results for the measurement of impulsiveness, and Figure 10e shows the duration of each cycle for the analysed data.

It is clearly visible that the first three parameters were significantly higher for the hydraulic hammer than for the electric hammer. This means that the registered acoustic signal was more impulsive. Figure 10c, especially, shows a significant reduction in the amplitudes of the peaks needed to break oversized pieces—that is, in the required result. The difference between the hydraulic and electric hammer was not as significant for parameter $P4$ as it was for parameters $P1$–$P3$; however, the decrease of $P4$ is clear, as presented in Figure 10d. The last figure (Figure 10e) is related to the duration of each cycle. No significant improvement is visible; however, it should be mentioned that each cycle consisted of two important parts: working movements and spreading the material and proper rock fragmentation. Therefore, the duration measurement may have been biased.

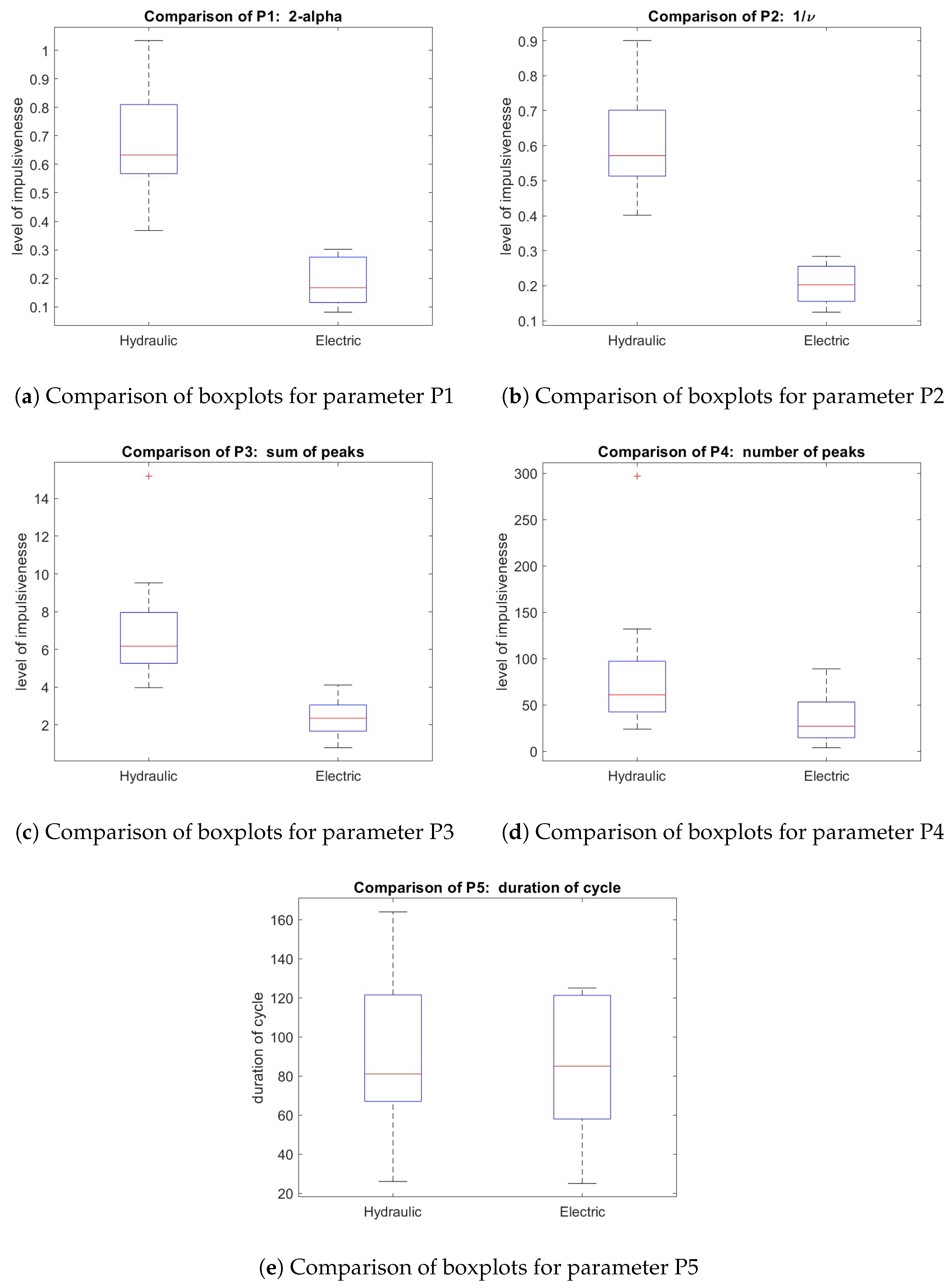
To aggregate the results presented in the previous figures, boxplots for each parameter are presented. Again, it is clear that the difference between the hydraulic and electric hammers expressed by the parameters $P1$:$P3$ is significant (Figure 11a–c).

Although parameter $P4$ followed a trend similar to the previous parameters, its proportional advantage for the electric hammer was significantly smaller. A comparison of the boxplots for parameter $P5$ confirmed our conclusion that it is not appropriate in its current form for performance evaluation (Figure 11e). The information on the size of individual rocks seems in this case crucial for the correct results.

5.2. Sound Data in the Context of Direct Hammer Signals—Vibration and Current

The measurement of acoustic signals may be disturbed by other acoustic sources. The reliability of the audio data in the context of the hammer performance analysis was confirmed by comparing them to the electric current data and vibration signal measured at the same time on the hammer (see Figure 12). This was additionally important, as the visible correlation shows that the components of the process that manifested in vibration and current data existed also in the audio data.

The electric current was measured directly from the hammer power supply circuit. Thus, the current variation may have been related to the movement of the boom as well as the fragmentation of the rock piece by the hammer. The first source could be neglected, as it was noticeably smaller and non-impulsive. The vibration signal measured by an accelerometer in a similar way may contain a variety of information but, again, the impulses visible in the signal are related to the hammer operation. All three methods have some drawbacks; however, they deliver approximately similar information. The sound-based approach was selected, due to its contactless character.

5.3. Using Video Context for Validation of Performance Analysis of Breaking Hammers Based on Parameters P3 and P4

The method was also validated by an expert using video analysis. First, the number of impacts was manually analysed and compared with detection based on audio analysis. Another important issue was the granulation of the delivered material. By image analysis of extracted frames, pieces of rocks were detected, and then the size (surface) of a given oversized block was measured. Finally, the number of blocks was counted and classified into three categories: small (1), average (2), and large (3). It was a very rough estimate to understand the significant influence it may have had on the analysis.

Examples of the frames extracted from the video recordings are presented in Figure 13. The frames were individually assessed, and each rock piece was classified into one of three size categories, as explained in the methodology section. By associating this information with audio data, the number of impacts could be easily attached to the size.

The results for parameters $P1$–$P3$ presented in the previous sections are clear, while the results for $P4$ and, especially, for $P5$ need more explanation. It is not possible to directly demonstrate a significant increase in efficiency in terms of the number of impacts or duration of the cycle by applying a novel electric hammer. Thus, additional information from manual video analysis with extracted parameters was combined, and the results are presented in Figure 14 and

Table 8. Comparison of hydraulic and electric hammer efficiency.

Hammer	Class 1	Class 2	Class 3	Mean
Impacts per rock
Hydraulic hammer	7.2	19.8	22.8	11.3
Electric hammer	2.8	5.4	6.4	3.1
Time(s) per rock
Hydraulic hammer	3.0	7.9	7.1	4.2
Electric hammer	1.2	1.5	2.2	1.3

.

All the data in Figure 14 were analysed by the corresponding three size categories (1, 2, 3) described earlier for each piece of processed rock, and they were then averaged over the number of loaders/trucks. In this way, the data were made comparable under different working conditions, providing a unified metric for the rock-breaking process.

It is visible from Figure 14 that the mean values of impacts/rock and time/rock in every loader/truck were significantly lower for the electric hammer. Although both hammers had significant deviations in rock fragmentation, an almost flat line of time/rock parameter is observable for the electric hammer, which reflects the smoothness and stability of the rock processing at the dumping point.

Table 8 shows that the mean number of impacts per rock processing of the hydraulic hammer (11.3) was 261% higher than that of the electric hammer (3.1). This ratio was also significant—158%, 269%, and 259%—for the three classes of rock sizes: 1, 2, and 3, respectively.

The mean time (s) for the rock processing of the hydraulic hammer (4.2) was 230% greater than that of the electric hammer (1.3). This ratio was also significant when divided into the three classes of rock sizes: 146%, 417%, and 217% for classes 1, 2, and 3, respectively.

Considering the hammering performance by the rock size classes, the maximum effect of the electric hammer is observable for class 2, and the minimum is observable for class 1 (small rocks). This was due to their unstable position on the grizzly screen, which required a greater number of hammer impacts and longer processing times. The lower efficiency ratio of the class 3 rock processing can be attributed to the damping effect of the layer of smaller fraction rocks lying beneath the large pieces. The number of impacts required and the time per rock increased from class 1 to class 3 for both hammers.

6. Summary and Conclusions

Rock fragmentation is one of the most important and energy-consuming processes in the mining industry. As in underground scenarios, initial breaking is usually realised by breaking hammers; their performance assessment is crucial for optimisation of the production workflow. This includes a comparison of the efficiency between different types of hammers that, due to the different principles of operation (such as hydraulic and electric hammers), can be difficult to measure. Furthermore, due to the character of underground mining operations and the impact of the hammer work routine, there is a great incentive for the development of contactless methodologies, which can be provided by analysis of data from acoustic measurements.

For this purpose, the authors conducted research based on unique data collected from hydraulic and electric hammers that worked under the conditions of ongoing mining operations. The proposed algorithms were developed and tested on the acoustic part of the data as the main source of information. Video data were used as an auxiliary measurement that allowed one to consider the size of an individual rock piece. The analysis of the proposed parameters included the following:

• stability index in $\alpha$-stable distribution ($P1$), number of degrees of freedom in Location–Scale distribution ($P2$), sum ($P3$) of peaks as parameters calculated from acoustic data, as a method to analyse signal impulsiveness;
• number of impacts calculated and duration of the cycle of processing material per truck, as a direct way of efficiency comparison.

Due to the possible, extreme cases of significantly uneven material loads (calculated per truck), an additional verification methodology was applied. The material was further categorised into three size-based categories, identified by video frame analysis. This allowed for the identification of outliers and the normalisation of the obtained results.

The time difference between consecutive measurements would have a minimal impact on the measurement (unless the difference is significant, counted in months). If the measurement sessions were carried out in close time proximity, only the initial fragmentation of the rocks might slightly differ (though not much more than it does between consecutive trucks during the same measurement day), as the parameters of the rock should stay the same (and usually will not change even in a long time frame). However, this should be neglected the higher data sample (due to averaging of the values).

In addition, different types of data were measured during the experiment, together with acoustic and video data. The vibration and electric current measurements proved to have similar signal waveforms (understood as characteristic amplitude peaks relative to impacts). This allowed for the implementation of the proposed methodology through data from different sources in scenarios where useful acoustic data would be hard to obtain, due to external factors (such as noise not related to the hammer workflow). The obvious disadvantage of such data would be the necessary installation of sensors, which in continuous operation conditions is not always possible without disturbing the work cycle.

In the case of the experiments carried out, the methodology allowed for demonstration of the significantly higher efficiency of the electric hammer over the hydraulic hammer in both the time required for the processing of the unloaded material and the number of necessary impacts. The most important thing about the methodology is that it is applicable to comparing the efficiency of hammers with different operational parameters.

It is important to note that this article focused on performance related to ongoing mine operations (the operational reliability and process cycle constraints posed by the frequency of unloaded material) rather than direct comparison of energy efficiency, which would require a different type of experiment to be carried out. This calculation would require tracking the energy flow and its losses throughout the process, which in the conditions of ongoing mine operations would be hard to conduct if not impossible (for safety and accessibility reasons). Research related to hammer energy losses under laboratory conditions is planned as future work, as it would both increase the value of this article and be valuable in itself.

The proposed methodology creates a potential diagnostic application due to the possibility of identifying underperforming hammer stations through a comparison with the ideal modelled station that could be obtained through a much larger number of experiments. An early identification of the outlier performance would then provide information that further and more thorough inspection was necessary. This could be considered as a possible continuation of the presented research.