Design and Optimization of a Contour Deep Loosening and Stubble Pressing Mechanism Suitable for Strip Tillage
Abstract
1. Introduction
2. Materials and Methods
2.1. Whole Machine Structure
2.2. Operating Principle
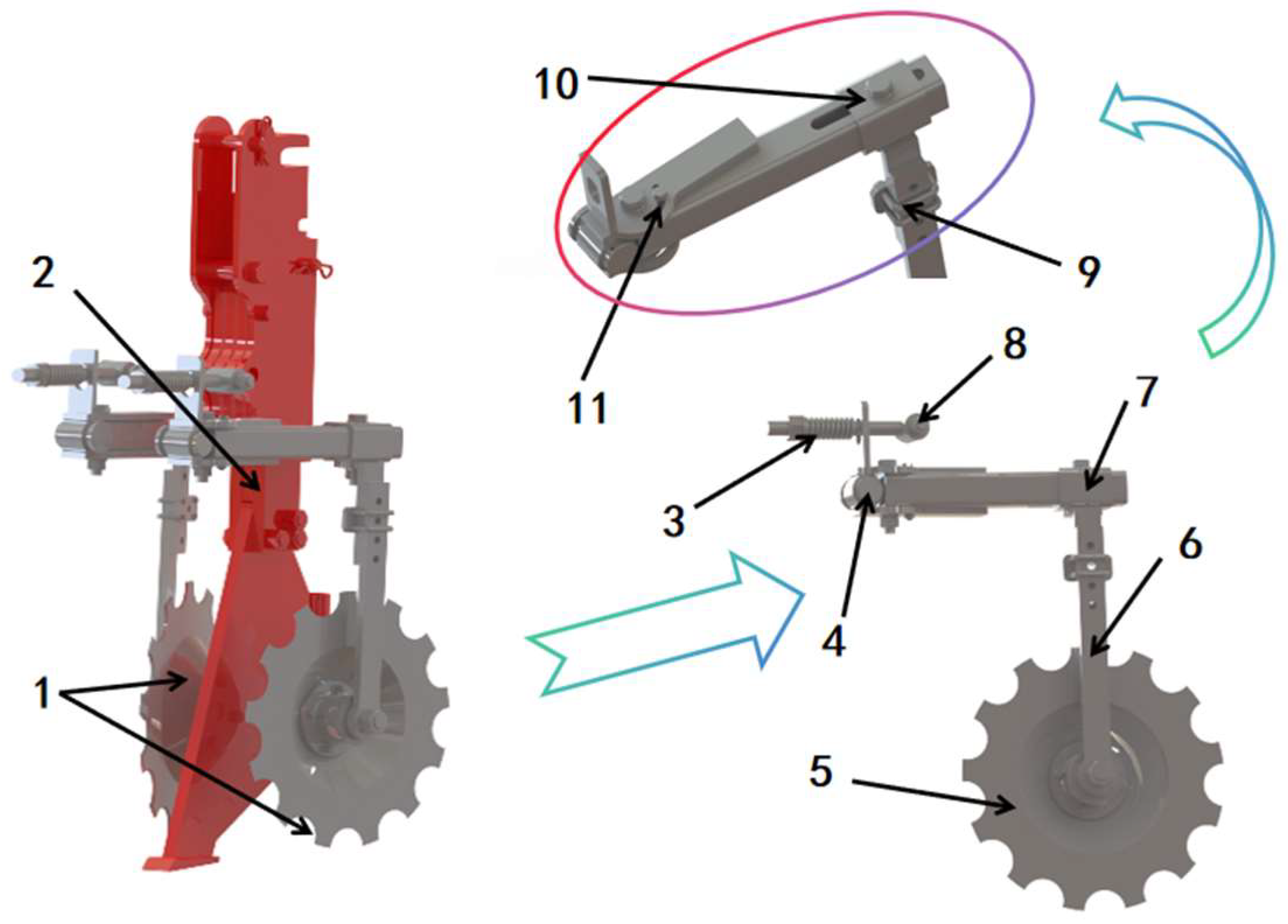
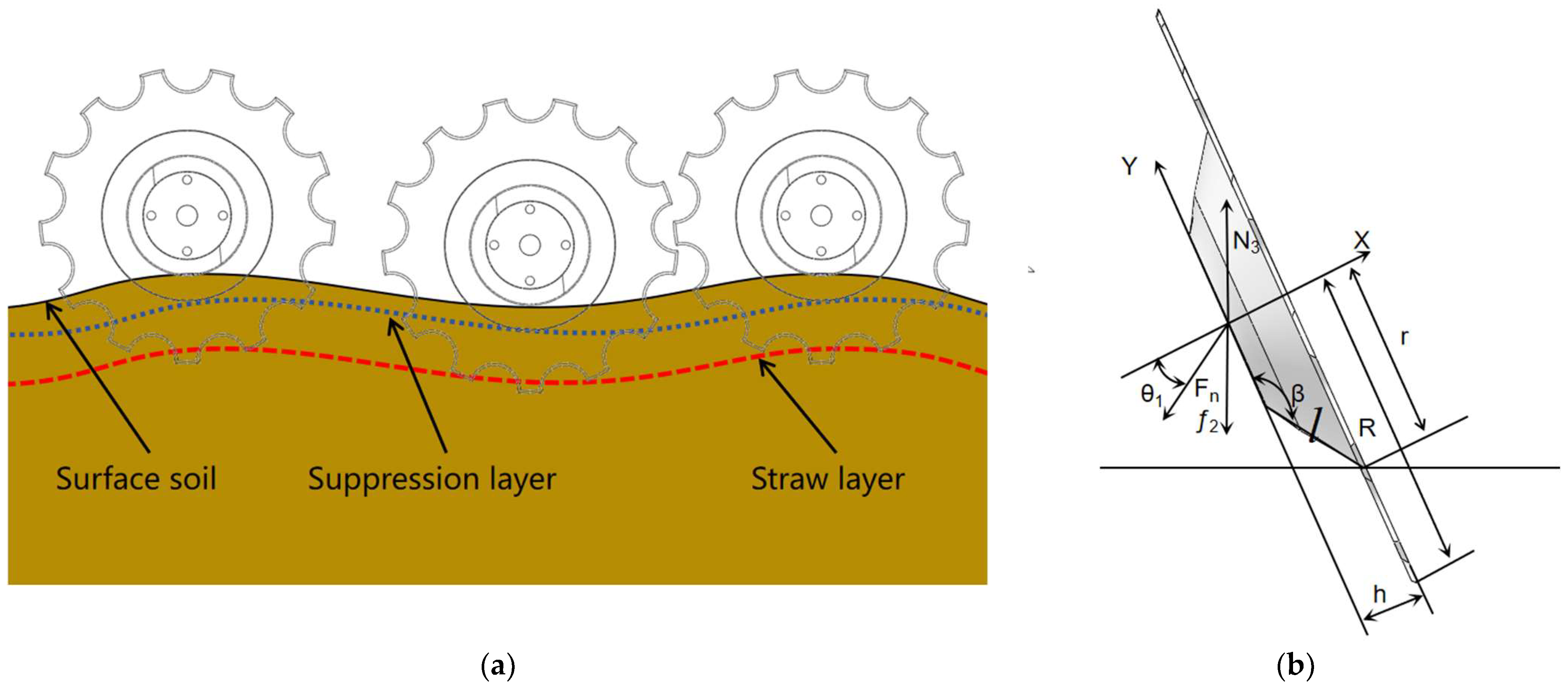
2.3. Key Component Design
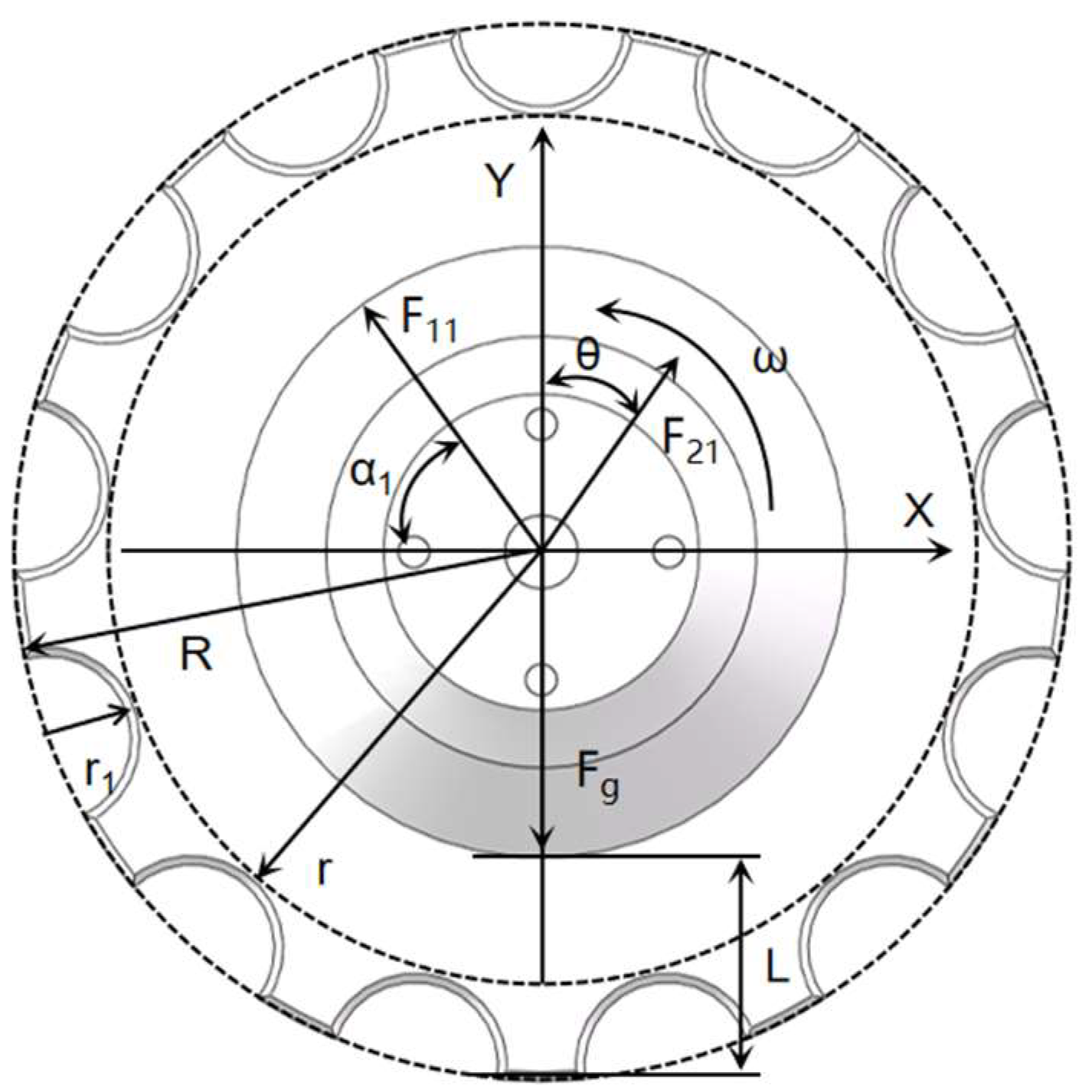
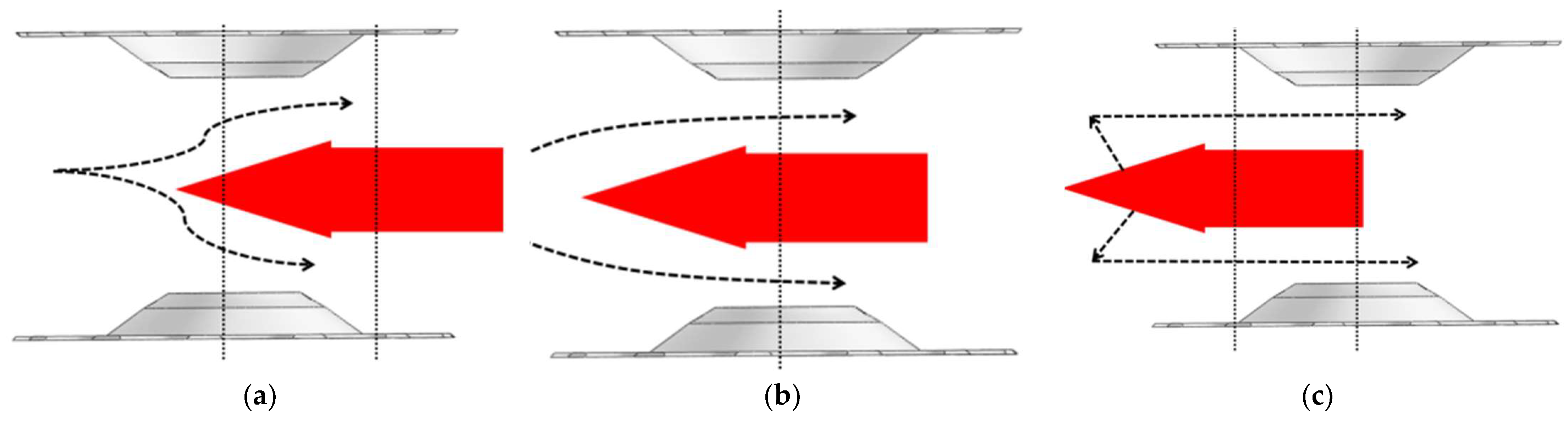
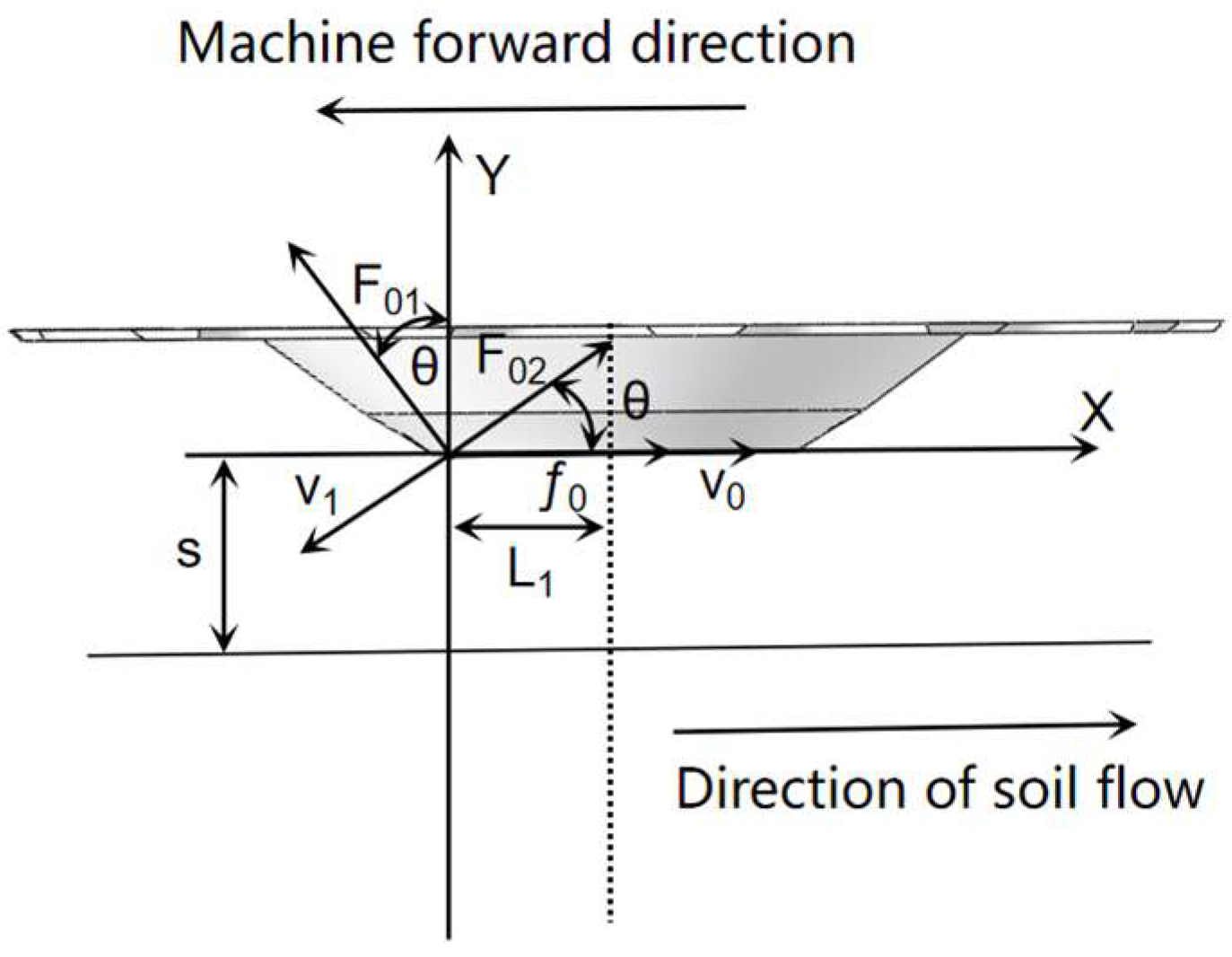
Design of Diversion and Pressure Wheel
2.4. Component Parameter Optimization
2.4.1. Optimization of Front and Rear Position Parameters of Guide Wheel
2.4.2. Optimization of Diversion Offset Angle Parameters
3. Discrete Element Simulation Experiment
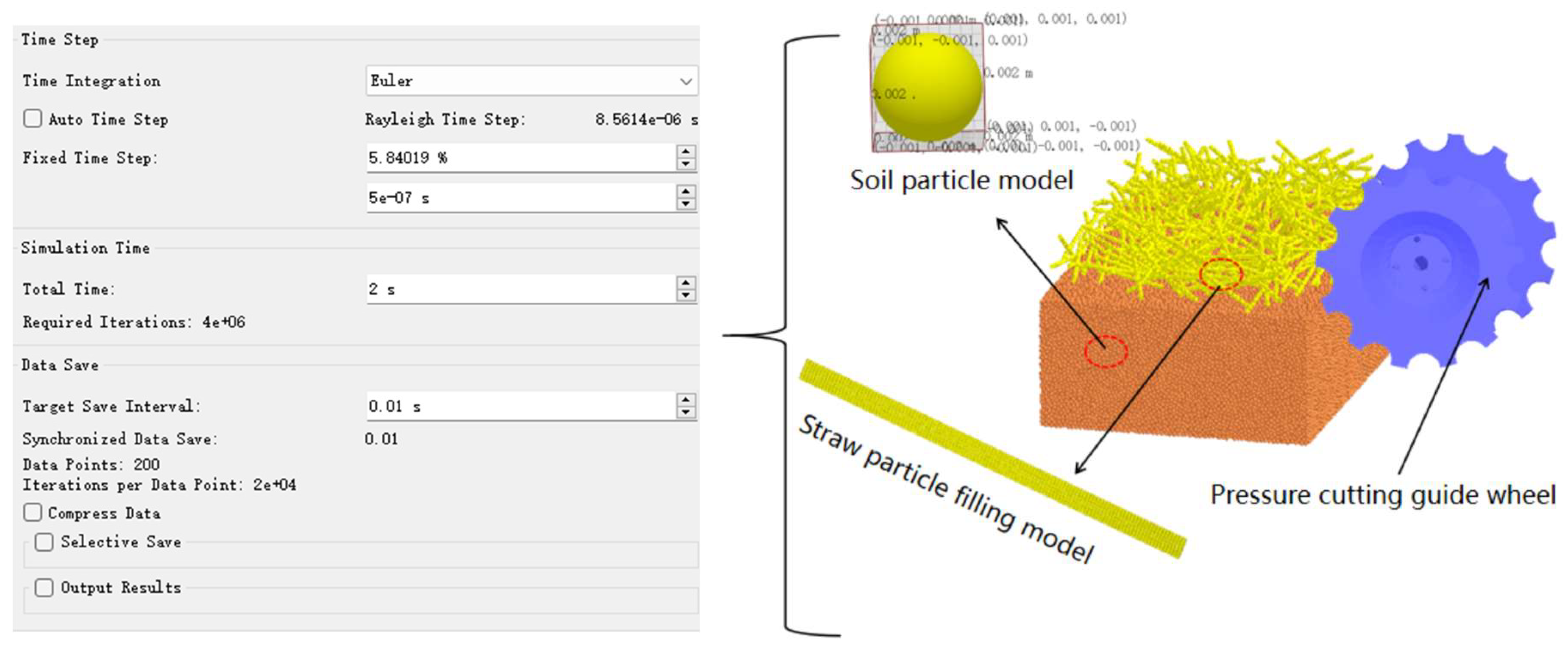
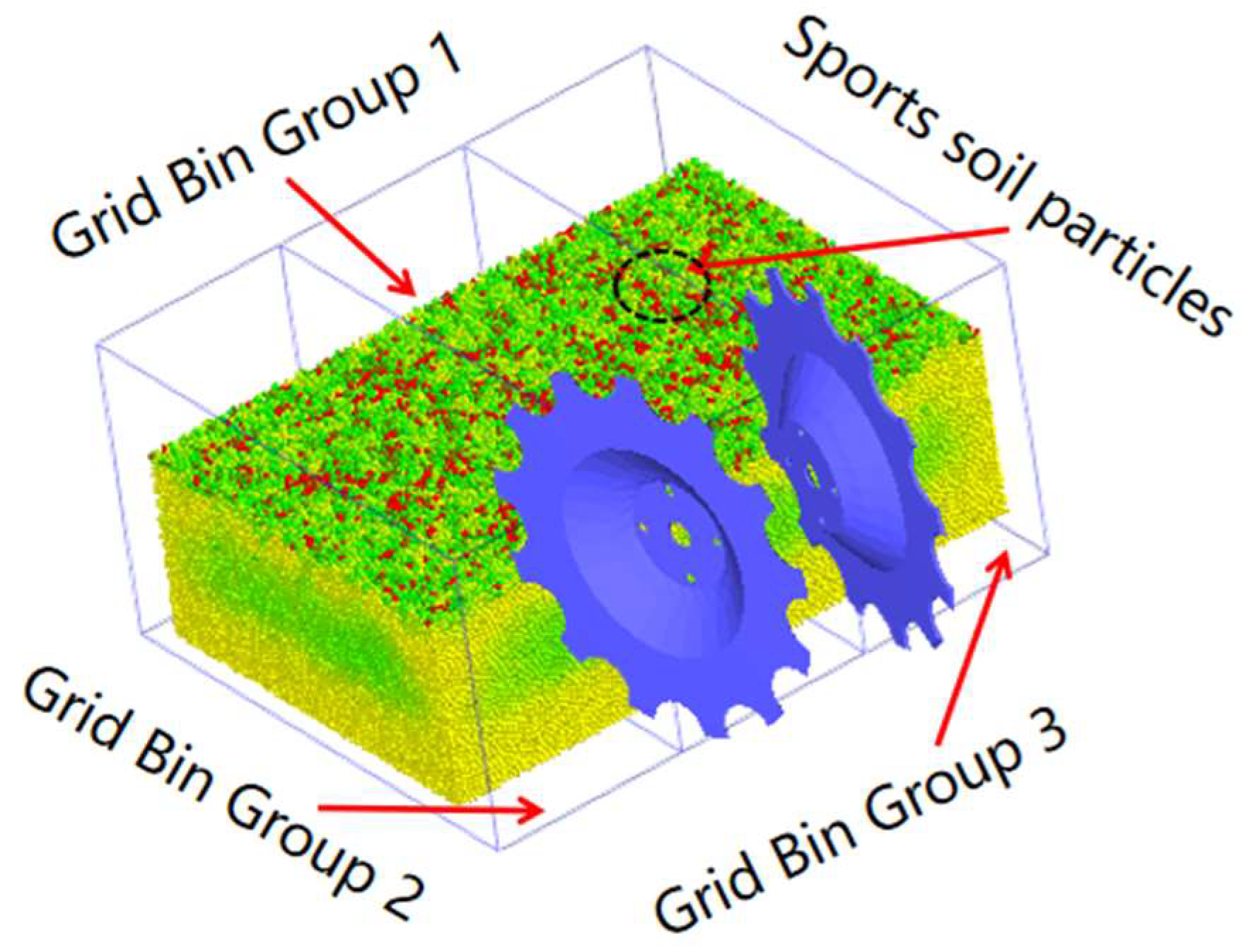
3.1. Establishment of Simulation Test Model
3.2. Simulation Test Method
4. Results and Discussion
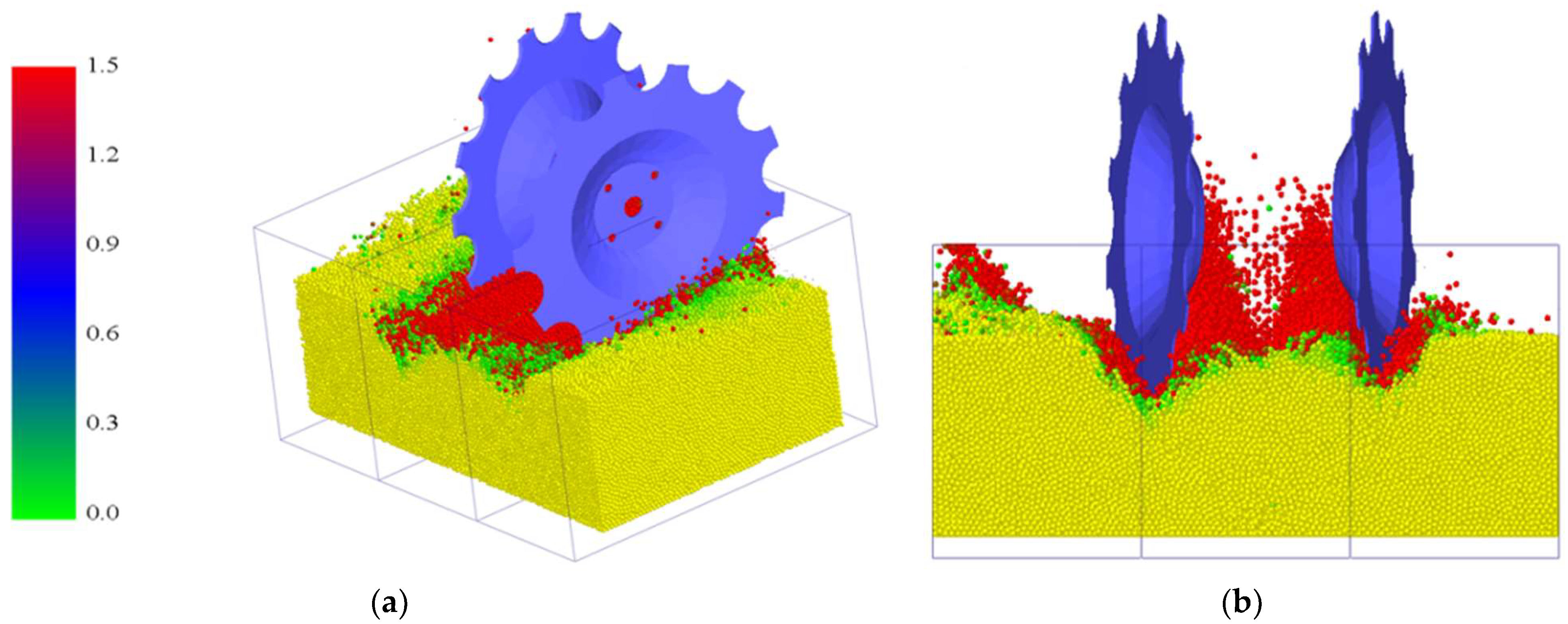
4.1. Analysis of Simulation Experiment Results
4.2. Establishment and Significance Analysis of Regression Equations
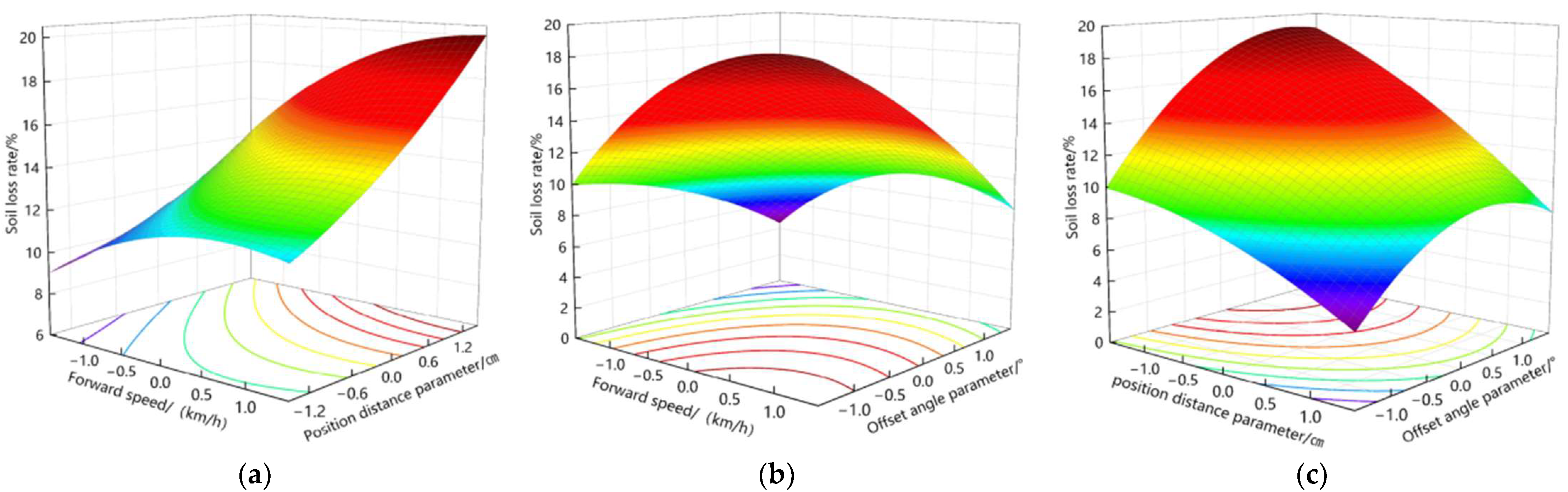
4.3. Response Surface Analysis
4.4. Parameter Optimization
5. Field Experiments
5.1. Test Conditions and Equipment
5.2. Test Method
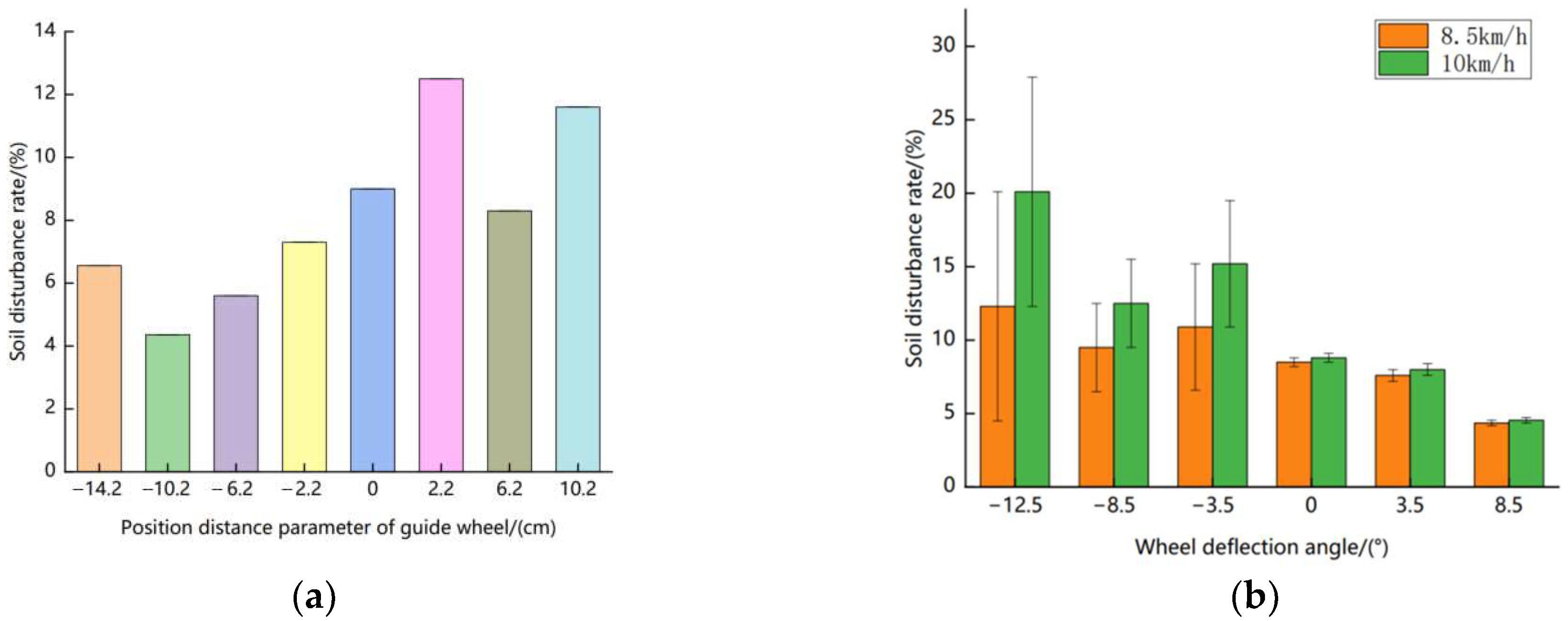
5.3. Analysis of Test Results
6. Conclusions
- (1)
- This article designs a copying deep loosening and stubble pressing mechanism suitable for strip tillage, which integrates profiling, depth limiting, diversion, and stubble pressing. The working principle of the device was expounded, the tooth shape parameters, convex structure parameters, and distribution mode of the mechanism were determined, the working process was optimized and analyzed, and the parameter range of the actual operation of the mechanism was verified through theoretical analysis and calculation.
- (2)
- The machine parameters obtained through discrete element simulation tests were as follows: forward speed of 7.383 km/h, front–rear position distance parameter of −10.131 cm, deflection angle of 8.608°, and soil loss rate of the seedling belt of 5.486%. Preliminary tests showed that after the machine operated, soil disturbance was reduced and machine performance was improved.
- (3)
- Based on the actual operation conditions and requirements, the working parameters of the mechanism were optimized, and field tests were conducted. Taking the soil disturbance rate and straw return status as the test indices, an optimization analysis of the design parameters was carried out. Field test data showed that the machine achieved the best operation performance when the forward speed was 8.5 km/h, the front–rear position distance parameter was −10.2 cm, and the deflection angle was 8.5°. Under these conditions, there was no large clod of soil remaining in the seedling belt after operation, and the surface soil was flat. The tests also revealed that no obvious straw sliding occurred after operation, and only a small amount of straw remained in the planting seedling belt, which did not affect the subsequent sowing quality. After parameter optimization, the operation performance of the machine was significantly improved.
- (4)
- The optimal combination of deflection angle and front–rear relative position parameters derived from this research can serve as specific reference criteria for manufacturers to optimize the structure of existing equipment. It can help enterprises address the issues of high tillage resistance, soil clogging, and uneven crushing that exist in traditional products, and holds practical reference significance for improving the efficiency of machinery in the industry.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tang, Q.X.; Li, S.K.; Xie, R.Z.; Zhang, J.X.; Ren, T.Z.; Lin, T.; Gao, S.J. Effects of Conservation Tillage on Crop Yield: A Case Study in the Part of Typical Ecological Zones in China. Agric. Sci. China 2011, 10, 860–866. [Google Scholar] [CrossRef]
- Hu, R.W.; Liu, Y.J.; Chen, T.; Zheng, Z.Y.; Peng, G.J.; Zou, Y.D.; Tang, C.G.; Shan, X.H.; Zhou, Q.M.; Li, J. Responses of soil aggregates, organic carbon, and crop yield to short-term intermittent deep tillage in Southern China. J. Clean. Prod. 2021, 298, 126767. [Google Scholar] [CrossRef]
- Askari, M.; Shahgholi, G.; Abbaspour-Gilandeh, Y. New wings on the interaction between conventional subsoiler and paraplow tines with the soil: Effects on the draft and the properties of soil. Arch. Agron. Soil Sci. 2019, 65, 88–100. [Google Scholar] [CrossRef]
- Afzalinia, S.; Zabihi, J. Soil compaction variation during corn growing season under conservation tillage. Soil Tillage Res. 2014, 137, 1–6. [Google Scholar] [CrossRef]
- Afshar, R.K.; Cabot, P.; Ippolito, J.A.; Dekamin, M.; Reed, B.; Doyle, H.; Fry, J. Corn productivity and soil characteristic alterations following transition from conventional to conservation tillage. Soil Tillage Res. 2022, 220, 105351. [Google Scholar] [CrossRef]
- Pöhlitz, J.; Rücknagel, J.; Koblenz, B.; Schlüter, S.; Vögel, H.J.; Christen, O. Computed tomography and soil physical measurements of compaction behaviour under strip tillage, mulch tillage and no tillage. Soil Tillage Res. 2018, 175, 205–216. [Google Scholar] [CrossRef]
- Murmu, K.; Thakur, T.C. Design and Development of Combined Conservation Tillage Machine with Chiselers and Clod Pulverizing Roller. Ama-Agric. Mech. Asia Afr. Lat. Am. 2019, 50, 66–72. [Google Scholar]
- Salar, M.R.; Esehaghbeygi, A.; Hemmat, A. Soil loosening characteristics of a dual bent blade subsurface tillage implement. Soil Tillage Res. 2013, 134, 17–24. [Google Scholar] [CrossRef]
- Loghin, F.; Capatîna, I. Aspects Regarding the Reduction of Penetration Resistance of Soil as a Consequence Soil Working. Environ. Eng. Manag. J. 2010, 9, 1619–1622. [Google Scholar] [CrossRef]
- Shahgoli, G.; Saunders, C.; Desbiolles, J.; Fielke, J. The effect of oscillation angle on the performance of oscillatory tillage. Soil Tillage Res. 2009, 104, 97–105. [Google Scholar] [CrossRef]
- Hou, S.Y.; Wang, S.Z.; Ji, Z.C.; Zhu, X.X. Design and Test of the Clearing and Covering of a Minimum-Tillage Planter for Corn Stubble. Agriculture 2022, 12, 1209. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, S.; Li, H.; Li, X.F.; Song, C.Y.; Cruse, R.M.; Zhang, X.Y. Effects of conservation tillage on corn and soybean yield in the humid continental climate region of Northeast China. Soil Tillage Res. 2011, 115, 56–61. [Google Scholar] [CrossRef]
- Zeng, Z.W.; Chen, Y. Performance evaluation of fluted coulters and rippled discs for vertical tillage. Soil Tillage Res. 2018, 183, 93–99. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, B.; Sun, M.J.; Sun, X.B.; Zhou, W.Q.; Tang, H.; Wang, J.W. Design and Testing of an Automatic Strip-Till Machine for Conservation Tillage of Corn. Agriculture 2023, 13, 2357. [Google Scholar] [CrossRef]
- Feng, X.; Yao, J.Y.; Gao, Y.P.; Zeng, L.C.; Wang, L.J.; Wang, B.; Yang, Z.L. Review of Root-Stubble Characteristics and Root-Stubble Crushing and Clearing Technologies for Conservation Tillage. Sustainability 2024, 16. [Google Scholar] [CrossRef]
- Overstreet, L.F. Strip tillage for sugarbeet production. Int. Sugar J. 2009, 111, 361–368. [Google Scholar]
- Li, C.R.; Liu, Z.N.; Liu, M.; Xu, T.Y.; Ji, C.; Qiao, D.; Wang, Y.; Jiang, L.M.; Wang, J.L.; Feng, W.Z. Design and Testing of Key Components for a Multi-Stage Crushing Device for High-Moisture Corn Ears Based on the Discrete Element Method. Appl. Sci. 2024, 14, 9108. [Google Scholar] [CrossRef]
- Yuan, Y.W.; Wang, J.Y.; Zhang, X.; Zhao, S.H. Effect of Rotary Speed on Soil and Straw Throwing Process by Stubble-Crushing Blade for Strip Tillage Using DEM-CFD. Agriculture 2023, 13, 877. [Google Scholar] [CrossRef]
- Hou, S.Y.; Xue, D.H.; Ji, Z.C.; Zhou, C.; Chen, H.T. Parameter Combination Optimization of the Lateral Straw Clearing and Throwing Knife Based on Discrete Element Simulation. Agronomy 2023, 13. [Google Scholar] [CrossRef]
- Liu, X.T.; Qi, H.Y.; Wang, S.; Xu, Z.H.; Gao, P.; Fu, D.P.; Ma, Y.H. The Design and Experimentation of a Wing-Shaped Stubble-Breaking Device for Maize Stubbles. Agriculture 2024, 14, 2108. [Google Scholar] [CrossRef]
- Bai, S.H.; Yang, Q.Z.; Niu, K.; Zhao, B.; Zhou, L.M.; Yuan, Y.W. Discrete Element-Based Optimization Parameters of an Experimental Corn Silage Crushing and Throwing Device. Trans. Asabe 2021, 64, 1019–1026. [Google Scholar] [CrossRef]
- Xu, Z.; Shi, A.; Zhang, M.; Liu, L.; Zhou, Z.; Ding, L. Design and Testing of Air-Separation-Type Tillage Layer Residual Film Recovery Machines. AgriEngineering 2025, 7, 262. [Google Scholar] [CrossRef]
- Li, H.S.; Yang, L.; Zhang, D.X.; Tao, C.; He, X.T.; Xie, C.J.; Li, C.; Du, Z.H.; Xiao, T.P.; Li, Z.M.; et al. Design and optimization of a high-speed maize seed guiding device based on DEM-CFD coupling method. Comput. Electron. Agric. 2024, 227, 109604. [Google Scholar] [CrossRef]
- Zhu, H.B.; Wu, X.; Qian, C.; Bai, L.Z.; Ma, S.A.; Zhao, H.R.; Zhang, X.; Li, H. Design and Experimental Study of a Bi-Directional Rotating Stubble-Cutting No-Tillage Planter. Agriculture 2022, 12, 1637. [Google Scholar] [CrossRef]
- Zhu, A.W.; Xu, C.T.; Liu, Y.F.; Wang, J.S.; Tan, X.D. Design and Experiment of Oblique Stubble-Cutting Side-Throwing Anti-Blocking Device for No-Tillage Seeder. Agriculture 2024, 14, 2250. [Google Scholar] [CrossRef]
- Yazgi, A.; Taylor, R.K.; Navid, H.; Weckler, P. Performance Modeling and Seed Releasing Characteristics of a Corn Planter Metering Unit Using Response Surface Methodology. Appl. Eng. Agric. 2017, 33, 181–189. [Google Scholar] [CrossRef]






| Model | Contact Parameters | Numerical Value |
|---|---|---|
| Straw residue model | Poisson’s ratio | 0.39 |
| Solid density/(kg/m3) | 1678 | |
| Shear modulus/(pa) | 1.696 × 107 | |
| Straw residue straw model | Collision recovery coefficient | 0.65 |
| Static friction coefficient | 0.3 | |
| Dynamic friction coefficient | 0.01 | |
| Straw residue cleaning wheel model | Collision recovery coefficient | 0.32 |
| Static friction coefficient | 0.33 | |
| Dynamic friction coefficient | 0.05 | |
| Soil particle model | Poisson’s ratio | 0.43 |
| Solid density/(kg/m3) | 1364 | |
| Shear modulus/(pa) | 1 × 108 | |
| Soil particle soil model | Collision recovery coefficient | 0.25 |
| Static friction coefficient | 0.66 | |
| Dynamic friction coefficient | 0.29 | |
| Soil particle cleaning wheel model | Collision recovery coefficient | 0.51 |
| Static friction coefficient | 0.63 | |
| Dynamic friction coefficient | 0.29 | |
| Soil particle straw residue model | Collision recovery coefficient | 0.51 |
| Static friction coefficient | 0.29 | |
| Dynamic friction coefficient | 0.06 | |
| Cleaning wheel model | Poisson’s ratio | 0.29 |
| Solid density/(kg/m3) | 7852 | |
| Shear modulus/(pa) | 3.5 × 109 |
| Encoding | Consideration | ||
|---|---|---|---|
| Traction Speed, X1 (km/h) | Distance Between Front and Rear Positions, X2 (cm) | Deflection Angle of Guide Wheel, X3 (°) | |
| −1.471 | 6 | −15 | −13 |
| −1 | 7.28112 | −10.1958 | −8.83636 |
| 0 | 10 | 0 | 0 |
| 1 | 12.7189 | 10.1958 | 8.83636 |
| 1.471 | 14 | 15 | 13 |
| Test Serial Number | x1/(km/h) | x2/(cm) | x3/(°) | Soil Disturbance Rate/% |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 15.3 |
| 2 | 1 | −1 | 1 | 7.3 |
| 3 | 0 | 0 | 1.471 | 12.6 |
| 4 | 1.471 | 0 | 0 | 16.2 |
| 5 | 0 | 0 | 0 | 14.5 |
| 6 | −1 | −1 | 1 | 5.6 |
| 7 | 0 | 0 | 0 | 12.5 |
| 8 | 0 | 1.471 | 0 | 18.6 |
| 9 | −1 | 1 | 1 | 10.5 |
| 10 | −1.471 | 0 | 0 | 7.5 |
| 11 | −1 | −1 | −1 | 9.6 |
| 12 | 1 | 1 | −1 | 26.8 |
| 13 | 1 | −1 | −1 | 11.6 |
| 14 | 0 | −1.471 | 0 | 14.5 |
| 15 | 0 | 0 | −1.471 | 15.1 |
| 16 | 1 | 1 | 1 | 13.1 |
| 17 | 0 | 0 | 0 | 17.8 |
| 18 | 0 | 0 | 0 | 10.9 |
| 19 | −1 | 1 | −1 | 19.5 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| MODEL | 355.86 | 9 | 39.54 | 3.97 | 0.0260 |
| X1 | 56.53 | 1 | 56.53 | 5.68 | 0.0410 |
| X2 | 141.94 | 1 | 141.94 | 14.27 | 0.0044 |
| X3 | 97.54 | 1 | 4.81 | 9.80 | 0.0121 |
| X1X2 | 4.81 | 1 | 3.13 | 0.4829 | 0.5046 |
| X1X3 | 3.13 | 1 | 25.92 | 0.3141 | 0.5889 |
| X2X3 | 25.92 | 1 | 18.29 | 2.61 | 0.1410 |
| X12 | 18.29 | 1 | 5.62 | 1.84 | 0.2082 |
| X22 | 5.62 | 1 | 2.10 | 0.5648 | 0.4715 |
| X32 | 2.10 | 1 | 9.95 | 0.2107 | 0.6571 |
| Residual | 89.55 | 9 | 12.30 | ||
| Lack of Fit | 61.51 | 5 | 7.01 | 1.75 | 0.3029 |
| Pure Error | 28.04 | 4 | |||
| Cor. Total | 445.41 | 18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, W.; Liu, K.; Li, Z.; Wang, Z.; Wei, G.; Zhou, J.; Shi, S. Design and Optimization of a Contour Deep Loosening and Stubble Pressing Mechanism Suitable for Strip Tillage. Appl. Sci. 2025, 15, 10062. https://doi.org/10.3390/app151810062
Yan W, Liu K, Li Z, Wang Z, Wei G, Zhou J, Shi S. Design and Optimization of a Contour Deep Loosening and Stubble Pressing Mechanism Suitable for Strip Tillage. Applied Sciences. 2025; 15(18):10062. https://doi.org/10.3390/app151810062
Chicago/Turabian StyleYan, Wenjie, Kaichang Liu, Zongxin Li, Zongshuai Wang, Guojian Wei, Jilei Zhou, and Song Shi. 2025. "Design and Optimization of a Contour Deep Loosening and Stubble Pressing Mechanism Suitable for Strip Tillage" Applied Sciences 15, no. 18: 10062. https://doi.org/10.3390/app151810062
APA StyleYan, W., Liu, K., Li, Z., Wang, Z., Wei, G., Zhou, J., & Shi, S. (2025). Design and Optimization of a Contour Deep Loosening and Stubble Pressing Mechanism Suitable for Strip Tillage. Applied Sciences, 15(18), 10062. https://doi.org/10.3390/app151810062





