Analysis of the Application of Analytical and Numerical Methods for the Dimensioning of Pin Connections of Folding Bridges
Abstract
1. Introduction
- -
- The amount of steel required in the girders was reduced, e.g., by removing the sections from the neutral axis of the girder cross-section in the storied arrangement [16]. The construction solution used was noted as an invention (number P.438762).
- -
- An innovative solution for the cross-beam was used, and a plate and grating system was designed; this allowed a significant reduction in the weight of this element. The construction solution used was claimed as an invention (number P.448192).
- -
- The number of elements in the structure has been reduced while ensuring the possibility of constructing a number of variants of the structural system; this will allow the crossing to be easily adapted to local conditions and the needs of the users.
- -
- Modern composite materials, which are widely applied in civil engineering, were used to make deck slabs [17,18,19,20,21,22]; the slabs were shaped with pre-set gradients and a built-in drainage system, which ensures that rainwater is drained from the deck surface in accordance with modern environmental requirements.
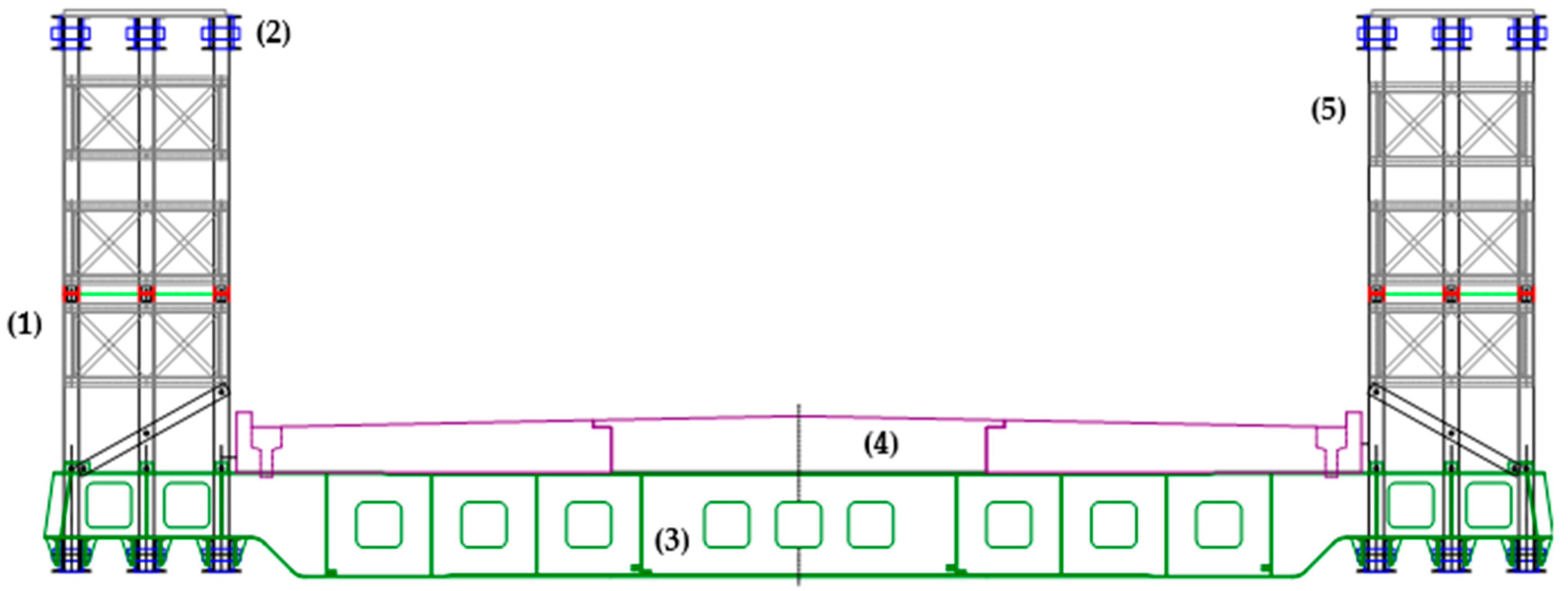
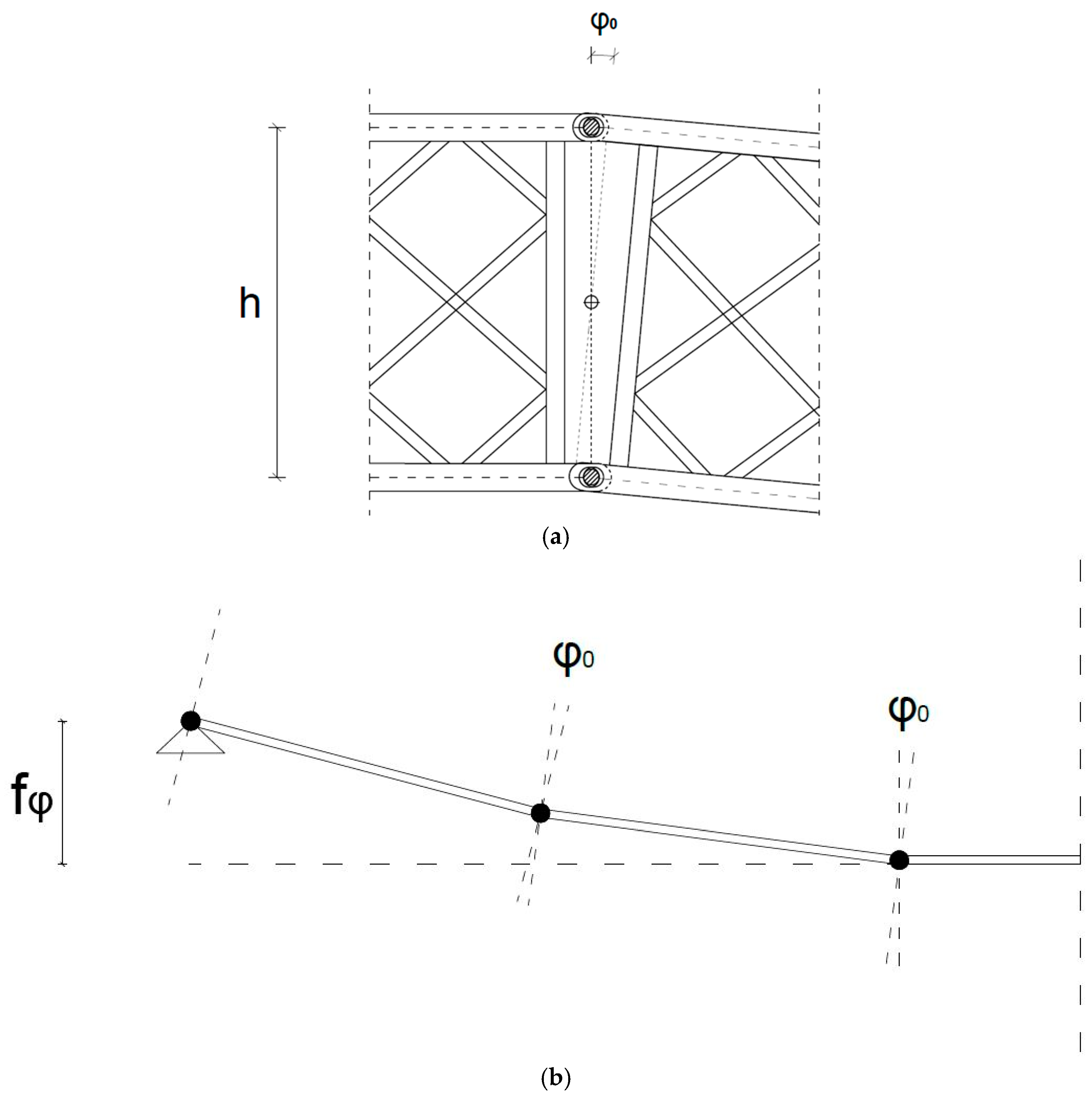
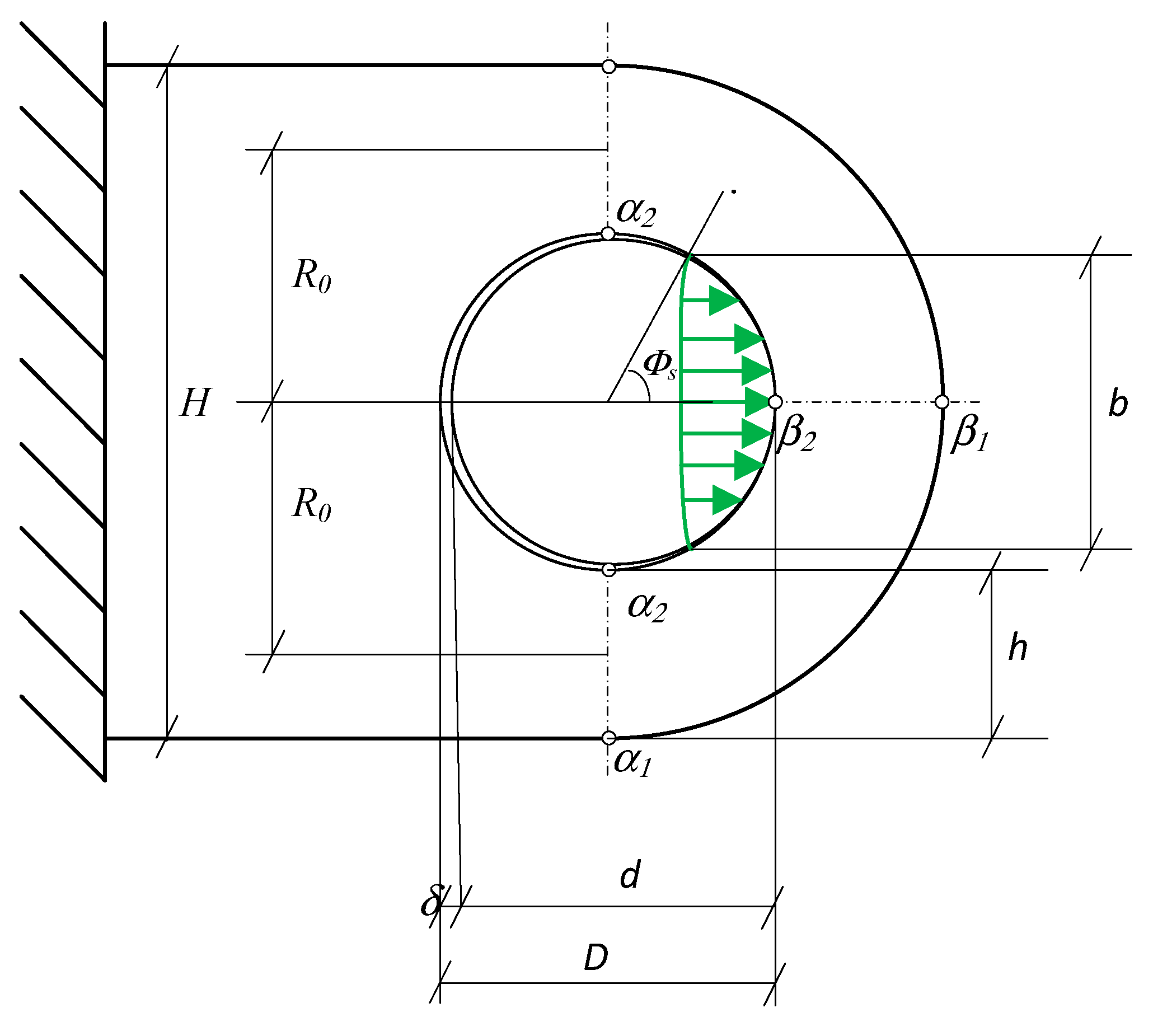
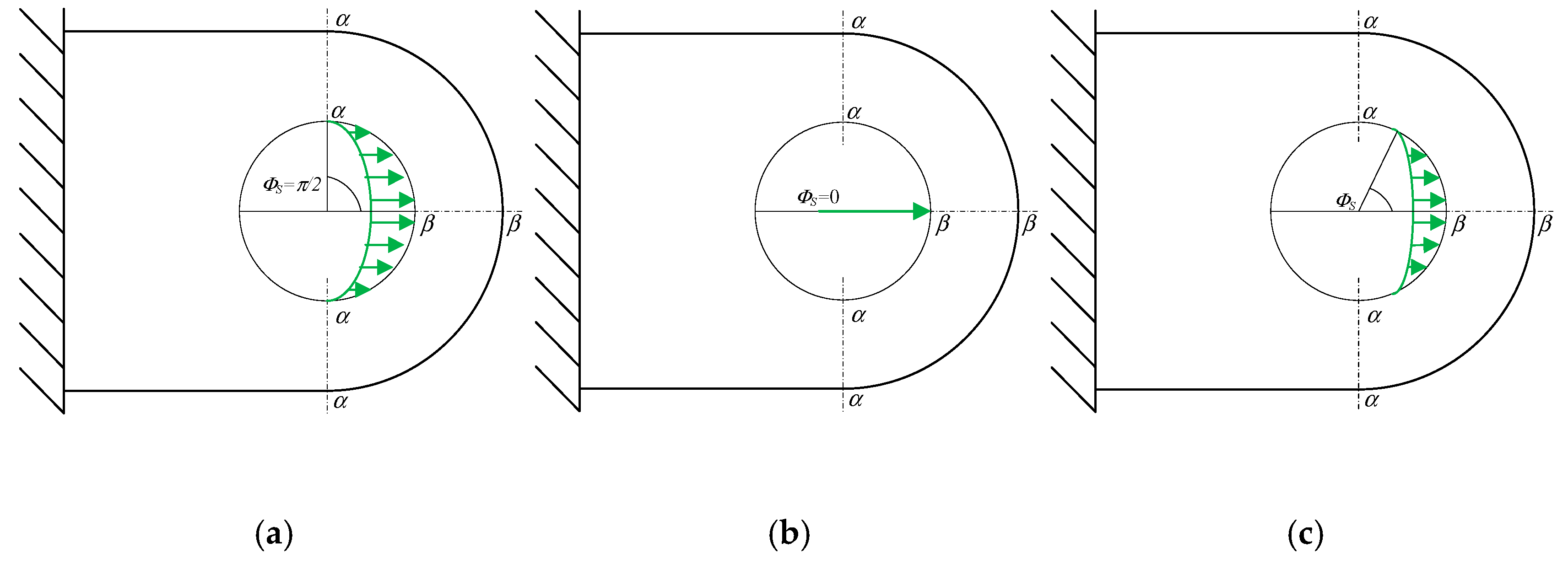
2. Influence of Pin Connection Assembly Clearances on the Distribution of Internal Forces in Folding Bridges
3. Bridge Pin Connection Concept MSC 23-150
- -
- Pin shear;
- -
- The pressure of the pin on the brackets or the mutual compression of the pin and the brackets;
- -
- Stretching of the net section of a single bracket or stretching of a single bracket;
- -
- Pin bending.
- -
- Checking the shear stress values when the pin is subjected to shearing:
- -
- Checking the clamping stresses in the connection brackets (the least favourable value is taken into account for the calculation, usually the clamping stress on a single connection):
- (a)
- Initial clamping stress in a single connection:
- (b)
- Initial clamping stress in the double connection:
- -
- Checking the tension in the pin from bending:
- -
- Checking the tensile stress in the net section of a single connection, i.e., the cross-sectional area reduced by the cross-sectional area of the pin hole:
- -
- Pin shear force stress, which is the basic factor determining the suitability of individual fasteners for transferring loads through a connection of a given type:
- -
- Clamping stress in a single pin connection bracket, under full load:
- -
- Normal pin bending moment stress:
- -
- Tensile stress in the net section of the single pin connection bracket (average in section α-α, i.e., without taking stress concentration factors into account):
- -
- At a point outside the pin eye:
- -
- At a point inside the pin eye:
- -
- At a point outside the pin eye:
- -
- At a point inside the pin eye:
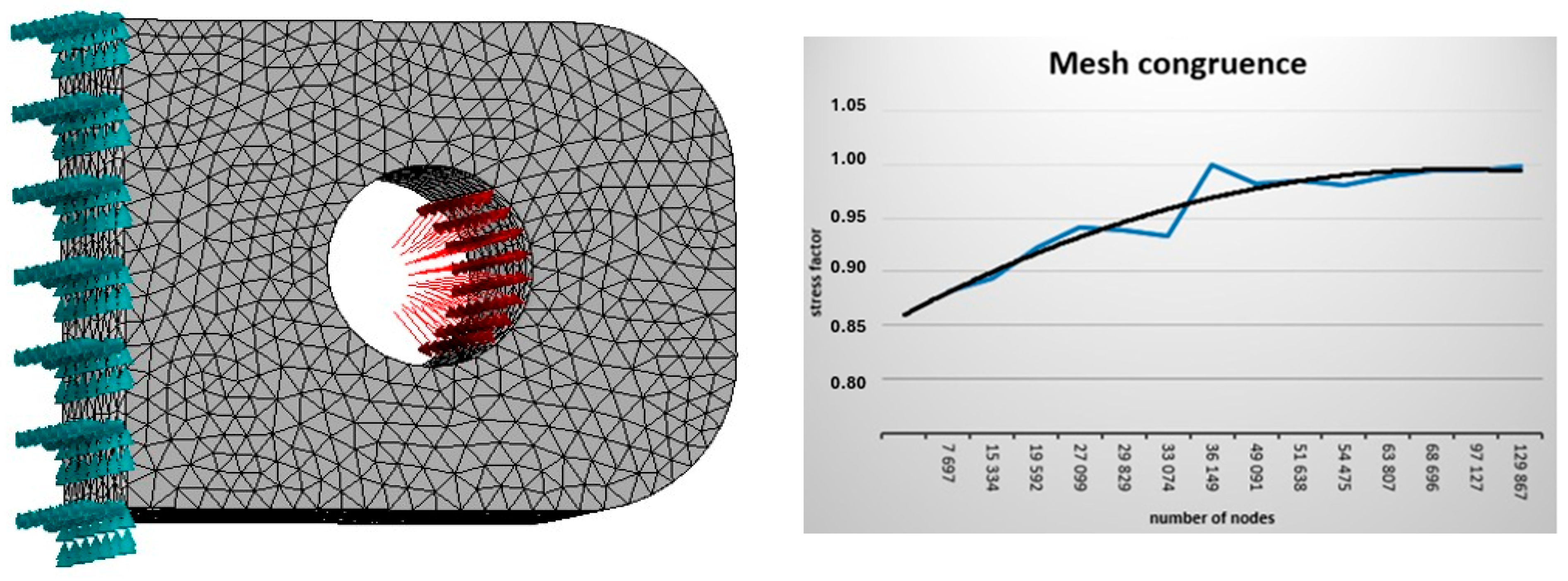
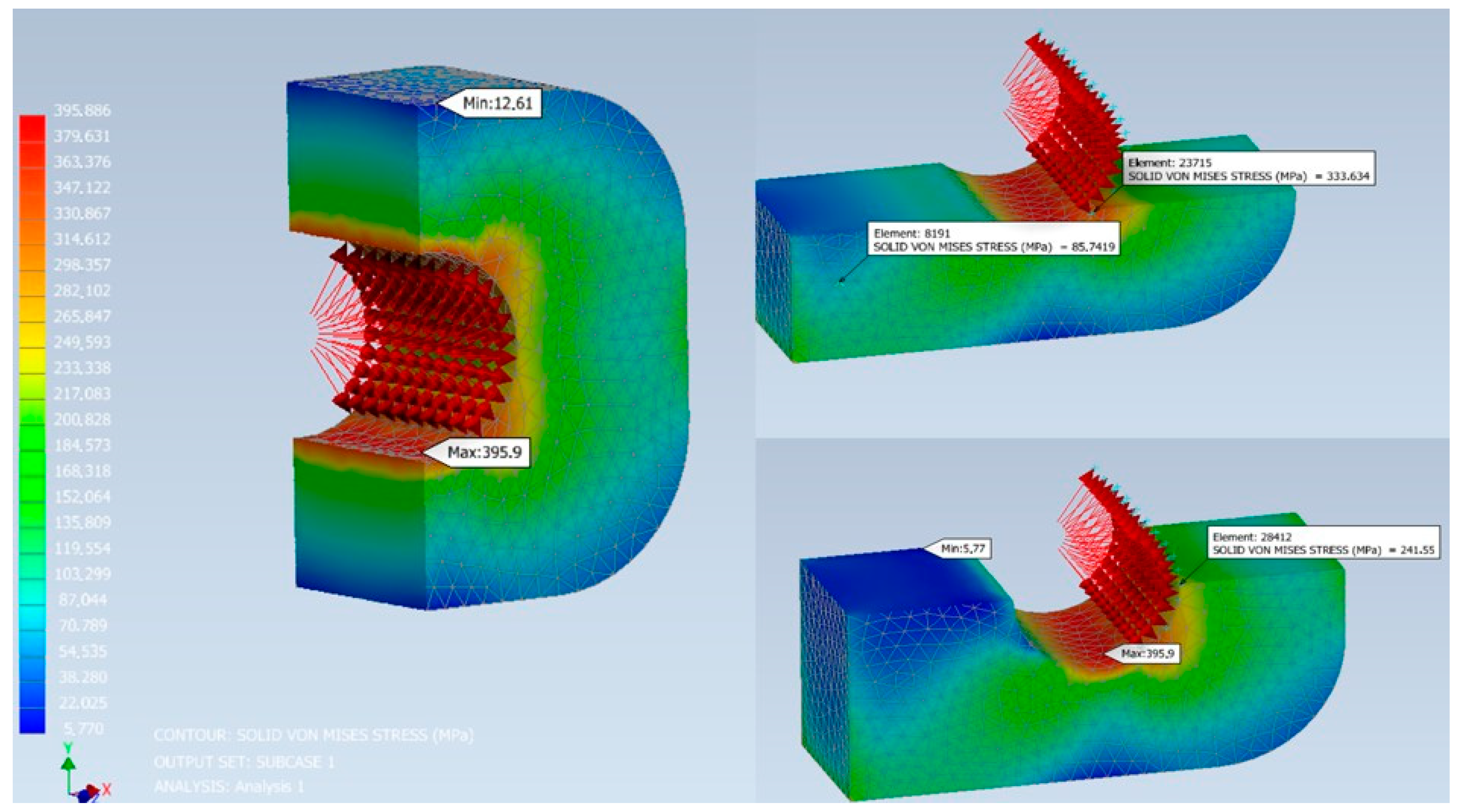
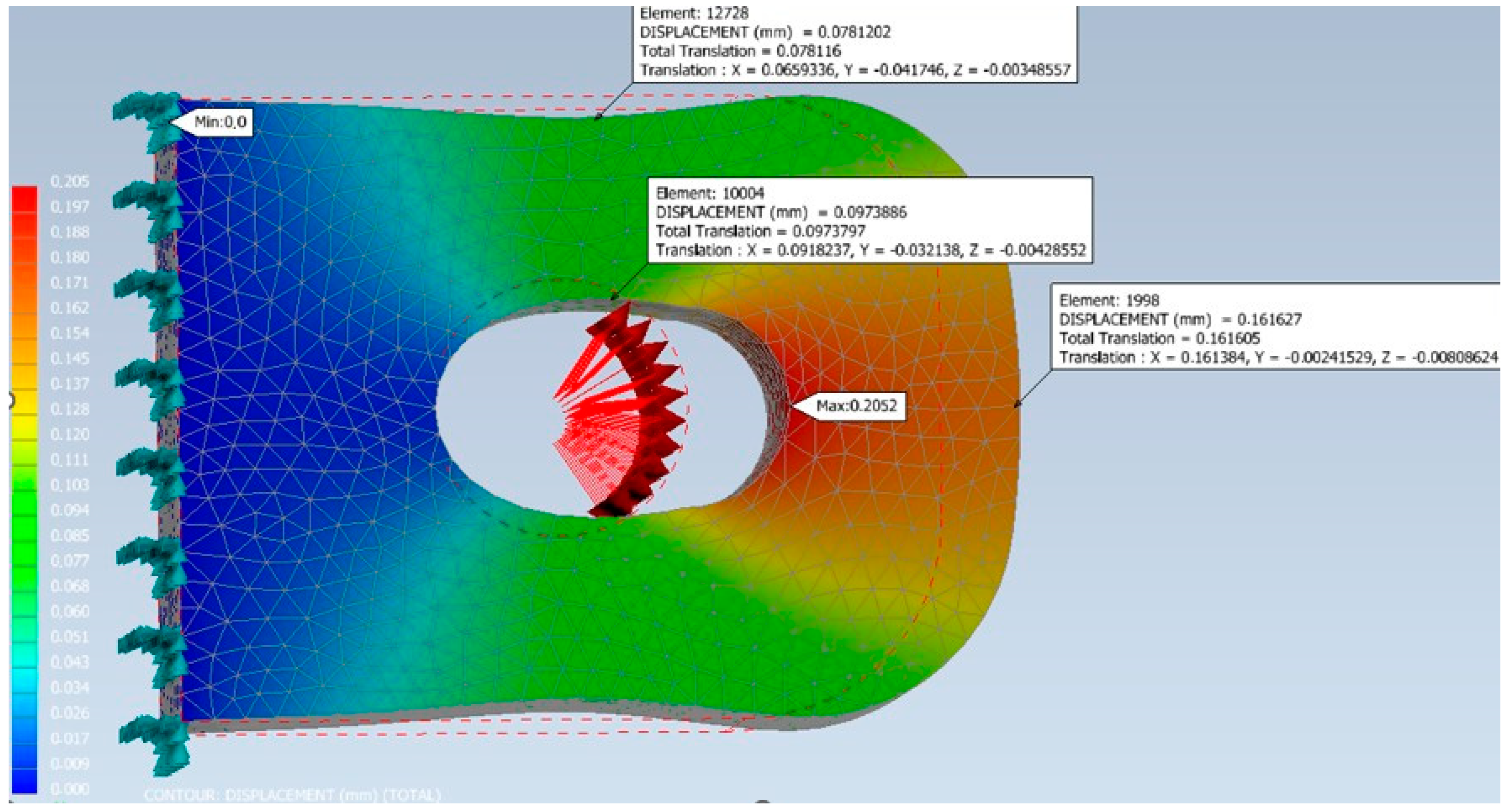
4. Pin Connection Model Analysis
5. Discussion
6. Conclusions
- Due to the nature of folding bridge structures and in order to ensure the structural and operational safety of the bridges, material plasticisation is not permissible. This also applies to the pin connections themselves, both the eyes and the pins. Permanent deformation of the connector eyes can lead to an increase in kinematic deflection, while such deformation of the pins can make it impossible to reassemble the structure using them.
- Based on the assumed pin connection meeting the load-bearing requirements for MSC 23-150 and based on calculations using the Herz formula [24,25,26], a method was proposed for taking assembly clearances into account in a bolted connection when calculating the stress on its components. The analytically obtained values were confirmed by the results obtained in numerical calculations, which proves the usefulness of this method.
- Through use of an analytical method based on taking into account the actual contact area and a numerical method, the load-bearing capacity of the proposed connector was positively verified, which allows it to be used in the construction of the MSC 23-150 bridge. It is worth adding that preliminary calculations of the MSC 23-150 bridge showed that it would be possible to build crossings from this structure under the maximum military loads specified by MLC 150 (Military Load Classification). This will require the use of girders in a two-storey, three-wall arrangement and will enable free-span beam crossings of more than 80 m, with a limit of one vehicle per bridge span. The designed structure makes it possible to achieve significantly higher efficiencies, expressed in the square of the span by the weight [16], compared to the structures currently in use. The proposed solution enables the construction of crossings using proven technology by sliding the structure along an assembly track.
- The designed connection will carry all loads that may be imposed on the bridge structure during its construction and use. Because of the significant reduction in the load-bearing capacity of the bridge structure due to potential asymmetry of the pin connection, efforts should be made to minimise the assembly clearance (gaps) between the connection eyes. The proposed slots of 0.6 mm on each side of the connection allow the structure to be assembled with the least possible asymmetric load on the pin. In addition, it minimises the risk of buckling of the top chord of the bridge structure in the horizontal plane.
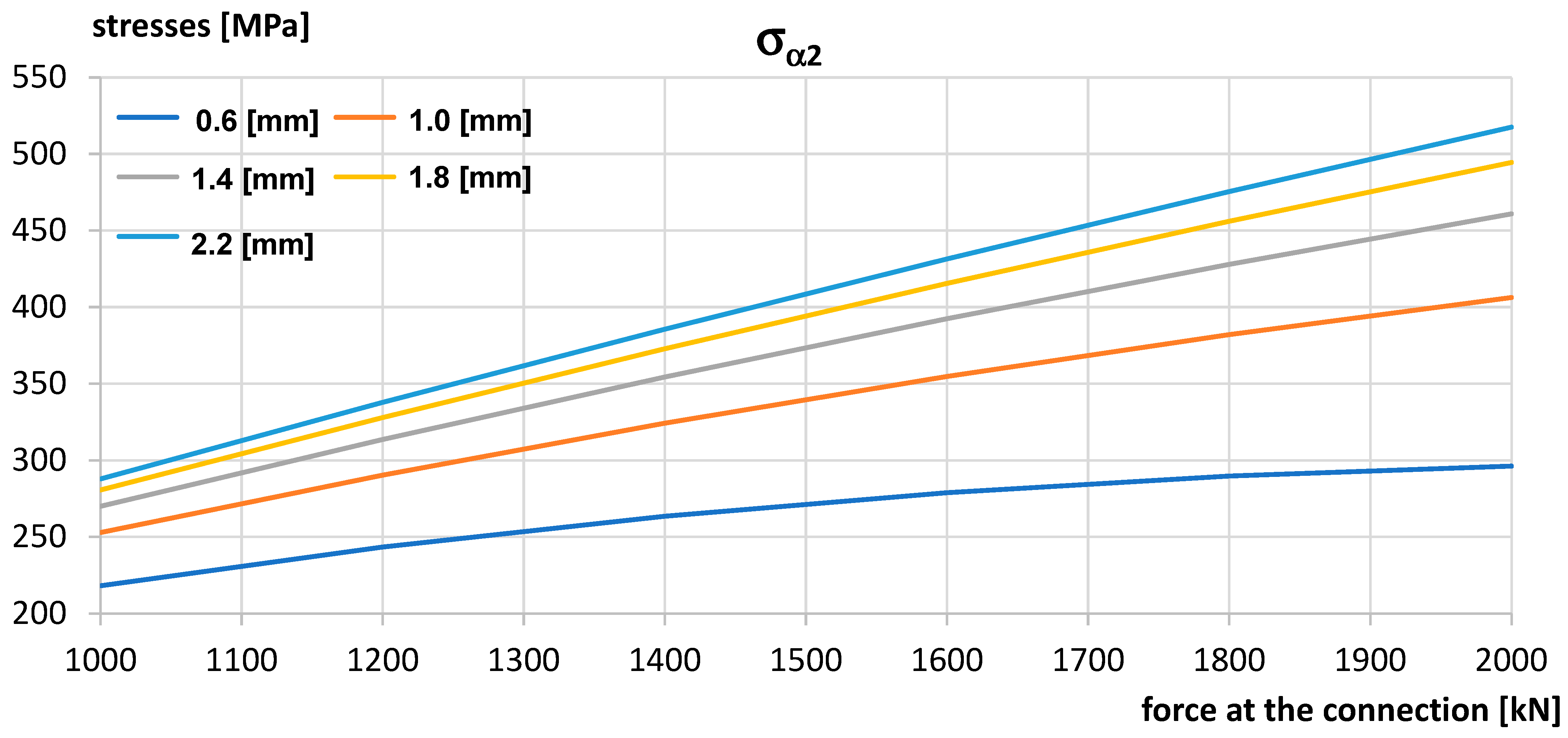
- In the analysis of pin connections, similar results were obtained using analytical and numerical methods. Based on convergence of analytical and numerical method results, it can be concluded that the proposed analytical method is a good tool to take into account the backlash on the design resistance of pin couplings in built-up bridges. Unfortunately, like any method, the numerical analysis is limited and makes certain assumptions. In view of the above, it is estimated that the margin of error for both methods may range from 5 to 10%. This is mainly due to the selection of the mesh size in the case of the numerical method and the approximations used for the analytical method. The analyses carried out in this paper are based on the assumption that the bridge pin connection only works in the elastic range, due to the cyclic nature of bridge rigging and the fact that bridge structures should not work in the plastic range. For the purpose of the analysis, it was assumed that the force acts on the joint in the direction parallel to the bridge axis. A further simplification is that the force acting on the joint is assumed to be a statically acting force. It is also worth mentioning the contact area between the pin and the joint component. The contact area of these elements was assumed on the basis of analytical calculations. Nevertheless, the results of the numerical and analytical analyses are similar, which demonstrates the suitability of the analytical method presented in this article for the calculation of pin joints of collapsible bridges.
- The results of the analysis clearly indicate that as the force in the belts increases, the significance of the influence of assembly clearance on stress concentration decreases due to an increase in the contact area for specific assembly clearance values. However, taking the stress concentration factor into account causes an increase in the maximum normal stress in the bolted joint by up to 300%, which has a fundamental impact on determining the load-bearing capacity of this type of connection.
- The next stage of research should be the validation of the numerical model and testing of the use of pins made of different materials or with different cross-section parameters, e.g., different stiffness. This is due to the simultaneous need to minimise assembly clearances in the connection and reduce the weight of the bolt. It is possible that bolts made of different material or composite material will exhibit different stiffness, which will affect the size of the so-called contact area between the pin and the bridge connector.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EC | Eurocode |
| MLC | Military Load Classification |
References
- Białobrzeski, T. Portable Bridge; Communication and Connectivity Publishing House: Warsaw, Poland, 1978. [Google Scholar]
- Marszałek, J.; Jarzyna, J.; Bryda, P.; Chmielewski, R.; Jakubowski, G.; Marcinkowski, R.; Rymsza, J. Portable bridge. In Design, Construction, and Operation; GDDKiA: Warsaw, Poland, 2005. [Google Scholar]
- Benda, M.; Coufal, D.; Sobotka, J. Specific Aspects of Bridge Construction in the Central African Republic. Adv. Mil. Technol. 2016, 11, 253–260. [Google Scholar] [CrossRef]
- Ostrowska, A.; Chmielewski, R. Overview of the organisation and technology of portable panel bridges. Inżynieria Bezpieczeństwa Obiektów Antropog. 2023, 1, 46–52. [Google Scholar] [CrossRef]
- Wolniewicz, A.; Chmielewski, R. Diagnostics and operation of folding bridge structures used in civil transport construction. Logistyka 2016, 1, 137–143. [Google Scholar]
- Drozdowska, K. Concept for adapting the DMS-65 military folding bridge into a permanent structure. Bezpieczeństwo I Ekol. 2016, 6, 156–159. [Google Scholar]
- Andre, A.; Fernandes, J.; Ferraz, I.; Pacheco, P. New Modular Bridges Solutions, 9th International Symposium on Steel Bridges. Mater. Sci. Eng. 2018, 419, 012021. [Google Scholar] [CrossRef]
- Benda, M. Reach back possibility temporary bridges after floods in 2013. In Proceedings of the Medzinárodná Vedecká Konferencia, Riešenie Krízových Situácií v Špecifickom Prostredí, Žilina, Slovakia, 21–22 May 2014; pp. 59–66. [Google Scholar]
- Falkowski, M.; Mondel, A. Overview of US Army military bridges. Zesz. Nauk. WSOWL 2010, 156, 158–177. [Google Scholar]
- Russell, B.R.; Thrall, A.P. Portable and Rapidly Deployable Bridges: Historical Perspective and Recent Technology Developments. J. Bridge Eng. 2012, 18, 1074–1085. [Google Scholar] [CrossRef]
- Chmielewski, R.; Wolniewicz, A. Classification of the modernized DMS-65 folded bridge structure according to STANAG 2021 requirements. Roads Bridge—Drog. I Most. 2017, 16, 147–158. [Google Scholar] [CrossRef]
- Xu, G.Y.; Chu, O.; Jie, Z. Development of ZJ200 Portable Steel Bridge. Appl. Mech. Mater. 2012, 188, 123–129. [Google Scholar] [CrossRef]
- Defense Standard NO-54-A203:2020; Portable Bridges—General Requirements. MON: Warsaw, Poland, 2020.
- NATO Standardization Agency. STANAG 2021 JAS (Edition 6)—Military Load Classification of Bridges, Ferries, Rafts and Vehicles; NSA: Brussels, Switzerland, 2006. [Google Scholar]
- EN 1991-2; Eurocode 1: Actions on Structures—Part 2: Traffic Loads on Bridges. CEN: Brussels, Switzerland, 2003.
- Wang, Y.; Thrall, A.P.; Zoli, T.P. Adjustable module for variable depth steel arch bridges. J. Constr. Steel Res. 2016, 126, 163–173. [Google Scholar] [CrossRef]
- Zobel, H.; Karwowski, W. Polymer composites in bridge engineering: Multilayer bridges. Geoinżynieria: Drog. Mosty I Tunele 2006, 9, 42–49. [Google Scholar]
- Siwowski, T.; Zobel, H.; Al-Khafaji, T.; Karwowski, W. FRP Bridges in Poland: State of practice. Arch. Civ. Eng. 2021, 67, 5–27. [Google Scholar] [CrossRef]
- Lu, C.; Wang, X.; Ning, Y.; Wen, K.; Wang, Q. Numerical Investigation on the Structural Behavior of a Short-Span Cable-Stayed Bridge with Steel and CFRP Hybrid Cables. Materials 2024, 17, 2032. [Google Scholar] [CrossRef]
- Alomari, Q.A.; Linzell, D.G.; Zouriq, M.F.A. Response of Bare and CFRP-Retrofitted Multi-Column Piers Under Post-Fire-Coupled Vehicle Collision and Air Blast. Materials 2025, 18, 1449. [Google Scholar] [CrossRef]
- Dervishhasani, G.; Sennah, K.; Afefy, H.M.; Diab, A. Ultimate Capacity of a GFRP-Reinforced Concrete Bridge Barrier–Deck Anchorage Subjected to Transverse Loading. Appl. Sci. 2025, 15, 7771. [Google Scholar] [CrossRef]
- Xiong, J.; Ai, P.; Xu, J.; Yang, J.; Feng, P. A comprehensive study on CFRP rapid portable bridge: Design, experimental investigation and finite element analysis. Compos. Struct. 2022, 289, 115439. [Google Scholar] [CrossRef]
- Bursztynowski, Z. Stress analysis in folding bridge joints. Drog. Kolejowe 1990, 11, 177–180. [Google Scholar]
- Hertz, H. Über die Berührung fester elastischer Körper. J. Reine Angew. Mathem. 1881, 92, 156–171. [Google Scholar]
- Timoshenko, S.; Goodier, J.N. Theory of Elasticity; McGraw-Hill: New York, NY, USA, 1951. [Google Scholar]
- Duerr, D. Pinned connection strength and behaviour. J. Struct. Eng. 2006, 132, 182–194. [Google Scholar] [CrossRef]
- Choo, Y.S.; Choi, K.C.; Lee, K.H. The effects of eye bar shape and pin/hole tolerance on its ultimate strength. J. Constr. Steel Res. 1993, 26, 153–169. [Google Scholar] [CrossRef]
- Harms, I. Pinned Connections. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2015. [Google Scholar]
- Conde, J.; da Silva, L.S.; Tankova, T.; Simões, R.R.; Abecasis, T. Design of pin connections between steel members. J. Constr. Steel Res. 2023, 201, 107752. [Google Scholar] [CrossRef]
- EN 1993-1-8; Eurocode 3: Design of Joints. CEN: Brussels, Switzerland, 2005.
- Montgomery, J.; Higgins, C.D.; Liu, J. Capacities of Pin and Hanger Assemblies. In Phase 1—Report Number: CA18-3023; Oregon State University: Corvallis, OR, USA, 2018. [Google Scholar]
- Cios, K.; Krasoń, W. Selected aspects of numerical analysis of a scissor bridge joint. Mechanik 2015, 7, 592–594. [Google Scholar] [CrossRef]
- Autodesk Inventor Nastran; Software for 3D Modeling and Numerical Calculations; Autodesk Company: San Francisco, CA, USA, 2022.




| Force at the Connection [kN] | Contact Area Height b [mm] | Contact Angle of the Contact Area 2Φs [°] |
|---|---|---|
| 1000 | 59.69 | 81.97 |
| 1200 | 63.43 | 88.37 |
| 1400 | 66.77 | 94.40 |
| 1600 | 69.81 | 100.19 |
| 1800 | 72.60 | 105.85 |
| 2000 | 75.20 | 111.45 |
| Force at the Connection [kN] | Maximum Stress in Section β-β in a Single Pin Connection Eye | Percentage Increase in the Stress Value [%] | |
|---|---|---|---|
| [MPa] | [MPa] | ||
| 1000 | 113.38 | 187.29 | 65.19 |
| 1200 | 136.05 | 214.66 | 57.77 |
| 1400 | 158.73 | 240.67 | 51.62 |
| 1600 | 181.41 | 265.78 | 46.51 |
| 1800 | 204.08 | 290.37 | 42.28 |
| 2000 | 226.76 | 317.19 | 39.88 |
| Force at the Connection [kN] | Unit Stress [MPa] | [MPa] | |
|---|---|---|---|
| 1000 | 79.10 | 3.20 | 252.87 |
| 1200 | 94.92 | 3.06 | 290.31 |
| 1400 | 110.74 | 2.93 | 324.22 |
| 1600 | 126.56 | 2.80 | 354.78 |
| 1800 | 142.38 | 2.68 | 382.09 |
| 2000 | 158.20 | 2.57 | 406.34 |
| Force at the Connection [kN] | Stress (Analytical Method) [MPa] | Stress From the Model (Numerical Method) σβM [MPa] | Maximum Model Stress (Numerical Method) σβMmax [MPa] | [%] |
|---|---|---|---|---|
| 1000 | 187.29 | 148.00 | 192.59 | 102.83% |
| 1200 | 214.66 | 164.63 | 217.72 | 101.43% |
| 1400 | 240.67 | 185.50 | 256.34 | 106.51% |
| 1600 | 265.78 | 196.10 | 272.26 | 102.44% |
| 1800 | 290.37 | 218.33 | 298.57 | 102.82% |
| 2000 | 317.19 | 241.55 | 333.63 | 105.18% |
| Force at the Connection [kN] | Stress (Analytical Method) [MPa] | Stress from the Model (Numerical Method) σαM [MPa] | [%] |
|---|---|---|---|
| 1000 | 252.87 | 227.4 | 89.93% |
| 1200 | 290.31 | 263.5 | 90.76% |
| 1400 | 324.22 | 296.1 | 91.33% |
| 1600 | 354.78 | 330.2 | 93.07% |
| 1800 | 382.09 | 363.1 | 95.03% |
| 2000 | 406.34 | 395.9 | 97.43% |
| Force at the Connection [kN] | Intensity in Cross Section α-α | Net Cross-Sectional Stress Obtained on the Basis of EC | Intensity in Cross Section β-β | Compressive Stress Obtained on the Basis of EC |
|---|---|---|---|---|
| 2000 | 0.92 | 0.72 | 0.72 | 0.86 |
| Force at the Connection [kN] | Displacement [mm] | Displacement [mm] | Displacement [mm] | Displacement [mm] |
|---|---|---|---|---|
| 1000 | 5.95 × 10−2 | 4.73 × 10−2 | 12.53 × 10−2 | 9.58 × 10−2 |
| 1200 | 6.85 × 10−2 | 5.49 × 10−2 | 14.46 × 10−2 | 11.17 × 10−2 |
| 1400 | 7.63 × 10−2 | 6.12 × 10−2 | 16.12 × 10−2 | 12.49 × 10−2 |
| 1600 | 8.22 × 10−2 | 6.69 × 10−2 | 17.58 × 10−2 | 13.70 × 10−2 |
| 1800 | 8.65 × 10−2 | 7.20 × 10−2 | 18.94 × 10−2 | 14.81 × 10−2 |
| 2000 | 9.33 × 10−2 | 7.81 × 10−2 | 20.52 × 10−2 | 16.15 × 10−2 |
| Clearance [mm] | 0.6 | 1.4 | 1.8 | 2.2 | ||||
|---|---|---|---|---|---|---|---|---|
| Force [kN] | b [mm] | 2Φs [°] | b [mm] | 2Φs [°] | b [mm] | 2Φs [°] | b [mm] | 2Φs [°] |
| 1000 | 70.87 | 102.30 | 53.27 | 71.67 | 48.92 | 65.04 | 45.69 | 60.27 |
| 1200 | 75.31 | 111.70 | 56.61 | 76.94 | 51.98 | 69.68 | 48.55 | 64.48 |
| 1400 | 79.28 | 121.20 | 59.60 | 81.83 | 54.73 | 73.94 | 51.11 | 68.34 |
| 1600 | 82.89 | 131.25 | 62.31 | 86.43 | 57.22 | 77.92 | 53.43 | 71.92 |
| 1800 | 86.21 | 142.65 | 64.80 | 90.82 | 59.51 | 81.68 | 55.57 | 75.28 |
| 2000 | 89.29 | 157.75 | 67.12 | 95.05 | 61.64 | 85.27 | 57.56 | 78.47 |
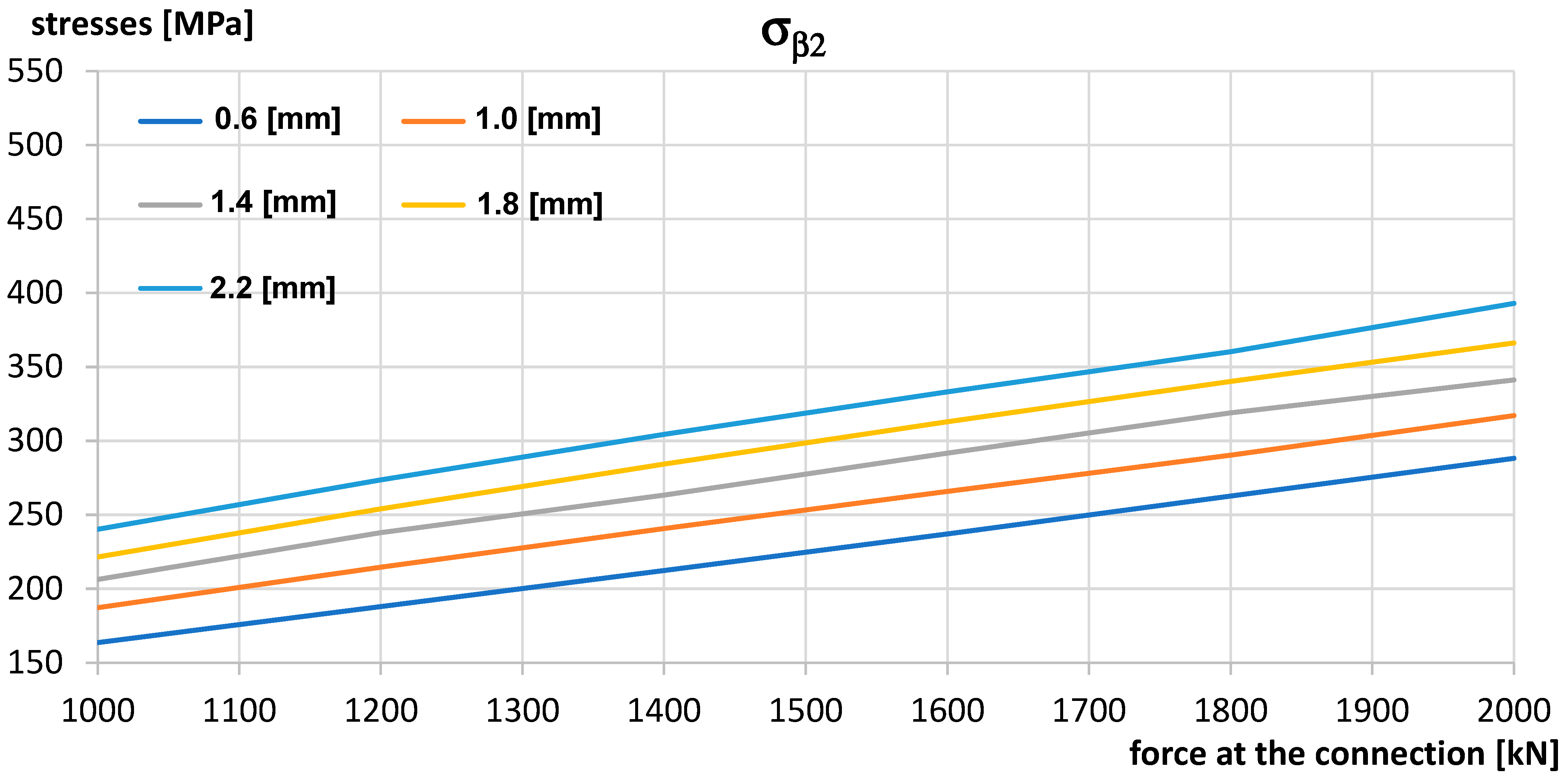
| Clearance [mm] | 0.6 | 1.4 | 1.8 | 2.2 | ||||
|---|---|---|---|---|---|---|---|---|
| Force [kN] | [MPa] | [MPa] | [MPa] | [MPa] | [MPa] | [MPa] | [MPa] | [MPa] |
| 1000 | 218.18 | 163.69 | 270.06 | 206.34 | 280.63 | 221.54 | 287.89 | 240.25 |
| 1200 | 243.32 | 188.00 | 313.62 | 238.01 | 327.94 | 254.04 | 337.79 | 273.62 |
| 1400 | 263.47 | 212.31 | 354.36 | 263.38 | 372.87 | 284.36 | 385.60 | 304.40 |
| 1600 | 278.87 | 237.09 | 392.41 | 291.71 | 415.54 | 312.94 | 431.45 | 333.12 |
| 1800 | 289.73 | 262.67 | 427.91 | 318.96 | 456.05 | 340.15 | 475.41 | 360.23 |
| 2000 | 296.24 | 288.30 | 460.94 | 341.22 | 494.49 | 366.28 | 517.55 | 392.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mikulski, E.; Chmielewski, R.; Wolniewicz, A.; Ostrowska, A. Analysis of the Application of Analytical and Numerical Methods for the Dimensioning of Pin Connections of Folding Bridges. Appl. Sci. 2025, 15, 10047. https://doi.org/10.3390/app151810047
Mikulski E, Chmielewski R, Wolniewicz A, Ostrowska A. Analysis of the Application of Analytical and Numerical Methods for the Dimensioning of Pin Connections of Folding Bridges. Applied Sciences. 2025; 15(18):10047. https://doi.org/10.3390/app151810047
Chicago/Turabian StyleMikulski, Erik, Ryszard Chmielewski, Andrzej Wolniewicz, and Alicja Ostrowska. 2025. "Analysis of the Application of Analytical and Numerical Methods for the Dimensioning of Pin Connections of Folding Bridges" Applied Sciences 15, no. 18: 10047. https://doi.org/10.3390/app151810047
APA StyleMikulski, E., Chmielewski, R., Wolniewicz, A., & Ostrowska, A. (2025). Analysis of the Application of Analytical and Numerical Methods for the Dimensioning of Pin Connections of Folding Bridges. Applied Sciences, 15(18), 10047. https://doi.org/10.3390/app151810047





