Data-Driven Tracing and Directional Control Strategy for a Simulated Continuum Robot Within Anguilliform Locomotion
Abstract
1. Introduction
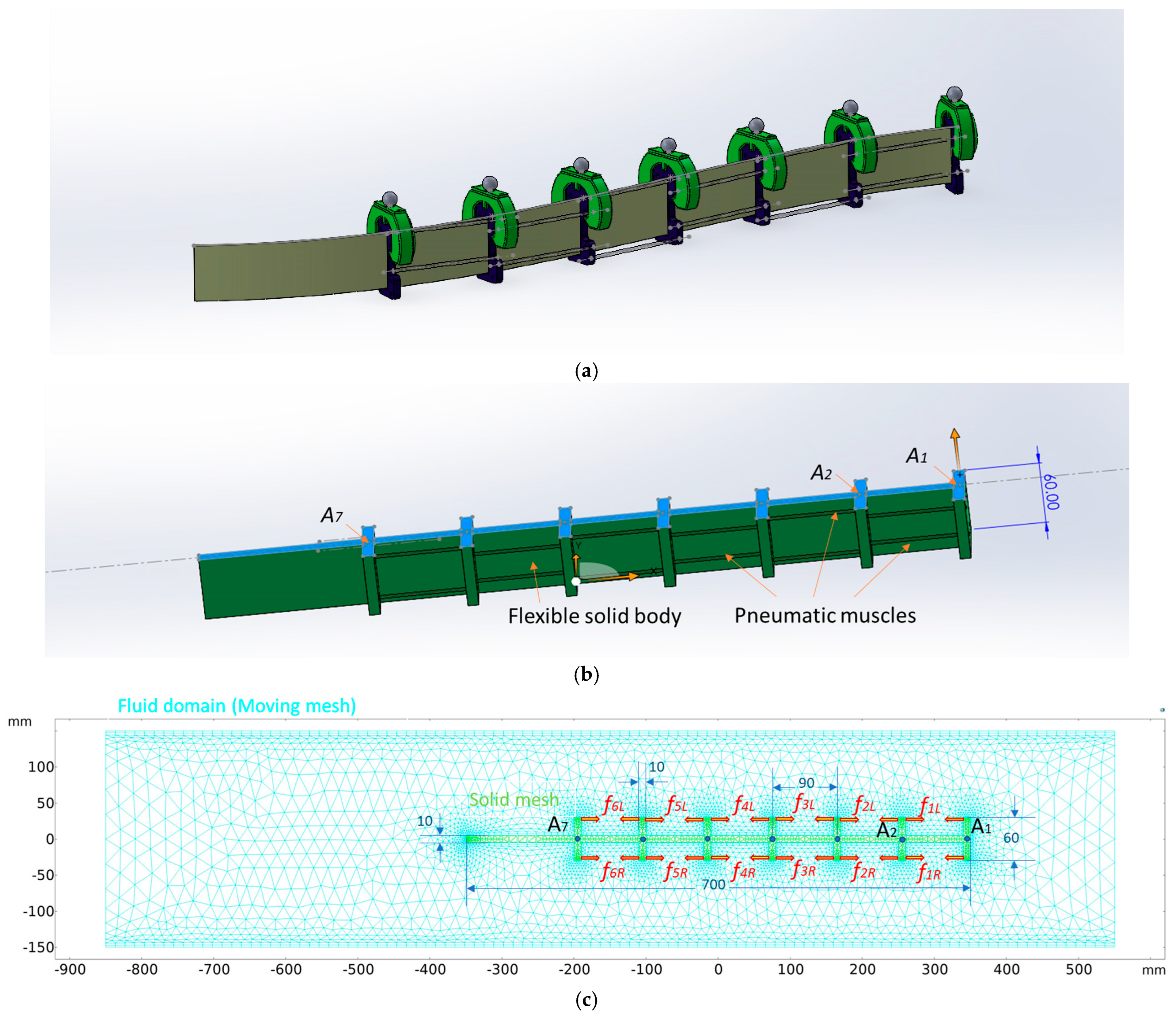
2. Materials and Methods
2.1. The Problem of Directional Stability
2.2. The Proposed CDE DMD Algorithm
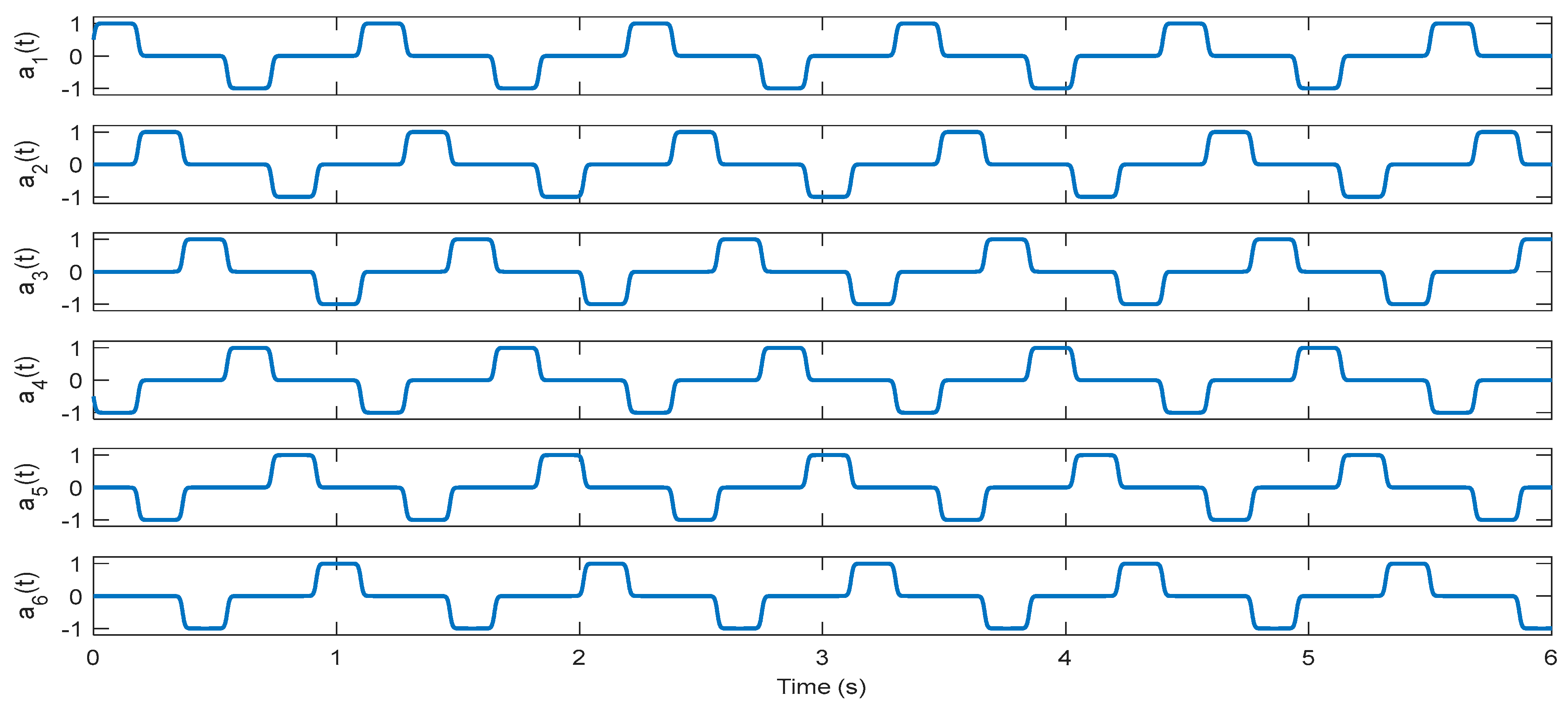
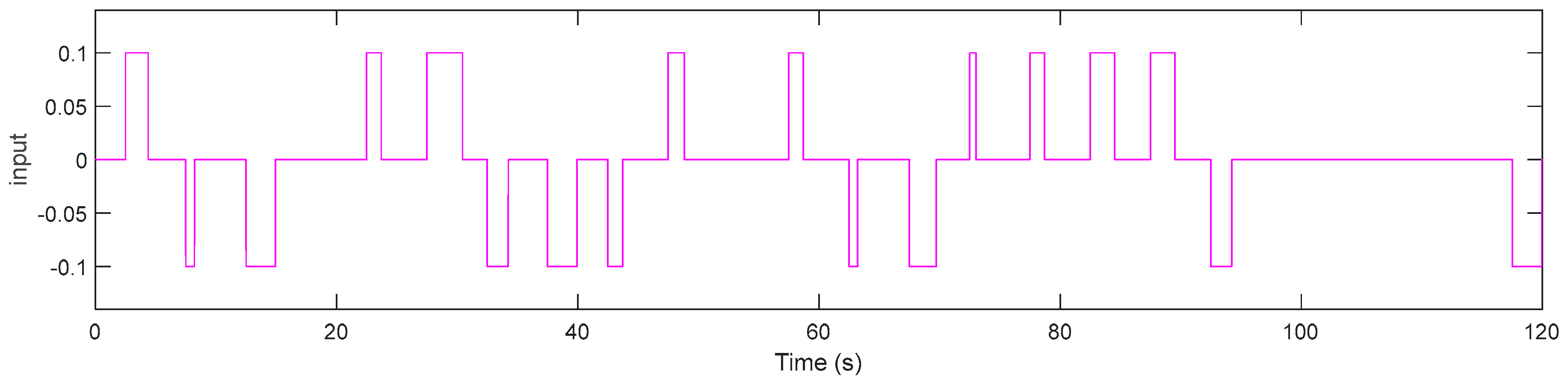
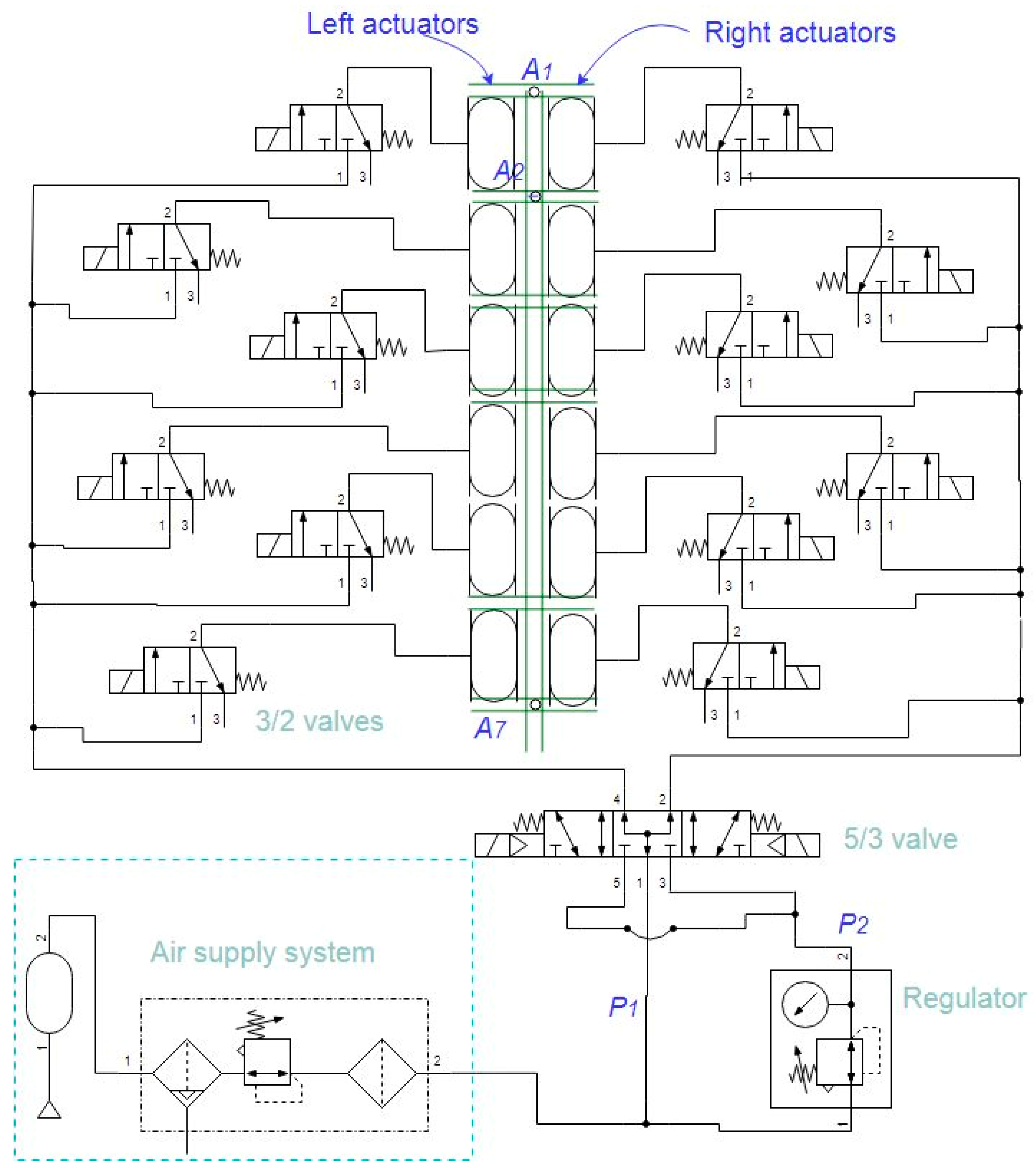
2.3. Actuation Mechanism
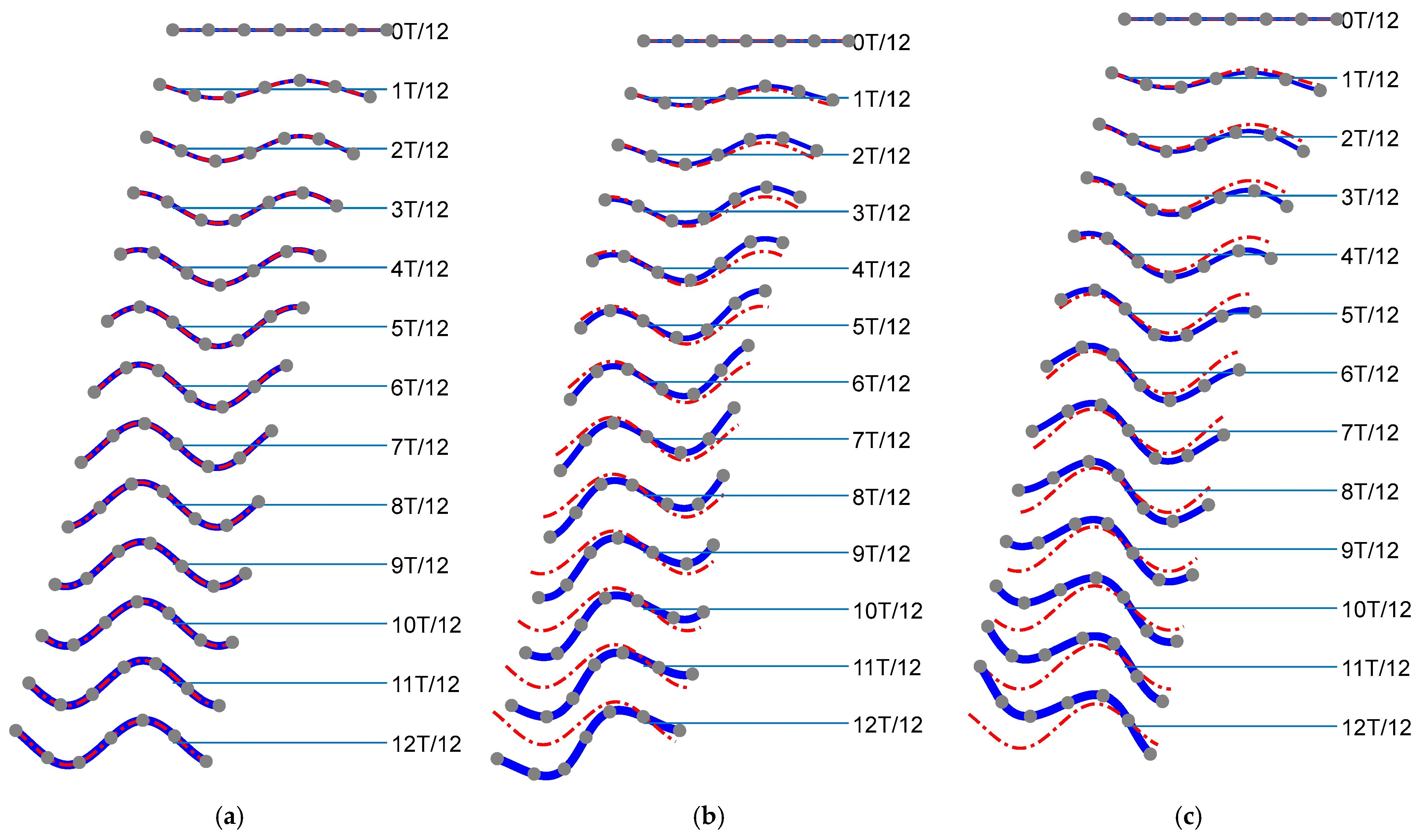
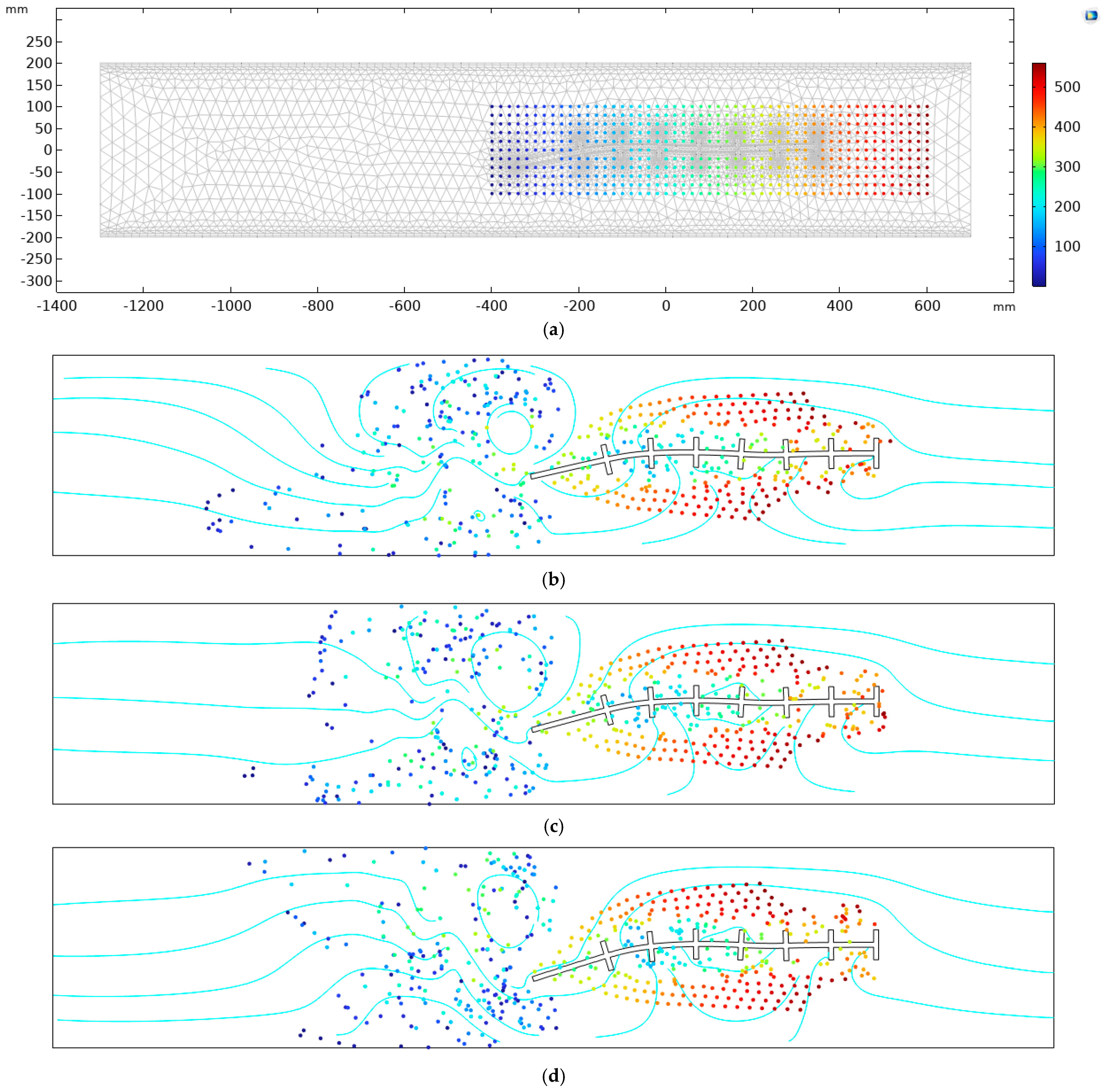
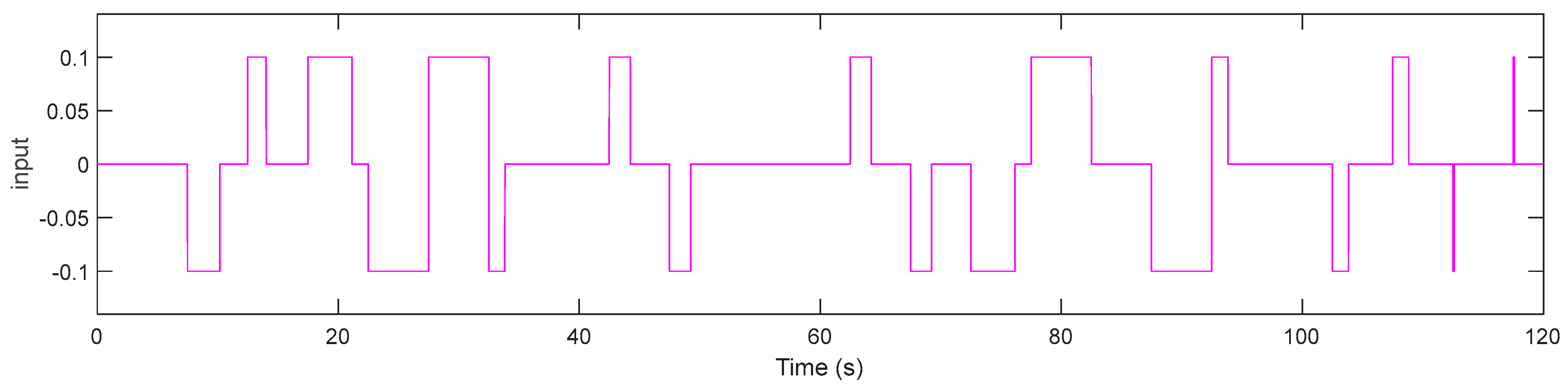
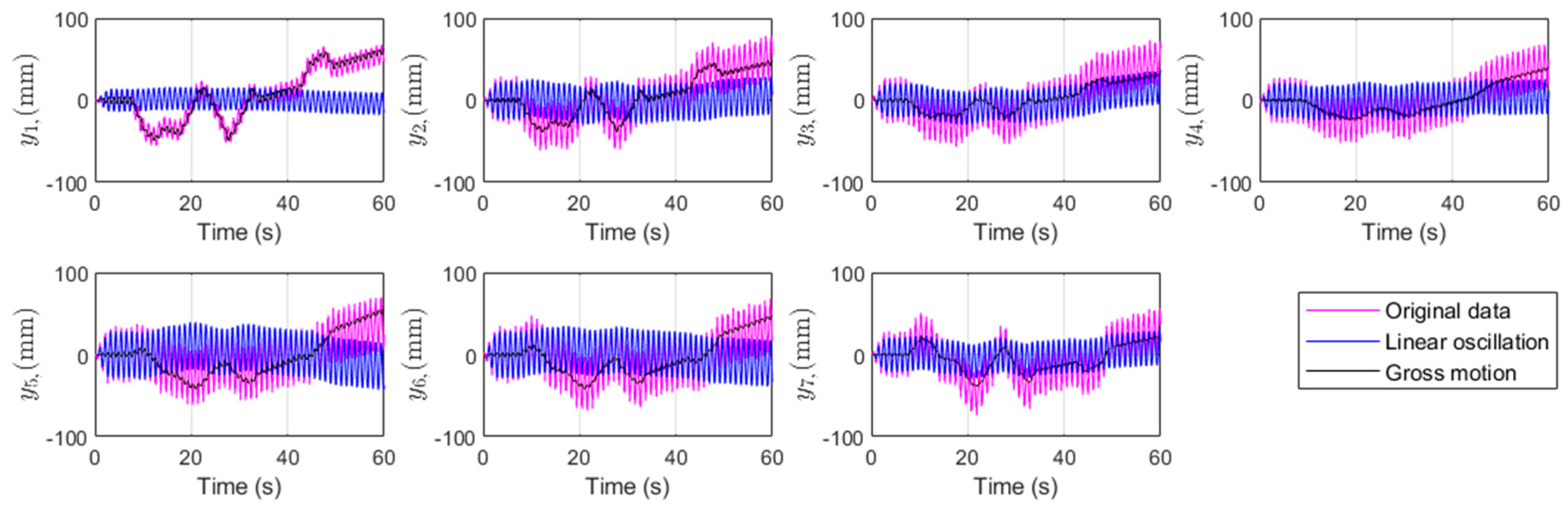
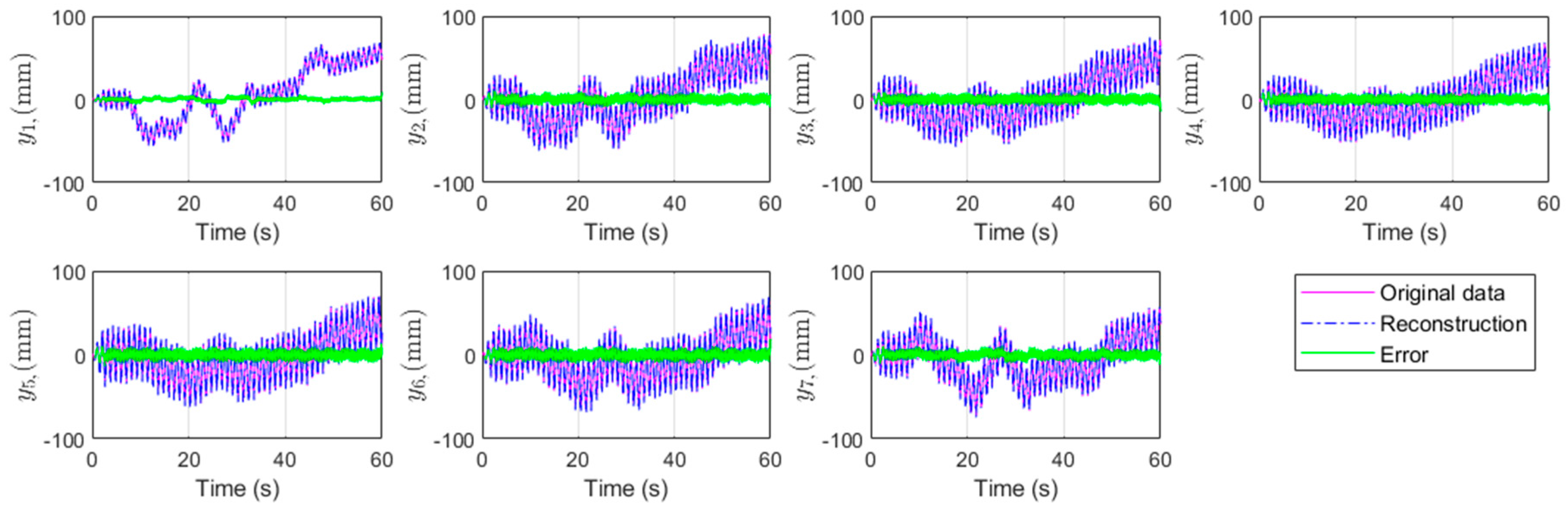
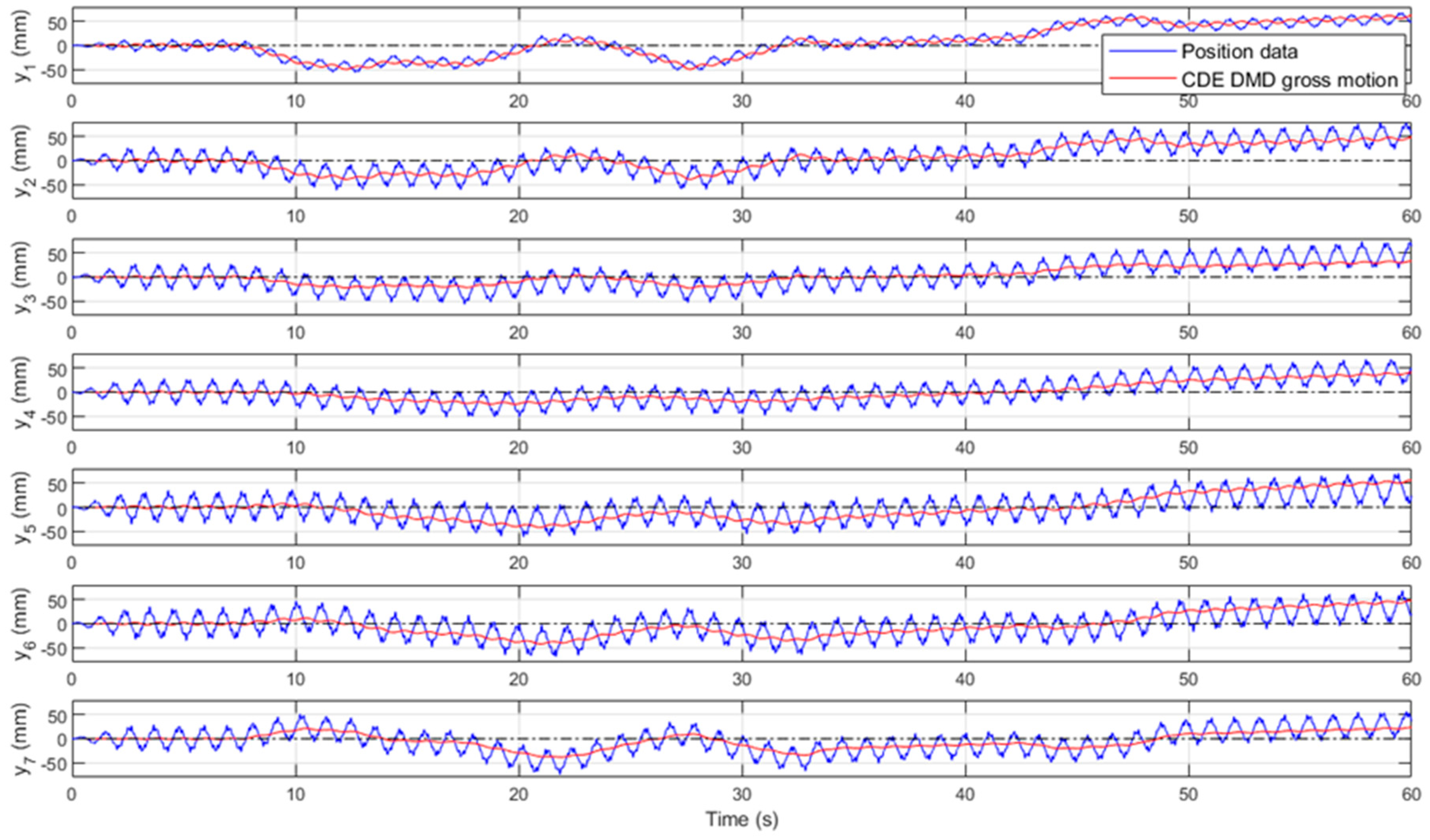
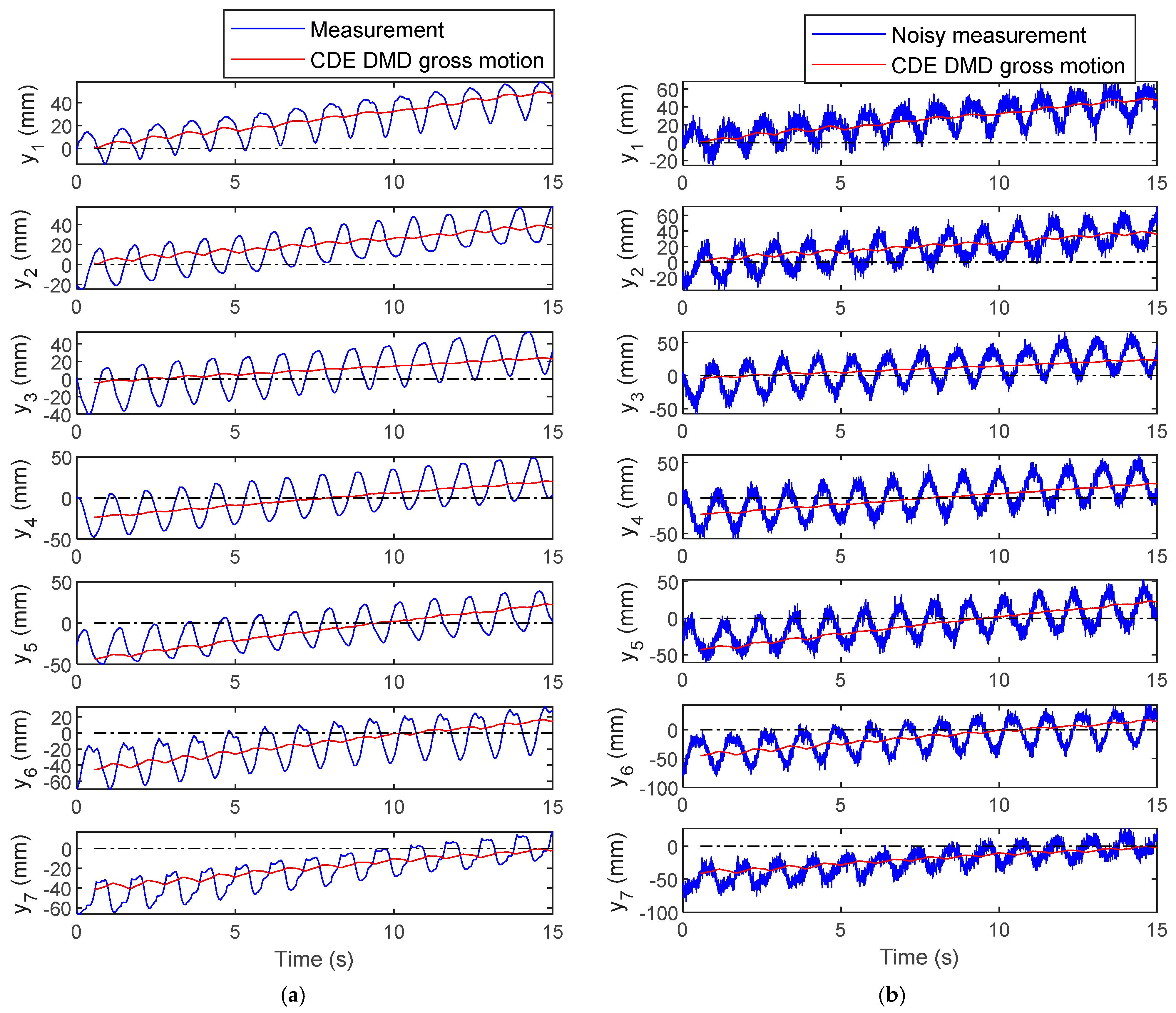
3. Results
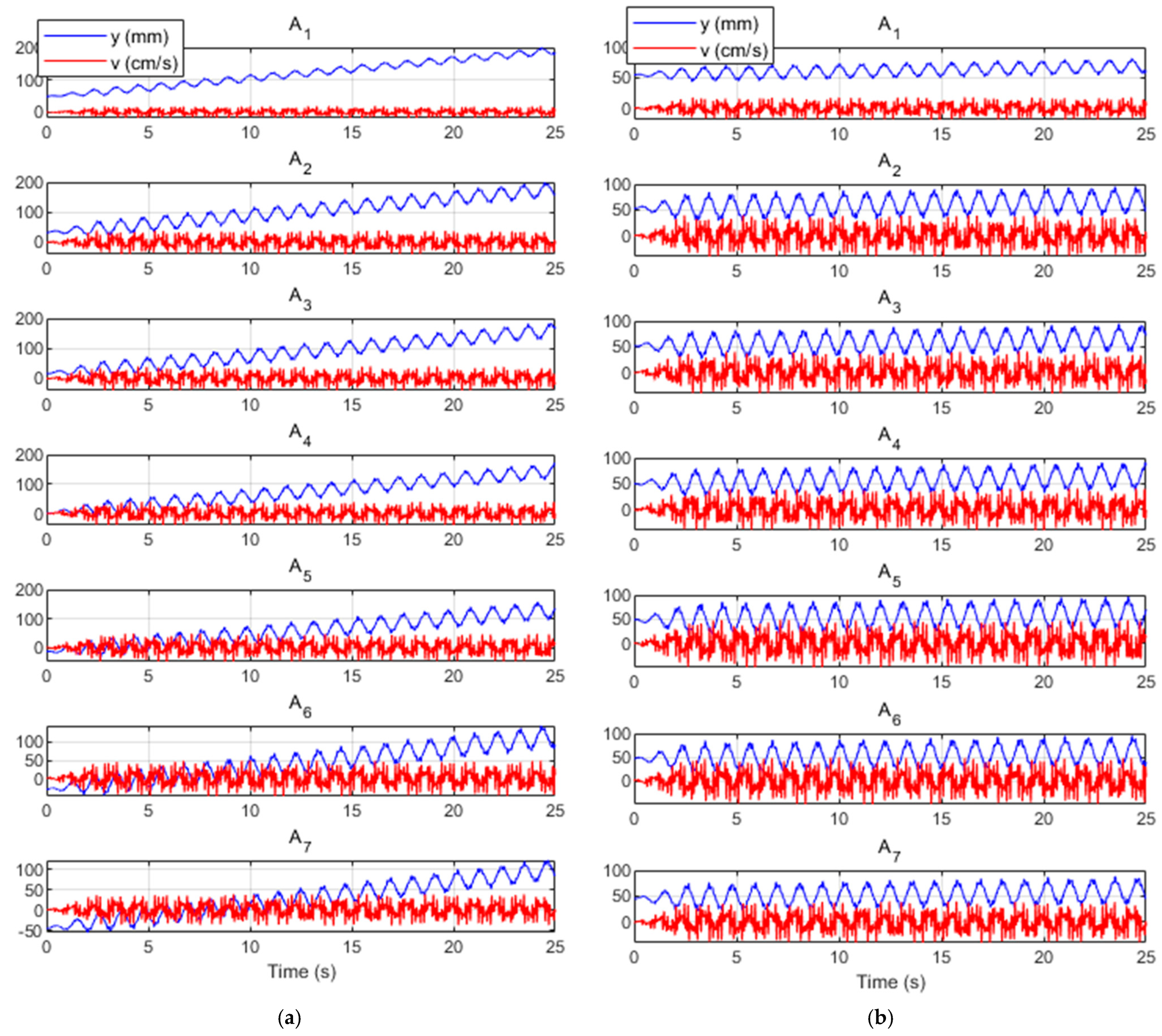
3.1. Particle Tracing
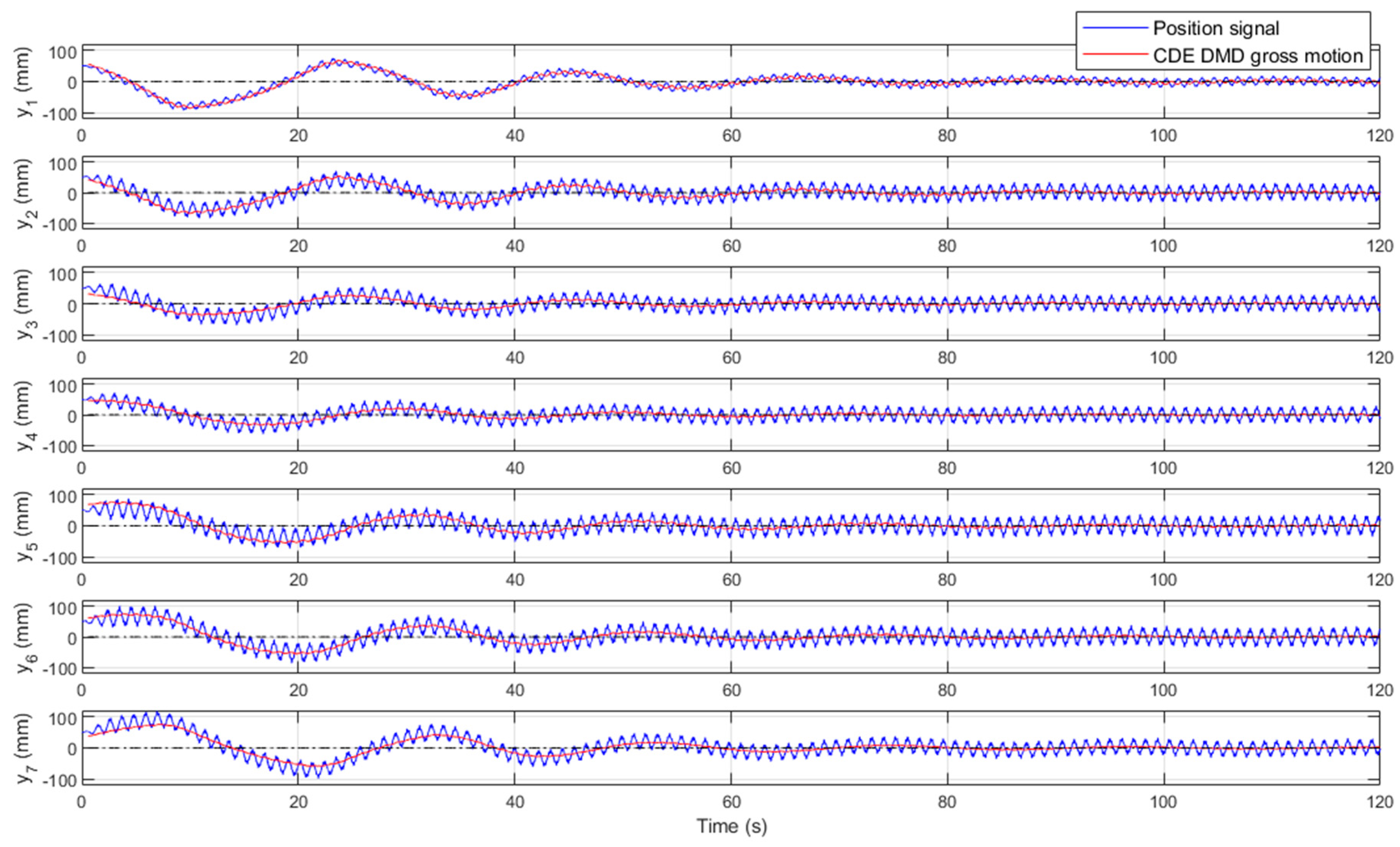
3.2. Implementation of the CDE DMD
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ALE | Arbitrary Lagrangian–Eulerian |
| CDE | Complex-variable Delay Embedding |
| CFD | Computational Fluid Dynamics |
| DMD | Dynamic Mode Decomposition |
| FE | Finite Elements |
| FPT | Fluid-Particle Tracing |
| FSI | Fluid–Structure Interaction |
| ML | Machine Learning |
| Re | Reynolds Number |
| SPF | Single-Phase Flow |
| SVD | Singular Value Decomposition |
References
- Sfakiotakis, M.; Lane, D.M.; Davies, J.B.C. Review of fish swimming modes for aquatic locomotion. IEEE J. Ocean. Eng. 2002, 24, 237–252. [Google Scholar] [CrossRef]
- Lindsey, C.C. Form, function, and locomotory habits in fish. In Fish physiology; Elsevier: Amsterdam, The Netherlands, 1978; Volume 7, pp. 1–100. [Google Scholar]
- Satoi, D.; Hagiwara, M.; Uemoto, A.; Nakadai, H.; Hoshino, J. Unified motion planner for fishes with various swimming styles. ACM Trans. Graph. 2016, 35, 1–15. [Google Scholar] [CrossRef]
- Hasib, S.A.; Gulzar, M.M.; Oishy, S.R.; Maaruf, M.; Habib, S.; Shakoor, A. An investigation of innovative strategies in underwater soft robotics. Eng. Sci. Technol. Int. J. 2025, 70, 102123. [Google Scholar] [CrossRef]
- Mathew, A.T.; Feliu-Talegon, D.; Abdullahi Adamu, Y.; Ben Hmida, I.; Armanini, C.; Stefanini, C.; Seneviratne, L.; Renda, F. Zodiaq: An isotropic flagella-inspired soft underwater drone for safe marine exploration. Soft Robot. 2025, 12, 410–422. [Google Scholar] [CrossRef]
- Ma, H.; Zhou, J.; Yeow, R. Soft Robotic Snake with Tunable Undulatory Gait for Efficient Underwater Locomotion. Adv. Robot. Res. 2025, 0, e2500061. [Google Scholar] [CrossRef]
- Alexandris, C.; Papageorgas, P.; Piromalis, D. Positioning systems for unmanned underwater vehicles: A comprehensive review. Appl. Sci. 2024, 14, 9671. [Google Scholar] [CrossRef]
- Tytell, E.D.; Lauder, G.V. The hydrodynamics of eel swimming: I. Wake structure. J. Exp. Biol. 2004, 207, 1825–1841. [Google Scholar] [CrossRef] [PubMed]
- Gregorio, E.; Godoy-Diana, R.; Herrel, A. Turning without Fins: How Snakes Achieve High Maneuverability While Swimming. 2025. HAL Preprints 2025. hal-04876557. Available online: https://hal.archives-ouvertes.fr/hal-04876557 (accessed on 11 September 2025).
- Yu, L.; Lai, J.; Huang, J.; Liu, H.; Pi, X. Wireless motion control of a swimming eel-machine hybrid robot. Bioinspir. Biomim. 2025, 20, 036010. [Google Scholar] [CrossRef]
- Xu, J.-X.; Niu, X.-L.; Ren, Q.-Y.; Wang, Q.-G. Collision-free motion planning for an Anguilliform robotic fish. In Proceedings of the 2012 IEEE International Symposium on Industrial Electronics, Hangzhou, China, 28–31 May 2012; pp. 1268–1273. [Google Scholar]
- Melsaac, K.; Ostrowski, J.P. A geometric approach to anguilliform locomotion: Modelling of an underwater eel robot. In Proceedings of the IEEE International Conference on Robotics and Automation, Detroit, MI, USA, 10–15 May 1999; pp. 2843–2848. [Google Scholar]
- Raj, A.; Kumar, A.; Thakur, A. Automated locomotion parameter tuning for an anguilliform-inspired robot. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016; pp. 002564–002569. [Google Scholar]
- Thati, S.K.; Raj, A.; Thakur, A. Optimal and Dynamically Feasible Path Planning for an Anguilliform Fish-Inspired Robot in Presence of Obstacles. In Proceedings of the ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Quebec, QC, Canada, 26–29 August 2018. [Google Scholar]
- Niu, X.; Xu, J.; Ren, Q.; Wang, Q. Locomotion generation and motion library design for an anguilliform robotic fish. J. Bionic Eng. 2013, 10, 251–264. [Google Scholar] [CrossRef]
- Yu, F.; Wu, Z.; Wang, J.; Yu, L.; Feng, Y.; Tan, M.; Yu, J. Learning From Fish: A Two-Stage Transfer Learning Method for a Bionic Robotic Fish. IEEE Trans. Autom. Sci. Eng. 2025, 22, 18796–18808. [Google Scholar] [CrossRef]
- Shi, H.; Meng, Y.; Cui, W.; Rao, M.; Wang, S.; Xie, Y. Biomimetic Underwater Soft Snake Robot: Self-Motion Sensing and Online Gait Control. IEEE Trans. Robot. 2025, 41, 1193–1210. [Google Scholar] [CrossRef]
- He, J.; Wu, C.; Li, Q.; Cui, Y. Efficient anguilliform swimming simulations via coupled overset mesh and RBF mesh deformation techniques. Arch. Appl. Mech. 2025, 95, 104. [Google Scholar] [CrossRef]
- Huang, X.-T.; Sun, P.-N.; Lyu, H.-G.; Zhong, S.-Y. Study of 3D self-propulsive fish swimming using the δ+-SPH model. Acta Mech. Sin. 2023, 39, 722053. [Google Scholar] [CrossRef]
- Wu, T.Y.-T. Hydromechanics of swimming propulsion. Part 1. Swimming of a two-dimensional flexible plate at variable forward speeds in an inviscid fluid. J. Fluid Mech. 1971, 46, 337–355. [Google Scholar] [CrossRef]
- Sayahkarajy, M.; Witte, H. Analysis of Robot–Environment Interaction Modes in Anguilliform Locomotion of a New Soft Eel Robot. Actuators 2024, 13, 406. [Google Scholar] [CrossRef]
- Sayahkarajy, M.; Witte, H. Temporal Evolution of the Hydrodynamics of a Swimming Eel Robot Using Sparse Identification: SINDy-DMD. J 2025, 8, 2. [Google Scholar] [CrossRef]
- Schmid, P.J. Application of the dynamic mode decomposition to experimental data. Exp. Fluids 2011, 50, 1123–1130. [Google Scholar] [CrossRef]
- Duke, D.; Soria, J.; Honnery, D. An error analysis of the dynamic mode decomposition. Exp. Fluids 2012, 52, 529–542. [Google Scholar] [CrossRef]
- Colbrook, M.J.; Drysdale, C.; Horning, A. Rigged dynamic mode decomposition: Data-driven generalized eigenfunction decompositions for Koopman operators. SIAM J. Appl. Dyn. Syst. 2025, 24, 1150–1190. [Google Scholar] [CrossRef]
- Chávez-Dorado, J.; Scherl, I.; DiBenedetto, M. Wave and turbulence separation using dynamic mode decomposition. J. Atmos. Ocean. Technol. 2025, 42, 509–526. [Google Scholar] [CrossRef]
- Asada, H.; Kawai, S. Exact parallelized dynamic mode decomposition with Hankel matrix for large-scale flow data. Theor. Comput. Fluid Dyn. 2025, 39, 8. [Google Scholar] [CrossRef]
- Sayahkarajy, M.; Witte, H. Empirical Data-Driven Linear Model of a Swimming Robot Using the Complex Delay-Embedding DMD Technique. Biomimetics 2025, 10, 60. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Ye, B. Similarity of signal processing effect between Hankel matrix-based SVD and wavelet transform and its mechanism analysis. Mech. Syst. Signal Process. 2009, 23, 1062–1075. [Google Scholar] [CrossRef]
- Wang, J.; Chen, H. BSAS: Beetle swarm antennae search algorithm for optimization problems. arXiv 2018, arXiv:1807.10470. [Google Scholar] [CrossRef]





| % Initialization 1: | ||
| for n = d:−1:0 | % for loop from d to 0 by step −1 | |
| Measure z | % current state vector z is measured | |
| zm_past(n) z | ||
| end | ||
| while (true) | % while loop (main code) | |
| Measure z | % current state vector z is measured | |
| is updated: | ||
| zm(0) z | ||
| for n = 1:1:d | ||
| zm(n) zm_past(n − 1) | ||
| zm_past(n − 1) zm(n − 1) | ||
| end | ||
| % Future gross motion: | ||
| % use (16) | ||
| % Controller update | ||
| Calculate and pressure | % use (19) and (18) | |
| Apply the pressure to the system (simulation/experimental model) | ||
| end | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sayahkarajy, M.; Witte, H. Data-Driven Tracing and Directional Control Strategy for a Simulated Continuum Robot Within Anguilliform Locomotion. Appl. Sci. 2025, 15, 10045. https://doi.org/10.3390/app151810045
Sayahkarajy M, Witte H. Data-Driven Tracing and Directional Control Strategy for a Simulated Continuum Robot Within Anguilliform Locomotion. Applied Sciences. 2025; 15(18):10045. https://doi.org/10.3390/app151810045
Chicago/Turabian StyleSayahkarajy, Mostafa, and Hartmut Witte. 2025. "Data-Driven Tracing and Directional Control Strategy for a Simulated Continuum Robot Within Anguilliform Locomotion" Applied Sciences 15, no. 18: 10045. https://doi.org/10.3390/app151810045
APA StyleSayahkarajy, M., & Witte, H. (2025). Data-Driven Tracing and Directional Control Strategy for a Simulated Continuum Robot Within Anguilliform Locomotion. Applied Sciences, 15(18), 10045. https://doi.org/10.3390/app151810045








