Heuristic, Hybrid, and LLM-Assisted Heuristics for Container Yard Strategies Under Incomplete Information: A Simulation-Based Comparison

Abstract

Efficient container stacking is a critical factor for the performance of intermodal terminals. This study evaluates how classical, hybrid, and LLM-assisted heuristic stacking strategies perform when terminals operate under incomplete or uncertain schedule information. A simulation model of a 4 × 5 × 3 yard was developed, comparing three strategies: a layer-based rule (LAY), a hybrid heuristic (SVD), and an adaptive heuristic supported by a large language model (ChatGPT-4), rather than a full ML/RL model. Each scenario (0%, 25%, 50%, and 100% schedule visibility) was repeated 10 times with controlled random seeds. Results show that under full schedule information, the LLM-assisted strategy reduced relocations by up to 35% and crane operating time by 28% compared to deterministic methods. However, its performance degraded with partial visibility, sometimes falling behind the hybrid strategy, which remained more stable across scenarios. Standard deviations confirmed that differences between methods were statistically significant. The findings highlight both the potential and the limitations of LLM-assisted heuristics: they can outperform classical approaches in data-rich environments but may overreact to incomplete inputs without explicit data quality assessment. This study should therefore be regarded as a simulation-based proof-of-concept, with further validation on real operational data required to confirm its applicability.

1. Introduction

Effective yard management is a critical factor influencing the performance of container terminals, especially within intermodal transport systems. The choice of a container stacking strategy directly impacts key operational indicators such as crane productivity, container handling time, yard congestion, and schedule adherence.

Meanwhile, many container terminals face serious challenges related to operational inefficiency. For example, automated terminals frequently encounter container misplacements and losses, which require costly relocations and prolong handling times [1]. Yard congestion and suboptimal resource allocation lead to longer truck turnaround times and may generate multimillion-dollar annual losses [2]. In middle-income countries, technical inefficiency often stems from poor organizational design and lack of system integration [3]. According to the Inter-American Development Bank, improving terminal operations could reduce transport costs by up to 15% [4].

Moreover, terminal pricing policies often do not reflect the actual quality of operations. It is estimated that differentiating services based on efficiency could generate up to USD 3 billion in added value annually [5].

Given these findings, the need for adaptive strategies capable of responding to volatile operating conditions and incomplete information is becoming increasingly evident. While static strategies—such as random or layered stacking—are widely used, they often lack the flexibility needed in the dynamic environment of terminal operations. In academic studies, stacking strategies are typically evaluated under the assumption of complete knowledge of container arrival and departure schedules—an assumption rarely met in real-world settings.

The aim of this paper is to evaluate the effectiveness of three container stacking strategies under conditions of limited schedule visibility: (1) the layered stacking strategy, (2) the SVD hybrid strategy by M. Zając, which combines block and layered approaches, and (3) an adaptive strategy based on artificial intelligence techniques. A simulation model of a terminal is used to assess the performance of these approaches at four levels of schedule visibility: 0%, 25%, 50%, and 100%.

This study investigates the effectiveness of classical, hybrid, and adaptive container stacking strategies under varying levels of schedule awareness. The central research question is: how do different placement strategies perform when terminals operate under incomplete or uncertain data—conditions common in real-world yard operations?

The main contribution lies in demonstrating that adaptive strategies, supported by large language models (LLMs) and real-time data analysis, can enhance responsiveness and reduce inefficiencies, even when information is limited. By evaluating these strategies in a simulated container terminal, this study highlights the practical potential of AI-assisted heuristics in dynamic and uncertain environments. Optimizing yard operations in such conditions supports more resilient and sustainable supply chains.

The term “AI-based strategy” in this paper refers to a heuristic method developed using interactions with a large language model (ChatGPT-4). While it leverages adaptive scoring and iterative evaluation, it does not represent a self-trained or data-driven ML model. This distinction is important for proper interpretation of the results and reproducibility of the findings.

The remainder of the paper is organized as follows. Section 2 presents a review of the related literature, focusing on classical, hybrid, and AI-based container stacking strategies under uncertainty. Section 3 describes the simulation methodology, including the model structure, decision logic, and data assumptions. Section 4 presents and analyzes the results of simulation experiments. Section 5 discusses the findings in the context of previous studies, identifies practical implications, and outlines the study’s limitations.

2. Literature Review

Effective container stacking in intermodal terminal yards is one of the most important aspects influencing the overall efficiency of cargo handling processes. In the literature, this issue has been analyzed from various perspectives: from relatively simple organizational strategies to advanced optimization models and artificial intelligence approaches. At the same time, many studies simplify real-world terminal conditions by assuming full knowledge of the operational schedule and perfect information availability.

The aim of this review is to organize and synthetically present existing solutions for container stacking strategies, with a particular focus on their limitations in real-world environments characterized by incomplete information. This review is structured as follows: the first part discusses traditional stacking strategies commonly used in terminal operations and their limitations. The next part covers optimization approaches developed in the scientific literature, including heuristic, programming, and simulation models. Recent research directions involving artificial intelligence and decision-support systems in terminal environments are then presented. Finally, a research gap is identified regarding the limited scope of studies addressing operations under incomplete information, thus justifying the approach adopted in this paper.

2.1. Stacking Strategies and Optimization Methods

The problem of container allocation in terminal yards has been widely studied, with a primary focus on reducing the number of non-productive moves (relocations), shortening container handling cycles, and optimizing space utilization. Among the most frequently cited approaches are FIFO and LIFO rules, grouping containers by logical attributes, and block stacking.

The study by [6] provides a comprehensive literature review on container terminal operation planning. The authors point out that most strategies are based on the assumption of static conditions and full access to operational data. Typical methods assign container positions based on departure dates [7], batch affiliation [8], or allocation to buffer zones [9].

In terminal practice, many of these strategies have been implemented in Asian and European ports, particularly in automated environments or high-throughput operations. For example, terminals in Singapore and Rotterdam use slot assignment systems based on estimated departure times while imposing limits on stack heights [10].

Despite their effectiveness under controlled conditions, these methods have several limitations. Primarily, they

• fail to account for operational variability (e.g., unexpected delays, route changes, load reorganizations);
• rely on full schedule knowledge, which is rarely available in practice;
• do not adapt to real-time yard occupancy levels or predict operational conflicts.

Moreover, as noted by [11], many of these methods are designed around a single optimization criterion (e.g., minimizing relocations), often ignoring concurrent operational goals such as minimizing delays or reducing the energy consumption of handling equipment.

The literature thus shows that while traditional stacking strategies are well-established and grounded in practice, their limited flexibility and static nature make them difficult to apply in environments with dynamically changing information availability. This motivates the exploration of more advanced approaches, which will be discussed in the following subsections.

In response to the limitations of classical strategies, a wide range of optimization approaches have been developed in the academic literature. These aim to reduce the number of relocations, increase yard throughput, and shorten container handling times. The most common methods include mixed-integer linear programming (MILP), heuristic and metaheuristic algorithms, and simulation models. MILP models, such as the one proposed in [12], allow for precise representation of slot allocation problems, incorporating spatial and scheduling constraints. However, they suffer from high computational complexity, which limits their practical applicability in large terminals or real-time operations. As a result, simplified versions of these models or their implementations in simulation environments are frequently encountered in the literature.

To improve scalability, many authors propose the use of heuristic and metaheuristic algorithms—such as genetic algorithms, simulated annealing, particle swarm optimization (PSO), and tabu search. For instance, ref. [13] presents an approach to the container relocation problem using a branch-and-price algorithm, demonstrating its high flexibility and ability to generate near-optimal solutions. These methods have been applied in crane scheduling and stack reorganization tasks.

Another significant stream of research involves simulation models, which allow for the representation of physical and operational terminal behaviors under varying assumptions. Studies [14,15] show that combining control algorithms with discrete event simulation enables dynamic testing of strategies under different yard occupancy scenarios and schedule variations.

Despite the high effectiveness of optimization models in controlled conditions, their application in real-world environments is limited due to:

• the requirement for complete input data;
• lack of flexibility in dealing with delays and unplanned events;
• long computation times for large-scale instances.

For these reasons, such models are increasingly treated as supporting components within broader decision-making systems, rather than as standalone operational tools.

In recent years, optimization approaches have significantly expanded, particularly in integrating multiple layers of terminal operations. In [16], the authors analyzed the performance of integrated optimization models that simultaneously consider crane scheduling, container placement, and truck handling. Such models show a clear advantage over hierarchical approaches, particularly in reducing handling times and improving operational flow [17].

One rapidly developing area is the management of container relocations under movement constraints. Study [18] introduces the Restricted Container Relocation Problem (RCRP), which aims to minimize the number of relocations while maintaining the operational feasibility of container retrieval.

Space optimization in feeder–mother port terminals is also gaining importance. Study [19] focuses on dynamic slot allocation considering vessel sizes, berth times, and container priority classes, requiring more advanced decision-making tools.

In [20], the authors emphasize the need for flexible yard space management. Their findings suggest that rigid slot assignment systems are outperformed by adaptive solutions that respond to real-time changes in data availability and carrier behavior.

These studies identify several critical challenges for effective yard management in automated container terminals. They point to the insufficient integration of terminal management systems, which hinders coordination between operational modules. Attention is also drawn to the limited adaptability of existing algorithms, which often fail to adjust to dynamic working conditions or respond effectively to uncertainty in container flows. A major issue remains the underutilization of available operational data—despite its volume, it is rarely leveraged for real-time decision-making. Authors also highlight the lack of standardized terminal processes, which complicates scalability and automation deployment across different operational contexts. Finally, infrastructural constraints, such as yard layout and equipment availability, continue to pose significant barriers to the implementation of fully automated solutions.

2.2. Adaptive Strategies and the Application of Artificial Intelligence in Yard Management

The ongoing digitization of terminal operations and the growing complexity of logistics chains foster the development of adaptive strategies that can respond to changing terminal conditions in real time. In recent years, there has been increasing interest in the application of artificial intelligence (AI) methods, particularly machine learning, reinforcement learning (RL), and predictive-decision-support systems integrated into Terminal Operating Systems (TOS).

One of the earliest milestones in this direction involved the use of supervised learning to predict slot demand and future handling operations. Study [21] demonstrated that random forest-based regression can accurately forecast container pickup times, supporting more informed decisions about container placement.

More recently, models have emerged that not only predict events but also make operational decisions autonomously. For example, reinforcement learning algorithms allow for adaptive container movement control without manually coded rules. In [22], a Deep Q-Network was applied to dynamically assign containers to slots under uncertain arrival times, reducing the number of MOVE operations by more than 30% compared to deterministic strategies.

In [23], a hybrid system combining an LSTM-based predictive model with a resource allocation algorithm was proposed, which continuously updated the yard strategy based on schedule changes. The authors noted that the greatest benefit stemmed not from prediction accuracy, but from the model’s real-time adaptability.

Agent-based simulations are gaining popularity as tools for modeling complex decision-making processes in container terminals, particularly when multiple autonomous entities (e.g., cranes, drivers, containers) must coordinate under limited information. Agent-Based Modeling (ABM) enables capturing the interactions between system components, and with the integration of RL, these agents can learn cooperative strategies autonomously.

Study [24] applied a Multi-Agent Reinforcement Learning (MARL) approach to optimize cooperation between multiple cranes. Each agent (crane) learned policies to minimize container wait times, resulting in significantly shorter handling durations compared to sequential approaches. However, the authors noted that decision conflicts arose in the absence of communication mechanisms between agents.

In [25], it was shown that integration with predictive systems enhances terminal performance in disruption-prone and data-sparse scenarios. Agents collaboratively developed container relocation strategies based on predicted schedule changes.

Such approaches are particularly promising for next-generation terminals that may require decentralized traffic management. Major challenges include scalability, the need for large datasets for training, and the complexity of interpreting multi-agent system behavior.

Despite the growing potential of AI, most studies remain limited to scenarios with full information or idealized simulation environments. Few approaches formally analyze the impact of incomplete information on the performance of intelligent strategies, and even fewer compare these methods against heuristic or hybrid models. Therefore, this study proposes an adaptive AI-based yard strategy and compares its performance with classical solutions under varying information conditions.

In recent years, deep reinforcement learning (DRL) has attracted particular attention, applied to container relocation optimization under partial information [26] and to scheduling automated guided vehicles (AGVs) with energy-efficiency considerations [27]. DRL techniques enable the development of adaptive control policies learned end-to-end from operational data, indicating their strong potential for real-world terminal applications.

In ref. [28], DRL was applied for outbound container stacking, showing that learning-based policies can adapt to highly dynamic operational scenarios with partial schedule visibility. In [29], the Authors demonstrated the effectiveness of simulation-based policy refinement using agent-based models, which emulate autonomous behaviors of yard equipment under varying traffic and information levels. The present study contributes to this line of inquiry by evaluating a lightweight AI-driven stacking strategy under different visibility conditions and by benchmarking it against a hybrid model (SVD) and deterministic baseline (LAY). Although the AI strategy used here is not a full DRL agent, its structure mimics priority learning and adaptive allocation mechanisms, reflecting the broader trend toward self-tuning and context-aware logistics systems.

However, despite their adaptability, DRL methods face practical limitations, including a lack of validation on real-world data, high computational requirements, and limited interpretability of decision-making processes for operators. Moreover, many studies assume complete information environments, limiting their comparability with real terminal operations characterized by inherent uncertainty.

Many of the current studies still rely on simplified simulation models and assume full access to input data, overlooking the volatility and uncertainty of operational environments. Furthermore, integrating AI technologies with existing TOS platforms, terminal equipment, and management procedures remains a major implementation challenge [30].

2.3. Research Gap and Justification of the Research Approach

Despite significant advances in modeling container yard operations, much of the existing literature continues to assume full availability of input data—especially container arrival and departure schedules. This applies to both heuristic and optimization strategies [31], as well as AI-based solutions [32].

In practice, container terminals often operate under incomplete or delayed information due to factors such as transport delays, lack of advance confirmations, or dynamically changing orders. Although this is a common characteristic of operational environments, only a few studies systematically examine the effect of information availability on the effectiveness of storage strategies. For example, ref. [33] mentions data uncertainty but does not formally differentiate schedule awareness across experimental scenarios.

Moreover, nearly all comparative analyses focus either on classical strategies or various AI versions—neglecting direct comparisons between static, hybrid, and adaptive strategies within the same operational setting. There is thus a lack of cohesive research that:

• differentiates levels of schedule information availability (e.g., 0%, 25%, 50%, 100%);
• tests different strategy classes (random, heuristic, adaptive);
• and evaluates their operational robustness under dynamic terminal conditions.

Table 1. Comparative overview of stacking strategies with respect to information requirements and adaptability.

Approach Type	Example Methods	Requires Full Schedule	Adaptability to Uncertainty	Computational Complexity	Reproducibility	Key References
Classical (Rule-Based)	LAY, EET, Min-Relocation	Yes	Low	Low	High	[6,7,10]
Heuristic (Hybrid)	SVD, Decision Trees	Partial	Medium	Medium	Medium	[8,12,13]
ML-Based	Random Forest, XGBoost	Optional	Medium–High	High	Medium	[16,26]
RL/DRL	Q-Learning, PPO, DQN	Optional	High	Very High	Medium	[22,28,30]
LLM-Assisted Heuristic	ChatGPT-4 scoring (this study)	Optional	Medium	Low	Low	This study

summarizes the reviewed approaches, comparing their data requirements, adaptability under uncertainty, computational complexity, and reproducibility.

The comparison in Table 1 shows that no single class of strategies is universally superior. Classical rule-based methods remain simple and highly reproducible, but their reliance on full schedule knowledge makes them fragile under uncertainty. Heuristic hybrids provide better adaptability; yet, they still depend on fixed rules and often lack scalability. Machine learning methods, such as Random Forest or XGBoost, demonstrate stronger predictive power but require curated datasets and do not always generalize well to volatile yard conditions. Reinforcement learning approaches achieve high adaptability but at the cost of very large training data requirements, heavy computation, and limited interpretability, which restrict their use in operational practice. Finally, LLM-assisted heuristics, as tested in this study, offer a lightweight and flexible alternative that does not require prior training data. However, their reproducibility is low, transparency is limited, and the black-box nature of large language models raises concerns about explainability (XAI). From a sustainability perspective, strategies that minimize unproductive moves directly reduce crane energy use and related emissions, linking operational efficiency to environmental performance. These trade-offs highlight the importance of testing multiple approaches under incomplete information, where robustness and transparency are as critical as raw efficiency.

This paper addresses these gaps by evaluating three stacking strategies—deterministic (LAY), hybrid rule-based (SVD), and adaptive AI—under simulated uncertainty scenarios. Unlike prior research focusing on either purely deterministic models or advanced but computationally intensive DRL agents, our study tests a lightweight, simulation-friendly AI strategy that can adapt to partial schedule information without large training datasets. Furthermore, the model is benchmarked using operational metrics directly linked to sustainability indicators, such as energy use and equipment movement, contributing to the applied relevance of the research.

3. Research Methodology

The objective of this simulation-based study was to compare the effectiveness of three container storage strategies under varying levels of access to operational schedule information. This research was designed to replicate realistic working conditions at a container terminal, where data regarding future operations may be incomplete, delayed, or uncertain. The simulations aimed to

• determine the extent to which adaptive strategies based on artificial intelligence outperform classical and hybrid approaches in information-uncertain environments;
• assess the impact of schedule visibility (0%, 25%, 50%, 100%) on the performance of each strategy;
• identify strategies that are most operationally resilient to disturbances and variability in information.

3.1. Simulation Setup and Procedure

To carry out the experiments, a simulation model was developed to replicate a section of a container yard. The layout consisted of 60 storage slots arranged in a three-dimensional grid: 4 slots along the X-axis (width), 5 along the Y-axis (length), and 3 along the Z-axis (stack height), presented in Figure 1. Handling operations were executed by a single gantry crane with the following directional parameters:

X-axis travel speed: 105 m/min

Y-axis travel speed: 75 m/min

Lifting/lowering speed (Z-axis): 10 m/min

The simulation scenario assumed the handling of 100 containers, including an initial state with 30 containers randomly placed in the yard. Each container was assigned a unique ID, arrival and pickup time, and additional attributes, such as priority class and carrier.

The simulation reflected the heterogeneous nature of container flows, using non-uniform distributions to generate 50 inbound (SET) and 50 outbound (GET) operations. These operations followed empirically observed patterns: higher inbound activity in the morning and early afternoon, and outbound peaks aligned with dispatch cut-offs. Variability in time windows and inter-arrival gaps was modeled with random noise applied to baseline daily profiles.

Each information availability scenario simulated a different degree of knowledge about future operations:

at 0%, no future events were known;

at 25% and 50%, only partial information was available;

at 100%, the full schedule was disclosed.

In scenarios with incomplete information, operational details (arrival/departure times) were unlocked 60 min prior to their occurrence, simulating real-life data delays.

The level of schedule awareness was defined as the percentage of operations (deliveries and pickups) whose full timing and metadata were available at the moment of container allocation:

• In the 0% scenario, only current operations were known, and no information about future containers was accessible.
• In the 25% and 50% scenarios, respectively, 25 or 50 out of 100 scheduled container operations were randomly revealed at the beginning of the simulation.
• In the 100% scenario, the system had access to the complete operational schedule, including all arrival and pickup times.

Dataset description

The simulation used a synthetic dataset of 100 containers, designed to replicate the heterogeneity of real flows observed in intermodal terminals. Each container was characterized by the following attributes:

−

Unique ID—sequential identifier used for tracking operations.

−

hourly distribution reflecting empirical patterns, with inbound peaks in the morning and early afternoon.

−

Pickup time—assigned within predefined daily windows, with outbound peaks aligned with dispatch cut-offs.

−

Priority class—categorical attribute (high, medium, low) influencing retrieval urgency, generated with probabilities of 0.2, 0.5, and 0.3, respectively.

−

Carrier—categorical variable with four classes representing different operators, randomly assigned with equal probability.

−

Operation type—inbound (SET) or outbound (GET), fixed at a 50/50 split.

Initial conditions included 30 containers placed randomly in the yard at the start of each simulation run. Inter-arrival times and operation windows were generated with stochastic noise (±15% of baseline values) to simulate variability in real operations. Random seeds were fixed across scenarios to ensure comparability between strategies.

ChatGPT-4 integration

A large language model (ChatGPT-4) was used in two distinct phases of the simulation: schedule generation and adaptive strategy scoring.

Schedule generation. The LLM received structured prompts describing the following:

−

the number of inbound and outbound containers (50 each),

−

time horizon of 24 h,

−

required clustering of arrivals (morning) and departures (afternoon/evening),

−

assignment of priority classes and carriers.

The model returned candidate schedules in JSON format (time stamps and attributes), which were post-processed to ensure feasibility and consistency with yard capacity.

Adaptive strategy scoring. During container placement, the LLM-assisted module was queried with the current yard state (occupied slots, stack heights) and the metadata of the arriving container (priority, estimated departure time, carrier). The model produced heuristic weights for candidate slots, reflecting expected relocation risk and travel distance. These weights were then normalized and integrated into the utility function described in Equation (5).

To ensure reproducibility, all prompts and model responses were logged, and random seeds controlling partial schedule visibility were fixed. Although ChatGPT-4 was used to generate predictive scores, the final allocation decisions were deterministic given the same yard state and model outputs.

The containers revealed in the partial-information scenarios were selected using a consistent random seed across strategy comparisons, ensuring identical conditions for each experimental run.

Three container stacking strategies were implemented and tested under identical simulation conditions:

• Layer-based strategy (LAY),
• Hybrid strategy based on Zając’s model (SVD),
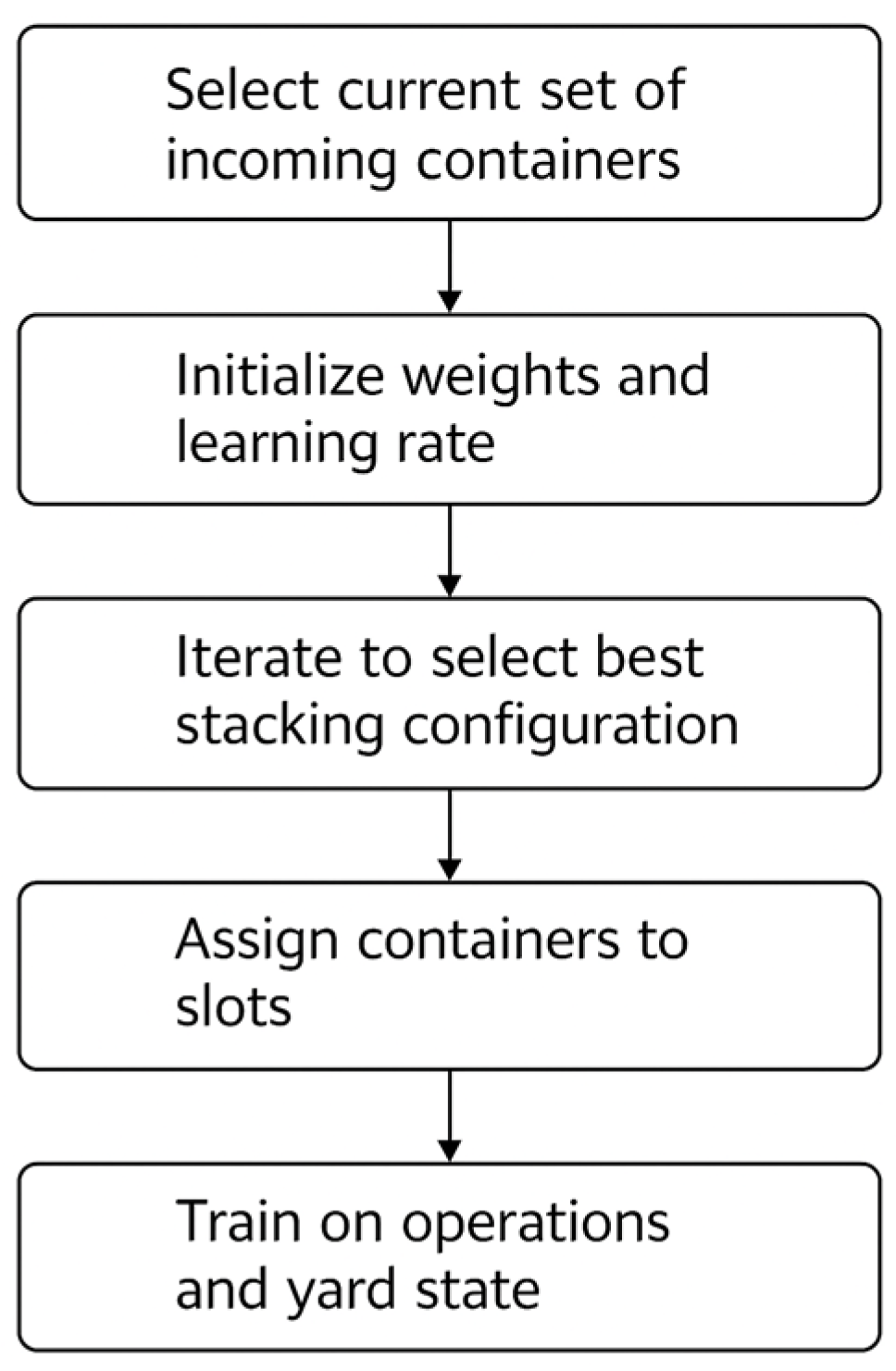
• Adaptive AI-based strategy (AI), featuring predictive and rule-based modules.

The computational procedure consisted of the following seven steps, visualized in Figure 2:

• Setting up the simulation environment: initializing the yard structure and assigning container metadata.
• Schedule generation: producing 100 operations (50 SET, 50 GET) based on realistic timing logic.
• Information scenario setup: determining which data points were hidden or revealed depending on the information level.
• Strategy implementation: executing storage allocation using one of the three defined approaches.
• Crane operation simulation: calculating movement time, vertical operations, and resolving conflicts.
• Multiple experimental runs: performing 10 repetitions for each strategy–information pair (totaling 120 runs).
• Data collection and analysis: aggregating all relevant metrics—operation counts, durations, travel distances, and delays.

The simulation was implemented in Python 3.10 using NumPy and pandas. All strategy modules were integrated into the simulation framework as callable functions. The AI-based strategy utilized real-time decision-making through predictive logic, though no historical training data was used. Instead, operational scenarios were analyzed dynamically during simulation runs.

While the raw empirical data used in this study are not publicly available due to confidentiality agreements with the terminal operator, all simulation parameters and performance assumptions reflect the collected data and are available upon reasonable request.

The procedure consists of the following steps:

• Setting up the simulation environment

The yard layout was defined as a 3D grid (4 × 5 × 3). The simulation code supported SET, GET, MOVE, and MOVE_EMPTY operations. Each container received a unique ID, arrival time, and pickup time.

2.

Schedule generation

Each simulation included 100 operations (50 deliveries, 50 pickups). A scheduling algorithm generated realistic schedules with operational logic (e.g., time windows, event spacing, seasonal effects). Attributes such as carrier, priority, and operation class were assigned randomly.

Schedules were generated via scripted prompts to the ChatGPT-4 system using random hourly distributions, seasonal conditions, and priority structures derived from empirical observations in terminals. Detailed prompts are available upon editorial request.

3.

Introducing the information level

Each experiment was defined by an information scenario. Depending on the level (0–100%), part of the future operations data was hidden at the time of the allocation decision. These data were revealed 60 min before the planned operation time, simulating real delays in reporting by clients or planning systems.

4.

Implementation of storage strategies

Three strategies were implemented in separate modules, described later in the article:

Layer-based strategy (layer_based()),

Hybrid strategy based on Zając’s model (zajac_hybrid_allocation()),

Adaptive AI-based strategy (adaptive_AI_strategy()), with prediction and decision-making submodules.

5.

Crane operation simulation

For each operation, travel time, vertical movement time, and total duration were calculated. Acceleration and deceleration were included, as well as slot conflicts and relocations.

6.

Multiple experimental runs

Each combination (strategy × information level) was run 10 times with different random seeds. A total of 160 runs were performed (4 strategies × 4 levels × 10 repetitions).

7.

Data collection and analysis

Each simulation recorded the following:

number of GET, SET, MOVE, and MOVE_EMPTY operations,

time and distance of each operation,

delay compared to the scheduled time,

number of relocations.

The simulation parameters used in this study—such as crane speeds, stacking logic, and operational delays—were derived from real-world observations conducted at a Polish intermodal container terminal during field studies carried out in 2024. As part of the research, empirical data were collected on the duration of container pickup and placement operations, the frequency of non-productive moves, and crane travel distances under typical operating conditions. These data served as the basis for defining model constraints and validating the logic of individual stacking strategies. While the model remains a conceptual representation, it reflects operational patterns observed during field audits and test deployments. The raw operational data collected during this study are not publicly available due to confidentiality agreements with the terminal operator, but aggregated metrics and performance assumptions are fully reflected in the simulation setup and available upon reasonable request.

To maintain conceptual clarity and reduce the number of experimental variables, the model assumes a simplified infrastructure: a single rail-mounted gantry crane operating over a static yard layout, with no parallel cranes or yard trucks. The simulation does not explicitly include ramp operations or workforce scheduling. Container weights were assumed to be uniform and within standard handling limits, consistent with ISO container norms. The simulation logic incorporated a first-come-first-served policy for arrivals and prioritized pickups based on scheduled departure times. No time-based penalties or load class distinctions were applied. These simplifications were introduced to focus the analysis on the impact of stacking strategies and schedule visibility, while maintaining computational feasibility.

Each experimental configuration (strategy × information level) was repeated 10 times with different random seeds. To account for variability, both mean values and standard deviations were reported for all performance indicators (relocations, crane time, distance). Ninety-five percent confidence intervals were calculated, and differences between strategies were tested for statistical significance using one-way ANOVA with post hoc Tukey tests. This ensured that observed performance differences were not due to random fluctuations but reflected consistent patterns across repetitions.

3.2. Storage Strategies

This study compares three storage strategies that differ in organizational complexity and the decision-making method for container placement.

Layer-based strategy—LAY

Containers are stacked in successive levels—first filling the lowest tier, then the next, until the entire available volume is used. The aim of this strategy is to reduce vertical interference (i.e., avoid containers blocking others from being accessed). It is more orderly than random placement but ignores container retrieval times, which may lead to unnecessary relocations in highly congested yards.

Hybrid strategy based on M. Zając’s model—SVD

This hybrid approach combines block storage rules (grouping based on logical attributes such as departure time or transport direction) with layer-based placement (even distribution across stack levels). Additionally, the model considers yard occupancy levels and adjusts the placement method depending on terminal load, aiming to minimize non-productive relocations. The strategy is described in detail in [34].

Adaptive AI-based strategy—AI

In this approach, container locations are dynamically selected based on real-time and predicted operational data. The algorithm has access to full yard state and container schedules and makes decisions in real time. The goal is to minimize the number of relocations and crane travel distance. The strategy is designed to react to unexpected delays or sudden changes in workload. It employs predictive algorithms that

−

analyze container movement data in real time;

−

forecast future retrieval or relocation operations;

−

dynamically assign storage locations to optimize crane routing and minimize empty travel.

This system can also operate under partial schedule visibility, flexibly adapting to updates or incomplete information. It is the most advanced strategy, but it requires substantial computational resources and high-quality data.

3.3. Information Levels and Performance Indicators

To reflect real-world terminal conditions, four levels of schedule awareness were applied in the simulations:

−

0%—no knowledge of future events,

−

25%—limited access to the schedule (every fourth container known),

−

50%—partial awareness (every second container known),

−

100%—full knowledge of the entire schedule.

In incomplete information scenarios, arrival or departure times were revealed one hour before the planned operation, simulating real-world reporting delays from clients or planning systems. All strategies were evaluated using the following operational metrics:

−

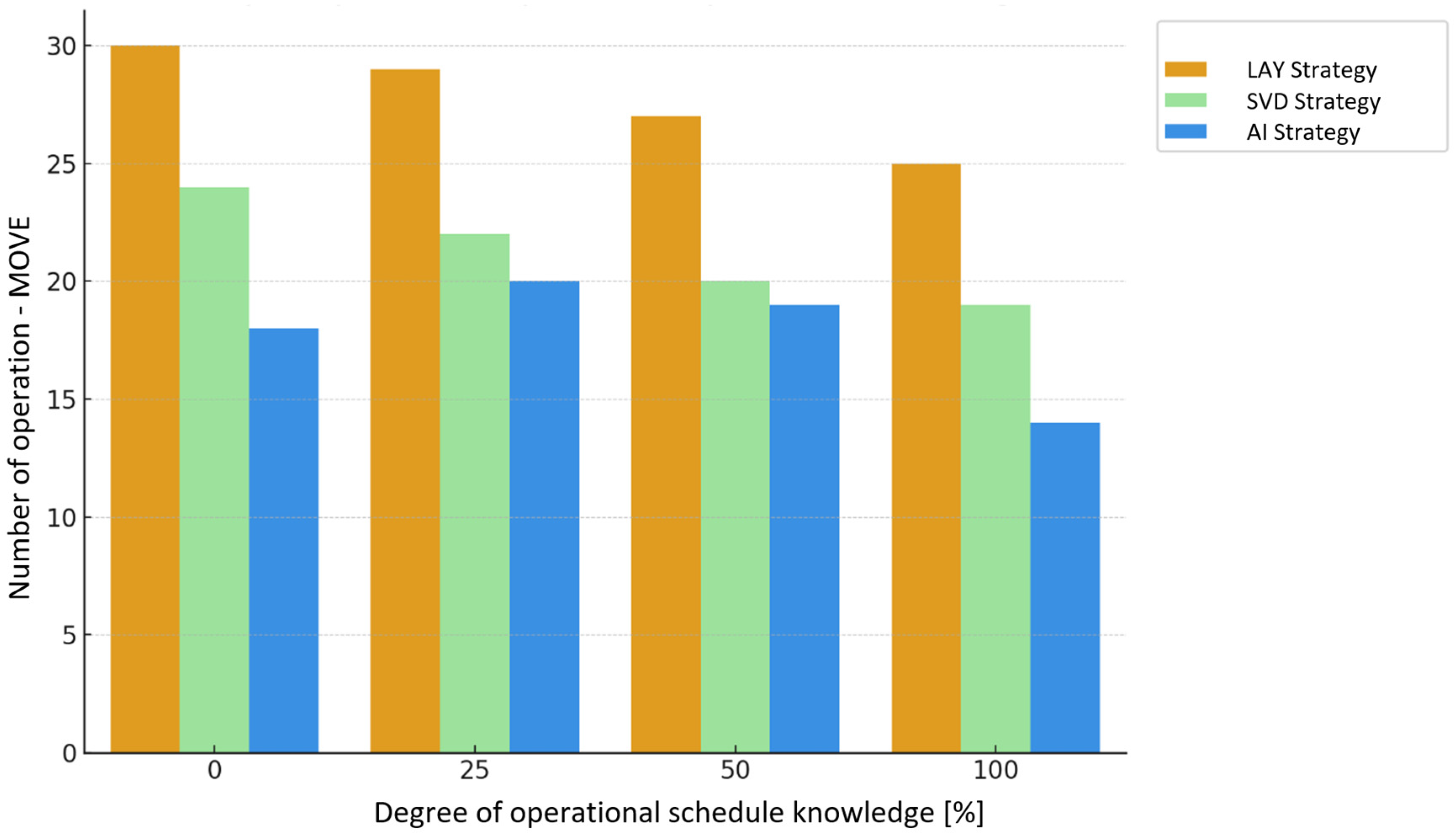
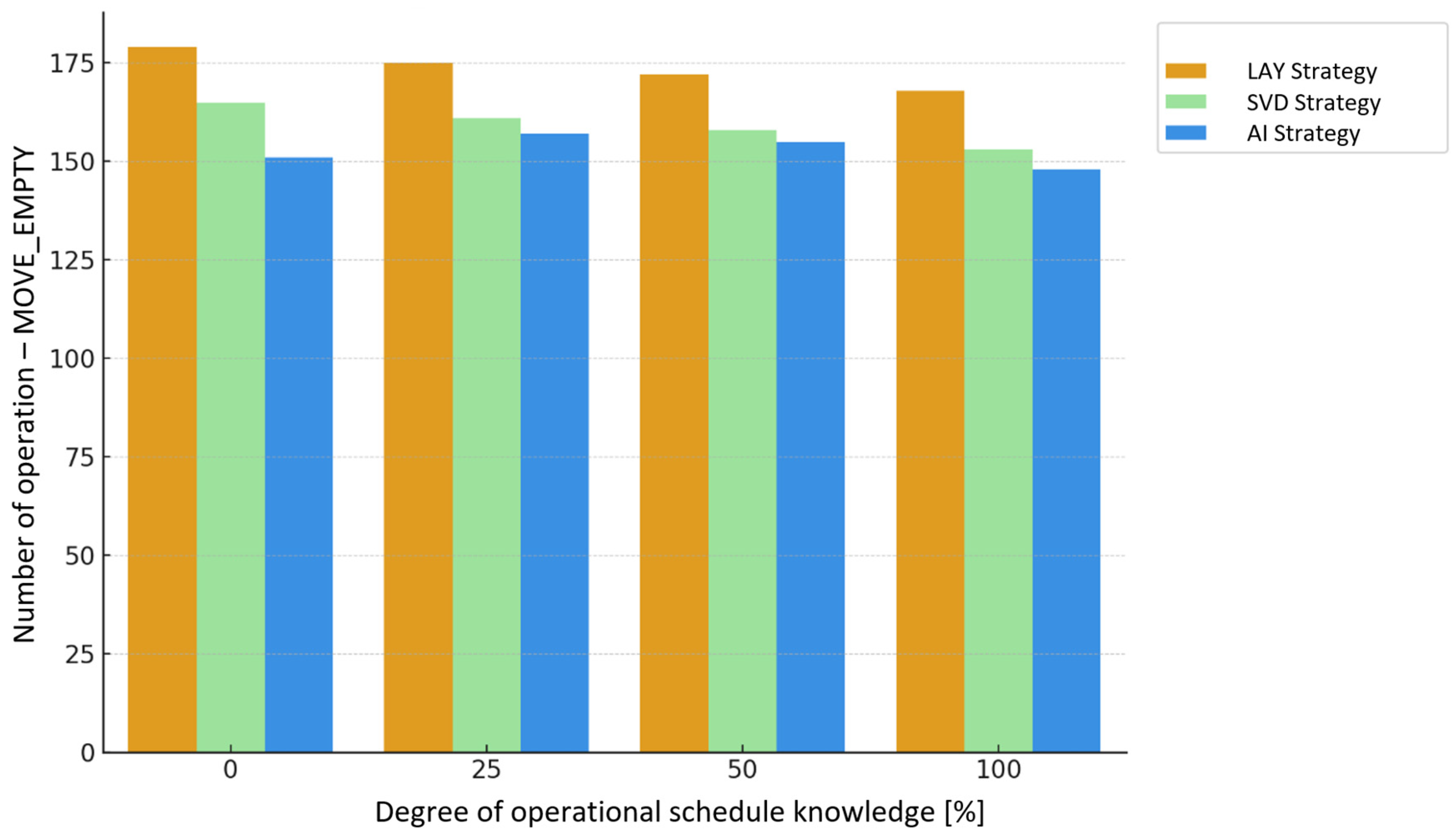
Numberofoperations:

• SET—placing a container in the yard,
• GET—retrieving a container from the yard,
• MOVE—relocation of a container (non-productive move),
• MOVE_EMPTY—crane movement without a load between tasks,

−

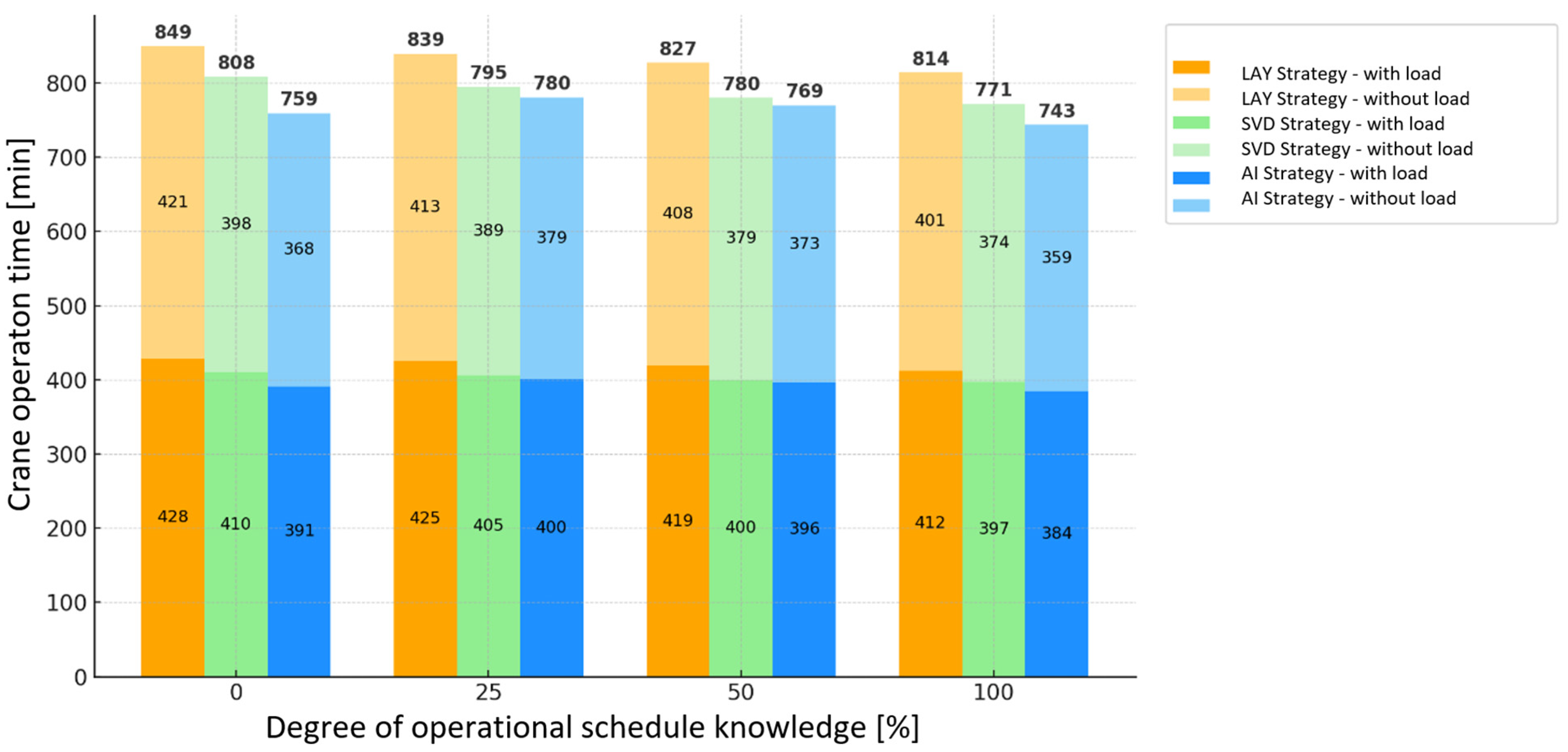
Operation duration—average and total,

−

Crane travel distance—separately for each type of operation,

−

Delays—number and time of operations completed after the scheduled time.

3.4. Formalization of the Decision Problem

To enable transparent evaluation of stacking strategies and reproducibility of results, we provide a formal definition of the decision problem considered in the simulation model.

Let:

• i = 1, 2, …, N: index of container
• $t_i^{arr}$: arrival time of container i,
• $t_i^{dep}$: departure time of container i,
• x, y, z: coordinates of a yard slot in a 3D grid, where $x\in \{1,\dots ,X\}$, $y\in \{1,\dots ,Y\}$,$z\in \{1,\dots ,Z\}$,
• $S=\left\{\right(x, y, z\left)\right\}$: set of all possible storage slots

$A_i\in S$: decision variable—slot assigned to container i

Objective:

Minimize the total number of non-productive relocations (MOVE operations), the crane travel time, or a weighted combination of both, e.g.,

$$min{\sum }_{i=1}^N(\alpha ·R_i+\beta ·T_i)$$

(1)

where:

• $R_i$: number of relocations caused by container i,
• $T_i$: total crane handling time related to container i,
• α, β: weight coefficients (experimentally set or equal).

Constraints:

Each container must be assigned to exactly one available slot:

$$A_i\in S,{\forall }_i$$

(2)

A slot can only hold one container at a time:

$A_i\ne A_j$ for all $i\ne j$ at overlapping times

Stack height limit:

$$z\le Z$$

Strategy-specific allocation logic:

Layered strategy (LAY):

Containers are assigned to the lowest available layer (z = 1z = 1 first), then filled upwards.

No look-ahead or prioritization is used:

$$A_i=\mathrm{m}\mathrm{i}\mathrm{n}\left\{\right(x,y,z)ϵS\left|available\}\right.$$

(3)

Hybrid strategy (SVD):

Containers are grouped by departure time windows into zones (blocks), e.g., early, medium, late.

Within each group, containers are assigned by layered priority:

If $t_i^{dep}ϵ{window}_k\Rightarrow A_iϵ{zone}_k$

and within

$${zone}_k:A_i=\mathrm{m}\mathrm{i}\mathrm{n}\left\{\right(x,y,z)ϵ{zone}_k\left|availabe\}\right.$$

(4)

This formalization creates a reference framework for analyzing the effects of different stacking strategies under varying levels of schedule visibility. The adaptive AI-based strategy does not follow a fixed rule set but instead dynamically chooses $A_i$ based on predicted operations and yard state.

AI strategy (adaptive)

Containers are assigned to storage slots dynamically based on a learned utility function, which combines operational parameters such as estimated departure time, expected relocations, travel distance, and other contextual features. Unlike the LAY and SVD strategies, the AI-based method does not rely on fixed allocation rules but instead computes priorities using a data-driven model.

The strategy operates in the following way:

Each candidate slot $(x$,$y,z)ϵS$ is evaluated using a scoring function $U_{i(x,y,z)}$, derived from a trained utility model:

$$U_{i,(x,y,z)}=f(t_i^{dep},relocations,d_{i,(x,y,z)},servicetime,\dots )$$

(5)

The decision variable $A_i$ is then chosen as the slot with the lowest utility score:

$$A_i={arg}_{(x,y,x)ϵS_{available}}min{U}_{i(x,y,z)}$$

(6)

The function $f$ is a heuristic scoring model generated by ChatGPT-4 using a learning loop. It simulates multiple stacking configurations and selects the one that minimizes the chosen performance metrics (relocations, travel time, etc.).

This procedure simulates a lightweight training phase for each instance, adjusting slot priorities iteratively across multiple simulated stackings. After evaluating each configuration, the system updates internal weights to guide future decisions, balancing between early departure accessibility and stack stability. The flowchart presented in Figure 3 illustrates the adaptive AI-based stacking strategy.

The system initializes configuration parameters and iteratively evaluates multiple container stacking layouts based on predicted utility scores. After each evaluation, internal weights are updated to improve subsequent slot assignments. This lightweight learning loop enables the algorithm to adapt to yard conditions and departure schedules dynamically, even under incomplete information scenarios. The AI-based strategy is composed of an adaptive decision loop that aims to select optimal container slots based on partial or complete schedule information.

At the beginning of each simulation run, the current layout of the yard, container metadata (arrival time, expected departure), and available slots are loaded. All slots are initialized with equal base priority weights.

For each arriving container, the system performs the following steps sequentially for each container that is to be placed on the yard. A set of feasible locations is identified, taking into account structural constraints (e.g., stack height) and crane accessibility. Each candidate slot is evaluated based on a utility function. The utility function combines multiple factors:

• estimated departure time of the container,
• slot depth and height (e.g., penalizing deep stacks),
• predicted risk of blocking future operations,
• distance from crane’s current position.

The system tentatively assigns the container to each candidate slot and simulates the downstream effects (e.g., expected number of future relocations). Each configuration is scored based on the predicted impact on operational efficiency. Based on the evaluation, the algorithm adjusts the priority weights for each slot type using a reinforcement-style update rule. Slots leading to fewer future relocations or faster handling are favored. The final decision is made by choosing the slot with the highest composite score. This slot is assigned to the container in the simulation.

The same process is repeated for the remaining containers. With each step, the internal weights are refined, reflecting the dynamic conditions of the yard and updating based on observed results. After completing the stacking of all containers, the algorithm performs an optional feedback step: if the simulation indicates poor performance (e.g., excessive relocations), it updates its internal heuristics for future runs.

To ensure the transparency and reproducibility of the AI-based stacking strategy, the key steps of the procedure are summarized below in the form of simplified pseudocode (Figure 4). This pseudocode illustrates the internal logic guiding the selection of storage locations under varying information levels.

This structured approach ensures that the AI model considers not only static slot availability but also the dynamic cost implications of each decision. The reinforcement step is optional but allows the system to adapt to recurring patterns or errors detected during simulation runs. Each component of the utility function can be adjusted via weights (e.g., prioritizing distance minimization over relocation risk), enabling strategy calibration to different terminal configurations or performance goals.

Although the AI-based stacking strategy implemented in this study does not follow a classical training procedure over large datasets, it incorporates a lightweight, scenario-driven refinement mechanism. During each simulation episode, the model evaluates multiple allocation possibilities and records the resulting outcomes (e.g., number of relocations or crane travel distance). These results are used to update internal priorities through a feedback loop, allowing the strategy to adapt slot selection rules based on the outcomes observed during earlier operations. This simulation-specific adaptation leads to gradual improvement of decision quality even within a single run, as the system “learns” which allocation patterns are more efficient under current operating conditions. While not a full-fledged reinforcement learning process, this iterative updating of priorities constitutes a form of local policy evolution embedded into the simulation cycle.

To provide additional points of reference, three baseline allocation rules were implemented. These methods are simple and widely documented in the literature, allowing for benchmarking against both deterministic and adaptive strategies:

−

Random placement—containers are assigned uniformly at random to any available slot, without considering future retrieval times or stack depth. This strategy reflects the absence of planning and provides a lower bound of performance.

−

Earliest-Departure-Time (EDT)—each container is placed in a slot minimizing the risk of blocking containers scheduled to depart earlier. This strategy is commonly used in practice to reduce relocations.

−

Min-Relocation—each new container is placed to minimize the expected number of future relocations, given the current yard state. This rule is computationally simple and directly targets relocation efficiency.

These baseline strategies were not designed to achieve optimality but rather to illustrate the relative advantages and disadvantages of more advanced methods. Their inclusion enables a more balanced evaluation of the proposed hybrid and LLM-assisted approaches.

4. Results

The conducted experiments compared the effectiveness of three container stacking strategies: the layer-based strategy (LAY), the hybrid strategy based on M. Zając’s model (SVD), and the adaptive strategy based on artificial intelligence (AI). The analysis was performed for four levels of operational schedule awareness: 0%, 25%, 50%, and 100%.

For each strategy and scenario, the following metrics were recorded: the number of operations (SET, GET, MOVE, MOVE_EMPTY), the duration of operations with and without load, the total crane operating time, the average operation time, and the total travel distance.

A comparison of the number of non-productive “MOVE” operations depending on the percentage of schedule awareness for the layer-based strategy, Zając’s hybrid model, and the AI-based strategy is presented in the chart (Figure 5).

The number of non-productive “MOVE” operations for the layer-based strategy and Zając’s model strategy steadily decreases as the level of schedule awareness increases. This is a logical phenomenon that highlights how critical schedule information about the inflow and outflow of cargo units is for the operation of the entire transshipment system. With gradually increasing knowledge of these events, it is possible to avoid a small but significant number of non-productive crane movements.

However, the data related to the number of “MOVE” operations for the strategy based on artificial intelligence tools presents an interesting pattern. The simulation with full schedule awareness resulted in the lowest number of “MOVE” operations, but surprisingly, the second-best result was observed in the simulation with no schedule information at all. This suggests a scenario in which the AI responsible for container allocation on the terminal, in this type of strategy, performs less efficiently despite having more information about the process.

This outcome could be attributed to multiple factors. One possible reason is that, under partial schedule awareness, the AI attempts to optimize the yard layout by mixing different allocation algorithms, introducing organizational chaos. This results in a higher number of non-productive moves compared to the strategy that has no prior information and follows a uniform placement plan for cargo units.

A comparison of the number of empty crane moves (“MOVE_EMPTY”) depending on the percentage level of schedule awareness for the layer-based strategy, Zając’s model, and the AI-based strategy is shown in the chart (Figure 6).

This chart shows an almost identical relationship between the level of schedule awareness and the number of crane movements without load, mirroring the results observed for the “MOVE” operations.

A comparison of crane working time depending on schedule awareness at the container terminal, divided into operations with and without load, is presented in the chart (Figure 7).

In the case of crane working time, both the layer-based strategy and the strategy based on M. Zając’s model also achieve better results as the level of schedule knowledge increases. Crane working time is closely tied to the number of operations performed. Therefore, for the AI-based strategy, a similar pattern of decreased efficiency under partially known container terminal schedules can be observed.

The analysis of storage strategies under incomplete information conditions indicated that artificial intelligence in planning systems requires not only data, but also the ability to assess data quality. Better results with no more information than with partial schedule awareness suggest that the AI model does not differentiate the level of trust in data and may overestimate its value, which introduces decision-making errors. This is a valuable signal for further improvement of AI-based strategies, especially in the context of adapting to incomplete, dynamic operational data. The drop in efficiency in these situations may also be due to insufficient fallback procedures when full schedule data is unavailable, as the strategy was designed to minimize the number of operations and reduce crane travel distances under full schedule visibility.

Nevertheless, the AI-based strategy demonstrated the highest efficiency, consistently achieving the lowest number of operations and crane working times across all simulations. The strategy based on M. Zając’s model showed the greatest resilience to dynamically changing conditions at the container terminal, proving its excellent suitability for real-world implementation.

Figure 8 presents a comparison of the three storage strategies depending on the level of available operational schedule information. For the LAY and SVD strategies, a clear, systematic relationship is observed: the greater the knowledge about planned container pickup times, the fewer the relocation operations (MOVE). Increased information levels allow these strategies to make more accurate location decisions, reducing unproductive container movements.

The AI strategy, in contrast, follows a different trajectory. Even with low information levels, it yields relatively good results, and its efficiency improves more rapidly than deterministic methods as more data becomes available. The AI line takes on a distinct, more dynamic shape, reflecting the strategy’s ability to act adaptively under uncertainty and to flexibly adjust to current operational conditions. This behavior demonstrates a significant advantage of AI-based strategies in situations where information is incomplete, volatile, or delayed.

The divergent shape of the AI strategy’s curve, compared to LAY and SVD, primarily results from its adaptive capabilities and dynamic decision-making approach. Unlike the other two methods that follow predefined, deterministic rules, the AI strategy analyzes the current yard state and available schedule data in real time. This not only allows it to better respond to changing operational conditions but also to more effectively anticipate upcoming operations through a predictive component built upon ChatGPT-4.

Even with limited schedule knowledge (e.g., 25% or 50%), the AI strategy can effectively estimate the needs of future operations and assign containers to slots that minimize relocation risk. This leads to a sharp decline in MOVE and MOVE_EMPTY operations as the level of information increases. It is evident that the AI strategy instantly benefits from any available operational data, while the LAY and SVD strategies react to increasing data availability more gradually—their curves are smoother and show no sharp improvement in efficiency.

The AI strategy not only reduces the number of relocations but also demonstrates the ability to respond dynamically to changing conditions, which translates into shorter operation times and reduced crane travel distances. In scenarios with full information (100%), it achieves the lowest values in all analyzed indicators, highlighting its high effectiveness in leveraging available data. While not an optimization strategy in the formal sense—lacking an explicit objective function and not guaranteeing a global optimum—its behavior relies on adaptive and predictive capabilities that enable it to make practically desirable decisions.

By contrast, LAY and SVD strategies follow fixed decision rules that do not adapt to new data. As a result, their performance improvements with increasing information levels are limited and more linear. The AI curve, on the other hand, exhibits a nonlinear shape, demonstrating a stronger response to improved data quality, which proves its superior operational flexibility compared to deterministic methods.

All performance indicators were accompanied by standard deviations to capture the variability across the 10 repetitions of each scenario. Ninety-five percent confidence intervals were computed for relocations, crane operating time, and travel distance. One-way ANOVA tests confirmed that the observed differences between strategies were statistically significant at the 0.05 level. Post hoc Tukey comparisons further indicated that the LLM-assisted strategy achieved significantly lower relocation counts than the baseline and hybrid strategies under full schedule visibility, while differences were not significant in the partial-information scenarios. These results confirm that the nonlinear behavior of the adaptive strategy is not a product of random variation but reflects genuine sensitivity to the quality of schedule data.

5. Discussion

The results obtained confirm the importance of operational data availability in making container placement decisions. This aligns with previous findings indicating that the level of information directly influences the number of relocations and unproductive handling operations [31,33]. Both the layer-based (LAY) and hybrid (SVD) strategies showed gradual improvements as schedule awareness increased, reflecting mechanisms previously described in heuristic and zone-based models [4].

The most intriguing observation is the nonlinear behavior of the AI strategy, whose performance strongly depends on either full information or none at all. This may be explained by the fact that AI tools—especially without appropriate data quality assessment mechanisms—may respond too optimistically to incomplete input data. This is consistent with criticisms found in recent reviews [35,36], which emphasize the need to adapt AI algorithms to real-world uncertainty and informational delays. Notably, despite lacking a clearly defined objective function, the AI strategy achieved the lowest values across nearly all indicators in the full-information scenario, confirming the potential of this method class as a decision-support tool in dynamic terminal environments.

The SVD strategy demonstrated strong stability and resilience to disturbances, supporting the validity of combining layer-based and zone-based approaches. The results align with growing interest in hybrid models, which—as noted in [26]—can better balance efficiency with operational simplicity.

From the perspective of IT system designers and container terminal operators, these findings suggest that even partial schedule awareness, if not properly processed by the decision system, may reduce operational efficiency. Therefore, collecting data is not enough; it must also be filtered, quality-assessed, and interpreted. In the context of implementing AI tools, incorporating uncertainty management mechanisms and ensuring transparency of predictive algorithms is especially crucial.

Deploying adaptive strategies can significantly improve terminal performance, but this requires proper digital infrastructure and access to real-time data. Terminal operators can use the findings of this study to guide investment decisions in decision-support systems (DSS) that dynamically adjust to the level of operational information.

The main limitation of this study is the lack of validation on real operational data. Although crane parameters and the schedule structure were modeled based on data collected from container terminals, the model itself was not tested in real-world conditions. Additionally, the yard layout (4 × 5 × 3) and simplified operation logic do not reflect the complexity of full-scale terminals. The model also does not account for weather conditions, equipment failures, staffing levels, or crane spatial constraints.

While the adaptive strategy demonstrated clear advantages in data-rich scenarios, several limitations must be acknowledged. First, the synthetic dataset used in this study cannot fully capture the complexity and variability of operational container flows; validation against real terminal logs or TOS data remains essential. Second, the LLM-assisted component should be interpreted as a heuristic rather than a fully trained ML or RL model. Although this design reduces computational requirements and avoids the need for historical training data, it also limits reproducibility and transparency. The scoring function produced by ChatGPT-4 operated as a black box, with inputs and updates defined procedurally but not derived from an interpretable mathematical model. This raises challenges for explainability (XAI), which is increasingly critical in operational decision-support systems. Finally, the yard layout considered was simplified, involving a single crane and small-scale storage grid, which restricts the generalizability of findings to large or multi-crane terminals. These limitations should be considered when interpreting the results and point directly to future research directions.

For the AI strategy, a predictive component generated by the ChatGPT-4 system was used without explicit control over the model’s structure or training on historical data. This limits the interpretability of the results in terms of classical machine learning methods. It should be emphasized that the present study constitutes a proof-of-concept based on synthetic data, parameterized by field observations at a Polish terminal. While these operational observations informed crane speeds and activity profiles, the model itself was not validated against full-scale TOS logs. A systematic validation with historical datasets is therefore a priority for future work. Another limitation concerns the scope of baselines. This study included classical heuristics (Random, Earliest-Departure-Time, Min-Relocation) but did not incorporate machine learning or reinforcement learning benchmarks (e.g., Random Forest, XGBoost, or DRL agents). This omission was deliberate, as validated training datasets were not available. Benchmarking against ML/RL methods remains an essential next step. Beyond confidence intervals and ANOVA, no explicit uncertainty metrics (e.g., entropy or reliability scores) were applied; these will be incorporated in future work to strengthen robustness analysis.

Future work should focus on:

• validating the proposed model in a real-world environment using data from Terminal Operating Systems (TOS),
• extending the model with additional infrastructure elements, including more than one crane and a larger yard,
• testing AI strategy performance under different levels of noise and errors in the schedule data,
• comparing the strategy with other predictive algorithms, such as LSTM, XGBoost, or Reinforcement Learning models,
• implementing a confidence estimation module to mitigate the risk of overinterpreting incomplete data.

Additionally, integration with real DSS used in terminals and experiments using historical data collected by handling equipment should be considered.

The observed nonlinear performance of the AI-based strategy suggests that its internal scoring mechanism evolves during the simulation. In scenarios with limited information, it may initially prioritize accessibility but later adapt to minimize relocations as the yard fills up. While not a full reinforcement learning implementation, this behavior reflects a form of policy adaptation driven by in-scenario feedback. Future research may explore persistent learning frameworks to retain knowledge across sessions and improve performance stability.

Beyond its localized application at the container yard level, the proposed approach supports the broader vision of AI-enhanced supply chain management. By enabling more predictable and energy-efficient operations under volatile schedule information, adaptive stacking contributes to seamless intermodal handovers, reduced bottlenecks, and improved utilization of shared infrastructure. As AI continues to redefine the logistics landscape, integrating such decision-support mechanisms becomes essential for building resilient, agile, and data-informed transport networks.

6. Conclusions

This simulation-based study confirmed that the choice of container stacking strategy significantly affects the operational efficiency of a container terminal, especially under incomplete schedule information. The comparison of three strategies—layer-based (LAY), hybrid (SVD), and LLM-assisted heuristic—showed clear differences in relocations, crane operating time, and travel distance.

The adaptive strategy supported by ChatGPT-4 achieved the best results under full information, reducing relocations by up to one-third compared to deterministic methods. However, with partial information, its performance was unstable, sometimes falling below the hybrid approach, which proved more resilient. This instability reflects the absence of explicit data quality assessment and the sensitivity of LLM-generated heuristics to incomplete inputs.

Importantly, the proposed method should be regarded as a lightweight heuristic informed by a large language model rather than a fully trained ML or RL system. While this design offers flexibility without requiring historical datasets, it also limits reproducibility, interpretability, and scalability. These constraints, combined with the simplified yard layout and reliance on synthetic data, represent major limitations of the present study.

Future research should therefore focus on:

−

validating the model with operational logs from Terminal Operating Systems,

−

benchmarking against classical ML (e.g., Random Forest, XGBoost) and RL/DRL methods,

−

integrating explainability mechanisms (XAI) to mitigate the black-box nature of LLM scoring,

−

and developing modules for assessing the reliability of incomplete or noisy input data.

From a practical perspective, the findings suggest that hybrid strategies remain the most stable choice under uncertainty, whereas LLM-assisted heuristics can provide efficiency gains in data-rich environments if coupled with transparency and robustness mechanisms. Extending the scope of analysis to larger and more complex terminal layouts, diverse handling equipment (e.g., reach stackers, RMG, AGVs), and environmental performance indicators will further strengthen the applied value of this research. It should be emphasized that this study represents a simulation-based proof-of-concept. Validation with operational logs and large-scale yard configurations is required before the proposed method can be implemented in practice.