Wheel–Rail Vertical Vibration Due to Random Roughness in the Presence of the Rail Dampers with Mixed Damping System
Abstract
1. Introduction
2. Mechanical Model of a Moving Wheel on a Rail with Rail Dampers
- -
- For the rail:
- -
- For the sleeper ‘i’
- -
- For the rail damper ‘i’
3. Numerical Application
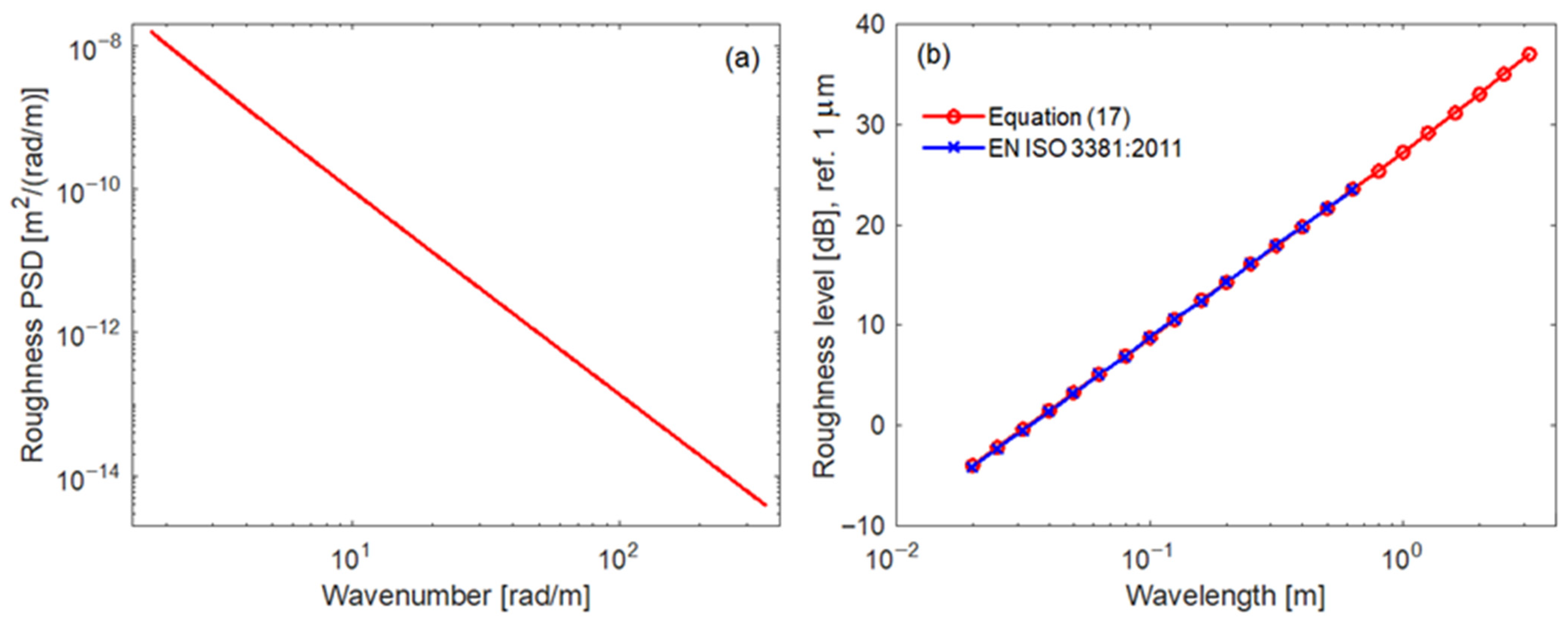
3.1. Pseudo-Random Function of the Roughness
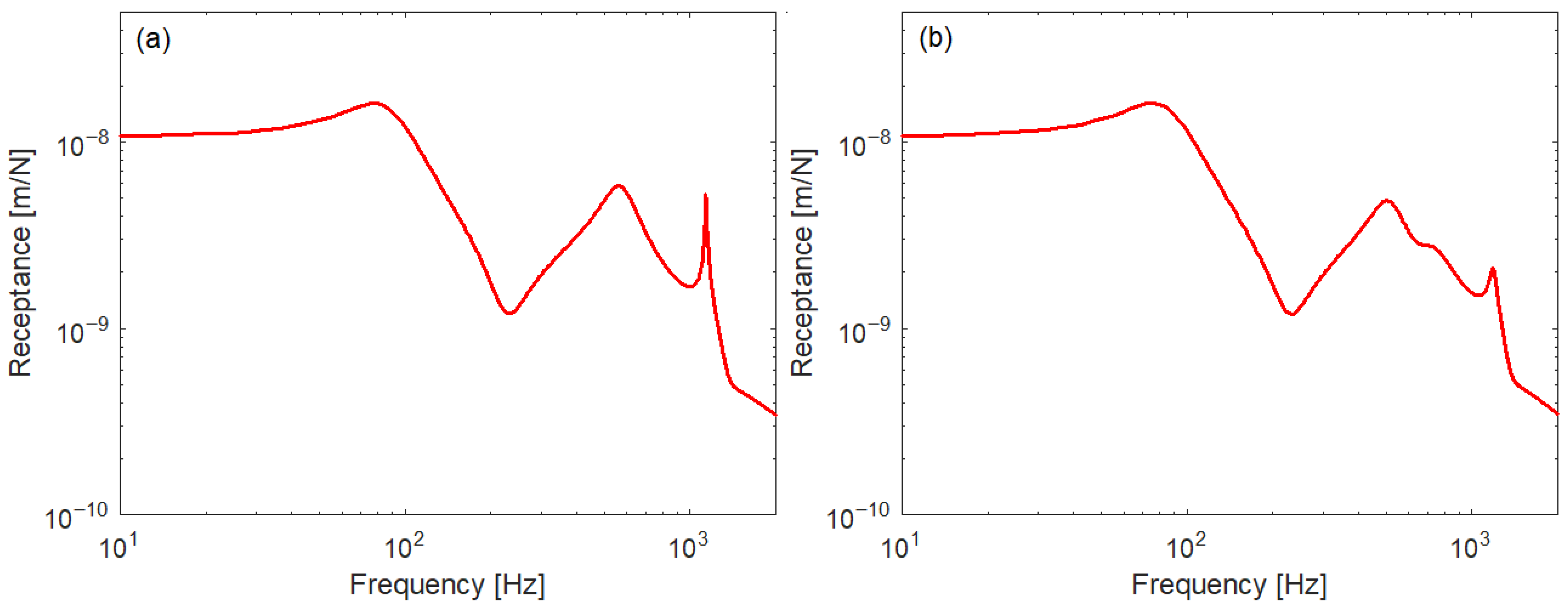
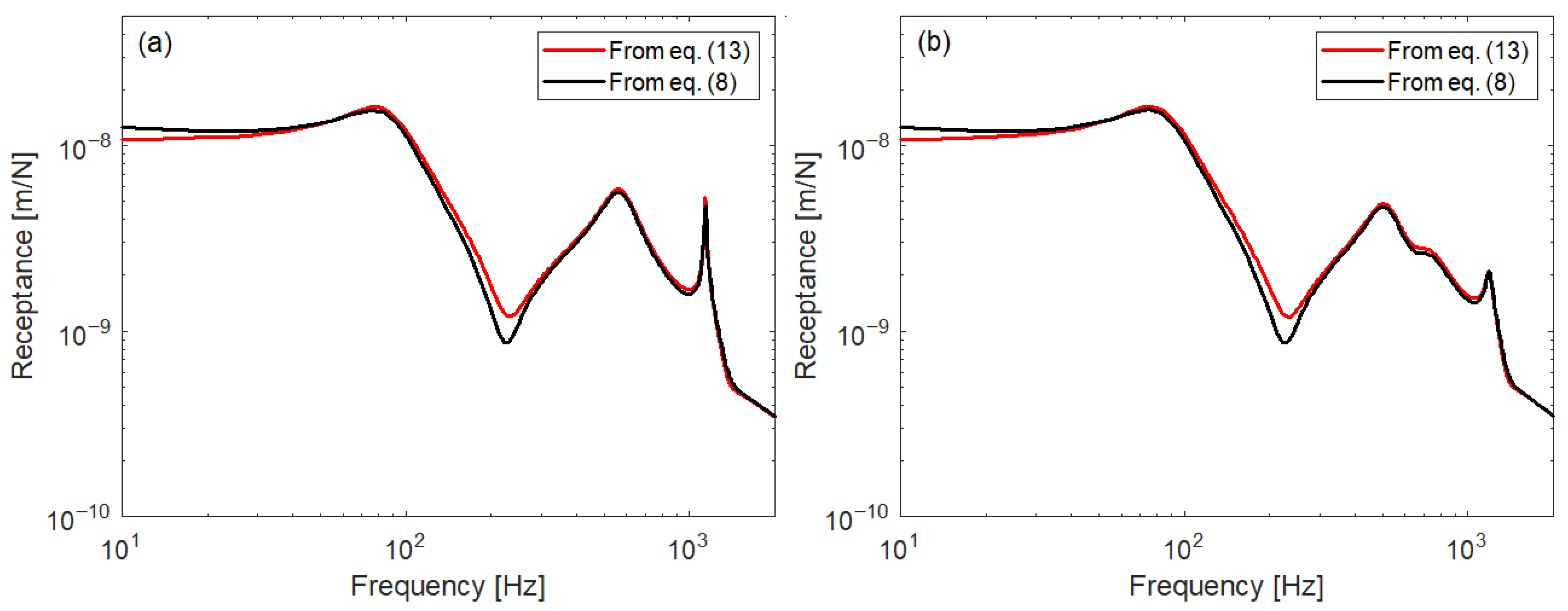
3.2. Green Functions
3.3. Wheel–Rail Steady-State Vibration
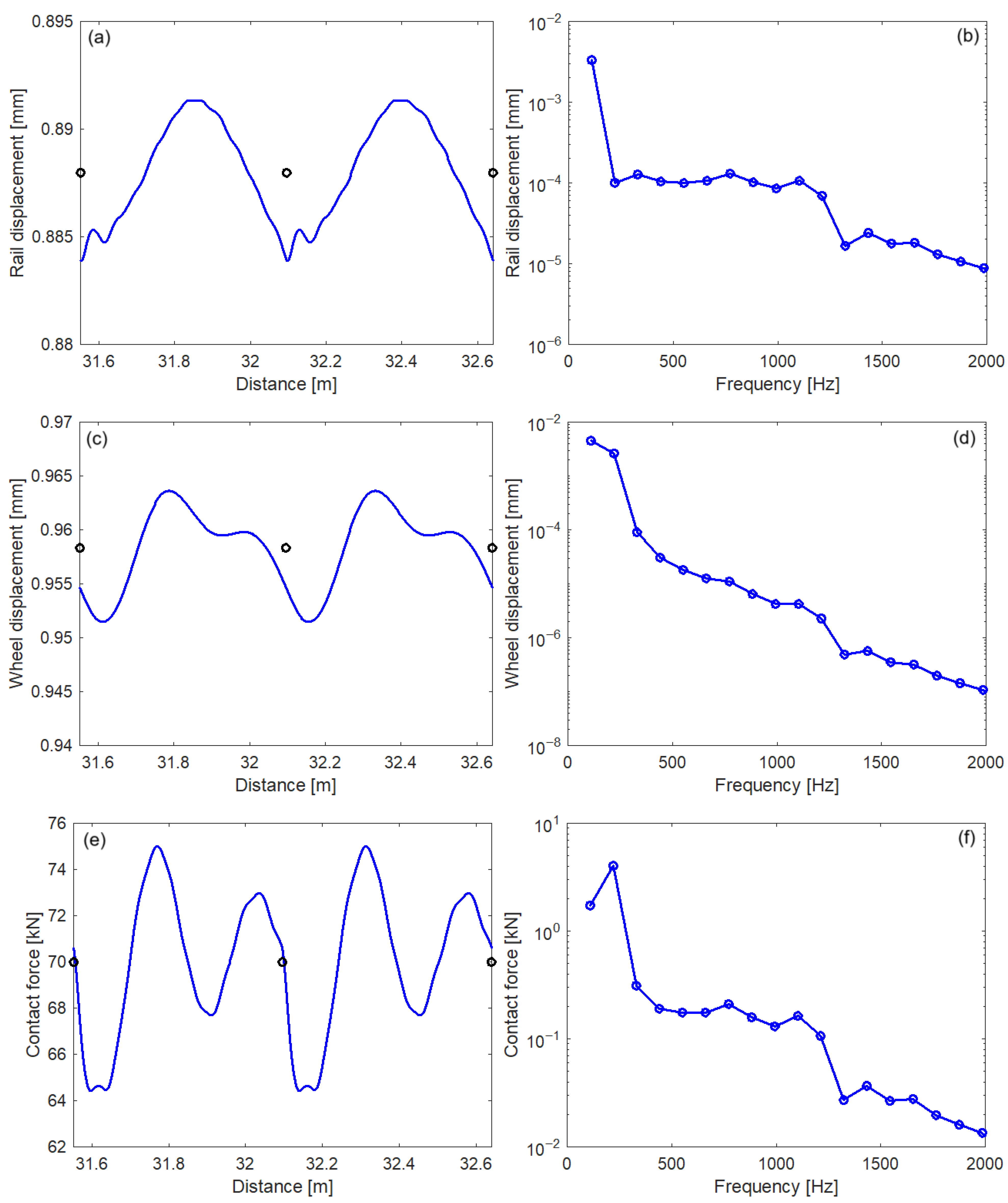
3.4. Wheel–Rail Vibration Due to Random Roughness
4. Conclusions
- (1)
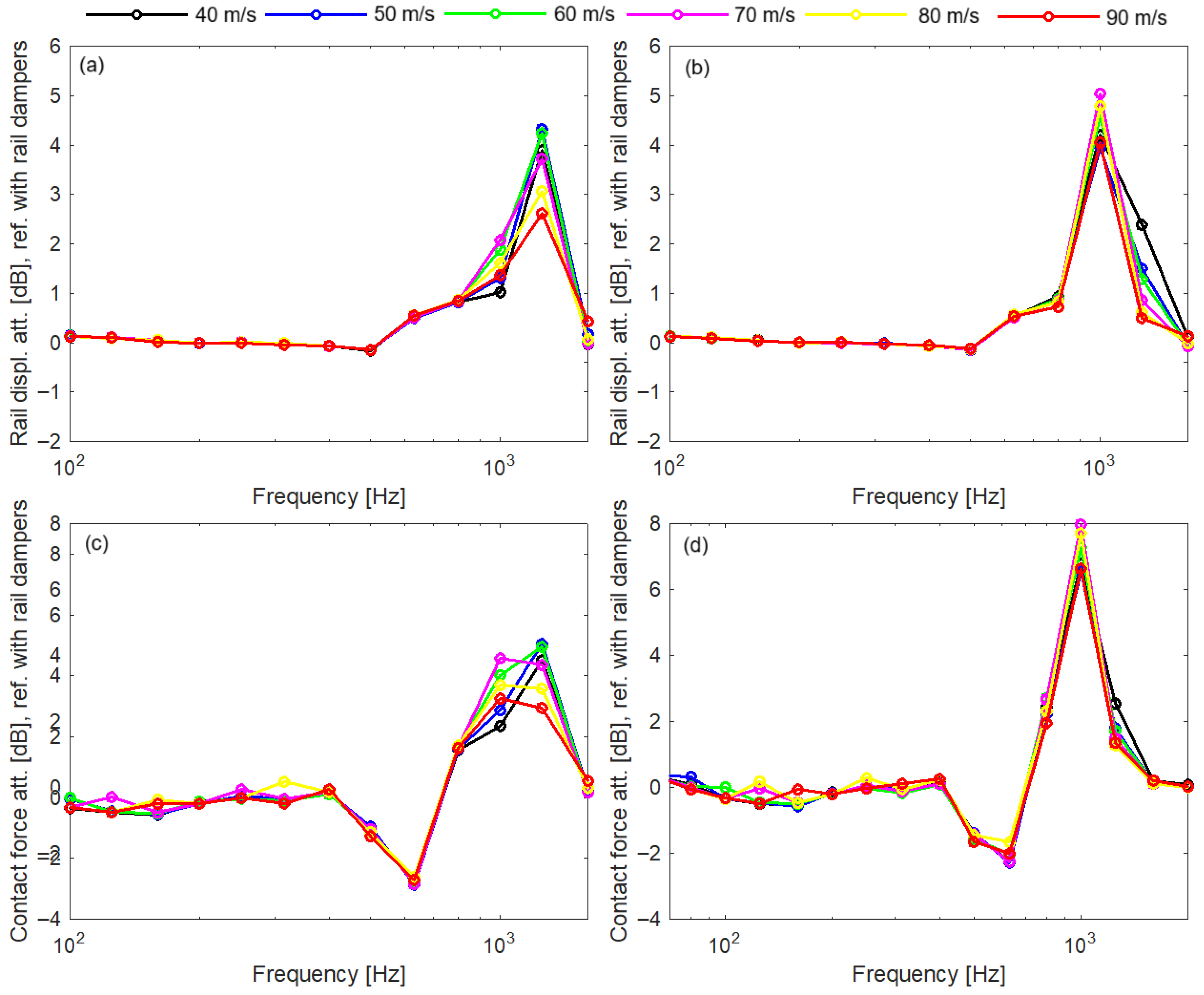
- Because rail dampers are attached directly to the rail, they primarily affect the rail dynamics and wheel–rail contact force over a relatively wide frequency range, starting at 500–600 Hz for stiff rail pads and 200–300 Hz for soft rail pads, and extending up to nearly 1600 Hz;
- (2)
- Rail dampers significantly reduce the level of rail vibration and the wheel–rail contact force when stiff rail pads are used;
- (3)
- With soft rail pads, the reduction in the vibration and contact force level is considerably lower;
- (4)
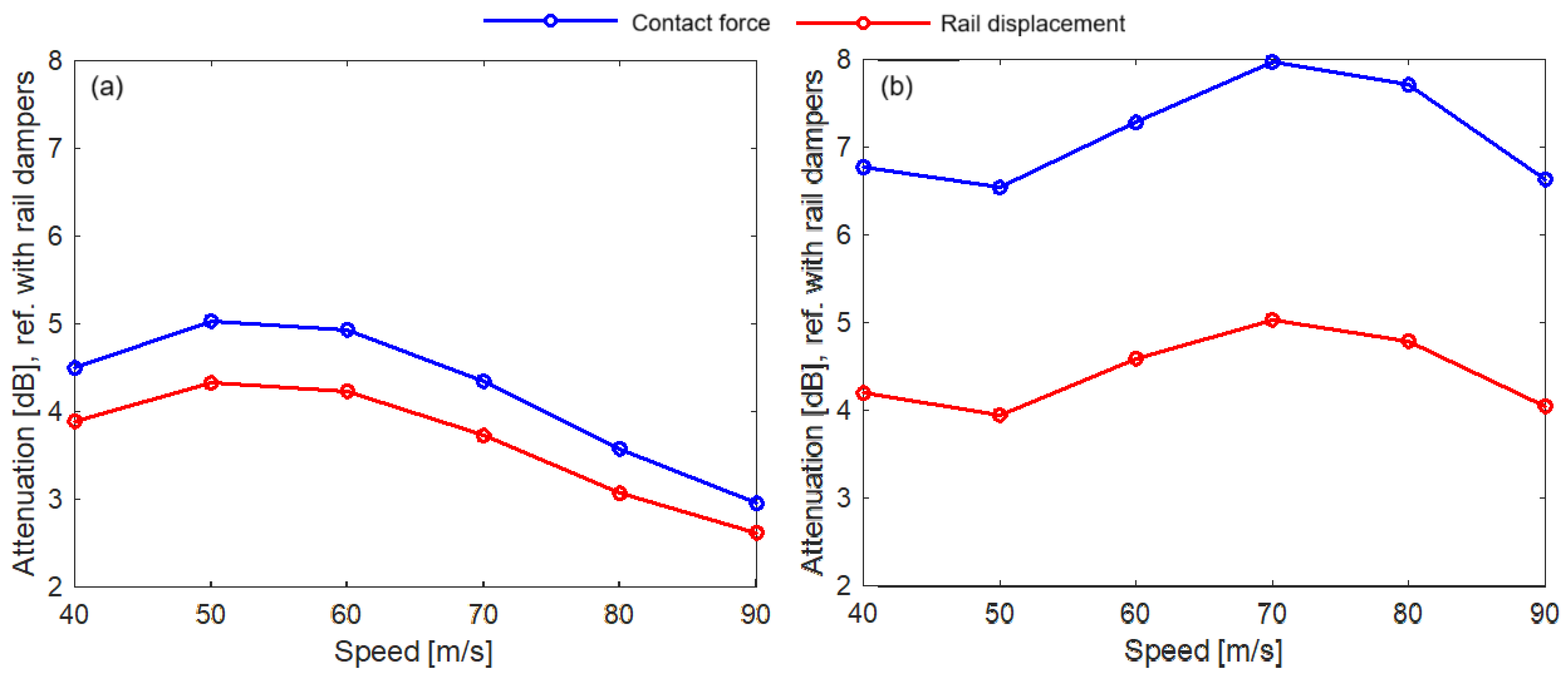
- The largest reduction in vibration level and contact force is observed with a long sleeper bay;
- (5)
- However, rail dampers slightly amplify the contact force at the lower edge of their effective frequency range;
- (6)
- Effectiveness of the rail dampers depends on wheel speed, reaching its maximum at a certain value and subsequently decreasing as the speed increases.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mazilu, T. Comfort at the Rolling Stock; Matrixrom: Bucharest, Romania, 2003. (In Romanian) [Google Scholar]
- Hemsworth, B. Environmental Noise Directive Development of Action Plans for Railways, Prepared for International Union of Railways. 2008. Available online: https://uic.org/IMG/pdf/action_planning_paper_final-2.pdf (accessed on 16 October 2024).
- Thompson, D. Railway Noise and Vibration: Mechanisms, Modelling and Means of Control, 2nd ed.; Elsevier Ltd.: London, UK, 2024. [Google Scholar]
- Mazilu, T. Vibrations; Matrixrom: Bucharest, Romania, 2012. (In Romanian) [Google Scholar]
- Wang, Y.; Dimitrovová, Z.; Yau, J.D. Laboratory Vibration Studies of Metro Tracks Equipped with Tuned Rail Dampers. J. Vib. Eng. Technol. 2023, 11, 2659–2669. [Google Scholar] [CrossRef]
- Chen, J.; Liu, W.; Sun, X. Effects of Tuned Rail Damper on Track Dynamic Characteristics Optimization. Procedia Eng. 2017, 199, 1616–1622. [Google Scholar] [CrossRef]
- Merideno, I.; Nieto, J.; Gil-Negrete, N.; Ortiz, J.G.G.; Landaberea, A.; Iartza, J. Theoretical prediction of the damping of a railway wheel with sandwich–type dampers. J. Sound Vib. 2014, 333, 4897–4911. [Google Scholar] [CrossRef]
- Peng, Y.; Zhang, D.; Sheng, X.; Thompson, D. A fundamental study on the performance of tuned mass dampers installed periodically on a fast-rotating train wheel. J. Sound Vib. 2024, 576, 118271. [Google Scholar] [CrossRef]
- Thompson, D.J.; Jones, C.J.C.; Waters, T.P.; Farrington, D. A tuned damping device for reducing noise from railway track. Appl. Acoust. 2007, 68, 43–57. [Google Scholar] [CrossRef]
- Wu, T.X. Effects on short pitch rail corrugation growth of a rail vibration absorber/damper. Wear 2011, 271, 339–348. [Google Scholar] [CrossRef]
- Mazilu, T.; Fologea, D. Experimental study on the performance of a rail damper. IOP Conf. Ser. Mater. Sci. Eng. 2018, 400, 620186. [Google Scholar] [CrossRef]
- Michalczyk, R.; Brzeziński, K.; Zbiciak, A. Numerical Vibration Response of Railway Track Retrofitted with Single Degree of Freedom Rail Dampers. IOP Conf. Ser. Mater. Sci. Eng. 2019, 661, 2–8. [Google Scholar] [CrossRef]
- Maes, J.; Sol, H. A double tuned rail damper—Increased damping at the two first pinned–pinned frequencies. J. Sound Vib. 2003, 267, 721–737. [Google Scholar] [CrossRef]
- Liu, H.P.; Wu, T.X.; Li, Z.G. Theoretical modelling and effectiveness study of rail vibration absorber for noise control. J. Sound Vib. 2009, 323, 594–608. [Google Scholar] [CrossRef]
- Dumitriu, M.; Cruceanu, I.C. On the Rolling Noise Reduction by Using the Rail Damper. J. Eng. Sci. Technol. Rev. 2017, 10, 87–95. [Google Scholar] [CrossRef]
- Jones, C.J.C.; Thompson, D.J.; Diehl, R.J. The use of decay rates to analyse the performance of railway track in rolling noise generation. J. Sound Vib. 2006, 293, 485–495. [Google Scholar] [CrossRef]
- Ryue, J.; Thompson, D.J.; White, P.R.; Thompson, D.R. Decay rate of propagating waves in railway tracks at high frequencies. J. Sound Vib. 2009, 320, 955–976. [Google Scholar] [CrossRef]
- EN ISO 3095:2013; Acoustics—Railway Applications—Measurement of Noise Emitted by Railbound Vehicles. British Standards Institution: London, UK, 2013.
- Wu, T.X. On the railway track dynamics with rail vibration absorber for noise reduction. J. Sound Vib. 2008, 309, 739–755. [Google Scholar] [CrossRef]
- Poisson, F.; Margiocchi, F. The use of dynamic on the rail to reduce the noise of steel railway bridges. J. Sound Vib. 2006, 293, 944–952. [Google Scholar] [CrossRef]
- Wu, T.X. Attenuating Railway Track Vibration by Rail Absorber for Noise Reduction. Noise Vib. Worldw. 2008, 39, 14–23. [Google Scholar] [CrossRef]
- Wu, T.X.; Liu, H.P. Reducing the rail component of rolling noise by vibration absorber: Theoretical prediction. Proc. IMechE Part F J. Rail Rapid Transit 2009, 223, 473–483. [Google Scholar] [CrossRef]
- Li, W.; Wang, A.; Gao, X.; Ju, L.; Liu, L. Development of multi-band tuned rail damper for rail vibration control. Appl. Acoust. 2021, 184, 108370. [Google Scholar] [CrossRef]
- Liu, H.; Wu, T.X. The influences on railway rolling noise of a rail vibration absorber and wave reflections due to multiple wheels. Proc. IMechE Part F J. Rail Rapid Transit 2010, 224, 227–235. [Google Scholar] [CrossRef]
- Liu, H.; Yang, J.; Wu, T. The influences of rail vibration absorber on normal wheel–rail contact forces due to multiple wheels. J. Vib. Control 2015, 21, 275–284. [Google Scholar] [CrossRef]
- Parker, A.; Weber, C. Rail Dampers—The First Australian Field Trial. In Proceedings of the 20th International Congress on Acoustics, ICA 2010, Sydney, Australia, 23–27 August 2010. [Google Scholar]
- Squicciarini, G.; Toward, M.G.R.; Thompson, D.J. Experimental procedures for testing the performance of rail dampers. J. Sound Vib. 2015, 359, 21–39. [Google Scholar] [CrossRef]
- Sun, F.; Sun, Z.; Liang, R.; Ding, D.; Ma, M. Experimental Study on the Rail Damper for Vibration and Noise Control and Rail Corrugation Suppression. Urban Rail Transit 2025, 11, 207–220. [Google Scholar] [CrossRef]
- Qian, W.J.; Huang, Z.Q.; Ouyang, H.; Chen, G.X.; Yang, H.J. Numerical investigation of the effects of rail vibration absorbers on wear behaviour of rail surface. Proc. IMechE Part J J. Eng. Tribol. 2018, 233, 424–438. [Google Scholar] [CrossRef]
- Qian, W.J.; Wu, Y.F.; Chen, G.X.; Ouyang, H. Experimental and numerical studies of the effects of a rail vibration absorber on suppressing short pitch rail corrugation. J. Vibroeng. 2016, 18, 1133–1144. [Google Scholar] [CrossRef]
- Croft, B.E.; Jones, C.J.C.; Thompson, D.J. Modelling the effect of rail dampers on wheel–rail interaction forces and rail roughness growth rates. J. Sound Vib. 2009, 323, 17–32. [Google Scholar] [CrossRef]
- EN 13674-1:2003; Railway Applications—Track—Rail Part 1: Vignole Railway Rails 46 kg/m and Above. British Standards Institution: London, UK, 2003.
- Fologea, D.; Mazilu, T.; Gheți, M.A.; Apostol, I.I. Parametric Study on the Effect of Rail Dampers on Track Decay Rate. Appl. Sci. 2024, 14, 9541. [Google Scholar] [CrossRef]
- Maia, N. Reflections on the hysteretic damping model. Shock Vibr. 2009, 16, 529–542. [Google Scholar] [CrossRef]
- Macris, N. Causal hysteretic element. J. Eng. Mech. 1997, 123, 1209–1214. [Google Scholar] [CrossRef]
- Mazilu, T. Green’s functions for analysis of dynamic response of wheel/rail to vertical excitation. J. Sound Vib. 2007, 306, 31–58. [Google Scholar] [CrossRef]
- Cruceanu, I.C. Research on Wheel–Rail System Vibrations. Doctoral Thesis, University Politehnica of Bucharest, Bucharest, Romania, 2021. (In Romanian). [Google Scholar]
- EN ISO 3381:2011; Railway Applications—Acoustics—Measurement of Noise Inside Railbound Vehicles. British Standards Institution: London, UK, 2011.
- Wu, T.X.; Thompson, D.J. On the parametric excitation of the wheel/track system. J. Sound Vib. 2004, 278, 725–747. [Google Scholar] [CrossRef]
- Wu, T.X. Parametric excitation of wheel/track system and its effects on rail corrugation. Wear 2008, 265, 1176–1182. [Google Scholar] [CrossRef]
- Mazilu, T. Wheel\Rail Interaction Due to Parametric Excitation. U.P.B. Sci. Bull. Ser. D 2007, 69, 23–38. [Google Scholar]
- Abe, K. Rail model for parametric excitation analysis of a discretely supported track. J. Sound Vib. 2025, 618, 119309. [Google Scholar] [CrossRef]




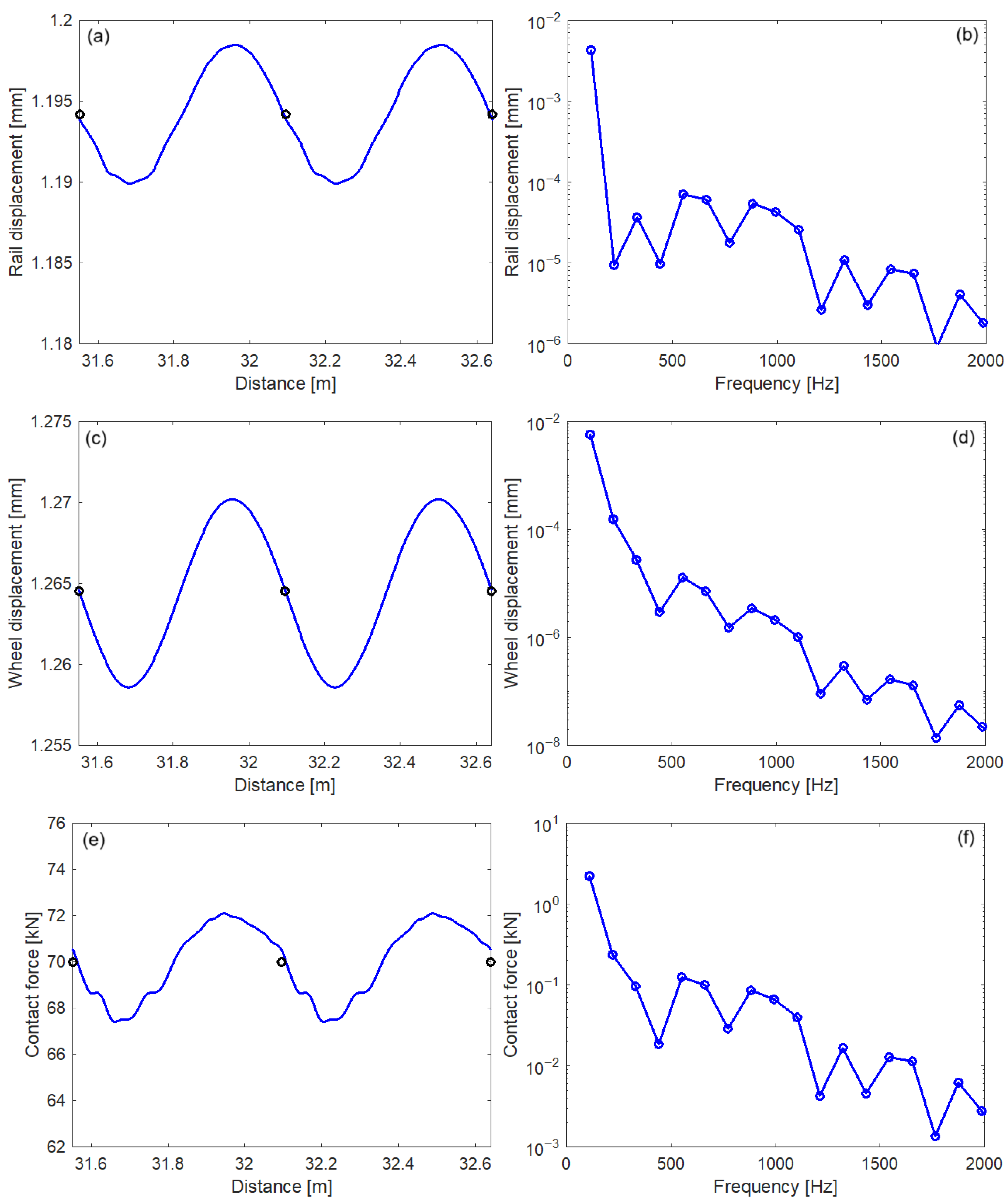
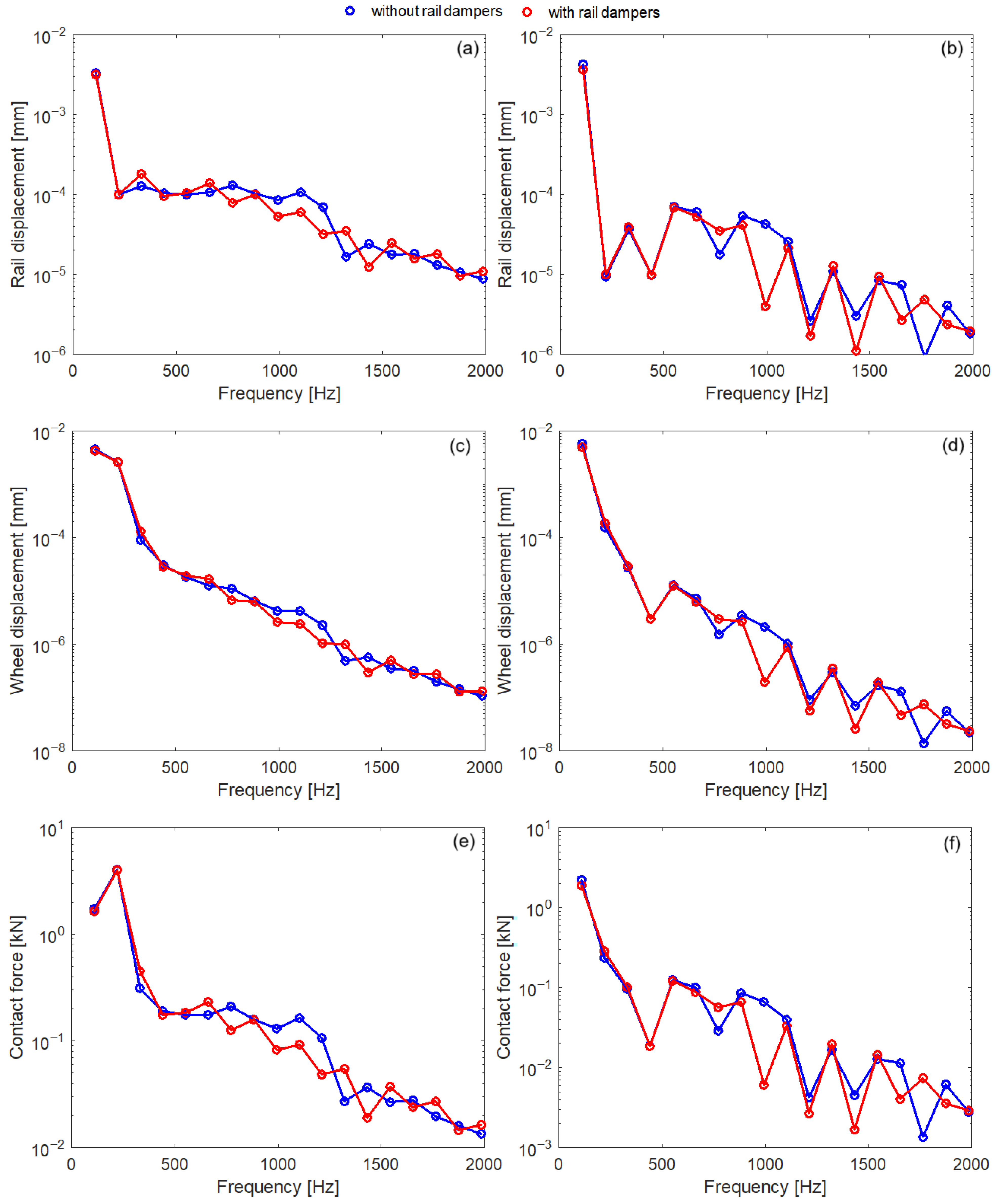
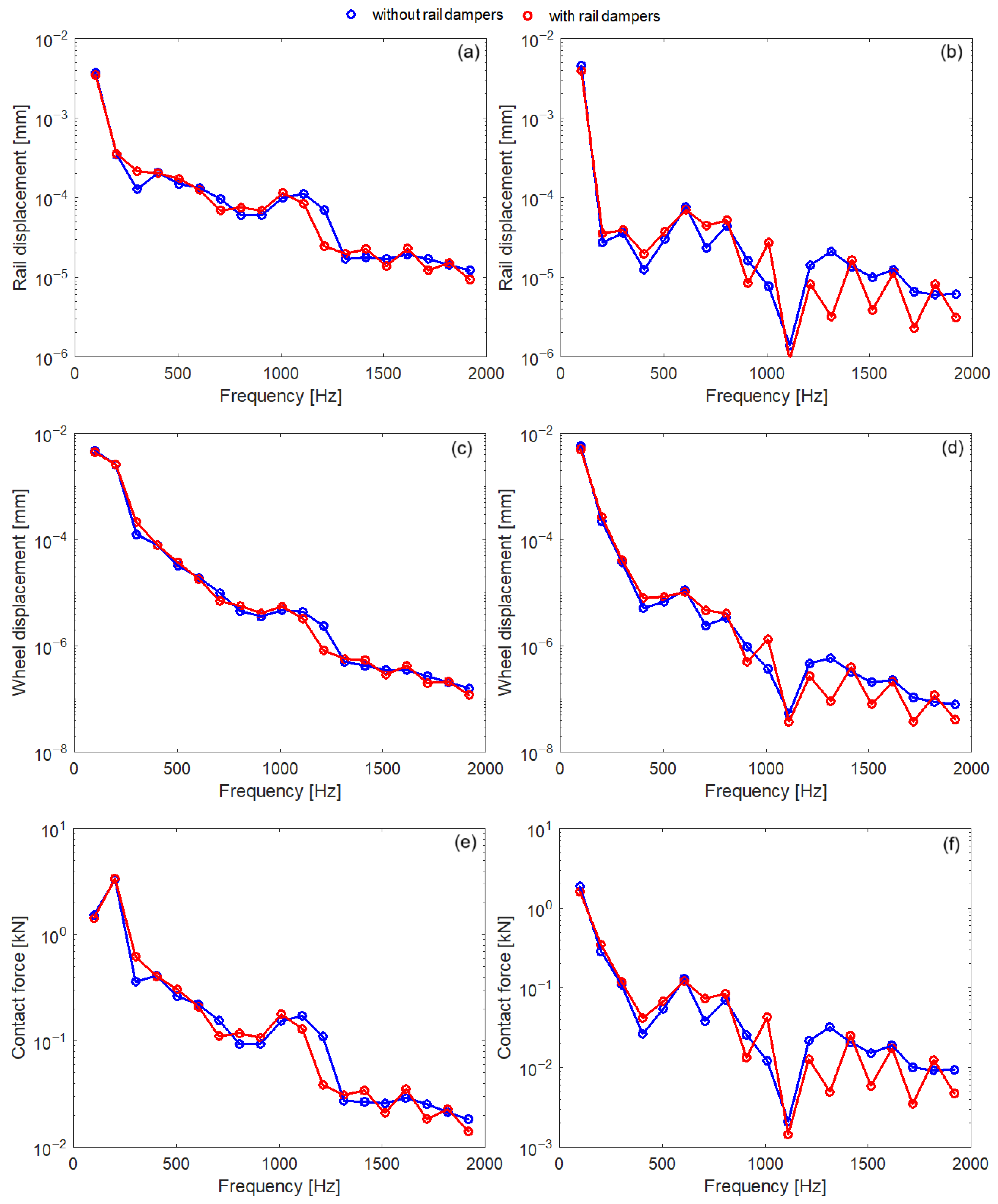
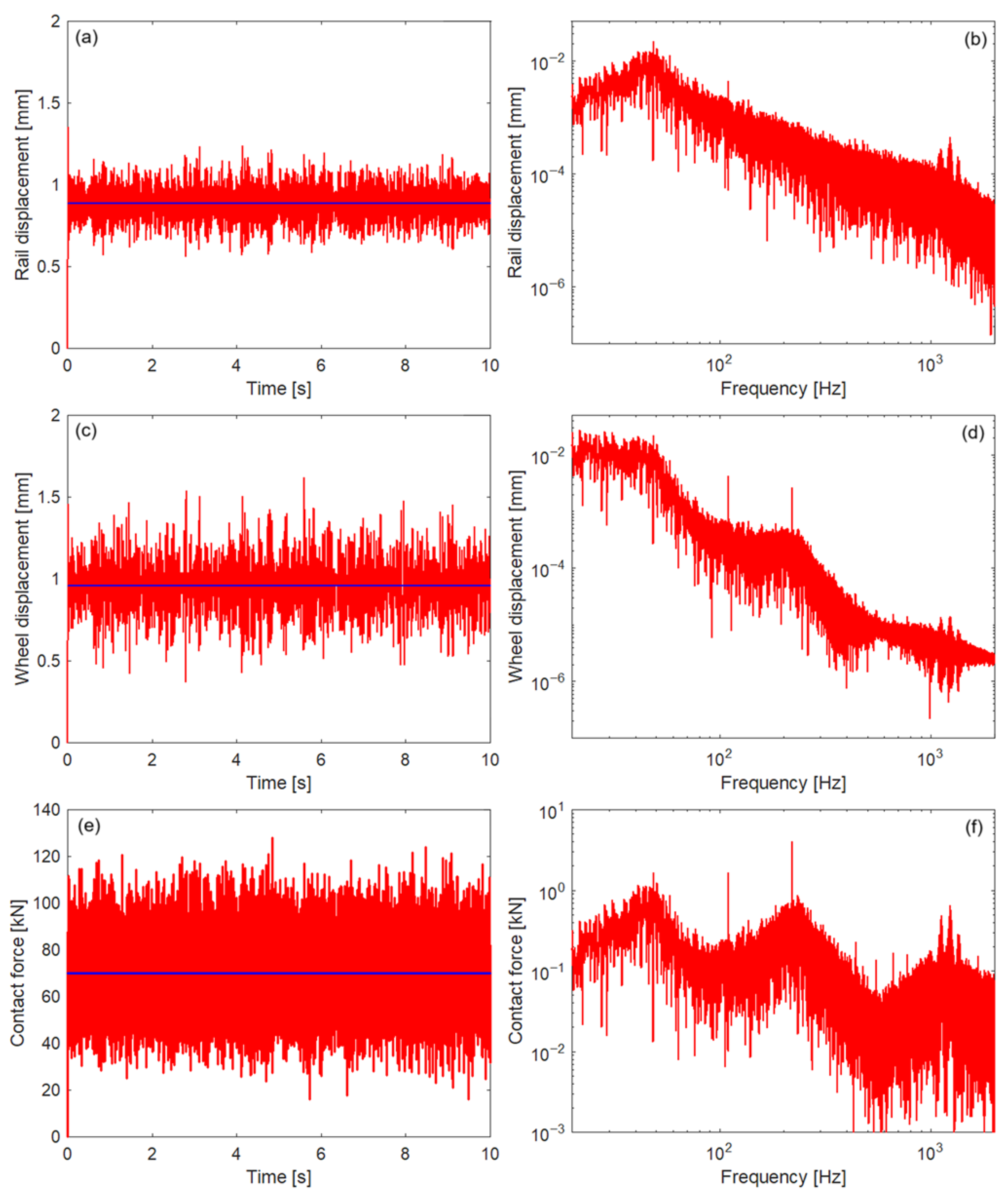
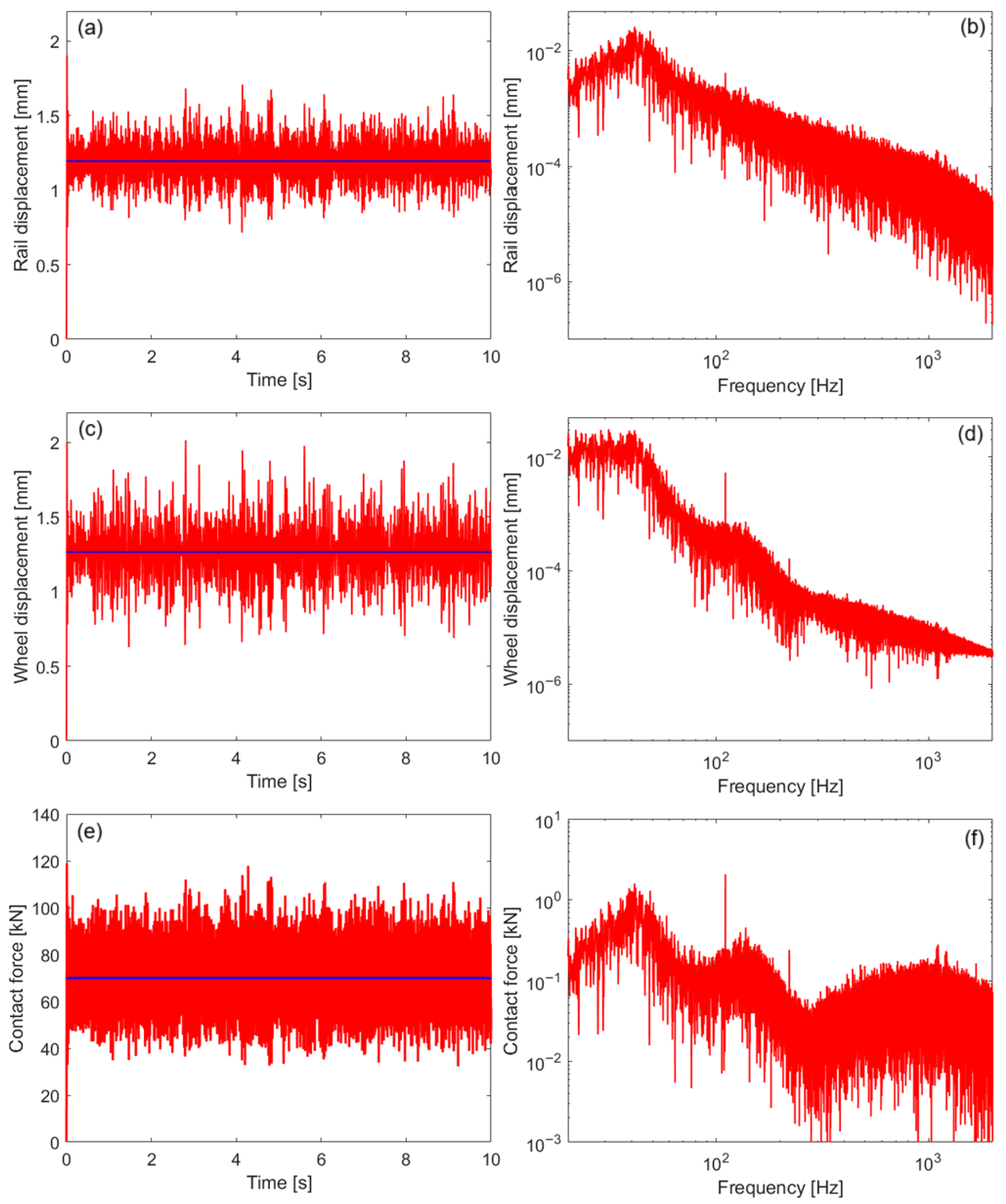
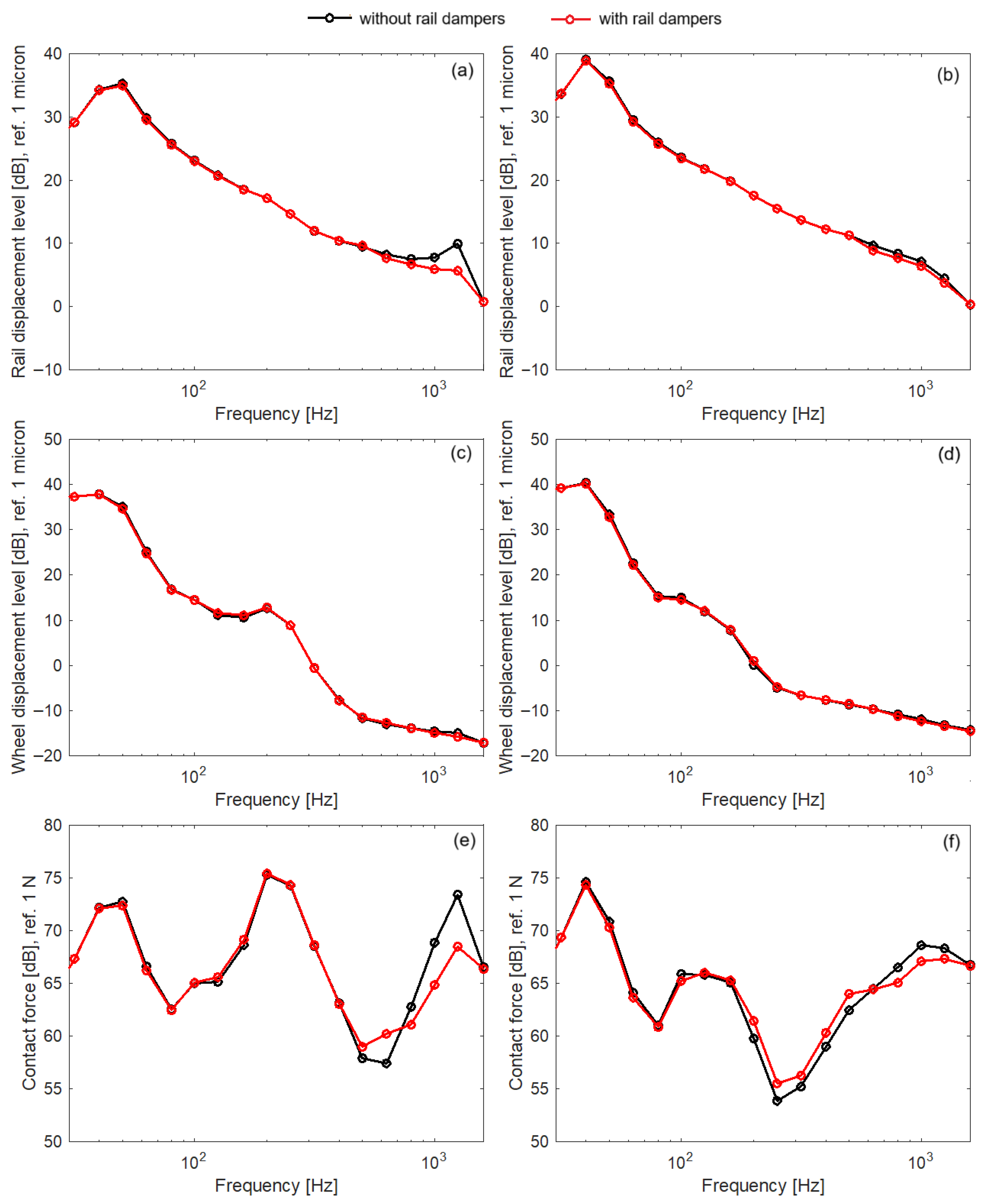

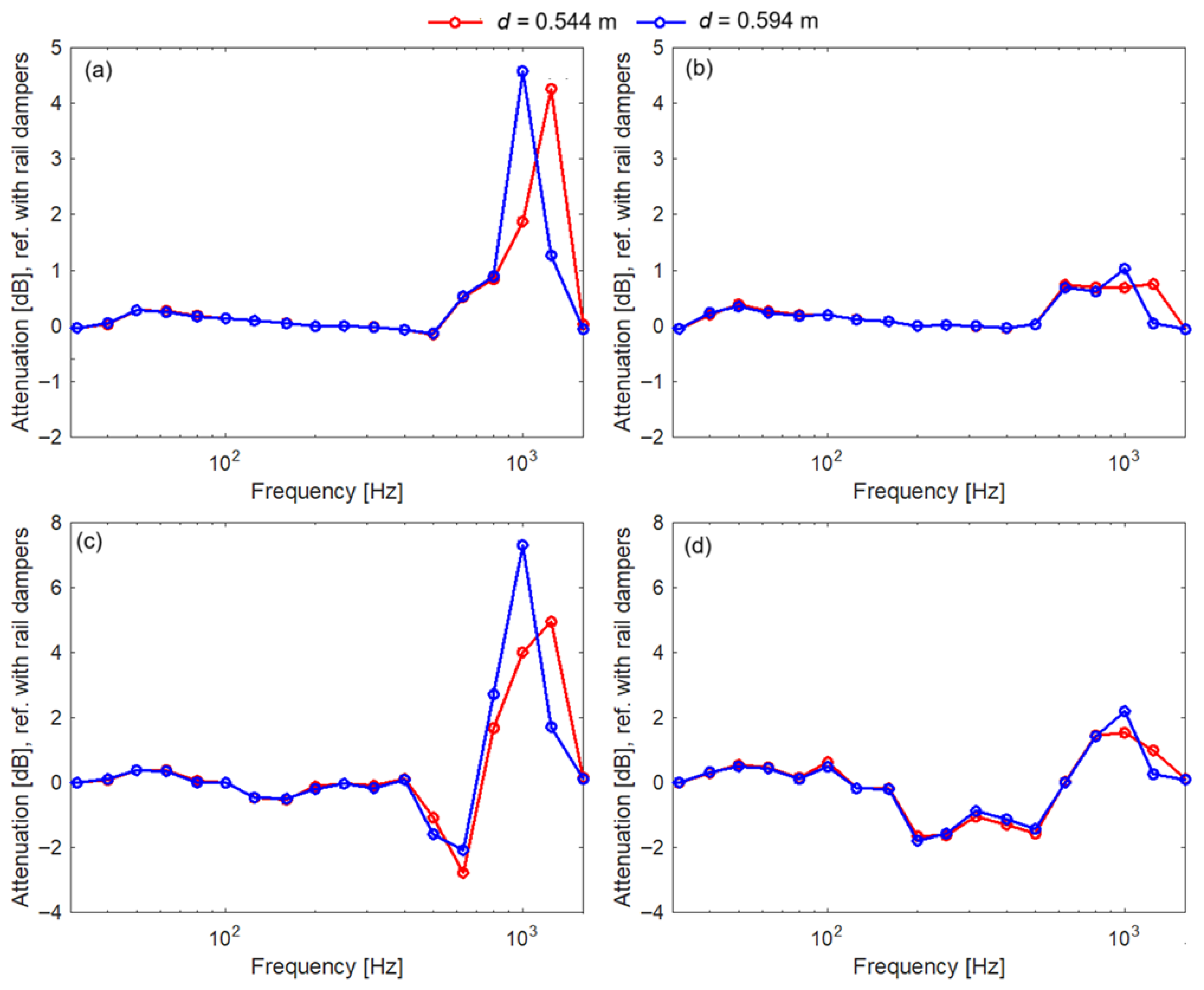
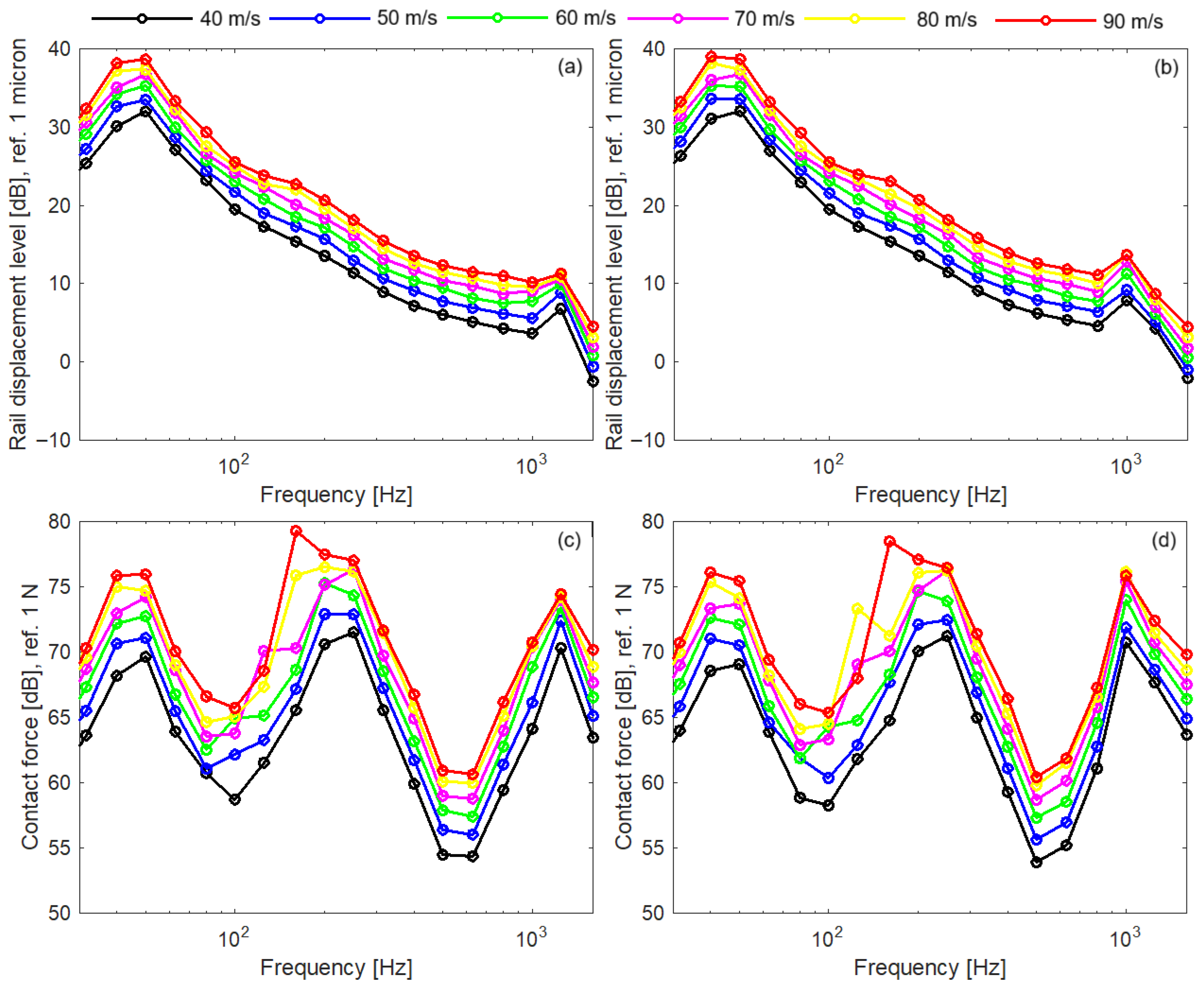
| Parameter | Notation | Value | |
|---|---|---|---|
| Wheel mass | Mw | 800 kg | |
| Hertzian constant | CH | 118.6 GN/m3/2 | |
| Static load | Qo | 70 kN | |
| Rail mass per unit length | m | 49.4 kg/m | |
| Rail density | r | 7850 kg/m3 | |
| Young’s modulus of elasticity | E | 210 GPa | |
| Shear modulus of elasticity | G | 81 GPa | |
| Rail loss factor | η | 0.01 | |
| Cross-section area | S | 62.92 × 10−4 m2 | |
| Area moment of inertia | I | 18.16 × 10−6 m4 | |
| Shear coefficient | κ | 0.40 | |
| Sleeper mass (half) | Mt | 131 kg | |
| Rail pad stiffness | kp | Soft | 60 MN/m |
| Stiff | 300 MN/m | ||
| Rail pad loss factor | ηp | 0.30 | |
| Ballast stiffness | kb | 40 MN/m | |
| Ballast loss factor | ηb | 0.60 | |
| Sleeper bay | l | Short | 0.544 m |
| Long | 0.595 m | ||
| First body mass | M1 | 3.650 kg | |
| Second body mass | M2 | 3.514 kg | |
| First elastic element stiffness | k1 | 50.62 MN/m | |
| First elastic element loss factor | η1 | 0.35 | |
| Second elastic element stiffness | k2 | 5.617 MN/m | |
| Second elastic element loss factor | η2 | 0.25 | |
| Coefficient of roughness PSD | Kr | 6.04 × 10−8 m0.18rad1.82 | |
| Contant of roughness PSD | Ωo | 3.1 × 10−8 rad2.82/m0.82 | |
| Exponent of roughness PSD | n | 3.82 | |
| Minimum value of the wavenumber range | Ωmin | 1.777 rad/m | |
| Maximum value of the wavenumber range | Ωmax | 352.988 rad/m | |
| Wavenumber-domain discretization step | DΩ | 0.001 rad/m | |
| Time-domain discretization step | Dt | 2/60 ms | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazilu, T.; Fologea, D.; Gheți, M.-A. Wheel–Rail Vertical Vibration Due to Random Roughness in the Presence of the Rail Dampers with Mixed Damping System. Appl. Sci. 2025, 15, 10027. https://doi.org/10.3390/app151810027
Mazilu T, Fologea D, Gheți M-A. Wheel–Rail Vertical Vibration Due to Random Roughness in the Presence of the Rail Dampers with Mixed Damping System. Applied Sciences. 2025; 15(18):10027. https://doi.org/10.3390/app151810027
Chicago/Turabian StyleMazilu, Traian, Dorina Fologea, and Marius-Alin Gheți. 2025. "Wheel–Rail Vertical Vibration Due to Random Roughness in the Presence of the Rail Dampers with Mixed Damping System" Applied Sciences 15, no. 18: 10027. https://doi.org/10.3390/app151810027
APA StyleMazilu, T., Fologea, D., & Gheți, M.-A. (2025). Wheel–Rail Vertical Vibration Due to Random Roughness in the Presence of the Rail Dampers with Mixed Damping System. Applied Sciences, 15(18), 10027. https://doi.org/10.3390/app151810027







