Research on Active Suppression Methods for End-Effector Residual Vibration of Heavy-Load Collaborative Robots in Arbitrary Poses
Abstract
1. Introduction
2. Modeling and Parameter Estimation of Residual Vibration at the End of a Manipulator in Arbitrary Poses
2.1. Modeling of Residual Vibration at the End of a Manipulator
2.2. Parameter Estimation of Residual Vibration at the End of a Robotic Arm in Arbitrary Poses
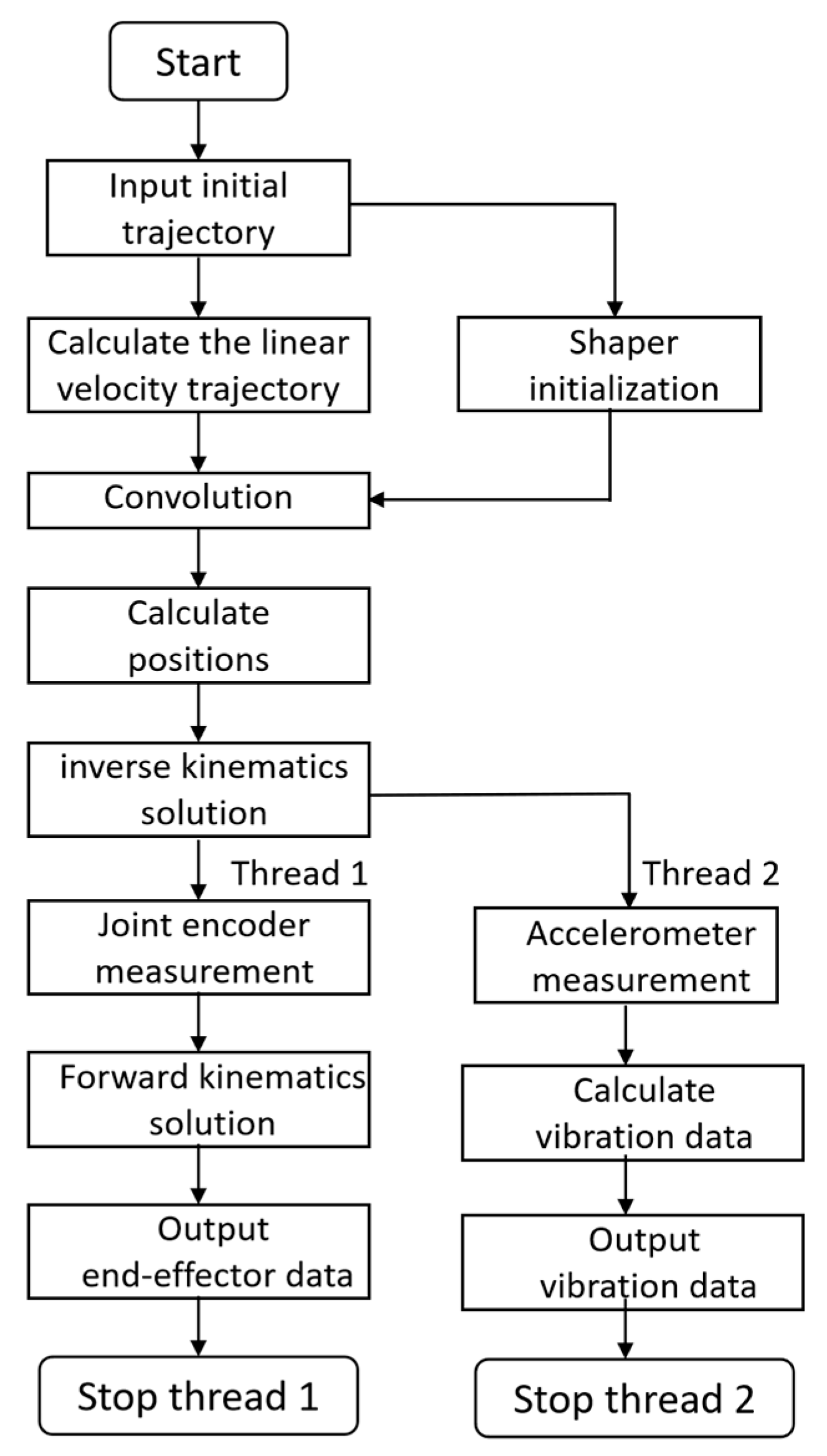
3. Active Suppression of Residual Vibration of Manipulators Based on Input Shapers
3.1. ZV Input Shaper
3.2. ZVD Input Shaper
3.3. EI Input Shaper
4. Experiments and Analysis
4.1. Experiment on Vibration Suppression of a Single-Joint Manipulator
4.2. Experiment on Heavy-Load Six-Axis Collaborative Robot
4.2.1. Introduction to the Experimental Platform
4.2.2. Vibration Parameter Identification for Arbitrary Poses
4.2.3. Active Suppression of Manipulator in Arbitrary Poses
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aliev, K.; Antonelli, D. Proposal of a monitoring system for collaborative robots to predict outages and to assess reliability factors exploiting machine learning. Appl. Sci. 2021, 11, 1621. [Google Scholar] [CrossRef]
- Liu, L.; Guo, F.; Zou, Z.; Duffy, V.G. Application, development and future opportunities of collaborative robots (cobots) in manufacturing: A literature review. Int. J. Hum.–Comput. Interact. 2024, 40, 915–932. [Google Scholar] [CrossRef]
- Xiang, Q.; Chen, C.; Jiang, Y. Vibration Suppression of Collaborative Robot Servo with Dual Encoders. Appl. Sci. 2025, 15, 2548. [Google Scholar] [CrossRef]
- Han, X.; Wu, K.; Hui, N. Co-Optimization of Vibration Suppression and Data Efficiency in Robotic Manipulator Dynamic Modeling. Appl. Sci. 2025, 15, 7679. [Google Scholar] [CrossRef]
- Wang, G.; Fang, S.; Xu, Q. Robot Joint Vibration Suppression Method Based on Improved ADRC. Appl. Sci. 2025, 15, 5476. [Google Scholar] [CrossRef]
- Min, F.; Cai, Y.; She, Y.; Wang, G.; Li, D. Robot collisions classification based on variational mode decomposition of vibration measurements. IEEE Trans. Instrum. Meas. 2024, 73, 1–16. [Google Scholar] [CrossRef]
- Bandopadhya, D.; Bhogadi, D.K.; Bhattacharya, B.; Dutta, A. Active Vibration Suppression of a Flexible Link Using Ionic Polymer Metal Composite. In Proceedings of the 2006 IEEE Conference on Robotics, Automation and Mechatronics, Bangkok, Thailand, 1–3 June 2006; pp. 1–6. [Google Scholar]
- Bajkowski, J.M.; Dyniewicz, B.; Bajer, C.I. Semi-Active Damping Strategy for Beams System with Pneumatically Controlled Granular Structure. Mech. Syst. Signal Process. 2016, 70–71, 387–396. [Google Scholar] [CrossRef]
- Cannon, R.H., Jr.; Schmitz, E. Initial Experiments on the End-Point Control of aFlexible One-Link Robot. Int. J. Robot. Res. 1984, 3, 62–75. [Google Scholar] [CrossRef]
- Preumont, A. Vibration Control of Active Structures; Springer: Berlin/Heidelberg, Germany; Brussels, Belgium, 2011; p. 49. [Google Scholar]
- Meckl, P.H.; Arestides, P.B. Optimized S-Curve Motion Profiles for Minimum Residual Vibration. In Proceedings of the 1998 American Control Conference (ACC), Philadelphia, PA, USA, 26 June 1998; Volume 5, pp. 2627–2631. [Google Scholar]
- Kuck, E.; Sands, T. Space robot sensor noise amelioration using trajectory shaping. Sensors 2024, 24, 666. [Google Scholar] [CrossRef]
- Magistri, F.; Marcuzzi, R.; Marks, E.; Sodano, M.; Behley, J.; Stachniss, C. Efficient and accurate transformer-based 3d shape completion and reconstruction of fruits for agricultural robots. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; pp. 8657–8663. [Google Scholar]
- Dona, D.; Bettega, J.; Tamellin, I.; Boscariol, P.; Caracciolo, R. Minimum-Energy Trajectory Planning for an Underactuated Serial Planar Manipulator. Robotics 2025, 14, 98. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Kim, J.J.; Hudson, J. Input Shaping Control of a Flexible Structure for Rest-to-Rest and Non-Rest-to-Rest Maneuvers. Appl. Sci. 2025, 15, 2952. [Google Scholar] [CrossRef]
- Singer, N.C.; Seering, W.P. Preshaping Command Inputs to Reduce System Vibration. Automatica 1990, 23, 76–82. [Google Scholar]
- Smith, O.J. Posicast Control of Damped Oscillatory Systems. Proc. IRE 1957, 45, 1249–1255. [Google Scholar] [CrossRef]
- Pao, L.Y.; Lau, M.A. Expected Residual Vibration of Traditional and Hybrid Input Shaping Designs. J. Guid. Control Dyn. 1999, 22, 162–165. [Google Scholar] [CrossRef]
- Pao, L.Y. Multi-input Shaping Design for Vibration Reduction. Automatica 1999, 35, 81–89. [Google Scholar] [CrossRef]
- Tuttle, T.D.; Seering, W.P. A Zero-Placement Technique for Designing Shaped Inputs to Suppress Multiple-Mode Vibration. In Proceedings of the American Control Conference (ACC), Baltimore, MD, USA, 29 June–1 July 1994; Volume 3, pp. 2533–2537. [Google Scholar]
- Zhao, Y.; Tomizuka, M. Modified Zero Time Delay Input Shaping for Industrial Robot With Flexibility. In Proceedings of the ASME 2017 Dynamic Systems and Control Conference, Tysons, VA, USA, 11–13 October 2017; Volume 3, pp. 1–6. [Google Scholar]
- Zhao, Y. Intelligent Control and Planning for Industrial Robots. Ph.D. Dissertation, University of California, Berkeley, CA, USA, 2018; pp. 21–46. [Google Scholar]
- Huang, J.; Maleki, E.; Singhose, W. Dynamics and Swing Control of Mobile Boom Cranes Subject to Wind Disturbances. IET Control Theory Appl. 2013, 7, 1187–1195. [Google Scholar] [CrossRef]
- Peng, J.; Huang, J.; Singhose, W. Payload Twisting Dynamics and Oscillation Suppression of Tower Cranes During Slewing Motions. Nonlinear Dyn. 2019, 98, 1041–1048. [Google Scholar] [CrossRef]
- Huang, B.; Gan, Y.; Fang, F.; Zhou, B.; Dai, X. Research on vibration suppression for industrial robots based on dynamic feedforward control. In Proceedings of the IEEE 2024 43rd Chinese Control Conference (CCC), Kunming, China, 28–31 July 2024; pp. 4398–4403. [Google Scholar]
- Tang, X.; Xun, T.; Yang, J.; Ding, H. Vibration suppression of series elastic actuator used for robotic grinding based on reconstructed hybrid optimized input shaper. Mech. Syst. Signal Process. 2025, 223, 111817. [Google Scholar] [CrossRef]
- Tong, S.; Zeng, J.; Miao, Z.; Chen, G. Parameter optimization of tuned inerter damper for vibration suppression in structures with damping. J. Sound Vib. 2025, 597, 118827. [Google Scholar] [CrossRef]
- Kenderi, G.; Fidlin, A. Nonparametric Identification of Nonlinear Dynamic Systems Using a Synchronisation-Based Method. J. Sound Vib. 2014, 333, 6405–6423. [Google Scholar] [CrossRef]
- Masri, S.F.; Chassiakos, A.G.; Caughey, T.K. Identification of Nonlinear Dynamic Systems Using Neural Networks. J. Appl. Mech. 1993, 60, 123–133. [Google Scholar] [CrossRef]
- Juang, J.N.; Pappa, R.S. An Eigen System Realization Algorithm for Modal Parameter Identification and Model Reduction. J. Guid. Control Dyn. 1985, 8, 620–627. [Google Scholar] [CrossRef]
- Nadkarni, I.; Bhardwaj, R.; Ninan, S.; Chippa, S.P. Experimental Modal Parameter Identification and Validation of Cantilever Beam. Mater. Today Proc. 2021, 38, 319–324. [Google Scholar] [CrossRef]
- Doughty, T.A.; Davies, P.; Bajaj, A.K. A Comparison of Three Techniques Using Steady State Data to Identify Non-Linear Model Behavior of an Externally Excited Cantilever Beam. J. Sound Vib. 2002, 249, 785–813. [Google Scholar] [CrossRef]
- Cheng, M.; Zhang, X.; Ding, R.; Zhang, J.; Xu, B. Residual vibration suppression of large-size flexible hydraulic manipulator under external disturbance with accurate positioning. Mechatronics 2025, 110, 103355. [Google Scholar] [CrossRef]
- Alghanim, K.; Alenezi, H.; Mohammed, A.; Alfadhli, A. Enhanced Vibration Suppression for Overhead Cranes Over a Range of Cable Lengths. J. Vib. Eng. Technol. 2025, 13, 318. [Google Scholar] [CrossRef]
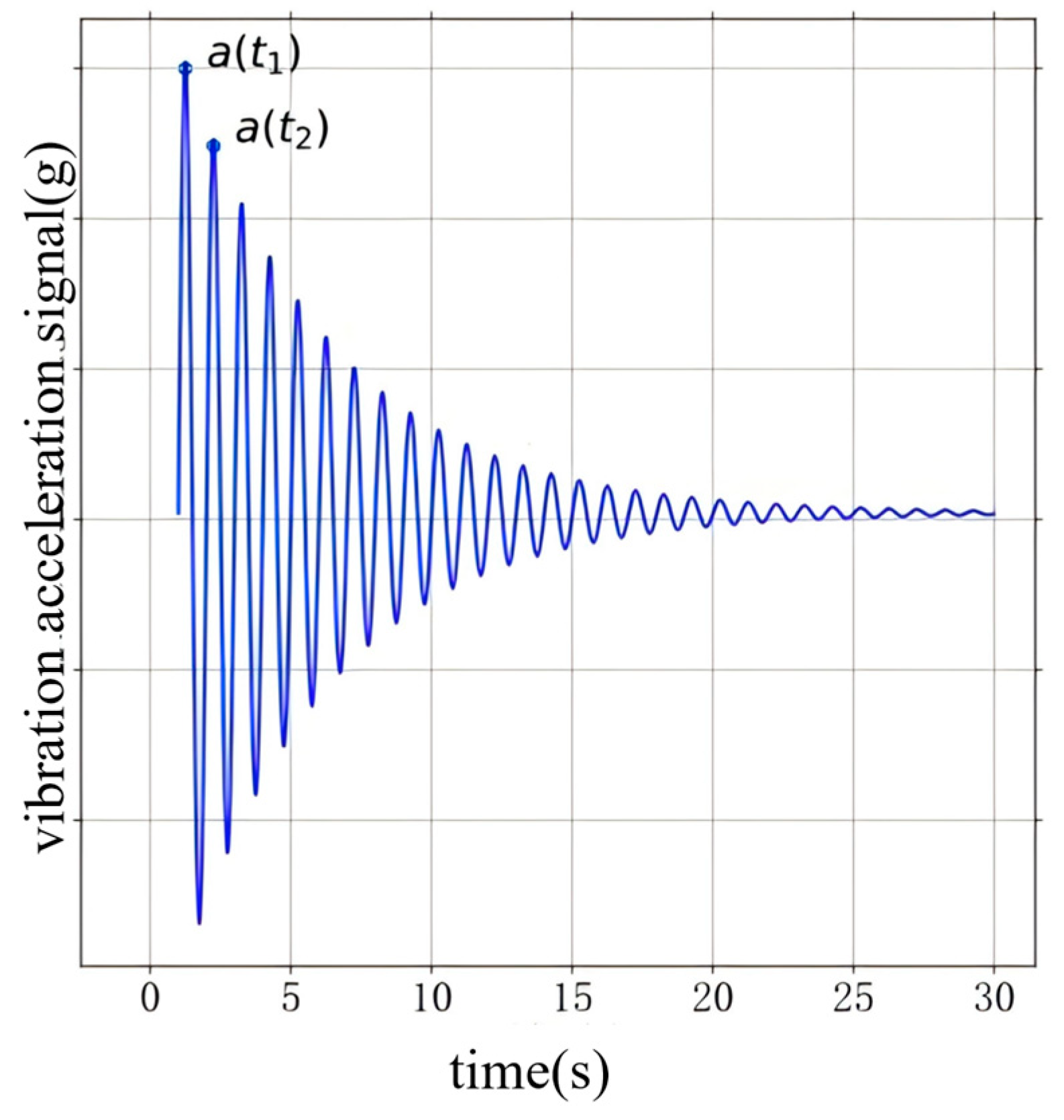



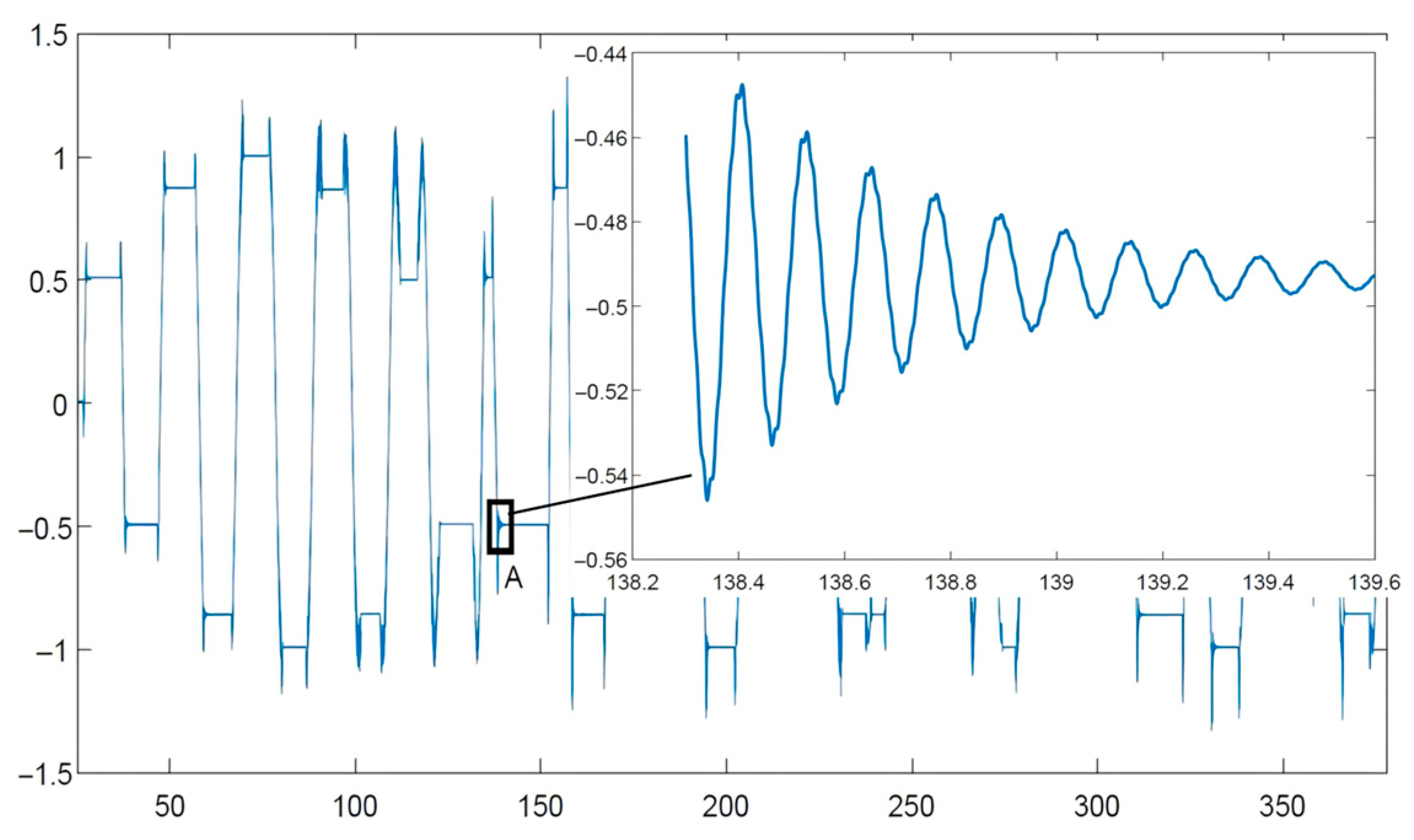

| Items | Maximum Amplitude (m/s2) | Optimization Effect |
|---|---|---|
| NO Input Shaper | 1.263 | / |
| ZV Input Shaper | 0.510 | 59.7% |
| ZVD Input Shaper | 0.393 | 68.9% |
| EI Input Shaper | 0.375 | 70.3% |
| Items | Joints | Parameters |
|---|---|---|
| Robot weight (kg) | / | 40 |
| Rated load (kg) | / | 16 |
| Working radius (mm) | 1000 | |
| Maximum operating speed(m/s) | 3 | |
| Joint range of motion (°) | J1 | ±360 |
| J2 | ±360 | |
| J3 | ±160 | |
| J4 | ±360 | |
| J5 | ±360 | |
| J6 | ±360 | |
| Maximum joint speed (°/s) | J1/J2 | 120 |
| J3/J4/J5/J6 | 180 | |
| Repeat positioning accuracy (mm) | / | ±0.03 |
| Power consumption (W) | / | 350 |
| The range of accelerometer (g) | / | ±16 |
| The resolution of accelerometer (mg/LSB) | / | 0.488 |
| The sampling frequency of accelerometer (kHz) | / | 26.667 |
| (°) | (°) | (°) | (°) | m (kg) | ()% | ()% | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 8 | 58.28 | 76.28 | 30.88 | 0.0089 | 0.0106 | 19.10 |
| 30 | 0 | 0 | 0 | 8 | 62.53 | 63.53 | 1.590 | 0.0091 | 0.0087 | 4.390 |
| 30 | 30 | 0 | 0 | 8 | 68.34 | 64.34 | 5.850 | 0.0089 | 0.0108 | 21.34 |
| 30 | 30 | 30 | 0 | 8 | 69.07 | 73.07 | 5.790 | 0.0091 | 0.0092 | 1.090 |
| 30 | 30 | 30 | 30 | 8 | 69.89 | 62.89 | 10.01 | 0.0094 | 0.0088 | 6.380 |
| 60 | 30 | 30 | 0 | 8 | 69.15 | 59.15 | 14.46 | 0.0099 | 0.0088 | 11.11 |
| 60 | 30 | 60 | 0 | 8 | 69.73 | 62.73 | 10.03 | 0.0100 | 0.0086 | 14.00 |
| 60 | 30 | 60 | 30 | 8 | 70.02 | 77.02 | 9.990 | 0.0087 | 0.0086 | 1.140 |
| 60 | 60 | 0 | 0 | 8 | 76.46 | 82.46 | 7.840 | 0.0092 | 0.0101 | 9.780 |
| 90 | 0 | 0 | 0 | 16 | 58.46 | 44.05 | 24.65 | 0.0099 | 0.0094 | 5.050 |
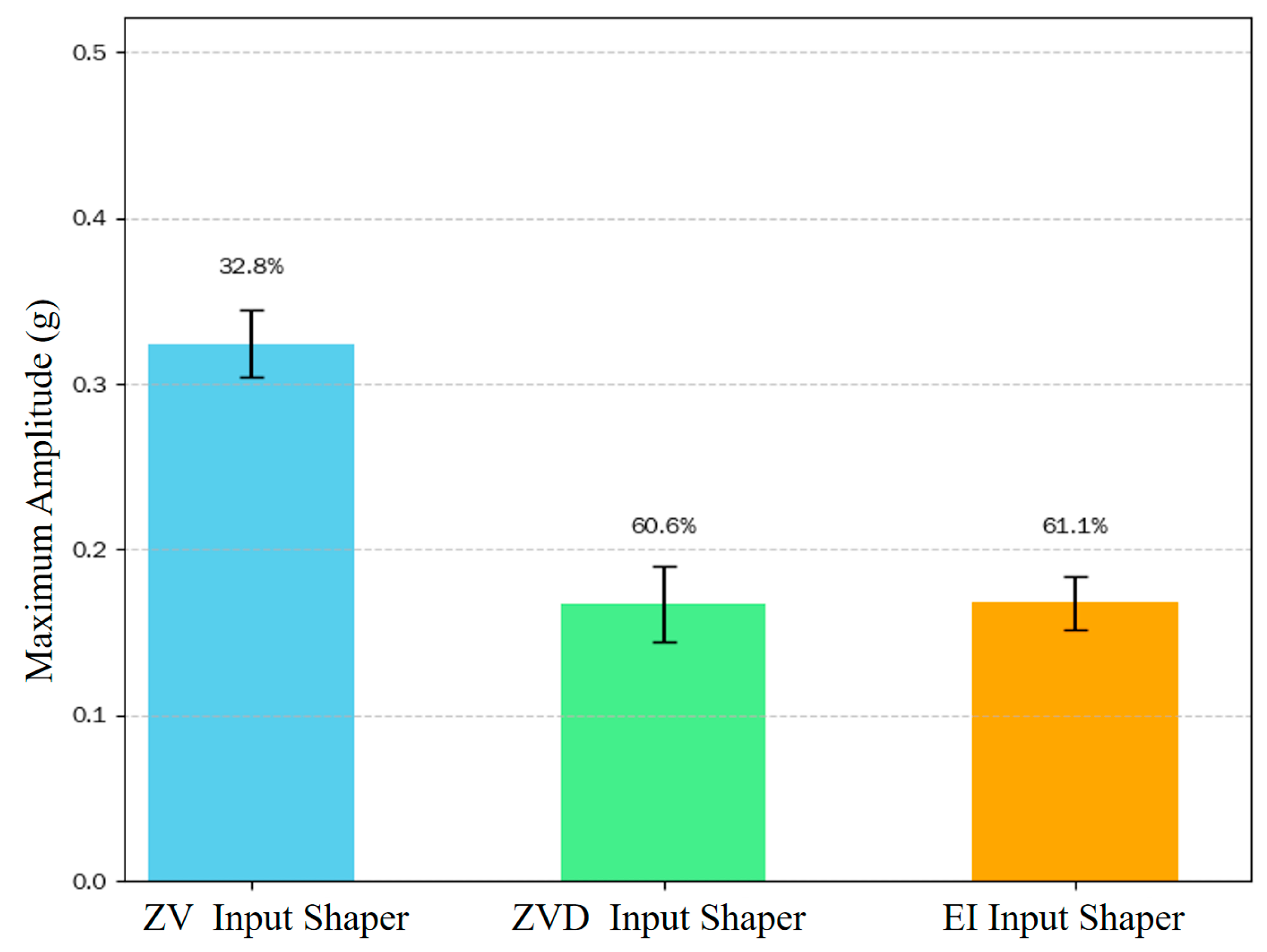
| Items | Maximum Amplitude (g) | Optimization Effect |
|---|---|---|
| NO Input Shaper | 0.4692 | / |
| ZV Input Shaper | 0.3155 | 32.8% |
| ZVD Input Shaper | 0.1849 | 60.6% |
| EI Input Shaper | 0.1825 | 61.1% |
| θ1(°) | θ2(°) | θ3(°) | θ4(°) | θ5(°) | θ6(°) | m (kg) | ZV(°) | ZVD(°) | EI(°) |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 8 | 25.82 | 40.73 | 43.02 |
| 0 | 30 | 0 | 0 | 0 | 0 | 8 | 55.46 | 78.07 | 77.41 |
| 0 | 30 | 30 | 0 | 0 | 0 | 8 | 49.25 | 66.67 | 66.57 |
| 0 | 30 | 30 | 30 | 0 | 0 | 8 | 45.58 | 62.60 | 65.44 |
| 0 | 30 | 30 | 30 | 30 | 0 | 8 | 38.67 | 62.89 | 10.01 |
| 0 | 60 | 30 | 30 | 0 | 0 | 8 | 39.85 | 57.92 | 57.34 |
| 0 | 60 | 30 | 60 | 0 | 0 | 8 | 37.86 | 65.14 | 68.30 |
| 0 | 60 | 30 | 60 | 30 | 0 | 8 | 40.05 | 60.25 | 62.37 |
| 0 | 60 | 60 | 0 | 0 | 0 | 8 | 36.72 | 59.98 | 62.95 |
| 0 | 90 | 0 | 0 | 0 | 0 | 16 | 28.43 | 45.89 | 46.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, R.; Fan, S.; Li, Z.; Lou, Y. Research on Active Suppression Methods for End-Effector Residual Vibration of Heavy-Load Collaborative Robots in Arbitrary Poses. Appl. Sci. 2025, 15, 10011. https://doi.org/10.3390/app151810011
Shi R, Fan S, Li Z, Lou Y. Research on Active Suppression Methods for End-Effector Residual Vibration of Heavy-Load Collaborative Robots in Arbitrary Poses. Applied Sciences. 2025; 15(18):10011. https://doi.org/10.3390/app151810011
Chicago/Turabian StyleShi, Ran, Shengsi Fan, Zhibin Li, and Yunjiang Lou. 2025. "Research on Active Suppression Methods for End-Effector Residual Vibration of Heavy-Load Collaborative Robots in Arbitrary Poses" Applied Sciences 15, no. 18: 10011. https://doi.org/10.3390/app151810011
APA StyleShi, R., Fan, S., Li, Z., & Lou, Y. (2025). Research on Active Suppression Methods for End-Effector Residual Vibration of Heavy-Load Collaborative Robots in Arbitrary Poses. Applied Sciences, 15(18), 10011. https://doi.org/10.3390/app151810011





