Abstract
With the rapid development of edge computing and deep learning, the efficient deployment of deep neural networks (DNNs) on resource-constrained terminal devices faces multiple challenges (background), such as execution delay, high energy consumption, and resource allocation costs. This study proposes an improved Multi-Objective Particle Swarm Optimization (MOPSO) algorithm for PSO. Unlike the conventional PSO, our approach integrates a historical optimal solution detection mechanism and a dynamic temperature regulation strategy to overcome its limitations in this application scenario. First, an end–edge–cloud collaborative computing framework is constructed. Within this framework, a multi-objective optimization model is established, aiming to minimize time delay, energy consumption, and cloud configuration cost. To solve this model, an optimization method is designed that integrates a historical optimal solution detection mechanism and a dynamic temperature regulation strategy into the MOPSO algorithm. Experiments on six types of DNNs, including the Visual Geometry Group (VGG) series, have shown that this algorithm reduces execution time by an average of 58.6%, the average energy consumption by 61.8%, and optimizes cloud configuration costs by 36.1% compared to traditional offloading strategies. Its Global Search Capability Index (GSCI) reaches 92.3%, which is 42.6% higher than the standard PSO algorithm. This method provides an efficient, secure, and stable cooperative computing solution for multi-constraint task unloading in an edge computing environment.
1. Introduction
With the rapid development of Artificial Intelligence (AI) technology, especially the widespread application of deep learning (DL), deep neural networks (DNNs) have become the core technology for processing complex tasks. DNNs have achieved significant results in fields such as image recognition [1], speech recognition [2], and natural language processing [3], and it has been widely applied in the field of Internet of Things (IoT) [4]. However, the high computational resource requirements, energy consumption, and cost issues of DNNs pose serious challenges to terminal devices such as smartphones and IoT devices. The hardware performance of terminal devices is limited, making it difficult to meet the high computing requirements of DNNs, resulting in high application response latency and insufficient device endurance [5]. These issues not only affect user experience, but also bring environmental and energy consumption problems [6]. In order to ensure the efficient execution of DNNs while avoiding the limitations of traditional computing modes [7], it is of great significance to study an offloading strategy that comprehensively considers running time, device configuration costs, and energy consumption.
Traditional offloading strategies often only focus on a single optimization objective, making it difficult to fully meet practical needs. In existing research, Chen Huimin et al. [8] studied the low energy consumption problem of the edge–cloud collaborative distributed task offloading strategy, focusing on delay-sensitive tasks, but did not fully consider computational delay and economic costs. Mengwei Xu et al. [9] studied the strategy of offloading deep learning tasks from wearable devices to mobile devices, optimizing security and computational latency, but did not consider energy consumption and economic costs. Gao Han et al. [10] designed a multi-objective offloading strategy based on end–edge–cloud, optimizing energy consumption and response time, but did not consider cloud configuration costs. In order to reduce task completion time, Su Zhi et al. [11] proposed a joint optimization algorithm based on a genetic algorithm for the task offloading ratio, channel bandwidth, and MEC computing resources, but did not consider multi-edge server scenarios. Hu Yi et al. [12] optimized service placement and task migration problems using heuristic algorithms under the constraints of service deployment costs and system latency. However, traditional algorithm research is still limited by local optima and efficiency issues.
At present, the deployment and execution methods of DNNs are mainly divided into two types: local computing based on terminal devices and complete offloading based on cloud servers [13]. Although local computing avoids data transmission delays, it is difficult to efficiently handle complex tasks and consumes high energy due to the limited computing power of terminal devices. Completely uninstalling [14] transfers computing tasks to the cloud, utilizing the powerful computing power of cloud servers to reduce computation time and terminal device energy consumption. However, data transmission may experience delays due to network congestion, and cloud configuration costs are relatively high [15]. Obviously, neither of these methods can fully meet the optimal requirements. In scenarios with large data transmission but small computational tasks, local computing has more advantages [16]; in scenarios with small data transmission but heavy computational tasks, cloud computing is more efficient [17].
The progress of deep learning and reinforcement learning has also provided new technological approaches for optimizing computation offloading strategies [18]. The method based on deep reinforcement learning can adjust policies in real-time in dynamic environments and optimize resource utilization [19]. Chen Jia et al. [20] proposed a deep network based on dual branch convolution to minimize the cost and latency of service migration. Furthermore, Yan L et al. [21] proposed a cloud–edge collaborative load balancing optimization algorithm based on deep reinforcement learning, which reduces task packet loss rate, average latency, and terminal device energy consumption. Ren et al. [22] proposed a joint optimization strategy based on computational resources and wireless network resources, using a partial computation offloading strategy to solve the multi-user delay minimization problem in MEC. Tang T [23] studied the task-dependent edge computing offload strategy in the cloud–edge collaboration architecture to minimize the average energy consumption and time delay of all IoT devices. Ren et al. [24] proposed a new partial computation offloading model that optimizes computing resources and network communication resources, reducing the latency of user devices. The above research has made further research on task offloading in the edge computing environment and achieved good results. However, considering the running time, equipment configuration cost and energy consumption are still major problems in the offloading of edge computing.
This study seeks to minimize three competing objectives simultaneously: total task completion time, total system energy consumption, and total economic cost. The solution must meet the following constraints: the execution order between tasks defined by the DNN computation graph must be followed, the total computational load allocated to any server must not exceed its computing capacity, and the total completion time must meet the deadline specified by the user.
Traditional mathematical programming methods face challenges of low efficiency or difficulty in converging on such complex problems [25]. Therefore, adopting MOPSO has become a necessary and reasonable choice.
Considering the above issues, the focus of this study is to propose an offloading strategy that can comprehensively optimize the running time, device configuration cost, and energy consumption of DNNs. By dynamically adjusting the search strategy, this strategy can adapt to the complexity and characteristics of different problems, and optimize in multiple dimensions such as task response delay, device configuration cost, and energy consumption. The contributions of this study are summarized as follows:
- This study proposes a novel multi-objective optimization model for DNN task offloading in an end–edge–cloud collaborative framework. This model simultaneously minimizes execution time, energy consumption, and cloud leasing cost, and innovatively incorporates time constraints as a hard indicator in the fitness calculation.
- This study proposes designing an enhanced MOPSO algorithm to solve the proposed model. Key improvements include a hybrid encoding scheme to seamlessly represent complex offloading decisions, a dynamic temperature regulation strategy, and an adaptive restart mechanism. These enhancements effectively prevent premature convergence, a common drawback of traditional PSO, as evidenced by a 42.6% higher Global Search Capability Index (GSCI).
- This study proposes conducting extensive simulations on six mainstream DNN models (e.g., VGG series) to validate our approach. The results demonstrate that our strategy significantly outperforms existing baselines, reducing average execution time by 58.6%, energy consumption by 61.8%, and cloud cost by 36.1%.
The rest of this paper is structured as follows. Section 2 details the system model and problem formulation, including the DNN task model and the mathematical models for time delay, energy consumption, and cost. Section 3 elaborates on the proposed Multi-Objective Particle Swarm Optimization (MOPSO) algorithm, explaining the hybrid encoding scheme, fitness function, and the improved strategy to avoid local optima. Section 4 presents the simulation setup, experimental results, and a comprehensive performance comparison with other baseline strategies. Finally, Section 5 concludes the work and suggests potential directions for future research.
2. Materials and Methods
In the offloading strategy model, there are issues related to data transmission between different devices, data representation of deep neural network hierarchical structures, and load calculation at various levels of deep neural networks. When using multi-objective optimization algorithms based on particle swarm optimization, it is necessary to calculate the fitness values of particles. A specific fitness value calculation method model is established based on the calculation time, equipment configuration cost, and energy consumption of the deep neural network determined by the objective function. The DNN structure digital model and load calculation model used in the system model are used as auxiliary models to establish a simulation offloading platform. Different deep neural network structures are converted into specific topological matrices, and the floating-point calculation amount of each layer is determined through the load calculation model to simulate the specific offloading scenario realistically and assist in calculating the specific offloading plan.
We build simulation experiment programs by constructing system models, DNN computing task models, time models, energy consumption models, and ordering cost models.
2.1. System Model
This article constructed a three-tier “end–edge–cloud” collaborative computing framework. Within this framework, we distinguish three distinct computational entities:
- The user equipment: This refers to the physical device that generates the data and ultimately consumes the computation results;
- Edge Server: This refers to the computing infrastructure deployed at the network edge;
- Cloud Server: This refers to virtualized or physical server clusters located in remote data centers, possessing powerful and elastic computational resources.
The origin of deep neural network tasks is always the user equipment, and the input data always exists directly in the terminal device [26]. When terminal devices need to send computing requests to edge servers or cloud servers, they need to transmit data to the corresponding devices through a Wide Area Network (WAN) or a Local Area Network (LAN). After receiving the data, the edge server or cloud server performs calculations and sends the calculation results to the next device. After several rounds of calculations, the final calculation results need to be transmitted back to the terminal device. The distance between the terminal device and the edge server is relatively close, and the data is transmitted between the two pairs through the LAN, while the cloud server is far away from the terminal device and the edge server, and the data is transmitted between the two pairs through the same WAN [27], as shown in Figure 1. This paper deploys the complete DNN model layers to various computing resources in the mobile edge computing environment.
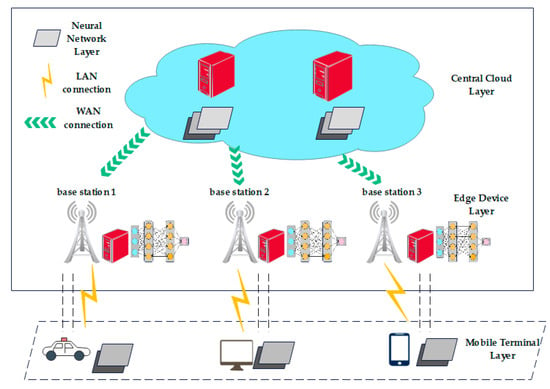
Figure 1.
Deep neural network system model.
2.2. DNNs Computing Task Model
This paper refers to one complete DNN inference as an inference task and decomposes it into multiple fine-grained layer tasks, each corresponding to a layer in the network. Each layer of tasks may have data associations, and two layers of tasks with data associations are connected by directed edges to form a directed graph , where and , respectively, represent the starting input and ending output of data, for each layer of tasks in the deep neural network, and represents the data association between each layer in the deep neural network, that is, the directed edge. If there are directed edges from point to point in the graph, it indicates that the output data of the layer task is the input data of the layer task. The DNNs task graph composed of DNNs is shown in Figure 2.
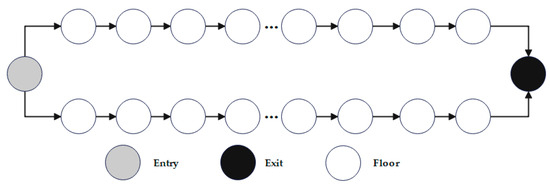
Figure 2.
DNNs task diagram.
This represents the task graph of DNNs using an adjacency matrix D:
Among them, if dj,k = 1, it indicates the existence of a directed edge from vj to vk, and if dj,k = 0, it indicates the absence.
Split the entire DNNs into multiple single-layer computing tasks, each task represented by a point. If there is a directed edge from point i to point j, it indicates that the output data of the i layer task is the input data of the j layer task. Use a directed graph to represent DNNs, where each point represents a task and the directed edge represents data association. Transform the directed graph into an adjacency matrix, where the elements in the matrix represent data association. If there are directed edges from j to k, the elements in the j row and k column of the adjacency matrix are 1; otherwise, they are 0.
A simple DNN neural network model is shown in Figure 3, with the leftmost input layer, rightmost output layer, and middle hidden layer.
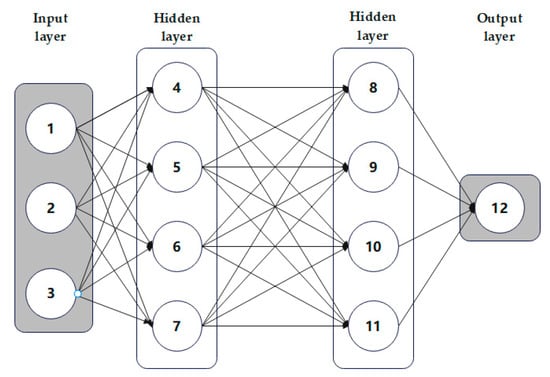
Figure 3.
Example diagram of DNN model.
Assuming that the neural network is used as a separate task and each node is individually numbered, according to the above transformation rules, the following adjacency matrix can be obtained:
2.3. Load Model
For each different deep neural network, its structural hierarchy is determined, so the computation process within each layer is also determined. For each deep neural network model, the number of floating-point operations (FLOPs) per layer can be calculated [28]. Therefore, the number of floating-point operations calculated can be used as the main indicator for calculating and quantifying the computational complexity of each layer in the DNN. This paper introduces the layer computational index to represent the total number of floating-point operations in the i-th layer of the network. In today’s DNN models, convolutional and fully connected layers are the two most commonly used and computationally intensive deep network layers, while other types of neural network layers have simpler FLOP calculation models. Therefore, this article presents the calculation models for convolutional and fully connected layer FLOPs [29].
The convolutional layer load, , is calculated using Equation (1):
The fully connected layer, , is calculated using Equation (2):
In the formula, is the number of floating-point operations (FLOPs) required for the i-th layer, and represent the width and height of the output feature map, represents the width of the convolution kernel, and represent the number of channels in the input and output feature maps, and and represent the number of input and output neurons, respectively.
2.4. Task Offloading Time Model
When calculating the task offloading time, set the time at the beginning of the task, considering the computation processing time of the task and the data transmission time between different levels. The computation processing time of the layer task on the device is
, and if the output of the layer task is used as the input of the layer task, the transmission time is
The transmission time for the final result of the deep neural network to be transmitted back to the terminal server is
In the formula, represents the computing speed of the i device (FLOPS/s), represents the size of the output data for the layer task (MB), represents the size of the final output data to the terminal (MB), and represent the transmission rates of the local and metropolitan area networks, represents the device number where the j layer task is executed, , , and represent the terminal device number, the set of all edge server device numbers, and the set of all cloud server device numbers, respectively.
The required data arrival time for the layer task is
The data completion time required for the layer task is
The offloading time for the entire deep neural network task is
The completion time for a task is determined by the latest finishing precedent task plus the required transmission time, following the classic critical path analysis method for task scheduling. This approach has been effectively applied in edge computing offloading scenarios [22,23].
2.5. Task Offloading Energy Consumption Model
Each layer of tasks in deep neural networks has a certain amount of computation. When these tasks are assigned to different devices, the corresponding devices will perform calculations on them, and the central processor needs to consume energy during the calculation process. Energy consumption optimization is an important problem of deep neural networks in edge computing scenarios. By simulating and running deep neural network models, the energy consumption of edge devices can be analyzed and optimized. By optimizing the structure, parameter configuration, and allocation of computing tasks of the network, it is possible to avoid excessive energy consumption and improve energy utilization efficiency. For the same device, the energy consumption is directly proportional to the number of floating-point operations, but the energy consumption may vary for different devices. The total usage time of the device is
, and represents the total usage time of device , represents the computation time of task , represents the condition for task to be assigned to device , and represents the total number of tasks.
The energy consumption of device is
In the formula, represents the unit time energy consumption rate (J/h) of the device.
The total energy consumption when running a deep neural network is
The energy consumption of a device is calculated as the product of its power consumption rate and the total time it is active, which is a widely adopted model in the energy-aware computing literature [5].
2.6. Task Offloading Cost Model
When using a multi-objective optimization task offloading strategy to schedule deep neural networks, there will be a cost of renting servers, which can be divided into on-demand ordering and package time ordering. For on-demand ordering, the rental cost of each server only needs to be calculated based on its actual usage time; for package time ordering, when calculating the rental cost of the server, it is necessary to consider not only the actual usage time of the server, but also the package time cost of the server. Generally speaking, the unit time usage cost of servers ordered during packaging is much lower than the unit time usage cost of on-demand ordering.
The on-demand ordering and usage cost of device is
The cost of ordering and using the package for device is
In the formula, is the unit time usage cost of on-demand ordering for device , is the unit time usage cost ordered for the package of device , and is the unit time ordering cost for the package of device .
The total cost of cloud configuration during the entire operation of deep neural networks is
The cost model for cloud server leasing follows the mainstream pricing schemes of public cloud providers: on-demand and reservation [30]. The total cost is the sum of the cost for all leased instances.
2.7. Problem Formulation
The objective of our optimization is to minimize three objectives: completion_time, Power_Cost, and purchase_cost. Each candidate offloading strategy can be evaluated by these three objective functions to obtain its raw performance metrics.
However, the PSO algorithm requires a single scalar value to compare particles and guide the search. Therefore, we define a fitness function that aggregates the three objective values into one. This fitness function incorporates the weighting of different objectives and, crucially, a penalty term for violating the deadline constraint to enforce it as a hard requirement. The fitness value for a particle is calculated as follows:
Among them, represents the fitness value, represents the server procurement cost (the value from the purchase_cost objective function), represents the completion time of DNN calculation (the value from the completion_time objective function), represents the calculated total energy consumption (the value from the Power_Cost objective function), represents the deadline, and all represent weight coefficients (used to adjust the contribution of different indicators).
3. Task Offloading Strategy Based on Multi-Objective Particle Swarm Optimization Algorithm
3.1. Multi-Objective Particle Swarm Optimization
Particle swarm optimization (PSO) is a classic meta-heuristic algorithm that simulates the social foraging behavior of bird flocks or fish schools to solve optimization problems [31]. However, the standard PSO algorithm is prone to premature convergence, often trapping itself in local optima and struggling to maintain a balance between exploration and exploitation, which significantly limits its performance in complex multi-objective optimization scenarios. To address these limitations, this paper proposes an enhanced Multi-Objective Particle Swarm Optimization (MOPSO) algorithm that innovatively integrates a historical optimal solution detection mechanism and a dynamic temperature regulation strategy. These improvements prevent the swarm from stagnating prematurely by adaptively accepting suboptimal solutions with a certain probability, thereby enhancing the diversity of the Pareto frontier. The three core components of the algorithm include velocity updating based on elite guidance, archive maintenance for non-dominated solutions, and temperature-controlled stochastic acceptance.
This study aims to minimize the multi-objective optimization problem of execution time, energy consumption, and economic cost, and there are multiple metaheuristic solving methods available. There are Pareto frontier-based methods, which can generate a set of non-dominated solutions and are popular, and other methods, such as indicator-based or interactive methods; we use the scalar method because in the real-world edge computing system, what is needed is a single, determined unloading strategy to implement. Although Pareto-optimal sets are useful for analysis, they require higher-level decision-makers to make choices after optimization, which increases complexity and latency; The weights f1, f2, and f3 in the fitness function provide system designers with an intuitive and transparent mechanism to express their priorities, such as preferring low latency over cost savings; the fitness function elegantly incorporates the deadline constraint as a hard penalty term, which is naturally integrated into the scalarization objective function. This effectively narrows down the search space to solutions that meet user latency requirements.
3.2. Algorithm Design
The position of particle i in n-dimensional space in the particle swarm optimization algorithm is represented as vector , and the flight velocity of the particle is represented as vector . Each particle has a fitness value determined by the objective function and knows the best position of the group it has discovered so far and its current position . In each iteration, particles determine their motion speed and update their individual positions based on individual and group experience, and ultimately find the optimal position or solution through continuous iteration.
3.2.1. Hybrid Encoding Scheme and Justification
The offloading decision in our context is a complex, mixed-variable optimization problem. A viable strategy must simultaneously determine
- The number of servers to rent (Server Count);
- The hardware type for each server (Server Type);
- The purchasing model (e.g., on-demand or reserved) for each server (Purchase Mode);
- The mapping of each DNN layer task to a local device (Task Mapping).
Traditional encoding schemes, such as pure binary or integer encoding, struggle with this complexity due to the variable-length nature of the solution and the heterogeneity of the decision variables.
To address this, we designed a structured hybrid encoding scheme that maps a continuous particle position vector Xi into a complete offloading strategy. This design is justified by its ability to seamlessly integrate all required decisions into a unified representation that is well-suited for the continuous optimization mechanics of PSO.
Completeness and Structured Representation: The particle position vector is partitioned into sequential segments, each responsible for a specific aspect of the decision-making, as shown in Equation (16). The first dimension determines the number of servers K. The subsequent K dimensions determine the type of each server, and the next K dimensions determine the purchase mode. The final segment, whose length equals the number of DNN tasks, handles the task-to-server mapping. This structure ensures that every possible solution within the defined constraints (e.g., max servers M) can be represented.
Efficiency and Direct Feasibility: The encoding is highly compact. The solution length grows linearly with the sum of the maximum number of servers M and the number of tasks N, avoiding the combinatorial explosion typical of naive encoding. Furthermore, the transformation rules directly generate executable strategies.
Suitability for PSO: This encoding elegantly embeds the discrete decision space into a continuous hypercube [0, 1]n. The PSO algorithm operates naturally in this space, with velocity updates guiding particles toward promising regions. The decoding process (Equation (16)) acts as a deterministic projection from the continuous space to the discrete solution space. This allows PSO to leverage its strengths in exploring continuous landscapes to effectively solve the underlying discrete combinatorial problem.
This hybrid encoding scheme is not merely a transformation rule but a core methodological choice that enables the effective application of a continuous optimizer to a complex discrete problem, ensuring both comprehensive coverage of the solution space and algorithmic efficiency.
3.2.2. Transformation Rules and Examples
In terms of offloading strategy, an offloading decision model is constructed to utilize deep neural networks to make migration decisions for tasks between cloud servers and edge devices. This model can make dynamic offloading decisions based on the characteristics of tasks, the status of edge devices and cloud servers, and network load, achieving optimized resource utilization.
The position of particles in the particle swarm optimization algorithm is represented as the unloading strategy scheme [32], and its transformation rule is as follows:
and represent rounding up and rounding down, respectively; M represents the maximum order quantity of the server max_purchase; A represents the maximum category number alternative_instance_type; and B represents the maximum type number alternative_purchase_type.
If the position of the particle is
then simultaneously define the maximum order quantity, maximum type number, and maximum type number:
The example of particle position is shown in Figure 4:
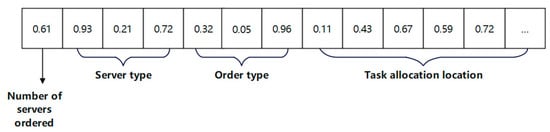
Figure 4.
Example of particle position.
The sequence of offloading strategy schemes obtained by converting particle positions is
An example of particle position encoding is shown in Figure 5:
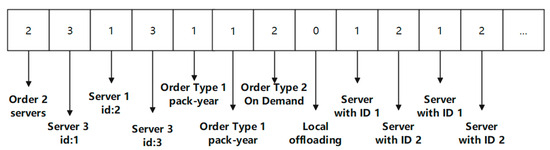
Figure 5.
Example of particle position encoding.
The i + 7th item represents the server ID assigned to the i layer task (i > 0).
3.3. Simulation Algorithm
The simulation process for evaluating a given offloading strategy follows the workflow depicted in Figure 6.
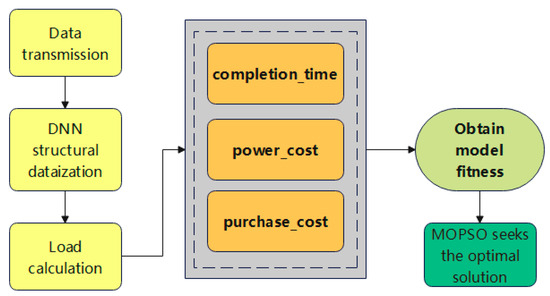
Figure 6.
The workflow for calculating the fitness value of an offloading strategy.
First, the DNN model is digitized into an adjacency matrix, and the computational load of each layer is calculated. Then, based on the device assignment specified by the particle, the completion time, energy consumption, and monetary cost are simulated according to the models in Section 2. Finally, these three objective values are aggregated into a single fitness value using Equation (15). The pseudo-code of this simulation process is described in Algorithm 1.
| Algorithm 1 Simulation Algorithm | |
| Input: Task topology diagram task, execution_time of each layer task on different devices, task_ allocation method, instance type instance_id, task quantity task_ num, output data volume task_out for each layer, input data volume task_ in for the first layer | |
| Data volume size | |
| Output: The completion time of each layer task is finish_time, and the usage time of the ordered instance is time_stpan | |
| 1. | The current task is set as the first level task |
| 2. | while (there are tasks that have not been computed) |
| 3. | if (whether the previous task is the first layer task) |
| 4. | The ready time of the current task is set to the transmission time of task_in; |
| 5. | end if |
| 6. | The start time of the current task=max (the readiness time of the current task and the readiness time of the server assigned by the current task); |
| 7. | completion time=start time+execution time; |
| 8. | The usage time of the server assigned to the current task=the usage time of the server assigned to the current task + the task execution time; |
| 9. | Determine the next level task of the current task through the adjacency matrix; |
| 10. | Calculate the transmission time of the current layer’s output data volume based on the server type assigned by the next layer task; |
| 11. | The readiness time of the next layer task=the completion time of the current task+the transmission time of the output data volume; |
| 12. | end while |
| 13. | return the completion time of each layer task and the usage time of the ordered server; |
3.4. The Overall Flow of the Algorithm
Based on the characteristics of DNNs, the particle swarm optimization algorithm is improved to optimize the shortcomings of the particle swarm optimization algorithm (that is, it is easy to fall into the local optimal solution), while improving the long search time. The deep neural network offloading strategy of the multi-objective optimization algorithm based on particle swarm optimization in edge computing is designed. The algorithm flow chart is shown in Figure 7.
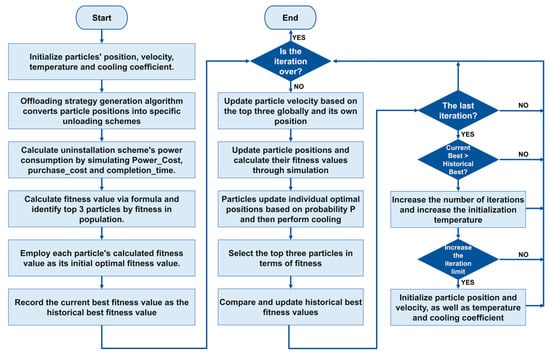
Figure 7.
Flowchart of multi-objective optimization algorithm based on particle swarm optimization.
The workflow of the proposed algorithm is presented in Algorithm 2.
| Algorithm 2 Multi-objective optimization algorithm based on particle swarm optimization | |
| Input: algorithm iteration times MaxNum, population size particle size, convolutional neural network C, server package annual rental price reserved_price, server on-demand rental price on_demand_price, server energy consumption rate W, data transmission rate translate_rate; | |
| Output: Energy consumption, time consumption, price optimization offloading plan best and scheduling fitness value best_ralue | |
| 1. | Randomly initialize the particle swarm, with particles obtaining initialization position xx and flying speed v; |
| 2. | Offloading strategy generation algorithm, transforming particle positions into offloading strategy schemes; |
| 3. | Calculate the particle initialization fitness value f; |
| 4. | Initialize the individual optimal fitness value f_best and position x of the particles; |
| 5. | Find the optimal fitness value Gbest_ralue and position Gbest for the group; |
| 6. | The best historical value is best all = Gbest value |
| 7. | Identify the positions p1, p2, and p3 of the top three particles in the group; |
| 8. | Initialization temperature T = max (f) - min (f); |
| 9. | Initialization speed a = 0.9; |
| 10. | while (T == 0) |
| 11. | Reinitialize the particle swarm algorithm; |
| 12. | Reinitialize temperature T; |
| 13. | end while |
| 14. | time_num = MaxNum; |
| 15. | time = 1; |
| 16. | while(time != time_num) |
| 17. | for k = 1:particlesize |
| 18. | Update particle velocity based on the position of the top three particles; |
| 19. | Speed out of bounds processing, which ensures that each dimension of particle velocity is between - vmax and vmax; |
| 20. | Update particle position xx; |
| 21. | Particle out of bounds processing, which ensures that each dimension of particle position is between 0 and 1; |
| 22. | Offloading strategy generation algorithm, transforming particle positions into offloading strategy schemes; |
| 23. | Calculate the fitness value f; |
| 24. | Compare the size of f_best and f, accept the better value and position with a probability of 1, and accept the worse value and position with a probability of p; |
| 25. | end for |
| 26. | Find the optimal fitness value Gbest1_value and position Gbest1 for the group; |
| 27. | Identify the positions p1, p2, and p3 of the top three particles in the group; |
| 28. | Compare the size of Gbest-value and Gbest1_value, accept the better value and position with a probability of 1, and accept the worse value and position with a |
| 29. | probability of p; |
| 30. | Cooling T = aT; |
| 31. | time = time + 1; |
| 32. | if (time == time_num && Gbest_value > best_all) |
| 33. | the optimal iteration result is worse than the historical best, increase the number of iterations and iterate again; |
| 34. | time_num = time_num + MaxNum; |
| 35. | T = T/a; |
| 36. | a = 0.9a; Accelerate the cooling speed |
| 37. | If (a < 0.5) |
| 38. | If there are too many iterations and the optimal iteration value has not been obtained, reinitialize the iteration; |
| 39. | Randomly initialize particle position xx and particle flight velocity v again; |
| 40. | Calculate the particle fitness value f; |
| 41. | Reinitialize the initial temperature T; |
| 42. | end if |
| 43. | end if |
| 44. | if (Gbest_value < best_all) |
| 45. | best_all = Gbest_value; |
| 46. | end if; |
| 47. | end while |
Particle k velocity update formula:
Among them: represents the velocity vector of particle k at time t + 1, represents the inertia weight, represents the i-th acceleration coefficient (c1, c2, c3, c4), represents the random vector within the [0, 1] interval (corresponding to rand in the original equation), represents element-wise multiplication (Hadamard product), Pi represents the reference position vector (P1 = p1, P2 = p2, P3 = p3, P4 = xxk), and represents the position vector of particle k at time t.
The particle position update formula is
4. Simulation Experiment and Analysis
The selection of DNN models for evaluation is a critical design choice. In this section, we selected VGG series [33], gogglenet, and darknet53 as experimental subjects, which, despite not being the most efficient, provide a clear and consistent hierarchical structure that is ideal for analyzing fine-grained layer-wise offloading strategies. Their high and well-documented computational cost (FLOPs) also serves as a stress test for our optimization algorithm, making performance improvements more pronounced and easier to analyze. While modern architectures like ResNet and EfficientNet incorporate skip connections or compound scaling, their more complex data dependencies would introduce additional variables into the offloading problem. We focus on VGG to first establish a strong baseline understanding of our algorithm’s performance on a classic topology.
4.1. Experimental Environment and Parameter Settings
Under the terminal non-offloading strategy based on six different deep neural networks, the running time Timep is set with different termination times , where .
At 0.8 CNY/h, the package time subscription price is 300 CNY/month and 280 CNY/month, and the package time subscription unit time cost is 0.18 CNY/h and 0.15 CNY/h; for end–cloud server equipment, its unit time energy consumption rate is 4 J/h, the on-demand subscription unit time cost is 2 CNY/h, the package time subscription price is 600 CNY/month, and the package time subscription unit time cost is 0.4 CNY/h. Unless otherwise specified, the data in the table will be used as the parameters.
4.2. Experimental Results and Analysis
To comprehensively evaluate the performance of our proposed MOPSO algorithm, we compared it with various advanced metaheuristic algorithms. This includes the standard particle swarm optimization algorithm (PSO), genetic algorithm (GA), and gray wolf optimization algorithm (GWO).
All comparison algorithms use the same simulation environment, fitness function (Formula (15)), and parameter settings (as shown in Table 1) to ensure fair comparison.

Table 1.
Simulation data.
Compared to other metaheuristic algorithms, MOPSO continues to outperform GA and GWO algorithms. Although the GA has a decent convergence speed in the early stages, its search efficiency decreases in the later stages, and the quality of the final solution is far inferior to MOPSO. The convergence effect of the GWO algorithm is better than other algorithms, but the convergence speed is slightly slower than MOPSO. This result strongly proves that the improvement strategy proposed by us is not only effective for PSO, but also an overall better solution to the complex problem of edge computing task unloading.
Figure 8 shows the convergence curves of the optimal fitness values of various optimization algorithms with the number of iterations.
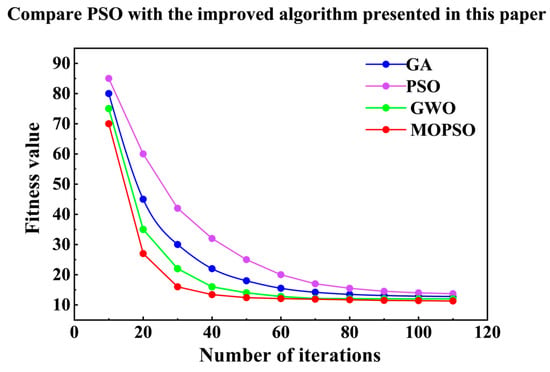
Figure 8.
The fitness convergence curves of different algorithms.
To further explore the effectiveness of the proposed algorithm and verify the influence of neural networks on optimization strategies, this paper conducts simulation comparisons based on six types of convolutional neural networks. Design four different offloading strategies: Local-Only Particle Swarm Optimization strategy (LOPSO), Full Offloading to Cloud with Particle Swarm Optimization strategy (FOCPSO), Partial Offloading with Particle Swarm Optimization strategy (POPSO), and Multi-Objective Particle Swarm Optimization strategy based on end–edge–cloud (MOPSO).
The graph of the number of floating-point operations for the six different deep neural networks is shown in Figure 9, where VGG19 has the highest number of floating-point operations, and googlenet has the lowest number of floating-point operations. This indicates that as the structure of the network is more complex, it requires more computational resources to complete, which leads to longer execution time, especially on end devices with limited computational power; the more computation, the more energy consumed by the device, which leads to a shorter battery life of the end device.
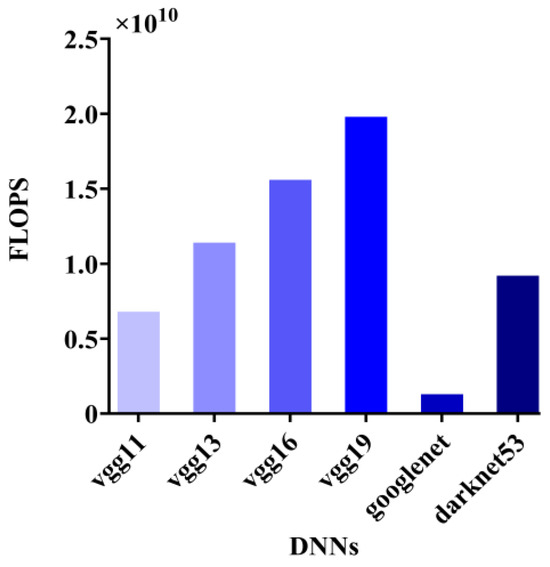
Figure 9.
Floating-point operations per second.
From Figure 10, it can be clearly seen that as the network structure becomes more complex, the execution time of all algorithms also increases. Specifically, the local execution scheme showed the most significant increase in execution time, indicating its low efficiency under higher computational loads. Compared to it, the MOPSO algorithm demonstrated a more stable performance advantage throughout the entire process, with the lowest execution time. The optimization strategy proposed in this article is more efficient in terms of execution time compared to the local execution (LOPSO) scheme, the cloud completely offloading (FOCPSO) scheme, and the end–cloud (POPSO) optimization scheme: The execution time was reduced by 55.4%, 10.7%, and 21.6%, respectively, in the VGG11 neural network environment. The execution time was reduced by 55.2%, 10.4%, and 20.9%, respectively, in the VGG13 neural network environment. The execution time was reduced by 58.1%, 16.2%, and 36.9% in the VGG16 neural network environment, respectively. The execution time was reduced by 56.5%, 13.1%, and 37.9%, respectively, in the VGG19 neural network environment. The execution time was reduced by 59.0%, 18.0%, and 27.4%, respectively, in the Googlenet neural network environment. The execution time was reduced by 52.8%, 5.7%, and 29.6%, respectively, in the Darknet53 neural network environment.
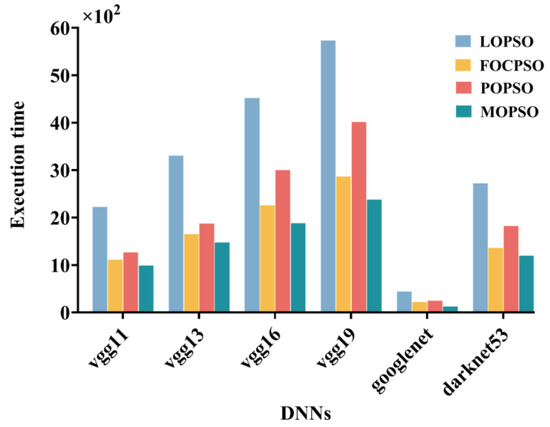
Figure 10.
Comparison chart of execution time.
It can be clearly observed from Figure 11 that as the complexity of the neural network increases, the energy consumption of all optimization algorithms also increases. Specifically, the POPSO algorithm exhibits the most significant energy consumption under high computational loads. In contrast, the MOPSO algorithm consistently maintains the lowest energy consumption among all tested networks, while meeting normal communication requirements and bringing certain cost reduction and efficiency improvement benefits. In the VGG11 neural network environment, energy consumption was reduced by 37.77%, 62.65%, and 70.90%, respectively. In the VGG13 neural network environment, energy consumption was reduced by 41.42%, 64.84%, and 75.08%, respectively. In the VGG16 neural network environment, energy consumption was reduced by 34.80%, 62.73%, and 79.12%, respectively. In the VGG19 neural network environment, energy consumption was reduced by 36.18%, 65.09%, and 76.80%, respectively. In the Googlenet neural network environment, energy consumption was reduced by 5.43%, 43.27%, and 57.14%, respectively. In the Darknet53 neural network environment, energy consumption was reduced by 39.77%, 63.86%, and 78.36%, respectively.
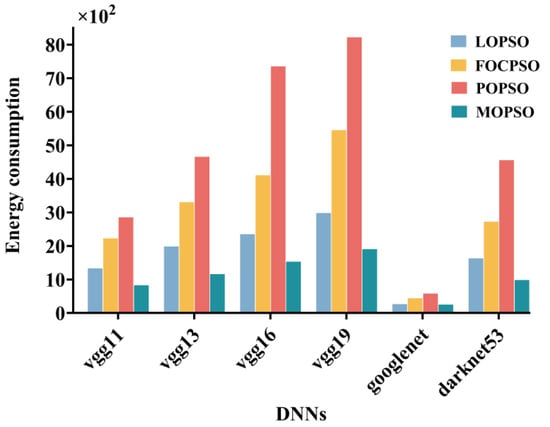
Figure 11.
Energy consumption comparison chart.
The comparison chart of cloud configuration prices for six different deep neural networks is shown in Figure 12. Local offloading does not use cloud services, so there is no cloud configuration cost. Compared to the other three strategies, it can be found that MOPSO has lower cloud configuration costs on the six deep neural networks than the other two offloading strategies, which has a significant improvement effect on saving cloud configuration prices. This is because MOPSO can choose the appropriate cloud server type and rental method based on the computing and data volume of the task, such as on-demand or yearly rental, thereby reducing cloud configuration costs.
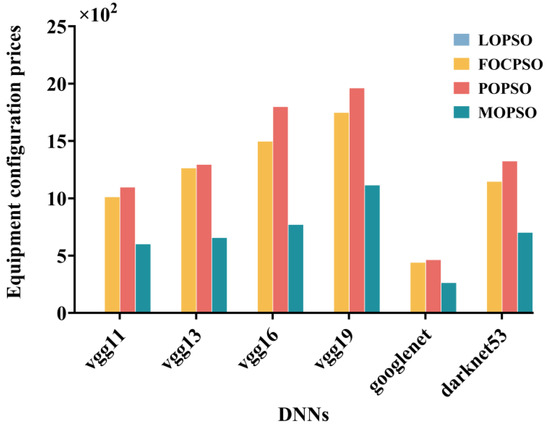
Figure 12.
Comparison chart of equipment configuration prices.
Calculate the optimal scheduling scheme and fitness value for the four offloading strategies mentioned above. The comparison of the optimal fitness values calculated for the four offloading strategies is shown in Figure 13.
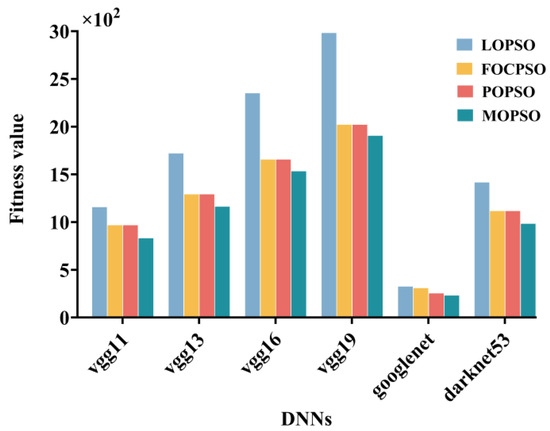
Figure 13.
Comparison chart of fitness values.
Compare the fitness values of the optimization scheme proposed in this article with the local execution scheme, cloud complete uninstallation scheme, and end–cloud partial uninstallation scheme: In the VGG11 neural network environment, the fitness values decreased by 28.20%, 14.13%, and 14.13%, respectively. In the VGG13 neural network environment, the fitness values decreased by 32.44%, 10.07%, and 10.07%, respectively. The fitness values of VGG16 decreased by 34.80%, 7.42%, and 7.42%, respectively, in the network environment. In the VGG19 neural network environment, the fitness values decreased by 36.14%, 5.72%, and 5.72%, respectively. In the Google Net neural network environment, the fitness values decreased by 9.10%, 18.94%, and 1.38%, respectively. In the darknet53 neural network environment, the fitness values decreased by 30.54%, 11.97%, and 11.97%, respectively.
Through simulation experiments, the running time, equipment rental cost, and energy consumption of six different deep neural networks, vgg11, vgg13, vgg16, vgg19, darknet53, and googlenet, under four different offloading strategies, were compared. It can be concluded that under the specified time constraints, the running time and energy consumption values of the six deep neural networks under the multi-objective optimization offloading strategy based on end–edge–cloud are better than the other three offloading strategies, and the fitness value is the lowest.
5. Conclusions
This paper deeply analyzes the strategy of task offloading in an edge computing environment and proposes a multi-objective optimization algorithm to optimize the selection of computing task offloading. Considering the structural characteristics of deep neural networks in the edge computing environment, this research constructs a computing problem model, which aims to minimize the weighted sum of time delay, energy consumption, and cost, so as to achieve an efficient solution of computing problems. A multi-objective optimization algorithm based on particle swarm optimization has been proposed, which incorporates the concept of historical optimality into traditional particle swarm optimization algorithms. It can detect whether the algorithm has fallen into local optima, while reducing the cooling coefficient to make the temperature drop faster, increasing the current temperature value, and expanding the search range.
Simulation experiments show that our proposed MOPSO algorithm is not only the best in the PSO family, but its performance is also significantly better than other types of metaheuristic algorithms. This fully demonstrates the effectiveness, superiority, and robustness of our algorithm, making it a powerful tool to solve the multi-objective task unloading problem in edge computing. We believe that testing on more modern architectures, such as ResNet or EfficientNet, is a valuable direction for future work. Future work will focus on implementing these improvements, which will help demonstrate the universality of our method across different model architectures.
Author Contributions
Conceptualization, L.Y. and W.W.; methodology, L.Y. and S.W.; software, L.Y. and S.W.; validation, W.Z. and B.J.; investigation, X.Y. and Z.T.; writing—original draft preparation, S.W. and W.Z.; writing—review and editing, L.Y. and S.W.; supervision, L.Y. and W.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the following scientific research projects: “Research on Key Technologies for Task Unloading of Chronic Disease Diagnosis in edge computing” (Project Number: JJKH20251101KJ), which is a scientific research project funded by Jilin Provincial Department of Education; Research and Development of Intelligent Assisted Obstacle Avoidance System (Project Number: 2024JBH05LU5), sponsored by Changchun Tianqin Environmental Engineering Co., Ltd.; Development of a Path Planning System for Visually Impaired Persons (Project Number: 2023JBH05L54), supported by Changchun AsiaInfo Technology Co., Ltd.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sathiyapriya, G.; Anita Shanthi, S. Image Classification Using Convolutional Neural Networks. In Proceedings of the 2022 First International Conference on Electrical, Electronics, Information and Communication Technologies (ICEEICT), Trichy, India, 16–18 February 2022. [Google Scholar]
- Ayadi, S.; Lachiri, Z. Deep neural network architectures for audio emotion recognition performed on song and speech modalities. Int. J. Speech Technol. 2023, 26, 1165–1181. [Google Scholar] [CrossRef]
- Olusegun, R.; Oladunni, T.; Audu, H.; Houkpati, Y.; Bengesi, S. Text Mining and Emotion Classification on Monkeypox Twitter Dataset: A Deep Learning-Natural Language Processing (NLP) Approach. IEEE Access 2023, 11, 49882–49894. [Google Scholar] [CrossRef]
- Seo, W.; Kim, S.; Hong, S. Partitioning Deep Neural Networks for Optimally Pipelined Inference on Heterogeneous IoT Devices with Low Latency Networks. In Proceedings of the 2024 IEEE 44th International Conference on Distributed Computing Systems (ICDCS), Jersey, NJ, USA, 23–26 July 2024; pp. 1255–1279. [Google Scholar]
- Wang, Y.; Chen, M.; Li, Z.; Hu, Y. Joint Allocations of Radio and Computational Resource for User Energy Consumption Minimization Under Latency Constraints in Multi-Cell MEC Systems. IEEE Trans. Veh. Technol. 2023, 72, 3304–3320. [Google Scholar] [CrossRef]
- Jafari, V.; Rezvani, M.H. Joint optimization of energy consumption and time delay in IoT-fog-cloud computing environments using NSGA-II metaheuristic algorithm. J. Ambient. Intell. Humaniz. Comput. 2023, 14, 1675–1698. [Google Scholar] [CrossRef]
- Huang, J.; Wan, J.; Lv, B.; Ye, Q.; Chen, Y. Joint Computation Offloading and Resource Allocation for Edge-Cloud Collaboration in Internet of Vehicles via Deep Reinforcement Learning. IEEE Syst. J. 2023, 17, 2500–2511. [Google Scholar] [CrossRef]
- Chen, H.; Hu, Y. Task offloading model under 5G edge cloud collaborative distributed network architecture. Mob. Commun. 2021, 45, 144–148. [Google Scholar]
- Xu, M.; Qian, F.; Zhu, M.; Huang, F.; Pushp, S.; Liu, X. Deepwear: Adaptive local offloading for on-wearable deep learning. IEEE Trans. Mob. Comput. 2019, 19, 314–330. [Google Scholar] [CrossRef]
- Gao, H.; Li, X.; Zhou, B.; Liu, X.; Xu, J. Energy efficient computing task offloading strategy for deep neural networks in mobile edge computing. Comput. Integr. Manuf. Syst. 2020, 26, 1607–1615. [Google Scholar]
- Li, Z. Research on Computing Offloading and Resource Allocation Algorithm Based on MEC. Master’s Thesis, Nanjing University of Posts and Telecommunications, Nanjing, China, March 2021. [Google Scholar]
- Hu, Y.; Wang, H.; Wang, L.; Hu, M.; Peng, K.; Veeravalli, B. Joint deployment and request routing for microservice call graphs in data centers. IEEE Trans. Parallel Distrib. Syst. 2023, 34, 2994–3011. [Google Scholar] [CrossRef]
- Gao, H. Research on Edge Cloud Collaborative Computing Framework and Unloading Strategy for Deep Learning Applications. Ph.D. Thesis, Anhui University, Hefei, China, 2021. [Google Scholar]
- Elouali, A.; Mora, H.M.; Mora-Gimeno, F.J. Data transmission reduction formalization for cloud offloading-based IoT systems. J. Cloud Comput. 2023, 12, 48. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Li, K.; Li, K. Minimal Cost Server Configuration for Meeting Time-Varying Resource Demands in Cloud Centers. IEEE Trans. Parallel Distrib. Syst. 2018, 29, 2503–2513. [Google Scholar] [CrossRef]
- Teymoori, P.; Todd, T.D.; Zhao, D.; Karakostas, G. Efficient Mobile Computation Offloading with Hard Task Deadlines and Concurrent Local Execution. In Proceedings of the GLOBECOM 2020, Taipei, Taiwan, 7–11 December 2020; pp. 1–6. [Google Scholar]
- Lipsa, S.; Dash, R.K.; Ivkovic, N.; Cengiz, K. Task Scheduling in Cloud Computing: A Priority-Based Heuristic Approach. IEEE Access 2023, 11, 27111–27126. [Google Scholar] [CrossRef]
- Geng, L.; Zhao, H.; Wang, J.; Kaushik, A.; Yuan, S.; Feng, W. Deep-reinforcement-learning-based distributed computation offloading in vehicular edge computing networks. IEEE Internet Things J. 2023, 10, 12416–12433. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, H.; Geng, L.; Feng, W. A policy gradient based offloading scheme with dependency guarantees for vehicular networks. In Proceedings of the 2020 IEEE Globecom Workshops (GC Wkshps), Taipei, Taiwan, 7–11 December 2020. [Google Scholar]
- Chen, J.; Yi, C.; Wang, R.; Zhu, K.; Cai, J. Learning aided joint sensor activation and mobile charging vehicle scheduling for energy-efficient WRSN-based industrial IoT. IEEE Trans. Veh. Technol. 2023, 72, 5064–5078. [Google Scholar] [CrossRef]
- Yan, L.; Chen, H.; Tu, Y.; Zhou, X. A Task Offloading Algorithm With Cloud Edge Jointly Load Balance Optimization Based on Deep Reinforcement Learning for Unmanned Surface Vehicles. IEEE Access 2022, 10, 16566–16576. [Google Scholar] [CrossRef]
- Ren, J.; Yu, G.; Cai, Y.; He, Y. Latency optimization for resource allocation in mobile-edge computation offloading. IEEE Trans. Wirel. Commun. 2018, 17, 5506–5519. [Google Scholar] [CrossRef]
- Tang, T.T.; Li, C.; Liu, F.G. Collaborative cloud-edge-end task offloading with task dependency based on deep reinforcement learning. Comput. Commun. 2023, 209, 78–90. [Google Scholar] [CrossRef]
- Ren, J.; Yu, G.; Cai, Y.; He, Y.; Qu, F. Partial offloading for latency minimization in mobile-edge computing. In Proceedings of the GLOBECOM 2017, Singapore, 4–8 December 2017; pp. 1–6. [Google Scholar]
- Talbi, E.-G. Combining metaheuristics with mathematical programming, constraint programming and machine learning. Ann. Oper. Res. 2016, 240, 171–215. [Google Scholar] [CrossRef]
- Xue, M.; Wu, H.; Peng, G.; Wolter, K. DDPQN: An Efficient DNN Offloading Strategy in Local-Edge-Cloud Collaborative Environments. IEEE Trans. Serv. Comput. 2022, 15, 640–655. [Google Scholar] [CrossRef]
- Wang, D.; Wang, Z.; Yu, L.; Wu, Y.; Yang, J.; Mei, K.; Wang, J. A Survey of Stochastic Computing in Energy-Efficient DNNs On-Edge. In Proceedings of the ISPA/BDCloud/SocialCom/SustainCom 2021, New York, NY, USA, 30 September–3 October 2021; pp. 1554–1561. [Google Scholar]
- Guo, F.; Tang, B.; Tang, M. Joint optimization of delay and cost for microservice composition in mobile edge computing. World Wide Web 2022, 25, 2019–2047. [Google Scholar] [CrossRef]
- Xu, B.; Deng, T.; Liu, Y.; Zhao, Y.; Xu, Z.; Qi, J.; Wang, S.; Liu, D. Optimization of cooperative offloading model with cost consideration in mobile edge computing. Soft Comput. 2023, 27, 8233–8243. [Google Scholar] [CrossRef]
- Yuan, H.; Zheng, Z.; Bi, J.; Zhang, J.; Zhou, M. Energy-Optimized Task Offloading with Genetic Simulated-Annealing-Based PSO for Heterogeneous Edge and Cloud Computing. Proc. IEEE Int. Conf. Syst. Man Cybern. 2024, 13, 1446–1470. [Google Scholar]
- Li, Z.; Yu, H.; Fan, G.; Zhang, J.; Xu, J. Energy-efficient offloading for DNN-based applications in edge-cloud computing: A hybrid chaotic evolutionary approach. J. Parallel Distrib. Comput. 2024, 187, 104850. [Google Scholar] [CrossRef]
- Zhou, W.; Chen, L.; Tang, S.; Lai, L.; Xia, J.; Zhou, F.; Fan, L. Offloading strategy with PSO for mobile edge computing based on cache mechanism. Clust. Comput. 2022, 25, 2389–2401. [Google Scholar] [CrossRef]
- Kaya, V.; Akgül, İ. VGGNet model yapilari kullanılarak cilt kanserinin siniflandirilmasi. GUFBD/GUJS 2023, 13, 190–198. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).