Virtual Measurement of Explosion-Proof Performance: Application of an Improved RBF-GMSE-Based Surrogate Model to the Safety Performance Characterization of Coal Mine Equipment

Abstract

Explosion-proof safety evaluation is critical for coal mine equipment operating in hazardous environments. Traditional methods rely on physical explosion testing, which is time-consuming, costly, and impractical for large-scale or complex systems. We propose a real-time virtual measurement method based on an improved combined surrogate model to address these limitations. A digital twin framework is constructed by integrating internal explosion transmission data with physical models of gas deflagration and enclosure impact mechanics. A transient multi-physical reduced-order model is developed using Latin hypercube sampling and machine learning. The core prediction model, RBF-GMSE, combines a radial basis function surrogate model and a generalized mean square error model through adaptive weighting. This model is trained on dimension-reduced finite element data and used to predict explosion-induced stress, strain, and displacement in real time. A virtual measurement system is implemented using this framework, enabling accurate, dynamic safety evaluation of explosion-proof equipment. Validation against simulation data shows a maximum prediction error below 1.89% and an average correlation coefficient of 0.9779, confirming the model’s high accuracy and robustness. This approach offers an intelligent solution for efficient and precise acquisition of explosion-proof safety characteristics in coal mine equipment.

1. Introduction

Coal mine explosion-proof is a prerequisite for the application of underground equipment. According to the ‘Coal Mine Safety Regulations’, the measurement of explosion-proof safety characteristics of coal mine explosion-proof equipment is significant research content to ensure mine safety [1]. In October 2021, China updated and issued GB/T 3836 [2] series standards, which provided a basis for the detection of explosion-proof performance of coal mine explosion-proof equipment and the design of explosion-proof products [3]. Meanwhile, other countries and regions, such as the European Union with the ATEX regime, the International Electrotechnical Commission with the IECEx scheme and U.S. mining safety and health regulations, have also established comprehensive standards for explosive atmospheres. These international standards emphasize the importance of both structural integrity and preventive measures against ignition sources [4]. In recent years, the State Administration of Mine Safety Supervision has carried out the “14th Five-Year” mine safety production plan [5], aiming to develop major disaster prevention and control technology and equipment. The development of intelligent technologies and equipment for gas and coal dust explosion isolation and suppression has become a key strategy for enhancing the evaluation capabilities of explosion-proof equipment in China’s coal mines. However, the long testing cycle, low efficiency, high costs, and difficulty in assessing large-scale equipment have hindered the establishment of an intelligent evaluation system. Therefore, conducting in-depth research on efficient, safe, and accurate virtual measurement methods is of great significance for improving the assessment of explosion-proof safety characteristics in China’s coal mine equipment.

Aiming at the measurement of explosion-proof safety characteristics of coal mine explosion-proof equipment, many scholars at home and abroad have studied the combustion and explosion process of combustible gas by using computational fluid dynamics (CFD) theory. Based on the requirements of the explosion pressure test in the national standard GB 3836.2-2010 [2] and the study of a large number of test results, Zhou [6] analyzed the pressure generated by the ignition of explosive gas in the explosion-proof enclosure and the process of pressure change. Based on the constant volume explosion model and specific samples, Zhang [7] carried out the theoretical analysis and practical test of the explosion pressure of the explosion-proof enclosure, and summarized and analyzed the influencing factors of the explosion pressure of the explosion-proof enclosure. Based on the theory of combustible gas explosion, Lu et al. [8] simulated the explosion process inside the explosion-proof enclosure through ANSYS 2019, and analyzed the mechanical properties of the enclosure under the two-way coupling of the internal high-pressure flow field and the wall surface. Peschel et al. [9] reproduced the temporal pressure development inside a flameproof enclosure during a thermal runaway of a lithium-ion cell by gas explosions. With the assistance of MATLAB 2018b and ANSYS 2018 software, Ahirwal et al. [10] designed a large Ex d flameproof enclosure for gas group IIB hazardous areas; stress analysis of the plates and cover under internal pressure indicates that the enclosure remains within safety limits. Based on the explosion theory and CFD software(CEBAM), CLUTTER et al. [11] established the state and energy equation of combustible gas combustion and explosion, and compiled the numerical simulation software. It can be seen that the explosion-proof safety characteristics of the explosion-proof enclosure of coal mine explosion-proof equipment have been supplemented in theory, but these studies cannot solve the fundamental problems existing in the current pressure, overpressure and detonation test.

With the rapid development of big data, cloud computing and artificial intelligence, the physical world and the digital world are increasingly linked. Digital twin technology realizes the monitoring, optimization and prediction of real systems by establishing virtual models and docking with physical systems, and provides a new method for structural mechanical performance monitoring [12,13,14]. Latsou et al. [15] introduces a unified framework for DT development, emphasizing reusability and scalability. Gautam et al. [16] presents a digital twin-assisted online monitoring and control system for machining operations, robust process monitoring and control can be achieved while anomalies and false alarms are avoided. Addressing the harsh operating environment and large blind spots of boom-type coal roadheaders, Hao et al. [17] proposed a mixed-reality (MR)–based digital-twin monitoring system for EBZ-series roadheaders. Addressing the complex attitudes of hydraulic supports caused by undulations of the coal-seam floor, Zhou et al. [18] proposed a digital-twin-driven method for reconstructing the relative pose (position and orientation) of the hydraulic supports. Lai et al. [19] proposed a shape-property integrated digital twin (SPI-DT) enabling technology to predict the real-time performance of devices through the artificial intelligence (AI) model. In order to solve the timeliness problem of digital twins, the surrogate model can replace high-dimensional simulation with low computational cost, which significantly improves the analysis efficiency [20,21,22]. Hu [23] proposed research on the evaluation of the structural bearing capacity of mobile cranes based on digital twins, which provides a new way and strategy for the evaluation of the structural bearing capacity of cranes during service. Wang et al. [24] proposed a reliability decoupling optimization method of crane metal structure based on a dynamic Kriging surrogate model with a multi-point addition strategy, which solved the complexity and time-consuming problem of the double-cycle method for reliability optimization design of crane metal structure based on a static surrogate model. Zhang et al. [25] proposed a structural performance monitoring method for the head sheave of a mine hoist based on a digital twin. The surrogate model was developed by training preprocessed finite element data, resulting in a structural performance prediction model for the head sheave. This demonstrates that digital twin surrogate models have been successfully applied in the monitoring of mechanical equipment operation and structural performance. However, research on the measurement of explosion-proof safety characteristics in coal mine equipment remains limited, and real-time computation of the equipment’s transient response has yet to be achieved.

In summary, this paper investigates a virtual measurement method for evaluating the explosion-proof safety characteristics of coal mine equipment. By constructing a digital twin of the equipment, the approach addresses the limitations of traditional testing methods, such as lengthy test cycles, low efficiency, high costs, and the difficulty of evaluating large-scale equipment. An improved combined surrogate model is introduced to replace traditional finite element simulations, thereby overcoming the challenges of high computational complexity and nonlinearity in the explosion process, which previously hindered real-time and efficient dynamic safety evaluation. This method offers both theoretical support and practical tools for intelligent explosion-proof detection in coal mine equipment.

2. Digital Twin System Framework of Explosion-Proof Safety Characteristics of Coal Mine Explosion-Proof Equipment

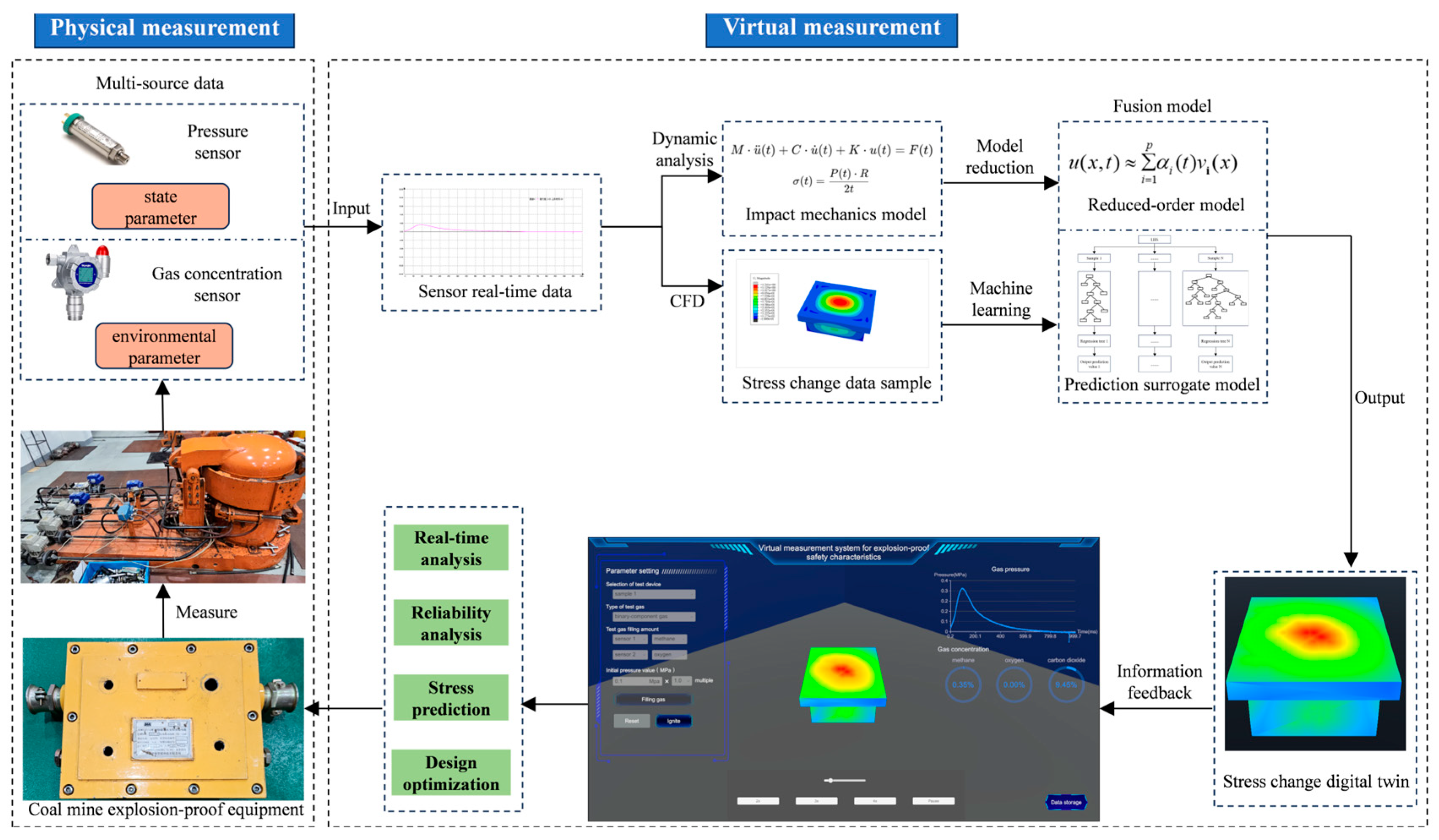
To improve the evaluation efficiency of explosion-proof safety characteristics in coal mine equipment and to visualize the mechanical behavior during the testing process, a virtual measurement method driven by real-time data is developed. This method enables dynamic assessment of explosion-proof safety characteristics and forms the basis of a virtual measurement system, which comprises five layers: the physical entity layer, the twin model layer, the twin data layer, the information transmission layer, and the application service layer, as illustrated in Figure 1.

(1)

Physical Entity Layer

The physical entity consists of the coal mine explosion-proof equipment and its associated sensing system. Sensors are deployed on the exterior of the physical equipment to collect operational state parameters and environmental data in real time during testing. Based on the structure and function of the equipment, the system is divided into mechanical, sensing, and communication subsystems.

(2)

Twin Model Layer

The twin model is a digital representation of the physical entity, enabling dynamic simulation of the equipment’s mechanical behavior through multidisciplinary modeling and data-driven approaches. Based on the geometric dimensions of the detection equipment within the virtual measurement system, a 3D model of the physical entity is constructed using 3D modeling software, and the virtual geometry is built to match the actual operating environment.

In a confined space, a spark plug ignites combustible gas to trigger a deflagration, producing a high-pressure shock wave that propagates at supersonic speed. When this wave strikes the surface of the explosion-proof equipment, it reflects and overlaps with the subsequent incoming wave. This interference creates dynamic pressure oscillations, subjecting the surface to alternating tensile and compressive impact loads. The superposition of wave fronts leads to stress concentration zones. This phenomenon is used to develop the impact mechanics model for the coal mine explosion-proof equipment, forming the basis for constructing the twin model.

(3)

Twin Data Layer

Twin data serves as the core link between the physical and virtual entities and is essential for model-driven simulation. It includes static, dynamic, and predictive data. Static data encompasses geometric dimensions, assembly relationships, material properties, constraint conditions, performance parameters, and historical records, supporting the development of the virtual geometry and explosion-proof performance prediction models.

Dynamic data includes real-time operational and environmental data collected during testing, such as gas pressure, concentration, and volume inside the equipment. Finite element analysis is performed on the impact mechanics model under different initial conditions, generating training data for a neural network model. This model forms the basis of the explosion-proof safety characteristics prediction system. By integrating real-time sensing data with model predictions, the system enables real-time safety assessments of coal mine explosion-proof equipment.

(4)

Information Transmission Layer

The information transmission layer enables real-time, bidirectional communication and synchronization between the physical and virtual entities, supporting continuous updates to the digital twin. This layer processes and analyzes geometric features and sensor data, stores the information in a database, and uses node data and predicted safety characteristics from the twin model as input to maintain accurate, real-time mapping and prediction of explosion-proof performance.

(5)

Application Service Layer

The application service layer encapsulates various types of data, models, algorithms, simulations, and outputs necessary for the operation of the digital twin system. Depending on user needs, services are categorized into functional services and business services. Functional services provide technical support for the implementation and execution of business services.

3. Twin Modeling and Simulation of Coal Mine Explosion-Proof Equipment

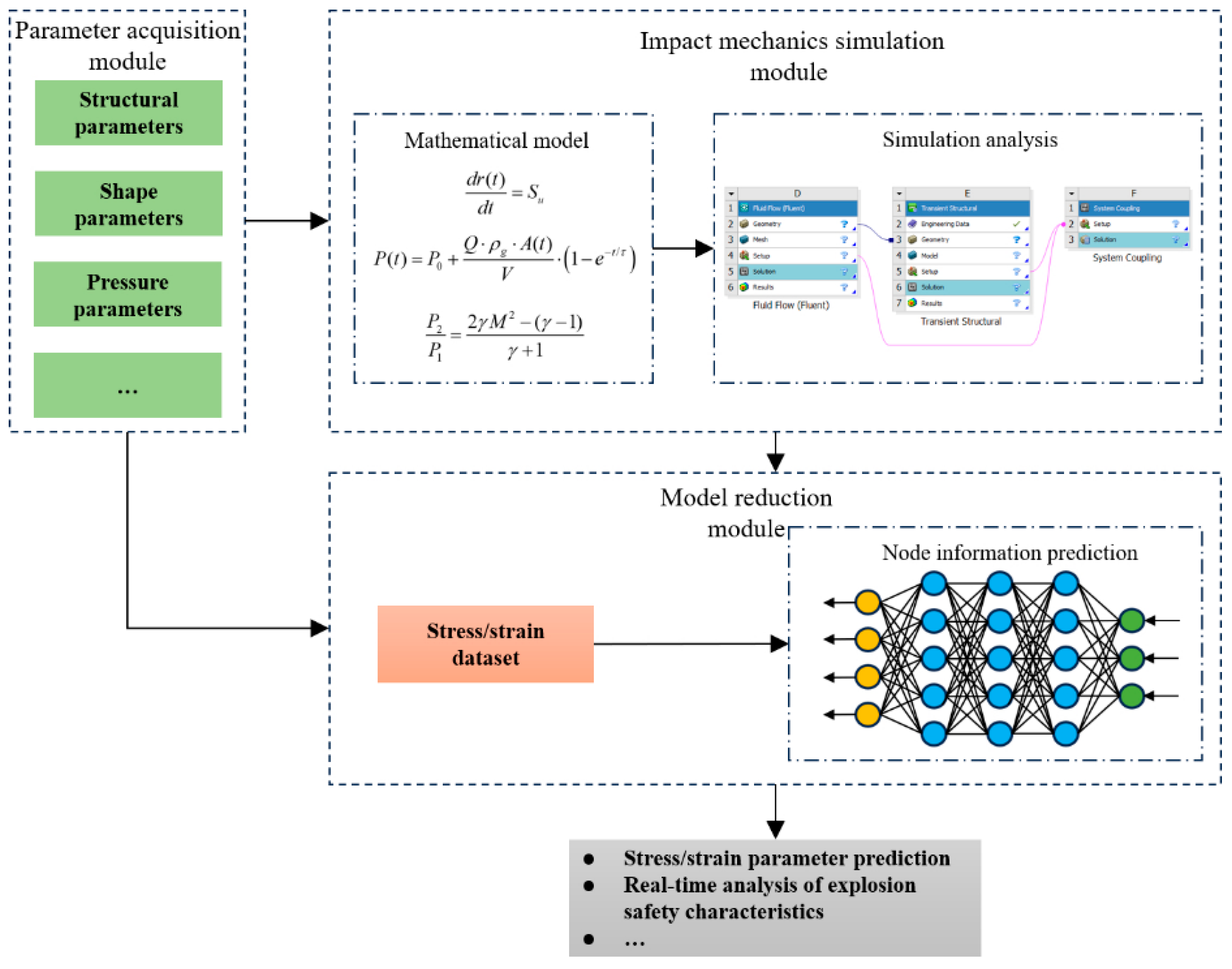
The basic framework for digital twin modeling and simulation of coal mine explosion-proof equipment is illustrated in Figure 2. It comprises three core modules: a parameter acquisition module, an impact mechanics modeling and simulation module, and a model lightweighting module. The key technologies supporting digital twin modeling and simulation for explosion-proof equipment in coal mines include: (1) Gas explosion impact mechanics modeling; (2) Finite element analysis; (3) Simulation model lightweighting techniques.

Due to inherent deviations between the digital twin model and the physical structure, the model’s fidelity is reduced, making it difficult to accurately reflect the actual condition of the equipment enclosure after a gas explosion during testing. To address this issue, the twin model is modified or updated using real-time data from internal detonation tests, thereby improving its fidelity. For the digital twin of coal mine explosion-proof equipment, in addition to basic information such as structural, geometric, and material parameters, the most critical input is real-time data—particularly the actual force on the enclosure and the internal gas pressure. These data are acquired from various field test sensors.

In terms of simulation model construction, digital twin models related to structural strength and gas explosion impact mechanics are developed to simulate the corresponding mechanical behaviors. The simulation model is built using structural finite element modeling and mechanical analysis techniques, providing a comprehensive and rapid simulation tool for evaluating the mechanical properties, structural strength, fatigue, and damage of coal mine explosion-proof equipment. Through efficient lightweight modeling techniques, a surrogate model is constructed to enable real-time output and rapid prediction of mechanical performance and structural damage. This ensures that the digital twin meets the timeliness and responsiveness requirements of explosion-proof safety evaluations.

3.1. Coal Mine Explosion-Proof Equipment Impact Mechanics Simulation Modeling

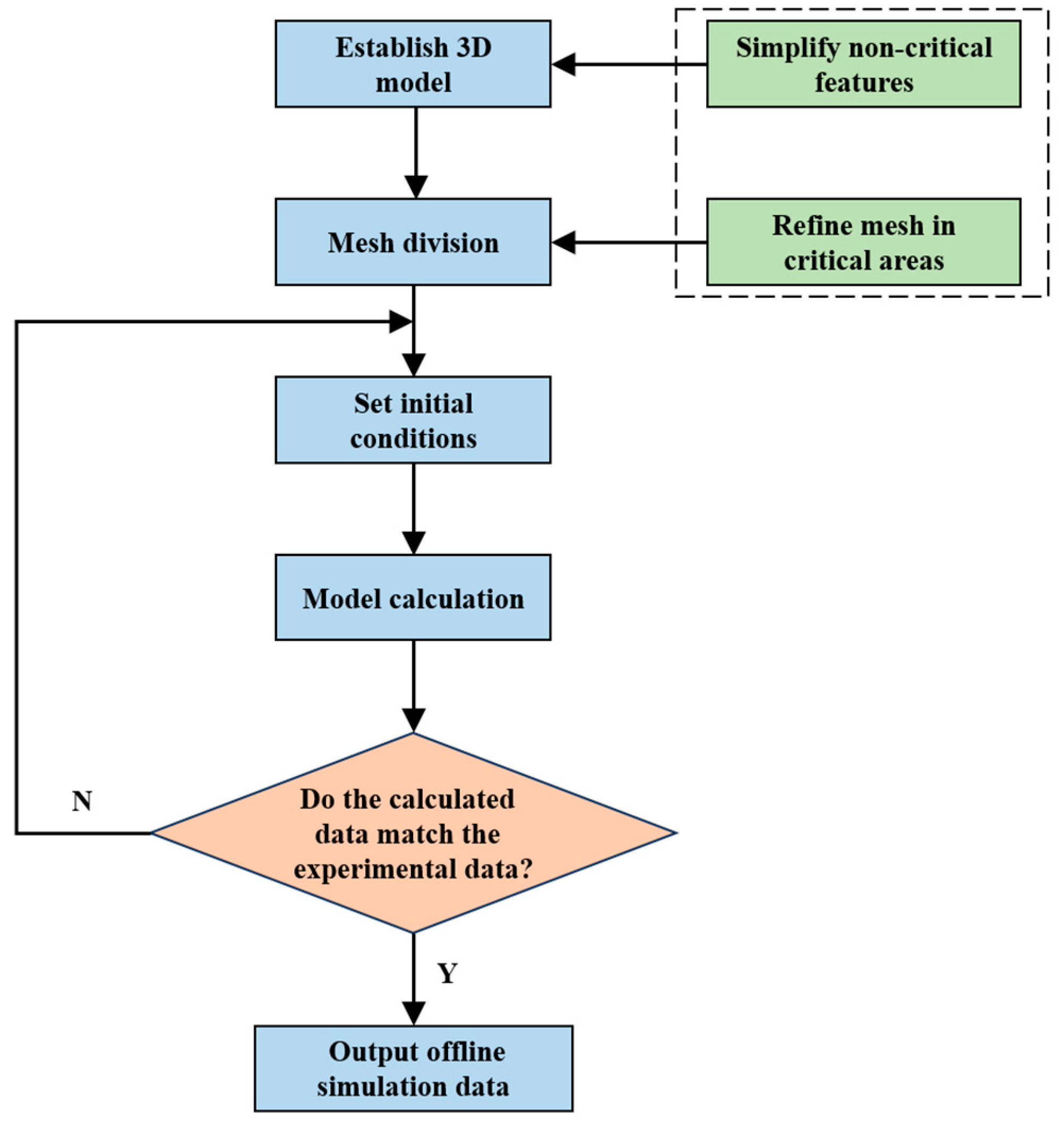
At present, CFD [26] simulation models of combustible gas explosions are mostly limited to simplified geometries such as long, wide roadways or regular cuboid and cylindrical models. These models often neglect complex geometries and fail to account for the two-way coupling between the explosion flow field and the enclosure walls. To address these limitations, this study couples a flow field analysis model based on Fluent with a transient structural analysis model to simulate both the internal explosion process and the dynamic structural response of the explosion-proof enclosure. The detailed simulation modeling process is illustrated in Figure 3.

3.2. Construction of Impact Mechanics Model

3.2.1. Physical Model

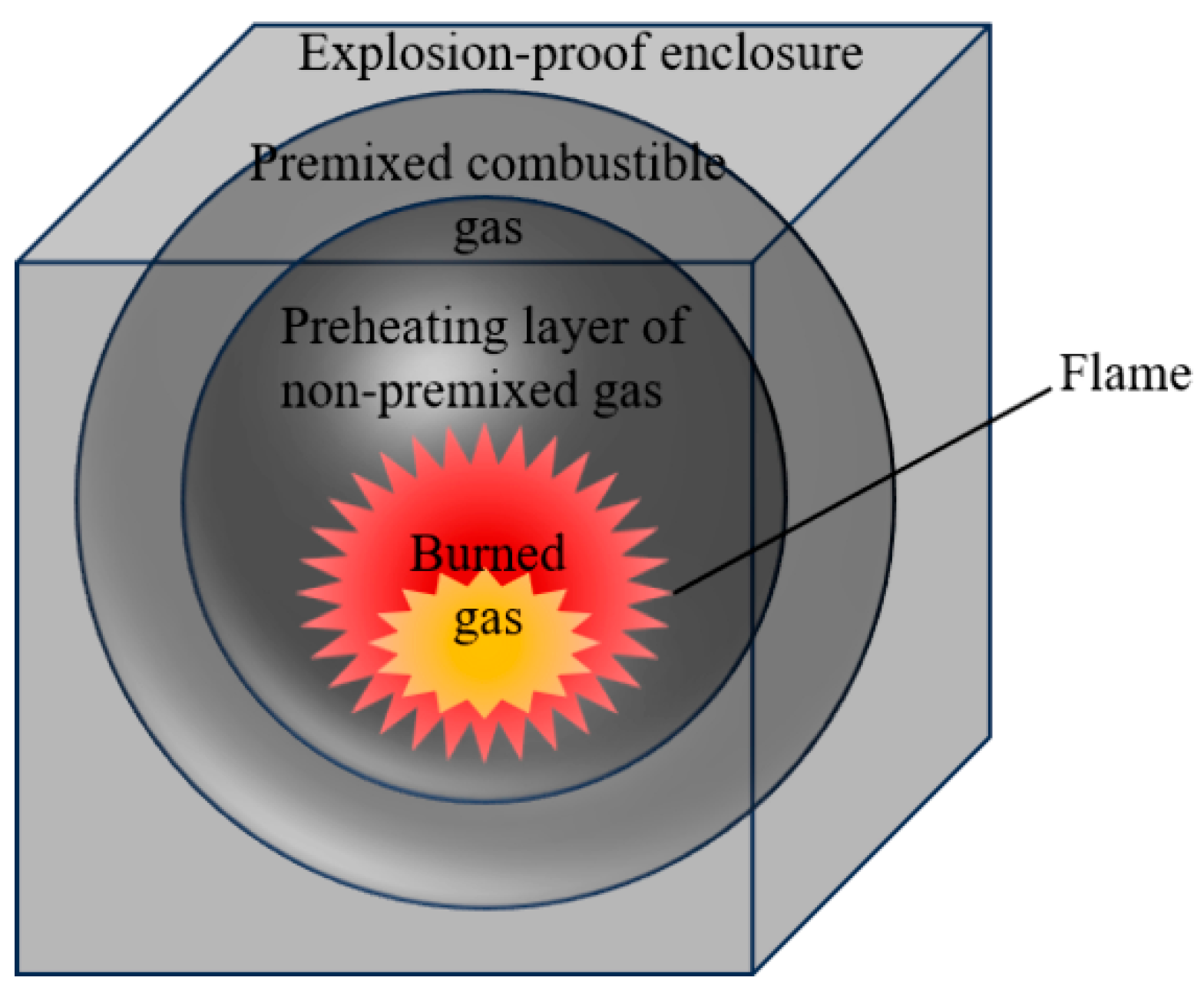
A gas explosion is a rapid combustion phenomenon triggered by an ignition source. Intense chemical reactions occur at the interface between the combustible gas and the unburned gas, resulting in the transformation of matter and energy. The most prominent physical characteristics of an explosion include high temperature, high pressure, and combustion flames. When a combustible gas is uniformly premixed with air and its concentration falls within the explosive limit range, its explosion and combustion behavior can be described by the physical model shown in Figure 4. Upon ignition, a small fireball forms at the ignition point and becomes the central fire source. A combustion wave develops around this point, propagating outward as a spherical wave, and the flame begins to expand in all directions. The premixed gas surrounding the initial fire source is ignited, forming a larger fireball. This generates a new combustion wavefront that continues to expand, causing the spherical, enclosure-shaped reaction zone to grow layer by layer. If the combustion occurs within a confined container, the temperature of the combustion products rises significantly, and the resulting pressure increases sharply. This rapid pressure buildup leads to an explosion capable of causing severe damage.

3.2.2. Explosion Model

Gas deflagration is mathematically simulated as the heating expansion of ideal gas. Gas dynamics can be expressed by a series of basic equations, such as continuity equation, momentum equation and energy equation. In this paper, the turbulent combustion time-averaged equations are used to describe the flow field, the k-ε turbulence model [27] is used to describe the turbulence change in the combustion process, the β-flame model is used to describe the change in the combustion reaction rate in the combustion process, and the wall function method is used to deal with the change in the flow field in the near wall region. A Reynolds-Averaged Navier–Stokes (RANS) formulation with the standard k-ε model is used to represent turbulent transport (${\mathrm{C}}_{\mathsf{\mu }}=0.09$, ${\mathrm{C}}_{\mathsf{\epsilon }1}=1.44$, ${\mathrm{C}}_{\mathsf{\epsilon }2}=1.92$, ${\mathsf{\sigma }}_{\mathrm{k}}=1.0$, ${\mathsf{\sigma }}_{\mathsf{\epsilon }}=1.3$). Near-wall treatment employed standard wall functions with automatic switching in cells satisfying 30 < $y^{+}$ < 300. The governing equation of the model is

$$\rho {\displaystyle \frac{\partial k}{\partial t}}+\rho {\displaystyle \frac{\partial }{\partial x_{\mathrm{j}}}}(U_{\mathrm{j}}k)=P_{\mathrm{k}}-\rho \epsilon +{\displaystyle \frac{\partial }{\partial x_{\mathrm{j}}}}\left[\left(\mu +{\displaystyle \frac{{\mu }_t}{{\sigma }_{\mathrm{k}}}}\right){\displaystyle \frac{\partial k}{\partial x_{\mathrm{j}}}}\right]$$

(1)

$$\rho {\displaystyle \frac{\partial \epsilon }{\partial t}}+\rho {\displaystyle \frac{\partial }{\partial x_{\mathrm{j}}}}(U_{\mathrm{j}}\epsilon )={\displaystyle \frac{\epsilon }{k}}({\mathrm{C}}_{\mathsf{\epsilon }1}{P}_{\mathrm{k}}-{\mathrm{C}}_{\mathsf{\epsilon }2}\rho \epsilon )+{\displaystyle \frac{\partial }{\partial x_{\mathrm{j}}}}\left[\left(\mu +{\displaystyle \frac{{\mu }_t}{{\sigma }_{\mathsf{\epsilon }}}}\right){\displaystyle \frac{\partial \epsilon }{\partial x_{\mathrm{j}}}}\right]$$

(2)

In the formula: $\rho$ is the density, $U_{\mathrm{j}}$ is the velocity vector, $k$ is the turbulent kinetic energy, $\mu$ is the laminar viscosity coefficient, ${\mu }_t$ is the turbulent viscosity coefficient, $P_k$ is the turbulent kinetic energy generation term, $\epsilon$ is the turbulent kinetic energy dissipation rate, $t$ is the time variable, $x_{\mathrm{j}}$ is the space tensor, ${\mathrm{C}}_{\mathsf{\epsilon }1}$, ${\mathrm{C}}_{\mathsf{\epsilon }2}$ are constants.

3.2.3. Impact Mechanics Model

The combustion wave propagates in a spherical form, and its dynamic process can be simplified as the expansion of the radius of the combustion wave with time.

$${\displaystyle \frac{dr(t)}{dt}}=S_{\mathrm{u}}$$

(3)

In the formula: $r(t)$ is the radius of the combustion wave, $S_{\mathrm{u}}$ is the combustion velocity (related to the concentration of the mixed gas and the turbulence intensity).

Based on the energy conservation and the ideal gas state equation, the combustion releases heat and causes the pressure to rise. The dynamic equation of the pressure in the enclosure of the coal mine explosion-proof equipment is

$$P(t)=P_0+{\displaystyle \frac{Q\cdot {\rho }_{\mathrm{g}}\cdot A(t)}{V}}\cdot \left(1-e^{-t/\tau }\right)$$

(4)

In the formula: $P_0$ is the initial pressure, ${\rho }_{\mathrm{g}}$ is the gas density, $A(t)$ is the combustion wave surface area, $V$ is the enclosure volume, $\tau$ is the pressure rise characteristic time.

When the combustion wave reaches the wall of the enclosure, the shock wave is formed by reflection, and the peak pressure is calculated by Rankine-Hugoniot equation.

$${\displaystyle \frac{P_2}{P_1}}={\displaystyle \frac{2\gamma M^2-(\gamma -1)}{\gamma +1}}$$

(5)

In the formula: $P_1$ is the pressure before the arrival of the combustion wave, $P_2$ is the shock wave reflection pressure, $M$ is the combustion wave Mach number, $\gamma$ is the specific heat capacity ratio.

This study employs a bidirectional fluid–structure interaction (FSI) approach. The bidirectional FSI numerical simulation provides an effective computational framework for solving coupled fluid–solid dynamics. The method achieves coupling between the fluid and solid domains through a bidirectional transfer of physical quantities while rigorously enforcing dynamic equilibrium at the interface. Considering the strongly nonlinear interaction between the explosion shock wave of a methane–air premix and the explosion-proof enclosure, a strongly coupled, multiphysics iterative algorithm is adopted to ensure convergence of interface variables at every time step and to guarantee computational accuracy.

Within the Ansys co-simulation framework, the enclosure–gas contact surface is defined as the fluid–solid coupling interface. Based on the principle of energy conservation, an implicit coupling scheme enables real-time, bidirectional transfer of the pressure field in the fluid domain and the displacement field in the solid domain. At each iterative step, the transient fluid solver (Ansys Fluent) and the transient nonlinear structural solver exchange converged data via the System Coupling module for the dynamic load (shock wave pressure) and the structural response (displacement field and deformation tensor). This study focuses on the blast’s action on the shell over a very short time scale; heat absorbed by the shell is negligible, so heat transfer is omitted from the data exchange in System Coupling. In the coupled solution, the solid’s displacement field is obtained using a nonlinear finite-element method and then fed back to the fluid solver through interface compatibility conditions. During each iteration, a dynamic-mesh technique updates the flow-domain topology, simultaneously adjusting the shock-wave propagation path and load distribution. Through successive iterative cycles, the peak overpressure and the shell’s plastic deformation approach prescribed convergence thresholds, and by the end of the time step a stable flow-field distribution and structural dynamic response that satisfy the residual tolerances are obtained.

3.3. Lightweight Simulation Model

The geometric mesh model of coal mine explosion-proof equipment is composed of triangular patches. Due to the large number of these patches, the computational load becomes significant, resulting in long processing times that fail to meet the real-time requirements of digital twin applications. Therefore, it is necessary to simplify the mesh model by reducing the number of triangular facets without compromising the geometric integrity of the structure. This reduction decreases the volume of data required for performance prediction and enables real-time prediction of explosion-proof safety characteristics.

The edge collapse algorithm based on the Quadratic Error Metric (QEM) [28] is a widely used mesh simplification method. Its basic principle involves iteratively collapsing edges of the triangular mesh to reduce the overall number of facets. The edge folding mechanism is illustrated in Figure 5.

In the process of edge folding, the square of the distance between the simplified point and the corresponding local area of the original surface is used as the error measure, and the edge with the smallest error is selected for folding. When performing an edge folding, define the two points of the collapse edge as $v_1$, $v_2$, and the folded point was $\overline{v}$, $\mathrm{p}(v)$ represented the set of triangular patches with vertex $v$, and the optimization goal is:

$$\overline{v}=\sum _{p\in \mathrm{p}(v)}{(v^{\mathrm{T}}p)}^2==v^{\mathrm{T}}(\sum _{p\in \mathrm{p}(v)}{K}_p)v=v^{\mathrm{T}}Qv$$

(6)

$$K_p=p{p}^{\mathrm{T}}=\left(\begin{array}{cccc}{a}^2& ab& ac& ad\\ ab& b^2& bc& bd\\ ac& bc& c^2& cd\\ ad& bd& cd& d^2\end{array}\right)$$

(7)

$$Q=\sum _{p\in \mathrm{p}(v)}{K}_p$$

(8)

In the formula: ${(v^{\mathrm{T}}p)}^2$ represents the distance between the new vertex and the triangular patches before folding. The expression of plane $p$ is $ax+by+cz+d=0$, and $a^2+b^2+c^2=1$.

Define the error metric matrix of $v_1$, $v_2$ shrinking to point $\overline{v}$ as:

$$\overline{Q}=Q_1+Q_2$$

(9)

The collapse error can be obtained as:

$$\Delta (\overline{v})={\overline{v}}^{\mathrm{T}}\overline{Q}\overline{v}$$

(10)

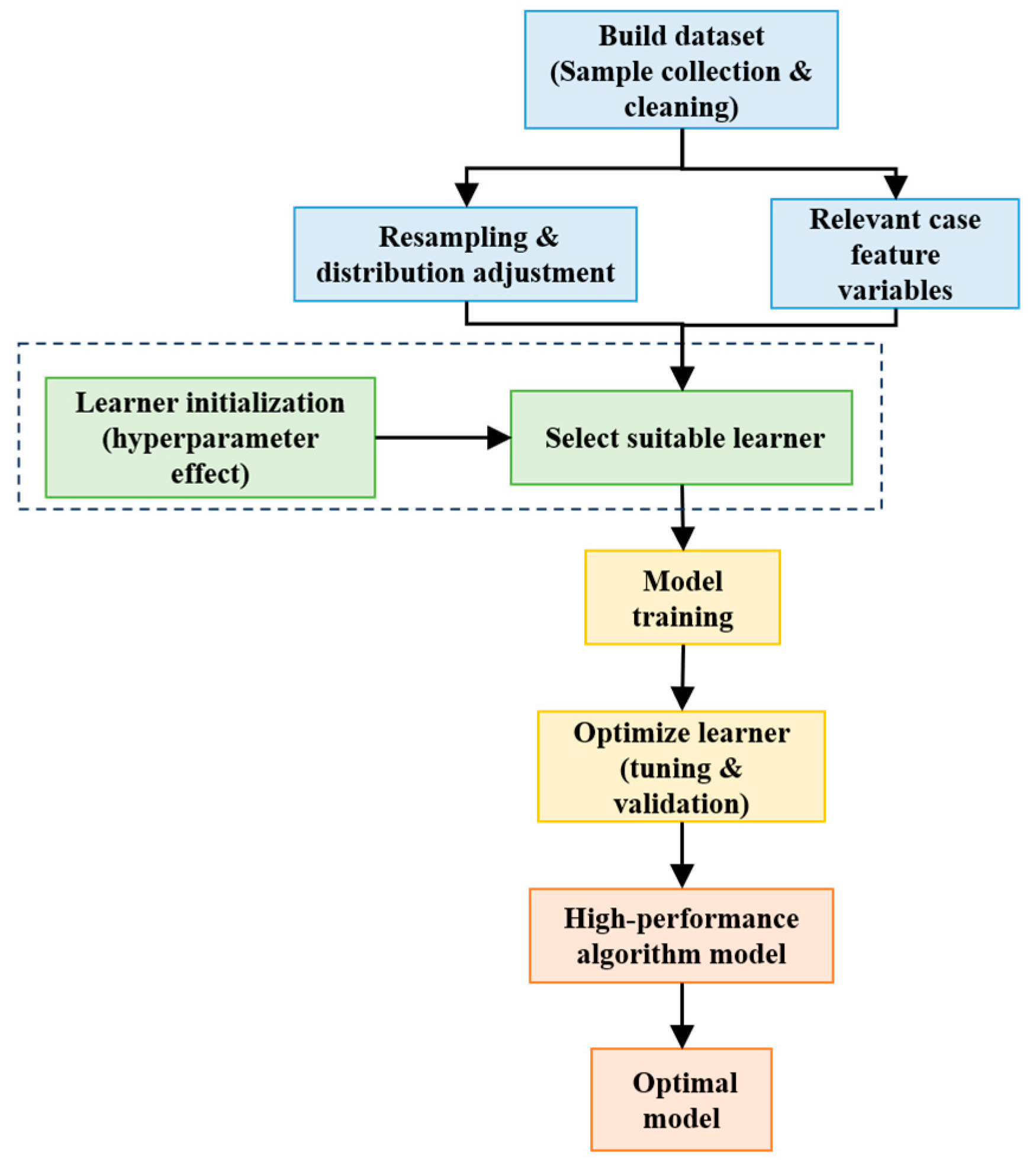
Model lightweighting refers to the simplification of high-fidelity models, aiming to significantly reduce computational time and storage requirements while preserving essential information and key effects. It is a core enabling technology for the development of digital twins. Currently, model lightweighting approaches can be categorized into three main types: the simplified model method, the projection method, and the surrogate model method. The simplified model method utilizes domain-specific knowledge to appropriately reduce model detail and complexity, and is typically based on the physical structure of the model. The projection method reduces the dimensionality of the model space by projecting the governing equations into a lower-dimensional subspace. The surrogate model method builds mathematical relationships between input and output variables using limited sample data. Common techniques include response surface methodology, Gaussian process regression, support vector regression, and artificial intelligence-based machine learning approaches.

With the rapid advancement of artificial intelligence, more efficient methods for constructing lightweight models can be developed by leveraging recent progress in computer science. The process begins with the data preparation stage, which involves data collection and preprocessing, the construction of the dataset $D=\{x_1,x_2,\dots ,x_n\}$, which $x_i$ is the feature of the input data, $n$ is the number of samples, and the dataset $D$ includes all the data in the training process. Then, the LHS method is used to uniformly sample from the original dataset $D$ to generate a new dataset $D^{*}=\mathrm{LHS}(D)$ to ensure that it can uniformly cover the sample space in each dimension. Before selecting the appropriate learner, it is necessary to initialize the learner, which has a crucial impact on the convergence and performance of the model. According to the task requirements, the appropriate learning algorithm (such as linear regression, decision tree, neural network, etc.) is selected, $L=\mathrm{choose}(L_0,A)$, which $A$ is a set of candidate algorithms and $L_0$ is an initialized learner. Then the model is trained $L^{*}=\mathrm{train}(L,D^{*})$, which $L^{*}$ is the learner obtained after training, and $D^{*}$ is the dataset after resampling. Finally, some parameters of the learner are adjusted by optimizing the relevant feature variables to improve the computational efficiency of the algorithm, avoid over-fitting, and obtain the optimal algorithm model $M^{*}$. The method flow of constructing machine learning algorithm model is shown in Figure 6.

The lightweight model offers significant advantages in terms of computational timeliness, as demonstrated by the comparison results shown in

Table 1. Comparison of model timeliness.

Lightweight Model	t/s	QEM Improved Model	t/s
Stress lightweight model	4	Stress QEM improved model	1
Strain lightweight model	4	Strain QEM improved model	1
Displacement lightweight model	4	Displacement QEM improved model	1

. The impact mechanics lightweight model delivers results within 4 s, while the inclusion of mesh simplification preprocessing using the QEM algorithm reduces the output time to just 1 s. In contrast, real-time simulation using finite element analysis software and the impact mechanics model requires approximately 7180 s. This indicates that the lightweight model combined with the QEM algorithm is an order of magnitude faster. Therefore, model lightweighting is a critical technology for ensuring the real-time performance of digital twins.

4. Construction of Surrogate Model for Explosion-Proof Safety Characteristics Prediction

To meet the requirements of real-time analysis and high-precision prediction of coal mine explosion-proof safety characteristics during testing, a surrogate prediction model for coal mine explosion-proof equipment is developed. The surrogate modeling approach includes both single surrogate models and combined surrogate models. Compared with single models, combined surrogate models integrate the strengths of individual models and offer improved prediction accuracy. Therefore, this study adopts a combined surrogate model, whose structure is illustrated in Figure 7, and enhances it using an adaptive weighting coefficient. Based on this, a prediction model for the explosion-proof safety characteristics of coal mine explosion-proof equipment is established.

4.1. Construction of Stress/Strain Cloud Dataset

Based on gas explosion theory, a mechanical simulation model of the gas explosion shock wave within the explosion-proof equipment enclosure is developed using simulation analysis software. Finite element simulation is then conducted to analyze the structural response under the effect of the explosion shock. Considering the influence of three external conditions—methane volume fraction, ignition location, and initial temperature—on the explosion-proof safety characteristics of coal mine explosion-proof equipment, the methane volume fraction range is set from 9.3% to 10.3%, with each increment of 0.2% representing one characteristic condition, resulting in 6 conditions in total. The ignition locations are set at the geometric center of the equipment and the centers of each surface, providing 5 conditions. The initial temperature range is set from 294 K to 303 K, with each increment of 3 K representing one characteristic condition, resulting in 4 conditions. Based on the above description, a total of 120 condition sets are generated as the original training dataset. As a result, stress–strain and displacement contour plots of the explosion-proof enclosure are obtained, which are used to generate the dataset for training the subsequent surrogate prediction model.

4.2. Combined Surrogate Model Theory

The combined surrogate model [29] is composed of multiple meta-surrogate models by means of weighted average, and its general expression is

$${\stackrel{⌣}{y}}_{\mathrm{p}}(x)=\sum _{i=1}^M{\omega }_i(x){\stackrel{⌣}{y}}_i(x)$$

(11)

$$\sum _{i=1}^M{\omega }_i(x)=1$$

(12)

In the formula: $x$ is the input variable; ${\stackrel{⌣}{y}}_{\mathrm{p}}(x)$ is the predicted value of the combined surrogate model; $M$ is the number of meta-models; ${\omega }_i$ is the weight of the $i$-th meta-model; ${\stackrel{⌣}{y}}_i$ is the predictive value of the $i$-th meta-model.

In order to optimize the weight coefficient of the combined surrogate model and make the combined surrogate model have more accurate prediction effect, this paper uses the leave-one-out cross-validation method to minimize the generalized mean square error, and then determines the weight coefficient of each meta-model.

$$E_{\text{LOO-CV}}={\displaystyle \frac{1}{N}}\sum _{j=1}^N{\left[y_i-{\widehat{y}}_i\right]}^2$$

(13)

In the formula: $N$ is the total number of training points; $y_i$ is the real value at the $i$-th training point; ${\widehat{y}}_i$ is the predicted value at point $i$ of the model constructed with the remaining training points after removing the point $i$;

Assuming that the accuracy index of the combined surrogate model is unbiased and irrelevant, the proportion of each meta-surrogate model index to the total is calculated in an inverse proportion as the weight coefficient of the combined surrogate model.

$${\omega }_i={\displaystyle \frac{{{\omega }_i}^{*}}{{\displaystyle \sum _{j=1}^m}{{\omega }_j}^{*}}}$$

(14)

$$\begin{array}{l}{{\omega }_i}^{*}={(E_i+\alpha \overline{E})}^{\beta }\\ \alpha <1, \beta <0\end{array}$$

(15)

$$\overline{E}={\displaystyle \frac{1}{m}}\sum _{i=1}^m{E}_i$$

(16)

In the formula: ${\omega }_i$ is the weight coefficient of the $i$-th meta-model in the normalized combined surrogate model; ${\omega }_i^{*}$ is the initial weight coefficient of the $i$-th meta-model; ${\omega }_j^{*}$ is the initial weight coefficient of the $j$-th meta-model; $E_i$ is the importance of the $i$-th meta-model; $\overline{E}$ is the average importance of all meta-surrogate models; $\alpha$ and $\beta$ are the two parameters controlling $\overline{E}$ and $E_i$, respectively, when $\alpha$ = 0.05, $\beta$ = −1, the combined surrogate model has good stability.

Radial basis function (RBF) [30] surrogate model is a model that uses discrete data to fit multivariate functions. It can be regarded as a constrained quadratic optimization problem. The goal of this method is to approximate a given dataset by functions. Compared with other traditional single surrogate models, it has good flexibility, simple structure, fast training speed and good fitting effect. Therefore, this paper chooses RBF surrogate model to construct combined surrogate model.

$$f\left(x\right)=\sum _{i=1}^n{\lambda }_i\varphi \left(r_i\right)$$

(17)

In the formula: $n$ is the total number of basis functions; ${\lambda }_i$ is the weight coefficient; $\varphi$ is a distance basis function, representing the correlation between training points; $r_i$ is the Euclidean distance between the predicted point $x$ and the center point of the $i$-th basis function, $r_i=\parallel x-c_i\parallel$.

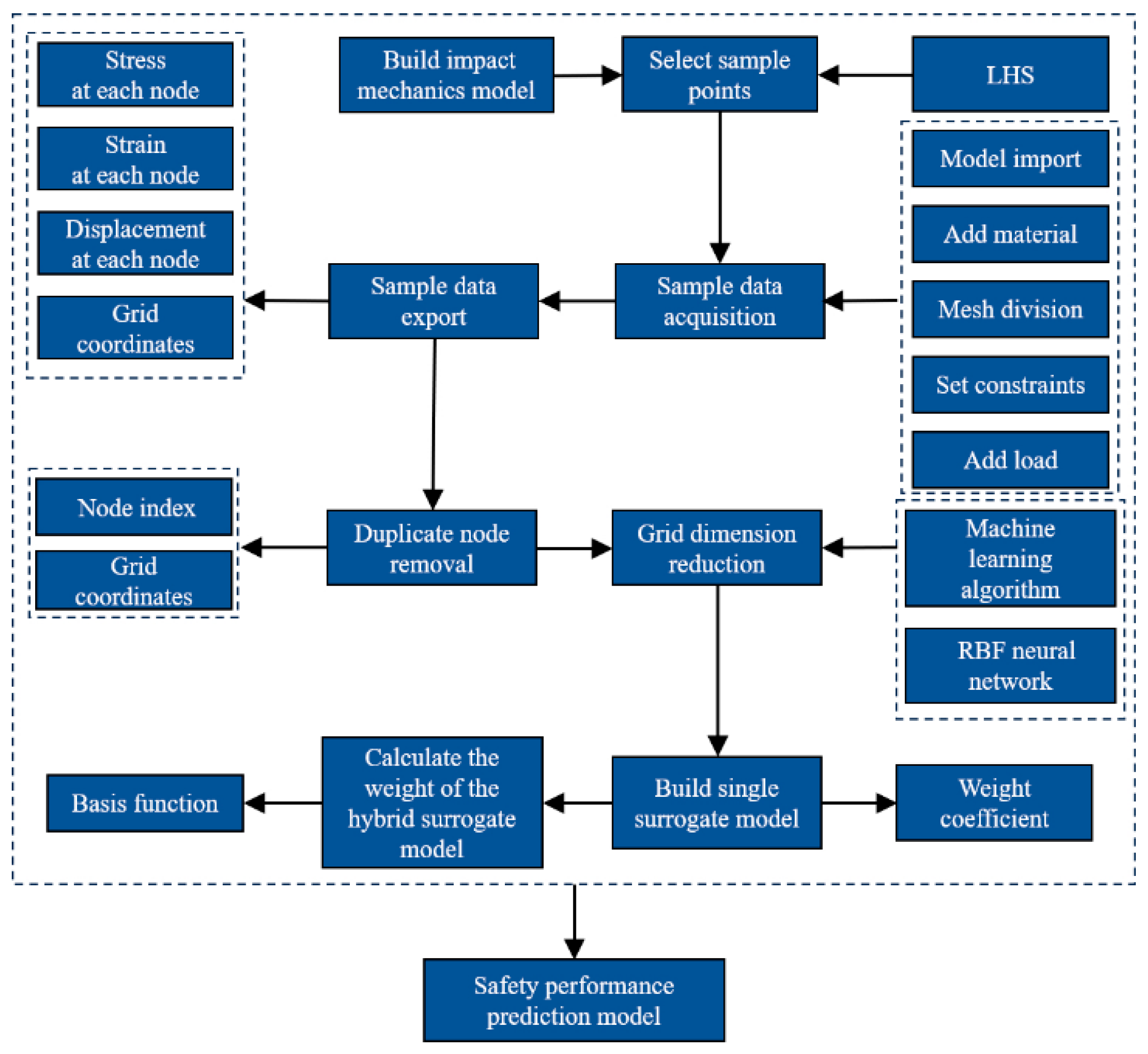
4.3. Construction of Safety Characteristics Prediction Model

In order to realize the real-time monitoring of explosion-proof safety characteristics of coal mine explosion-proof equipment, it is necessary to construct a safety characteristic prediction model, and the construction process is shown in Figure 8.

(1)

Based on the theoretical foundation and practical engineering requirements of coal mine explosion-proof equipment, an impact mechanics model is developed to support subsequent finite element analysis. The Latin Hypercube Sampling (LHS) method is employed to perform uniform random sampling within the initial parameter ranges that may influence the final results, and 30 representative sample points are selected.

(2)

A three-dimensional model of the explosion-proof equipment is imported into the finite element analysis software, where material properties are defined and the model is meshed. Boundary conditions are applied according to the actual test parameters of gas explosions, and the impact load is introduced to obtain corresponding finite element data. The mesh is divided into fine and coarse levels: the fine mesh is used for finite element simulation, while the coarse mesh is utilized in subsequent mesh simplification procedures.

(3)

Grid data, along with strain, stress, and displacement data, are exported. Position nodes of the coarse mesh are deduplicated to obtain non-redundant node coordinates and indices. Since the coarse mesh lacks structural performance data, the corresponding data from the fine mesh are mapped using a combination of the machine learning algorithm and a RBF neural network. This process generates performance data for non-redundant nodes and effectively reduces mesh dimensionality.

(4)

A single RBF surrogate model is trained using the processed finite element data. Based on the generalized mean square error (GMSE), the weight of each single surrogate model within the combined surrogate model is determined. Finally, a combined surrogate model composed of two single surrogate models is constructed, resulting in the explosion-proof safety characteristic prediction model.

5. Virtual Measurement Method of Explosion-Proof Safety Characteristics and System Test Analysis

5.1. Test Platform and Design

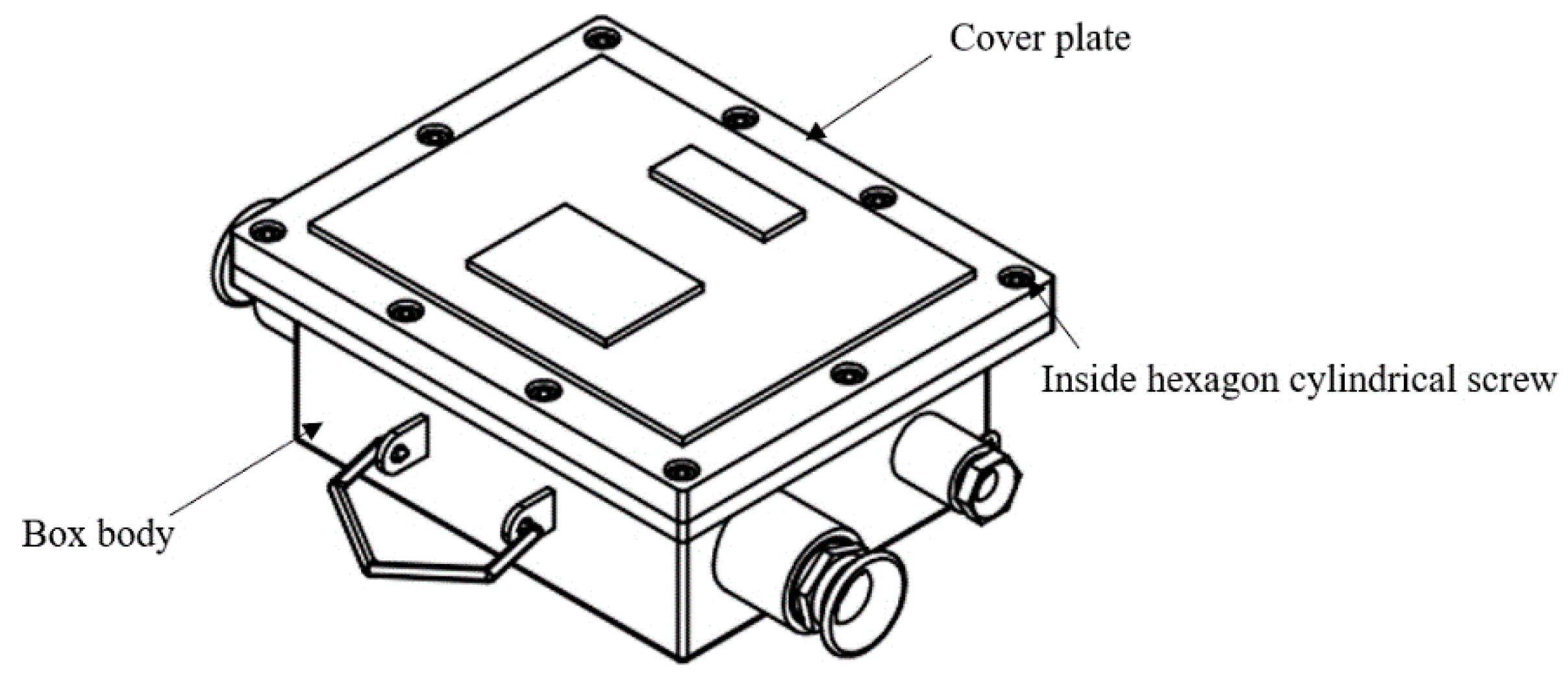
The structure of the coal mine explosion-proof equipment selected in this paper is shown in Figure 9. In Figure 9, the research object is KDW127 explosion-proof DC power supply, which is mainly composed of cover plate, box body, inner hexagonal cylinder head screw and so on. The length of the box is 378 mm, the width of the cover plate is 230 mm, and the height of the whole enclosure is 120 mm. The material properties of the explosion-proof equipment are shown in

Table 2. Material properties table.

Material	Density /(kg/m3)	Elastic Modulus/GPa	Poisson Ratio	Yield Strength/MPa	Tensile Strength/MPa
Q345B	7850	210	0.3	345	470

. In Table 2, the explosion-proof equipment studied in this paper selects Q345B as the material of the whole enclosure structure.

As shown in Figure 10, this is a device for internal explosion test of coal mine explosion-proof equipment. Based on an MD-G102 high-frequency pressure sensor(the device supports a sampling rate up to 10 kHz, 0~2.5 MPa range, ±0.0125 MPa accuracy), the gas pressure in the enclosure is collected. The concentration of the test gas is controlled by mass flow controllers, and the error in gas concentration detected by the sensor is <±0.5%.

The test device is mainly composed of gas distribution system, ignition device, pressure measurement system, console and test tank. The block diagram of the structure is shown in Figure 11. The experimental procedure is as follows:

(1)

Drill multiple holes in the test prototype and install the pressure sensors, ignition device, and gas delivery lines.

(2)

Check that the pressure sensors and the ignition device operate correctly.

(3)

Place the prototype into the explosion-proof test tank and close the tank via the control console.

(4)

Evacuate the specimen, then charge it with the pre-mixed methane–air gas through the gas distribution system.

(5)

When the gas analyzer indicates that the concentration meets the specified standard, trigger the ignition device to conduct the test.

(6)

The pressure-measurement module captures the blast pressure and transmits it to the data-processing module to generate the pressure–time curve.

After each test, holes are drilled on each surface of the test prototype, with a total of 6 tests conducted.

5.2. Introduction and Development Process of Virtual Measurement System

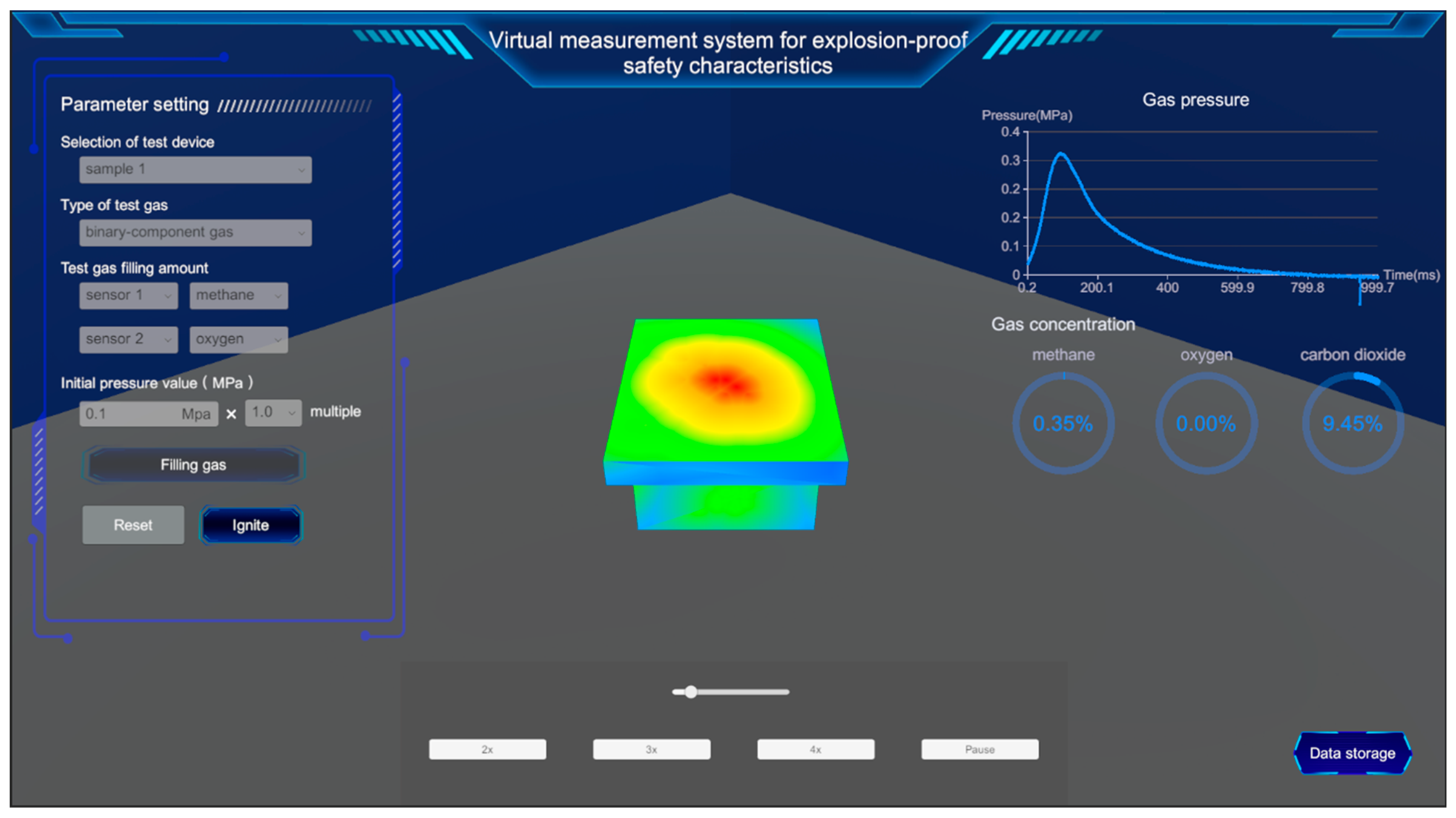
According to the framework proposed in this paper, a virtual measurement system for explosion-proof safety characteristics of coal mine explosion-proof equipment is built with the help of Unity3D 2022.3.50f1 platform, as shown in Figure 12. The virtual measurement system is mainly composed of test parameter setting module, explosion-proof safety characteristic visualization module, real-time data display module and data management module.

To establish a dynamic link between internal explosion testing and the virtual measurement of coal mine explosion-proof equipment—and to enable real-time measurement and prediction of explosion-proof safety characteristics—the system development process is illustrated in Figure 13. The virtual measurement system for explosion-proof safety characteristics integrates multiple components, including virtual entity data processing, stress–strain data acquisition, safety level evaluation, and more. Its development involves the coordinated integration of various software platforms. SolidWorks 2022 is used for the creation of the precise 3D model of the explosion-proof equipment based on its engineering drawings. The model is exported in STL (.stl) format to 3DS Max 2022 for model simplification, UV unwrapping, and material setup. The simplified visualization mesh (.fbx) is then imported into Unity 2022.3.50f1 for the digital twin front-end display. Stress–strain datasets are generated through joint simulations using Fluent and transient structural analysis. Data expansion and prediction of stress–strain behavior are performed using Python 3.11 algorithms and a RBF surrogate model. A dynamic evaluation method is then implemented to assess the explosion-proof safety characteristics of the equipment in real time. Finally, through Socket communication, data visualization and user interaction are realized using Xcharts 3.2.0 and a custom user interface (UI).

5.3. Test Results and Analysis

After the original finite element mesh model is processed by the mesh simplification process described in Section 3, the number of vertices and triangle meshes of the model is simplified. Figure 14 is a comparison of the simplification effect of the three-dimensional model of the experimental prototype. The simplification rates of different structural components and the number of triangle meshes before and after simplification are shown in

Table 3. Comparison of the mesh-simplification effect.

Structure	Before Simplification	After Simplification	Simplification Rate
Cover plate	32902	16045	51.2%
Box body	50440	27320	45.9%

.

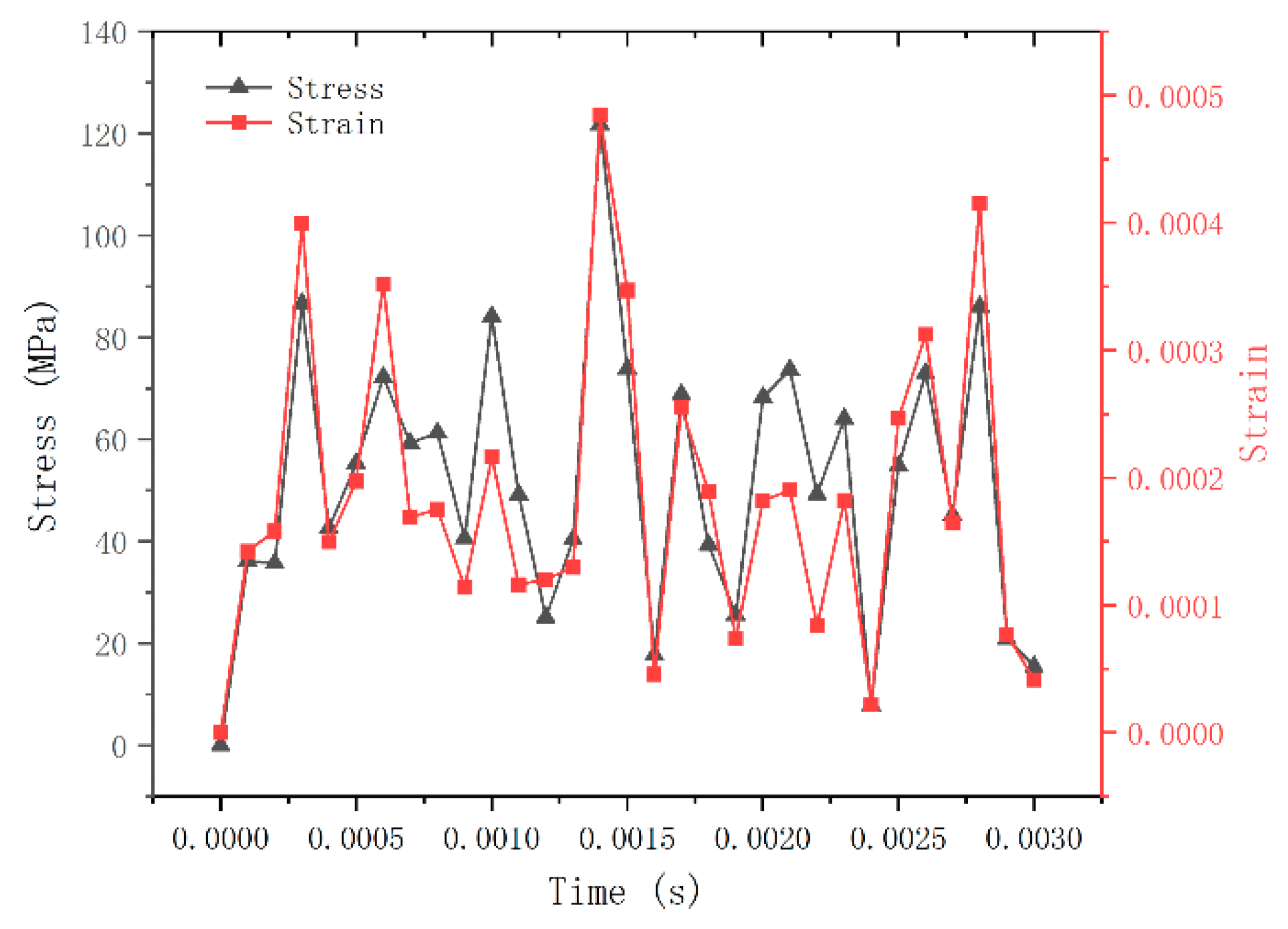
To verify the accuracy of the mechanical twin model for internal explosion impact in coal mine explosion-proof equipment, the enclosure is initially filled with a methane–oxygen gas mixture. The methane volume fraction is 9.8%, the initial pressure is 1 standard atmosphere, and the temperature is set to 300 K. The ignition zone is positioned at the center of the enclosure and modeled as a spherical region with a diameter of 1 cm and an ignition temperature of 2000 K. In this study, the species transport model and turbulence model in Fluent are selected as the combustion model to achieve two-way coupling between the high-pressure gas and the enclosure walls. The variations in stress, strain, and displacement over time during the gas combustion and explosion process are computed accordingly. The central point on the top surface of the mesh is chosen as a representative feature point, and its stress and strain trends are shown in Figure 15.

As shown in Figure 14, during the initial pressure impact stage, an instantaneous high-pressure shock wave is generated at the moment of the gas explosion, causing the inner wall of the enclosure to be rapidly subjected to an impact load, and resulting in a sharp rise in stress to its peak value. In the subsequent stage of stress wave propagation and reflection, the stress wave propagates from the inner wall toward the outer surface of the enclosure, where it reflects upon contact. This leads to noticeable fluctuations and oscillations in the stress distribution, with multiple stress peaks observed. In the final stage—characterized by stress attenuation and stabilization—the impact energy gradually dissipates, the stress amplitude decreases, and the system reaches a relatively stable state. The strain exhibits a similar trend to the stress during all three stages.

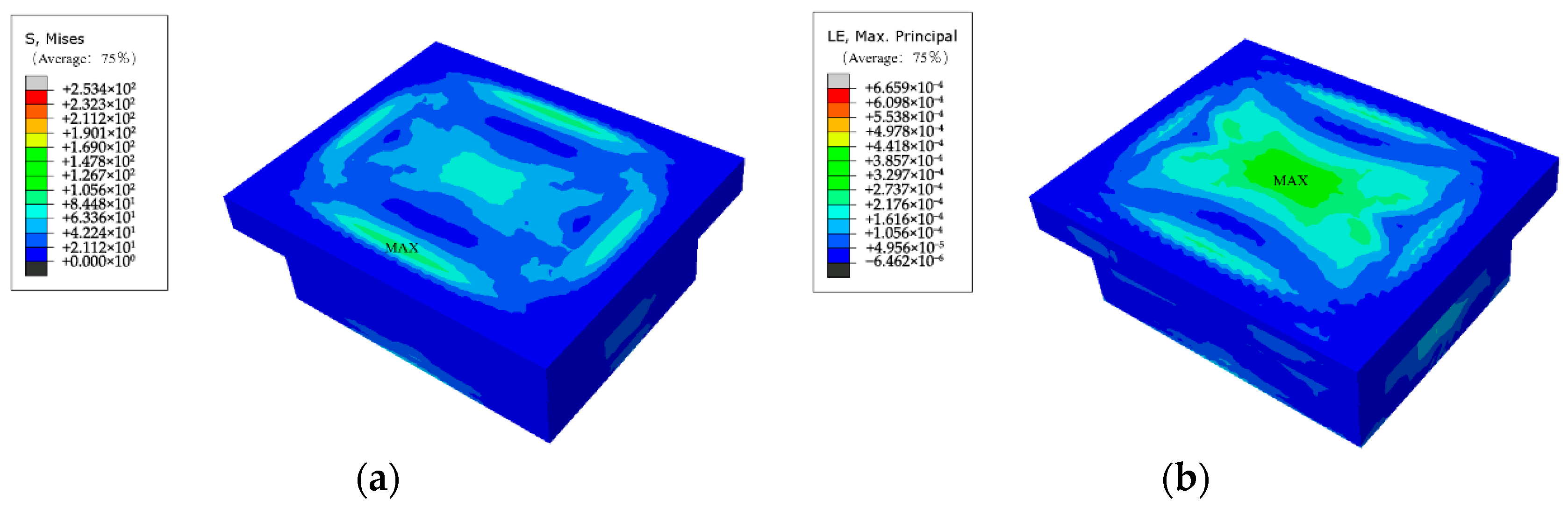
At approximately 0.0015 s, both stress and strain reach their respective peak values. The corresponding stress and strain contour plots are shown in Figure 16. It can be observed that the stress and strain concentration areas are symmetrically distributed. The highest values are primarily located near the edge of the enclosure’s upper cover and at the central regions of each surface. These areas are the most significantly affected by the explosion-induced impact load and thus represent critical zones for structural optimization. The maximum stress is approximately 121.7 MPa, which is well below the yield strength of the enclosure material, indicating that the structural integrity requirements of the explosion-proof equipment are met.

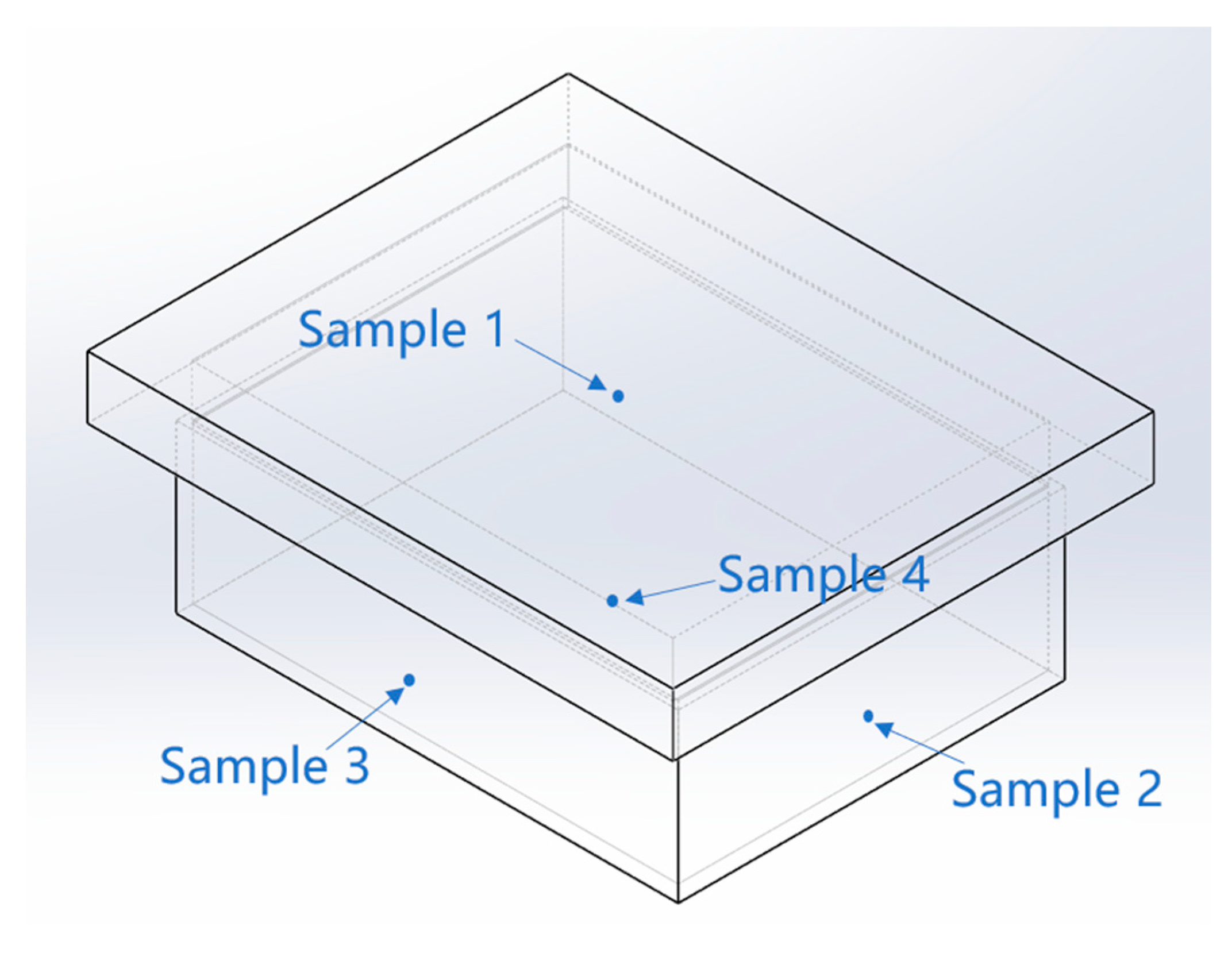
The stress concentration points of the four surfaces of the explosion-proof equipment enclosure are selected as the sample points, see Figure 17, and the stress, strain and displacement data of different sample points are obtained, respectively. The stress, strain and displacement curves of the four sample points are shown in Figure 18.

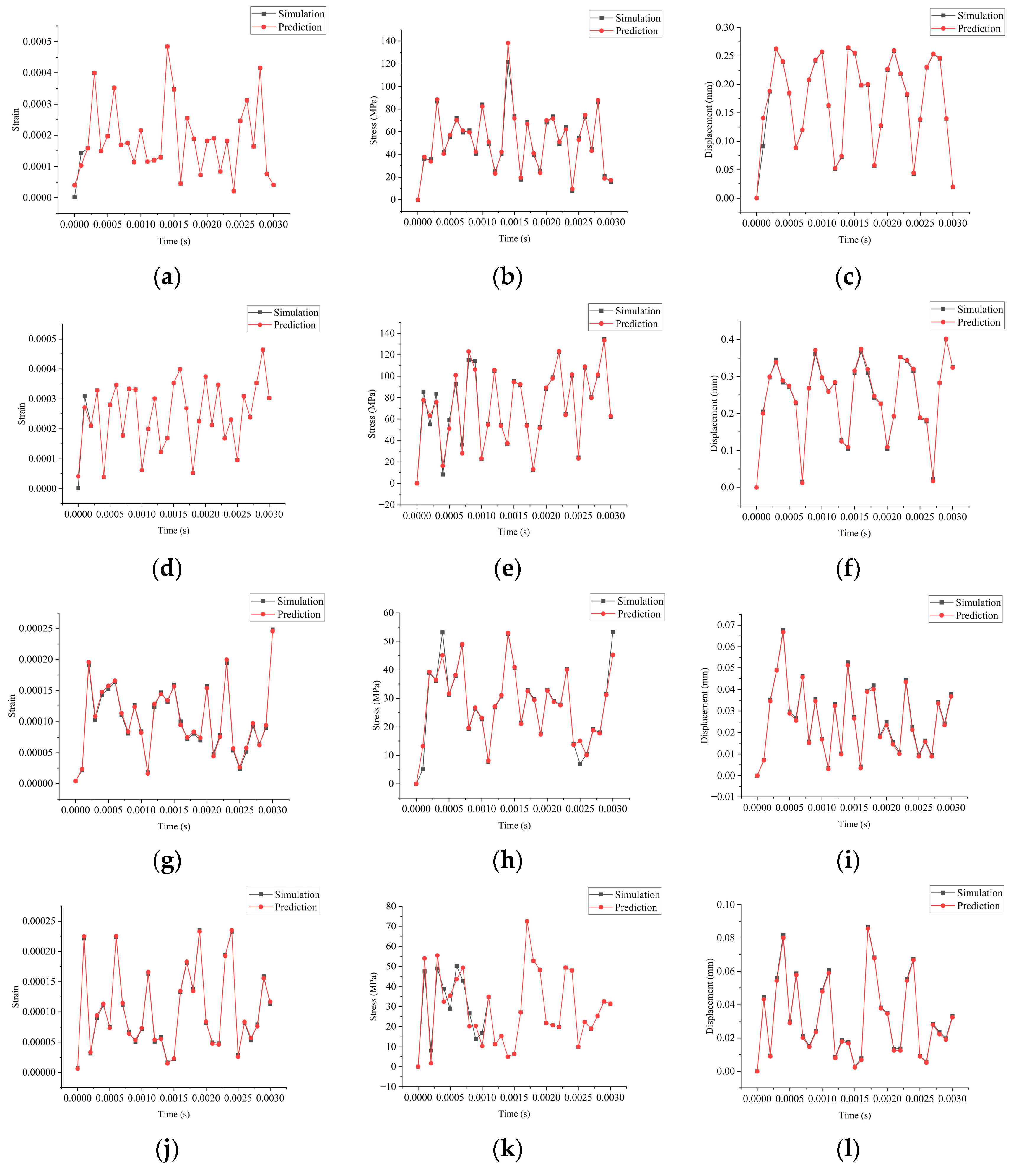
As shown in Figure 18, Subfigures (a), (b), and (c) present the strain, stress, and displacement curves of Sample Point 1, along with their corresponding prediction curves. It can be observed that the predicted strain and displacement curves closely match the simulation results. However, the predicted stress curve shows a noticeable error at the peak value, while the prediction errors at other time points are minimal. Subfigures (d), (e), and (f) display the results for Sample Point 2. The predicted strain and displacement curves again exhibit high consistency with the simulation data. The predicted stress curve has a slight deviation in the initial stage, but the prediction error at other time points remains very small. Similarly, Subfigures (g), (h), and (i) correspond to Sample Point 3. The predicted strain and displacement curves are almost identical to the simulation curves, whereas the predicted stress curve shows minor deviations at the beginning and end of the time series, with negligible error in between. Subfigures (j), (k), and (l) illustrate the results for Sample Point 4. While the strain and displacement predictions are consistent with the simulation results, the predicted stress curve exhibits a larger error in the first half of the time series and a smaller error in the second half. Overall, across all sample points, the predicted and simulated curves follow the same trend. The prediction data align well with the simulation results, demonstrating the high accuracy of the surrogate prediction model.

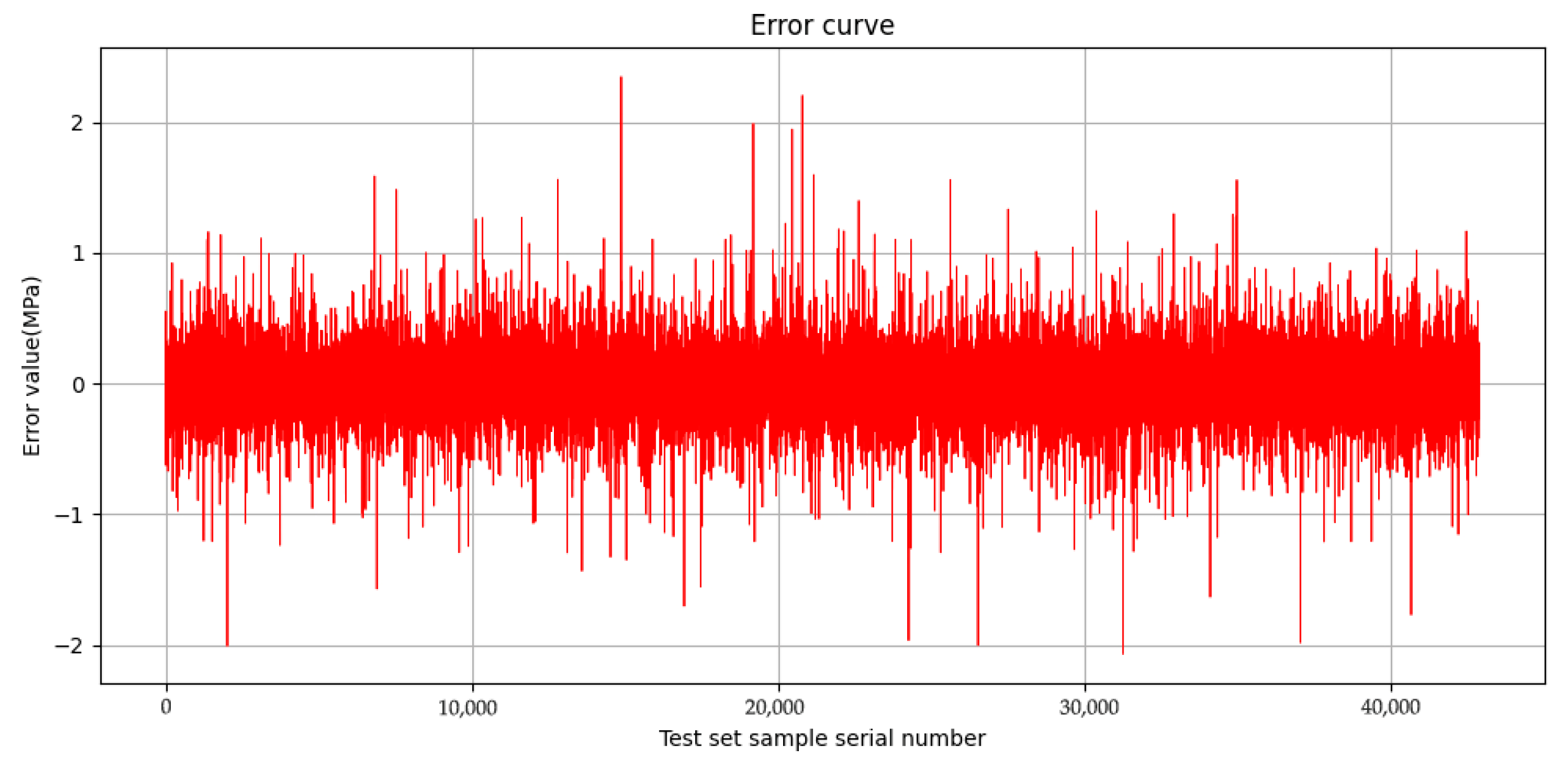
To verify the accuracy of the prediction model, Figure 19. presents the stress error between the finite element analysis (FEA) results and the prediction results of the surrogate model for over 40,000 sample points in the test set. The error is primarily concentrated within the range of ±1 MPa, with the vast majority of values distributed closely around zero. Only a small number of points exhibit errors exceeding ±2 MPa, and the maximum prediction error does not exceed 1.89%. These results indicate that the prediction model demonstrates a high level of consistency with the FEA simulation results. The model exhibits excellent accuracy and strong overall fitting performance.

The determination coefficient $R^2$ is selected as the global evaluation criterion to reflect the correlation between the simulation data and the prediction data. The mean square error ($MSE$), root mean square error ($RMSE$) and mean absolute error ($MAE$) are used for more comprehensive evaluation. See

Table 4. Prediction error estimation of different sample points.

Sample Point	Safety Characteristic Parameters	R2	MSE	RMSE	MAE
Sample point 1	Stress prediction	0.9624	12.1940	3.4920	2.3564
	Strain prediction	0.9930	9.59 × 10−11	9.79 × 10−6	2.76 × 10−6
	Displacement prediction	0.9852	8.36 × 10−5	9.14 × 10−3	2.67 × 10−3
Sample point 2	Stress prediction	0.9585	20.7910	4.5597	3.1990
	Strain prediction	0.9926	9.58 × 10−11	9.79 × 10−6	2.82 × 10−6
	Displacement prediction	0.9752	2.33 × 10−4	1.53 × 10−2	3.57 × 10−3
Sample point 3	Stress prediction	0.9549	7.9300	2.8160	1.3916
	Strain prediction	0.9906	2.30 × 10−11	4.79 × 10−6	2.34 × 10−6
	Displacement prediction	0.9883	4.00 × 10−6	2.00 × 10−3	1.59 × 10−3
Sample point 4	Stress prediction	0.9495	13.9091	3.7317	2.1906
	Strain prediction	0.9974	1.18 × 10−11	3.44 × 10−6	1.13 × 10−6
	Displacement prediction	0.9871	7.95 × 10−6	2.82 × 10−3	2.26 × 10−3

, the value range of $R^2$ is [0, 1], and the larger the value, the higher the correlation.

$$R^2=1-{\displaystyle \frac{{\displaystyle \sum _{b=1}^n}{(y_b-{\widehat{y}}_b)}^2}{{\displaystyle \sum _{b=1}^n}{(y_b-\overline{y})}^2}}$$

(18)

$$MSE={\displaystyle \frac{1}{n}}\sum _{b=1}^n{(y_b-{\widehat{y}}_b)}^2$$

(19)

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}\sum _{b=1}^n{(y_b-{\widehat{y}}_b)}^2}$$

(20)

$$MAE={\displaystyle \frac{1}{n}}\sum _{b=1}^n\left|y_b-{\widehat{y}}_b\right|$$

(21)

In the formula: $n$ is the number of sample points; $y_b$ is the actual response value of the $b$ sampling point $x_b$; ${\widehat{y}}_b$ is the corresponding predicted value; $\overline{y}$ is the average value of $n$ sample $y$.

It can be seen from Table 4 that the simulation data and prediction data of stress, strain and displacement of the four sample points are all greater than 0.94, with an average of 0.9779, indicating that there is a high correlation, and it can be concluded that the prediction model of safety characteristics has a good prediction effect.

6. Conclusions

To address the challenges of long testing cycles, low efficiency, high costs, and the difficulty of evaluating large-scale equipment in internal explosion tests of coal mine explosion-proof systems, a virtual measurement method is proposed for assessing explosion-proof safety characteristics. By constructing a virtual measurement system framework, a modeling and simulation approach is developed for the digital twin of internal explosion impact mechanics. This framework enables dynamic interaction and real-time synchronization between the physical entity and its virtual counterpart. Furthermore, an improved combined surrogate model is introduced for predicting explosion-proof safety characteristics, effectively solving the problem of real-time computation for transient internal explosion impacts in coal mine explosion-proof equipment.

(1)

A virtual measurement system framework for evaluating the explosion-proof safety characteristics of coal mine equipment is constructed. A mechanical twin model of internal explosion impact is established, enabling the visualization of mechanical behavior during explosion-proof safety tests.

(2)

A transient multi-physical field reduced-order model based on Latin Hypercube Sampling (LHS) and machine learning is proposed, significantly improving the modeling efficiency of the twin model under transient impact conditions.

(3)

A prediction method based on a Radial Basis Function–Generalized Mean Square Error (RBF–GMSE) combined surrogate model, improved by an adaptive weighting coefficient, is introduced. This approach addresses the limitations of single surrogate models in achieving high-precision prediction for transient processes.

(4)

A virtual measurement system is developed that visualizes the mechanical characteristics of the test process and enables real-time, accurate virtual measurement and prediction of key explosion-proof safety indicators in coal mine equipment.

(5)

The proposed prediction method is validated through experiments. Results show that the improved combined surrogate model achieves high prediction accuracy for stress, strain, and displacement, with a maximum error not exceeding 1.89% and an average prediction accuracy of 0.9779, confirming the model’s validity and reliability.

The comparisons with other methods, the limitations of the present work, and directions for future research are as follows:

Compared with traditional approaches that rely on physical testing and high-fidelity simulations [6,7], the virtual measurement system proposed herein offers marked advantages in efficiency, cost-effectiveness, and real-time assessment capability. Whereas prior studies have mainly focused either on CFD of the explosion process [8,9,10,11] or on structural-health digital twins under static loads [23,24,25], this work integrates both aspects into a coherent, dynamic, and real-time predictive framework. The adaptive weighting mechanism in the ensemble surrogate model effectively mitigates the limitations of single-model predictions and enhances robustness under transient shock scenarios.

The model developed in this study is based on the assumptions of an ideal gas and homogeneous, isotropic material properties; real-world cases involving complex gas mixtures or material defects may introduce biases. Future research will incorporate a broader range of influential factors by introducing more sophisticated material and combustion models to investigate the impact mechanics of explosion-proof equipment under multiphysics coupling. We will also integrate in situ measurement data to construct higher-fidelity finite-element models and surrogate predictors, enabling online model updating and self-calibration toward a fully adaptive digital twin.