Hybrid-Domain Synergistic Transformer for Hyperspectral Image Denoising

Featured Application

Hyperspectral denoising technology can improve the quality of remote sensing images and is applicable to fields such as environmental monitoring and precision agriculture.

Abstract

Hyperspectral image (HSI) denoising is challenged by complex spatial-spectral noise coupling. Existing deep learning methods, primarily designed for RGB images, fail to address HSI-specific noise distributions and spectral correlations. This paper proposes a Hybrid-Domain Synergistic Transformer (HDST) integrating frequency-domain enhancement and multiscale modeling. Key contributions include (1) a Fourier-based preprocessing module decoupling spectral noise; (2) a dynamic cross-domain attention mechanism adaptively fusing spatial-frequency features; and (3) a hierarchical architecture combining global noise modeling and detail recovery. Experiments on realistic and synthetic datasets show HDST outperforms state-of-the-art methods in PSNR, with fewer parameters. Visual results confirm effective noise suppression without spectral distortion. The framework provides a robust solution for HSI denoising, demonstrating potential for high-dimensional visual data processing.

1. Introduction

Image denoising, a traditional image processing technique, aims to recover clean information from observed signals and finds extensive applications in tasks such as remote sensing [1,2], target recognition [3], and 3D reconstruction [4]. Traditional methods such as wavelet transform [5], nonlocal means [6] rely on hand-crafted priors and are inadequate for handling complex noise distributions. In recent years, deep learning-based denoising models such as DnCNN [7] and SwinIR [8] have significantly improved performance through powerful image feature extraction capabilities.

These image denoising algorithms primarily focus on RGB images, which typically have only 3 channels and a simple structure. However, hyperspectral images (HSI), widely used in numerous scientific and applied fields, capture the spectral-spatial information of scenes through hundreds of consecutive narrow spectral bands, significantly expanding the dimension and capability of information expression. Since the late 1960s, hyperspectral imaging technology has been mainly applied in areas such as agriculture, mineral exploration, and satellite remote sensing monitoring [9]. Typical applications include crop health assessment, mineral identification, and land use classification based on satellite and airborne systems [9]. In recent years, with the continuous advancement of sensor technology and analytical methods, the applications of hyperspectral images have expanded to multiple cutting-edge fields, including agriculture, military [10], art and cultural heritage protection [11], food safety, and medical diagnosis [12]. For instance, in geophysical exploration, HSIs are used to invert the composition of surface materials [13]; in heritage science, they assist in the non-destructive identification of art materials and the restoration of historical documents [11]; moreover, in security and industrial testing, HSIs are also widely applied in chemical identification, material classification [14], and pollutant diffusion tracking. These applications demonstrate the unique advantages of hyperspectral images in acquiring information from complex scenes, while also placing higher-dimensional and more refined requirements on the research of HSI-related algorithms. Traditional algorithms cannot be directly applied to HSI denoising due to their neglect of channel correlations [15]. Compared to RGB images, HSI denoising presents the following unique challenges:

• Coupled multidimensional noise and cross-band correlations: Noise is non-uniformly distributed across spatial dimensions and complexly coupled with spectral dimensions, exhibiting inter-band dependencies [16].
• Sensitivity to high-frequency information: Inconsistent imaging equipment causes HSIs to frequently have bit depths different from RGB. Weak spectral features are easily drowned out by noise, requiring fine-grained frequency-domain guidance [1].
• Detail preservation and computational efficiency: Hundreds of channels substantially increase computational complexity. Traditional methods lack efficiency and capability in jointly modeling local spatial details and global spectral continuity [17].

Traditional HSI denoising methods based on frequency domain processing primarily utilize Fourier transform and wavelet transform techniques [18,19]. The Fourier transform distinguishes noise and signal distributions through frequency domain conversion, where low-pass filters can suppress high-frequency noise but tend to lose image details while showing limited effectiveness for complex noise. Similarly, wavelet transform decomposes HSI into sub-bands of different frequencies and achieves denoising by processing coefficients within these sub-bands [5,20]. When noise energy dominates certain sub-bands, thresholding can be applied to suppress noise components. However, this approach faces critical challenges in selecting appropriate wavelet basis functions and determining optimal thresholds, where improper threshold selection may cause over-denoising (resulting in image blurring) or under-denoising (leaving significant noise) [20]. These traditional methods primarily consider frequency domain perspectives without fully integrating spatial and spectral characteristics of HSI, making them increasingly unsuitable for modern high-quality HSI processing requirements.

Early attempts to apply deep learning to HSI denoising encountered significant challenges. For instance, Xie and Li [21] pioneered the use of deep CNNs with trainable nonlinear functions for this task, but extending 2D models to 3D HSI data faced obstacles including under-utilization of spatial-spectral correlations, high computational complexity, and insufficient training data [22]. To address these limitations, Dong et al. developed a 3D denoising framework using an improved U-net architecture [22]. Their approach employed separable filtering that decomposes 3D operations into 2D spatial and 1D spectral components to reduce complexity, supplemented by transfer learning to mitigate data scarcity, ultimately outperforming model-based methods. Recent innovations have further advanced deep learning approaches: Liang et al.’s HSSD [23] combines CNN and Transformer architectures with a decoupling strategy to capture both local/nonlocal details and global spectral correlations, achieving superior spatial-spectral reconstruction, while Fu et al.’s GMSC-Net [24] adopts a model-based approach using sparse representation and iterative optimization, addressing the lack of clean-noisy pairs through clustering techniques.

In recent years, frequency domain analysis, when integrated with deep learning, has demonstrated unique advantages in image restoration tasks [25,26], leveraging frequency transformations to decouple noise and signal spectra while utilizing the nonlinear modeling capabilities of deep networks. Successful applications in RGB denoising include Fourier convolutions in FADformer [27] and cross-domain filtering in FCENet [28], while other exemplary approaches span tasks like deraining—such as Gao et al.’s contrastive regularization-based frequency domain method for improved feature distinguishability [27]—deblurring via Kong et al.’s Frequency-domain Self-Attention Solver (FSAS) with Discriminative Frequency-domain Feed-forward Network (DFFN) that applies convolution theorem principles [29], and adaptive fusion of NIR and RGB images through Wang et al.’s FCENet to exploit frequency domain complementarity [30]. Cross-domain fusion frameworks have also gained traction, as seen in Zhang et al.’s FS-Net, which separates frequency components of underwater images combined with spatial filtering for contrast enhancement [25], alongside HSI-specific implementations like Wang et al.’s UOANet [31] and Sheng et al.’s SANet [32] that optimize denoising through spectrum-spatial fusion and frequency-guided processing—though the adaptation of earlier RGB-focused methods to HSI remains largely unexplored.

Complementary to frequency approaches, Atrous Spatial Pyramid Pooling (ASPP) [33] captures multi-frequency noise components through multiscale atrous convolutions, with its feature extraction capabilities validated in diverse tasks like semantic segmentation [34]. This module finds wide application in image processing; for example, ASPP-DF-PVNet [35] enhances model generalizability by capturing multi-level details. When combined with frequency analysis, ASPP’s multi-dilation design can be mapped to multi-band frequency processing, enabling specific separation of periodic stripe noise spectra (characterized by low-frequency directional energy [33]) from high-frequency random sensor noise in HSI. This integration provides physically meaningful frequency priors for cross-domain feature fusion, though effectively combining frequency analysis with HSI’s spatial-spectral duality requires further investigation.

To this end, this paper proposes an HSI denoising framework based on frequency domain enhancement and multiscale modeling, achieving spatial-frequency-channel three-dimensional collaborative processing. Specifically, building upon Spectral Enhanced Rectangle Transformer (SERT) [36], it innovatively deeply integrates frequency domain noise decoupling with spatial multiscale modeling: (1) Introducing a fast Fourier transform (FFT) preprocessing module to transform HSI into the frequency domain for noise separation, combined with ASPP multiscale atrous convolution [33] to suppress noise components of different frequencies; (2) designing a dynamic cross-domain attention module to adaptively fuse spatial-frequency features through a learnable gating mechanism, such as enhancing noise suppression in low-frequency regions dominated by the frequency domain and preserving ground object textures in high-frequency regions dominated by the spatial domain; and (3) constructing a shallow global-deep local hierarchical architecture, utilizing the global average pooling branch of ASPP to capture noise statistical characteristics and guide detail recovery in deep networks. Experiments show that this framework improves the quality of HSI restoration in mixed noise scenarios while maintaining the efficiency of SERT [36] to a certain extent. This framework has verified its effectiveness in HSI denoising tasks, and it may be extended to a universal post-processing framework in the future. In general, our contributions can be summarized as follows:

• Propose a spatial-frequency-channel three-dimensional collaborative dynamic cross-domain feature fusion framework, combining spatial domain Transformer with FFT-based frequency domain feature extraction in a post-processing manner. It realizes adaptive weight allocation of dual-domain features through a learnable gating mechanism, enabling cross-domain attention for dual-domain collaborative processing to address the coupling of HSI noise in spatial, spectral, and frequency dimensions.
• Firstly, introduce spatial pyramid pooling into the joint processing of both spatial and frequency domains; while constructing a hierarchical denoising chain of global statistical guidance-local detail recovery, it forms cross-denoising capabilities of spatial multi-resolution + frequency multi-band.
• Compared to the baseline, our model achieves a PSNR improvement of 0.94 dB on Realistic dataset and a maximum PSNR improvement of 0.52 dB on ICVL synthetic dataset.

2. Methods

Spatial domain methods are widely used in image restoration and can generally achieve relatively good denoising levels [37]. To enable our proposed frequency domain theoretical framework to be transplanted and applied to a large number of spatial domain denoising models, we integrate the idea of post-processing into the frequency domain theoretical framework while ensuring that the overall input and output of this framework maintain the same dimensional size, allowing information captured in the frequency domain to assist in improving the overall performance of the network.

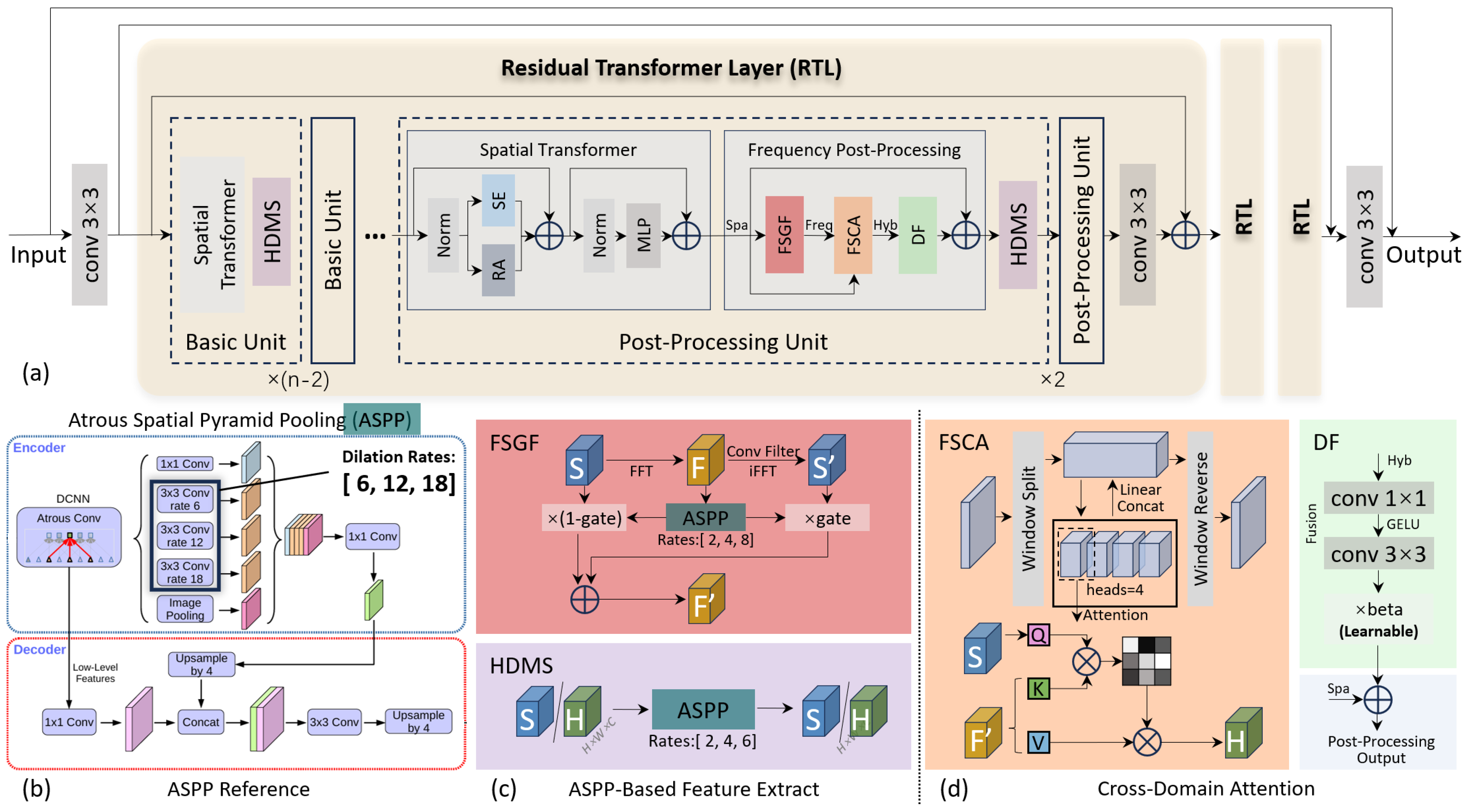
The overall framework of the proposed method is shown in Figure 1, which is based on the Spectral Enhanced Rectangle Transformer (SERT) [36]. To further reduce high-frequency signals caused by noise, this paper proposes a frequency post-processing (FPP) module based on both frequency and spatial domains, along with a learnable gating mechanism to achieve adaptive weight allocation of dual-domain features.

2.1. Review of SERT

Spectral Enhanced Rectangle Transformer (SERT) [36] employs 3 Residual Transformer Layers (RTL), each cascading 6 transformer blocks. Its core modules include (1) the Rectangular Attention (RA) module, which realizes multidirectional nonlocal interaction through horizontal and vertical rectangular window partitioning and spectral shuffling; and (2) the Spectral Enhancement (SE) module, which utilizes a global memory unit to store spectral priors and enhances spectral-spatial correlations while suppressing noise through a dynamic low-rank selection mechanism. These two modules work synergistically to effectively address the issues of multidimensional noise coupling and cross-band correlations in HSI, integrating the spatial and channel information of the image.

However, effective information in HSI is mostly concentrated in low- and medium-frequency regions, while random noise manifests itself as random fluctuations in pixel values in the spatial domain, and its energy is often widely distributed in high-frequency parts when transformed to the frequency domain. Therefore, SERT cannot effectively distinguish between stripe noise and edge textures in HSI space, leading to loss of image details after denoising.

2.2. Hybrid-Domain Synergistic Transformer Network (HDST)

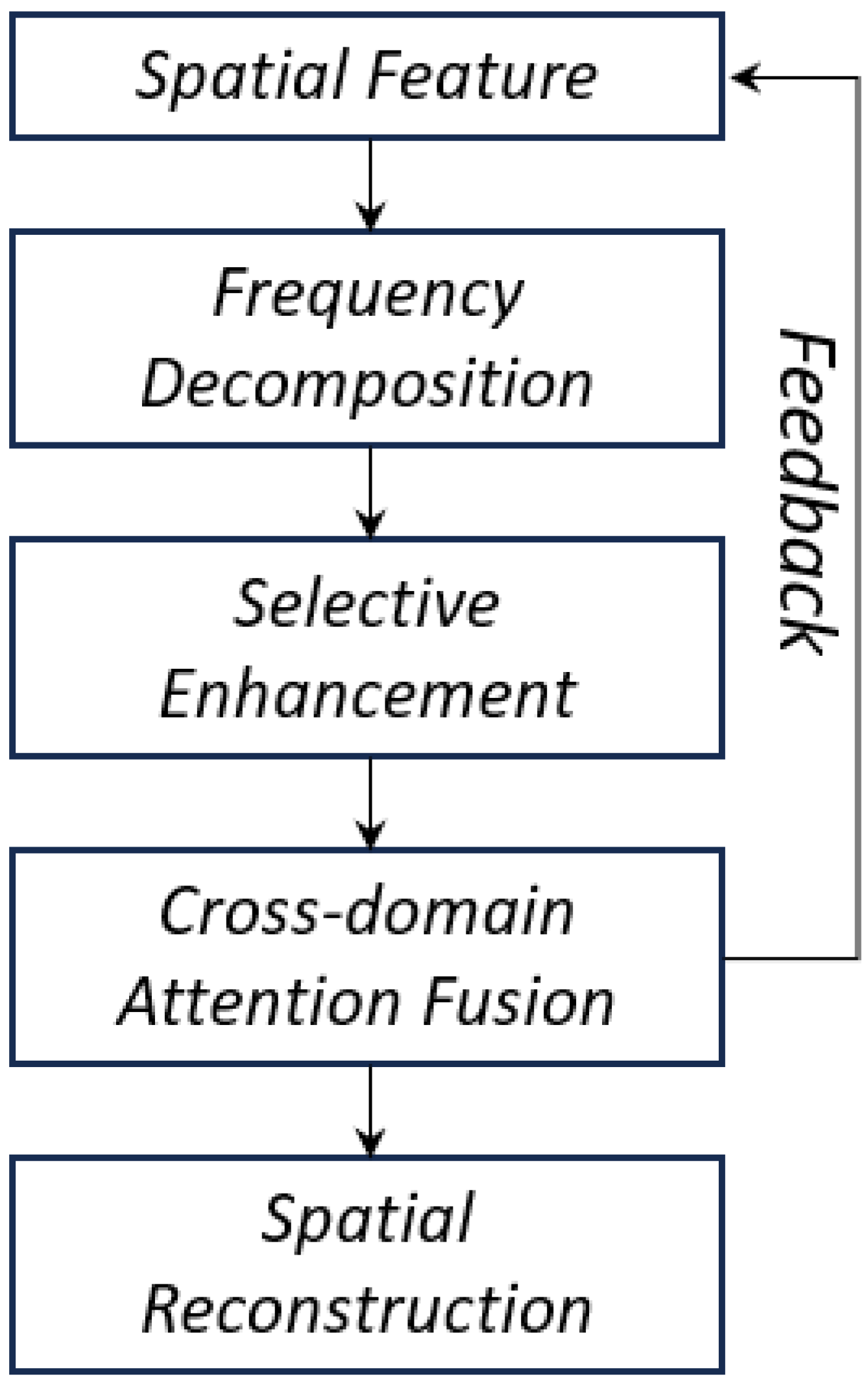
This framework takes RTL as the basic skeleton and innovatively introduces a frequency domain post-processing unit and a hybrid domain multiscale module, constructing a closed-loop optimization process of “spatial feature extraction–frequency domain noise decoupling–cross-domain information calibration”. The loop is shown in Figure 2.

Specifically, hierarchical domain adaptation is performed for the cascaded Transformer structure within RTL. Shallow Transformers capture long-range spatial dependencies and low-rank spectral characteristics through the RA and SE modules, laying the foundation for feature representation; FPP units are embedded in the deepest two layers of Transformers to decouple noise spectral components through frequency domain transformation, avoiding blurring of shallow details due to premature frequency domain processing.

Within the FPP unit, through a three-stage chain of frequency domain multiscale filtering–cross-domain feature calibration–dynamic residual fusion, frequency domain noise patterns are converted into guiding signals for spatial domain denoising. Through the frequency-spatial collaborative attention mechanism, frequency domain noise priors such as specific frequency noise patterns are fed back to spatial domain feature calibration, and then adaptive control of feature enhancement is achieved through learnable residual connections, ultimately forming a complete optimization chain of “noise decoupling–feature calibration–error compensation”.

Meanwhile, multiscale cross-enhancement is widely used to improve feature extraction capability. After each Transformer block, the HDMS module is used for multiscale sampling, covering multilevel information from edge details to global structures, providing a richer feature base for frequency domain processing; ASPP-FFT located within FSGF realizes refined separation of wide-band noise in the frequency domain through multi-dilation rate atrous convolution, effectively achieving two-dimensional multiscale analysis.

2.2.1. Atrous Spatial Pyramid Pooling (ASPP)

Atrous Spatial Pyramid Pooling (ASPP) is a module proposed in the DeepLab system [33]. It contains the following 5 parallel branches:

$$\left\{\begin{array}{cc}1\times 1\mathit{convolution}\hfill & \left(\mathit{preserve}\mathit{resolution}\right)\hfill \\ \mathit{Dilated}\mathit{conv}(\mathit{dilation}=[6,12,18\left]\right)\hfill & \left(\mathit{multiscale}\mathit{context}\right)\hfill \\ \mathit{Global}\mathit{Avg}\mathit{Pool}\stackrel{1\times 1\mathit{Conv}}{\to }\mathit{Upsample}\hfill & \left(\mathit{global}\mathit{statistics}\right)\hfill \end{array}\right..$$

(1)

The features are concatenated and fused by $1\times 1$ convolution. The structure is also shown in the ASPP Reference section of Figure 1, with dilation rates [6,12,18].

Innovatively, we adapt this spatial domain module for frequency domain processing by employing multiscale frequency domain convolutions with dilation rates [2,4,8], and we name this module ASPP-FFT. This enables the extraction of both local frequency-band correlations and cross-band global contextual information, which subsequently drives the generation of frequency-guided spatial gating signals. Since the frequency domain inherently represents global information, the redundant global statistics branch is removed to avoid disturbance.

$$\left\{\begin{array}{cc}1\times 1\mathit{convolution}\hfill & \left(\mathit{preserve}\mathit{resolution}\right)\hfill \\ \mathit{Dilated}\mathit{conv}(\mathit{dilation}=[2,4,8\left]\right)\hfill & \left(\mathit{multiscale}\mathit{context}\right)\hfill \end{array}\right..$$

(2)

2.2.2. FFT-Scale Gated Fusion (FSGF)

To achieve precise decoupling and adaptive fusion of noise in the frequency domain and spatial domain, we perform FFT on the input spatial feature S, separate the real and imaginary parts, and concatenate them into $F_c$. Multiscale feature extraction in the frequency domain is achieved through the ASPP-FFT module. This enables wide-band noise filtering in the frequency domain, forming a spatial-frequency dual-dimensional multiscale analysis. Its forward propagation can be expressed as

$$F=FFT\left(S\right),F_c=Concat(F.real,F.imag),$$

(3)

$$F_{proc}=\mathit{ASPP-FFT}(F_c,dilation=[2,4,8]),$$

(4)

where S represents the input spatial domain information, F is the frequency domain result obtained after a fast Fourier transform, and the feature $F_c$, formed by concatenating the real and imaginary parts of F, is used for multiscale ASPP-based analysis. The combination of $F_c$ fully preserves complex phase information and adapts to real-valued convolution, enabling noise frequency band separation and alignment in the domain.

Subsequently, a dynamic gating mechanism generates a spectral mask $Gate$, which adaptively selects the fusion path based on noise intensity. The hyperparameter $\alpha$ is used to control the injection intensity of the information from the frequency domain. This process is expressed by the following formulas:

$$S^{\prime }=Con{v}_{3\times 3}\left(IFFT\left(F_{proc}\right)\right),$$

(5)

$$Gate=\sigma \left(Con{v}_{1\times 1}\left(F_{proc}\right)\right),$$

(6)

$$F^{\prime }=S\odot Gate+\alpha ·S^{\prime }\odot (1-Gate),$$

(7)

where $S^{\prime }$ is the spatial feature reconstructed from the frequency domain processing result, and $3\times 3$ convolution denotes the reconstruction convolution operation; ⊙ represents element-wise multiplication; $\sigma$ represents the sigmoid activation function; Gate retains target areas ($\mathrm{Gate}\to 1$) and replaces noisy regions ($\mathrm{Gate}\to 0$).

2.2.3. Frequency-Spatial Collaborative Attention (FSCA)

To establish cross-domain correlations between frequency-domain noise priors and spatial-domain features, the frequency-domain fusion features output by FSGF and the original input features are divided into non-overlapping windows, and cross-domain associations are established through a multi-head attention mechanism: using spatial features as queries (Q) and frequency-domain features as keys (K) and values (V), realizing the interaction logic of spatial positions querying their corresponding frequency-domain noise patterns. The spatial map S and the map $F^{\prime }$ generated by combining original and reconstructed features with the mask are divided into M × M non-overlapping windows and flattened to reduce computational complexity. Then, unbiased multi-head attention calculation is performed on the flattened sequences, expressed as

$$Q=S_{flat}{W}_Q^T,K=F_{flat}{W}_K^T,V=F_{flat}{W}_V^T,$$

(8)

$$X_i=X[:,:,i{C}_h:(i+1)C_h],X\in \{Q,K,V\},$$

(9)

$$AttnHea{d}_i=Softmax\left({\displaystyle \frac{Q_i·K_i^T}{\sqrt{C_h}}}\right)·V_i,$$

(10)

$$H=Concat\left(AttnHea{d}_i\right)·W_O^T,$$

(11)

where $W_Q$, $W_K$, $W_V$, and $W_O$ are learnable weight matrices, projecting input features to query, key, value, and output spaces; $C_h$ represents the dimension of a single attention head, and the multi-head attention mechanism is implemented by dividing features by dimension; $Q_i$, $K_i$, and $V_i$ represent the query, key, and value vectors of the i-th head.

2.2.4. Dynamic Fusion

Residual calculation is performed on the calibrated feature H output by FSCA through a learnable parameter $\beta$ and a lightweight convolution fusion network, achieving dynamic fusion of “original features + frequency domain enhanced residuals”. Its forward propagation can be expressed as

$$H_{fused}=Con{v}_{3\times 3}\left(GELU\left(Con{v}_{1\times 1}\left(H\right)\right)\right),$$

(12)

$$Output=S+\beta ·H_{fused},$$

(13)

where $H_{f}used$ is the residual output enhanced by the fusion network. The $3\times 3$ convolution restores dimensions and introduces spatial context information and continuity constraints, avoiding block effects that may arise from frequency domain reconstruction; $\beta$ is a learnable fusion coefficient initialized to 0.1, ensuring stability in the early training stage and intensity of enhancement after convergence, preventing overshoot of features or loss of information.

2.2.5. Hybrid-Domain Multiscale Module (HDMS)

As a basic component throughout each RTL layer, the HDMS module performs multiscale atrous convolution with dilation rates [2,4,6] on spatial features after each Transformer block. Small dilation rates capture edge and texture details, and larger dilation rates aggregate target structures and globally associated features. Through multi-branch parallel sampling, it compensates for the deficiency of single-scale convolution in handling complex noise, providing more stable feature input for subsequent frequency domain processing and significantly enhancing feature robustness.

Shallow HDMS strengthens the noise resistance of local details, while deep HDMS provides spatial feature bases containing multiscale semantics for FPP units, enabling frequency domain noise decoupling to more accurately adapt to content structures at different levels, achieving cross-layer information paving.

3. Results

To evaluate the proposed HDST framework, experiments are conducted against model-based and deep-learning hyperspectral denoising methods. Further ablation studies and computational efficiency analyses are performed to validate the contribution of key components and the practical viability of HDST.

Today, deep learning denoising combined with the frequency domain has been involved in RGB image processing [38]. However, HSI denoising methods that integrate deep learning with frequency domain processing are relatively rare. When applying related RGB image processing methods to HSI image denoising tasks, the increase in the number of channels will lead to potential performance degradation. Therefore, the method of comparative experiments is still based on comparison with commonly used hyperspectral denoising methods.

The comparison methods include several traditional model-based hyperspectral image denoising methods, such as the filter-based method (Block-Matching 4D algorithm (BM4D [39])), the orthogonal basis-based method (Non-local Graph Matching (NGMeet [40])), and the wavelet-based method (3D wavelets [41]); also included are three deep learning-based methods, namely Hyperspectral Image Denoising Convolutional Neural Network (HSID-CNN [42]), Multi-Attention Fusion Network (MAC-Net [43]), and a relatively new spatial-spectral recurrent transformer U-Net (SSRT-UNet [44]).

The proposed model is implemented using Pytorch 2.4.1, and experiments are carried out on a server equipped with an Intel Xeon Processor CPU and a GeForce RTX 3090 GPU running Ubuntu 22.04. This server is located in Inner Mongolia, China, and was assembled by AutoDL.

We selected a widely used metric from each three perspectives: image restoration, visual perception, and spectral similarity to fully characterize the performance of the model.

• PSNR [45] (Peak Signal-to-Noise Ratio) focuses on pixel-level errors, calculating the mean square error between the original and distorted images, comparing it with the square of the maximum signal value, and expressing quality in decibels (larger values mean less distortion).

  $$\mathrm{PSNR}=10{log}_{10}\left({\displaystyle \frac{L^2}{\mathrm{MSE}}}\right),\mathrm{MSE}={\displaystyle \frac{1}{N}}\sum _{i=1}^N{(x_i-y_i)}^2.$$

  (14)
• SSIM [45] (Structural Similarity) emphasizes image structure and perceptual quality, evaluating similarity via structure, luminance, and contrast. Its evaluation results are more consistent with human visual perception. Ranging 0–1, values closer to 1 indicate higher quality.

  $$\mathrm{SSIM}(\mathbf{x},\mathbf{y})={\displaystyle \frac{(2{\mu }_x{\mu }_y+c_1)(2{\sigma }_{xy}+c_2)}{({\mu }_x^2+{\mu }_y^2+c_1)({\sigma }_x^2+{\sigma }_y^2+c_2)}}.$$

  (15)
• SAM [17] (Spectral Angle Mapping) focuses on spectral similarity, measuring it via the angle between spectral vectors; smaller angles mean more similar spectra and better quality.

  $$\mathrm{SAM}=arccos\left({\displaystyle \frac{\langle {\mathbf{x}}_{spec},{\mathbf{y}}_{spec}\rangle }{\parallel {\mathbf{x}}_{spec}{\parallel }_2·{\parallel {\mathbf{y}}_{spec}\parallel }_2}}\right).$$

  (16)

This paper introduces the L2 loss function [46] for network training. Let the noisy data be x and the corresponding ground truth be y; the loss function can be expressed as:

$$arg\underset{f_{\theta }}{min}{\parallel f_{\theta }\left(x\right)-y\parallel }_2^2.$$

(17)

3.1. Performance on Realistic Dataset

For the Realistic dataset [47], our experimental method is generally consistent with the training of the original SERT [36] network. The data set contains 59 noisy hyperspectral images and their corresponding clean, noise-free hyperspectral images. We followed the SERT division method, using the same 44 images and 15 images for training and testing. Each hyperspectral image channel contains 34 bands, ranging from 400 to 700 nm, and the image size within a single channel is 696 × 520. Overlapping 128 × 128 spatial regions are cropped, and data augmentation is performed for training [47]. Sufficient training can be achieved by setting the number of training epochs to 500. The learning rate is set to $1e-4$ for the first 200 epochs, changed to $5e-5$ at 200 epochs, and set to $1e-5$ at 400 epochs.

Table 1. Average results of different denoising methods on the Realistic dataset.

Category	Method	PSNR	SSIM	SAM	Time
-	Noisy	23.26	0.7609	17.329	-
Traditional	BM4D [39]	29.04	0.9471	3.087	11.83 m
	Wavelet [41]	28.05	0.9046	5.85	3.25 m
	NGMeet [40]	28.72	0.9511	2.735	17.88 m
Deep Learning	HSID-CNN [42]	26.44	0.8992	5.242	1.345 s
	MAC-Net [43]	29.2	0.9489	4.099	2.157 s
	SSRT-UNet [44]	30.17	0.9549	2.506	20.566 s
	SERT [36]	29.68	0.9533	2.536	0.551 s
	HDST (ours)	30.62	0.9555	2.417	0.607 s

All values are averaged over 15 test images. Higher PSNR/SSIM and lower SAM indicate better performance. Bold indicates best performance. (Based on PSNR.).

shows the average results of different methods on the Realistic dataset. Our proposed HDST method significantly outperforms SERT [36] as the baseline and several other hyperspectral image denoising methods, with a maximum PSNR improvement of 0.94 dB, indicating the effectiveness of our method in handling real noise. In terms of inference time, the average processing time of our proposed HDST method on the Realistic dataset is only 0.607 s, demonstrating excellent computational efficiency. This time is significantly superior to that of traditional methods and also competitive among deep learning methods, being faster than MAC-Net and SSRT-UNet. Although the inference time of HDST is slightly longer than that of its baseline SERT by 0.056 seconds, this minimal cost is exchanged for a significant improvement in image quality. This reflects the good balance achieved by the model between performance and efficiency and inherits the lightweight architectural design of SERT.

We also show the denoising results of the above real noisy hyperspectral images in Figure 3. In terms of noise removal and detail preservation, the results of our improved method are superior to traditional denoising methods and deep learning methods. Note that the noisy images in these datasets generally feature lower brightness than the GroundTruth images. Therefore, during the model training process, to reduce L2 loss, the algorithm may appropriately increase the saturation of the reconstructed images to make them closer to the GroundTruth. In addition, since all HSI images used in these datasets are in 16-bit format, their high numerical values appear as white, barely distinguishable to the naked eye on a grayscale display, and this exceeds the color rendering capability of most monitors. Thus, the white areas in the visualization results do not indicate local overexposure or reconstruction failure.

3.2. Performance on ICVL Synthetic Dataset

For the ICVL synthetic dataset [48,49], which contains 201 HSIs with a size of 1392 × 1300, each hyperspectral image channel contains 31 bands, ranging from 400 to 700 nm. We followed the SERT [36] division method, using the same 100 images, 5 images, and 50 images for training, validation, and testing. Training images are cropped to a size of 64 × 64 at different ratios. In the testing phase, HSI is cropped to 512 × 512 × 31 to obtain affordable computational costs. The number of training epochs is set at 100, with the learning rate set to $1e-4$ for the first 50 epochs and changed to $1e-5$ for the last 50 epochs.

The noise setting method partially follows the baseline settings, using the noise patterns in the literature [48] for simulation. The noise patterns are independently and identically distributed Gaussian noise with random settings between levels 10 and 70, non-independently and identically distributed Gaussian noise (non-i.i.d Gaussian noise), Gaussian + Stripe noise, Gaussian + Deadline noise, Gaussian + Impulse noise, and Mixture noise, which contains stripe, deadline, and impulse noise.

Table 2. Average results of different denoising methods on various noise types in the synthetic dataset.

Method	Gaussian+Mixture			Gaussian+Deadline			Gaussian+Impulse
	PSNR	SSIM	SAM	PSNR	SSIM	SAM	PSNR	SSIM	SAM
Noisy	13.91	0.3396	51.53	17.5	0.4770	47.55	14.93	0.3758	46.98
BM4D	28.01	0.8419	23.59	33.77	0.9615	6.85	29.79	0.8613	21.59
Wavelet	26.09	0.7945	32.83	32.57	0.9476	8.87	28.87	0.8856	17.59
NGMeet	26.13	0.7796	31.89	33.41	0.9665	6.55	27.02	0.7884	31.20
HSID-CNN	35.30	0.9588	6.29	38.33	0.9783	3.99	36.21	0.9663	5.48
MAC-Net	30.59	0.9300	14.51	36.68	0.9860	5.63	34.54	0.9553	10.20
SSRT-UNet	40.17	0.9902	2.96	44.01	0.9960	1.66	42.59	0.9932	2.17
SERT	40.00	0.9937	2.84	43.66	0.9969	1.99	42.67	0.9959	2.30
HDST (ours)	40.52	0.9947	2.51	43.81	0.9966	1.83	42.89	0.9963	1.96
Method	Gaussian+Stripe			Non-i.i.d Gaussian			Gaussian 10–70
	PSNR	SSIM	SAM	PSNR	SSIM	SAM	PSNR	SSIM	SAM
Noisy	17.51	0.4867	46.98	18.29	0.5116	46.2	17.24	0.4782	41.94
BM4D	35.63	0.9730	6.26	36.18	0.9767	5.78	36.62	0.9770	5.51
Wavelet	34.17	0.9648	6.73	34.29	0.9658	6.62	36.51	0.9874	3.52
NGMeet	34.88	0.9665	5.42	34.90	0.9745	5.37	41.67	0.9937	2.19
HSID-CNN	38.09	0.9765	4.59	39.28	0.9819	3.80	39.04	0.9776	3.71
MAC-Net	39.03	0.9910	4.03	39.98	0.9662	4.55	41.31	0.9941	2.52
SSRT-UNet	43.75	0.9953	1.79	44.05	0.9962	1.69	43.27	0.9947	1.89
SERT	43.68	0.9969	1.97	44.20	0.9971	1.69	42.82	0.9957	1.88
HDST (ours)	43.88	0.9963	1.76	44.37	0.9970	1.62	43.01	0.9967	1.83

All values are averaged over 50 test images. Bold text (except for the headers in the two columns at the top and middle of the table) indicates the best performance. Underlined indicates worst performance. (All based on PSNR.).

presents the comparison results. The proposed HDST method also outperforms SERT [36] as the baseline among the noise methods selected. In the case of small amounts of structured noise, some of the latest comparative methods perform excellently, even surpassing our proposed model; however, HDST demonstrates significant comprehensive advantages in mixed noise scenarios, enabling it to better adapt to denoising complex noise patterns such as those in real-world scenes.

Figure 4 presents the visualized comparison results. Our improved method has achieved relatively ideal visual effects, outperforming denoising methods with fewer noise points in some areas.

3.3. Ablation Study and Analysis

3.3.1. Module Interaction Analysis

To verify the theoretical analysis and understand the actual role of modules, in addition to the baseline and the proposed model, we additionally set up four groups of comparative models for experiments. Comparative Network 1 only adds frequency domain processing (FSGF + FSCA) to test the independent role of the frequency domain module. Comparative Network 2 adds dynamic fusion based on Network 1 to test the tuning ability of residual gating. Comparative Network 3 only adds multiscale pyramids (HDMS) to test the collaboration between multiscale and frequency domain ASPP. Comparative Network 4 includes frequency domain processing (without dynamic fusion) + multiscale pyramids (ASPP-FFT and HDMS) to analyze the bottleneck of cross-domain feature fusion and assist in verifying the collaborative role of modules. The performance results of each comparative network on the Realistic dataset and its corresponding training environment are shown in

Table 3. Ablation study on the Realistic dataset.

Model	Frequency	Residual	ASPP	PSNR	SSIM	SAM	Para
Baseline [36]				29.68	0.9533	2.536	1.91M
Net1	✓			29.73	0.9529	2.528	2.25M
Net2	✓	✓		29.89	0.9541	2.508	2.53M
Net3			✓	30.27	0.9539	2.475	2.46M
Net4	✓		✓	30.46	0.9550	2.433	2.80M
HDST	✓	✓	✓	30.62	0.9555	2.417	3.08M

✓ indicates the component is included. Frequency: frequency post-processing module. Residual: dynamic fusion. ASPP/HDMS: ASPP-FFT & Hybrid-Domain multiscale module.

.

The experimental results of Net1 and Net2 show that the processing of the independent frequency domain module may destroy spatial continuity, leading to a slight increase in parameters such as PSNR; while under the correction of the dynamic fusion module, the frequency domain module can achieve effective improvement; the experimental results of Net3 show that the pure multiscale module brings a large single-module gain, verifying that multiscale modeling is a key pillar for performance improvement; the experimental results of Net4 show that the combination of frequency domain and multiscale methods achieves great improvement, proving that multiscale feature extraction provides a frequency spectrum decomposition basis with clear physical meaning for frequency domain processing.

The incremental growth in parameters of the entire ablation network (from Net1 to Net4) also confirms that frequency domain processing (0.34 M), dynamic fusion (0.28 M), and ASPP (0.55 M) contribute to the parameter count in a relatively balanced manner. This benefit stems from the low-parameter design approach adopted for each module, which effectively controls the complexity of every individual module.

Both theoretical analysis and the above experiments show that multiscale methods can effectively collaborate with frequency domain methods, and the design of each module in the improved model is reasonable.

3.3.2. Multiscale Dilation Rate Comparison

To investigate the differences in the impact of dilation rate configurations in the multiscale module on spatial domain and frequency domain processing, we designed six groups of comparative experiments with different dilation rates for HDMS and FSGF, respectively. Specifically, we tested classic spatial pyramid configurations such as [2,4,6], [4,8,12], and [6,12,18], as well as unconventional configurations such as [1,3,5] and [2,4,8]. Meanwhile, an extremely large dilation rate [16,32,32] was established as a boundary condition. In all experiments, the parameters of other modules were kept consistent on Realistic dataset. As shown in

Table 4. ASPP dilation rate comparison on the Realistic dataset.

ASPP Rates	[6,12,18]	[1,3,5]	[2,4,6]	[2,4,8]	[4,8,12]	[16,32,32]
HDMS	−0.17	−0.09	(30.62)	−0.04	−0.11	−0.2
FSGF	−0.13	−0.07	−0.02	(30.62)	−0.05	−0.27

The values in the table represent the differences between the PSNR at the current rate and the PSNR at the optimal rate (marked as (30.62)).

, we recorded the deviation values of each configuration relative to the optimal PSNR. This presentation method intuitively reflects the sensitivity of different scale combinations to the two heterogeneous modules, providing data support for subsequent domain-specific optimization strategies.

As can be seen from the data in Table 4, HDMS and FSGF exhibit differences in their sensitivity to dilation rates. For HDMS, its optimal dilation rate configuration is [2,4,6], with a PSNR difference of 0.04 dB compared to the suboptimal configuration [2,4,8]. This slight gap indicates that spatial domain modeling needs to align closely with local structural features. Specifically, when using small dilation rates [1,3,5], the PSNR decreases by 0.09 dB due to insufficient receptive fields; while excessively large dilation rates [16,32,32] disrupt local continuity, leading to a 0.2 dB reduction in PSNR.

In contrast, the optimal dilation rate configuration for FSGF is [2,4,8], suggesting that the frequency domain module requires a relatively wider receptive field to achieve effective separation of broadband noise. When dilation rates reach [16,32,32], the loss of high-frequency details caused by over-smoothing also verifies the global characteristics of the frequency domain module.

The technical reason for this difference lies in the fact that ASPP-FFT in the frequency domain needs to balance frequency resolution, where small dilation rates are advantageous, and noise separation capability, where large dilation rates are more beneficial. However, HDMS emphasizes texture preservation, dominated by small dilation rates. This phenomenon echoes the design innovation of “domain-specific multiscale design”, confirming the rationality and effectiveness of differentiated designs tailored to the characteristics of different domains.

3.4. Model Computational Efficiency Analysis

3.4.1. Complexity-Parameter Trade-Off

We conducted statistics on the number of parameters and the operation speed on the Realistic dataset and its corresponding training environment, and the statistical results are shown in

Table 5. Model complexity analysis on the Realistic dataset.

Metric	Baseline [36]	HDST	$\mathbf{\Delta }$(%)
GFLOPS	4086.2	4686.8	+14.7
Params (M)	1.91	3.08	+61.2
Inference Time (ms)	551	607	+10.1

Tested on GeForce RTX 3090 GPU.

. During the upgrade of the baseline structure, we observed that the number of parameters increased from 1.91 M to 3.08 M, an increase of 61%, while the amount of computation (GFLOPS) increased only approximately 14%.

The core reason is that the newly added modules adopt a parameter-intensive but computationally efficient design strategy, achieving decoupling of the two. The multiscale method uses multi-branch 1 × 1 convolution to build a spatial pyramid, whose parameters are concentrated in the channel projection layer, but the amount of computation is compressed through depth-wise separable convolution; the frequency domain processing module introduces fully connected layer parameters through real and imaginary part separation and dynamic gating but controls the computational increment using the zero-parameter characteristics of the FFT transform and dimensionality reduction strategy. Finally, the cross-domain attention mechanism limits the attention range through window partitioning.

The asymmetric growth of parameters and computation reflects the idea of “trading parameters for efficiency”, i.e., enhancing the model’s expressive ability by adding lightweight parameter modules and suppressing computational overhead through optimization, improving model capacity while maintaining computational efficiency.

3.4.2. Cross-Model Parameter-Performance Comparison

To demonstrate the advantages of the HDST model in balancing parameter efficiency and performance, we selected three of the most representative models for comparative analysis: the lightweight convolutional network MAC-Net [43], the Transformer-based SSRT-UNet [44], and the Transformer model SERT [36]. We statistically analyzed the parameter counts and performance metrics of the above models, compiled the data into

Table 6. PSNR and parameter count comparison.

Metric	MAC-Net [43]	SSRT-UNet [44]	SERT [36]	HDST
PSNR (dB)	29.2	30.17	29.68	30.62
Params (M)	0.43	10.2	1.91	3.08

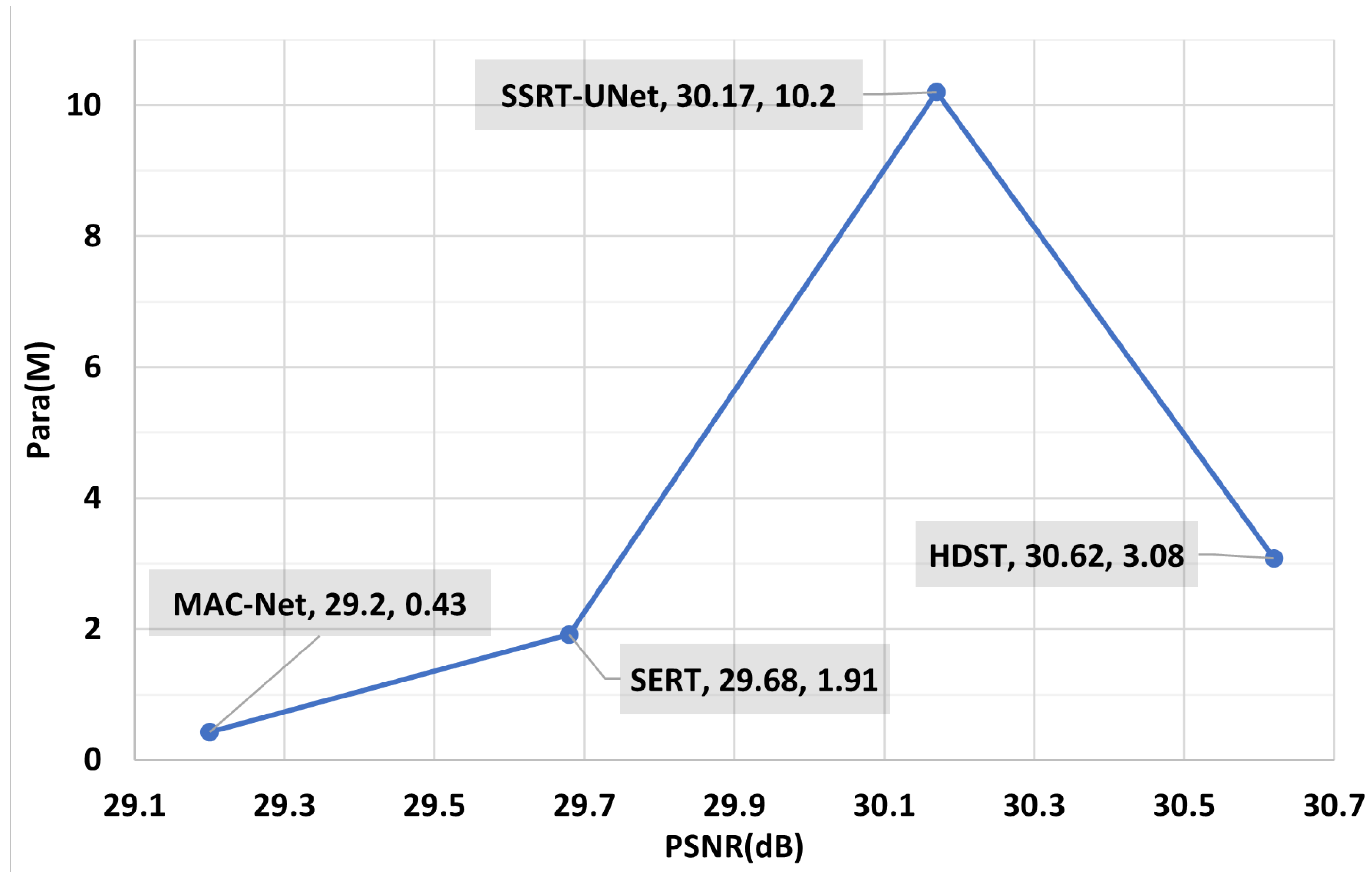
Tested on the Realistic dataset.

, and plotted them in the model complexity-performance relationship graph in Figure 5.

In terms of efficiency advantages, as demonstrated in Table 6 and Figure 5, HDST achieves a notable PSNR with a relatively small number of parameters, demonstrating remarkable superiority over existing models. Compared to the lightweight MAC-Net [43], which with 0.43 M parameters attains a PSNR of 29.2 dB, HDST delivers a significant performance gain of 1.42 dB, clearly proving the effective conversion of its increased parameters into tangible performance improvements. Compared with the more parameter-heavy SSRT-UNet [44], HDST also achieves a better restoration quality while using $30\%$ of SSRT-UNet’s parameter count.

Figure 5 uses a scatter plot to compare the parameter counts and denoising performance (PSNR) of different models, clearly showing that HDST has achieved an optimal balance in terms of parameter efficiency (Pareto optimum), i.e., it obtains leading performance with relatively low model complexity.

This advantage is an intuitive confirmation of the complexity analysis in Section 3.4.1 and is fundamentally derived from the inherent efficiency of the hybrid-domain collaborative design paradigm proposed in this paper. The FPP module leverages the parameter-free nature of FFT/IFFT to achieve powerful noise decoupling capabilities, and subsequent lightweight dynamic gating and convolutional layers further bring significant performance gains. HDMS and ASPP-FFT adopt parameter-efficient depthwise separable convolutions and a multi-branch design, which greatly enrich the feature expression capability while moderately controlling the total number of parameters. In addition, FSCA constrains computational complexity by window partition. This collaborative design strategy of “parameter dense yet computationally efficient” collectively enables HDST to achieve a disproportionately large improvement in PSNR with a $61\%$ increase in parameter count, thus occupying the advantageous position at the lower right of Figure 5.

Hyperspectral imaging often relies on platforms with limited on-device computing resources, such as satellites and unmanned aerial vehicles (UAVs). The framework, characterized by high performance, a moderate number of parameters, and high inference efficiency, exhibits excellent potential for practical application and engineering deployment. Through port-based packaging and model pre-training, this model can be applied to numerous scenarios, including remote sensing-based precision agriculture, medical image enhancement, and industrial vision. For embedded or real-time systems with constrained computing resources, such as satellite and airborne platforms, model pruning and quantization can be employed to further reduce their memory and computational overhead, thereby meeting the stringent requirements of practical applications.

4. Discussion

Analysis of experimental results across different datasets reveals that the performance improvement of the HDST model on the Realistic dataset (real-world data) is significantly superior to that on the ICVL synthetic dataset. This discrepancy underscores a profound connection between the frequency-domain processing mechanism and the physical characteristics of noise. From the perspective of hyperspectral imaging physics, real HSI noise exhibits typical spatial non-uniformity and frequency-domain energy aggregation, which precisely align with the core innovation of HDST: multiscale spatial-frequency collaboration. This alignment between physical properties and algorithmic design amplifies the model’s advantages in real-world scenarios.

Further analysis indicates that the excellent performance in complex noise scenarios stems from the cascaded enhancement effect of multiscale spatial-frequency features. Specifically, the shallow HDMS module employs a combination of small dilation rates [2,4,6], simulating the local perception mechanism of the human visual system to preserve critical edge information for subsequent processing. In contrast, the deep FSGF captures global frequency-domain patterns through larger dilation rates. Their synergistic operation enhances image restoration performance. This closed-loop optimization process, "spatial detail guidance-frequency domain noise decoupling”, maintains texture continuity when handling complex scenes with mixed stripe and impulse noise, validating the necessity of cross-domain modeling.

In particular, the limited performance improvement on synthetic data exposes the limitations of existing simulation methods. The uniform noise distribution in synthetic data creates a performance bottleneck, suggesting that future research should focus more on realistic modeling of noise physical models rather than solely relying on the generalization ability of synthetic data. Although the sample size of the Realistic dataset is relatively small, which may raise concerns about statistical robustness, the HDST model still maintains certain advantages compared with all the methods included in the comparison. In addition, the baseline improvement achieved by HDST under complex noise conditions in the synthetic dataset is superior to that under other noise conditions. This indirectly demonstrates the performance of HDST in handling real-world noise, which echoes the results obtained from the real-world dataset. In the future, we will seek more public real-world hyperspectral image denoising datasets and evaluate HDST on these datasets to comprehensively verify the robustness and generalization of the model under different imaging conditions and noise distributions.

From an engineering application perspective, HDST demonstrates a favorable balance of computation performance. Despite a 61% increase in parameters, the inference latency increases only by 10.1% due to low-computation design strategies, making it well suited for scenarios requiring both speed and high accuracy. If further validated, the dimension-preserving post-processing model proposed herein may be widely transplanted to various image denoising frameworks.

The limitations of this work and future improvement directions merit discussion: First, the gate generation mechanism should be further optimized to capture frequency-domain characteristics. Second, since frequency band analysis still relies on preset dilation rates, developing adaptive spectral perception modules is necessary. Finally, efforts should be made to further encapsulate the model and attempt its transplantation to more existing methods to enhance its universality. These challenges provide clear technical pathways for future research.

In summary, the success of HDST essentially stems from the precise matching between physical properties and algorithmic design. This establishes an important design paradigm for frequency-domain enhanced denoising models: under the premise of maintaining computational efficiency, achieve collaborative optimization of noise frequency-domain attributes and network architecture through mechanisms such as multiscale perception, cross-domain attention, and dynamic gating. This approach can be extended to other imaging modalities, offering new methodological references for various fields.

5. Conclusions

Hyperspectral image denoising needs to simultaneously address spatially non-uniform noise and spectral correlation interference. Traditional methods ignore the inherent multidimensional noise coupling and cross-band correlations of HSI images, leading to the limitation of single-domain processing being unable to balance detail preservation and noise suppression. This framework takes residual Transformer layers as the basic skeleton and constructs a closed-loop optimization process of “spatial feature extraction–frequency domain noise decoupling–cross-domain information calibration” through cross-layer collaboration between frequency domain post-processing units and hybrid domain multiscale modules. This work demonstrates that hybrid domain learning is not merely algorithmic fusion but creates emergent properties: the closed-loop spatial-frequency interaction enables noise component transferability that single-domain methods cannot achieve. A large number of experimental results also prove the effectiveness of the proposed method.

This framework is particularly suitable for denoising images with complex noise in real-world environments. In most cases, it can achieve state-of-the-art quality in the field and enables inference with a moderate number of parameters and high inference speed, endowing it with excellent potential for engineering deployment in tasks such as agricultural remote sensing, medical image enhancement, archaeological document restoration, and industrial non-destructive testing. Optimization strategies like model pruning and quantization can meet the requirements of resource-constrained platforms, while further porting and model pre-training can enhance the model’s usability. Future research will focus on testing the generalization ability of the modules and the model to promote the application of this method in a wider range of scenarios.