Quantitative Talent Identification Reimagined: Sequential Testing Reduces Decision Uncertainty

Abstract

Background/Objectives: Quantitative approaches to talent identification in youth soccer often rely on either closed-skill assessments or small-sided games, but each carries inherent uncertainties that can reduce selection accuracy. Effective talent selection requires integrating both sources of data while accounting for their limitations. This study aimed to develop and validate a framework that combines closed-skill tests with competitive 1v1 game outcomes to optimize early-stage player selection. Methods: We assessed the dribbling and sprinting performances of 30 Brazilian youth players and used 1308 individual 1v1 bouts (70–90 bouts/individual) to estimate competitive abilities using a Bayesian ordinal regression model. Based on our empirical results, we then ran simulations to determine how many players should be selected when the aim is to reduce a player pool of 100 individuals so that the ‘true’ top 10 performers are reliably included and to determine how the weighting between data from closed-skill tests and games should change with increasing match observations. Results: Dribbling speed was a strong predictor of 1v1 success (β = –0.76, 95% CI: [–1.16, –0.40]), while sprint speed (β = 0.01, 95% CI: [–0.36, 0.40]) showed no significant association with 1v1 success. Simulations revealed that 26.0 ± 2.5 players were needed after five 1v1 contests per player to capture the true top 10% and then decreased to 18.0 ± 1.5 players after 20 contests. Optimal weighting shifted from a greater reliance on dribbling-based data (α > 0.80 at Game 0) to more match-based data after 10–20 contests per player (α = 0.16 at Game 20), but utilizing both sources of data improved selection accuracies and efficiencies. Conclusions: This study provides an uncertainty-aware protocol for talent identification that optimizes the integration of data from closed-skill tests and in-game performances within a dynamic selection framework that enhances precision and forms the basis for efficient early-stage scouting of large cohorts of players.

1. Introduction

Many existing quantitative methodologies in youth soccer focus on closed-skill tests—controlled assessments of individual motor skills isolated from real-game scenarios [1,2,3,4]. Closed-skill tests considered useful are those that can discriminate between players at different representative levels or are predictive of match success [5,6,7,8]. However, assessments of closed skills are frequently criticized as tools in talent identification because tests are performed without the dynamic environmental complexities of real matches and typically explain only a modest proportion of variance in complex, game-realistic performances [2,3,4,9,10,11]. Yet, these criticisms should not preclude the use of closed-skill tests in talent identification when utilized appropriately. Even tests with limited predictive power can be valuable if the magnitude of the uncertainty is understood and integrated [12,13]. While assessments from competitive games or small-sided matches may better capture player abilities under the more dynamic conditions associated with matches, they introduce their own challenges. Quantifying individual performances within games is complicated by the influence of teammates and opponents [14], and large, randomized tournaments are required to reliably estimate ability within cohorts of players under game-realistic settings [14]. Moreover, even under ideal conditions, performance metrics from games are still estimates of true ability and can be logistically complex to obtain [15,16]. An effective talent identification protocol using data should therefore aim to: (i) leverage closed-skill assessments to reduce evaluation time without introducing excessive selection errors, and (ii) minimize the number of logistically complex competitive games required, while maintaining acceptable estimation accuracy [10,17].

This study aimed to develop a framework that integrates assessments of closed skills and competitive ability in small-sided games, while explicitly accounting for the uncertainties inherent in measuring and selecting based on these traits. We focus on a simplified subset of soccer—1v1 contests—as a model system for developing and testing this approach. Our goal was to design a method for optimally selecting players for their ability in 1v1 soccer contests that is based on using data to reduce the pool of players efficiently and accurately to a more manageable number suitable for further observations by trained scouts. Demonstrating the utility of this framework in the controlled, simplified context of 1v1 contests may support its future application to the more complex 11v11 games. The 1v1 contests in soccer are complex, multi-faceted games that rely on the perceptual, cognitive, and motor skills of both individuals [18,19], and are important to success in elite competitions [20]. When attacking with the ball, players may succeed through tight ball control and rapid changes in direction in confined spaces, or through a combination of close control and sprinting in more open areas. One established closed-skill test that is predictive of success in these contests is dribbling speed along paths of known distance and curvature [18,19]. Such metrics are reliable, repeatable, and predictive of 1v1 attacking success [18], goal-scoring in training games [21], defensive success in 1v1 contests [19], and overall performance in 3v3 small-sided games [22]. However, like other tests of closed-skills, there is substantial unexplained variance in 1v1 competitive ability, indicating that relying on dribbling metrics alone to predict success would introduce considerable estimation error during player selection. Directly measuring competitive ability through paired 1v1 contests offers a more direct approach but presents logistical challenges and may still retain high variance in estimates of ability, especially when only a small number of games are observed. In addition, it is impractical to run all possible paired matchups among a large group of players, and even extensive tournaments can only estimate competitive ability with uncertainty. However, utilizing both sets of data with the awareness of the inherent uncertainties for each can still support efficient early-stage scouting for large cohorts of players.

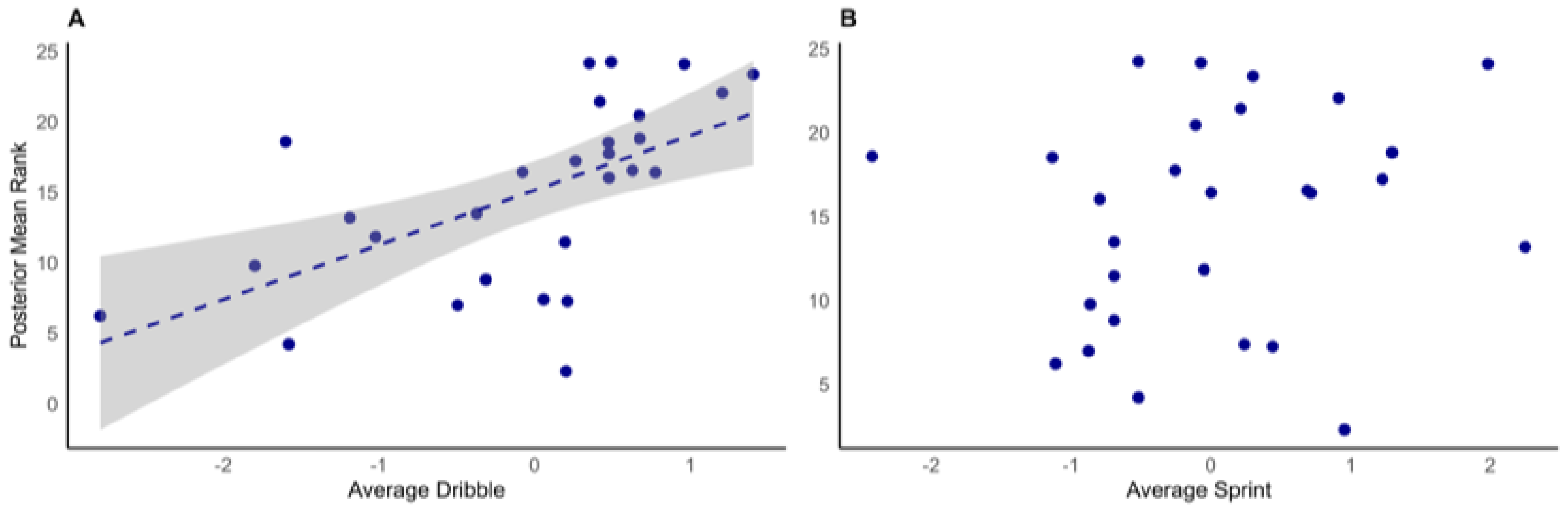
In this study, we quantified the uncertainties around estimating player ability from closed-skill tests and game data in the specific context of 1v1 contests. We assessed dribbling and sprinting performances in 30 youth players from a Brazilian soccer academy and examined how these closed-skill tests related to individual competitive ability in 1v1 games. In addition, we estimated each player’s competitive ability using a tournament structure of randomly paired 1v1 contests, with player rankings derived from the Bradley-Terry-Davidson model that accounts for draws and varying margins of victory [23]. Based on previous research, we predicted that dribbling performance would be significantly associated with the probability of winning 1v1 contests. Building on these empirical results, we then conducted simulations to estimate how many players should be selected to ensure, with 95% confidence, that the top 10% of performers are captured. The philosophy of our design is to use closed-skill tests in combination with games to rapidly and efficiently reduce the number of players needed to be considered further by scouts or coaches for ultimate selection. We used simulations because they allow us to estimate, under realistic conditions of uncertainty, how different selection strategies are likely to affect the likelihood of selecting the top 10% of players, thereby providing practical guidance for optimizing scouting and talent identification. Our simulations addressed two key questions: (i) how does the number of 1v1 games played per individual affect the number of players that must be selected to ensure the inclusion of the top 10%?, and (ii) given that dribbling speed offers a priori information about actual competitive ability (with uncertainty), what is the optimal weighting between closed-skill (dribbling) performance and in-game performance when cutting down the player pool? We predicted that when fewer games are played, greater reliance should be placed on dribbling speed, whereas as more in-game data becomes available, selection should increasingly favor in-game performance metrics.

2. Methods

2.1. Overall Study Design

We first assessed players’ dribbling and sprinting abilities along a curved track, then estimated their competitive ability through a series of 1v1 contests analyzed with a Bayesian ordinal regression model. Building on these empirical data, we conducted simulations to determine how many players must be selected—and how to optimally weight closed-skill versus in-game performance data—to ensure, with 95% confidence, that the top 10% of players are included. This sequential approach integrates controlled testing with competitive outcomes to guide efficient and accurate early-stage selection.

2.2. Study Participants

This study involved 30 junior football players from an elite Brazilian football academy that competes in state-level tournaments. Written consent was obtained from guardians in compliance with the ethical standards of the University of Queensland (Australia) and the University of São Paulo, Ribeirão Preto campus (Brazil). Players’ ages were recorded on the first day of testing, with an average of 12.67 ± 0.27 years (Range 12.15–13.11 years). All eligible U13 players from the academy participated in three two-hour testing sessions. Before assessments, players completed their standard 15 min warm-up under coach supervision. For the technical assessments, players were split into groups of four and rotated through stations in a fixed sequence: dribbling and then sprinting. Sessions 1 and 2 were dedicated to technical skill testing for all players, while the 1v1 competition took place in Session 3.

2.3. Dribbling and Sprinting Performance

Dribbling and sprinting performances were evaluated on a 30 m curved track based on that described in Wilson et al. [18]. The track was a 1 m wide channel bordered by black and yellow plastic chains (Kateli, Brazil) and included a mix of 15 directional changes: four 45° turns, four 90° turns, two 135° turns, and five 180° turns. The total curvature of the path was 1.03 radians·m⁻¹. Timing gates (Rox Pro laser system, A-Champs Inc., Barcelona, Spain) placed at the path’s entrance and exit recorded performance time. Players began each trial with their front foot placed 0.1 m before the starting gate and either sprinted without a ball or dribbled a size 5 ball through the course. During sprint trials, athletes had to keep both feet within the marked path while for dribbling only the ball was required to remain within bounds and the players’ feet could extend beyond the chains. If a player cut corners, the trial was stopped and repeated after a minimum 30 s rest. Average speed was calculated by dividing the track distance (30 m) by the time taken. Each player completed three dribbling and two sprinting trials per path. For each path, dribbling and sprinting performance was quantified using the mean speed from their respective trials, resulting in one score for each metric.

2.4. 1v1 Contests

To replicate game-relevant scenarios, players participated in 1v1 attacker-versus-defender bouts. Matches took place on a 20 m × 13 m pitch with a designated scoring zone (3 m × 13 m) at one end. Each player faced 10–15 different opponents across 1v1 matchups, completing 6 bouts per matchup (3 as attacker, 3 as defender) (N = 1308 bouts). Bouts started with the attacker at one end of the pitch and the defender at the edge of the scoring zone who passed the ball to the attacker. The defender’s objective was to stop the attacker from entering the scoring zone while dribbling. Each bout ended when: (i) the ball exited the field or scoring zone (defensive success, attacker failure), (ii) the attacker reached the scoring zone and touched the ball within the zone (defensive failure, attacker success), or (iii) 15 s passed without a score (defensive success, attacker failure). The competition used a round-robin tournament format. Players were first randomized into five groups of 5–6 and played all others in their group. This process was repeated in two additional rounds, with new randomized groupings. Between bouts, players rested for 3–10 min while awaiting their next matchup.

2.5. Simulating Player Performance and Determining Selection Size

We conducted a simulation to estimate the minimum number of players that would need to be selected to ensure inclusion of the top 10 ‘true’ performers, based on progressively accumulating more match data. First, we generated a population of 100 players per replicate, assigning each a latent “true ability” drawn from a normal distribution (mean = 0, standard deviation = 1). Across 20 independent replicates, we simulated competitive outcomes by randomly pairing players (a round of games) and repeating this process across 50 rounds of matches per replicate. In each match, the outcome was determined by the difference in true abilities between paired players, rounded to the nearest integer to reflect realistic score variability, as per Wilson et al. 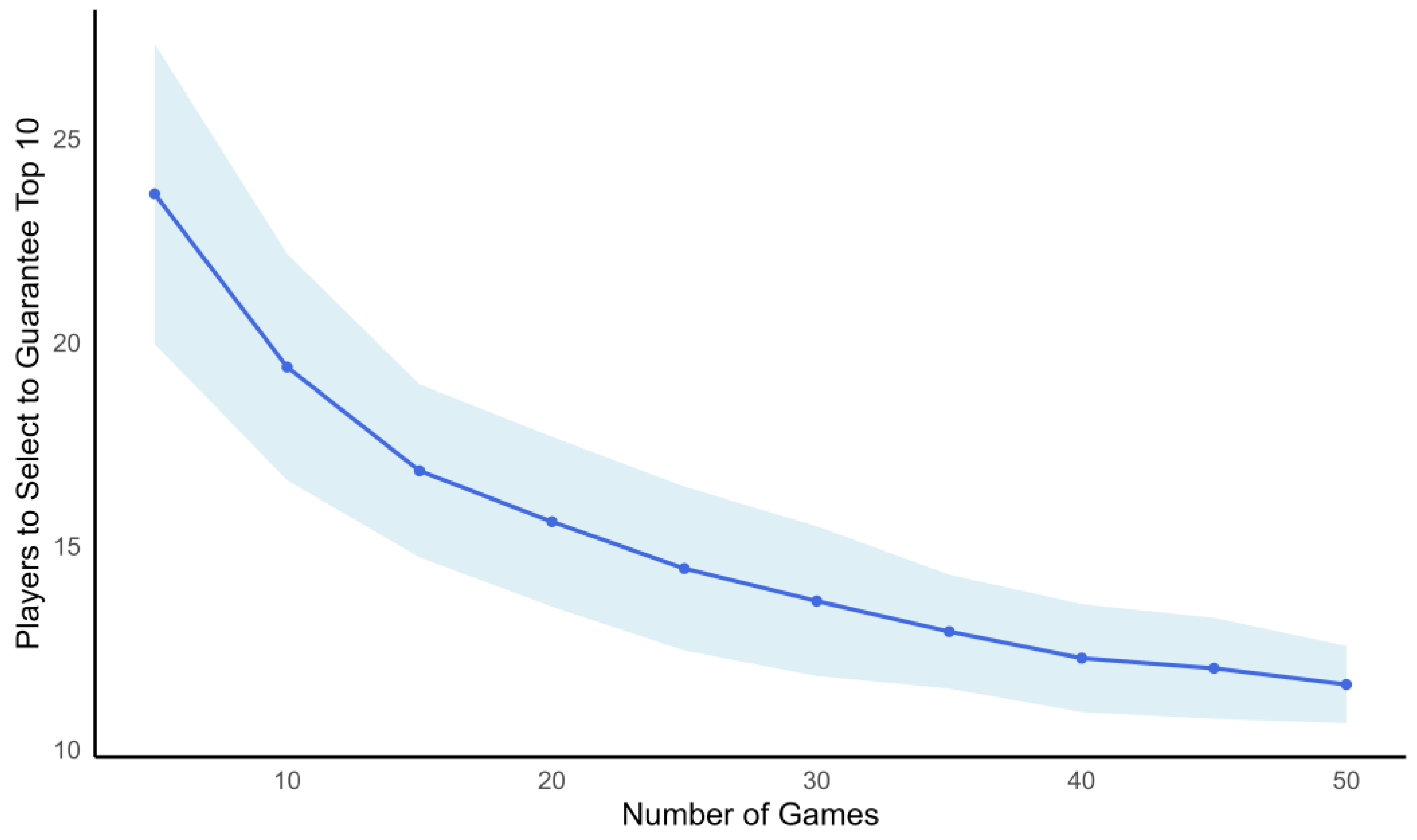[14]. For each match, players were awarded points based on the rounded score difference: If Player A’s ability exceeded Player B’s, Player A received a positive score equivalent to the rounded difference, and Player B received zero. Conversely, if Player B had the higher ability, they were awarded the positive value of the rounded score difference, and Player A received zero. Scores were accumulated across rounds. At every fifth round (i.e., after 5, 10, 15, …, 50 rounds), cumulative scores were used to generate a ranking of players using the Bayesian cumulative ordinal regression model (see below). We then determined, at each round cutoff, the minimum number of top-ranked players that would need to be selected to ensure the inclusion of all true top 10 performers (defined based on the original latent abilities). For each round cutoff, we progressively increased the number of players selected (starting from 10) until all true top 10 players were included in the selected set. If no selection could guarantee complete capture, all players (n = 100) were considered required. Across 20 replicates, we calculated the average number of players required at each game cutoff point (5 to 50 rounds). We summarized the results by plotting the mean number of players needed against the number of games played, with 95% confidence intervals based on the standard error of the mean.

2.6. Simulating Optimal Selection When Using Both Game Data and Dribbling Speed

We conducted a simulation to determine the optimal weighting of closed skills (e.g., dribbling speed) versus observed game performance when ranking players for selection. This simulation experiment was based on a complete population of 100 simulated players and measured how the number of games played influenced the efficiency of selecting the top-performing individuals. As above, we generated a population of 100 players per replicate, assigning each a latent “true ability” drawn from a normal distribution (mean = 0, standard deviation = 1). Dribbling ability was simulated as a linear function of latent ability with added Gaussian noise to reflect measurement variability (SD = 0.7), with the function taken from that determined using the empirical results from the 30 players. This yielded a moderate correlation between dribbling ability and 1v1 ability, consistent with previous studies [14]. Players competed in a series of paired games, with pairings randomly assigned each round. Match outcomes were determined by comparing the players’ latent abilities with added noise, as calculated above. Performance scores were averaged for each player over the range of rounds from 0 to 50.

2.7. Hybrid Score and Alpha Weighting

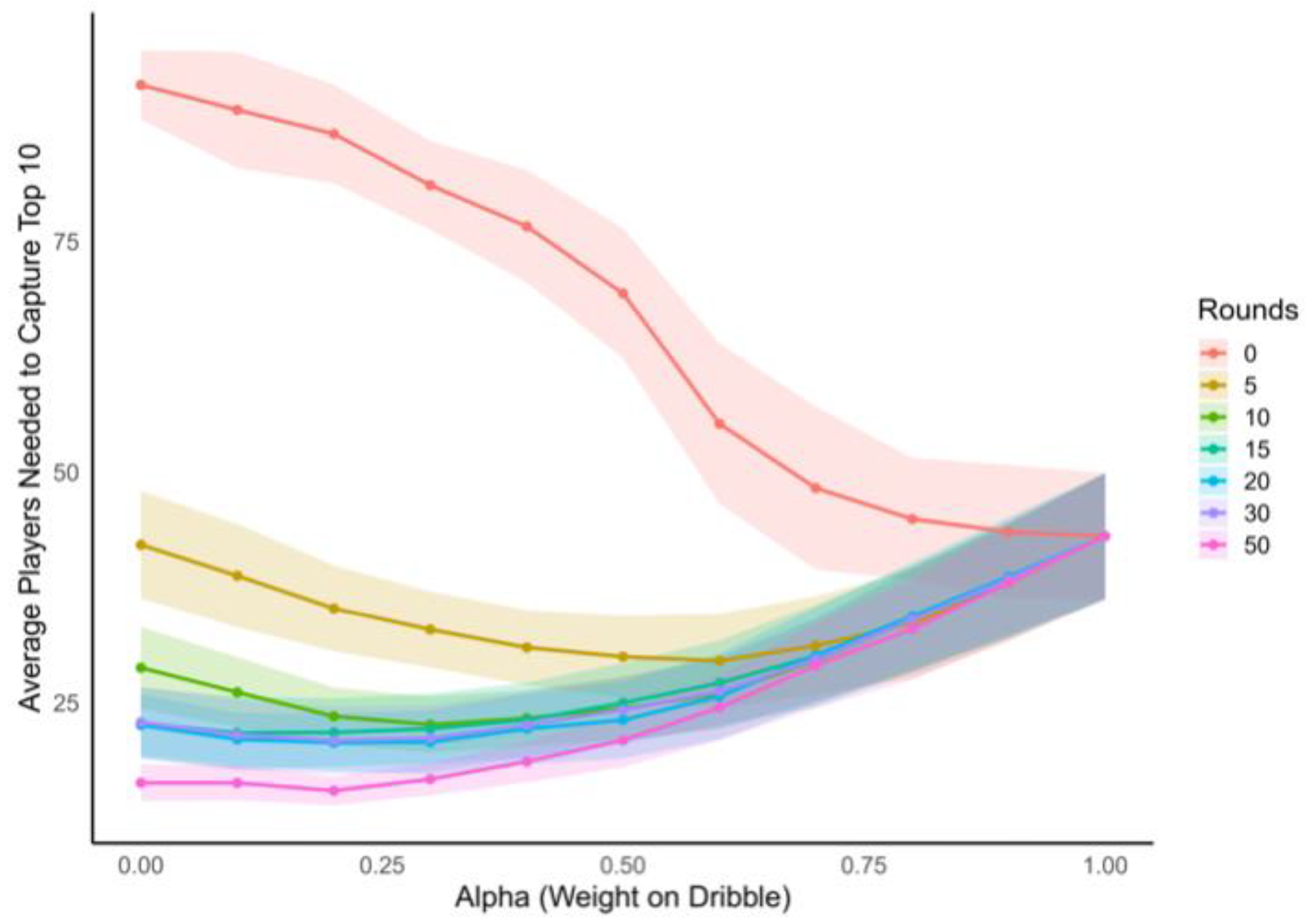
To calculate the hybrid score between dribble speed and in-game performance, we used the following equation: Hybrid_i = α × z(Dribble_i) + (1 − α) × z(Performance_i). The parameter α indicated the hybrid score between dribble speed and in-game performance, which ranged from 0 (game performance only) to 1 (dribble only) in increments of 0.1. This α represents the weighting one would place on the dribble speed versus in-game performance for estimating the performance of each player before applying a selection cutoff. For each value of α and number of rounds, we calculated how many of the top ranked players (by hybrid score) were needed to guarantee the inclusion of the top 10 players (based on latent ability). This procedure was repeated across 20 replicate simulations. For each replicate and round, we determined the α value that minimized the number of players needed to reliably include the true top 10 players (optimal α). We determined the: (i) optimal α as a function of games played, showing how reliance on skill versus performance should shift over time, and (ii) the average number of players needed to select the top 10 at each round for various α values.

2.8. Statistical Analyses

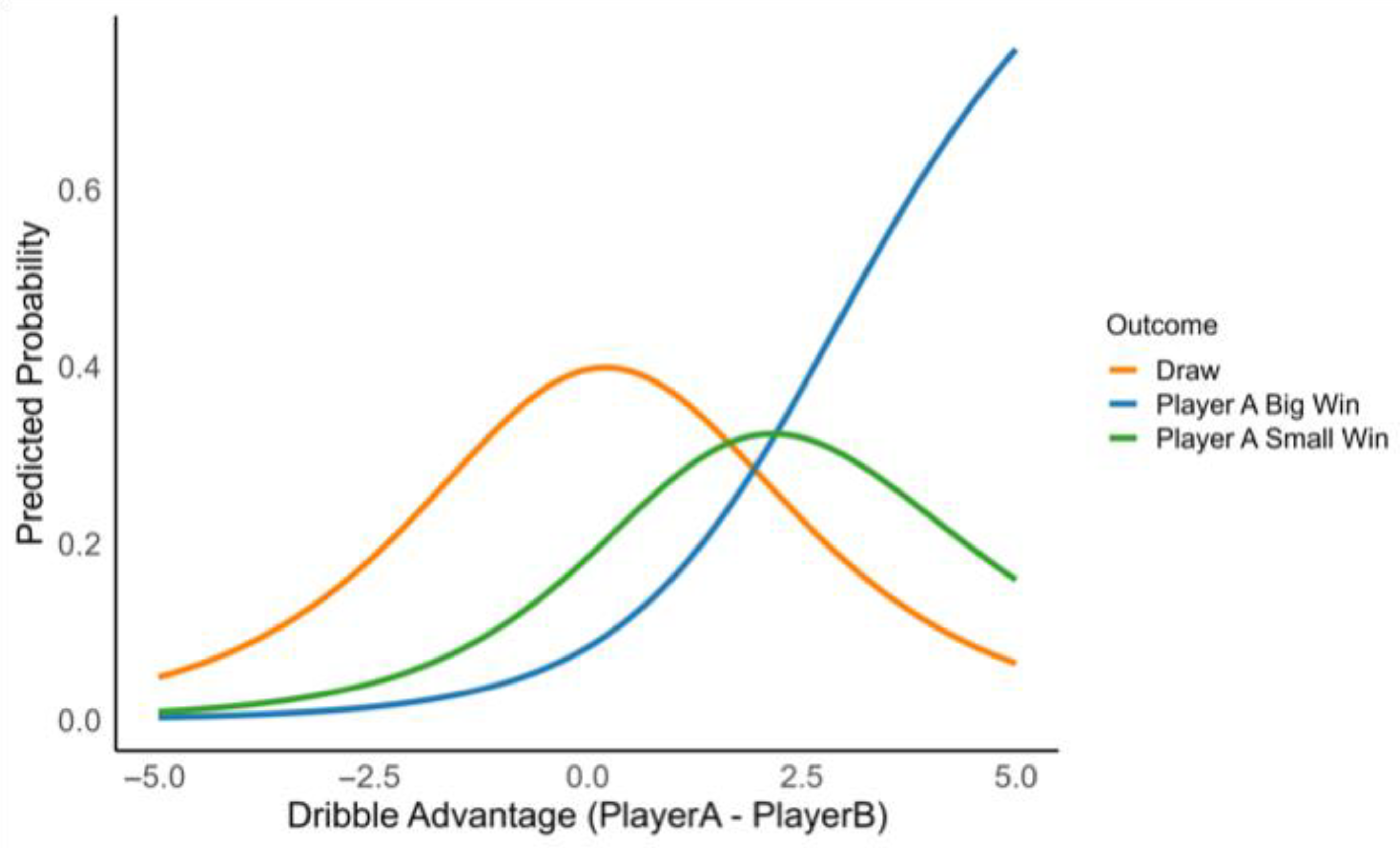
A Bayesian cumulative ordinal regression model was fitted to match outcome data of 1v1 competitive games using the brms package in R [24]. The response variable was an ordered factor representing the match result (large win = +2 goals, small win = +1 goal, draw, small loss = −1 goals, or large loss = −2 goals). The predictors included differences in dribbling speed and sprint speed between Player A and Player B (dribble_diff, sprint_diff). The model incorporated random intercepts for both Player A and Player B to account for player-specific variability. A logit link function was used, and sampling was performed using the No-U-Turn Sampler (NUTS) with two chains of 2000 iterations each, including 1000 warmup iterations. To explore how differences in dribbling skill influenced predicted match outcomes, new prediction data were created where the difference in dribbling between each pair of players (dribble_diff) varied from −5 to +5, while the difference in sprinting between each pair of players (sprint_diff) was held constant at zero. Expected probabilities for each outcome category were computed using the posterior_epred() function in brms, taking the mean across posterior samples. Posterior samples of player-specific random intercepts were extracted, and player rankings were calculated for each posterior draw. The mean rank and either the standard deviation (SD) or 95% credible intervals (CIs) of the rank were computed for each player. Player IDs were mapped to letter labels (A, B, C, etc.) matching those used in the network diagram visualization. Ranking plots with uncertainty bars (SD or CI) were created using ggplot2 [25], showing Posterior Mean Rank on the x-axis and Player Labels on the y-axis.

To examine the relationship between the number of games played and the number of players needed to be selected to capture the true top 10% in our simulation, we fitted a generalized additive model (GAM) [26] using the mgcv package [26] in R [27]. The GAM modeled the number of players needed as a smooth function of games played with a basis dimension k = 10, allowing flexibility to capture potential nonlinearities without overfitting. Model diagnostics, including estimated degrees of freedom (EDF), F-statistic, and p-values for smooth terms, were extracted and summarized.

To evaluate how the optimal weighting of player selection traits (specifically the parameter α, representing the relative weight on dribble skill versus performance score) influenced the number of players required to capture the top 10 true performers, we fitted a series of generalized additive models (GAMs) using the mgcv package in R [26]. The response variable was the average number of players needed to include the top 10 true performers at each level of α (ranging from 0 to 1), across multiple stages of player observation (Rounds: 0–50). Rounds was treated as a fixed factor to model differences in baseline player selection efficiency across stages. Smoothing parameter estimation was performed via restricted maximum likelihood (REML). Visual inspection of residuals and diagnostic plots confirmed the adequacy of model fit. To test whether the relationship between α and the number of players required differed significantly between stages of observation, we conducted pairwise comparisons of smooth terms. In addition, we conducted post hoc comparisons of the predicted number of players needed at fixed α values using the emmeans package [28]. Estimated marginal means for each Rounds-level were calculated at α values between 0 and 1 (in 0.1 increments), and pairwise contrasts were performed using Tukey’s adjustment for multiple comparisons. This enabled identification of specific round-to-round differences in selection efficiency at fixed α levels.

All simulations and analyses were conducted using R version 4.3.2 [26] utilizing the dplyr [29] and ggplot2 packages for data manipulation and visualization, respectively.

3. Results

3.1. Performance Parameters

Average dribbling speed for this cohort of players was 2.08 ± 0.15 m·s⁻¹ and varied from a low of 1.67 m·s⁻¹ to a high of 2.30 m·s⁻¹. Average sprinting speed was 3.41 ± 0.16 m·s⁻¹ and varied from a low of 3.03 m·s⁻¹ to a high of 3.76 m·s⁻¹.

3.2. 1v1 Competitive Ability

The average percentage success for individuals when attacking was 33.1 ± 13.5% and varied from 6.7 to 55.6%. The average defending success for individuals, which was when they prevented attackers from touching the ball in the scoring zone, was 66.5 ± 11.3% and varied from 40.0 to 84.4%.

Top-performing players consistently showed lower mean ranks and narrower uncertainty intervals, while players with fewer matches or similar abilities displayed wider uncertainty around their estimated ranks. Bayesian cumulative ordinal regression indicated excellent model convergence (all Rhat = 1.00; ESS > 1500) (

Table 1. Posterior estimates from a Bayesian cumulative ordinal regression model predicting match outcomes based on skill differences. Estimates are presented as posterior means with associated 95% credible intervals. Fixed effects correspond to differences in dribbling and sprinting performances between players. Random effects represent player-specific variability not explained by covariates. Intercepts define latent thresholds between outcome categories. Convergence diagnostics (Rhat ≈ 1.00) and effective sample sizes were satisfactory across all parameters.

Parameter	Mean	SD	2.5%	97.5%	Rhat	ESS_Bulk	ESS_Tail
dribble_diff	−0.76	0.19	−1.16	−0.40	1.00	1800	1700
sprint_diff	0.01	0.19	−0.36	0.40	1.00	1850	1750
SD (Player A Intercept)	0.87	0.27	0.44	1.44	1.00	1600	1500
SD (Player B Intercept)	0.91	0.26	0.46	1.44	1.00	1650	1550
Intercept-1	−2.45	0.41	−3.23	−1.77	1.00	1900	1800
Intercept-2	−1.02	0.34	−1.67	−0.37	1.00	1950	1850
Intercept-3	2.48	0.39	1.76	3.30	1.00	1980	1870

). Among fixed effects, only the difference in dribbling speed between competing individuals (dribble_diff) showed a credible effect on match outcomes (mean = −0.76, 95% CI: [−1.16, −0.40]), with greater differences in dribble speed associated with a greater probability in Player A’s chance of winning (Table 1) (Figure 1). The greater the advantage in dribbling speed for an individual (higher dribble_diff) the greater the probability of winning by a larger margin and a lower probability of a draw. The difference in sprinting speed between competing individuals (sprint_diff) demonstrated no credible association (mean = 0.01, 95% CI: [−0.36, 0.40]) (Table 1).

Players with higher rankings in the 1v1 competition were more likely to have higher dribbling performances (R² = 0.354; p < 0.001) but not sprinting performances (R² = 0.031; p = 0.370) (Figure 2).

3.3. Simulations

There was a significant nonlinear relationship between the number of games an individual played and the number of players needed to be selected to reliably include the true top 10% of players (adjusted R² = 0.82; edf = 3.62, F = 97.4, p < 0.001) (Figure 3) (

Table 2. The parametric terms from the generalized additive model (GAM) evaluating how the number of rounds played influences the number of players that need to be selected to ensure the true top 10% of players are included.

Term	Estimate	Standard Error	t-Value	p-Value
Intercept	66.377	0.06	1069.4	<0.0001
Rounds5	−31.318	0.09	−356.8	<0.0001
Rounds10	−37.273	0.09	−424.6	<0.0001
Rounds15	−38.250	0.09	−435.7	<0.0001
Rounds20	−38.877	0.09	−442.9	<0.0001
Rounds25	−39.977	0.09	−455.4	<0.0001
Rounds30	−38.650	0.09	−440.3	<0.0001
Rounds35	−40.073	0.09	−456.5	<0.0001
Rounds40	−40.327	0.09	−459.4	<0.0001
Rounds45	−40.809	0.09	−464.9	<0.0001
Rounds50	−41.627	0.09	−474.2	<0.0001

Note: The intercept represents the estimated average number of players needed to identify the top 10 performers at Round 0. Negative estimates for other rounds indicate a reduction in the number of players required relative to Round 0.

). After 5 games, an average of 26.0 ± 2.5 players were needed to be selected to guarantee inclusion of the true top 10 performers. The number of players decreased to 18.0 ± 1.5 players after 20 games and then plateaued at around 15 players after 30 games. Thus, using data from a greater number of games reduced uncertainty and improved player identification efficiency but there were diminishing gains beyond 30 games. The true top individual player in each simulated group had a mean rank of 2.80 ± 2.09 (Range: 1 to 9) after 5 rounds of games and 1.95 ± 1.90 by round 10 (Range: 1 to 8) (Figure 4). By round 20, the true top individual player in each simulated group had a mean rank of 1.65 ± 1.09 (Range: 1 to 5).

The optimal weighting between dribble skill and game-match data significantly influenced the number of players needed to correctly identify the top 10 performers, and this relationship varied across observation rounds (

Table 3. A summary of smooth terms from the generalized additive model (GAM) examining the effect of alpha within each observation round.

Smooth Term	EDF	Ref. DF	F-Value	p-Value
s(Alpha):Rounds0	8.870	8.995	10,208	<0.0001
s(Alpha):Rounds5	7.635	8.541	638	<0.0001
s(Alpha):Rounds10	7.673	8.564	1253	<0.0001
s(Alpha):Rounds15	6.804	7.924	1625	<0.0001
s(Alpha):Rounds20	7.515	8.465	1758	<0.0001
s(Alpha):Rounds25	7.103	8.168	2078	<0.0001
s(Alpha):Rounds30	7.096	8.163	1692	<0.0001
s(Alpha):Rounds35	6.702	7.836	2318	<0.0001
s(Alpha):Rounds40	6.856	7.968	2301	<0.0001
s(Alpha):Rounds45	6.863	7.974	2521	<0.0001
s(Alpha):Rounds50	7.385	8.377	2654	<0.0001

). As rounds increased from 0 to 50, the average number of players that were needed to be selected decreased markedly from around 66 at Round 0 to approximately 25 at Round 50 (all p < 0.0001), indicating improved selection efficiency with more data (Figure 4). Smooth terms for α were highly significant across all rounds (all p < 0.0001), highlighting a nonlinear impact of α on player selection outcomes (Table 3). Pairwise comparisons at α = 0.0 showed large and consistent reductions in player requirements across rounds.

The relationship between the number of rounds played and the optimal α weighting (on dribble) was highly significant and nonlinear, as indicated by the smooth term (edf = 7.82, F = 289.9, p = 0.0034) (Figure 5). The optimal α (weighting towards dribbling data) decreased with increasing number of games from an α of 0.80 ± 0.14 at Game 0, 0.28 ± 0.17 at Game 10, to 0.16 ± 0.16 at Game 50 (Figure 5). The model demonstrated excellent fit, with the low generalized cross-validation (GCV = 0.00083) and scale estimate (0.00016) further support model accuracy.

4. Discussion

This study aimed to develop and validate a framework for talent identification in youth soccer that combines closed-skill assessments with competitive game data, while explicitly accounting for the uncertainties inherent in both. We found dribbling speed significantly predicted 1v1 in-game performance, aligning with previous findings linking it to both attacking and defensive success [18,19]. A Bayesian regression model showed that greater positive differences in dribbling ability between two players significantly increased the likelihood of winning 1v1 contests. Using simulations that were informed by these empirical data, we show that even when closed-skill tests explain only a limited portion of in-game performance variance, they can still play a vital role in the early stages of selection when used appropriately. Thus, data from tests of closed skill can support more informed and efficient early-stage player selections, especially in contexts where time, data, and staffing are limited. When more in-game data are available, our simulations show that it is more profitable to rely on the logistically complex and time-intensive collection of game-data when reducing player pools down to more manageable numbers. Thus, when the aim of a quantitative talent identification program is to reduce a large, logistically challenging number of players down to a more manageable group for subsequent assessment by experienced scouts and coaches then a strategic integration of skill testing and match-based data can reduce uncertainty and enhance selection precision.

Quantitative talent identification programs often advocate for the assessment of multiple traits—technical, tactical, psychological, and cognitive—to reflect the multifaceted nature of soccer [2,30,31,32]. While this approach is intuitively appealing, it often overlooks the core challenge of large-scale talent identification: the need for rapid, efficient, and accurate screening [4,33,34]. Including all traits associated with success is unnecessary—and potentially counterproductive—if it does not enhance these aspects of the identification process [35,36]. Closed-skill tests can be highly efficient even when they predict less than half the variance in individual match performance. For example, dribbling speed—as measured in this study—can be assessed in roughly three minutes per player. When such tests show even modest predictive value for match performance, they can effectively and rapidly narrow the pool of candidates. Based on our simulations, approximately 50% of the candidates could be excluded after an initial dribbling speed assessment—without excluding any of the top 10%—with 95% confidence. Thus, this closed-skill test serves as an efficient early-stage filter.

Assessments of players using in-game performances are more accurate for evaluating player abilities, but the collection of these data is logistically complex and inefficient at scale. Therefore, it is most practical to use game data after initial screening through closed-skill tests or in combination with closed-skill data to balance predictive value and feasibility. Based on our simulations of in-game data alone, an average of 26 out of 100 players needed to be selected after 5 games per player to ensure the true top 10% of players were included. This number declined with additional games, plateauing at around 15 players after 30–40 matches. This nonlinear, asymptotic relationship highlights diminishing returns with over-sampling and provides a guidance for real-world resource allocation in scouting. Thus, our results show that both closed-skill and in-game data carry uncertainty, and the optimal weighting of each evolves as more data become available. Our simulations revealed that, early in the process, closed-skill assessments such as dribbling speed should be weighted heavily (optimal alpha ≈ 0.80 at Game 0). Before any match data are collected, selection decisions must rely entirely on closed-skill performance. However, as we accumulate more in-game data, the reliance on skill assessments should decrease (alpha ≈ 0.28 at Game 10; ≈0.16 by Game 50). This dynamic weighting emphasizes the importance of flexible selection criteria, as a fixed reliance on either data source is suboptimal. It should also be noted that the relative reliance on using data from closed-skill tests versus in-game data when determining selection cutoffs will vary with context and group. For example, our simulations were based on our empirically estimated relationship between dribbling speed and 1v1 performance that had a SD of 0.7. The SD is likely to vary in the relationship between each different closed-skill test and in-game performance, but knowledge of this variance is critical for estimating selection cutoffs and appropriate alphas. Higher SDs will lead to fewer players being cut when based on closed-skill tests alone, and also lead to a faster shift towards reliance on in-game data when they become available. Our findings suggest a more adaptive approach: begin with closed-skill testing for large groups (with knowledge of SDs), then shift toward match-based evaluations as more data accumulate. This strategy better reflects actual player development trajectories and improves decision-making.

Our framework addresses two of the most difficult challenges in talent identification: the large volume of players needing assessment and the inherent error in selection judgments [2,15,32]. First, it offers a practical method for reducing large cohorts to manageable sizes. Second, it incorporates a statistical understanding of uncertainty, guiding scouts on how to balance predictive accuracy with logistical feasibility. While top performers are rare, our approach increases the likelihood of identifying them early, with fewer false negatives (cutting players that are in the true top 10%). Moreover, our study offers a structure for integrating data in a sequential scouting strategy: closed-skill tests serve as efficient initial filters, while in-game metrics become more prominent as match data accumulate. This framework model leverages the predictive power of skill tests while recognizing that performance in a controlled environment does not guarantee success in match contexts. Yet, our simulations also show that in-game metrics are not free of uncertainty. Therefore, selection models should treat all performance estimates probabilistically, rather than as definitive rankings.

Our focus on 1v1 contests in this study was strategically used to demonstrate the conceptual framework of an adaptive model of talent identification. Future research should examine how this framework performs in small-sided or full-sided matches where team dynamics and tactical demands are more pronounced. In addition, the predictive validity of our closed-skill tests for predicting in-game performance, and thus the utility of a sequential framework, may differ across age groups, cohorts, or contexts. Incorporating additional skill tests, such as technical skill tests under pressure or that incorporate more of the complexities of decision-making in games, could enhance assessments before progressing to in-game metrics. Finally, while our model focused on identifying the top 10% of players, future applications may target different selection thresholds (e.g., top 5%, top 20%) depending on the quality of the player pool, scouting goals or the size of the cohort that needs to be selected.

One of the most challenging tasks coaches face during selection trials is evaluating a large pool of players and narrowing it down to a final team. It is virtually impossible for coaches to give each player the individual attention required to accurately assess their suitability when dealing with such large numbers. To address this, we propose a sequential selection strategy that helps reduce the player pool to a manageable size, allowing coaches to dedicate meaningful time to evaluating the most promising candidates. The process begins with a test of a key performance skill that is central to match success, such as dribbling ability, which can quickly eliminate less-suitable players. Subsequently, small-sided games can be used to further refine the group. This two-step approach enables coaches to focus their attention on a smaller cohort, with the assurance, at a 95% confidence level, that the top 10% of players will still be included. While the number of players eliminated in the early, closed-skill phase may vary across groups, there is now sufficient empirical evidence linking these tests to in-game performance to support the use of data-driven cutoff points.

5. Conclusions

Our study provides a sequential, data-driven framework for youth soccer talent identification that integrates closed-skill assessments and in-game performance data, while accounting for uncertainty. By illustrating how to balance these inputs over time and quantifying the link between data availability and selection accuracy, we offer practical guidance for optimizing early-stage evaluations. Although no model can eliminate the uncertainty of forecasting talent, embracing and accounting for that uncertainty can enable more consistent, fair, and effective selection strategies.