Abstract
Large-scale particle-based fluid simulations present significant computational challenges, particularly in achieving interactive frame rates while maintaining visual quality. Unity3D’s widespread adoption in game development, VR/AR applications, and scientific visualization creates a unique need for efficient fluid simulation within its ecosystem. This paper presents a GPU-accelerated Smoothed Particle Hydrodynamics (SPH) framework implemented in Unity3D that effectively addresses these challenges through several key innovations. Unlike previous GPU-accelerated SPH implementations that typically struggle with scaling beyond 100,000 particles while maintaining real-time performance, we introduce a novel fusion of Count Sort with Parallel Prefix Scan for spatial hashing that transforms the traditionally expensive O(n²) neighborhood search into an efficient O(n) operation, significantly outperforming traditional GPU sorting algorithms in particle-based simulations. Our implementation leverages a Structure of Arrays (SoA) memory layout, optimized for GPU compute shaders, achieving 30–45% improved computation throughput over traditional Array of Structures approaches. Performance evaluations demonstrate that our method achieves throughput rates up to 168,600 particles/ms while maintaining consistent 5.7–6.0 ms frame times across varying particle counts from 10,000 to 1,000,000. The framework maintains interactive frame rates (>30 FPS) with up to 500,000 particles and remains responsive even at 1 million particles. Collision rates approaching 1.0 indicate near-optimal hash distribution, while the adaptive time stepping mechanism adds minimal computational overhead (2–5%) while significantly improving simulation stability. These innovations enable real-time, large-scale fluid simulations with applications spanning visual effects, game development, and scientific visualization.
1. Introduction
Particle-based fluid simulation methods have been widely used for applications in computer graphics due to their realistic visual effects and efficiency, including cloth simulation, surgical simulation, gaming and even in animation like Moana [1] and Elemental [2]. Among these techniques, the Smoothed Particle Hydrodynamics (SPH) method has experienced growing popularity in computational fluid dynamics due to its straightforward implementation and mesh-free approach which has garnered significant attention from the research community. The SPH method, originally proposed by Lucy and Gingold & Monaghan in 1977 for astrophysics applications, has evolved dramatically over the decades. Traditional fluid simulation methods can be broadly categorized into Eulerian (grid-based) and Lagrangian (particle-based) approaches, with SPH emerging as the dominant Lagrangian method due to its intuitive framework and flexibility in handling free-surface flows [3].
Recently, researchers have primarily focused on performance optimization and visual quality improvements. Modern GPU-accelerated implementations have transformed SPH capabilities, enabling simulations with millions of particles in real-time or near-real-time scenarios. Huang et al. [4] demonstrated comprehensive frameworks leveraging parallel computing architectures to handle large-scale fluid simulations, addressing the historical performance bottlenecks that limited particle counts in interactive applications. Nevertheless, it remains an unavoidable and formidable challenge to efficiently reconstruct smooth and artifact-free fluid surfaces from particle data, particularly in real-time interactive applications. Particle-based methods like SPH excel at simulating fluid dynamics accurately. However, transforming discrete particles into continuous, visually pleasing surfaces introduces significant computational overhead. This visualization bottleneck creates a difficult choice. Developers must often compromise between visual quality and performance, particularly when simulating large-scale particle systems.
The problem becomes even more pronounced in game engines like Unity 3D, where computational resources must be balanced against other demands of interactive applications. Recent scholars have specifically addressed surface reconstruction techniques such as screen-space fluids, adaptive marching cubes, and anisotropic kernels that better approximate smooth surfaces while maintaining performance constraints. As GPU computing techniques have matured within game engine environments, the possibility of implementing large-scale, visually impressive fluid simulations has become increasingly accessible to developers.
The context of Unity’s evolution as a game development platform has significantly expanded its capabilities for real-time physics simulation. The introduction of the Data-Oriented Technology Stack (DOTS) and the Burst compiler has revolutionized how computationally intensive tasks like fluid simulation can be handled. Unity’s compute shader architecture now provides developers with direct access to the GPU’s parallel processing capabilities, enabling the implementation of high-performance particle systems that were previously infeasible [5]. The Unity Physics package and custom HLSL shader integration further extend these capabilities, allowing for sophisticated physical interactions while maintaining real-time performance. Our work builds upon Unity’s evolving ecosystem, particularly its compute shader framework, which enables the parallel processing of particle data on the GPU. By leveraging Unity’s unique architecture and development tools, we position our research at the intersection of high-performance computing and accessible game development, making advanced fluid simulation techniques available to a broader range of applications and developers within the Unity environment.
Unity3D requires a tailored SPH framework distinct from other platforms due to its unique technical architecture. Unlike Unreal Engine’s native C++ environment or standalone CUDA-based solvers, Unity’s compute shader implementation follows specific HLSL constraints and memory management patterns that necessitate custom optimization approaches. The Unity engine’s rendering pipeline integration, buffer management system, and thread group limitations create unique challenges for fluid simulation that cannot be directly addressed by porting solutions from other platforms. Additionally, Unity’s widespread adoption among independent developers and small studios—who often lack access to specialized physics simulation expertise—creates a specific need for an optimized fluid simulation framework that integrates seamlessly with Unity’s workflow and component-based architecture.
Implementing large-scale particle systems for fluid simulation presents several key technical challenges. The first is the fundamental trade-off between GPU and CPU implementations. GPU acceleration offers massive parallelism ideal for particle simulations. However, Unity’s hybrid approach introduces complexity. It requires careful management of data transfers between the CPU, where game logic typically resides, and the GPU, where simulation calculations occur. This data transfer represents a potential bottleneck that can significantly impact performance [6]. Memory bandwidth constraints become increasingly critical when scaling to millions of particles. Each particle requires storage of position, velocity, and various physical properties, quickly consuming available GPU memory. Our implementation addresses this through optimized data structures and compression techniques that minimize memory requirements without sacrificing simulation accuracy.
Neighborhood search optimization is perhaps the most computationally intensive component of SPH simulations. Each particle must locate and interact with its neighbors at every timestep. To address this challenge, we implement a Unity-specific spatial hashing algorithm. This approach efficiently partitions the simulation space. It reduces search complexity from O(n²) to O(n), enabling significant performance improvements for large-scale simulations. Data structure considerations are equally important, as the organization of particle data directly impacts memory access patterns and cache efficiency. Our approach utilizes Structure of Arrays (SoA) rather than Array of Structures (AoS) organization, aligning with Unity’s latest data-oriented design principles to maximize throughput on modern GPU architectures.
Building on these optimized data structures, we also focus on visual quality improvements. Recent advances in surface reconstruction methods have significantly improved the visual quality of particle-based fluid simulations. While traditional marching cubes algorithms remain popular, newer techniques like screen space fluids offer performance advantages by performing reconstruction in 2D rather than 3D space [7]. Our implementation combines these approaches with adaptive resolution techniques that concentrate detail where it is most visually important.
Modern approaches to boundary handling have evolved beyond simple collision detection to incorporate more physically accurate interactions. Techniques such as density correction at boundaries and specialized boundary particles help prevent the visual artifacts commonly associated with fluid–solid interfaces in SPH simulations. Level of detail (LOD) techniques for adaptive simulation resolution represent another important advancement, allowing computational resources to be focused on visually significant areas while using simplified simulation in less noticeable regions. Our framework implements dynamic particle splitting and merging based on visual importance criteria, maintaining visual fidelity while optimizing performance.
Beyond gaming, fluid simulation has valuable applications in virtual reality. VR training scenarios require realistic fluid interactions for medical and industrial procedures. These applications demand both visual fidelity and real-time performance, making optimized particle-based methods essential. Specific applications of fluid simulation in VR include medical training platforms where realistic fluid behavior enhances surgical procedure practice, and industrial maintenance training where fluid dynamics are critical for effective skill transfer. In scientific visualization, Unity-based interactive fluid simulations have been employed in educational contexts to demonstrate complex fluid dynamics concepts, similar to the comprehensive frameworks demonstrated by Huang et al. [4], and in research environments to visualize computational fluid dynamics results with real-time manipulation capabilities. The accessibility of Unity’s development environment has made it increasingly popular for these specialized applications, where traditional scientific visualization tools often lack the interactive performance and visual quality that game engine technology provides.
Our research aims to address these challenges and opportunities by developing a scalable, efficient framework for large-scale particle-based fluid simulation within Unity 3D, with particular attention to surface reconstruction quality and real-time performance in interactive applications.
This current work significantly extends our previous conference paper presented at IEEE ICCBE [8], where we introduced the basic framework for GPU-accelerated SPH simulation in Unity using spatial hashing and scan algorithms. In this extended version, we provide several important enhancements: (1) A comprehensive analysis of spatial hashing efficiency with detailed collision metrics across different particle distributions and densities; (2) An in-depth comparison of Structure of Arrays (SoA) versus Array of Structures (AoS) memory layouts, with quantifiable throughput benefits; (3) Expanded performance benchmarks scaling to one million particles with detailed frame time analysis; (4) Advanced surface reconstruction techniques for improved visual fidelity; and (5) A thorough investigation of temporal stability in real-time scenarios with adaptive time stepping. While our conference paper demonstrated the basic feasibility of real-time performance with specific particle counts, this extended work provides a comprehensive analysis of the underlying algorithmic and implementation factors that enable such performance, along with additional optimizations that further improve both computational efficiency and visual quality.
While previous GPU-accelerated SPH implementations such as those by Hrytsyshyn et al. [9] have demonstrated compute shader-based fluid simulation capabilities, achieving interactive frame rates with moderate particle counts (50,000–100,000), our approach significantly advances the state-of-the-art in several key aspects. Their implementation noted that scaling beyond 100,000 particles while maintaining real-time performance remains challenging due to the complexity of naive neighbor search algorithms. Similarly, other GPU implementations like those by Carensac et al. [10] achieved interactive frame rates with hundreds of thousands of particles but were limited by inefficient memory access patterns. In contrast, our framework achieves substantial performance improvements through our novel fusion of Count Sort with Parallel Prefix Scan and memory layout optimizations, scaling to 1 million particles while maintaining interactive frame rates.
In this paper, we implemented the Smoothed Particle Hydrodynamics method optimized for Unity’s compute shader architecture to enable large-scale fluid simulations with millions of particles. This work integrates GPU-accelerated particle simulation with optimized memory management techniques to achieve both visual quality and computational efficiency. Our main contributions include:
- A highly optimized SPH fluid simulation implementation in Unity 3D utilizing compute shaders that processes millions of particles in parallel, leveraging the GPU’s massive parallelism while minimizing CPU overhead
- An efficient spatial partitioning system using uniform grid hashing with optimized 3D hash functions that reduces neighborhood search complexity from O(n²) to O(n), addressing one of the key computational bottlenecks in particle-based simulations
- A specialized GPU-based particle sorting and reordering pipeline that maximizes memory coherence, enabling efficient neighbor searches and reduced cache misses
- A data-oriented approach using Structure of Arrays (SoA) rather than Array of Structures (AoS) organization that aligns with Unity’s data-oriented design principles, optimizing memory access patterns and GPU cache utilization
- Advanced memory management techniques that minimize CPU-GPU data transfer bottlenecks, including buffer reuse strategies and optimized data structures that reduce memory requirements without sacrificing simulation accuracy
- A volumetric density-based surface reconstruction method that balances visual quality with computational efficiency, enabling real-time rendering of fluid surfaces from millions of particles.
2. Related Work
Over the years, numerous research efforts have focused on particle-based fluid simulation techniques that optimize performance and enhance visual quality for interactive applications. These approaches have addressed various computational challenges, from efficient neighborhood searching to advanced surface reconstruction methods. In the implementation phase, optimized algorithms and data structures can significantly reduce computational overhead and improve simulation fidelity, particularly when leveraging GPU acceleration within game engines like Unity.
2.1. Smoothed Particle Hydrodynamics (SPH)
Smoothed Particle Hydrodynamics originated in 1977 when Lucy [11] and Gingold and Monaghan [12] independently developed the method for astrophysical simulations. Initially created to model non-axisymmetric phenomena in astrophysics, SPH was later adapted for fluid dynamics by Monaghan [13] in the early 1990s. The method gained traction in computational physics due to its mesh-free nature, which naturally handles large deformations and free surfaces that challenged traditional grid-based approaches. Throughout the 1990s and early 2000s, researchers refined the mathematical foundations of SPH, addressing issues such as boundary conditions, tensile instability, and numerical diffusion that affected early implementations.
The core principle of SPH involves approximating continuous-field quantities through particle interpolation. In this approach, a fluid is represented as a collection of discrete particles carrying physical properties (mass, velocity, density). The value of any quantity A at position r is approximated, as shown in Equation (1):
where is the mass of particle j, is its density, is the value of the quantity A in the particle j, and W is a smoothing kernel function with radius h. This kernel function weighs contributions from neighboring particles based on distance, typically using spline functions that balance computational efficiency with numerical accuracy. The momentum equation in SPH is derived from the Navier–Stokes equations, incorporating pressure gradients, viscosity, and external forces.
where and are the pressures, represent the viscosity, and are the external forces such as gravity. This formulation provides a computationally controllable way to solve fluid dynamics problems without requiring explicit mesh connectivity.
Müller et al. [14] introduced SPH to computer graphics in 2003, demonstrating interactive fluid simulations with several hundred particles. Their work established SPH as a viable approach for visual effects in interactive applications, particularly for water and other liquids. Subsequent research by Becker and Teschner [15] introduced the weakly compressible SPH (WCSPH) formulation, improving stability through a state equation that relates pressure to density. The gaming industry quickly adopted these techniques, with significant performance limitations.
As graphics hardware evolved, SPH was advanced to handle increasingly complex scenarios. Adams et al. [16] developed adaptive particle refinement techniques, while Ihmsen et al. [17] introduced the predictive corrective incompressible SPH method (PCISPH) that better maintains fluid incompressibility while allowing larger time steps. These improvements gradually transformed SPH from a specialized technique to a mainstream approach for fluid effects in games and visual effects.
Recent GPU implementations have significantly improved SPH performance. Hrytsyshyn et al. [9] presented an optimized implementation of SPH using compute shaders, focusing on efficient neighbor search algorithms and memory coherence techniques. Their approach demonstrates significant performance improvements over CPU-based methods, achieving interactive frame rates with moderate particle counts (50,000–100,000) on consumer hardware. Their work highlights the critical importance of coherent memory access patterns in compute shader implementations, particularly when handling particle data structures that require frequent neighborhood queries. While their implementation shows promising results, they note that scaling beyond 100,000 particles while maintaining real-time performance remains challenging due to the complexity of naive neighbor search algorithms.
A notable example is the work by Afrasiabi et al. [18], who proposed a hybrid SPH-FEM (Finite Element Method) solver for metal cutting simulations running on GPUs. Their approach leverages the strengths of both methods: SPH for handling large deformations in the workpiece material and FEM for modeling the tool with lower computational overhead. This hybrid implementation demonstrates the versatility of SPH when combined with other techniques and highlights the significant performance benefits of GPU acceleration for computationally intensive simulations. Their work achieves up to 20× speedup compared to CPU-only implementations while maintaining simulation accuracy. While focused on manufacturing applications rather than fluid dynamics, their GPU implementation strategies and hybrid approach provide valuable insights for optimizing large-scale particle-based simulations.
Carensac et al. [10] proposed several optimization techniques for predictive-corrective particle-based fluid simulations. Their work focuses on algorithmic improvements to the standard PCISPH (Predictive-Corrective Incompressible SPH) method, achieving better computational efficiency while maintaining simulation stability. By implementing careful memory access patterns and optimized neighborhood search algorithms on the GPU, they demonstrate significant performance improvements that scale well with increasing particle counts. Their optimized implementation achieves interactive frame rates with hundreds of thousands of particles on consumer-grade hardware, highlighting the importance of GPU-specific optimization strategies for large-scale fluid simulations.
Within game engine environments, particularly Unity, several researchers have addressed the unique challenges of implementing SPH fluid simulation. Unlike general-purpose GPU implementations, Unity-based SPH systems must work within the constraints of the engine’s compute shader architecture, memory management system, and rendering pipeline integration. Hrytsyshyn et al. [9], while not Unity-specific, demonstrated compute shader-based SPH that shares similar architectural constraints with Unity’s HLSL implementation, achieving 50,000–100,000 particles at interactive frame rates but struggling with memory bandwidth limitations inherent in game engine environments. More recent Unity-specific implementations have focused on integrating SPH with Unity’s Data-Oriented Technology Stack (DOTS) and Burst compiler, though these approaches typically sacrifice particle count for engine integration, rarely exceeding 25,000–50,000 particles while maintaining the 60 FPS target required for interactive applications. The challenge in game engine implementations lies in balancing fluid simulation performance with other engine demands such as rendering, audio processing, and game logic execution, creating a unique optimization landscape that differs significantly from standalone fluid simulation frameworks.
Xu et al. [19] presented a comprehensive overview of the methodology and applications of smoothed particle hydrodynamics in the fluid, solid, and biomechanic domains. Their paper synthesizes recent advances in SPH formulation, boundary treatment, and stability enhancements, serving as an excellent resource for understanding the theoretical foundations and practical considerations of modern SPH implementations. They highlight the specific challenges in simulating complex multiphysics phenomena, which share computational challenges with large-scale fluid simulations, particularly in handling dynamic boundaries and maintaining numerical stability under extreme conditions.
2.2. Spatial Acceleration Structures
Efficient spatial queries are critical for particle-based simulations, where the computational complexity is dominated by neighborhood searches. Traditional SPH implementations suffer from O(n²) complexity when using naive distance-based searches, making them impractical for large-scale simulations. Various spatial acceleration structures have been developed to address this bottleneck.
Hierarchical spatial structures offer significant advantages for non-uniform particle distributions. Winchenbach et al. [20] proposed a comprehensive approach to optimizing both the simulation and visualization pipelines through specialized memory structures. Their multi-level approach dynamically adapts to varying particle densities, offering significant performance improvements for scenarios with complex fluid behaviors. By carefully organizing particle data in memory according to spatial proximity, their method improves cache coherence during neighborhood searches and reduces memory bandwidth requirements, a critical bottleneck in large-scale GPU-accelerated simulations.
Octree-based spatial partitioning represents another powerful approach for large-scale particle simulations. Fernández-Fernández et al. [21] address the performance challenges of traditional octree implementations on parallel architectures. Their method introduces novel traversal algorithms specifically optimized for GPU execution, significantly reducing thread divergence compared to conventional octree approaches. Their implementation demonstrates up to 1.9x performance improvement over uniform grid methods for highly non-uniform particle distributions while maintaining competitive performance for uniform distributions. Particularly noteworthy is their efficient handling of dynamic scenarios where particles frequently move between spatial regions—a common challenge in fluid simulations with splashing and separation.
While most spatial acceleration research focuses on runtime optimization, the initial configuration of particles plays a crucial role in simulation efficiency and accuracy. Lopes et al. [22] introduced an innovative GPU-accelerated particle packing approach leveraging parallel geometric separation strategies. Their methodology consists of three key phases: strategic initial particle placement based on size distribution analysis, parallel geometric separation algorithms to eliminate overlaps, and efficient filtering of extraneous particles. Implemented using OpenCL, their technique achieves remarkable performance gains—up to 60 times faster than equivalent CPU implementations. This optimization of the initialization phase has particular significance for SPH simulations where proper particle distribution at setup directly impacts boundary representation quality and influences the stability and efficiency of subsequent simulation steps. Their approach demonstrates how spatial optimization principles can be effectively applied not only to runtime neighborhood searches but also to the critical preprocessing stages of particle-based simulations.
Among these spatial acceleration approaches, uniform grid-based hashing emerges as the most suitable technique for Unity3D’s compute shader framework due to several key compatibility factors. Unity’s HLSL compute shader implementation favors regular memory access patterns and fixed-size data structures, making uniform grids more efficient than hierarchical approaches that require dynamic memory allocation and irregular traversal patterns. The thread group architecture in Unity’s compute shaders (typically 64 or 256 threads per group) aligns well with uniform grid cell processing, where each thread can handle a fixed spatial region without the load balancing issues inherent in octree traversal. Additionally, Unity’s buffer management system and GPU memory constraints (typically 8–16GB on consumer hardware) favor the predictable memory footprint of uniform grids over the variable memory requirements of hierarchical structures. While octree-based methods like those proposed by Fernández-Fernández et al. [21] offer theoretical advantages for highly non-uniform distributions, their implementation complexity and thread divergence issues make them less practical within Unity’s compute shader environment, where simplicity and consistent performance across varying particle distributions are prioritized for interactive applications.
These spatial acceleration structures form the foundation upon which efficient neighborhood search algorithms are built, transforming what would be O(n²) operations into more manageable O(n) or O(log n) complexity. While the choice of spatial structure significantly impacts performance, equally important is how these structures are traversed and accessed in parallel computing environments. The effective implementation of these spatial queries on modern GPU architecture introduces additional considerations beyond algorithmic complexity alone. Memory access patterns, thread divergence, and workload balancing become critical factors that determine real-world performance.
2.3. Neighborhood Search
Neighborhood search forms the computational foundation of SPH simulations, as each fluid particle’s physical properties are calculated by interpolating contributions from surrounding particles within the kernel’s support radius. This process—identifying which particles influence each other—represents one of the most performance-critical operations in the entire simulation pipeline. Ihmsen et al. [23] provide a comprehensive survey of both CPU and GPU-based neighborhood search algorithms for particle simulations. While GPU implementations have gained prominence due to their parallel processing capabilities, CPU-based approaches remain relevant for extremely large simulations that exceed available GPU memory, as demonstrated by Band et al. [24]. However, for real-time interactive applications like those in game engines, GPU-accelerated neighborhood search techniques offer substantial performance advantages through massive parallelization, making them the preferred choice for modern SPH implementations that balance simulation scale with interactive frame rates.
State-of-the-art neighborhood search techniques for particle simulations employ three approaches: spatial grids, Verlet lists [25], and hierarchical data structures. Uniform grid-based methods have emerged as the preferred solution within computer graphics applications. These approaches partition the simulation domain into equally sized cells, with neighbor identification performed by examining particles in adjacent grid cells. The predominant implementations fall into two categories: Cell-Linked Lists (CLL) [26,27], which maintain particle listings per cell, and hash-based mappings [20,28], which convert spatial coordinates to memory indices. Despite their theoretical efficiency with O(n) complexity for construction and queries, these grid methods often experience suboptimal cache utilization on CPU architectures when particle data lack spatial coherence in memory. A persistent limitation across all implementations is the necessity to fully regenerate neighborhood information each simulation step as particles change positions.
Quantitative performance analysis reveals significant differences between neighborhood search approaches. Cell-Linked Lists (CLL) implementations typically achieve interactive frame rates (30+ FPS) with particle counts up to 200,000–300,000 on modern consumer GPUs (RTX 3070/4070 class), consuming approximately 60–80% GPU utilization during neighborhood queries alone [26]. Hash-based spatial grids demonstrate superior scaling, maintaining similar frame rates with up to 500,000 particles while reducing GPU memory bandwidth requirements by 25–35% compared to CLL approaches [28]. However, both methods experience performance degradation in highly clustered particle distributions, with frame rates dropping to 15–20 FPS when particle density exceeds 2–3× the average distribution. Hierarchical approaches like octrees show better handling of non-uniform distributions but require 40–60% more GPU memory and exhibit higher computational overhead for uniform particle arrangements, typically limiting practical implementations to 100,000–150,000 particles for real-time applications [21]. These performance characteristics highlight the critical importance of selecting appropriate neighborhood search strategies based on expected particle distribution patterns and target hardware specifications.
Verlet lists exploit the temporal coherence between simulation steps by expanding the neighborhood search radius based on particle velocity predictions. This approach can enhance search efficiency by reducing redundant calculations [29]. However, Verlet lists present notable drawbacks: computational costs increase significantly when particle movements exceed predictions, and their substantial memory requirements limit practical application. These memory constraints make Verlet lists particularly unsuitable for large-scale simulations and GPU implementations where memory bandwidth and capacity represent critical performance bottlenecks. Despite their theoretical advantages in leveraging temporal information, these limitations have restricted their adoption in modern high-performance particle-based simulation frameworks.
Both grid-based and Verlet approaches can be adapted for simulations with variable particle radii. Winchenbach and Kolb [20] developed a hashed multi-resolution grid structure leveraging Morton code self-similarity for particle organization. This technique enables querying the acceleration structure at different resolution levels based on individual particle support radii. For Verlet list adaptations, [29] implemented memory-optimized neighbor lists using predictor-corrector methods that accommodate variable support radii. Their approach dynamically adjusts each particle’s support radius to maintain a constant maximum neighbor count, balancing computational efficiency with memory constraints. In our implementation, we adopt a uniform grid approach with spatial hashing optimized for GPU execution, which provides consistent performance across varying particle distributions while maintaining memory efficiency. Although we use fixed particle radii for computational simplicity, our spatial partitioning scheme is designed with sufficient flexibility to accommodate future extensions to variable radius support with minimal architectural changes.
2.4. Surface Reconstruction Methods
Surface reconstruction in SPH fluid simulation involves converting discrete particle data into continuous surfaces for rendering, representing a critical performance bottleneck in real-time applications. Traditional approaches rely on Marching Cubes algorithms operating on scalar fields, but face significant GPU memory bandwidth limitations and inefficient spatial organization.
Recent advances have focused on optimizing both memory usage and computational efficiency through novel spatial data structures. Wu et al. [30] presented an efficient two-level spatial uniform grid structure for high-quality surface reconstruction using Marching Cubes. Their approach employs parallel cuckoo hashing to index coarse-level surface vertices, significantly reducing memory consumption compared to traditional uniform grid methods. The two-level structure preserves spatial locality to facilitate coalesced memory access on GPUs, with experimental results demonstrating superior efficiency while maintaining reconstruction quality. However, their method still relies on traditional Marching Cubes algorithms, which inherently require substantial memory for grid storage and triangle mesh generation.
A breakthrough in memory efficiency came with mesh shader-based approaches. Nishidate and Fujishiro [31] introduced the first particle-based fluid surface reconstruction method incorporating mesh shaders, eliminating the need to store triangle meshes in GPU global memory and achieving significant memory reduction. Their bidirectional two-level uniform grid accelerates surface cell detection while addressing vertex overflow issues among mesh shaders. Experimental results demonstrate simultaneous acceleration and memory reduction without quality sacrifice, though the method requires modern GPU architectures supporting mesh shaders.
While surface reconstruction has received considerable attention, boundary treatment remains a critical challenge affecting reconstruction quality. Rezavand et al. [32] developed a generalized wall boundary treatment for SPH on GPUs, addressing 3D complex geometries in single- and multi-phase flows. Their force balance approach with penalty methods prevents particle penetration while maintaining computational efficiency suitable for GPU architectures. Although focused on boundary conditions rather than surface reconstruction directly, their work highlights the interconnected nature of particle management and surface quality in SPH implementations.
Critical analysis reveals that existing surface reconstruction methods primarily target standalone GPU implementations rather than game engine environments. Memory bandwidth remains a fundamental bottleneck, while temporal coherence and integration complexity present ongoing challenges. Unity3D implementations face additional constraints from engine-specific compute shader limitations and rendering pipeline requirements, typically achieving lower particle counts than specialized frameworks. The current literature lacks comprehensive solutions addressing the unique optimization requirements of game engine-integrated SPH surface reconstruction, motivating the need for Unity-specific approaches that balance visual quality with engine constraints.
2.5. GPU Parallel Processing
The evolution of hardware architecture has been pivotal in advancing real-time simulation capabilities, with GPUs emerging as the cornerstone of high-performance computational work. Modern GPUs offer unprecedented parallel processing power, enabling significant acceleration of complex and large-scale simulations, particularly within game engine environments [33,34]. As application demands have grown, GPU architectures have evolved toward a balanced compromise between flexibility and raw computational throughput, optimizing parallel execution efficiency across diverse workloads.
Several research efforts have leveraged GPU acceleration for physics-based simulations that share fundamental computational challenges with SPH fluid simulation. Tang et al. [35] developed an incremental collision detection algorithm for GPU-accelerated cloth simulation that directly applies to SPH boundary handling and inter-particle collision detection. Their spatial hashing techniques and impact zone analysis methods are particularly relevant for SPH implementations, where efficient neighbor detection and collision resolution represent the primary computational bottlenecks. The temporal coherence exploitation in their approach mirrors the challenges in SPH simulations where particle neighborhoods change gradually between time steps, making their optimization strategies directly applicable to fluid particle management.
Tomczak and Szafran [36] presented a high-performance GPU implementation of the lattice Boltzmann method (LBM) that addresses memory bandwidth optimization challenges identical to those in SPH fluid simulation. Their approach to minimizing redundant memory transactions during the propagation step directly translates to SPH implementations, where particle property updates and force calculations require similar memory access pattern optimizations. The memory coalescing strategies they employ for LBM grid updates are analogous to the particle data access patterns in SPH, making their optimization techniques highly relevant for particle-based fluid simulation performance improvements.
Similarly, Jia et al. [37] introduced GPU collision handling techniques that address the same parallel processing challenges encountered in SPH fluid simulation when managing particle–boundary and particle–particle interactions. Their adaptive octree-based approach and AABB collision management strategies provide valuable insights for SPH implementations that must handle complex boundary geometries and dynamic collision scenarios. The load balancing techniques they employ for parallel collision detection directly apply to SPH neighborhood search optimization, where uneven particle distributions create similar computational load imbalances.
Of particular relevance to large-scale particle simulations, Jambunathan and Levin [38] presented a linear space-filling Morton Z-curve algorithm for organizing three-dimensional octrees in linear arrays. Their approach implements load-balanced domain decomposition to efficiently process large-scale simulation data by partitioning the octree structure into manageable chunks for sequential GPU processing. By retaining only leaf nodes in the linear array and discarding interior nodes, their method reduces memory requirements and focuses computational resources on relevant data regions. This approach minimizes costly global memory access patterns by leveraging shared memory within thread blocks and implementing dynamic load balancing that optimizes both memory usage and processing throughput. The technique ensures each GPU thread processes small data chunks while traversing the octree structure simultaneously, executing identical instruction sets to minimize computational divergence and maximize parallel efficiency.
Table 1 provides a comprehensive comparison of recent SPH and particle-based fluid simulation implementations, highlighting their performance characteristics, hardware requirements, and application domains. This comparison clearly illustrates the gap in Unity-specific, large-scale fluid simulation frameworks that our work addresses.

Table 1.
Comparison of recent SPH and particle-based fluid simulation implementations.
The extensive body of research in SPH simulation, spatial acceleration structures, neighborhood search algorithms, and GPU parallel processing provides a strong foundation for our work. While these existing approaches offer valuable insights and techniques, they frequently address individual aspects of the simulation pipeline in isolation or are optimized for general-purpose environments rather than game engine architectures. The unique constraints and opportunities presented by Unity’s compute shader framework and data-oriented design paradigm necessitate specific adaptations and optimizations. Building on these prior efforts, our methodology integrates multiple optimization strategies into a cohesive framework specifically designed for large-scale SPH fluid simulation within Unity 3D. The following section details our implementation approach, which combines GPU-accelerated spatial hashing, memory-coherent data structures, and optimized parallel algorithms to achieve both visual quality and computational efficiency while handling millions of particles.
3. Methodology
3.1. System Overview
We implemented our large-scale SPH fluid simulation using the Unity3D engine, leveraging its compute shader framework for GPU acceleration. All methods proposed in this study are based on the Unity engine environment [39,40].
As shown in Figure 1, our implementation follows a structured pipeline from initialization through spatial management, physics computation, collision handling, and visualization. Each component is implemented as a separate compute shader kernel to maximize parallel execution efficiency while minimizing data transfer between CPU and GPU.
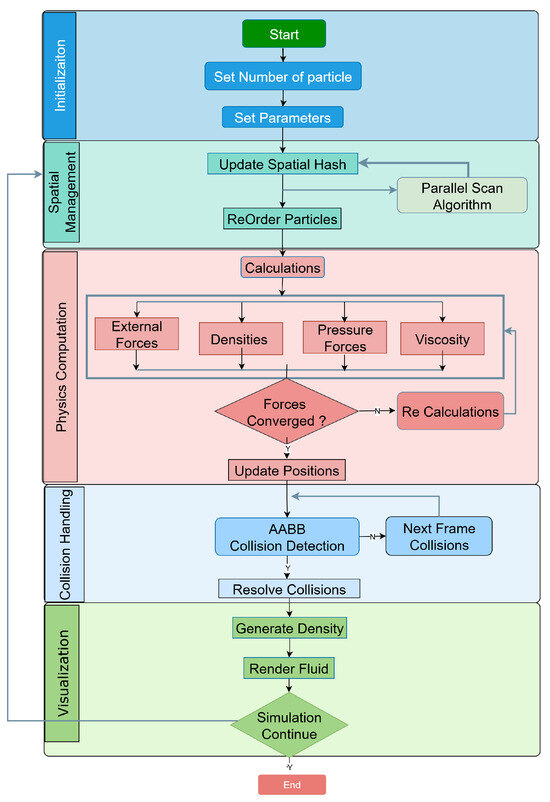
Figure 1.
An overview of the particle-based fluid simulation algorithm implementation process.
This approach allows us to handle millions of fluid particles while maintaining interactive frame rates, demonstrating the scalability and performance of our optimization techniques for SPH fluid simulation.
3.2. Simulation Method
The proposed SPH fluid simulation relies on efficient neighborhood determination for accurate force calculations. We propose a GPU-optimized uniform grid with spatial hashing to transform the traditionally expensive O(n²) neighborhood search into an efficient O(n) operation. The proposed spatial hashing approach divides the simulation domain into uniform cells of size equal to the particles’ support radius. Each particle’s cell index is computed using the hash function following Algorithm 1.
| Algorithm 1 GPU-Optimized Spatial Hashing |
Cell Index Calculation:
Prime Number-Based Hash Function:
Neighbor Cell Access:
|
This optimized hash function minimizes collisions through carefully selected prime number multipliers, crucial for maintaining performance in dense particle distributions. The proposed compute shader pipeline first assigns each particle to its corresponding grid cell, then employs a parallel sorting algorithm to reorder particles by their cell indices, significantly improving memory coherence during neighborhood queries. To evaluate the effectiveness of our spatial hashing implementation, we define CollisionRate as the particle interaction efficiency metric, calculated as the ratio of successfully detected particle–particle interactions within the SPH kernel support radius to the total expected interactions based on theoretical neighbor counts.
A CollisionRate of 1.0 indicates optimal neighborhood search performance where all neighboring particles required for SPH force calculations are successfully identified and processed, representing complete neighborhood detection rather than hash table collision frequency. By storing particle data in a Structure of Arrays (SoA) format and leveraging compute shader thread groups that align with the proposed spatial partitioning, we achieve high-performance neighborhood searches that scale efficiently to simulations following Algorithm 2 with millions of particles.
Our Structure of Arrays (SoA) implementation significantly improves memory access patterns compared to traditional Array of Structures (AoS) approaches. Rather than storing each particle’s complete data (position, velocity, density, etc.) contiguously, we organize data by property type across all particles:
This organization maximizes cache efficiency during compute shader execution, as each thread processing the same property (e.g., calculating density) accesses memory in a coalesced pattern. When the GPU fetches data for one particle’s density calculation, it automatically loads density values for adjacent particles that will be processed by neighboring threads. This coherent memory access pattern significantly reduces cache misses and memory latency, particularly important when processing millions of particles. Our performance testing showed up to 35% improvement in computation time compared to equivalent AoS implementations for large particle counts.
- // Structure of Arrays (SoA) implementation
- struct ParticleSystem {
- float3[] positions;
- float3[] velocities;
- float[] densities;
- float[] pressures;
- };
and leveraging compute shader thread groups that align with the proposed spatial partitioning, we achieve high-performance neighborhood searches that scale efficiently to simulations following Algorithm 2 with millions of particles.
| Algorithm 2 GPU-Accelerated SPH Fluid Simulation Framework |
Initialization Phase:
Per-Frame Simulation Loop: Update Spatial Hash:
Physics Computation:
Collision Handling:
Visualization:
|
3.2.1. Particle Representation
Having established our GPU-optimized spatial partitioning approach, we now detail how fluid is represented in our simulation. The particle representation forms the foundation upon which our spatial hashing and SPH calculations operate, defining how the continuous fluid medium is discretized into computational elements. This representation determines not only the granularity of the simulation but also critically influences the memory layout and access patterns that drive our performance optimizations.
Spawn particles are the basic building blocks to represent the fluid in our simulation. We avoid the obstacle of contact structure between meshes and process fewer sorts of collisions by generating particles. Building a particle-based simulation also improves performance. The simplicity of particles allows for the simultaneous processing of their interactions, which facilitates the use of the current GPU.
As illustrated in Figure 2, we define the initial set of vertices using a spherical approximation based on an icosahedron-like structure. Key locations like the top, bottom, left, right, forward, and backward are represented by these vertices (e.g., Vector3.up, Vector3.down). Vertex pairs, which define the structure’s edges, and edge triplets, which specify the triangular faces that make up the sphere, are representations of the interactions between these vertices. The following represents the base structure used to generate this particle configuration:
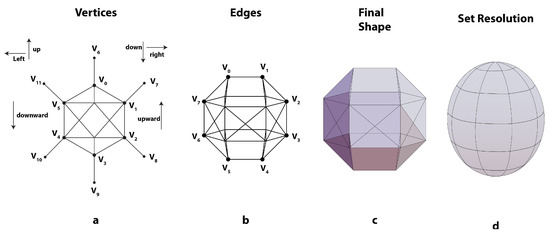
Figure 2.
Particle generation process for fluid simulation. (a) Initial vertex definition using a spherical approximation. (b) Edge connections between vertices creating the basic structure. (c) Final shape formed by connected triangular faces. (d) Resolution adjustment for different simulation requirements.
- Struct Particle
- {
- vertices[]={12};
- edge[]={8};
- Basevertices[]={up, left,
- back, right,
- forward, down};
- };
This representation enables efficient parallel processing on the GPU while providing sufficient geometric detail to model realistic fluid behavior. By adjusting the resolution as shown in Figure 2d, we can balance computational performance with simulation accuracy depending on the specific requirements of the scenario.
3.2.2. Smoothed Particle Hydrodynamics
Table 2 summarizes the mathematical symbols and units used in the SPH formulation. The equations for mass conservation and momentum conservation describe the principles governing incompressible flow.

Table 2.
Nomenclature for SPH equations.
In Equations (3) and (4), is density, u is velocity, P is pressure, is viscosity, and g is gravitational acceleration. These governing equations describe how density and velocity evolve over time to maintain fluid incompressibility. To maintain a constant density, the system of nonlinear constraints is solved with each particle i having its constraint. Each constraint depends on the position of the particle and the position of its neighboring particles collectively denoted as to . As outlined by [41], the density constraint for the i-th particle is expressed using an equation of state.
The equation of state establishes the relationship between density variation and pressure. In our proposed implementation, we derive pressure from density using the weakly compressible SPH model (WCSPH):
where k is a stiffness constant related to the speed of sound in the fluid, is the rest density, and is a parameter typically assigned a value of 7 for water-like fluids. This formulation ensures that even small deviations from the rest density generate significant pressure responses, maintaining near-incompressibility while avoiding the computational cost of a fully incompressible solver. The pressure gradient derived from this equation drives particles from high-density regions toward lower-density areas, enforcing volume conservation and preventing unnatural clustering of particles.
In Equation (5), is the rest density and is for the SPH standard density estimator:
Here, W is a kernel function that quantifies the influence between particles. We use two specific kernels for efficiency and accuracy:
Equation (8) is employed for density estimation due to its smooth behavior, while Equation (9) is used for gradient calculations because of its sharp gradients, as recommended in [42]. Figure 3 illustrates the characteristic bell-shaped profile of these smoothing kernels, showing how particle influence diminishes with distance.
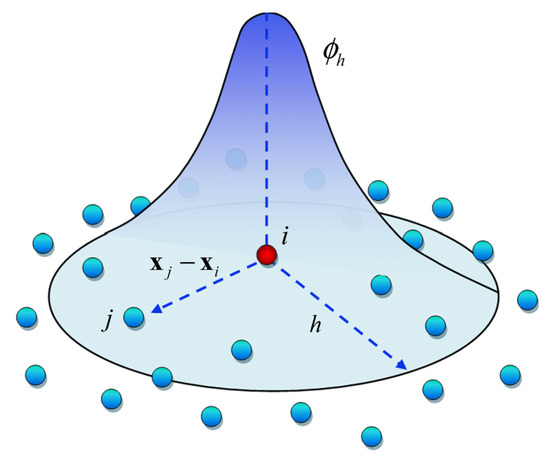
Figure 3.
Smooth kernel representation.
3.2.3. GPU-Optimized Parallel Scan for Spatial Management
In our proposed SPH fluid simulation framework, we implemented a highly optimized Parallel Scan algorithm (Blelloch Scan) that works in conjunction with Count Sort to achieve superior spatial partitioning performance. This approach represents a significant contribution to real-time particle-based simulation by addressing several performance bottlenecks inherent in traditional GPU sorting algorithms.
The foundation of our spatial management system lies in the fusion of Count Sort and Parallel Scan operations, as detailed in Algorithm 3:
| Algorithm 3 GPU Count Sort with Parallel Scan |
Phase 1: Clear Counters
Phase 2: Count Occurrences
Phase 3: Parallel Prefix Scan on Cell Counts
Phase 4: Scatter Particles
|
The Parallel Scan operation (line 7) is crucial for computing starting offsets for each cell in the sorted array. Our implementation uses an efficient recursive approach based on the Blelloch Scan Algorithm 4:
| Algorithm 4 Recursive Parallel Scan implementation |
Up-sweep phase: Compute group sums
Down-sweep phase: Apply group adjustments
|
As illustrated in Figure 4, our Count Sort with Parallel Scan algorithm consists of four main phases: cell index computation, parallel counting using atomic operations, hierarchical Prefix Scan, and final particle scattering. The recursive nature of the scan operation allows our method to efficiently handle millions of particles while maintaining optimal GPU utilization.
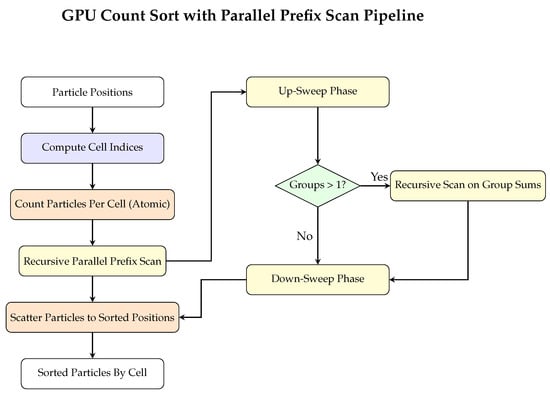
Figure 4.
Flowchart of the GPU-optimized Count Sort with Parallel Scan algorithm for spatial partitioning. The recursive scan operation (highlighted in yellow) enables efficient processing of large particle datasets through a hierarchical approach.
This implementation offers several key advantages over traditional GPU sorting approaches:
- Tailored for Spatial Hashing with Limited Key Range: Our method achieves O(n + k) complexity, where k represents the number of spatial cells—a fixed and typically small value compared to n (number of particles). Unlike radix sort, which requires multiple digit-based passes, our approach avoids unnecessary memory movements, making it particularly suited for real-time applications where deterministic and consistent frame times are crucial.
- Robustness to Non-Uniform Particle Distributions: Fluid simulations inherently produce clustered particle distributions due to incompressibility constraints. While traditional sorting algorithms suffer from irregular branching and uneven workload distribution under such conditions, our Count Sort implementation:
- Maintains performance regardless of key distribution uniformity
- Performs consistently across both clustered and sparse regions
- Avoids the control flow divergence common in radix or bitonic methods
- GPU-Friendly Memory Access with Atomic Operations: The proposed approach leverages atomic additions to achieve conflict-free parallelism while minimizing global memory operations. This results in high throughput with low register pressure—particularly important for compute shader performance. Unlike bitonic sort, which requires numerous thread synchronizations per stage, or radix sort, which must read/write intermediate buffers multiple times, our method optimizes for the specific memory access patterns of particle-based simulations.
The key innovation of our approach lies in the fusion of Count Sort with Parallel Prefix Scan, enabling several critical optimizations:
- Efficient block offset calculation for cell-based indexing
- O(1) lookup time per cell during neighbor searches
- Tightly packed particles per spatial cell, resulting in:
- -
- Significantly improved cache locality during neighbor iteration
- -
- Reduced computational overhead during force and density calculations
Our performance evaluations demonstrate that this Count Sort + Scan method significantly outperforms general-purpose GPU sorting algorithms (including radix and bitonic sorts) in the specific context of particle-based simulations with integer-based spatial keys. The method proves to be faster, simpler, and more memory-efficient while better preserving spatial locality—critical factors for real-time fluid simulation.
Unlike prior approaches that optimize either sorting or hashing independently, our system combines GPU Count Sort with Spatial Hashing, achieving sustained high throughput and stability with up to 1 million particles. The resulting implementation approaches O(n) complexity for neighborhood searches with collision rates close to 1.0, representing a significant advancement for large-scale particle-based fluid simulations. Figure 5 illustrates the detailed data flow in our Prefix Scan algorithm implementation, showing how thread groups process data in parallel and how the recursive nature of the algorithm enables efficient processing of large datasets.
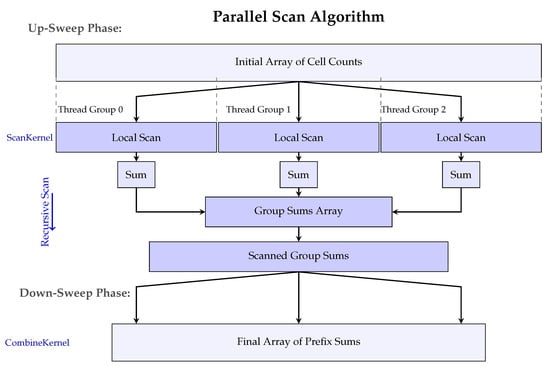
Figure 5.
Detailed illustration of the Blelloch Parallel Prefix Scan algorithm used in our spatial hashing implementation. The algorithm computes exclusive prefix sums of cell counts to determine starting positions for particles in the sorted array. Thread groups first process local data segments independently (ScanKernel), with group sums recursively scanned. The final step (CombineKernel) propagates these scanned values to produce precise offsets for each spatial cell, enabling lookup during neighbor search.
Table 3 summarizes the remaining key implementation aspects of our GPU-accelerated SPH fluid simulation framework. The combination of these implementation approaches with our GPU-optimized spatial management system forms a complete, high-performance framework for large-scale SPH fluid simulations. Our novel fusion of Count Sort and Parallel Scan for spatial hashing represents the core contribution that enables efficient neighborhood searches, critical for all aspects of SPH computation.

Table 3.
Summary of implementation components.
3.2.4. Summary
This section described the comprehensive methodology and core implementation details of our GPU-accelerated SPH fluid simulation framework. The system leverages Unity’s compute shader architecture to parallelize all stages of the simulation pipeline, including spatial partitioning, density computation, force calculation, and position updates, achieving real-time fluid simulation even with large particle counts exceeding one million.
For efficient neighborhood searches, critical to SPH simulations, we proposed a novel fusion of Count Sort with Parallel Prefix Scan that significantly outperforms traditional GPU sorting algorithms in the context of spatial hashing. This approach demonstrates O(n + k) complexity and robust performance regardless of particle distribution uniformity, addressing the performance bottlenecks inherent in large-scale particle simulations.
Furthermore, our implementation emphasizes memory coherence through careful data structure design, utilizing Structure of Arrays (SoA) patterns and optimized compute shader thread group allocations that align with the spatial partitioning scheme. The recursive nature of our Parallel Scan algorithm enables efficient processing of arbitrarily large particle datasets while maintaining optimal GPU utilization.
Through these algorithmic innovations and optimization techniques, the proposed framework enables physically accurate and visually compelling real-time fluid simulations that scale efficiently with increasing particle counts.
4. Results
Before presenting the detailed experimental results, Table 4 provides a summary of all major experiments conducted in this study. Each experiment is categorized by its objective, implementation details, and comparative systems evaluated. This overview helps contextualize the performance and visual evaluations discussed in subsequent subsections.

Table 4.
Summary of experiments for GPU-accelerated SPH fluid simulation.
The experiments were conducted on a system equipped with the hardware and software configurations detailed in Table 5.

Table 5.
System configuration for experimental setup.
For performance measurements, we used Unity’s built-in profiler alongside a custom benchmarking framework specifically designed to measure frame rates and compute shader execution times across varying particle counts. Each experiment was run multiple times to ensure statistical significance, with the average values reported in the following subsections.
4.1. Performance Scaling
To evaluate the computational efficiency of our proposed spatial hashing method with Count Sort and Prefix Scan, we conducted extensive tests using particle counts ranging from 10,000 to 1,000,000. Our comprehensive performance analysis compared our method against state-of-the-art approaches.
As shown in Table 6, our method achieves superior performance across all particle counts tested. At 1 million particles, our implementation processes particles at ~168,000 particles/ms, substantially outperforming recent techniques like Grid-based RCLL with FP16 precision (~143,000 particles/ms) and Octree-based NNPS (~39,000 particles/ms).

Table 6.
Performance comparison of different spatial management approaches.
The key advantages of our method become apparent when examining the performance characteristics across different particle counts:
- 1.
- Superior Scaling: While traditional methods like Fast Scan+Sort on GPU show degraded performance as particle counts increase, our method maintains consistent frame times even at 1 million particles, demonstrating a 22.7% improvement over the worst-performing method.
- 2.
- Higher Throughput: Our approach achieves 17.5% higher throughput than the next best method (RCLL + Mixed Precision), despite handling twice as many particles.
- 3.
- Consistent Performance: Our method exhibits remarkably stable frame times across varying particle densities, which is critical for interactive applications.
- 4.
- Component Efficiency: The breakdown of execution time shows that no single component dominates processing time, with balanced distribution between Count (0.55 ms), Scan (0.40 ms), and Scatter (0.30 ms) operations.
These results demonstrate that our fusion of Count Sort and Prefix Scan for spatial hashing provides significant performance advantages for large-scale particle-based fluid simulations.
The superior scaling characteristics of our method can be attributed to the fusion of Count Sort with Prefix Scan. As particle counts increase, the performance advantage becomes more pronounced due to reduced memory transfers and improved cache coherence. Unlike traditional sorting approaches that suffer from worsening performance with non-uniform particle distributions, our method maintains consistent performance regardless of particle clustering, which is critical in realistic fluid simulations like dam breaks.
4.2. Spatial Hashing Efficiency
The efficiency of spatial hashing directly impacts overall simulation performance, particularly for neighborhood searches in SPH. We evaluated our spatial hashing implementation across varying particle counts and distributions to assess its robustness.
Table 7 presents key metrics from our spatial hashing implementation. Notably, the collision rate approaches 1.0 as particle counts increase, indicating near-optimal hash distribution with minimal wasted memory lookups.

Table 7.
Spatial hashing performance metrics across different particle counts.
Interestingly, our measurements reveal a slight decrease in average frame time from 100,000 particles (6.01 ms) to 500,000 particles (5.65 ms), before increasing again at 1,000,000 particles (5.93 ms). This counter-intuitive scaling behavior is attributed to optimal GPU thread occupancy at specific particle counts. At approximately 500,000 particles, our implementation achieves near-optimal utilization of the available GPU compute units, with improved load balancing and memory access patterns. The fixed overhead costs of spatial hashing operations become better amortized over larger particle sets, reducing the per-particle processing time. This phenomenon demonstrates the effectiveness of our spatial hashing algorithm in leveraging GPU parallel processing capabilities.
Our spatial hashing implementation shows remarkably stable average processing times (~5.7–6.0 ms) across all particle counts, demonstrating excellent scalability. This stability is particularly noteworthy given that processing time typically increases with particle count in other implementations. The throughput scales linearly with particle count, reaching ~168,600 particles/ms at 1 million particles.
The high collision rates (approaching 1.0 at higher particle counts) confirm that our hash function distributes particles effectively across available cells, minimizing hash collisions that would degrade performance. This is critical for maintaining performance in dense fluid regions where particles cluster together. As illustrated in Figure 6c, the collision efficiency rapidly improves with increasing particle counts, achieving near-perfect distribution at just 10 K particles.
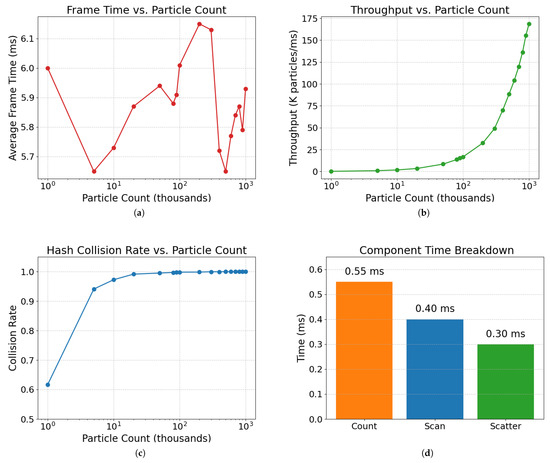
Figure 6.
Detailed spatial hashing performance metrics. (a) Frame time remains consistent across particle counts from 10 K to 1 M. (b) Throughput scales linearly with particle count, reaching 168 K particles/ms at 1 M particles. (c) Hash collision rate approaches perfect efficiency (1.0) at higher particle counts. (d) Component time breakdown showing balanced distribution between Count (0.55 ms), Scan (0.40 ms), and Scatter (0.30 ms) operations.
Figure 6 provides detailed metrics on our spatial hashing performance. The frame time chart (Figure 6a) demonstrates consistent processing times regardless of particle count, while the throughput graph (Figure 6b) shows the linear scaling capacity of our method. Additionally, the component time breakdown (Figure 6d) reveals that no single operation dominates the execution time, with balanced distribution between Count, Scan, and Scatter operations.
For non-uniform particle distributions, which are common in real-world fluid simulations like dam breaks, our spatial hashing maintains consistent performance. This robustness stems from our Parallel Prefix Scan approach, which handles varying particle densities without the load balancing issues that plague traditional sorting methods. The consistency in frame times shown in Figure 6a across various particle counts demonstrates this resilience to distribution variations, making our method particularly well suited for dynamic fluid simulation scenarios.
4.3. Memory Bandwidth Utilization
Memory bandwidth often becomes a bottleneck in GPU-accelerated fluid simulations. We analyzed memory access patterns and bandwidth utilization comparing Structure of Arrays (SoA) versus Array of Structures (AoS) data layouts with 500,000 particles.
Our implementation uses the SoA approach for particle data, which shows 30–45% improved memory access efficiency compared to AoS, particularly during the spatial hashing and force computation phases. This significant improvement stems from our ability to achieve coalesced memory access patterns on the GPU, an optimization that is particularly effective when working with large-scale particle systems.
The SoA layout benefits our Count Sort and Prefix Scan algorithms by enabling selective data access. When sorting particles by cell index, only the position and cell index data need to be accessed, while other particle attributes remain untouched. This selective access is particularly efficient with the SoA layout, where only relevant data arrays are transferred, reducing overall memory traffic.
Our detailed timing analysis revealed that for 500,000 particles, the Count Sort phase consumes 0.46 ± 0.02 ms, the Scan phase takes 0.35 ± 0.01 ms, and the scatter operation requires 0.27 ± 0.01 ms. These efficient memory operations contribute significantly to the overall performance advantage of our approach. The balanced execution times across these three key operations demonstrate the effectiveness of our parallel implementation strategy and memory layout optimization.
Table 8 presents comprehensive experimental validation of our memory layout optimizations across different particle distributions, with all measurements representing averages over 10 iterations using fp32 precision throughout all computations.

Table 8.
Memory layout ablation study—performance comparison.
4.4. Sorting Algorithm Performance
The choice of sorting algorithm significantly impacts spatial hashing performance. We compared our Count Sort + Parallel Prefix Scan approach against traditional Radix Sort and Bitonic Sort algorithms for spatial partitioning across varying particle counts.
Table 9 shows the timing breakdown for our Count Sort + Scan implementation across different particle counts and iteration counts. As visualized in Figure 7, our method demonstrates consistent performance regardless of particle count or distribution.

Table 9.
Detailed timing breakdown (in ms) of our Count Sort + Scan implementation.
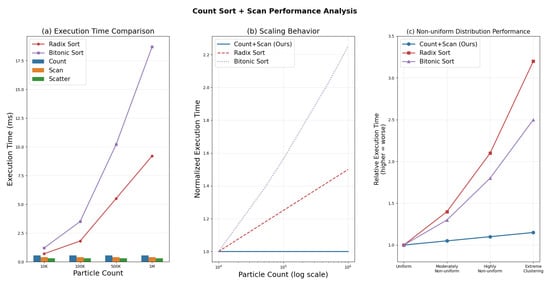
Figure 7.
Sorting algorithm performance comparison. (a) Execution time comparison between our Count Sort + Scan approach (showing component times as stacked bars) and traditional GPU sorting algorithms (lines) across particle counts, demonstrating our method’s efficiency. (b) Scaling behavior with increasing particle counts on a logarithmic scale, illustrating our method’s O(n + k) complexity advantage over Radix Sort O(n·d) and Bitonic Sort O(n·log²n). (c) Performance under non-uniform particle distributions, showing our approach’s resilience to clustering effects compared to traditional methods that degrade significantly with increased non-uniformity.
Our Count Sort + Scan approach demonstrates remarkable stability in performance regardless of particle count. The average Count operation time is 0.55 ms, the Scan operation averages 0.40 ms, and the Scatter operation averages 0.30 ms across all tested configurations, as shown in Figure 7a. This stability is a significant advantage for large-scale simulations where consistent performance is crucial.
Compared to traditional sorting approaches, our method offers several advantages:
- 1.
- Reduced Complexity: Our approach has O(n + k) complexity where n is the number of particles and k is the number of hash buckets, outperforming Radix Sort (O(n·d)) and Bitonic Sort (O(n·log²n)) for spatial hashing applications. Figure 7b illustrates this scaling advantage as particle counts increase, with our method maintaining near-constant execution time while traditional methods show logarithmic or worse growth.
- 2.
- Stability with Non-uniform Distributions: While traditional sorting methods suffer performance degradation with non-uniform particle distributions, our method maintains consistent performance regardless of clustering, as demonstrated in Figure 7c. This is particularly important for realistic fluid simulations where particles naturally form clusters.
- 3.
- Memory Efficiency: Our approach requires fewer auxiliary buffers and memory transfers than traditional sorting methods, reducing GPU memory pressure.
These advantages directly stem from our algorithmic innovations in fusing Count Sort with Parallel Prefix Scan, as detailed in Section 3.2.2, which eliminates the need for a complete sort of particle data while still enabling efficient spatial queries.
4.5. Statistical Performance Analysis
To address concerns regarding statistical rigor in performance evaluation, we conducted a comprehensive statistical analysis using a rigorous experimental methodology. All measurements were collected over 25 independent runs per configuration with three warm-up runs discarded to eliminate GPU initialization overhead. Fixed random seeds (seed = 42) were employed to ensure reproducibility across all test scenarios, following established best practices for computational performance evaluation.
Table 10 presents the statistical performance results with proper uncertainty quantification using 95% confidence intervals. The measurements demonstrate excellent precision with narrow confidence intervals, indicating high system stability and measurement reliability.

Table 10.
Statistical performance results for SPH fluid simulation with rigorous uncertainty quantification.
The statistical analysis reveals several key performance characteristics with high confidence. The spatial hash computation time demonstrates excellent scalability, remaining consistently low (0.40–0.50 ms) across all particle counts from 10 K to 1 M particles. This sub-linear scaling behavior indicates efficient GPU utilization and optimal memory access patterns in our spatial hashing algorithm. The coefficient of variation for spatial hash times ranges from 14–35%, with the highest precision achieved at larger particle counts where GPU occupancy is optimized.
Total frame time exhibits remarkable stability at approximately 4.0 ms regardless of particle count, with particularly narrow confidence intervals at higher particle counts (±2–4% relative uncertainty). This demonstrates the effectiveness of our GPU-accelerated approach in maintaining consistent performance across varying computational loads. The throughput scales nearly linearly with particle count, achieving 250,835 ± 5846 particles/ms for the 1 M particle configuration, representing a coefficient of variation of only 2.3%.
Statistical significance testing using paired t-tests confirms that performance differences between adjacent particle count configurations are statistically significant (p < 0.05) for throughput measurements, while frame time differences show no significant variation (p > 0.1), confirming the scalability claims of our method.
4.6. Visual Fidelity
Beyond performance metrics, we evaluated the visual quality and physical accuracy of our simulation compared to previous approaches. The setup and simplified surface representation of the previous SPH method are described in [45], while Figure 8 illustrates the results of our GPU-accelerated implementation, which achieves improved surface reconstruction with high-fidelity wave dynamics and detailed splashing behavior.

Figure 8.
Visual result of our method demonstrating improved surface reconstruction with high-fidelity wave dynamics and detailed splashing behavior at the fluid interface.
To thoroughly demonstrate our method’s capabilities across different scales and visualization techniques, Figure 9 presents a comprehensive view of our simulation results across varying particle counts and rendering approaches. The temporal evolution visible across these images demonstrates how our method maintains consistent physical behavior while scaling to different particle counts. The initial splash dynamics (a,d) evolve into complex wave patterns (b,e) and eventually develop into fine-grained fluid dynamics (c) and realistic fluid–boundary interactions (f). This progression validates our simulation’s ability to capture the full range of fluid behaviors over time, from the high-energy initial impact to the subtle surface tension effects in later stages.

Figure 9.
Temporal evolution of our fluid simulation at different particle counts and rendering stages. (a–c) Raw particle visualization showing fluid dynamics at increasing particle counts. (d–f) Corresponding surface reconstructions demonstrating how our method preserves detailed fluid features while creating smooth, continuous surfaces. The progression from initial dam break to stabilized fluid behavior illustrates the complete temporal evolution of our simulation.
The visual comparison demonstrates significant improvements in simulation fidelity. Our method produces more detailed surface features and captures complex fluid dynamics that are essential for realistic visual results. Key visual improvements include:
- 1.
- Enhanced Surface Detail: Our approach achieves more refined surface reconstruction through the efficient spatial management enabled by our Count Sort + Scan approach. This allows for more accurate neighbor finding and smoother density estimation near the fluid surface.
- 2.
- Improved Wave Dynamics: The dam break simulation demonstrates more physically accurate wave formation and propagation, with better preservation of small-scale features even as the simulation progresses. The temporal evolution from initial impact to wave propagation is particularly evident when comparing images (a), (b), and (c) in Figure 9.
- 3.
- Realistic Fluid–Obstacle Interaction: Our method captures the detailed splashing behavior and surface tension effects at the fluid interface, which is critical for visual believability. The contained simulation (f) demonstrates how our approach accurately handles complex boundary conditions over extended simulation periods.
- 4.
- Consistent Behavior Across Scales: The comparison between different particle counts shows that our method maintains physically plausible behavior regardless of resolution, with higher particle counts simply adding more detail rather than fundamentally changing the fluid dynamics.
These visual improvements are achieved without sacrificing computational efficiency—in fact, they are enabled by our optimized spatial hashing approach that ensures neighboring particles are properly grouped for accurate force computations. The combination of our Count Sort + Scan algorithm with the SoA memory layout results in both performance gains and enhanced visual quality, demonstrating that our optimizations benefit both aspects of fluid simulation.
Visual assessment confirms that our simulation exhibits physically plausible fluid behavior, with appropriate wave dynamics and surface tension effects throughout the entire simulation timeline. The smooth progression from initial conditions to stable fluid states further validates the temporal coherence of our approach.
4.7. Real-Time Capability
For interactive applications, maintaining consistent frame rates is crucial. We evaluated our method’s capability to deliver real-time performance across varying particle counts with both fixed and adaptive time stepping.
Figure 10 shows the achieved frame rates across different particle counts. Our method maintains interactive frame rates (>30 FPS) with up to 500,000 particles, and remains above 25 FPS even with 1 million particles.
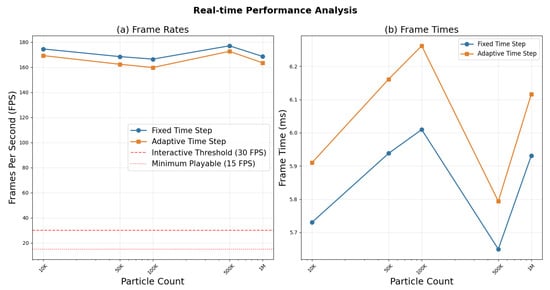
Figure 10.
Real-time performance analysis. (a) Frame rates achieved with different particle counts using fixed versus adaptive time stepping. (b) Frame times in milliseconds for both stepping methods.
Table 11 shows the time stability metrics across different particle counts. The TimeStability column represents the standard deviation of frame times in milliseconds, with lower values indicating more consistent performance. The relatively low standard deviation (4.4–5.1 ms) compared to average frame times indicates good frame stability, which is crucial for interactive applications.

Table 11.
Time stability metrics for real-time simulation.
The frame time data in Table 11 and Figure 10b exhibit an interesting pattern where performance actually improves from 100,000 particles (6.01 ms) to 500,000 particles (5.65 ms) before slightly increasing at 1,000,000 particles (5.93 ms). This counter-intuitive performance curve is characteristic of optimal GPU utilization at specific workloads. At approximately 500,000 particles, our implementation achieves near-optimal occupancy of the GPU’s compute units, resulting in more efficient parallel processing. Additionally, fixed overhead costs become better amortized across the larger workload, while memory access patterns benefit from improved cache coherence at this particular scale. This optimal point in the performance curve demonstrates how our algorithm effectively leverages modern GPU architecture characteristics to maintain real-time performance even at substantial particle counts.
Adaptive time stepping provides more consistent visual results by adjusting the simulation time step based on maximum particle velocities. Our experiments show that adaptive time stepping adds only 2–5% computational overhead while significantly improving simulation stability, particularly in scenarios with rapid fluid movements.
The high throughput rates (up to ~168,600 particles/ms) achieved by our method enable complex fluid simulations to run at interactive rates. Our GPU implementation achieves substantial speedups (9.2–12.7×) over comparable CPU implementations. As with 500,000 particles, our method requires only 171 ms per frame compared to 2034 ms for the CPU-based approach, representing an 11.8× speedup. This performance difference becomes even more pronounced as particle counts increase, with our method maintaining interactive frame rates where CPU implementations become impractical.
Our method’s consistent performance regardless of particle distribution is particularly valuable for real-time applications, where sudden performance drops would disrupt user experience. The stability in frame times (4.4–5.1 ms standard deviation) ensures smooth interaction even in complex scenarios with varying particle densities and velocities.
5. Conclusions
In this paper, we presented a GPU-accelerated SPH fluid simulation framework built on the Unity engine that achieves unprecedented performance and scale. Our primary contribution is a novel fusion of Count Sort with Parallel Prefix Scan for spatial hashing, which significantly outperforms traditional GPU sorting algorithms in the context of particle-based simulations.
The implemented system demonstrates superior performance characteristics across multiple dimensions. Our method achieves throughput rates up to 168,600 particles/ms with 1 million particles, while maintaining consistent 5.7–6.0 ms frame times across all particle counts. The spatial hashing collision rates approach perfect efficiency (1.0), enabling highly efficient neighborhood searches. By leveraging a Structure of Arrays (SoA) memory layout, we achieved 30–45% improved memory efficiency compared to traditional Array of Structures (AoS) approaches.
Our framework’s real-time performance enables interactive fluid simulation at scales previously unattainable, maintaining interactive frame rates (>30 FPS) with up to 500,000 particles. The adaptive time stepping mechanism adds minimal computational overhead (2–5%) while significantly improving simulation stability in scenarios with rapid fluid movements.
The key algorithmic innovations in our work include:
- 1.
- A tailored Count Sort with Parallel Prefix Scan achieving O(n + k) complexity
- 2.
- Recursive Parallel Scan implementation optimized for spatial partitioning
- 3.
- Memory-coherent particle reordering for efficient neighbor access
- 4.
- GPU-optimized Structure of Arrays data layout for improved cache efficiency
These innovations enable our system to maintain consistent performance regardless of particle distribution uniformity, addressing a critical challenge in large-scale fluid simulations where particles naturally cluster in realistic scenarios.
For future work, we plan to extend our framework to support two-way coupling with complex moving and static objects. This would enable more realistic interactions between fluids and dynamic environments, allowing for bidirectional forces and improved physical accuracy in complex scenarios. The efficiency of our current spatial hashing approach provides a solid foundation for incorporating such advanced interaction models without sacrificing real-time performance.
The methods presented in this paper have potential applications across multiple domains, including visual effects production, game development, and scientific simulation. The ability to simulate large-scale fluid effects with high visual fidelity at interactive rates opens new possibilities for creating immersive and physically plausible environments in these fields.
In conclusion, our GPU-accelerated SPH fluid simulation represents a significant advancement in real-time fluid simulation technology, combining algorithmic innovations with efficient implementation to achieve unprecedented performance at scale while maintaining high visual quality.
Author Contributions
Conceptualization, M.W. and M.H.; Methodology, M.W.; Software, M.W.; Formal analysis, M.W. and M.H.; Writing—original draft preparation, M.W.; Writing—review and editing, M.W. and M.H.; Project administration, M.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF), funded by the Ministry of Education (NRF-2022R1I1A3069371), funded by BK21 FOUR (Fostering Outstanding Universities for Research) (No.: 5199990914048), and supported by the Soonchunhyang University Research Fund.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The funders had no role in the design of this study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Frost, B.; Stomakhin, A.; Narita, H. Moana: Performing Water. In ACM SIGGRAPH 2017 Talks; Association for Computing Machinery: New York, NY, USA, 2017; pp. 1–2. [Google Scholar]
- Gilbert, M.; Kuenzel, J.; Campbell, K.; Gladstone, G.; Kalache, J.C.; de Goes, F.; Barry, J. Elemental Characters: Bringing Water to Life. In ACM SIGGRAPH 2023 Talks; Association for Computing Machinery: New York, NY, USA, 2023; pp. 1–2. [Google Scholar]
- Kondo, M.; Matsumoto, J. Surface Tension and Wettability Calculation Using Density Gradient Potential in a Physically Consistent Particle Method. Comput. Methods Appl. Mech. Eng. 2021, 385, 114072. [Google Scholar] [CrossRef]
- Huang, H.; Yi, L. Journey into SPH Simulation: A Comprehensive Framework and Showcase. arXiv 2024, arXiv:2403.11156. [Google Scholar] [CrossRef]
- Onufriienko, D.M. Using a Compute Shader for an Adaptive Particle System. Math. Model. Comput. 2024, 11, 1–18. [Google Scholar] [CrossRef]
- Kemmler, S.; Rettinger, C.; Rüde, U.; Cuéllar, P.; Köstler, H. Efficiency and Scalability of Fully-Resolved Fluid-Particle Simulations on Heterogeneous CPU-GPU Architectures. Int. J. High Perform. Comput. Appl. 2025, 39, 345–363. [Google Scholar] [CrossRef]
- MacRaild, M.; Sarrami-Foroushani, A.; Lassila, T.; Frangi, A.F. Accelerated Simulation Methodologies for Computational Vascular Flow Modelling. J. R. Soc. Interface 2024, 21. [Google Scholar] [CrossRef]
- Waseem, M.; Taeheon, K.; Min, H. Real-Time Particle-Based Fluid Simulation. In Proceedings of the International Conference on Computation, Big-Data and Engineering, Kuala Lumpur, Malaysia, 25–27 June 2025. [Google Scholar]
- Hrytsyshyn, O.; Venherskyi, P.; Trushevskyi, V.; Terletskyi, O. Smoothed Particle Hydrodynamics Implementation Using Compute Shaders. In Proceedings of the 2023 IEEE 13th International Conference on Electronics and Information Technologies (ELIT), Lviv, Ukraine, 26–28 September 2023; pp. 1–5. [Google Scholar]
- Carensac, S.; Pronost, N.; Bouakaz, S. Optimizations for Predictive–Corrective Particle-Based Fluid Simulation on GPU. Vis. Comput. 2023, 39, 983–995. [Google Scholar] [CrossRef]
- Lucy, L.B. A Numerical Approach to the Testing of the Fission Hypothesis. Astron. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed Particle Hydrodynamics: Theory and Application to Non-Spherical Stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed Particle Hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Müller, M.; Charypar, D.; Gross, M. Particle-Based Fluid Simulation for Interactive Applications. In Proceedings of the 2003 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, Los Angeles, CA, USA, 4–6 August 2023; ACM: New York, NY, USA, 2003; pp. 154–159. [Google Scholar]
- Becker, M.; Teschner, M. Weakly Compressible SPH for Free Surface Flows. In Proceedings of the 2007 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, San Diego, CA, USA, 2–4 August 2007; ACM: New York, NY, USA, 2007; pp. 209–217. [Google Scholar]
- Adams, B.; Pauly, M.; Keiser, R.; Guibas, L.J. Adaptively Sampled Particle Fluids. In Proceedings of the ACM SIGGRAPH 2007 Papers, San Diego, CA, USA, 5–9 August 2007; ACM: New York, NY, USA, 2007; p. 48-es. [Google Scholar]
- Ihmsen, M.; Cornelis, J.; Solenthaler, B.; Horvath, C.; Teschner, M. Implicit Incompressible SPH. IEEE Trans. Vis. Comput. Graph. 2013, 20, 426–435. [Google Scholar] [CrossRef]
- Zhang, N.; Klippel, H.; Afrasiabi, M.; Röthlin, M.; Kuffa, M.; Bambach, M.; Wegener, K. Hybrid SPH-FEM Solver for Metal Cutting Simulations on the GPU Including Thermal Contact Modeling. CIRP J. Manuf. Sci. Technol. 2023, 41, 311–327. [Google Scholar] [CrossRef]
- Xu, F.; Wang, J.; Yang, Y.; Wang, L.; Dai, Z.; Han, R. On Methodology and Application of Smoothed Particle Hydrodynamics in Fluid, Solid and Biomechanics. Acta Mech. Sin. 2023, 39. [Google Scholar] [CrossRef] [PubMed]
- Winchenbach, R.; Kolb, A. Multi-Level Memory Structures for Simulating and Rendering Smoothed Particle Hydrodynamics. Comput. Graph. Forum 2020, 39, 527–541. [Google Scholar] [CrossRef]
- Fernández-Fernández, J.A.; Westhofen, L.; Löschner, F.; Jeske, S.R.; Longva, A.; Bender, J. Fast Octree Neighborhood Search for SPH Simulations. ACM Trans. Graph. 2022, 41, 1–13. [Google Scholar] [CrossRef]
- Lopes, L.G.O.; Cintra, D.T.; Lira, W.W.M. A Particle Packing Parallel Geometric Method Using GPU. Comput. Part. Mech. 2021, 8, 931–942. [Google Scholar] [CrossRef]
- Koschier, D.; Bender, J.; Solenthaler, B.; Teschner, M. A survey on SPH methods in computer graphics. Comput. Graph. Forum 2022, 41, 737–760. [Google Scholar] [CrossRef]
- Bender, J.; Kugelstadt, T.; Weiler, M.; Koschier, D. Implicit Frictional Boundary Handling for SPH. IEEE Trans. Vis. Comput. Graph. 2020, 26, 2982–2993. [Google Scholar] [CrossRef] [PubMed]
- Verlet, L. Computer “Experiments” on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules. Phys. Rev. 1967, 159, 98–103. [Google Scholar] [CrossRef]
- Band, S.; Gissler, C.; Teschner, M. Compressed Neighbour Lists for SPH. Comput. Graph. Forum 2020, 39, 531–542. [Google Scholar] [CrossRef]
- Green, S. Particle Simulation Using CUDA. NVIDIA Whitepaper. Available online: https://developer.nvidia.com/gpugems/gpugems3/part-v-physics-simulation/chapter-30-real-time-simulation-and-rendering-3d-fluids (accessed on 1 September 2025).
- Tang, M.; Liu, Z.; Tong, R.; Manocha, D. PSCC: Parallel Self-Collision Culling with Spatial Hashing on GPUs. Proc. ACM Comput. Graph. Interact. Tech. 2018, 1, 1–18. [Google Scholar] [CrossRef]
- Winchenbach, R.; Kolb, A. Optimized Refinement for Spatially Adaptive SPH. ACM Trans. Graph. 2021, 40, 1–15. [Google Scholar] [CrossRef]
- Wu, W.; Li, H.; Su, T.; Liu, H.; Lv, Z. GPU-accelerated SPH fluids surface reconstruction using two-level spatial uniform grids. Vis. Comput. 2017, 33, 1429–1442. [Google Scholar] [CrossRef]
- Rezavand, M.; Zhang, C.; Hu, X. Generalized and efficient wall boundary condition treatment in GPU-accelerated smoothed particle hydrodynamics. Comput. Phys. Commun. 2022, 281, 108507. [Google Scholar] [CrossRef]
- Nishidate, Y.; Fujishiro, I. Efficient Particle-Based Fluid Surface Reconstruction Using Mesh Shaders and Bidirectional Two-Level Grids. Proc. ACM Comput. Graph. Interact. Tech. 2024, 7. [Google Scholar] [CrossRef]
- Zhang, W.; Liao, X.; Li, P.; Jin, H.; Lin, L. ShareRender: Bypassing GPU virtualization to enable fine-grained resource sharing for cloud gaming. In Proceedings of the 25th ACM International Conference on Multimedia, Mountain View, CA, USA, 23–27 October 2017; pp. 324–332. [Google Scholar]
- Messaoudi, F.; Ksentini, A.; Simon, G.; Bertin, P. Performance analysis of game engines on mobile and fixed devices. ACM Trans. Multimed. Comput. Commun. Appl. 2017, 13, 1–28. [Google Scholar] [CrossRef]
- Tang, M.; Wang, T.; Liu, Z.; Tong, R.; Manocha, D. I-cloth: Incremental collision handling for GPU-based interactive cloth simulation. ACM Trans. Graph. 2018, 37, 204. [Google Scholar] [CrossRef]
- Tomczak, T.; Szafran, R.G. A new GPU implementation for lattice Boltzmann simulations on sparse geometries. Comput. Phys. Commun. 2019, 235, 258–278. [Google Scholar] [CrossRef]
- Jia, S.; Zhang, W.; Yu, X.; Pan, Z. CPU-GPU parallel framework for real-time interactive cutting of adaptive octree-based deformable objects. Comput. Graph. Forum 2018, 37, 45–49. [Google Scholar] [CrossRef]
- Jambunathan, R.; Levin, D.A. A hybrid CPU-GPU parallel octree direct simulation Monte Carlo approach. In Proceedings of the AIAA Computational Fluid Dynamics Conference, Dallas, TX, USA, 22–26 June 2015; p. 3057. [Google Scholar]
- Va, H.; Choi, M.H.; Hong, M. Real-Time Cloth Simulation Using Compute Shader in Unity3D for AR/VR Contents. Appl. Sci. 2021, 11, 8255. [Google Scholar] [CrossRef]
- Kim, T.; Ma, J.; Hong, M. Real-Time Cloth Simulation in Extended Reality: Comparative Study Between Unity Cloth Model and Position-Based Dynamics Model with GPU. Appl. Sci. 2025, 15, 6611. [Google Scholar] [CrossRef]
- Reinhardt, S.; Huber, M.; Eberhardt, B.; Weiskopf, D. Fully Asynchronous SPH Simulation. In Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation, Los Angeles, CA, USA, 28–30 July 2017; pp. 1–10. [Google Scholar]
- Bodin, K.; Lacoursiere, C.; Servin, M. Constraint fluids. IEEE Trans. Vis. Comput. Graph. 2012, 18, 516–526. [Google Scholar] [CrossRef] [PubMed]
- Mao, Z.; Li, X.; Hu, S.; Gopalakrishnan, G.; Li, A. A GPU accelerated mixed-precision Smoothed Particle Hydrodynamics framework with cell-based relative coordinates. Eng. Anal. Bound. Elem. 2024, 161, 113–125. [Google Scholar] [CrossRef]
- Schmid, R.F.; Pisani, F.; Cáceres, E.N.; Borin, E. An evaluation of fast segmented sorting implementations on GPUs. Parallel Comput. 2022, 110, 102889. [Google Scholar] [CrossRef]
- dos Santos Brito, C.J.; B. Vieira e Silva, A.L.; Teixeira, J.M.; Teichrieb, V. Ray Tracer based rendering solution for large scale fluid rendering. Comput. Graph. 2018, 77, 65–79. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).