Distributed Robust Routing Optimization for Laser-Powered UAV Cluster with Temporary Parking Charging
Abstract
1. Introduction
- A UAV cluster scheduling model is proposed for communication restoration in the distribution network post-disaster by optimizing task allocation and execution pathways. This concept enhances the efficiency of UAV collaboration while accounting for energy limitations. Furthermore, we implemented laser charging technology to develop an effective charging-operation cluster scheduling model.
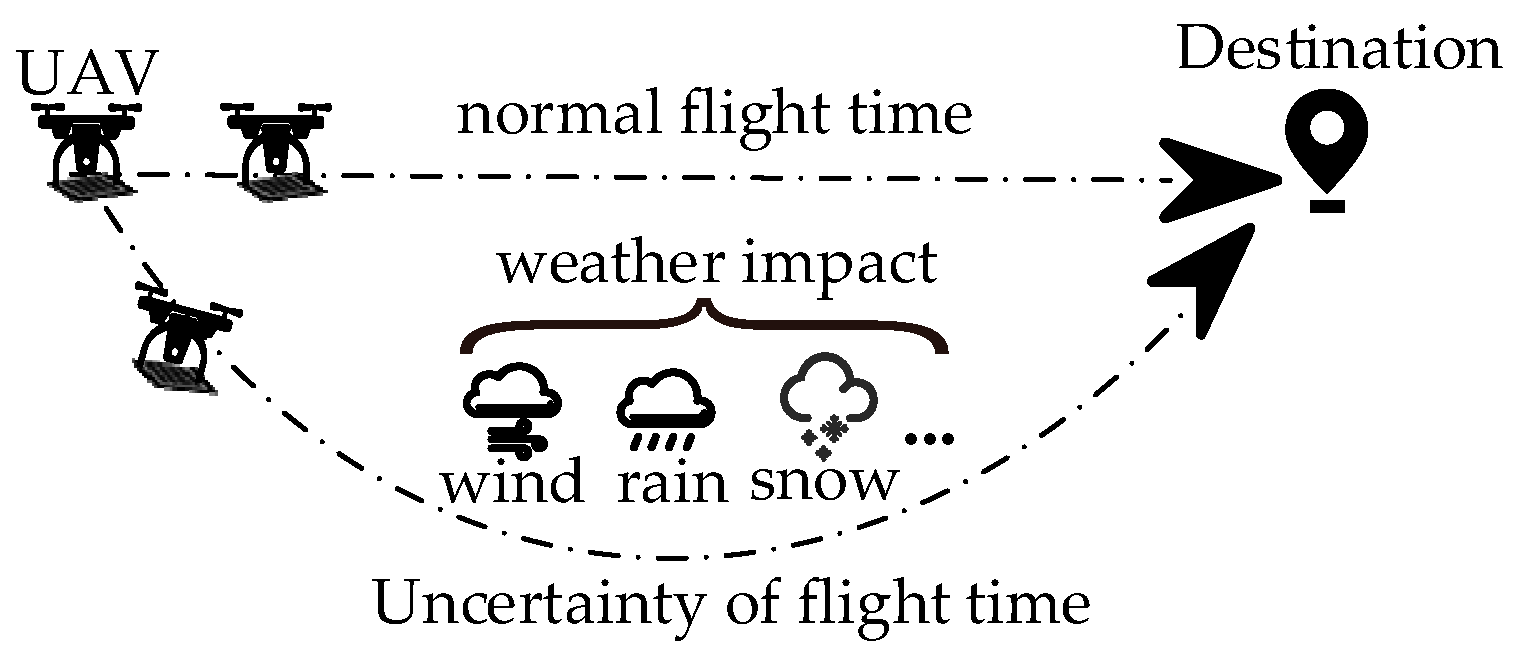
- A distributed robust optimization (DRO) model is proposed that explicitly accounts for spatiotemporal meteorological uncertainty (e.g., rainfall, wind dynamics, and atmospheric disturbances) in long-range laser UAV operations. This model guarantees reliable task scheduling under weather-induced perturbations.
2. Related Work
3. Theoretical Framework
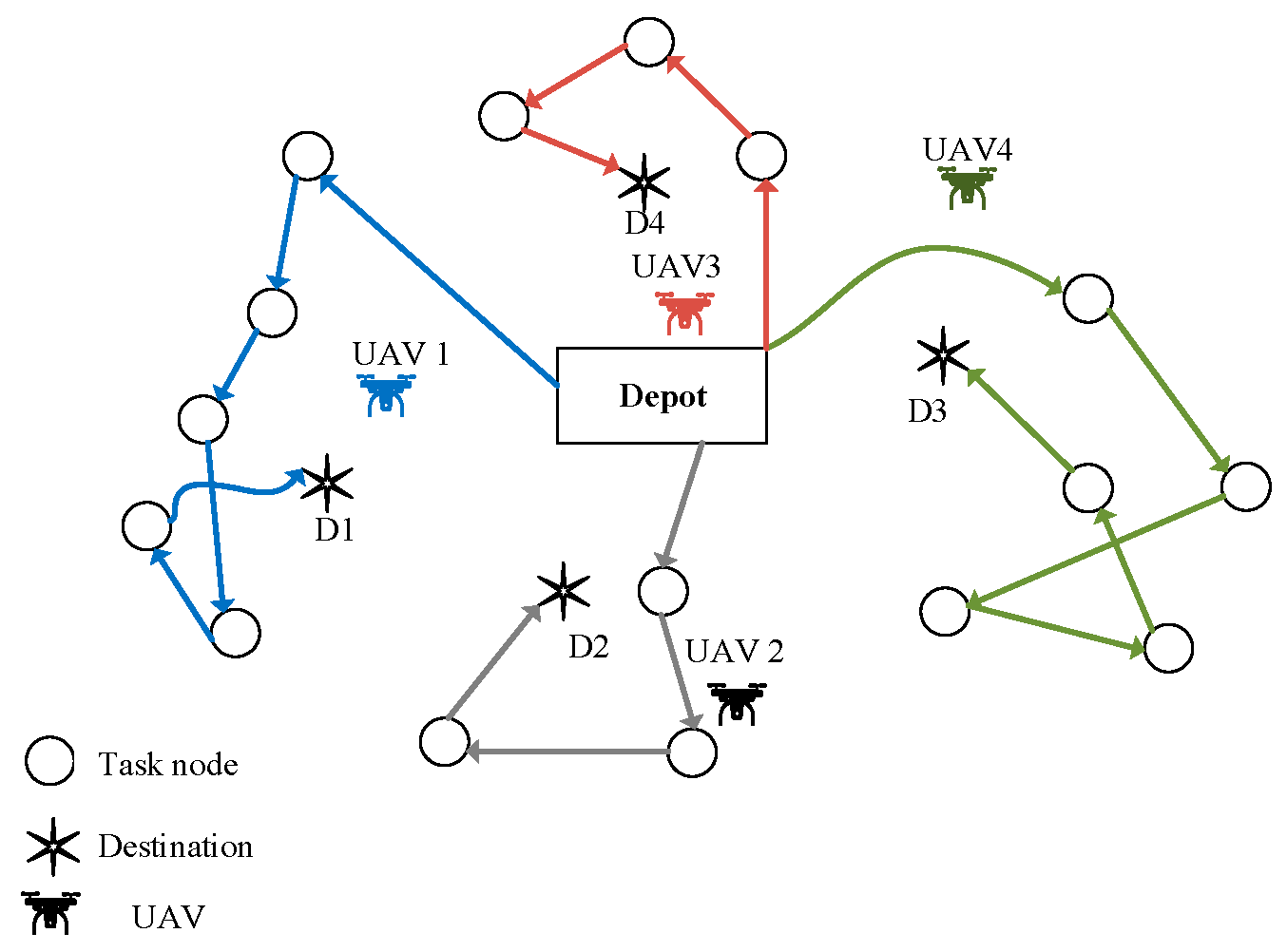
3.1. MVRP Formulation for UAV Scheduling
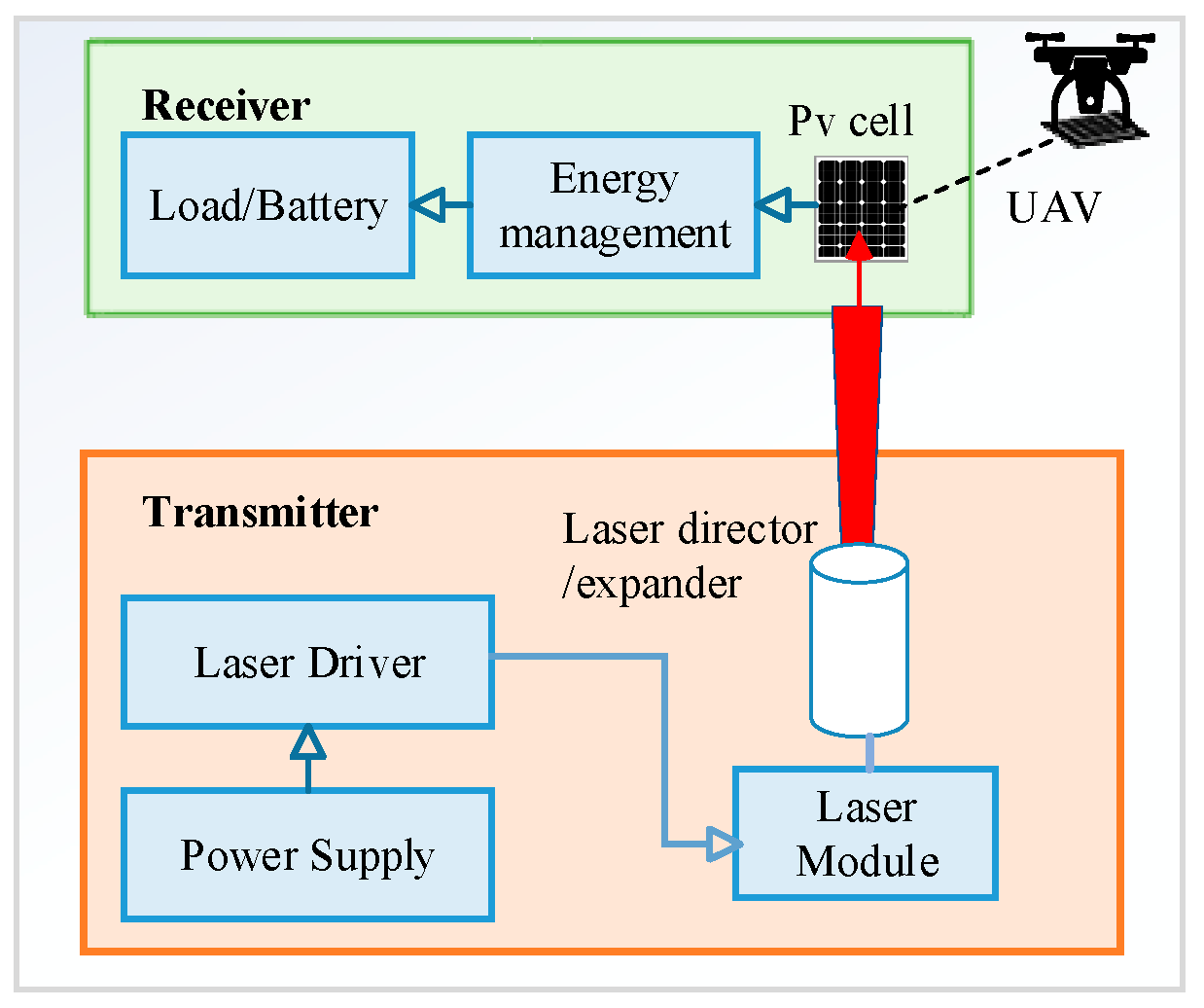
3.2. The Basic Principles of Laser Charging for UAV
4. System Model
- UAV Operation Constraints: The UAV cluster departs from the dispatch center, visits designated work points, and returns to the dispatch center. Each UAV has identical energy capacity and experiences uniform path loss during flight.
- Energy Consumption Model: The energy consumption of UAVs is dominated by hovering and mobility, while communication energy costs are negligible.
- Fault Point Handling: The coordinates of fault points are assumed known, and UAVs are equipped with laser-based charging systems to replenish their energy when servicing fault points.
- Charging rules: The charging protocol initiates upon arrival at the designated task point, where laser charging systems distribute energy evenly across all UAVs in the cluster to maintain approximate state-of-charge parity among units.
4.1. Laser UAV Model
4.2. DRO Model Formulation
5. Simulation Results
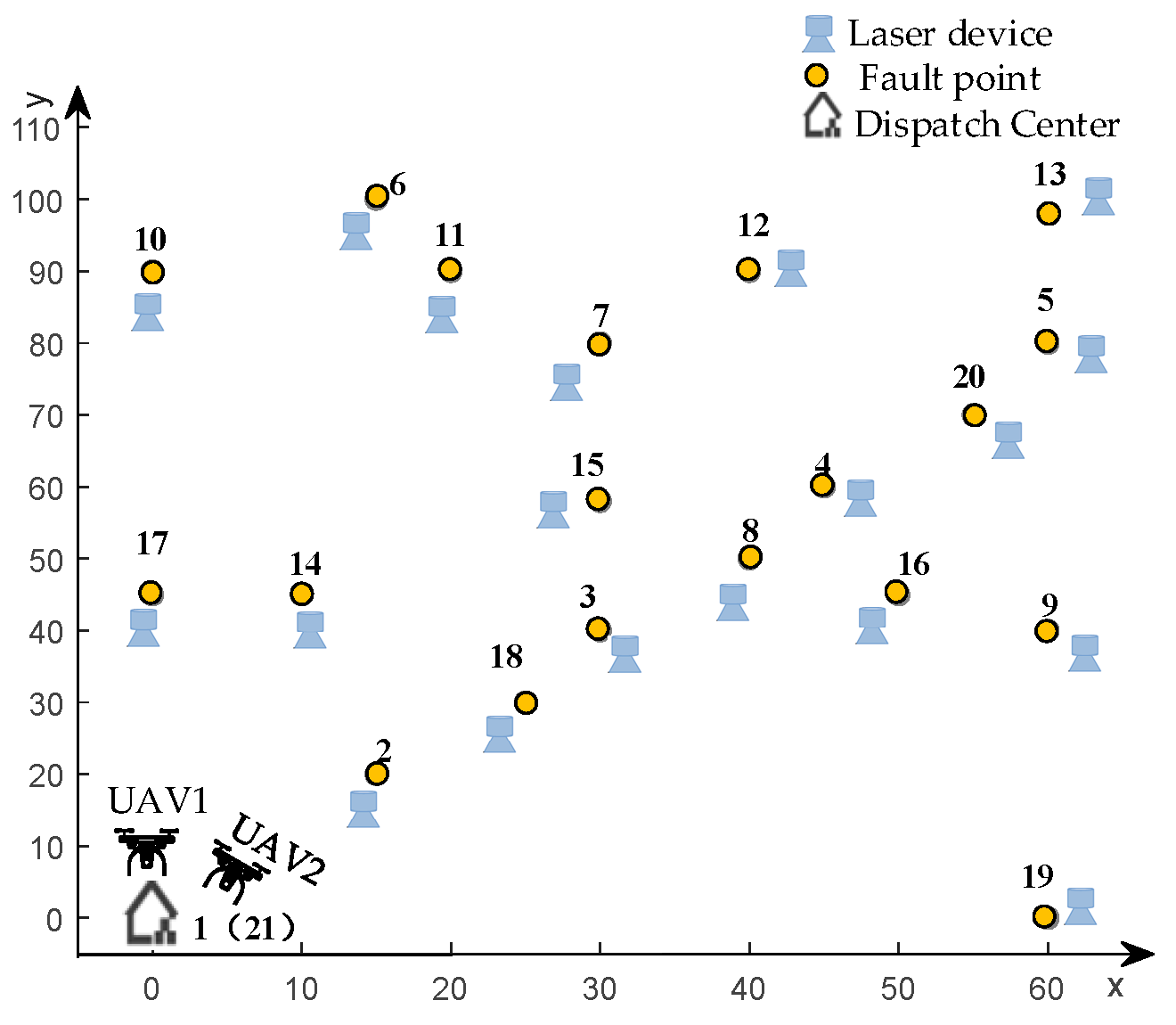
5.1. Simulation Setup
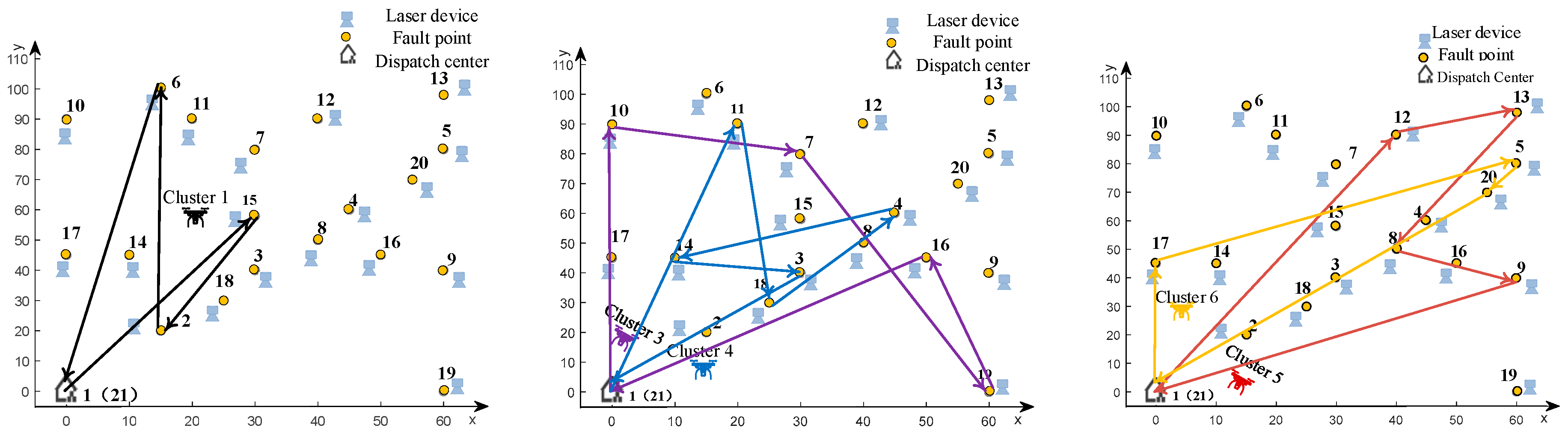
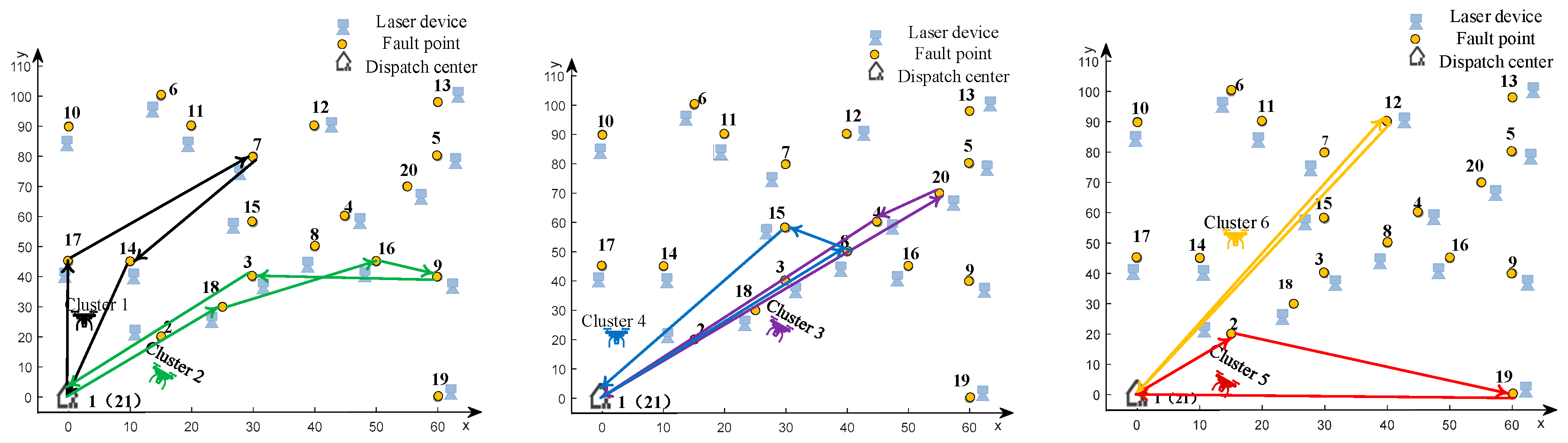
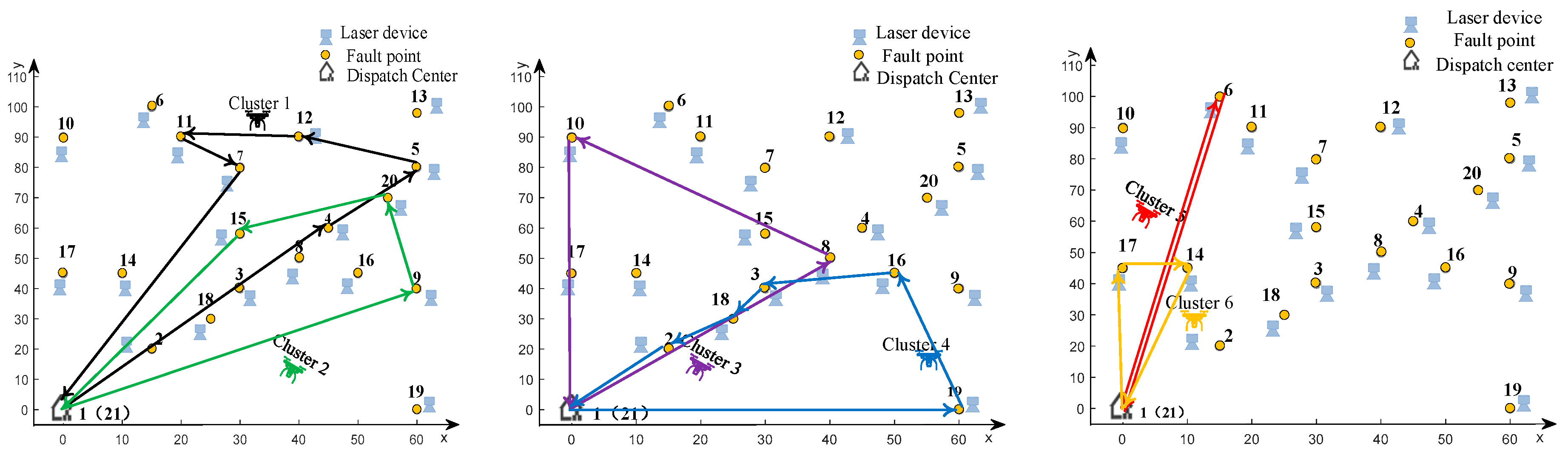
5.2. Comparative Analysis of Scheduling Strategies
- Baseline model: traditional MVRP scheduling without considering any UAV operational constraints.
- Energy constraint modeling: adding UAV energy constraints to the baseline model.
- Charging extension model: adding laser charging to the range constraint model
- Robust optimization model: introducing flight robustness constraints based on the charging extension model. Considering the uncertain parameters, we set for DRO model. In particular, , are randomly generated from [−1, 1], and σij are randomly generated from [0, 0.1], ∀i, j∈θ, ϵ = 0.1.
5.3. Sensitivity Analysis
5.4. Computational Efficiency
6. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hao, Z.; Yu, H.; Yu, W.; Binbin, L.; Yi, C.; Cong, W.; Ning, Z. Design and Implementation of UAV Inspection and Control Platform for Transmission Lines. In Proceedings of the 2023 8th International Conference on Information Systems Engineering (ICISE), Dalian, China, 23–25 June 2023. [Google Scholar]
- Wang, R.; Wu, W.; Fu, Z.; Chen, B.; Wu, X. Task Scheduling Optimization for UAV Electrical Image Fault Detection with Wireless Power Transfer. J. Circuits Syst. Comput. 2024, 33, 2450213. [Google Scholar] [CrossRef]
- Ojetunde, B.; Ano, S.; Sakano, T. A Practical Approach to Deploying a Drone-Based Message Ferry in a Disaster Situation. Appl. Sci. 2022, 12, 6547. [Google Scholar] [CrossRef]
- Huang, H.; Savkin, A.V. Deployment of Charging Stations for Drone Delivery Assisted by Public Transportation Vehicles. IEEE Trans. Intell. Transp. Syst. 2022, 23, 15043–15054. [Google Scholar] [CrossRef]
- Townsend, A.; Jiya, I.N.; Martinson, C.; Bessarabov, D.; Gouws, R. A Comprehensive Review of Energy Sources for Unmanned Aerial Vehicles, Their Shortfalls and Opportunities for Improvements. Heliyon 2020, 6, e05285. [Google Scholar] [CrossRef]
- Chittoor, P.K.; Chokkalingam, B.; Mihet-Popa, L. A Review on UAV Wireless Charging: Fundamentals, Applications, Charging Techniques and Standards. IEEE Access 2021, 9, 69235–69266. [Google Scholar] [CrossRef]
- Blackwell, T. Recent Demonstrations of Laser Power Beaming at DFRC and MSFC. In AIP Conference Proceedings; American Institute of Physics: Melville, NY, USA, 2005. [Google Scholar]
- Yadav, K.; Kumar, B. Swaroop Mitigation of Mismatch Power Losses of PV Array under Partial Shading Condition Using Novel Odd Even Configuration. Energy Rep. 2020, 6, 427–437. [Google Scholar] [CrossRef]
- Sprangle, P.; Hafizi, B.; Ting, A.; Fischer, R. High-Power Lasers for Directed-Energy Applications. Appl. Opt. 2015, 54, F201-9. [Google Scholar] [CrossRef]
- AUVSI: LaserMotive, Lockheed Demonstrate Real-World Laser Power. Available online: https://www.flightglobal.com/auvsi-lasermotive-lockheed-demonstrate-real-world-laser-power/106546.article (accessed on 31 August 2025).
- Nguyen, D.H. Dynamic Optical Wireless Power Transfer for Electric Vehicles. IEEE Access 2023, 11, 2787–2795. [Google Scholar] [CrossRef]
- Hassija, V.; Saxena, V.; Chamola, V. Scheduling Drone Charging for Multi-Drone Network Based on Consensus Time-Stamp and Game Theory. Comput. Commun. 2020, 149, 51–61. [Google Scholar] [CrossRef]
- Zhao, L.; Yao, Y.; Guo, J.; Zuo, Q.; Leung, V.C.M. Collaborative Computation Offloading and Wireless Charging Scheduling in Multi-UAV-Assisted MEC Networks: A TD3-Based Approach. Comput. Netw. 2024, 251, 110615. [Google Scholar] [CrossRef]
- Montemanni, R.; Dell’Amico, M.; Corsini, A. Parallel Drone Scheduling Vehicle Routing Problems with Collective Drones. arXiv 2023, arXiv:2307.03523. [Google Scholar] [CrossRef]
- Yang, J.; You, X.; Wu, G.; Hassan, M.M.; Almogren, A.; Guna, J. Application of Reinforcement Learning in UAV Cluster Task Scheduling. Future Gener. Comput. Syst. 2019, 95, 140–148. [Google Scholar] [CrossRef]
- Jin, Y.; Xu, J.; Wu, S.; Xu, L.; Yang, D.; Xia, K. Bus Network Assisted Drone Scheduling for Sustainable Charging of Wireless Rechargeable Sensor Network. J. Syst. Arch. 2021, 116, 102059. [Google Scholar] [CrossRef]
- Nguyen, M.A.; Hà, M.H. The Parallel Drone Scheduling Traveling Salesman Problem with Collective Drones. Transp. Sci. 2023, 57, 866–888. [Google Scholar] [CrossRef]
- Wang, X.; Poikonen, S.; Golden, B. The Vehicle Routing Problem with Drones: Several Worst-Case Results. Optim. Lett. 2017, 11, 679–697. [Google Scholar] [CrossRef]
- Sacramento, D.; Pisinger, D.; Ropke, S. An Adaptive Large Neighborhood Search Metaheuristic for the Vehicle Routing Problem with Drones. Transp. Res. Part C Emerg. Technol. 2019, 102, 289–315. [Google Scholar] [CrossRef]
- Das, D.N.; Sewani, R.; Wang, J.; Tiwari, M.K. Synchronized Truck and Drone Routing in Package Delivery Logistics. IEEE Trans. Intell. Transp. Syst. 2021, 22, 5772–5782. [Google Scholar] [CrossRef]
- Deng, D.; Jing, W.; Fu, Y.; Huang, Z.; Liu, J.; Shimada, K. Constrained Heterogeneous Vehicle Path Planning for Large-Area Coverage. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 4–8 November 2019. [Google Scholar]
- Jung, M.; Oh, H. Heterogeneous Mission Planning for a Single Unmanned Aerial Vehicle (UAV) with Attention-Based Deep Reinforcement Learning. PeerJ Comput. Sci. 2022, 8, e1119. [Google Scholar] [CrossRef]
- Li, H.; Wang, H.; Chen, J.; Bai, M. Two-Echelon Vehicle Routing Problem with Time Windows and Mobile Satellites. Trans. Res. Part B Methodol. 2020, 138, 179–201. [Google Scholar] [CrossRef]
- Wu, Q.; Zeng, Y.; Zhang, R. Joint Trajectory and Communication Design for Multi-UAV Enabled Wireless Networks. IEEE Trans. Wirel. Commun. 2018, 17, 2109–2121. [Google Scholar] [CrossRef]
- Chowdhery, A.; Jamieson, K. Aerial Channel Prediction and User Scheduling in Mobile Drone Hotspots. IEEE ACM Trans. Netw. 2018, 26, 2679–2692. [Google Scholar] [CrossRef]
- Liu, H.; Liu, T.; Huang, K. A Real-Time System for Scheduling and Managing UAV Delivery in Urban. arXiv 2024, arXiv:2412.11590. [Google Scholar] [CrossRef]
- Golden, B.; Raghavan, S.; Wasil, E.A. (Eds.) The Vehicle Routing Problem: Latest Advances and New Challenges. In Operations Research/Computer Science Interfaces Series, 2008th ed.; Springer: New York, NY, USA, 2008; ISBN 9780387777771. [Google Scholar]
- Xu, W.; Wang, X.; Li, W.; Li, S.; Lu, C. Research on Test and Evaluation Method of Laser Wireless Power Transmission System. EURASIP J. Adv. Signal Process. 2022, 2022, 20. [Google Scholar] [CrossRef]
- Balkan, N.; Erol, A. Light Emitting Diodes and Semiconductor Lasers. In Graduate Texts in Physics; Springer International Publishing: Cham, Switzerland, 2021; pp. 219–278. ISBN 9783319449340. [Google Scholar]
- Zhang, Q.; Fang, W.; Liu, Q.; Wu, J.; Xia, P.; Yang, L. Distributed Laser Charging: A Wireless Power Transfer Approach. IEEE Internet Things J. 2018, 5, 3853–3864. [Google Scholar] [CrossRef]
- Krupke, W.F. DPAL: A New Class of Lasers for Cw Power Beaming at Ideal Photovoltaic Cell Wavelengths. In AIP Conference Proceedings; American Institute of Physics: Melville, NY, USA, 2004. [Google Scholar]
- Wang, X. Guizhou Power Grid Intelligent Operations Center Successfully Developed a UAV Remote Charging System. Available online: https://www.csg.cn/epaper/epaper/nfdwb/html/2024-11/26/content_4137.htm (accessed on 31 August 2025).
- James, J.; Iyer, V.; Chukewad, Y.; Gollakota, S.; Fuller, S.B. Liftoff of a 190 Mg Laser-Powered Aerial Vehicle: The Lightest Wireless Robot to Fly. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018. [Google Scholar]
- Wolsey, L.A.; Nemhauser, G.L. Integer and Combinatorial Optimization. In Wiley Series in Discrete Mathematics and Optimization, 1st ed.; John Wiley & Sons: Nashville, TN, USA, 2014; ISBN 9780471359432. [Google Scholar]
- Babic, D. Piecewise Polynomial Approximation Based on Taylor Series with Efficient Realization Using Farrow Structure. In Proceedings of the 2009 9th International Conference on Telecommunication in Modern Satellite, Cable, and Broadcasting Services, Nis, Serbia, 7–9 October 2009. [Google Scholar]




| Symbol | Notations |
|---|---|
| θ = {θ1,θ2…,θn} | Fault points (task points) and dispatch centers set data Numbered sets of UAV clusters |
| U = {1,2,3…u} | |
| N | Total number of UAVs |
| Pch | Laser charging power |
| eij | Power consumption for passage between nodes i, j |
| Battery capacity of UAV cluster u | |
| xi,j,u | Task selection variable |
| nu | Number of UAVs in UAV cluster u |
| Electricity of UAV cluster u when leaving node i | |
| Electricity of UAV cluster u when reaching node i | |
| The task time for UAV cluster u at node i | |
| The task time for single UAV at node i | |
| ti,j | The time it takes for the UAV to fly from node i to node j |
| The charging time of UAV cluster u at node i UAV | |
| The dwell time of UAV cluster u at node i | |
| Ph | Hovering power |
| Pf | Flight power consumption |
| Set of critical points to be recovered | |
| Wi | Node i communication recovery status |
| Conforming load recovery after node i is communication resumption | |
| Ta | Task scheduling limit time |
| Parameter | Value |
|---|---|
| Battery capacity Hovering power consumption | 4276 mAh |
| 90 W | |
| Flight power consumption | 80 W |
| Laser charging power | 125 W |
| Total number of UAVs | 100 |
| Flight speed | 15 m/s |
| Number of UAV clusters | 6 |
| Nominal battery voltage | 14.6 V |
| Battery energy | 62.5 Wh |
| Task scheduling limit time | 60 min |
| U | Case1 | Case2 | Case3 | Case4 | ||||
|---|---|---|---|---|---|---|---|---|
| nu | ρ/p.u | nu | ρ/p.u | nu | ρ/p.u | nu | ρ/p.u | |
| 1 | 15 | 0.93 | 23 | 0.75 | 45 | 1.3 | 32 | 0.75 |
| 2 | 0 | 0 | 22 | 1.15 | 13 | 0.85 | 21 | 0.55 |
| 3 | 40 | 1.05 | 15 | 0.45 | 15 | 0.35 | 15 | 0.9 |
| 4 | 23 | 1.15 | 21 | 0.6 | 18 | 1.3 | 21 | 1.05 |
| 5 | 15 | 1.0 | 10 | 0.5 | 5 | 0.28 | 9 | 0.53 |
| 6 | 7 | 0.75 | 9 | 0.25 | 4 | 0.5 | 2 | 0.25 |
| Total | 100 | 4.88 | 100 | 3.60 | 100 | 4.58 | 100 | 4.03 |
| Ta/min | Confidence Interval | Total Load Restored/p.u |
|---|---|---|
| 40 | 75% | 3.65 |
| 80% | 3.60 | |
| 85% | 3.38 | |
| 90% | 3.20 | |
| 95% | 3.00 | |
| 50 | 75% | 4.18 |
| 80% | 4.18 | |
| 85% | 4.08 | |
| 90% | 3.98 | |
| 95% | 3.83 | |
| 60 | 75% | 4.48 |
| 80% | 4.34 | |
| 85% | 4.25 | |
| 90% | 4.03 | |
| 95% | 3.93 | |
| 80 | 75% | 4.73 |
| 80% | 4.58 | |
| 85% | 4.30 | |
| 90% | 4.18 | |
| 95% | 3.98 |
| Nodes | MIP Gap | Objective Functions | Computation Time/s |
|---|---|---|---|
| 15 | 60% | 2.4 | 53 |
| 40% | 2.85 | 94 | |
| 30% | 2.9 | 101 | |
| 20% | 3.13 | 107 | |
| 20 | 60% | 3.08 | 1047 |
| 40% | 3.78 | 1125 | |
| 30% | 3.89 | 1578 | |
| 20% | 4.05 | 1726 | |
| 25 | 60% | 4.42 | 1225 |
| 40% | 4.94 | 1576 | |
| 30% | 5.03 | 2063 | |
| 20% | 5.08 | 2454 | |
| 30 | 60% | 5.07 | 1084 |
| 40% | 5.49 | 1551 | |
| 30% | 5.70 | 2883 | |
| 20% | / | >4500 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Zhong, Y.; Li, H. Distributed Robust Routing Optimization for Laser-Powered UAV Cluster with Temporary Parking Charging. Appl. Sci. 2025, 15, 9676. https://doi.org/10.3390/app15179676
He X, Zhong Y, Li H. Distributed Robust Routing Optimization for Laser-Powered UAV Cluster with Temporary Parking Charging. Applied Sciences. 2025; 15(17):9676. https://doi.org/10.3390/app15179676
Chicago/Turabian StyleHe, Xunzhuo, Yuanchang Zhong, and Han Li. 2025. "Distributed Robust Routing Optimization for Laser-Powered UAV Cluster with Temporary Parking Charging" Applied Sciences 15, no. 17: 9676. https://doi.org/10.3390/app15179676
APA StyleHe, X., Zhong, Y., & Li, H. (2025). Distributed Robust Routing Optimization for Laser-Powered UAV Cluster with Temporary Parking Charging. Applied Sciences, 15(17), 9676. https://doi.org/10.3390/app15179676





