Abstract
Distribution System Operators (DSOs) increasingly need planning tools that coordinate utility-influenced assets—such as electric-vehicle charging stations (EVCS) and voltage-support resources—with customer-sited distributed generation (DG). We present a Nash-equilibrium-based Iterative Best Response Algorithm (IBRA-NE) for joint planning of DG and EVCS in radial distribution networks. The framework supports two applicability modes: (i) a DSO-plannable mode that co-optimizes EVCS siting/sizing and utility-controlled reactive support (DG operated as VAR resources or functionally equivalent devices), and (ii) a customer-sited mode that treats DG locations as fixed while optimizing DG reactive set-points/sizes and EVCS siting. The objective minimizes network losses and voltage deviation while incorporating deployment costs and EV charging service penalties, subject to standard operating limits. A backward/forward sweep (BFS) load flow with Monte Carlo simulation (MCS) captures load and generation uncertainty; a Bus Voltage Deviation Index (BVDI) helps identify weak buses. On the EEU 114-bus system, the method reduces base-case losses by up to 57.9% and improves minimum bus voltage from 0.757 p.u. to 0.931 p.u.; performance remains robust under a 20% load increase. The framework explicitly accommodates regulatory contexts where DG siting is customer-driven by treating DG locations as fixed in such cases while optimizing EVCS siting and sizing under DSO planning authority. A mixed scenario with 5 DGs and 3 EVCS demonstrates coordinated benefits and convergence properties relative to PSO, GWO, RFO, and ARFO. Additionally, the proposed algorithm is also tested on the IEEE 69-bus system and results in acceptable performance. The results indicate that game-theoretic coordination, applied in a manner consistent with regulatory roles, provides a practical pathway for DSOs to plan EV infrastructure and reactive support in networks with uncertain DER behavior.
1. Introduction
The modern power grid is undertaking a transformation—driven by growing energy demands, climate imperatives, and the global shift toward decentralized, renewable generation. At the forefront of this change are Distributed Generators (DGs), which offer a promising solution to boost the stability, efficiency, and reliability of power systems. Fueled by clean sources like solar photovoltaic (SPV) and wind turbines (WTs), DGs also bring the added benefit of environmental sustainability. Yet, this potential comes with a caveat: the benefits of DGs are not guaranteed by mere integration. In fact, if DGs are poorly placed or inadequately sized, they can trigger the very issues they are meant to solve—causing voltage instability, increased losses, and even equipment overloads [1].
To unlock their full potential, DGs must be deployed with strategic precision—taking into account both technical constraints and dynamic system behavior. However, as the number of DGs increases, so does the complexity of their coordination. The challenge lies not just in finding one optimal solution, but in navigating a shifting landscape of interdependent decisions, renewable uncertainty, and evolving grid conditions [2]. Traditional optimization techniques such as Genetic Algorithms (GAs), Whale Optimization Algorithms (WOAs), Particle Swarm Optimization (PSO), and Grey Wolf Optimization (GWO) have been applied to this problem with varying degrees of success.
Optimal placement and sizing of DG units in radial distribution networks is a complex problem due to the nonlinear, multi-objective, and interactive nature of the electrical system. Traditional optimization methods often rely on centralized control and deterministic models, which may not fully capture the strategic behavior of individual DG units or their impact on overall system performance. While effective in reducing power losses or improving voltage profiles, these methods often treat each DG in isolation—overlooking the strategic interactions that emerge in multi-DG environments. Furthermore, they can struggle with computational load, convergence reliability, and adaptability in large-scale systems.
Radial distribution networks increasingly host a mix of customer-sited DG and DSO-influenced assets (e.g., electric vehicle charging station (EVCS), reactive power devices). While DG can reduce losses and support voltage when properly integrated, uncoordinated siting and operation may worsen voltage drops and raise feeder losses. Traditional metaheuristics (e.g., PSO, GWO, RFO) have been widely used for DG placement/sizing; however, these methods typically assume centralized control and do not fully reflect multi-agent strategic interactions among many devices. Moreover, they rarely reconcile the regulatory reality that DSOs often do not control where customers install DG, and that confidential network data are not available to customers for “optimal siting”.
To bridge this gap, we use game theory to model DG/EVCS decisions as interdependent strategies. In our approach, the IBRA-NE iteratively updates each player’s strategy until no unilateral improvement is possible, ensuring consistent convergence in practice. We extend the standard technical objectives (loss and voltage deviation) to include deployment costs and EV charging service quality and embed the model in a probabilistic BFS to reflect uncertainty. Crucially, we position the framework for two real-world modes: a DSO-plannable mode (EVCS + VAR support siting/sizing) and a customer-sited mode (DG locations fixed, with set-point optimization), thereby aligning the optimization scope with who actually has siting authority.
Game theory offers a powerful alternative by modeling the interactions among multiple decision-makers—each DG and EVCS unit—as strategic players in a game. Game theory is a mathematical framework for analyzing strategic interactions among rational agents, where the outcome for each participant depends on both their own decisions and those of others. It provides tools to model problems involving competition, cooperation, and negotiation [3]. In DG/EVCS planning, this approach enables decentralized decision-making by allowing each unit to optimize its performance while accounting for the strategies of other units. A central concept in this framework is the Nash Equilibrium (NE), which represents a stable operating point where no player can improve their outcome unilaterally.
This study proposes a game-theoretic optimization framework based on NE principles. By modeling each DG as a strategic player within a non-cooperative game, we capture the real-world dynamics of competition and interdependence. The Iterative Best Response Algorithm (IBRA) guides each DG to iteratively adjust its strategy—placement and size—based on the evolving choices of its peers, leading to a stable and efficient system-wide configuration [3].
This innovative framework advances distribution system optimization by directly addressing the multi-agent nature of DG integration. It improves not only power loss minimization but also enhances voltage stability and operational resilience under varying conditions. Ultimately, the proposed method supports the seamless and sustainable integration of renewable energy into the power grid—aligning technical performance with global energy goals.
The proposed IBRA model formulates multi-DG placement and sizing as a game-theoretic problem, where players (DG) iteratively optimize their locations and sizes based on a utility function balancing cost, power losses, voltage stability, and revenue. The model incorporates power system constraints and addresses IBRA optimization. The proposed study framework is shown in Figure 1.
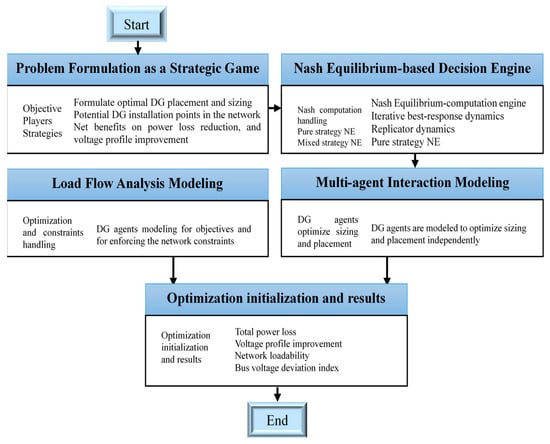
Figure 1.
Expanded diagram for the proposed study.
Ignoring uncertainty in multi-DG placement and sizing leads to inefficient and impractical solutions for modern power systems. It risks suboptimal performance, constraint violations, and reduced resilience, mainly in systems with high renewable penetration. By addressing uncertainty through Monte Carlo simulations (MCS), the optimization process can yield more robust and adaptable solutions, ensuring reliable operation across a range of scenarios and supporting the integration of DGs in modern grids.
A comparative analysis is conducted involving PSO, GWO, RFO, and ARFO. These algorithms are chosen for comparison, since we aim to include metaheuristics that span classical, nature-inspired, and recently enhanced adaptive paradigms to provide a balanced comparative landscape. These proposed comparative methods are computationally efficient, well-documented in power systems, and easily reproducible in the MATLAB environment. Each of the selected algorithms has been successfully applied to distribution system optimization tasks.
1.1. Statement of the Problem
The deployment of DGs within power distribution networks holds tremendous potential—but only when executed with precision. Improper placement and sizing can degrade system performance, triggering voltage instability, overloading, and increased energy losses. In a grid increasingly reliant on renewable energy sources, the margin for error is shrinking.
Existing optimization techniques often fall short. They treat DGs as isolated entities, ignoring the strategic interplay that arises when multiple DGs compete for limited grid resources. This lack of coordination leads to suboptimal outcomes—where local gains come at the expense of global performance. Moreover, traditional algorithms struggle to simultaneously satisfy the complex objectives of reducing losses, improving voltage profiles, and maintaining overall system stability, especially in large-scale or dynamically changing environments. They lack the computational agility and strategic foresight needed for today’s evolving power systems.
What is missing is an optimization framework that mirrors reality: one where multiple agents—DGs—make decisions based on not only their own goals but also the actions of others. This study addresses that gap by leveraging game theory, specifically an IBRA-based NE, to model DG interactions as a dynamic, multi-agent optimization problem. This approach promises coordinated, efficient, and stable DG integration across diverse operating conditions.
Conventional DG planning studies often presume that a single planner can freely choose both the locations and sizes of multiple DG units. In practice, DG siting is typically decided by customers, while the DSO is responsible for safe, efficient, and reliable operation of the network. This mismatch creates three problems:
- Optimizing DG locations is often infeasible for DSOs, whereas EVCS siting and reactive support assets are more directly plannable.
- Independently sited devices interact through the grid, but most algorithms ignore strategic interactions, potentially yielding suboptimal network-level outcomes.
- Deterministic planning overlooks variability in loads and DER outputs, leading to fragile solutions.
Therefore, there is a need for a planning framework that (i) models multi-agent interactions, (ii) aligns optimization decisions with DSO vs. customer control, (iii) co-optimizes EVCS and voltage support with explicit cost and service terms, and (iv) remains robust under uncertainty.
1.2. Objectives of the Study
1.2.1. General Objective
The general objective is to develop and validate an NE-based planning framework (IBRA-NE) for radial distribution networks that co-optimizes EVCS siting/sizing and DG operation (and DG siting) to reduce losses, improve voltage profiles, and account for costs and EV service quality under uncertainty.
1.2.2. Specific Objectives
The specific objectives are as follows:
- To develop a IBRA-NE principle to capture multi-objective dynamics in DG and EVCS placement and sizing;
- To formulate both basic and probabilistic BFS load flow models;
- To extend the BFS load flow to incorporate EVCS as PQ buses and DG as controllable injections;
- To integrate MCS and a BVDI to identify weak nodes under uncertainty;
- To co-optimize EVCS siting/sizing and utility-controlled DG reactive support;
- To benchmark the performance of the IBRA-NE algorithm against conventional optimization methods such as RFO, PSO, GWO, and ARFO;
- To evaluate the impact of the optimized DG configuration on system metrics, including voltage profile, loss reduction, and load adaptability;
- To provide a cost parameterization and budget sensitivity, demonstrating trade-offs between electrical and economic outcomes.
1.3. Contribution of This Study
Unlike conventional methods, the proposed approach models DGs as strategic agents in a non-cooperative game, enabling coordinated decision-making that enhances system stability and efficiency.
It provides a game-theoretic optimization framework that accounts for DG interactions, with integration of probabilistic load flow analysis using MCS. Through comprehensive MCS, this study establishes that DG improves voltage profile, minimizes variability, and enhances energy efficiency in distribution systems operating under uncertain load and DG power generation conditions.
This study adopts the DSO planning perspective; in jurisdictions where DSO cannot site DG, we fix DG locations and optimize reactive set-points while co-optimizing EVCS siting/sizing.
2. Literature Review
2.1. Review of Related Papers
Many studies use various metaheuristic algorithms, like GWO, PSO, and modified flower pollination algorithms, to optimize the placement and sizing of distributed generation (DG) in radial distribution systems with the goal of enhancing system performance during peak load times [4,5,6,7,8].
Despite being based on base load conditions, these studies employ different optimizations, like Comprehensive Learning Particle Swarm Optimization (CLPSO) and PSO, for determining the optimal solution of DG without considering the uncertainty condition [9,10].
Numerous studies investigate the placement and sizing of multiple distributed generation (DG) units under similar conditions but adopt different algorithms such as GA, the jaya optimization algorithm, and the shuffled frog leap algorithm, each offering distinct advantages and limitations [11,12].
Many researchers have investigated network reconfiguration in distribution systems, especially considering the integration of distributed generation (DG), to improve system performance and reduce losses [13,14,15,16,17].
Dawit et al. investigated radial distribution system reconfiguration using a hybrid particle swarm optimization (PSO) and genetic algorithm (GA) to minimize power losses. However, their study focuses solely on loss reduction through reconfiguration, without considering reactive power support, which is commonly addressed in multi-DG planning [18].
Muluneh et al. explored the reduction of real power losses in the RDS through optimal installing of single D-STATCOM [19].
To integrate DSR with DG active power scheduling, Dawit et al. proposed a modified particle swarm optimization that considers DG type, generation limits, and allowable penetration levels [20].
Prakash et al. used the Whale Optimization Algorithm (WOA) for multiple DG placements in radial distribution systems, demonstrating two cases: type-1 DGs (active power only) and type-2 DGs (active and reactive power). However, the study lacks a comprehensive comparison of different algorithms [21].
Dawit et al. explored disruptive DER technologies to reduce reactive power drawn from the primary distribution system. However, the study lacks a global optimization algorithm for integrating DERs to minimize losses and improve voltage profiles [22]. Mahesh et al. presented a comprehensive review on optimal DG placement and sizing in RDS, highlighting numerous methods but overlooking uncertainty considerations [23]. Yang et al. proposed optimizing line loss management in medium-level distribution systems using big data analysis. However, the study focuses mainly on real power, without adequately considering reactive power support from DG [24].
Aamir et al. proposed an improved large-scale multi-objective evolutionary algorithm for optimal DG placement and sizing at peak load, enhancing system performances while addressing renewable variability. However, the study does not consider DG output as an unexpected load in real-time systems [25].
Tri et al. combined the symbiosis organism search and neural network algorithm (SOS-NNA) for optimal DG and capacitor bank operation in radial distribution networks. However, when DGs operate at unity power factor, they cannot provide reactive power, limiting voltage drop reduction along feeders [26].
Bineeta et al. reviewed optimal PV-DG and BESS placement and network reconfiguration using PSO, proposing advanced approaches for multi-objective, dynamic, and static load conditions. However, these methods were not tested on large-scale networks, and no comparative analysis with other optimization algorithms was performed [27].
Waseen et al. discussed DG placement in radial distribution systems, highlighting DGs’ capability to dynamically inject active power [1].
Kumari et al. proposed an ANN-based intelligent method for optimal placement and sizing of multiple DERs in distribution systems. However, the study lacked DG interaction modeling [28]. Saidah et al. examined the impact of DG integration on power quality in distribution systems [29].
Eshan et al. proposed the multileader particle swarm optimization (MLPSO) algorithm for optimal DG placement and sizing in distribution systems. However, the approach neglects reactive power support, limiting DG’s effectiveness in loss reduction [30].
Imene et al. emphasized that DG installation in radial distribution systems is vital for voltage stability and loss reduction. However, using average daily instead of peak load demand may affect DG sizing accuracy and lead to suboptimal siting [31].
2.2. Identified Research Gaps
Based on the review of the related papers, the following gaps are identified:
Limited Application of game theory in the DG and EVCS Optimization: Although GT can provide a robust framework for optimizing DG and EVCS placement by addressing stakeholder interactions, balancing objectives, and adapting to uncertainties, leading to efficient, fair, and resilient power systems, there is limited application of GT.
Underexplored IBRA for Multi-DG Optimization: Though best response dynamic has shown promise in several optimization problems, its application to multi-DG placement and sizing in power systems is largely unexplored. The application of IBRA to multi-DG placement and sizing is underexplored due to the complexity of power system dynamics, convergence and scalability issues, the need for multi-objective and stakeholder-specific modeling, and the dominance of established optimization methods. Addressing these challenges requires significant theoretical and computational advancements, which remain open research areas.
Although uncertainty incorporation into the optimization process presents critical opportunities, its consideration is limited in current studies
3. Methodology
3.1. Materials and Methods
The proposed framework was validated on the Ethiopian Electric Utility (EEU) 114-bus system and IEEE 69-bus radial distribution system. the EEU 114-bus system data were adopted from Ref. [32], and IEEE 69-bus system data were adopted from standard test system specifications.
All simulations and algorithmic implementations were conducted using MATLAB R2018b, Intel Core i7, 8 GB RAM Windows 10 PC (Taipei, Taiwan), and custom-built scripts for metaheuristics (PSO, GWO, RFO, ARFO, and IBRA-NE). Performance was evaluated based on total power loss, voltage deviation and convergence characteristics.
Each algorithm (PSO, GWO, RFO, ARFO, and IBRA-NE) executed 30 independent runs to ensure statistical significance and to account for stochastic variability. To ensure fairness in comparison, the parameter settings for each algorithm were adopted from the original papers and tuned through preliminary trials to achieve optimal performance in our case study. The configurations used are summarized in Table 1.

Table 1.
Configuration parameters of each algorithm.
All model configurations and datasets are presented as Supplementary Materials, and source code are available upon reasonable request for validation and reproducibility purposes.
3.2. Backward/Forward Sweep Load Flow Mathematical Modeling
A BFS load flow algorithm mathematical model is developed to represent the power system. The BFS method is a popular iterative algorithm for load flow analysis in radial distribution systems [33]. It is computationally efficient and suitable for networks with a tree-like structure.
3.2.1. Basic Steps of BFS Method
- (a)
- Backward Sweep: The backward sweep calculates the branch currents by summing the power flows from downstream buses toward the source.
- Current through a line:
- where Pj and Qj are the total active and reactive power demand at bus j (including its load and power flowing to downstream buses), Iij is the current flowing in line i to j, and Vj is the voltage magnitude at bus j.
- Total power flowing through bus i (including downstream contributions):
- where Pi and Qi are active and reactive power demands at bus i.
- Current summation into a node:
- (b)
- Forward Sweep: The forward sweep calculates the voltages at each bus, starting from the source (slack bus) and moving downstream.
- Voltage drop across a branch:
- where Vi is voltage at the upstream bus, Zij is impedance of the branch between i and j, and Iij is the current flowing through the branch.
- (c)
- Convergence Criterion: The iterations between the BFS continue until the maximum absolute power differences converge:
- where ϵ is a predefined tolerance, k is the iteration count, and Scalc and SD are the calculated and actual apparent power.
3.2.2. BFS Formulation with Multiple DGs and EVCSs
Integrating multiple DGs and EVCSs into the BFS method requires adjustments to the load flow formulation to account for the active and reactive power contributions of the DGs and EVCSs. Voltage-controlled DGs are used to regulate voltage fluctuations in distribution networks [34], while EVCS are treated as PQ buses.
- Steps for BFS with Multiple DGs
- (a)
- Identify DG Placement: DGs are treated as reactive power injection nodes in the network. For each DG, reactive power output is determined using NE-algorithm.
- (b)
- EVCS consumes active power and are treated as PQ buses. For each EVCS, active power output is determined using NE-algorithm.
- (c)
- Modify Load Flow Inputs: For a bus j with DG and EVCS, the net active and reactive power demand is found as follows:
The power injections by DGs and EVCSs alter the load demand at the buses and need to be included in the power balance equations.
- (d)
- Backward Sweep: We compute the branch currents using the net load demands:
- (e)
- Forward Sweep: We update bus voltages using the branch currents in Equation (4).
3.2.3. Bus Voltage Deviation Index Formulation
A bus voltage deviation index (BVDI) measures the proximity of the current operating point to nominal bus voltage magnitude violation. For a radial distribution system:
- Bus voltage magnitude largely depends on load levels and power flow.
- Weak buses, typically at the ends of radial feeders, are more prone to instability.
The assumptions for developing a proposed BVDI are as follows:
- The radial distribution system is balanced.
- Loads are modeled with voltage-dependent characteristics.
- Buses with higher BVDI values are closer to voltage drop.
The proposed bus voltage deviation index is derived as follows:
where BVDIj represents the bus voltage deviation margin for bus j, Vactual is computed from the load flow equation (Equation (4)), and Vref is taken as 1.0 p.u.
Interpretation of BVDI:
3.3. NE-Based Optimization Framework
The optimization algorithm determines the placement and sizing of the DG and EVCS devices. Given the complexity of the radial distribution system and non-linearity of power flow equations, NE is developed to solve the optimization problem.
The algorithm is designed to optimize the placement and sizing of multiple DGs and EVCS by:
- ✓
- Modelling the interactions between multiple DGs and EVCS using the NE concept.
- ✓
- Developing the IBRA to explore the solution space.
3.3.1. Objective Functions and Constraints
In practical distribution systems, modern DSOs often manage or influence not only DGs but also other controllable assets such as EVCS. To enhance the applicability of the proposed NE-based IBRA framework, we extend the optimization model to jointly determine the optimal siting and sizing of DGs and EVCS. This joint formulation allows for coordinated planning of reactive and active power sources as well as new load components, improving overall network performance under rising EV penetration.
Decision Variables
DG units: for each DG i ∈ NDG, the strategy is si = (Li,Qi), where Li is the selected bus index from a candidate set and Qi is the DG’s reactive or apparent power capacity.
EVCS units: for each EVCS m ∈ NEV, the strategy is sm = (Lm,cm,Pm), where Lm is the bus location, cm is the installed charging capacity (kW), and Pm is the operational charging power. Since in our case vehicle-to-grid (V2G) capability is disabled, Pm ≥ 0.
The augmented fitness function is formulated as follows:
- →
- Minimize active power loss:
- →
- Reduce bus voltage deviation:
- →
- EV service quality: unmet charging power penalty and/or peak-coincident demand penalty. Given an exogenous EV charging request cm, it penalizes shortfall as:
- →
- Deployment/size cost (economic part of the objective):
The overall objective function is modeled as follows:
where ws are weighting factors (w1+…+w4 = 1).
- Constraints:
- Voltage limits:
- DG capacity and position limits:
- EVCS siting/sizing:
- Budget and count limits:
3.3.2. Non-Cooperative Game Formulation
In non-cooperative games, players independently optimize their strategies, potentially leading to NE. In this case, the competing generation company determines reactive power outputs to minimize costs. NE ensures no player can improve their payoff unilaterally. In a non-cooperative game, each player independently optimizes its strategy to maximize its own payoff (minimizing more power losses) while considering the actions of others static.
- Players
- DG units i ∈ I represent the set of DG players.
- EVCS operators m ∈ M represent the set of EVCS players.
- Strategies
- Let Sp = (Lp, Cp) denote the strategy of player p, where Lp is candidate buses for DG placement and Cp is DG capacity.
- Let Sm = (Lm,cm,Pm), where Lm is the bus index, cm is the capacity in kW (or number of plugs), and Pm is an operational setpoint (net power at the bus). Since we are considering without V2G: Pm ≥ 0 (net load).
- The strategy profile is S = (Sp, Sm), where Sp, Sm represents the strategy of player p.
- Payoff Function: The payoff function Ji(Sp, S-p) for each player depends on:
- (a)
- System Losses, L(Sp): This is a function of total power loss (Equation (10)).
- (b)
- Voltage Deviation, ∆V(Sp): This represents penalties for voltage violations (Equation (11)).
- (c)
- Charging energy, ∆P(Sm): This represents the peak-coincident demand penalty (Equation (12)).
- (d)
- Deployment cost, C(Sp,Sm): This represents the economic part of the objective (Equation (13)).
The payoff function is:
where ws are weights parameters. Weighting factors used to balance objectives are determined using the analytic hierarchy process (AHP) [35]. With help of AHP, prioritizing power loss, the weights are w1 = 0.4, w2 = 0.2, w3 = 0.25, w4 = 0.15, normalized such that w1 + … + w4 = 1.
- Nash Equilibrium: A Nash equilibrium S* satisfies the following:
At the NE, no player can improve their payoff by unilaterally deviating from their strategy.
- Proposed Framework for DG and EVCS Coordination Using GT:
Players: DG and EVCS devices. Each DG unit seeks to reduce its own reactive power generation and compensation expenses, which are quantified by the voltage variation and total power loss. EVCS seeks to reduce active power injections.
Strategies: DG placement (bus indices) and reactive power injection levels. Each agent (DG and EVCS) chooses its size and position in order to offset total power losses and increase the overall efficiency of the system. The voltage levels and reactive power demands at the buses have an impact on this approach.
Payoff: This is associated with improved voltage profile and decreased total power losses, unmet charging power, and deployment cost. The goal of each DG is to lower the overall reactive power demand from the grid and minimize its own share of overall losses. The goal of each EVCS is to lower the overall active power demand from the grid and minimize its own share of overall losses.
To find NE, we used the best response dynamic iterative algorithm. IBRA follows a GT approach, where each player iteratively selects its optimal strategy (placement and size) by minimizing an objective function while considering the strategies of other players.
- 1.
- Problem Definition: We considered a radial distribution system with N buses, M candidate locations for placing DGs with k DG units, and D candidate locations for placing EVCSs with y EVCS units.
For each DG, we choose a random bounded location xk ∈ {2,…,N} (bus number) and random bounded size Qk ∈ [Qmin, Qmax] (in kVAR).
For each EVCS, we choose a random bounded location xy ∈ {2,…,N} (bus number) and random bounded size Py ∈ [Pmin, Pmax] (in kW).
Players (DGs and EVCS) act iteratively to minimize the fitness function until NE is reached.
- 2.
- Objective Function:
Each DG and EVCS aims to reduce the overall fitness function given in Equation (19), subject to the constraints in Equations (15)–(18).
Iterative best response mechanism: The optimization is performed iteratively, where each DG and EVCS chooses its best response while keeping the others fixed.
Step 1: Initialize DG and EVCS Locations and Sizes
Randomly initialize xk(0), xy(0) and Qk(0), Py(0).
Step 2: Iterative Update for Each DG and EVCS
For each player (k,y), the best response function is:
Subject to:
Step 3: Nash Equilibrium Check
Check convergence criteria:
where ϵ is a tolerance value (ϵ = 0.001 for this study). If the condition holds for all DGs and EVCS, stop the algorithm. Otherwise, update the state variables (location and size) and continue.
- 3.
- Adaptive step size for DG size selection: To enhance convergence, we used an adaptive step size α(t) to adjust DG and EVCS sizes smoothly:
- 4.
- Ensuring unique DG and EVCS locations: To avoid placing multiple DGs (EVCSs) at the same bus, we introduced a penalty function. To avoid two assets at the same bus if required by planning rules, we imposed a penalty constraint:
This ensures that no two DGs (EVCS) can be assigned to the same bus.
The IBRA-NE ensures that DGs and EVCS individually optimize their placement and sizing while considering system-wide effects by incorporating adaptive step size, penalty functions for unique locations, and power loss minimization. This approach efficiently finds an NE for DG and EVCS placement in power distribution networks.
3.3.3. Potential Function Structure and Game Properties
While the proposed problem is initially framed as a non-cooperative static game, the implementation adopts an IBRA, which indeed corresponds to a dynamic learning process where each player (i.e., placement agent) updates its strategy sequentially based on the others’ most recent decisions.
An ordinal potential game potential function, Φ(s) over the strategy profile s = (s1,s2,…,sN) of all players, such that any unilateral change in a player’s strategy leads to a change in the potential function aligned with the player’s own utility improvement, is developed as:
where ui is the utility (or cost function) of player i, si is the current strategy of player i, si’ is the alternative strategy of player i, and s−i are the strategies of all other players.
Since each player’s cost function is aligned with a global system-level cost, such as total power loss and voltage deviation, the global objective function is served as a potential function in our case.
The cost function for each agent is constructed to minimize global performance metrics (power loss, voltage deviation, charging power, and deployment cost), along with local penalties. Hence, the game exhibits the characteristics of an ordinal potential game.
3.4. Cost Modeling
To reflect the economic trade-offs in joint DG–EVCS planning, the objective incorporates fixed and variable costs associated with each asset. The cost component of the joint objective is expressed in Equation (13). The considered cost parameters for simulation are shown in Table 2. These cost assumptions are consistent with DOE/NREL EVSE reports (2023) and Lazard LCOE estimates (2024). Costs are normalized for integration with technical objectives. This cost modeling ensures that the optimal solution balances technical benefits with investment feasibility.

Table 2.
Considered cost parameters for simulation.
Thus, the EVCS cost can be computed as follows:
3.5. AHP Procedure
A summary of the AHP procedure is presented as follows:
Step 1: Define Criteria: the considered two performance objectives in the optimization problem are power loss minimization and voltage profile improvement.
Step 2: Construct Pairwise Comparison Matrix: The relative importance between objectives was evaluated based on expert judgment and system reliability considerations. Power loss is prioritized due to its direct impact on energy efficiency, operational cost, and thermal stress on equipment. The pairwise comparison matrix is shown in Table 3.

Table 3.
Pairwise comparison matrix.
Step 3: Normalize the Matrix and Compute Priority Vector: Floss column sum = 2.5, Fvdev column sum = 5, Funserv column sum = 4, Fcap column sum = 6.67. By dividing each element by its column sum (normalizing the matrix), the row averages (priority vector) are found as about w1 = 0.4, w2 = 0.2, w3 = 0.25, w4 = 0.15, respectively.
Step 4: Consistency Check: The principal eigenvalue (λmax) is computed by multiplying the original matrix by the weight vector and dividing each element of the result by the corresponding weight. Calculating the Consistency Index (CI) = (λmax − n)/(n − 1), where n = 4, and comparing it with the Random Index (RI) (for n = 4, RI ≈ 0.9), the Consistency Ratio (CR) was found to be less than 0.1, confirming that the pairwise judgments are consistent.
Rationale for Prioritization: The prioritization reflects a focus on operational performance (Floss and Funserv) over financial considerations (capital cost). Floss (0.4) and Funserv (0.25) together account for 65% of the weight, emphasizing efficiency and reliability, which are core to power system performance. Fvdev (0.2) supports operational stability but is less critical, and Fcap (0.15) is a long-term concern that can be managed through planning. Floss and Funserv have direct customer and regulatory implications. Fvdev has a less immediate impact, and Fcap are internal to utility planning. This prioritization, derived via AHP, balances operational performance with financial constraints, aligning with typical utility goals of efficiency, reliability, and cost management.
3.6. Probabilistic BFS Model
After determination of optimal DG and EVCS sizes and locations, the uncertainty analysis is conducted whether the proposed optimal values meet the system requirements or not.
The basic BFS method is improved to enhance its applicability to real-world networks. The use of probabilistic load models is considered to make the method more realistic for real-world scenarios instead of assuming constant power loads. The integration of probabilistic analysis with the BFS method involves incorporating uncertainties in load into the load flow analysis.
The uncertainty modeling considered in this study is the system load and DG uncertainties using probability distributions. Modeling the system load and DGs’ power generations uncertainties using probability distributions is chosen because these variabilities are dominant factors affecting DG placement and sizing, and probability distributions offer a practical and mathematically robust way to capture this uncertainty.
The active and reactive power load (Pi and Qi) is modeled with a normal probability distribution as follows:
where μp, μq is the mean value.
Monte Carlo Simulation: MCS is a widely used probabilistic technique [32]. The steps are:
Generate uncertain power: Sample Pi sand Qi, from their respective distributions. For a random variable, solve Equation (6).
Conduct BFS load flow: For each sample, perform BFS load flow analysis.
Update state variables: For each Monte Carlo iteration, update Equations (1)–(4).
Statistical Post-Processing: After N iterations:
- → Mean Voltage:
- → Voltage Standard Deviation:
The proposed study flowchart, representing an IBRA-NE optimization framework for DG optimization in a distribution system integrating load flow analysis, MCS for uncertainty, and an IBRA-NE as the core engine to solve the multi-DG optimization, is shown in Figure 2.

Figure 2.
Overall flowchart of the proposed study.
4. Results and Analysis
4.1. Optimization Parameters and Proposed System Design
The proposed system consists of 114 nodes connected in a radial fashion. The total active and reactive power demand of the proposed distribution system is about 12.28 MW and 10.982 MVAR, respectively, which is fed from the main substation with base voltage of 15 kV and power transformer rating of 25 MVA operating at 50 Hz, with 0.85 lagging power factor.
The parameters utilized for the development and investigation of the proposed IBRA-NE algorithm and load flow analysis are presented in Table 4. The total DG maximum and minimum sizes are bounded by the total reactive power demand of the existing system. The total DG capacity is expected to not exceed the peak reactive power demand in the network to maintain system stability and avoid reverse power flow issues. Depending on the power demand data of the EVs in the town, the total size of the EVCSs should be bounded to be 12% of the total power demand of the system. The number of dimensions represent the sizes and locations of the DGs and EVCSs.

Table 4.
System and algorithm parameters.
With the given parameters, the DG locations during base load scenario analysis are found as the 35th, 77th, and 102th buses, with optimal sizes of about 3042.0533, 2082.2072, and 3250.82kVAR, respectively. The IBRA-based NE-algorithm convergence curve of the proposed algorithm is shown in Figure 3.
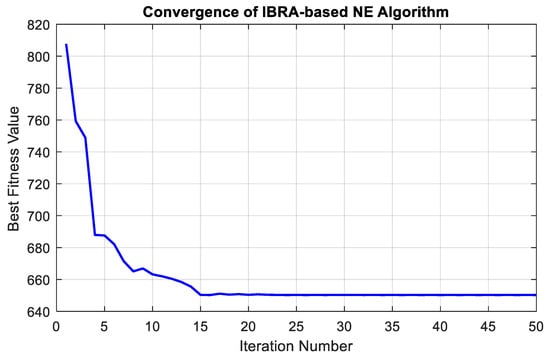
Figure 3.
Convergence curve of proposed IBRA-based NE-algorithm.
The EVCS locations during the base load scenario load flow analysis are found as the 12th, 37th, and 64th buses, with optimal sizes of about 642.33, 327.94, and 467.58 kW, respectively.
Figure 4 shows the proposed radial power distribution system with the proposed DG locations. The positions of DG1, DG2, and DG3 suggest they are strategically placed at nodes where they can effectively support the network, determined through IBRA-NE optimization.

Figure 4.
Proposed radial power distribution system with DGs.
4.2. Load Flow Analysis Results
As shown in Figure 5, at buses closer to the source, the voltage remains close to 1.0 p.u for both scenarios. The voltage drop below 0.9 p.u is more pronounced under the load increase scenario, indicating potential under-voltage problems at the farthest buses. The BVDI is used to assess the proximity of buses to the nominal voltage violation. With DG, the voltage deviation index remains at a much lower value and is within an acceptable range compared to without DGs, suggesting that DGs help in maintain bus voltages.
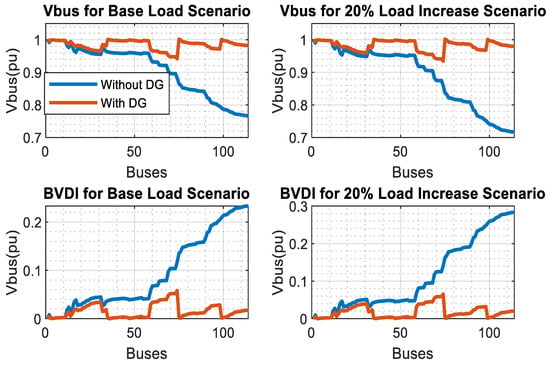
Figure 5.
Bus voltage profile without and with DG case analysis.
With the integration of the proposed DGs within the proposed power system, the minimum bus voltage profile is increased from 0.757 p.u to 0.9306 p.u. The overall voltage deviation without and with DGs is about 166.5% and 5.67%, respectively. The total active power loss without and with DGs during the base load scenario are 1543.5055 and 649.7669 kW, respectively. The total reactive power loss without and with DGs is 1356.3068 and 574.3493 kVAR, respectively. The active and reactive power loss reduction rates are 57.90% and 57.65%, respectively.
As shown in Figure 6, the 20% load increase shows a steeper decline compared to the base load, indicating increased power losses in the system. With the load increment scenario analysis, the minimum bus voltage magnitude without DGs is 0.717 at bus 114, while with DG integration, the minimum bus voltage magnitude becomes 0.9240 at bus 76. The overall bus voltage magnitude deviation without and with DGs is found to be about 243.3483% and 7.3357%, respectively. The total active and reactive power loss for the 20% load scenario is found to be about 2237.819kW and 1967.921kVAR, respectively. The active and reactive power loss reduction rates are 61.47% and 61.27%, respectively.
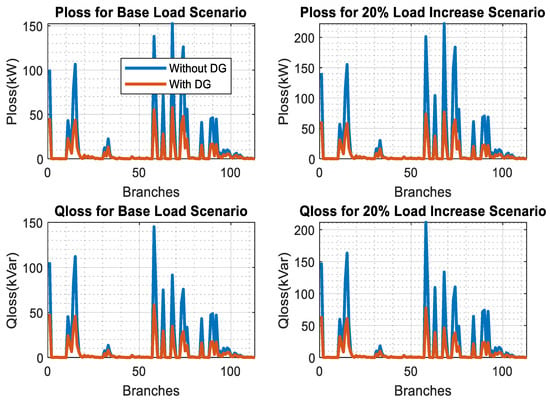
Figure 6.
Power loss without and with DGs.
The branches in the middle (Branches 60–80) show the most pronounced increases. The higher current flow from the load increase leads to quadratic growth in losses, which explains the steep rise in losses. The increased power losses in the system indicate reduced efficiency under higher load conditions. Certain branches are under stress, suggesting a need for targeted interventions to reduce losses and improve overall performance.
4.3. Uncertainty Analysis
From without and with-DG case load flow analysis, the standard deviation of bus voltage magnitudes for both scenarios are found as 7.88% and 4.48%, respectively. Considering the higher standard deviation of 7.88% (~8%), the system random load samples are generated. This assumes the variability in power demand follows a normal distribution with a standard deviation proportional to the mean considering 1000 MCS samples. Each iteration generates a random sample of active and reactive power demands to model uncertainty. By generating random samples of power demands based on normal distributions, we simulated the system to examine how variability in load affects the system.
As shown in Figure 7, DG typically improves voltage profiles by providing local power injections near load centers. The "with DG" curve shows improved voltage levels, especially at buses farther from the substation. The voltage drop gradient across buses is less steep with DG present. The “evolution” aspect suggests that the figure captures dynamic changes caused by the Monte Carlo simulations for uncertainty analysis.

Figure 7.
Bus voltage profile evolution without and with DGs.
As shown in Figure 8, without DGs, the distribution of the voltage levels skewed toward lower voltages, while with DGs, the distribution is more centered on the nominal voltage. The distribution with DGs is tighter (less variance) due to the DGs’ good voltage regulation providence. The bus voltages standard deviations are found as about 0.0766 and 0.0356 without and with DGs, respectively, indicating improved voltages. With DGs, the frequency of voltages falling below acceptable limits is reduced, and the likelihood of over-voltages (above 1.05 pu) increase slightly, depending on DG penetration and control strategies.

Figure 8.
Bus voltage magnitude and distribution frequency without and with DGs.
As shown in Figure 9, DG reduces power losses by serving local loads and reducing current flow through distribution lines. Under uncertainty (variable loads), the power losses show a wide range, with some scenarios resulting in significantly high losses due to unfavorable voltage profiles. In an uncertainty scenario, the figure reflects results from multiple simulations (MCS) to capture the range of possible outcomes. A reduction in power losses with DGs indicates improved system efficiency, while the distribution of losses provides insights into the system’s sensitivity to uncertain parameters.
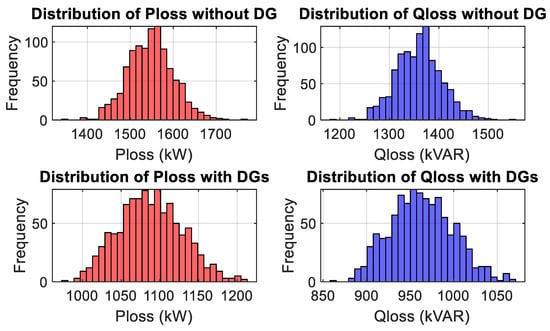
Figure 9.
Power loss without and with DGs for uncertainty scenario.
4.4. Comparative Analysis
Case I: EEU 114-bus system with 3 DGs
In this study, an NE is designed to enhance the standard IBRA performance. To evaluate the efficacy of the proposed algorithm, its performance is compared against PSO, GWO, RFO, and ARFO. The comparative load flow analysis during the base load scenario analysis focuses on convergence speed and solution accuracy to highlight the strengths and limitations of each algorithm.
A comparison of the performance of various optimization algorithms in addressing the problem of minimizing power loss and improving the voltage profile in a power system is presented in Table 5. Elapsed time denotes the computation time required by each algorithm to converge to a solution. Optimal locations refer to the specific buses in the power system where DGs should be placed to achieve the desired system performance. Optimal sizes represent the required reactive power capacities of the DGs at the identified locations. Overall percentage bus voltage deviation indicates the percentage deviation in bus voltages across the system after compensation, reflecting the effectiveness of the voltage profile maintenance.

Table 5.
Performance of different optimization algorithms.
As shown in Figure 10, IBRA-NE and GWO perform the best in terms of minimizing power loss (kW and kVAR) and overall bus voltage deviation. IBRA-NE is the most effective algorithm for this problem. GWO also performs well, making it a strong alternative.

Figure 10.
Convergence curves of each algorithm.
As shown, IBRA-NE converges the fastest, achieving a stable fitness value earlier than the other algorithms. GWO and ARFO show competitive performance, converging slightly slower than NE but achieving a fitness value close to IBRA-NE. IBRA-NE shows rapid improvement within the first 15 iterations, reflecting its efficiency in finding optimal solutions quickly. RFO exhibits a much slower improvement rate during the early iterations. IBRA-NE showed best convergence speed and lowest final fitness value. ARFO and GWO were slightly slower than IBRA-NE but achieved competitive results.
Case II: EEU 114-bus system with 5 and 10 DGs
Table 6 presents a comparison of the performance of the algorithms in optimally placing and sizing DGs in a power distribution system. This highlights that the algorithms differ not only in optimal locations but also in how aggressively they size DGs, with IBRA-NE and PSO offering steadier, more evenly distributed capacities and RFO concentrating on higher reactive support, which could yield greater loss reductions but may pose higher cost and voltage-regulation challenges.

Table 6.
Performance of different optimization algorithms with 5 and 10 DGs.
The convergence behavior of different optimization algorithms applied to the EEU 114-bus distribution system under two scenarios (with 5 and 10 DGs) is illustrated in Figure 11. The convergence speed varies significantly among the algorithms. The IBRA-NE algorithm achieved near-optimal solutions in fewer iterations, indicating faster convergence than the other variants. With 10 DGs, most of the algorithms exhibited a smoother and lower convergence path, suggesting that more DG units allow for better optimization and deeper reductions in objective values.
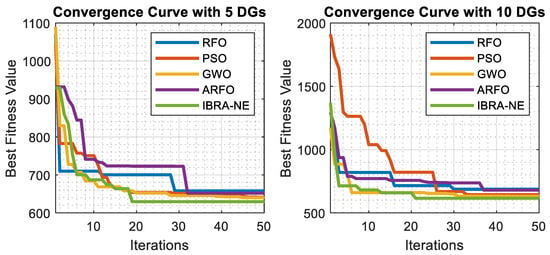
Figure 11.
Convergence of each algorithm for EEU 114-bus system with 5 and 10 DGs.
Case III: EEU 114-bus system with 5 DGs and 3 EVCSs
Considering the availability of electric vehicles in the town, three EVCS are considered to be erected under proposed study. A MATLAB simulation is conducted to evaluate the performance of the proposed IBRA-NE algorithm. Although the convergence varies significantly among the algorithms, the IBRA-NE algorithm achieves lower fitness solutions than the other variants, as shown in Figure 12. With 5 DGs and 3 EVCS, most algorithms exhibit varying convergence paths.

Figure 12.
Convergence of each algorithm for EEU 114-bus with 5 DGs and 3 EVCSs.
4.5. EVCS Deployment Cost of the Selected Plan
Under the base-load scenario, the IBRA–NE solution places EVCS at buses 12, 37, and 64 with capacities of 642.33, 327.94, and 467.58 kW, respectively. Using the planning cost model (Equation (13)) with Fm = USD 40,000, Cm = USD 1200/kW, and a grid-upgrade adder Gm, the total deployment cost is USD 2.44 million. A tiered per-kW schedule reduces the total to USD 2.20 million. Since procurement often happens in modules (150 kW DCFC cabinets), each site is rounded to the nearest multiple of 150 kW (ceil). When capacities are rounded to commercial 150 kW charger modules (750, 450, 600 kW), the BOM-plus-site cost is USD 1.56 million; including the same grid adders yields USD 2.19 million. These numbers illustrate that (i) procurement granularity and (ii) grid upgrade assumptions materially affect total cost, which motivates the budget-constrained variants analyzed in Equation (18).
For the base-load scenario, the joint DG–EVCS plan achieves a 57.9% reduction in feeder losses and raises the minimum bus voltage from 0.757 p.u. to 0.931 p.u. Using the rounded-module cost estimate of about USD 2.19 million (Table 7), this corresponds to a cost of about USD 37,800 per 1% loss reduction (2.19 M/57.9) and roughly USD 128,800 per 0.01 p.u. improvement in minimum voltage (2.19 M/[(0.931–0.757)/0.01]). These values are within the reported planning ranges for EV infrastructure and reactive support programs, and they illustrate that the proposed method delivers tangible network benefits for reasonable investment levels. Such normalized metrics allow DSOs and planners to compare alternative portfolios or evaluate budget-constrained variants of the solution.

Table 7.
Rounded-module cost estimate.
- Case IV: IEEE 69-bus system with 5 DGs
The convergence comparison for the IEEE 69-bus test system with 5 DGs to track how different optimization algorithms evolve the objective function over iterations is presented in Figure 13. The IEEE 69-bus system allows for faster convergence due to reduced dimensionality. From the convergence trends, IBRA-NE was identified as the algorithm that adapted best to a smaller fitness value.

Figure 13.
Convergence of each algorithm for IEEE 69-bus system with 5 DGs scenario.
General Insights: Increasing the DG count (from 5 to 10) generally improves the optimization results in larger systems. Algorithm performance depends on the system size, number of DGs, and optimization complexity. The proposed IBRA-NE algorithm consistently demonstrates superior performance in convergence speed, stability, and final solution quality.
4.6. Practical Applicability and Regulatory Perspective
A critical consideration in DG and EVCS planning is the distinction between assets controlled by the Distribution System Operator (DSO) and those owned by customers or third parties. In many jurisdictions, DG siting decisions are made by customers and cannot be centrally optimized by DSOs, who also cannot disclose confidential network data to DG owners. The proposed IBRA–NE framework accommodates this regulatory context through two applicability modes:
- (1)
- DSO-plannable mode, where the DSO co-optimizes EVCS siting/sizing and utility-owned or managed reactive support assets (e.g., DGs operated as VAR resources, D-STATCOMs, or batteries).
- (2)
- Customer-sited mode, where DG locations are taken as fixed inputs from interconnection data and only their reactive set-points/sizes are optimized, while EVCS siting and sizing remain under DSO planning control.
By including explicit cost terms and optional budget limits, the framework aligns with real-world planning processes and regulatory roles, providing DSOs with a practical decision-support tool for EV integration and voltage support in networks with uncertain DER behavior.
The effect of penalty weight on 3 DG placement outcomes within the EEU 114-bus system is presented in Table 8. As shown, the higher penalty values reduced DG placement conflicts and improved convergence behavior.

Table 8.
Effect of penalty weight on DG placement outcomes. Higher penalty values reduce DG placement conflicts and improve convergence behavior.
Table 9 summarizes the statistical performance of the proposed IBRA-NE algorithm under 30 independent Monte Carlo runs. The results indicate a high level of consistency and robustness, as evidenced by the low standard deviations and narrow min–max ranges across all key performance metrics. This highlights the algorithm’s ability to maintain optimal or near-optimal solutions under varying system conditions, confirming its suitability for real-world deployment in uncertain distribution environments.

Table 9.
Statistical analysis of IBRA-NE algorithm robustness over 30 independent runs.
5. Conclusions
This study proposed a novel IBRA-NE algorithm to optimize the placement and sizing of multiple DGs and EVCSs. The objective was to develop a robust optimization framework that leverages GT to model strategic interactions among DGs and EVCSs, optimizing distribution system performance effectively. The specific goals included formulating an optimization model for DG and EVCS placement, applying IBRA-NE to model these interactions for the multi-objective nature of the problem, evaluating the IBRA-NE algorithm’s effectiveness, and analyzing its impact on the power system.
The basic BFS is developed with probabilistic load models, accounting for uncertainties in system loads by utilizing MCS. When integrating multiple DGs, modifications in the load flow are necessary to incorporate their reactive power effects. A BVDI was developed to assess voltage deviations, focusing on weak buses and their susceptibility to instability based on load and power flow.
The optimization framework employed the IBRA-NE algorithm for effective placement and sizing of DGs and EVCSs, leveraging NE concepts to model DG and EVCS interactions. To explore the solution space, non-cooperative GT was applied to optimize reactive power outputs among competing companies. In this framework, players represent DGs and EVCSs with strategies involving reactive power injection and active power consumption. The payoff function, dependent on system losses, voltage deviations, charging power, and deployment cost, guides players towards a NE, where no player can improve their payoff unilaterally. The IBRA-NE algorithm, implemented in MATLAB, adjusted the DG and EVCS configuration to improve the system.
The proposed distribution system, consisting of 114 nodes in a radial configuration, was analyzed under various operating conditions. The analysis included scenarios with normal load and a 20% load increase, revealing a trend of decreasing bus voltages as the bus number increases, which is common in radial systems. Power losses escalated significantly with the 20% load increase, showing total active and reactive losses arising from about 1543.506 kW and 1356.307 kVAR under the base load to about 2237.819 kW and 1967.921 kVAR under the increased load. Overall, the results indicated the system’s sensitivity to changes in load and the potential for voltage drop and increased losses.
In the multi-DG and EVCS analysis, the parameters for the IBRA-NE algorithm and load flow analysis ere defined, ensuring that the total DG and EVCS capacity did not exceed the peak reactive and active power demand. The identified optimal DG locations during base load analysis were the 35th, 77th, and 102nd buses with sizes of about 3042.0533, 2082.2072, and 3250.8200 kVAR, respectively. The identified EVCS locations were found as the 12th, 37th, and 64th buses with optimal sizes of about 642.33, 327.94, and 467.58 kW, respectively.
The base load case study showed that the integration of DGs and EVCSs markedly enhances system performance. Total active and reactive power losses also decreased significantly, achieving reduction rates of 57.90% and 57.65% with the help of DGs. Overall, DG integration notably decreases power losses, suggesting improved efficiency and performance within the network. In the load increment case, the optimal DG configurations are consistent with the base load scenario, leading to improved voltage profiles and decreased power losses. The proposed optimization algorithm identified DG and EVCS locations and sizes for diverse loading conditions, indicating its robustness. The overall bus voltage deviations were significantly reduced from 166.5% to 5.67% when DGs were utilized.
This study proposed and evaluated the IBRA-NE algorithm. Comparative analysis with RFO, PSO, GWO, and Adaptive-RFO highlighted IBRA-NE’s superior performance in reducing power loss, improving voltage profiles, and achieving minimal bus voltage deviation. To evaluate the performance of the proposed algorithm, scenarios involving the inclusion of 5 and 10 DGs were considered on the EEU 114-bus system, while the IEEE 69-bus system was evaluated with 5 DGs. Additionally, the algorithm was tested with consideration of five DGs and three EVCSs within the system configuration. MATLAB simulations demonstrated that the IBRA-NE algorithm outperformed the compared metaheuristic algorithms.
This study analyzed the impact of DG and EVCS on distribution system performance under load uncertainty using MCS with 8% standard deviation. The results showed that DG improves voltage profiles across the system and reduces voltage variability (standard deviation reduced from 0.0766 to 0.0356). The presence of DG shifted voltage distributions closer to nominal values and decreased the frequency of under-voltage occurrences, though a slight increase in over-voltage risk was noted. In terms of efficiency, DG reduced overall power losses by serving local loads and lessening line currents, with loss distributions under uncertainty showing narrower and lower ranges. Overall, DG enhanced voltage stability, reduced variability, and improved efficiency, demonstrating its value in increasing system resilience against load uncertainties.
While the current study provides a framework for optimizing DG placement, several avenues exist for future study to enhance the applicability of the approach. Future studies could incorporate cost–benefit analysis and market dynamics to extend the optimization framework into a techno-economic model. The present model assumes a balanced system, which simplifies analysis but may not fully capture the characteristics of practical distribution networks. Adapting the framework to accommodate three-phase unbalanced conditions would increase realism. Future work could also integrate robust control techniques to handle uncertainties in renewable generation. Investigating how the proposed method scales to meshed networks and interfaces with smart meters and IoT devices would strengthen its relevance in the context of emerging smart grid infrastructures. The proposed approach is also extensible to other DSO-managed assets such as distribution-level storage, ensuring broader applicability even in jurisdictions where DG siting decisions remain outside DSO control.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/app15179668/s1, Table S1: Wolaita Sodo 114-Bus Radial Distribution Network Data.
Author Contributions
Conceptualization: K.L.L.; Methodology: K.L.L., D.B.B. and A.T.T.; Software: A.T.T. and D.B.B.; Validation: K.L.L., C.-C.K., D.B.B. and A.T.T.; Formal analysis: D.B.B. and A.T.T.; Resources: K.L.L. and C.-C.K.; Original draft preparation: A.T.T. and D.B.B.; Review and Editing: D.B.B.; Supervision: K.L.L. and C.-C.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the Supplementary Materials. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Haider, W.; Hassan, S.J.U.; Mehdi, A.; Hussain, A.; Adjayeng, G.O.M.; Kim, C.-H. Voltage profile enhancement and loss minimization using optimal placement and sizing of distributed generation in reconfigured network. Machines 2021, 9, 20. [Google Scholar] [CrossRef]
- Saxena, V.; Manna, S.; Rajput, S.K.; Kumar, P.; Sharma, B.; Alsharif, M.H.; Kim, M.-K. Navigating the complexities of distributed generation: Integration, challenges, and solutions. Energy Rep. 2024, 12, 3302–3322. [Google Scholar] [CrossRef]
- Heinrich, T.; Jang, Y.; Mungo, L.; Pangallo, M.; Scott, A.; Tarbush, B.; Wiese, S. Best-response dynamics, playing sequences, and convergence to equilibrium in random games. Int. J. Game Theory 2023, 52, 703–735. [Google Scholar] [CrossRef] [PubMed]
- Bendriss, B.; Sayah, S.; Hamouda, A. Efficient multi-objective optimization approach for solving optimal DG placement and sizing problem in distribution systems. J. Eng. Res. 2024, in press. [Google Scholar] [CrossRef]
- Salam, I.U.; Yousif, M.; Numan, M.; Zeb, K.; Billah, M. Optimizing distributed generation placement and sizing in distribution systems: A multi-objective analysis of power losses, reliability, and operational constraints. Energies 2023, 16, 5907. [Google Scholar] [CrossRef]
- Parah, S.A.; Jamil, M. Optimal DG placement for power loss reduction using GWO algorithm. In Proceedings of the 2023 International Conference on Recent Advances in Electrical, Electronics & Digital Healthcare Technologies (REEDCON), New Delhi, India, 1–3 May 2023; pp. 583–587. [Google Scholar]
- Adegoke, S.A.; Sun, Y.; Adegoke, A.S.; Ojeniyi, D. Optimal placement of distributed generation to minimize power loss and improve voltage stability. Heliyon 2024, 10, e39298. [Google Scholar] [CrossRef]
- Ramshanker, A.; Isaac, J.R.; Jeyeraj, B.E.; Swaminathan, J.; Kuppan, R. Optimal DG placement in power systems using a modified flower pollination algorithm. Energies 2022, 15, 8516. [Google Scholar] [CrossRef]
- Liu, W.; Wu, J.; Wang, F.; Huang, Y.; Dai, Q.; Yang, L. Multi-objective Optimization of Accommodation Capacity for Distributed Generation Based on Mixed Strategy Nash Equilibrium, Considering Distribution Network Flexibility. Appl. Sci. 2019, 9, 4395. [Google Scholar] [CrossRef]
- Alyu, A.B.; Yetayew, T.T. Optimal Placement and Size of Multiple PV-DG Units for Power Loss Reduction and Voltage Profile Improvement in Dilla Distribution Network. In Advancement of Science and Technology: Materials and Energy; Springer: Berlin/Heidelberg, Germany, 2023; pp. 179–198. [Google Scholar]
- Sunil, A.; Kongala, S.; Venkaiah, C. Metaheuristic techniques based optimal placement and sizing of multiple distributed generations in radial distribution system. In Proceedings of the 2021 13th IEEE PES Asia Pacific Power & Energy Engineering Conference (APPEEC), Kerala, India, 21–23 November 2021; pp. 1–6. [Google Scholar]
- Almabsout, E.A.; El-Sehiemy, R.A.; Bayoumi, A.S.A. Enhanced real coded genetic algorithm for optimal DG placement in a radial distribution system. J. Electr. Eng. Technol. 2023, 18, 2581–2597. [Google Scholar] [CrossRef]
- Shaik, M.A.; Mareddy, P.L. Enhancement of Voltage Profile in the Distribution system by Reconfiguring with DG placement using Equilibrium Optimizer. Alex. Eng. J. 2022, 61, 4081–4093. [Google Scholar] [CrossRef]
- Raut, U.; Mishra, S. An improved sine–cosine algorithm for simultaneous network reconfiguration and DG allocation in power distribution systems. Appl. Soft Comput. 2020, 92, 106293. [Google Scholar] [CrossRef]
- Rao, G.P.; Babu, P.R. Network reconfiguration and optimal allocation of multiple DG units in radial distribution system. Int. J. Adv. Technol. Eng. Explor. 2021, 8, 1019. [Google Scholar] [CrossRef]
- Tran, T.T.; Truong, K.H.; Vo, D.N. Stochastic fractal search algorithm for reconfiguration of distribution networks with distributed generations. Ain Shams Eng. J. 2020, 11, 389–407. [Google Scholar] [CrossRef]
- Ntombela, M.; Musasa, K.; Leoaneka, M.C. Power loss minimization and voltage profile improvement by system reconfiguration, DG sizing, and placement. Computation 2022, 10, 180. [Google Scholar] [CrossRef]
- Teshome, D.F.; Lian, K.L. An improved distribution system reconfiguration using hybrid GA with PSO. In Proceedings of the 2015 IEEE 15th International Conference on Environment and Electrical Engineering (EEEIC), Rome, Italy, 13 June 2015; pp. 77–82. [Google Scholar]
- Woldesemayat, M.L.; Biramo, D.B.; Tantu, A.T. Assessment of power distribution system losses and mitigation through optimally placed D-STATCOM. Cogent Eng. 2024, 11, 2330824. [Google Scholar] [CrossRef]
- Teshome, D.F.; Lian, K.L. A smart distribution system reconfiguration algorithm with optimal active power scheduling considering various types of distributed generators. IEEJ Trans. Electr. Electron. Eng. 2016, 11, 564–576. [Google Scholar] [CrossRef]
- Prakash, D.; Lakshminarayana, C. Multiple DG placements in radial distribution system for multi objectives using Whale Optimization Algorithm. Alex. Eng. J. 2018, 57, 2797–2806. [Google Scholar] [CrossRef]
- Teshome, D.F.; Xu, W.; Bagheri, P.; Nassif, A.; Zhou, Y. A reactive power control scheme for DER-caused voltage rise mitigation in secondary systems. IEEE Trans. Sustain. Energy 2018, 10, 1684–1695. [Google Scholar] [CrossRef]
- Kumar, M.; Soomro, A.M.; Uddin, W.; Kumar, L. Optimal multi-objective placement and sizing of distributed generation in distribution system: A comprehensive review. Energies 2022, 15, 7850. [Google Scholar] [CrossRef]
- Emrani, A.; Achour, Y.; Sanjari, M.J.; Berrada, A. Adaptive energy management strategy for optimal integration of wind/PV system with hybrid gravity/battery energy storage using forecast models. J. Energy Storage 2024, 96, 112613. [Google Scholar] [CrossRef]
- Ali, A.; Abbas, G.; Keerio, M.; Mugheri, N.; Memon, S.; Saand, A. Optimization of distributed energy resources planning and battery energy storage management via large-scale multi-objective evolutionary algorithm. Energy 2024, 311, 133463. [Google Scholar] [CrossRef]
- Nguyen, T.P.; Nguyen, T.A.; Phan, T.V.-H.; Vo, D.N. A comprehensive analysis for multi-objective distributed generations and capacitor banks placement in radial distribution networks using hybrid neural network algorithm. Knowl.-Based Syst. 2021, 231, 107387. [Google Scholar] [CrossRef]
- Mukhopadhyay, B.; Das, D. Multi-objective dynamic and static reconfiguration with optimized allocation of PV-DG and battery energy storage system. Renew. Sustain. Energy Rev. 2020, 124, 109777. [Google Scholar] [CrossRef]
- Sandhya, K.; Chatterjee, K. Two-stage ANN based intelligent technique for optimal positioning and sizing of DERs in distribution system. Eng. Appl. Artif. Intell. 2023, 121, 105932. [Google Scholar] [CrossRef]
- Masrufun, M. Optimization of DG placement and size using PSO based on GUI. In Proceedings of the 2020 International Conference on Smart Technology and Applications (ICoSTA), Surabaya, Indonesia, 20–20 February; pp. 1–6.
- Karunarathne, E.; Pasupuleti, J.; Ekanayake, J.; Almeida, D. Optimal placement and sizing of DGs in distribution networks using MLPSO algorithm. Energies 2020, 13, 6185. [Google Scholar] [CrossRef]
- Khenissi, I.; Sellami, R.; Fakhfakh, M.A.; Neji, R. Power loss minimization using optimal placement and sizing of photovoltaic distributed generation under daily load consumption profile with PSO and GA algorithms. J. Control Autom. Electr. Syst. 2021, 32, 1317–1331. [Google Scholar] [CrossRef]
- Tantu, A.T.; Biramo, D.B. Power flow control and reliability improvement through adaptive PSO based network reconfiguration. Heliyon 2024, 10, e36668. [Google Scholar] [CrossRef] [PubMed]
- Das, D.; Kothari, D.; Kalam, A. Simple and efficient method for load flow solution of radial distribution networks. Int. J. Electr. Power Energy Syst. 1995, 17, 335–346. [Google Scholar] [CrossRef]
- Hu, X.; Liu, Z.-W.; Wen, G.; Yu, X.; Liu, C. Voltage control for distribution networks via coordinated regulation of active and reactive power of DGs. IEEE Trans. Smart Grid 2020, 11, 4017–4031. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision making with the analytic hierarchy process. Int. J. Serv. Sci. 2008, 1, 83–98. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).