Development and Analysis of a Fast-Charge EV-Charging Station Model for Power Quality Assessment in Distribution Systems
Abstract
1. Introduction
1.1. Related EV Charging Literature Review
1.2. Contribution
- Assessment of grid impact and power quality standards in a real Thai distribution system. This work investigated the influence of EV fast charging on the electrical distribution network using a Thailand case study parameterized with utility-representative data (e.g., 24-kV MV feeders and 24/0.4-kV Δ–Y transformers). Compliance with accepted power quality standards—particularly harmonic distortion per IEEE Std 519-2014—was evaluated, providing evidence-based guidance for the strategic expansion of EV fast-charging stations in Thailand.
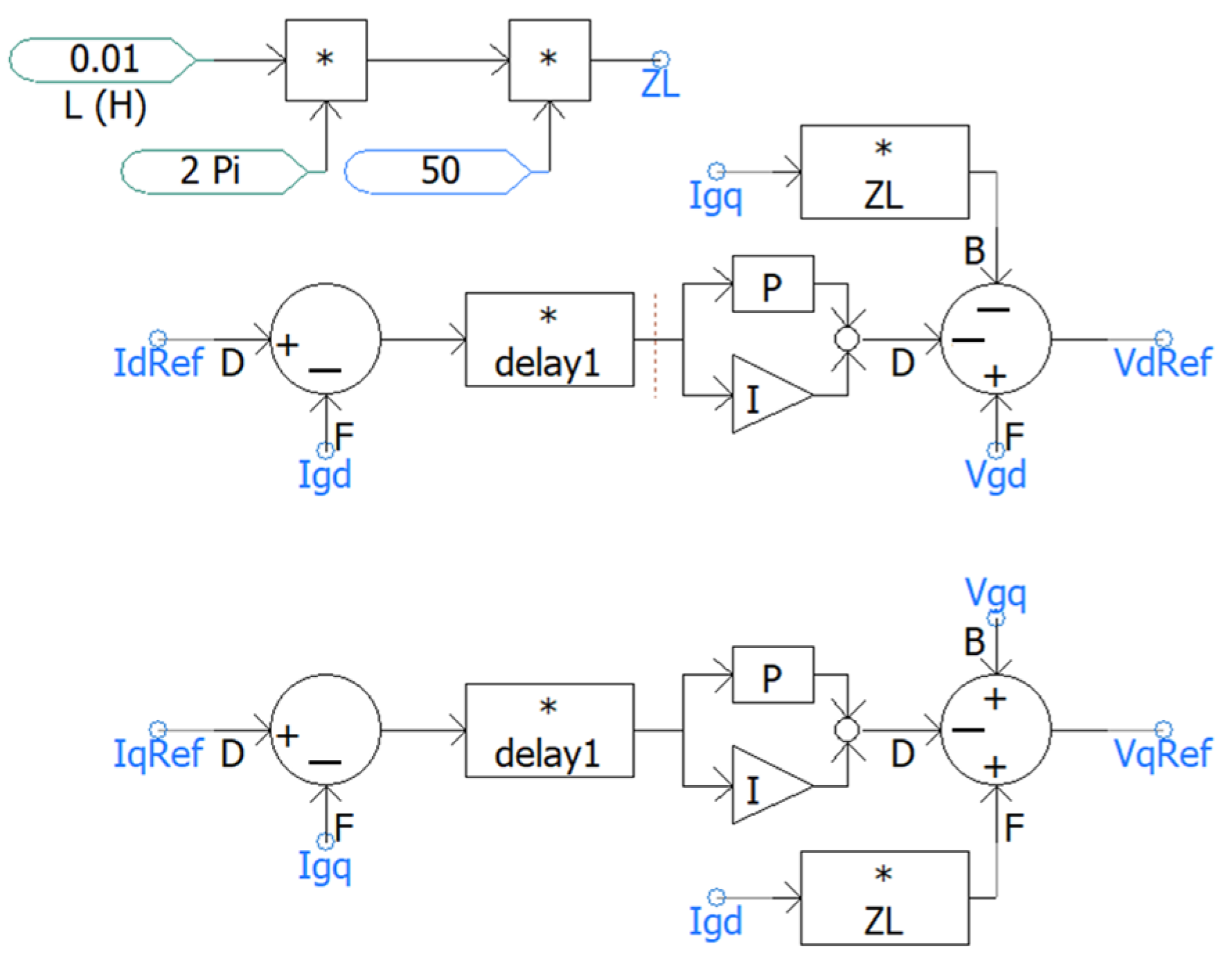
- Development of a control-oriented EV fast-charging station model built from standard PSCAD/EMTDC components and calibrated with Thai network parameters. The station model uses library VSC/transformer/feeder and DC–DC buck elements calibrated to local (MEA-consistent) parameters. Grid-side vector control maps to dq-axis current references are tracked by proportional–integral (PI) loops and synthesized via sinusoidal pulse-width modulation (SPWM) for the voltage-source converter (VSC), while the DC side enforces CC–CV charging.
- Model validation and system-wide power-quality evaluation. Validation was performed through PSCAD/EMTDC simulations spanning a matrix of battery state-of-charge (SoC) levels and staggered/simultaneous charging schedules, together with a multi-node assessment at the transformer secondary, charger AC terminals, and DC adapters. Monitored quantities include active power, current, voltage, and THDi/THDv to quantify disturbances and identify potential reliability constraints. Across all cases, the system maintains THDi ≤ 5% and THDv ≤ 1.5%—even under concurrent multi-EV sessions—confirming compliance with IEEE Std 519-2014 and practical deployability.
1.3. Organization
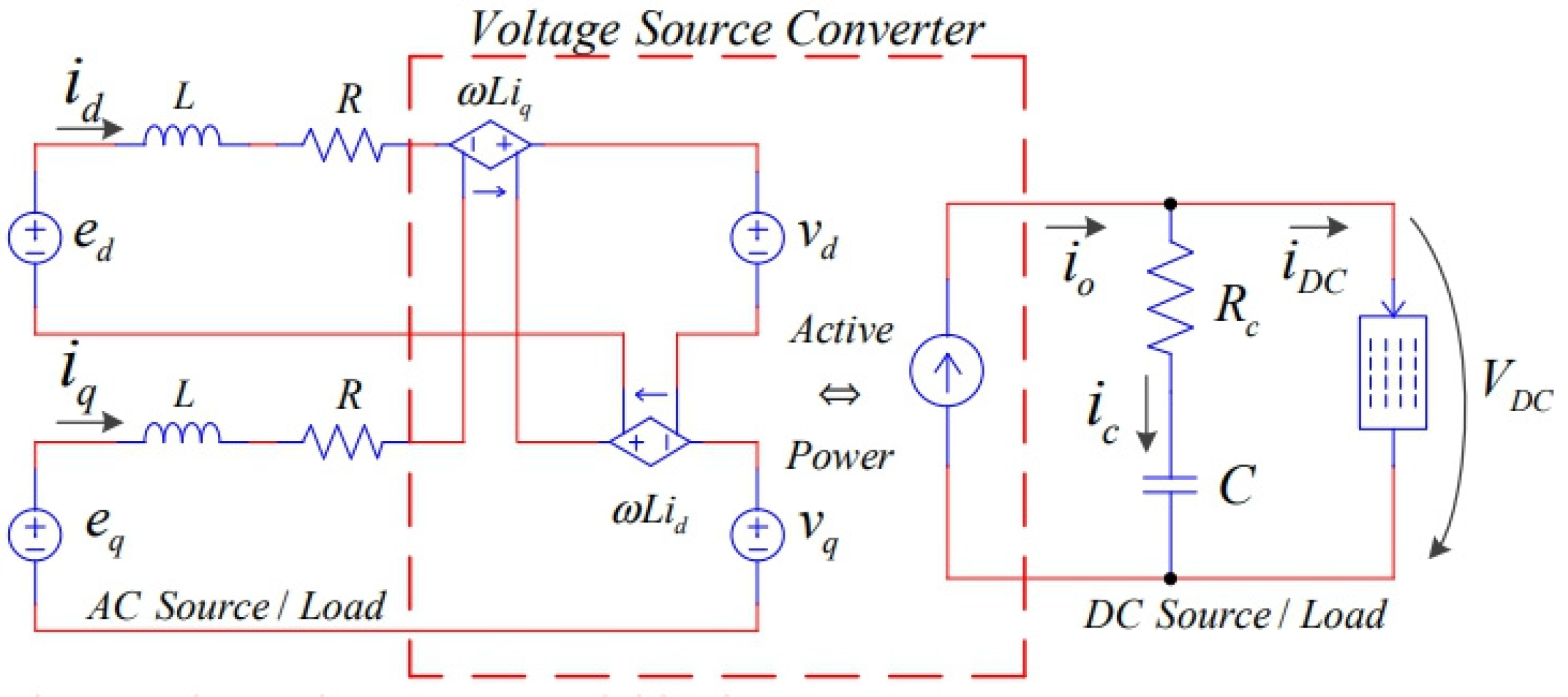
2. Electric Vehicle-Charging Station
2.1. Mathematical Charger Model
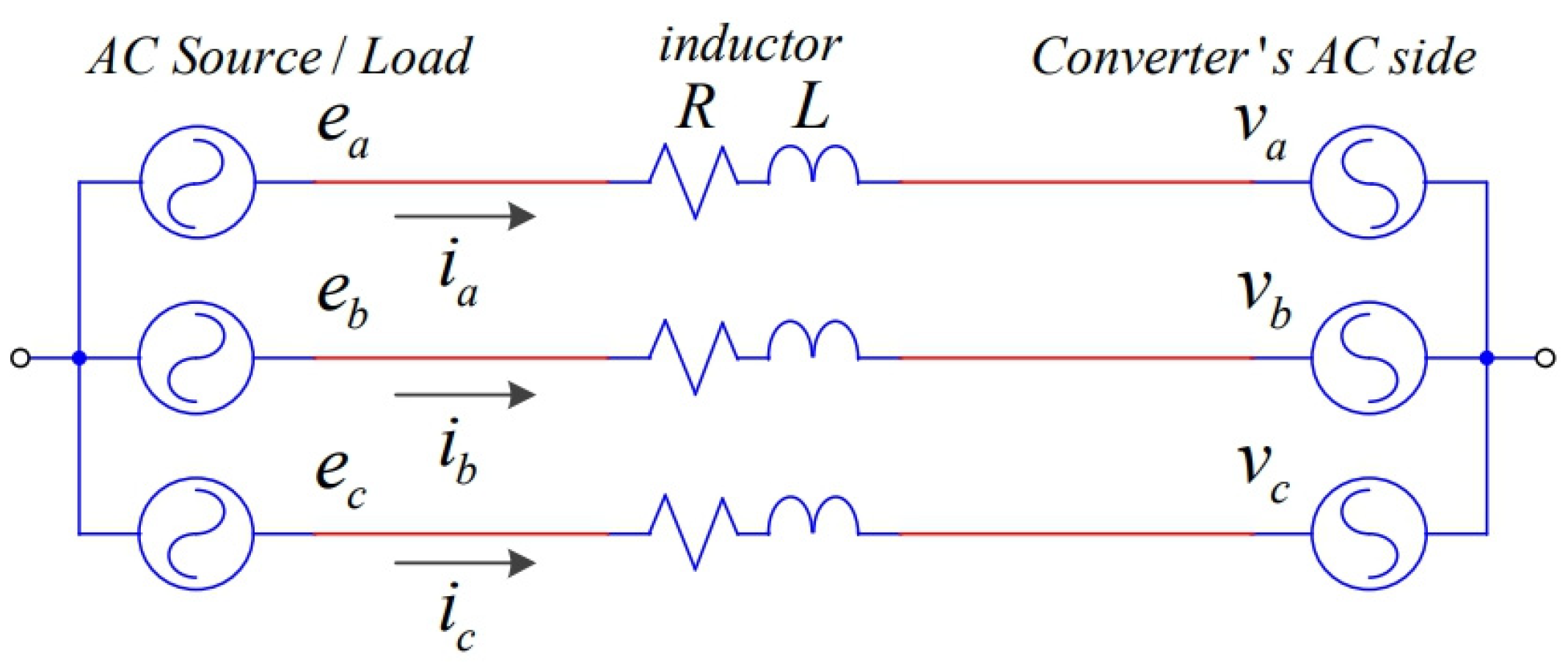
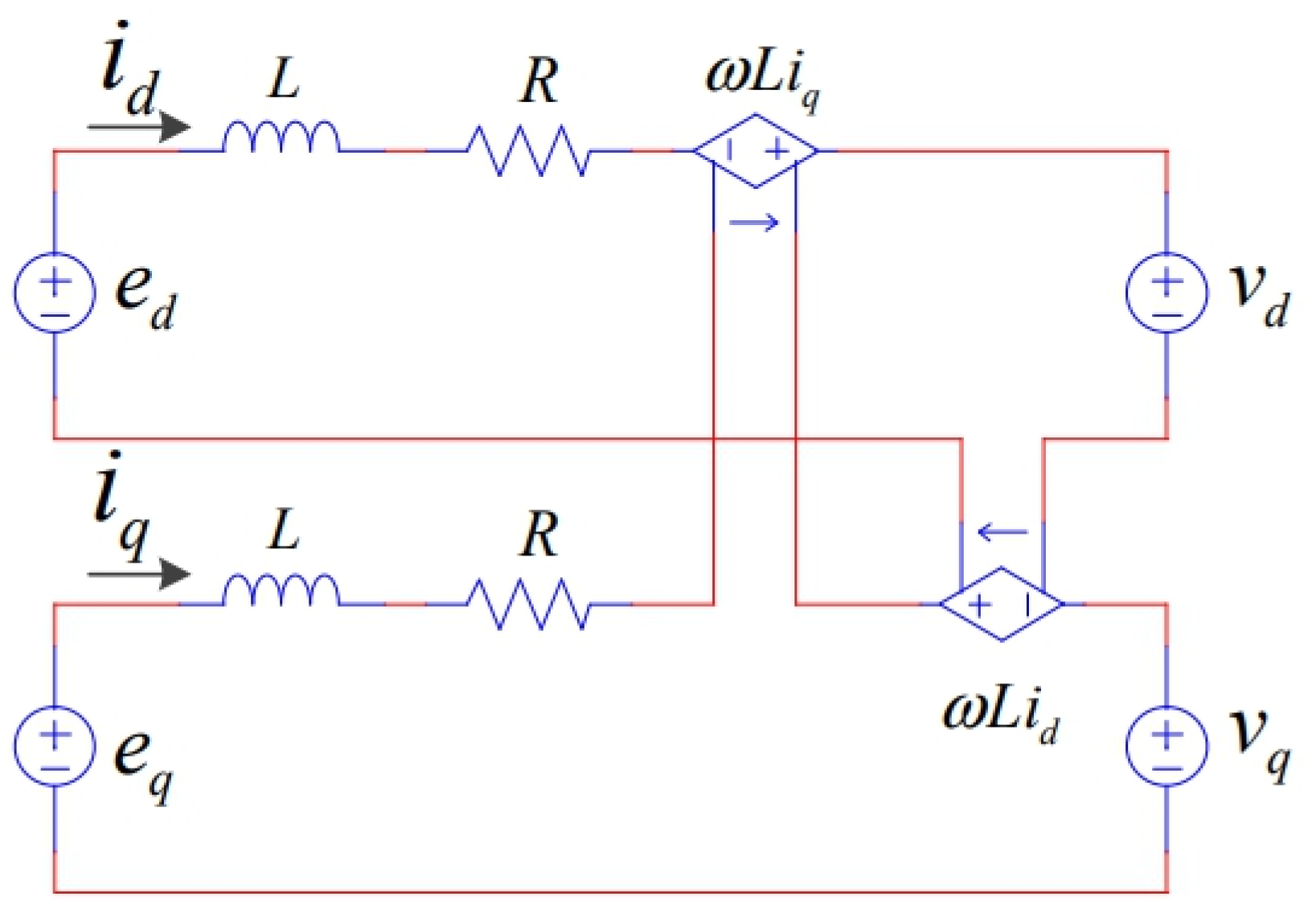
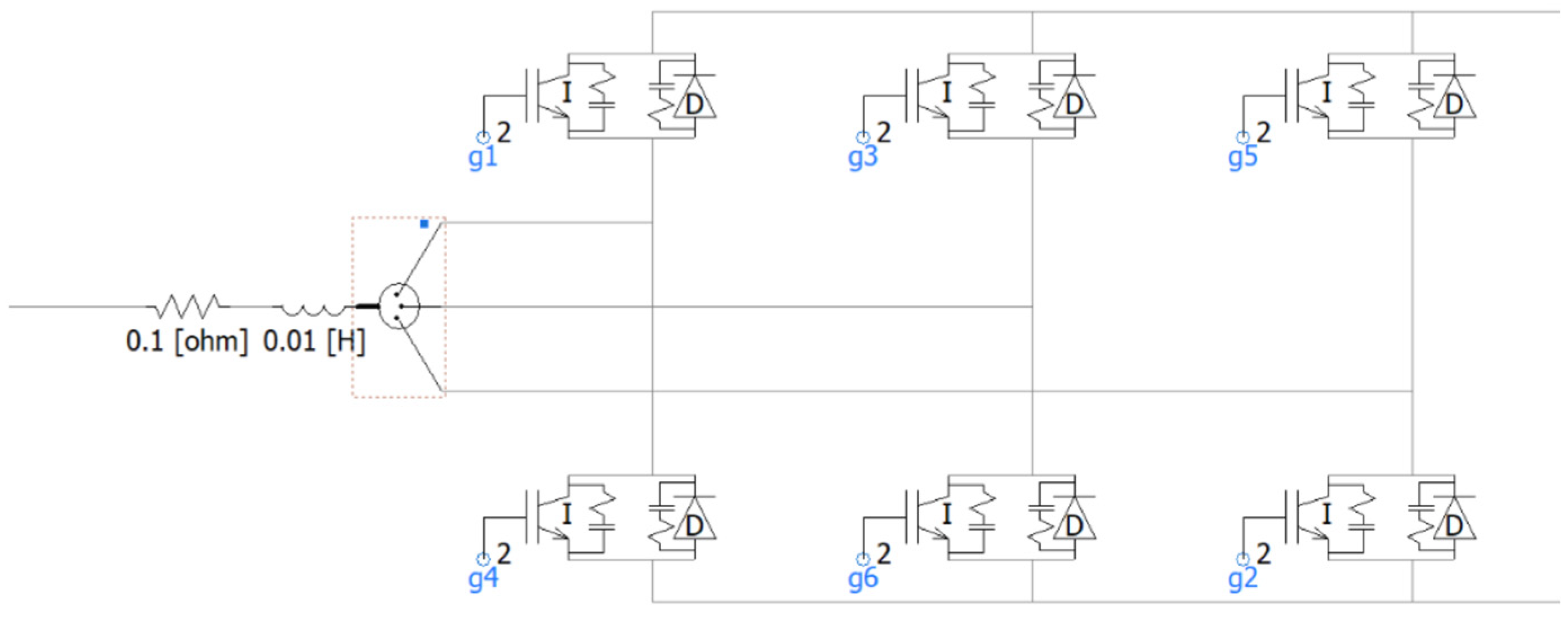
2.1.1. AC-Side Model of the Three-Phase Voltage-Source Converter
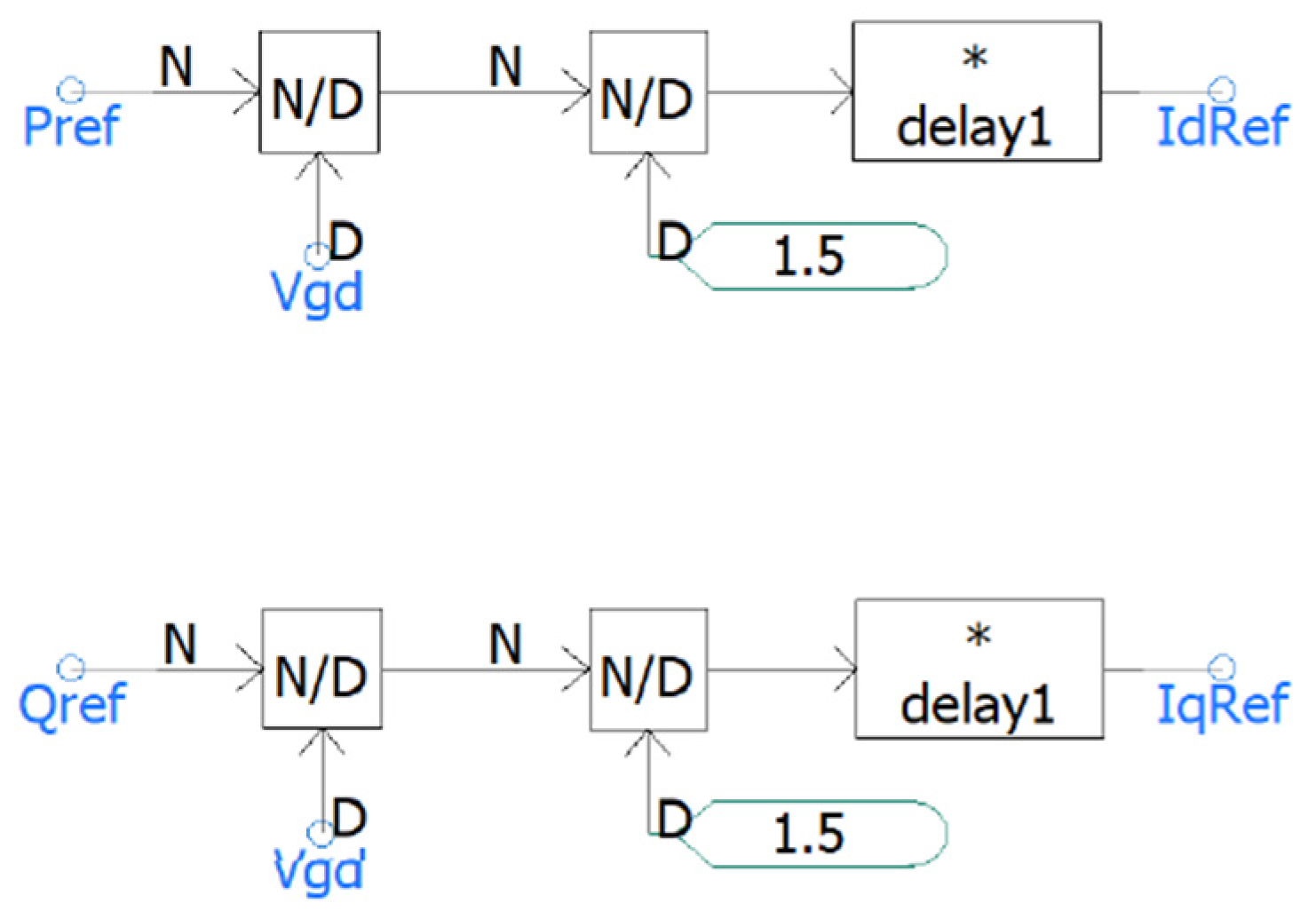
2.1.2. Converter Voltage Control
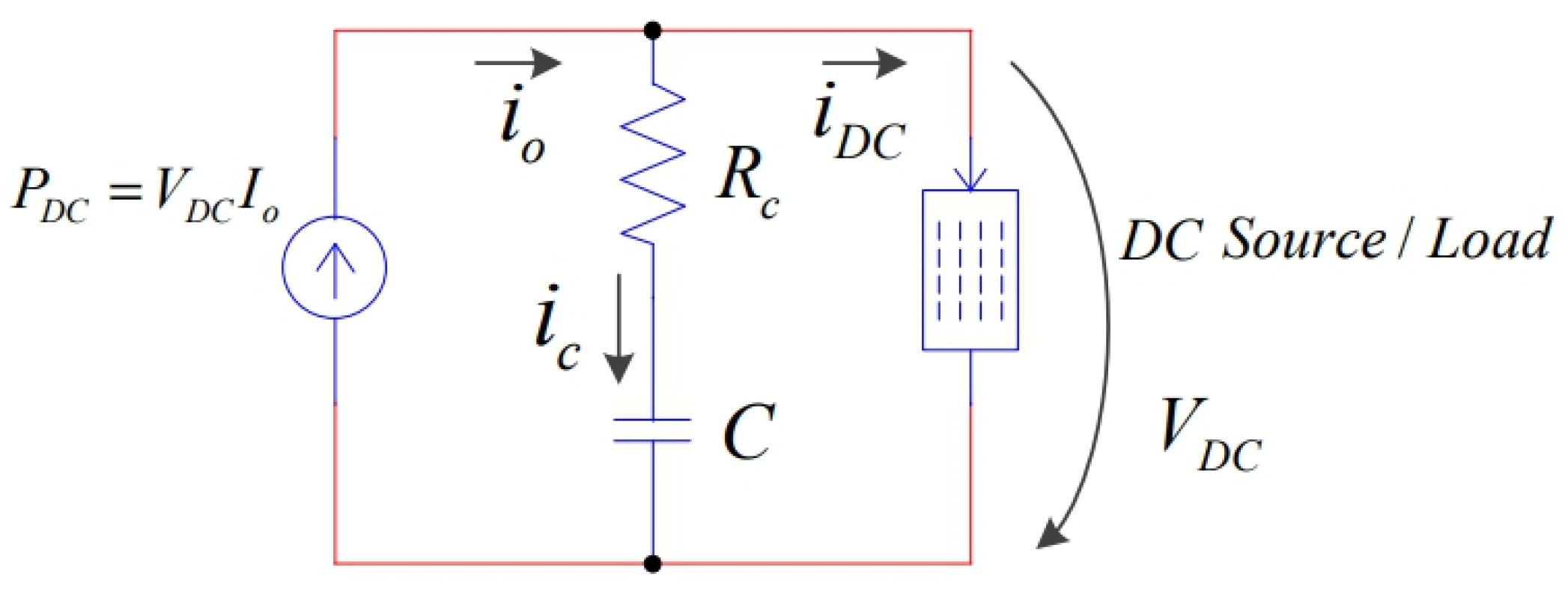
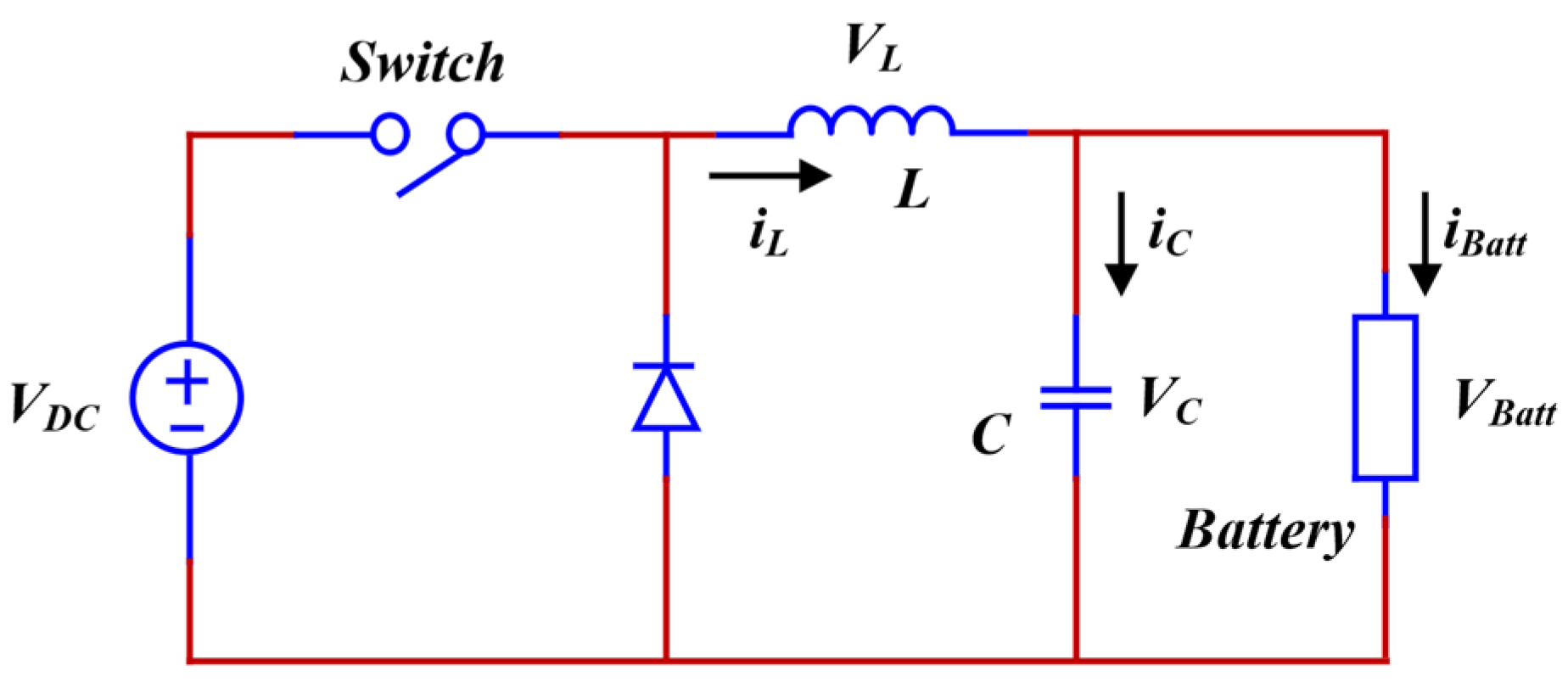
2.1.3. Buck Converter Governing the Battery Charger
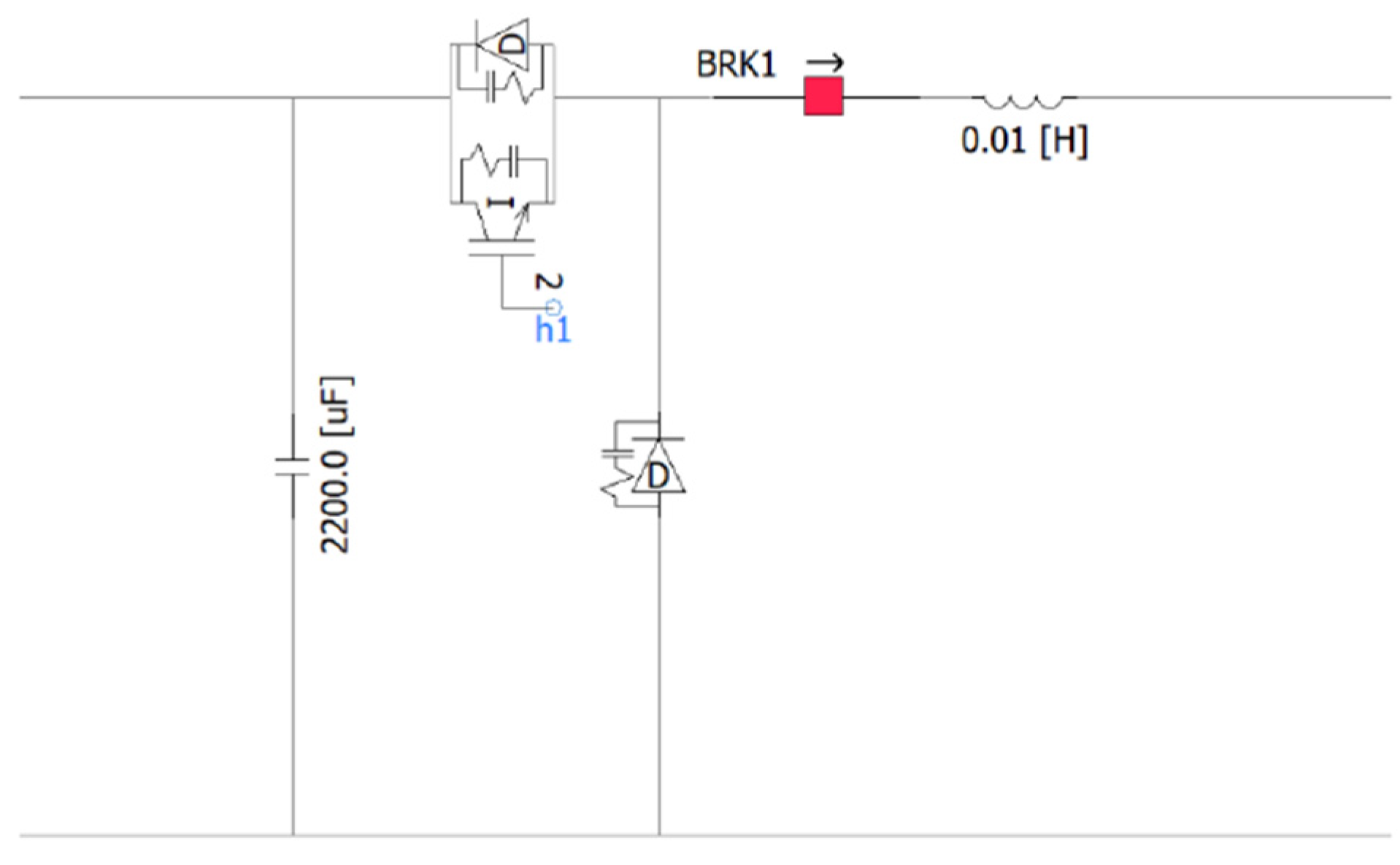
2.2. Electric Vehicle-Charging Station Model
- Voltage drop and transformer loading: At full load (300 kW), the transformer approaches 100% capacity, inducing measurable voltage drops across the 400 V bus.
- Power quality: High current switching of DC fast chargers introduces harmonics, particularly if pulse-width modulation (PWM)-based converters are used. IEEE Std 519-2014 recommends limiting THD < 5%.
- Energy losses and efficiency: Power losses in cables and the transformer were evaluated to determine system efficiency and thermal stress.
- Charging time and SoC dynamics: Based on EV battery ratings and charger power, charging durations were estimated (e.g., 30 min for 0–80% SoC at 100 kW).
3. Case Study and Results
- Front side of transformer (before step-down transformation or primary side):
- This point is located on the medium-voltage (MV) side of the transformer and represents the electrical conditions supplied by the main distribution grid (24 kV). It is used to assess grid-side impacts and monitor incoming power quality.
- Behind side of transformer (after step-down transformation or secondary side):
- Positioned at the low-voltage (LV) side of the transformer (0.4 kV), this point provides insight into voltage regulation performance, voltage drop, and transformer efficiency under varying load conditions.
- G1—input to charger unit 1:
- This point captures electrical parameters at the input of the first AC–DC conversion unit. It is useful for analyzing the power drawn by the inverter system and its conversion efficiency.
- G2—input to charger unit 2:
- Similar to G1, this monitors the input of the second charger unit, enabling phase-by-phase comparison under different EV charging loads.
- G3—input to charger unit 3:
- Measures power input to the third charger and contributes to a complete evaluation of total station consumption and power distribution among chargers.
- DC11—output of charging adapter 1 (charger 1):
- Located at the first output port of charger 1, this point monitors the DC voltage and current supplied to the connected EV. It assists in validating proper current sharing and voltage regulation during fast charging.
- DC12—output of charging adapter 2 (charger 1):
- The second output port of charger 1 is measured here, ensuring consistent performance across both ports of the same charger.
- DC21—output of charging adapter 1 (charger 2):
- Positioned at the first output of charger 2, this enables performance comparison across different charger units.
- DC22—output of charging adapter 2 (charger 2):
- Monitors the second charging outlet of charger 2, contributing to load balancing and real-time power flow analysis.
- DC31—output of charging adapter 1 (charger 3):
- Captures charging behavior at the first output of charger 3.
- DC32—output of charging adapter 2 (charger 3):
- Measures the final outlet in the system, offering a complete view of all charging interactions.
3.1. Base Case (Without EV Charging)
3.2. Various EV-Charging Scenarios
3.2.1. Transformer-Side Analysis
3.2.2. Charging Adapter Analysis
4. Discussion
5. Conclusions
- Base case: There was minimal disturbance, with a total active power of 1.6 kW from internal standby loads. Harmonic distortion was well within IEEE Std 519-2014. Voltages were highly stable at 24 kV (primary) and at the secondary (400 V AC at transformer secondary, and 500 V DC at adapter side).
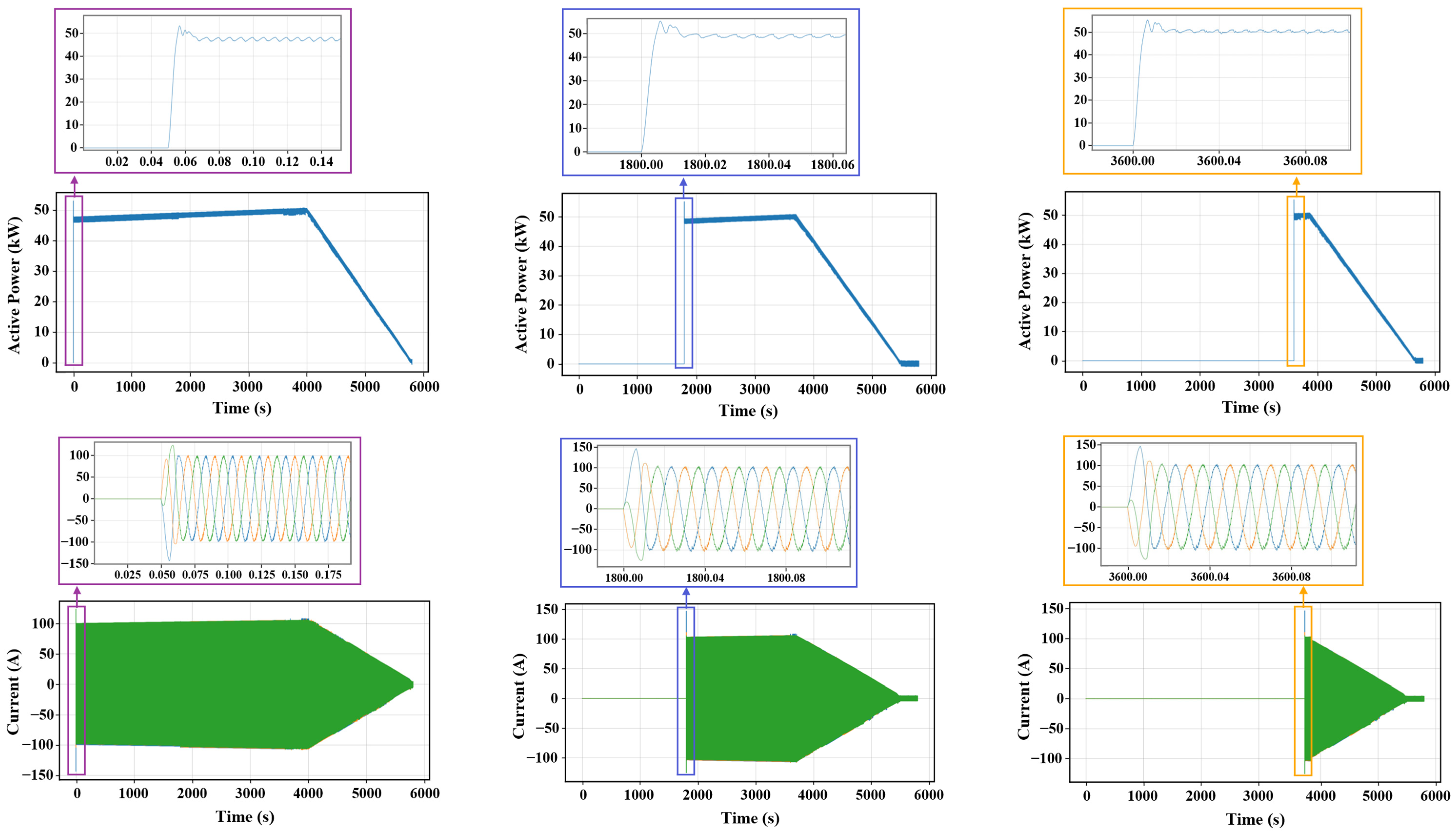
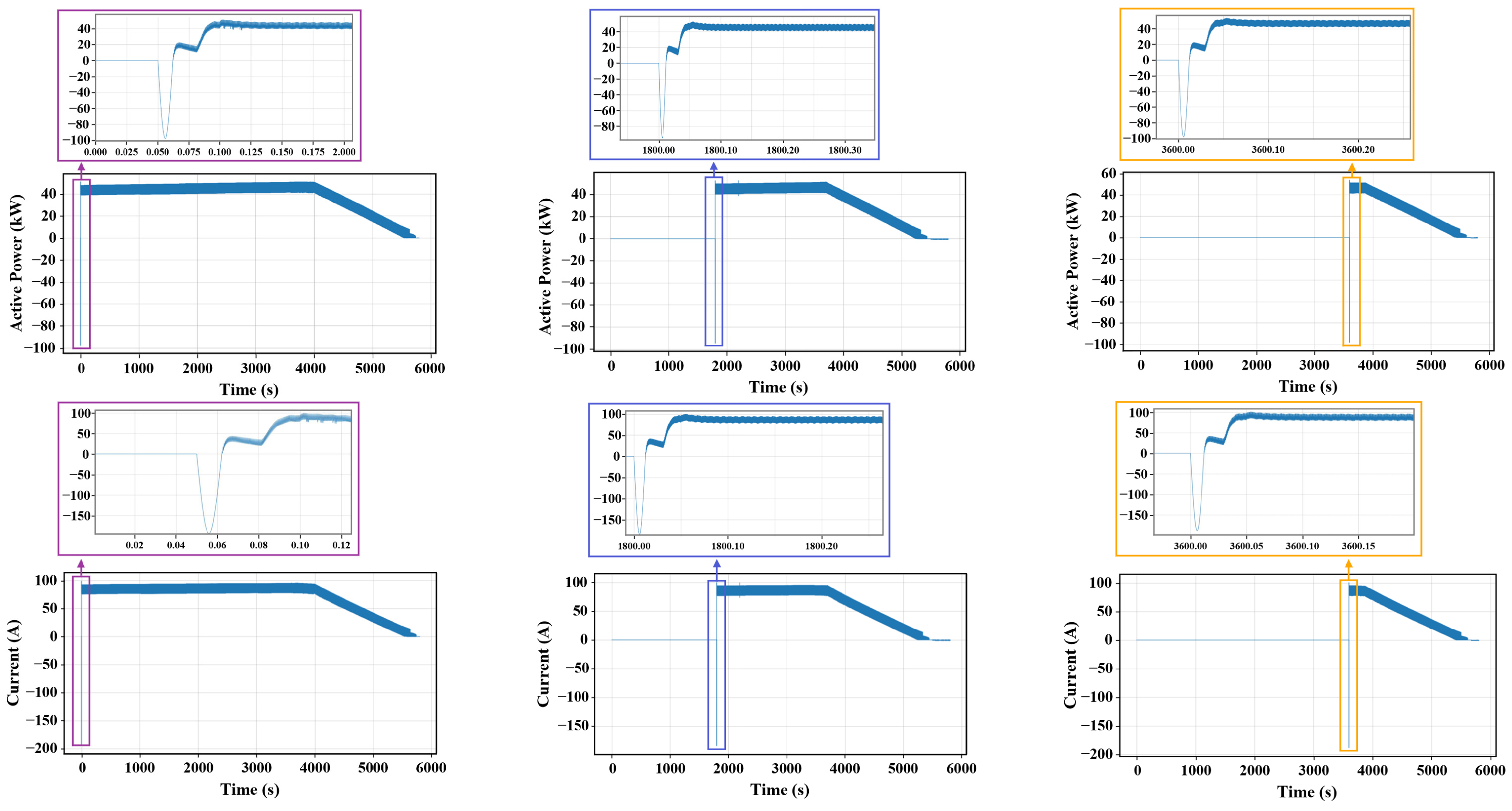
- EV-charging scenario: System loading increased markedly, peaking at 140 kW during concurrent charging of three EVs. Secondary-side currents rose to 300 A, while voltage waveforms remained stable and nearly sinusoidal, indicating robust regulation.
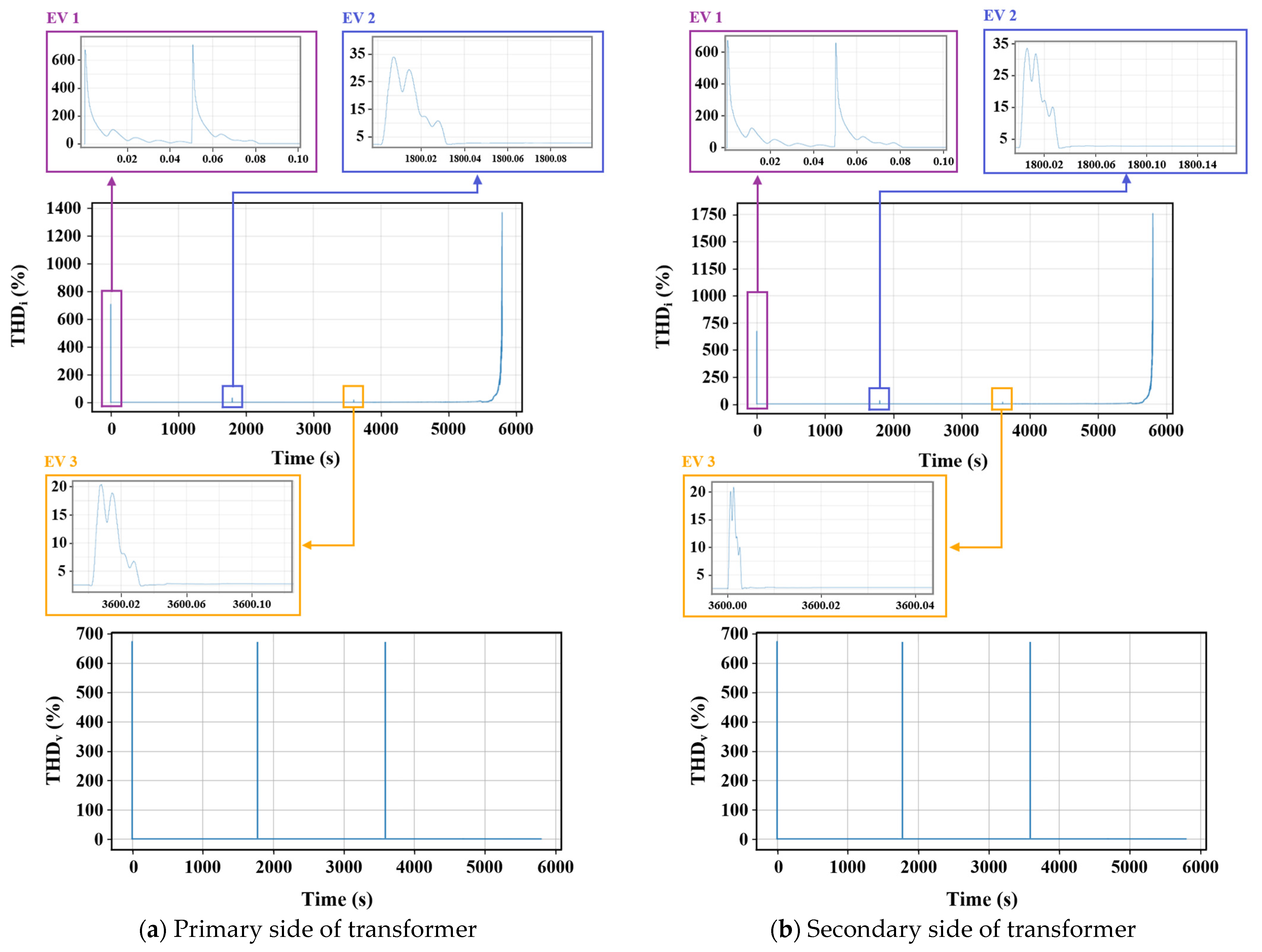
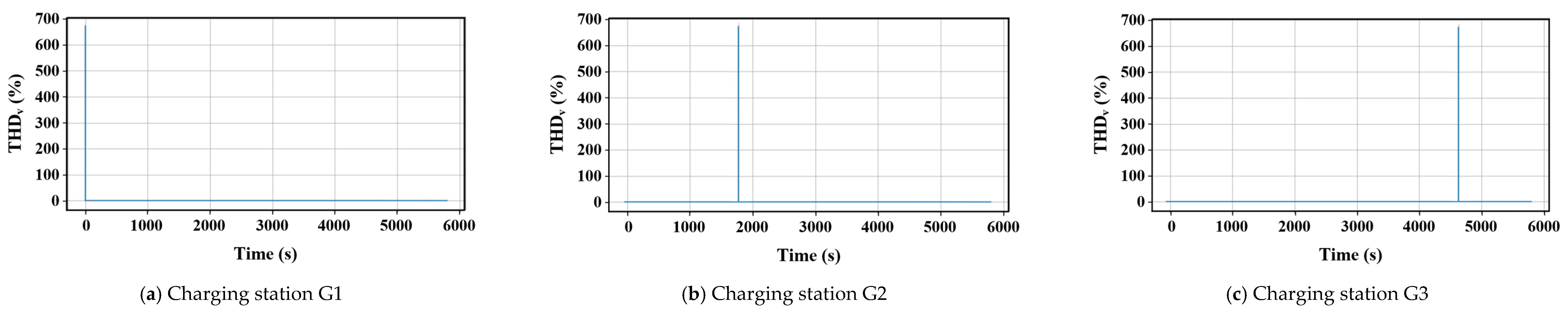
- THD behavior: The THDi showed brief spikes at charging initiation due to power-converter energization and then fell below 5% in the steady state. The THDv consistently remained < 1.5%, evidencing effective harmonic control.
- Charging profiles and DC adapters: Chargers followed the expected CC–CV profiles with asynchronous operation that helped distribute demand over time. DC adapters delivered smooth power transitions and tracked SoC requirements, dynamically regulating output voltages between 520 V and 620 V.
- Standards compliance (all nodes): Across all scenarios and measurement points (transformer secondary, charger AC terminals, and DC adapters), the steady-state THDi < 5% and THDv < 1.5% were maintained in accordance with IEEE Std 519-2014.
- Transient THD note: Transient apparent THD spikes at plug-in, caused by a temporarily small fundamental in short analysis windows, were brief and were excluded from compliance metrics by using fundamental-synchronized steady-state windows.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- International Energy Agency. Global EV Outlook 2025: Expanding Sales in Diverse Markets; IEA Publications: Paris, France, 2025. [Google Scholar]
- Electric Vehicle Association of Thailand (EVAT). Thailand Electric Vehicle Outlook 2022; EVAT: Bangkok, Thailand, 2022. [Google Scholar]
- IEEE Std 519-2014; Recommended Practice and Requirements for Harmonic Control in Electric Power Systems. IEEE Standards Association: New York, NY, USA, 2014.
- TIS 61851-1:2021; Electric Vehicle Conductive Charging System—Part 1: General Requirements. Thai Industrial Standards Institute (TISI), Ministry of Industry: Bangkok, Thailand, 2021.
- TIS 62196-1/2/3; Plugs, Socket-Outlets, Vehicle Connectors and Vehicle Inlets for EVs. Thai Industrial Standards Institute (TISI), Ministry of Industry: Bangkok, Thailand, 2022.
- TIS 60364-7-722; Low-Voltage Electrical Installations—Part 7-722: Supplies for Electric Vehicles. Thai Industrial Standards Institute (TISI), Ministry of Industry: Bangkok, Thailand, 2018.
- Metropolitan Electricity Authority. Technical Requirements for Connecting EV Chargers to the MEA Distribution Network. Available online: https://www.mea.or.th (accessed on 17 July 2025).
- Provincial Electricity Authority. Guideline for EV Charger Installation and Grid Interconnection for Customers. Available online: https://www.pea.co.th (accessed on 17 July 2025).
- UL 2202; Standard for Electric Vehicle (EV) Charging System Equipment. Underwriters Laboratories, UL Standards: Northbrook, IL, USA, 2016.
- UL 2231; Standard for Personnel Protection Systems for Electric Vehicle (EV) Supply Circuits. Underwriters Laboratories, UL Standards: Northbrook, IL, USA, 2016.
- Burra, L.T.; Al-Khasawneh, M.B.; Cirillo, C. Impact of charging infrastructure on electric vehicle adoption: A synthetic population approach. Travel Behav. Soc. 2024, 37, 100834. [Google Scholar] [CrossRef]
- Luo, Y.; Xu, X.; Yang, Y.; Liu, Y.; Liu, J. Impact of electric vehicle disordered charging on urban electricity consumption. Renew. Sustain. Energy Rev. 2025, 212, 115449. [Google Scholar] [CrossRef]
- Lin, W.; Wei, H.; Yang, L.; Zhao, X. Technical review of electric vehicle charging distribution models with considering driver behaviors impacts. J. Traffic Transp. Eng. (Engl. Ed.) 2024, 11, 643–666. [Google Scholar] [CrossRef]
- Ahmad, S.; Chaveesuk, S.; Chaiyasoonthorn, W. Impact of charging infrastructure on willingness to pay for EV: Mediating role of driving experience and behavior intentions. Acta Psychol. 2025, 254, 104833. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Guo, F.; Sivakumar, A. Analysing the impact of electric vehicle charging on households: An interrelated load profile generation approach. Energy Build. 2025, 335, 115558. [Google Scholar] [CrossRef]
- Li, B.; Chang, X. EV Charging Station Load Prediction in Coupled Urban Transportation and Distribution Networks. Energy Eng. 2024, 121, 3001–3018. [Google Scholar] [CrossRef]
- Abiassaf, G.A.; Arkadan, A.A. Impact of EV Charging, Charging Speed, and Strategy on the Distribution Grid: A Case Study. IEEE J. Emerg. Sel. Top. Ind. Electron. 2024, 5, 531–542. [Google Scholar] [CrossRef]
- Su, L.; Gurumurthy, K.M.; Kockelman, K.M. Siting and sizing of public–private charging stations impacts on household and electric vehicle fleets. Transp. Res. Part A Policy Pract. 2025, 195, 104436. [Google Scholar] [CrossRef]
- Yao, H.; Xiang, Y.; Gu, C.; Liu, J. Optimal Planning of Distribution Systems and Charging Stations Considering PV-Grid-EV Transactions. IEEE Trans. Smart Grid 2025, 16, 691–703. [Google Scholar] [CrossRef]
- Khan, M.O.; Kirmani, S.; Rihan, M. Impact assessment of electric vehicle charging on distribution networks. Renew. Energy Focus 2024, 50, 100599. [Google Scholar] [CrossRef]
- Barnabé, G.P.; Tofoli, F.L.; Mello, L.S.; Sampaio, R.F.; Antunes, F.L.M.; Leão, R.P.S. Non-intrusive demand response management strategy to mitigate the impacts of residential electric vehicle charging on distribution systems. Electr. Power Syst. Res. 2024, 235, 110849. [Google Scholar] [CrossRef]
- Brodnicke, L.; Kachirayil, F.; Gabrielli, P.; Sansavini, G.; McKenna, R. Transforming decentralized energy systems: Flexible EV charging and its impact across urbanization degrees. Appl. Energy 2025, 384, 125303. [Google Scholar] [CrossRef]
- Heider, A.; Moors, F.; Hug, G. Impact of Smart Charging and Vehicle-to-Grid Technologies on Flexibility and Grid Expansion Requirements in German Distribution Networks. IEEE Trans. Ind. Appl. 2025, 61, 4822–4832. [Google Scholar] [CrossRef]
- Bernal-Sancho, M.; Rocca, R.; Fernández-Aznar, G.; Comech, M.P.; Galán-Hernández, N. Grid Impact of Frequency Regulation Provided by V2Gs Aggregated at HV, MV, and LV Level. IEEE Access 2023, 11, 76768–76780. [Google Scholar] [CrossRef]
- Heider, A.; Helfenbein, K.; Schachler, B.; Röpcke, T.; Hug, G. On the Integration of Electric Vehicles Into German Distribution Grids Through Smart Charging. IEEE Trans. Ind. Appl. 2025, 61, 2001–2010. [Google Scholar] [CrossRef]
- Chen, J.; Aurangzeb, M.; Iqbal, S.; Shafiullah, M.; Harrison, A. Advancing EV fast charging: Addressing power mismatches through P2P optimization and grid-EV impact analysis using dragonfly algorithm and reinforcement learning. Appl. Energy 2025, 394, 126157. [Google Scholar] [CrossRef]
- Zhu, X.; Mishra, P.; Mather, B.; Zhang, M.; Meintz, A. Grid Impact Analysis and Mitigation of En-Route Charging Stations for Heavy-Duty Electric Vehicles. IEEE Open Access J. Power Energy 2023, 10, 141–150. [Google Scholar] [CrossRef]
- Roy, P.; Ilka, R.; He, J.; Liao, Y.; Cramer, A.M.; Mccann, J. Impact of Electric Vehicle Charging on Power Distribution Systems: A Case Study of the Grid in Western Kentucky. IEEE Access 2023, 11, 49002–49023. [Google Scholar] [CrossRef]
- Zou, Q.; Qian, S.; Detwiler, D.; Chhajer, R. Impacts of vehicle electrification on large-scale transportation and charging infrastructure: A dynamic network modeling approach. Case Stud. Transp. Policy 2025, 20, 101401. [Google Scholar] [CrossRef]
- Wu, Y.; Aziz, S.M.; Haque, M.H.; Kauschke, T. New staggered time-of-use tariffs to mitigate the impact of electric vehicle charging demand on distribution networks. Sustain. Energy Grids Netw. 2025, 42, 101682. [Google Scholar] [CrossRef]
- Sarmokadam, S.; Suresh, M.; Mathew, R. Power flow control strategy for prosumer based EV charging scheme to minimize charging impact on distribution network. Energy Rep. 2025, 13, 3794–3809. [Google Scholar] [CrossRef]
- James, J.; Jasmin, E.A. Stochastic modeling of electric vehicle charging and impacts on the grid. Electr. Power Syst. Res. 2025, 246, 111659. [Google Scholar] [CrossRef]
- Gnann, T.; Yu, S.; Stute, J.; Kühnbach, M. The value of smart charging at home and its impact on EV market shares—A German case study. Appl. Energy 2025, 380, 124997. [Google Scholar] [CrossRef]
- Chemudupaty, R.; Bahmani, R.; Fridgen, G.; Marxen, H.; Pavić, I. Uncertain electric vehicle charging flexibility, its value on spot markets, and the impact of user behaviour. Appl. Energy 2025, 394, 126063. [Google Scholar] [CrossRef]
- Yu, Y.; De Herdt, L.; Shekhar, A.; Mouli, G.R.C.; Bauer, P. EV Smart Charging in Distribution Grids–Experimental Evaluation Using Hardware in the Loop Setup. IEEE Open J. Ind. Electron. Soc. 2024, 5, 13–27. [Google Scholar] [CrossRef]
- Li, X.; Han, Q. An EV Charging Station Load Prediction Method Considering Distribution Network Upgrade. IEEE Trans. Power Syst. 2024, 39, 4360–4371. [Google Scholar] [CrossRef]
- Xia, Y.; Gu, X.; Fu, D.; Chen, X. Large Scale EV Charging Allocation in Unbalanced Multi-Microgrid System. IEEE J. Emerg. Sel. Top. Circuits Syst. 2023, 13, 797–805. [Google Scholar] [CrossRef]
- Gönül, Ö.; Duman, A.C.; Güler, Ö. Sizing of interoperable EV charging stations on highways with a coordinated charging scheduling strategy. Eng. Sci. Technol. Int. J. 2025, 65, 102035. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.; Razzaghi, R.; Jalili, M.; Liebman, A. Multi-objective coordinated EV charging strategy in distribution networks using an improved augmented epsilon-constrained method. Appl. Energy 2024, 369, 123547. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, Y.; Qu, J.; Ji, H.; Yu, J.; Song, G.; Sun, B.; Zhao, J. A privacy-protected distributed operation method for flexible distribution networks with EV charging load clusters. Energy 2025, 327, 136409. [Google Scholar] [CrossRef]
- Li, X.; Yip, C.; Dong, Z.Y.; Zhang, C.; Wang, B. Hierarchical control on EV charging stations with ancillary service functions for PV hosting capacity maximization in unbalanced distribution networks. Int. J. Electr. Power Energy Syst. 2024, 160, 110097. [Google Scholar] [CrossRef]
- Nakhodchi, N.; Bollen, M.H.J. Impact of modelling of MV network and remote loads on estimated harmonic hosting capacity for an EV fast charging station. Int. J. Electr. Power Energy Syst. 2023, 147, 108847. [Google Scholar] [CrossRef]
- Visakh, A.; Selvan, M.P. Analysis and mitigation of the impact of electric vehicle charging on service disruption of distribution transformers. Sustain. Energy Grids Netw. 2023, 35, 101096. [Google Scholar] [CrossRef]
- Fani, H.; Hashmi, M.U.; Deconinck, G. Impact of electric vehicle charging simultaneity factor on the hosting capacity of LV feeder. Sustain. Energy Grids Netw. 2024, 40, 101581. [Google Scholar] [CrossRef]
- Deshmukh, S.; Tariq, H.; Amir, M.; Iqbal, A.; Marzband, M.; Al-Wahedi, A.M.A.B. Impact Assessment of Electric Vehicles Integration and Optimal Charging Schemes Under Uncertainty: A Case Study of Qatar. IEEE Access 2024, 12, 131350–131371. [Google Scholar] [CrossRef]
- Vasconcelos, S.D.; da Costa Castro, J.F.; Gouveia, F.; de Moura Lacerda Filho, A.V.; Buzo, R.F.; de Medeiros, L.H.A. Assessment of Electric Vehicles Charging Grid Impact via Predictive Indicator. IEEE Access 2024, 12, 163307–163323. [Google Scholar] [CrossRef]
- Sarda, J.; Patel, N.; Patel, H.; Vaghela, R.; Brahma, B.; Bhoi, A.K.; Barsocchi, P. A review of the electric vehicle charging technology, impact on grid integration, policy consequences, challenges and future trends. Energy Rep. 2024, 12, 5671–5692. [Google Scholar] [CrossRef]
- Mojlish, S.A.K.; Sutanto, D.; Muttaqi, K.M. Impacts of ultra-fast charging of electric vehicles on power grids: State-of-the-art technologies, case studies, and a proposed improvement using a solid-state transformer. J. Energy Storage 2025, 107, 114913. [Google Scholar] [CrossRef]
- Senol, M.; Bayram, I.S.; Hunter, L.; Sevdari, K.; McGarry, C.; Gaona, D.C. Harmonics Measurement, Analysis, and Impact Assessment of Electric Vehicle Smart Charging. IEEE Open J. Veh. Technol. 2025, 6, 109–127. [Google Scholar] [CrossRef]
- Kazemtarghi, A.; Chandwani, A.; Ishraq, N.; Mallik, A. Active Compensation-Based Harmonic Reduction Technique to Mitigate Power Quality Impacts of EV Charging Systems. IEEE Trans. Transp. Electrif. 2023, 9, 1629–1640. [Google Scholar] [CrossRef]
- Jin, Y.; Acquah, M.A.; Seo, M.; Han, S. Optimal Siting and Sizing of EV Charging Station Using Stochastic Power Flow Analysis for Voltage Stability. IEEE Trans. Transp. Electrif. 2024, 10, 777–794. [Google Scholar] [CrossRef]
- Subash Kumar, C.S.; Saravanan, R.; Sankarakumar, S.; Srinivas, G. Optimizing power quality and placement of EV charging stations in a DC grid with PV-BESS using hybrid DOA-CHGNN approach. Electr. Power Syst. Res. 2025, 245, 111595. [Google Scholar] [CrossRef]



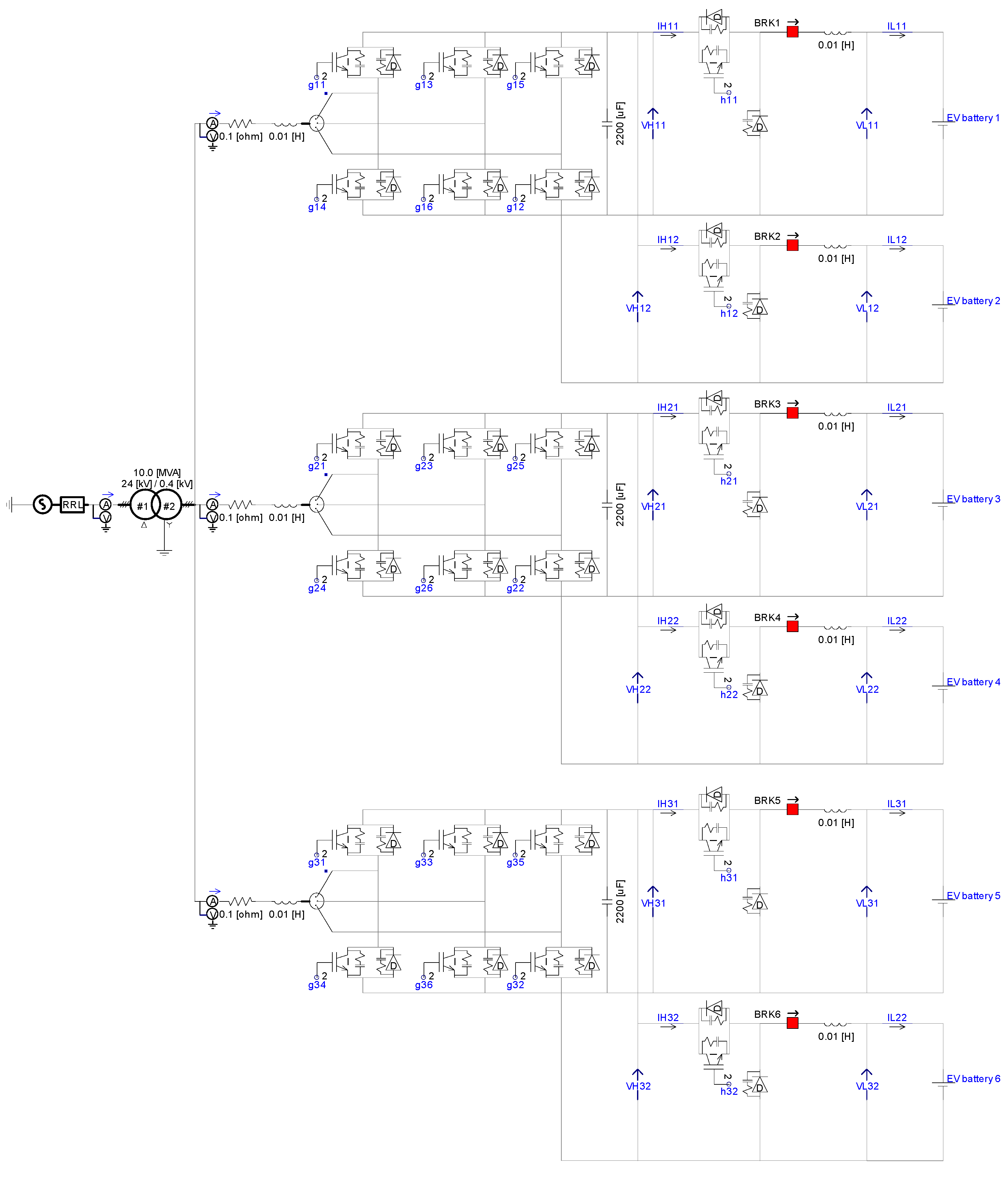




| Category | Standard/Guideline | Governing Body | Description |
|---|---|---|---|
| Product (EVSE) | TIS 61851-1 (based on IEC 61851-1) [4] | TISI | Mandatory standard for conductive EV-charging systems, including charging modes 1–4 |
| TIS 62196-1/2/3 (based on IEC 62196) [5] | TISI | Specifies EV connectors, plugs, and sockets (type 1, type 2, CCS, and CHAdeMO) | |
| Installation | TIS 60364-7-722 (based on IEC 60364-7-722) [6] | TISI | Installation requirements for EV-charging systems in low-voltage environments |
| MEA/PEA EV Charger Installation Guidelines [7,8] | MEA/PEA | Technical requirements for safely connecting EV chargers to the utility grid | |
| Power quality | IEEE Std 519-2014 (referenced by MEA/PEA) [3] | Referenced in grid codes | Regulates harmonic distortion: THDi ≤ 5%; THDv ≤ 5% at the point of common coupling (PCC) |
| Electrical safety | UL 2202/UL 2231 (for imported chargers) [9,10] | TISI/ERC | Applies to personal protection and safety of EV chargers |
| Research Work | Grid Impact and Mitigation Strategies | Charging and Control Strategies | Behavior, User Adoption, and Urban Integration | Power Quality and Harmonics |
|---|---|---|---|---|
| [11] | X | |||
| [12] | X | |||
| [13] | X | |||
| [14] | X | |||
| [15] | X | |||
| [16] | X | |||
| [17] | X | X | X | |
| [18] | X | |||
| [19] | X | |||
| [20] | X | |||
| [21] | X | X | ||
| [22] | X | X | X | |
| [23] | X | X | ||
| [24] | X | |||
| [25] | X | |||
| [26] | X | X | ||
| [27] | X | |||
| [28] | X | |||
| [29] | X | X | ||
| [30] | X | X | ||
| [31] | X | |||
| [32] | X | |||
| [33] | X | |||
| [34] | X | X | ||
| [35] | X | X | ||
| [36] | X | X | ||
| [37] | X | |||
| [38] | X | |||
| [39] | X | X | ||
| [40] | X | X | ||
| [41] | X | |||
| [42] | X | |||
| [43] | X | |||
| [44] | X | X | ||
| [45] | X | X | ||
| [46] | X | X | ||
| [47] | X | X | X | |
| [48] | X | X | ||
| [49] | X | X | ||
| [50] | X | |||
| [51] | X | |||
| [52] | X | X | ||
| This paper | X | X | X | X |
| Description | Specification |
|---|---|
| Nominal voltage | 500 V |
| Battery capacity | 120 Ah |
| Nominal capacity | 42.2 kWh |
| Number of cells | 96 |
| Storage technology | Lithium-ion batteries |
| Loss of capacity at nominal current in an hour | 0.1% |
| Initial state of charge | 1.26% |
| Measuring Points | Active Power (kW) | Reactive Power (kVar) | Voltage (V) | Current (A) | THDi (%) | THDv (%) |
|---|---|---|---|---|---|---|
| Front TR | 0.48 | 0 | 24,000 | 0 | 0.5 | 0.6 |
| Behind TR | 0.48 | 0 | 400 | 0 | 0.4 | 0.2 |
| Charging unit no. G1 | 0.16 | 0 | 400 | 0 | 0.4 | 0.2 |
| Charging unit no. G2 | 0.16 | 0 | 400 | 0 | 0.4 | 0.2 |
| Charging unit no. G3 | 0.16 | 0 | 400 | 0 | 0.4 | 0.2 |
| Adapter DC11 | 0 | 0 | 500 | 0 | 0 | 0 |
| Adapter DC12 | 0 | 0 | 500 | 0 | 0 | 0 |
| Adapter DC21 | 0 | 0 | 500 | 0 | 0 | 0 |
| Adapter DC22 | 0 | 0 | 500 | 0 | 0 | 0 |
| Adapter DC31 | 0 | 0 | 500 | 0 | 0 | 0 |
| Adaptor DC32 | 0 | 0 | 500 | 0 | 0 | 0 |
| Papers | Core Idea and Scope | Power Quality Focus and Representative Findings | Strengths | Gaps Versus This Work |
|---|---|---|---|---|
| [17] | Methodology to project EV demand and grid impact to 2050; sensitivity to charging speed and user preferences; evaluates voltage and line limits. | Planning-level power quality and hosting impacts; explores DG/RES as mitigation. | Strategic view; captures behavior and adoption scenarios. | Not an EMT converter-level study; lacks station-level THD compliance under asynchronous fast charging. |
| [39] | Multi-objective scheduling on IEEE-33 bus; optimizes DNO cost, DN losses, and user cost. | Cuts DN power loss (6%→2%); improves voltage stability. | Rigorous trade-offs; Pareto-efficient solutions. | Assumes schedules; no EMT coupling of VSC control with CC–CV charging and measured THDi/THDv at the station. |
| [42] | Hosts a fast-charging station near a transformer; compares harmonic-voltage limits vs. transformer rating with stochastic analysis. | Shows harmonic constraints can be binding; network impedance detail matters. | Sound power quality framing; data-informed. | Does not provide a station control recipe achieving THDi/THDv limits under asynchronous sessions. |
| [43] | Assesses overload/thermal risk (IEEE C57.91) and shows controlled charging reduces disruption. | Thermal indices (top-oil/hotspot) as primary risk metrics. | Practical transformer-centric guidance. | Thermal focus; not harmonic-compliance of a specific electric vehicle supply equipment control. |
| [45] | Monte Carlo EV loads; DIgSILENT assessment; PV + reward scheme improves voltages. | Voltage profile mitigation with PV and incentives. | End-to-end uncertainty treatment. | Does not verify station-level THD with practical control. |
| [46] | Composite index (demand, SCC, THD, PF) from models + measurements. | Aids early screening of EVSE impact. | Managerial tool; predictive capability. | Indicator-level; not control-design/EMT validation. |
| [49] | Lab/field harmonics vs. current level; Monte Carlo aggregation. | Worst-case aggregate 25% THD; cancellation sometimes helps. | Empirical power quality evidence. | Highlights risk; does not show a station control that guarantees THD limits. |
| [50] | Active compensation to cut 3rd harmonic in PFC; THD 4.88%→4.03%. | Component-level THD reduction. | Concrete hardware/control refinement. | Charger-front-end micro-level; not system EMT with grid coupling. |
| [52] | Hybrid optimizer for DC-grid EVCS siting and quality; reports THD = 0.9%. | PQ + cost + efficiency in DC grid. | Strong optimization outcome. | Different grid paradigm; not AC distribution EMT with Thai parameters. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiradeja, P.; Yoomak, S.; Srisuksai, P.; Klomjit, J.; Ngaopitakkul, A.; Ananwattanaporn, S. Development and Analysis of a Fast-Charge EV-Charging Station Model for Power Quality Assessment in Distribution Systems. Appl. Sci. 2025, 15, 9645. https://doi.org/10.3390/app15179645
Chiradeja P, Yoomak S, Srisuksai P, Klomjit J, Ngaopitakkul A, Ananwattanaporn S. Development and Analysis of a Fast-Charge EV-Charging Station Model for Power Quality Assessment in Distribution Systems. Applied Sciences. 2025; 15(17):9645. https://doi.org/10.3390/app15179645
Chicago/Turabian StyleChiradeja, Pathomthat, Suntiti Yoomak, Panu Srisuksai, Jittiphong Klomjit, Atthapol Ngaopitakkul, and Santipont Ananwattanaporn. 2025. "Development and Analysis of a Fast-Charge EV-Charging Station Model for Power Quality Assessment in Distribution Systems" Applied Sciences 15, no. 17: 9645. https://doi.org/10.3390/app15179645
APA StyleChiradeja, P., Yoomak, S., Srisuksai, P., Klomjit, J., Ngaopitakkul, A., & Ananwattanaporn, S. (2025). Development and Analysis of a Fast-Charge EV-Charging Station Model for Power Quality Assessment in Distribution Systems. Applied Sciences, 15(17), 9645. https://doi.org/10.3390/app15179645









