Determination of the Radius of the Ring Current in the Earth’s Core According to the Data of the INTERMAGNET Network Observatories
Abstract
1. Introduction
- -
- The liquid core of the Earth, generating the main dipole field;
- -
- The lithospheric field created by magnetized rocks;
- -
- The external field created by currents flowing in the ionosphere;
- -
- Electromagnetic induction field created by currents of the crust and outer mantle [2].
2. Materials and Methods
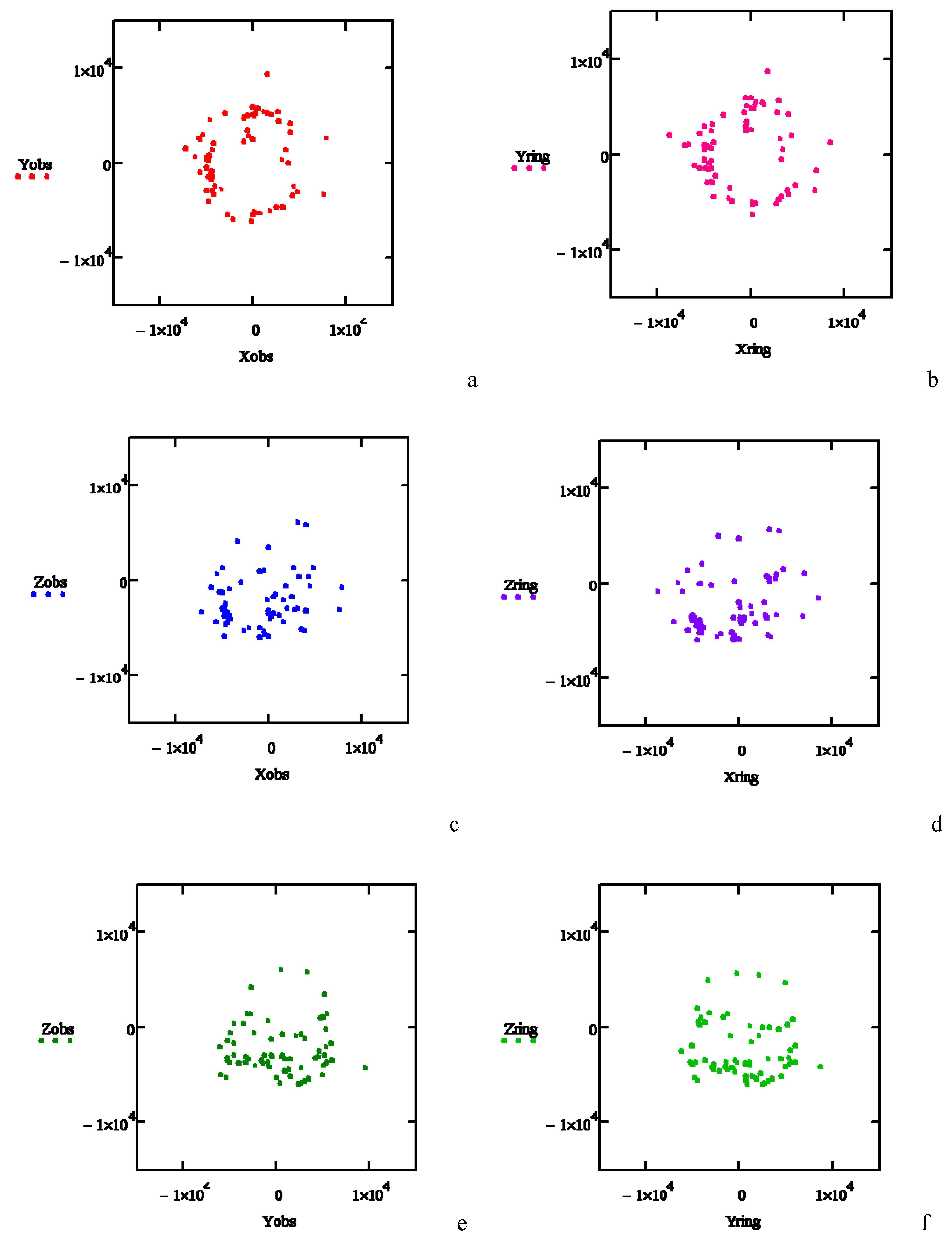
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cawood, J. Terrestrial magnetism and the development of international collaboration in the early nineteenth century. Ann. Sci. 1977, 34, 551–587. [Google Scholar] [CrossRef]
- Lanza, R.; Meloni, A. The Earth’s Magnetic Field. In The Earth’s Magnetism; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1–66. [Google Scholar] [CrossRef]
- Roberts, P.H.; King, E.M. On the genesis of the Earth’s magnetism. Rep. Prog. Phys. 2013, 76, 096801. [Google Scholar] [CrossRef] [PubMed]
- Dmitriev, A.N. A New Look On the Nature of the Earth’s Magnetic Field. IOP Conf. Ser. Earth Environ. Sci. 2016, 44, 022001. [Google Scholar] [CrossRef]
- Qin, S. Theoretical Explanation and Experimental Design of the Origin of Earth’s Magnetic Field, Stellar Magnetic Field, and Neutron Star Magnetic Field. Preprints 2023, 2023040009. [Google Scholar] [CrossRef]
- Olsen, N.; Moretto, T.; Friis-Christensen, E. New approaches to explore the Earth’s magnetic field. J. Geodyn. 2002, 33, 29–41. [Google Scholar] [CrossRef]
- Friis-Christensen, E.; Lühr, H.; Hulot, G. Swarm: A constellation to study the Earth’s magnetic field. Earth Planets Space 2006, 58, 351–358. [Google Scholar] [CrossRef]
- Hammer, M.D.; Cox, G.A.; Brown, W.J.; Beggan, C.D.; Finlay, C.C. Geomagnetic Virtual Observatories: Monitoring geomagnetic secular variation with the Swarm satellites. Earth Planets Space 2021, 73, 54. [Google Scholar] [CrossRef]
- Alldredge, L.R.; Stearns, C.O. Dipole model of the sources of the Earth’s magnetic field and secular change. J. Geophys. Res. 1969, 74, 6583–6593. [Google Scholar] [CrossRef]
- Kuppers, F.; Untiedt, J.; Baumjohann, W.; Lange, K.; Jones, A. A two-dimensional magnetometer array for ground-based observations of auroral zone electric currents during the International Magnetospheric Study (IMS). J. Geophys. 1979, 46, 429–450. Available online: https://journal.geophysicsjournal.com/JofG/article/view/160 (accessed on 29 August 2025).
- Connors, M.; Schofield, I.; Reiter, K.; Chi, P.J.; Rowe, K.M.; Russell, C.T. The AUTUMNX magnetometer meridian chain in Québec, Canada. Earth Planet Space 2016, 68, 2. [Google Scholar] [CrossRef]
- Kochnev, V. Distribution of Sources of Magnetic Field in the Earth’s Core Obtained by Solving Inverse Magnetometry Problem. In Practical and Theoretical Aspects of Geological Interpretation of Gravitational, Magnetic and Electric Fields; Nurgaliev, D., Khairullina, N., Eds.; Springer Proceedings in Earth and Environmental Sciences: Springer, Cham, 2019. [Google Scholar] [CrossRef]
- Holschneider, M.; Lesur, V.; Mauerberger, S.; Baerenzung, J. Correlation-based modeling and separation of geomagnetic field components. J. Geophys. Res. Solid Earth 2016, 121, 3142–3160. [Google Scholar] [CrossRef]
- Li, B.; Yang, B.; Xiang, F.; Guo, J.; Li, H. The Source Structure Design of the Rotating Magnetic Beacon Based on Phase-Shift Direction Finding System. Sensors 2022, 22, 8304. [Google Scholar] [CrossRef] [PubMed]
- Perov, N.S.; Granovskij, S.A.; Strelkov, N.V.; Shapaeva, T.B.; Makarova, L.A.; Shapaev, B.A. Izuchenie Postojannogo Magnitnogo Polja. Chislennoe Modelirovanie i Jeksperiment [Study of a Constant Magnetic Field. Numerical Simulation and Experiment]. Moscow 2017, 23p. Available online: http://magn.phys.msu.ru/Rus/praki/magneticfield.pdf (accessed on 29 August 2025). (In Russian).
- Vassilyev, I.V.; Mendakulov, Z.K.; Fedulina, I.N.; Zhumabayev, B.T. Method for revealing the violation of synchronization in the operation of geomagnetic observatories of INTERMAGNET network. Acta Geophys. 2025, 73, 3045–3055. [Google Scholar] [CrossRef]
- Aksenov, V.V. Modelirovanie toroidal’nyh i poloidal’nyh elektromagnitnyh polej [Modeling of toroidal and poloidal electromagnetic fields]. Mat. Model. 2014, 26, 3–24. (In Russian). [Google Scholar]
- Deguen, R. Structure and dynamics of Earth’s inner core. Earth Planet. Sci. Lett. 2012, 333–334, 211–225. [Google Scholar] [CrossRef]
- Ishii, M.; Dziewoński, A.M. The innermost inner core of the earth: Evidence for a change in anisotropic behavior at the radius of about 300 km. Proc. Natl. Acad. Sci. USA 2002, 99, 14026–14030. [Google Scholar] [CrossRef] [PubMed]
- Jacobs, J. The Earth’s Inner Core. Nature 1953, 172, 297–298. [Google Scholar] [CrossRef]
- Smylie, D.E.; McMillan, D.G. Viscous and rotational splitting of the translational oscillations of Earth’s solid inner core. Phys. Earth Planet. Inter. 1998, 106, 1–18. [Google Scholar] [CrossRef]
- Tkalčić, H.; Wang, S.; Phạm, T. Shear Properties of Earth’s Inner Core. Annu. Rev. Earth Planet. Sci. 2022, 50, 153–181. [Google Scholar] [CrossRef]
- Vassilyev, I.V.; Fedulina, I.N. Certificate of Entry of Information into the State Register of Rights to Objects Protected by Copyright № 57172 of the Republic of Kazakhstan. Determination of coordinates of magnetic field sources according to INTERMAGNET Observatories. 24 April 2025. Available online: https://copyright.kazpatent.kz/?!.iD=wQEy (accessed on 29 August 2025).
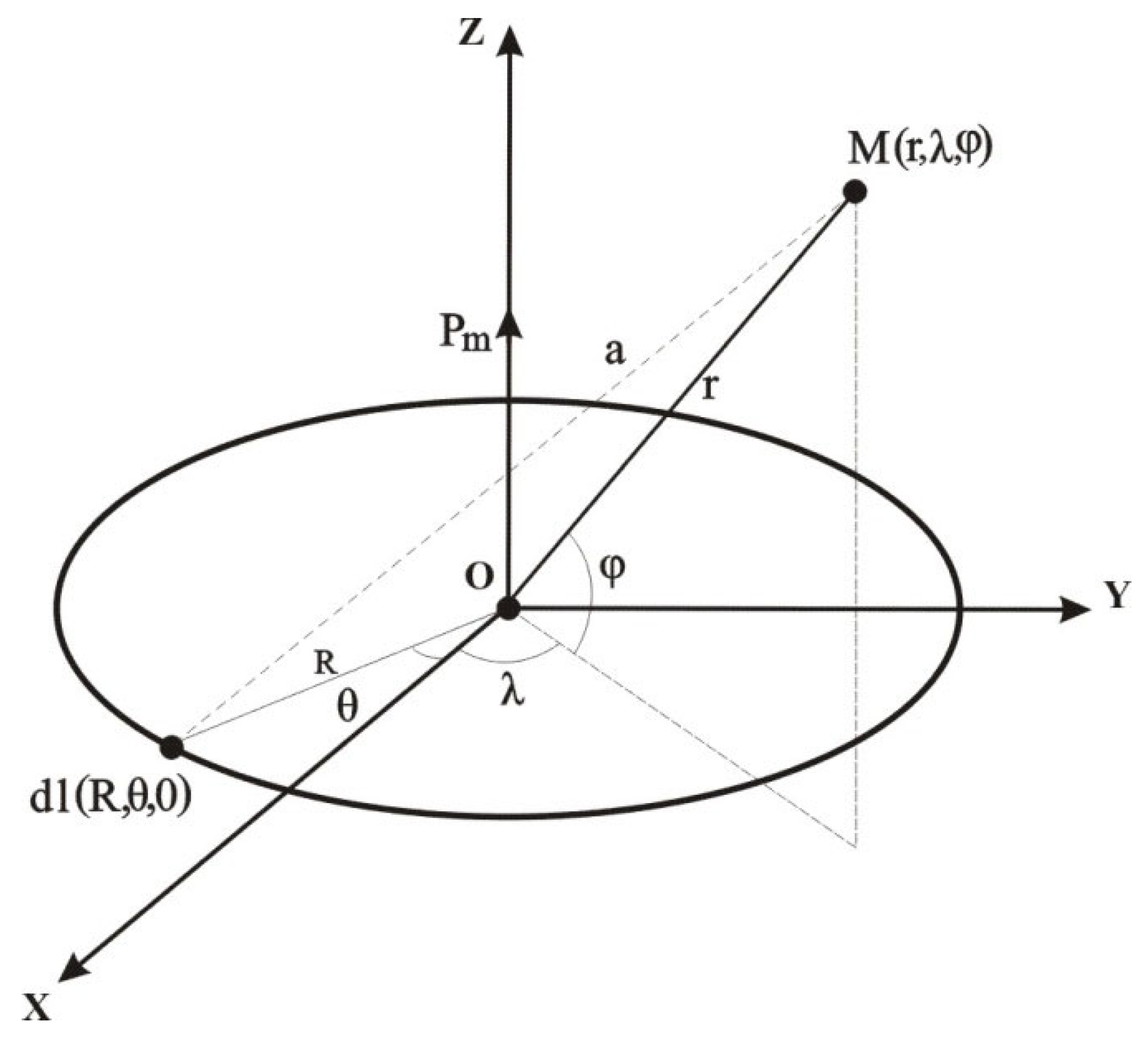
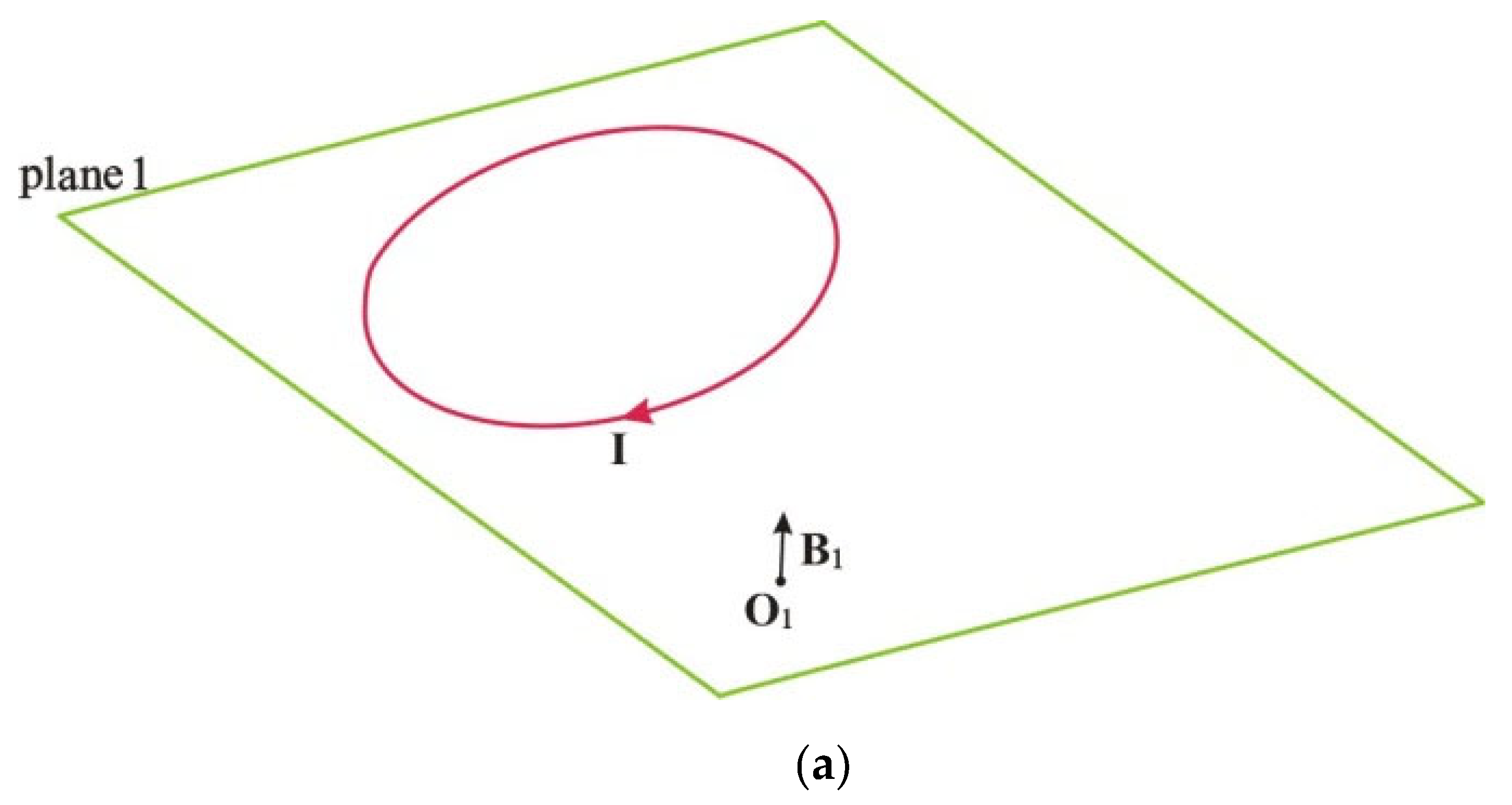
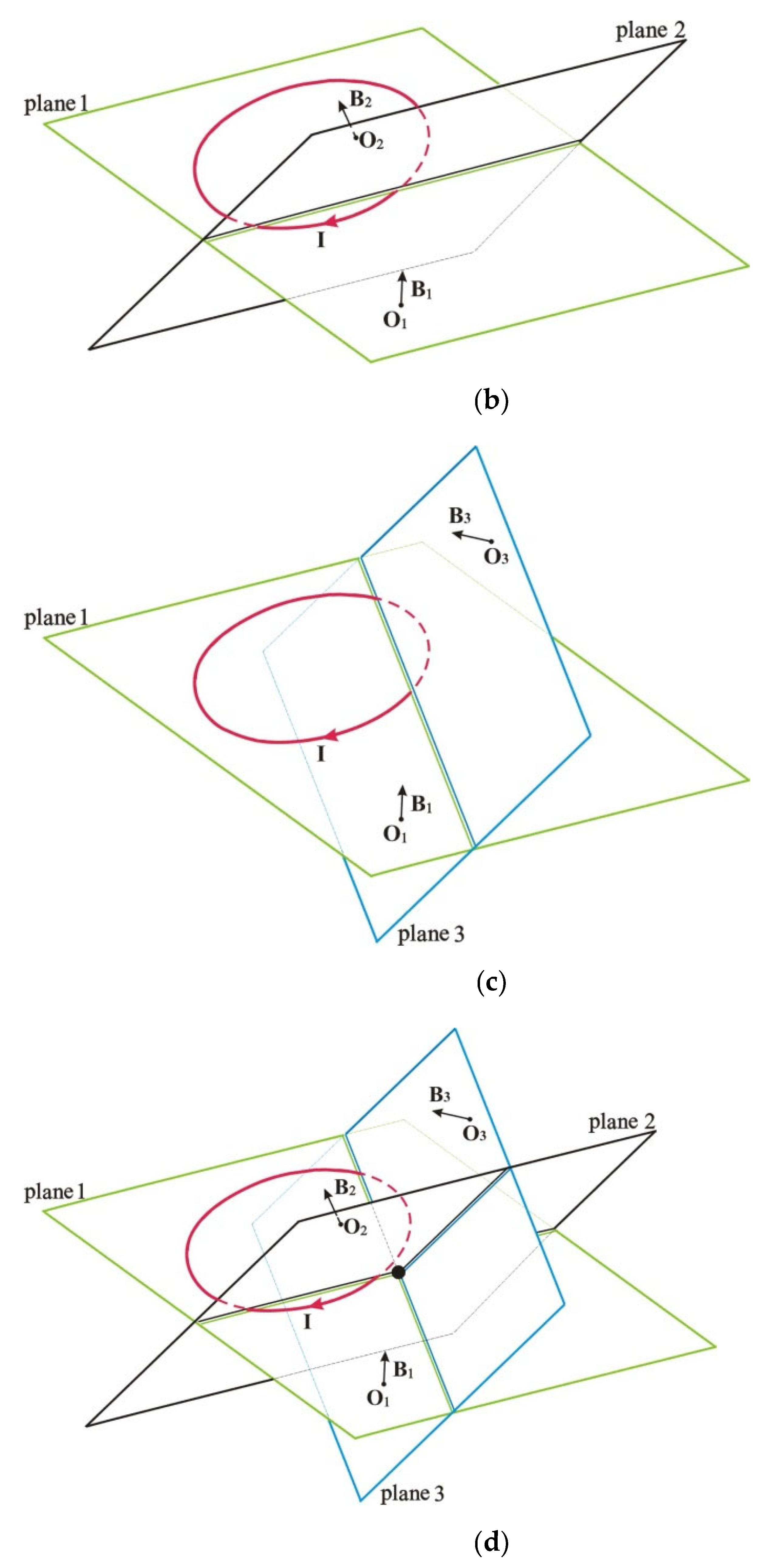
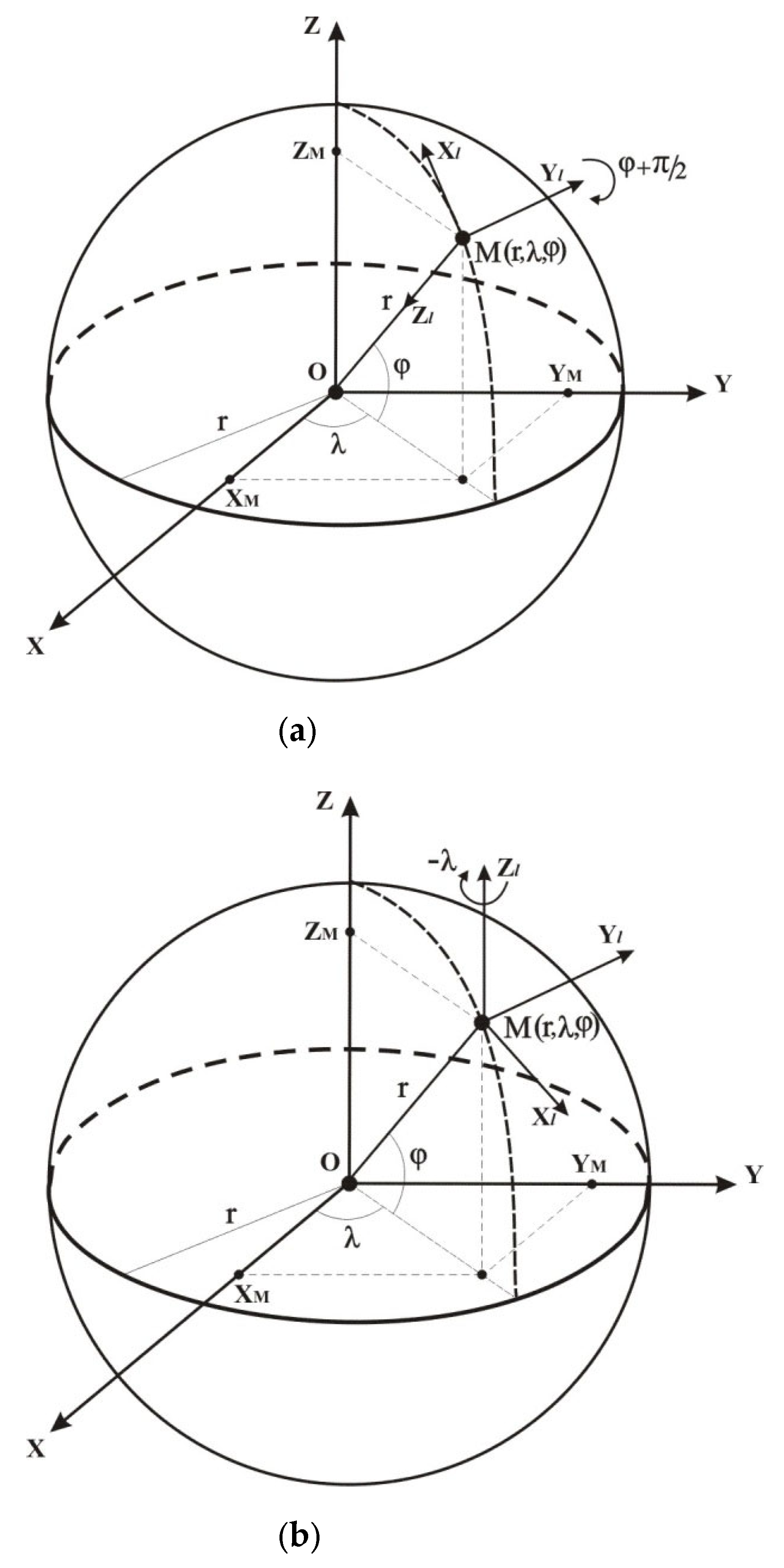
| φ0(°) | 0 | 5 | 10 | 20 | 30 | 40 | 50 | 60 | |
|---|---|---|---|---|---|---|---|---|---|
| Δ(°) | r/Δz | ||||||||
| 0.1 | r (km) | 4354 | 4408 | 4554 | 5001 | 5459 | 5817 | 6063 | 6221 |
| Δz (km) | 0 | −10 | −76 | −519 | −1405 | −2567 | −3778 | −4856 | |
| 1 | r (km) | 4355 | 4418 | 4572 | 5023 | 5478 | 5831 | 6073 | 6227 |
| Δz (km) | 0 | −13 | −86 | −549 | −1453 | −2622 | −3830 | −4900 | |
| 2 | r (km) | 4358 | 4431 | 4592 | 5049 | 5500 | 5847 | 6084 | 6235 |
| Δz (km) | 0 | −16 | −98 | −584 | −1507 | −2684 | −3889 | −4948 | |
| 5 | r (km) | 4376 | 4480 | 4663 | 5133 | 5574 | 5903 | 6125 | 6263 |
| Δz (km) | 0 | −29 | −137 | −694 | −1671 | −2869 | −4065 | −5094 | |
| 10 | r (km) | 4444 | 4595 | 4811 | 5298 | 5718 | 6017 | 6211 | 6328 |
| Δz (km) | 0 | −57 | −215 | −891 | −1956 | −3185 | −4361 | −5338 | |
| 15 | r (km) | 4559 | 4756 | 5000 | 5496 | 5890 | 6157 | 6321 | 6415 |
| Δz (km) | 0 | −96 | −311 | −1109 | −2256 | −3509 | −4664 | −5586 | |
| 20 | r (km) | 4727 | 4967 | 5233 | 5729 | 6093 | 6323 | 6455 | 6523 |
| Δz (km) | 0 | −145 | −424 | −1349 | −2574 | −3847 | −4975 | −5841 | |
| φ0(°) | 0 | 5 | 10 | 20 | 30 | 40 | 50 | 60 | |
|---|---|---|---|---|---|---|---|---|---|
| Δ(°) | r/Δz | ||||||||
| 0.1 | r (km) | 4675 | 4746 | 4932 | 5432 | 5851 | 6113 | 6256 | 6328 |
| Δz (km) | 0 | −16 | −116 | −733 | −1809 | −3048 | −4206 | −5152 | |
| 1 | r (km) | 4676 | 4759 | 4953 | 5454 | 5867 | 6123 | 6261 | 6331 |
| Δz (km) | 0 | −20 | −131 | −773 | −1864 | −3103 | −4253 | −5189 | |
| 2 | r (km) | 4679 | 4776 | 4978 | 5481 | 5885 | 6134 | 6268 | 6334 |
| Δz (km) | 0 | −26 | −149 | −818 | −1924 | −3164 | −4306 | −5230 | |
| 5 | r (km) | 4703 | 4838 | 5063 | 5566 | 5947 | 6174 | 6293 | 6350 |
| Δz (km) | 0 | −45 | −207 | −958 | −2107 | −3347 | −4465 | −5352 | |
| 10 | r (km) | 4790 | 4983 | 5237 | 5731 | 6070 | 6258 | 6351 | 6392 |
| Δz (km) | 0 | −89 | −320 | −1204 | −2415 | −3652 | −4726 | −5553 | |
| 15 | r (km) | 4937 | 5180 | 5454 | 5925 | 6217 | 6366 | 6430 | 6452 |
| Δz (km) | 0 | −146 | −453 | −1465 | −2730 | −3957 | −4988 | −5755 | |
| 20 | r (km) | 5151 | 5435 | 5717 | 6152 | 6391 | 6495 | 6527 | 6529 |
| Δz (km) | 0 | −218 | −606 | −1744 | −3053 | −4267 | −5251 | −5958 | |
| φ0(°) | 0 | 5 | 10 | 20 | 30 | 40 | 50 | 60 | |
|---|---|---|---|---|---|---|---|---|---|
| Δ(°) | r/Δz | ||||||||
| 0.1 | r (km) | 5850 | 6000 | 6211 | 6373 | 6373 | 6357 | 6354 | 6361 |
| Δz (km) | 0 | −110 | −576 | −2021 | −3395 | −4458 | −5230 | −5767 | |
| 1 | r (km) | 5852 | 6022 | 6227 | 6376 | 6372 | 6357 | 6354 | 6361 |
| Δz (km) | 0 | −137 | −631 | −2088 | −3450 | −4499 | −5258 | −5786 | |
| 2 | r (km) | 5861 | 6048 | 6245 | 6380 | 6373 | 6358 | 6356 | 6363 |
| Δz (km) | 0 | −168 | −693 | −2161 | −3509 | −4543 | −5290 | −5808 | |
| 5 | r (km) | 5916 | 6139 | 6308 | 6399 | 6382 | 6365 | 6362 | 6369 |
| Δz (km) | 0 | −270 | −878 | −2374 | −3684 | −4674 | −5384 | −5872 | |
| 10 | r (km) | 6100 | 6323 | 6433 | 6454 | 6415 | 6391 | 6384 | 6387 |
| Δz (km) | 0 | −464 | −1188 | −2712 | −3960 | −4882 | −5534 | −5976 | |
| 15 | r (km) | 6383 | 6544 | 6584 | 6533 | 6468 | 6432 | 6418 | 6414 |
| Δz (km) | 0 | −678 | −1500 | −3034 | −4222 | −5080 | −5680 | −6078 | |
| 20 | r (km) | 6763 | 6802 | 6761 | 6633 | 6538 | 6486 | 6460 | 6450 |
| Δz (km) | 0 | −910 | −1813 | −3345 | −4473 | −5272 | −5822 | −6179 | |
| UTC | 0–3 | 3–6 | 6–9 | 9–12 | 12–15 | 15–18 | 18–21 | 21–24 |
| ap | 4 | 2 | 2 | 2 | 3 | 3 | 3 | 0 |
| Observatory 1 | Observatory 2 | Observatory 3 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Code | Latitude | Longitude | Code | Latitude | Longitude | Code | Latitude | Longitude | |
| 1 | aaa | 43.25 | 76.92 | nvs | 54.85 | 83.23 | lzh | 36.09 | 103.84 |
| 2 | abk | 68.36 | 18.82 | ups | 59.90 | 17.35 | bel | 51.84 | 20.79 |
| 3 | aia | −65.25 | 295.74 | trw | −43.27 | 294.62 | pst | −51.70 | 302.11 |
| 4 | asc | −7.95 | 345.62 | vss | −22.40 | 316.35 | mbo | 14.39 | 343.04 |
| 5 | asp | −23.76 | 133.88 | kdu | −12.69 | 132.47 | lrm | −22.22 | 114.10 |
| 6 | bdv | 49.08 | 14.02 | fur | 48.17 | 11.28 | mab | 50.30 | 5.68 |
| 7 | bel | 51.84 | 20.79 | abk | 68.36 | 18.82 | nur | 60.51 | 24.66 |
| 8 | bfe | 55.63 | 11.67 | mab | 50.30 | 5.68 | aqu | 42.38 | 13.32 |
| 9 | blc | 64.32 | 263.99 | fcc | 58.76 | 265.91 | pbq | 55.28 | 282.25 |
| 10 | bmt | 40.30 | 116.20 | gzh | 23.97 | 112.45 | kny | 31.42 | 130.88 |
| 11 | bou | 40.14 | 254.77 | dlr | 29.49 | 259.08 | tuc | 32.17 | 249.27 |
| 12 | box | 58.07 | 38.23 | qsb | 33.87 | 35.64 | sod | 67.37 | 26.63 |
| 13 | brw | 71.32 | 203.38 | cmo | 64.87 | 212.14 | shu | 55.35 | 199.54 |
| 14 | cbb | 69.12 | 254.97 | res | 74.69 | 265.11 | fcc | 58.76 | 265.91 |
| 15 | clf | 48.02 | 2.26 | ebr | 40.96 | 0.33 | aqu | 42.38 | 13.32 |
| 16 | cta | −20.09 | 146.26 | cnb | −35.32 | 149.36 | asp | −23.76 | 133.88 |
| 17 | dlr | 29.49 | 259.08 | tuc | 32.17 | 249.27 | fcc | 58.76 | 265.91 |
| 18 | dou | 50.10 | 4.60 | ebr | 40.96 | 0.33 | fur | 48.17 | 11.28 |
| 19 | ebr | 40.96 | 0.33 | spt | 39.55 | −4.35 | dou | 50.10 | 4.60 |
| 20 | esk | 55.31 | 356.79 | dou | 50.10 | 4.60 | ebr | 40.96 | 0.33 |
| 21 | fcc | 58.76 | 265.91 | pbq | 55.28 | 282.25 | frd | 38.21 | 282.63 |
| 22 | frn | 37.09 | 240.28 | tuc | 32.17 | 249.27 | new | 48.27 | 242.88 |
| 23 | fur | 48.17 | 11.28 | wng | 53.73 | 9.05 | bfe | 55.63 | 11.67 |
| 24 | gck | 44.63 | 20.77 | abk | 68.36 | 18.82 | nur | 60.51 | 24.66 |
| 25 | gdh | 69.25 | 306.47 | naq | 61.17 | 314.57 | sjg | 18.11 | 293.85 |
| 26 | gui | 28.32 | 343.56 | mbo | 14.39 | 343.04 | sfs | 36.67 | 354.06 |
| 27 | gzh | 23.97 | 112.45 | lrm | −22.22 | 114.10 | phu | 21.03 | 105.96 |
| 28 | had | 51.00 | 355.52 | ler | 60.14 | 358.82 | ebr | 40.96 | 0.33 |
| 29 | hbk | −25.88 | 27.71 | her | −34.43 | 19.23 | aae | 9.04 | 38.77 |
| 30 | her | −34.43 | 19.23 | tsu | −19.20 | 17.58 | hbk | −25.88 | 27.71 |
| 31 | hrn | 77.00 | 15.55 | ngk | 52.07 | 12.68 | nck | 47.63 | 16.72 |
| 32 | hua | −12.05 | 284.67 | sjg | 18.11 | 293.85 | teo | 19.75 | 260.82 |
| 33 | iqa | 63.75 | 291.48 | thl | 77.47 | 290.77 | gdh | 69.25 | 306.47 |
| 34 | irt | 52.27 | 104.45 | lzh | 36.09 | 103.84 | nvs | 54.85 | 83.23 |
| 35 | kak | 36.23 | 140.19 | mmb | 43.91 | 144.19 | gua | 13.59 | 144.87 |
| 36 | kdu | −12.69 | 132.47 | asp | −23.76 | 133.88 | cta | −20.09 | 146.26 |
| 37 | kny | 31.42 | 130.88 | kdu | −12.69 | 132.47 | kak | 36.23 | 140.19 |
| 38 | kou | 5.21 | 307.27 | sjg | 18.11 | 293.85 | vss | −22.40 | 316.35 |
| 39 | ler | 60.14 | 358.82 | had | 51.00 | 355.52 | clf | 48.02 | 2.26 |
| 40 | lrm | −22.22 | 114.10 | kny | 31.42 | 130.88 | kdu | −12.69 | 132.47 |
| 41 | lvv | 49.90 | 23.75 | abk | 68.36 | 18.82 | nur | 60.51 | 24.66 |
| 42 | lzh | 36.09 | 103.84 | irt | 52.27 | 104.45 | gzh | 23.97 | 112.45 |
| 43 | mab | 50.30 | 5.68 | clf | 48.02 | 2.26 | wng | 53.73 | 9.05 |
| 44 | mbo | 14.39 | 343.04 | asc | −7.95 | 345.62 | kou | 5.21 | 307.27 |
| 45 | mcq | −54.50 | 158.95 | sba | −77.85 | 166.76 | eyr | −43.47 | 172.39 |
| 46 | mmb | 43.91 | 144.19 | kak | 36.23 | 140.19 | kny | 31.42 | 130.88 |
| 47 | naq | 61.17 | 314.57 | stj | 47.59 | 307.32 | gdh | 69.25 | 306.47 |
| 48 | nck | 47.63 | 16.72 | ngk | 52.07 | 12.68 | ups | 59.90 | 17.35 |
| 49 | new | 48.27 | 242.88 | tuc | 32.17 | 249.27 | mea | 54.62 | 246.65 |
| 50 | ngk | 52.07 | 12.68 | aqu | 42.38 | 13.32 | fur | 48.17 | 11.28 |
| 51 | nvs | 54.85 | 83.23 | aaa | 43.25 | 76.92 | irt | 52.27 | 104.45 |
| 52 | paf | −49.35 | 70.26 | maw | −67.60 | 62.88 | czt | −46.43 | 51.86 |
| 53 | pbq | 55.28 | 282.25 | fcc | 58.76 | 265.91 | ott | 45.40 | 284.45 |
| 54 | phu | 21.03 | 105.96 | irt | 52.27 | 104.45 | gzh | 23.97 | 112.45 |
| 55 | ppt | −17.57 | 210.43 | hon | 21.32 | 202.00 | frn | 37.09 | 240.28 |
| 56 | res | 74.69 | 265.11 | cbb | 69.12 | 254.97 | blc | 64.32 | 263.99 |
| 57 | sba | −77.85 | 166.76 | mcq | −54.50 | 158.95 | drv | −66.67 | 140.01 |
| 58 | sfs | 36.67 | 354.06 | val | 51.93 | 349.75 | had | 51.00 | 355.52 |
| 59 | shu | 55.35 | 199.54 | brw | 71.32 | 203.38 | sit | 57.06 | 224.67 |
| 60 | spt | 39.55 | −4.35 | had | 51.00 | 355.52 | clf | 48.02 | 2.26 |
| 61 | stj | 47.59 | 307.32 | kou | 5.21 | 307.27 | sjg | 18.11 | 293.85 |
| 62 | tan | −18.92 | 47.55 | hbk | −25.88 | 27.71 | czt | −46.43 | 51.86 |
| 63 | teo | 19.75 | 260.82 | tuc | 32.17 | 249.27 | bou | 40.14 | 254.77 |
| 64 | thl | 77.47 | 290.77 | iqa | 63.75 | 291.48 | stj | 47.59 | 307.32 |
| 65 | thy | 46.90 | 17.89 | aqu | 42.38 | 13.32 | gck | 44.63 | 20.77 |
| 66 | tuc | 32.17 | 249.27 | mea | 54.62 | 246.65 | bou | 40.14 | 254.77 |
| 67 | ups | 59.90 | 17.35 | bfe | 55.63 | 11.67 | aqu | 42.38 | 13.32 |
| 68 | val | 51.93 | 349.75 | sfs | 36.67 | 354.06 | gui | 28.32 | 343.56 |
| 69 | vic | 48.52 | 236.58 | new | 48.27 | 242.88 | frn | 37.09 | 240.28 |
| 70 | wng | 53.73 | 9.05 | mab | 50.30 | 5.68 | fur | 48.17 | 11.28 |
| Rring | 0.05RE | 0.1RE | 0.15RE | 0.17RE | 0.2RE | 0.22RE | 0.25RE |
| 730 | 727 | 724 | 723 | 723 | 723 | 725 | |
| 650 | 651 | 653 | 654 | 657 | 658 | 662 | |
| Rring | 0.3RE | 0.4RE | 0.5RE | 0.6RE | 0.7RE | 0.8RE | 0.9RE |
| 734 | 789 | 917 | 1154 | 1616 | 2064 | 2295 | |
| 672 | 703 | 764 | 903 | 1602 | 2012 | 912 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vassilyev, I.; Fedulina, I.; Mendakulov, Z.; Zhumabayev, B.; Kozin, I. Determination of the Radius of the Ring Current in the Earth’s Core According to the Data of the INTERMAGNET Network Observatories. Appl. Sci. 2025, 15, 9633. https://doi.org/10.3390/app15179633
Vassilyev I, Fedulina I, Mendakulov Z, Zhumabayev B, Kozin I. Determination of the Radius of the Ring Current in the Earth’s Core According to the Data of the INTERMAGNET Network Observatories. Applied Sciences. 2025; 15(17):9633. https://doi.org/10.3390/app15179633
Chicago/Turabian StyleVassilyev, Ivan, Inna Fedulina, Zhassulan Mendakulov, Beibit Zhumabayev, and Igor Kozin. 2025. "Determination of the Radius of the Ring Current in the Earth’s Core According to the Data of the INTERMAGNET Network Observatories" Applied Sciences 15, no. 17: 9633. https://doi.org/10.3390/app15179633
APA StyleVassilyev, I., Fedulina, I., Mendakulov, Z., Zhumabayev, B., & Kozin, I. (2025). Determination of the Radius of the Ring Current in the Earth’s Core According to the Data of the INTERMAGNET Network Observatories. Applied Sciences, 15(17), 9633. https://doi.org/10.3390/app15179633






