Causal Correction and Compensation Network for Robotics: Applications and Validation in Continuous Control

Abstract

Deep Reinforcement Learning (DRL) has achieved remarkable success in robotic control, autonomous driving, and game-playing agents. However, its decision-making process often remains a black box, lacking both interpretability and verifiability. In robotic control tasks, developers cannot pinpoint decision errors or precisely adjust control strategies based solely on observed robot behaviors. To address this challenge, this work proposes an interpretable DRL framework based on a Causal Correction and Compensation Network (C²-Net), which systematically captures the causal relationships underlying decision-making and enhances policy robustness. C²-Net integrates a Graph Neural Network-based Neural Causal Model (GNN-NCM) to compute causal influence weights for each action. These weights are then dynamically applied to correct and compensate the raw policy outputs, thereby balancing performance optimization and transparency. This work validates the approach on OpenAI Gym’s Hopper, Walker2d, and Humanoid environments, as well as the multi-agent AzureLoong platform built on Isaac Gym. In terms of convergence speed, final return, and policy robustness, experimental results show that C²-Net achieves higher performance over both non-causal baselines and conventional attention-based models. Moreover, it provides rich causal explanations for its decisions. The framework represents a principled shift from correlation to causation and offers a practical solution for the safe and reliable deployment of multi-robot systems.

1. Introduction

DRL has made significant progress in robotic control, autonomous driving, and game-playing agents. However, its decision-making process often functions as a black box, lacking both interpretability and verifiability. In high-risk applications such as multi-robot collaboration, medical assistance, and financial decision-making, the transparency and auditability of decisions are critical [1]. Traditional visualization and local linearization reveal only limited sensitivities to input features. They fail to identify the causal impact of actions on outcomes and do not generalize well across tasks.

In robotic control, understanding the causal relationships among state, action, and reward is vital for both decision explanation and safety. Classical control methods, such as PID (Proportional–Integral–Derivative) control, Model Predictive Control (MPC), and rule-based expert systems, are easy to understand. These methods naturally provide strong interpretability and stability due to their clear mathematical models or rule-based logic [2]. Their convergence and robustness can be rigorously verified using Lyapunov methods or frequency-domain analysis [3]. However, these approaches heavily rely on precise physical dynamics models and expert knowledge. In complex tasks involving high degrees of freedom or multi-robot coordination, the manual design and maintenance of controllers and rule bases become extremely costly, and such methods cannot adaptively learn and improve from operational data.

DRL is a key approach for high-dimensional, continuous control. However, its black-box nature raises concerns about interpretability and safety. For example, recent work on Interpretable Continuous Control Trees (ICCTs) has shown that tree-based models can be easier to simulate, faster to verify [4], and more interpretable than neural networks, while still delivering competitive performance.

Causal inference offers a rigorous mathematical framework for reinforcement learning by treating each agent’s action as an intervention on the environment. Structural Causal Models (SCMs) systematically capture the causal dependencies among state variables, actions, and outcomes, enabling contrastive explanations (“Why action A instead of B?”) and counterfactual reasoning to enhance explanation fidelity and trustworthiness. However, applying causal inference directly to complex multi-agent systems still faces challenges due to limited model expressiveness. Many Explainable Reinforcement Learning approaches borrow saliency or attention techniques from Explainable Artificial Intelligence [5,6]. However, these methods were not designed for sequential decision-making and struggle to account for temporal dependencies in DRL.

In recent years, many scholars have conducted a lot of research on Explainable Reinforcement Learning to improve the interpretability of reinforcement learning. Wang [7] and Yang [8] leveraged causal inference to enhance algorithmic robustness against confounding variables and adversarial interventions. Seitzer et al. [9] improved exploration strategies by detecting the causal effects of actions, while Wang [10] and Ding [11] investigated causal world models. However, these works focus primarily on using causality to boost generalization rather than to generate explanations. True advances in explainability via causal models remain scarce. Madumal et al. [12] introduced the Action Influence Model (AIM), a causal model specifically tailored for reinforcement learning to produce explanations of agent behavior; later work combined AIM with decision trees to improve explanation quality [13]. Yet these methods require limited action spaces, a priori expert-provided causal structures, and only support low-fidelity models unsuitable for policy learning. Volodin et al. [14] proposed an approach to abstract latent variables from high-dimensional observations and learn their sparse causal graph, deepening environmental understanding but without offering detailed insights into agent behaviors. Nevertheless, significant gaps remain in leveraging causal relationships to adjust and optimize DRL and robotic control strategies within interpretable reinforcement learning.

Subsequently, several studies have attempted to explain specific aspects of the decision-making process, such as observations, actions, policies, and rewards. However, these efforts rarely integrate explanations into the environment’s dynamics, which is crucial for understanding the long-term effects of the agent’s actions [15,16]. Traditional DRL methods often struggle to reveal the causal relationships between state variables, action choices, and final rewards in a policy. This makes it difficult for users to infer or predict the system’s behavior in complex or unusual scenarios. The lack of interpretability and safety hinders their deployment on real robots [17].

In the field of robotic control, using Causal Policy Learning (CPL) can enhance the robustness and interpretability [18]. Li et al. [19] used a knowledge graph to deduce relationships in reinforcement learning, and the prior knowledge can reveal which relationships are important. Zhu [20] used causal inference techniques to compute the importance of different samples for offline data, adjusting their influence on the loss function to ensure safety under perturbations. This method can be flexibly integrated with existing model-free DRL algorithms, such as Soft Actor-Critic and Deep Q-Learning. Tang [21] proposed a CD-DRL-MP (Causal Deconfounding Deep Reinforcement Learning for Mobile Robot Motion Planning) method that infers causal relationships via Structural Causal Models (SCMs) and blocks backdoor paths in the model using a representation set, allowing the learning of causal effects between states and actions. Guo et al. [22] used a dual-correction-strategy-based Markov boundary (DCMB) method, based on Bayesian network (BN) datasets, to remove false positives from the features currently selected. This method improved the learning accuracy of the Markov boundary. These studies focus on optimizing sample data via causal inference to improve RL training efficiency. However, agents following a fixed policy still require retraining for alignment.

To avoid retraining and enhance generalization, causal correction is a feasible solution. In complex robotic tasks, action execution is influenced by multiple environmental variables. Diehl and Ramirez-Amaro [23] used Bayesian Neural Networks (BNNs) to infer causal structures, enabling robots to predict and avoid erroneous actions. This strategy builds on their earlier work [24], which improved performance by predicting and avoiding mistakes. However, it did not enhance reward guidance. Causal correction computes the causal influence weight of each action on key states and final rewards and uses this to automatically adjust errors or disturbances in action selection. This allows robots to consistently choose actions that are truly effective for task outcomes, even under perturbations, thereby improving policy convergence speed, performance, and reliability.

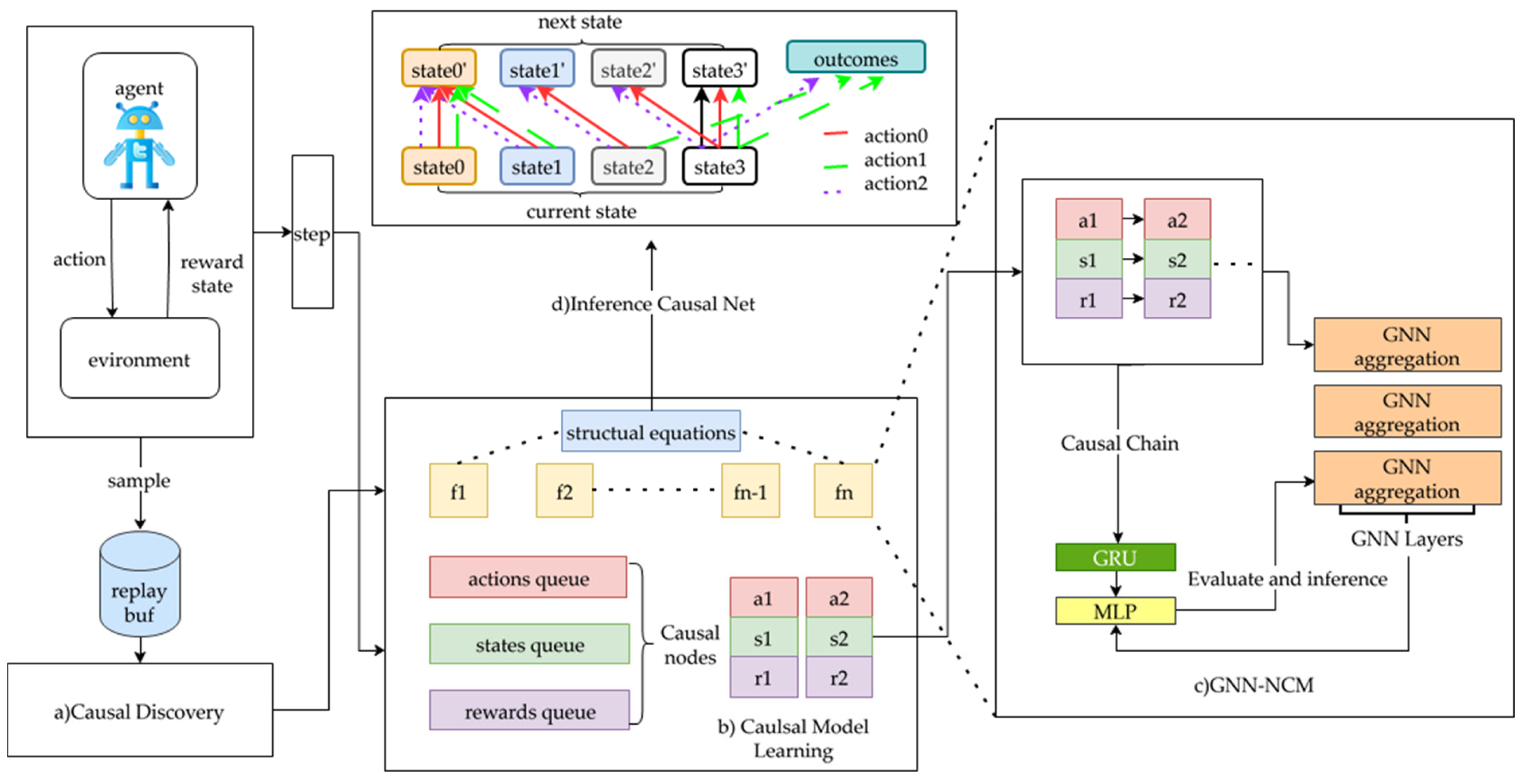
Against this background, an interpretable reinforcement learning framework based on the Causal World Model is introduced, with the following primary contributions:

• Causal World based on GNN-NCM: To capture environment dynamics and action–reward causal relationships in RL, we propose a Causal-World-Model-based RL framework that integrates a novel GNN-NCM architecture. It replaces traditional attention mechanisms with multilayer message passing and neighborhood aggregation. The framework more precisely infers causal influence weights, thereby modeling state transitions and reward generation more effectively.
• C²-Net: We propose the C²-Net correction algorithm, which incorporates causal weights inferred from GNN-NCM into dynamic action adjustment and compensation. By explicitly leveraging action–state–reward causal relationships, C²-Net enhances reward acquisition and improves policy exploration, thereby enhancing both performance and generalization.

2. Materials and Methods

2.1. Structural Causal Model

A Structural Causal Model (SCM) formalizes the causal relationships among variables by combining exogenous variables $V$, endogenous variables $U$, and a set of structural equations $F=\left\{\mathit{f}1,\dots ,\mathit{f}\mathit{q}\right\}$, forming the tuple $\left(\mathit{U},\mathit{V},F\right)$ [25]. Here is the collection of structural equations, each quantitatively describing how each variable is determined by other variables. The SCM can be visualized as a directed acyclic graph. The nodes correspond to the elements, and the edges are determined by the structural equations. Edges in the graph reflect the causal relationships between nodes. For an intervention, the post-intervention distribution can be computed using the SCM’s “prune-and-replace” rule as follows:

$$P\left(V\mid do\left(\mathit{X}={\mathit{x}}^{\mathit{*}}\right)\right)={\prod }_{v_i\in V\backslash X} P\left(v_j\mid \mathit{P}\mathit{A}\left(v_j\right)\right) \mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h} \mathit{P}\mathit{A}\left(v_j\right)$$

(1)

Building upon SCM, the Action Influence Model (AIM) incorporates an action space vector into the structural equations. This explicitly models how each exogenous variable is influenced by an action. Compared to a standard SCM, AIM more directly accounts for the impact of an agent’s or robot’s actions on the entire system, enabling more effective causal action analysis. To quantify the causal effect of a single action on a future state or reward, consider a given state-action pair at time t, and let $Y_t$ denote the next-step variable of interest (either a specific state dimension or the reward). The single-step causal influence of on is defined as follows:

$$\mathrm{I}\mathrm{n}\mathrm{f}\left({\mathit{A}}_{\mathit{t}}\to Y_{t+1}\right)=D\left(\begin{array}{c}P\left(Y_{t+1}\mid {\mathit{S}}_t,do\left({\mathit{A}}_{\mathit{t}}=\mathit{a}\right)\right)\parallel \\ P\left(Y_{t+1}\mid {\mathit{S}}_t,do({\mathit{A}}_{\mathit{t}}=\tilde{\mathit{a}})\right)\end{array}\right)$$

(2)

Finally, by ranking all possible pairs ${\mathit{A}}_{\mathit{t}}\to Y_{t+1}$ according to their influence scores and retaining only those edges whose scores exceed a threshold (usually set to 0.1), one can construct an explanatory causal subgraph.

2.2. Graph Neural Networks

The Graph Neural Networks (GNNs) naturally excel at processing graph-structured data and can model interactions among agents and environmental elements in multi-robot systems. By treating state variables or agents as nodes and interactions or communication links as edges, GNNs use message-passing mechanisms to efficiently aggregate neighborhood information. This provides a structured foundation for causal inference. Combining causal inference with GNNs preserves both interpretability and scalability. This endows DRL with greater robustness and generalization in complex scenarios.

As mentioned above, causal models are mostly presented in the form of graphs. Graph Neural Networks excel at handling relational data, making them well-suited to model interactions in multi-agent and physics-based environments [26,27]. GNNs introduce a powerful “relational inductive bias,” enabling them to process arbitrarily structured graph data. Building on this, researchers have integrated GNNs into multi-agent reinforcement learning frameworks to improve coordination performance and robustness. Jiang et al. [28] proposed Graph Convolutional Reinforcement Learning (GCRL) at ICLR 2020, treating the environment as a dynamic graph and using learnable relation kernels to capture agent interactions. Prior work integrates GNNs into MARL to improve coordination and robustness. These results indicate that GNNs are a versatile foundation for explainable RL.

Benham and Wang [29] adopted a similar mechanism for causal model interpretation, in line with the recent “causal explanation” trend in GNN research. Their method trains a GNN augmented by a small multilayer perceptron (MLP) to assign a causal score to each edge, thereby constructing a neural causal model:

$${\mathit{h}}_u^{\left(k\right)}=UPDATE\left({\mathit{h}}_u^{\left(k-1\right)},AGGREGATE\{{\mathit{h}}_v^{(k-1)}:v\in \mathcal{N}(u\left)\right\}\right)$$

(3)

Here, ${\mathit{h}}_u^{\left(k\right)}$ denotes the hidden representation of node $u$ after the $k$-th iteration, and $\mathcal{N}\left(u\right)$ is the set of neighbors of $u.$ GNNs are well-suited to model data consisting of entities (nodes) and their relations (edges). This structured inductive bias allows interpretability techniques to capture the spatiotemporal dependencies an agent perceives—dependencies that attention-based methods often fail to capture. Consequently, GNNs can provide deeper insights into why an agent behaves as it does.

RL environments evolve through highly correlated transitions. Attention alone may miss the key spatiotemporal structure. Joint spatial–temporal encoding with GNNs better captures critical interactions and supports clearer decision explanations. In this study, since it is necessary to process a large number of causal structures arising from robot–environment interactions, we employ Graph Neural Networks (GNNs) to handle the causal structure processing. By learning and aggregating information from causal structures through GNNs, the inferred causal structures become more precise.

An MLP is used to score the aggregated outputs and update the GNN parameters by minimizing the mean squared error between the long-term causal return predicted by the GNN and the Monte Carlo return:

$${\mathcal{L}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}}={\mathbb{E}}_{t_0}\left[{\left({\widehat{G}}_{t_0}^{\mathrm{c}\mathrm{a}\mathrm{u}\mathrm{s}\mathrm{a}\mathrm{l}}-G_{t_0}\right)}^2\right]$$

(4)

A sparsity regularization term is also applied to the cross-step edge weights $e_{uv}^{\left(L\right)}$, encouraging concise causal chains:

$${\mathcal{L}}_{\mathrm{s}\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{s}\mathrm{e}}=\lambda \sum _{(u\to v)\in E} \left|e_{uv}^{\left(L\right)}\right|$$

(5)

The total loss function is then defined as follows:

$$\mathcal{L}={\mathcal{L}}_{\mathrm{s}\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{s}\mathrm{e}}+{\mathcal{L}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}}$$

(6)

By modeling and explaining the causal dependencies in the state–action–reward process, the inference network ultimately outputs an explanatory causal graph.

2.3. Causal Discovery and Inference

As shown in Figure 1a), experience tuples $(s,s’,a,r)$ are sampled from the replay buffer for causal analysis. We treated state $s$ and action $a$ as input variables: $U=\left\{u_i\right\}=(s,a)=(s_1\dots \dots s_n,a_1\dots \dots a_n)$, and the next-state and outcome r as output variables: $V=\left\{v_j\right\}$ = $(s’,r$) = (${s’}_1{,\dots \dots s’}_n,r_1\dots \dots r_n$). Assuming each input renders the outputs conditionally independent, the system decomposes into independent components. This assumption enables the orientation of each causal edge, which may then be validated through additional constraints, expert priors, or formal causal-inference rules.

For every candidate pair $(u_i\to v_j)$, a test is performed to determine the existence of a causal edge. Prior studies have demonstrated that Conditional Independence Testing (CIT) efficiently uncovers sparse causal structures [10,30]. The CIT computation is given as follows:

$$u_i\in \mathit{P}\mathit{A}\left(v_j\right)⟺\left(u_i\nparallel v_j|u_{-i}\right)$$

(7)

Here, $\mathit{P}\mathit{A}\left(v_j\right)$ denotes the set of parent variables for $v_j$. Conditional Independence Testing (CIT) assesses whether two variables $X$ and $Y$ remain statistically dependent when conditioned on another set of variables $Z$. By iteratively applying CIT to remove non-existent edges, a sparse yet valid causal graph is obtained.

Extending the Causal World Model framework, edge strengths are estimated by learning node embeddings with a Graph Neural Network, yielding a fully differentiable, end-to-end causal evaluation mechanism. Parameterizing these edge weights makes it possible to infer causal influence paths directly from the GNN representations.

After the causal graph has been discovered and back-door adjustments applied (see Figure 1b), a GNN-based inference module is constructed (Figure 1c). At each time step, state and action nodes are projected into a shared embedding space and propagated through the causal graph via message passing. All state and action nodes are linearly projected into a shared hidden space to obtain initial embeddings. The resulting embeddings are scored using an MLP, and the GNN parameters are updated by minimizing the mean-squared error between the GNN’s long-term causal return ${\widehat{G}}_{t_0}^{\mathrm{c}\mathrm{a}\mathrm{u}\mathrm{s}\mathrm{a}\mathrm{l}}$ and the Monte Carlo return $G_{t_0}$.

Treat the entire causal graph as a heterogeneous graph with “state→output” and “action→output” edges and input it to the GNN for aggregation and causal weight computation. By modeling and explaining the causal dependencies in the state–action–reward process, the inference network (Figure 1d) ultimately outputs an explanatory causal graph.

2.4. C²-Net

A direct application of discovered causal structures and causal weights might involve reward shaping or full policy retraining. However, reward shaping can introduce unintended biases into the learning objective and requires extensive manual tuning. In contrast, full policy retraining is computationally expensive and risks undermining established policy behaviors. To address these challenges, a lightweight, modular correction mechanism—the C²-Net—is introduced. C²-Net leverages precomputed causal weights to adjust policy actions dynamically at decision time, enabling precise, real-time intervention without modifying the reward function or retraining the entire policy network.

C²-Net is designed to adjust and refine policy actions through causal inference, thereby enhancing safety and interpretability in reinforcement learning. First, causal weights serve as an intuitive form of explanation: by leveraging the Structural Causal Model and GNN-NCM, C²-Net automatically identifies which state variables and action components exert genuine causal influence on the final return, rather than mere correlations. This precision ensures that corrections target only truly “harmful” or “inefficient” action elements, thereby avoiding indiscriminate intervention across the entire policy.

As shown in Figure 2, C²-Net integrates the Causal World Model with GNNs and consists of two main components:

• Causal Inference with Multilayer GNN-NCM: This component learns the causal relationships among state variables, actions, and rewards by constructing a causal graph where nodes represent states and actions, and edges represent latent causal influences or interactions. Each state–action pair is linearly projected into initial node embeddings in a shared hidden space. Through several layers of message passing and neighborhood aggregation, the GNN-NCM computes causal influence weights, producing a causal weight matrix that quantifies each action’s influence on each reward variable.
• Weight Partitioning, Vectorization, and Activation: The causal weight matrix $W_c$ is partitioned into blocks corresponding to the action dimensions. Each block is reduced to a scalar causal weight $c_j$ via a predefined mapping rule. These weights are then normalized by a temperature-adjusted Softmax function:

  $$w_i={\displaystyle \frac{\mathrm{e}\mathrm{x}\mathrm{p}(c_i/\tau )}{\sum _{j=1}^d \mathrm{e}\mathrm{x}\mathrm{p}(c_j/\tau )}},i=1,\dots ,d.$$

  (8)

In this work, we leverage the causal weights learned by the GNN to perform the fine-grained correction of the original policy’s action outputs, aiming to better optimize the long-term cumulative return. Specifically, at time step t, the original policy outputs an action vector.

$${\mathbf{a}}^{\mathrm{r}\mathrm{a}\mathrm{w}}={\left(a_1^{\mathrm{r}\mathrm{a}\mathrm{w}},\dots ,a_d^{\mathrm{r}\mathrm{a}\mathrm{w}}\right)}^{\mathrm{\top }}$$

(9)

Meanwhile, the causal discovery module computes the causal contribution (or “weight”) of each action dimension to the future reward as follows:

$$\mathbf{c}={\left(c_1,\dots ,c_d\right)}^{⊺}$$

(10)

Higher values of $c_j$ result in larger normalized weights ${ w}_i$. Finally, the raw action ${\mathbf{a}}^{\mathbf{r}\mathbf{a}\mathbf{w}}$ is corrected as follows:

$${\mathbf{a}}^{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}}={\mathbf{a}}^{\mathrm{r}\mathrm{a}\mathrm{w}}\left(1+\alpha \left(\mathbf{w}-{\displaystyle \frac{1}{d}}\mathbf{1}\right)\right)$$

(11)

where $\alpha \in \left[\mathrm{0,1}\right]$ controls the interpolation strength between the unmodified action ($\alpha =0$) and the fully causally corrected action ($\alpha =1$), and 1/d serves as a de-centering baseline to maintain overall amplitude balance.

By combining these two steps, C²-Net can identify and suppress potentially dangerous actions in real time while promoting causally beneficial behaviors, ensuring policy robustness, safety, and interpretability under high-risk and complex conditions.

3. Results

To comprehensively evaluate the performance and interpretability of the proposed C²-Net in reinforcement learning tasks, this chapter first introduces the experimental environments and evaluation metrics, then describes the baseline algorithms and evaluation protocols. 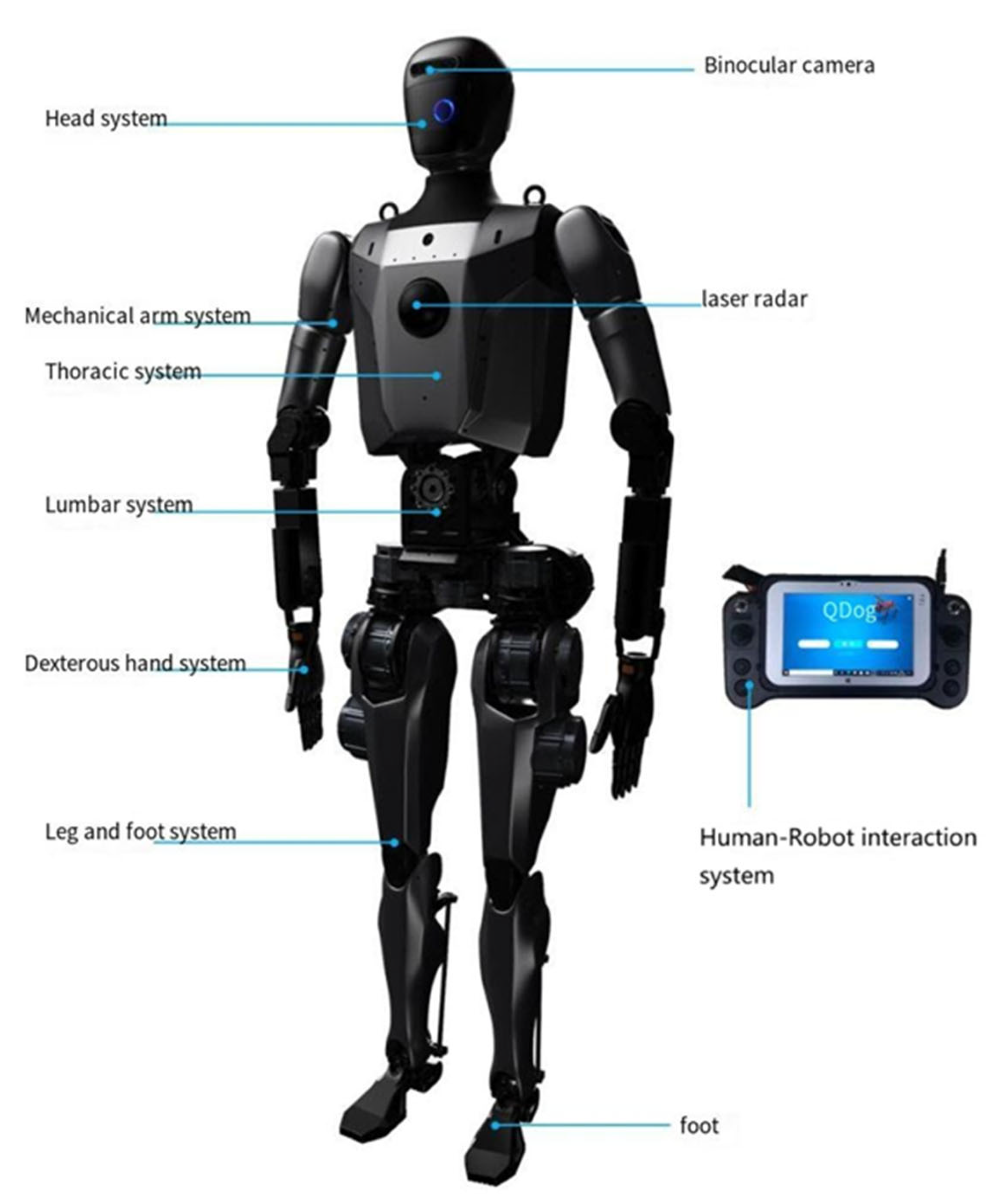The experiments include two main categories: single-agent control tasks on OpenAI Gym’s classic continuous control benchmarks (Hopper, Walker2d, Humanoid)—these environments are all open-sourced, and the definitions and models can be found using the following link: https://gymnasium.farama.org/environments/mujoco/ (accessed on 29 August 2025), used to assess convergence speed and final return. The second main category is multi-agent collaboration tasks on the AzureLoong platform built on NVIDIA Isaac Gym, used to examine coordination capabilities and explainability under complex dynamic interactions. The physical AzureLoong robot is shown in Figure 3. All related documentation and information have been published on the open-source community at https://www.openloong.org.cn/cn/documents (accessed on 29 August 2025). Evaluation metrics cover average return, policy entropy analysis, and explainability measures. To ensure fairness and reproducibility, all algorithms are executed under identical hyperparameter settings and random seeds, and are compared against baselines from various reinforcement learning algorithms.

We train baselines with Stable-Baselines3 as a comparison. Stable-Baselines3 provides standardized, reliable implementations of widely used reinforcement learning algorithms based on OpenAI Baselines (e.g., PPO, DDPG, SAC, TD3, A2C) and ensures reproducibility through unified interfaces and thorough documentation. The algorithms and parameter settings related to Stable-Baselines can be found at https://github.com/DLR-RM/stable-baselines3 (accessed on 29 August 2025). PPO and SAC, two widely used algorithms in reinforcement learning control tasks, are adopted as baselines. After completing the baseline training, causal relationships are inferred using the GNN-NCM Causal World Model, and C²-Net is applied for correction. The performance of the baseline and the corrected model is compared under the same number of simulation steps. Then, we used a t-test to assess the differences between the baseline and our method. By comparing the reward values with established baselines and conducting statistical analysis, the advantages of the proposed algorithm can be intuitively demonstrated.

3.1. LunarLander Environment: Causal World Model Construction

To demonstrate C²-Net’s effectiveness, it is first essential to ensure the accuracy of the causal weights produced by the Causal World Model. Accordingly, an experiment was designed to compare and validate the quality of the causal inference results.

Experience tuples sampled from the replay buffer—20,000$(\mathit{s},\mathit{a},\mathit{r},\mathit{s}\mathrm{’})$ entries—were used to train and construct the Causal World Model via GNN-NCM in the OpenAI Gym LunarLander environment, with a causal weight threshold of 0.1. A Structural Causal Model (SCM) uncovers the causal graph linking states, actions, and rewards while computing corresponding edge weights. Then, train and update the causal weights of all the edges using GNN. In this work, the GNN uses three layers, using ReLU for activation and 128 dimensions in each layer. The MLP score uses ReLU for activation, too, where ${\mathbf{h}}_i {\mathbf{h}}_o$ presents the embedded vector of node I, the output node ${\mathbf{W}}_1{\mathrm{W}}_2$ is the weight of the hidden layer, and ${\mathbf{b}}_1$ and $b_2$ are the biases.

$${\mathbf{z}}_{i\to o}=\mathrm{R}\mathrm{e}\mathrm{L}\mathrm{U}\left({\mathbf{W}}_1\left[{\mathbf{h}}_i;{\mathbf{h}}_o\right]+{\mathbf{b}}_1\right)$$

(12)

$$s_{i\to o}={\mathbf{w}}_2^{\mathrm{\top }}{\mathbf{z}}_{i\to o}+b_2$$

(13)

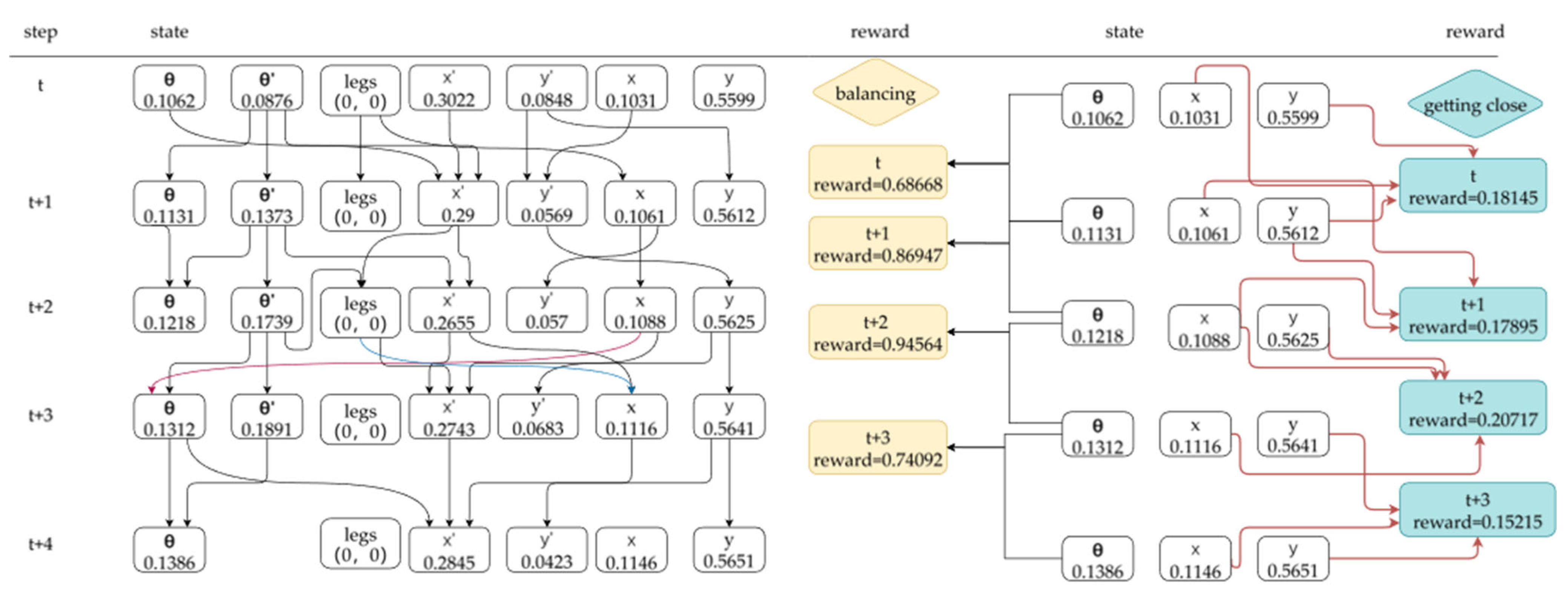
The causal chain graph inferred via GNN-NCM is shown in Figure 4. Taking five-time steps as an example, the state space $x,y,x^{\mathrm{\prime }},y^{\mathrm{\prime }},\theta ,\theta \mathrm{\prime }$, legs represent: (1) Horizontal position, (2) Vertical position, (3) Horizontal velocity, (4) Vertical velocity, (5) Aircraft angle, (6) Angular velocity, and (7) Whether the two legs are in contact with the ground (1 for contact, 0 for suspended). The reward “balancing” shows how well the agent keeps balance, and “getting close” shows how far to reach the destination. The graph illustrates the causal relationships among states, actions, and rewards in the LunarLander environment, that is, “what causes what.”

To assess both the interpretability of the inferred graph and its short-term prediction accuracy, a linear regression baseline was defined: only statistically significant causal edges were retained to form a subgraph, whose parent nodes then predicted the next-step state or reward. Prediction quality was evaluated using the root-mean-square error (RMSE) against ground truth, with comparisons made to two baselines:

Attention-Based Causal World Model [30]: uses an attention mechanism to assign causal weights;

MLP-Scored World Model: Only employs a multilayer perceptron to score all candidate causal edges.

As shown in

Table 1. Comparison of causal prediction accuracy errors.

Rewards	ATTN	MLP	GNN-NCM (Ours)
Getting close	0.168 × 10−1	0.172 × 10−1	0.016 × 10−1
Slowing down	3.356	4.319	2.007
Balancing	1.083 × 10−1	0.197 × 10−1	0.327 × 10−1
Fuel cost	0.213 × 10−1	0.213 × 10−1	0.111 × 10−1

, the GNN-NCM-based Causal World Model achieves lower RMSE and provides higher-quality explanations than both baselines, demonstrating its superiority in causal inference accuracy and interpretability. Based on this inferred causal chain structure, the subsequent experiments in this study apply causal correction to other environments.

3.2. Task: Gym Hopper-v4

In the OpenAI Gym Hopper-v4 environment, the agent and physics simulator are initialized. The observation space comprises a 17-dimensional state vector, and the action space consists of a three-dimensional joint-torque vector. The Causal World Model is defined by the following:

Inputs: the current state $s_t$ and the previous action $a_{t-1}$.

Outputs: the causal components of the next state $s_{t+1}$ and the immediate reward $r_t$ based on the forward distance.

A Structural Causal Model (SCM) is then employed to uncover the direct causal relationships between state variables and actions, and the resulting causal graph is used to train the GNN-NCM. All SCM and GNN-NCM training parameters match those specified in Section 3.1. Subsequently, a baseline policy is trained using Stable-Baselines3 with parameters shown in

Table 2. Hopper-V4 training parameters.

Parameters	Value	Description
Learning_rate	0.0003	-
N_epochs	10	Number of training Epochs per update
n_envs	4	Number of concurrent environments
Batch_size	256	Number of steps per epoch
Total_steps	100,000	Total training time steps

. For each scenario, the causal inference module generates explanations that are then subjected to blind expert evaluation. Running reward curves and final returns are recorded, with their means and standard deviations reported. Two off-the-shelf algorithms from Stable-Baselines3—PPO (Proximal Policy Optimization) and SAC (Soft Actor-Critic)—serve as baselines. Causal analysis reveals that the “forward” component dominates sensitivity (all other components have causal weights ≤ 0.1); therefore, comparative evaluation focuses on this metric. All charts and statistical analyses are produced in GraphPad Prism (version 9.5.1) with a 95% confidence interval.

Figure 5 and Figure 6 show the comparison of rewards between the baseline and after correction using C²-Net, more data are displayed in

Table 3. Data analysis of Hopper-v4 under the SAC algorithm.

	Baseline with SAC	C2-Net
Mean Reward	2.795	3.361
Number of Sampled Steps	300	300
Fall	Yes	No
SEM	0.04503	0.05872
ΔR% (Reward Increase)		20.2%

and

Table 4. Data analysis of Hopper-v4 under the PPO algorithm.

	Baseline with PPO	C2-Net
Mean Reward	2.902	3.328
Number of Sampled Steps	300	300
Fall	Yes	Yes
SEM	0.05637	0.05653
ΔR% (Reward Increase)		14.6%

. The experimental results demonstrate that the C²-Net-corrected policy outperforms common baselines on several key metrics. Compared with the PPO baseline, C²-Net achieves a 14.6% increase in average cumulative return; versus the SAC baseline, the gain is 20.2%.

Within a 300-step window, PPO and SAC baselines occasionally collapse. In contrast, the C²-Net-corrected agent remains upright and continues moving forward, indicating effective prevention of unsafe actions. Despite this, C²-Net’s state-prediction RMSE is slightly higher than the baselines—2% above PPO and 30% above SAC—reflecting the added variability from the causal reasoning process. Nonetheless, the overall improvements in performance and safety clearly validate the effectiveness and practical value of causal correction.

We conduct independent t-tests with our algorithm against the baseline data to obtain statistical results. At a 95% confidence level, the p-values for both algorithms were < 0.0001, indicating a significant difference between the C²-Net–based correction and the baseline. The differences between means of SAC and PPO algorithm, compared with the baseline, were 0.5663 ± 0.07400 and 0.4264 ± 0.07983, with corresponding Cohen’s d values of −0.6245 and 0.4368, respectively, indicating that the C²-Net correction has a medium-to-large effect.

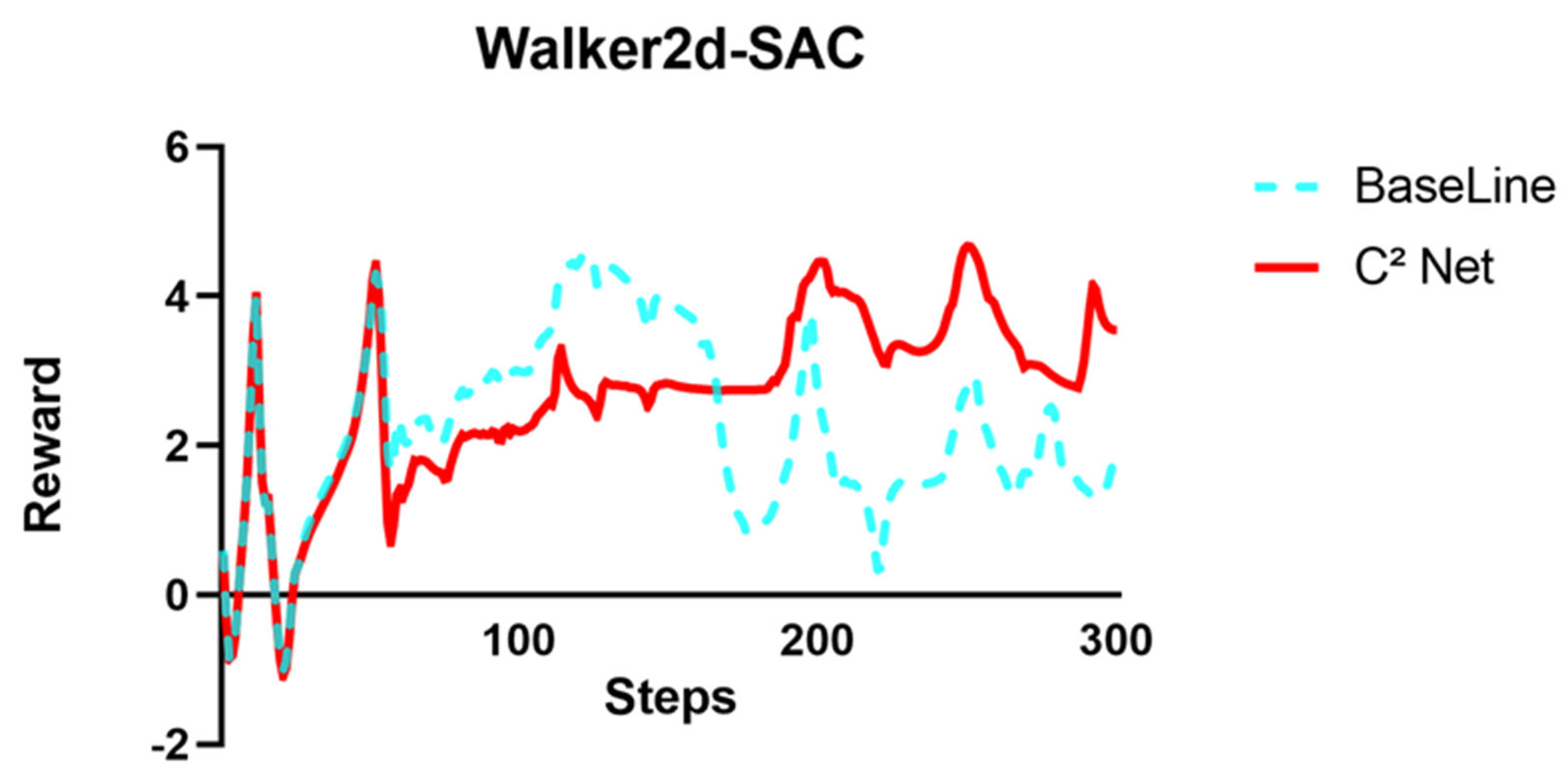
3.3. Task: Gym Walker2d-v4

In the OpenAI Gym Walker2d-v4 environment, both the agent and the physics simulator are initialized. The observation space comprises a 17-dimensional state vector—including torso position, joint angles, and velocities—while the action space is a six-dimensional vector of joint torques. To construct the Causal World Model, the inputs and outputs are defined by the following:

Inputs: the current state $s_t$ and the previous action $a_{t-1}$.

Outputs: the causal components of the next state $s_{t+1}$ and the immediate reward $r_t$ based on the forward distance.

A Structural Causal Model (SCM) is then employed to uncover the direct causal relationships between state variables and actions, and the resulting causal graph is used to train the GNN-based Neural Causal Model (GNN-NCM). All SCM and GNN-NCM training parameters match those specified in Section 3.1. Subsequently, a baseline policy is trained using Stable-Baselines3 with the parameters shown in

Table 5. Training parameters of Walker2d-V4.

Parameters	Value	Description
Learning_rate	0.0003	-
N_epochs	10	Number of training Epochs per update
n_envs	8	Number of concurrent environments
Batch_size	256	Number of steps per epoch
Total_steps	100,000	Total training time steps

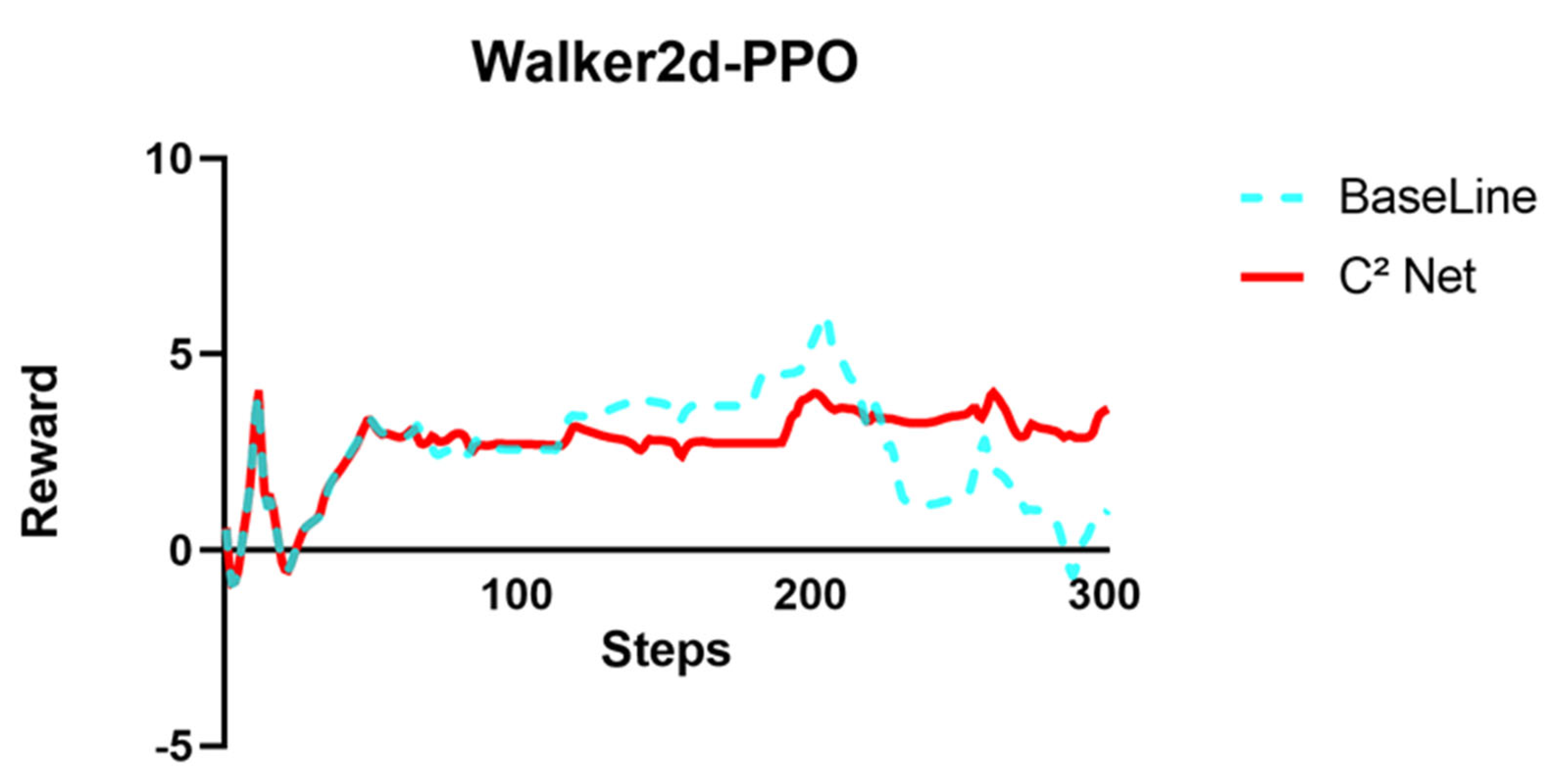
. Figure 7 and Figure 8 show the comparison of rewards between the baseline and after correction by C²-Net, more data are displayed in

Table 6. Data analysis of Walker2d-v4 under the PPO algorithm.

	Baseline with PPO	C2-Net
Mean Reward	2.035	2.950
Number of Sampled Steps	300	300
Fall	Yes	Yes
SEM	0.07198	0.06262
ΔR% (Reward Increase)		44.9%

and

Table 7. Data analysis of Walker2d-v4 under the SAC algorithm.

	Baseline with SAC	C2-Net
Mean Reward	2.253	2.671
Number of Sampled Steps	300	300
Fall	Yes	No
SEM	0.04506	0.04537
ΔR% (Reward Increase)		18.5%

Interesting observations emerge during the under-converged phase of the Walker2d task. The unmodified policy routinely collapsed within approximately 300 samples due to executing unsafe actions. After applying C²-Net correction, the agent’s trajectories avoid these dangerous motions, maintain upright locomotion, and achieve higher immediate rewards. Quantitatively, the corrected policy’s reward increased by 18% compared to the baseline. This result validates both the accuracy of the causal model in inferring action–state dependencies and the effectiveness of the causally weighted compensation strategy in ensuring action safety and improving overall performance.

Statistically, we conduct independent t-tests with our algorithm against the baseline data to obtain statistical results. At a 95% confidence level, the p-values for both algorithms were <0.0001, indicating a significant difference between the C²-Net–based correction and the baseline. The differences between means of SAC and PPO algorithms, compared with the baseline, were 0.4186 ± 0.09550 and 0.9144 ± 0.09541, with corresponding Cohen’s d values of 0.6068 and 0.3585, respectively, indicating that the C²-Net correction has a medium-to-large effect.

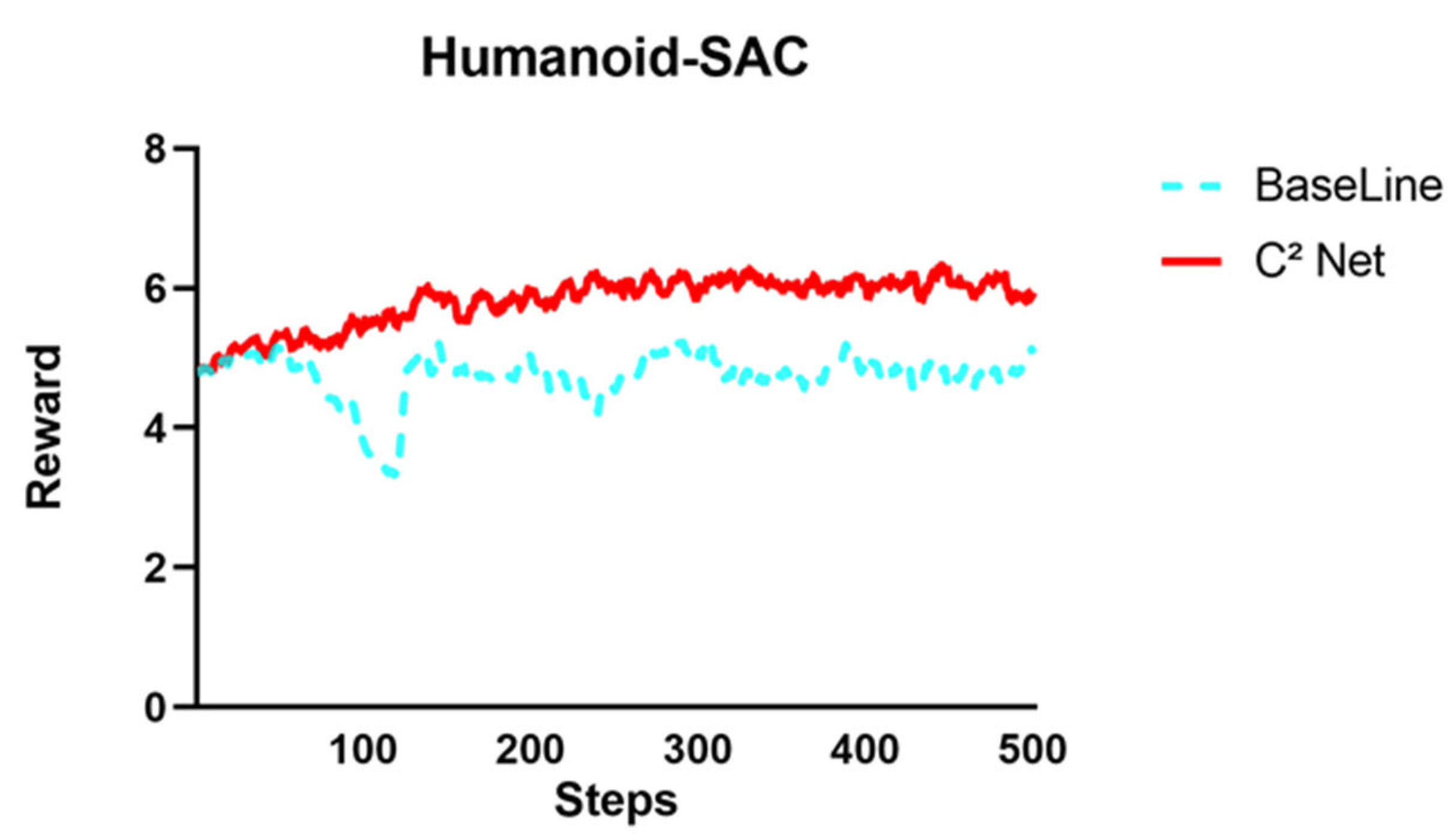
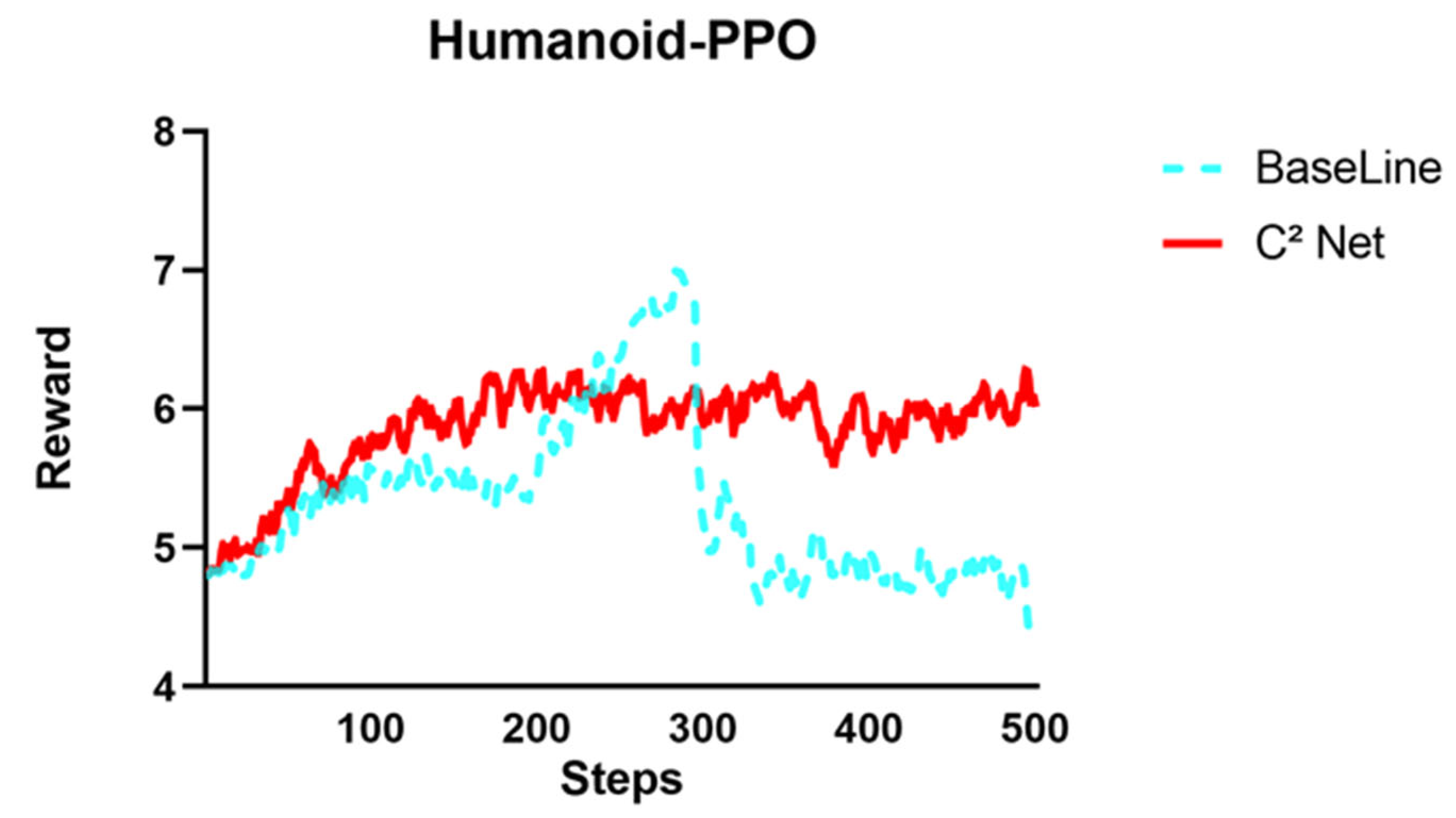
3.4. Task: Gym Humanoid-v4

In the OpenAI Gym Humanoid-v4 environment, C²-Net’s capabilities are assessed on a high-dimensional, high-degree-of-freedom control task. The observation space consists of a 376-dimensional vector—encompassing joint positions, velocities, angles, and related physical quantities—while the action space comprises a 17-dimensional joint-torque vector. The Causal World Model is constructed exactly as described in Section 3.1, using identical SCM and GNN-NCM training parameters. The environment is initialized through Gym, and the baseline policy is trained with Stable-Baselines3 using the following parameters in

Table 8. Training parameters of Humanoid-V4.

Parameters	Value	Description
Learning_rate	0.0003	-
N_epochs	10	Number of training Epochs per update
n_envs	8	Number of concurrent environments
Batch_size	256	Number of steps per epoch
Total_steps	100,000	Total training time steps

.

Following environment initialization, a baseline policy is trained via Stable-Baselines3 with the hyperparameter settings shown in Table 8. Figure 9 and Figure 10 show the comparison of rewards between the baseline and after correction using C²-Net; more data are displayed in

Table 9. Data analysis of Humanoid-v4 under the SAC algorithm.

	Baseline with SAC	C2-Net
Mean Reward	4.747	5.809
Number of Sampled Steps	500	500
Fall	No	No
SEM	0.01559	0.01606
ΔR% (Reward Increase)		22.3%

and

Table 10. Data analysis of Humanoid-v4 under the PPO algorithm.

	Baseline with PPO	C2-Net
Mean Reward	5.332	5.861
Number of Sampled Steps	500	500
Fall	Yes	No
SEM	0.02702	0.01484
ΔR% (Reward Increase)		9.92%

.

The results in the Humanoid-v4 environment demonstrate the effectiveness of C²-Net. Introducing C²-Net increased the average return by 9.92%. Moreover, over 500 sampling steps, the C²-Net-corrected agent never fell, confirming that the causal corrections effectively suppress dangerous actions. The variance of the corrected policy’s returns decreased by approximately 54% in the policy trained by PPO, indicating that C²-Net not only enhances performance but also significantly improves the stability and reliability of the control strategy. Furthermore, these outcomes show that C²-Net adapts well to high-dimensional continuous control scenarios—such as Humanoid with 376-dimensional observations and 17-dimensional actions—suggesting potential for scalability and generalization.

We conduct independent t-tests with our algorithm against the baseline data to obtain statistical results. At a 95% confidence level, the p-values for both algorithms were <0.0001, indicating a significant difference between the C²-Net–based correction and the baseline. The differences between means of SAC and PPO algorithms, compared with the baseline, were 1.062 ± 0.02238 and 0.5286 ± 0.03083, with corresponding Cohen’s d values of 3.0040 and 1.0857, respectively, indicating that the C²-Net correction has a large effect.

3.5. AzureLoong Simulation Environment

To further validate C²-Net’s generality and effectiveness in complex agent scenarios, conducted a comparative experiment on the AzureLoong multi-robot collaboration environment built on NVIDIA Isaac Gym. The AzureLoong platform simulates the Chinese open-source “Qinglong” humanoid robot, which features a human-like skeletal structure with up to 43 active degrees of freedom, enabling bipedal walking, balance control, and fine manipulation. The robot stands approximately 185 cm tall, weighs around 80 kg, and delivers peak joint torques of up to 400 N·m, giving it high agility and rapid obstacle-avoidance capabilities. Developed by the Humanoid Robot Innovation Center in Shanghai, the Qinglong design—including both hardware and software parameters—has been open-sourced to the OpenLoong community. Figure 11 shows Qinglong performing robot DRL on real objects.

In simulation, AzureLoong leverages the NVIDIA Isaac Gym/Isaac Sim platform to achieve large-scale parallel physics simulation and training. By utilizing Isaac Lab’s highly efficient GPU-accelerated physics engine, the environment supports hundreds to thousands of parallel instances, delivering high throughput without sacrificing simulation fidelity. This platform allows us to model multi-robot collaboration tasks—such as object transport, dynamic obstacle avoidance, and formation keeping—and to focus the analysis on two characteristic behaviors of the Qinglong robot: “in-place stepping” and “forward locomotion”.

First, train the multi-agent system with the PPO algorithm to achieve the baseline strategy. The training code can be obtained from the OpenLoong documentation at https://github.com/loongOpen/Openloong-gymloong (accessed on 29 August 2025). The parameters are shown in

Table 11. Training parameters of AzureLoong.

Parameters	Value	Description
Learning_rate	0.0001	-
n_epochs	5	Number of training Epochs per update
n_envs	4096	Number of concurrent environments
num_steps_per_env	24	Number of steps per epoch in each environment (batch_size=num_envs×nsteps)
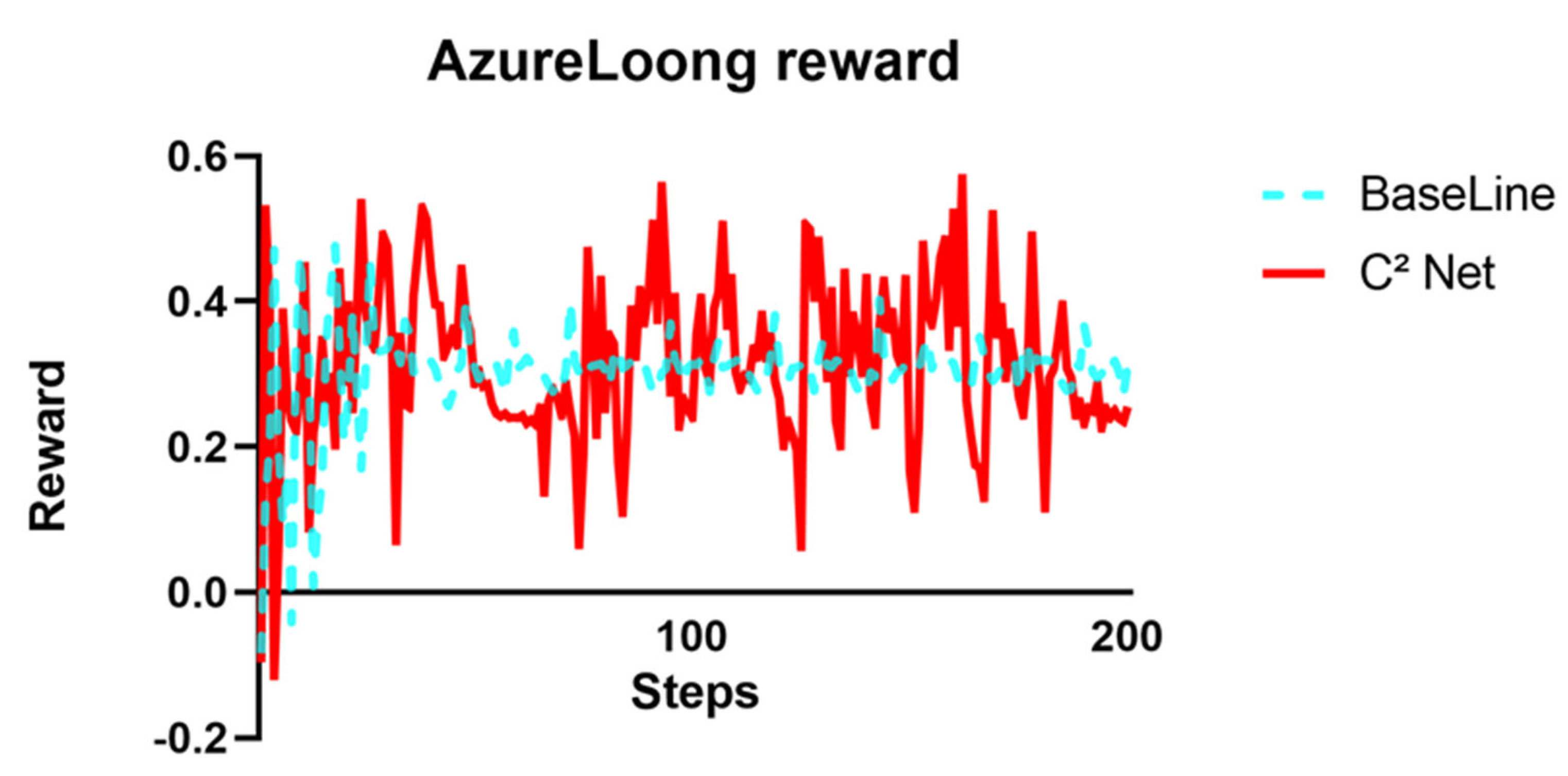
Total_iterations	10,000	Total training iterations

. In the AzureLoong environment—where the state space spans 173 dimensions and the reward derives from multiple state variables—causal analysis and correction were focused on two key metrics: body energy consumption and forward distance. With 20,000 training samples available, additional data were collected for both environment states and agent actions to construct the Causal World Model and train C²-Net. The comparison data and rewards are displayed in

Table 12. Comparison in AzureLoong before and after correction.

	Baseline with PPO	C2-Net
Mean Reward	0.3034	0.3143
Number of Sampled Steps	200	200
Fall	No	No
SEM	0.004507	0.007859
ΔR% (Reward Increase)		3.6%

and Figure 12; the rewards are given by the original AzureLoong environment.

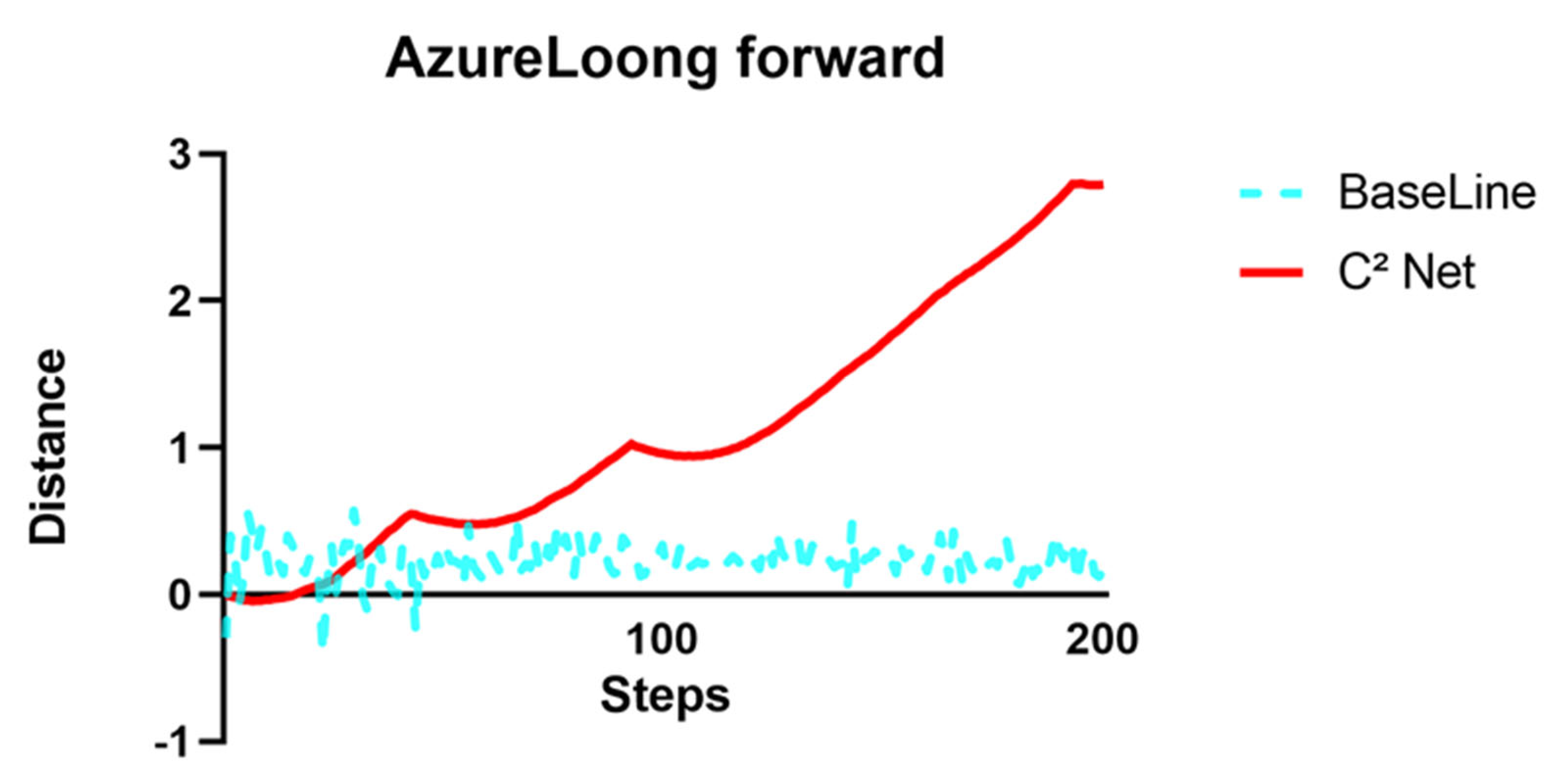
Time-series plots of energy consumption and forward distance reveal that causal correction increased average reward by 3.6% compared to the unmodified PPO policy, albeit with a notable rise in reward variance—a reflection of the high-dimensional complexity that amplifies fluctuations in state estimation and causal inference. An examination of forward-distance curves and rendered trajectories shows that the baseline policy remains in “in-place stepping” to maintain balance, whereas the C²-Net-corrected policy, guided by the causal weight on forward distance, achieves continuous forward locomotion. These findings confirm that the causal inference and correction mechanism can substantially improve behavior even under sparse training conditions.

We conduct independent t-tests with our algorithm against the baseline data to obtain statistical results. At a 95% confidence level, the p-value was < 0.0001, indicating a significant difference between the C²-Net–based correction and the baseline. The differences between means, compared with the baseline, were 0.01093 ± 0.009059, with corresponding Cohen’s d values of 0.1210, respectively, suggesting that the C²-Net correction exhibits a small to medium effect.

Figure 13 shows the displacement generated by the robot performing ‘forward locomotion’ in the environment. It is observed that the uncorrected AzureLoong robot, after an initial external perturbation, could use balance control to right itself and maintain a relatively stable reward; however, its behavior remained largely “in-place stepping,” and yielded almost zero forward progress. After applying C²-Net correction, the model dynamically identified and amplified that action components positively correlated with forward distance, actively driving the robot to move ahead.

Figure 14 and Figure 15 show the key video frames before and after applying C²-Net correction in the simulation. The corrected robot exhibited a more fluid gait and clear forward propulsion; the reward curve reveals higher instantaneous peaks, indicating a more aggressive achievement of task goals. Although the corrected policy’s reward fluctuations increased slightly, the results show that under the learned causal model, C²-Net can guide the robot to increase a given reward, such as “forward” in the test environment to improve strategy exploration.

4. Discussion

Figure 16 summarizes the results across all environments. Here, reward_raw denotes the mean return before correction, and reward_crr represents the mean return after applying C²-Net. Overall, C²-Net consistently improves the agent’s average return across all tasks. For example, in the Hopper environment with SAC and PPO algorithms, the mean return increased by 14.6% and 20.2%, with a value of Cohen’s d indicating a medium-to-large effect. Similar trends are observed in Walker2d (SAC: 18.5% and PPO: 44.9%), Humanoid (SAC: +22.3%; PPO: +9.92%), and AzureLoong (+3.6%). These effect sizes range from small to large according to Cohen’s convention, underscoring the contribution of causal correction across diverse benchmarks.

However, the T-shaped error bars indicate that the standard deviation also increased in certain scenarios. For instance, in the Hopper-SAC task, the variance rose from 0.04503 to 0.05872, and in the AzureLoong environment, it increased from 0.004507 to 0.007859. This suggests that although causal correction improves the mean performance, it also introduces greater policy variability. Such an increase in variance is expected, as C²-Net explicitly models the causal dependencies among states, actions, and rewards, providing a principled basis for the agent’s action selection. By guiding the correction process using reward information, the agent can explore multiple near-optimal behaviors under uncertainty or perturbations, thereby enhancing system robustness and adaptability. At the same time, this increased variance highlights the inherent trade-off between exploratory behavior and policy stability.

Conventional reinforcement learning methods, such as PPO and SAC, primarily regulate policy variance through reward shaping or entropy regularization. In contrast, C²-Net provides an alternative and potentially more principled approach by explicitly modeling causal dependencies among states, actions, and rewards. While this causal-driven exploration helps to interpret both the improvement in average performance and the observed variance, it also highlights a potential trade-off between adaptability and stability. Specifically, greater variance may yield diverse behavioral trajectories beneficial for long-term exploration, yet it can also increase the difficulty of convergence and control in safety-critical environments.

5. Conclusions

This paper presents an interpretable reinforcement learning framework based on the Causal Correction and Compensation Network (C²-Net) to address the ‘black box’ nature of deep RL models. The framework systematically integrates causal inference with GNNs to enhance both interpretability and policy robustness. A Structural Causal Model is employed to uncover intrinsic causal relationships among states, actions, and rewards, resulting in a Causal World Model that provides a solid theoretical foundation for subsequent inference. Building on this model, a GNN-NCM replaces traditional attention mechanisms. Through multilayer message passing, the causal influence weights of actions on key variables are computed. These weights drive the C²-Net module, which dynamically corrects and compensates the original policy’s actions, preserving performance while making the decision-making process fully interpretable.

The framework’s effectiveness and generality are validated through extensive experiments across various tasks. In single-agent continuous control benchmarks (Hopper, Walker2d, Humanoid) on OpenAI Gym, after applying C²-Net correction, the average returns improved compared with the standard PPO and SAC baselines. In the Humanoid and Walker2d tasks, the correction further prevented falling, thereby enhancing the stability of the robot’s policy. These results demonstrate the framework’s potential in complex continuous control. On the AzureLoong multi-agent platform built on Isaac Gym, C²-Net markedly reduces “in-place stepping” behavior, increases team average return by approximately 3.6%, and drives the robot forward under the guidance of the corrective policy to obtain rewards. Causal correction of high-dimensional metrics such as body energy consumption and forward distance further demonstrates adaptability to complex systems. Although state-prediction RMSE is slightly increased by the causal compensation mechanism, a reduction in return variance underscores the practical benefits of causal inference in improving performance, safety, and stability.

Future work may integrate self-supervised causal feature learning and optimize the GNN architecture to further improve inference accuracy and computational efficiency. At the same time, the framework can be extended to real-world domains—such as autonomous driving and smart grids—to explore cross-domain transfer and generalization capabilities. Interactive visualization interfaces for human–machine collaborative debugging would allow practitioners to fine-tune policies in real time using causal explanations. This approach can advance the adoption of explainable RL in both industrial and research settings. This work offers new conceptual and practical pathways for the safe and reliable deployment of high-risk continuous control and multi-agent systems, and provides potential ideas for future application exploration in real robots and industrial scenarios.