Multimodal Emotion Recognition Based on Graph Neural Networks

Abstract

Emotion recognition remains a challenging task in human–computer interaction. With advancements in multimodal computing, multimodal emotion recognition has become increasingly important and significant. To address the existing limitations in multimodal fusion efficiency, emotional–semantic association mining, and long-range context modeling, we propose an innovative graph neural network (GNN)-based framework. Our methodology integrates three key components: (1) a hierarchical sequential fusion (HSF) multimodal integration approach, (2) a sentiment–emotion enhanced joint learning framework, and (3) a context-similarity dual-layer graph architecture (CS-BiGraph). The experimental results demonstrate that our method achieves 69.1% accuracy on the IEMOCAP dataset, establishing a new state-of-the-art performance. For future work, we will explore robust extensions of our framework under real-world scenarios with higher noise levels and investigate the integration of emerging modalities for broader applicability.

1. Introduction

Multimodal dialogue emotion recognition, which integrates textual, acoustic, and visual cues, is a pivotal research area with significant applications in human–computer interaction, clinical diagnosis, and cognitive science [1]. By leveraging multiple modalities, machines can achieve a more comprehensive and accurate understanding of human emotional states. However, effectively modeling the complex interplay between modalities, speakers, and contextual dependencies within a conversation remains a formidable challenge.

The existing methods face three primary limitations. Firstly, many approaches struggle to capture the rich dynamic interactions between modalities, often resorting to simple fusion techniques that neglect semantic alignment and complementary information [2,3]. Secondly, while sentiment analysis is closely related to emotion recognition, most models fail to effectively leverage fine-grained sentiment features to enhance emotion classification, or lack mechanisms for dynamic emotional weight optimization [4]. Lastly, capturing long-range contextual dependencies is crucial, yet traditional RNN-based models suffer from vanishing gradient issues [5,6], while recent GNN-based approaches are often constrained by fixed dialogue order and predefined graph structures [7,8]. These challenges collectively hinder the performance and robustness of current emotion recognition systems.

To overcome these limitations, we propose a novel integrated framework centered around the context-similarity bilevel graph (CS-BiGraph) model. Our framework introduces a sophisticated multimodal fusion method (HSF) and a sentiment-enhanced learning framework (SE) to provide high-quality sentiment-aware features. The core of our work, the CS-BiGraph model, innovatively constructs a bilevel graph to capture both global context similarity and local conversational relationships, leveraging a graph autoencoder for adaptive structure learning. This allows our model to overcome the constraints of fixed graph structures and effectively model long-range dependencies.

The main contributions of this paper are summarized as follows:

• We propose a novel sentiment-enhanced learning framework (SE) that integrates a RoBERTa-based fine-grained feature extractor with a dynamic emotional weight optimization module, effectively sharpening emotion classification boundaries.
• We introduce the context-similarity bilevel graph (CS-BiGraph) model, which decouples global and local contextual modeling. Its structure self-learning mechanism, driven by a graph autoencoder, adaptively captures long-range dependencies, overcoming the limitations of conventional GNNs.
• We conduct extensive experiments on the IEMOCAP and MOSEI datasets. Our integrated framework achieves state-of-the-art performance, demonstrating the effectiveness of our proposed methods, particularly in recognizing neutral and happy emotions.

2. Related Work

2.1. Multimodal Fusion Strategies

Effective fusion of information from different modalities is a cornerstone of multimodal emotion recognition. Early works often employed feature-level or decision-level fusion. For instance, Poria et al. [3] developed dedicated models for each modality before fusing their outputs. Zhou et al. [2] proposed a semi-supervised multipath generative network for fusion. A significant breakthrough came with attention-based mechanisms and transformers, which allow for more dynamic inter-modal interactions. Tsai et al. [9] introduced the cross-modal transformer, which effectively aligns features across modalities. Shou et al. [10] proposed a Low-Rank Matching Attention Method (LMAM), which utilizes low-rank decomposition to significantly reduce the number of parameters in the cross-modal attention mechanism. However, many of these methods still process modalities in a parallel fashion, which may not fully capture the temporal and hierarchical dependencies inherent in human communication. Our HSF fusion method builds upon this by introducing a sequential weighting mechanism to achieve progressive temporally synchronized fusion.

2.2. Sentiment-Enhanced Emotion Recognition

The intrinsic link between sentiment (positive, negative, and neutral) and discrete emotions (happy, sad, and angry) has inspired research into joint learning frameworks. Wu et al. [11] treated emotion classification as the primary task and sentiment classification as an auxiliary task, using shared information to boost performance. More recently, UniMSE [4] proposed a comprehensive knowledge sharing framework across features, labels, and models. While these methods validate the benefit of leveraging sentiment information, they often lack the capacity for fine-grained sentiment analysis or mechanisms to dynamically optimize how much sentiment information should influence the final emotion prediction. Our SE framework addresses this gap by combining a powerful pre-trained language model (RoBERTa) for fine-grained feature extraction with a dynamic weight optimization module.

2.3. Contextual Modeling in Dialogues

Modeling the conversational context is critical for understanding emotional dynamics. Early approaches relied on Recurrent Neural Networks (RNNs) and their variants. ICON [5] and CMN [12] used RNNs to capture inter-utterance temporal relationships. Subsequent models like DialogueRNN [6], SGED [13], and RTER [14] introduced more complex architectures to handle speaker-specific information and long-range dependencies, but the inherent limitations of sequential modeling remained.

To better capture non-sequential relationships, graph neural networks (GNNs) have become a popular choice. Models like DialogueGCN [7], RGAT [15], and ConGCN [8] structure dialogues as graphs, with utterances as nodes and relationships as edges. This allows for more flexible modeling of contextual influences. Nevertheless, these GNN-based methods are typically constrained by fixed graph construction rules (e.g., relying only on speaker order) and limited receptive fields (e.g., fixed window sizes), which hinders their ability to capture complex long-range dependencies adaptively. Our CS-BiGraph model is specifically designed to overcome these constraints by learning the graph structure itself.

2.4. LLM-Based and Prompt-Driven Methods

Another promising direction is the application of prompt learning to emotion recognition. For instance, Wu et al. [16] proposed the MERC-PLTAF framework, which ingeniously constructs both textual and ‘acoustic prompts’ to guide a pre-trained language model. Their work demonstrates the power of leveraging the structured knowledge within LLMs through explicit prompting.

3. Method

The focus of this study is to perform emotion recognition by integrating multimodal data. First, the hierarchical sequential fusion (HSF) method is employed to fuse different modalities. Simultaneously, textual information is input into the sentiment-enhancement (SE) framework to predict sentiment labels for utterances, which assists emotion recognition. The emotion labels and fused multimodal data are then processed through a contextual extractor and input into the context-similarity bilevel graph (CS-BiGraph) model to generate graph structures. Subsequently, the outputs from CS-BiGraph are processed via relational graph convolutional network (RGCN) and graph transformer, with the final emotion recognition results obtained through a classifier. The overall process is shown in Figure 1.

3.1. Feature Extraction

(1) Textual Modality Features: The sBert (sentence-BERT) [17] model is employed to extract key textual features. After processing through sBert, each sentence yields a 768-dimensional feature vector $u^t$, which we denote as $u^t\in {\mathbb{R}}^{L_t\times d_t}$, where $L_t$ is the sequence length and $d_t$ = 768.

(2) Audio Modality Features: The open-source toolkit OpenSmile [18] is utilized to extract acoustic features. Acoustic descriptors such as Mel-Frequency Cepstral Coefficients (MFCCs), Fundamental Frequency Contour (F0), and over 64 other acoustic features are extracted to establish mappings between speech signals and emotional states. A total of 6373 acoustic descriptors are used to construct speech emotion features. The feature matrix undergoes standardization preprocessing and is subsequently processed through a fully connected neural network layer for dimensionality reduction, resulting in a 100-dimensional audio feature vector denoted as $u^a\in {\mathbb{R}}^{L_a\times d_a}$, where $d_a$ = 100.

(3) Video Modality Features: The OpenFace [19] toolkit is used to extract facial keypoints and derive rich feature representations. After processing with OpenFace, a 512-dimensional sequential feature vector $u^v$ is obtained as the final video modality representation, denoted as $u^v\in {\mathbb{R}}^{L_v\times d_v}$, where $d_v$ = 512.

3.2. Hierarchical Sequential Fusion

HSF is the multimodal fusion module designed in this study. As illustrated in Figure 2, its architecture comprises three parallel cross-fusion blocks designed to enrich each modality’s features by incorporating information from the others.

3.2.1. Cross-Attention Mechanism

At the core of our fusion block is the cross-attention mechanism, which enables a target modality to selectively integrate information from a source modality. To facilitate this, the input feature sequences are linearly projected into three distinct representations: the query ($\mathbf{Q}$), the key ($\mathbf{K}$), and the value ($\mathbf{V}$). The $\mathbf{Q}$ representation is derived from the target modality’s features, while the $\mathbf{K}$ and $\mathbf{V}$ representations are derived from the source modality’s features. This projection is governed by three learnable weight matrices: ${\mathbf{W}}_Q$, ${\mathbf{W}}_K$, and ${\mathbf{W}}_V$. The attention scores are then computed based on the similarity between queries and keys, which in turn weight the values to produce the final fused output.

3.2.2. Fusion Process

The fusion process within HSF unfolds in two stages.

First, the audio and video modalities are enhanced in parallel. The audio feature sequence ${\mathbf{u}}^a$ is enriched by attending to both the text features ${\mathbf{u}}^t$ and the video features ${\mathbf{u}}^v$. This results in two intermediate representations, ${\mathbf{A}}_{a\leftarrow t}$ and ${\mathbf{A}}_{a\leftarrow v}$, computed as shown in Equation (1) and Equation (2), respectively.

$${\mathbf{A}}_{a-t}=\mathrm{softmax}\left({\displaystyle \frac{\left({\mathbf{u}}^a{\mathbf{W}}_Q\right){\left({\mathbf{u}}^t{\mathbf{W}}_K\right)}^T}{\sqrt{d_k}}}\right)\left({\mathbf{u}}^t{\mathbf{W}}_V\right)$$

(1)

$${\mathbf{A}}_{a-v}=\mathrm{softmax}\left({\displaystyle \frac{\left({\mathbf{u}}^a{\mathbf{W}}_Q\right){\left({\mathbf{u}}^v{\mathbf{W}}_K\right)}^T}{\sqrt{d_k}}}\right)\left({\mathbf{W}}_V{\mathbf{u}}^v\right)$$

(2)

where $d_k$ is the dimension of the key vectors for normalization. These two enhanced representations are then fused using the Hadamard product (⊙), which performs element-wise multiplication. We chose this operation because it acts as a non-linear feature-gating mechanism, amplifying features that receive strong signals from both the text and video sources while suppressing those supported by only one. The result is then passed through a normalization layer to produce the final enhanced audio features, ${\mathbf{u}}^{\prime a}$. The video features are similarly enhanced in parallel to produce ${\mathbf{u}}^{\prime v}$.

Second, in our sequential strategy, the text modality serves as the final integration point. It attends to the already enhanced audio (${\mathbf{u}}^{\prime a}$) and video (${\mathbf{u}}^{\prime v}$) features to produce its final representation, ${\mathbf{u}}^{\prime t}$. For instance, text attending to the enhanced audio features is formulated as

$${\mathbf{A}}_{t\leftarrow a^{\prime }}=\mathrm{softmax}\left({\displaystyle \frac{\left({\mathbf{u}}^t{\mathbf{W}}_Q\right){\left({\mathbf{u}}^{\prime a}{\mathbf{W}}_K\right)}^T}{\sqrt{d_k}}}\right)\left({\mathbf{u}}^{\prime a}{\mathbf{W}}_V\right)$$

(3)

All normalization steps employ a residual connection with a learnable coefficient $\alpha$, as shown in Equation (4). Finally, the three fully enhanced feature sequences are concatenated to form the final multimodal representation ${\mathbf{X}}^{\mathrm{atv}}$ (Equation (5)).

$${\mathbf{u}}_{\mathrm{out}}=\mathrm{LayerNorm}({\mathbf{u}}_{\mathrm{in}}+\alpha ·\mathbf{F})$$

(4)

$${\mathbf{X}}^{\mathrm{atv}}=\mathrm{concat}({\mathbf{u}}^{\prime a},{\mathbf{u}}^{\prime t},{\mathbf{u}}^{\prime v})$$

(5)

3.3. Sentiment-Enhancement Framework

To predict sentiment labels for utterances and enhance emotion recognition, we design the SE module with the architecture shown in Figure 3.

(1) Embedding Layer: For sentence-level sentiment analysis, inputs are unified as word sequences S = [$w_1$, $w_2$, …, $w_n$ ]. The pre-trained RoBERTa model converts inputs into continuous vector representations. Each word $w_i$∈ S is mapped to a continuous vector $x_i$∈$R^{d^{\prime }}$ (where $d^{\prime }$ denotes the embedding dimension). By stacking these word vectors, we obtain the word embedding matrix X ∈$R^{\mathrm{n}\times {\mathrm{d}}^{\prime }}$.

(2) Global Locator: The architecture of global locator is shown on the left in Figure 4. The word embedding matrix X is fed into the global locator to capture sentence-level contextual information. LSTM Processing: X is input to an LSTM to generate hidden states Ht. Attention Mechanism: Ht is linearly transformed into query (Q), key (K), and value (V) representations, as computed in Equation (6).

$$A_L=\mathrm{softmax}\left({\displaystyle \frac{Q{K}^T}{\sqrt{d}}}\right)V$$

(6)

Residual Processing: The attention output is combined with the original input through residual connections to produce the final global locator output.

(3) Local Locator: The architecture of global locator is shown on the left in Figure 4. This component employs an Encoder–Locator Combination (ELC) mechanism. Encoder Guidance: For the k-th ELC (k > 1), the encoder derives hidden states $h_k$∈$R_d$ by weighted summation of rows in $C_{k-1}$ (masked context matrix). The weights are determined by $l_{k-1}$∈$R_n$ (projected weights from the previous ELC).

Masking Strategy: Before core computations in the k-th ELC, $C_{k-1}$ undergoes Bernoulli masking with predefined probability Pmask. Each row in $C_{k-1}$ is independently masked (set to zero) based on weights in $l_{k-1}$. This operation is only activated during training (demonstrated in Figure 4).

(4) Linear Layer: A single-layer feedforward neural network constructs the linear layer Equation (7).

$$D=\left({\displaystyle \frac{1}{k}}\sum _k{h}_k\right)W^{\mathrm{dis}}+b^{\mathbf{dis}}$$

(7)

The output D represents sentiment features extracted by the SE module, which are concatenated with multimodal fusion features from HSF for downstream processing.

3.4. Contextual Extractor

The fused features $X^{atv}$ generated by HSF and sentiment features D obtained from the SE module are concatenated and input into the contextual extractor. This module takes the fused features as inputs for each dialogue utterance ($u_i$; i = 1, …, n) and employs a transformer encoder to capture contextual dependencies. The architecture is illustrated in Figure 1.

3.5. CS-BiGraph

Our CS-BiGraph model addresses a fundamental limitation in existing GNN-based methods for conversational emotion recognition, such as DialogueGCN and COGMEN [20]. While these models have successfully introduced graphs to model conversational context, they typically construct a single monolithic graph based on rigid predefined rules (e.g., speaker turn order and fixed-size temporal windows). This approach suffers from two key drawbacks: (1) it conflates local turn-by-turn conversational flow with global long-range semantic dependencies, treating them within the same structural representation; and (2) its fixed structure is unable to adapt to the highly dynamic and non-sequential nature of human dialogues, where an utterance might be semantically closer to a much earlier turn than its immediate predecessor.

To overcome these challenges, our CS-BiGraph introduces a novel bilevel architectural paradigm that explicitly decouples these two distinct types of contextual relationships. While the CS-BiGraph paradigm is constructed using established techniques such as K-nearest neighbor (KNN) and graph autoencoder (GAE), its fundamental novelty lies in their architectural orchestration. This specific integration is engineered to create a disentangled bilevel structure that directly addresses a core limitation in prior models: the conflation of local turn-by-turn conversational flow with global long-range semantic dependencies. Therefore, the primary contribution is the design of this specialized architecture, which systematically separates these two contextual facets and models them with dedicated graph structures to achieve a more robust understanding of the dialogue’s emotional landscape.

A Global Similarity Graph: This layer is specifically designed to capture the non-sequential topic-driven semantic relationships across the entire conversation. By connecting nodes based on feature similarity (via KNN and cosine distance), it builds a “shortcut” network that allows information to flow between semantically related but temporally distant utterances, overcoming the limitations of fixed window sizes.

A Local Speaker Relationship Graph: This layer focuses on modeling the turn-by-turn speaker-dependent conversational dynamics. Crucially, instead of using fixed rules, we employ a graph autoencoder (GAE) to adaptively learn the optimal structure of these local interactions directly from the data. This allows the model to dynamically adjust the graph’s connectivity based on the specific dialogue rather than relying on a one-size-fits-all heuristic.

This explicit decoupling of global semantic context from local conversational structure is the fundamental architectural difference between CS-BiGraph and prior GNN-based models. By modeling these two facets of context with specialized mechanisms and then integrating them, our framework achieves a more comprehensive and robust understanding of the dialogue’s emotional landscape. The following describes the implementation details of each graph component.

The CS-BiGraph model consists of a global similarity-based neighbor graph and a speaker relationship graph based on graph autoencoders, as illustrated in Figure 5.

The dialogue is defined as D = $U^{s_1}$, $U^{s_2}$, …, $U^{s_M}$, where $U^{s_1}$ = $u_1^{s_1}$, $u_2^{s_1}$, …, $u_n^{s_1}$ represents the utterances from speaker 1, as illustrated in Figure 6.

In this study: Intra-speaker relationships $R_{\mathrm{intra}}=\left\{U_i^{\mathbf{S}}\to U_i^{\mathbf{S}}\right\}$ are relationships between utterances from the same speaker. Inter-speaker relationships $R_{\mathrm{inter}}\in {\left\{U^{{\mathbf{S}}_i}\to U^{{\mathbf{S}}_j}\right\}}_{i\ne j}$ are relationships between utterances from different speakers. (1) Global Similarity-Based Neighbor Graph: After feature extraction, the K-nearest neighbor (KNN) algorithm calculates node similarities using Equation (8):

$$\mathrm{dis}=\sqrt{\sum _{i,j}{(u_i-u_j)}^2}$$

(8)

where d denotes the feature dimension. Smaller distances indicate higher similarity. Subsequently, cosine distances between nodes are computed, and edges are removed if distances exceed a threshold $\tau$ (hyperparameter), reducing redundant information and enhancing discriminative features.

(2) Speaker Relationship Graph via Graph Autoencoder (GAE): The graph autoencoder (GAE), an unsupervised graph neural network (GNN) method, optimizes graph structures by reconstructing adjacency matrices through node representation learning. It comprises the following:

Encoder: Maps node features to a low-dimensional latent space via graph convolutional networks (GCNs), learning node embeddings Z. Decoder: Reconstructs the adjacency matrix $\widehat{A}$ using Z, as defined in Equation (9):

$$\widehat{A}=\sigma \left(Z{Z}^{\mathrm{T}}\right)$$

(9)

where $\sigma$ denotes the sigmoid function, mapping similarities to the range [0, 1].

3.6. Prediction Result Generation

After graph construction, the relational graph convolutional network (R-GCN) is employed to train the graph structure, effectively capturing dependencies between inter-speaker and intra-speaker connected utterances, as defined in Equation (10).

$$x_i^{\prime }={\theta }_{\mathrm{root}}·z_i+\sum _{r\in \mathcal{R}}\sum _{j\in {\mathcal{N}}_r\left(i\right)}{\displaystyle \frac{1}{|{\mathcal{N}}_r\left(i\right)|}}{\theta }_r·z_j$$

(10)

where ${\mathcal{N}}_r\left(i\right)$ indicates neighbor indices of node $\mathit{i}$ under relation $\mathit{r}\in \mathit{R}$; ${\theta }_{root},{\theta }_r$ represent learnable parameters of R-GCN; $|{\mathcal{N}}_r\left(i\right)|$ denotes normalization constant; and $\mathit{z}$ indicates utterance-level features from the contextual extractor. The processed graph representations are then fed into a graph transformer layer with ReLU activation and softmax normalization, followed by a classifier to generate final emotion label predictions. The complete pipeline is illustrated in Figure 7.

4. Experiment

4.1. Experimental Environment

Our experimental environment is shown in

Table 1. Computational resources and model statistics.

Component	Specification
Hardware and System
GPU	NVIDIA RTX 3070 Ti (NVIDIA Corporation, Santa Clara, CA, USA) (8 GB VRAM)
Operating System	Ubuntu 22.04
Software
Python Version	3.10
PyTorch Version	1.12.1
Model Statistics and Training Time
Total Trainable Parameters	7.5 M
Training Time per Epoch (IEMOCAP)	Approx. 7 min
Total Training Time (IEMOCAP)	Approx. 9 h

.

4.2. Test Dataset Description

IEMOCAP Dataset [21]: Comprises 151 dyadic dialogues with 7433 utterances, each annotated by experts with six emotion labels: happiness, sadness, calmness, anger, excitement, and depression.

CMU-MOSEI Dataset [22]: Contains over 23,000 monologue video clips from YouTube, annotated for sentiment and emotion. Sentiment labels range from −3 (strongly negative) to +3 (strongly positive), while emotion labels include happiness, sadness, disgust, fear, surprise, and anger. Due to multi-label emotion annotations, sentiment labels are prioritized for evaluation. The CMU-MOSEI dataset features multi-label emotion annotations, where a single utterance can be associated with multiple emotion categories. To ensure a fair and consistent comparison with prior works, we follow a standard evaluation protocol for this dataset. Specifically, we transform the multi-label problem into a multi-class classification problem by prioritizing the sentiment labels, which are single-label annotations ranging from −3 (strongly negative) to +3 (strongly positive), resulting in a 7-class classification task. For binary sentiment classification (positive/negative), we treat sentiment scores $>0$ as the positive class and scores $<0$ as the negative class, excluding neutral samples. The reported accuracy (Acc) metric in our experiments corresponds to the standard classification accuracy on this primary sentiment task.

4.3. Evaluation Metrics

To assess model performance across scenarios, predictions are evaluated on the IEMOCAP test set (1623 utterances) and CMU-MOSEI test set (4662 utterances). Performance is measured using standard metrics: precision, recall, and F1-score, which comprehensively evaluate the model’s ability to accurately recognize diverse emotion categories.

4.4. Computational Complexity Analysis

To provide a formal assessment of our framework’s theoretical underpinnings, we analyze its computational complexity. The overall complexity is primarily determined by its three main components: the hierarchical sequential fusion (HSF), sentiment-enhancement (SE), and CS-BiGraph modules.

Let N be the number of utterances in a dialogue and L be the sequence length of each utterance. The complexity of the feature extractors (e.g., sBERT) is typically $O\left(L^2\right)$ per utterance. For our main components, the complexities are as follows:

• HSF Module: The complexity is dominated by the cross-attention mechanisms. For three modalities, this results in a complexity of $O(N·L^2)$.
• SE Module: The RoBERTa-based embedding, along with the subsequent LSTM and attention layers, contribute a complexity of $O(N·L^2)$.
• CS-BiGraph Module: This module’s complexity is driven by two parts: the Global Similarity Graph construction using KNN, which is $O(N^2·d)$, and the GNN operations (GAE and R-GCN), which are approximately $O(E·d)$, where d is the feature dimension and E is the number of edges.

Therefore, the total computational complexity of our framework is approximately $O(N·L^2+N^2·d+E·d)$. The quadratic term $O(N^2·d)$ from the KNN graph construction is the dominant factor for long dialogues. This analysis highlights a trade-off between our model’s ability to capture long-range dependencies and its scalability.

5. Results

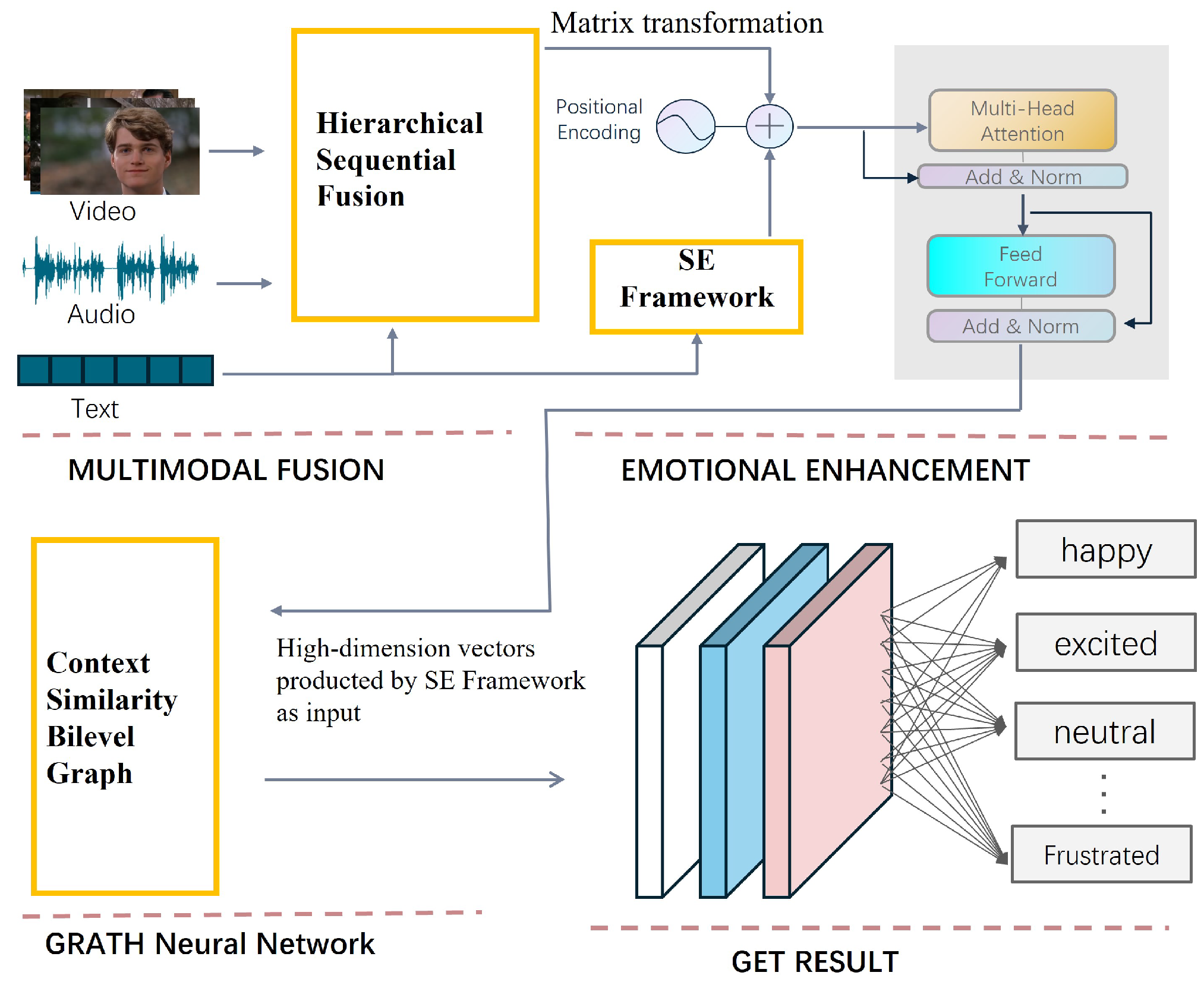
5.1. Ablation Study

To validate the effectiveness of each proposed component, ablation experiments are conducted by removing individual modules and substituting alternatives: HSF module removal replaced with simple feature concatenation, SE module removal replaced with RNN, and CS-BiGraph removal replaced with conventional GCN. The key findings are presented below (

Table 2. Overall ablation study results on the IEMOCAP dataset.

	Happy	Sad	Neutral	Angry	Excited	Frustrated	Avg
Model	F1 (%)	F1 (%)	F1 (%)	F1 (%)	F1 (%)	F1 (%)	F1 (%)
Ours	54.2	79.3	69.9	68.3	72.9	68.4	70.0
w/o HSF	57.9	78.1	65.4	66.8	76.6	64.7	68.7
w/o SE	56.1	81.1	66.9	67.4	73.4	66.6	69.3
w/o CS-BiGraph	49.8	78.5	65.3	68.7	76.8	67.1	68.8
w/o HSF, SE	47.1	75.5	69.1	66.7	73.3	69.4	68.7
w/o HSF, CS-BiGraph	55.4	81.7	64.1	68.6	74.0	64.4	68.4
w/o SE, CS-BiGraph	51.1	81.1	65.1	66.2	74.4	65.3	68.2

and

Table 3. Accuracy (Acc) scores (%) of the proposed model in ablation studies on the MOSEI dataset.

Method	CMU-MOSEI
Ours	48.6
w/o HSF	48.5
w/o SE	47.9
w/o CS-BiGraph	48.2
w/o HSF, SE	47.8
w/o HSF, CS-BiGraph	48.3
w/o SE, CS-BiGraph	47.6

):

Module Complementarity:

HSF + CS-BiGraph achieves the highest F1-score (56.1%) for happy emotion, demonstrating the synergy between hierarchical sequential fusion and bilevel graph optimization in positive emotion recognition.

Sentiment-Topology Synergy: SE + CS-BiGraph improves the excited emotion F1-score to 76.6%, verifying the benefits of combining sentiment enhancement with global graph modeling.

To further analyze the effectiveness of each component in the bilevel graph structure, we conducted a decomposition analysis of the CS-BiGraph module, with the results shown in

Table 4. Accuracy (Acc) scores (%) of Cs-BiGraph in ablation studies on two datasets.

Method	IEMOCAP	MOSEI
Cs-BiGraph	68.9	47.8
w/o Cosine	68.2	46.5
w/o Similarity Graph	65.7	44.9
w/o GAE	67.9	46.3
w/o Cosine, GAE	66.3	45.6
w/o Similarity Graph, GAE	64.5	43.9

. The removal of the Global Similarity Graph (w/o Similarity Graph) and graph autoencoder (w/o GAE) led to significant performance drops of 3.2% and 1.0%, respectively, on the IEMOCAP dataset, demonstrating the foundational role of graph structure optimization in complex emotion recognition. Notably, when CS-BiGraph remains intact, the synergistic gains between HSF and SE reach their maximum (+1.7%). This enhancement effect is particularly pronounced in long-tail categories such as neutral (69.9%) and angry (68.3%). Compared to the baseline model COGMEN (w/o Similarity Graph, GAE), the triple-module integrated model (HSF + SE + CS-BiGraph) achieves a 1.9× greater improvement (+3.4%) in complex emotion categories than in ordinary ones.

The optimized graph structure enables efficient fusion of HSF’s local temporal features and SE’s global semantic information through its hierarchical information propagation channels. This triple synergistic effect ultimately yields an average F1-score of 70.0%, significantly outperforming single-module (max 68.7%) and dual-module combinations (max 69.3%).

Impact of Pre-Trained Feature Extractors

To address the framework’s dependency on large pre-trained models, we conducted a quantitative analysis by replacing the sBERT textual feature extractor with a lighter non-contextual GloVe model [23]. All the other framework components remained unchanged. The comparative results on the IEMOCAP dataset are presented in

Table 5. Impact of replacing the textual feature extractor on IEMOCAP (Avg F1-%).

Textual Feature Extractor	Average F1-Score (%)
sBERT (our main model)	70.0
GloVe (300d vectors)	64.8

.

The results show a significant performance drop of 5.2%, empirically confirming the importance of high-quality contextual embeddings from models like sBERT. Notably, even with a simpler GloVe extractor, our framework achieves a respectable F1-score of 64.8%. This demonstrates that the architectural design of our framework contributes significantly to its effectiveness, independent of the feature extractor’s power.

5.2. Hyperparameter Analysis

Hyperparameter Settings For the IEMOCAP dataset: Dropout = 0.1, GNNhead = 7, SeqContext = 4, Learning Rate = 1 × 10⁻⁴. For the CMU-MOSEI dataset: Dropout = 0.3, GNNhead = 2, SeqContext = 1, Learning Rate = 1 × 10⁻³.

5.2.1. Number of Attention Layers

To investigate the impact of attention layers in the SE module’s global locator, we fix other hyperparameters and vary the number of attention layers h ∈ {1, 2, 3, 4, 5}. The results (Figure 8) are presented as follows:

Initial performance gain: Increasing $\mathit{h}$ from 1 to 2 enhances key sentiment feature capture, improving accuracy. Diminishing returns: Beyond $\mathit{h}$ = 5, model complexity surges, causing overfitting and reduced generalization.

5.2.2. Number of Neighbor Nodes

To analyze the impact of neighbor quantity in k-NN graph construction, we fix other hyperparameters and vary n ∈ {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. The results (Figure 9) reveal the following:

Sparse regime ($\mathit{n}\le 3$): Insufficient neighbors restrict feature propagation due to sparse graph connectivity. Optimal range ($4\le \mathit{n}\le 6$): Balanced local associations and mitigated sparsity yield peak performance. Overdense regime ($\mathit{n}\ge 7$): Excessive edges introduce low-similarity noise, degrading model robustness.

5.2.3. Similarity Threshold $\tau$

Similarity Threshold $\tau$: To analyze the impact of similarity threshold $\tau$ on model performance during graph construction, we fix other hyperparameters and vary $\tau \in$ {0, 0.1, 0.2, …, 1.0}. The results (Figure 10) demonstrate the following:

Low $\tau$ regime ($\tau \le 0.3$): Excessive low-similarity edges introduce significant noise, diluting discriminative emotional associations despite expanded feature propagation.

Optimal range ($0.4\le \tau \le 0.6$): Balanced edge density and noise suppression achieve peak performance, retaining high-confidence emotional connections while avoiding isolated nodes.

High $\tau$ regime ($\tau \ge 0.7$): Over-sparse graphs impair context aggregation due to insufficient neighbor connections, causing severe performance degradation.

5.3. Statistical Significance Analysis

To validate that the performance improvements of our proposed framework are statistically significant and not due to random chance, we conducted a statistical analysis on the IEMOCAP dataset, which serves as our primary benchmark. We specifically compared our full model against a strong baseline, COGMEN.

Following common practice, we performed multiple independent training runs (five runs) for both our model and the baseline, each with different random seeds. We then collected the F1-score for each run and performed a two-sample t-test to assess the significance of the difference between the two sets of results.

The mean F1-score for our model was 70.2 with a standard deviation of 0.53. In comparison, the mean F1-score for the baseline was 67.6 with a standard deviation of 0.72. The t-test yielded a p-value 0.00084. Since $p<0.05$, we can conclude that the performance gain achieved by our model is statistically significant. This analysis provides strong evidence that the architectural innovations in our framework, particularly the CS-BiGraph module, lead to a genuine and reliable improvement in performance.

5.4. Comparison with Existing Works

In this subsection, we further compare the proposed method with state-of-the-art multimodal emotion classification models on the IEMOCAP and CMU-MOSEI datasets.

To provide a comprehensive and up-to-date comparison, we have included several strong baselines as well as two very recent state-of-the-art methods from 2025, LMAM and MERC-PLTAF [16]. The overall performance comparison on the IEMOCAP dataset, which features rich dyadic dialogues and serves as our primary benchmark, is visualized in Figure 11.

As illustrated in Figure 11, our integrated framework outperforms established baselines such as GraphMFT, BiGraph [24], TelME [25], and COGMEN. We also observe that the recently proposed LMAM and MERC-PLTAF achieve higher overall scores. This warrants a deeper analysis into the architectural philosophies of these methods.

The strong performance of the LMAM can be attributed to its highly specialized and parameter-efficient cross-modal fusion module, which excels at its specific subtask. MERC-PLTAF’s success lies in its innovative use of a prompt-based learning paradigm, effectively converting the multimodal problem into a format that maximally leverages the power of large pre-trained language models.

In contrast, our work’s primary contribution is a holistic three-component architecture that addresses multiple distinct challenges in the CER pipeline simultaneously. Our key innovation, the CS-BiGraph module, provides a unique capability in adaptively learning complex non-sequential conversational structures—a mechanism not present in the aforementioned models. As demonstrated in our extensive ablation studies (Table 1), this graph-based contextual modeling is the cornerstone of our framework’s performance. Therefore, we posit that our work offers a complementary and architecturally novel approach, focusing on robust conversational structure modeling, while methods like LMAM and MERC-PLTAF provide powerful solutions for modality fusion and alignment, respectively. Future work could explore integrating these specialized modules into our comprehensive framework.

To provide a more fine-grained analysis of our model’s capabilities,

Table 6. F1-scores of existing models for each emotion category on the IEMOCAP dataset.

Model	Happy	Sad	Neutral	Angry	Excited	Frustrated
	F1 (%)	F1 (%)	F1 (%)	F1 (%)	F1 (%)	F1 (%)
BC-LSTM	35.6	69.2	53.5	66.3	61.1	62.4
CMN	32.6	72.9	56.2	64.6	67.9	63.1
ICON	32.8	74.4	60.6	68.2	68.4	66.2
DialogueRNN	32.8	78.0	59.1	63.3	73.6	59.4
DialogueGCN	42.8	84.5	63.5	64.2	63.1	67.0
MMGCN	42.3	78.7	61.7	69.0	74.3	62.3
COGMEN	44.4	77.5	63.1	62.2	72.1	58.6
GraphMFT	46.0	83.1	63.1	70.0	76.9	63.8
BiGraph	47.1	79.4	66.7	67.0	74.7	64.0
Ours	54.2	79.3	69.9	68.3	72.9	68.4

details the F1-scores for each of the six emotion categories on the IEMOCAP dataset, comparing our model with several classic and strong baselines for which this detailed data is available, such as BC-LSTM [26], CMN, ICON, DialogueRNN, DialogueGCN, MMGCN [27], TBJE [28], and Multilogue-Net [29]. For the CMU-MOSEI dataset, which consists primarily of monologues, the overall accuracy scores are presented in

Table 7. Accuracy (Acc) scores (%) of existing models on the CMU-MOSEI dataset.

Model	Acc (%)
TBJE	44.4
Multilogue-Net	44.83
Graph-MFN	45.0
COGMEN	43.9
BiGraph	47.2
Ours	48.6
TAILOR	48.8
CARAT	49.4

.

As noted in our dataset description, CMU-MOSEI primarily consists of monologues. It serves as a crucial benchmark for multi-label classification on single-speaker data streams. Our framework achieves a competitive accuracy score, as shown in Table 7, where we also include results from recent state-of-the-art models for a comprehensive comparison.

As shown in Table 7, our model’s accuracy (48.6%) is competitive, although slightly below recent SOTA models like TAILOR (48.8%) [30] and CARAT (49.4%) [31]. We attribute this difference to a fundamental divergence in research paradigms. These state-of-the-art methods achieve high performance by developing sophisticated intra-task mechanisms, such as TAILOR’s label-specific feature generation or CARAT’s reconstruction-based fusion.

In contrast, our work explores a complementary inter-task approach. The novelty of our SE module lies in leveraging an auxiliary task—sentiment polarity analysis—to provide external knowledge that constrains and guides the primary emotion recognition task. This strategy aims to reduce emotional ambiguity by using broader sentiment cues, a method that proves particularly effective on conversational datasets like IEMOCAP (see Table 6).

Thus, while SOTA models advance intra-task representation learning, our framework contributes an orthogonal perspective on inter-task knowledge integration. We believe these approaches are not mutually exclusive; future work could explore combining our sentiment-enhancement strategy with the advanced fusion mechanisms of models like TAILOR and CARAT.

5.5. Discussion

Our experimental results, presented in Table 6 and Table 7, demonstrate that our proposed framework achieves competitive or state-of-the-art performance compared to a wide range of baseline models. A key strength of our approach is evident on the IEMOCAP dataset, where our model shows a significant 7.1% F1-score improvement on the “happy” emotion over the second-best model from our baseline set—a category where many models traditionally struggle. This highlights our framework’s enhanced discriminative power in handling challenging non-canonical emotional expressions.

However, a critical analysis of our results also reveals important limitations and areas for future improvement, which we discuss in detail below.

5.5.1. Challenges in Distinguishing Semantically Similar Emotions

A primary challenge, reflected in the fine-grained results of Table 6, is the model’s difficulty in distinguishing between semantically similar emotion categories. For instance, while achieving strong performance in most categories, the F1-scores for “angry” (68.3%) and “frustrated” (68.4%) are lower than for “sad” (79.3%) or “excited” (72.9%). This suggests a degree of confusion between emotions that share similar valence and arousal levels, such as the overlap between anger and frustration. This issue stems from two factors. First, the inherent ambiguity in human expression means that these emotions often share highly similar acoustic features (e.g., increased vocal intensity) and lexical cues. Second, capturing the subtle contextual shifts that differentiate them (e.g., frustration often implies an unfulfilled goal, while anger can be more direct) remains a non-trivial task.

Our framework is architecturally designed to mitigate this. The SE module provides a foundational layer of sentiment polarity, helping to separate positive from negative emotions. More critically, our CS-BiGraph module aims to resolve ambiguity by modeling long-range context, learning, for example, that an utterance following a series of failed attempts is more likely to be “frustrated” than “angry”. However, our results indicate that, when local immediate multimodal signals are particularly strong and ambiguous, they can occasionally override the model’s broader contextual understanding. This points to a need for future work on more robust arbitration mechanisms that can better balance local evidence with global context.

5.5.2. The Impact of Data Imbalance and Future Directions

A second factor influencing performance is the well-known class imbalance in the IEMOCAP dataset. As shown in our ablation studies (Table 1), our model achieves its highest F1-score in the “neutral” category (69.9%), which is also the most frequent class. This high performance, while positive, may also indicate a slight bias, where the model learns to default to “neutral” in cases of high uncertainty. This is a common issue that can lead to suboptimal performance on less frequent minority emotion classes.

While the focus of this paper was on architectural innovation, we acknowledge that addressing this data imbalance is a critical next step for improving generalizability. We did not employ explicit mitigation strategies in this work, but future iterations of our framework could readily incorporate them. Promising directions include the following:

(1) class-balanced loss functions, such as focal loss or weighted cross-entropy, to assign higher penalties for misclassifying minority classes;

(2) advanced data augmentation, particularly for synthesizing realistic multimodal data for underrepresented emotions; and

(3) balanced sampling strategies, such as oversampling minority classes during batch creation. We hypothesize that integrating these data-centric strategies with our model-centric innovations will lead to more robust and equitable performance across all emotion categories.

Despite these limitations, by integrating results from both datasets, our model consistently demonstrates strong performance, proving the effectiveness and reliability of its core architectural design in practical applications.

6. Limitations and Future Work Directions

(1) The current multimodal fusion method has only validated the effectiveness of text/audio/video modalities. Future work should extend to additional modalities (e.g., gestures) to verify generalizability.

(2) The emotion modeling focuses solely on polarity dimensions without fully exploring fine-grained features like intensity. Subsequent research could integrate multi-dimensional emotion-labeled datasets and incorporate external knowledge (e.g., gestures and micro-expressions) to enhance model performance.

(3) The dual-graph structure (speaker relationship graph and similarity graph) lacks interactive mechanisms. Future improvements may involve dynamic collaborative graph networks through cross-graph information propagation (e.g., similarity-weighted speaker relationship modeling and structural feature sharing).

(4) The current model has only validated the effectiveness of this method under ideal data conditions. Further research is required to determine whether the model performance remains consistent when one or more modalities are partially missing or contain noise.

(5) Our framework’s performance is inherently linked to the capabilities of the large pre-trained models used for feature extraction (e.g., sBERT and RoBERTa). While leveraging these models provides a strong foundation, the stability and reproducibility of our results are dependent on them. Future work should investigate the framework’s robustness with different, potentially lighter, feature extractors to better assess its architectural modularity and efficiency.

These advancements will enhance the model’s ability to deeply mine multimodal emotional features and further break through the performance bottleneck in emotion recognition.

7. Conclusions

Emotion recognition is a prominent research direction in machine learning and plays a critical role in affective computing. However, challenges such as insufficient multimodal fusion interaction, lack of dynamic emotional weight optimization, and long-range dependency modeling in dialogue history persist.

To address these issues, we propose three innovations: HSF, a hierarchical sequential fusion method; SE, a sentiment-enhanced joint learning framework; and CS-BiGraph, a context-similarity bilevel graph model for dialogue modeling. The integrated framework achieves 69.9% accuracy on the IEMOCAP dataset, setting new benchmarks in “Neutral” and “Happy” emotion recognition. This work demonstrates significant performance improvements and paves the way for future research in emotion recognition applications. Specifically, our framework lays the groundwork for real-world applications such as developing more empathetic chatbots and advanced tools for mental health monitoring.