Key Operator Vectorization for LeNet and ResNet Based on Buddy Compiler

Abstract

Deep learning has emerged as a prominent focus in both academia and industry, with a wide range of models being applied across diverse domains. Fast and efficient model inference is essential for the practical deployment of deep learning models. Under specific hardware constraints, accelerating inference remains a key research challenge. Common techniques for model acceleration include quantization, pruning, and vectorization. Although quantization and pruning primarily reduce model precision or complexity to enhance efficiency, this paper concentrates on vectorization, a technique that accelerates models by increasing the parallelism of operator execution. Based on the open-source Buddy-MLIR project, this work implements vectorization optimizations for Matmul, Conv2d, and Max Pooling operations to improve inference performance. These optimizations are designed as compiler passes and integrated into the Buddy-MLIR framework, offering a general solution for vectorizing such operators. Two optimization approaches are proposed: general vectorization and adaptive vectorization. Compared to the standard MLIR lowering pipeline and the fully optimized LLVM backend, the proposed general and adaptive vectorization methods reduce the inference latency of LeNet-5 by $26.7\%$ and $37.3\%$, respectively. For the more complex ResNet-18 model, these methods achieve latency reductions of $79.9\%$ and $82.6\%$, respectively.

1. Introduction

In recent years, deep learning research has advanced rapidly [1], becoming a central focus in both academia and industry. This technology has been widely adopted in a variety of fields, particularly in computer vision [2] and natural language processing [3], where deep learning models have demonstrated exceptional performance. Among these models, convolutional neural networks (CNNs) [4] have achieved remarkable success in tasks such as image recognition and object detection due to their local receptive field properties and the dimensionality reduction capabilities of pooling layers [5]. With the growth in computational power and the availability of large-scale datasets, CNNs have become foundational technologies in both computer vision and natural language processing.

As a pioneering model in convolutional neural networks (CNNs), LeNet-5 [6] (LeNet refers to LeNet-5 in this paper) was initially developed for handwritten digit recognition. Although its architecture is relatively simple compared to more recent models, such as AlexNet [7] and Transformer-based architectures, its foundational design makes it an ideal candidate for investigating optimization techniques that can be generalized to more complex networks. Through the optimization of LeNet, valuable information can be obtained on how vectorization strategies can be effectively applied across different CNN architectures. LeNet comprises two convolutional (Conv2d) Proof (Operations), two max pooling (Max Pooling) operations, and three matrix multiplication (Matmul) operations. This streamlined but effective architecture laid the foundation for the subsequent development of more sophisticated models. The success of LeNet played a crucial role in catalyzing the evolution of deep neural networks, as demonstrated by the emergence of ResNet [8], which significantly extended the reach of deep learning in various domains. ResNet addresses challenges such as vanishing gradients and network degradation by incorporating residual blocks and skip connections. It has become a widely adopted backbone for advanced computer vision tasks, including image classification, object detection, and semantic segmentation. A representative variant, ResNet-18 (ResNet refers to ResNet-18 in this paper), features a compact architecture and high computational efficiency, making it well suited for fundamental vision tasks such as image classification. The model consists of 18 trainable layers, primarily composed of stacked basic residual blocks. Each block includes two 3 × 3 convolutional layers and a residual connection that adds the input directly to the output, effectively mitigating the problem of vanishing gradients in deep networks. Despite these architectural advances, the computational intensity of deep learning models remains a significant challenge. In real-world applications, both computational cost and latency overhead are critical considerations [9].

Therefore, achieving fast and efficient model inference has become critical to the successful deployment of deep learning models. Under specific hardware constraints, accelerating model inference is a prominent research focus. Optimization efforts can be directed toward the architecture, parameters, and computational operations of the model, with common approaches including quantization, pruning [10], and vectorization. Quantization reduces both computational and memory overhead by lowering the precision of numerical representations. Pruning eliminates redundant neurons in the neural network, thereby decreasing the structural complexity and computational burden of the model. For example, modifying the number of output units in LeNet to suit a binary classification task [11] or removing the C5 layer to adjust the number of neurons in each layer [12] can improve the network structure and parameter efficiency. Although these methods improve inference speed, they often do so at the cost of reduced model accuracy.

Vectorization transforms computational tasks into vector operations by leveraging the SIMD (Single Instruction, Multiple Data) instruction sets available on modern CPUs and GPUs [13]. This approach enhances the parallelism of data processing in model operators, thereby accelerating model inference without compromising the accuracy of the results. For example, in the optimization of the Metropolis algorithm, vectorization increases the amount of data processed simultaneously during the generation of random numbers and the evaluation of the exponential function, thus enhancing the parallelism of the sweep algorithm [14]. In stencil computations, vectorization resolves data alignment conflicts and improves computational parallelism through SIMD instructions. When combined with tiling techniques, it also improves data locality, further improving the performance [15]. In practical deep learning frameworks such as TensorFlow, vectorization optimizations are applied to built-in operations, core functions, and tensor expressions to improve the efficiency of model training and deployment [16]. XLA (Accelerated Linear Algebra) employs hardware-level vectorization instructions and compiler-level optimizations, including operator fusion, computation graph optimization, and automatic tensor scheduling, to significantly improve the execution efficiency of deep learning models [17].

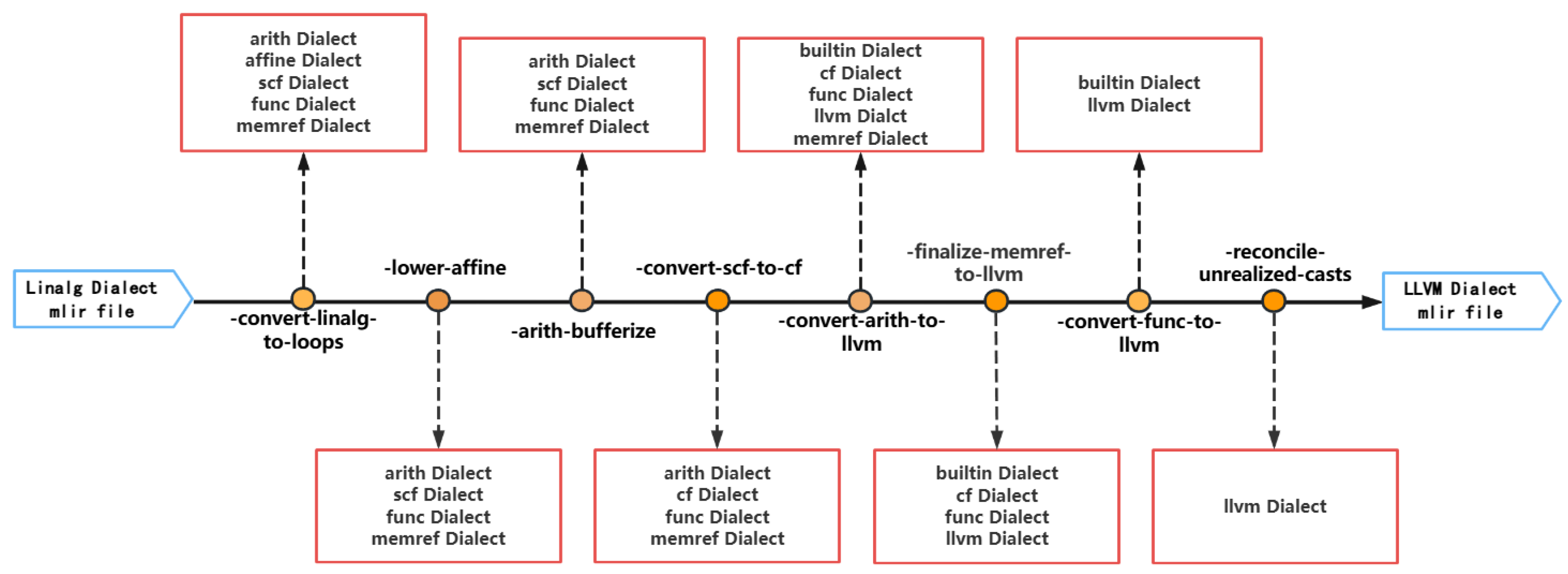
In the field of deep learning compiler optimization, targeting diverse hardware architectures is a crucial research direction. Section 5.1 (Multi-Level Intermediate Representation), a compiler framework that supports multilevel abstractions and transformations, has been widely adopted for deep learning acceleration. As illustrated in Figure 1, MLIR enables hierarchical optimization across various abstraction levels. Built on top of MLIR and tailored for the RISC-V architecture, the open-source project Section 5.2 introduces a hardware–software co-design framework. This framework enables fine-grained optimizations at multiple levels of intermediate representation, effectively accelerating the inference of deep learning models.

Based on the Buddy-MLIR open-source project, this paper focuses on how to use vectorization techniques to optimize key operators (Matmul, Conv2d, and Max Pooling) in LeNet and ResNet to accelerate model inference. By combining multilevel intermediate representations and compilation optimization techniques, this paper proposes vectorization optimization for the Matmul, Conv2d, and Max Pooling operators at the Vector Proof (Dialect) level. The optimization is applied to sequential memory access under the NHWC data format, with the aim of increasing the parallelism of operator computations while maximizing data locality, thus improving inference efficiency. Based on this optimization approach, an optimization Proof (Pass) is designed and added to Buddy-MLIR. This pass not only supports flexible vectorization size configurations but also ensures data alignment requirements, providing a general solution for further operator-level optimizations.

In addition, these operators are widely employed in more complex deep learning models, such as VGG [18], YOLO [19], and GPT [20]. Given their ubiquity in modern deep learning architectures, optimizing these operators not only significantly accelerates inference in models like LeNet and ResNet, but also offers effective acceleration strategies for more sophisticated deep learning tasks.

In summary, the main contributions of this study are as follows:

• A vectorization optimization method is proposed for the Matmul, Conv2d, and Max Pooling operators, providing sequential memory access under the NHWC data format and maximizing data locality, achieving better acceleration than the standard optimization path and the LLVM backend.
• A general optimization pass from the Linalg dialect level to the Vector dialect level is implemented and integrated into the Buddy-MLIR project, adding a vectorization optimization module to Buddy-MLIR.
• A specific optimization scheme is proposed to achieve model inference acceleration that outperforms general vectorized optimization. It adaptively sets the appropriate vectorization length based on the number of operators in the operation.

2. Operator Optimization Design

In MLIR, data computations at the Linalg dialect level are represented as complex operators (Matmul, Conv2d, etc.). These operators are typically computed element-by-element in the standard lowering process, resulting in relatively low computational efficiency. To address this issue, MLIR provides the Vector dialect, which abstracts code at the vector level and focuses on defining efficient operations with vector types. Therefore, operators such as Matmul, Conv2d, and Max Pooling can be lowered from the Linalg dialect to the Vector dialect, transforming these complex operators into basic operators and refining the granularity of data flow computation. Then, through the Vector dialect, element-wise operations are transformed into vector operations, leveraging SIMD (Single Instruction, Multiple Data) technology to accelerate the computation of target operators and significantly improve computational efficiency. This section will illustrate the optimization design approach for the Matmul, Conv2d, and Max Pooling operators.

2.1. Operator Computation Principle

At the Linalg dialect level, the Matmul, Conv2d, and Max Pooling operators, respectively, invoke the operations $linalg.batchmatmul$, $linalg.conv2dnhwcfhwc$, and $linalg.poolingnhwcmax$. In the general downgrade process, these operators follow similar computational patterns based on the SISD (Single Instruction Single Data) approach. Specifically, these operations extract data from the operands sequentially along a dimension, perform calculations, and store the results back in the output tensor. Taking the more complex $linalg.conv2dnhwcfhwc$ as an example, the $NHWC$ data format follows a specific layout during storage (as shown in Figure 2). To improve data locality, the computation is performed in the order of $C{W}_k{H}_{k}F{W}_o{H}_{o}N$ (from the inner loop to the outer loop). Here, k denotes the convolution kernel and o represents the output tensor. In each iteration of the loop, the following three operations are performed sequentially:

• Load: Data are read from memory.
• FMA: Multiply and add operations are performed.
• Store: The result of the computation is stored back in the output tensor.

Although this computation process aligns with the SISD approach, it has relatively low computational efficiency due to its reliance on element-wise processing, especially when handling large-scale data, which may result in significant latency and low throughput.

2.2. Vectorization Optimization

The general vectorization strategy leverages SIMD (Single Instruction, Multiple Data) while preserving data locality. For each operator, vectorization is achieved by performing Load and Store operations along a designated dimension, i.e., the computation is vectorized along that dimension and executed at the vector level. However, due to the uniqueness of each operator, two key aspects must be determined based on the operator’s characteristics: 1. the preferred dimension for the Load and Store operations; 2. the appropriate computational instructions to be applied during the execution of the vector level.

2.2.1. Matmul

At the Linalg dialect level, the Matmul operator uses $linalg.batchmatmulop$, with the operand data format being $CHW$. Therefore, to maintain data locality, the preferred dimensions for the Load and Store operations in the Batchmatmul operation should be W. At the same time, based on the computation method of $linalg.batchmatmulop$ and the data types being processed, the computational operations should be selected as $arith.fma$ to meet the requirements for vectorized FMA operations.

2.2.2. Conv2d

The Conv2d operator is implemented using $linalg.conv2dnhwcfhwcop$, where the input tensor and the convolution kernel follow the $NHWC$ and $FHWC$ data layouts, respectively, at the Linalg dialect level. To preserve data locality, the C dimension is typically preferred for Load and Store operations.

However, suppose the input tensor is X (the data format is $N{H}_x{W}_{x}C$), the convolution kernel is W (the data format is $F{H}_w{W}_{w}C$), and the output tensor is Y (the data format is $N{H}_y{W}_{y}F$). $Y[n,h_y,w_y,f]$ is an element of Y, where $n\in [0,N-1],h_y\in [0,H_y-1],w_y\in [0,W_y-1],f\in [0,F-1]$:

$$Y[n,h_y,w_y,f]=\sum _{h_w=0}^{H_w-1}\sum _{w_w=0}^{W_w-1}\sum _{c=0}^{C-1}\left(X[n,h_y+h_w,w_y+w_w,c]·W[f,h_w,w_w,c]\right)$$

(1)

The input tensor is affected by the convolution kernel, and both cannot have good data locality at the same time. Considering the better data locality of the convolution kernel, the data locality of the convolution kernel should be maintained. Furthermore, based on the computation method of $linalg.conv2dnhwcfhwcop$ and the types of data being processed, the computational operations should include $arith.mulfop$ or $arith.muliop$, as well as $vector.reductionop$.

2.2.3. Max Pooling

At the Linalg dialect level, the Max Pooling operator uses $linalg.poolingnhwcmaxop$, where the operands’ data format is $NHWC$. To maintain data locality, the preferred dimensions for Load and Store operations should be C. Since the Pooling computation only involves vectors from the input and output tensors, the calculation only needs to focus on the vectors obtained from the input and output tensors. Depending on the type of data that is being processed, $arith.maxi$ or $arith.maxf$ should be used to obtain the maximum value. This ensures an efficient Max Pooling operation, fully utilizing the advantages of vectorization during execution.

Based on these insights, the vectorization algorithm is shown in Algorithm 1, using Conv2d as an example.

Algorithm 1 Conv2D vectorization optimization.

Require: X: 4D tensor of $N{H}_x{W}_{x}C$. W: 4D tensor of $F{H}_w{W}_{w}C$. Y: 4D tensor of $N{H}_y{W}_{y}F$.       $vlStep$: vectorization size. Ensure: $Y\Leftarrow conv2d(X,W)$ 1: for $n=0$ to $N-1$ do 2:    for $h_y=0$ to $H_y-1$ do 3:        for $w_y=0$ to $W_y-1$ do 4:           for $f=0$ to $F-1$ do 5:               $c\Leftarrow 0$ 6:               while $c<(C-vlStep+1)$ do 7:                   for $h_w=0$ to $H_w-1$ do 8:                       for $w_w=0$ to $W_w-1$ do 9:                          $yVal\Leftarrow$ take a data from $Y[n,h_y,w_y,f]$ 10:                          $xVec\Leftarrow$ take a vector from $X[n,h_y+h_w,w_y+w_w,c]$ 11:                          $wVec\Leftarrow$ take a vector from $W[f,h_w,w_w,c]$ 12:                          $newVec\Leftarrow Mul(xVec,wVec)$ 13:                          $newVal\Leftarrow Reduction\left(newVec\right)$ 14:                          $yVal\Leftarrow Add(newVal,yVal)$ 15:                          Store $yVal$ to $Y[n,h_y,w_y,f]$ 16:                       end for 17:                   end for 18:                   $c\Leftarrow c+vlStep$ 19:               end while 20:               Tail-end processing 21:           end for 22:        end for 23:    end for 24:  end for

2.2.4. Load and Store External Optimization

To further enhance the effects brought about by the above general optimization, some Load and Store operations can be moved to the outer loop, thereby reducing their execution frequency.

Taking the most complex calculation process, Conv2d, as an example, in the general computation flow, Load operations for the input tensor, convolution kernel, and output tensor are typically performed in the innermost loop. After multiplication and accumulation calculations, the new result is then stored back in the output tensor via a Store operation. This process is repeated in every iteration of the inner loop, causing the time overhead of data access to account for a large proportion of the computation time for the Conv2d operator.

To minimize data access overhead, the order of the loop variable can be adjusted and an intermediate variable can be introduced to accumulate the results from each iteration. After calculating one element of the output tensor, it is stored back in the output tensor. By adjusting the loop order and moving the Load and Store operations of the output tensor outside of vectorization, the number of Load and Store operations for the output tensor in each iteration can be reduced. This can effectively reduce the number of access operations, significantly lowering the access overhead. With these insights, we devise the vectorization optimization outlined in Algorithm 2.

Algorithm 2 Conv2D Load and Store external vectorization optimization.

Require: X: 4D tensor of $N{H}_x{W}_{x}C$. W: 4D tensor of $F{H}_w{W}_{w}C$. Y: 4D tensor of $N{H}_y{W}_{y}F$.       $vlStep$: vectorization size. Ensure:  $Y\Leftarrow conv2d(X,W)$ 1:for $n=0$ to $N-1$ do 2:    for $h_y=0$ to $H_y-1$ do 3:        for $w_y=0$ to $W_y-1$ do 4:           for $f=0$ to $F-1$ do 5:               $yVal\Leftarrow$ take a data from $Y[n,h_y,w_y,f]$ 6:               $c\Leftarrow 0$ 7:               while $c<(C-vlStep+1)$ do 8:                   for $h_w=0$ to $H_w-1$ do 9:                       $h_{new}\Leftarrow h_y+h_w$ 10:                       for $w_w=0$ to $W_w-1$ do 11:                          $w_{new}\Leftarrow w_y+w_w$ 12:                          $xVec\Leftarrow$ take a vector from $X[n,h_{new},w_{new},c]$ 13:                          $wVec\Leftarrow$ take a vector from $W[f,h_w,w_w,c]$ 14:                          $newVec\Leftarrow Mul(xVec,wVec)$ 15:                          $tmpVal\Leftarrow Reduction\left(newVec\right)$ 16:                          $yVal\Leftarrow Add(tmpVal,yVal)$ 17:                       end for 18:                   end for 19:                   $c\Leftarrow c+vlStep$ 20:               end while 21:               Tail-end processing 22:           end for 23:           Store $yVal$ to $Y[n,h_y,w_y,f]$ 24:        end for 25:    end for 26:  end for

• Lines 5–20: Compute an element of Y and store it back in the corresponding position.
• Lines 7 and 18: Accesses to Y occur outside the vectorized loop, a calculation that makes fewer multiple data accesses compared to the regular pass.
• Line 7: The dimension C uses a step size of vlStep.
• Lines 10–14: One computation of Conv2d is completed with slices of X and W as operands.
• Line 18: The tail processing of Conv2d vectorization is collapsed.

This approach not only enables vectorization but also reduces the number of element-wise Load and Store operations by $H_w\times W_w$ times each, as well as decreases the number of element-wise additions by $W_w$ times.

2.3. Specific Optimization

By analyzing the operands used by the Conv2d and Max Pooling operators at the Linalg dialect level for LeNet and ResNet, it can be observed that the sizes of the dimensions to be vectorized are not the same. The use of the same vectorization length in generic vectorization obviously sacrifices some of the performance. Therefore, it is possible to attempt to fold these dimensions that need to be vectorized, adaptively setting the vectorization length for each operation to the size of these dimensions. This approach is referred to as “Adaptation Vectorization” in this paper. The benefits of adaptive vectorization are as follows: (a) Each operator in the model can adaptively set an appropriate vectorization length. (b) The vectorization length is set more accurately, avoiding unnecessary computations caused by the mismatch between the amount of tail data and the vectorization length in general algorithms, thus eliminating the overhead of operations like $vector.maskloadop$ and $vector.maskstoreop$.

In order to collapse the dimension that needs to be vectorized, it is necessary to obtain the size c of this dimension during the MLIR generation process, set the vectorized length $vl$ from c, and cancel the tail-end processing. To avoid register overflow and cache misses that may occur when the channel dimension c is excessively large, we define $maxVl$, which indicates the maximum value of vectorized length, and the vectorization length $vl$ can be computed as follows:

$$vl=\left\{\begin{array}{cc}\lfloor {\displaystyle \frac{c}{2}}\rfloor \hfill & \mathrm{if}maxVl>0andc>maxVl\hfill \\ c\hfill & \mathrm{if}maxVl\le 0orc\le maxVl\hfill \end{array}\right.$$

3. Optimization Pipeline Construction

After determining the optimization strategy, the next step is to design the optimization pass and register it in the optimization tools provided by the Buddy Compiler for use in the optimization pipeline. Then both the regular optimization pipeline and the Vector dialect optimization pipeline are constructed. Since the LeNet model and its operators become lengthy when lowered to the Vector dialect level, this section will use the Conv2d operator as an example to introduce the process of building the optimization pipeline and present the optimized results.

3.1. Regular Optimization Pipeline

In the regular optimization pipeline, assuming an MLIR file composed of the Linalg dialect as the starting point for optimization, the dialect structures in the MLIR file will continuously change through successive transformations provided by the core passes in MLIR. As this process progresses, more computation details of the operators gradually emerge. Ultimately, the MLIR file, initially composed of the Linalg dialect, will be transformed into a file composed of the LLVM dialect, which can then be handed over to the LLVM backend for further backend optimization or execution.

Figure 3 presents an example of the optimization pipeline described above, showing the passes used in this process and the changes in the types of dialect used in the MLIR file.

The goal of this paper is to perform vectorization at the Vector dialect level, so we need to focus more on the MLIR file obtained after lowering with the $-convert-linalg-to-loops$ pass. The original operator $linalg.conv2dnhwcfhwcop$ was lowered from the Linalg dialect level to the Memref dialect level. (In fact, at this point, the MLIR file consists of the Arith, Affine, Scf, Func, and Memref dialects. However, for convenience, we use the dialect that best reflects this level of computation as a representative, and this approach will be used consistently throughout the paper.) At the Memref dialect level, more details of the Conv2d operator’s computation are exposed, such as the nested-loop order and the basic operators used in the computation. According to the implementation, at the Memref dialect level, the Conv2d operator performs element-wise computation.

3.2. Vectorization Optimization Pipeline

In order to perform vectorization at the Vector dialect level, it is necessary to first optimize the Matmul, Conv2d, and Max Pooling operators individually at the Linalg dialect level by using $-batchmatmul-optimize$, $-conv2d-nhwc-fhwc-vectorization$, and $-pooling-nhwc-max-vectorization$. After applying the vectorization pass to lower these three operators to the Vector dialect, the regular optimization pipeline continues to perform multilevel optimization across all dialects (the remaining operators that do not require vectorization are still lowered via the $-convert-linalg-to-loops$ pass). This process continues until the level of the LLVM dialect is reached.

However, since the Vector dialect is involved, an additional $-convert-vector-to-llvm$ pass is needed during the lowering process to lower the Vector-dialect-related operations to the LLVM dialect level. As shown in Figure 4, using the optimization of the Conv2d operator as an example, the sequence of all passes should follow this order.

After adding these two passes, the MLIR file obtained after optimizing the $-conv2d-nhwc-fhwc-vectorization$ pass and lowering the $-convert-linalg-to-loops$ pass is shown in Algorithm 2.

4. Results

In this section, we evaluate the performance of each operator under different vectorization lengths in Buddy-Benchmark, a benchmark module provided by the Buddy-MLIR project, and then take the best vectorization length of each operator to perform joint optimization. We further assess whether the optimized model incurs any significant accuracy degradation, subject to an error tolerance of 0.0001. A baseline optimization method is established, and both the proposed vectorization optimization and adaptive vectorization optimization are compared against this baseline.

4.1. Experimental Setup

Environmental Setup. The hardware platform used for the experiment is a dual-socket Intel Xeon Gold 5218R processor system. Each processor contains 20 physical cores and supports hyperthreading, providing a total of 80 logical processing threads. The maximum clock frequency of each core is 4.00 GHz, and the minimum clock frequency is 800 MHz. In terms of memory, the system is equipped with a three-level cache hierarchy: L1 cache of 1.3 MiB, L2 cache of 40 MiB, and L3 cache of 55 MiB.

Model and Data Configuration. Our research is based on the LeNet model, with an input tensor of size $1\times 1\times 28\times 28$. All elements of the tensor data are generated using a random number generator to produce random single-precision floating-point numbers (that is, of type f32) uniformly distributed between $0.0$ and $1.0$. For the Matmul, Conv2d, and Max Pooling operators, three sets of input tensors are configured for comparison experiments against the baseline.

LeNet and ResNet are optimized using the core passes provided by MLIR to generate an executable program. The execution time of the models is then collected as the baseline, referred to as the “Scalar,” and compared with the two vectorization optimization methods proposed in this paper.

4.2. LeNet Optimization Analysis

To isolate the impact of per-operator vectorization on LeNet’s inference latency, we conduct individual operator analyses. MatMul exclusively employs general vectorization, while Conv2D and Max Pooling undergo both general and adaptive vectorization approaches. Under controlled environmental conditions, we systematically increment vectorization lengths, apply corresponding optimizations, and measure pre/post-optimization latency. The LeNet inference results are presented in Figure 5.

As shown in Figure 5, all three vectorized operators exhibit a similar trend with increasing vectorization lengths. Inference latency initially decreases to an optimal point before gradually increasing. Compared to the baseline, vectorization significantly improves the computational efficiency of the MatMul operator while satisfying the specified error constraint. The increased vectorization scale enhances operator parallelism and reduces the loop count, leading to lower latency. However, excessively large vectorization scales introduce redundant computation and increased per-iteration overhead, offsetting these benefits and potentially causing performance degradation. The adaptive vectorization approach for MatMul and Max Pooling maintains optimal performance by consistently selecting the most efficient scale.

The optimal vectorization length for general vectorization varies between operators due to differing vectorization methods and operand sizes. Conv2D, with the highest computational complexity, shows the most significant improvement ($19.3\%$ latency reduction) at an optimal length of 4. MatMul achieves the next best improvement ($16.3\%$) at length 8. Max Pooling, which is inherently simpler, exhibits limited improvement; its optimal length fluctuates between 4, 8, and 16 in experiments, producing an average latency reduction of only $4.4\%$. In contrast, adaptive vectorization enables Conv2D and Max Pooling to achieve greater latency reductions of $28.1\%$ and $5.9\%$, respectively.

Applying the optimal vectorization length per operator (considering the three candidate lengths for Max Pooling), the data in Figure 6 show that, among the general methods, the LeNet inference latency is reduced to between 0.332 and 0.339 ms. This represents an average decrease of $26.7\%$ from the baseline. However, the adaptive vectorization method achieves a significantly lower latency reduction of $37.3\%$, substantially outperforming general vectorization. Moreover, all methods satisfy the error constraint without causing significant accuracy degradation in LeNet.

4.3. ResNet Optimization Analysis

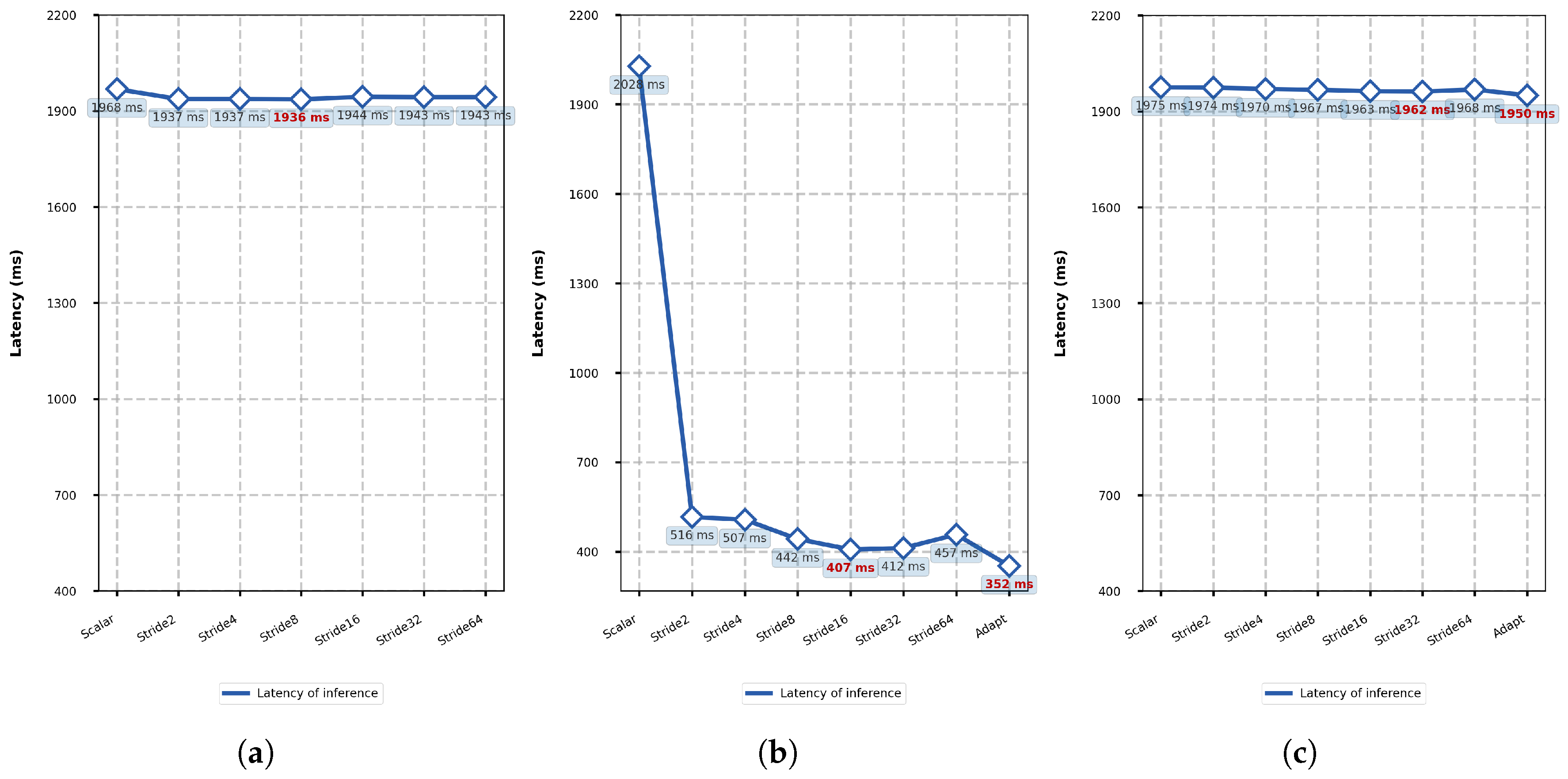
Compared to LeNet, ResNet has a greater model complexity. To evaluate the effects of MatMul, Conv2D, and Max Pooling vectorization on ResNet inference latency, controlled experiments were carried out under identical conditions. Each operator’s vectorization was applied individually with incremental vectorization lengths, and the pre/post-optimization latency was measured. Upon identifying the optimal vectorization scheme, we further evaluated changes in CPU usage time to analyze the corresponding impact on power consumption.

Figure 7 reveals that vectorizing MatMul and Max Pooling still accelerates ResNet inference relative to the baseline. However, MatMul vectorization exhibits no consistent pattern due to its single invocation with fixed dimensionality (1000), obscuring measurable trends. Max Pooling vectorization follows the characteristic decrease-then-increase curve, peaking at length 32. And lower inference latency is also obtained by going further with adapt vectorization. But they all contribute negligibly to overall optimization due to its single execution.

Compared to the baseline, the vectorization of Conv2D also accelerates model inference and causes the inference latency to first decrease and then increase as the vectorization size increases, and the optimal vectorization length for Conv2D is 16, which reduces the ResNet inference latency by $79.9\%$, decreases CPU resource utilization by $77.3\%$, and satisfies the error constraint. Meanwhile, the performance of Adapt vectorization is even better, reducing the ResNet inference latency by $80.5\%$ and CPU resource utilization by $83.5\%$, while also meeting the error constraint. The inference latency for all vectorization lengths tested is significantly lower than the benchmark level, indicating that the method is significantly optimized for ResNet. In addition, the optimized model significantly reduces CPU usage time, indicating that the proposed method not only accelerates inference but also reduces CPU power consumption. Since Conv2D is called 20 times in ResNet, its computational share is much greater than those of the other two operators and becomes the dominant factor in the inference latency. Consequently, joint operator optimization was not explored, which established Figure 7b results as conclusive.

5. Related Work

5.1. MLIR

MLIR is a flexible, reusable, and scalable infrastructure used for compiler construction [21]. It is a subproject of the LLVM project [22], with its key feature being multilevel intermediate representation, allowing transformations, optimizations, and code generation across different abstraction levels. MLIR aims to address the problem of software fragmentation, improve compilation for heterogeneous hardware, significantly reduce the cost of building domain-specific compilers, and help integrate existing compilers. MLIR provides a unified, scalable, multilevel intermediate representation for problem solving and optimization, as well as support for specific hardware systems. However, MLIR does not handle low-level operations such as register allocation and instruction scheduling, which are typically managed by the underlying optimizer, LLVM.

Through a hybrid intermediate representation, MLIR supports multiple and diverse requirements in a unified architecture, such as the ability to represent data flow graphs [23].

Proof. (Dialect).

MLIR uses dialects to define a uniform IR (intermediate representation) format, each with its own unique namespace [24], enables progressive lowering through Pass, and provides custom IR components to manage extensibility.    □

Proof. (Operations).

Operations, referred to as Ops, are the smallest semantic units in MLIR, and all computational logic (e.g., arithmetic operations, function calls) is modeled as Ops. Instead of presetting a fixed set of Ops, MLIR supports user-defined Ops through a dialect mechanism to support user-defined Ops [25].    □

Proof. (Pass).

Pass is the core mechanism in MLIR for implementing IR transformation and optimization, which is essentially an iterative reconstruction of the IR structure. IR is modified through a set of predefined rules, which can be used to perform the user-defined Pass.    □

5.2. Buddy MLIR

The Buddy-MLIR is a domain-specific compiler framework built on MLIR and RISC-V, aimed at creating a unified ecosystem to drive hardware–software co-design and optimize the compilation process from DSL (Domain-Specific Language) to DSA (Domain-Specific Architecture). MLIR [24] is an innovative multilevel intermediate representation and compiler architecture that provides reusable and scalable mechanisms. RISC-V [26] is an open-source instruction set architecture with a modular design and support for custom extensions. The combination of the two provides an ideal platform for hardware–software co-design, and their modularity and scalability lay a solid foundation for building this ecosystem.

The Buddy-MLIR consists of two main modules: the compiler module and the benchmark framework module. As shown in Figure 8, the compiler module is used to develop the compiler toolchain, while the benchmark framework module is used to evaluate domain-specific compilers and libraries. The compiler framework is based on the MLIR and LLVM backend tools, designed to build domain-specific compilers. This framework is divided into three parts: frontend, middle-end, and backend. The frontend primarily supports DSL (Domain-Specific Language); the middle-end focuses on domain-specific MLIR dialects, IR-level optimization, and automatic backend configuration mechanisms; and the backend focuses on hardware-specific code generation and the application of the MLIR toolchain. The benchmark framework is an extensible evaluation platform that is intended to test the performance of domain-specific compilers. It integrates Google’s benchmarking infrastructure and provides a unified benchmark by collecting domain-specific operators, models, and other cases, helping users evaluate the effectiveness of optimization methods or compilers. The benchmark framework works in conjunction with the compiler framework to assess the performance of the code generated by the compiler toolchain.

5.3. Operator Optimization

In the development of deep learning compilers, different systems have introduced distinctive intermediate representations (IRs) and optimization strategies tailored for operator-level optimization, aiming to improve model execution efficiency on specific hardware platforms.

TVM first converts models into a high-level IR known as Relay, which is subsequently transformed into a fine-grained low-level IR called a TIR. Execution of tensor operations is controlled via a set of abstract operations referred to as scheduling primitives, enabling a wide range of operator-level optimizations within TIR. Glow converts models into a domain-specific high-level IR, performs target-independent graph-level optimizations and then decomposes this IR into linear algebra primitives through node lowering. This is followed by target-specific optimizations and finally a transformation into a low-level instruction-based IR that supports memory-centric optimizations. TensorRT emphasizes hardware–software co-design in its operator optimization strategies. It utilizes internal IRs specifically designed for efficient inference on an NVIDIA GPU, delivering high-performance implementations—particularly for computationally intensive operators.

While these compilers adopt operator-centric optimization strategies around a fixed IR, MLIR offers a more generalized solution. Its multilevel IR framework enables optimization and code generation across different abstraction levels, thereby improving portability and reusability. As a result, compilers such as TVM and Glow can adopt MLIR as their underlying infrastructure, facilitating compatibility and the extension of existing optimization pipelines.

6. Conclusions

In this paper, we propose an approach based on the Buddy-MLIR framework that uses MLIR’s multilevel intermediate representation to lower operators from the Linalg dialect to the Vector dialect, enabling vectorization optimizations for Matmul, Conv2d, and Max Pooling operations. Building on this general vectorization optimization, we further introduce an adaptive vectorization technique. For general vectorization, applying vectorization with optimal vector sizes yields substantial performance gains for both LeNet and ResNet models. Moreover, the adaptive vectorization method surpasses the general approach, further demonstrating the effectiveness of vectorization in deep learning inference.

Future work will focus on the following areas:

• Based on the results obtained from the Conv2d and Max Pooling operators, the Matmul operator is also expected to benefit from adaptive vectorization and should therefore be further implemented and evaluated.
• The operators proposed in this paper have been tested only on LeNet and ResNet. To demonstrate the generality of the vectorization optimization designed in this paper, further testing will be conducted on more CNN models, and even models based on Transformer architectures.
• In the analysis of the results, the operand data format used by the operators in the LeNet model is $NHWC$, and the small size of the dimension C limits the optimization effect of the vectorization. In the future, we will attempt to change the operand data format of the operators in the LeNet model to $NCHW$, as the dimension W is more suitable for vectorization compared to the dimension C. An example of LeNet vectorization under the $NHWC$ data format is provided in Appendix A.1. Furthermore, changing the data format facilitates vectorization optimization for the Conv2D operator by overcoming the limitations introduced by $vector.reductionop$. A detailed analysis of the drawbacks of this operator is provided in Appendix A.2.