Improvement and Radiation-Resistance Study of an Optical Displacement Sensing System Based on a Position Sensitive Detector
Abstract
1. Introduction
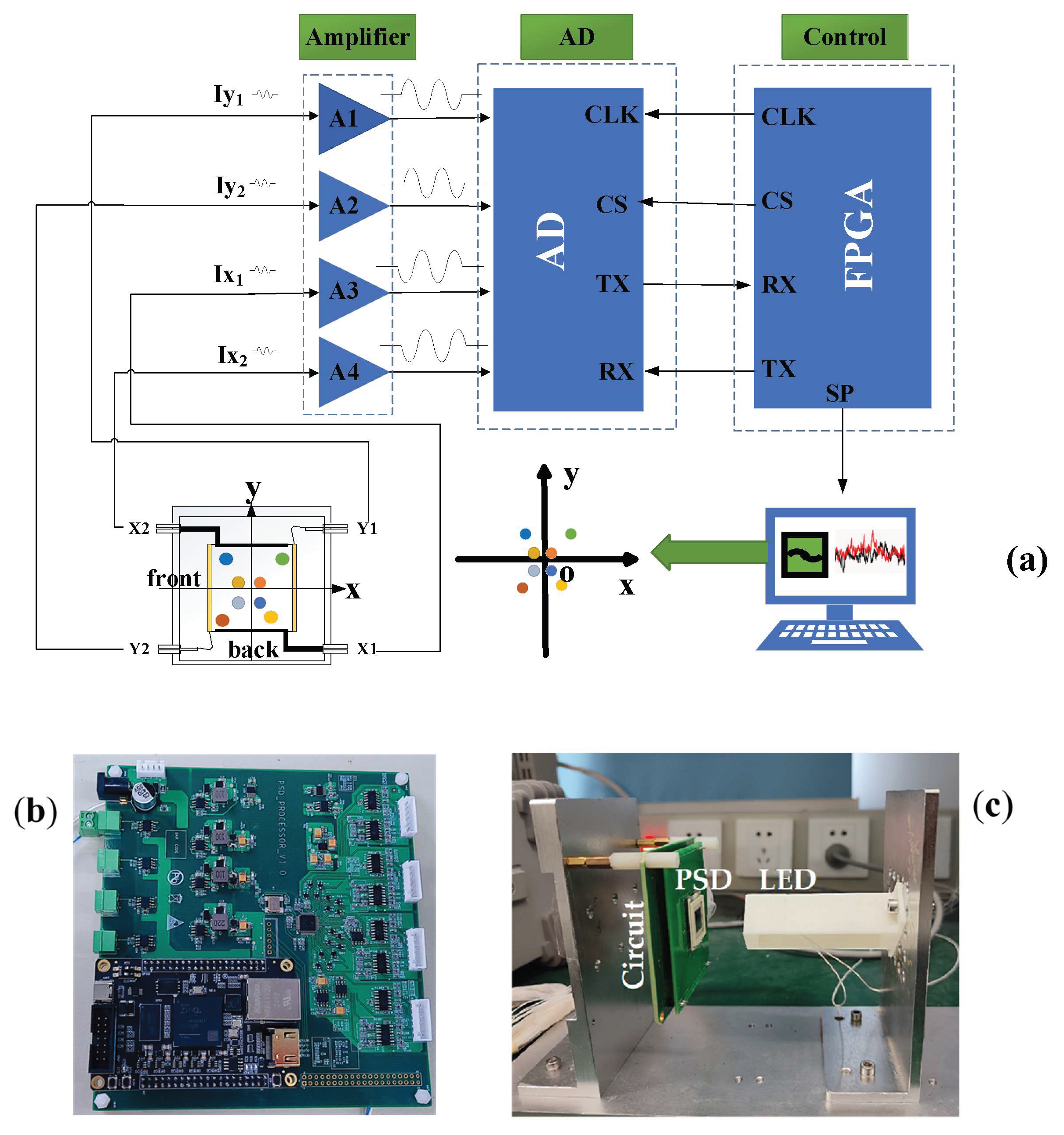
2. Methods
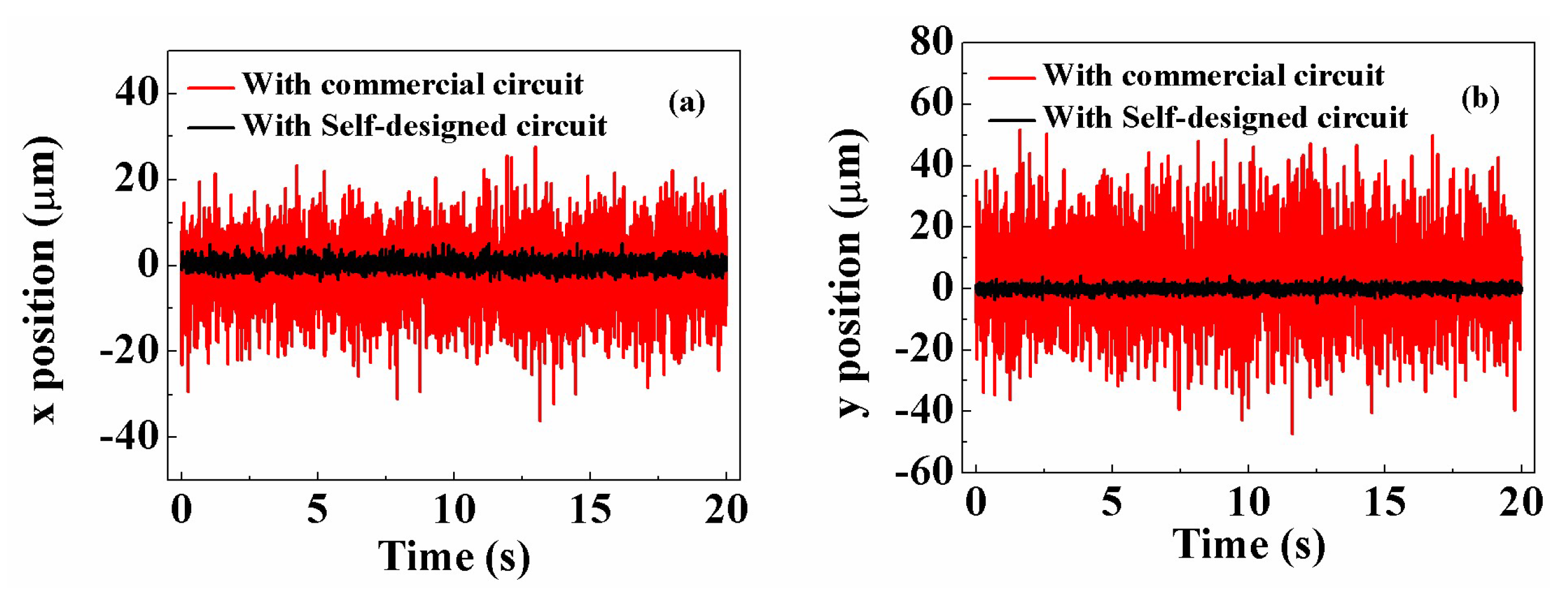
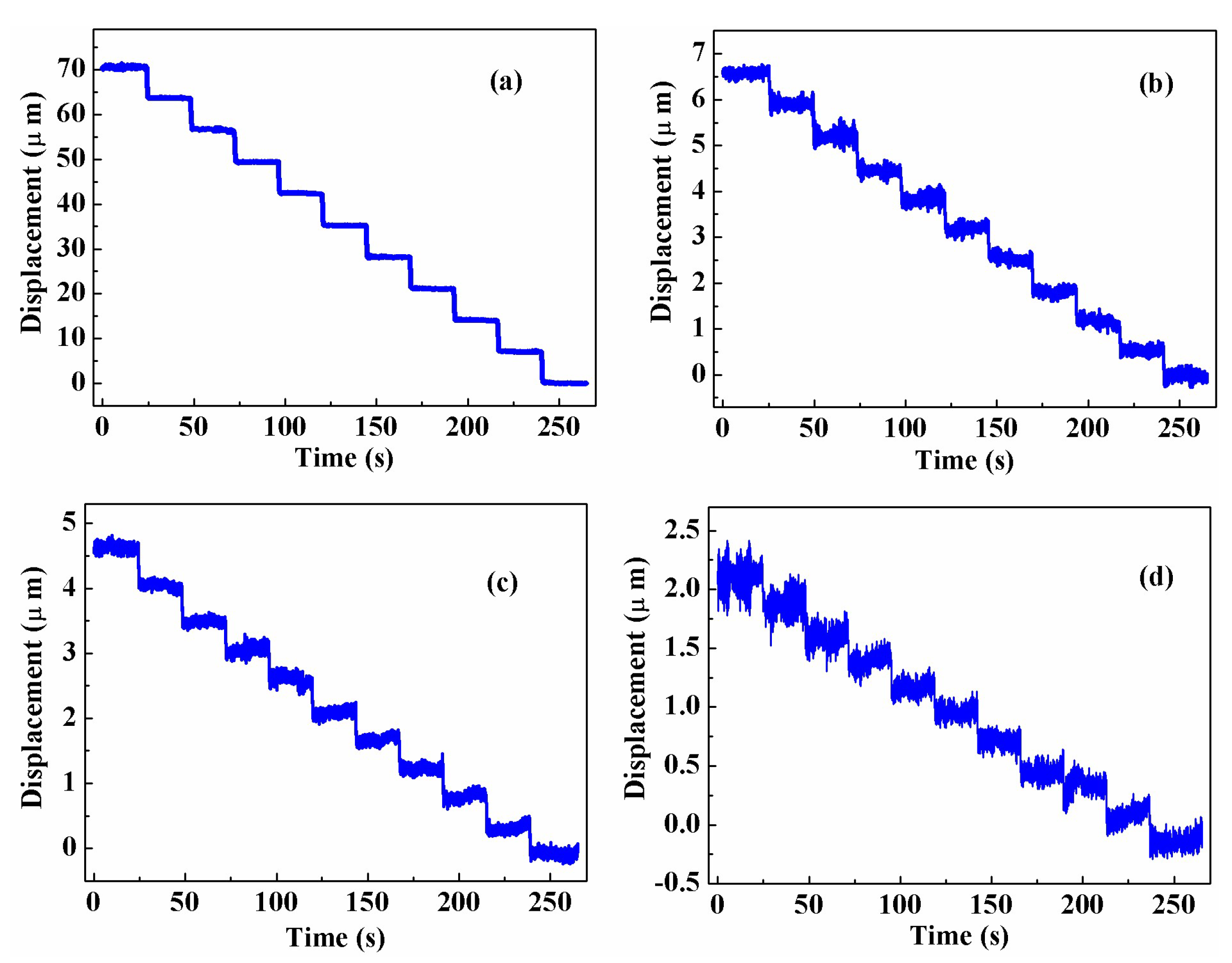
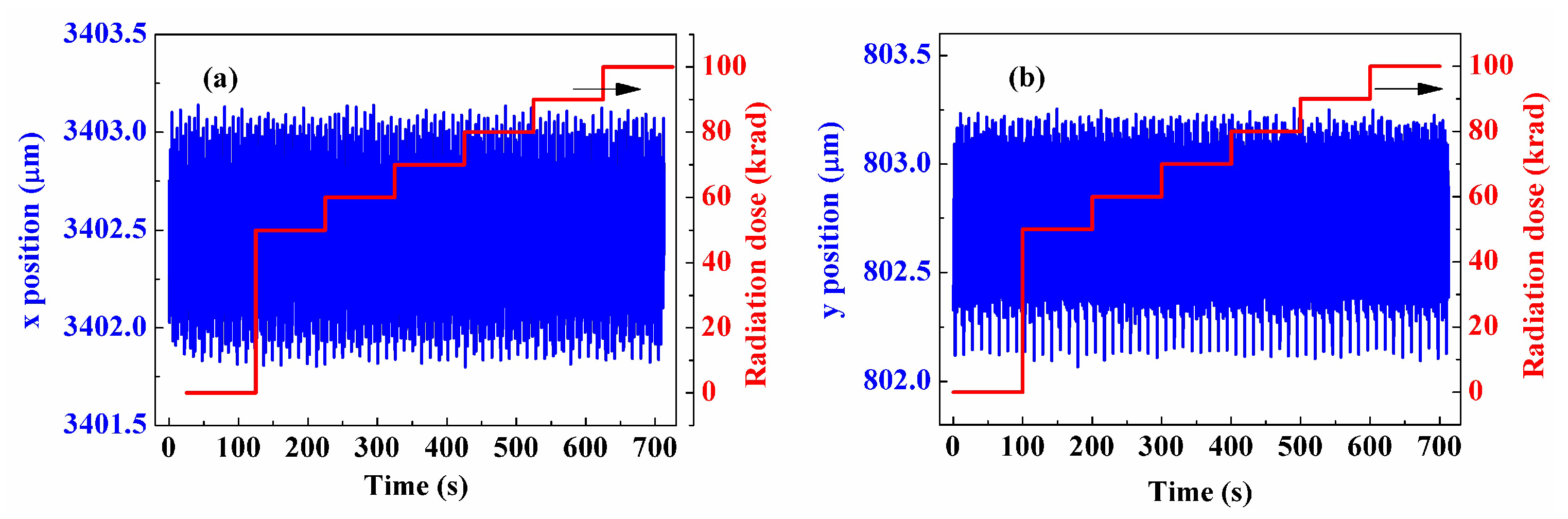
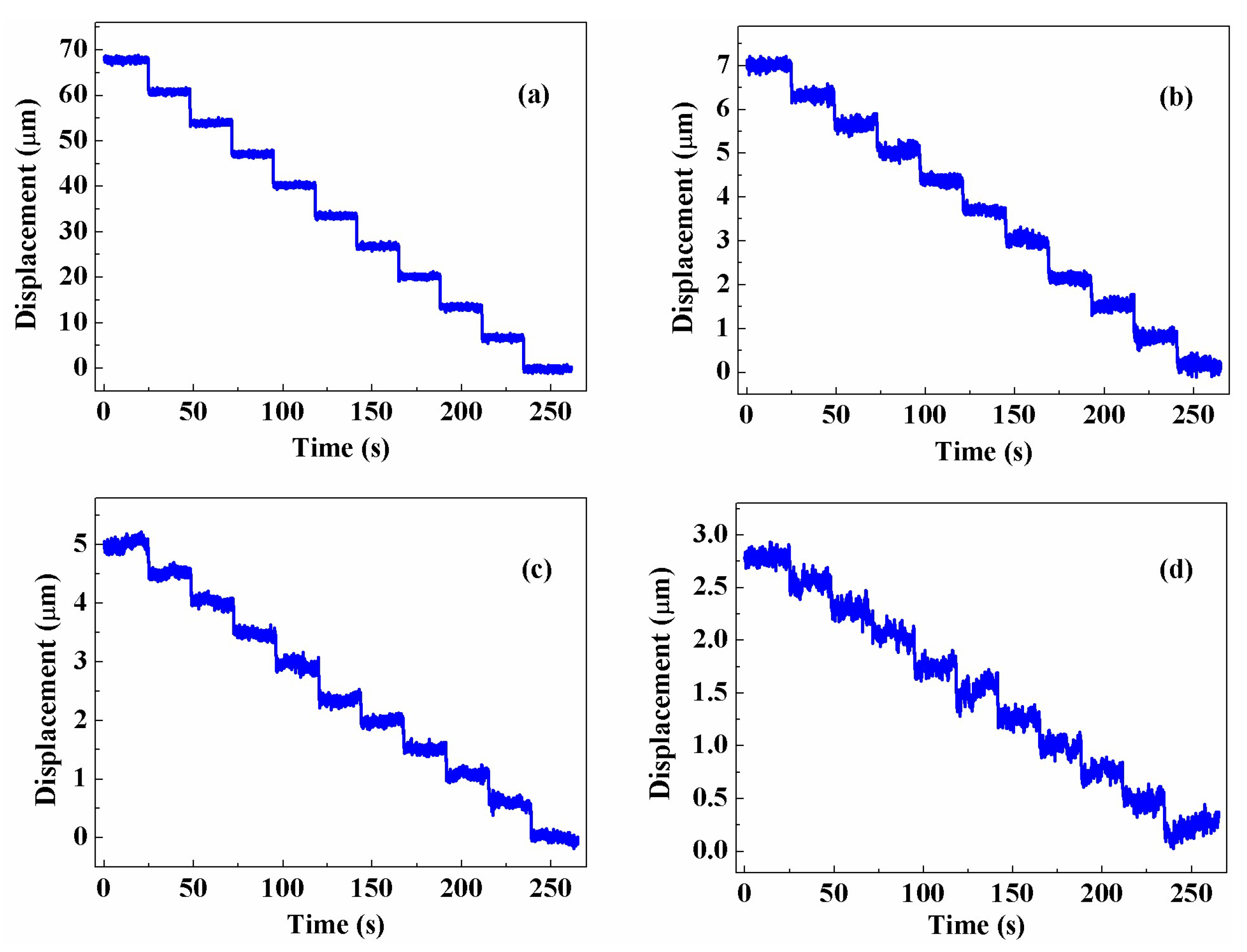
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Preumont, A. Active Damping, Vibration Isolation, and Shape Control of Space Structures: A Tutorial. Actuators 2023, 12, 122. [Google Scholar] [CrossRef]
- Liu, C.; Jing, X.; Daley, S.; Li, F. Recent advances in micro-vibration isolation. Mech. Syst. Signal Process. 2015, 56–57, 55–80. [Google Scholar] [CrossRef]
- Tu, H. An overview of the development of intelligent materials and active vibration isolation systems for vehicles. J. Phys. Conf. Ser. 2023, 2649, 012020. [Google Scholar] [CrossRef]
- Schmidt, R.H. Ultra-precision engineering in lithographic exposure equipment for the semiconductor industry. Philos. Trans. A Math. Phys. Eng. Sci. 2012, 370, 3950–3972. [Google Scholar] [CrossRef]
- Li, H.; Li, D.; Lou, Q.; Liu, C.; Lan, T.; Yu, X. Advancements in Optical Resonator Stability: Principles, Technologies, and Applications. Sensors 2024, 24, 6473. [Google Scholar] [CrossRef]
- Gong, W.; Li, A.; Huang, C.; Che, H.; Feng, C.; Qin, F. Effects and Prospects of the Vibration Isolation Methods for an Atomic Interference Gravimeter. Sensors 2022, 22, 583. [Google Scholar] [CrossRef]
- Yuan, Z.; Zhang, Z.; Zeng, L.; Li, X. Key technologies in active microvibration isolation systems: Modeling, sensing, actuation, and control algorithms. Measurement 2023, 222, 113658. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, X.; Wang, C.; Yan, R. Active vibration control technology in China. IEEE Instrum. Meas. Mag. 2022, 25, 36–44. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, X. A Review of Low-Frequency Active Vibration Control of Seat Suspension Systems. Appl. Sci. 2019, 9, 3326. [Google Scholar] [CrossRef]
- Meng, X.; Sun, S.; Yan, X.; Liu, F.; Cao, L.; Wang, Q.; Sun, Y. Six-Degree-of-Freedom Posture Measurement Technologies Using Position Sensitive Detectors (PSDs): State of the Art. Micromachines 2022, 13, 1903. [Google Scholar] [CrossRef]
- Yu, H.S.; Yu, N.C.; Rim, J.A.; Jo, M.J. Widely sensitive optical humidity module by using acrylic resin and a position sensitivity detector. Opt. Quantum Electron. 2020, 52, 469. [Google Scholar] [CrossRef]
- Zhou, G.; Li, L.; Zhou, Y.; Chen, X. High-Sensitivity Seawater Refraction Index Optical Measurement Sensor Based on a Position-Sensitive Detector. Sensors 2024, 24, 2050. [Google Scholar] [CrossRef]
- Zhou, G.; Liu, Q.; Wang, H.; Li, L.; Zhou, Y.; Chen, X. Optical Detection of Underwater Propeller Wake Based on a Position-Sensitive Detector. Photonics 2024, 11, 732. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, L.; Li, G.; Zheng, H.; Pang, C. High-Precision Main Shaft Displacement Measurement for Wind Turbines Using an Optimized Position-Sensitive Detector. Electronics 2024, 13, 5055. [Google Scholar] [CrossRef]
- Bello, V.; Bodo, E.; Merlo, S. Optical Identification of Parenteral Nutrition Solutions Exploiting Refractive Index Sensing. Sensors 2022, 22, 6815. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Y.; Wang, X.; Zhang, D.; Qin, L.; Liu, J.; Li, M.; Liu, J.C. Field calibration method for industrial robots based on single position sensitive device. IEEE Trans. Instrum. Meas. 2023, 72, 7506112. [Google Scholar] [CrossRef]
- Blank, S.; Shen, Y.; Xi, N.; Zhang, C.; Wejinya, U.C. High precision PSD guided robot localization: Design, mapping, and position control. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 52–57. [Google Scholar]
- Fortunato, E.; Lavareda, G.; Martins, R.; Soares, F.; Fernandes, L. Large-area 1D thin-film position-sensitive detector with high detection resolution. Sens. Actuators A Phys. 1995, 51, 135–142. [Google Scholar] [CrossRef]
- Hu, C.; Wang, X.; Song, B. High-performance position-sensitive detector based on the lateral photoelectrical effect of two-dimensional materials. Light Sci. Appl. 2020, 9, 88. [Google Scholar] [CrossRef]
- Wang, W.; Lu, J.; Ni, Z. Position-sensitive detectors based on two-dimensional materials. Nano Res. 2020, 14, 1889–1900. [Google Scholar] [CrossRef]
- Jiang, H.; Fu, J.; Nie, C.; Sun, F.; Tang, L.; Sun, J.; Meng, Z.; Shen, J.; Feng, S.; Shi, H.; et al. Gate modulation enhanced position-sensitive detectors using graphene/silicon-on-insulator structure. Carbon 2021, 184, 445–451. [Google Scholar] [CrossRef]
- Song, H.X.; Wang, X.D.; Ma, L.Q.; Cai, M.Z.; Cao, T.Z. Design and Performance Analysis of Laser Displacement Sensor Based on Position Sensitive Detector (PSD). J. Phys. Conf. Ser. 2006, 48, 217–222. [Google Scholar] [CrossRef]
- Rahimi, M.; Luo, Y.; Harris, F.C.; Dascalu, S.M.; Shen, Y. Improving measurement accuracy of position sensitive detector (PSD) for a new scanning PSD microscopy system. In Proceedings of the 2014 IEEE International Conference on Robotics and Biomimetics (ROBIO 2014), Bali, Indonesia, 5–10 December 2014; pp. 1685–1690. [Google Scholar]
- Sun, S.; Zheng, Q.; Meng, X.; Sun, P.; Liu, F.; Cao, L. High positional resolution pin-cushion position sensitive detector by deliberately introducing barrel distortion. IEEE Sens. J. 2021, 22, 1280–1286. [Google Scholar] [CrossRef]
- Narayanan, C.; Buckman, A.B.; Busch-Vishniac, I. Noise analysis for position-sensitive detectors. IEEE Trans. Instrum. Meas. 1997, 46, 1137–1144. [Google Scholar] [CrossRef]
- Ivan, I.A.; Ardeleanu, M.; Laurent, G.J. High dynamics and precision optical measurement using a position sensitive detector (PSD) in reflection-mode: Application to 2D object tracking over a Smart Surface. Sensors 2012, 12, 16771–16784. [Google Scholar] [CrossRef]
- Geng, L.; Cao, G.; Shang, C.; Ding, H. Absolute Photoelectric Encoder Based on Position-Sensitive Detector Sensor. Electronics 2024, 13, 1446. [Google Scholar] [CrossRef]
- Xie, L.Q.; Song, H.B.; Wang, P.C.; Zhang, Y.F.; Gu, H.C.; Liu, X.G. Dosimetry of a 3-5 MeV linear electron accelerator for radiation processing. In Proceedings of the 6th Japan-China bilateral symposium on radiation chemistry, Tokyo, Japan, 6–11 November 1994; pp. 338–343. [Google Scholar]
- SiTek Electro Optics. Available online: https://www.sitek.se/ (accessed on 11 August 2025).
- Hamamatsu Photon Is Our Business. Available online: https://www.hamamatsu.com/us/en/product/optical-sensors/distance-position-sensor/psd/psd-circuit.html (accessed on 11 August 2025).



| SPC02 Circuit | Self-Designed Circuit | |
|---|---|---|
| Noise voltage | 3 mV | 0.1 mV |
| Bandwidth | 400 kHz | 5 MHz |
| Dimension (Amplification part) | 21 mm × 21 mm | 33 mm × 33 mm |
| Operating temperature | 70 °C maximum | −40~125 °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, X.; Chen, G.; Yu, M.; Zheng, T.; Ding, K.; Chen, H.; Yan, Z.; Xiao, A. Improvement and Radiation-Resistance Study of an Optical Displacement Sensing System Based on a Position Sensitive Detector. Appl. Sci. 2025, 15, 9383. https://doi.org/10.3390/app15179383
Ren X, Chen G, Yu M, Zheng T, Ding K, Chen H, Yan Z, Xiao A. Improvement and Radiation-Resistance Study of an Optical Displacement Sensing System Based on a Position Sensitive Detector. Applied Sciences. 2025; 15(17):9383. https://doi.org/10.3390/app15179383
Chicago/Turabian StyleRen, Xiaojing, Guansheng Chen, Mengxi Yu, Tuo Zheng, Kai Ding, Huiyuan Chen, Zhanyuan Yan, and Aimin Xiao. 2025. "Improvement and Radiation-Resistance Study of an Optical Displacement Sensing System Based on a Position Sensitive Detector" Applied Sciences 15, no. 17: 9383. https://doi.org/10.3390/app15179383
APA StyleRen, X., Chen, G., Yu, M., Zheng, T., Ding, K., Chen, H., Yan, Z., & Xiao, A. (2025). Improvement and Radiation-Resistance Study of an Optical Displacement Sensing System Based on a Position Sensitive Detector. Applied Sciences, 15(17), 9383. https://doi.org/10.3390/app15179383






