Dictionary Learning-Based Data Pruning for System Identification
Abstract
1. Introduction
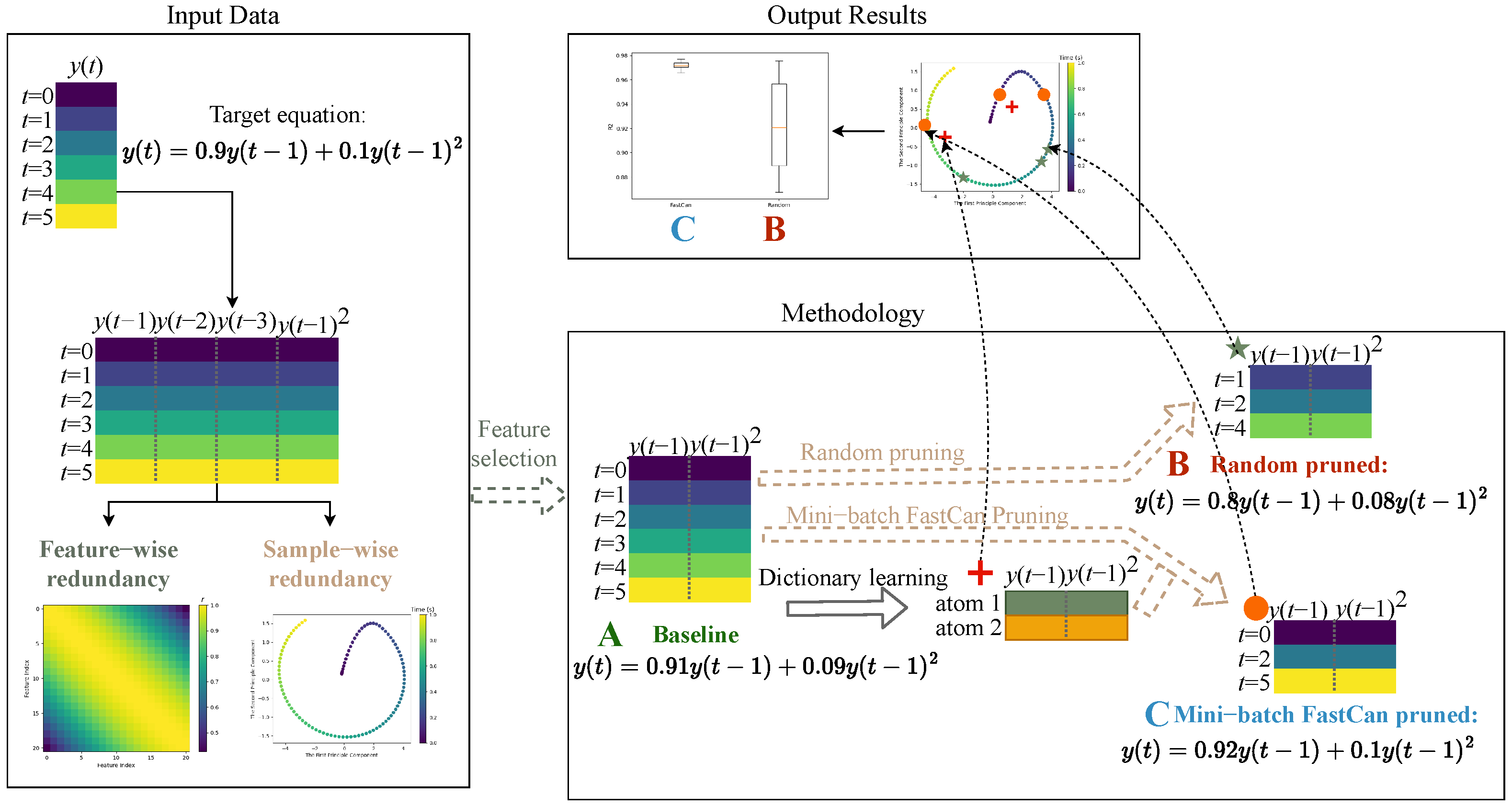
2. Methodology
2.1. Reduced Polynomial NARX
2.2. Data Pruning with Mini-Batch FastCan
| Algorithm 1: Mini-batch FastCan | ||||||
| Input: ; | ▹ Sample matrix | |||||
| ; | ▹ Number of atoms in a dictionary | |||||
| ; | ▹ Batch size; Optional | |||||
| ; | ▹ Number of samples to select | |||||
| Output: ; | ▹ Selected indices | |||||
| Step 1: | ||||||
| Apply the k-means-based dictionary learning [29] to with q clusters; | ||||||
| The resulting q cluster centres form the columns of a dictionary ; | ||||||
| ▹ Target matrix | ||||||
| Step 2: | ||||||
| if p is not specified or then | ||||||
| Set ; | ||||||
| if then | ||||||
| Set ; | ||||||
| Step 3: | ||||||
| Generate the batch matrix , where , and ; | ||||||
| Step 4: | ||||||
| Initialize the candidate sample matrix and the target matrix ; | ||||||
| for to q do | ||||||
| Let ; | ||||||
| for to t do | ||||||
| Select samples from by using the canonical-correlation-based fast selection method [21], with serving as the target vector | ||||||
| Append the indices of the selected samples to ; | ||||||
| Remove the selected samples from the candidate matrix ; | ||||||
| return s; | ||||||
3. Numerical Case Studis
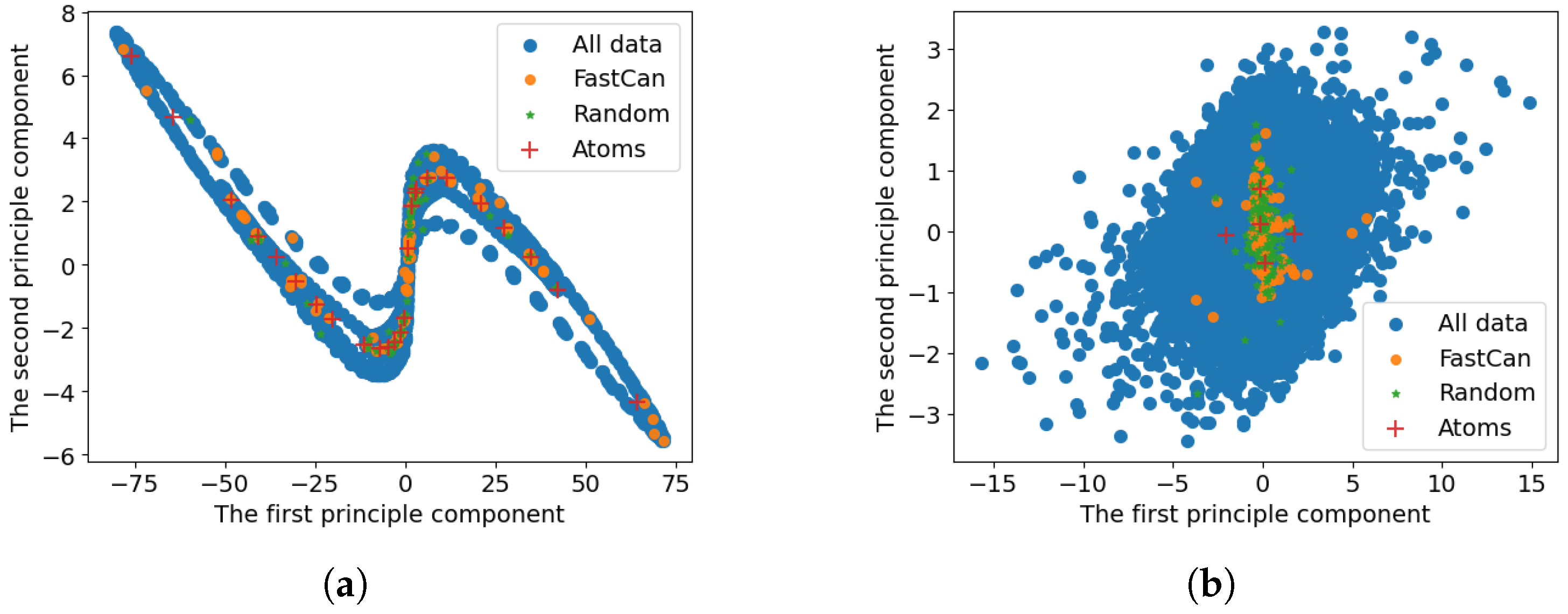
3.1. Visualisation of Sample Redundancy in System Identification
3.2. Data with Dual Stable Equilibria
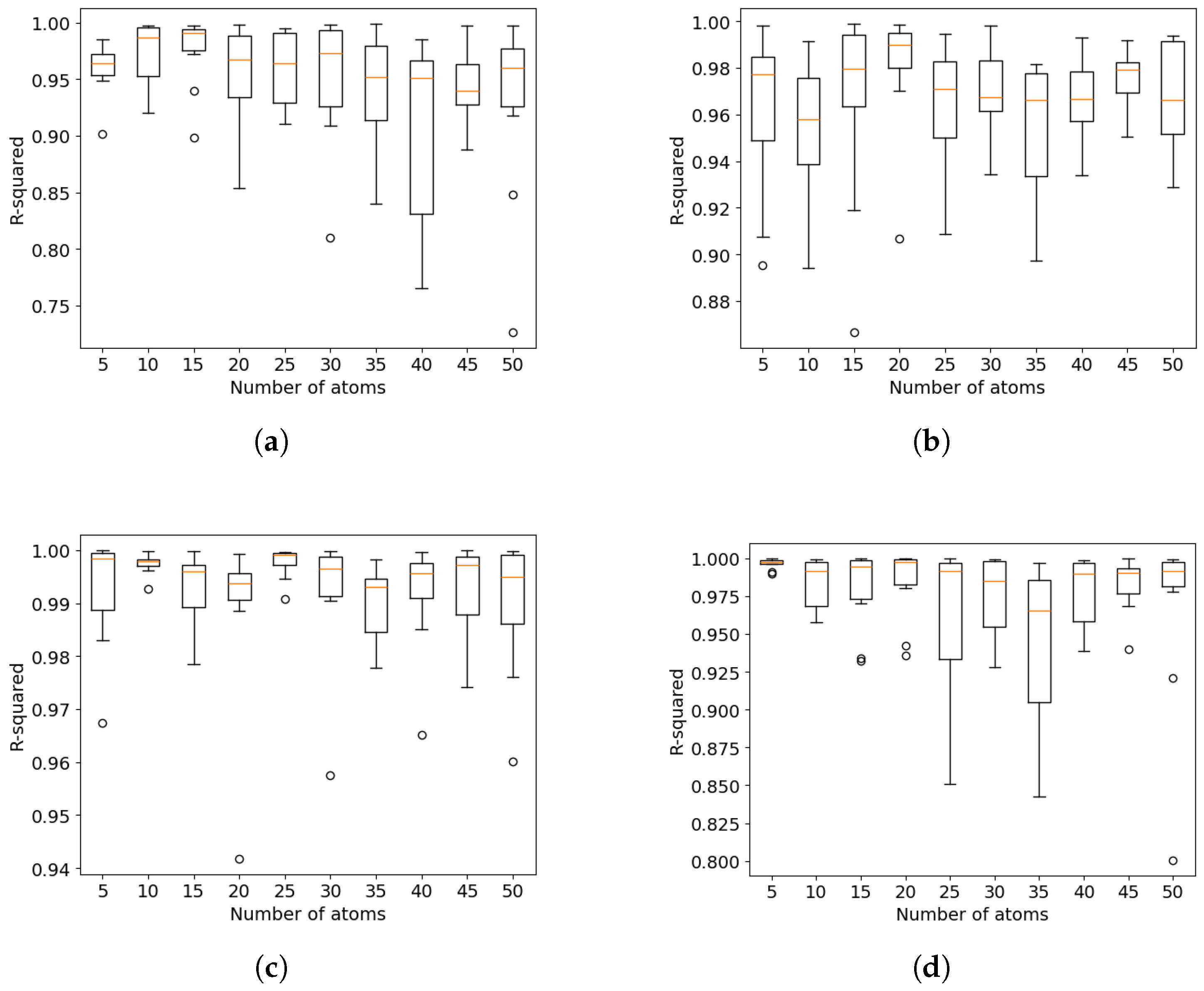
4. Case Studies on the Benchmark Datasets
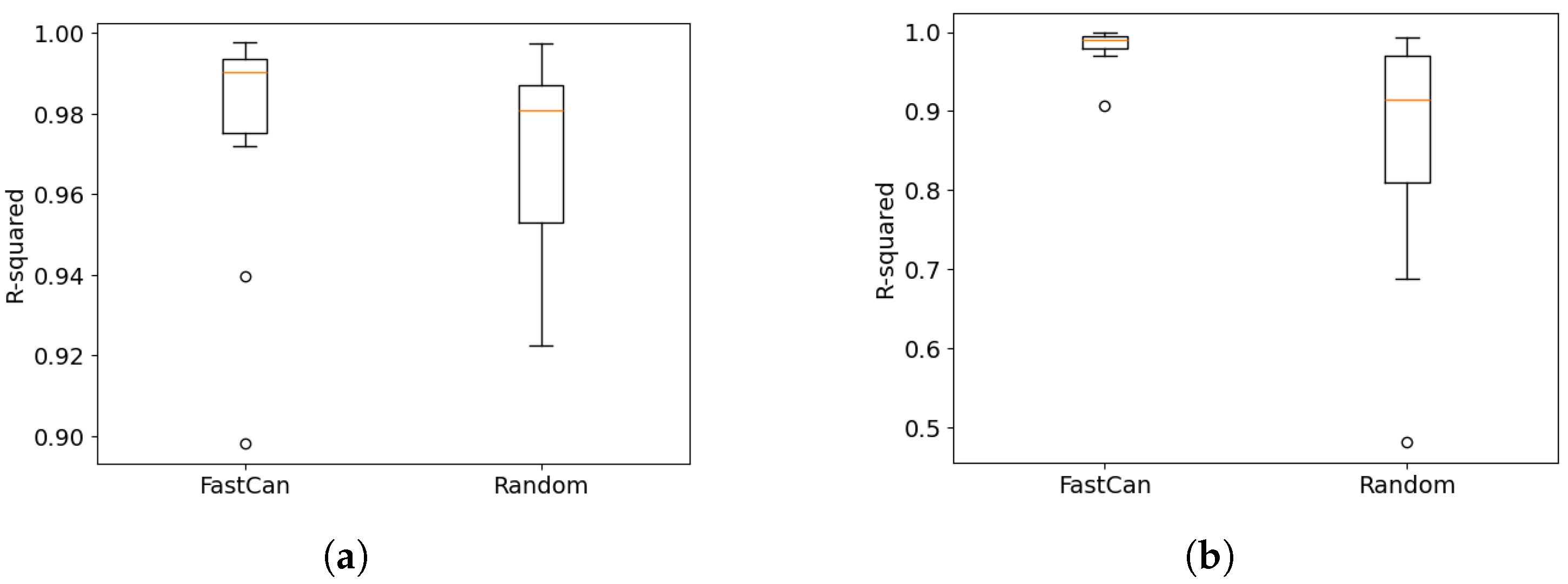
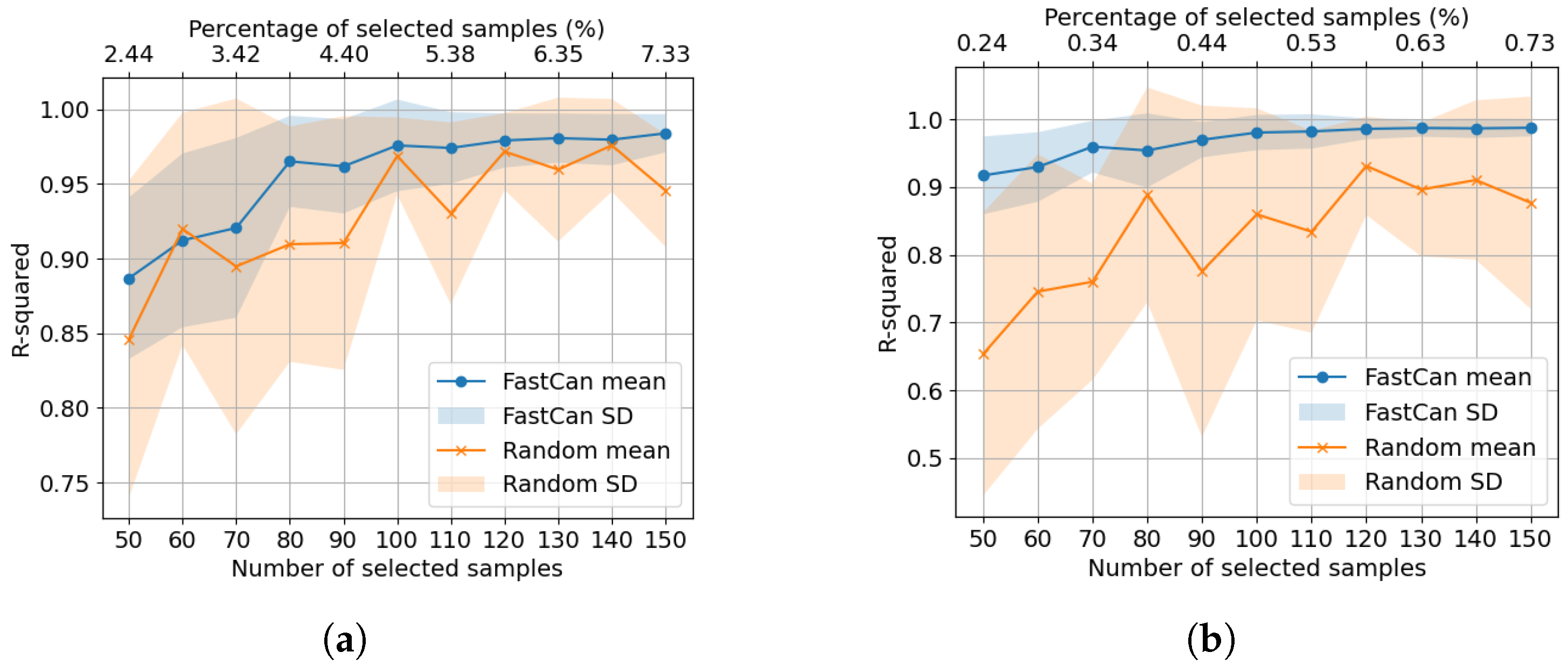
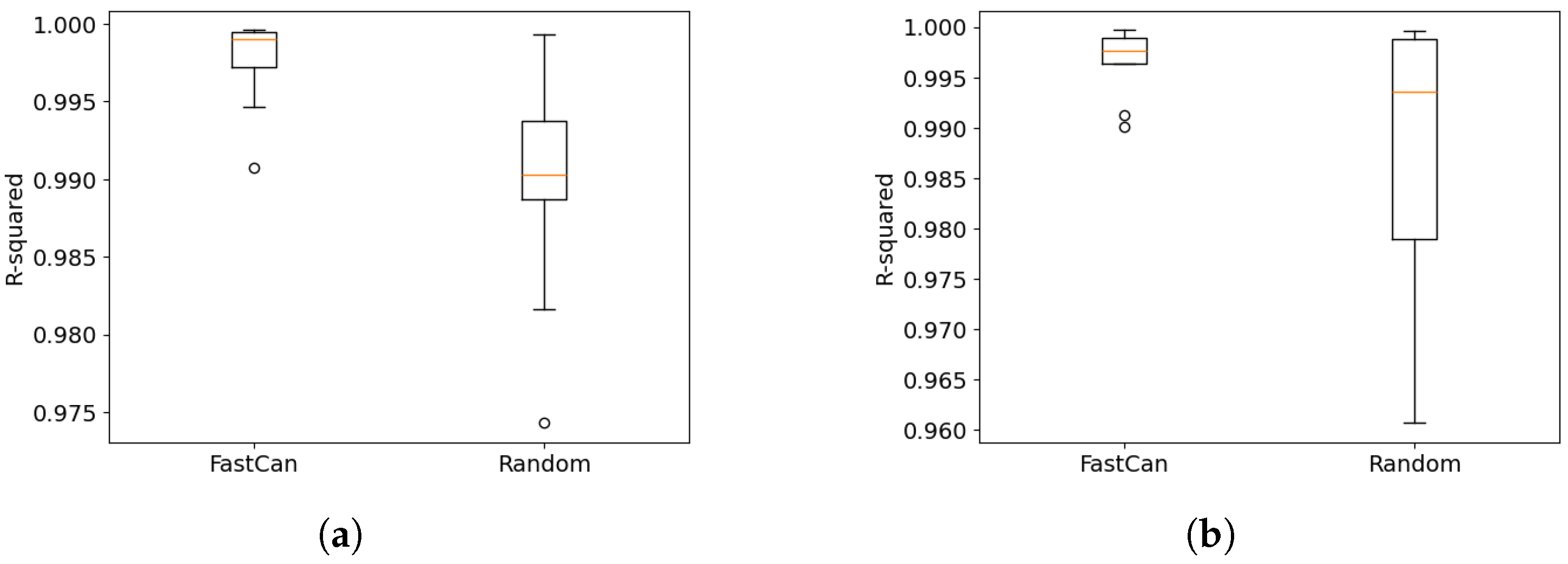
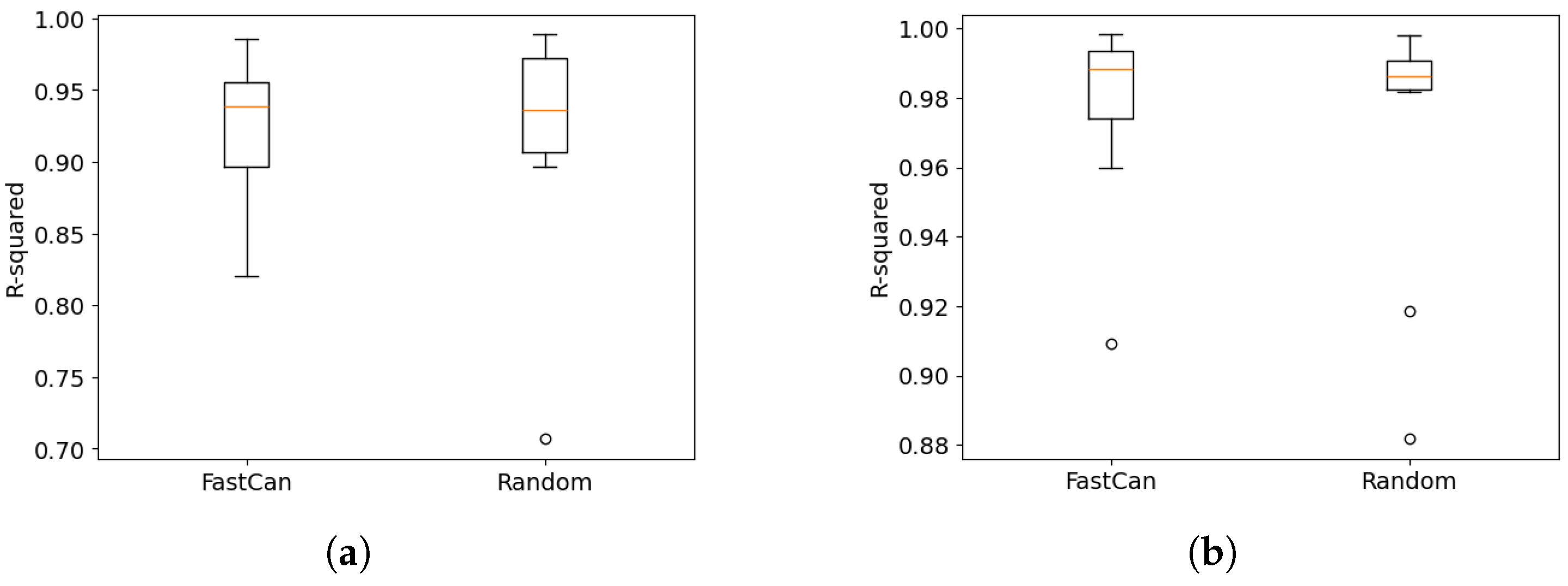
4.1. Data from the Electro-Mechanical Positioning System
4.2. Data from the Wiener–Hammerstein System
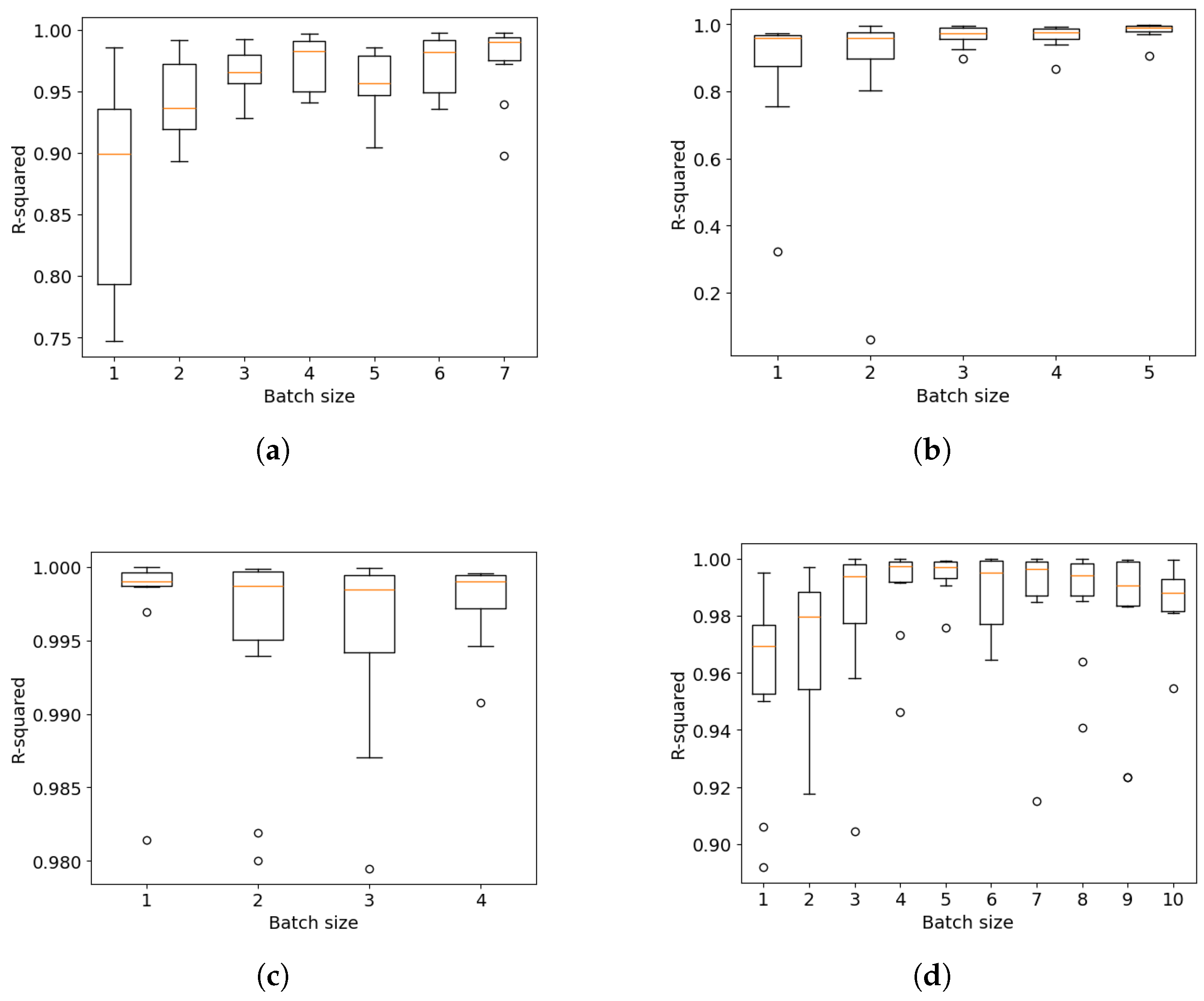
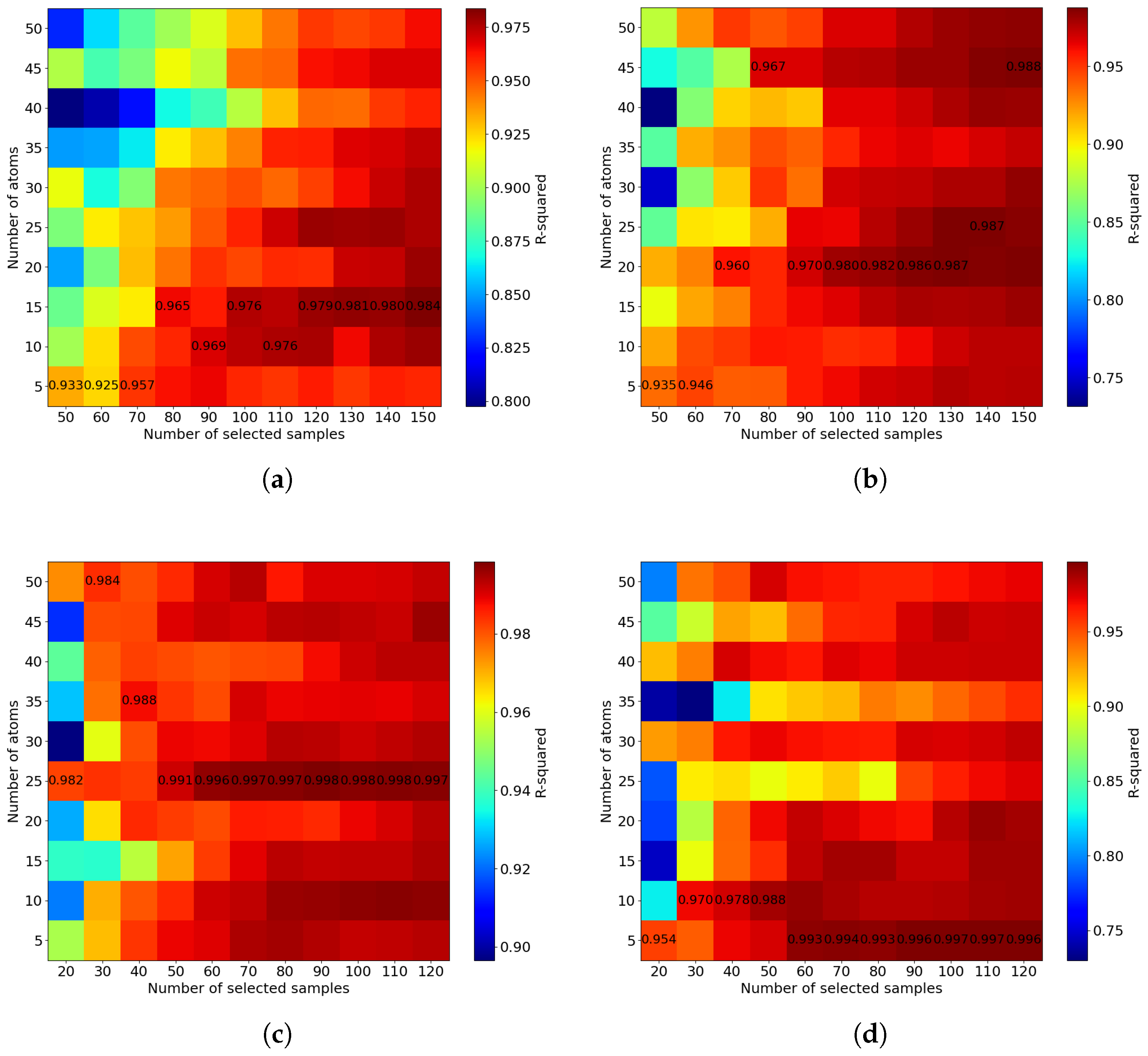
5. The Effect of Hyperparameters on the Mini-Batch FastCan Method
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| NARX | Nonlinear autoregressive with eXogenous inputs |
| FastCan | Fast selection method based on canonical correlation |
| PCA | Principal component analysis |
| SDSE | Symmetrical dual-stable equilibria |
| ADSE | Asymmetrical dual-stable equilibria |
| EMPS | Electro-mechanical positioning system |
| WHS | Wiener–Hammerstein system |
Appendix A. Prediction Performance of Baseline NARX
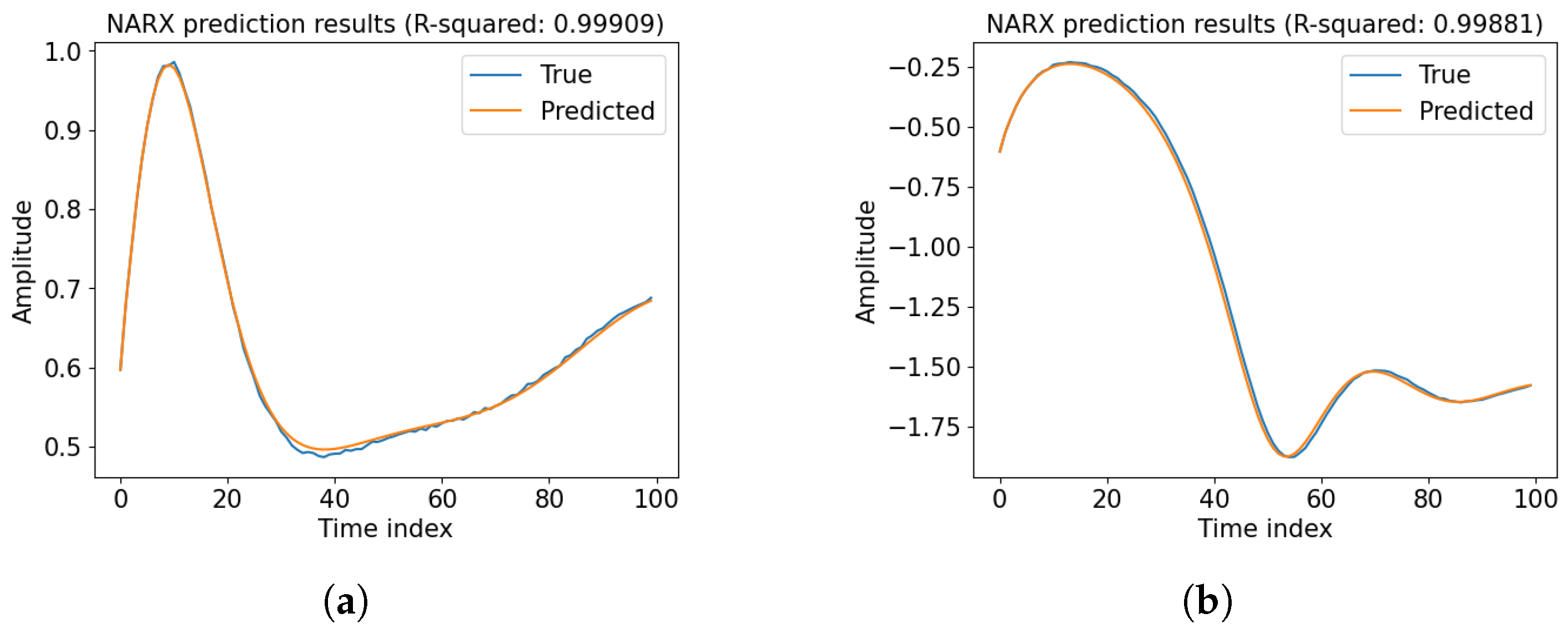
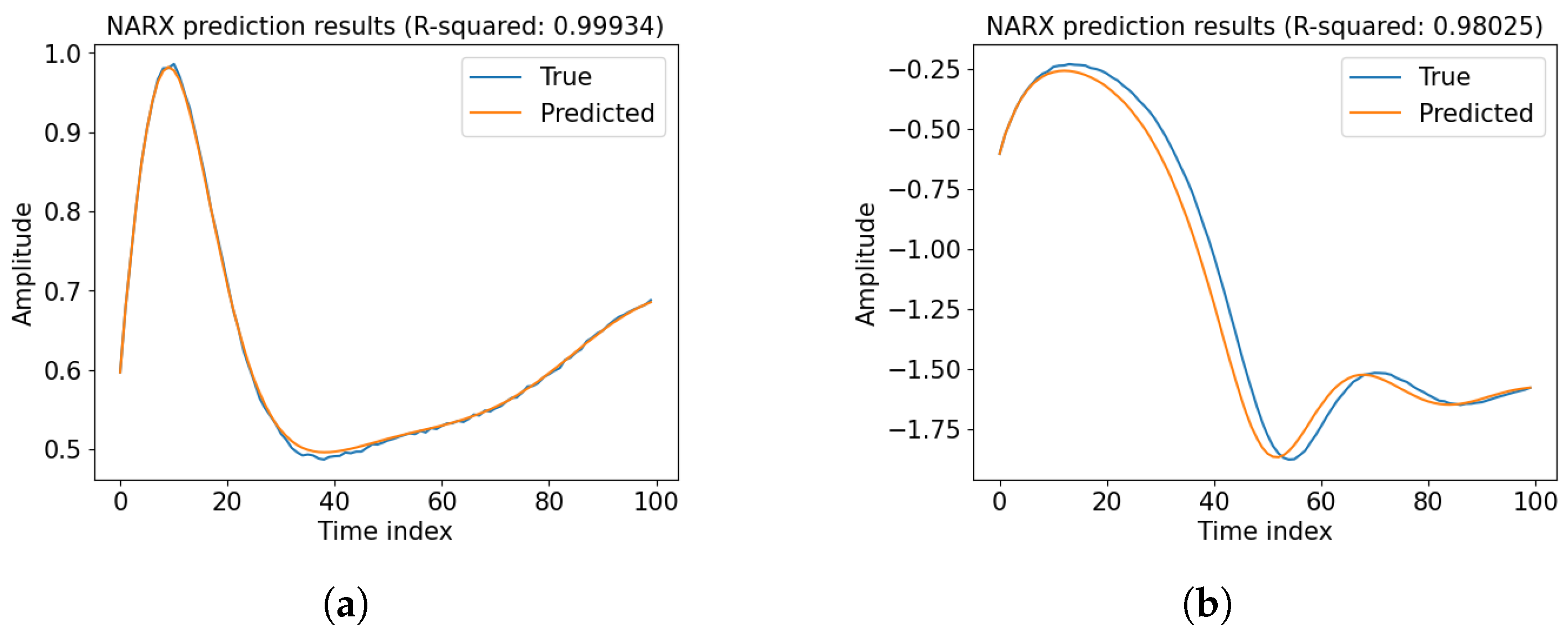

References
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control, 5th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015; Chapter 1; pp. 1–2. [Google Scholar]
- Billings, S.A. Nonlinear System Identification: NARMAX Methods in the Time, Frequency, and Spatio-Temporal Domains; John Wiley & Sons, Ltd.: West Sussex, UK, 2013; Chapter 1; pp. 9–10. [Google Scholar]
- Nelles, O. Nonlinear System Identification: From Classical Approaches to Neural Networks and Fuzzy Models; SpringerLink: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Miller, W.T.; Sutton, R.S.; Werbos, P.J. Neural Networks for Control; The MIT Press: London, UK, 1990. [Google Scholar]
- Jenkins, G.M.; Watts, D.G. Spectral Analysis and Its Applications; Holden-Day, Inc.: San Francisco, CA, USA, 1968. [Google Scholar]
- Schetzen, M. The Volterra and Wiener Theories of Nonlinear Systems; John Wiley & Sons Inc.: New York, NY, USA, 1980. [Google Scholar]
- Chen, S.; Billings, S.A. Representations of non-linear systems: The NARMAX model. Int. J. Control 1989, 49, 1013–1032. [Google Scholar] [CrossRef]
- Kukreja, S.L.; Galiana, H.L.; Kearney, R.E. NARMAX representation and identification of ankle dynamics. IEEE Trans. Biomed. Eng. 2003, 50, 70–81. [Google Scholar] [CrossRef] [PubMed]
- Boynton, R.; Balikhin, M.; Wei, H.; Lang, Z. Applications of NARMAX in space weather. In Machine Learning Techniques for Space Weather; Elsevier: Amsterdam, The Netherlands, 2018; pp. 203–236. [Google Scholar]
- Korenberg, M.; Billings, S.A.; Liu, Y.; McIlroy, P. Orthogonal parameter estimation algorithm for non-linear stochastic systems. Int. J. Control 1988, 48, 193–210. [Google Scholar] [CrossRef]
- Chen, S.; Billings, S.A.; Luo, W. Orthogonal least squares methods and their application to nonlinear system identification. Int. J. Control 1989, 50, 1873–1896. [Google Scholar] [CrossRef]
- Hong, X.; Mitchell, R.J.; Chen, S.; Harris, C.J.; Li, K.; Irwin, G.W. Model selection approaches for non-linear system identification: A review. Int. J. Syst. Sci. 2008, 39, 925–946. [Google Scholar] [CrossRef]
- Goodwin, G.C. Optimal input signals for nonlinear-system identification. Proc. Inst. Electr. Eng. 1971, 118, 922–926. [Google Scholar] [CrossRef]
- Mehra, R. Optimal inputs for linear system identification. IEEE Trans. Autom. Control 1974, 19, 192–200. [Google Scholar] [CrossRef]
- Raju, R.S.; Daruwalla, K.; Lipasti, M. Accelerating deep learning with dynamic data pruning. arXiv 2021, arXiv:2111.12621. [Google Scholar] [CrossRef]
- Sorscher, B.; Geirhos, R.; Shekhar, S.; Ganguli, S.; Morcos, A.S. Beyond neural scaling laws: Beating power law scaling via data pruning. Adv. Neural Inf. Process. Syst. 2022, 35, 19523–19536. [Google Scholar]
- Yang, Z.; Yang, H.; Majumder, S.; Cardoso, J.; Gallego, G. Data pruning can do more: A Comprehensive data pruning approach for object re-identification. arXiv 2024, arXiv:2412.10091. [Google Scholar] [CrossRef]
- Marion, M.; Üstün, A.; Pozzobon, L.; Wang, A.; Fadaee, M.; Hooker, S. When less is more: Investigating data pruning for pretraining LLMs at scale. arXiv 2023, arXiv:2309.04564. [Google Scholar] [CrossRef]
- Jin, R.; Xu, Q.; Wu, M.; Xu, Y.; Li, D.; Li, X.; Chen, Z. LLM-based knowledge pruning for time series data analytics on edge-computing devices. arXiv 2024, arXiv:2406.08765. [Google Scholar]
- Zhang, S.; Lang, Z.Q. Orthogonal least squares based fast feature selection for linear classification. Pattern Recognit. 2022, 123, 108419. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, T.; Worden, K.; Sun, L.; Cross, E.J. Canonical-correlation-based fast feature selection for structural health monitoring. Mech. Syst. Signal Process. 2025, 223, 111895. [Google Scholar] [CrossRef]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Mairal, J.; Bach, F.; Ponce, J. Task-driven dictionary learning. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 34, 791–804. [Google Scholar] [CrossRef] [PubMed]
- Vu, T.H.; Monga, V. Fast low-rank shared dictionary learning for image classification. IEEE Trans. Image Process. 2017, 26, 5160–5175. [Google Scholar] [CrossRef] [PubMed]
- Ayed, F.; Hayou, S. Data pruning and neural scaling laws: Fundamental limitations of score-based algorithms. arXiv 2023, arXiv:2302.06960. [Google Scholar] [CrossRef]
- Janot, A.; Gautier, M.; Brunot, M. Data set and reference models of EMPS. In Proceedings of the Nonlinear System Identification Benchmarks, Eindhoven, The Netherlands, 10–12 April 2019. [Google Scholar]
- Schoukens, J.; Ljung, L. Wiener-Hammerstein Benchmark; Technical Report; Linköping University Electronic Press: Linköping, Sweden, 2009. [Google Scholar]
- Billinge, S. bg-mpl-stylesheets. 2024. Available online: https://github.com/Billingegroup/bg-mpl-stylesheets (accessed on 21 July 2025).
- Sculley, D. Web-scale k-means clustering. In Proceedings of the 19th International Conference on World Wide Web, Raleigh, NC, USA, 26–30 April 2010; pp. 1177–1178. [Google Scholar]
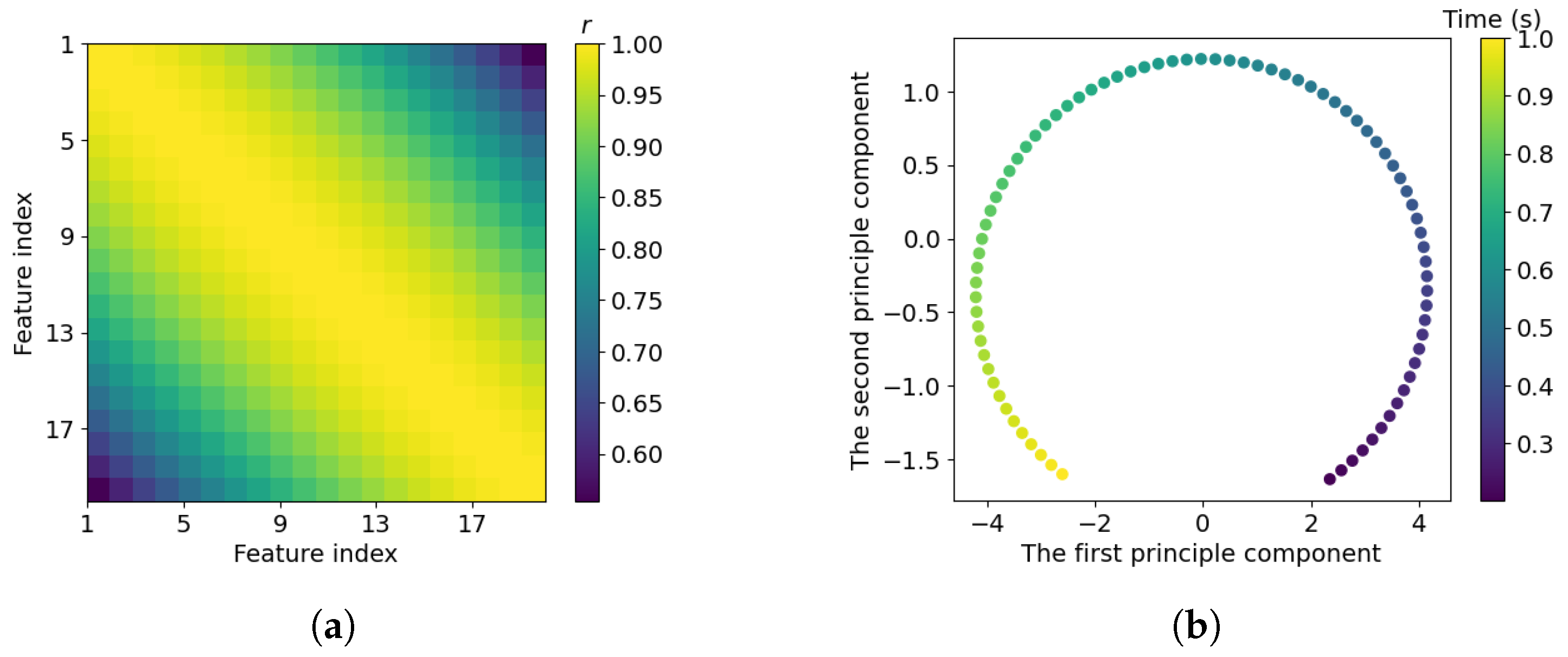



| t (s) | y(t − Δt) | y(t − 2Δt) | y(t − 3Δt) | … | y(t − 20Δt) |
|---|---|---|---|---|---|
| 0 | NaN | NaN | NaN | … | NaN |
| 0.01 | 0.000 | NaN | NaN | … | NaN |
| 0.02 | 0.063 | 0.000 | NaN | … | NaN |
| 0.03 | 0.127 | 0.063 | 0.000 | … | NaN |
| 0.04 | 0.189 | 0.127 | 0.063 | … | NaN |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋱ | ⋮ |
| 0.99 | −0.063 | −0.127 | −0.189 | … | −0.955 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Zhang, S.; Song, M.; Sun, L. Dictionary Learning-Based Data Pruning for System Identification. Appl. Sci. 2025, 15, 9368. https://doi.org/10.3390/app15179368
Wang T, Zhang S, Song M, Sun L. Dictionary Learning-Based Data Pruning for System Identification. Applied Sciences. 2025; 15(17):9368. https://doi.org/10.3390/app15179368
Chicago/Turabian StyleWang, Tingna, Sikai Zhang, Mingming Song, and Limin Sun. 2025. "Dictionary Learning-Based Data Pruning for System Identification" Applied Sciences 15, no. 17: 9368. https://doi.org/10.3390/app15179368
APA StyleWang, T., Zhang, S., Song, M., & Sun, L. (2025). Dictionary Learning-Based Data Pruning for System Identification. Applied Sciences, 15(17), 9368. https://doi.org/10.3390/app15179368








