Properties of Stress and Deformation of Internal Geomembrane–Clay Seepage Control System for Rockfill Dam on Deep Overburden
Abstract
1. Introduction
2. Numerical Simulation
2.1. Methods
2.2. Numerical Model and Material Parameters
2.2.1. Numerical Model
2.2.2. Material Parameters
2.2.3. Numerical Cases
3. Results and Analysis
3.1. Stress–Deformation Behavior of Dam and Geomembrane Under Normal Reservoir Water Level
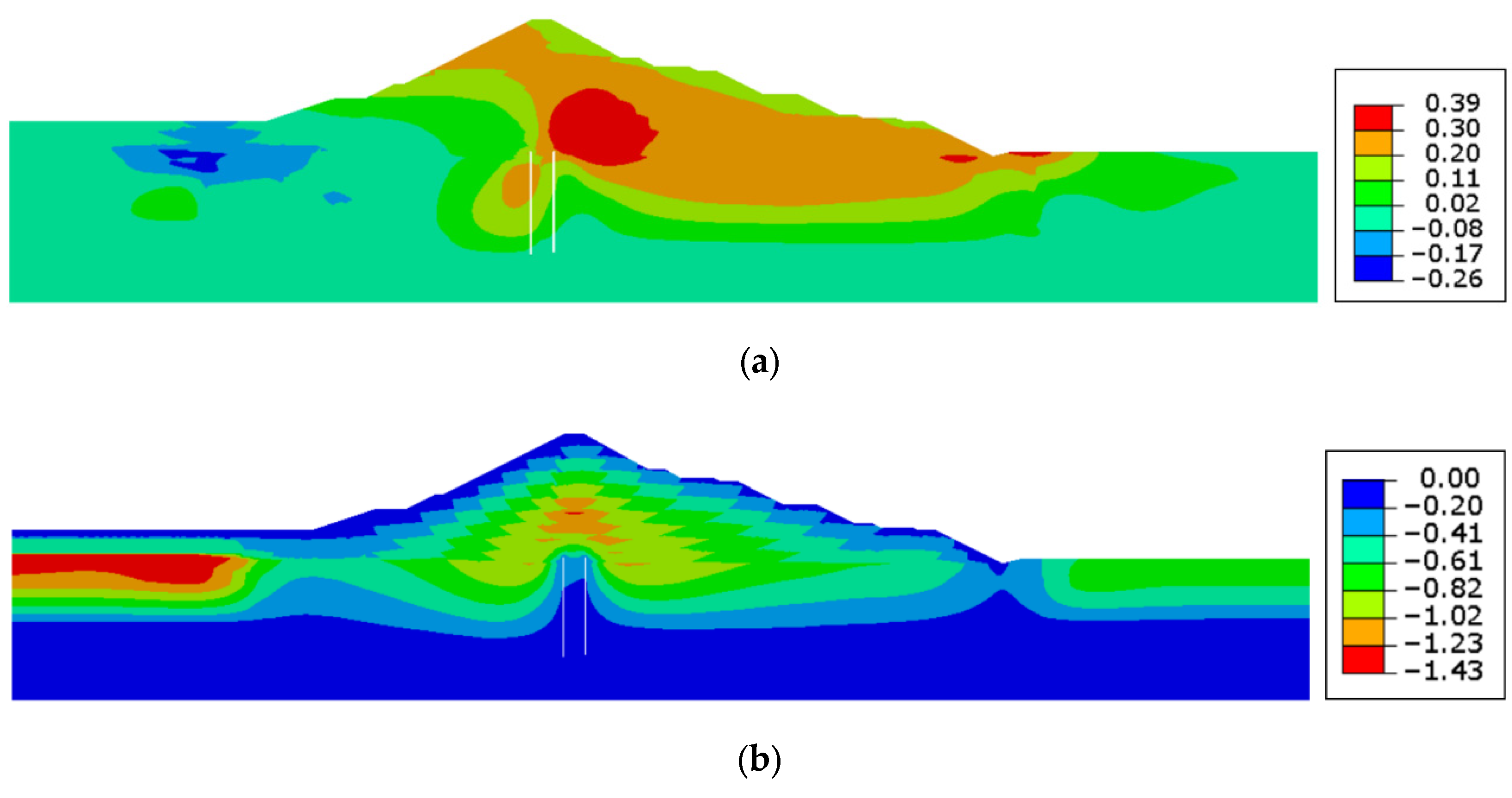
3.1.1. Stress–Deformation Behavior of the Dam
3.1.2. Stress–Deformation Behavior of GMB
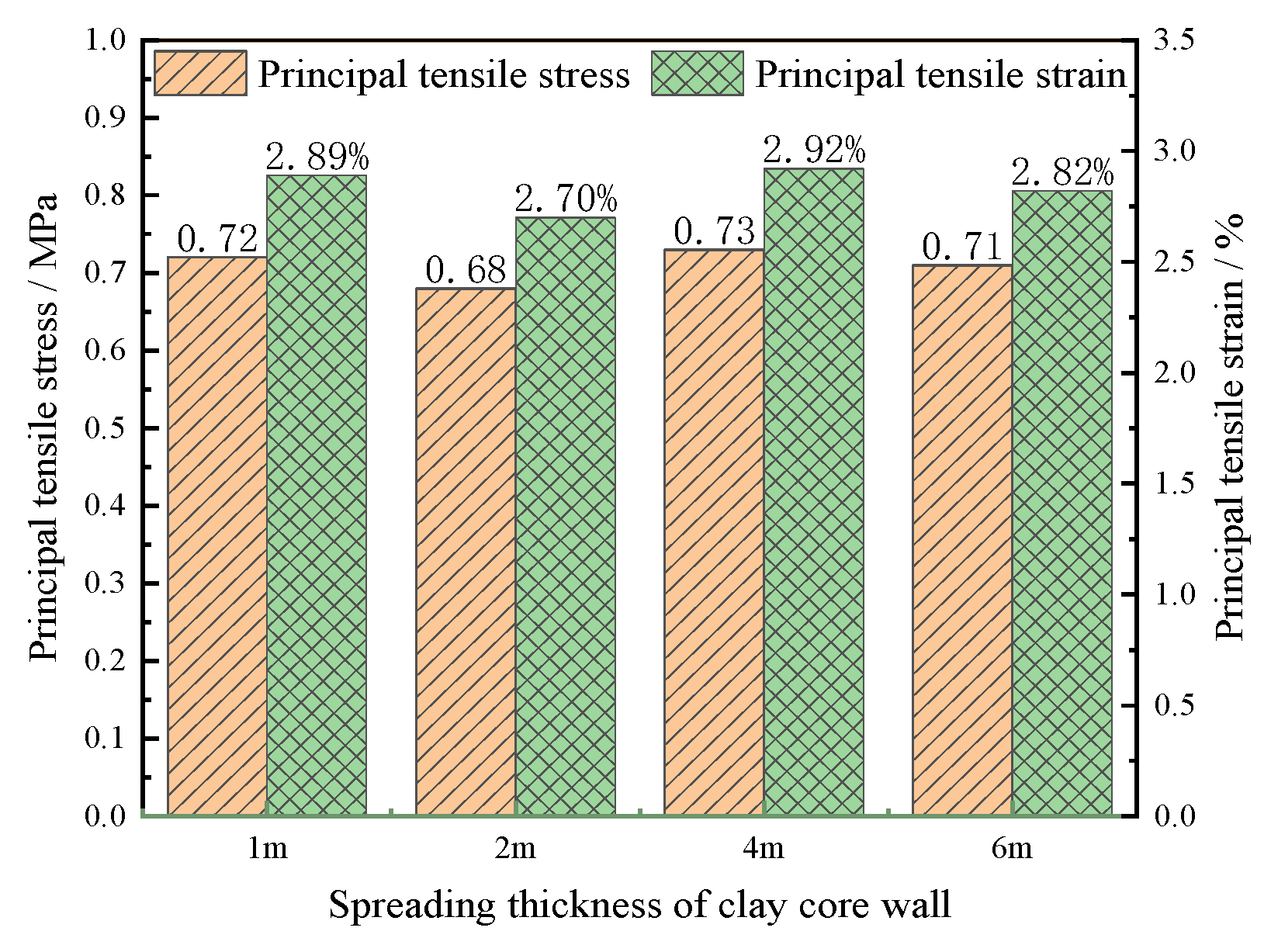
3.2. Influence of Clay Core-Wall Spreading Thickness on Stress–Deformation Response of GMB
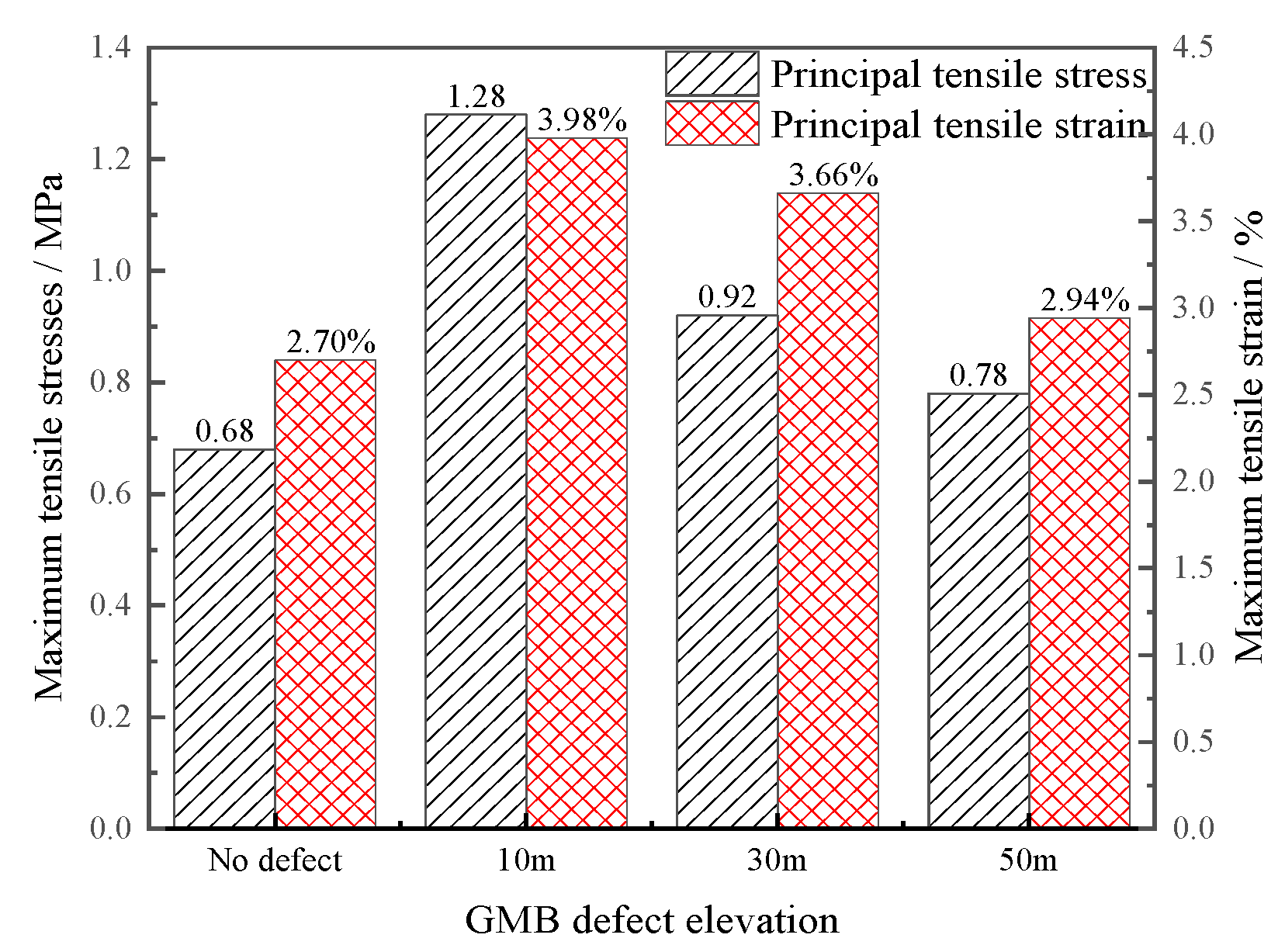
3.3. Influence of Defect Location on Stress–Deformation Behavior of GMB
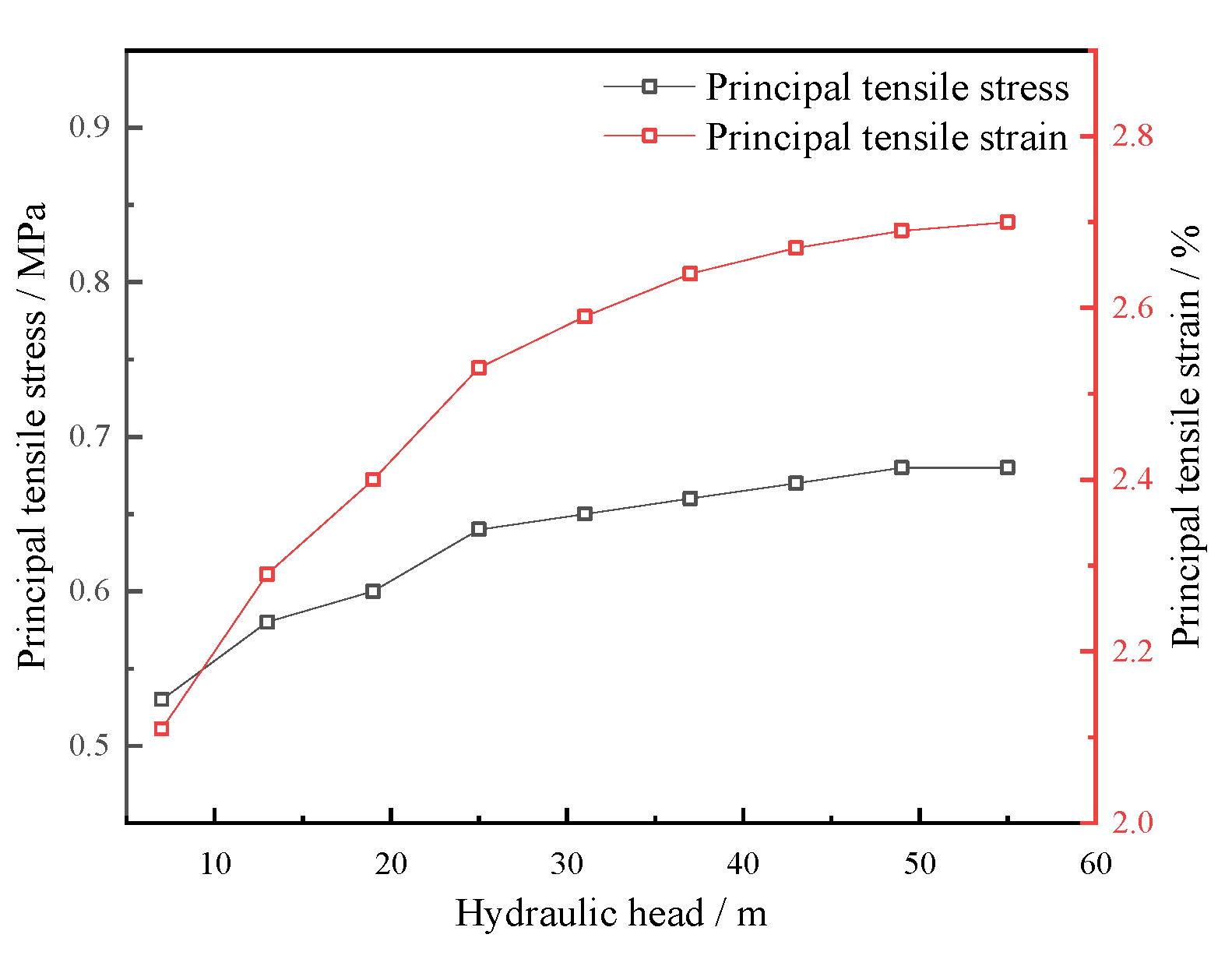
3.4. Influence of Hydraulic Head Magnitude on Stress–Deformation Behavior of Geomembrane
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xing, Y.L.; Shu, Y.M.; Hua, J.F.; Li, Y.H.; Zhou, W.Y. Improvement of Arch Action at Clay Core-Wall of High Rockfill Dam by United Seepage Control with Geomembrane; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Xing, Y.L.; Shu, Y.M.; Hua, J.F.; Li, Y.H.; Zhou, W.H. Effect of geomembrane and core-wall united impervious system on arch effect of core-wall in high earth-rock dams. J. Hohai Univ. 2007, 4, 456–459. [Google Scholar] [CrossRef]
- Shu, Y.M.; Li, Y.H. Design of impervious structure with geomembrane for high earth rock dams. J. Hohai Univ. 2006, 1, 60–64. [Google Scholar] [CrossRef]
- Lin, D.X. Study on Some Key Issues in Design and Construction of Geomembrane Central Core Earth and Rockfll Dams. Master’s Thesis, Dalian University of Technology, Dalian, China, 2002. [Google Scholar]
- Jiang, H.B. Stress and Strain of High Earth-rock Dam with Composite Geomembrane Core-wall and Inclined-wall. J. Chang. River Sci. Res. Inst. 2014, 31, 53–57+76. [Google Scholar] [CrossRef]
- Honkanadavar, N.P.; Kumar, N.; Ratnam, M. Modeling the behavior of alluvial and blasted quarried rockfill materials. Geotech. Geol. Eng. 2014, 32, 1001–1015. [Google Scholar] [CrossRef]
- Sharma, P.; Mahure, N.V.; Ratnam, M. Influence of different stress conditions on behavior of rockfill materials. Geotech. Geol. Eng. 2011, 29, 1035–1048. [Google Scholar] [CrossRef]
- Wu, H.M.; Zhang, Z.; Shu, Y. Stress and Deformation Property of Geomembrane Surface Barrier for High Rock-fill Dam. MATEC Web Conf. 2019, 275, 03003. [Google Scholar] [CrossRef]
- Ding, D.Y.; Ren, J.M. Analysis of Stress Deformation Characteristics of Composite Geomembrane Rock-Fill Dam with Core Wall. Appl. Mech. Mater. 2014, 470, 962–965. [Google Scholar] [CrossRef]
- Koerner, R.M.; Hsuan, Y.G. Lifetime Prediction of Polymeric Geomembranes Used in New Dam Construction and Dam Rehabilitation. 2003. Available online: https://www.researchgate.net/publication/238679247 (accessed on 28 June 2025).
- Yao, T.B.; Ding, D.Y.; Ren, J.M. Stress deformation analysis of composite geomembrane wall rock-fill dam under earthquake. South North Water Transf. Water Sci. Technol. 2015, 13, 127–131+144. [Google Scholar] [CrossRef]
- Xu, H.; Li, B.; Pan, J.J.; Li, H.-M. Stress and Deformation Characteristics of Composite Geomembrane Cofferdam with Different Patterns of Laying and Connection. J. Chang. River Sci. Res. Inst. 2022, 39, 111–115. [Google Scholar] [CrossRef]
- Fox, P.J.; Ross, J.D.; Sura, J.M.; Thiel, R. Geomembrane damage due to static and cyclic shearing over compacted gravelly sand. Geosynth. Int. 2011, 18, 272–279. [Google Scholar] [CrossRef]
- Li, T.Y.; Sun, D.A.; Fu, X.L.; Chen, Z.; Wang, L.; Du, Y.J. Two-dimensional migration characteristics of contaminants considering time-dependent contaminant sources and GM defects. Chin. J. Geotech. Eng. 2024, 46, 2450–2456. [Google Scholar] [CrossRef]
- Rowe, R.K. Systems engineering: The design and operation of municipal solid waste landfills to minimize contamination of groundwater. Geosynth. Int. 2011, 18, 391–404. [Google Scholar] [CrossRef]
- Giroud, J.; Bonaparte, R. Leakage through liners constructed with geomembranes—Part, I. Geomembrane liners. Geotext. Geomembr. 1989, 8, 27–67. [Google Scholar] [CrossRef]
- Giroud, J.P.; Gross, B.A.; Bonaparte, R.; McKelvey, J. Leachate Flow in Leakage Collection Layers Due to Defects in Geomembrane Liners. Geosynth. Int. 1997, 4, 215–292. [Google Scholar] [CrossRef]
- Rowe, R.K. Geosynthetics the minimization of contaminant migration through barrier systems beneath solid waste. In Proceedings of the 6th International Conference on Geosynthetics, Atlanta, GA, USA, 25–29 March 1998; Industrial Fabrics Association International: Roseville, MN, USA, 1998; pp. 27–103. [Google Scholar]
- Rowe, R.K. Long-term performance of contaminant barrier systems. Geotechnique 2005, 55, 631–678. [Google Scholar] [CrossRef]
- Rowe, R.K. Short-long-term leakage through composite liners. The 7th arthur casagrande lecture 1This lecture was presented at the 14th pan-American conference on soil mechanics geotechnical engineering Toronto ont October 2011, and a pre-print appeared in the conference proceedings. Can. Geotech. J. 2012, 49, 141–169. [Google Scholar] [CrossRef]
- Rowe, R.K. Protecting the environment with geosynthetics: 53rd Karl Terzaghi lecture. J. Geotech. Geoenviron. Eng. 2020, 146, 4020081. [Google Scholar] [CrossRef]
- Huang, J.; Wang, J.J.; Yi, L. Study on the Working Characteristics of Core Wall Rockfill Dam Considering Geomembrane Permeation. Water Resour. Power 2024, 42, 142–146. [Google Scholar] [CrossRef]
- Weber, C.T. Leakage Through Defects in Geomembrane Liners under High Hydraulic Heads. Master’s Thesis, University of Texas at Austin, Austin, TX, USA, 2008. [Google Scholar]
- Yang, Z.Y.; Gong, C.Y.; Xing, H.T.; Lv, H. Equivalent treatment methods for geomembrane defects in earth-rockfill dam seepage control systems and dam breach mechanisms induced by severe defects. Water Resour. Hydropower Eng. 2025, 1–15. Available online: https://link.cnki.net/urlid/10.1746.tv.20250709.1523.004 (accessed on 28 June 2025).
- Zhuang, Z. The Beginner’s Guide to ABAQUS Finite Element Software, Version 6.4; Tsinghua University Press: Beijing, China, 2004.
- Li, Z.M. Earth and Rockfill Dam FEM Automatic Mesh Generation Process. Master’s Thesis, Dalian University of Technology, Dalian, China, 2009. [Google Scholar]
- Wu, H.M.; Shu, Y.M.; Dai, L.J.; Teng, Z.M.; Jiang, S.P. Development verification of composite geomembrance-cushioninterface constitutive model in FLAC 3D. J. Hydraul. Eng. 2014, 45 (Suppl. S2), 167–174. [Google Scholar] [CrossRef]
- Bacas, B.M.; Canizal, J.; Konietzky, H. Frictional behaviour of three critical geosynthetic interfaces. Geosynth. Int. 2015, 22, 355–365. [Google Scholar] [CrossRef]
- Gunaratne, M.; Demirdogen, S. Discussion on stability analysis of embankment dams with defective internal geomembrane liners. Int. J. Geotech. Eng. 2022, 16, 1165–1175. [Google Scholar] [CrossRef]
- Sun, D.; Shen, Z.Z.; Cui, J.J. Seepage Numerical Simulation of Geomembrane Gravel Dam Caused by Geomembrane Defect. Water Resour. Power 2013, 31, 69–73. [Google Scholar] [CrossRef]
- Wang, B.; Shen, X.D. Stress and Strain Calculation of Asphalt Concrete Core for Earth-rock Dam. J. Eng. Heilongjiang Univ. 2008, 2, 52–55. [Google Scholar] [CrossRef]
- Zhao, H.Y.; Wu, H.M.; Shu, Y.M.; Yi, F. Experimental Study on Elastic Deformation Property of Geomembrane used as barrier in Upper Reservoir of Pumped Storage Power Station. Chin. J. Geotech. Eng. 2024. Available online: https://link.cnki.net/urlid/32.1124.TU.20240905.1724.002 (accessed on 28 June 2025).
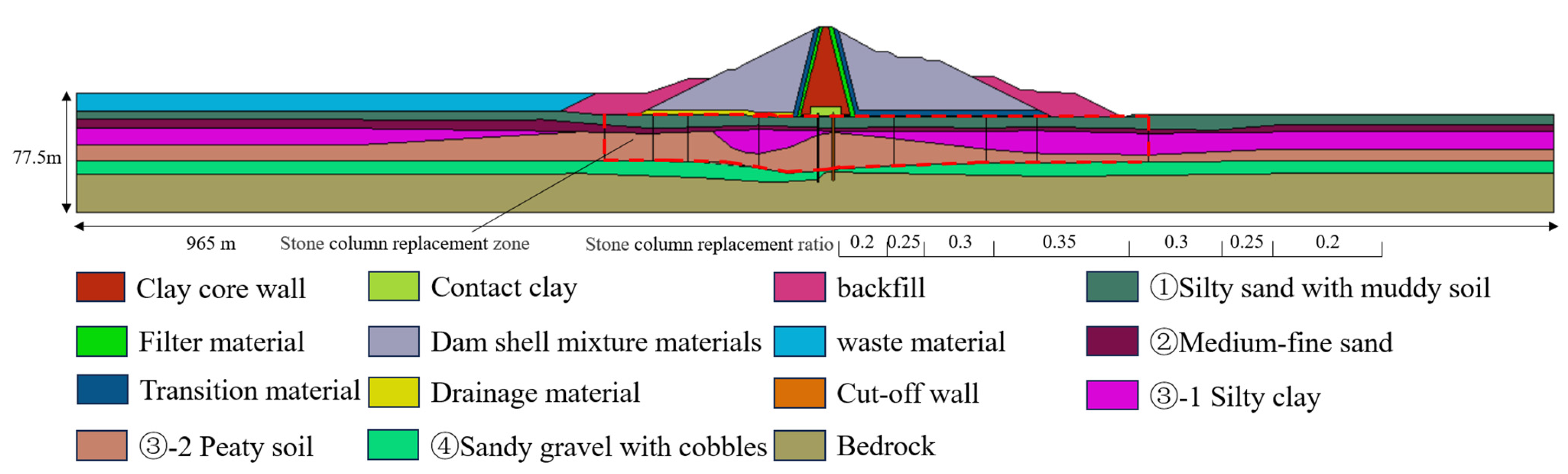
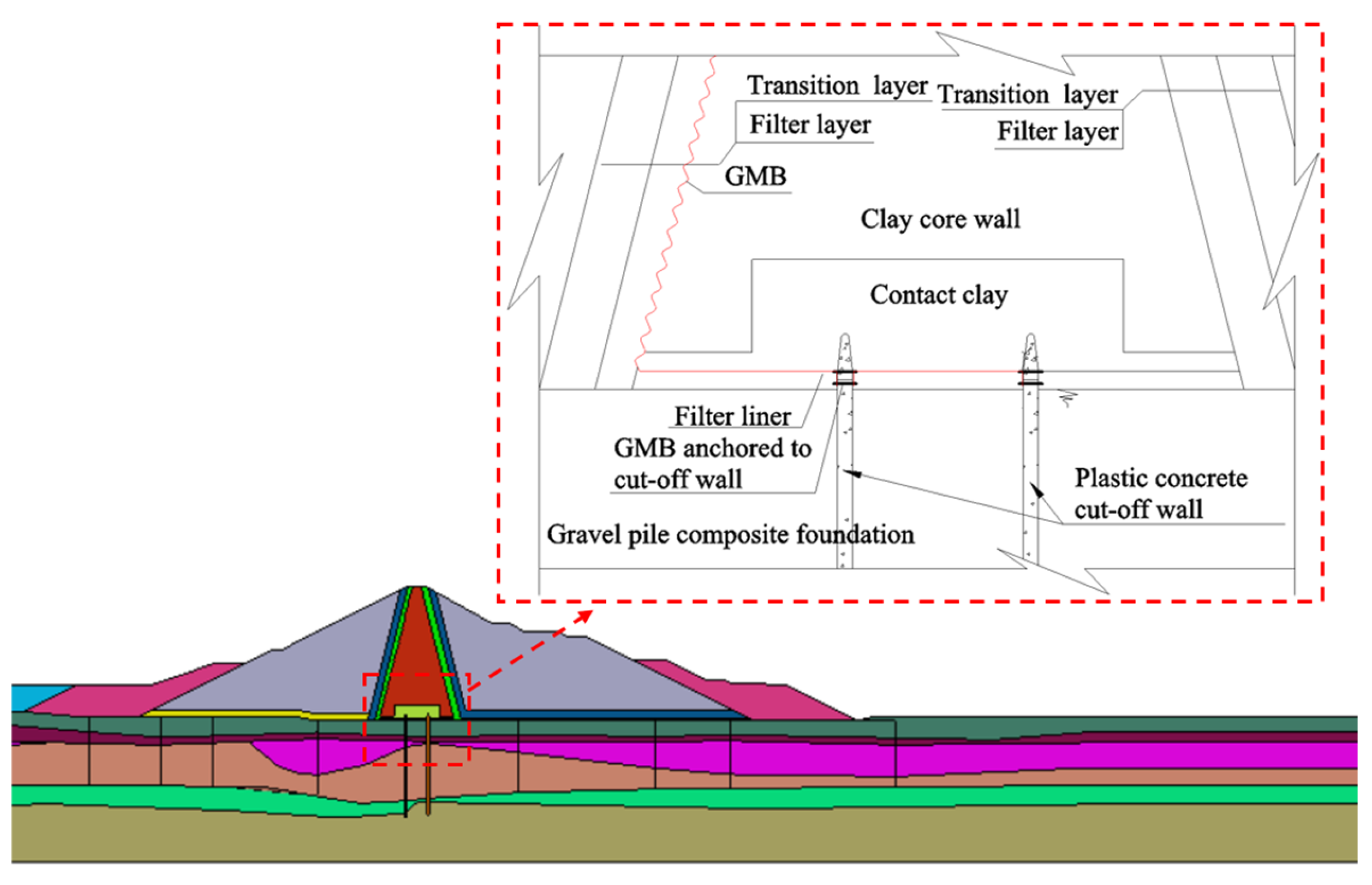





| Materials | ρsat (g/cm3) | Ρ (g/cm3) | n0 | Sr0 | c/kPa | φo (°) | Δφ (°) | K | n | Rf | Kur | Kb | m |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Clay core-wall | 1.73 | 1.66 | 0.47 | 0.85 | 30 | 25 | 0 | 180 | 0.5 | 0.80 | 540 | 90 | 0.6 |
| Filter material | 2.01 | 1.96 | 0.23 | - | - | 50.1 | 8.4 | 630 | 0.33 | 0.74 | 1260 | 250 | 0.31 |
| Transition material | 2.15 | 2.12 | 0.23 | - | - | 52.5 | 8.0 | 750 | 0.25 | 0.71 | 1500 | 300 | 0.30 |
| Dam shell mixture materials | 2.01 | 1.96 | 0.23 | - | - | 43.3 | 3.9 | 500 | 0.38 | 0.63 | 1000 | 200 | 0.32 |
| Drainage material | 2.06 | 2.01 | 0.26 | - | - | 45.0 | 6.0 | 600 | 0.36 | 0.65 | 1200 | 240 | 0.31 |
| Backfill and waste material | 1.92 | 1.81 | 0.28 | - | 67.9 | 28.3 | 0 | 220 | 0.46 | 0.67 | 440 | 90 | 0.40 |
| Contact clay | 1.69 | 1.62 | 0.5 | 0.85 | 5 | 16 | 0 | 108 | 0.35 | 0.6 | 270 | 45 | 0.45 |
| ①Silty sand with muddy soil | 1.96 | 1.96 | 0.60 | 0.95 | 3 | 13 | - | 40 | 0.75 | 0.70 | 120 | 16 | 0.7 |
| ②Medium-fine sand | 2.0 | 2.0 | 0.3 | 0.95 | 0 | 27 | - | 300 | 0.4 | 0.7 | 600 | 120 | 0.5 |
| ③-1 Silty clay | 1.53 | 1.53 | 0.64 | 1.00 | 28.8 | 22.8 | - | 52 | 0.50 | 0.6 | 156 | 15 | 0.45 |
| ③-2 Peaty soil | 1.59 | 1.59 | 0.62 | 1.00 | 30.3 | 23.0 | - | 53 | 0.50 | 0.6 | 159 | 15 | 0.60 |
| ④Sandy gravel with cobbles | 2.05 | 2.03 | 0.28 | 1.00 | 0 | 38 | 0 | 510 | 0.45 | 0.68 | 1000 | 230 | 0.28 |
| Concrete cut-off wall | 2.4 | 2.4 | - | - | 1006 | 39 | - | 16,628 | 0.24 | 0.63 | 19,954 | 1699.8 | −0.015 |
| Materials | Stone Column Replacement Ratio: 0.35 | Stone Column Replacement Ratio: 0.3 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| c (kPa) | φ(◦) | K | n | Kur | Kb | m | c (kPa) | φ(◦) | K | n | Kur | Kb | m | |
| Post-reinforcement Layer ① | 2.0 | 24.6 | 411 | 0.57 | 822 | 195.9 | 0.55 | 2.1 | 21.8 | 358 | 0.59 | 716 | 170.2 | 0.57 |
| Post-reinforcement Layer ② | 0 | 32.0 | 580 | 0.37 | 1160 | 263.5 | 0.19 | 0 | 30.8 | 540 | 0.38 | 1080 | 243 | 0.19 |
| Post-reinforcement Layer ③-1 | 19.4 | 29.8 | 418.8 | 0.44 | 837.6 | 195.3 | 0.39 | 22.3 | 28.1 | 366.4 | 0.45 | 732.8 | 169.5 | 0.40 |
| Post-reinforcement Layer ③-2 | 20.7 | 29.7 | 419.5 | 0.44 | 839 | 195.2 | 0.35 | 20.9 | 28.1 | 367.1 | 0.45 | 734.2 | 169.5 | 0.36 |
| Materials | Stone column replacement ratio: 0.25 | Stone column replacement ratio: 0.20 | ||||||||||||
| c (kPa) | φ (◦) | K | n | Kur | Kb | m | c (kPa) | φ(◦) | K | n | Kur | Kb | m | |
| Post-reinforcement Layer ① | 2.3 | 20.4 | 305 | 0.61 | 610 | 144.5 | 0.59 | 2.4 | 19.0 | 252 | 0.66 | 536 | 118.8 | 0.61 |
| Post-reinforcement Layer ② | 0 | 30.2 | 500 | 0.38 | 1000 | 222.5 | 0.18 | 0 | 29.5 | 460 | 0.38 | 920 | 202 | 0.17 |
| Post-reinforcement Layer ③-1 | 23.9 | 27.2 | 314 | 0.46 | 628 | 143.8 | 0.41 | 23.0 | 26.4 | 261.6 | 0.46 | 564.8 | 118 | 0.41 |
| Post-reinforcement Layer ③-2 | 22.4 | 27.3 | 314.8 | 0.46 | 629.5 | 143.8 | 0.37 | 24.2 | 26.5 | 262.4 | 0.46 | 567.2 | 118 | 0.37 |
| Materials | Permeability (cm/s) | Materials | Permeability (cm/s) |
|---|---|---|---|
| Clay core-wall | 1 × 10−5 | ③-1Silty clay | 1 × 10−6 |
| Filter material | 5 × 10−3 | ③-2Peaty soil | 1 × 10−7 |
| Transition material | 5 × 10−2 | ④ Sandy gravel with cobbles | 5 × 10−3 |
| Dam shell mixture materials | 5 × 10−3 | Concrete cutoff wall | 1 × 10−7 |
| Drainage material | 1 × 10−2 | Bedrock | 1 × 10−5 |
| Backfill and waste material | 1 × 10−3 | Post-reinforcement Layer ① (0.35/0.3/0.25/0.2) | 1.76 × 10−3/1.51 × 10−3/ 1.26 × 10−3/1.01 × 10−3 |
| Contact clay | 1 × 10−6 | Post-reinforcement Layer ② (0.35/0.3/0.25/0.2) | 1.82 × 10−3/1.57 × 10−3/ 1.33 × 10−3/1.08 × 10−3 |
| ① Silty sand with muddy soil | 1 × 10−5 | Post-reinforcement Layer ③-1 (0.35/0.3/0.25/0.2) | 1.75 × 10−3/1.50 × 10−3/ 1.25 × 10−3/1.0 × 10−3 |
| ② Medium-fine sand | 1 × 10−4 | Post-reinforcement Layer ③-2 (0.35/0.3/0.25/0.2) | 1.75 × 10−3/1.50 × 10−3/ 1.25 × 10−3/1.0 × 10−3 |
| Number | The Spreading Thickness of the Clay Core-Wall/m | Water Level/m | The Height of the GMB Defect Location/m |
|---|---|---|---|
| GK1 | 1 | 55 | No defect |
| GK2 | 2 | 55 | No defect |
| GK3 | 4 | 55 | No defect |
| GK4 | 6 | 55 | No defect |
| GK5 | 2 | 7 | No defect |
| GK6 | 2 | 13 | No defect |
| GK7 | 2 | 19 | No defect |
| GK8 | 2 | 25 | No defect |
| GK9 | 2 | 31 | No defect |
| GK10 | 2 | 37 | No defect |
| GK11 | 2 | 43 | No defect |
| GK12 | 2 | 49 | No defect |
| GK13 | 2 | 55 | 50 |
| GK14 | 2 | 55 | 30 |
| GK15 | 2 | 55 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Wu, H.; Wang, W.; Liu, Q. Properties of Stress and Deformation of Internal Geomembrane–Clay Seepage Control System for Rockfill Dam on Deep Overburden. Appl. Sci. 2025, 15, 9324. https://doi.org/10.3390/app15179324
Liu B, Wu H, Wang W, Liu Q. Properties of Stress and Deformation of Internal Geomembrane–Clay Seepage Control System for Rockfill Dam on Deep Overburden. Applied Sciences. 2025; 15(17):9324. https://doi.org/10.3390/app15179324
Chicago/Turabian StyleLiu, Baoyong, Haimin Wu, Wansheng Wang, and Qiankun Liu. 2025. "Properties of Stress and Deformation of Internal Geomembrane–Clay Seepage Control System for Rockfill Dam on Deep Overburden" Applied Sciences 15, no. 17: 9324. https://doi.org/10.3390/app15179324
APA StyleLiu, B., Wu, H., Wang, W., & Liu, Q. (2025). Properties of Stress and Deformation of Internal Geomembrane–Clay Seepage Control System for Rockfill Dam on Deep Overburden. Applied Sciences, 15(17), 9324. https://doi.org/10.3390/app15179324





