From Mathematical Modeling and Simulation to Digital Twins: Bridging Theory and Digital Realities in Industry and Emerging Technologies

Featured Application

The concepts discussed outline how mathematical modeling, real-time simulation, and data-driven optimization can be integrated to develop self-adaptive digital twins for smart manufacturing applications such as additive manufacturing and process automation. This work highlights how such digital twins can improve operational resilience, efficiency, and product customization.

Abstract

Against the background of the unprecedented advancements related to Industry 4.0 and beyond, transitioning from classical mathematical models to fully embodied digital twins represents a critical change in the planning, monitoring, and optimization of complex industrial systems. This work outlines the subject within the broader field of applied mathematics and computational simulation while highlighting the critical role of sound mathematical foundations, numerical methodologies, and advanced computational tools in creating data-informed virtual models of physical infrastructures and processes in real time. The discussion includes examples related to smart manufacturing, additive manufacturing technologies, and cyber–physical systems with a focus on the potential for collaboration between physics-informed simulations, data unification, and hybrid machine learning approaches. Central issues including a lack of scalability, measuring uncertainties, interoperability challenges, and ethical concerns are discussed along with rising opportunities for multi/macrodisciplinary research and innovation. This work argues in favor of the continued integration of advanced mathematical approaches with state-of-the-art technologies including artificial intelligence, edge computing, and fifth-generation communication networks with a focus on deploying self-regulating autonomous digital twins. Finally, defeating these challenges via effective collaboration between academia and industry will provide unprecedented society- and economy-wide benefits leading to resilient, optimized, and intelligent systems that mark the future of critical industries and services.

1. Introduction

Historically, mathematical modeling and simulation have been essential components of scientific and technological advancement, offering a structured framework for comprehending, forecasting, and optimizing the behavior of complex systems [1]. These tools have become essential in today’s industry for addressing problems that require precise data-supported decision making in the face of uncertainty and growing system complexity. From designing advanced manufacturing processes to managing large-scale industrial operations, mathematical models enable scientists and engineers to translate physical principles and empirical observations into predictive insights. The development of innovative products, process optimization for sustainability and efficiency, and risk mitigation related to expensive experimental trials or full-scale prototyping are all supported by these insights [2]. The need for accurate, flexible, and computationally efficient models is increasing as industries embrace more automated, integrated, and intelligent production workflows, reaffirming the critical role of applied mathematics in technological advancement.

In parallel, simulation technologies have undergone significant evolution, leveraging exponential advances in computing power, numerical algorithms, and high-fidelity data acquisition. Contemporary simulation environments allow practitioners to replicate physical processes virtually, explore design alternatives rapidly, and perform extensive scenario analyses that would be infeasible or prohibitively expensive through physical experimentation alone [3]. These capabilities have greatly assisted industries such as aerospace, energy, automotive, and biomedical engineering, where virtual prototyping and computational experimentation have become integral to innovation pipelines [4]. Moreover, the integration of simulation with real-time data streams and feedback loops is laying the groundwork for a new generation of applications—notably, digital twins [5]—that converge theoretical models and physical assets [6]. In this context, the synergy of rigorous mathematical modeling and computational simulation emerges as a strategic enabler of resilient, efficient, and intelligent systems across diverse industrial domains.

Thus, this perspective paper aims to highlight the essential role of robust mathematical foundations in shaping the next generation of industrial and technological solutions. While the digital twin concept has attracted significant attention in recent years, its practical realization depends fundamentally on the development, refinement, and validation of mathematical models that faithfully capture the behavior of complex physical systems [7]. By articulating how theoretical modeling, numerical simulation, and real-time data integration can be systematically combined, this work seeks to clarify the scientific underpinnings that make digital twins more than mere digital replicas, positioning them instead as adaptive, predictive, and decision support tools deeply rooted in applied mathematics.

Moreover, this perspective emphasizes that a true synthesis of mathematical rigor and computational innovation is indispensable for addressing the multifaceted chal-lenges posed by contemporary industrial contexts. These include not only the technical demands of real-time monitoring and control, but also the need for scalable interoperable frameworks that can integrate multi-physics multi-scale models with vast streams of heterogeneous data [8]. By outlining the opportunities and open questions at this intersection, this paper aspires to foster interdisciplinary dialogue, encourage methodological advances, and inspire new applications that bridge traditional modeling paradigms with the dynamic data-centric architectures that define Industry 4.0 and beyond [9].

A diverse range of emerging technologies exemplifies how this convergence of mathematical modeling, simulation, and data-driven intelligence is being practically implemented to transform industrial practice. Applications such as predictive maintenance in manufacturing [10], the real-time optimization of energy systems [11], and the management of autonomous vehicles [12] all illustrate the growing need for integrated digital twin solutions that leverage high-fidelity models and continuous data flows. Among these, additive manufacturing—commonly known as 3D printing—stands out as a particularly vivid demonstration of how rigorous modeling and real-time simulation can revolutionize production processes [13]. Modern 3D printing workflows increasingly rely on mathematical models to predict material behavior, optimize part geometry, and control process parameters with high precision [14]. Computational simulations inform layer-by-layer deposition strategies, thermal management, and structural integrity assessments before and during fabrication [15]. When integrated into a digital twin framework, these models enable adaptive process control, quality assurance, and closed-loop feedback that enhance efficiency and minimize defects [16]. As such, 3D printing exemplifies the tangible benefits of simultaneously exploiting applied mathematics, computational power, and data-driven insights to enable agile, resilient, and innovative production systems.

Collectively, these advancements depict the reach of a critical point for the disci-plines of applied mathematics and computational modeling, wherein the traditional boundaries between theoretical abstraction and practical application meet the dynamic data-driven frameworks such as digital twins. This work aims to elucidate how rigorous mathematical methodologies, coupled with state-of-the-art simulation technologies and real-time data assimilation, can be systematically integrated to address the multifaceted demands of modern industry and emerging technological domains. By articulating the scientific principles, computational challenges, and practical opportunities inherent in this convergence—and by highlighting representative applications such as additive manufacturing—the sections that follow seek to provide a coherent knowledge body for advancing the design, implementation, and utilization of digital twin technology. In doing so, it investigates the indispensable role of mathematical modeling and simulation in enabling resilient, adaptive, and intelligent systems that can meet the evolving demands of contemporary industrial practice and future innovation.

This review adopts a structured literature synthesis approach, drawing from peer-reviewed journal articles, conference proceedings, and authoritative technical reports published primarily within the past decade. The search strategy combined targeted keywords related to computational modeling, digital twin architectures, and real-time simulation across major scientific databases (e.g., Scopus, Web of Science, IEEE Xplore). Inclusion criteria emphasized works that present original methods, significant application case studies, or critical analyses relevant to the integration of modeling techniques with digital twin systems. The final selection was guided by the aim of covering both foundational concepts and state-of-the-art advancements, ensuring a balanced treatment of theoretical underpinnings, enabling technologies, and practical implementations. This methodological framework underpins the organization of the paper and informs the thematic progression from fundamentals to advanced applications.

The remainder of this work is structured as follows. Section 2 outlines the founda-tional principles of applied mathematics and computational modeling, presenting key techniques that underpin modern simulation practices. Section 3 examines representative industrial and technological applications, with emphasis on smart manufacturing, innovative services, and enabling infrastructures. Section 4 explores the transition from conventional modeling approaches to fully developed digital twin frameworks, detailing their characteristics, architectures, and enabling technologies. Section 5 discusses the current challenges, emerging research directions, and interdisciplinary opportunities that define the digital twin era. Finally, Section 6 offers future perspectives, highlighting potential technological, ethical, and collaborative pathways toward advancing self-adaptive and autonomous digital twins.

2. Foundations: Applied Mathematics and Computational Modeling

At the heart of modern industrial problem solving lies a robust framework of core mathematical principles that underpin the formulation, analysis, and resolution of complex phenomena. Differential equations—both ordinary and partial—form the backbone of this framework, providing a rigorous means to describe the dynamic behavior of physical, chemical, and biological systems across multiple spatial and temporal scales [17]. For example, the general form of a partial differential equation (PDE) [18] encapsulates conservation laws where u represents a state variable (such as temperature, pressure, or concentration), $\mathbf{F}\left(\mathrm{u}\right)$ denotes the flux, and $S$ is a source term. The analytical and numerical treatment of such equations enables the prediction of system responses under varying boundary and initial conditions, which is essential in domains ranging from fluid dynamics and heat transfer to structural mechanics and chemical process engineering. To make these continuous models tractable on modern computing architectures, advanced numerical methods—such as finite difference [19], finite volume [20], or spectral schemes [21]—are employed to approximate solutions with high fidelity and computational efficiency.

$${\displaystyle \frac{\partial \mathrm{u}}{\partial \mathrm{t}}}+\nabla \cdot \mathbf{F}\left(\mathrm{u}\right)=\mathrm{S}\left(\mathrm{u},\mathrm{x},\mathrm{t}\right),$$

(1)

Optimization theory [22,23] further extends this mathematical foundation by offering systematic approaches to enhance the performance, efficiency, and sustainability of engineered systems. In its simplest form, an optimization problem seeks to determine the variable vector $\mathbf{x}$ that minimizes an objective function $\mathit{f}\left(\mathit{x}\right)$ subject to constraints.

$$\underset{x}{\mathit{min}} f\left(\mathit{x}\right) subject to g_{i }\left(x\right)\le 0, h_{j }\left(x\right)=0$$

(2)

Here, ${\mathit{g}}_{\mathit{i}}$ and ${\mathit{h}}_{\mathit{j}}$ represent inequality and equality constraints, respectively, which define the feasible solution space. Such formulations are ubiquitous in the design and operation of modern industrial systems from optimizing material usage and energy consumption to balancing trade-offs among competing performance metrics. Collectively, these mathematical building modules—differential equations, numerical methods, and optimization frameworks—equip engineers, scientists, and technologists with the analyt-ical rigor and computational tools needed to overcome the inherent complexity of contemporary industrial applications and to build upon a solid theoretical basis for advanced simulation and digital twin development.

2.1. Overview of Computational Modeling Techniques

Building upon the foundational mathematical principles, computational modeling techniques provide the means to translate abstract equations into practical, solvable representations of real-world systems. Among the most widely adopted methods is the Finite Element Method (FEM), which enables the numerical solution of complex partial differential equations over domains with arbitrary geometries and boundary conditions. In FEM, the domain is discretized into smaller subdomains (elements), and the solution is approximated by piecewise continuous functions [24]. The governing equations are reformulated in a weak form, for example,

$${\int }_{\Omega }\mathsf{\nabla }u · \mathsf{\nabla }v d\Omega ={\int }_{\Omega }fv d\Omega ,$$

(3)

where $\mathsf{\Omega }$ denotes the problem domain, $u$ is the unknown field variable, $\mathit{v}$ is a test function, and $\mathit{f}$ is a source term. This variational approach provides the flexibility and robustness needed to handle multi-physics phenomena, such as fluid–structure interaction, thermo-mechanical coupling, and electromagnetic field analysis, which are common in advanced industrial applications.

In industrial deployments, the weak form FEM formulation presented in Equation (3) is well suited for real-time updates, as it allows for the localized recalibration of the discretized system without the need to recompute global matrices from scratch. By exploiting sparse system structures and employing reduced-order approximations, the FEM framework can efficiently incorporate streaming sensor data into boundary conditions, material parameters, or loading vectors. This adaptability is further enhanced when combined with data assimilation methods such as the Ensemble Kalman Filter or moving-horizon estimation, which provide recursive schemes for embedding measurements into the FEM solution. In practice, this hybridization of weak form discretization with assimilation techniques ensures that the digital twin remains dynamically synchronized with its physical counterpart, enabling predictive monitoring and adaptive control in real time.

In parallel, alternative modeling paradigms such as Agent-Based Modeling (ABM) offer complementary capabilities for simulating systems characterized by discrete entities and complex interactions [25]. Unlike continuum-based methods, ABM captures the emergent behavior of large populations of autonomous agents that follow simple rules but collectively give rise to non-linear system-wide dynamics. The evolution of each agent’s state ${\mathit{s}}_{\mathit{i}}$ at time $\mathit{t}+\mathbf{1}$ can be represented generically as follows:

$$s_i\left(t +1\right) =f\left(s_i \left(t\right), {\left\{s_j \left(t\right)\right\}}_{j\ne i},\mathit{p}\right),$$

(4)

where the next state depends on its own current state, the states of neighboring agents, and a set of model parameters $\mathit{p}$. This approach has proven invaluable in domains such as supply chain modeling, crowd dynamics, epidemiology, and socio-technical systems, where the collective outcome cannot be adequately described by continuum equations alone [25,26,27,28]. Together, these computational techniques—spanning mesh-based numerical solvers and agent-based discrete simulations—demonstrate the versatility of modern computational modeling and underscore its essential role in translating mathematical theory into actionable insights for complex industrial and technological challenges.

In practical implementations, FEM solvers often employ sparse matrix representations and iterative solution schemes—such as the Conjugate Gradient [29] or Generalized Minimal Residual (GMRES) [30] methods—optimized for parallel execution on high-performance computing architectures. For transient, non-linear, or multi-physics problems, adaptive meshing and time-stepping algorithms are integrated to balance accuracy with computational cost. In the ABM context, efficient event-driven simulation engines and data structures such as k-d trees or spatial hashing are used to accelerate neighbor searches, enabling the simulation of large agent populations with minimal performance degradation.

The real value of modern modeling and simulation lies in the seamless synergy between rigorous theoretical frameworks and advanced computational implementa-tions. While mathematical formulations provide the necessary precision, generality, and explanatory depth to represent complex systems, computational techniques operationalize these models at scales and levels of detail that would be impractical to address analytically alone. This integration enables practitioners to tackle multi-physics, multi-scale, and highly non-linear problems, perform extensive parametric studies, and assimilate real-time data for continuous model refinement.

2.2. The Synergy of Theory and Computation for Complex Problem Solving

The ability of contemporary applied mathematics to convert theoretical concepts into workable solutions through the systematic integration of computation is one of its distinguishing advantages. Although mathematical theory establishes the fundamental laws and relationships that govern physical and engineered systems, which are frequently expressed through differential equations, variational principles, or optimization formulations, it is the conversion of these formulations into computationally tractable forms that makes it possible to apply them to real-world problems of unpredicted complexity and scale. Iterative algorithms [31], numerical solvers [32], and high-fidelity discrimination techniques [33] bridge this gap by enabling the exploration of parametric sensitivities, the simulation of multi-scale phenomena, and the validation of models against experimental or operational data. This collaboration enables researchers and engineers to go beyond idealized scenarios and capture the inherent non-linearity, heterogeneity, and stochasticity that define contemporary industrial systems and emerging technologies.

Crucially, this interplay between theory and computation leads to a dynamic iterative approach to complex problem solving. Advances in computing power, numerical algorithms, and data acquisition have given rise to simulation-based design and virtual experimentation, wherein theoretical models are continuously refined in light of empirical evidence and evolving operational conditions [34]. Such feedback loops enable predictive maintenance strategies, real-time process optimization, and rapid prototyping without the prohibitive costs of full-scale physical trials. Furthermore, this integrated framework lays the groundwork for the next evolutionary step—the digital twin—by combining physics-based models with real-time data streams to create living, adaptive, and digital representations of physical assets and processes [35].

Based on this, the PDE formulation introduced in Equation (1) can be explicitly connected to digital twin calibration methods through advanced numerical strategies. In digital twin contexts, calibration entails continuously updating the governing PDE parameters as new sensor data streams, ensuring that the computational model re-mains aligned with the evolving physical system. Sequential data assimilation techniques such as the Extended Kalman Filter (EKF), Ensemble Kalman Filter (EnKF), and Particle Filters provide efficient recursive schemes for this purpose, while reduced-order modeling approaches—including proper orthogonal decomposition (POD) and Dynamic Mode Decomposition (DMD)—enable real-time applicability by reducing computational burden without sacrificing predictive accuracy. Optimization-based schemes, particularly adjoint methods, further support the rapid recalibration of PDE coefficients and boundary conditions in high-dimensional settings. Increasingly, these numerical approaches are coupled with machine learning surrogates that approximate PDE solutions under varying operational scenarios, thereby accelerating calibration and facilitating predictive control. Together, these methods form the basis of real-time model updating, linking rigorous mathematical formulations with the adaptive data-driven requirements of digital twins.

To further illustrate this process, Figure 1 presents a workflow diagram of the data assimilation loop between physical sensors and digital twin models. It highlights how sensor data are continuously collected, integrated into computational models for calibration and updating, and then used to generate feedback that enhances the fidelity and predictive capabilities of the twin.

3. Modeling and Simulation in Industry and Emerging Technologies

3.1. Application Examples: Industrial Systems, Smart Manufacturing, and Innovative Services

The optimization and management of complex industrial systems is perhaps where mathematical modeling and computational simulation have the greatest practical impact. For example, advanced models of production lines, supply chains, and process flows in manufacturing enable engineers to forecast system bottlenecks, balance resource allocation, and implement lean manufacturing strategies that minimize waste and maximize throughput [36]. The design of scheduling algorithms, inventory management policies, and logistics networks that are resilient to disruptions and responsive to shifting market demands is supported by traditional operations research methods, which are reinforced by contemporary computational tools. In the energy sector, system-level models integrate fluid dynamics, thermodynamic principles, and network optimization to manage grid stability, distribution efficiency, and power generation in increasingly complex infrastructures that incorporate renewable resources, storage systems, and demand-side management [37]. These examples demonstrate how the interaction of theory and computation directly results in quantifiable improvements in sustainability, cost effectiveness, and productivity.

A particularly transformative application area is smart manufacturing, which leverages real-time monitoring, automation, and data-driven feedback to enhance traditional production systems [38]. Here, mathematical models form the backbone of digital representations of equipment, processes, and entire production lines, enabling virtual commissioning, predictive maintenance, and adaptive process control [39]. For example, multi-physics simulations can predict thermal stresses during welding, casting operations, or additive manufacturing (3D printing) processes, while real-time sensor data can be assimilated to update these models continuously, informing operators of deviations and potential failures before they occur [40]. In the context of Industry 4.0, the fusion of physics-based modeling, embedded computational intelligence, and cyber–physical systems (CPS) has redefined manufacturing as a highly interconnected self-optimizing environment [41]. Such capabilities allow manufacturers to switch rapidly between product variants, scale production efficiently, and respond dynamically to supply chain fluctuations and customized consumer demands. Figure 2 depicts the prominent components of a CPS incorporated in the Industry 4.0 context.

Beyond traditional industrial contexts, modeling and simulation increasingly drive the development of innovative services that deliver value through digitalization and data analytics. Applications range from smart city infrastructure planning and traffic flow management to personalized healthcare solutions and remote asset monitoring [42]. For example, urban planners optimize public transportation routes [43], emergency evacuation plans [44], and pedestrian and vehicle movements [45] by using computational fluid dynamics and agent-based models. In the medical field, patient-specific organ models and physiological procedures enable personalized treatment planning and surgical practice, enhancing results while lowering risks [46]. To assess risk portfolios, forecast market dynamics, and guide decision making without uncertainty, financial and insurance services also rely on stochastic modeling and large-scale simulations [47,48]. The integration of advanced modeling techniques with real-time data streams, cloud computing, and intuitive user interfaces underpins the shift towards services that are predictive, adaptable, and capable of delivering customized solutions at scale in all of these domains.

3.2. Case Examples: Predictive Maintenance, Process Optimization, and System Prototyping

Predictive maintenance is one of the most common uses of modeling and simulation in modern business. Its goal is to predict when equipment will fail before it happens, which reduces unplanned downtime and extends the life of assets [49]. Engineers can use physics-based degradation models, statistical analysis, and machine learning algorithms to predict how things will wear out and fail under different operating conditions [50]. For instance, mathematical models of thermal ageing or fatigue crack propagation can be used with real-time sensor data, like vibration, temperature, and sound emissions, to find early signs of mechanical stress or component damage [51]. Condition-based maintenance strategies replace routine time-based inspections with targeted interventions exactly when they are needed [52]. This has become feasible due the combination of modeling, simulation, and continuous data acquisition. These kinds of predictive methods lower maintenance costs, make things safer, and make operations more efficient in a wide range of fields, including manufacturing, energy production, transportation, and critical infrastructure [53].

Process optimization represents another core domain where the integration of mathematical modeling and simulation delivers tangible industrial benefits [3]. By formulating detailed process models—whether for chemical reactors, thermal systems, or complex assembly lines—engineers can identify key variables and constraints that govern system performance. Techniques such as process simulation and optimization algorithms enable the exploration of design spaces, determination of optimal operating conditions, and evaluation of trade-offs between competing objectives such as cost, throughput, energy consumption, and environmental impact [54]. For instance, in the petrochemical industry, multi-phase flow models and reaction kinetics are coupled with numerical solvers to simulate refinery operations under various scenarios, informing decisions on catalyst selection, heat exchanger networks, and process intensification [55]. The result is a significant reduction in trial-and-error experimentation, shorter development cycles, and the ability to implement innovative solutions with a high degree of confidence in their viability and performance [56].

Beyond incremental improvements to existing systems, modeling and simulation also play a transformative role in system prototyping, enabling the rapid design, testing, and validation of novel products and technologies in a virtual environment [57]. Digital prototyping significantly reduces the need for costly and time-consuming physical iterations by allowing engineers to assess structural integrity, functional performance, and manufacturability at an early stage [58]. For example, in the development of complex mechanical assemblies or advanced materials, finite element analysis (FEA) and computational fluid dynamics (CFD) simulations are employed to predict stress distributions, heat transfer, and fluid behavior under operational loads [59,60]. In the context of additive manufacturing, virtual prototyping is particularly valuable for optimizing part geometries, minimizing support structures, and ensuring printability before physical fabrication begins [61,62].

3.3. Role of High-Performance Computing (HPC) and Cloud Computing

The increasing complexity and scale of modern mathematical models and simulations would be impractical to address without the computational capabilities provided by high-performance computing (HPC) [63]. Many of the physical processes modeled in advanced industrial applications—such as turbulent fluid flow [64], multi-phase reac-tions [65], or structural dynamics under extreme loads [66]—require the resolution of large systems of non-linear equations across fine spatial and temporal grids. HPC clusters and supercomputers, utilizing parallel architectures and distributed memory systems, enable the execution of these large-scale simulations within feasible timeframes. Numerical methods such as finite element analysis, direct numerical simulation, and large eddy simulation rely heavily on HPC resources to deliver results with high fidelity and acceptable turnaround times [67]. In this context, HPC sets to be an indispensable enabler, allowing researchers and engineers to test hypotheses, optimize designs, and validate models that would otherwise remain computationally inaccessible [68].

Complementing traditional HPC infrastructures, cloud computing has emerged as a flexible and scalable alternative for deploying computationally intensive modeling and simulation workflows [69]. Cloud platforms provide on-demand access to virtually unlimited computing power and storage capacity, democratizing the use of advanced simulations beyond institutions that own dedicated supercomputing facilities [70]. Engineers and researchers can run parameter sweeps, uncertainty quantification studies, and sensitivity analyses across distributed cloud environments, significantly accelerating development cycles while minimizing capital investments in hardware [71]. Moreover, cloud-based platforms often integrate seamlessly with collaborative tools, data lakes, and specialized simulation software, enabling geographically dispersed teams to co-develop models, share results, and coordinate complex engineering projects in real time [72]. This elasticity and accessibility have made cloud computing an increasingly attractive complement to traditional HPC, particularly for small- and medium-sized enterprises seeking to harness sophisticated modeling capabilities without prohibitive upfront costs [73].

Importantly, the convergence of HPC and cloud computing with emerging paradigms such as digital twins underscore their transformative role in the future of industrial simulation and control [74]. The vast data streams generated by IoT-enabled assets require significant computational resources for real-time assimilation, model updating, and decision support [75]. Hybrid computational frameworks that leverage both on-premise HPC clusters for intensive batch processing and cloud resources for elastic scaling provide a robust foundation for these data-driven applications. For example, in additive manufacturing, high-fidelity process simulations and in situ monitoring data can be integrated in near real time to adapt printing parameters dynamically, ensuring quality and efficiency [76]. As the volume, variety, and velocity of industrial data continue to expand, the strategic deployment of HPC and cloud resources will remain central to enabling predictive analytics, continuous optimization, and the full realization of adaptive and resilient digital twins.

4. From Simulation to Digital Twins

The concept of the digital twin represents one of the most significant advances in the application of modeling and simulation to modern industry and emerging technologies [77]. A digital twin extends the traditional notion of a numerical model by coupling it with continuous data streams from its physical counterpart, creating a dynamic virtual representation that evolves in real time [78]. This brings abstract simulations and operational reality closer, enabling predictive, adaptive, and prescriptive capabilities that were previously unattainable [79]. As industries constantly push to optimize performance, ensure reliability, and respond to changing operational contexts, the digital twin has emerged as an enabling tool, fusing robust mathematical models, advanced computation, and pervasive data integration into a single intelligent framework.

4.1. Defining a Digital Twin: Characteristics and Enabling Technologies

Fundamentally, a digital twin is a living virtual replica of a physical asset, procedure, or system that stays in sync with its real-world counterpart throughout its operational lifecycle [80]. It is more than just a high-fidelity simulation. By continuously assimilating real-time sensor data, which is used to update the state variables, boundary conditions, and model parameters of the underlying mathematical representation, this synchronization is achieved. A digital twin’s unique features include its capacity to replicate the physical entity’s current state, model its future behavior in various scenarios, and aid in decision making by offering actionable insights [81]. A digital twin, in contrast to static models, is intrinsically dynamic and adaptive, capable of changing as new operational data become available [82]. This feedback loop transforms the model into a predictive and prescriptive tool, offering significant advantages for asset management, process optimization, and risk mitigation [83].

The realization of digital twins relies on a suite of enabling technologies that bring together core disciplines such as computational modeling, data science, and high-performance computing [84]. Fundamental to this integration are IoT-enabled sensor networks, which generate the high-resolution data streams necessary for continuous model calibration and validation [85]. Cloud computing and edge computing architectures provide the computational power and scalability to process these data in near real time, facilitating the rapid updating of models and the delivery of insights to decision-makers on the ground [86]. Equally critical are data-driven algorithms, including machine learning techniques, which complement physics-based models by capturing behaviors that may be difficult to describe analytically [87]. For instance, surrogate modeling and reduced-order models can be employed to approximate complex phenomena efficiently, enabling fast simulations that are feasible for real-time applications [88]. Effective model integration in digital twin frameworks frequently requires co-simulation platforms capable of synchronizing heterogeneous solvers in both time and state space. Techniques such as the Functional Mock-up Interface (FMI) standard [89] enable model exchange and co-simulation between tools developed in different programming languages or modeling environments. Time synchronization is typically achieved via master algorithms that coordinate fixed- or variable-step solvers, while data mapping ensures that variables with different units, resolutions, or coordinate frames are consistently translated across models. This integration layer is critical for maintaining numerical stability and physical consistency when coupling multi-physics models with real-time data streams. Together, these technologies form the backbone of the digital twin ecosystem, ensuring its capacity to handle vast data volumes and deliver robust actionable outputs.

A distinctive aspect of the digital twin concept is its capacity to act not only as a passive mirror, but also as an active participant in the operation and control of its physical counterpart. Through advanced analytics and closed-loop feedback mechanisms, a digital twin can detect anomalies, predict system failures [90], and recommend or even autonomously implement corrective actions [91]. In manufacturing, for example, a digital twin of a production line can simulate the impact of adjusting process parameters in response to changing material properties or unexpected disturbances, thereby maintaining product quality and throughput [92]. Digital twins of bridges, buildings, or energy networks can predict structural deterioration or performance under stress in infrastructure management, enabling timely interventions that extend lifespans and improve safety [93]. The digital twin’s ability to adapt behavior, which is based on the combination of mathematical modeling, continuous sensing, and intelligent algorithms, makes it a key enabler of the shift to intelligent, resilient, and sustainable systems. Figure 3 depicts the digital twins’ pillar technologies.

4.2. The Transition from Static Models to Dynamic Continuously Updated Virtual Replicas

A fundamental change in how industries approach the monitoring, control, and optimization of complex systems can be seen in the transition from static mathematical models to dynamic continuously updated virtual replicas. Mathematical models have historically been powerful tools for design and off-line analysis, offering insight into system behavior under fixed parameters and assumed conditions. Static models are useful for scenario planning and design validation, but they are severely limited in their ability to reflect the real-time state of physical assets because they operate under changing conditions and external influences [94]. These restrictions frequently result in a discrepancy between theoretical predictions and actual system performance, necessitating frequent calibration, manual intervention, and conservative safety margins to account for uncertainty and variability.

By integrating mathematical models into a continuous data feedback loop, the digital twin paradigm bridges this gap and converts them from static approximations into dynamic self-updating representations of their physical counterparts [95]. In order to improve the digital twins’ predictions and keep them in line with reality, real-time sensor data streams provide current information about operational states, environmental factors, and system responses [96]. In order to ensure that the virtual replica accurately reflects the changing physical system, techniques like data assimilation, Kalman filtering, and adaptive parameter estimation enable the continuous calibration of model inputs and boundary conditions [97]. By incorporating continuous dynamic characteristics, this linkage enhances predictive maintenance, risk assessment, and resource allocation by enabling operators to simulate hypothetical scenarios, test control strategies, and forecast future states with a level of confidence that static models alone cannot provide.

The transition to dynamic virtual replicas is further supported by advances in data-driven modeling techniques that complement traditional physics-based formulations. Machine learning and statistical inference methods are increasingly integrated into digital twins to capture complex non-linear behaviors that may elude purely analytical descriptions [98]. For example, in additive manufacturing, real-time monitoring data on temperature gradients, layer deposition quality, and material properties can be fed into hybrid models that blend first-principles equations with trained predictive algorithms [99]. This synergy enhances the twins’ capacity to adapt to unexpected process variations, correct deviations autonomously, and optimize performance in situ.

While the conceptual advantages of transitioning to dynamic continuously updated digital twins are clear, their practical implementation presents a series of technical and operational challenges. Foremost among these is the integration of heterogeneous data sources, which often vary in sampling rates, formats, and quality, requiring robust pre-processing pipelines and data fusion algorithms to ensure coherence and reliability. Achieving low-latency synchronization between the physical and virtual systems demands both high-throughput communication infrastructures and computational architectures capable of sustaining real-time updates without compromising numerical stability. Furthermore, the continuous calibration of physics-based models with streaming data introduces non-trivial complexity in parameter estimation, particularly when dealing with noisy, incomplete, or asynchronous measurements. Ensuring interoperability across multi-physics and multi-scale models remains an equally significant barrier, as industrial digital twin deployments frequently necessitate the coupling of domain-specific solvers and legacy systems within a unified framework. Addressing these challenges requires not only advances in algorithms and computing resources, but also standardized protocols, scalable architectures, and cross-disciplinary collaboration between domain experts, data scientists, and software engineers.

4.3. Examples of Digital Twin Architectures: Cyber–Physical Systems and IoT Integration

Digital twin deployment relies heavily on robust cyber–physical system (CPS) architectures that seamlessly integrate control systems, sensor networks, and computational models into a single operational ecosystem [100]. Physical assets like machines, vehicles, or infrastructure components are outfitted with embedded sensors and actuators that gather and send real-time operational data in a typical CPS framework [101]. Computational models operating on edge devices, local servers, or cloud platforms then process this data, producing insights and control signals that affect the physical system’s behavior. A closed feedback loop created by the bi-directional communication between the digital and physical domains enables the system to continuously adjust to changing circumstances [102]. A CPS-enabled production line, for instance, can modify machining parameters in response to tool wear or material inconsistencies in smart manufacturing, preserving product quality and reducing waste with little assistance from humans [103]. To complement this discussion and provide a concise visual comparison,

Table 1. Comparison of representative digital twin architectures.

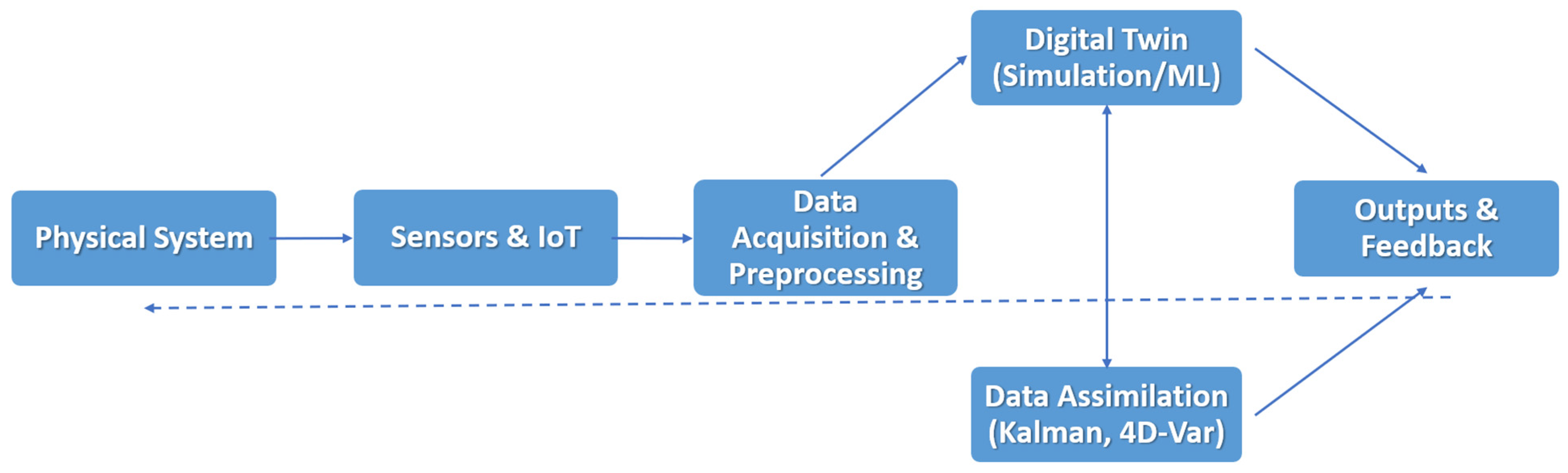
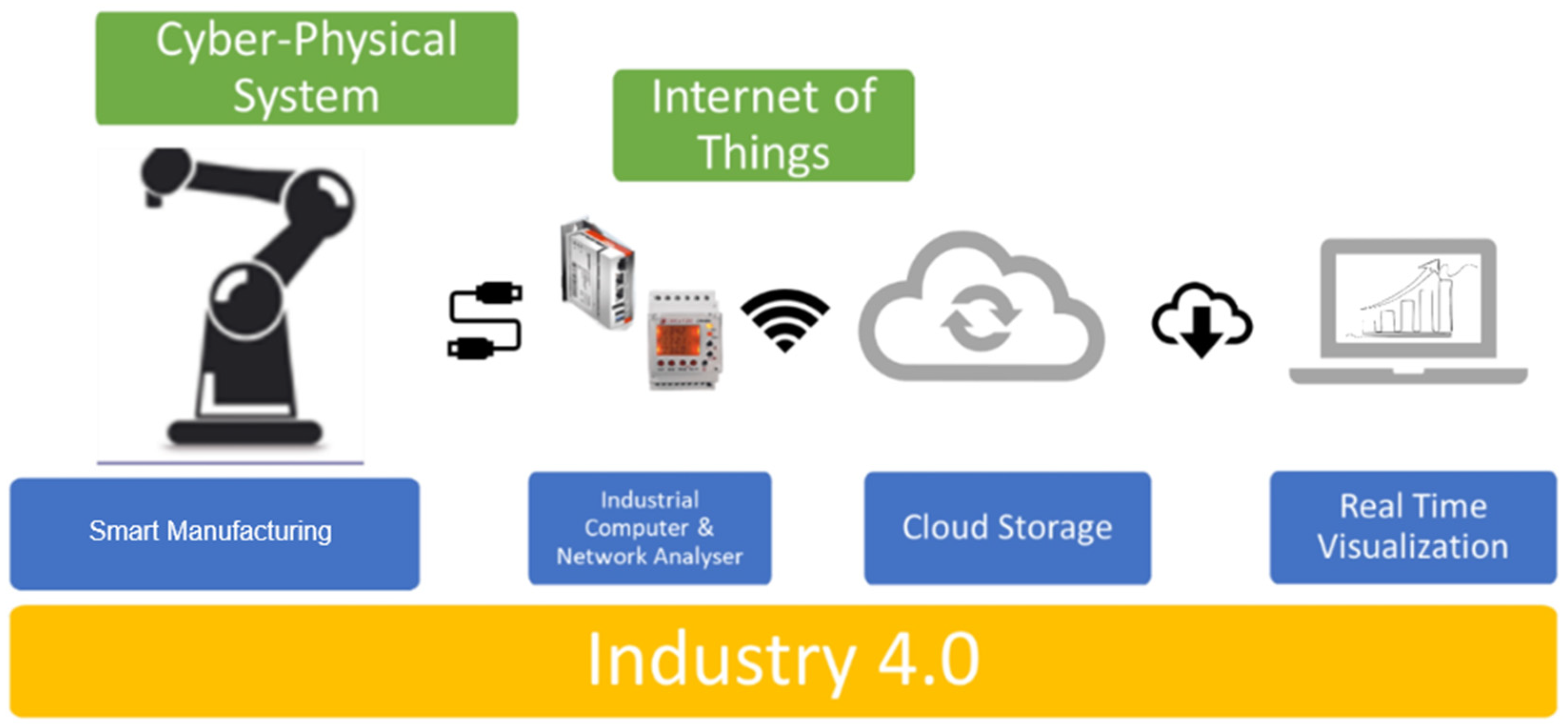
Architecture Type	Key Features	Advantages	Limitations	Example Applications	Real-Time Updating Method
Centralized Cloud-Based	All model computation and data processing handled in cloud servers	Scalable resources; easy remote access; integration with big data analytics	Higher latency; dependence on internet connectivity; potential data security concerns; susceptibility to WiFi latency in large-scale settings	Predictive maintenance in distributed manufacturing	Batch assimilation of sensor data into weak form FEM via cloud-based Kalman filtering
Edge-Enhanced Digital Twin	Real-time computation on local edge devices with selective cloud offloading	Low latency; resilient to connectivity disruptions; supports time-critical decision making	Limited computational power at the edge; higher hardware cost	Adaptive control in additive manufacturing processes	Localized FEM matrix recalibration with streaming sensor input; reduced-order modeling
Hybrid Cloud–Edge Architecture	Tasks split between edge (real-time control) and cloud (heavy analytics, long-term optimization)	Combines scalability with responsiveness; optimized workload distribution	Requires sophisticated orchestration; increased system complexity; latency bottlenecks if reliant on WiFi in distributed deployments	Smart grids, autonomous vehicles	Moving-horizon estimation for edge-level updates; cloud-based assimilation of long-term data
On-Premises HPC-Integrated Digital Twin	High-performance computing clusters within organization’s infrastructure	Handles very large-scale simulations; ensures data sovereignty	High capital and maintenance costs; limited elasticity	Aerospace simulation, nuclear plant operations	High-fidelity FEM weak form recalibration using parallel solvers and data assimilation filters
Federated/Distributed Digital Twin Network	Multiple interconnected twins sharing models/data without centralization	Enables cross-domain integration; preserves local data privacy	Complex coordination; risk of inconsistent model states	Urban infrastructure management across city districts	Distributed Kalman filtering and consensus-based FEM updating across nodes

summarizes representative digital twin architectures, outlining their key features, advantages, limitations, and example applications across different industrial domains.

A further limitation that warrants emphasis is the impact of WiFi latency in large-scale digital twin implementations. While cloud-based and hybrid architectures benefit from scalable computation and centralized data integration, reliance on standard WiFi connections introduces non-negligible delays when streaming high-frequency sensor data across multiple nodes. These delays, often in the order of tens to hundreds of milliseconds, can significantly degrade synchronization accuracy in latency-sensitive applications such as real-time process control, autonomous systems, or precision manufacturing. Moreover, as the number of connected devices increases, contention and packet loss can exacerbate latency issues, leading to instability in the feedback loop between the physical system and its digital counterpart. Addressing these limitations typically requires the adoption of advanced communication protocols (e.g., 5G, WiFi 6) or hybrid architectures that shift time-critical tasks to edge devices, thereby reducing dependence on high-latency wireless links.

A key enabler of such architectures is the widespread adoption of Internet of Things (IoT) technologies, which provide the connectivity and interoperability required to support large-scale distributed data acquisition and exchange [104]. IoT devices, ranging from simple wireless sensors to complex multi-modal measurement systems, generate the high-resolution continuous data streams that feed digital twins with up-to-date information about operational status, environmental context, and system performance [105]. IoT platforms also facilitate integration with enterprise resource planning (ERP) systems, supply chain management tools, and other business-level applications, allowing digital twins to serve not only as engineering tools, but also as strategic assets for decision support [106].

Examples of digital twin architecture that are representative of various industrial and technological domains show their versatility and transformative power. Drawing from the work on a Model-Based Design (MBD)-enhanced Asset Administration Shell for generic production line design [107], this case demonstrates how standardized digital representation and consistent model integration can enable scalable digital twin deployment in complex manufacturing environments. In this application, an MBD-augmented Asset Administration Shell encapsulates both semantic metadata and interlinked functional models across the production line, enabling the digital twin to not only replicate physical asset behavior, but also to adapt dynamically as configurations evolve. The approach enhances interoperability by using standardized object models, while also enabling real-time synchronization between design, simulation, and operational data, thus supporting modular design reuse, streamlined commissioning, and digital validation across heterogeneous components.

Also, in another published literature study [108], the authors develop a spatial-temporal interactive integration network (STIIN) embedded within a digital twin framework. The STIIN architecture combines a time–memory gate and spatial–temporal fusion gate to extract robust features even from limited thermal data, enabling the digital twin to perform real-time thermal error compensation with exceptional accuracy. Empirical results show an over 90% reduction in positioning error and an over 80% reduction in machining error, demonstrating that digital twin systems can deliver high-fidelity error mitigation even under small-sample data constraints. This highlights the twins’ potential in precision machining, where continuous adaptation to thermal dynamics is essential for maintaining accuracy and productivity.

Digital twins of additive manufacturing processes in advanced manufacturing use multi-physics models in conjunction with Internet of Things-enabled process monitoring to guarantee consistent layer quality, minimize errors, and optimize print parameters in real time [108]. In the transportation industry, digital twins of railway systems integrate IoT sensors mounted on rolling stock and tracks with predictive wear and vibration models, enabling proactive maintenance scheduling and enhanced passenger safety [109,110]. Urban infrastructure is another rapidly evolving domain, where digital twins of bridges, tunnels, and smart buildings combine structural health monitoring, real-time data feeds, and simulation models to predict degradation, assess risk, and inform maintenance strategies [111]. These examples highlight the essential role of CPS and IoT integration in making digital twins a practical, scalable reality, transforming them from static engineering tools into intelligent adaptive systems that deliver measurable value across the entire lifecycle of physical assets and processes. To illustrate the defining features, technological enablers, and representative applications discussed in this section,

Table 2. Key characteristics, enabling technologies, and representative applications of digital twins.

Aspect	Description	Representative Application	Associated Mathematical Techniques
Core Characteristics	Dynamic real-time virtual replica synchronized with its physical counterpart via continuous data feedback	Predictive asset management for wind turbines	Kalman Filtering (EKF, EnKF), Particle Filtering, Data Assimilation Schemes
Data Integration	High-resolution sensor networks, IoT-enabled data streams, seamless assimilation into computational models	Smart grids with real-time demand response	Bayesian Inference, Sensor Fusion Algorithms, Statistical Signal Processing
Computational Backbone	High-performance computing (HPC), cloud and edge computing for real-time simulation and analytics	Adaptive process control in additive manufacturing	Reduced-Order Modeling (POD, DMD), Parallel Numerical Solvers, Multi-Scale Simulation
Hybrid Modeling	Combination of physics-based models and data-driven algorithms for adaptive non-linear behavior	Condition monitoring and anomaly detection in complex machinery	Hybrid PDE–ML Frameworks, System Identification Methods, Neural ODEs
Cyber–Physical Architecture	Closed-loop feedback between physical systems and digital models through embedded control systems	Smart production lines with automated parameter adjustment	Optimal Control Theory, Model Predictive Control (MPC), Stability Analysis
Scalability and Interoperability	Integration with ERP systems, supply chain tools, and multi-stakeholder platforms	Urban infrastructure digital twins for bridges and tunnels	Graph Theory, Network Optimization, Distributed Computing Methods
Key Benefits	Enhanced operational efficiency, predictive maintenance, optimized resource allocation, risk mitigation	Oil and gas pipeline monitoring and failure prevention	Reliability Modeling, Probabilistic Risk Assessment, Uncertainty Quantification

summarizes the core characteristics and practical examples of digital twin implementations across various industrial contexts.

5. Challenges and Future Directions for Applied Mathematics in the Digital Twin Era

As digital twin technology develops further, it raises a number of immense computational and mathematical challenges that need to be resolved in order to realize its full potential. New algorithms that can assimilate continuous data streams, maintain numerical stability, and ensure interoperability across multi-physics and multi-scale domains are needed to make the transition from static modeling to dynamic, real-time, and data-enriched virtual replicas. At the same time, sophisticated techniques that connect rigorous theory with real-world implementation in HPC and cloud environments are required to quantify uncertainty, validate hybrid models, and ensure computational efficiency at industrial scales. Because of these technical requirements, applied mathematics can flourish and spur innovation at the sectors of systems engineering, data science, modeling, and simulation. Mathematical sciences are in a position to facilitate the development of the next generation of automation techniques, decision support tools, and resilient services that will characterize the future of intelligent, adaptable industrial ecosystems by addressing these issues through interdisciplinary cooperation.

5.1. Algorithmic and Computational Challenges

The creation of reliable algorithms for real-time model updating, data assimilation, and numerical stability is a key obstacle to realizing the full potential of digital twins. Digital twins require constant synchronization between the physical system and its virtual counterpart through a continuous influx of heterogeneous frequently high-frequency data streams, unlike traditional static simulations. Advanced data assimilation techniques, such as Kalman filtering, sequential Monte Carlo methods, and ensemble-based approaches, must be customized for complex high-dimensional industrial systems in order to integrate these data effectively. These techniques must handle sensor noise, missing data, and potential anomalies without compromising computational tractability, in addition to accurately updating statistics. It is equally important to maintain numerical stability during continuous updates; robust solvers, adaptive time-stripping, and error control are required to ensure that evolving models remain consistent, dependable, and convertible with physical constraints over extended operational lifetimes.

Scalability, computational efficiency, and flexible deployment represent additional pillars that must be addressed to transition digital twin concepts from laboratory-scale demonstrations to industrial-scale implementations [112,113,114]. Many high-fidelity simulations—particularly those involving multi-physics, large domains, or fine resolutions—impose prohibitive computational costs if executed serially or on limited hardware [115]. High-performance computing (HPC) environments provide the parallelism required for such intensive workloads, but practical deployment increasingly demands the elasticity and accessibility offered by cloud computing and edge computing paradigms [116]. Efficient load balancing, distributed processing, and model partitioning are essential to ensure that real-time performance requirements are met, even as system complexity grows [117]. Emerging approaches such as surrogate modeling, reduced-order models, and adaptive mesh refinement offer promising avenues for retaining accuracy while dramatically reducing computational demands. Together, these advances enable digital twins to deliver timely insights without incurring prohibitive resource expenditures, a prerequisite for widespread industrial adoption.

Equally important is achieving interoperability among multi-physics and multi-scale models, which is vital for representing the full spectrum of physical phenomena that modern engineered systems embody [118]. Many industrial applications, from aerospace to energy networks, require the simultaneous resolution of coupled processes such as fluid dynamics [119], structural mechanics [120], thermal effects [121], and chemical reactions [122], often across scales ranging from microscopic material properties to system-level behavior. Developing frameworks that can integrate these disparate domains into cohesive numerically stable simulations remains a formidable challenge. Coupled solvers, co-simulation platforms, and standardized data exchange protocols play key roles in enabling modular flexible architectures that allow various specialized models to interact seamlessly [123,124]. Achieving this level of interoperability not only enhances the physical realism of digital twins, but also supports their scalability and maintainability, laying the groundwork for robust, extensible, and virtual ecosystems that evolve alongside technological and operational demands.

5.2. Managing Uncertainty and Validation

A fundamental requirement for the credibility and practical utility of digital twins is the rigorous treatment of uncertainty quantification (UQ) [125] and risk assessment [126]. Unlike deterministic simulations that assume perfectly known parameters and boundary conditions, real-world systems inevitably involve uncertainties stemming from material properties, environmental conditions, operational variability, and measurement noise. Robust UQ methods—such as probabilistic modeling, stochastic differential equations, and Monte Carlo sampling—enable the systematic propagation of these uncertainties through the computational models [127]. This allows stakeholders to quantify confidence intervals, identify critical risk factors, and assess the probability of rare but high-impact events. By explicitly capturing uncertainty, engineers can design systems and control strategies that are resilient to variability and robust against unexpected deviations, thereby minimizing downtime, ensuring safety, and informing strategic decision making under uncertainty [128].

Model calibration and validation become particularly challenging when the available data are incomplete, noisy, or collected under non-ideal operating conditions, a common scenario in industrial environments [129]. To maintain accuracy and relevance, digital twins must be continuously calibrated against empirical observations to reconcile discrepancies between predicted and observed behavior. This demands advanced parameter estimation techniques, inverse modeling, and optimization frameworks capable of handling sparse or noisy datasets [130]. Bayesian inference and regularization methods are frequently employed to stabilize the calibration process, providing plausible parameter distributions rather than point estimates [131]. Equally important is validation, which involves comparing model predictions with independent datasets to confirm that the twins’ behavior remains consistent across different conditions and timeframes [132]. This iterative process of calibration and validation is crucial for building trust in the digital twins’ outputs, especially when these outputs inform critical operational decisions.

As digital twins increasingly integrate hybrid physics-based and data-driven models, ensuring their reliability and trustworthiness introduces new layers of complexity [133]. Hybrid models capitalize on the strengths of both approaches, using mechanistic equations to anchor physical realism while employing machine learning to capture complex relationships that elude analytical description [134]. However, such combinations can introduce unintended biases, overfitting, or instabilities if not carefully designed and validated [135]. Rigorous frameworks are needed to test hybrid models under a wide range of scenarios, verify consistency with fundamental physical laws, and quantify residual uncertainties introduced by the data-driven components. Explainable AI methods and transparent model structures are gaining traction as means to enhance interpretability and stakeholder confidence in these complex systems [136]. Ultimately, the credibility of hybrid digital twins rests on their ability to deliver reliable predictions, maintain physical consistency, and adapt responsibly to changing data streams [137], a goal that demands continuous methodological refinement at the interface of applied mathematics, computational science, and domain-specific engineering.

5.3. Emerging Research Frontiers

With the potential to unlock greater levels of adaptability and predictive power, the rapidly changing landscape of digital twins is advancing new research frontiers in hybrid modeling and digital twin enrichment with machine learning. Physics-based models may struggle to capture complex non-linear interactions or unknown phenomena that are not present in real-world systems, even though they offer interpretability and a foundation in established laws. Conversely, pure data-driven models are capable of learning subtle patterns from empirical data, but they frequently lack generalizability outside of training conditions. By integrating machine learning components into physics-based frameworks, hybrid modeling aims to combine these advantages and create adaptive models that can learn corrections or parameter updates in real time [138]. Research is moving closer to integrating techniques like neural operators, Physics-Informed Neural Networks (PINNs), and surrogate modeling to create digital twins that dynamically refine their predictions in response to new data, bridging theory and data in previously unimaginable ways [139].

Another critical direction involves model order reduction [140] and real-time optimization [141], both of which are essential for making high-fidelity simulations practical for operational use. High-dimensional multi-physics models, while accurate, are often too computationally demanding for real-time application in industrial settings. Model order reduction techniques—such as proper orthogonal decomposition, balanced truncation, and reduced basis methods—systematically distill large models into lower-dimensional representations that preserve the dominant dynamics with minimal loss of fidelity [142]. These compact surrogates allow for rapid simulation, sensitivity analysis, and control synthesis on time scales compatible with online decision making. Coupled with advanced real-time optimization algorithms, reduced-order models empower digital twins to continuously evaluate alternative scenarios, adjust control variables, and recommend interventions, all while maintaining the computational responsiveness required by modern smart factories, infrastructure systems, and autonomous operations [143].

A further frontier is the development of adaptive algorithms for streaming data and continuous decision support, which is critical for deploying digital twins in complex rapidly changing environments [144]. In contrast to traditional batch-processing approaches, modern applications demand algorithms that can ingest, process, and learn from incoming data streams without interruption [145]. Techniques such as online learning [146], incremental parameter estimation [147], and adaptive filtering [148] enable digital twins to update predictions and control strategies on the fly, maintaining relevance even as system behavior evolves due to wear, external influences, or unforeseen disturbances. Research into robust data fusion, outlier detection, and anomaly response is equally important for ensuring that digital twins remain resilient to imperfect or malicious data [149]. These adaptive capabilities position digital twins not merely as passive monitoring tools, but as intelligent agents for continuous decision support, capable of informing human operators, driving automated control, and supporting the transition to next-generation autonomous and resilient industrial systems.

5.4. Enabling Interdisciplinary Innovation

The full realization of digital twin technologies depends not only on advances in mathematics and computational methods, but also on fostering synergies between mathematicians, engineers, and data scientists. Modern industrial problems rarely align neatly within a single disciplinary domain; instead, they demand integrated solutions that combine rigorous mathematical modeling, practical engineering insights, and sophisticated data analytics. Mathematicians contribute by developing robust theoretical frameworks, numerical methods, and algorithms that underpin the stability and accuracy of digital twins. Engineers provide domain-specific knowledge, operational expertise, and the physical context necessary to translate models into deployable tools. Data scientists enrich this collaboration with expertise in large-scale data handling, machine learning, and artificial intelligence. Effective digital twin projects thrive when these communities collaborate closely, co-design models, and iterate solutions in response to real-world challenges. Such synergies accelerate technological adoption and help ensure that digital twins deliver tangible measurable value to industry [149].

To harness these synergies, new collaborative frameworks for cross-domain problem solving are emerging as essential enablers. These frameworks take the form of interdisciplinary research consortia, joint academic–industrial laboratories, and open innovation ecosystems that bring together diverse stakeholders under a shared mission. Modern digital twin development often involves co-simulation platforms, shared data environments, and standardized interoperability protocols that allow teams to integrate disparate modeling components and data sources into cohesive systems. Collaborative software environments and version-controlled digital twin repositories further facilitate distributed development while preserving intellectual rigor and traceability [150]. By embedding collaboration into the technical workflow, these frameworks ensure that digital twins remain adaptable, extensible, and aligned with evolving industrial needs, creating an innovation pipeline that is responsive, inclusive, and ready to tackle the next generation of complex systems.

The impact of these interdisciplinary advances extends far beyond improved technical performance; they fundamentally reshape decision making, automation, and next-generation innovative services [151]. As digital twins mature, they serve as powerful decision support tools that allow stakeholders to test scenarios, evaluate risks, and identify optimal courses of action with unprecedented speed and confidence. Integrated with automated control systems, they enable dynamic process adaptation and self-optimizing operations that enhance efficiency and resilience [152]. In sectors such as healthcare [153], energy [154], transportation [155], and smart cities [156], the digital twin technology is already delivering new service models, from predictive diagnostics and personalized treatment planning to intelligent grid management and responsive urban infrastructure. These contemporary applications illustrate how the convergence of applied mathematics, engineering expertise, and data science does not merely solve today’s problems, but actively shapes the industrial and societal systems of tomorrow. To consolidate the core challenges, research directions, and interdisciplinary opportunities outlined in this section,

Table 3. Summary of mathematical and computational challenges and emerging opportunities in the development of digital twins.

Focus Area	Key Aspects	Illustrative Context
Real-Time Algorithms	Model updating, data assimilation, numerical stability	Continuous monitoring in smart grids
Scalability and Efficiency	HPC and cloud integration, surrogate modeling, computational cost reduction	Large-scale simulations for aerospace or energy systems
Multi-Physics Interoperability	Coupling of diverse models, modular frameworks, standardized data exchange	Co-simulation of thermal–structural interactions in engines
Uncertainty Management	Uncertainty quantification (UQ), risk assessment, propagation of parameter variability	Predictive maintenance for critical infrastructure
Calibration and Validation	Parameter estimation with sparse/noisy data, Bayesian inference, model trustworthiness	Industrial process control and fault detection
Hybrid Modeling Frontiers	Integration of machine learning with physics-based models, surrogate modeling, PINNs	Adaptive quality control in additive manufacturing
Real-Time Optimization	Model order reduction, fast scenario analysis, dynamic control synthesis	Autonomous robotics and smart factories
Adaptive Algorithms	Streaming data, online learning, anomaly detection, continuous decision support	Real-time urban mobility management
Interdisciplinary Collaboration	Synergy among mathematicians, engineers, and data scientists; open innovation frameworks; co-development tools	Multi-partner industrial–academic digital twin consortia
Societal and Industrial Impact	Decision support, automation, next-generation services	Smart cities, resilient infrastructure, personalized medicine

presents a concise summary highlighting the key focus areas shaping the future of applied mathematics within the context of digital twins.

6. Future Perspectives

• The role of emerging technologies: AI, edge computing, and 5G/6G.

As digital twins evolve in complexity and scale, emerging enabling technologies such as artificial intelligence (AI), edge computing, and next-generation communication infrastructures like 5G and forthcoming 6G networks will play an indispensable role in unlocking their full potential [157]. AI offers unprecedented capabilities for learning from vast heterogeneous datasets, enabling digital twins to infer latent relationships, adapt to unforeseen system behaviors, and make predictive or prescriptive recommendations beyond what deterministic models can achieve alone [158]. Edge computing complements these advances by relocating data processing and analytics closer to the source of data generation, thereby reducing latency, minimizing bandwidth requirements, and enabling near-instantaneous feedback loops, which are essential for mission-critical applications [159]. Meanwhile, 5G and future 6G networks promise ultra-reliable low-latency communications with massive device connectivity, making it feasible to deploy vast sensor networks and distributed twin instances across geographically dispersed assets [160]. Together, these technologies have the ability to transform digital twins from complementary technologies to a vital tool in modern industry.

• Toward self-adaptive autonomous digital twins.

A transformative frontier for digital twins lies in their progression from reactive human-supervised tools to fully self-adaptive and autonomous systems capable of acting on insights without direct operator intervention. Achieving this vision requires embedding advanced cognitive capabilities into digital twin architectures, enabling them to perceive operational changes, learn optimal responses, and implement corrective actions in real time [161]. This evolvement demands breakthroughs in online learning algorithms, robust self-optimization techniques, and resilient control strategies that maintain safe reliable performance under dynamic conditions [162]. In autonomous manufacturing, for example, a self-adaptive digital twin could detect a deviation in process quality, adjust production parameters instantly, and coordinate with other machines to rebalance workloads, all while keeping human oversight minimal but informed [163]. The integration of such autonomous behaviors has the potential to lead to next-generation smart factories, critical infrastructure systems, and adaptive supply chains that continuously self-correct and optimize, embodying the core principles of Industry 5.0 and beyond.

• Ethical, security, and governance aspects.

The proliferation of digital twins across safety-critical sectors and data-rich environ-ments inevitably raises profound ethical, security, and governance challenges that must be addressed proactively to ensure responsible deployment [164]. As digital twins depend on the continuous acquisition and processing of sensitive operational data, robust cybersecurity measures become non-negotiable to safeguard intellectual property, protect privacy, and defend against malicious attacks that could disrupt physical operations [165]. Beyond technical security, ethical considerations include the transparency and explainability of hybrid models, the risk of algorithmic biases embedded in data-driven components, and the accountability for decisions made by partially or fully autonomous systems [166]. Governance frameworks must, therefore, evolve to define clear regulatory standards, certification protocols, and accountability structures that balance innovation with societal trust [167]. Establishing these standards will prove crucial in securing stakeholder confidence and legitimizing the widespread adoption of digital twins in critical sectors such as healthcare, energy, and transportation.

• Vision for academia–industry synergy and skill development.

Realizing the full promise of the digital twin technolgy requires cultivating a collab-orative ecosystem that bridges academia and industry while fostering the development of the specialized skills needed to sustain this rapidly advancing field [168]. Universities, research institutes, and industrial partners must co-create curricula, joint research programs, and experiential learning opportunities that prepare the next generation of engineers, data scientists, and applied mathematicians to work seamlessly across disciplinary boundaries [169]. Multidisciplinary training in computational science, systems engineering, data analytics, and domain-specific knowledge will be crucial to address the growing demand for professionals capable of designing, implementing, and governing complex digital twin solutions [170]. Simultaneously, industry-driven innovation hubs and testbeds can provide real-world contexts for applied research, accelerating the translation of theoretical advances into deployable technologies [171]. By nurturing this academia–industry synergy, the global community should ensure a robust talent pipeline and an innovation ecosystem ready to shape the resilient, adaptive, and intelligent systems that the digital twin vision ultimately promises.

Future research should focus on the development of modular open-source digital twin frameworks that can be readily adapted across diverse industrial domains without incurring prohibitive customization costs. Advancements in real-time multi-physics simulation—particularly when integrated with edge-computing capabilities—will be critical to enabling on-site analytics and control in latency-sensitive environments. Parallel efforts are needed to establish scalable uncertainty quantification methodologies coupled with decision support algorithms capable of functioning reliably under conditions of incomplete or noisy data. The incorporation of AI-driven anomaly detection within digital twin systems offers significant potential for predictive diagnostics and self-healing capabilities. Progress in these areas will depend on coordinated cross-disciplinary initiatives uniting computational sciences, control engineering, data analytics, and domain-specific expertise to translate digital twin concepts from proof-of-concept prototypes into robust large-scale operational solutions.

Building on these thematic priorities, several specific research questions emerge. How can model order reduction techniques be systematically integrated with streaming data assimilation to enable real-time control in computationally intensive multi-physics environments? Which hybrid modeling strategies best reconcile the interpretability of physics-based methods with the adaptability of machine learning, particularly under evolving and unpredictable operating conditions? What standardized interoperability protocols can ensure seamless coupling among domain-specific solvers, legacy systems, and distributed cloud-edge infrastructures? In uncertainty quantification, which approaches are most effective for propagating and managing stochastic effects in high-dimensional time-dependent systems? Finally, as self-adaptive digital twins mature, what governance frameworks and validation procedures will guarantee transparent, trustworthy, and human-aligned decision making? Addressing these questions will require sustained interdisciplinary collaboration that combines advances in applied mathematics, computational modeling, domain engineering, and ethical oversight.

Collectively, these perspectives outline a forward-looking operational paradigm in which cutting-edge computational technologies, autonomous capabilities, robust governance mechanisms, and strong industry–academia partnerships converge to re-define the scope and impact of digital twin systems. By simultaneously advancing technical innovation and addressing ethical, regulatory, and societal considerations, the international research and industrial communities can position digital twins as secure, intelligent, and durable facilitators of next-generation innovation.

7. Conclusions

This work has explored the multidisciplinary evolving sector where rigorous mathematical modeling, advanced computational methods, and real-time data integration converge to shape the digital twin technology. By tracing the evolution from foundational applied mathematics through computational modeling and high-performance simulation to the deployment of cyber–physical systems enriched by IoT and AI, we have underscored how digital twins transform static models into dynamic, adaptive, and operationally impactful tools. Examples including smart manufacturing, additive technologies, critical infrastructure, and emerging service models illustrate the breadth of applications already benefiting from this synthesis. Equally, this work has highlighted the algorithmic, computational, and validation challenges that must be addressed to maintain trust, scalability, and physical fidelity as these virtual representations become increasingly autonomous and embedded within industrial operations.

Looking ahead, there is a clear need for intensified research in the sectors of of applied mathematics, computational science, and systems engineering to advance the capabilities of next-generation digital twins. Priorities include developing hybrid modeling frameworks that unify physics-based rigor with adaptive data-driven learning, designing robust methods for uncertainty quantification and validation, and building resilient ethical governance models to guide deployment in sensitive domains. The societal and economic potential is immense: digital twins promise to enhance operational efficiency, accelerate innovation cycles, support sustainable resource use, and enable smarter decision making in sectors ranging from manufacturing and healthcare to cities and energy grids. Realizing this vision dictates sustained interdisciplinary collaboration, targeted skill development, and a global commitment to translating mathematical excellence into transformative industrial and societal outcomes.