Abstract
Integrating renewable energy, particularly wind power, into modern power systems introduces challenges concerning stability and reliability. These issues require enhanced regulation to balance power supply with load demand. Flexible loads and energy storage provide viable solutions to stabilize the grid without relying on new resources. This paper proposes building thermostatically controlled loads (BTLs), such as heating, ventilation, and air conditioning (HVAC) systems, as flexible demand-side management tools to address the challenges of intermittent energy sources. A new concept is introduced, portraying BTLs as a stochastic battery with losses, offering a compact representation of their dynamics. BTLs’ thermal characteristics, user-defined set points, and ambient temperature changes determine the power limits and energy capacity of this stochastic battery. The model is simulated using DIgSILENT Power Factory, which includes thermal power plants, gas turbines, wind power plants, and BTLs. A dynamic dispatch strategy optimizes power generation while utilizing BTLs to balance grid fluctuations caused by variable wind energy. Performance analysis shows that integrating BTLs with conventional thermal plants can reduce variability and improve grid stability. The study highlights the dual role of simulating overall flexibility and applying dynamic dispatch strategies to enhance power systems with high renewable energy integration.
1. Introduction
The uncertainty and variability in the electrical power supply systems have been observed due to the massive integration of intermittent wind energy into modern power grids. While traditional power plants can be controlled to generate power at certain times, wind-generated power varies with the weather and is inconsistent. This intermittency presents significant difficulties in managing the real-time balance of supply and demand needed for steady grid operations [1,2]. These fluctuations must be corrected immediately by grid operators to avoid power quality problems, frequency variations, and, in extreme cases, grid instability. Power balancing operations have emerged as the key concern in modern grid management to meet these challenges. The balance between supply and demand has been maintained using fast-start-up thermal power stations or spinning reserves. However, these methods are expensive, time-consuming, and often negatively impact the environment [3]. The growing share of variable renewable power sources requires using other, more innovative, less costly supply-side and demand-side resources and a sophisticated control system [4,5].
Of the emerging strategies, demand-side flexibility, especially building thermostatically controlled loads (BTLs), has received considerable interest. BTLs include heating, ventilation, and air conditioning (HVAC) systems commonly installed in residential, commercial, and public buildings and provide a large amount of flexible load potential [6,7]. When grouped and managed effectively, BTLs can offer important secondary services such as load following, peak clipping, and frequency regulation to improve the grid’s stability while maintaining the users’ comfort [8,9,10]. This paper proposes a detailed framework for utilizing the loading capacities of BTLs to offer grid ancillary services through Automatic Generation Control (AGC) in modern power systems with integrated large-scale wind power. The proposed strategy also mitigates the problem of forecasting errors through the demand response of BTLs integrated with thermal energy systems to improve the stability of the grid and the overall operation.
1.1. Related Work
Variabilities in wind power generation have remained a major issue in modern power systems. Previous works tackled this problem by constructing mathematical models to predict wind variability and control strategies to reduce its detrimental effects on the grid [11,12,13]. Nevertheless, the reliance on conventional reserves, including thermal and gas-fired power plants, was expensive and detrimental to the environment [5,14]. Recent work has moved to the demand side to add flexibility for dealing with wind-related imbalances [5,14]. For instance, studies showed that when BTLs are connected in parallel, they can store excess wind power during times of excess and provide cover during scarce supply [15,16]. This dual capability made BTLs an attractive solution for connecting wind energy to the grid. The capability of BTLs as demand-side resources for grid balancing has been studied widely. Initial studies proved that they could perform frequency regulation and load-following services by flexibly controlling their operation based on the grid needs [17,18]. BTLs could substantially decrease the traditional requirement for spinning and non-spinning reserves while simultaneously ensuring customer satisfaction [19,20]. Based on this, other studies focused on the interaction between BTLs and AGC systems, an essential mechanism in frequency control. When AGC was enabled for BTLs, the proposed approach demonstrated the ability to quickly compensate for the grid imbalances due to fluctuations in renewable resources such as wind power. These studies affirmed that BTLs could be a prospective and affordable solution to conventional reserves for handling short-term grid volatility [21,22].
Recently, there has been rapid progress in real-time and distributed control strategies that have increased the use of BTLs in grid services. Multilevel control structures are developed that allow BTLs to function autonomously and integrate with grid-level systems such as AGC [13,23]. One significant improvement was applying dynamic dispatch strategies involving power control from conventional generation units and flexible loads [6,24]. These strategies have been used in the BTLs, wind power, and thermal generation models to demonstrate the effectiveness of forecasting and reduction in errors to enhance the ability of the grid [25,26]. Some pilot and case studies have described real-world applications of BTL-based flexibility [22,27]. These studies may comprise large-scale simulations of power systems with wind, thermal generation, and flexible loads. Several studies reveal that when BTLs are synchronized with AGC, the problem of over- or under-generation can be solved, and there is no need for conventional backup power [28,29]. For example, one research study showed that pooling the flexibility of BTLs enabled optimal integration of renewable electricity resources without compromising grid stability during high load demand [30,31].
1.2. Research Gap
Despite the advancement in modelling BTLs and exploring the use of BTLs for grid services, some gaps exist. First, existing studies are based on assumptions about users’ behaviour and environment, which are often oversimplified. Moreover, although the stochastic battery model estimates overall flexibility, its application in conjunction with dynamic grid processes, including AGC, is still limited. Further, few studies have addressed integrating the total flexibility of BTLs with dispatch techniques that optimally balance supply and demand resources. Consequently, as more grids integrate intermittent renewable resources, there is a growing demand for models and approaches that estimate BTL flexibility and showcase its application in managing supply-demand imbalance from intermittent renewable energy sources.
1.3. Paper Contribution
This paper presents an innovative, dynamic power system AGC solution designed for intermittent power grids, ensuring system stability by effectively regulating frequency fluctuations. Additionally, operating reserves are integrated through BTLs, enhancing AGC functionality by supporting active power balancing services. A key feature of this work is the representation of BTL flexibility via a stochastic battery model. This model offers a concise and efficient description of power constraints and energy storage capacity, influenced by critical parameters such as thermal properties, ambient temperature, and user-defined settings. A strategic dispatch framework is developed to allocate power from the inherent flexibility of BTLs along with the Thermal power plant to optimize grid balancing. The proposed methodology is modelled and simulated using DIgSILENT PowerFactory (https://www.digsilent.de/en/), demonstrating its effectiveness in managing grids with high levels of wind power integration. The results underscore the model’s potential to enhance grid stability and operational efficiency in systems with fluctuating renewable energy contributions.
1.4. Organization of the Paper
2. System Modelling and Methodology
The proposed system model is shown in Figure 1, showing the functioning of the AGC system, which is essential for the balance, stability, and efficiency of a power system of 6022 MVA. The AGC is responsible for the operation of power generation from various sources such as the Thermal Power Station (TPS), Wind Energy Generation Station (WEGS), and Gas-Fired Power Station (GFPS). Also, the model incorporates the BTLs that serve as an energy storage system that can either receive or provide power during peak demand and an external grid connection that can buy or sell power at any time. The AGC continuously supervises the Area Control Error (ACE), a crucial parameter of the mismatch between planned and actual power in the system. The AGC can control each source’s power output by monitoring real-time power deviations to maintain the grid’s stability. This involves ensuring that the system frequency is within a certain range, the supply is equal to the demand, and that no component is overloaded. For wind power, the AGC also considers available wind energy to enhance its contribution to the grid. Moreover, the external grid connection is another advantage of the system since it allows it to buy power in case of power rationing or sell excess power when production exceeds the demand. This real-time integration makes it possible to coordinate all the power supply and storage systems in real time, increasing the power grid’s efficiency. The capacities of the conventional and wind-generating systems are shown in Figure 1.
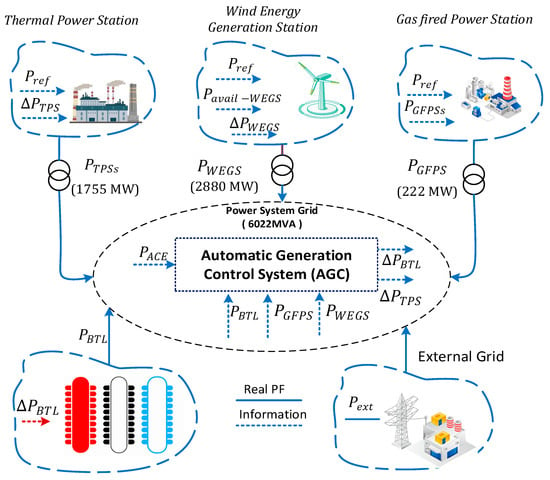
Figure 1.
Proposed Model of the Automatic Generation Control System; the real PF shows the power flow between generation units and the power grid, Pref denotes the reference power.
2.1. Modelling of the Building Thermostatic Loads
Generalized Battery Model
Generalized battery models create basic representations of groups of power signals. These models provide essential functionality for measuring the total flexibility of several connected loads. The generalized battery model utilizes several signals that fulfil particular requirements.
Positive parameters specify the model written completely as stochastic battery model . The effective energy capacities (down) of are defined as: .
2.2. BTL Individual Model
2.2.1. Modelling of Dead Band
A baseline hybrid-system representation of a Building Thermostatic Load (BTL) is introduced, serving as the foundation for the simulation analyses carried out in this study. In this model, the temperature evolution of a BTL is expressed as
The binary signal represents the unit’s state, where = 0 denotes OFF and = 1 denotes ON. The unit changes its operating state whenever the temperature surpasses the predefined threshold limits set by the user.
In this context, Δ denotes the dead band, Here is the dead band, which represents the temperature setpoint, and the process noise captures the impact of external disturbances. The constants are defined in terms: .
The constant exists between thermal resistance, thermal capacitance and coefficient of performance as defined [8,32]. The power rating of cooling systems has positive values, contrary to the negative values used by heating systems. Table 1 presents a residential air conditioning system’s key operational parameters and standard reference values. The first-order hybrid model serves as a dimensional basic approximation but requires advanced models for particular scenarios that involve west-facing home attic cooling systems exposed to external elements. This paper does not include a complete analysis of modelling uncertainty in Equation (2). A BTL expends average power at rates during its cycle operation.

Table 1.
Representative parameter values commonly used for modelling a residential air-conditioning system.
Here, measures the duration of the ON state and defines the total cycle time between ON states. The proof of this statement is straightforward, where .
2.2.2. Continuous Power Model
Examining the continuous thermal model represents an easier way to interpret the dead-band model. All analytical work will rely on this model for approximation [33]. The BTLs operate within a power range from when accepting continuous power input according to this dynamics model
The model contains which shows zero-mean properties according to [34]. A mean value of disturbance could be eliminated through an appropriate modification of parameter . The power signal requires limitations to sustain temperature within the specified dead-band region . The initial temperature evaluation for this uninterrupted model requires the condition . This continuous power model obtains its specification from parameters . The BTL requires nominal power according to its set point for maintenance purposes, as expressed below.
2.2.3. Aggregate Flexibility
Consider a diverse collection of BTLs indexed by k. Let denote the nominal power consumed by the kth BTL. Each BTL can accommodate fluctuations in power consumption around its nominal value, provided they remain within user-defined comfort thresholds, defined as:
This power signal set quantifies the kth BTL’s flexibility relative to the nominal. Their Minkowski sum gives the aggregate flexibility of BTLs.
The geometry of this set is inherently complex. We aim to derive concise characterizations of the aggregate flexibility set and show that generalized battery models can bind it.
Theorem 1.
A collection consisting of heterogeneous BTLs modelled by the continuous-power model with parameters χk will produce aggregate flexibility U through where the parameters
are given by
and ,, where
and is arbitrary . The following examination focuses on sufficient descriptions of U. The available set of battery parameters B(∅)⊆U contains several options. The following observations are presented:
Theorem 2.
Consider a collection of heterogeneous BTLs modelled by the continuous-power model with parameters χk. Fix α > 0, and define . Fix With Let satisfy the constant
The overall flexibility of the collection fulfils these conditions Where . Further, if , the causal power allocation strategy satisfies the dead-band constraints .s.
According to Theorem 2, the aggregate flexibility set U can be characterized sufficiently by multiple battery models from . Different situations may require sufficient battery models that achieve maximum energy capacity C, maximum charge power limit or maximum discharge power limit . Table 2 demonstrates three distinct scenarios, including the maximum capacity C and the highest limits for charging rate or discharging rate . Theorem 2 leads to the results by using as , , . The relationship between the necessary battery specifications from and sufficient specifications from contains a gap throughout the U segment. The exact characterization of our battery model works for identical BTL populations. More specifically, we have:

Table 2.
Evaluating Generalized Battery Models for Diverse BTL Collections.
Corollary 1.
Consider a collection of homogeneous BTLs, modelled by the continuous-power model with parameters . Then where , , , and .
2.3. Modelling of the Power Plant Units
This subsection elaborates on modelling TPS, WEGS, and GFPS, drawing upon previously established methodologies [10]. These models align with the guidelines set by the International Council on Large Electric Systems (CIGRE), conforming to international best practices for power system modelling and performance analysis. The primary focus of this model is to achieve effective active power control and accurately simulate the long-term dynamic characteristics of WEGSs. The WEGS, as mentioned in Figure 2, the power controller generates a turbine reference signal ( and adjusts operations in response to variations in the system’s reference signal (. This process considers the governor’s feedback () and the power recorded at the point of common coupling . The system employs the signal to constrain the output of the PI controller, which directs the generator to produce the current active power component () based on the wind turbine’s reference input. Wind energy systems offer faster dynamic responses than hydroelectric systems, typically reacting to grid demand changes within 2–4 s. While hydroelectric plants often take longer to provide the secondary response for AGC, solar energy systems lack rotational inertia. This absence limits their capability to stabilize the grid during sudden load or generation fluctuations, making wind turbines more efficient in maintaining grid stability.
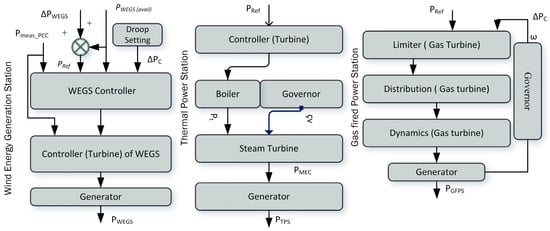
Figure 2.
Modelling of WEGS, TPS, and GFPS Units.
As illustrated in Figure 2, the TPS model is intended to manage the active power by operating its mechanisms. The steam turbine block provides mechanical output power () in the form of rotational speed, which is a shaft speed. The effects of steam pressure have been incorporated into the model by using the symbol () steam in the equation and the governor control (cv). The process starts with the load reference set point, one of the main parameters affecting the boiler’s work. The boiler controls steam pressure in real-time to match the turbine output to the grid requirements and the time of steam generation processes. This paper highlights the benefits of integrating power generation systems with rotational inertia, including wind turbines and TPS, in tackling grid stability issues and renewable energy integration. With their response capability and inertia, wind power plants are a significant advantage over hydroelectric and inertia-less solar power stations. These models stress using fast-response energy sources such as WEGS and TPS for new, renewable-based power systems.
2.4. Control Architecture
The system aims to provide a reliable frequency regulation service through active control of BTL aggregations. The system operator defines a regulation signal at 4 s sampling intervals based on ACE to become the AGC command. We have selected a centralized control system design for the implementation. Participation in the regulation of ancillary service markets requires this selection based on reliability standards. At each sampling instant, the aggregator compares r(t) with the measured aggregate power deviation . The instantaneous power drawn by BTLs equals while represents their baseline power. Ahead of time, the aggregation needs an agreed-upon contractual arrangement to set as the base power consumption for its future delivery period. The population of BTLs needs power release to the grid when causing some ON units to be switched OFF. The population of BTLs will require additional energy consumption when r(t) exceeds δ(t). An operating protocol must activate some inactive units. A priority-stack-based control strategy determines which BTLs must change their status between ON and OFF for optimal results. The strategy operates as a feedback controller to provide resistance against disturbances caused by occupancy patterns and solar radiation, together with model error in TCL dynamics, while maintaining system stability. The system control framework appears in Figure 1.
2.4.1. Priority Stacks
The current moment brings forward a situation where remains inferior to . All BTL operating units need to decrease their power usage. The population needs to shut down operational units which are currently active. Turning OFF units that will switch off sooner provides the most beneficial solution. To calculate natural imminence, BTLs utilize temperature distance to switch boundaries through the measurement , under the condition that . The temperature distance receives normalization treatment as part of heterogeneity management. A stack of ON priority units contains the devices that are currently turned ON. The components in this stack follow their ordering according to the priority measure . We establish the OFF-priority stack of units which are OFF by sorting them according to with . The distance to the switching boundary represents an additional way to determine imminence. The ON priority stack functions to prioritize units that will automatically switch OFF by directing them toward the top of the list immediately after power activation. The system begins by activating the unit with the top priority, followed by activating units with successively lower priority settings until the necessary control objective is met. The stack-based priority control system uses a minimum ON/OFF control method, preventing equipment from short-cycling while decreasing mechanical wear. The illustration of priority stacks appears in Figure 3 [33]. The accessible units located in the lower parts of the ON stack receive index values starting from 1 and going upwards to N, while the units of the OFF stack get their indexes inverted from N0 downward to 1. The system enables units to activate or deactivate when equals the calculated amount between r(t) and δ(t). Algorithm 1 summarizes the priority stack-based control algorithm.
| Algorithm 1. Hierarchical Priority-Based Control Algorithm for Aggregated BTL Management |
| Loop |
| Obtain |
| Develop a well-defined hierarchical priority framework. |
| read ; |
| Compute ; |
| If |
| Find ; |
| Activate units identified by |
| Else if Then |
| Find ; |
| De-activate units identified by |
| End if |
| End loop |
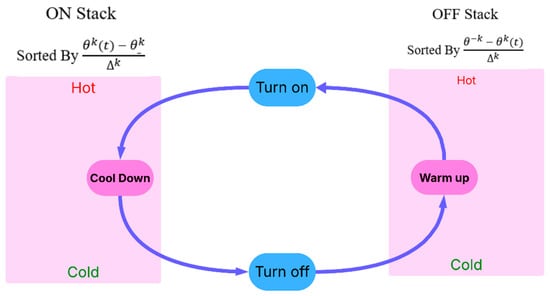
Figure 3.
Priority-based activation and deactivation queues.
2.4.2. Practical Considerations
The implementation of direct load control depends on minimum sensor measurements of power and temperature at a 0.25 Hz sampling rate for each BTL. The thermostat directly provides set points and temperature measurements, but implementing the necessary power measurement solution requires extra equipment. To determine with and estimate values from the temperature data run-time algorithms can be applied to each BTL for system identification. Subsequently, a locally embedded controller calculates for each device. Each aggregator receives the priority criterion together with the power consumption from all BTLs. Using the collected data, the aggregator constructs the priority stack to compute the control action of the upcoming sample. The BTLs receive the command from the aggregator through broadcast transmission, which their local controllers execute. The delay found in the control loop system determines the quality of power rate regulations that can be delivered. The scheme poses low operational costs for both computation and communication infrastructure.
3. Performance Validation
The system model in Figure 1 is simulated in DIgSilent PowerFactory to leverage the ancillary services from BTLs in modern power systems. In this regard, the generation profiles of WEGS and TPS over 10 h are shown in Figure 4. Substantial differences between actual and forecasted wind power plant outputs are considered in this paper, which generates the area control error. The TPS and BTL operating reserves suppress the resultant error between the load and generation. Figure 5 shows the dispatch strategy to effectively allocate the secondary reserves from TPS or BTLs.
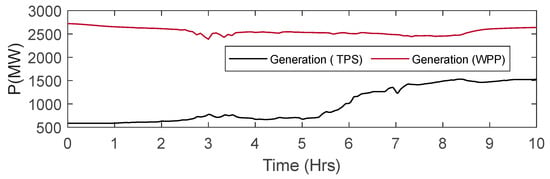
Figure 4.
Generation from the wind energy generation system and the thermal power station; TPS: Thermal power station, WPP: Wind power plant.
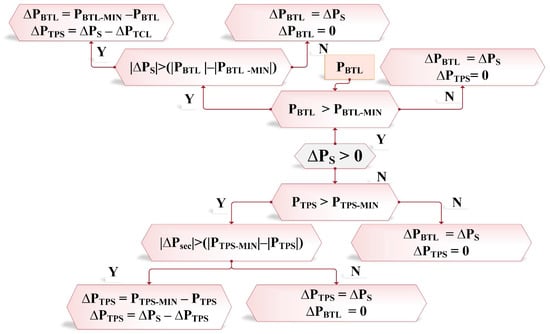
Figure 5.
Proposed Dynamic Dispatch Strategy.
A total of 1000 diverse BTLs form the population under examination. The simulations utilize a high-precision hybrid modelling approach for each BTL, ensuring enhanced accuracy and reliability in the computational analysis. Table 3 lists the model parameters operating under their nominal condition. The BTL parameters in heterogeneous collections receive their values randomly from a uniform distribution that extends 10% above and below the nominal values. Each thermal device resistance value is drawn randomly from , when stands for nominal resistance value. The ambient temperature maintains a static position at 32 °C while the BTL population operates with randomized initial temperatures and states.

Table 3.
Reserves capacities.
In Figure 5, in the case of positive regulation (Δ, the AGC immediately directs the BTLs to adjust their consumption, while TPSs respond more swiftly to negative regulation than BTL systems. Reducing power generation from wind power stations is more beneficial and cost-effective than increasing the load on BTLs. TPSs can be quickly adjusted, providing a flexible and efficient solution for grid balancing. Contrarily, augmenting the load on BTLs is less efficient and incurs higher costs. These discrepancies disturb the power grid’s supply-demand equilibrium and grid frequency, requiring prompt corrective measures to maintain stability. The simulations evaluate the effectiveness of the proposed model, and the capacities and regulating power reserves of the WEGS, TPS, and BTLs are provided in Table 3.
Therefore, any frequency variation in the system generates the ACE. Subsequently, the creation of the ACE activates the AGC service to harness the power supply from the TPS and BTLs. The power imbalances between varying load and supply in Figure 6a are reduced using reserve power from TPS and BTL. The GFPS and WEGS contribute to the primary response, while BTLs and TPS provide only a secondary response, as shown in Figure 6b. BTL units offer a significant ±21.5 MW capacity for power regulation within the AGC framework.
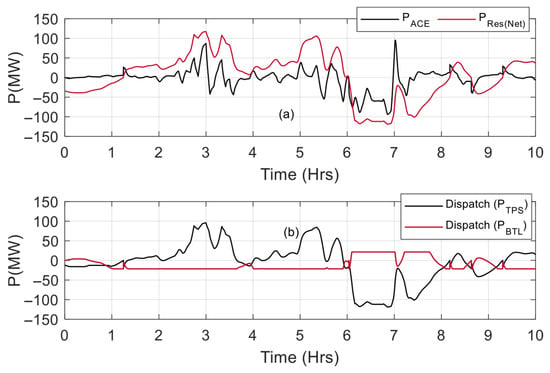
Figure 6.
(a) Secondary Reserves and ACE signal, (b) Dispatch Power from TPS and BTL.
Figure 7 illustrates the change in ACE with and without using AGC. The red line depicts ACE when AGC is not in operation and values are relatively farther from the zero line, suggesting frequent changes in power discrepancy. Contrarily, the black line, which depicts ACE with AGC, has smaller fluctuations, which proves that AGC minimizes errors and maintains system stability. This emphasizes AGC’s responsibility to reduce fluctuations and ensure the integrity of the grid through constant control of the power supply to meet the demand.
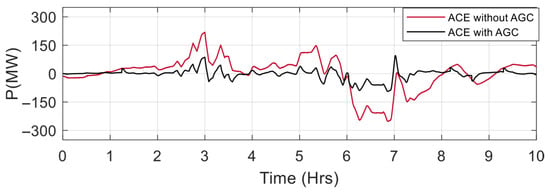
Figure 7.
Area Control Error Comparison with and without AGC.
The comparative bar chart, as shown in Figure 8, indicates that AGC significantly reduces ACE compared to the scenario without AGC. Without AGC, errors exhibit larger deviations, reaching peaks of ±150 MW, particularly at time intervals 4–8. With AGC, these deviations are effectively minimized, keeping errors within tighter bounds (e.g., reduced to ±90 MW), improving power system stability, and ensuring better frequency and power balance. This highlights AGC’s critical role in maintaining grid reliability. Figure 9 shows frequency deviations (Δf) reduced by the AGC, keeping them tightly controlled around the nominal value of 50 MW over 10 h. Despite minor fluctuations, especially between 4 and 7 h, AGC effectively stabilizes the frequency within a narrow range (49.98 MW to 51.02 MW), ensuring system stability.
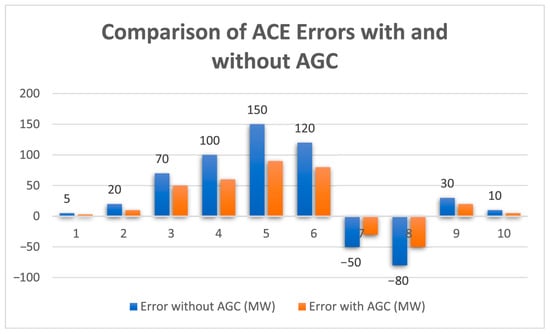
Figure 8.
Error Comparison.
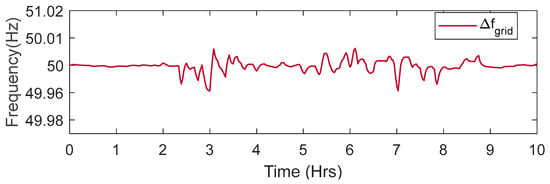
Figure 9.
Frequency deviations after the AGC response.
4. Conclusions and Future Work
The large-scale integration of intermittent wind energy into modern power systems presents significant grid reliability and stability challenges. This paper addresses these challenges by demonstrating the potential of Building Thermostatically Controlled Loads (BTLs), such as HVAC systems, as a flexible demand-side management tool. By modelling the aggregated flexibility of BTLs as a stochastic battery with losses, we provide a concise yet comprehensive representation of their thermal and operational dynamics, offering a novel approach to grid balancing. The simulation model developed in DIgSILENT PowerFactory successfully integrates diverse systems, including large gas turbines, thermal power plants, wind energy, and BTLs. The proposed dynamic dispatch strategy effectively utilizes BTL flexibility to mitigate fluctuations caused by intermittent wind energy, optimizing the operation of conventional generating units while ensuring grid stability. The results confirm that BTLs, when integrated with both traditional and renewable power generation sources, can significantly reduce variability and intermittency, thereby enhancing grid resilience and serving as an economically viable resource for systems with high renewable penetration. This work highlighted the dual advantages of representing BTL flexibility through a stochastic model and applying dynamic dispatch strategies to improve large-scale renewable-integrated power systems’ performance, stability, and reliability.
Future research will focus on integrating AI-based forecasting for load and renewable generation, developing adaptive real-time dispatch under uncertainty, and scaling the approach to urban and regional systems. Additional directions include coupling BTLs with other flexible resources and aligning the methodology with market and policy frameworks to enable broader adoption. These advancements will further improve renewable-rich power systems’ sustainable and reliable operation.
Author Contributions
Conceptualization, Z.U.; Methodology, Z.U.; Software, Z.U.; Validation, G.G.; Formal analysis, G.G.; Investigation, K.U. and A.S.; Resources, K.U. and A.S.; Writing—original draft, Z.U. and K.U.; Writing—review & editing, G.G. and A.S.; Visualization, K.U.; Supervision, G.G.; Project administration, A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
This publication was produced while attending the course doctoral programme in electrical engineering at the Polytechnic Institute of Milan, XXXVIII cycle, with the support of a scholarship funded by Ministerial Decree No. 351 of 9.4.2022, under the PNRR—funded by the European Union—NextGenerationEU—Mission 4 “Education and Research,” Component 1 “Strengthening the supply of education services: from kindergartens to universities”—Investment 3.4 “Advanced university teaching and skills,” and Investment 4.1 “Expanding the number of PhDs and innovative PhDs for public administration and cultural heritage”.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Li, Y.; Shen, X. An Operational Situations Characterization Methodology for Wind Speed Sensors of Wind Farms Against Natural Weather Events. IEEE Trans. Ind. Inform. 2024, 20, 9244–9254. [Google Scholar] [CrossRef]
- Rosales-Asensio, E.; Diez, D.B.; Sarmento, P. Electricity balancing challenges for markets with high variable renewable generation. Renew. Sustain. Energy Rev. 2024, 189, 113918. [Google Scholar] [CrossRef]
- Shahzad, S.; Jasińska, E. Renewable Revolution: A Review of Strategic Flexibility in Future Power Systems. Sustainability 2024, 16, 5454. [Google Scholar] [CrossRef]
- Chen, W.; Yang, W.; Qi, H.; Shi, Z.; Geng, H. Coordinated Power Reserve Control of Wind Farm for Frequency Regulation. IEEE Access 2023, 11, 55465–55473. [Google Scholar] [CrossRef]
- Ullah, K.; Tunio, M.A.; Ullah, Z.; Ejaz, M.T.; Anwar, M.J.; Ahsan, M.; Tandon, R. Ancillary Services from Wind and Solar Energy in Modern Power Grids: A Comprehensive Review and Simulation Study. J. Renew. Sustain. Energy 2024, 16, 3. [Google Scholar] [CrossRef]
- Granitsas, I.M. Aggregation of Thermostatically Controlled Loads for Fast Power System Services: From Theory to Practice. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2024. [Google Scholar] [CrossRef]
- Wei, C.-G.; Shangguan, X.-C.; He, Y.; Zhang, C.-K.; Xu, D. Delay-Dependent Stability Evaluation for Temperature Control Load Participating in Load Frequency Control of Microgrid. IEEE Trans. Ind. Electron. 2024, 72, 449–459. [Google Scholar] [CrossRef]
- Ullah, Z.; Ullah, K.; Gruosso, G. Using Controlled Thermostatic Loads in Buildings as Auxiliary Services to the Power Grid: An Investigation with Thoroughly Simulated Case Study. Int. J. Energy Res. 2024, 1, 5581128. [Google Scholar] [CrossRef]
- Sekyere, Y.O.; Effah, F.B.; Okyere, P.Y. Optimally Tuned Cascaded FOPI-FOPIDN with Improved PSO for Load Frequency Control in Interconnected Power Systems with RES. J. Electr. Syst. Inf. Technol. 2024, 11, 25. [Google Scholar] [CrossRef]
- Ullah, Z.; Gruosso, G.; Ullah, K.; Mehmood, F. Leveraging Ancillary Services from Building Thermostatic Loads in Power Grids. In Proceedings of the 2024 3rd International Conference Energy Transition Mediterranean Area (SyNERGY MED), Limassol, Cyprus, 21–23 October 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Gui, Y.; Jiang, S.; Bai, L.; Xue, Y.; Wang, H.; Reidt, J. Review of Challenges and Research Opportunities for Control of Transmission Grids. IEEE Access 2024, 12, 94543–94569. [Google Scholar] [CrossRef]
- Timmers, V.; Egea-Àlvarez, A.; Gkountaras, A.; Xu, L. Control and power balancing of an off-grid wind turbine with co-located electrolyzer. IEEE Trans. Sustain. Energy 2024, 15, 2349–2360. [Google Scholar] [CrossRef]
- Li, C.; Feng, C.; Li, J.; Hu, D.; Zhu, X. Comprehensive Frequency Regulation Control Strategy of Thermal Power Generating Unit and ESS Considering Flexible Load Simultaneously Participating in AGC. J. Energy Storage 2023, 58, 106394. [Google Scholar] [CrossRef]
- Hussain, S.; Lai, C.; Eicker, U. Flexibility: Literature Review on Concepts, Modeling, and Provision Method in Smart Grid. Sustain. Energy Grids Netw. 2023, 35, 101113. [Google Scholar] [CrossRef]
- Ullah, Z.; Ullah, K.; Diaz-Londono, C.; Gruosso, G.; Basit, A. Enhancing Grid Operation with Electric Vehicle Integration in Automatic Generation Control. Energies 2023, 16, 7118. [Google Scholar] [CrossRef]
- Enescu, D.; Mazza, A.; Chicco, G. Concepts and Representations to Analyse the Grid Services Provided by Electrical Systems and Buildings. In Sustainability in Energy and Buildings 2023; Springer: Cham, Switzerland, 2024; pp. 771–782. [Google Scholar] [CrossRef]
- Córdova, S.; Cañizares, C.A.; Lorca, Á.; Olivares, D.E. Aggregate Modeling of Thermostatically Controlled Loads for Microgrid Energy Management Systems. IEEE Trans. Smart Grid 2023, 14, 4169–4181. [Google Scholar] [CrossRef]
- Tian, X.; Liu, L.; Shen, G. A Review on the Mathematical Models of Thermostatically Controlled Load. Archit. Intell. 2024, 3, 33. [Google Scholar] [CrossRef]
- Langner, F.; Wang, W.; Frahm, M.; Hagenmeyer, V. Model Predictive Control of Distributed Energy Resources in Residential Buildings Considering Forecast Uncertainties. Energy Build. 2024, 303, 113753. [Google Scholar] [CrossRef]
- Barala, C.P.; Firdous, A.; Mathuria, P.; Bhakar, R. Bi-level Framework for Coordination between Thermostatically Controlled Loads and Distribution System for Flexibility. Electr. Power Syst. Res. 2024, 230, 110221. [Google Scholar] [CrossRef]
- Ahumada, C.; Cárdenas, R.; Saez, D.; Guerrero, J.M. Secondary Control Strategies for Frequency Restoration in Islanded Microgrids with Consideration of Communication Delays. IEEE Trans. Smart Grid 2015, 7, 1430–1441. [Google Scholar] [CrossRef]
- Bashash, S.; Fathy, H.K. Modeling and Control of Aggregate Air Conditioning Loads for Robust Renewable Power Management. IEEE Trans. Control Syst. Technol. 2012, 21, 1318–1327. [Google Scholar] [CrossRef]
- Ranginkaman, S.; Mashhour, E.; Saniei, M. Bidding Strategy of the Virtual Power Plant Consisting of Thermal Loads Controlled by Thermostats for Providing Primary Frequency Control Ancillary Service. Sustain. Energy Grids Netw. 2024, 38, 101242. [Google Scholar] [CrossRef]
- Gasca, M.V.; Ibáñez, F.; Pozo, D. Flexibility Quantification of Thermostatically Controlled Loads for Demand Response Applications. Electr. Power Syst. Res. 2022, 202, 107592. [Google Scholar] [CrossRef]
- Parshin, M.; Majidi, M.; Ibanez, F.; Pozo, D. On the Use of Thermostatically Controlled Loads for Frequency Control. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Ma, K.; Liu, P.; Yang, J.; Guan, X. Control and Communication for Demand Response with Thermostatically Controlled Loads; Springer: Cham, Switzerland, 2023. [Google Scholar] [CrossRef]
- Lakshmanan, V.; Marinelli, M.; Hu, J.; Bindner, H.W. Experimental Analysis of Flexibility Change with Different Levels of Power Reduction by Demand Response Activation on Thermostatically Controlled Loads. Electr. Power Compon. Syst. 2017, 45, 88–98. [Google Scholar] [CrossRef]
- Ma, K.; Yuan, C.; Yang, J.; Liu, Z.; Guan, X. Switched Control Strategies of Aggregated Commercial HVAC Systems for Demand Response in Smart Grids. Energies 2017, 10, 953. [Google Scholar] [CrossRef]
- Zhao, B.; Cao, X.; Zhang, S.; Ren, J.; Li, J. Day-Ahead Energy Management of a Smart Building Energy System Aggregated with Electrical Vehicles Based on Distributionally Robust Optimization. Build. Simul. 2025, 18, 339–352. [Google Scholar] [CrossRef]
- Lakshmanan, V.; Marinelli, M.; Hu, J.; Bindner, H. Provision of Secondary Frequency Control via Demand Response Activation on Thermostatically Controlled Loads: Solutions and Experiences from Denmark. Appl. Energy 2016, 173, 470–480. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, P.; Li, N.; Yan, W.J. Multi-Period Optimal Scheduling of Building Loads Based on Accurate Virtual Battery Model. Energy Build. 2025, 327, 115046. [Google Scholar] [CrossRef]
- Mathieu, J.L.; Koch, S.; Callaway, D.S. State Estimation and Control of Electric Loads to Manage Real-Time Energy Imbalance. IEEE Trans. Power Syst. 2012, 28, 430–440. [Google Scholar] [CrossRef]
- Hao, H.; Sanandaji, B.M.; Poolla, K.; Vincent, T.L. Aggregate Flexibility of Thermostatically Controlled Loads. IEEE Trans. Power Syst. 2014, 30, 189–198. [Google Scholar] [CrossRef]
- Malhame, R.; Chong, C.-Y. Electric Load Model Synthesis by Diffusion Approximation of a High-Order Hybrid-State Stochastic System. IEEE Trans. Autom. Control 1985, 30, 854–860. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).