An Efficient and Practical 2D FEM-Based Framework for AC Resistance Modeling of Litz Wire Windings
Abstract
1. Introduction
2. High-Frequency Loss Mechanisms in Conductors
2.1. Frequency-Dependent Loss Mechanisms in Conductors: Skin and Proximity Effects
2.2. Analytical Solutions for an Infinitely Long Isolated Conductor
3. Segment-Based Geometric Modeling and Mesh Optimization
3.1. Polygonal Discretization of Circular Conductors in 2D FEM
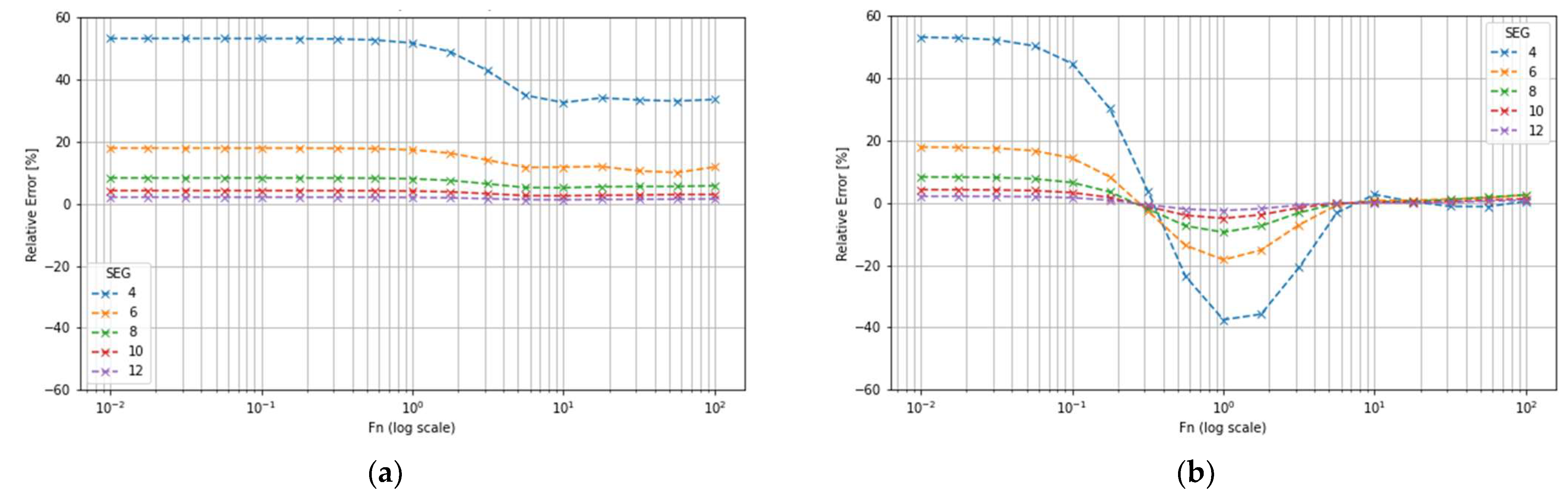
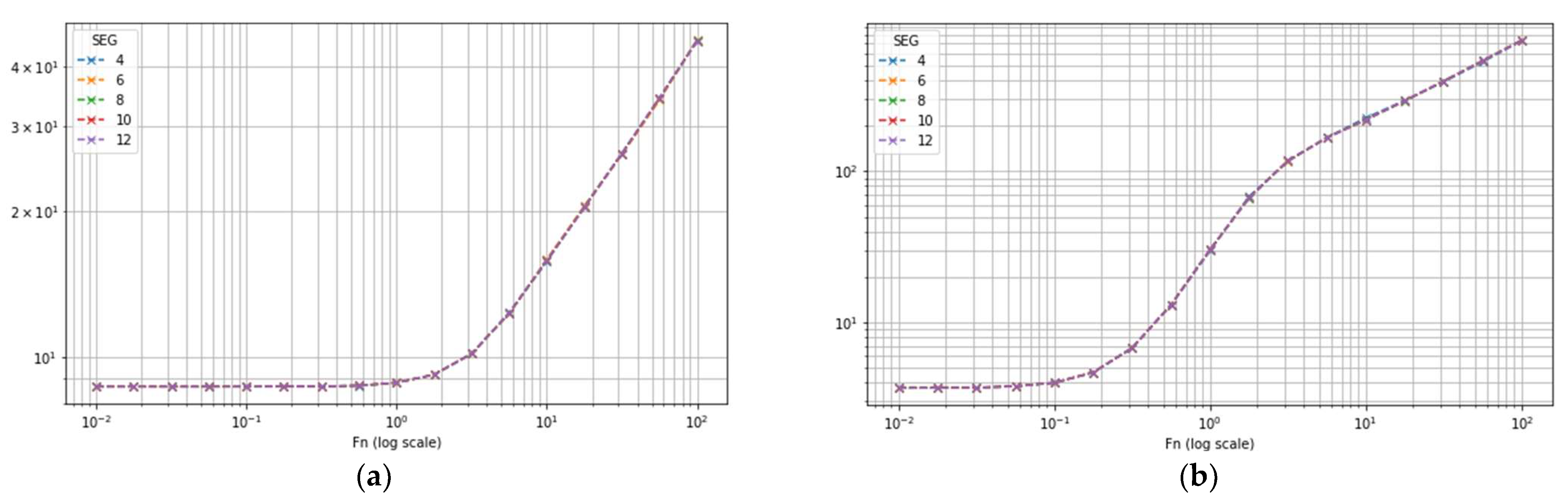
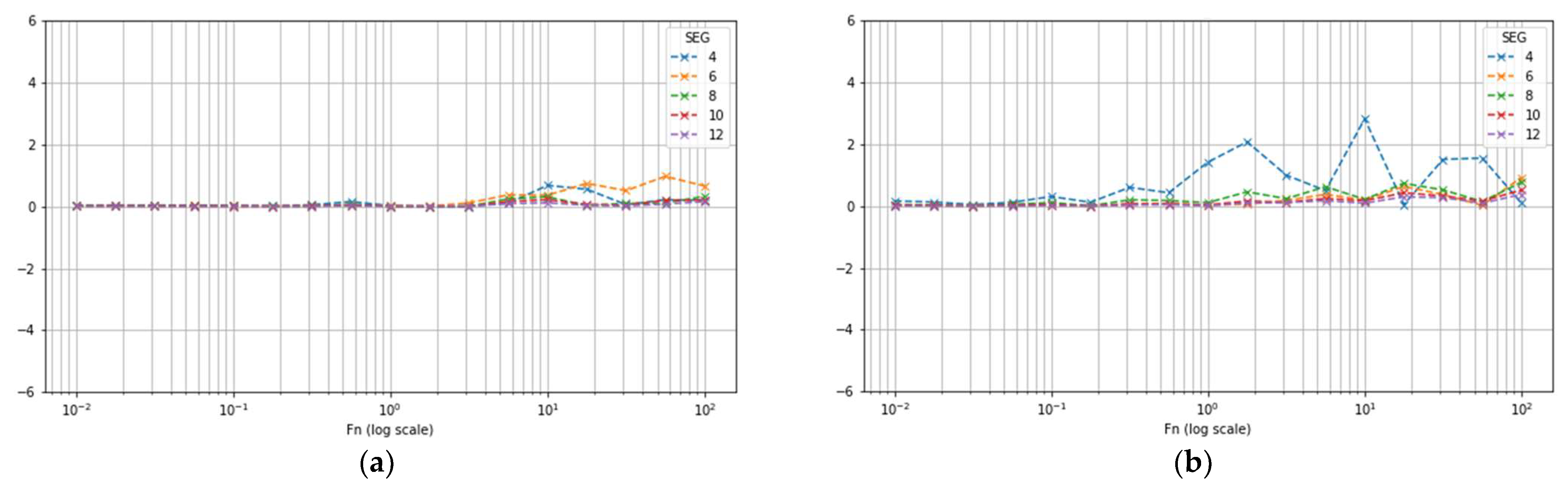
3.2. Segment-Based Error Compensation Through Mathematical Fitting Models
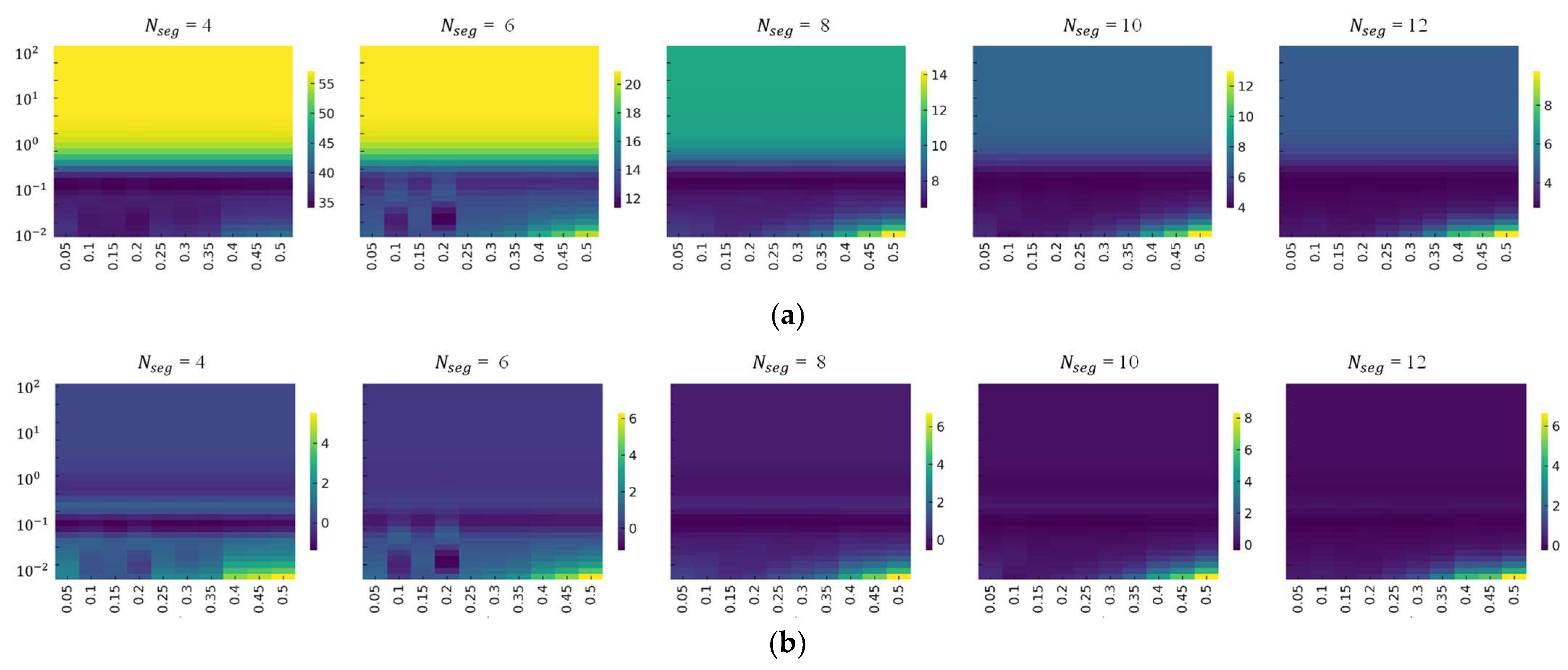
3.3. Meshing Optimization for Low Element Count
4. Experimental Validation of the Proposed 2D FEM-Based Modeling Approach
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jaritz, M.; Biela, J. Analytical Model for the Thermal Resistance of Windings Consisting of Solid or Litz Wire. In Proceedings of the 2013 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–10. [Google Scholar]
- Baek, S.; Bhattacharya, S. Analytical Modeling and Implementation of a Coaxially Wound Transformer with Integrated Filter Inductance for Isolated Soft-Switching DC–DC Converters. IEEE Trans. Ind. Electron. 2018, 65, 2245–2255. [Google Scholar] [CrossRef]
- Ahmed, D.; Wang, L. Optimal Area-Product Model (OAPM) Based Non-Iterative Analytical Design Methodology for Litz-Wired High-Frequency Gapped-Transformer (LHFGT) in LLC Converters. IEEE Access 2020, 8, 18134–18148. [Google Scholar] [CrossRef]
- Deng, Q.; Liu, J.; Czarkowski, D.; Kazimierczuk, M.K.; Bojarski, M.; Zhou, H. Frequency-Dependent Resistance of Litz-Wire Square Solenoid Coils and Quality Factor Optimization for Wireless Power Transfer. IEEE Trans. Ind. Electron. 2016, 63, 2825–2837. [Google Scholar] [CrossRef]
- Prosen, N.; Domajnko, J.; Milanovič, M. Wireless Power Transfer Using Double-DD Coils. Electronics 2021, 10, 2528. [Google Scholar] [CrossRef]
- Dowell, P.L. Effects of Eddy Currents in Transformer Windings. Proc. IEE 1966, 113, 1387–1394. [Google Scholar] [CrossRef]
- Ferreira, J.A. Improved Analytical Modeling of Conductive Losses in Magnetic Components. IEEE Trans. Power Electron. 1994, 9, 127–131. [Google Scholar] [CrossRef]
- Ferreira, J.A. Appropriate Modelling of Conductive Losses in the Design of Magnetic Components. In Proceedings of the 21st Annual IEEE Conference on Power Electronics Specialists (PESC), San Antonio, TX, USA, 11–14 June 1990. [Google Scholar]
- Albach, M. Two-Dimensional Calculation of Winding Losses in Transformers. In Proceedings of the 2000 IEEE 31st Annual Power Electronics Specialists Conference (PESC), Galway, Ireland, 23–23 June 2000. [Google Scholar]
- Vandelac, J.P.; Ziogas, P.D. A Novel Approach for Minimizing High-Frequency Transformer Copper Losses. IEEE Trans. Power Electron. 1988, 3, 266–277. [Google Scholar] [CrossRef]
- Hurley, W.G.; Gath, E.; Breslin, J.G. Optimizing the AC Resistance of Multilayer Transformer Windings with Arbitrary Current Waveforms. IEEE Trans. Power Electron. 2000, 15, 369–376. [Google Scholar] [CrossRef]
- Wallmeier, P. Improved Analytical Modeling of Conductive Losses in Gapped High-Frequency Inductors. IEEE Trans. Ind. Appl. 2001, 37, 1045–1054. [Google Scholar] [CrossRef]
- Lotfi, A.W.; Lee, F.C. A High Frequency Model for Litz Wire for Switch-Mode Magnetics. In Conference Record of the 1993 IEEE Industry Applications Conference Twenty-Eighth IAS Annual Meeting, Toronto, ON, Canada, 2–8 October 1993; Volume 2, pp. 1169–1175. [Google Scholar]
- Arruti, E.; Stevanovic, M.; Krizmanic, K.; Hjuler, K. Evolution of Classical 1-D Based Models and Improved Approach for the Characterization of Litz Wire Losses. IEEE Trans. Power Electron. 2024; early access. [Google Scholar] [CrossRef]
- Sullivan, C.R. Optimal Choice for Number of Strands in a Litz-Wire Transformer Winding. IEEE Trans. Power Electron. 1999, 14, 283–291. [Google Scholar] [CrossRef]
- Sullivan, C.R.; Zhang, R.Y. Simplified Design Method for Litz Wire. In Proceedings of the IEEE Power Electronics Specialists Conference (PESC), Fort Worth, TX, USA, 16–20 March 2014; pp. 2667–2674. [Google Scholar]
- Sullivan, C.R.; Zhang, R.Y. Analytical Model for Effects of Twisting on Litz-Wire Losses. In Proceedings of the IEEE Workshop on Control and Modeling for Power Electronics (COMPEL), Santander, Spain, 22–25 June 2014; pp. 1–10. [Google Scholar]
- Tang, X.; Sullivan, C.R. Stranded Wire with Uninsulated Strands as a Low-Cost Alternative to Litz Wire. In Proceedings of the 34th Annual Conference on Power Electronics Specialists (PESC ‘03), Acapulco, Mexico, 15–19 June 2003. [Google Scholar]
- Ahmadi, S.; Khan, S.H.; Grattan, K.T.V. Impact of Twisting on Skin and Proximity Losses in Segmented Underground Cables: A 3D Finite-Element Study. Appl. Sci. 2025, 15, 2814. [Google Scholar] [CrossRef]
- Rossmanith, H.; Dobrotenko, M.; Albach, M.; Exner, D. Measurement and Characterization of High Frequency Losses in Nonideal Litz Wires. IEEE Trans. Power Electron. 2018, 33, 7828–7840. [Google Scholar] [CrossRef]
- Plumed, E.; Acero, J.; Lope, I.; Carretero, C. 3D Finite Element Simulation of Litz Wires with Multilevel Bundle Structure. In Proceedings of the 2018 IEEE 44th IECON, Washington, DC, USA, 21–23 October 2018; pp. 3479–3484. [Google Scholar]
- Otomo, Y.; Igarashi, H.; Sano, H.; Yamada, T. Analysis of Litz Wire Losses Using Homogenization-Based FEM. IEEE Trans. Magn. 2021, 57, 7402409. [Google Scholar] [CrossRef]
- Zhang, R.Y.; White, J.K.; Sullivan, C.R. Realistic Litz Wire Characterization Using Fast Numerical Simulations. IEEE Trans. Power Electron. 2020, 35, 12642–12655. [Google Scholar]
- Lyu, J.; Chen, H.; Zhang, Y.; Du, Y.; Cheng, Q.S. Fast Simulation of Litz Wire Using Multilevel PEEC Method. IEEE Trans. Power Electron. 2020, 35, 12612–12623. [Google Scholar] [CrossRef]
- Ehrlich, S.; Rossmanith, H.; Sauer, M.; Joffe, C.; März, M. Fast Numerical Power Loss Calculation for High-Frequency Litz Wires. IEEE Trans. Power Electron. 2021, 36, 2018–2031. [Google Scholar] [CrossRef]
- Zhang, R.Y.; White, J.K.; Sullivan, C.R.; Kassakian, J.G. Fast Simulation of Complicated 3D Structures above Lossy Magnetic Media. In Proceedings of the 2017 IEEE 18th Workshop on Control and Modeling for Power Electronics (COMPEL), Stanford, CA, USA, 9–12 July 2017; pp. 1–7. [Google Scholar]

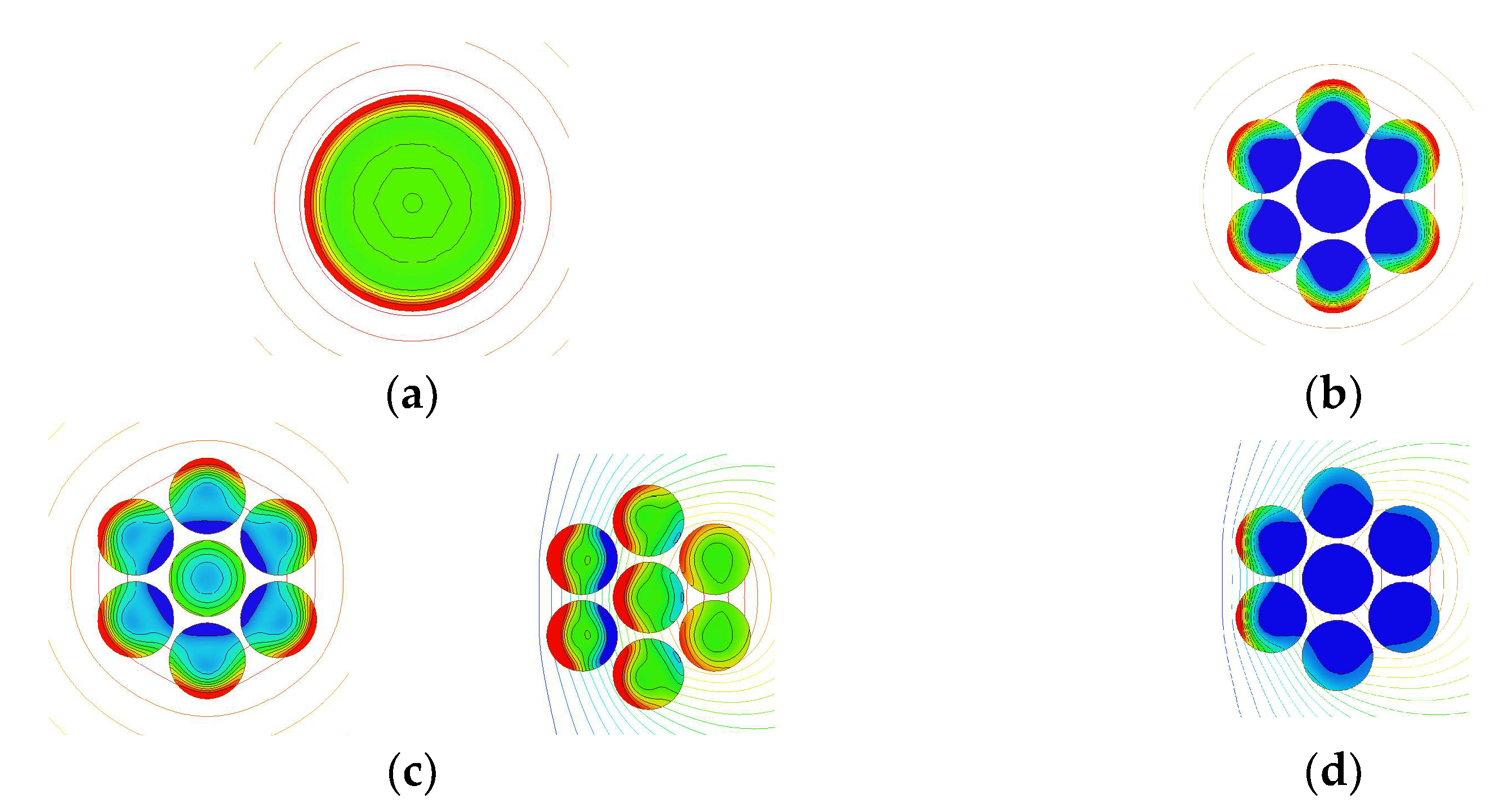
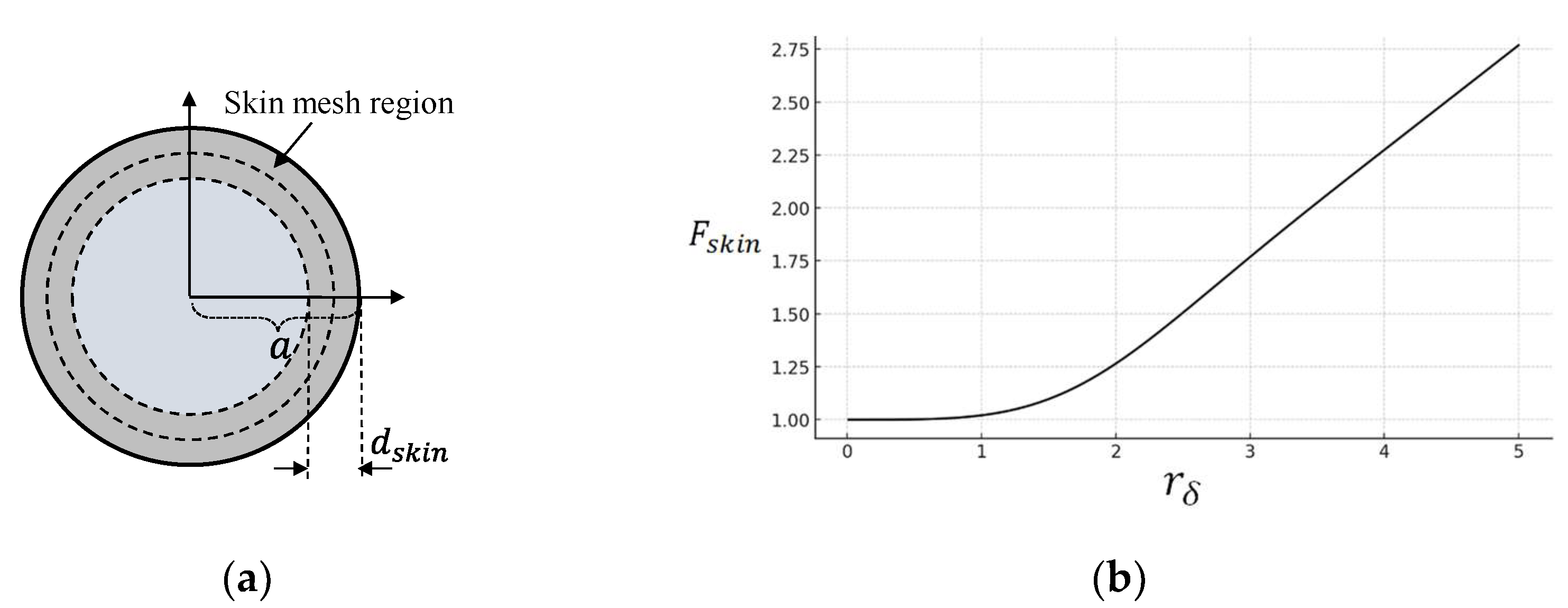

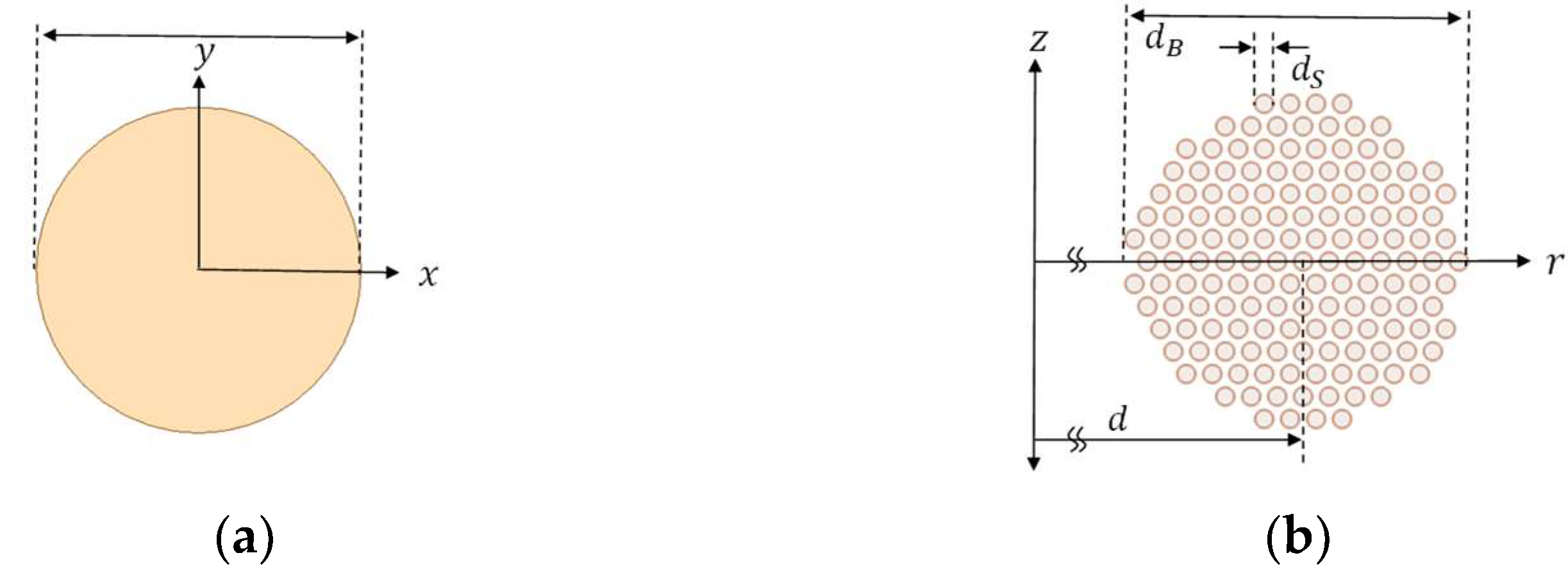
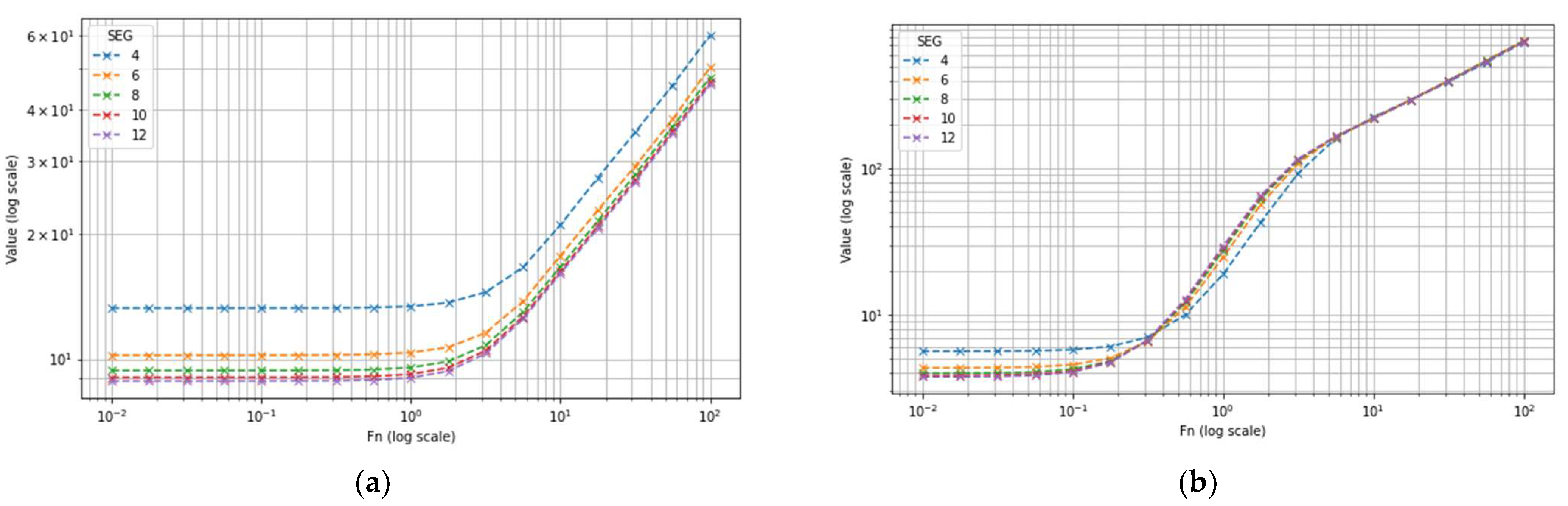

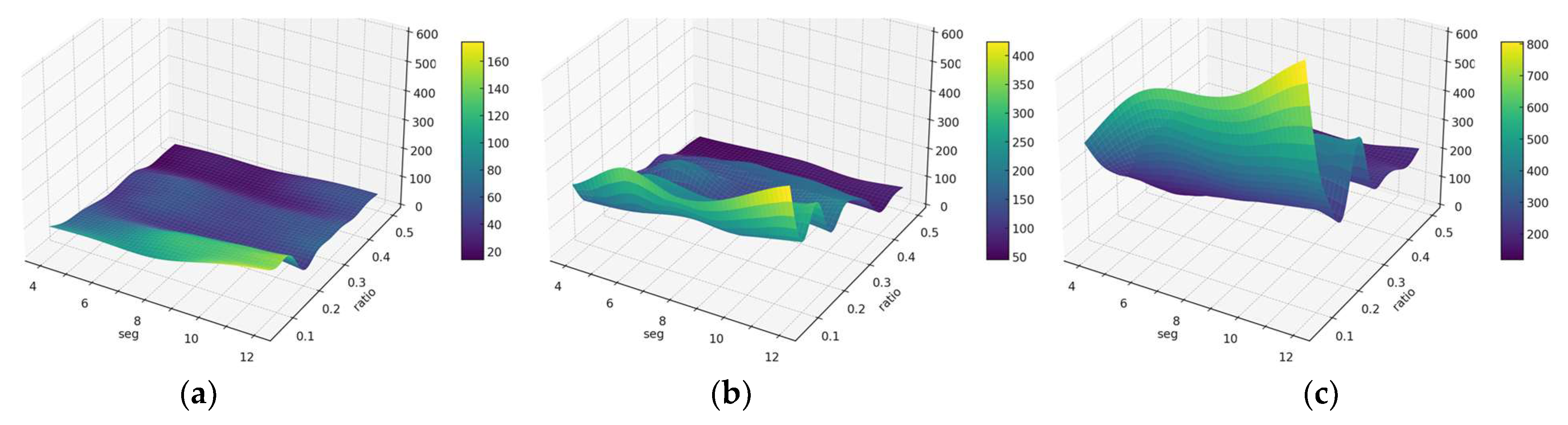

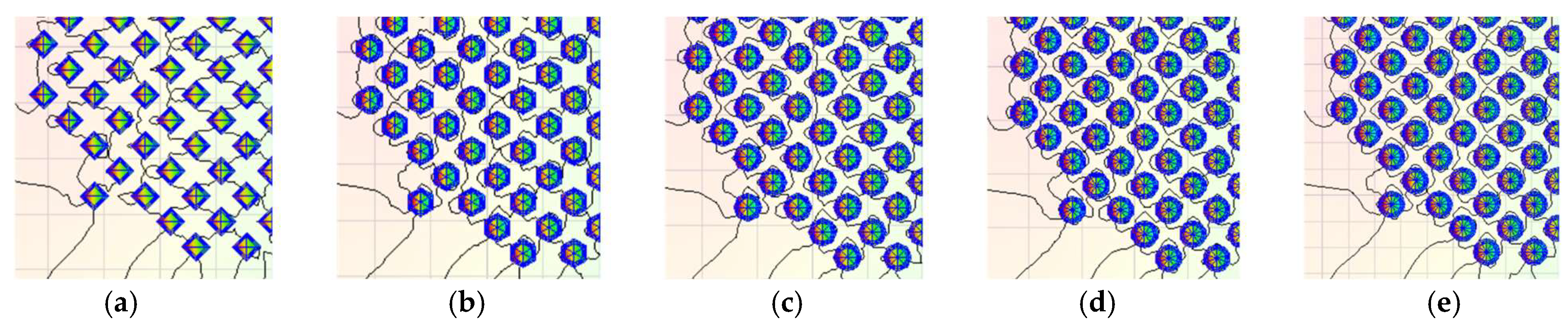
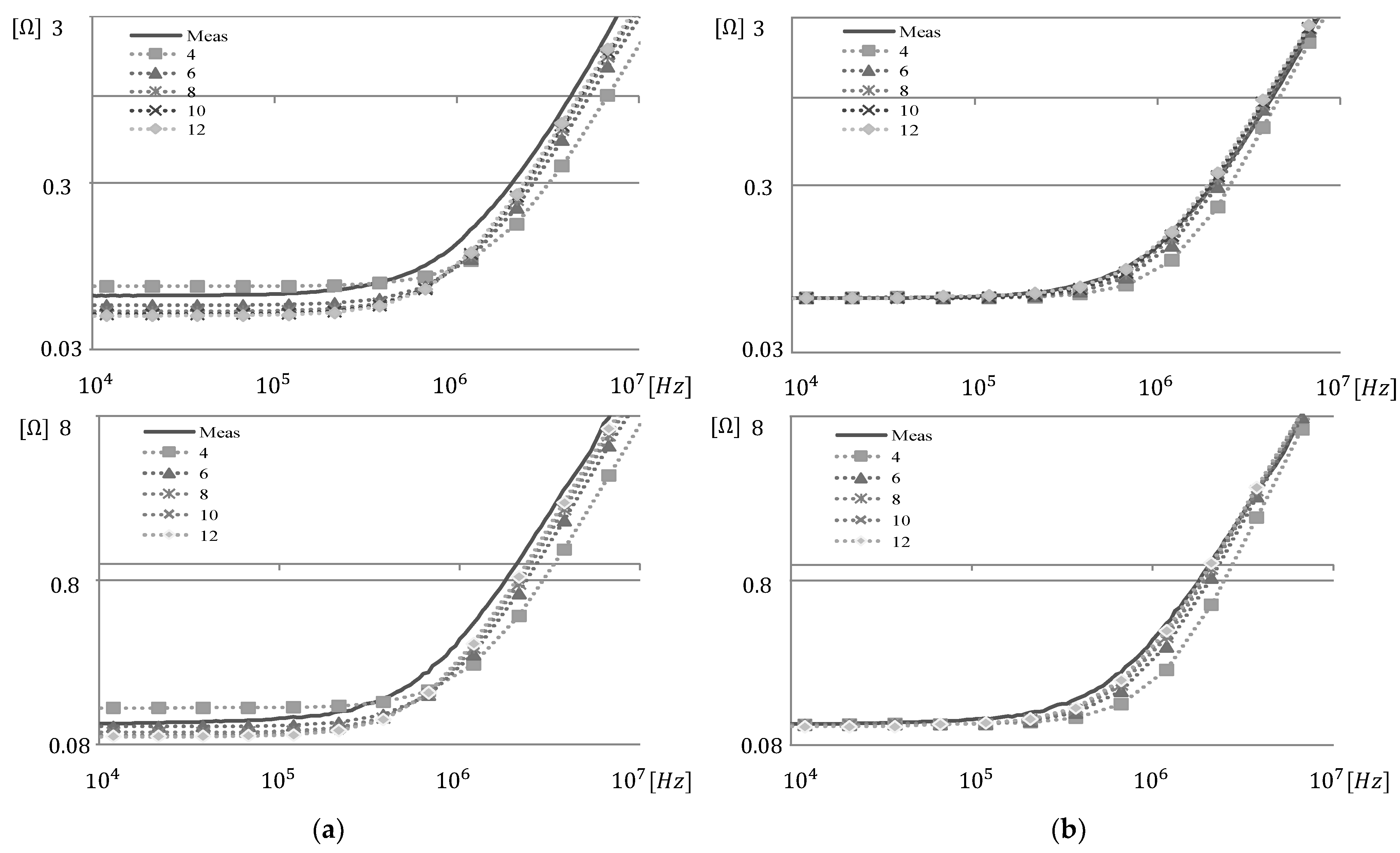
| Segment | 4 | 6 | 8 | 10 | 12 |
|---|---|---|---|---|---|
| A single conductor | 45.174 | 15.135 | 7.0495 | 3.559 | 1.751 |
| a 150-44 AWG Litz wire | 24.307 | 9.204 | 4.571 | 2.331 | 1.166 |
| Segment | |||||||
|---|---|---|---|---|---|---|---|
| 4 | 4.462 | 2.308 | −1.804 | 4.561 | −2.268 | 1.785 | 1.431 |
| 6 | 1.006 | 1.222 | −0.701 | 1.040 | −1.213 | 0.713 | 1.144 |
| 8 | 5.057 | 9.686 | −5.894 | 5.071 | −6.591 | 4.112 | 1.068 |
| 10 | 2.791 | 9.190 | −5.592 | 2.798 | −6.644 | 4.126 | 1.034 |
| 12 | 2.157 | 9.343 | −5.659 | 2.160 | −7.041 | 4.334 | 1.016 |
| Segment | |||||||
|---|---|---|---|---|---|---|---|
| 4 | 0.224 | 1.847 | −2.060 | 0.487 | −1.074 | −1.256 | 1.265 |
| 6 | 0.131 | 1.260 | −1.116 | 0.213 | −1.020 | −1.144 | 1.096 |
| 8 | 5.696 | 0.757 | 0.303 | 5.729 | −0.762 | −0.329 | 1.050 |
| 10 | 0.062 | 0.848 | −0.363 | 0.079 | −0.910 | −0.814 | 1.024 |
| 12 | 2.242 | 0.751 | 0.363 | 2.250 | −0.755 | −0.381 | 1.012 |
| Segment | 4 | 6 | 8 | 10 | 12 |
|---|---|---|---|---|---|
| A single conductor | 0.128 | 0.224 | 0.073 | 0.056 | 0.030 |
| A 150-44 AWG Litz wire | 0.756 | 0.174 | 0.258 | 0.139 | 0.093 |
| The Number of Layers/Turns | Bundle/Strand | |
|---|---|---|
| Winding A | 2/12 | 150-strand (44 AWG) enameled wire, copper, |
| Winding B | 3/13 |
| Operating System | Processor/RAM | Frequency Range | Percent Error |
|---|---|---|---|
| Windows 11 x64-based PC | Intel® Core™ i7-14700KF 3.40GHz /64GB | 4.71 kHz~47.1 MHz logarithmic scale, 4 points/decade | 0.6% |
| Validation | Meshing | Analysis | Total Elapsed Time | |
|---|---|---|---|---|
| 4 | 1459 | 38 | 1775 | 3272 |
| 6 | 2044 | 45 | 2427 | 4516 |
| 8 | 2501 | 53 | 2945 | 5499 |
| 10 | 3014 | 61 | 3549 | 6624 |
| 12 | 3607 | 73 | 4206 | 7886 |
| Memory Usage [GB] | Total Number of Elements in Strands | The Average Number of Elements in a Strand | |
|---|---|---|---|
| 4 | 12.0 | 18,889 | 10.49 |
| 6 | 17.8 | 29,871 | 16.60 |
| 8 | 23.7 | 37,759 | 20.98 |
| 10 | 29.5 | 45,756 | 25.42 |
| 12 | 35.4 | 57,158 | 31.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baek, S. An Efficient and Practical 2D FEM-Based Framework for AC Resistance Modeling of Litz Wire Windings. Appl. Sci. 2025, 15, 9185. https://doi.org/10.3390/app15169185
Baek S. An Efficient and Practical 2D FEM-Based Framework for AC Resistance Modeling of Litz Wire Windings. Applied Sciences. 2025; 15(16):9185. https://doi.org/10.3390/app15169185
Chicago/Turabian StyleBaek, Seunghun. 2025. "An Efficient and Practical 2D FEM-Based Framework for AC Resistance Modeling of Litz Wire Windings" Applied Sciences 15, no. 16: 9185. https://doi.org/10.3390/app15169185
APA StyleBaek, S. (2025). An Efficient and Practical 2D FEM-Based Framework for AC Resistance Modeling of Litz Wire Windings. Applied Sciences, 15(16), 9185. https://doi.org/10.3390/app15169185





