Fault Detection in Power Distribution Systems Using Sensor Data and Hybrid YOLO with Adaptive Context Refinement
Abstract
1. Introduction
Contributions
- Integration of ACR into multi-generation YOLO architectures for insulator inspection: Enhances YOLOv8–YOLOv12 detectors with a context-aware refinement stage that adaptively exploits surrounding visual cues, improving robustness in challenging conditions.
- Adaptive multi-scale context extraction: Introduces a size-aware strategy that dynamically adjusts the contextual region based on the relative object area, improving the detection of small, partially occluded, or low-contrast faults in high-voltage insulators.
- Lightweight dual-attention refinement network: Employs spatial and channel attention modules to refine bounding boxes and recalibrate confidence scores with minimal computational overhead, maintaining suitability for real-time UAV-based inspection.
- Comprehensive cross-architecture evaluation: Assesses the proposed approach across 25 YOLO model variants (YOLOv8 to YOLOv12), showing consistent mAP gains—up to 22.9% improvement for resource-constrained nano models—while preserving efficiency.
- Validation on real-world UAV datasets: Demonstrates robustness and applicability under diverse environmental and fault conditions using high-resolution UAV imagery from actual power transmission and distribution networks.
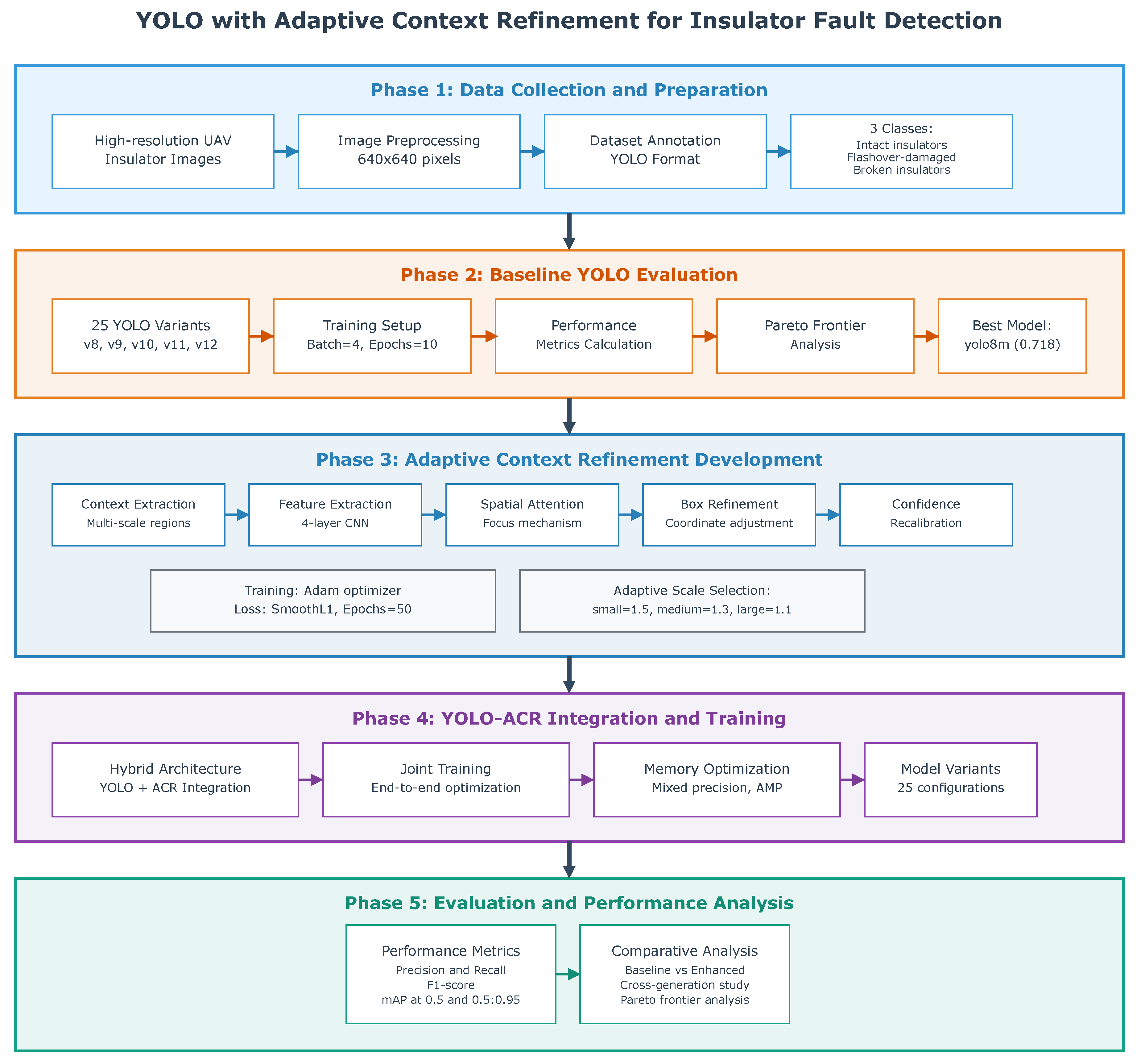
2. Methodology
2.1. YOLO Detection Framework
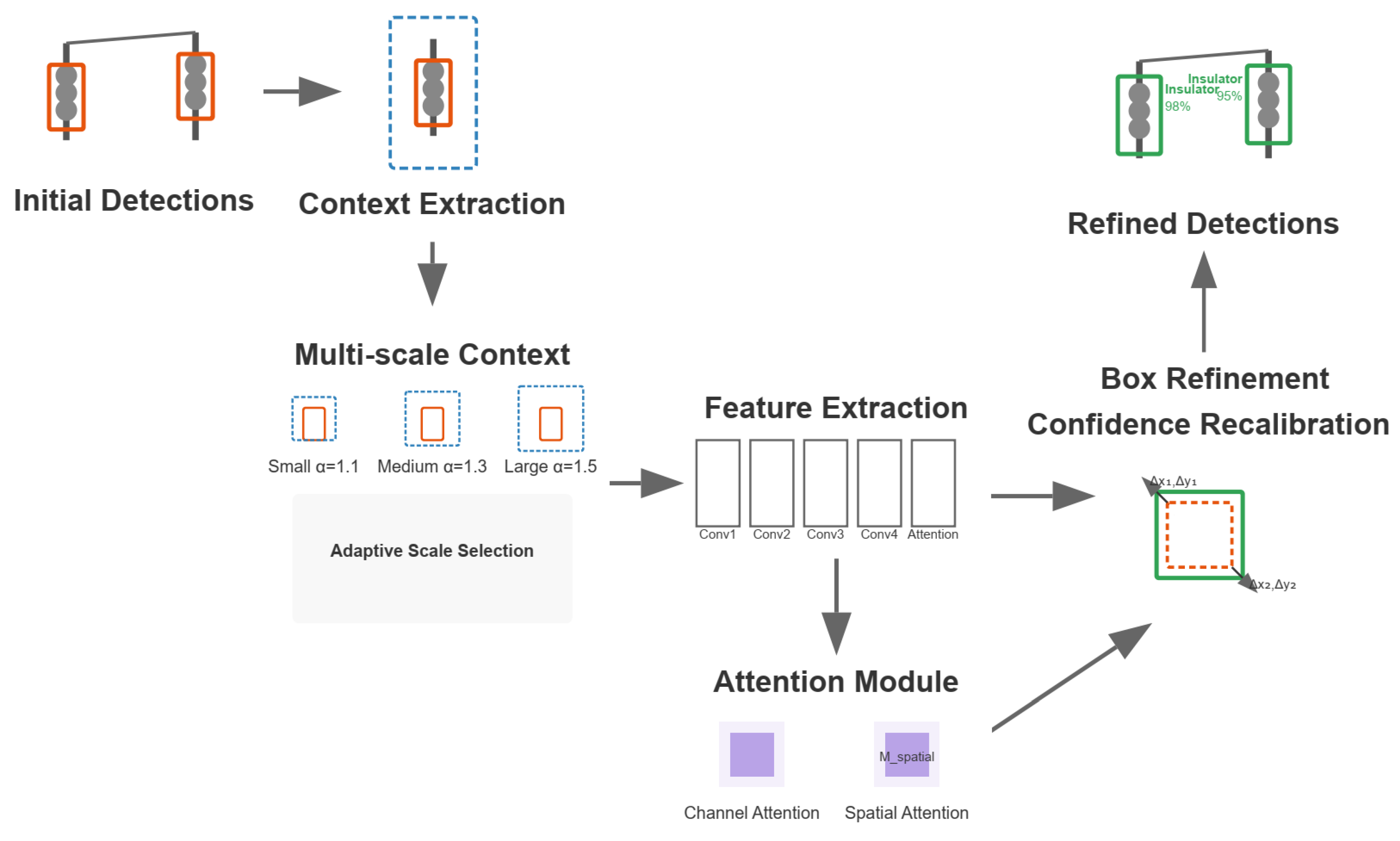
2.2. Adaptive Context Refinement
2.3. Context Extraction and Neural Architecture
2.4. Spatial Attention and Feature Fusion
2.5. Box Refinement and Confidence Recalibration
2.6. Training Methodology
3. Implementation and Validation Framework
3.1. Performance Evaluation Metrics
3.2. Dataset
4. Results and Discussion
4.1. Training Methodology
4.2. Implementation Details
- Data Configuration: A custom YAML configuration generator that creates the required dataset specification with appropriate paths and class definitions.
- Memory Management: Implementation of memory optimization techniques, including the following:
- Dynamic garbage collection.
- CUDA cache emptying between training runs.
- Automatic mixed precision (AMP) to reduce memory footprint.
- Minimal worker threads to reduce parallel processing overhead.
- Adaptive Training: The framework includes fallback mechanisms to handle potential memory limitations as follows:
- Automatic reduction in batch size and image resolution if out-of-memory errors occur.
- Optional subset training on reduced dataset samples for preliminary model validation.
- Device-agnostic implementation with CPU fallback capability.
- Evaluation Metrics: The training process tracks multiple performance indicators, including the following:
- Precision and recall for class-specific performance.
- mAP at IoU thresholds of 0.5 (mAP@0.5) and 0.5:0.95 (mAP@0.5:0.95).
- F1-score for balanced evaluation of precision and recall.
4.3. Experimental Framework
4.4. Baseline Analysis with YOLO Variants
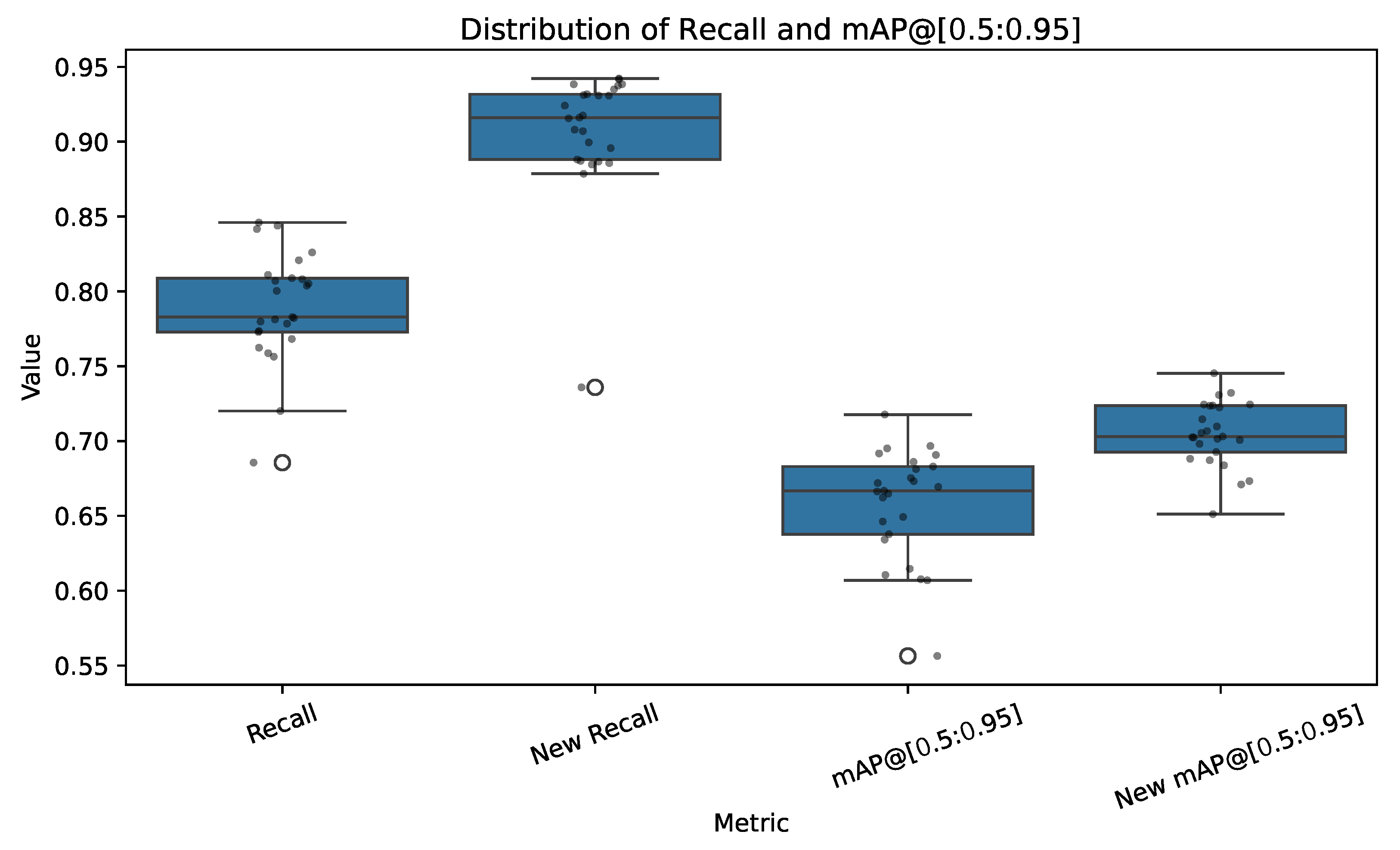
4.5. Refinement Analysis and Cross-Generation Comparison
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ahmed, M.; Mohanta, J.; Sanyal, A. Inspection and identification of transmission line insulator breakdown based on deep learning using aerial images. Electr. Power Syst. Res. 2022, 211, 108199. [Google Scholar] [CrossRef]
- Arias Velásquez, R.M. Insulation failure caused by special pollution around industrial environments. Eng. Fail. Anal. 2019, 102, 123–135. [Google Scholar] [CrossRef]
- Seman, L.O.; Stefenon, S.F.; Mariani, V.C.; Coelho, L.S. Ensemble learning methods using the Hodrick–Prescott filter for fault forecasting in insulators of the electrical power grids. Int. J. Electr. Power Energy Syst. 2023, 152, 109269. [Google Scholar] [CrossRef]
- Aljalaud, F.; Kurdi, H.; Youcef-Toumi, K. Autonomous Multi-UAV Path Planning in Pipe Inspection Missions Based on Booby Behavior. Mathematics 2023, 11, 2092. [Google Scholar] [CrossRef]
- Gong, Y.; Zhou, W.; Wang, K.; Wang, J.; Wang, R.; Deng, H.; Liu, G. Defect detection of small cotter pins in electric power transmission system from UAV images using deep learning techniques. Electr. Eng. 2023, 105, 1251–1266. [Google Scholar] [CrossRef]
- Yi, J.; Mao, J.; Zhang, H.; Chen, Y.; Liu, T.; Zeng, K.; Xie, H.; Wang, Y. Balancing Accuracy and Efficiency With a Multiscale Uncertainty-Aware Knowledge-Based Network for Transmission Line Inspection. IEEE Trans. Ind. Inform. 2025, 21, 2829–2838. [Google Scholar] [CrossRef]
- Labrador Rivas, A.E.; Abrão, T. Faults in smart grid systems: Monitoring, detection and classification. Electr. Power Syst. Res. 2020, 189, 106602. [Google Scholar] [CrossRef]
- Preduș, M.F.; Popescu, C.; Răduca, E.; Hațiegan, C. Study of the Accelerated Degradation of the Insulation of Power Cables under the Action of the Acid Environment. Energies 2022, 15, 3550. [Google Scholar] [CrossRef]
- You, X.; Zhao, X. A insulator defect detection network based on improved YOLOv7 for UAV aerial images. Measurement 2025, 253, 117410. [Google Scholar] [CrossRef]
- Liao, W.; Zhu, R.; Ge, L.; Cao, D.; Yang, Z. Mitigating Class Imbalance Issues in Electricity Theft Detection via a Sample-Weighted Loss. IEEE Trans. Ind. Inform. 2025, 21, 1754–1763. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, C.; Zhang, Q.; Zhang, J.; Wang, G. IF-YOLO: An Efficient and Accurate Detection Algorithm for Insulator Faults in Transmission Lines. IEEE Access 2024, 12, 167388–167403. [Google Scholar] [CrossRef]
- Zhao, W.; Xu, M.; Cheng, X.; Zhao, Z. An Insulator in Transmission Lines Recognition and Fault Detection Model Based on Improved Faster RCNN. IEEE Trans. Instrum. Meas. 2021, 70, 5016408. [Google Scholar] [CrossRef]
- Shuang, F.; Wei, S.; Li, Y.; Gu, X.; Lu, Z. Detail R-CNN: Insulator Detection Based on Detail Feature Enhancement and Metric Learning. IEEE Trans. Instrum. Meas. 2023, 72, 2524414. [Google Scholar] [CrossRef]
- Zhou, M.; Wang, J.; Li, B. ARG-Mask RCNN: An Infrared Insulator Fault-Detection Network Based on Improved Mask RCNN. Sensors 2022, 22, 4720. [Google Scholar] [CrossRef] [PubMed]
- Liang, H.; Zuo, C.; Wei, W. Detection and Evaluation Method of Transmission Line Defects Based on Deep Learning. IEEE Access 2020, 8, 38448–38458. [Google Scholar] [CrossRef]
- Costa, A.; Cortes, C.O. A Convolutional Neural Network for Detecting Faults in Power Distribution Networks along a Railway: A Case Study Using YOLO. Appl. Artif. Intell. 2021, 35, 2067–2086. [Google Scholar] [CrossRef]
- Qiu, Z.; Zhu, X.; Liao, C.; Shi, D.; Qu, W. Detection of Transmission Line Insulator Defects Based on an Improved Lightweight YOLOv4 Model. Appl. Sci. 2022, 12, 1207. [Google Scholar] [CrossRef]
- Liquan, Z.; Mengjun, Z.; Ying, C.; Yanfei, J. Fast Detection of Defective Insulator Based on Improved YOLOv5s. Comput. Intell. Neurosci. 2022, 2022, 8955292. [Google Scholar] [CrossRef]
- Gong, C.; Jiang, W.; Zou, D.; Weng, W.; Li, H. An Insulator Fault Diagnosis Method Based on Multi-Mechanism Optimization YOLOv8. Appl. Sci. 2024, 14, 8770. [Google Scholar] [CrossRef]
- Tao, Z.; He, Y.; Lin, S.; Yi, T.; Li, M. SnakeNet: An adaptive network for small object and complex background for insulator surface defect detection. Comput. Electr. Eng. 2024, 117, 109259. [Google Scholar] [CrossRef]
- He, M.; Qin, L.; Deng, X.; Liu, K. MFI-YOLO: Multi-Fault Insulator Detection Based on an Improved YOLOv8. IEEE Trans. Power Deliv. 2024, 39, 168–179. [Google Scholar] [CrossRef]
- Zhang, L.; Li, B.; Cui, Y.; Lai, Y.; Gao, J. Research on improved YOLOv8 algorithm for insulator defect detection. J. Real-Time Image Process. 2024, 21, 22. [Google Scholar] [CrossRef]
- Zhao, J.; Miao, S.; Kang, R.; Cao, L.; Zhang, L.; Ren, Y. Insulator Defect Detection Algorithm Based on Improved YOLOv11n. Sensors 2025, 25, 1327. [Google Scholar] [CrossRef]
- Zhou, Y.; Shao, H.; Wang, L.; Waslander, S.L.; Li, H.; Liu, Y. Smartrefine: A scenario-adaptive refinement framework for efficient motion prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 15281–15290. [Google Scholar]
- Chen, J.; Wang, Y.; Liu, X.; Zhou, G.; Zhou, Z. ARNet: Adaptive Refinement Network Using Context Filter for Motion Forecasting. In Proceedings of the 2024 8th CAA International Conference on Vehicular Control and Intelligence (CVCI), Chongqing, China, 25–27 October 2024; pp. 1–6. [Google Scholar]
- Huai, Z.; Ding, X.; Li, Y.; Li, X. Context-aware pseudo-label refinement for source-free domain adaptive fundus image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Vancouver, BC, Canada, 8–12 October 2023; Springer: Cham, Switzerland; pp. 618–628. [Google Scholar]
- Tan, X.; Hou, S.; Yang, F.; Li, Z. Transmission Lines Insulator State Detection Method Based on Deep Learning. Appl. Sci. 2025, 15, 526. [Google Scholar] [CrossRef]
- Lu, G.; Li, B.; Chen, Y.; Qu, S.; Cheng, T.; Zhou, J. Precision in Aerial Surveillance: Integrating YOLOv8 With PConv and CoT for Accurate Insulator Defect Detection. IEEE Access 2025, 13, 49062–49075. [Google Scholar] [CrossRef]
- Panigrahy, S.; Karmakar, S. Real-Time Condition Monitoring of Transmission Line Insulators Using the YOLO Object Detection Model With a UAV. IEEE Trans. Instrum. Meas. 2024, 73, 2514109. [Google Scholar] [CrossRef]
- Stefenon, S.F.; Seman, L.O.; Singh, G.; Yow, K.C. Enhanced insulator fault detection using optimized ensemble of deep learning models based on weighted boxes fusion. Int. J. Electr. Power Energy Syst. 2025, 168, 110682. [Google Scholar] [CrossRef]
- Lewis, D.; Kulkarni, P. Insulator Defect Detection. 2021. Available online: https://ieee-dataport.org/competitions/insulator-defect-detection (accessed on 8 May 2025).
- Stefenon, S.F. Inspection of Electrical Power Distribution Grid. 2023. Available online: https://github.com/SFStefenon/InspectionDataSet (accessed on 8 May 2025).


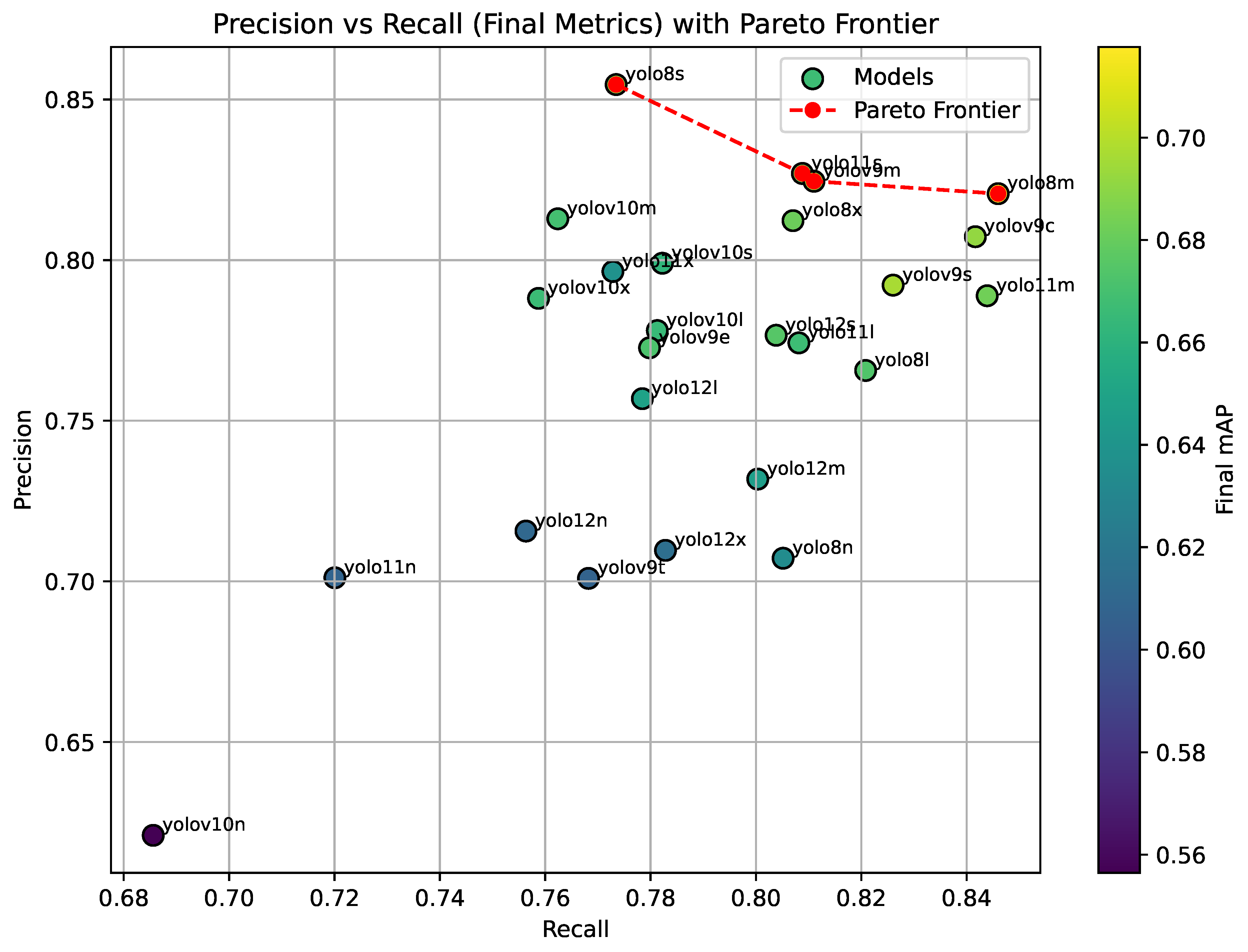
| Model | Final mAP | Final Precision | Final Recall |
|---|---|---|---|
| yolo8l | 0.673160 | 0.765651 | 0.820825 |
| yolo8m | 0.717706 | 0.820685 | 0.845983 |
| yolo8n | 0.634158 | 0.707193 | 0.805160 |
| yolo8s | 0.690742 | 0.854654 | 0.773468 |
| yolo8x | 0.681275 | 0.812279 | 0.807037 |
| yolov9c | 0.691740 | 0.807288 | 0.841653 |
| yolov9e | 0.671942 | 0.772708 | 0.779811 |
| yolov9m | 0.695113 | 0.824548 | 0.811013 |
| yolov9s | 0.696710 | 0.792208 | 0.826039 |
| yolov9t | 0.606963 | 0.700928 | 0.768216 |
| yolov10l | 0.664870 | 0.778065 | 0.781277 |
| yolov10m | 0.669379 | 0.812874 | 0.762396 |
| yolov10n | 0.556448 | 0.621034 | 0.685595 |
| yolov10s | 0.662223 | 0.799026 | 0.782245 |
| yolov10x | 0.666366 | 0.788095 | 0.758736 |
| yolo11l | 0.666793 | 0.774235 | 0.808157 |
| yolo11m | 0.682998 | 0.788911 | 0.843897 |
| yolo11n | 0.607671 | 0.701113 | 0.720074 |
| yolo11s | 0.686071 | 0.826978 | 0.808819 |
| yolo11x | 0.637785 | 0.796459 | 0.772851 |
| yolo12l | 0.649314 | 0.756868 | 0.778446 |
| yolo12m | 0.646290 | 0.731834 | 0.800345 |
| yolo12n | 0.610553 | 0.715652 | 0.756351 |
| yolo12s | 0.675353 | 0.776610 | 0.803838 |
| yolo12x | 0.614661 | 0.709647 | 0.782829 |
| Model | Recall | New Recall | % Gain Recall | mAP@[0.5:0.95] | New mAP@[0.5:0.95] | % Gain mAP@[0.5:0.95] |
|---|---|---|---|---|---|---|
| yolo8l | 0.821 | 0.931 | 13.398 | 0.673 | 0.703 | 4.433 |
| yolo8m | 0.846 | 0.938 | 10.924 | 0.718 | 0.724 | 0.835 |
| yolo8n | 0.805 | 0.896 | 11.245 | 0.634 | 0.687 | 8.364 |
| yolo8s | 0.773 | 0.931 | 20.393 | 0.691 | 0.715 | 3.454 |
| yolo8x | 0.807 | 0.937 | 16.153 | 0.681 | 0.703 | 3.130 |
| yolov9c | 0.842 | 0.935 | 11.091 | 0.692 | 0.725 | 4.736 |
| yolov9e | 0.780 | 0.924 | 18.503 | 0.672 | 0.702 | 4.533 |
| yolov9m | 0.811 | 0.938 | 15.707 | 0.695 | 0.724 | 4.213 |
| yolov9s | 0.826 | 0.932 | 12.791 | 0.697 | 0.723 | 3.702 |
| yolov9t | 0.768 | 0.885 | 15.176 | 0.607 | 0.673 | 10.929 |
| yolov10l | 0.781 | 0.887 | 13.558 | 0.665 | 0.745 | 12.097 |
| yolov10m | 0.762 | 0.886 | 16.173 | 0.669 | 0.724 | 8.100 |
| yolov10n | 0.686 | 0.736 | 7.337 | 0.556 | 0.684 | 22.887 |
| yolov10s | 0.782 | 0.879 | 12.318 | 0.662 | 0.731 | 10.356 |
| yolov10x | 0.759 | 0.887 | 16.865 | 0.666 | 0.732 | 9.880 |
| yolo11l | 0.808 | 0.931 | 15.176 | 0.667 | 0.710 | 6.435 |
| yolo11m | 0.844 | 0.942 | 11.649 | 0.683 | 0.701 | 2.592 |
| yolo11n | 0.720 | 0.888 | 23.334 | 0.608 | 0.651 | 7.163 |
| yolo11s | 0.809 | 0.942 | 16.429 | 0.686 | 0.693 | 0.966 |
| yolo11x | 0.773 | 0.916 | 18.535 | 0.638 | 0.702 | 9.990 |
| yolo12l | 0.778 | 0.908 | 16.643 | 0.649 | 0.698 | 7.513 |
| yolo12m | 0.800 | 0.916 | 14.401 | 0.646 | 0.707 | 9.347 |
| yolo12n | 0.756 | 0.907 | 19.931 | 0.611 | 0.671 | 9.900 |
| yolo12s | 0.804 | 0.917 | 14.140 | 0.675 | 0.705 | 4.449 |
| yolo12x | 0.783 | 0.899 | 14.904 | 0.615 | 0.688 | 11.964 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scapinello Aquino, L.; Rodrigues Agottani, L.F.; Seman, L.O.; Cocco Mariani, V.; Coelho, L.d.S.; González, G.V. Fault Detection in Power Distribution Systems Using Sensor Data and Hybrid YOLO with Adaptive Context Refinement. Appl. Sci. 2025, 15, 9186. https://doi.org/10.3390/app15169186
Scapinello Aquino L, Rodrigues Agottani LF, Seman LO, Cocco Mariani V, Coelho LdS, González GV. Fault Detection in Power Distribution Systems Using Sensor Data and Hybrid YOLO with Adaptive Context Refinement. Applied Sciences. 2025; 15(16):9186. https://doi.org/10.3390/app15169186
Chicago/Turabian StyleScapinello Aquino, Luiza, Luis Fernando Rodrigues Agottani, Laio Oriel Seman, Viviana Cocco Mariani, Leandro dos Santos Coelho, and Gabriel Villarrubia González. 2025. "Fault Detection in Power Distribution Systems Using Sensor Data and Hybrid YOLO with Adaptive Context Refinement" Applied Sciences 15, no. 16: 9186. https://doi.org/10.3390/app15169186
APA StyleScapinello Aquino, L., Rodrigues Agottani, L. F., Seman, L. O., Cocco Mariani, V., Coelho, L. d. S., & González, G. V. (2025). Fault Detection in Power Distribution Systems Using Sensor Data and Hybrid YOLO with Adaptive Context Refinement. Applied Sciences, 15(16), 9186. https://doi.org/10.3390/app15169186










