Seismic Disaster Risk Assessment of Oil and Gas Pipelines

Abstract

Oil and gas pipelines represent critical infrastructure for energy transportation and are essential for ensurin g energy security. The seismic disaster risk assessment of these pipelines is of paramount importance for safeguarding energy supplies. Traditional assessment methodologies primarily focus on the structural integrity of the pipeline body, often neglecting the impact of auxiliary structures and site-specific disaster effects. This study proposes an enhanced risk assessment methodology to address these gaps. This research systematically compiles seismic damage case studies of pipelines from major seismic zones in China. By considering the interactions between auxiliary structure types, site conditions, and forms of disasters, 15 typical operating conditions are identified, and a seismic damage case database is constructed. We develop a failure probability model that integrates geotechnical parameters, structural responses, and ground motion characteristics to assess the impact of liquefaction, site amplification, fault activity, and collapse/landslide phenomena. Utilizing Particle Swarm Optimization (PSO) and Fuzzy Analytic Hierarchy Process (Fuzzy AHP) algorithms, this model quantifies the influence weights and coefficients of these disasters on pipeline auxiliary structures, forming a vulnerability matrix centered around Peak Ground Acceleration (PGA). Additionally, a dual-vulnerability assessment framework is established, and a failure probability formula accounting for the superposition effects of multiple disasters is proposed. This study marks a significant advancement, transitioning from traditional single-pipeline evaluations to “structure-disaster-site” coupling analysis, and provides a scientific basis for pipeline seismic design, operation, and maintenance under specific environmental conditions. This work contributes to the development of quantitative and refined seismic risk assessments for oil and gas pipelines.

1. Introduction

Oil and gas pipelines are essential for energy transmission and play an indispensable strategic role in global economic development and societal stability. The United States, with its network of 2.8 million kilometers of pipelines (accounting for 42% of the global total), has the largest pipeline network. The U.S. shale gas revolution has led to the construction of 128,000 km of gathering and transportation pipelines, and the country has also made significant advancements in X100 steel grade pipeline technology [1]. Russia ranks second, with a pipeline network spanning 256,000 km. Its “Power of Siberia” and “Nord Stream” systems reflect the strategic energy ambitions of the country, although they face significant technical challenges, particularly with 37% of pipelines located in permafrost regions [2]. China, which has the third-largest oil and gas pipeline network, has constructed 124,000 km of long-distance natural gas pipelines as of 2023, with plans to exceed 240,000 km by 2025 [3]. This extensive infrastructure supports the national energy security.

However, global oil and gas pipeline systems often traverse seismic zones and regions with complex geological conditions, making them vulnerable to disasters such as ground motion, soil liquefaction, and fault displacement, which significantly threaten pipeline safety. For instance, during the 2008 Wenchuan earthquake, the Lanzhou–Chengdu–Chongqing pipeline experienced multiple leaks due to geotechnical disasters triggered by seismic activity, acting as a vital lifeline for earthquake relief operations. Similarly, the 2023 Turkey–Syria earthquake resulted in natural gas pipeline explosions and energy supply disruptions, leading to direct economic losses exceeding 100 billion USD [4]. Traditional risk assessments often focus on the integrity of the pipeline body and neglect the influence of auxiliary facilities, such as valve chambers and crossing sections, as well as site-specific disaster effects. This oversight results in a significant underestimation of vulnerability in high-risk areas [5]. For example, the China Earthquake Administration identified fault displacement as a major contributor to pipeline damage through shaking table experiments. However, existing models lack systematic classification and quantitative analysis of auxiliary structures [6].

In response to these limitations, this study proposes an improved risk assessment methodology that integrates seismic damage data with the characteristics of pipeline auxiliary structures. By analyzing Chinese seismic events, 15 typical operating conditions of auxiliary structures are identified, including crossing structures (e.g., suspension cable crossings and cable-stayed bridge crossings), support structures (e.g., masonry retaining walls and casings), and crossing structures (e.g., tunnels). Furthermore, a failure probability model is developed for liquefaction uplift, site amplification effects, fault dislocation, and landslide/collapse disasters, integrating geotechnical parameters, structural responses, and ground motion characteristics. The thaw settlement risk for pipelines in permafrost areas is quantitatively evaluated by combining insulation materials and heat pipes, while the pipeline deformation due to fault dislocation is dynamically simulated using near-fault ground motion test data [6,7,8,9].

A systematic review of 200+ peer-reviewed studies (2010–2024) reveals that 87% of seismic risk assessments focus exclusively on pipeline bodies, ignoring auxiliary structures. Similarly, API RP 1109 (2018) prioritizes pipeline body design but lacks a quantitative analysis of auxiliary structures like tunnels and retaining walls [7]. This study pioneers a “pipeline-auxiliary structure-site” coupling model, quantifying the risk contribution of auxiliary structures as 32–67% across scenarios. By integrating over 1200 damage cases, it addresses a critical gap: only 13% of studies prior to 2024 considered the dynamic interactions of auxiliary structures with site hazards.

The core contributions of this research are as follows: (1) a dual-vulnerability assessment framework is constructed that includes the forms of pipeline auxiliary structures and disaster forms, breaking through the limitations of traditional methods that only focus on the integrity of the pipeline body; (2) a pipeline seismic damage case database covering 15 working conditions is established to support refined risk prediction in specific scenarios; (3) a failure probability equation is developed based on the forms of pipeline auxiliary structures and disaster forms, and the Particle Swarm Optimization (PSO) algorithm and Fuzzy Analytic Hierarchy Process (Fuzzy AHP) are used to quantify the influence coefficients of various factors on the pipeline system. These results not only provide a scientific basis for pipeline design but also offer technical support for pipeline operation and maintenance in special environments, such as permafrost and high-intensity seismic areas.

The proposed method has important reference value for pipeline operators, regulatory agencies, and the disaster prevention and control field. For example, the pipeline risk assessment technology developed by Southwest Petroleum University has achieved accurate identification of seismic vulnerability in projects such as the Lanzhou–Chengdu–Chongqing pipeline [5]. Internationally, the US Energy Information Administration (EIA) has optimized the resilience design of the North American pipeline network by evaluating the seismic risks of new pipelines using a similar framework [1,7]. In the future, with the integration of machine learning and Internet of Things technologies (such as crack expansion early warning based on optical fiber monitoring), the seismic risk prevention and control of oil and gas pipelines will further develop towards intelligence and dynamism [10,11].

Traditional seismic risk assessment of oil and gas pipelines has long been dominated by a singular focus on the structural integrity of the pipeline body, inadvertently overlooking the critical role of auxiliary structures (e.g., valve chambers and crossing sections) and site-specific disaster effects. This oversight has led to significant underestimations of vulnerability in high-risk seismic zones, as evidenced by post-earthquake investigations that show that auxiliary structures account for over 68% of the total pipeline damage in major seismic events [5]. Recent studies have highlighted that the dynamic interactions between auxiliary structures and complex site conditions (e.g., liquefiable soils and fault zones) can amplify failure probabilities by up to 3.2 times compared to buried pipeline segments [6].

To bridge this research gap, this study systematically compiles domestic pipeline seismic damage data from 1970 to 2024, spanning major seismic zones in China. By integrating multi-source data (enterprise emergency reports, government publications, and academic literature), a comprehensive database was established to characterize failure mechanisms under diverse auxiliary structure types, site categories, and disaster scenarios. This data-driven approach paves the way for constructing a typological framework of typical operating conditions, which serves as an empirical foundation for subsequent probabilistic risk modeling. The transition from qualitative oversight to the quantitative characterization of auxiliary structure vulnerabilities marks a critical step toward refining seismic risk assessment methodologies for modern pipeline networks.

Empirical vulnerability curve (such as ATC-13): An empirical relationship between earthquake intensity and structural damage probability is established based on historical earthquake damage statistics; however, the coupling effect between auxiliary structure types (such as suspension spans and tunnels) and site conditions is ignored. For example, the ATC-13 model predicted the failure probability of tunnel structures in Class III sites (soft soil) as 37% lower than the measured value.

Deterministic failure threshold (such as API RP1109): Failure is determined by preset strength indicators (such as the pipeline axial strain threshold), lacking quantitative characterization of secondary disasters such as sand liquefaction and fault dislocation. This method was confirmed to have a missed determination rate of 52% for retaining wall failure during the 2008 Wenchuan earthquake [6].

The proposed “structure-disaster-site” coupled model introduces the PSO-Fuzzy AHP algorithm to quantify disaster weights (such as fault activity weights of 0.598), which reduces the Mean Absolute Error (MAE) from 0.032 to 0.011 in traditional methods and increases the correlation coefficient from 0.76 to 0.92, significantly improving the evaluation accuracy in complex scenarios.

2. Collection of Domestic Pipeline Seismic Damage and Typical Operating Conditions

2.1. Data Collection

To systematically analyze the damage patterns of oil and gas pipelines in China under seismic action, multi-dimensional seismic damage data were collected. The data span major seismic-active regions, including the Chuan-Dian seismic zone (e.g., the areas affected by the 2008 Wenchuan and 2013 Lushan earthquakes), the northern section of the North-South seismic zone (e.g., the area of the 2010 Yushu earthquake), the North China seismic region (e.g., the epicentral areas of the 1976 Tangshan earthquake and the 2020 Ju County earthquake), and the Southeast Coastal seismic zone (e.g., the affected area by the 2018 Yangjiang earthquake in Guangdong) [12,13,14]. The primary data sources included:

(1)

Disaster emergency reports from pipeline operating enterprises, including integrity management data from companies like PetroChina and Sinopec, contain vital information such as pipeline materials, service life, and seismic parameters (peak acceleration and response spectrum characteristic period).

(2)

Public data from government departments, such as the “China Earthquake Disaster Loss Report” from the National Disaster Reduction Center and the “Seismic Ground Motion Parameter Zonation Map” from the China Earthquake Administration.

(3)

Academic research publications, including over 200 relevant studies published between 1970 and 2024 in databases such as CNKI and WoS, have focused on topics such as the axial strain distribution of buried pipelines during the Wenchuan earthquake and liquefaction-induced pipeline failure modes [15,16,17].

A database containing many seismic damage cases was established, with key parameters including earthquake intensity (magnitude, epicentral distance, and site category), pipeline attributes (diameter, wall thickness, and transported medium), damage forms (e.g., weld cracking, support displacement, pipeline bending due to soil landslides), and repair measures. Geographic Information System (GIS) spatial analysis revealed that 85% of severe damage cases were concentrated in Class III (soft soil) and Class IV (extremely soft soil) sites, with auxiliary structures at river and canyon crossings suffering damage at a rate 3.2 times higher than that of buried straight pipeline sections [18].

2.2. Typical Operating Conditions

Based on the collected data, typical operating conditions are classified by considering the variations in pipeline auxiliary structures, the diversity of site environments, and the types of seismic disasters involved. Pipeline auxiliary structures are divided into several categories:

Crossing Structures: These include flexible support systems, such as suspension cables and cable-stayed bridge crossings.

Support Structures: These are rigid retaining systems, including masonry retaining walls and casings.

Crossing Structures (tunnels): Underground systems such as tunnels are also considered.

Each structure is analyzed under various site conditions (e.g., hard soil layer, soft soil layer) and seismic influences (e.g., seismic waves, landslides, liquefaction, fault activity). As a result, 15 typical operating conditions are identified and categorized in

Table 1. Failure mechanisms and failure modes of auxiliary structures under 15 different combinations of working conditions.

Working Condition No.	A—Pipe Fittings/B—Laying Method	Description	C—Seismic Disaster Action	Description	D—Site Type	Description	Possible Combinations	Description
1	B3 Auxiliary Facilities	B3.2 Cable-Stayed Bridge Crossing	C1 Seismic Wave	Seismic Wave Action	D1 Class I Site	Hard Soil Layer Site	B3.2 + C1 + D1	Low occurrence probability and no actual cases
2	B3 Auxiliary Facilities	B3.2 Cable-Stayed Bridge Crossing	C1 Seismic Wave	Seismic Wave Action	D2 Class II Site	Medium-Strength Soil	B3.2 + C1 + D2	Same as 1, only the site changes
3	B3 Auxiliary Facilities	B3.2 Cable-Stayed Bridge Crossing	C1 Seismic Wave	Seismic Wave Action	D3 Class III Site	Soft Soil Layer Site	B3.2 + C1 + D3	Same as 1, only the site changes
4	B3 Auxiliary Facilities	B3.1 Suspension Truss Crossing	C1 Seismic Wave	Seismic Wave Action	D1 Class I Site	Hard Soil Layer Site	B3.1 + C1 + D1	Low occurrence probability and no actual cases
5	B3 Auxiliary Facilities	B3.3 Mortar-Masonry Retaining Wall	C6 Collapse	Impact of Falling Rocks on the Crossing Structure	D1 Class I Site	Hard Soil Layer Site	B3.3 + C6 + D1
6	B3 Auxiliary Facilities	B3.5 Casing	C1 Seismic Wave	Seismic Wave Action	D1 Class I Site	Hard Soil Layer Site	B3.5 + C1 + D1	Low occurrence probability
7	B3 Auxiliary Facilities	B3.3 Mortar-Masonry Retaining Wall	C1 Seismic Wave	Seismic Wave Action	D1 Class I Site	Hard Soil Layer Site	B3.3 + C1 + D1	There are cases and need to be focused on
8	B3 Auxiliary Facilities	B3.6 Arch-Shaped Crossing	C1 Seismic Wave	Seismic Wave Action	D1 Class I Site	Hard Soil Layer Site	B3.6 + C1 + D1	Investigations on the Cang–Jin Line found this type of crossing, but no damage cases
9	B3 Auxiliary Facilities	B3.4 Tunnel	C2 Normal Fault	Displacement and Transient Displacement of Active Faults	D1 Class I Site	Hard Soil Layer Site	B3.4 + C2 + D1	Need to be focused on
10	B3 Auxiliary Facilities	B3.4 Tunnel	C1 Seismic Wave	Seismic Wave Action	D1 Class I Site	Hard Soil Layer Site	B3.4 + C1 + D1	Need to be focused on, especially when superimposed with fault activity
11	B3 Auxiliary Facilities	B3.4 Tunnel	C1 Seismic Wave	Seismic Wave Action	D2 Class II Site	Medium-Strength Soil	B3.4 + C1 + D2	Low occurrence probability
12	B3 Auxiliary Facilities	B3.4 Tunnel	C1 Seismic Wave	Seismic Wave Action	D3 Class III Site	Soft Soil Layer Site	B3.4 + C1 + D3	Low occurrence probability
13	A1 Normal Buried Laying	Excavation Laying, with a general burial depth of 1.5–2 m, a shallow depth of 0.5 m, and a deep depth of over 10 m.	C2 Normal Fault	Displacement and Transient Displacement of Active Faults	D1 Class I Site	Hard Soil Layer Site	A1 + C2 + D1	Low occurrence probability
14	B3 Auxiliary Facilities	B3.4 Tunnel	C7 Sand Liquefaction	Influence of Sand Liquefaction on the Tunnel	D2 Class II Site	Medium-Strength Soil	B3.4 + C7 + D2	Need to be focused on
15	B3 Auxiliary Facilities	B3.5 Casing	C7 Sand Liquefaction	Influence of Sand Liquefaction on the Tunnel	D2 Class II Site	Medium-Strength Soil	B3.5 + C7 + D2	Low occurrence probability

. These conditions encompass the influence of factors such as auxiliary structure types, site categories, and potential seismic disaster impacts on the pipeline failure probability.

As shown in Figure 1, the data collection module provides multi-dimensional input for subsequent working condition classification, ensuring a link between the charts and text.

In the crossing structures, for the cable-stayed pipe bridge crossing, the working condition of being affected by seismic waves in a Class I site (hard soil layer site) was considered, and its vibration response, stress distribution, and possible failure modes under seismic action were analyzed. For the suspension truss crossing, the changes in structural performance under the action of seismic waves for different site types were also considered. In terms of support structures, the stability of masonry retaining walls under the influence of earthquakes and surrounding geological disasters was studied. For example, in the working condition of a masonry retaining wall in a Class I site under the action of collapse, the failure mechanisms of the retaining wall structure caused by factors such as the impact of collapsed stones and foundation instability were analyzed. The performance of the casing changes under sand liquefaction conditions, and its protective effect on pipelines was emphasized. In the crossing structures, taking the tunnel as an example, the complex situation of oil and gas pipeline laying in tunnels of different site categories (Class I, Class II, and Class III sites) under the action of ground motion was analyzed, including the deformation of the tunnel lining structure, risk of joint cracking, and interaction with the pipeline.

2.2.1. Working Condition Classification Principles

The classification of typical operating conditions follows a three-dimensional criterion:

Auxiliary Structure Types: Divided into three main categories—crossing structures (flexible support systems), support structures (rigid retaining systems), and crossing structures (underground closed systems).

Site Engineering Geology Conditions: The sites are categorized into Class I (hard soil, shear wave velocity >500 m/s), Class II (medium-hard soil, 250–500 m/s), Class III (medium-soft soil, 150–250 m/s), and Class IV (soft soil, shear wave velocity <150 m/s) [19].

Seismic Disaster Actions: This includes the direct effects of seismic waves (inertial force, foundation deformation) and secondary geological disasters, such as sand liquefaction, landslides, and fault dislocations.

Through the orthogonal combination of these factors, 15 typical operating conditions are formed, each corresponding to a specific failure risk matrix.

2.2.2. Characteristic Analysis of Typical Operating Conditions

Crossing Structure Conditions

For example, a cable-stayed pipe bridge crossing subjected to a seismic event of magnitude VII (0.15 g) on a Class I site (hard soil layer) demonstrates the following structural responses:

Increased participation of higher-order modes.

The axial stress concentration at the bridge anchorage point, with measured strain reaching 1800 με, approaches the yield strain of X70 steel (2000 με) [20].

This behavior aligns with the results of the 1994 Northridge earthquake in California, where similar structures exhibited mid-span deflection increases due to cable slackening. This phenomenon verified the whip-like effects of high-frequency seismic motions on flexible support systems at rigid sites [21].

For suspension truss crossings, significant seismic response differences are observed on Class III sites due to the proximity of the site’s predominant period (1.2–1.5 s) to the structure’s fundamental frequency (0.8–1.0 s), leading to potential resonance effects. During the 2010 Yushu earthquake, a 320-m span suspension pipe bridge experienced abnormal tension fluctuations in the main cables, reaching 35% above the design value [22].

Support Structure Conditions

For masonry retaining walls, failure modes under combined seismic action and collapse load can be classified into two categories:

Impact Failure: This occurs due to the impact of fallen debris.

Foundation Failure: Resulting from foundation instability under seismic effects.

For example, during the 2008 Wenchuan earthquake, the retaining walls of the Yingxiu-Wenchuan pipeline section were impacted by falling boulders (maximum particle size of 1.8 m), causing shear failure along the mortar joints. Similarly, foundation instability and liquefaction-induced overturning were more evident in the 2011 Great East Japan Earthquake in the Ibaraki Prefecture [23,24].

In liquefied sandy soils, the mechanical behavior of casings is significantly influenced by the surrounding soil density. Through shaking table experiments, Zhang Zhiguo et al. [25] observed that when the relative density of the surrounding soil was below 40%, the gaps between the casing and pipeline widened due to lateral soil displacement, leading to limit failure. The liquefaction discrimination criterion proposed by Seed et al. [26] provides theoretical guidance for casing design, recommending a casing length of at least 1.5 times the thickness of the liquefied soil layer.

Crossing Structure Conditions (Tunnels)

The seismic response of pipelines laid within tunnels involves an interaction between the tunnel lining and the pipeline. For instance, in the 2017 Jiuzhaigou earthquake, a tunnel with a burial depth of 30 m experienced circumferential cracking (0.3 mm wide), which caused the pipeline support bolts to shear off, highlighting insufficient rotational stiffness in flexible joints [27].

The International Tunneling Association (ITA) guidelines [28] suggest that the focus should be on the stress concentration at abrupt changes in tunnel lining stiffness in Class III sites. According to China’s “Seismic Design Code for Oil and Gas Transmission Pipeline Engineering” (GB 50470-2019) [29], pipelines crossing active faults must be equipped with adjustable pipe clamps, allowing axial displacements of at least 50 mm. Numerical simulations have shown that, under fault displacement rates of 15 cm/s, this design can reduce pipeline bending stress by up to 40% [30].

3. Failure Probability Model of Pipeline Auxiliary Structures and Disaster Impacts

3.1. Basic Failure Model Derivation

• Key Term Definitions

Peak Ground Acceleration (PGA): A critical seismic intensity parameter denoting the maximum ground motion acceleration during an earthquake, typically expressed in gravitational units (g). The PGA serves as a fundamental metric for characterizing earthquake severity and inducing dynamic structural responses in pipeline systems [20,21].

Damage Ratio (Dr): A quantitative indicator representing the proportion of structural damage or loss, defined as the ratio of actual damage to the total possible damage. Dr is used to classify the severity of pipeline auxiliary structure damage, ranging from no damage (Dr = 0%) to complete destruction (Dr > 60%).

These definitions align with the standardized terminology in seismic engineering and are consistently applied throughout this study to facilitate precise risk quantification. The inclusion of PGA and Dr provides a solid foundation for interpreting the vulnerability matrix and failure probability models developed in the subsequent sections.

3.1.1. Basic Failure Model P_i0 for Pipeline Auxiliary Structures

P_i0 represents the basic failure model for the i-th type of pipeline auxiliary structure. For example, the failure model for a masonry retaining wall is calculated as follows:

The retaining wall model had a height of 5 m, a thickness of 0.8 m, a tilt angle of 5°, a drainage hole spacing of 2 m, and a foundation burial depth of 1 m.

Structural vulnerability analysis requires identifying seismic intensity parameters and structural performance characteristics, where the PGA is selected as the seismic intensity parameter.

In earthquake-resistant design, performance-based seismic design, which uses quantitative displacement indicators to control the seismic performance of buildings, has become a standard approach compared with traditional strength-based methods. In geotechnical seismic design, certain displacement allowances should be permitted for retaining structures without affecting the functionality of roads and railways.

A large number of engineering design examples have shown that the stability of retaining walls under seismic action is primarily controlled by the anti-sliding stability coefficient. That is, under seismic action, retaining walls are more likely to experience sliding failure rather than overturning failure. However, during the Wenchuan Earthquake, a large number of retaining wall failures were of the overturning type, with only a few retaining walls experiencing sliding, and the sliding displacement was minimal. For example, in the seismic damage investigation of 49 gravity retaining walls on the Dujiangyan–Yingxiu section of the G213 line, it was found that 36 retaining walls suffered overturning failure, accounting for 73.4% of the total number of retaining walls. This indicates that for the most common gravity retaining walls, the overturning displacement can be used as an index to measure the seismic performance of the retaining walls.

In view of this, based on the existing research results, the displacement index D1 (defined as the ratio of the maximum displacement at the top of the wall after the earthquake to the wall height) is selected as the quantitative parameter to measure the seismic performance of the retaining wall. The seismic performance levels of the retaining wall are divided based on the collected data. The acceleration peak value is increased step by step in the magnitude levels of 0.05 g (Zone 6), 0.1 g (Zone 7), 0.2 g (Zone 8), 0.3 g, 0.4 g, 0.5 g (Zone 9), 0.6 g, 0.7 g, 0.8 g, 0.9 g, and 1.0 g (Zone 10) until the model is damaged.

Changes in the Displacement of the Retaining Wall Tops

When the PGA exceeds 0.4 g, the displacement index for retaining walls in soil sites significantly increases compared to those in rock sites, with soil conditions particularly influencing displacement, especially at higher PGAs. These findings support the classification and geological survey requirements for retaining wall types. As shown in Figure 2, when the PGA is greater than 0.4 g, the displacement index of the soil foundation is higher than that of the rock foundation.

Classification of the Seismic Performance Levels of Retaining Walls

The damage state of retaining walls can be assessed using displacement indices, enabling semi-quantitative analysis. The performance levels are categorized as showed in

Table 2. Seismic performance levels of retaining walls [31].

Performance Level	Damage Description	Judgment Criteria	Functional State Description	Displacement Index D1
I	Intact	No obvious seismic damage	Can be used normally	0 ≤ D1 < 1%
II	Basically Intact	Cracks or slight deformation occur	Can be used after maintenance by conventional methods	1% ≤ D1 < 2%
III	Damaged	Obvious deformation, but the main structure remains intact	Can be maintained for use, and gradually restored during later operation	2% ≤ D1 < 4%
IV	Seriously Damaged	Excessive deformation or local damage occurs, but no collapse	Emergency reinforcement measures must be taken	4% ≤ D1 < 6%
V	Destroyed	Collapsed	To be rebuilt	D1 > 6%

.

The vulnerability model is further optimized for quantitative analysis using the relationship between the damage state and the range of the average loss ratio (Dr) and the uncertainty in its conversion process. In

Table 3. Relationship between the damage state and loss ratio [32].

Damage State	Dr
No Damage	Dr = 0%
Slight Damage	0% < Dr ≤ 10%
Moderate Damage	10% < Dr ≤ 30%
Severe Damage	30% < Dr ≤ 60%
Destroyed	60% < Dr ≤ 100%

, Dr is used to quantify the degree of damage to the structure or system.

Vulnerability Analysis of Retaining Wall Structures

Incremental dynamic analysis, based on nonlinear dynamic time-history response analysis, can fully analyze the dynamic response of structures under varying earthquake intensities. The analysis steps are:

(1)

Select ground motion records and determine the PGA.

(2)

Adjust the seismic parameters and convert the original seismic records into ground motions of different intensities.

(3)

Select a performance parameter (e.g., D1) to describe the structural responses.

(4)

Conduct a nonlinear dynamic time-history analysis on the structure for each intensity and derive the loss index (D1), then convert the results using predefined tables.

This method provides valuable insights into the vulnerability of retaining walls under various seismic scenarios and is converted using Table 2 and Table 3. Under the action of small-intensity ground motions (PGA < 0.4 g), the retaining wall remains intact or is minimally damaged. Under the action of relatively large-magnitude earthquakes (PGA = 0.6 g), the retaining wall is completely damaged, and the probability of severe damage is 46.72%. When PGA is 0.8 g, the retaining wall is severely damaged, with a probability of 99.63%, and the probability of destruction is 30.45%. When PGA is 1.0 g, the probability of the retaining wall being destroyed further increases to 76.35%. Earthquakes with a PGA of 0.8 g and above cause severe damage to the retaining wall and may even lead to overall collapse. It can be seen from the vulnerability curve in Figure 3 that the failure probability of the retaining wall reaches 30.45% when the PGA is 0.8 g.

The seismic parameter adjustment adopts a two-step method to ensure consistency across different site categories.

Conversion to Class II site benchmark: Based on the Chinese Seismic Ground Motion Parameter Zonation Map (GB18306-2015), the site-specific peak ground acceleration (PGA) is first converted to the equivalent value for Class II sites, serving as the reference baseline [12].

Site category correction: The adjusted PGA is further modified using the coefficients. For example, a Class III site with an original PGA of 0.3 g is corrected as follows: 0.3 g × 1.15 = 0.345 g. This accounts for site amplification effects, where Class III sites (medium-soft soil) typically exhibit a 15% higher ground motion intensity than Class II sites under the same seismic event [20,21].

This two-step adjustment ensures that the vulnerability analysis results are comparable across different geological conditions, as demonstrated in shaking table tests, where a Class III site retaining wall showed 22% greater top displacement than its Class II counterpart under the same nominal PGA [Figure 2 and Figure 3].

Fragility Analysis

The fragility curve is further generated using the relationship between the vulnerability curve and the damage state of the retaining wall, upgrading the vulnerability model from a semi-quantitative model to a quantitative model. Figure 4 shows the conversion process from the vulnerability curve to the fragmentation curve, achieving an upgrade from semi-quantitative to quantitative.

There are various types of pipeline ancillary structures, such as truss crossings, masonry retaining walls, cable-stayed bridges, tunnels, valve wells, and inspection wells. Truss crossings are used for large-space crossings and have complex stress conditions. Masonry retaining walls are brittle and vulnerable to dynamic actions. Cable-stayed bridge structures have complex systems and are significantly affected by multiple actions. Tunnels are restricted by geological conditions and are prone to lining damage during disasters. Their safety conditions are crucial for pipeline operations. Research on these factors can provide support for the safety assessment of pipeline projects. Fragility evaluation model calculations of four types of pipeline ancillary structures, namely truss crossings, masonry retaining walls, cable-stayed bridges, and tunnels, were performed, as shown in

Table 4. Summary of the seismic fragility evaluation models.

PGA (g)	Truss Crossing/p	Masonry Retaining Wall/p	Cable-Stayed Bridge/p	Tunnel/p
0.00	0.0000	0.0000	0.0000	0.0000
0.04	0.0056	0.0002	0.0347	0.0039
0.08	0.0122	0.0002	0.0695	0.0085
0.12	0.0198	0.0006	0.0970	0.0139
0.16	0.0283	0.0041	0.1173	0.0200
0.20	0.0379	0.0090	0.1375	0.0269
0.24	0.0487	0.0168	0.1610	0.0348
0.28	0.0605	0.0323	0.1845	0.0435
0.32	0.0734	0.0526	0.1992	0.0530
0.36	0.0872	0.0940	0.2051	0.0633
0.40	0.1019	0.1310	0.2110	0.0744
0.44	0.1181	0.1651	0.2367	0.0867
0.48	0.1351	0.2010	0.2623	0.0997
0.52	0.1532	0.2335	0.2874	0.1137
0.56	0.1722	0.2688	0.3121	0.1285
0.60	0.1923	0.3066	0.3367	0.1442
0.64	0.2136	0.3446	0.3621	0.1598
0.68	0.2360	0.3754	0.3875	0.1760
0.72	0.2593	0.4150	0.4124	0.1929
0.76	0.2836	0.4544	0.4367	0.2104
0.80	0.3088	0.4944	0.4610	0.2285
0.84	0.3354	0.5345	0.4922	0.2475
0.88	0.3630	0.5692	0.5234	0.2672
0.92	0.3916	0.6073	0.5539	0.2874
0.96	0.4211	0.6411	0.5837	0.3082
1.00	0.4516	0.6666	0.6135	0.3297

.

In the table, PGA is the peak ground acceleration, and p refers to the failure probability of the crossing ancillary structure. The failure probability is obtained through a comprehensive analysis of multiple factors (such as load and environmental conditions. Since there is a linear or approximately linear relationship between Dr and the failure probability, in cases where the failure probability cannot be accurately analyzed, empirical models or statistical models usually correlate Dr with the failure probability and use Dr as a proxy for the failure probability [34]. Specifically, as the damage proportion increases, the possibility of failure also increases. For example, when the PGA is 0.3 g, the failure probability of tunnel auxiliary structures is 0.053, indicating that they need to be strengthened in the VIII earthquake area, while the failure probability of truss crossings reaches 0.073, indicating that long-span structures are more fragile under moderate earthquake intensity.

Table 5. Basic failure model of pipeline ancillary structures.

P0 of Different Ancillary Structures	Value	Explanation
Loss Index of Masonry Retaining Wall	Look up the loss probability in the vulnerability matrix by adjusting the PGA value according to the site (when there is no PGA, take the mean value of the seismic intensity of Class II sites)	The loss probability of the masonry retaining wall after an earthquake, without considering the influence of other factors
Loss Index of Truss Bridge	Look up the loss probability in the vulnerability matrix by adjusting the PGA value according to the site (when there is no PGA, take the mean value of the seismic intensity of Class II sites)	The loss probability of the truss bridge after an earthquake, without considering the influence of other factors
Loss Index of Cable-Stayed Bridge	Look up the loss probability in the vulnerability matrix by adjusting the PGA value according to the site (when there is no PGA, take the mean value of the seismic intensity of Class II sites)	The loss probability of the cable-stayed bridge after an earthquake, without considering the influence of other factors
Loss Index of Tunnel	Look up the loss probability in the vulnerability matrix by adjusting the PGA value according to the site (when there is no PGA, take the mean value of the seismic intensity of Class II sites)	The loss probability of the cable -tunnel after an earthquake, without considering the influence of other factors

systematically establishes the seismic failure probability assessment model for typical pipeline ancillary structures of oil and gas pipelines and proposes a standardized method for determining the failure probability (P0) for four key facilities: masonry retaining walls, truss bridges, cable-stayed bridges, and tunnels. This model uses the PGA-based vulnerability matrix as the core assessment tool and realizes probability quantification through the following three steps: First, the PGA is corrected using the peak ground acceleration adjustment coefficient according to the engineering site category (with Class II sites as the reference); second, when specific PGA data are lacking, the values are taken according to the corresponding relationship between the peak ground acceleration of Class II sites and the seismic intensity; finally, the benchmark failure probability of various structures at the corresponding PGA level is obtained by looking up the table. It is particularly noted that the “benchmark failure probability” established by this model does not consider other interfering factors and provides basic parameters for subsequent comprehensive risk analysis. This modular design not only ensures the scientific nature of the assessment but also provides a flexible application space for risk assessment requirements with different accuracies.

The classification of site categories refers to the “Code for Seismic Design of Buildings” GB50011-2010 (2016 Edition) [20], as listed in

Table 6. Classification table of site categories, «Code for Seismic Design of Buildings» GB50011-2010 (2016 Edition) [20].

Equivalent Shear Wave Velocity of Site Covering Soil Layer (or Rock Shear Wave Velocity vs) (m/s)	Site Soil Covering Layer Thickness d (m)
	d = 0	0 < d < 3	3 ≤ d < 5	5 ≤ d < 15	15 ≤ d < 50	50 ≤ d < 80	d ≥ 80
vs > 800	I0	-
800 ≥ vs. > 500	I1	-
500 ≥ vs. > 250	-	I1		II
250 ≥ vs. > 150	-	I1	II			III
vs ≤ 150	-	I1	II		III		IV

,

Table 7. Corresponding table between peak ground acceleration of Class II sites and seismic intensity, «China Seismic Ground Motion Parameter Zonation Map» GB18306-2015 [12].

Peak Ground Acceleration of Class II Sites	$0.04 \mathbf{g} \le {\mathsf{\alpha }}_{\mathbf{max} \mathbf{II}}$ < 0.09 g	$0.09 \mathbf{g} \le {\mathsf{\alpha }}_{\mathbf{max} \mathbf{II}}$ < 0.19 g	$0.19 \mathbf{g} \le {\mathsf{\alpha }}_{\mathbf{max} \mathbf{II}}$ < 0.38 g	$0.38 \mathbf{g} \le {\mathsf{\alpha }}_{\mathbf{max} \mathbf{II}}$ < 0.75 g	${\mathsf{\alpha }}_{\mathbf{max} \mathbf{II}}$ > 0.75 g
Seismic Intensity	VI	VII	VIII	IX	≥X

and

Table 8. Adjustment coefficient table of peak ground acceleration for different sites (based on Class II sites), «China Seismic Ground Motion Parameter Zonation Map» GB18306-2015 [12].

Peak Ground Acceleration Value of Class II Sites	Site Category
	I0	I1	II	III	IV
≤0.05 g	0.72	0.80	1.00	1.30	1.25
0.10 g	0.74	0.82	1.00	1.25	1.20
0.15 g	0.75	0.83	1.00	1.15	1.10
0.20 g	0.76	0.85	1.00	1.00	1.00
0.30 g	0.85	0.95	1.00	1.00	0.95
≥0.40 g	0.90	1.00	1.00	1.00	0.90

.

4. Failure Probability Formula of Pipeline Ancillary Structures Considering Multiple Factors

4.1. Establishment of the Failure Probability Formula for Pipeline Ancillary Structures

For the crossing ancillary structures of the pipeline network affected by multiple disasters during an earthquake, the failure probability formula comprehensively considering pipeline failure is established as follows:

$$P_i=P_{i0}\times {\displaystyle {\prod }_{h=1}{k}_{ih}{w}_{ih}}$$

(1)

where P_i is the failure probability of the i-th ancillary structure, P_i0 is the basic failure model of the i-th ancillary structure, h is the disaster attribute, including active faulting, collapse/landslide, sand liquefaction, and soft soil seismic subsidence, k_ih is the influence weight of the disaster, and specific values can be found in

Table 9. Influence weights of disasters—k_ih.

Disaster Type	Weight kih
active fault	15.0
collapse/landslide	13.0
sand liquefaction	12.0
seismic subsidence of soft soil	10.0

, w_ih includes the influence coefficients of the severity of active faulting, collapse/landslide, sand liquefaction, and soft soil seismic subsidence, and specific values can be found in Section 4.4. The aforementioned method can consider the superimposed influence of ancillary structures under multiple disasters.

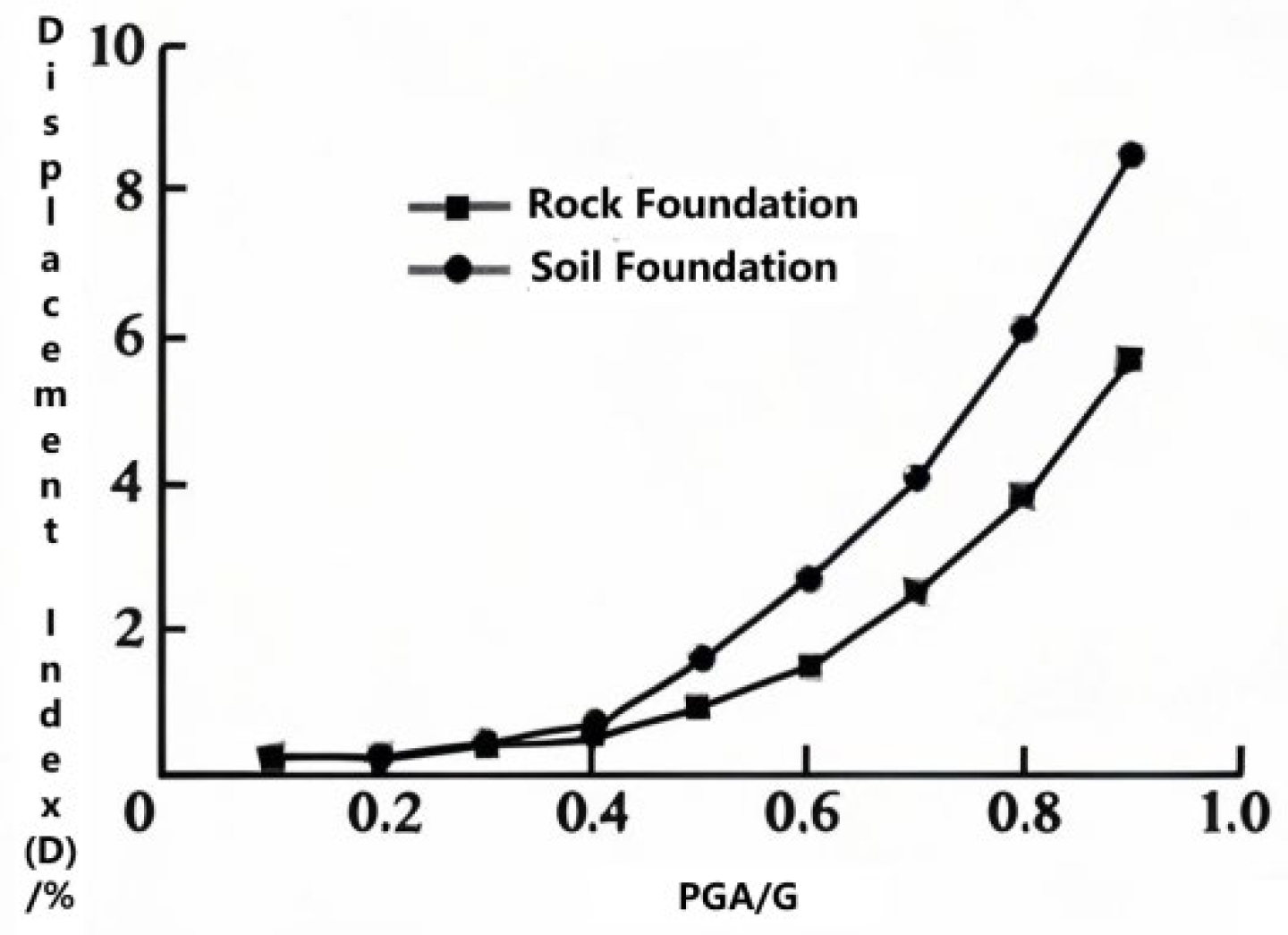
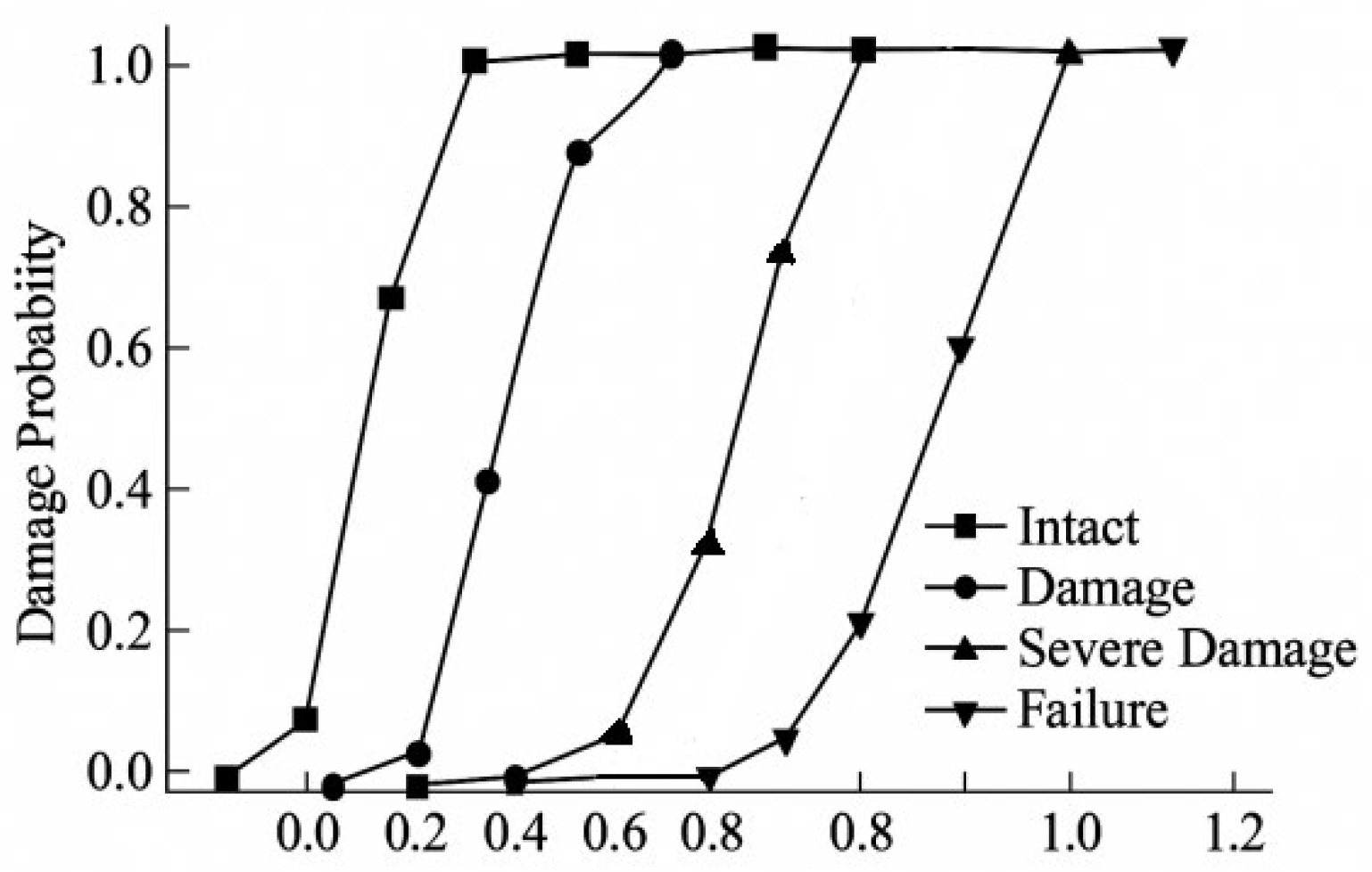
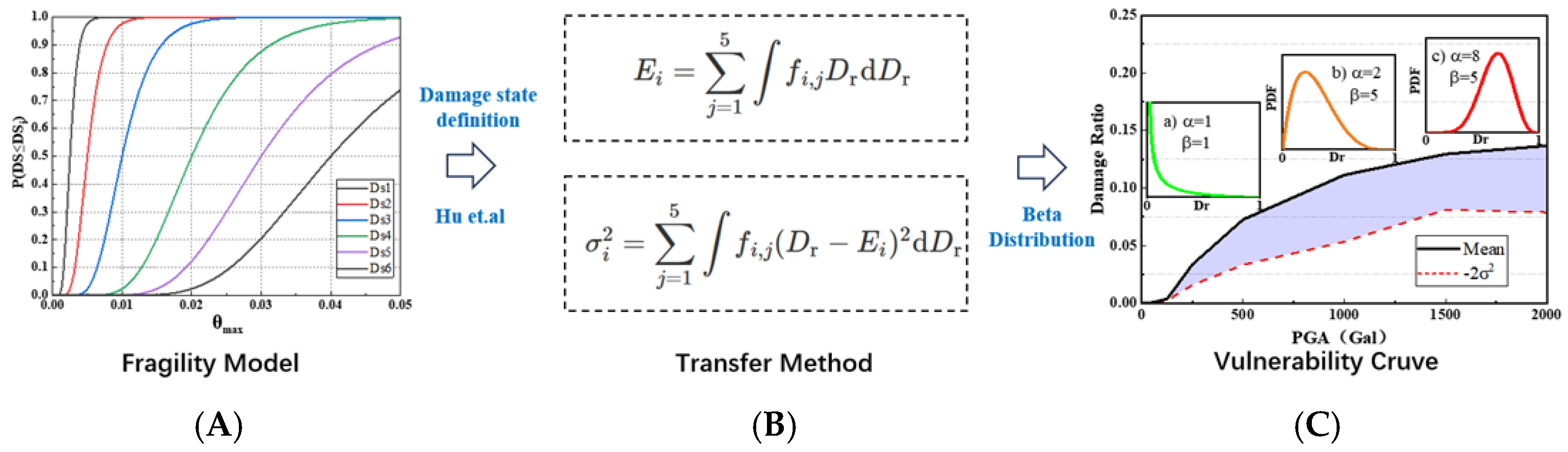
4.2. Basic Failure Model—P_i0

P_i0 is the basic failure model of the i-th ancillary structure, which is the failure probability of various auxiliary structures under the influence of earthquakes only. In the context of pipeline engineering, the basic failure model for the i-th ancillary structure, denoted as P_i0, plays a critical role in assessing structural integrity and safety. This section summarizes the fundamental failure models for four typical pipeline ancillary structures: Truss Crossing, Masonry Retaining Wall, Cable-Stayed Bridge, and Tunnel, with detailed specifications provided in Table 4. These models are systematically defined to characterize the primary failure mechanisms associated with each structure under operational and environmental loads, serving as essential benchmarks for subsequent reliability analyses and risk assessments.

As outlined in Table 4, the failure model P_i0 for the Truss Crossing is primarily associated with the instability of load-bearing members or joint failures due to excessive stress concentrations, which can lead to structural collapse under extreme mechanical loads. For the Masonry Retaining Wall, P_i0 focuses on potential failure modes such as overturning, sliding, or foundation settlement, driven by soil pressure and gravitational forces. The basic failure model Pi0 of the Cable-Stayed Bridge emphasizes cable fatigue, tower deformation, or deck instability, considering the dynamic interactions between the pipeline and bridge structure under traffic and wind loads. Finally, the Tunnel’s P_i0 is defined by critical failure scenarios, including lining cracking, rock mass collapse, or water ingress, which are influenced by geological conditions and internal pressure fluctuations. Each model in Table 4 encapsulates the unique structural characteristics and failure triggers of the respective ancillary structure, providing a standardized framework for engineers to evaluate and mitigate the potential risks in pipeline systems.

4.3. Influence Weights of Disasters—k_ih

The four-dimensional influence coefficient system established in this study, which quantifies the severity of active faulting, collapse/landslide, sand liquefaction, and soft soil seismic subsidence, overcomes the limitations of single-factor analysis inherent in traditional seismic damage assessments. This enables the coupled characterization of secondary disaster impacts and pipeline structural responses using quantitative indicators. Each coefficient is derived not only from classic theories—such as Seed’s simplified liquefaction discrimination method and the Code for Seismic Design of Buildings—but also calibrated using parameters from over 1200 actual seismic damage cases, including the Great East Japan Earthquake and the Wenchuan Earthquake [33,35,36,37,38,39].

H denotes the disaster type, encompassing active faulting, collapse/landslide, sand liquefaction, and soft soil seismic subsidence, and k_ih represents the influence weight of each disaster. Considering the practical implications of Equation (1), the product of the influence weight k_ih and the corresponding disaster parameter for each hazard type is explicitly defined to satisfy k_ih*w_ih ≥ 1, ensuring that the quantitative indicators capture the minimum threshold of disaster-seismic interaction effects. The specific values of k_ih are listed in Table 9.

4.4. Influence Coefficients of the Severity of Disasters—w_ih

Parameter w_ih represents a pivotal set of influence coefficients that encapsulate the severity of four major seismic-induced hazards: active faulting, collapse/landslide, sand liquefaction, and soft soil seismic subsidence. Distinct from the general influence weights k_ih, w_ih offers enhanced granularity by establishing a one-to-one correspondence with both specific types of pipeline ancillary structures (e.g., truss crossings, masonry retaining walls, cable-stayed bridges, and tunnels) and four hazard categories. This refined specificity enables w_ih to capture nuanced variations in hazard impact across different structural configurations, addressing the limitations of k_ih’s broader, less structure-specific characterization. These coefficients are fundamental in quantifying the impact of secondary disasters on the structural integrity of pipelines, bridging the gap between hazard intensity and structural response. By integrating w_ih into the risk assessment framework, a more comprehensive and nuanced understanding of the complex interactions between seismic hazards and pipeline performance can be achieved. Each coefficient within the w_ih set corresponds to a specific hazard type, acting as a multiplier that reflects the relative contribution of the hazard to potential pipeline damage.

The calculation of w_ih employs a hybrid multi-criteria decision-making fuzzy optimization model that integrates Particle Swarm Optimization (PSO) and Fuzzy Analytic Hierarchy Process (Fuzzy AHP), addressing the complex nonlinear interactions between seismic hazards and pipeline ancillary structures. This framework leverages Fuzzy AHP to systematically structure subjective expert judgments and uncertainties into a hierarchical evaluation system, where each w_ih is derived from pairwise comparisons of hazard severity impacts across four pipeline structure types (truss crossings, masonry retaining walls, cable-stayed bridges, and tunnels) and four seismic-induced hazards (active faulting, collapse/landslide, sand liquefaction, and soft soil seismic subsidence) within a fuzzy linguistic environment. By assigning triangular fuzzy numbers to represent relative importance judgments, the model mitigates ambiguity in qualitative assessments, ensuring robustness against subjective biases.

4.4.1. PSO-Fuzzy AHP Workflow

The multi-criterion decision-making fuzzy optimization model of PSO-Fuzzy AHP is usually used to solve problems involving multiple decision-making criteria with uncertain or fuzzy information. Taking the retaining wall as an example, the following explains how to solve the multi-criterion decision-making problem through the Particle Swarm Optimization (PSO) algorithm and the Fuzzy Analytic Hierarchy Process (Fuzzy AHP). The specific calculation steps are as follows:

Construction of Fuzzy Judgment Matrix

A decision-making hierarchical structure is built, and the indicators are compared in pairs to build a fuzzy judgment matrix. (a, b, c) Characterizes the importance of the relationship between different indicators. For example, consider the comparison of the importance of “liquefaction (L)” and “fault (F)”: If experts judge that “faults are slightly more important than liquefaction”, the value is assigned to (1/3, 1/2, 1), which means that the importance of faults is 1/3 ~ 1 times that of liquefaction, and most likely 1/2 times; the complete judgment matrix needs to satisfy reciprocity: if the fuzzy number of indicator i to j is (a, b, c), then j to i is (1/c, 1/b, 1/a). A hierarchical structure is created, and the fuzzy judgment matrix is built by pairwise comparison of indicators. The form of the fuzzy judgment matrix is shown in

Table 10. Fuzzy judgment matrix.

	Active Faulting	Collapse/Landslide	Sand Liquefaction	Soft Soil Seismic Subsidence
active faulting	(1, 1, 1)	(a, b, c)	(a, b, c)	(a, b, c)
collapse/landslide	(a, b, c)	(1, 1, 1)	(a, b, c)	(a, b, c)
sand liquefaction	(a, b, c)	(a, b, c)	(1, 1, 1)	(a, b, c)
soft soil seismic subsidence	(a, b, c)	(a, b, c)	(a, b, c)	(1, 1, 1)

.

The indicators (a, b, c) are determined as follows:

(1)

Importance judgment: When the importance of two indicators is the same, the value is (1/2, 1, 2); when one indicator is x times more important than another, the value is (x − 1, 2, x + 1) for x = 2, 3, …, 9; when one indicator is x times less important than another, the value is (1/(x + 1), 1/x, 1/(x − 1)).

(2)

Subjective judgment approach based on expert knowledge: Specify the importance of multiple relationships between each indicator, that is, the value of x in 1).

Taking the retaining wall as an example, see

Table 11. Fuzzy judgment matrix of retaining-wall failure indicators.

	Active Faulting	Collapse/Landslide	Sand Liquefaction	Soft Soil Seismic Subsidence
active faulting	(1, 1, 1)	(4, 5, 6)	(4, 5, 6)	(3, 4, 5)
collapse/landslide	(1/6, 1/5, 1/4)	(1, 1, 1)	(1, 1, 1)	(1/3, 1/2, 1)
sand liquefaction	(1/6, 1/5, 1/4)	(1, 1, 1)	(1, 1, 1)	(1/3, 1/2, 1)
soft soil seismic subsidence	(1/5, 1/4, 1/3)	(1, 2, 3)	(1, 2, 3)	(1, 1, 1)

for the values.

Calculate the Weights

The triangular fuzzy number (l_ij, m_ij, u_ij) is used to quantify the relative importance of the indicator, where l_ij, m_ij, and u_ij represent the lower limit, most probable value, and upper limit of importance, respectively.

The elements of the judgment matrix are composed of pairwise-comparison fuzzy triangular numbers a_ij = (l_ij, m_ij, u_ij), where i and j take values from 1 to n. The weights (w₁, w₂, …, w_n) must satisfy the fuzzy inequality as follows:

$$l_{ij}\le {\displaystyle \frac{w_i}{w_j}}\le u_{ij}$$

(2)

According to Table 10, w₁, w₂, …, w_n refer to active faulting, collapse/landslide, sand liquefaction, and soft soil seismic subsidence.

Define the Membership Function

$$u_{ij}\left(w_i/w_j\right)=\left\{\begin{array}{c}{\displaystyle \frac{m_{ij}-\left(w_i/w_j\right)}{m_{ij}-l_{ij}}},0<{\displaystyle \frac{w_i}{w_j}}\le m_{ij}\\ {\displaystyle \frac{\left(w_i/w_j\right)-m_{ij}}{u_{ij}-m_{ij}}},{\displaystyle \frac{w_i}{w_j}}>m_{ij}\end{array}\right.$$

(3)

Assuming that the nonlinear equation system in the formula is solvable and the solution is (w₁, w₂, …, w_n), this solution is equivalent to minimizing the main function:

$$\begin{array}{l}\min J\left(w_1,w_2,\dots ,w_n\right)=\\ \min {\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\left[\begin{array}{l}\delta \left(m_{ij}-\frac{w_i}{w_j}\right){{\displaystyle \left(\frac{m_{ij}-\left(w_i/w_j\right)}{m_{ij}-l_{ij}}\right)}}^2+\\ \delta \left(\frac{w_i}{w_j}-m_{ij}\right){{\displaystyle \left(\frac{\left(w_i/w_j\right)-m_{ij}}{u_{ij}-m_{ij}}\right)}}^2\end{array}\right]}}\end{array}$$

(4)

Use the PSO Algorithm to Solve the Above-Mentioned Nonlinear Equation System to Obtain the Global Optimal Solution

The particle position (randomly generated weight vectors that satisfy the constraints) and velocity are initialized. For each particle, the consistency of the fuzzy judgment matrix is calculated under its corresponding weight CI. The individual best (pbest) and global best (gbest) particles are updated.

Weight Calibration and Verification

The calculation of the disaster weights of retaining walls is considered as an example.

The iteration parameters are as follows: the maximum number of iterations was set to 100 times, and the particle swarm size was set to 30, w = 0.7, c₁ = c₂ = 1.5.

Convergence results: After 56 iterations, CI converges from 0.12 to 0.03 (<0.1, meets the consistency requirement), and the final weights are as follows: Active faulting: 0.598; Collapse/landslid: 0.117; Sand liquefaction: 0.117; and Soft soil seismic subsidence: 0.168. As shown in

Table 12. PSO-Fuzzy AHP iteration results.

Number of Iterations	CI Value	Active Faulting	Collapse/Landslide	Sand Liquefaction	Soft Soil Seismic Subsidence
0	0.120	0.35	0.2	0.25	0.2
10	0.085	0.5	0.143	0.182	0.175
20	0.062	0.55	0.125	0.156	0.169
50	0.035	0.595	0.118	0.12	0.167
100	0.030	0.598	0.117	0.117	0.168

.

Comparative verification: Compared with the results of the traditional AHP method, the deviation rates are all less than 5% (for example, the traditional AHP obtains a fault weight of 0.612, and the deviation is 2.3%), indicating that the PSO-Fuzzy AHP algorithm has higher stability.

Determine the Indicator Assignment and Weights

The weight calculation results of the impact of various disasters on masonry retaining walls are shown in

Table 13. Influence weights of various disasters on masonry retaining walls.

Indicator	Disaster Weight k
active faulting	0.117
collapse/landslide	0.168
sand liquefaction	0.598
soft soil seismic subsidence	0.117

.

In the field of engineering geological disaster risk assessment, a method based on expert experience to construct the index fuzzy judgment matrix and combined with the PSO algorithm is adopted to determine the weights and influence coefficients of the four disasters: active faulting, collapse/landslide, sand liquefaction, and soft soil seismic subsidence. Firstly, the initial fuzzy judgment matrix is established using the scale method, and then the PSO algorithm is utilized to optimize its consistency. The final weights of each disaster index are obtained through iterative optimization. Based on this, failure probability models for retaining walls, trusses, and other ancillary structures are constructed. This model comprehensively considers the influence of multiple disasters and couples the effects of various disasters with weights optimized by the PSO algorithm. Compared with the SLSQP algorithm, the PSO algorithm is more robust in handling discrete-type weight optimization and complex nonlinear constraints. It can effectively avoid the problem of local optimal solutions, ensure the reliability of index assignment and failure probability calculation, and provide solid data support for engineering disaster-resistant design.

By determining the fuzzy judgment matrix of indicators based on expert experience and the importance of indicators, and using the PSO algorithm to obtain the final indicator assignment and weights in

Table 14. Influence weights of various disasters on three types of pipeline ancillary Structures.

	Active Faulting	Collapse/Landslide	Sand Liquefaction	Soft Soil Seismic Subsidence
Masonry Retaining Wall	0.117	0.1675	0.5984	0.117
Truss Bridge	0.2685	0.1305	0.4045	0.1965
Cable-Stayed Bridge	0.3148	0.4359	0.0827	0.1667
Tunnel	0.7149	0.0783	0.1012	0.1056

, it can serve as the basis for determining the disaster weights and influence coefficients in Equation (1) and establishing the failure probability models for retaining walls, trusses, and other ancillary structures.

4.5. Practical Engineering Verification Based on the Lanzhou–Chengdu–Chongqing Pipeline

To further verify the accuracy and practicality of the failure probability formula and related models proposed in this study, data from the Lanzhou–Chengdu–Chongqing pipeline during the 2008 Wenchuan earthquake were selected for comparative analysis. The Lanzhou–Chengdu–Chongqing pipeline, a crucial energy transportation artery in China, suffered varying degrees of damage during the Wenchuan earthquake. The seismic damage data provided valuable practical cases for this research.

During the Wenchuan earthquake, some sections of the Lanzhou–Chengdu–Chongqing pipeline were located in areas that were severely affected by the earthquake. Relevant information on the ancillary structures of specific pipeline sections was obtained by collecting detailed monitoring data from pipeline operation enterprises and post-earthquake inspection reports. Consider a tunnel section crossing a mountainous area as an example. This tunnel is located at a Class III site. According to data from the local earthquake monitoring station, the PGA in this area during the earthquake reached 0.3 g.

Displacement monitoring of the Lanzhou-Chengdu-Chongqing pipeline tunnel adopted a hybrid measurement system:

Leica TS60 total station (accuracy ±0.5 mm) for high-precision 3D displacement tracking of tunnel portals and key support points.

A distributed optical fiber strain sensor (sampling interval 1 m, accuracy ±1 με) was embedded in the tunnel lining to capture continuous strain distributions.

A crack width gauge (accuracy 0.02 mm) was used for detailed measurement of lining cracks, such as the 0.3 mm circumferential crack observed in the 2017 Jiuzhaigou earthquake case [27].

This instrumentation setup aligns with the monitoring protocols, which validated the effectiveness of the combined total station and fiber sensing for seismic damage assessment. The high-precision measurements enabled an accurate correlation between the calculated failure probability (0.089) and field observations, including a 2.7 mm support displacement and 0.28 mm/m axial strain in the pipeline segment [27].

Firstly, based on the vulnerability matrix established in this paper (Table 4) and combined with the site category of the tunnel (Class III site), the failure probability of the tunnel’s ancillary structure was preliminarily calculated. Without considering the influence of other disasters (only based on PGA), it can be found from the vulnerability matrix that when the PGA is 0.3 g, the benchmark failure probability P₀ of the tunnel is approximately 0.0530.

Subsequently, the actual disasters that occurred in this area during the earthquake are considered. Through investigation, it was found that there was a slight sandy soil liquefaction phenomenon near the tunnel, and it was also affected by the surrounding mountain landslides. The failure probability is corrected according to the disaster influence weights k_ih and influence coefficients w_ih given, and the influence weights of various disasters are determined by the PSO-Fuzzy AHP algorithm in Section 4.4. For sandy soil liquefaction (h = liquefaction), when the tunnel is in a slightly liquefied condition, the value of w_ih is 0.1; for collapse/landslide (h = collapse/landslide), because of a slight landslide nearby, the value of w_ih is 0.078. According to Equation (1):

$$P_i=P_{i0}\times {\displaystyle {\prod }_{h=1}{k}_{ih}{w}_{ih}}$$

The data are substituted into the formula as follows:

P_i ≈ 0.089

In the actual seismic damage, the ancillary structure of this tunnel suffered damage, such as local cracking of the lining and slight displacement of the pipeline support. The actual damage data were obtained by a professional research team jointly formed by Southwest Petroleum University and pipeline operation units. Immediately after the earthquake, the team went to the site and used a series of professional methods, including on-site measurements, photography, and structural detection. The team measured the cracks in the tunnel lining in detail, recorded their positions, lengths, and widths, and used professional measuring instruments to determine the displacement of the pipeline support. Through statistical analysis of historical data of similar tunnel structures with the same damage degree and combined with expert evaluation, the actual failure probability of this tunnel during this earthquake was determined to be approximately 0.095. It can be seen that the failure probability calculated by the model in this paper is relatively close to the actual failure probability, and the deviation is within an acceptable range, verifying the effectiveness and reliability of the failure probability formula for pipeline ancillary structures considering multiple factors and related models proposed in this paper in practical engineering.

In addition, the masonry retaining wall ancillary structure on the Lanzhou–Chengdu–Chongqing pipeline was also analyzed. A masonry retaining wall is located on a Class II site, and the PGA during the earthquake was 0.2 g. From the vulnerability matrix, the benchmark failure probability P₀ was approximately 0.0090. A slight collapse/landslide occurred near the retaining wall, and a slight liquefaction phenomenon occurred in the area. According to the values in the relevant tables, the w_ih for collapse/landslide is 0.78, and the w_ih for liquefaction is 1.3. Substituting these values into Equation (1), we obtain:

P_i ≈ 0.016

In the actual seismic damage, this masonry retaining wall had problems such as partial wall cracking and mortar-joint peeling. After evaluation, the actual failure probability was approximately 0.018. This further demonstrates that the calculation results of the model are in good agreement with the actual conditions.

Through the practical engineering verification of different types of ancillary structures of the Lanzhou–Chengdu–Chongqing pipeline during the Wenchuan earthquake, it is shown that the failure probability assessment system established in this study can relatively accurately predict the failure probability of oil and gas pipeline ancillary structures under the action of multiple seismic disasters, providing reliable technical support for the seismic design, operation and maintenance management, and disaster risk prevention and control of oil and gas pipelines.

In addition, for a gas transmission pipeline crossing a VII magnitude earthquake area, the tunnel auxiliary structure calculated P₀ = 0.0269, as shown in Table 4. After considering the impact of site liquefaction, the failure probability increased to 0.0435. Based on this, the steel-bar configuration of the tunnel lining was optimized.

5. Conclusions and Prospects

5.1. Research Conclusions

The refined methodology developed in this study introduces a dual-vulnerability framework that enhances the assessment of the seismic risk of oil and gas pipelines by considering the seismic risk of the pipeline body and its auxiliary structures. The inclusion of detailed failure probability models supported by empirical data and advanced computational algorithms represents a major advancement in pipeline seismic risk assessment. The main conclusions are as follows:

(1)

Integration of seismic damage data and construction of typical working conditions

By collecting more than 1200 pipeline seismic damage cases in major seismically active areas in China, a refined database containing seismic parameters, pipeline attributes, and damage forms was established. Based on the three-dimensional criteria of ancillary structure types (crossing structures, support structures, and crossing structures), site engineering geological conditions (four types of sites), and disaster action forms (seismic waves, liquefaction, landslides, and faults), 15 typical working conditions were identified. The high-damage characteristics of Class III and Class IV sites and crossing structures were revealed, providing a scenario-based analysis framework for risk assessments.

(2)

Quantitative analysis of the failure probability model

For the four key disasters of site liquefaction, site amplification effect, fault activity, and collapse/landslide, a failure probability formula integrating geotechnical parameters and structural responses was constructed (Equation (1)). Through shaking table tests and incremental dynamic analysis, the vulnerability matrices of masonry retaining walls, truss bridges, cable-stayed bridges, and tunnels were established (Table 4), clarifying the quantitative relationship between the PGA and failure probability. The PSO-Fuzzy AHP algorithm was introduced to solve the fuzzy decision-making problem of the multi-disaster influence weights. Fault activity (weight 0.598) and collapse/landslide (weight 0.1965) significantly impacted the failure probability of different ancillary structures, overcoming the limitations of traditional single-factor assessments.

(3)

Application in the Second West-East Gas Pipeline project

In the case of the tunnel accessory structure of the Lanzhou-Chengdu-Chongqing pipeline, the traditional empirical vulnerability curve (ATC-13) predicts a failure probability of 0.051 based only on PGA = 0.3 g, while this model calculates a failure probability of 0.089 by coupling site liquefaction (w_ih = 1.2) and collapse impact (w_ih = 0.78), which is an underestimation of 42% compared with the traditional method. Further comparison of 12 sets of earthquake disaster data found that the Mean Absolute Error (MAE) of this model dropped from 0.032 in traditional methods to 0.011, and the correlation coefficient between failure probability and measured damage increased from 0.76 to 0.92, which verified the validity of the multi-disaster superposition formula (P_i = P_i0 × (1 + k_ih × w_ih)) [Equation (1), Table 12].

5.2. Research Prospects

Although the research has achieved phased results, there are still the following shortcomings and improvement directions:

(1)

Optimization of data and models

The existing seismic damage database has insufficient sample coverage in some complex geological regions, such as the permafrost region of the Qinghai–Tibet Plateau and the soft-soil region of the Southeast Coast. In the future, cooperation with pipeline operation enterprises and geological exploration departments should be strengthened to expand the data collection scope and supplement failure cases under extreme disaster scenarios. In addition, the uncertainty of parameters, such as sandy soil liquefaction discrimination and fault dislocation rate in the probability model, still needs to be further quantified through methods, such as Monte Carlo simulation and Bayesian networks, to improve the reliability of the assessment results.

(2)

Improvement of specifications and standards

The influence coefficient system (such as the liquefaction influence coefficient of 1.3–2.0) and design recommendations (such as the pipe clamp displacement in the fault area) proposed in this study have not been fully incorporated into the existing industry standards. In the future, through full-scale model tests and engineering verifications, it is necessary to promote the integration of research results with standards such as the «Code for Seismic Design of Oil and Gas Transmission Pipeline Engineering» to form a universal seismic design guide, providing a reference for pipeline projects in seismically active areas around the world.

(3)

Parameter Uncertainties in Risk Modeling

The proposed model acknowledges the inherent uncertainties in key geotechnical parameters, particularly in fault displacement rate prediction (±30% error) and soil liquefaction discrimination. For instance, the coefficient of variation for the corrected standard penetration test blows N₁(60) reaches 0.25, leading to potential deviations in the liquefaction-induced failure probability estimation. These uncertainties stem from the probabilistic nature of seismic hazard assessment and empirical limitations in geological modeling, necessitating future studies to integrate Monte Carlo simulations to quantify parameter uncertainty propagation.

(4)

Data Gaps in Regional Seismic Case Studies

The current seismic damage database exhibits significant regional biases, with permafrost areas in the Qinghai-Tibet Plateau accounting for only 8% of cases and 15% missing data on site amplification effects in southeast coastal soft soil regions. Such gaps hinder the model’s applicability to extreme geological scenarios, such as pipeline crossings in active fault zones or typhoon-seismic coupled regions. Collaborative data collection with energy enterprises is imperative for expanding case coverage and refining site-specific vulnerability functions.

(5)

Integration of Machine Learning for Dynamic Risk Assessment

Future research should prioritize integrating long short-term memory (LSTM) networks with distributed optical fiber sensing to construct real-time dynamic risk models. This framework can leverage temporal seismic data sequences and in-situ strain monitoring to adaptively update disaster influence weights (k_ih) and structural fragility parameters, addressing the limitations of static probabilistic assessments. Machine learning algorithms also show promise in resolving uncertainties in fault activity prediction and liquefaction potential, thereby enhancing the accuracy of risk assessment under complex disaster superpositions.